MetaTrader 5 / Tester
English Русский 中文 Español 日本語 Português
preview
Archery-Algorithmus (AA)

Archery-Algorithmus (AA)

MetaTrader 5 — Tester | 8 Mai 2025, 08:16
64 0
Andrey Dik
Andrey Dik

Inhalt

  1. Einführung
  2. Implementierung des Algorithmus
  3. Testergebnisse


Einführung

In einer Zeit, in der die Aufgaben immer komplexer und die Ressourcen immer knapper werden, wird die Optimierung nicht nur zu einer Notwendigkeit, sondern auch zu einer echten algorithmischen Kunst in der modernen Welt. Wie findet man die beste Lösung unter vielen möglichen? Wie lassen sich Kosten minimieren, die Effizienz steigern und maximale Gewinne erzielen? Diese Fragen betreffen Fachleute aus den verschiedensten Bereichen - von der Wirtschaft bis zum Ingenieurwesen, von sozialen Systemen bis zur Ökologie. Vor der Lösung eines Optimierungsproblems ist es wichtig, das Problem richtig zu modellieren, indem Schlüsselvariablen und mathematische Beziehungen ermittelt werden, die die Realität adäquat wiedergeben. Die Optimierung ist im Finanzwesen und im Handel weit verbreitet und hilft nicht nur bei der Entwicklung neuer Anlagestrategien, sondern auch bei der Verbesserung bestehender Strategien. Trotz der Universalität der Ansätze lassen sich die Optimierungsmethoden jedoch bedingt in zwei Kategorien einteilen: deterministisch und stochastisch.

Deterministische Methoden wie der Gradientenabstieg bieten strenge und vorhersehbare Lösungen, indem sie mathematische Ableitungen verwenden, um das Optimum zu finden, wodurch sie verschiedene Szenarien effektiv modellieren können. Sobald die Probleme jedoch nichtlinear oder multivariat werden, kann ihre Effektivität drastisch abnehmen. In solchen Fällen kommen stochastische Methoden zum Einsatz, die auf der Grundlage von Zufallsprozessen in der Lage sind, unter komplexen Bedingungen akzeptable Lösungen zu finden, was sie besonders auf volatilen Märkten nützlich macht.

Kombinationen von deterministischen und stochastischen Methoden spielen in modernen Optimierungsansätzen eine zentrale Rolle. Durch die Kombination dieser beiden Ansätze können Analysten flexiblere und anpassungsfähigere Modelle erstellen, die sowohl stabile als auch sich ändernde Bedingungen berücksichtigen können. Dadurch lässt sich nicht nur die Qualität der Prognosen verbessern, sondern auch das Risiko minimieren, was für ein erfolgreiches Investitionsmanagement entscheidend ist.

In diesem Artikel werde ich einen neuen Ansatz zur Lösung von Optimierungsproblemen vorstellen - den Archery Algorithm (AA). Der Algorithmus wurde von Fatemeh Ahmadi Zeidabadi und Kollegen entwickelt und im Februar 2022 veröffentlicht. Diese vom Bogenschießen inspirierte Methode erzeugt quasi-optimale Lösungen, indem sie die Position der Populationsmitglieder im Suchraum auf der Grundlage eines zufällig ausgewählten Elements aktualisiert. Wir werden die Effizienz von AA bei Standard-Zielfunktionen testen und die erzielten Ergebnisse mit uns bereits bekannten Algorithmen vergleichen. Indem wir in die Details eintauchen, werden wir zeigen, wie dieser innovative Ansatz die Art und Weise, wie wir über Optimierung denken, verändern und neue Horizonte für die Lösung komplexer Probleme eröffnen kann.


Implementierung des Algorithmus

Der Archery Algorithm (AA) ist eine völlig neue stochastische Optimierungsmethode, die entwickelt wurde, um optimale Lösungen für Optimierungsprobleme zu finden, und die durch das Verhalten eines Bogenschützen inspiriert wurde, der auf ein Ziel zielt. AA simuliert das Schießen von Pfeilen auf ein Ziel. Jedes Mitglied der Population stellt eine potenzielle Lösung für das Optimierungsproblem dar, und ihre Positionen im Suchraum werden auf der Grundlage der Leistung eines zufällig ausgewählten „Ziel“-Mitglieds aktualisiert, ähnlich wie Bogenschützen ihr Ziel anpassen, je nachdem, wo sie treffen wollen.

Die Grundgesamtheit wird als Matrix dargestellt, wobei jede Zeile einem Mitglied (Lösung) und jede Spalte einer Dimension des Problems entspricht. Dies ermöglicht eine strukturierte Bewertung und Aktualisierung von Entscheidungen auf der Grundlage ihrer Zielfunktionswerte. Die Leistung der einzelnen Mitglieder wird anhand einer Zielfunktion bewertet, die angibt, wie gut eine gefundene Lösung ist. Die Ergebnisse werden in einem Vektor gespeichert, der es dem Algorithmus ermöglicht, die Effizienz der verschiedenen Lösungen zu vergleichen.

Das Ziel ist in Abschnitte unterteilt, deren Breite der Produktivität der Bevölkerungsmitglieder entspricht. Eine Wahrscheinlichkeitsfunktion wird berechnet, um die Wahrscheinlichkeit zu bestimmen, mit der jedes Mitglied auf der Grundlage seines Zielfunktionswertes ausgewählt wird, wobei effizientere Bogenschützen eine höhere Wahrscheinlichkeit haben, ausgewählt zu werden. Ein Mitglied der Population wird nach dem Zufallsprinzip auf der Grundlage der kumulativen Wahrscheinlichkeit ausgewählt, was die Zielauswahl eines Bogenschützen simuliert. Diese Entscheidung wirkt sich darauf aus, wie die Positionen der anderen Mitglieder aktualisiert werden. Der Algorithmus aktualisiert die Position der einzelnen Bogenschützen im Suchraum anhand bestimmter Gleichungen. Die Aktualisierung hängt davon ab, ob der ausgewählte Bogenschütze einen besseren oder schlechteren Zielfunktionswert hat als der aktuelle. Bei diesem Verfahren wird der Suchraum nach dem Zufallsprinzip erkundet. AA arbeitet iterativ und aktualisiert die Population, bis eine Stopp-Bedingung (maximale Anzahl von Iterationen) erreicht ist. Während dieses Prozesses verfolgt der Algorithmus die beste gefundene Lösung.

Die ursprüngliche Version des oben vorgestellten AA-Algorithmus beschreibt die Matrix als eine Population und die Vektoren als Mitglieder der Population. Im Text werden jedoch keine spezifischen Operationen angegeben, die für die Arbeit mit Matrizen typisch sind. Tatsächlich beinhaltet der Algorithmus Standardaktionen mit Suchagenten, wie bei den meisten der zuvor diskutierten Algorithmen.

Die Formulierung „die Zielscheibe ist in Abschnitte unterteilt, deren Breite der Produktivität der Populationsmitglieder entspricht“ impliziert die Anwendung einer Roulette-Methode für die Auswahl. In diesem Fall ist die Wahrscheinlichkeit, einen Sektor zu wählen, proportional zu seiner Breite.

Auf diese Weise können komplexe Formulierungen, die viele Konzepte beschreiben, auf viel einfachere Weise erklärt werden, was die Umsetzung der Idee vereinfacht.

Der Bogenschießalgorithmus „Archery“ ist also eine populationsbasierte Optimierungsmethode, die die Prinzipien des Zielschießens nutzt, um die Suche nach optimalen Lösungen zu leiten. Es kombiniert Elemente des Zufalls mit der Normalverteilung, um den Suchraum zu erkunden und auszunutzen. Schlüsselkomponenten des Algorithmus:

1. Eine Population von Agenten (Bogenschützen)
2. Ein Vektor der Wahrscheinlichkeiten und kumulativen Wahrscheinlichkeiten
3. Ein Vererbungsmechanismus (in der ursprünglichen Version nicht vorhanden)
4. Ein Mechanismus zur Aktualisierung der Position
5. Parameter Trainingsintensität (I)

Lassen Sie uns zunächst den Pseudocode des Algorithmus vorstellen:

Initialisierung:
    Erstellen einer Population von popSize Agenten
    Für jeden Agenten:
        Initialisierung einer zufälligen Position innerhalb des Suchbereichs
        Initialisierung der vorherigen Position und Fitness

Hauptschleife:
    Bis zum Erreichen der Stopp-Bedingung:
        Für jeden Agenten i in der Population:
            Berechnen Sie den Vektor der Wahrscheinlichkeiten P und die kumulativen Wahrscheinlichkeiten C
            
            Für jede Koordinate c:
                Auswahl von k Bogenschützen mit kumulativer Wahrscheinlichkeit
                
                Wenn (random_number < inheritance_probability):
                    new_position [c] = k_archer_position [c]
                Andernfalls:
                    I = rounding (1 + random_number_from_0_to_1)  // Parameter für die Trainingsintensität
                    random_gaussian = generate_gaussian_number (mean = 0, min =-1, max = 1)
                    
                    Wenn (k_archer_fitness > i_agent_fitness):
                        new_position [c] = previous_position [c] + random_gaussian * (k_archer_position [c] - I * previous_position [c])
                    Andernfalls:
                        new_position [c] = previous_position [c] + random_gaussian * (previous_position [c] - I * k_archer_position [c])
                
                Begrenzung von new_position [c] innerhalb des Suchbereichs
            
            Aktualisierung der Position des Agenten i
        
        Bewerten der Fitness aller Agenten
        Aktualisierung der besten Gesamtlösung
        Für jeden Agenten:
            Wenn die neue Fitness besser ist als die vorherige:
                Aktualisieren der vorherige Position und Fitness

Rückgabe der besten gefundenen Lösung

Implementierungsmerkmale im Code:

1. Der Algorithmus verwendet einen probabilistischen Ansatz, um die Bogenschützen auszuwählen, von denen er lernen soll.
2. Der Vererbungsmechanismus ermöglicht es den Agenten, die Positionen erfolgreicher Bogenschützen mit einer gewissen Wahrscheinlichkeit direkt zu kopieren.
3. Bei der Aktualisierung der Positionen wird eine Gauß-Verteilung verwendet, um Zufälligkeit in den Lernprozess der Bogenschützen zu bringen.
4. Der Algorithmus speichert die vorherigen besten Positionen der Agenten, sodass er ein gewisses „Gedächtnis“ für gute Entscheidungen hat.
5. Die Implementierung wird einen Mechanismus zur Begrenzung neuer Positionen innerhalb des zulässigen Suchbereichs umfassen.
6. Der von den Autoren beschriebene Parameter der Trainingsintensität (I) wird verwendet, um den Grad des Einflusses der aktuellen Position auf die neue Position zu regulieren.

Der Parameter I (Trainingsintensität) ist eine Zufallsvariable, die den Wert 1 oder 2 annehmen kann. Sie ist wie folgt definiert: I = Rundung auf die nächste ganze Zahl (1 + zufällig erzeugte Zahl von 0 bis 1). Das bedeutet, dass I mit einer Wahrscheinlichkeit von 0,5 gleich 1 und mit derselben Wahrscheinlichkeit gleich 2 sein wird. Die Rolle des Parameters I im Algorithmus:

1. Wenn I = 1 ist, nimmt der Algorithmus kleinere Positionsanpassungen vor.
2. Wenn I = 2 ist, kann der Algorithmus drastischere Änderungen an einer Position vornehmen.

Kommen wir nun zum Algorithmus selbst. Beschreibung der Struktur des Bogenschützen, S_AA_Agent. Sie repräsentiert einen Agenten in einem Optimierungsalgorithmus mit einem Satz von Koordinaten im Lösungsraum und enthält Informationen über seine Effizienz in Form der Fitnessfunktion. 

  • cPrev [] - das Array speichert die vorherigen Koordinaten des Agenten.
  • fPrev - die Variable speichert den vorherigen Wert der Agentenfitness.   

Die Methode Init ermöglicht es uns, den Agenten auf die Arbeit vorzubereiten, indem wir Anfangswerte für seine Koordinaten und seine Fitness festlegen. Anschließend wird der Wert fPrev auf den kleinstmöglichen Wert für den Typ „double“ gesetzt, da die Fitness noch nicht berechnet wurde.

//——————————————————————————————————————————————————————————————————————————————
struct S_AA_Agent
{
    double cPrev []; // previous coordinates
    double fPrev;    // previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Werfen wir einen Blick auf die Klasse C_AO_AAm, die den Algorithmus selbst implementiert und von der Klasse C_AO abgeleitet wird. 

  • popSize - Größe der Population.
  • inhProbab - Wahrscheinlichkeit, ein Merkmal von einem anderen Bogenschützen zu erben.

Dann wird das Array params mit der Größe 2 initialisiert, in dem die Parameter des Algorithmus gespeichert werden: Populationsgröße und Vererbungswahrscheinlichkeit.

  • SetParams - Methode setzt die Parameter basierend auf den im Array params gespeicherten Werten. Es extrahiert Werte für popSize und inhProbab und wandelt sie in die entsprechenden Typen um.
  • Init - die Methode initialisiert den Algorithmus, indem sie die minimalen und maximalen Suchgrenzen, den Suchschritt und die Anzahl der Epochen übernimmt.
  • Moving und Revision - die Methoden sind für die Logik der Verschiebung von Agenten im Lösungsraum und deren Revision (Aktualisierung) verantwortlich. 

S_AA_Agent agent [] - Array von Agenten, die zur Durchführung der Optimierung verwendet werden sollen.

Die Klasse C_AO_AAm implementiert den Optimierungsalgorithmus, während SetParams, Init, Moving und Revision die Konfiguration und das Verhalten des Algorithmus während seines Betriebs verwalten. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AAm () { }
  C_AO_AAm ()
  {
    ao_name = "AAm";
    ao_desc = "Archery Algorithm M";
    ao_link = "https://www.mql5.com/en/articles/15782";

    popSize   = 50;    // population size
    inhProbab = 0.3;

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "inhProbab"; params [1].val = inhProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    inhProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // step search
             const int     epochsP = 0);  // number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double  inhProbab; //probability of inheritance

  S_AA_Agent agent [];

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

Die Methode Init in der Klasse C_AO_AAm ist für die Initialisierung des Optimierungsalgorithmus zuständig. Sie benötigt vier Parameter: Arrays für die minimalen und maximalen Suchgrenzen, den Suchschritt und die Anzahl der Epochen, die standardmäßig gleich Null sind.

  • Wenn die Standardinitialisierung erfolgreich ist, ändert die Methode die Größe des Agenten, sodass er der angegebenen Populationsgröße popSize entspricht. So können wir die erforderliche Anzahl von Agenten für den Algorithmus erstellen.
  • In der for-Schleife wird jeder Agent aus dem Array mit der Init-Methode initialisiert, die die Anfangskoordinaten für jeden Agenten angibt.

Am Ende gibt die Methode „true“ zurück, was den erfolgreichen Abschluss der Algorithmusinitialisierung anzeigt. Die Init-Methode stellt also sicher, dass der Algorithmus für den Betrieb vorbereitet ist, indem er die notwendigen Parameter einstellt und Agenten erstellt, die an der Optimierung teilnehmen werden.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAm::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving in der Klasse C_AO_AAm ist für die Bewegung der Agenten im Lösungsraum auf der Grundlage ihrer aktuellen Positionen und der Werte der Funktion, die sie optimieren, verantwortlich. Zerlegen wir sie in Teile:

  • Wird die Methode zum ersten Mal aufgerufen (Revision ist false), dann wird für jeden Agenten und jede Koordinate ein Zufallswert innerhalb der angegebenen Grenzen von rangeMin und rangeMax initialisiert.
  • Anschließend wird dieser Wert mit der Methode SeInDiSp angepasst, die sicherstellt, dass der Wert mit der angegebenen Stufe übereinstimmt.

Danach wird dem Flag für Revision true zugwiesen und die Methode beendet ihre Arbeit.

  • Als nächstes werden zwei Arrays erstellt: P für Wahrscheinlichkeiten und C für kumulative Wahrscheinlichkeiten.
  • Der schlechteste Wert der Funktion F_worst wird ermittelt, um die Werte der Fitnessfunktion für die Agenten zu normalisieren.
  • Die Wahrscheinlichkeiten für jeden Agenten werden dann berechnet und normalisiert, sodass sie in der Summe 1 ergeben.
  • Die kumulativen Wahrscheinlichkeiten C werden auf der Grundlage der Wahrscheinlichkeiten P berechnet.
  • Für jeden Agenten und jede Koordinate wird ein Partnerbogenschütze (ein Agent) auf der Grundlage der kumulativen Wahrscheinlichkeit ausgewählt.
  • Ist der Zufallswert kleiner als die angegebene Vererbungswahrscheinlichkeit inhProbab, nimmt der Agent die Koordinate des ausgewählten Agenten an (wodurch die Vererbung der Merkmale mit einer bestimmten Wahrscheinlichkeit gewährleistet ist).
  • Andernfalls aktualisiert der Agent seine Position auf der Grundlage einer Gleichung, die die aktuelle Position, den Zufallswert und die Position des Partnerschützen berücksichtigt.
  • Schließlich wird der neue Koordinatenwert auch mit der Methode SeInDiSp angepasst.

Die Methode Moving implementiert die Bewegung von Agenten im Lösungsraum unter Berücksichtigung ihrer aktuellen Positionen und Funktionswerte und verwendet probabilistische Methoden, um Bewegungsrichtungen auszuwählen und Positionen zu aktualisieren.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        // Update position using Eq. (5) and (6)
        double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);

        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision in der Klasse C_AO_AAm ist für die Aktualisierung der Informationen über die besten Agenten in der Population zuständig. Die Methode geht folgendermaßen vor:

  • Die Variable ind wird mit dem Wert -1 initialisiert. Sie wird verwendet, um den Index des Agenten mit dem besten Funktionswert zu speichern.
  • Die for-Schleife durchläuft alle Agenten in der Population popSize und prüft, ob der Wert der aktuellen Agentenfunktion a [i].f den aktuell besten Wert der Funktion fB übersteigt:
    • fB wird auf den neuen besseren Wert von a [i].f aktualisiert.
    • wird der Index dieses Bearbeiters in der Variablen ind gespeichert.
Nach Beendigung der Schleife wird, wenn ind ungleich -1 ist, die Funktion ArrayCopy aufgerufen. Es kopiert die Koordinaten des besten Agenten aus dem Array a in das Array cB. Die zweite for-Schleife durchläuft ebenfalls alle Bearbeiter in der Grundgesamtheit:

  • Wenn der Wert der aktuellen Agentenfunktion a [i].f den Wert der vorherigen des Agenten [i].fPrev übersteigt:
    • wird der vorherige Wert von fPrev für den Agenten aktualisiert.
    • werden die aktuellen Koordinaten des Agenten mittels ArrayCopy in das Array cPrev kopiert.

Die Methode Revision dient der Aktualisierung der Informationen über die beste globale Lösung sowie der Aktualisierung der besten Positionen der Agenten.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


Testergebnisse

Ich habe den Algorithmus leicht verändert. Der ursprüngliche Algorithmus sieht keinen direkten Informationsaustausch zwischen Bogenschützen vor. Der Austausch erfolgt indirekt durch die Interaktion der Koordinaten über die Normalverteilung, sodass ich es für notwendig hielt, den Austausch solcher Informationen hinzuzufügen. Zu diesem Zweck habe ich den zusätzlichen Algorithmus inhProbab hinzugefügt, der dafür zuständig ist, einen solchen Austausch mit einer bestimmten Wahrscheinlichkeit durchzuführen.

if (u.RNDbool () < inhProbab)
{
  x = a [k].c [c];
}

Die im Folgenden dargestellten Ergebnisse entsprechen der ursprünglichen Version des Algorithmus, wie sie von den Autoren beabsichtigt war.

AA|Archery Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6699547926310098
25 Hilly's; Func runs: 10000; result: 0.37356238340164605
500 Hilly's; Func runs: 10000; result: 0.257542163368952
=============================
5 Forest's; Func runs: 10000; result: 0.38166669771790607
25 Forest's; Func runs: 10000; result: 0.199300365268835
500 Forest's; Func runs: 10000; result: 0.15337954055780398
=============================
5 Megacity's; Func runs: 10000; result: 0.4076923076923077
25 Megacity's; Func runs: 10000; result: 0.17907692307692308
500 Megacity's; Func runs: 10000; result: 0.10004615384615476
=============================
All score: 2.72222 (30.25%)

Der Algorithmus erreicht im Test 30,25 %, aber mit meiner Änderung verbesserte er seine Leistung um mehr als 13 %. Nachstehend sind die Ergebnisse der geänderten Version aufgeführt:

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9353194829441194
25 Hilly's; Func runs: 10000; result: 0.6798262991897616
500 Hilly's; Func runs: 10000; result: 0.2596620178276653
=============================
5 Forest's; Func runs: 10000; result: 0.5735062785421186
25 Forest's; Func runs: 10000; result: 0.22007188891556378
500 Forest's; Func runs: 10000; result: 0.1486980566819649
=============================
5 Megacity's; Func runs: 10000; result: 0.6307692307692309
25 Megacity's; Func runs: 10000; result: 0.344
500 Megacity's; Func runs: 10000; result: 0.10193846153846249
=============================
All score: 3.89379 (43.26%)

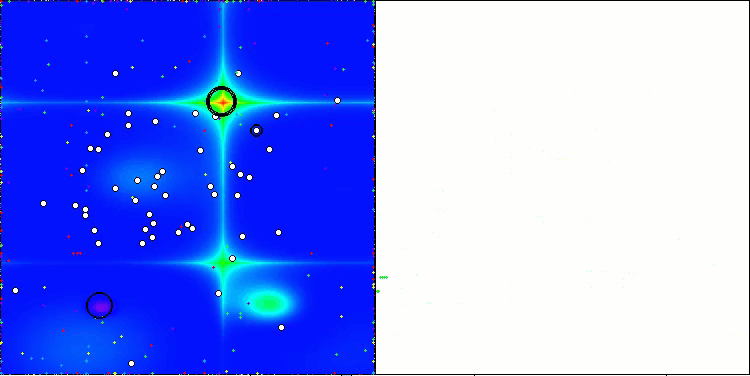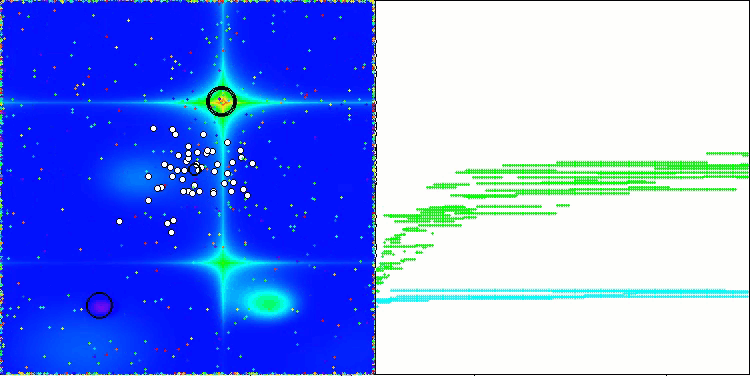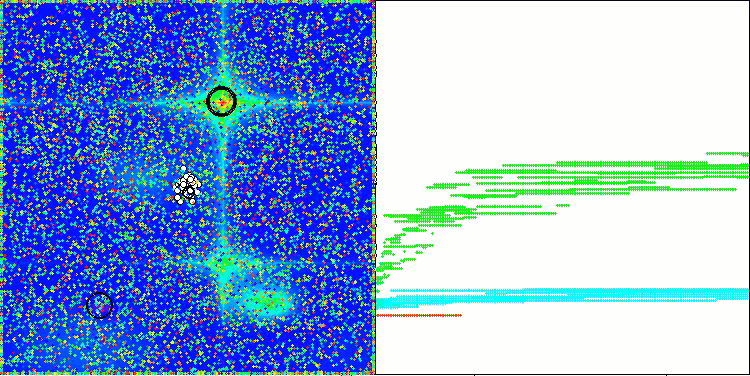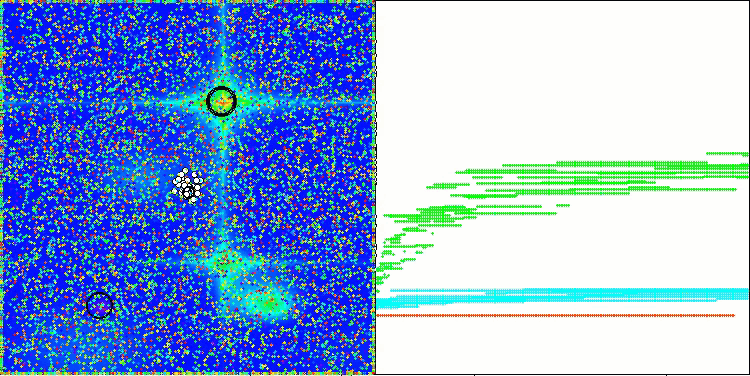
Ich habe also den geänderten Algorithmus ausgewählt und in die Bewertungstabelle aufgenommen. Unten sehen Sie die Visualisierung des Algorithmus. Ich denke, sie ist recht gut. Natürlich gibt es eine Streuung der Ergebnisse, die jedoch nicht kritisch ist und nur bei Funktionen mit einer kleinen Anzahl von Koordinaten auftritt.

Hilly

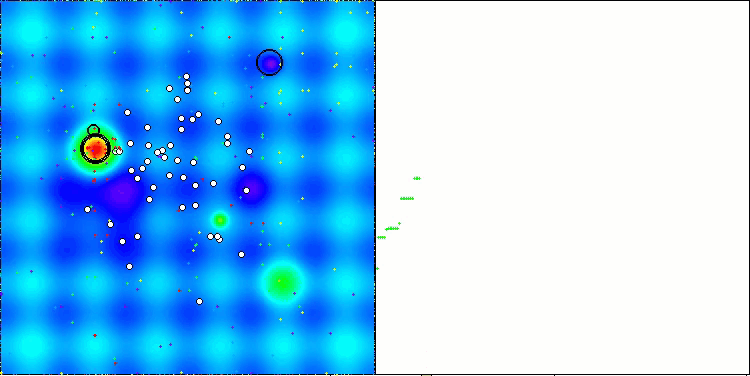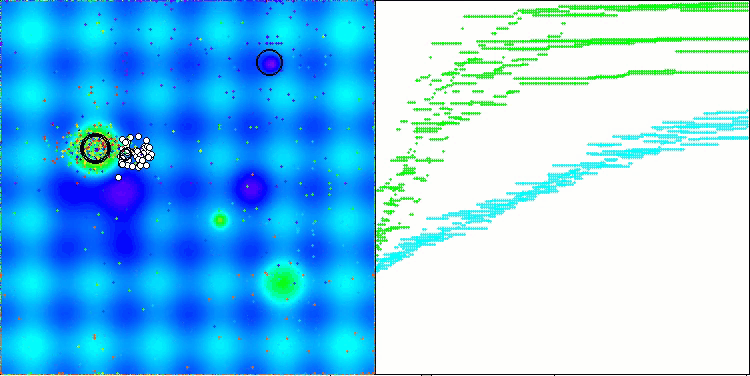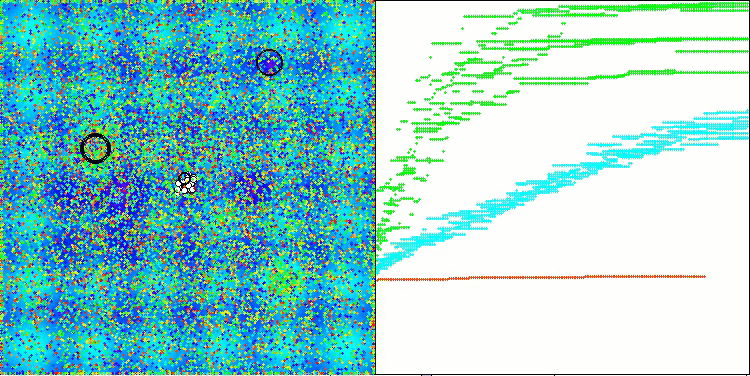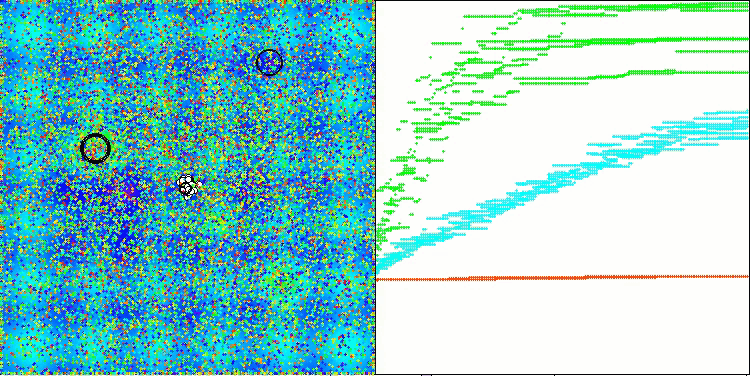
AAm mit der Testfunktion Hilly

Forest

AAm mit der Testfunktion Forest

Megacity

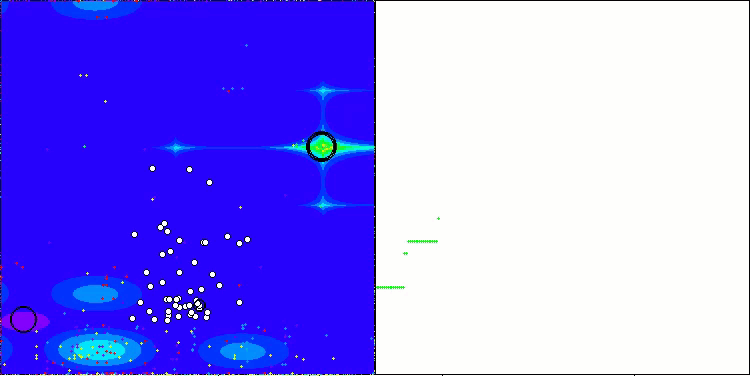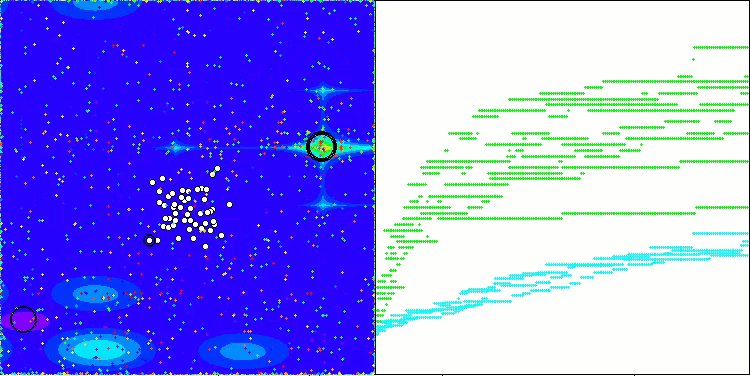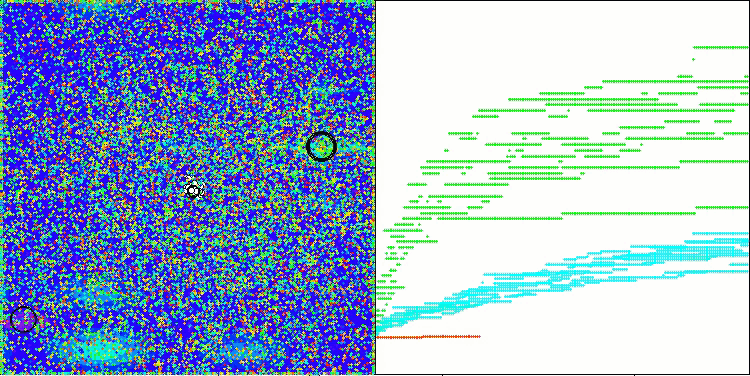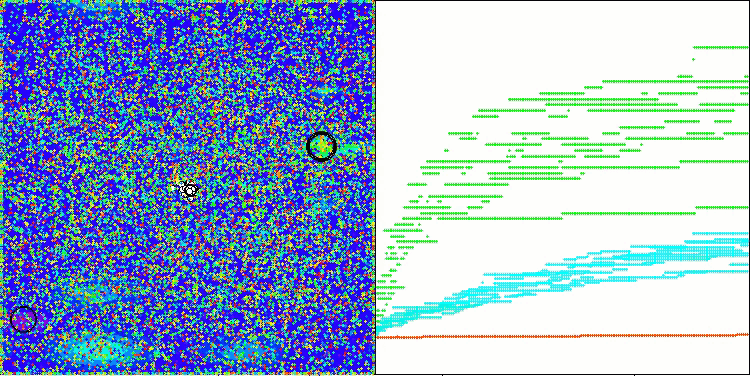
AAm mit der Testfunktion Megacity

Nach den Betriebsergebnissen belegt die modifizierte Version des Algorithmus den 26.

# AO Beschreibung HillyHilly final ForestForest final Megacity (discrete)Megacity final Final result % of MAX
10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)
1ANSSuche über die gesamte Nachbarschaft0.949480.847760.438572.235811.000000.923340.399882.323230.709230.634770.230911.574916.13468.15
2CLAСode Lock Algorithmus0.953450.871070.375902.200420.989420.917090.316422.222940.796920.693850.193031.683806.10767.86
3AMOmOptimierung der Tiermigration M0,903580,843170,462842,209590,990010,924360,465982,380340,567690,591320,237731,396755.98766,52
4(P+O)ES(P+O) Entwicklungsstrategien0.922560.881010.400212.203790.977500.874900.319452.171850.673850.629850.186341.490035.86665.17
5CTAKometenschweif-Algorithmus0.953460.863190.277702.094350.997940.857400.339492.194840.887690.564310.105121.557125.84664.96
6SDSmstochastische Diffusionssuche M0.930660.854450.394762.179880.999830.892440.196192.088460.723330.611000.106701.441035.70963.44
7ESGEntwicklung der sozialen Gruppen0.999060.796540.350562.146161.000000.828630.131021.959650.823330.553000.047251.423585.52961.44
8SIASimuliertes isotropes Abkühlen0.957840.842640.414652.215130.982390.795860.205071.983320.686670.493000.090531.270205.46960.76
9ACSkünstliche, kooperative Suche0.755470.747440.304071.806981.000000.888610.224132.112740.690770.481850.133221.305835.22658.06
10ASOAnarchische Gesellschaftsoptimierung0,848720,746460,314651,909830,961480,791500,238031,991010,570770,540620,166141,277525.17857,54
11TSEASchildkrötenpanzer-Evolutionsalgorithmus0.967980.644800.296721.909490.994490.619810.227081.841390.690770.426460.135981.253225.00455.60
12DEdifferentielle Evolution0.950440.616740.303081.870260.953170.788960.166521.908650.786670.360330.029531.176534.95555.06
13CROOptimierung chemischer Reaktionen0.946290.661120.298531.905930.879060.584220.211461.674730.758460.426460.126861.311784.89254.36
14BSAVogelschwarm-Algorithmus0.893060.649000.262501.804550.924200.711210.249391.884790.693850.326150.100121.120124.80953.44
15HSHarmoniesuche0.865090.687820.325271.878180.999990.680020.095901.775920.620000.422670.054581.097254.75152.79
16SSGSetzen, Säen und Wachsen0.778390.649250.395431.823080.859730.624670.174291.658690.646670.441330.105981.193984.67651.95
17BCOmOptimierung der bakteriellen Chemotaxis M0.759530.622680.314831.697040.893780.613390.225421.732590.653850.420920.144351.219124.64951.65
18(PO)ES(PO) Entwicklungsstrategien0.790250.626470.429351.846060.876160.609430.195911.681510.590000.379330.113221.082554.61051.22
19TSmTabu-Suche M0.877950.614310.291041.783300.928850.518440.190541.637830.610770.382150.121571.114494.53650.40
20BSOBrainstorming-Optimierung0.937360.576160.296881.810410.931310.558660.235371.725340.552310.290770.119140.962224.49849.98
21WOAmWal-Optimierungsalgorithmus M0.845210.562980.262631.670810.931000.522780.163651.617430.663080.411380.113571.188034.47649.74
22AEFAAlgorithmus für künstliche elektrische Felder0.877000.617530.252351.746880.927290.726980.180641.834900.666150.116310.095080.877544.45949.55
23ACOmAmeisen-Kolonie-Optimierung M0.881900.661270.303771.846930.858730.586800.150511.596040.596670.373330.024720.994724.43849.31
24BFO-GAOptimierung der bakteriellen Futtersuche - ga0.891500.551110.315291.757900.969820.396120.063051.428990.726670.275000.035251.036924.22446.93
25ABHAAlgorithmus für künstliche Bienenstöcke0.841310.542270.263041.646630.878580.477790.171811.528180.509230.338770.103970.951974.12745.85
26AAmAlgorithmus für das Bogenschießen M0.935320.679830.259661.874810.573510.220070.148700.942280.630770.344000.101941.076713.89443.26
27ASBOOptimierung des adaptiven Sozialverhaltens0.763310.492530.326191.582020.795460.400350.260971.456770.264620.171690.182000.618313.65740.63
28MECEvolutionäre Berechnung des Geistes0.695330.533760.326611.555690.724640.330360.071981.126980.525000.220000.041980.786983.47038.55
29IWOOptimierung mit invasiven Unkräutern0.726790.522560.331231.580580.707560.339550.074841.121960.423330.230670.046170.700173.40337.81
30Micro-AISKünstliches Mikro-Immunsystem0.795470.519220.308611.623300.729560.368790.093981.192330.376670.158670.028020.563353.37937.54
31COAmKuckuck-Optimierungsalgorithmus M0.758200.486520.313691.558410.740540.280510.055991.077040.505000.174670.033800.713473.34937.21
32SDOmOptimierung der Spiraldynamik M0.746010.446230.296871.489120.702040.346780.109441.158260.428330.167670.036630.632633.28036.44
33NMmNelder-Mead-Verfahren M0.738070.505980.313421.557470.636740.283020.082211.001970.446670.186670.040280.673623.23335.92
34FAmFirefly-Algorithmus M0.586340.472280.322761.381380.684670.374390.109081.168140.286670.164670.047220.498553.04833.87
35GSAAlgorithmus für die Schwerkraftsuche0.647570.491970.300621.440160.539620.363530.099451.002600.326670.122000.019170.467832.91132.34
36BFOOptimierung der bakteriellen Futtersuche0.611710.432700.313181.357590.544100.215110.056760.815970.421670.138000.031950.591622.76530.72
37ABCKünstliches Bienenvolk (Artificial Bee Colony, ABC)0.633770.424020.308921.366710.551030.218740.056230.826000.340000.142000.031020.513022.70630.06
38BAFledermaus-Algorithmus0.597610.459110.352421.409150.403210.193130.071750.668100.210000.101000.035170.346172.42326.93
39AAAKünstlicher Algenalgorithmus (AAA)0.500070.320400.255251.075720.370210.222840.167850.760890.278460.148000.097550.524022.36126.23
40SAsimuliertes Abkühlen0.557870.421770.315491.295130.349980.152590.050230.552800.311670.100330.028830.440832.28925.43
41IWDmintelligente Wassertropfen M0.545010.378970.301241.225220.461040.147040.043690.651770.258330.097000.023080.378422.25525.06
42PSOPartikelschwarmoptimierung0.597260.369230.299281.265770.372370.163240.070100.605720.256670.080000.021570.358232.23024.77
43GeboteBoids-Algorithmus0.433400.305810.254250.993460.357180.201600.157080.715860.278460.142770.098340.519572.22924.77
44MAAffen-Algorithmus0.591070.426810.318161.336040.311380.140690.066120.518190.228330.085670.027900.341902.19624.40
45SFLschlurfender Froschsprung0.539250.358160.298091.195510.371410.114270.040510.526180.271670.086670.024020.382352.10423.38



Zusammenfassung

Ich habe zwei Versionen des Algorithmus vorgestellt: die ursprüngliche und eine modifizierte Version, die geringfügige Änderungen enthält, aber eine deutliche Leistungsverbesserung bietet. Dieser Artikel zeigt deutlich, dass selbst geringfügige Anpassungen an der Logik eines Algorithmus zu erheblichen Effizienzsteigerungen bei verschiedenen Aufgaben führen können. Es wird auch deutlich, dass komplexe Beschreibungen das Verständnis für die Funktionsweise eines Algorithmus erschweren können, was wiederum seine Verbesserung behindert. Im Gegenteil: Komplexe Konzepte, die in einfacher Sprache ausgedrückt werden, eröffnen den Weg zu effizienteren Lösungen.

Tabelle

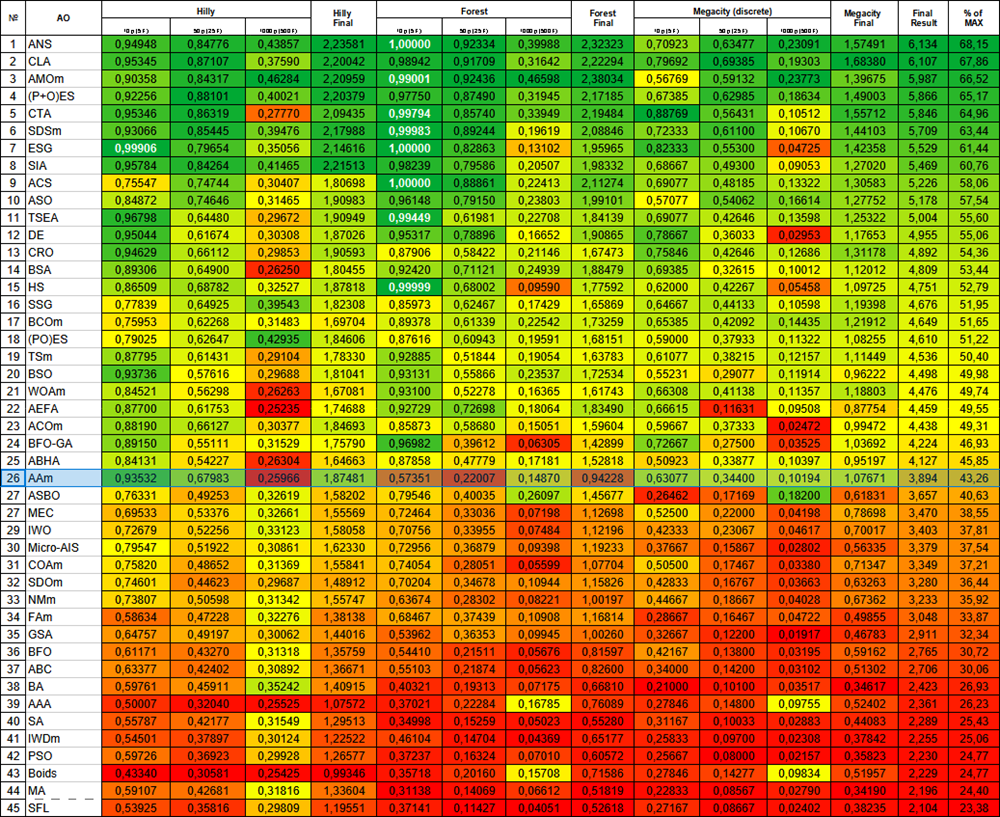
Abbildung 1. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

Histogramm

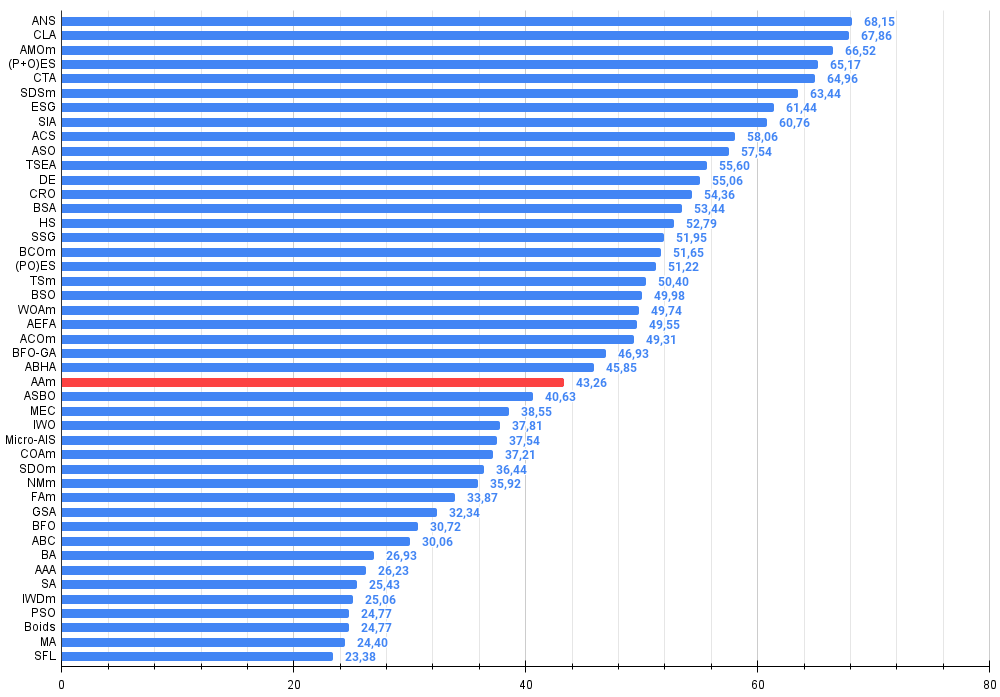
Abbildung 2. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)


Als der Artikel kurz vor der Veröffentlichung stand, hatte ich eine Idee, die ich testen wollte. Wie wäre es, wenn wir, der Logik der Autoren über Ziele und Bogenschützen folgend, die die „Roulette“-Methode für die Auswahl verwenden, die Größe der Ziele selbst umgekehrt proportional zur Qualität der gefundenen Lösungen ändern? Wenn sich die Lösung als gut erweist, sollte sie verfeinert und ihre Umgebung erkundet werden. Ist das Ergebnis unbedeutend, muss der Suchbereich erweitert werden, um neue, potenziell vielversprechende Gebiete zu ermitteln.

Ziele

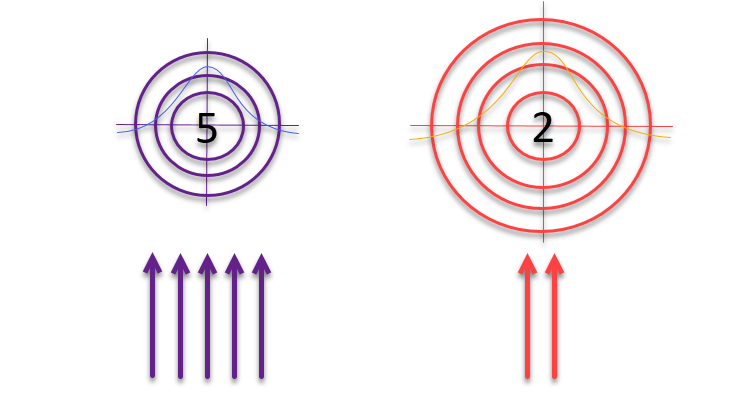
Abbildung 3. Die Anzahl der Pfeile, die die Ziele treffen, ist direkt proportional zur Qualität der Ziele selbst, während die Größe der Ziele umgekehrt proportional zu ihrer Qualität ist 

Schauen wir uns den Code an, der die Idee verwendet, Ziele umgekehrt proportional zu ihrer Qualität zu erhöhen. 

void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX; // a[ArrayMaximum(a, WHOLE_ARRAY, 0, popSize)].f;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst; ////F_worst - a[i].f;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;
  
  double maxFF = fB;
  double minFF = DBL_MAX;
  double prob1;
  double prob2;
  
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < minFF) minFF = a [i].f;
  } 

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        
        // Update position using Eq. (5) and (6)
        //double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);
        /*
        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
        */
        
        prob1 = u.Scale (a [i].f, minFF, maxFF, 0, 1);
        prob2 = u.Scale (a [k].f, minFF, maxFF, 0, 1);
        
        x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2);  
        
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//—

1. Der kommentierte Abschnitt in der ursprünglichen Version verwendete das bedingte Konstrukt if-else, um zu bestimmen, wie die Position des Agenten aktualisiert werden soll. Diese Logik wurde entfernt und durch eine neue Berechnung ersetzt.

2. Drei neue Zeilen Code:

prob1 = u.Scale(a[i].f, minFF, maxFF, 0, 1);
prob2 = u.Scale(a[k].f, minFF, maxFF, 0, 1);

x = agent[i].cPrev[c] + rnd * (a[k].c[c] - agent[i].cPrev[c]) * (1 - prob1 - prob2);

Mit diesen Zeilen wird ein neuer Ansatz zur Berechnung der aktualisierten Position eingeführt:

a) Zwei Wahrscheinlichkeitswerte (prob1 und prob2) werden mit der Funktion Scale berechnet, die die Fitnesswerte der Agenten i und k im Bereich von 0 bis 1 auf der Grundlage der minimalen und maximalen Fitnesswerte minFF und maxFF normalisiert.

b) Dann wird die neue Position x anhand dieser Wahrscheinlichkeiten berechnet. Dabei werden die vorherige Position i des Agenten agent [i].cPrev [c], die Position k des ausgewählten Bogenschützen a [k].c [c] und den Zufallsfaktor rnd verwendet.

c) Nun wird die Bewegung durch die Summe der Fitnesswerte beider Agenten, subtrahiert von 1, beeinflusst. Dieser Faktor dient als Skalierungsfaktor, der es ermöglicht, die Zielscheibe im umgekehrten Verhältnis zur Fitness der gewählten Bogenschützen zu vergrößern oder zu verkleinern. Je weniger erfahren die Bogenschützen sind, desto größer ist die Streuung der Pfeile, aber die Verteilung der Trefferwahrscheinlichkeiten folgt immer noch einer Normalverteilung.

Schauen wir uns nun die Ergebnisse an:

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9174358826544864
25 Hilly's; Func runs: 10000; result: 0.7087620527831496
500 Hilly's; Func runs: 10000; result: 0.42160091427958263
=============================
5 Forest's; Func runs: 10000; result: 0.9252690259821034
25 Forest's; Func runs: 10000; result: 0.7580206359203926
500 Forest's; Func runs: 10000; result: 0.353277934084795
=============================
5 Megacity's; Func runs: 10000; result: 0.6738461538461538
25 Megacity's; Func runs: 10000; result: 0.552
500 Megacity's; Func runs: 10000; result: 0.23738461538461658
=============================
All score: 5.54760 (61.64%)

Die Leistung des Algorithmus hat sich deutlich verbessert. In der folgenden Visualisierung sehen wir die sichere Konvergenz des Algorithmus und die Identifizierung signifikanter Bereiche der Funktionsoberfläche.

Hilly2

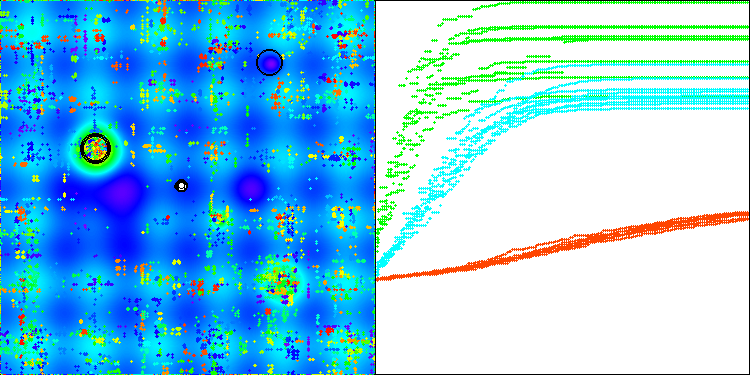
AAm mit der Testfunktion Hilly

Lassen Sie uns ein weiteres kleines Experiment durchführen. Die obigen Ergebnisse erhält man, indem man die Summe der Wahrscheinlichkeiten der Bogenschützen von eins subtrahiert.

//x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2); 
 x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (2 - prob1 - prob2);  

Die wichtigste Änderung besteht darin, dass die Summe nicht von eins, sondern von zwei subtrahiert wird. Schauen wir uns an, wie sich eine so einfache Aktion auf das Verhalten des Algorithmus auswirken kann:

  • In der vorherigen Version konnte das Ergebnis dieser Operation negativ sein, wenn die Fitness beider Bogenschützen hoch war, was zu einem „Mutationseffekt“ bei den Koordinaten des neuen Bogenschützen führte.
  • In der neuen Version wird der Multiplikator einen Wert von 0 bis 2 haben.

Diese Änderung führt dazu, dass sich die Agenten umfassender bewegen und den Lösungsraum aggressiver erkunden, da die Agenten bei jeder Positionsaktualisierung größere Schritte machen.

Wie aus dem Ausdruck der Ergebnisse des Algorithmus ersichtlich ist, verbesserte diese Änderung die Konvergenz des Algorithmus bei mittelgroßen Funktionen, führte aber auch zu einer Verschlechterung bei hochdimensionalen Funktionen (gelb markiert), obwohl der Algorithmus insgesamt einen höheren Endwert erzielte.

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9053229410164233
25 Hilly's; Func runs: 10000; result: 0.8259118221071665
500 Hilly's; Func runs: 10000; result: 0.2631661675236262
=============================
5 Forest's; Func runs: 10000; result: 0.9714247249319152
25 Forest's; Func runs: 10000; result: 0.9091052022399436
500 Forest's; Func runs: 10000; result: 0.2847632249786224
=============================
5 Megacity's; Func runs: 10000; result: 0.7169230769230768
25 Megacity's; Func runs: 10000; result: 0.6378461538461538
500 Megacity's; Func runs: 10000; result: 0.10473846153846252
=============================
All score: 5.61920 (62.44%)

Das vorherige Ergebnis erscheint praktischer und wird als Hauptvariante der modifizierten Version des AAm-Algorithmus beibehalten. Ich werde die Bewertungstabelle mit thermischer Abstufung noch einmal vorstellen. AAm belegt nun einen würdigen 7. Platz. Der Algorithmus kann als sehr ausgewogen bezeichnet werden (gute Konvergenz bei Funktionen verschiedener Dimensionen) und kann für die Lösung verschiedener Probleme empfohlen werden.

Tabelle2

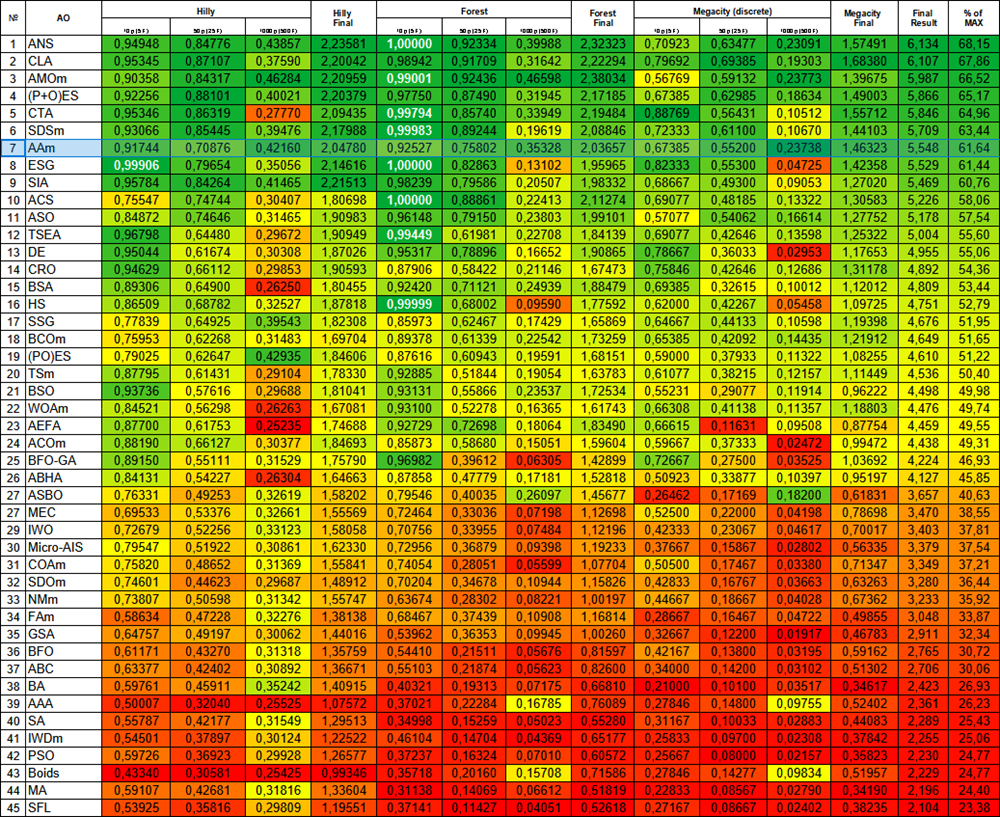
Abbildung 4. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

Vorteile und Nachteile von AAm:

Vorteile:

  1. Ziemlich schnell.
  2. Selbstanpassend.
  3. Nur ein externer Parameter.
  4. Gute Konvergenz.
  5. Gute Skalierbarkeit.
  6. Einfache Implementierung (trotz der komplexen Beschreibung durch die Autoren).

Nachteile

  1. Etwas anfällig für das Hängenbleiben bei niedrigdimensionalen Funktionen.

Die weitere Hinzufügung neuer Algorithmen zur Bewertungstabelle wird die Lesbarkeit erschweren. Daher habe ich beschlossen, die Zahl der Teilnehmer an der Bewertung auf 45 Algorithmen zu begrenzen, und der Wettbewerb wird nun im K.O.-Format durchgeführt. Um den Lesern den Zugang zu allen Artikeln in einer optisch ansprechenden Form zu erleichtern, habe ich eine HTML-Datei mit einer Liste aller bisher überprüften Algorithmen, sortiert nach ihrer Bewertung in einer Tabelle, vorbereitet. Diese Datei befindet sich schon seit einiger Zeit im Artikelarchiv, und wer sie zum ersten Mal öffnet, wird mit einer kleinen Überraschung konfrontiert.

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15782

Beigefügte Dateien |
ZIP herunterladen
AAm.zip (35.89 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Quantitativer Ansatz für das Risikomanagement: Anwendung des VaR-Modells zur Optimierung eines Multiwährungsportfolios mit Python und MetaTrader 5 Quantitativer Ansatz für das Risikomanagement: Anwendung des VaR-Modells zur Optimierung eines Multiwährungsportfolios mit Python und MetaTrader 5
In diesem Artikel wird das Potenzial des Value-at-Risk (VaR)-Modells für die Optimierung von Portfolios in mehreren Währungen untersucht. Mit Hilfe von Python und der Funktionalität von MetaTrader 5 demonstrieren wir, wie man eine VaR-Analyse für eine effiziente Kapitalallokation und Positionsverwaltung implementiert. Von den theoretischen Grundlagen bis zur praktischen Umsetzung behandelt der Artikel alle Aspekte der Anwendung eines der robustesten Risikoberechnungssysteme - VaR - im algorithmischen Handel.
Einfache Lösungen für die komfortable Handhabung von Indikatoren Einfache Lösungen für die komfortable Handhabung von Indikatoren
In diesem Artikel beschreibe ich, wie man ein einfaches Panel erstellt, um die Einstellungen des Indikators direkt im Chart zu ändern, und welche Änderungen am Indikator vorgenommen werden müssen, um das Panel zu verbinden. Dieser Artikel richtet sich an MQL5-Anfänger.
Neuronale Netze im Handel: Hierarchisches Lernen der Merkmale von Punktwolken Neuronale Netze im Handel: Hierarchisches Lernen der Merkmale von Punktwolken
Wir untersuchen weiterhin Algorithmen zur Extraktion von Merkmalen aus einer Punktwolke. In diesem Artikel werden wir uns mit den Mechanismen zur Steigerung der Effizienz der PointNet-Methode vertraut machen.
Von der Grundstufe bis zur Mittelstufe: Die Direktive Include Von der Grundstufe bis zur Mittelstufe: Die Direktive Include
Im heutigen Artikel werden wir eine Kompilierungsdirektive besprechen, die in verschiedenen Codes, die in MQL5 zu finden sind, häufig verwendet wird. Obwohl diese Direktive hier nur oberflächlich erklärt wird, ist es wichtig, dass Sie sich mit ihrer Verwendung vertraut machen, da sie bald unverzichtbar sein wird, wenn Sie sich auf höheren Ebenen der Programmierung bewegen. Der hier dargestellte Inhalt ist ausschließlich für Bildungszwecke bestimmt. Die Anwendung sollte unter keinen Umständen zu einem anderen Zweck als zum Erlernen und Beherrschen der vorgestellten Konzepte verwendet werden.