
Algorithmus für zyklische Parthenogenese (CPA)
Inhalt
Einführung
Von Naturphänomenen inspirierte Optimierungsalgorithmen spielen weiterhin eine wichtige Rolle bei der Lösung komplexer Optimierungsprobleme. Von besonderem Interesse sind Algorithmen, die auf dem Verhalten von sozialen Insekten wie Ameisen, Bienen und Blattläusen basieren. Wir haben bereits eine Reihe ähnlicher Algorithmen wie ACOm und ABHA diskutiert. In diesem Artikel wird der Cyclic Parthenogenesis Algorithm (CPA, zyklische Jungfernzeugung) vorgestellt, der die einzigartige Fortpflanzungsstrategie von Blattläusen nachahmt.
Blattläuse zeigen eine bemerkenswerte Anpassungsfähigkeit aufgrund ihres ungewöhnlichen Lebenszyklus, der sowohl ungeschlechtliche (Parthenogenese) als auch geschlechtliche Fortpflanzung umfasst. Unter günstigen Bedingungen vermehren sich Blattläuse parthenogenetisch, was ein schnelles Populationswachstum ermöglicht. Wenn sich die Bedingungen verschlechtern, gehen sie zur sexuellen Fortpflanzung über, was die genetische Vielfalt fördert und die Überlebenschancen in einer sich verändernden Umwelt erhöht.
CPA simuliert diese biologischen Mechanismen mathematisch, indem es ein Gleichgewicht zwischen der Ausnutzung gefundener Lösungen (durch Parthenogenese) und der Erkundung neuer Bereiche des Suchraums (durch sexuelle Fortpflanzung) herstellt. Der Algorithmus ahmt auch das soziale Verhalten von Blattläusen nach, indem er Entscheidungen innerhalb der Kolonie organisiert und einen Migrationsmechanismus zwischen ihnen einführt, der den Informationsaustausch erleichtert.
Die oben aufgeführten Eigenschaften sollten CPA besonders effizient für die Lösung mehrdimensionaler Optimierungsprobleme machen, bei denen ein Gleichgewicht zwischen lokaler und globaler Suche erforderlich ist. In diesem Artikel werden wir die Grundsätze des Algorithmus, sein mathematisches Modell und seine praktische Umsetzung im Detail untersuchen. Der Algorithmus der zyklischen Parthenogenese wurde von Ali Kaveh und Zolghadr vorgeschlagen. Es wurde erstmals 2019 veröffentlicht.Implementierung des Algorithmus
Stellen Sie sich vor, Sie beobachten eine Kolonie von Blattläusen in Ihrem Garten. Diese winzigen Lebewesen nutzen zwei Methoden der Fortpflanzung und passen sich sehr gut an ihre Umwelt an. Der Algorithmus der zyklischen Parthenogenese (CPA) simuliert genau dieses Verhalten, um komplexe Optimierungsprobleme zu lösen. Wie funktioniert das? Bei der anfänglichen Organisation werden mehrere Gruppen (Kolonien) von Lösungen gebildet, die jeweils „weibliche“ und „männliche“ Individuen enthalten.
Der Algorithmus schlägt zwei Wege vor, um neue Lösungen zu erstellen:- Die erste Methode ist die „Selbstreplikation“, bei der die besten Lösungen Kopien von sich selbst mit geringfügigen Änderungen erstellen.
- Die zweite Methode ist die traditionelle „paarige Reproduktion“, bei der zwei verschiedene Lösungen zu einer neuen kombiniert werden.
Manchmal „fliegt“ die beste Lösung von einer Kolonie zur anderen. Der Algorithmus prüft ständig, welche Lösungen am besten funktionieren, speichert die besten Ergebnisse und kombiniert erfolgreiche Optionen, während die Suche fortgesetzt wird. Und das alles, um die optimale Lösung zu finden. Das Hauptmerkmal des Algorithmus besteht darin, dass er ein Gleichgewicht zwischen der Verwendung bereits gefundener guter Lösungen und der Suche nach völlig neuen Optionen findet, ähnlich wie sich Blattläuse an Veränderungen in der Umwelt anpassen.
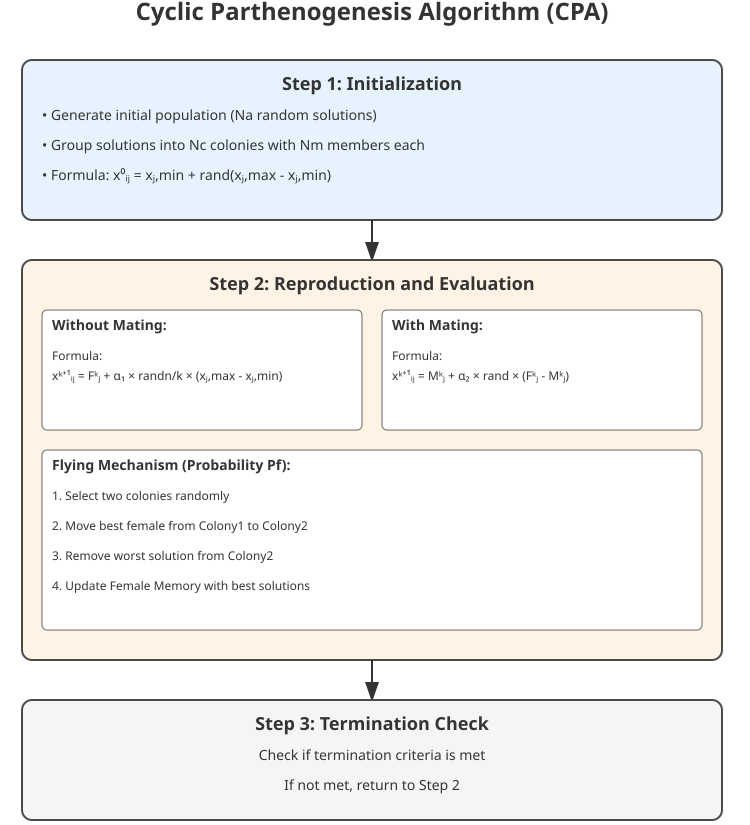
Abbildung 1. Aufbau des CPA-Algorithmus, grundlegende Gleichungen
Die wichtigsten Elemente in der Abbildung sind Kolonien, rosa Quadrate stehen für weibliche Individuen (Lösungen), blaue Quadrate für männliche Individuen (Lösungen) und die gestrichelte Linie zeigt den Flugweg zwischen den Kolonien. Die Illustration zeigt die Struktur der Kolonien, die Mechanismen der Fortpflanzung, den Flug zwischen den Kolonien und die Interaktion der Individuen innerhalb der Kolonien. Dies wird dazu beitragen, die Prinzipien des Algorithmus anhand einer visuellen Metapher mit echten Blattläusen besser zu verstehen.
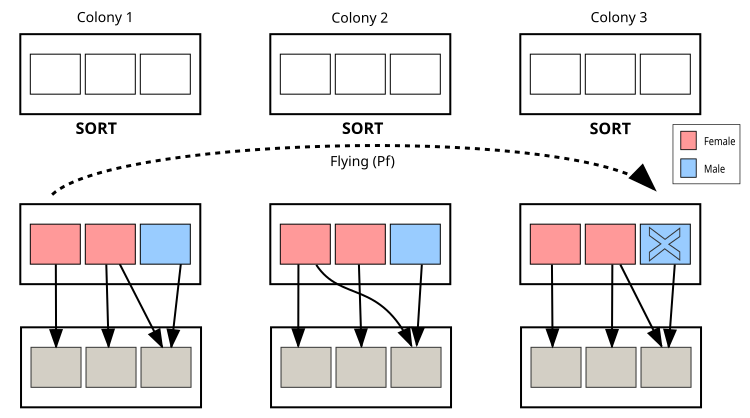
Abbildung 2. Blattlauskolonien und ihre Interaktionen im CPA-Algorithmus
Nachdem wir uns nun ein wenig mit der Beschreibung des Algorithmus vertraut gemacht haben, können wir mit dem Schreiben von Pseudocode fortfahren:
Initialisierung:
Erstellen Sie eine Population von Na-Individuen
Unterteilung der Bevölkerung in Nc Kolonien
In jeder Kolonie:
Bestimme die Anzahl der Weibchen (Fr * Nm)
Bestimme die Anzahl der Männchen (der Rest)
Stelle die Anfangsparameter ein:
alpha1 (Parthenogenese-Verhältnis)
alpha2 (Paarungsverhältnis)
Pf (Flugwahrscheinlichkeit)
Hauptzyklus (für jede Epoche):
Für jede Kolonie:
Für Weibchen:
Aktualisierung der Position durch Parthenogenese:
neue_Position = aktuelle_Position + alpha1 * k * N(0,1) * (max_range – min_range)
wobei k = (total_epochs – current_epoch) / total_epochs
N(0,1) – Normalverteilung
Für Männchen:
Wählen Sie ein zufälliges Weibchen aus derselben Kolonie
Aktualisieren Sie die Position über die Kopplung:
new_position = current_position + alpha2 * random[0,1] * (female_position - current_position)
Revision der Positionen:
Aktualisiere die beste gefundene Lösung
Speichere die aktuellen Positionen
Sortiere die Individuen in jeder Kolonie nach dem Wert der Zielfunktion
Migration (mit Pf-Wahrscheinlichkeit):
Wähle zwei zufällige Kolonien
Vergleiche ihre besten Lösungen
Verschiebe die beste Lösung in die schlechteste Kolonie
Ordne die Individuen in der Kolonie neu an
Alles ist bereit für das Schreiben des Algorithmus-Codes, machen wir weiter. Schreiben wir die Klasse C_AO_CPA, die von der Klasse C_AO abgeleitet wird. Diese Klasse implementiert den gesamten Algorithmus, eine kurze Beschreibung seiner Komponenten:
C_AO_CPA Konstruktor:
- Legt Parameter wie Populationsgröße, Koloniezahl, Weibchenanteil, Flugwahrscheinlichkeit und Skalierungsfaktoren für Parthenogenese und Paarung fest.
- Reserviert ein Array von Parametern und füllt es mit Werten.
Die Methode SetParams setzt die Werte der Parameter aus dem Array „params“ und konvertiert sie in die entsprechenden Typen.
Init, Moving und Revision Methoden:
- Init dient dazu, den Algorithmus mit den angegebenen Bereichen und der Anzahl der Epochen zu initialisieren.
- Verschieben und Überarbeiten – Methoden implementieren die Logik des Verschiebens und Überarbeitens innerhalb des Algorithmus.
Die Klassenmitglieder werden durch Variablen definiert, um Algorithmusparameter wie die Anzahl der Kolonien, das Verhältnis von Weibchen zu Männchen und Parameter zur Steuerung des Prozesses zu speichern.
Zu den privaten Mitgliedern gehören Variablen zur Verfolgung der aktuellen Epoche, der Anzahl der Mitglieder in der Kolonie und ein temporäres Array von Agenten.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the Cyclic Parthenogenesis Algorithm (CPA) // Inherited from the optimization base class class C_AO_CPA : public C_AO { public: C_AO_CPA (void) { ao_name = "CPA"; ao_desc = "Cyclic Parthenogenesis Algorithm"; ao_link = "https://www.mql5.com/en/articles/16877"; popSize = 50; // total population size Na Nc = 10; // number of colonies Fr = 0.2; // ratio of female individuals Pf = 0.9; // probability of flight between colonies alpha1 = 0.3; // scaling factor for parthenogenesis alpha2 = 0.9; // scaling factor for pairing ArrayResize (params, 6); // Setting algorithm parameters params [0].name = "popSize"; params [0].val = popSize; params [1].name = "Nc"; params [1].val = Nc; params [2].name = "Fr"; params [2].val = Fr; params [3].name = "Pf"; params [3].val = Pf; params [4].name = "alpha1_init"; params [4].val = alpha1; params [5].name = "alpha2_init"; params [5].val = alpha2; } void SetParams () { popSize = (int)params [0].val; Nc = (int)params [1].val; Fr = params [2].val; Pf = params [3].val; alpha1 = params [4].val; alpha2 = params [5].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // function for moving individuals void Revision (); // function for reviewing and updating positions //---------------------------------------------------------------------------- int Nc; // number of colonies double Fr; // ratio of female individuals double Pf; // probability of flight between colonies private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch int Nm; // number of individuals in each colony double alpha1; // scaling factor for parthenogenesis double alpha2; // scaling factor for pairing int fNumber; // number of females in the colony int mNumber; // number of males in the colony S_AO_Agent aT []; // temporary colony for sorting void SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count); // agent sorting function }; //——————————————————————————————————————————————————————————————————————————————
Implementierung der Init-Methode der Klasse C_AO_CPA, ihre Funktionalität:
Parameter der Methode:
- rangeMinP, rangeMaxP, rangeStepP – Arrays, die den minimalen und maximalen Wert des Bereichs sowie den Suchschritt definieren.
- epochsP – Anzahl der Epochen (Standardwert 0).
- Die Methode ruft zunächst StandardInit auf, um eine Standardinitialisierung mit den übergebenen Bereichen durchzuführen, wenn die Initialisierung fehlschlägt, gibt sie „false“ zurück,
- legt die Anzahl der Epochen und die aktuelle Epoche (epochNow) fest,
- berechnet die Anzahl der Mitglieder in einer Kolonie (Nm) auf der Grundlage der Bevölkerungsgröße und der Anzahl der Kolonien,
- ermittelt die Anzahl der Weibchen (fNumber) in der Kolonie und stellt sicher, dass sie nicht kleiner als 1 ist; die Anzahl der Männchen (mNumber) wird als Differenz zwischen der Gesamtzahl der Mitglieder und der Anzahl der Weibchen berechnet:
- reserviert das Array „aT“, um temporäre Kolonie-Agenten zu speichern.
- Die Methode gibt „true“ zurück, wenn die Initialisierung erfolgreich war.
Diese Methode legt die Parameter und die Struktur fest, mit denen der Algorithmus arbeiten soll, und gewährleistet eine ordnungsgemäße Initialisierung, bevor er mit der Ausführung beginnt.
//—————————————————————————————————————————————————————————————————————————————— // Initialization of the algorithm with the given search parameters bool C_AO_CPA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Calculating the colony size and the number of individuals of each gender Nm = popSize / Nc; fNumber = int(Nm * Fr); if (fNumber < 1) fNumber = 1; mNumber = Nm - fNumber; ArrayResize (aT, Nm); return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_CPA bewegt Agenten im Lösungsraum und passt ihre Koordinaten auf der Grundlage bestimmter Regeln und Zufallsfaktoren an. Schauen wir uns das Ganze Schritt für Schritt an:
Erhöhen der Epoche. Die Methode beginnt mit der Inkrementierung der aktuellen Epoche (epochNow), die anzeigt, dass ein weiterer Schritt im Optimierungs- oder Evolutionsprozess aufgerufen wurde.
Erster Schritt (wenn Revision nicht erforderlich ist) – wenn das Feld „revision“ auf „false“ gesetzt ist, werden die Koordinaten jedes Agenten in der Population (popSize) initialisiert:
- Jeder Agent (a[i]) erhält neue Koordinaten in jeder Dimension (coords) mit Hilfe der Funktion RNDfromCI, die Zufallswerte im angegebenen Bereich [rangeMin[c], rangeMax[c]] erzeugt.
- Die Koordinierung wird dann mit Hilfe der Funktion SeInDiSp geändert, die eine Korrektur der Werte entsprechend dem Diskretisierungsschritt (rangeStep[c]) vornimmt.
- Das Flag „revision“ wird auf „true“ gesetzt und die Methode wird beendet.
- Die Variable k wird als das Verhältnis der verbleibenden Anzahl von Epochen zur Gesamtzahl der Epochen berechnet. Auf diese Weise kann der Bewegungsspielraum der Agenten schrittweise eingegrenzt werden, wenn sich die Optimierung dem Ende nähert.
- Die Kolonien (col) und Funktionen (fNumber) werden iteriert, um die Koordinaten jedes Agenten für die ersten fNumber Agenten in der Kolonie auf der Grundlage ihrer vorherigen Koordinaten (cP) zu aktualisieren, wobei ein Zufallswert hinzugefügt wird, der mit Hilfe einer Normalverteilung (Gauß-Verteilung) erzeugt wird. Dieser Wert wird zwischen rangeMin und rangeMax skaliert.
- Für die verbleibenden Agenten (m von fNumber bis Nm) werden die Koordinaten ebenfalls aktualisiert, aber jetzt werden zufällig ausgewählte Koordinaten eines der besten Agenten in derselben Kolonie verwendet. Zu den Koordinaten jedes Agenten werden Zufallswerte hinzugefügt, wobei der Parameter alpha2 berücksichtigt wird.
- Das übergeordnete Ziel dieser Methode besteht darin, die Agenten auf der Grundlage ihrer vorherigen Position im Lösungsraum zu bewegen und ein Element des Zufalls in die Erkundung des Gebiets einzubringen, um die Wahrscheinlichkeit zu erhöhen, ein globales Optimum zu finden.
- Mit Parametern wie alpha1 und alpha2 lassen sich der Grad der Anpassung und die Zufälligkeit steuern.
Die Methode Moving im Zusammenhang mit dem Optimierungsalgorithmus ist also wichtig, um Agenten im Lösungsraum zu bewegen, wobei sowohl ihre eigenen früheren Positionen als auch die Positionen anderer Agenten berücksichtigt werden.
//—————————————————————————————————————————————————————————————————————————————— // The main function for moving individuals in the search space void C_AO_CPA::Moving () { epochNow++; //---------------------------------------------------------------------------- // Initial random initialization of positions if this is the first iteration if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a random position in a given range a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Calculate the search power decay rate over time double k = (epochs - epochNow)/(double)epochs; int ind = 0; int indF = 0; // Handling each colony for (int col = 0; col < Nc; col++) { // Updating the positions of female individuals (parthenogenesis) for (int f = 0; f < fNumber; f++) { ind = col * Nm + f; for (int c = 0; c < coords; c++) { // Parthenogenetic position update using normal distribution a [ind].c [c] = a [ind].cP [c] + alpha1 * k * u.GaussDistribution (0.0, -1.0, 1.0, 8) * (rangeMax [c] - rangeMin [c]); } } // Update positions of males (mating) for (int m = fNumber; m < Nm; m++) { ind = col * Nm + m; // Select a random female for mating indF = u.RNDintInRange (ind, col * Nm + fNumber - 1); for (int c = 0; c < coords; c++) { // Update position based on the selected female a [ind].c [c] = a [ind].cP [c] + alpha2 * u.RNDprobab () * (a [indF].cP [c] - a [ind].cP [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision der Klasse C_AO_CPA ist für die Aktualisierung des Zustands der Agenten in der Population auf der Grundlage ihrer Werte der Funktion f zuständig. Schauen wir uns das einmal genauer an:
Initialisierung – die Methode beginnt mit der Initialisierung der Variablen „ind“ mit dem Wert „-1“, die dazu verwendet wird, den Index des Agenten mit dem besten Wert der Funktion f zu speichern.
Suche nach dem besten Agenten – in der ersten „for“-Schleife werden alle Agenten in der Population (popSize) durchlaufen, und wenn der Wert der f-Funktion des aktuellen Agenten (a[i].f) größer ist als der aktuelle fB-Bestwert, dann:
- fB wird durch a[i].f aktualisiert.
- Der Index des besten Bearbeiters wird in der Variablen „ind“ gespeichert.
- Wenn nach Abschluss der Schleife ein Agent mit einem besseren Wert (ind != -1) gefunden wurde, werden seine Koordinaten (c) in das Array cB kopiert.
Kopieren der aktuellen Koordinaten. Die zweite „for“-Schleife kopiert die aktuellen Koordinaten (c) der einzelnen Agenten auf ihre vorherigen Koordinaten (cP). Dadurch kann der vorherige Zustand der Agenten für weitere Analysen gespeichert werden.
Sortiermittel. Die dritte „for“-Schleife durchläuft alle Kolonien (Nc), und für jede Kolonie wird die Methode SortFromTo aufgerufen, die die Agenten innerhalb der Kolonie nach ihren Werten der Funktion f sortiert. Der Sortierindex wird berechnet als (ind = col * Nm).
Probabilistische Aktualisierung. Die Methode prüft, ob der von der Funktion u.RNDprobab() erzeugte Zufallswert kleiner ist als der Schwellenwert von Pf:
- Wenn die Bedingung erfüllt ist, werden zwei zufällige Kolonie-Indizes (indCol_1 und indCol_2) ausgewählt, wobei sichergestellt wird, dass sie nicht gleich sind.
- Die Werte der f-Funktion von Agenten in diesen Kolonien werden verglichen. Wenn der Funktionswert in der ersten Kolonie kleiner ist als in der zweiten, werden die Indizes vertauscht.
- Dann werden die Koordinaten des ersten Agenten in der ersten Kolonie auf die Koordinaten des letzten Agenten in der zweiten Kolonie übertragen.
- Danach wird SortFromTo erneut aufgerufen, um die Reihenfolge der Agenten in der zweiten Kolonie zu aktualisieren.
Allgemeine Logik:
Die Revisionsmethode dient der Aktualisierung des Zustands der Agenten, der Speicherung von Informationen über den besten Agenten und der Möglichkeit, Informationen zwischen den Kolonien auszutauschen.
//—————————————————————————————————————————————————————————————————————————————— // Function for revising positions and exchanging information between colonies void C_AO_CPA::Revision () { // Find and update the best solution int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Save the current positions for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY); } // Sort individuals in each colony by the target function value for (int col = 0; col < Nc; col++) { ind = col * Nm; SortFromTo (a, aT, ind, Nm); } // Mechanism of flight (migration) between colonies if (u.RNDprobab () < Pf) { int indCol_1 = 0; int indCol_2 = 0; // Select two random different colonies indCol_1 = u.RNDminusOne (Nc); do indCol_2 = u.RNDminusOne (Nc); while (indCol_1 == indCol_2); // Ensure that the best solution is in the first colony if (a [indCol_1 * Nm].f < a [indCol_2 * Nm].f) { int temp = indCol_1; indCol_1 = indCol_2; indCol_2 = temp; } // Copy the best solution to the worst colony ArrayCopy (a [indCol_2 * Nm + Nm - 1].cP, a [indCol_1 * Nm].cP, 0, 0, WHOLE_ARRAY); // Re-sort the colony after migration SortFromTo (a, aT, indCol_2 * Nm, Nm); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode SortFromTo der Klasse C_AO_CPA dient dazu, ein Array von Bearbeitern auf der Grundlage ihrer Werte der Funktion f zu sortieren. Schauen wir uns das einmal genauer an:
Initialisierung von Variablen:
- Die Methode benötigt drei Parameter: p Array von Agenten, pTemp temporäres Array, „from“ Startindex für die Sortierung und „count“ Anzahl der Elemente für die Sortierung.
- Die Variablen cnt, t0 und t1 werden verwendet, um die Anzahl der Austauschvorgänge zu verfolgen und Werte zwischenzuspeichern.
- Die Arrays ind und val werden erstellt, um die Indizes bzw. Werte der Fitnessfunktion f zu speichern.
Füllen von Arrays mit Indizes und Werten. In der ersten „for“-Schleife werden die Arrays ind und val gefüllt:
- ind[i] liefert den Index des Bearbeiters in der Quellgruppe, beginnend mit „from“.
- val[i] liefert den Wert der Funktion f für den entsprechenden Bearbeiter.
Sortierung. Die „while“-Hauptschleife wird so lange ausgeführt, wie es Austauschvorgänge gibt (d. h. cnt > 0). Die innere „for“-Schleife iteriert durch das val-Array und vergleicht benachbarte Werte:
- Wenn der aktuelle Wert kleiner ist als der nächste (val[i] < val[i + 1]), werden die Indizes im Array ind und die Werte im Array val ausgetauscht.
- Der Zähler cnt wird inkrementiert, um anzuzeigen, dass ein Austausch stattgefunden hat.
- Dieser Prozess wird so lange fortgesetzt, bis eine vollständige Iteration ohne Austausch durchgeführt wurde.
Kopieren der sortierten Werte:
- Nachdem die Sortierung abgeschlossen ist, kopiert die erste „for“-Schleife die sortierten Bearbeiter aus dem temporären pTemp-Array zurück in das ursprüngliche p-Array, beginnend mit dem „from“-Index.
- Die zweite „for“-Schleife aktualisiert das ursprüngliche p-Array und ersetzt es durch die sortierten Werte.
//—————————————————————————————————————————————————————————————————————————————— // Auxiliary function for sorting agents by the value of the objective function void C_AO_CPA::SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count) { int cnt = 1; int t0 = 0; double t1 = 0.0; int ind []; double val []; ArrayResize (ind, count); ArrayResize (val, count); // Copy values for sorting for (int i = 0; i < count; i++) { ind [i] = i + from; val [i] = p [i + from].f; } // Bubble sort in descending order while (cnt > 0) { cnt = 0; for (int i = 0; i < count - 1; i++) { if (val [i] < val [i + 1]) { // Exchange of indices t0 = ind [i + 1]; ind [i + 1] = ind [i]; ind [i] = t0; // Exchange values t1 = val [i + 1]; val [i + 1] = val [i]; val [i] = t1; cnt++; } } } // Apply the sorting results for (int i = 0; i < count; i++) pTemp [i] = p [ind [i]]; for (int i = from; i < from + count; i++) p [i] = pTemp [i - from]; } //——————————————————————————————————————————————————————————————————————————————
Nachdem wir den Code des Algorithmus geschrieben und gründlich analysiert haben, gehen wir zu den Ergebnissen der Prüfung des CPA-Algorithmus über.
Testergebnisse
Als ich die interessante und einzigartige Logik des Algorithmus implementierte, dachte ich nicht einmal daran, dass er es nicht an die Spitze der Rangliste schaffen würde, und es gab eine gewisse Enttäuschung, als ich die Ergebnisse des CPA-Algorithmus-Tests im Detail betrachtete. Ausgehend von den Testergebnissen erzielte der Algorithmus höchstens 34,76 % des maximal möglichen Ergebnisses.
CPA|Cyclic Parthenogenesis Algorithm|50.0|10.0|0.2|0.9|0.3|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7166412833856777
25 Hilly's; Func runs: 10000; result: 0.4001377868508138
500 Hilly's; Func runs: 10000; result: 0.25502012607456315
=============================
5 Forest's; Func runs: 10000; result: 0.6217765628284961
25 Forest's; Func runs: 10000; result: 0.3365148812759322
500 Forest's; Func runs: 10000; result: 0.192638189788532
=============================
5 Megacity's; Func runs: 10000; result: 0.34307692307692306
25 Megacity's; Func runs: 10000; result: 0.16769230769230772
500 Megacity's; Func runs: 10000; result: 0.09455384615384692
=============================
All score: 3.12805 (34.76%)
Die Visualisierung veranschaulicht die für den Algorithmus charakteristische Bewegung der virtuellen Blattläuse im Suchraum. Dies macht sich besonders bei hochdimensionalen Problemen bemerkbar; einzelne Kolonien und die Bewegung virtueller Lebewesen in ihnen können sogar mit dem Auge erkannt werden.
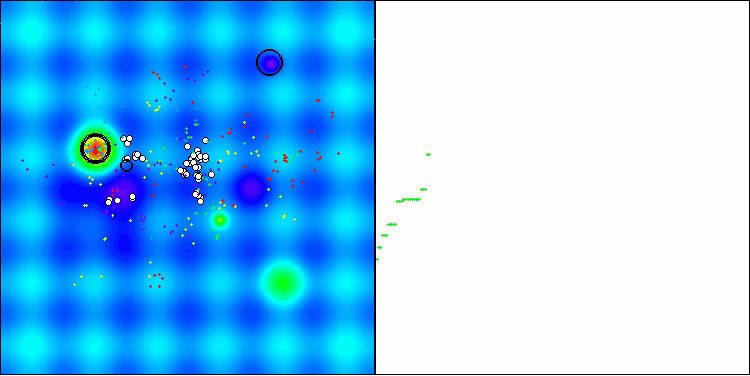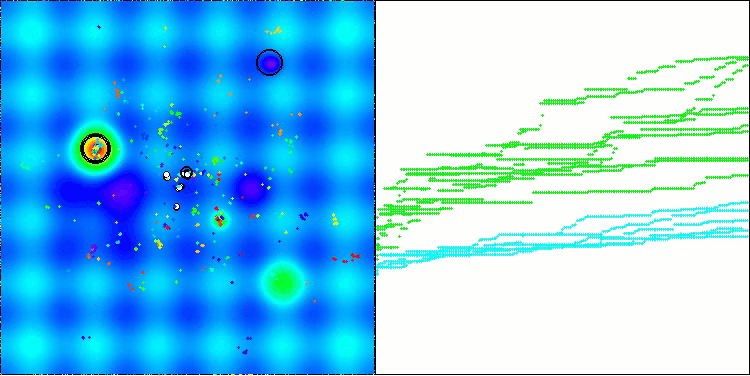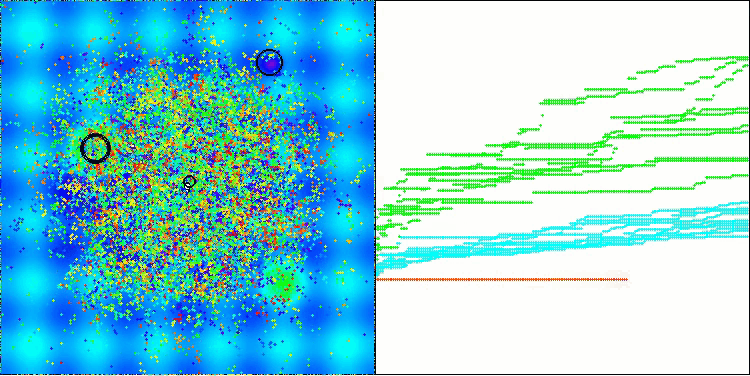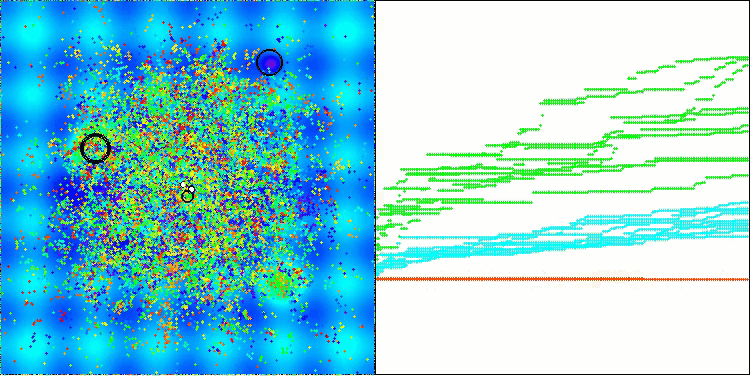
CPA mit der TestfunktionHilly
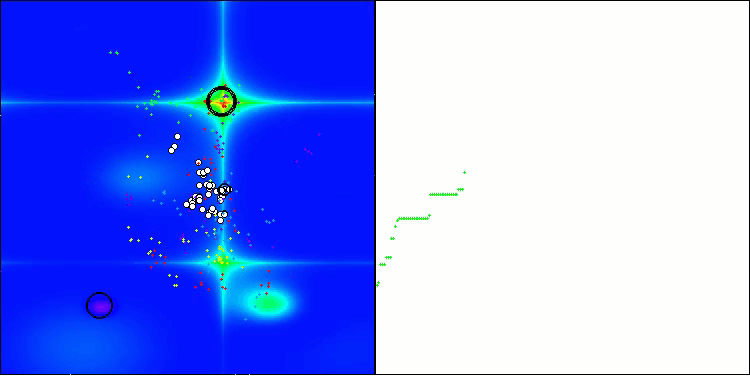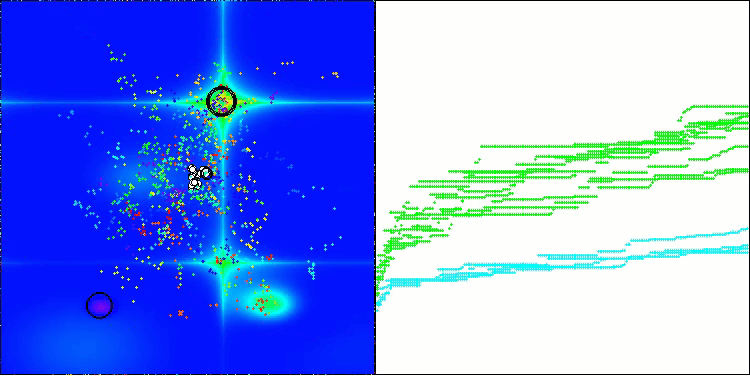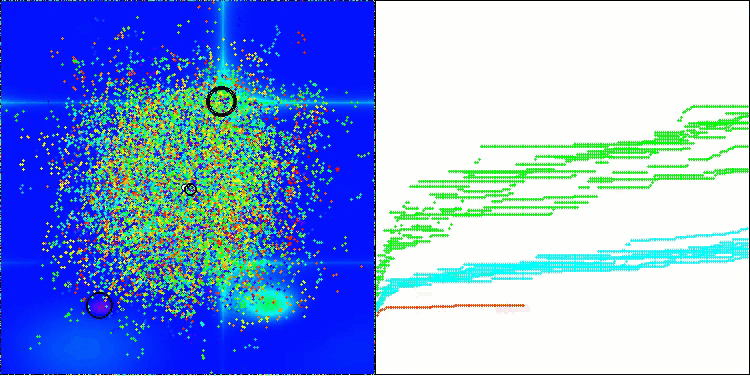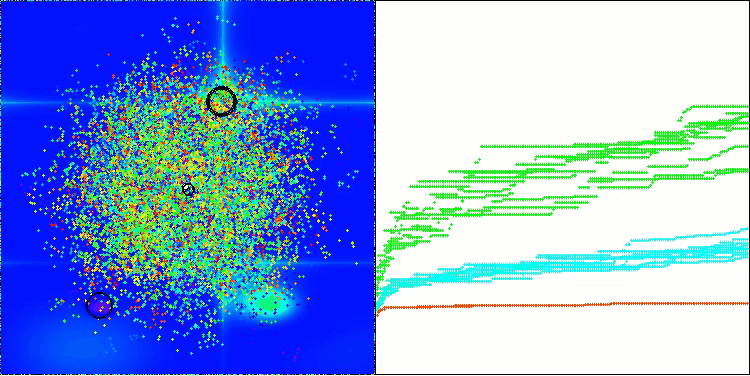
CPA mit der TestfunktionForest

CPA mit der TestfunktionMegacity
Nach den Tests belegte der CPA-Algorithmus den 44. Platz in der Rangliste und wurde in die Gruppe der 45 besten Algorithmen zur Bevölkerungsoptimierung aufgenommen.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 13 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | BBBC | Big-Bang-Big-Crunch-Algorithmus | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1.08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 44 | CPA | Algorithmus für die zyklische Parthenogenese | 0.71664 | 0.40014 | 0.25502 | 1.37180 | 0.62178 | 0.33651 | 0.19264 | 1.15093 | 0.34308 | 0.16769 | 0.09455 | 0.60532 | 3.128 | 34.76 |
| 45 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Die Arbeit an der Implementierung und Erprobung des CPA-Algorithmus hat uns zu interessanten Beobachtungen und Schlussfolgerungen geführt. Bei dem Algorithmus handelt es sich um eine populationsbasierte Optimierungsmethode, die auf dem Verhalten von Blattläusen basiert. Obwohl die Idee an sich vielversprechend erscheint, zeigen die Testergebnisse eine relativ geringe Leistung im Vergleich zu anderen populationsbasierten Algorithmen.
Die Hauptidee des Algorithmus besteht darin, zwei Arten der Fortpflanzung (mit und ohne Paarung) zu verwenden und die Population in Kolonien mit der Möglichkeit der Migration zwischen ihnen zu unterteilen. Die biologische Metapher ist hier recht elegant: Blattläuse nutzen sowohl die Parthenogenese als auch die sexuelle Fortpflanzung, um sich den Umweltbedingungen anzupassen. Die mathematische Umsetzung dieser Konzepte erwies sich jedoch als nicht so effektiv wie gewünscht.
Die Schwächen des Algorithmus zeigen sich in mehreren Aspekten. Erstens bietet die Aufteilung der Individuen einer Population in weibliche und männliche Individuen keine ausreichende Vielfalt und Qualität der Lösungen. Zweitens führt die Aufteilung in Kolonien, obwohl sie die Erkundung verschiedener Regionen des Suchraums erleichtern soll, in der Praxis oft zu einer vorzeitigen Konvergenz zu lokalen Optima. Die Effizienz des Flugmechanismus zwischen den Kolonien, der diesem Effekt entgegenwirken sollte, erwies sich als gering.
Auch die Abstimmung der Algorithmusparameter ist eine nicht triviale Aufgabe. Parameter wie die Koloniegröße (Nm), der Anteil der Weibchen (Fr), die Flugwahrscheinlichkeit (Pf) und die Skalierungsfaktoren (alpha1, alpha2) beeinflussen die Leistung des Algorithmus erheblich, und es ist schwierig, ihre optimalen Werte zu finden. Versuche, den Algorithmus durch die Einführung adaptiver Parameter zu verbessern, führten zwar zu einigen Verbesserungen, konnten aber seine Effizienz nicht wesentlich steigern. Dies deutet darauf hin, dass das Problem möglicherweise grundlegender ist und mit der Struktur des Algorithmus selbst zusammenhängt.
Die Arbeit an diesem Algorithmus war jedoch in mehrfacher Hinsicht nützlich. Erstens hat sie gute Erfahrungen mit der Analyse und Implementierung eines bioinspirierten Algorithmus geliefert. Zweitens half der Prozess der Fehlersuche und Optimierung, die Bedeutung des Gleichgewichts zwischen der Erkundung des Suchraums und der Ausnutzung der gefundenen Lösungen in metaheuristischen Algorithmen besser zu verstehen. Drittens ist dies ein gutes Beispiel dafür, dass sich eine schöne biologische Analogie nicht immer in einen effektiven Optimierungsalgorithmus umsetzen lässt.
Abschließend ist anzumerken, dass selbst die am wenigsten erfolgreichen Algorithmen zur Entwicklung des Bereichs der metaheuristischen Optimierung beitragen, indem sie neue Ideen und Ansätze liefern, die bei der Entwicklung effizienterer Methoden genutzt werden können. Trotz seiner Einschränkungen zeigt CPA einen interessanten Ansatz für die Abwägung zwischen verschiedenen Lösungssuchstrategien und kann als Ausgangspunkt für weitere Forschungen in dieser Richtung dienen.
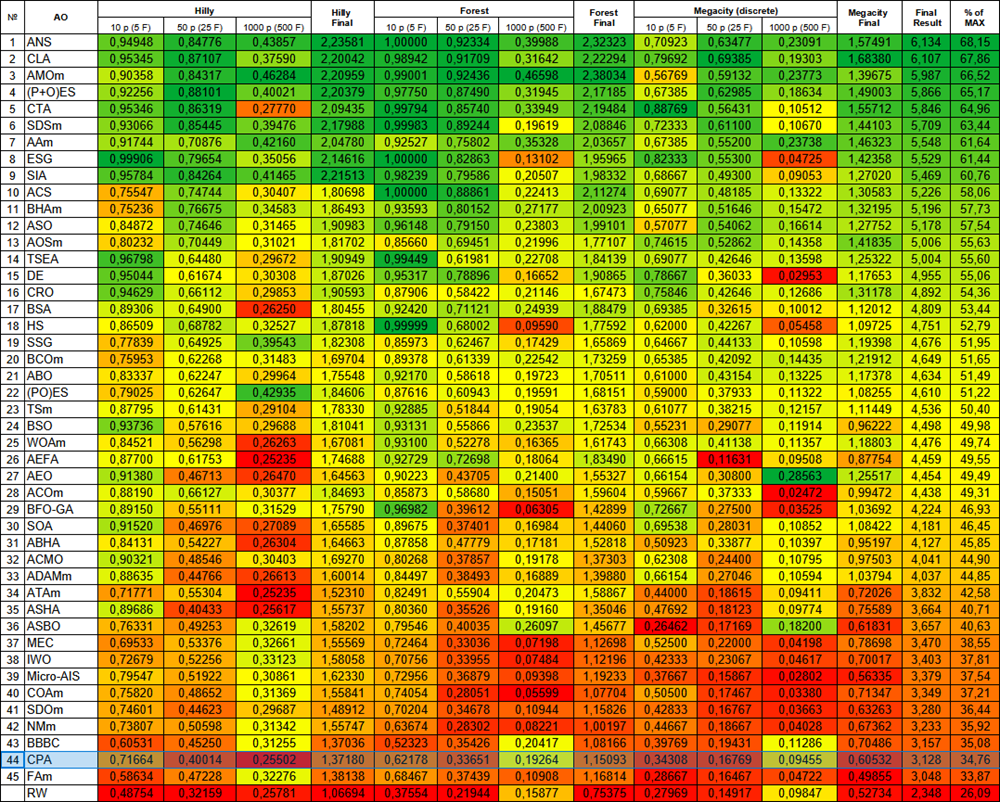
Abbildung 3. Farbabstufung der Algorithmen nach den entsprechenden Tests
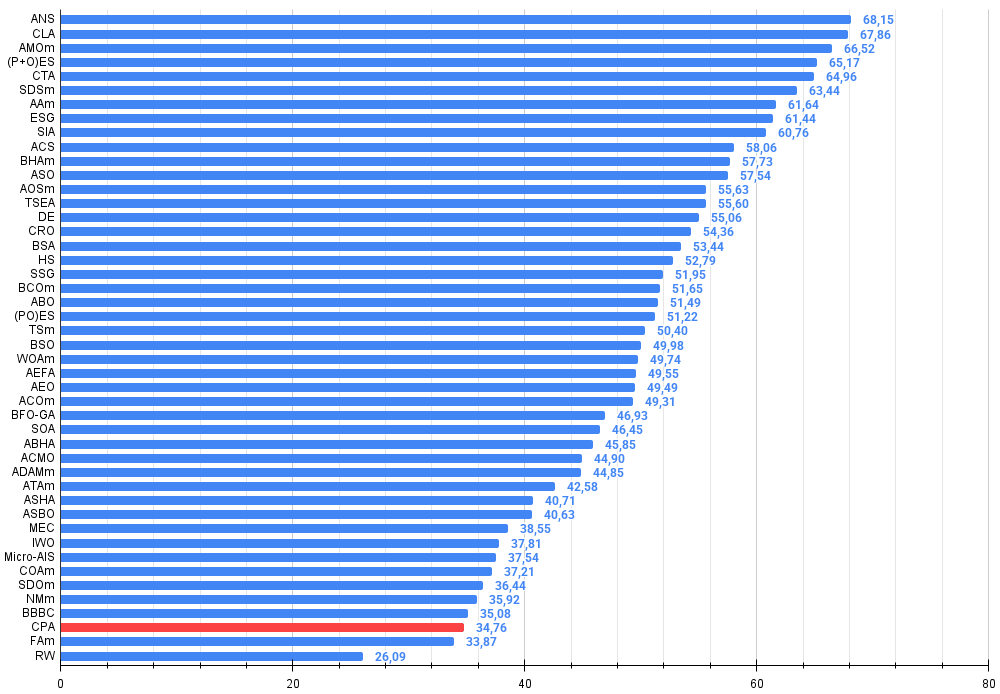
Abbildung 4. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
CPA Vor- und Nachteile:
Vorteile:
- Interessante Idee.
- Eine recht einfache Umsetzung.
- Funktioniert gut bei groß angelegten Problemen.
Nachteile
- Viele externe Parameter.
- Geringe Geschwindigkeit und Konvergenzgenauigkeit.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_CPA.mq5 | Skript | CPA-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16877
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Post-Factum-Handelsanalyse: Auswahl von Trailing-Stops und neuen Stoppstufen im Strategietester
Post-Factum-Handelsanalyse: Auswahl von Trailing-Stops und neuen Stoppstufen im Strategietester
 Evolutionärer Handelsalgorithmus mit Verstärkungslernen und Auslöschung von schwachen Individuen (ETARE)
Evolutionärer Handelsalgorithmus mit Verstärkungslernen und Auslöschung von schwachen Individuen (ETARE)
 Analyse des Binärcodes der Börsenkurse (Teil II): Umwandlung in BIP39 und Schreiben des GPT-Modells
Analyse des Binärcodes der Börsenkurse (Teil II): Umwandlung in BIP39 und Schreiben des GPT-Modells
 Neuronale Netze im Handel: Ein Agent mit geschichtetem Speicher
Neuronale Netze im Handel: Ein Agent mit geschichtetem Speicher
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.