Algorithmen zur Optimierung mit Populationen Grauer-Wolf-Optimierung (GWO)

MetaTrader 5 — Beispiele | 26 Januar 2023, 13:16

448

Andrey Dik

Inhalt

1. Einführung
2. Beschreibung des Algorithmus
3. Testfunktionen
4. Testergebnisse

1. Einführung

Der Graue-Wolf-Algorithmus ist ein metaheuristischer, stochastischer Schwarmintelligenz-Algorithmus, der 2014 entwickelt wurde. Seine Idee basiert auf dem Modell der Jagd auf graue Wolfsrudel. Es gibt vier Arten von Wölfen: Alpha, Beta, Delta und Omega. Der Alpha hat das meiste „Gewicht“ bei der Entscheidungsfindung und der Führung des Rudels. Danach kommen die Beta- und die Delta-Wölfe, die dem Alpha gehorchen und Macht über die übrigen Wölfe haben. Der Omega-Wolf gehorcht immer dem Rest der dominanten Wölfe.

Im mathematischen Modell der Wolfshierarchie wird der Alpha-α-Wolf als der dominante Wolf im Rudel angesehen, und seine Befehle sollten von den Mitgliedern des Rudels ausgeführt werden. Beta-β-untergeordnete Wölfe unterstützen das Alphatier bei der Entscheidungsfindung und gelten als die besten Kandidaten für die Rolle des Alphatiers. Delta-Wölfe δ sollten Alpha und Beta gehorchen und sie beherrschen Omega. Omega ω-Wölfe gelten als die Sündenböcke des Rudels und als die unwichtigsten Individuen. Sie dürfen erst zum Schluss essen. Alpha wird als die günstigste Lösung angesehen.

Die zweit- und drittbeste Lösung sind Beta bzw. Delta. Die übrigen Lösungen gelten als Omega. Es wird davon ausgegangen, dass die fittesten Wölfe (Alpha, Beta und Delta), d. h. diejenigen, die der Beute am nächsten sind, vom Rest der Wölfe angegangen werden. Nach jeder Annäherung wird festgestellt, wer in dieser Phase Alpha, Beta und Delta ist, und dann werden die Wölfe wieder neu geordnet. Die Formation erfolgt so lange, bis sich die Wölfe zu einem Rudel zusammenfinden, das die optimale Richtung für einen Angriff mit minimalem Abstand darstellt.

Während des Algorithmus werden 3 Hauptphasen durchgeführt, in denen die Wölfe nach Beute suchen, sie einkreisen und angreifen. Die Suche ergibt Alpha, Beta und Delta - die Wölfe, die der Beute am nächsten sind. Der Rest, der den dominanten Tieren gehorcht, kann beginnen, die Beute zu einzukreisen oder sich auf der Suche nach der besten Möglichkeit wahllos zu bewegen.

2. Beschreibung des Algorithmus

Die Hierarchie im Paket ist in Abbildung 1 schematisch dargestellt. Alpha spielt eine dominante Rolle.

Dominanz

Abb. 1. Soziale Hierarchie in einem Wolfsrudel

Mathematisches Modell und Algorithmus
Soziale Hierarchie:

Die beste Lösung in Form eines Alpha-Wolfs (α).
Die zweitbeste Lösung als Beta-Wolf (β).
Die drittbeste Lösung als Delta-Wolf (δ).
Andere mögliche Lösungen als Omega-Wölfe (ω).

Einkreisen der Beute: Wenn es bereits die besten Alpha-, Beta- und Delta-Lösungen gibt, hängen die weiteren Aktionen von Omega ab.

Phasen

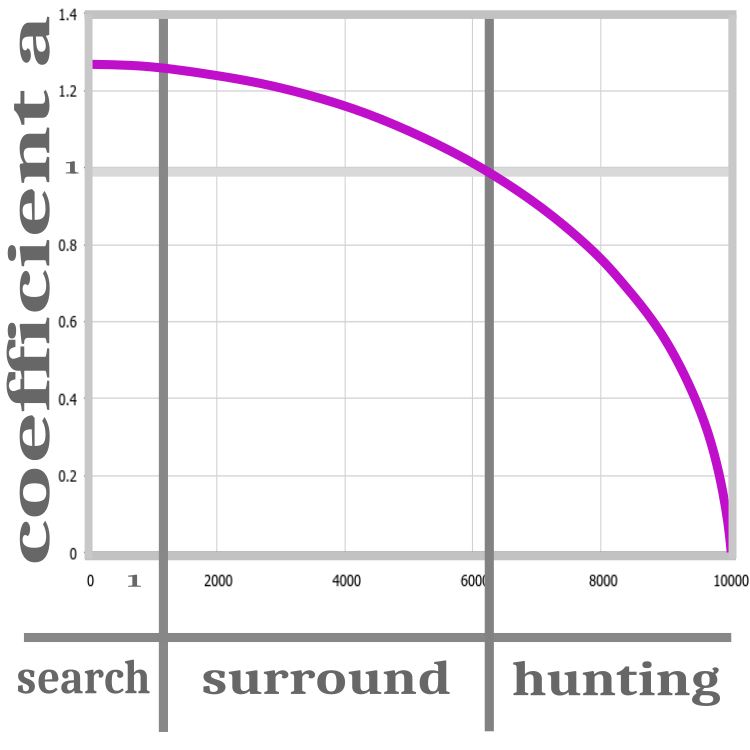
Abb. 2. Jagdphasen: Suche, Einkreisung, Angriff.

Alle Iterationen des Algorithmus werden durch drei Phasen dargestellt: Suche, Umkreisung und Jagd. Die kanonische Version des Algorithmus zeichnet sich durch einen Koeffizienten а aus, der zur Verbesserung der Konvergenz des Algorithmus eingeführt wurde. Der Koeffizient sinkt bei jeder Iteration auf Null. Solange der Koeffizient über 1 liegt, werden die Wölfe initialisiert. In dieser Phase ist die Position der Beute völlig unbekannt, sodass die Wölfe nach dem Zufallsprinzip verteilt werden sollten.

Nach der „Suchphase“ wird der Wert der Fitnessfunktion bestimmt, und erst dann kann man zur „Einkreisungsphase“ übergehen. In dieser Phase ist der Koeffizient a größer als 1. Dies bedeutet, dass sich Alpha, Beta und Delta von ihren vorherigen Positionen entfernen und somit die Position der geschätzten Beute verfeinert werden kann. Wenn der Koeffizient а gleich 1 wird, beginnt die „Angriffsphase“, während der Koeffizient vor dem Ende der Iterationen gegen 0 tendiert. Dies veranlasst die Wölfe, sich der Beute zu nähern, was darauf hindeutet, dass die beste Position bereits gefunden wurde. Wenn in dieser Phase einer der Wölfe eine bessere Lösung findet, werden zwar die Position der Beute und die Hierarchie der Wölfe aktualisiert, aber der Koeffizient tendiert weiterhin gegen 0. Der Prozess der Veränderung von a wird durch eine nichtlineare Funktion dargestellt. Die Phasen sind in Abbildung 2 schematisch dargestellt.

Das Verhalten der Omega-Wölfe ist in allen Epochen unverändert und besteht darin, der geometrischen Mitte zwischen den Positionen der derzeit dominanten Individuen zu folgen. In Abbildung 3 weichen Alpha, Beta und Delta von ihrer vorherigen Position in einer zufälligen Richtung mit einem Radius ab, der durch die Koeffizienten gegeben ist, und Omegas bewegen sich zur Mitte zwischen ihnen, weichen aber mit einer gewissen Wahrscheinlichkeit innerhalb des Radius von ihr ab. Die Radien bestimmen den Koeffizienten а, der sich, wie wir uns erinnern, ändert, wodurch die Radien proportional abnehmen.

Einkreisen

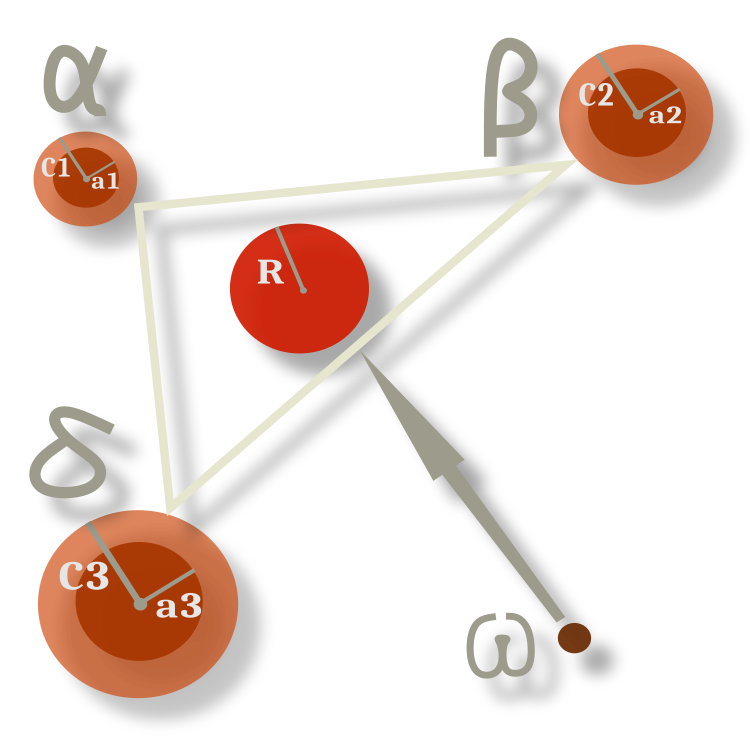
Abb. 3. Diagramm der Omega-Bewegung im Verhältnis zu Alpha, Beta und Delta

Der Pseudocode des GWO-Algorithmus lautet wie folgt:

1) Initialisieren der Population der Grauen Wölfe nach dem Zufallsprinzip.
2) Berechnen der Fitness der einzelnen Mitglieder der Population.
3) Rudelführer:
-α = Mitglied mit dem besten Fitnesswert
-β = zweitbestes Mitglied (in Bezug auf die Fitness)
-δ = drittbestes Mitglied (in Bezug auf den Fitnesswert)
Aktualisierung der Position aller Omega-Wölfe gemäß den Gleichungen, die von α, β, δ abhängen
4) Berechnen der Fitness der einzelnen Mitglieder der Population.
5) Schritt 3 wiederholen.

Kommen wir nun zum Algorithmus selbst. Die einzige Ergänzung, die ich gegenüber der ursprünglichen Version vorgenommen habe, ist die Möglichkeit, die Anzahl der Leitwölfe im Rudel festzulegen. Jetzt können wir eine beliebige Anzahl von Anführern festlegen, bis hin zum gesamten Rudel. Dies kann für bestimmte Aufgaben nützlich sein.

Wir beginnen, wie üblich, mit der elementaren Einheit des Algorithmus - dem Wolf, der eine Lösung des Problems darstellt. Dies ist eine Struktur, die eine Reihe von Koordinaten und einen Beutewert (Fitnessfunktionen) enthält. Die Struktur ist für Anführer und untergeordnete Mitglieder des Rudels gleich. Dies vereinfacht den Algorithmus und ermöglicht es uns, dieselben Strukturen in den Schleifenoperationen zu verwenden. Außerdem wechseln die Rollen der Wölfe während aller Iterationen mehrmals. Die Rollen sind eindeutig durch die Position im Array nach der Sortierung bestimmt. Die Anführer stehen am Anfang der Reihe.

//——————————————————————————————————————————————————————————————————————————————
struct S_Wolf
{
  double c []; //coordinates
  double p;    //prey
};
//——————————————————————————————————————————————————————————————————————————————

Das Wolfsrudel wird durch eine kompakte und verständliche Klasse repräsentiert. Hier geben wir die Bereiche und den Schritt der zu optimierenden Parameter, die beste Produktionsposition, den besten Lösungswert und Hilfsfunktionen an.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO //wolfpack
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Wolf wolves    []; //wolves of the pack
  public: double cB        []; //best prey coordinates
  public: double pB;           //best prey

  public: void InitPack (const int    coordinatesP,   //number of opt. parameters
                         const int    wolvesNumberP,  //wolves number
                         const int    alphaNumberP,   //alpha beta delta number
                         const int    epochCountP);   //epochs number

  public: void TasksForWolves      (int epochNow);
  public: void RevisionAlphaStatus ();


  //============================================================================
  private: void   ReturnToRange (S_Wolf &wolf);
  private: void   SortingWolves ();
  private: double SeInDiSp      (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI     (double Min, double Max);

  private: int    coordinates;     //coordinates number
  private: int    wolvesNumber;    //the number of all wolves
  private: int    alphaNumber;     //Alpha beta delta number of all wolves
  private: int    epochCount;

  private: S_Wolf wolvesT    [];   //temporary, for sorting
  private: int    ind        [];   //array for indexes when sorting
  private: double val        [];   //array for sorting

  private: bool   searching;       //searching flag
};
//——————————————————————————————————————————————————————————————————————————————

Traditionell folgt auf die Klassendeklaration die Initialisierung. Hier setzen wir auf den minimalen „double“ Wert der Fitness der Wölfe zurück und verteilen die Größe der Felder.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO::InitPack (const int    coordinatesP,   //number of opt. parameters
                         const int    wolvesNumberP,  //wolves number
                         const int    alphaNumberP,   //alpha beta delta number
                         const int    epochCountP)    //epochs number
{
  MathSrand (GetTickCount ());
  searching = false;
  pB        = -DBL_MAX;

  coordinates  = coordinatesP;
  wolvesNumber = wolvesNumberP;
  alphaNumber  = alphaNumberP;
  epochCount   = epochCountP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (ind, wolvesNumber);
  ArrayResize (val, wolvesNumber);

  ArrayResize (wolves,  wolvesNumber);
  ArrayResize (wolvesT, wolvesNumber);

  for (int i = 0; i < wolvesNumber; i++)
  {
    ArrayResize (wolves  [i].c, coordinates);
    ArrayResize (wolvesT [i].c, coordinates);
    wolves  [i].p = -DBL_MAX;
    wolvesT [i].p = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die erste öffentliche Methode, die bei jeder Iteration aufgerufen wird, ist am schwierigsten zu verstehen und am umfangreichsten. Hier ist die Hauptlogik des Algorithmus. Die Leistung des Algorithmus wird nämlich durch einen probabilistischen Mechanismus gewährleistet, der streng durch Gleichungen beschrieben wird. Gehen wir diese Methode Schritt für Schritt durch. Bei der ersten Iteration, wenn die Position der beabsichtigten Beute unbekannt ist, schicken wir die Wölfe nach der Überprüfung der Flag in eine zufällige Richtung, indem wir einfach Werte aus den Maximal- und Minimalwerten der optimierten Parameter generieren.

//----------------------------------------------------------------------------
//space has not been explored yet, then send the wolf in a random direction
if (!searching)
{
  for (int w = 0; w < wolvesNumber; w++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      wolves [w].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      wolves [w].c [c] = SeInDiSp  (wolves [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
   
  searching = true;
  return;
}

In der kanonischen Version der Algorithmusbeschreibung gibt es Gleichungen, die mit Vektoren arbeiten. In Codeform sind sie jedoch viel deutlicher. Die Berechnung der Omega-Wölfe wird vor der Berechnung der Alpha-, Beta- und Delta-Wölfe durchgeführt, da wir die vorherigen Leader-Werte verwenden müssen.

Die Hauptkomponente, die die drei Phasen der Jagd (Suchen, Einkreisen und Angriff) ermöglicht, ist der Koeffizient a. Er stellt eine nichtlineare Abhängigkeit von der aktuellen Iteration und der Gesamtzahl der Iterationen dar und tendiert gegen 0.
Die nächsten Komponenten der Gleichung sind Ai und Сi:

Ai = 2,0 * a * r1 - a;
Ci = 2,0 * r2;

wobei r1 und r2 Zufallszahlen im Bereich [0,0;1,0] sind.
In dem Ausdruck

Xn += wolves [abd].c [c] - Ai * (Ci * wolves [abd].c [c] - wolves [w].c [c]);

werden die Koordinaten der Wölfe entsprechend den Durchschnittswerten der Leitwölfe angepasst. Da in dem Algorithmus eine beliebige Anzahl von Anführern angegeben werden kann, wird die Summierung der Koordinaten in einer Schleife durchgeführt. Anschließend wird der sich ergebende Betrag durch die Anzahl der Anführer geteilt. Wir führen diesen Vorgang für jede Koordinate separat durch, wobei jedes Mal neue Werte für r1 und r2 erzeugt werden. Wie wir sehen können, wird die neue Position der Omega-Wölfe entsprechend den Positionen der Anführer unter Berücksichtigung ihrer eigenen aktuellen Position angepasst.

//----------------------------------------------------------------------------
double a  = sqrt (2.0 * (1.0 - (epochNow / epochCount)));
double r1 = 0.0;
double r2 = 0.0;

double Ai = 0.0;
double Ci = 0.0;
double Xn = 0.0;

double min = 0.0;
double max = 1.0;

//omega-----------------------------------------------------------------------
for (int w = alphaNumber; w < wolvesNumber; w++)
{
  Xn = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    for (int abd = 0; abd < alphaNumber; abd++)
    {
      r1 = RNDfromCI (min, max);
      r2 = RNDfromCI (min, max);
      Ai = 2.0 * a * r1 - a;
      Ci = 2.0 * r2;
      Xn += wolves [abd].c [c] - Ai * (Ci * wolves [abd].c [c] - wolves [w].c [c]);
    }

    wolves [w].c [c] = Xn /= (double)alphaNumber;
  }

  ReturnToRange (wolves [w]);
}

Hier werden die Anführer berechnet. Für sie werden die Koeffizienten a, Ai und Ci für jede Koordinate berechnet. Der einzige Unterschied besteht darin, dass sich die Position der Anführer im Verhältnis zu den besten Beutekoordinaten zum aktuellen Zeitpunkt und ihren eigenen Positionen ändert. Die Anführer kreisen die Beute ein, bewegen sich nach innen und außen und kontrollieren die kleineren Wölfe bei ihrem Angriff.

//alpha, beta, delta----------------------------------------------------------
for (int w = 0; w < alphaNumber; w++)
{
  for (int c = 0; c < coordinates; c++)
  {
    r1 = RNDfromCI (min, max);
    r2 = RNDfromCI (min, max);

    Ai = 2.0 * a * r1 - a;
    Ci = 2.0 * r2;

    wolves [w].c [c] = cB [c] - Ai * (Ci * cB [c] - wolves [w].c [c]);
  }

  ReturnToRange (wolves [w]);
}

Dies ist die zweite öffentliche Methode, die bei jeder Iteration aufgerufen wird. Der Status der Führenden im Rudel wird hier aktualisiert. Die Wölfe sind nämlich nach ihrem Fitnesswert sortiert. Wenn bessere Beutekoordinaten als die im Schwarm gespeicherten gefunden werden, aktualisieren wir die Werte.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO::RevisionAlphaStatus ()
{
  SortingWolves ();

  if (wolves [0].p > pB)
  {
    pB = wolves [0].p;
    ArrayCopy (cB, wolves [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testfunktionen

Sie kennen bereits die Funktionen Skin, Forest und Megacity. Diese Testfunktionen erfüllen alle Komplexitätskriterien für das Testen von Optimierungsalgorithmen. Es gibt jedoch eine Besonderheit, die nicht berücksichtigt wurde. Sie sollte eingeführt werden, um die Objektivität der Prüfung zu erhöhen. Die Anforderungen sind wie folgt:

Das globale Extremum sollte nicht an den Grenzen des Bereichs liegen. Verfügt der Algorithmus nicht über eine Bereichsüberschreitungsprüfung, sind Situationen möglich, in denen der Algorithmus hervorragende Ergebnisse liefert. Dies ist darauf zurückzuführen, dass die Werte aufgrund eines internen Fehlers an den Rändern liegen werden.
Das globale Extremum sollte nicht in der Mitte der Koordinaten des Bereichs liegen. In diesem Fall wird der Algorithmus, der in einem Bereich gemittelte Werte erzeugt, berücksichtigt.
Das globale Minimum sollte sich in der Mitte der Koordinaten befinden. Dies ist notwendig, um die auf S. 2 beschriebenen Situationen bewusst auszuschließen.
Bei der Berechnung der Ergebnisse der Testfunktion sollte der Fall berücksichtigt werden, dass zufällig erzeugte Zahlen über den gesamten Bereich der Funktion (wenn es sich um eine multivariable Funktion handelt) ein durchschnittliches Ergebnis von etwa 50 % des Maximums ergeben, obwohl diese Ergebnisse tatsächlich zufällig erzielt wurden.

Unter Berücksichtigung dieser Anforderungen wurden die Grenzen der Testfunktionen überarbeitet und die Mittelpunkte des Bereichs auf die Minima der Funktionswerte verschoben. Fassen wir noch noch einmal zusammen. Dies war notwendig, um eine größtmögliche Plausibilität und Objektivität der Ergebnisse der Testoptimierungsalgorithmen zu erreichen. Daher zeigte der Optimierungsalgorithmus, der auf der Erzeugung von Zufallszahlen basiert, bei neuen Testfunktionen ein natürlich niedriges Gesamtergebnis. Die aktualisierte Bewertungstabelle befindet sich am Ende des Artikels.

Die Skin-Funktion. Eine glatte Funktion, die mehrere lokale Extrema aufweist, die den Optimierungsalgorithmus verwirren können, da er in einem von ihnen stecken bleiben kann. Das einzige globale Extremum ist durch schwach wechselnde Werte in der Umgebung gekennzeichnet. Diese Funktion zeigt deutlich, dass der Algorithmus in verschiedene Bereiche unterteilt werden kann, anstatt sich auf einen einzigen Bereich zu konzentrieren. Insbesondere der Bienenvolk-Algorithmus (ABC) verhält sich auf diese Weise.

Skin

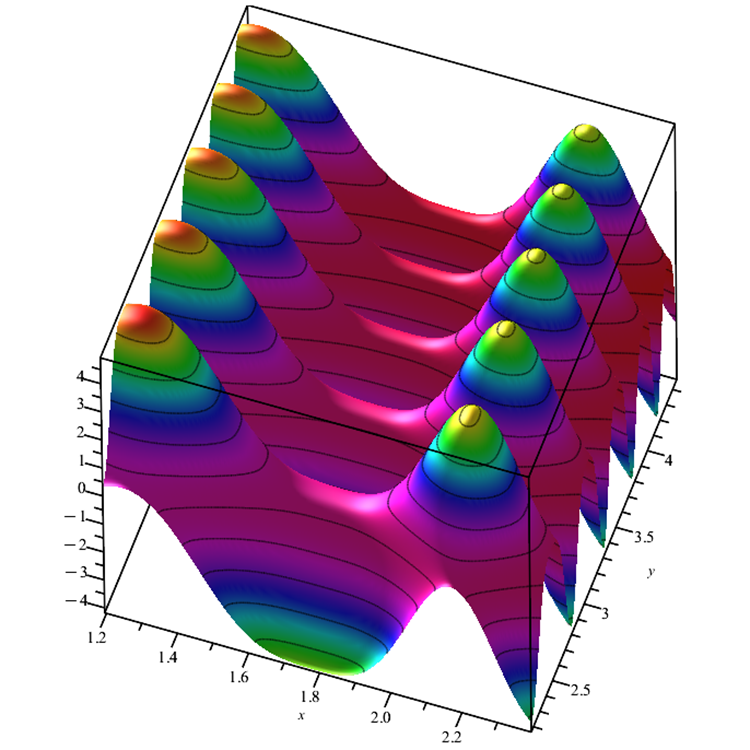
Abb. 4. Funktion des Skin-Tests

Die Forest-Funktion. Eine Funktion mit mehreren glatten und mehreren nicht-differenzierbaren Extrema. Dies ist ein wertvoller Test für Optimierungsalgorithmen, um eine „Nadel im Heuhaufen“ zu finden. Die Suche nach einem einzigen globalen Maximalpunkt ist eine sehr schwierige Aufgabe, insbesondere wenn die Funktion viele Variablen enthält. Der Ameisenkolonie-Algorithmus (ACO) zeichnet sich bei dieser Aufgabe durch das charakteristische Verhalten aus, das auf unglaubliche Weise Wege zum Ziel bahnt.

Forest

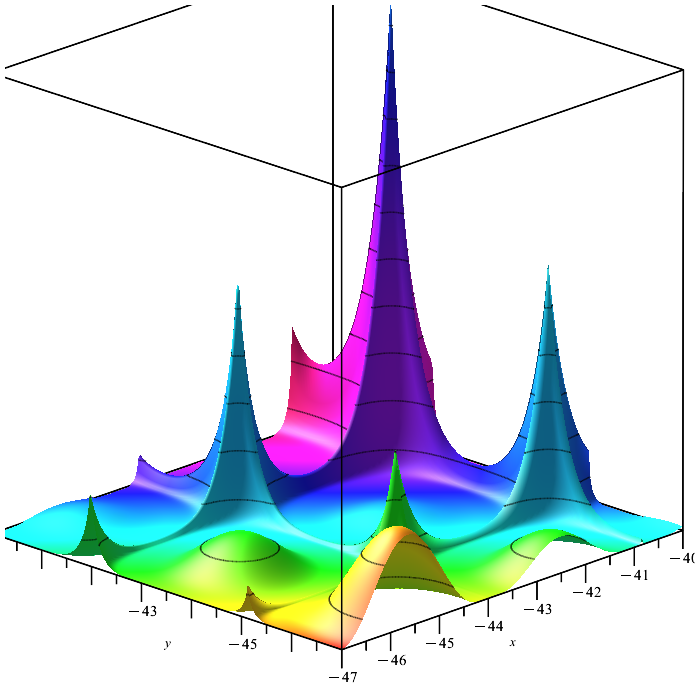
Abbildung 5, Testfunktion von Forest

Die Megacity-Funktion. Die Funktion ist ein diskretes Optimierungsproblem mit einem globalen und mehreren lokalen Extrema. Die extrem komplexe Oberfläche bietet einen guten Test für Algorithmen, die einen Gradienten benötigen. Eine zusätzliche Komplexität wird durch einen völlig ebenen „Boden“ hinzugefügt, der ebenfalls ein Minimum ist, das keine Informationen über die mögliche Richtung zum globalen Maximum gibt.

Megacity

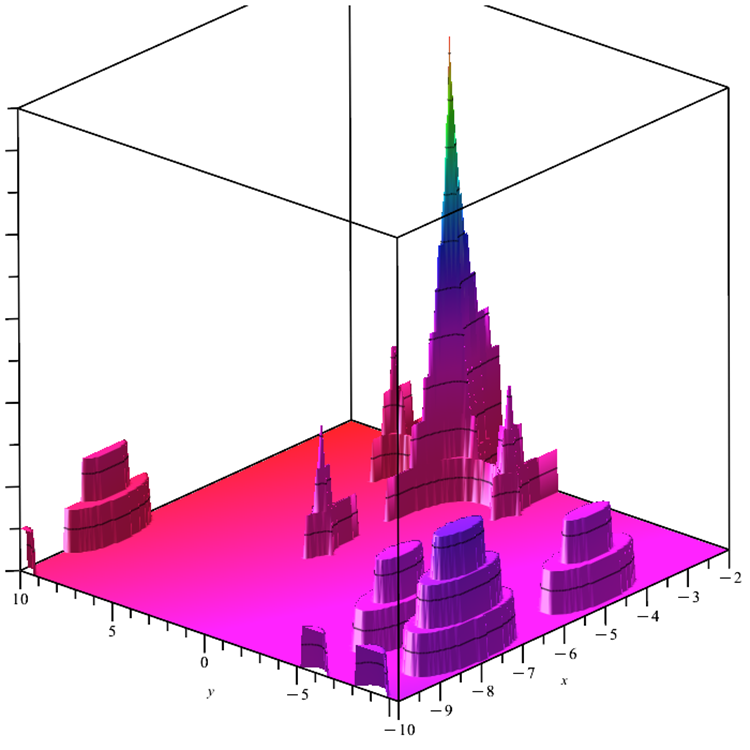
Abbildung 6, Testfunktion von Megacity

Der Code der Testfunktionen wurde um Überprüfungen der eingehenden Argumente auf Werte außerhalb des zulässigen Bereichs erweitert. In den früheren Versionen der Funktionen konnten Optimierungsalgorithmen auf unfaire Weise Funktionswerte erhalten, die größer waren als die tatsächlichen Werte der Funktion innerhalb ihres Definitionsbereichs.

4. Testergebnisse

Aufgrund der Änderungen der Prüffunktionen wurde auch der Prüfstand aktualisiert. Auf der rechten Seite des Standbildschirms sind weiterhin die Konvergenzkurven der Optimierungsalgorithmen zu sehen. Die grüne Linie steht für die Ergebnisse der Konvergenz bei Funktionen mit zwei Variablen. Die blaue Linie steht für die Funktionen mit 40 Variablen. Die rote Farbe steht für Funktionen mit 1000 Variablen. Der größere schwarze Kreis zeigt die Position des globalen Maximums der Funktion an. Der kleinere schwarze Kreis zeigt die Position des aktuellen Lösungswertes des Optimierungsalgorithmus an. Das Fadenkreuz aus weißen Linien zeigt den geometrischen Mittelpunkt der Testfunktionen und entspricht dem globalen Minimum. Dies wurde eingeführt, um das Verhalten der getesteten Algorithmen besser sichtbar zu machen. Die weißen Punkte zeigen gemittelte Zwischenlösungen an. Farbige kleine Punkte kennzeichnen Koordinatenpaare der entsprechenden Dimension. Die Farbe gibt die ordinale Position der Dimension der Testfunktion an.

Die aktualisierten Ergebnisse der Tests der in früheren Artikeln besprochenen Optimierungsalgorithmen auf dem neuen Stand sind in der aktualisierten Tabelle zu sehen. Für mehr visuelle Klarheit wurde die Zeile über die Konvergenzgeschwindigkeit aus der Tabelle entfernt - sie kann auf der Animation des Standes visuell bestimmt werden. Die Spalte mit der Algorithmusbeschreibung wurde hinzugefügt.

ACO (Ant Colony Optimization) Testergebnisse:

2022.11.28 12:17:00.468 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:17:06.382    Test_AO_ABCm (EURUSD,M1)    1 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.844203223078298
2022.11.28 12:17:06.382 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.98229.
2022.11.28 12:17:14.191    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.043383610736287
2022.11.28 12:17:14.191 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.79108.
2022.11.28 12:17:55.578    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.2580170651681026
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.12602.
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:18:01.491    Test_AO_ABCm (EURUSD,M1)    1 Forests; Funktionsdurchläufe 10000 Ergebnis: 1.7678766100234538
2022.11.28 12:18:01.491 Test_AO_ACO (EURUSD,M1) Ergebnis: 1.00000
2022.11.28 12:18:09.508    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 1.0974381500585855
2022.11.28 12:18:09.508 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.62077.
2022.11.28 12:18:53.348    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.20367726028454042
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.11521.
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:18:59.303    Test_AO_ABCm (EURUSD,M1)    1 Megacity; Funktionsdurchläufe 10000 Ergebnis: 4.6
2022.11.28 12:18:59.303 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.38333.
2022.11.28 12:19:07.598 Test_AO_ACO (EURUSD,M1) 20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 5.28.
2022.11.28 12:19:07.598 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.44000.
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) 500 Megacities; Funktionsdurchläufe 10000 Ergebnis: 0.2852.
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) Ergebnis: 0.02377.
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:19:53.172    Test_AO_M1 (EURUSD,M1)    Alle Ergebnisse für C_AO_ABC: 0.4980520084646583

ABCm (Künstliches Bienenvolk) Testergebnisse:

2022.11.28 12:35:47.181    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.28 12:35:52.581    Test_AO_ABCm (EURUSD,M1)    1 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.918379986612587
2022.11.28 12:35:52.581    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 1.00000
2022.11.28 12:35:59.454    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 3.4073825805846374
2022.11.28 12:35:59.454    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.63922.
2022.11.28 12:36:32.428    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.0684464927353337
2022.11.28 12:36:32.428    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.08076
2022.11.28 12:36:32.428    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.28 12:36:38.086    Test_AO_ABCm (EURUSD,M1)    1 Forest; Funktionsdurchläufe 10000 Ergebnis: 1.766245456669898
2022.11.28 12:36:38.086    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.99908.
2022.11.28 12:36:45.326    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.35556125136004335
2022.11.28 12:36:45.326    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.20112
2022.11.28 12:37:22.301    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.06691711149962026
2022.11.28 12:37:22.301    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.03785.
2022.11.28 12:37:22.301    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.28 12:37:28.047    Test_AO_ABCm (EURUSD,M1)    1 Megacity; Funktionsdurchläufe 10000 Ergebnis: 12.0.
2022.11.28 12:37:28.047    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 1.00000
2022.11.28 12:37:35.689    Test_AO_ABCm (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 1.9600000000000002
2022.11.28 12:37:35.689    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.16333.
2022.11.28 12:38:11.609    Test_AO_ABCm (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 10000 Ergebnis: 0.33880000000000005
2022.11.28 12:38:11.609    Test_AO_ABCm (EURUSD,M1)    Ergebnis1: 0.02823.
2022.11.28 12:38:11.609    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.28 12:38:11.609    Test_AO_ABCm (EURUSD,M1)    All score for C_AO_ABCm: 0.4610669021761763

ABC (Artificial Bee Colony) Testergebnisse:

2022.11.28 12:29:51.177 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:29:56.785    Test_AO_ABCm (EURUSD,M1)    1 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.890679983950205
2022.11.28 12:29:56.785 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.99339.
2022.11.28 12:30:03.880    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 3.8035430744604133
2022.11.28 12:30:03.880 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.73381.
2022.11.28 12:30:37.089    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.195840100227333
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.11118.
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:30:42.811    Test_AO_ABCm (EURUSD,M1)    1 Forests; Funktionsdurchläufe 10000 Ergebnis: 1.7667070507449298
2022.11.28 12:30:42.811 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.99934.
2022.11.28 12:30:50.108    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.3789854806095275
2022.11.28 12:30:50.108 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.21437.
2022.11.28 12:31:25.900    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.07451308481273813
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.04215.
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:31:31.510    Test_AO_ABCm (EURUSD,M1)    1 Megacities; Funktionsdurchläufe 10000 Ergebnis: 10.2
2022.11.28 12:31:31.510 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.85000.
2022.11.28 12:31:38.855    Test_AO_ABCm (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 2.02
2022.11.28 12:31:38.855 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.16833.
2022.11.28 12:32:14.623    Test_AO_ABCm (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 10000 Ergebnis: 0.37559999999999993
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) Ergebnis: 0.03130.
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:32:14.623    Test_AO_M1 (EURUSD,M1)    All score for C_AO_ABC: 0.46043003186219245

PSO (Partikelschwarm-Optimierung) Testergebnisse

2022.11.28 12:01:03.967 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:01:09.723    Test_AO_ABCm (EURUSD,M1)    1 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.90276049713715
2022.11.28 12:01:09.723 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.99627.
2022.11.28 12:01:17.064    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 2.3250668562024566
2022.11.28 12:01:17.064 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.38080.
2022.11.28 12:01:52.880    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 0.943331687769892
2022.11.28 12:01:52.881 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.05089.
2022.11.28 12:01:52.881 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:01:58.492    Test_AO_ABCm (EURUSD,M1)    1 Forests; Funktionsdurchläufe 10000 Ergebnis: 1.6577769478566602
2022.11.28 12:01:58.492 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.93772.
2022.11.28 12:02:06.105    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.25704414127018393
2022.11.28 12:02:06.105 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.14540.
2022.11.28 12:02:44.566    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.08584805450831333
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.04856.
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:02:50.268    Test_AO_ABCm (EURUSD,M1)    1 Megacities; Funktionsdurchläufe 10000 Ergebnis: 12.0.
2022.11.28 12:02:50.268 Test_AO_PSO (EURUSD,M1) Ergebnis: 1.00000
2022.11.28 12:02:57.649 Test_AO_PSO (EURUSD,M1) 20 Megacity's; Func läuft 10000 Ergebnis: 1.1199999999999999
2022.11.28 12:02:57.649 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.09333.
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) 500 Megacity's; Func läuft 10000 Ergebnis: 0.268
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) Ergebnis: 0.02233.
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) Alle Ergebnisse für C_AO_PSO: 0.40836715689743186

RND (Random) Testergebnisse:

2022.11.28 16:45:15.976 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:45:21.569    Test_AO_ABCm (EURUSD,M1)    1 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.915522750114194
2022.11.28 16:45:21.569 Test_AO_RND (EURUSD,M1) Ergebnis: 0.99932.
2022.11.28 16:45:28.607    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 2.584546688199847
2022.11.28 16:45:28.607 Test_AO_RND (EURUSD,M1) Ergebnis: 0.44276.
2022.11.28 16:46:02.695    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.0161336237263792
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) Ergebnis: 0.06827.
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:46:09.622    Test_AO_ABCm (EURUSD,M1)    1 Forests; Funktionsdurchläufe 10000 Ergebnis: 1.4695680943894533
2022.11.28 16:46:09.622 Test_AO_RND (EURUSD,M1) Ergebnis: 0.83126.
2022.11.28 16:46:17.675    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.20373533112604475
2022.11.28 16:46:17.675 Test_AO_RND (EURUSD,M1) Ergebnis: 0.11524.
2022.11.28 16:46:54.544    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.0538909816827325
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) Ergebnis: 0.03048.
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:47:00.219    Test_AO_ABCm (EURUSD,M1)    1 Megacities; Funktionsdurchläufe 10000 Ergebnis: 10.0.
2022.11.28 16:47:00.219 Test_AO_RND (EURUSD,M1) Ergebnis: 0.83333.
2022.11.28 16:47:08.145    Test_AO_ABCm (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 1.08
2022.11.28 16:47:08.145 Test_AO_RND (EURUSD,M1) Ergebnis: 0.09000.
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) 500 Megacity's; Func läuft 10000 Ergebnis: 0.28840000000000005
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) Ergebnis: 0.02403.
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) Alle Ergebnisse für C_AO_RND: 0.38163317904126015

Skin

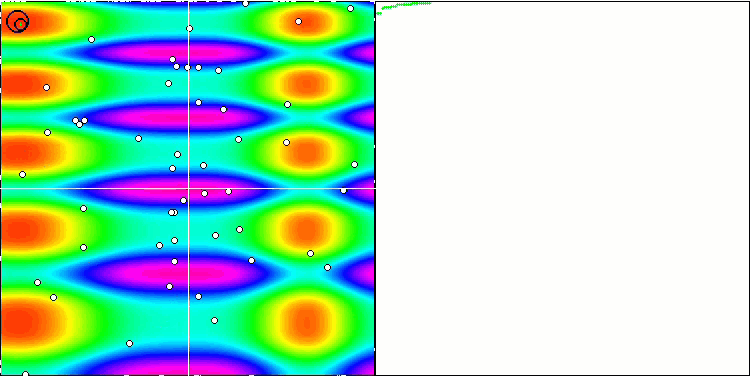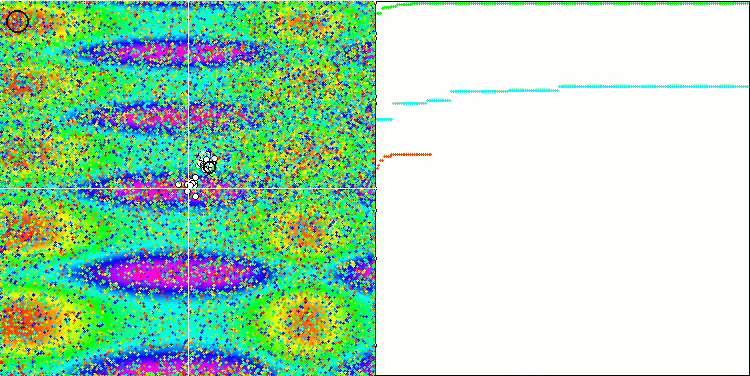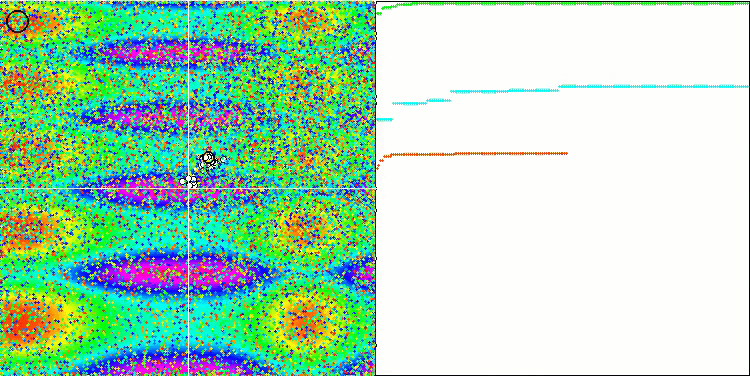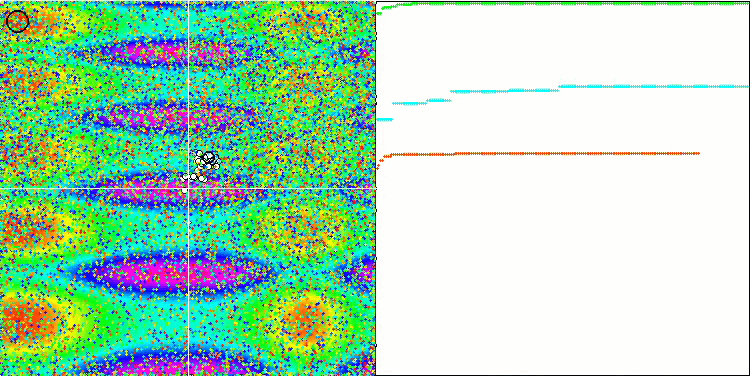
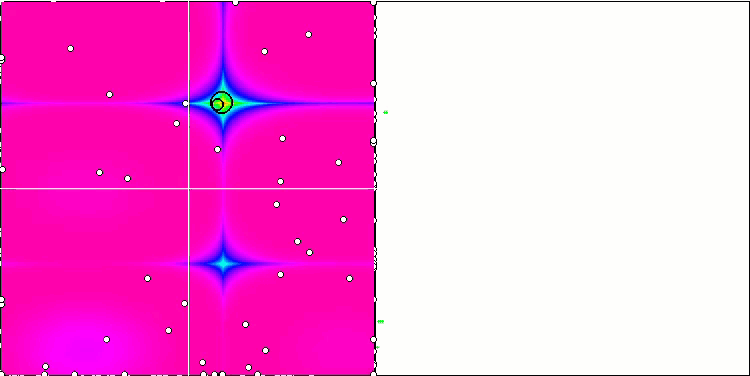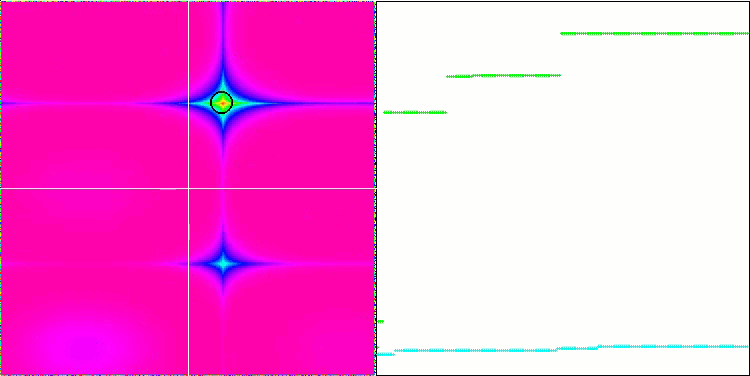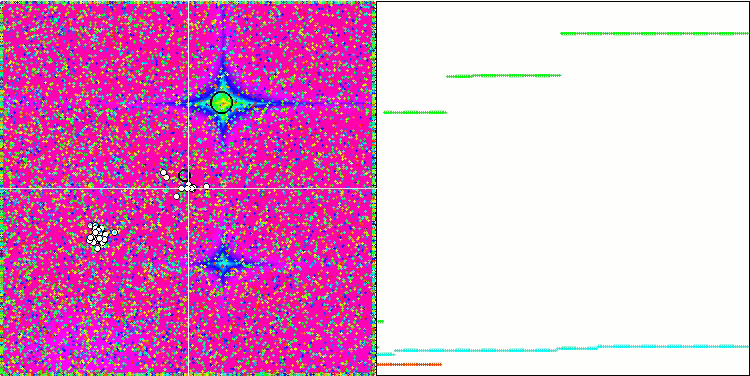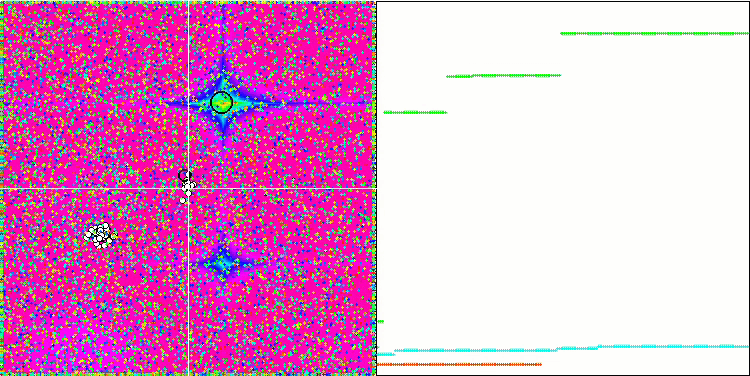
ACO mit der Testfunktion Skin

Forest

ACO mit der Testfunktion Forest

Megacity

ACO mit der Testfunktion Megacity

GWO-Testergebnisse.

2022.11.28 13:24:09.370 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:24:14.895    Test_AO_ABCm (EURUSD,M1)    1 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.914175888065222
2022.11.28 13:24:14.895 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.99900
2022.11.28 13:24:22.175    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 2.7419092435309405
2022.11.28 13:24:22.175 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.48033.
2022.11.28 13:25:01.381    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.5227848592798188
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.18924.
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:25:06.924    Test_AO_ABCm (EURUSD,M1)    1 Forests; Funktionsdurchläufe 10000 Ergebnis: 1.4822580151819842
2022.11.28 13:25:06.924 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.83844.
2022.11.28 13:25:14.551    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.15477395149266915
2022.11.28 13:25:14.551 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.08755.
2022.11.28 13:25:56.900    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.04517298232457319
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.02555.
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:26:02.305    Test_AO_ABCm (EURUSD,M1)    1 Megacity; Funktionsdurchläufe 10000 Ergebnis: 12.0.
2022.11.28 13:26:02.305 Test_AO_GWO (EURUSD,M1) Ergebnis: 1.00000
2022.11.28 13:26:09.475    Test_AO_ABCm (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 1.2
2022.11.28 13:26:09.475 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.10000
2022.11.28 13:26:48.980    Test_AO_ABCm (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 10000 Ergebnis: 0.2624.
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) Ergebnis: 0.02187.
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) Alle Ergebnisse für C_AO_GWO: 0.41577484361261224

Der Graue-Wölfe-Optimierungsalgorithmus (GWO) ist einer der jüngsten bio-inspirierten Optimierungsalgorithmen, der auf der simulierten Jagd eines Rudels grauer Wölfe basiert. Im Durchschnitt hat sich der Algorithmus bei verschiedenen Funktionstypen als recht effizient erwiesen, sowohl was die Genauigkeit bei der Suche nach einem Extremum als auch was die Konvergenzgeschwindigkeit betrifft. In einigen Tests hat sie sich als der beste herausgestellt. Die wichtigsten Leistungsindikatoren des Optimierungsalgorithmus „Graue Wölfe“ sind besser als die des Algorithmus der Partikelschwarmoptimierung, der als „konventionell“ in der Klasse der bio-inspirierten Optimierungsalgorithmen gilt.

Gleichzeitig ist die Rechenkomplexität des Graue-Wölfe-Optimierungsalgorithmus vergleichbar mit der des Partikelschwarm-Optimierungsalgorithmus. Aufgrund der zahlreichen Vorteile des GWO-Optimierungsalgorithmus sind in der kurzen Zeit seit der ersten Veröffentlichung des Algorithmus viele Arbeiten zu seiner Modifizierung erschienen. Der einzige Nachteil des Algorithmus ist die geringe Genauigkeit der gefundenen Koordinaten der Funktion sharp-maximum für Forest,

Die geringe Genauigkeit des gefundenen Extremwerts zeigte sich in allen Dimensionen der Forest-Funktion, und die Ergebnisse sind die schlechtesten unter allen Teilnehmern in der Tabelle. Der Algorithmus erwies sich bei der glatten Skin-Funktion als effizient, insbesondere bei der Skin-Funktion mit größerer Dimension. GWO ist auch der Dritte in der Tabelle, der bei der Funktion Megacity einen Treffer von 100 % beim globalen Maximum erzielt.

AO	Beschreibung	Skin			Forest			Megacity (diskret)			Endergebnis
AO	Beschreibung	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	Endergebnis
ACOm	Ameisenkolonie-Optimierung (ACO)	0.98229.	0.79108.	0.12602.	1.00000	0.62077.	0.11521.	0.38333.	0.44000.	0.02377.	0.49805222
ABCm	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	1.00000	0.63922.	0.08076	0.99908.	0.20112	0.03785.	1.00000	0.16333.	0.02823.	0.46106556
ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.99339.	0.73381.	0.11118.	0.99934.	0.21437.	0.04215.	0.85000.	0.16833.	0.03130.	0.46043000
GWO	Grauer-Wolf-Optimierung	0.99900	0.48033.	0.18924.	0.83844.	0.08755.	0.02555.	1.00000	0.10000	0.02187.	0.41577556
PSO	Partikelschwarmoptimierung	0.99627.	0.38080.	0.05089.	0.93772.	0.14540.	0.04856.	1.00000	0.09333.	0.02233.	0.40836667
RND	zufällig	0.99932.	0.44276.	0.06827.	0.83126.	0.11524.	0.03048.	0.83333.	0.09000.	0.02403.	0.38163222

Schlussfolgerungen:

Vorteile:
1. Hohe Geschwindigkeit.
2. Hohe Konvergenz für glatte Funktionen mit einer großen Anzahl von Variablen.

Nachteile
1. Nicht universell.
2. Feststecken in lokalen Extremen.
3. Geringe Skalierbarkeit bei diskreten und nicht-differenzierbaren Funktionen.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11785

Beigefügte Dateien |

ZIP herunterladen

l5_The_world_of_AO_oGWOv.zip (44.97 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Die Kategorientheorie in MQL5 (Teil 1)

Die Kategorientheorie ist ein vielfältiger und expandierender Zweig der Mathematik, der in der MQL-Gemeinschaft noch relativ unentdeckt ist. In dieser Artikelserie sollen einige der Konzepte vorgestellt und untersucht werden, mit dem übergeordneten Ziel, eine offene Bibliothek einzurichten, die zu Kommentaren und Diskussionen anregt und hoffentlich die Nutzung dieses bemerkenswerten Bereichs für die Strategieentwicklung der Händler fördert.

DoEasy. Steuerung (Teil 27): Arbeiten am WinForms Objekt der ProgressBar

In diesem Artikel werde ich die Entwicklung des ProgressBar-Steuerelements fortsetzen. Insbesondere werde ich die Funktionen zur Verwaltung des Fortschrittsbalkens und der visuellen Effekte erstellen.

Techniken des MQL5-Assistenten, die Sie kennen sollten (Teil 05): Markov-Ketten

Markov-Ketten sind ein leistungsfähiges mathematisches Werkzeug, das zur Modellierung und Vorhersage von Zeitreihendaten in verschiedenen Bereichen, einschließlich des Finanzwesens, verwendet werden kann. In der Finanzzeitreihenmodellierung und -prognose werden Markov-Ketten häufig zur Modellierung der zeitlichen Entwicklung von Finanzwerten wie Aktienkursen oder Wechselkursen verwendet. Einer der Hauptvorteile von Markov-Kettenmodellen ist ihre Einfachheit und Nutzerfreundlichkeit.

Algorithmen zur Optimierung mit Populationen Künstliches Bienenvolk (Artificial Bee Colony, ABC)

In diesem Artikel werden wir den Algorithmus eines künstlichen Bienenvolkes untersuchen und unser Wissen durch neue Prinzipien zur Untersuchung funktionaler Räume ergänzen. In diesem Artikel werde ich meine Interpretation der klassischen Version des Algorithmus vorstellen.