Algorithmen zur Optimierung mit Populationen: Ein dem Elektro-Magnetismus ähnlicher Algorithmus (ЕМ)

Inhalt:

1. Einführung
2. Der Algorithmus
3. Testergebnisse

1. Einführung

In den letzten Jahrzehnten haben Forscher auf der ganzen Welt zahlreiche metaheuristische Suchmethoden zur Lösung komplexer globaler Optimierungsprobleme entwickelt und Wege gefunden, diese zu verbessern.

Der elektromagnetismusähnliche (ЕМ) Algorithmus ist ein relativ neuer metaheuristischer Suchalgorithmus der auf der Simulation des Verhaltens von elektromagnetischen Teilchen im physikalischen Raum basiert und erstmals von I. Birbil und S.С. Fang im Jahr 2003 vorgestellt wurde. Er wird als evolutionärer Algorithmus mit zufälligem Rauschen und einer Population beschrieben, die auf der elektromagnetischen Kraft der Wechselwirkung zwischen geladenen Teilchen basiert.

Dieser Algorithmus wurde durch den Mechanismus der Anziehung und Abstoßung von Ladungen in der Theorie des Elektromagnetismus inspiriert, um nicht-lineare Optimierungsprobleme ohne Einschränkungen auf einen kontinuierlichen Bereich zu lösen. Aufgrund seiner Fähigkeit, komplexe globale Optimierungsprobleme zu lösen, wird EM in vielen Bereichen als Optimierungswerkzeug eingesetzt.

Interessante Fakten über Elektromagnetismus und elektrische Ladungen:

• Es gibt zwei Arten von elektrischen Ladungen: positive und negative. Alle Ladungen sind entweder positiv oder negativ.
• Das elektromagnetische Feld kann zur Übertragung von Informationen in Form von Radiowellen genutzt werden. Wir nutzen diese Funktion jeden Tag, wenn wir Radio hören oder fernsehen.
• Wir haben das Magnetfeld der Erde, das uns vor dem Sonnenwind und der kosmischen Strahlung schützt.
• Es gibt verschiedene Materialien, die magnetisiert werden können, und dies ermöglicht die Herstellung von Elektromagneten. Elektromagnete werden in verschiedenen Anwendungen eingesetzt, z. B. in Stromgeneratoren.
• Es gibt viele Anwendungen, die auf Elektromagnetismus basieren. So arbeiten beispielsweise Computer, Mobiltelefone und andere Geräte mit elektromagnetischer Technologie.
• Alle leuchtenden Objekte (z. B. Glühbirnen und Autolampen) geben elektromagnetische Strahlung ab.
• Auch in der Medizin spielt der Elektromagnetismus eine wichtige Rolle. Medizinische Geräte wie MRT und CT verwenden ein elektromagnetisches Feld, um Bilder aus dem Inneren des Körpers zu erzeugen.
• Einige Tiere, wie Haie und Zitteraale, können sich mithilfe von Elektromagnetismus im Wasser fortbewegen.
• Der Elektromagnetismus ist neben der Gravitationskraft, der schwachen und der starken Kraft eine der vier fundamentalen Kräfte der Natur.

2. Der Algorithmus

Auf der Grundlage der Theorie des Elektromagnetismus simuliert EM den Mechanismus der Anziehung und Abstoßung von Ladungen, um mit begrenzten Variablen eine globale optimale Lösung zu finden. In dem Algorithmus werden alle Lösungen als geladene Teilchen im Suchraum betrachtet, und die Ladung jedes Teilchens ist mit dem Wert der Zielfunktion verbunden. Teilchen mit einer besseren objektiven Leistung üben anziehende Kräfte aus, während Teilchen mit schlechteren objektiven Werten abstoßende Kräfte auf andere Teilchen ausüben. Je besser der Wert der Zielfunktion, desto größer ist die Anziehung oder Abstoßung zwischen den Teilchen.

Das Prinzip des Algorithmus besteht darin, dass in der Anfangsphase eine Population von Zufallslösungen gebildet wird, wobei jede Lösung durch einen Vektor von Koordinaten dargestellt wird, die den Ladungen der elektromagnetischen Teilchen entsprechen. Außerdem wird bei jeder Iteration des Algorithmus die Bewegung dieser Ladungen im Raum unter Einwirkung elektromagnetischer Kräfte simuliert. Während der Bewegung interagiert jede Ladung mit anderen Ladungen, was zu einer Änderung der Bewegungsrichtung und Geschwindigkeit führt. Infolgedessen kommt es zu einer allmählichen Konvergenz der Lösungen zum optimalen Wert der Zielfunktion.

Die wichtigsten Komponenten des EM-Algorithmus sind:

1. Bildung der Anfangspopulation von Lösungen (Ladungen), wobei jede Ladung durch einen Koordinatenvektor dargestellt wird und einer bestimmten Lösung des Optimierungsproblems entspricht.
2. Berechnung der elektromagnetischen Kraft der Wechselwirkung zwischen Ladungen. Die Berechnung wird bei jeder Iteration des Algorithmus durchgeführt und hängt vom Abstand zwischen den Ladungen (Lösungen) ab.
3. Bewegung von Ladungen im Raum unter dem Einfluss von elektromagnetischen Wechselwirkungskräften.
4. Aktualisierung der Lösungspopulation bei jeder Iteration durch die Zielfunktion (die Zielfunktion kann z. B. die Verlustfunktion bei Problemen des maschinellen Lernens sein).
5. Festlegung der Bedingung für das Anhalten des Algorithmus, z. B. das Erreichen eines bestimmten Wertes der Zielfunktion.

Die Teilchen interagieren miteinander, wobei sie sich je nach Ladung und Abstand voneinander anziehen oder abstoßen. Der Algorithmus wird in mehreren Iterationen ausgeführt, bei denen jeweils die Koordinaten und Ladungen der Partikel aktualisiert und die neuen Werte der Fitnessfunktion berechnet werden.

Die logische Einheit des EM-Optimierungsalgorithmus ist ein Partikel. Sie kann durch die Struktur S_Particle beschrieben werden, die einen Agenten im Suchraum darstellt. Jedes Teilchen hat Koordinaten, c[], die seine Position im Suchraum bestimmen, sowie die C-Ladung, die die Wechselwirkung mit anderen Teilchen beeinflusst. Für jedes Partikel wird der Wert der Fitnessfunktion f berechnet, mit der die Qualität der Lösung für die jeweilige Koordinate bewertet wird. Darüber hinaus werden für jedes Teilchen die Abstände R zu anderen Teilchen und die Kraftvektoren F berechnet, die die Richtung der Teilchenbewegung im Suchraum bestimmen.

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c  [];   //coordinates
  double C;       //charge
  double f;       //fitness
  double R  [];   //euclidean distance to other particles
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Die Klasse C_AO_EM ist eine Implementierung des elektromagnetischen Optimierungsalgorithmus. Es wird verwendet, um die optimalen Werte einer Funktion zu finden, die auf einer Menge von reellen Zahlen gegeben ist. Der Algorithmus basiert auf der Simulation der Interaktionsprozesse zwischen magnetischen und elektrischen Teilchen in einem physikalischen System.

Die Klasse enthält die folgenden Felder:

• S_Particle p[] - Array von Partikeln, die potenzielle Lösungen für das Optimierungsproblem darstellen.
• double rangeMax[] — Array der maximalen Suchbereichswerte für jede Koordinate.
• double rangeMin[] — Array der minimalen Suchbereichswerte für jede Koordinate.
• double rangeStep[] — Array der Suchschritte für jede Koordinate.
• double cB[] — Array der Koordinaten der besten Lösung.
• double fB[] — Wert der besten Lösungsfunktion.

Die Klasse enthält die folgenden Methoden:

• void Init() initialisiert den Algorithmus und setzt die Anzahl der Koordinaten, die Anzahl der Partikel, die Umgebungskonstante und den Bewegungsschritt.
• void Moving(int iter) iteriert den Algorithmus, der die Teilchen gemäß den Regeln für die Wechselwirkung von magnetischen und elektrischen Feldern bewegt.
• void Revision() führt eine Revision der Partikel durch, indem sie überprüft, ob sie den Suchbereich verlassen haben, und ihre Position gegebenenfalls anpasst.

Die Klasse enthält auch private Felder:

• int coordinatesNumber — Anzahl der Koordinaten.
• int particlesNumber — Anzahl der Partikel.
• double envConstant — Umgebungskonstante.
• double movConstant — Bewegungsschritt.
• double exponent — Abstandsexponent.
• double vect[] — Array von Vektoren.
• bool revision — Flag, die angibt, ob eine Partikelrevision erforderlich ist.

Die Klasse enthält private Methoden:

• double SeInDiSp(double In, double InMin, double InMax, double Step) verteilt Punkte auf einem einheitlichen Gitter.
• double RNDfromCI(double min, double max) erzeugt eine Zufallszahl im angegebenen Bereich.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_EM
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double envConstantP,       //environmental constant
                     const double movConstantP,       //movement step
                     const double exponentP);         //exponent

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double envConstant;       //environmental constant
  private: double movConstant;       //movement step
  private: double exponent;          //exponent
  private: double vect    [];        //vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Die Initialisierungsmethode des Optimierungsalgorithmus „elektromagnetischer Algorithmus“ beginnt mit dem Zurücksetzen des Zufallszahlengenerators und dem Festlegen von Anfangswerten für einige Variablen. Dann nimmt die Methode mehrere Parameter als Eingabe: die Anzahl der Koordinaten, die Anzahl der Partikel, den Wert der Umgebung und den Bewegungsschritt. Als Nächstes erstellt die Methode mehrere Arrays der erforderlichen Größe und füllt sie mit Anfangswerten.

In den Arrays werden die Höchst- und Mindestwerte des Bereichs für jede Koordinate, der Schritt der Koordinatenänderung, der Vektor und die aktuelle Position jedes Partikels gespeichert. Die Methode erzeugt dann ein Array von Partikeln und erstellt für jedes Partikel Arrays, um seine Koordinaten, die Matrix der Abstände zu anderen Partikeln, den Kraftvektor und den aktuell besten Wert der Funktion zu speichern. Am Ende erstellt die Methode ein Array, in dem die besten Koordinaten aller Partikel gespeichert werden. Auf diese Weise initialisiert die Methode alle notwendigen Variablen und Arrays, damit der Optimierungsalgorithmus „elektromagnetischer Algorithmus“ funktionieren kann.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Init (const int    coordinatesNumberP, //coordinates number
                    const int    particlesNumberP,   //particles number
                    const double envConstantP,       //environmental constant
                    const double movConstantP,       //movement step
                    const double exponentP)          //exponent
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  envConstant       = envConstantP;
  movConstant       = movConstantP;
  exponent          = exponentP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,  coordinatesNumber);
    ArrayResize (p [i].R,  particlesNumber);
    ArrayResize (p [i].F,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving() ist die erste, die bei jeder Iteration ausgeführt werden muss. Sie ist für die Bewegung der Partikel im Lösungssuchraum verantwortlich. Zunächst prüft die Methode, ob die Partikel bereits initialisiert worden sind. Wenn nicht, erhält jedes Teilchen zufällige Koordinaten innerhalb der vorgegebenen Grenzen und setzt seine aktuelle Schätzung und Ladung auf Null zurück. Der Vektor, vect[], der Differenzen zwischen den Höchst- und Mindestwerten in jeder Dimension des Suchraums wird ebenfalls berechnet.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].C     = 0.0;
      p [obj].f     = -DBL_MAX;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = rangeMax [c] - rangeMin [c];
  }

  revision = true;
}

Wurde die Initialisierung bereits durchgeführt, so berechnet die Methode die Ladung jedes Teilchens auf der Grundlage seiner Abweichung vom globalen Maximum, normiert auf die Summe der Abweichungen vom globalen Maximum aller Teilchen. Berechnung der Summe der Differenzen:

//calculate the sum of the differences of the fitness of the particles with the global value
for (int obj = 0; obj < particlesNumber; obj++)
{
  sumDiff += fB - p [obj].f;
}

Die Partikelladung wird nach der folgenden Gleichung berechnet:

p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));

Wie Sie sehen können, ist der Wert der Ladung in der Gleichung positiv. Das Vorzeichen der Ladung wird später im Algorithmus berücksichtigt. Ist die Summe der Differenzen der Abweichungen vom globalen Maximum gleich Null, so wird die Ladung des Teilchens als Null angenommen. Die berechnete Ladung des Teilchens bestimmt die Amplitude der Kraft, die von dem Teilchen auf andere relevante Teilchen während des Kraftberechnungsschritts wirkt. Der Code zur Berechnung der Ladung eines Teilchens sieht folgendermaßen aus:

//calculating the charge of particles=======================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  if (sumDiff == 0.0)
  {
    p [obj].C = 0.0;
  }
  else
  {
    p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
  }
}

Bevor wir mit der Berechnung der Abstände zwischen den Teilchen beginnen, ist es notwendig, das Feld der Abstände zwischen dem Teilchen und anderen Teilchen sowie den Vektor der auf das Teilchen wirkenden Kräfte zurückzusetzen:

//calculation of Euclidean distances between all particles==================
for (int obj = 0; obj < particlesNumber; obj++)
{
  ArrayInitialize (p [obj].R, 0.0);
  ArrayInitialize (p [obj].F, 0.0);
}

Dann werden die Abstände zwischen allen Teilchenpaaren und die zwischen ihnen wirkenden Kräfte berechnet. Dazu wird die Formel des Coulomb-Gesetzes verwendet, die die Wechselwirkung zwischen geladenen Teilchen beschreibt. Die auf jedes Teilchen wirkenden Kräfte werden als Vektorsumme aller Kräfte berechnet, die von anderen Teilchen auf das Teilchen wirken.

Nach der elektromagnetischen Theorie ist die Kraft, die von einem Teilchen auf ein anderes einwirkt, umgekehrt proportional zum Abstand zwischen den beiden Teilchen und direkt proportional zum Produkt ihrer Ladungen. Ein Teilchen mit einem niedrigeren Zielwert übt eine abstoßende Kraft auf ein Teilchen mit einem relativ höheren Zielwert aus. In ähnlicher Weise wird ein gutes Teilchen von einer Region mit einem schlechten Zielwert weggeschoben. Andererseits übt ein Teilchen mit einem höheren Zielwert eine Anziehungskraft auf Teilchen mit relativ niedrigeren Werten aus.

Unter Berücksichtigung aller relevanten Kräfte, die von allen anderen Teilchen erzeugt werden, wird der Gesamtkraftvektor für das Teilchen berechnet. Dieser kombinierte Kraftvektor bestimmt die Richtung, in die sich das Teilchen während der Bewegungsphase bewegen wird. Die Autoren des Algorithmus empfehlen, den Kraftvektor des Teilchens auf den Vektor der Kräfte zwischen allen Teilchen zu normieren. Meine Experimente haben gezeigt, dass die Ergebnisse ohne Normalisierung besser sind, und der Code wird ohne Normalisierung dargestellt.

Je nachdem, welches Teilchen den größeren Wert der Zielfunktion hat, legen wir die Richtung der Kraft fest (Nachahmung des Vorzeichens der Ladung).

for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int obj2 = 0; obj2 < particlesNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (p [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = p [obj].c [c] - p [obj2].c [c];
          p [obj].R [obj2] += diffDist * diffDist;
        }

        p [obj].R [obj2] = sqrt (p [obj].R [obj2]);
        p [obj2].R [obj] = p [obj].R [obj2];

        //calculation of the force------------------------------------------
        Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent));

        for (int c = 0; c < coordinatesNumber; c++)
        {
          if (p [obj].f > p [obj2].f)
          {
            p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;

          }
          else
          {
            p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
          }
        }
      }
    }
  }
}

Schließlich werden für jedes Teilchen auf der Grundlage seiner aktuellen Position und der auf es wirkenden Kraft neue Koordinaten berechnet. Die Teilchen haben keine Masse, was bedeutet, dass es keine Beschleunigung gibt. Im Gegensatz zu GSA, dem Gravitationssuchalgorithmus, bewegen sich die Teilchen sofort an einen neuen Ort. Die Bewegungskoordinaten sind durch den Suchbereich und den Änderungsschritt begrenzt.

Der auskommentierte Code gibt das Partikel auf der gegenüberliegenden Seite des Bereichs in einem Abstand von der entsprechenden Koordinate zurück, falls das Partikel außerhalb des Bereichs liegt.

//calculation of particle motions===========================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (0.0, 1.0);
    p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant;

    //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]);
    //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]);

    p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Die Methode Revision(), die zweite Methode, die bei jeder Iteration im EM-Optimierungsalgorithmus ausgeführt werden muss, ist für die Überprüfung der besten Position des Partikels in der aktuellen Iteration zuständig. Innerhalb der Methode durchläuft sie in einer Schleife alle Partikel und vergleicht den Wert ihrer Fitnessfunktion mit dem aktuell besten Wert von fB. Wenn der Wert der Fitnessfunktion des aktuellen Partikels größer als fB ist, wird fB aktualisiert und die Position des Partikels in das Array cB kopiert.

Die Methode Revision() ermöglicht es also, die beste Position des Partikels bei jeder Iteration des Algorithmus zu verfolgen und sie im Array cB zu speichern. Dies trägt zur Optimierung des Prozesses der Suche nach der optimalen Lösung bei und erhöht die Effizienz des Algorithmus.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Revision ()
{
  for (int s = 0; s < particlesNumber; s++)
  {
    if (p [s].f > fB)
    {
      fB = p [s].f;
      ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode SeInDiSp() im Optimierungsalgorithmus „Elektromagnetischer Algorithmus“ wird verwendet, um die Werte der Variablen In innerhalb eines bestimmten Bereichs [InMin, InMax] mit einem Schritt zu begrenzen. Wenn In kleiner oder gleich InMin ist, gibt die Methode InMin zurück. Wenn In größer oder gleich InMax ist, gibt die Methode InMax zurück. Ist der Schritt gleich Null, gibt die Methode den ursprünglichen In-Wert zurück. Andernfalls berechnet die Methode anhand der Gleichung einen neuen In-Wert: InMin + Step * (In - InMin) / Step, wobei MathRound() die Methode zur Rundung einer Zahl auf die nächste ganze Zahl ist.

Die Methode SeInDiSp() ermöglicht es also, die Änderung des Wertes der Variablen In innerhalb der festgelegten Grenzen und mit einem festgelegten Schritt zu kontrollieren, was zu einer effizienteren und schnelleren Optimierung der Funktion beiträgt.

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Ergebnisse des SSG-Prüfstands:

2023.03.26 18:27:39.259    C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259    =============================
2023.03.26 18:27:43.215    5 Rastrigins; Funkt.-Durchläufe 10000 Ergebnis: 59.939529106561224
2023.03.26 18:27:43.215    Score: 0.74268
2023.03.26 18:27:52.960    25 Rastrigins; Funkt.-Durchläufe 10000 Ergebnis: 59.780143424645416
2023.03.26 18:27:52.960    Score: 0.74071
2023.03.26 18:29:22.856    500 Rastrigins; Funkt.-Durchläufe 10000 Ergebnis: 63.94951378068386
2023.03.26 18:29:22.856    Score: 0.79237
2023.03.26 18:29:22.856    =============================
2023.03.26 18:29:28.901    5 Forests; Funkt.-Durchläufe 10000 Ergebnis: 0.28698617113254693
2023.03.26 18:29:28.901    Score: 0.16233
2023.03.26 18:29:38.103    25 Forests; Funkt.-Durchläufe 10000 Ergebnis: 0.1571444033424823
2023.03.26 18:29:38.103    Score: 0.08889
2023.03.26 18:30:53.341    500 Forests; Funkt.-Durchläufe 10000 Ergebnis: 0.11734383105881332
2023.03.26 18:30:53.341    Score: 0.06638
2023.03.26 18:30:53.341    =============================
2023.03.26 18:30:58.108    5 Megacities; Funkt.-Durchläufe 10000 Ergebnis: 1.3599999999999999
2023.03.26 18:30:58.108    Score: 0.11333
2023.03.26 18:31:08.897    25 Megacities; Funkt.-Durchläufe 10000 Ergebnis: 0.776
2023.03.26 18:31:08.897    Score: 0.06467
2023.03.26 18:32:23.199    500 Megacities; Funkt.-Durchläufe 10000 Ergebnis: 0.34320000000000006
2023.03.26 18:32:23.199    Score: 0.02860
2023.03.26 18:32:23.199    =============================
2023.03.26 18:32:23.199    All score: 2.79996

Wenn wir uns die Animation des ME-Algorithmus auf Testfunktionen ansehen, können wir uns eine Art „Elektrifizierung“ des Suchraumfeldes vorstellen. Die Partikel bilden Gruppen mit hoher Ladung, die den Merkmalen der Oberfläche der Testfunktion folgen. Leider ist die Qualität der Konvergenz spürbar niedrig, aber das Bild ist unbestreitbar schön.

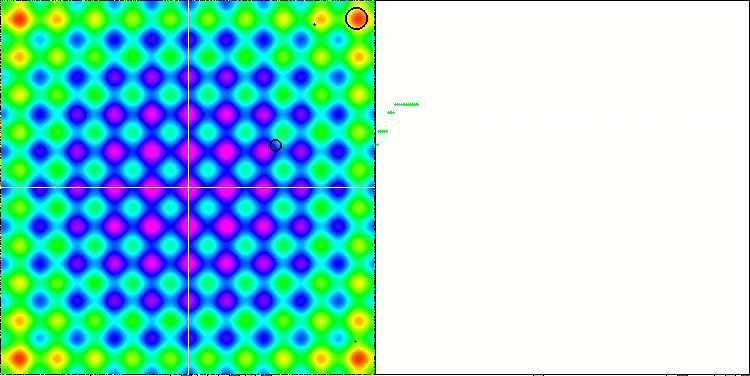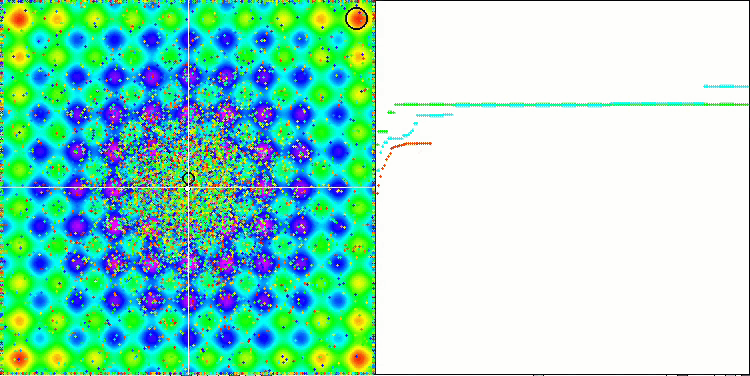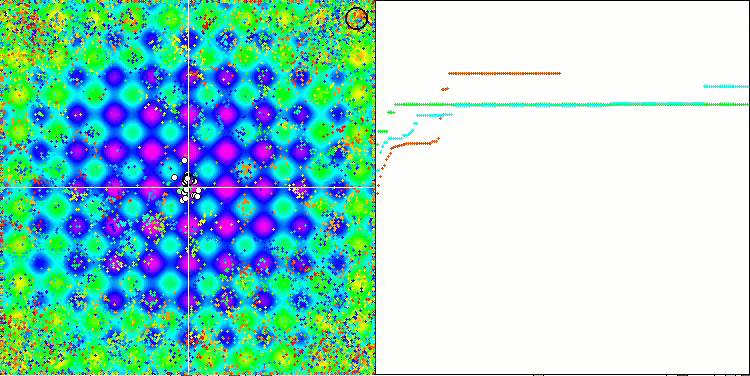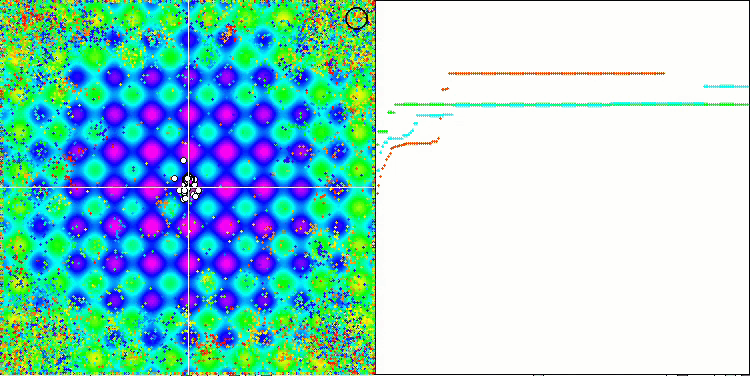
  EM mit der Rastrigin-Testfunktion.

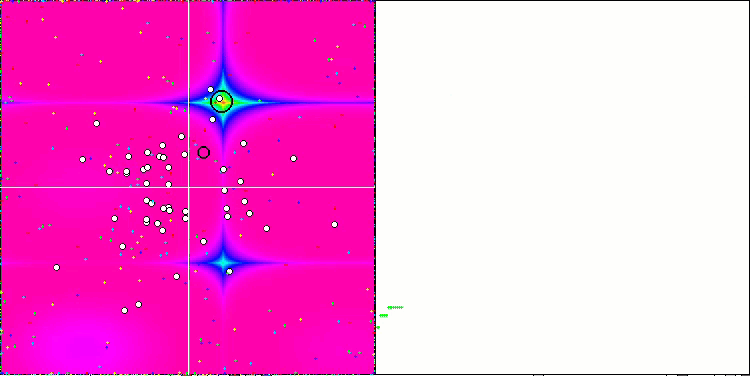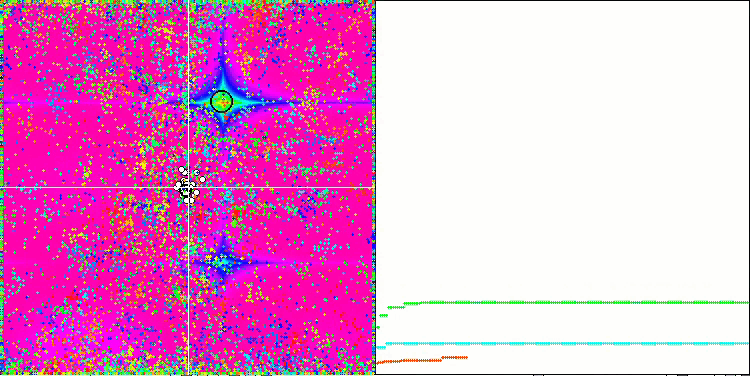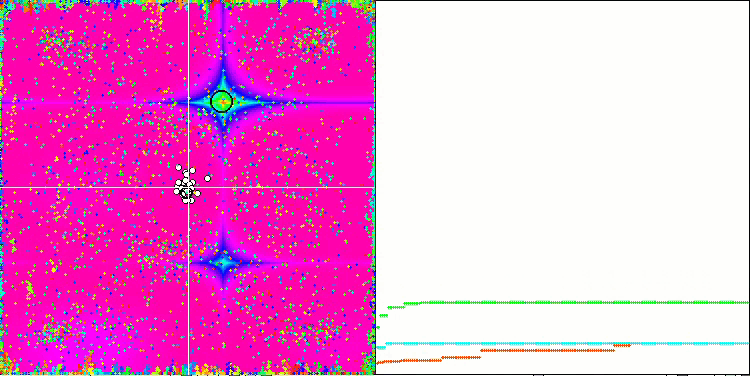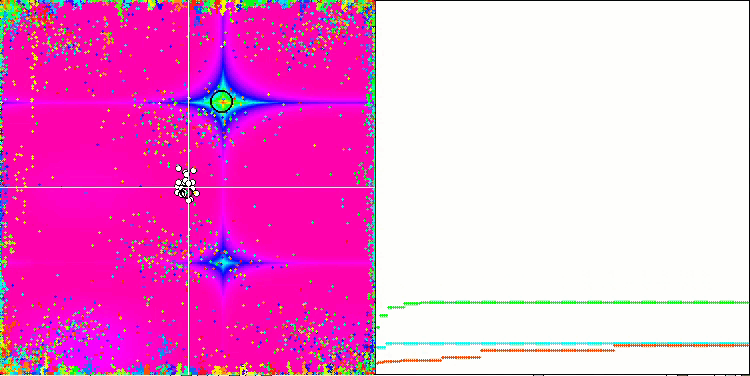
  EM mit der Forest-Testfunktion.

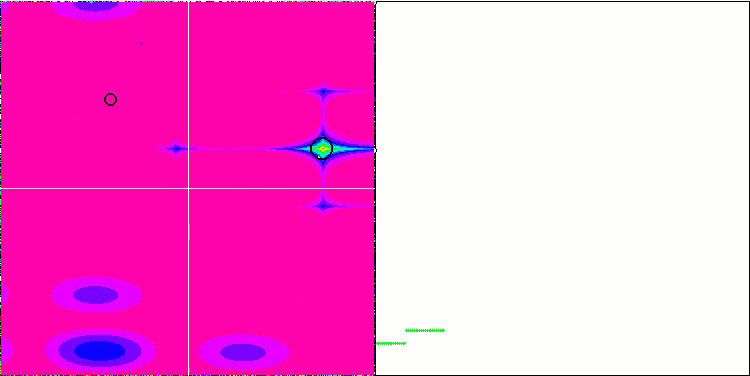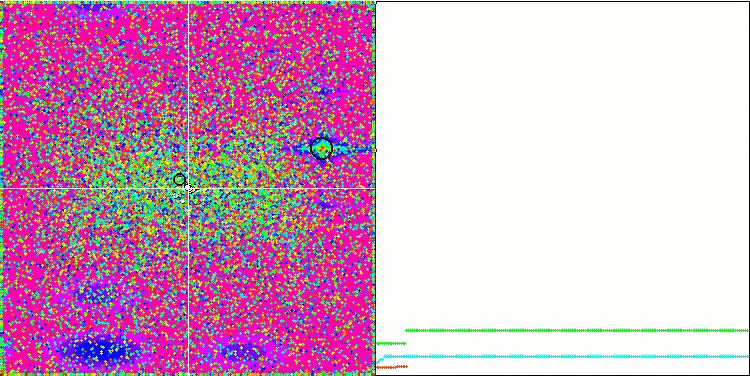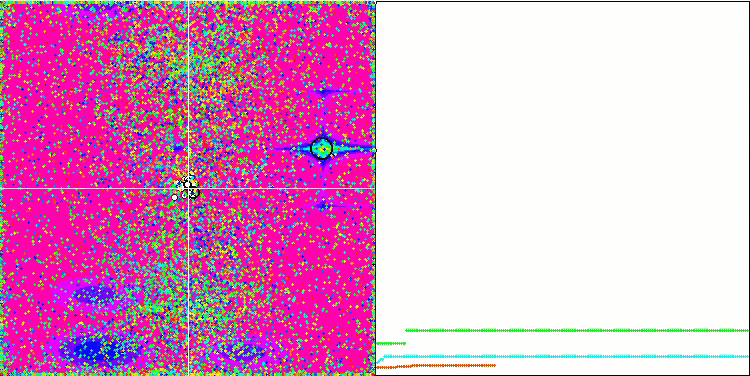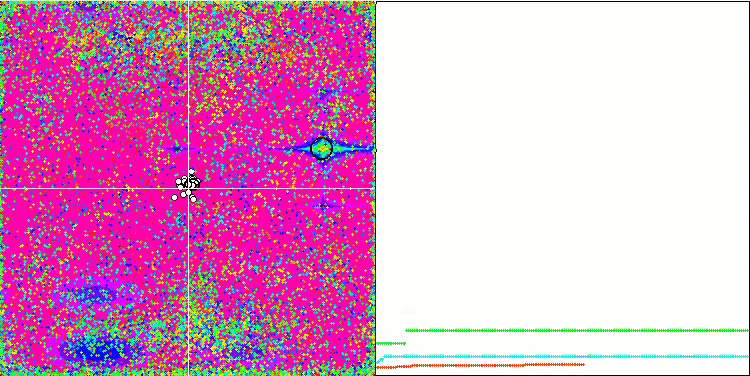
  EM mit der Megacity-Testfunktion.

Kommen wir nun zu den Testergebnissen des EM-Optimierungsalgorithmus. EM schnitt mit einem Endergebnis von 22 unterdurchschnittlich ab. Der Algorithmus zeigte in fast allen Tests schlechte Ergebnisse. Eine Ausnahme bildet der Rastrigin-Funktionstest mit 1000 Parametern, bei dem sich EM als besser erwies als so leistungsfähige Algorithmen wie SSG und BA. Darüber hinaus erwiesen sich die absoluten Werte der Funktion bei 1000 Parametern als höher als bei Tests mit 10 und 50 Parametern!

Dies ist das erste Mal, dass sich die Suchergebnisse verbessern, wenn die Anzahl der optimierten Parameter steigt. Höchstwahrscheinlich hängt dieses Phänomen mit den Eigenheiten der EM-Suchstrategie selbst zusammen. Es ist zu beachten, dass EM empfindlich auf das Vorhandensein eines Gradienten und die Differenzierbarkeit über den gesamten Bereich der untersuchten Funktionsdefinition reagiert.

AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Endergebnis
		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)
SSG	Setzen, Säen und Wachsen	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100.000
HS	Harmoniesuche	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
ACOm	Ameisen-Kolonie-Optimierung M	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
IWO	Optimierung mit invasiven Unkräutern	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
COAm	Kuckuck-Optimierungsalgorithmus M	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
FAm	Firefly-Algorithmus M	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
GSA	Algorithmus für die Schwerkraftsuche	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
BA	Fledermaus-Algorithmus	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
BFO	Optimierung der bakteriellen Futtersuche	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
EM	elektromagnetismusähnlicher Algorithmus	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
MA	Affen-Algorithmus	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
FSS	Fischschulsuche	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
PSO	Partikelschwarmoptimierung	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
RND	zufällig	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
GWO	Grauer-Wolf-Optimierung	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

Zusammenfassung

1. Der EM-Algorithmus ist ein effizientes Optimierungsverfahren, mit dem verschiedene Optimierungsprobleme gelöst werden können, insbesondere solche, die mit der Verarbeitung großer Datenmengen und hoher Dimensionalität bei glatten Funktionen verbunden sind.
2. Der Algorithmus basiert auf der Simulation des Verhaltens elektromagnetischer Teilchen im physikalischen Raum, wodurch eine hohe Genauigkeit des Ergebnisses bei der Arbeit mit komplexen mehrdimensionalen Funktionen erreicht werden kann.
3. Der EM-Algorithmus erfordert keine Gradientenberechnungen, was ihn vielseitiger und leichter auf verschiedene Probleme anwendbar macht, aber er reagiert empfindlich auf das Vorhandensein eines Gradienten in der zu optimierenden Funktion.
4. Der Algorithmus kann je nach spezifischem Optimierungsproblem verändert und angepasst werden, was ihn zu einem flexiblen Werkzeug für die Optimierung verschiedener Funktionen macht.
5. Es gibt verschiedene Modifikationen des EM-Algorithmus, die gegenüber der Grundversion verbessert und an spezifische Optimierungsprobleme angepasst werden können.
6. Der EM-Algorithmus kann in verschiedenen Bereichen wie dem maschinellen Lernen, der künstlichen Intelligenz, der Finanzmarktoptimierung und anderen eingesetzt werden.

Der Hauptvorteil des elektromagnetischen Algorithmus ist die Fähigkeit, Optimierungsprobleme in mehrdimensionalen Räumen und großen Dimensionen zu lösen und dabei eine hohe Genauigkeit des Ergebnisses beizubehalten.

Somit ist der EM-Algorithmus ein effektives Werkzeug für die Optimierung verschiedener Funktionen und kann bei einer Vielzahl von Optimierungsproblemen eingesetzt werden, insbesondere bei der Verarbeitung einer großen Datenmenge und/oder hoher Dimensionalität.

Diese Bewertung kann bei der Auswahl des am besten geeigneten Algorithmus für die Lösung eines bestimmten Optimierungsproblems hilfreich sein. Die Effizienz des Algorithmus hängt jedoch von vielen Faktoren ab, z. B. von der Größe des Problems, der Art der Funktion, der Anzahl der Variablen usw. Daher sollte die Wahl eines Algorithmus auf einer gründlichen Analyse eines bestimmten Problems beruhen.

Abbildung 1 zeigt die Testergebnisse der Algorithmen

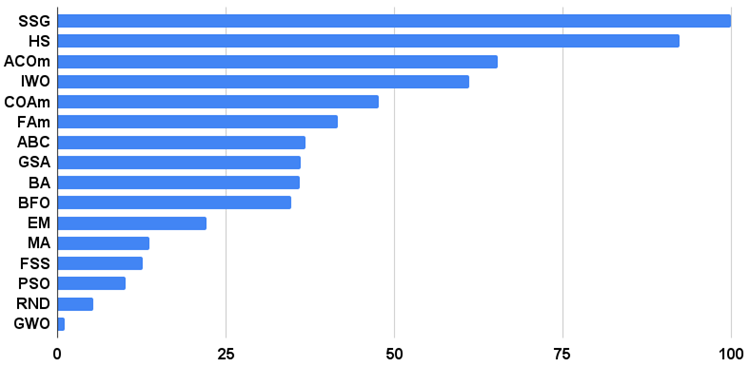
Bild 1. Histogramm der Testergebnisse der Algorithmen

Vor- und Nachteile des elektromagnetischen Algorithmus (EM):

Vorteile:
1. Einfache Implementierung.
2. Beeindruckende Skalierbarkeit bei glatten Funktionen.
3. Geringe Anzahl von externen Parametern.

Nachteile
1. Hohe rechnerische Komplexität.
2. Schlechte Ergebnisse bei diskreten Funktionen.
3. Hängenbleiben bei Funktionen mit flachen horizontalen „Plattformen“.

Jeder Artikel verfügt über ein Archiv, das aktualisierte aktuelle Versionen der Algorithmuscodes für alle früheren Artikel enthält. Der Artikel basiert auf den gesammelten Erfahrungen des Autors und stellt seine persönliche Meinung dar. Die Schlussfolgerungen und Urteile beruhen auf den Experimenten.