
Tabu Search (TS)
Inhalt
Einführung
Der Algorithmus beginnt mit der Auswahl einer Ausgangslösung und untersucht dann die benachbarten Optionen, wobei diejenigen bevorzugt werden, die das aktuelle Ergebnis verbessern. Um zu verhindern, dass man zu zuvor erforschten, erfolglosen Lösungen zurückkehrt, wird eine Tabu-Liste verwendet - eine Struktur, die „verbotene“ Bewegungen aufzeichnet. Dadurch können wir zyklische Prozesse vermeiden und den Suchraum effizienter erkunden. Beim Knapsack-Problem zum Beispiel könnte ein Algorithmus Elemente einzeln hinzufügen oder entfernen und versuchen, ihren Wert zu maximieren, während er es vermeidet, zu vorher in Betracht gezogenen Kombinationen zurückzukehren.
Die Grundlage der Tabu-Suche ist das adaptive Gedächtnis, das nicht nur die Rückkehr zu bereits gefundenen Lösungen verhindert, sondern auch den Suchprozess unter Berücksichtigung früherer Schritte steuert. Andere Forscher, wie Manuel Laguna und Rafael Marti, entwickelten den Algorithmus in der Folgezeit weiter und erweiterten seine Anwendung in Bereichen, die von der Produktionsplanung über die Finanzanalyse bis zur Telekommunikation reichen. Die Tabu-Suche ist nach wie vor ein wichtiges Instrument für die Lösung komplexer kombinatorischer Probleme, die eine gründliche Analyse und komplexe Berechnungen erfordern.
Tabu-Suche ist somit ein gutes Beispiel dafür, wie innovative Ideen die Methoden der Suchoptimierung verändern und neue Möglichkeiten in Wissenschaft und Technik eröffnen können. Obwohl der Algorithmus ursprünglich entwickelt wurde, um bestimmte kombinatorische Probleme zu lösen, wie z. B. das Problem des Handlungsreisenden und das Knapsack-Problem, wird in diesem Artikel eine Modifikation des klassischen Algorithmus erörtert, die es ihm ermöglicht, allgemeinere Optimierungsprobleme zu lösen, einschließlich Problemen in einem kontinuierlichen Suchraum.
Implementierung des Algorithmus
Betrachten wir die allgemeinen Gleichungen und Mechanismen, die im Tabu-Suche-Algorithmus zur Lösung kombinatorischer Optimierungsprobleme (dem herkömmlichen Algorithmus) verwendet werden:
1. Allgemeine Formulierung des Optimierungsproblems:
- f (x) Optimierung - Zielfunktion.
- x ∈ X, wobei X eine Menge von Nebenbedingungen für den Vektor der Variablen x ist.
2. Die Nachbarschaft der Lösungen:
- N (x) ist eine Menge von Lösungen, die von der aktuellen Lösung x aus mit einem „Zug“ erreicht werden können.
- N* (x) ist eine modifizierte Nachbarschaft, die die Suchhistorie (Kurz- und Langzeitgedächtnis) berücksichtigt.
3. Kurzzeitgedächtnis:
- Verfolgen von Attributen (Entscheidungsmerkmalen), die sich in der jüngsten Vergangenheit verändert haben.
- Verbot des Besuchs von Lösungen mit „tabu-aktiven“ Attributen.
4. Langzeitgedächtnis:
- Zählung der Häufigkeit von Attributänderungen/Vorkommen in besuchten Lösungen.
- Nutzung dieser Frequenzen zur Steuerung der Suchdiversifizierung.
5. Intensivierung:
- Auswahl des besten Zuges aus einer modifizierten Nachbarschaft N* (x).
- Zurück zu den vielversprechenden Bereichen des Lösungsraums.
6. Diversifizierung:
- Wählen Sie Züge aus, die neue, bisher unbekannte Attribute einführen.
- Suche nach Richtungen in einem anderen als dem bereits erkundeten Gebiet.
7. Strategische Fluktuationen:
- Änderung der Regeln für die Auswahl von Zügen bei Annäherung an eine „kritische Stufe“.
- Die Ebene durchlaufen und dann zurückkehren.
8. Verknüpfung von Pfaden:
- Erstellung von Verbindungslinien zwischen hochwertigen Unterstützungslösungen.
- Auswahl von Zügen, die die aktuelle Lösung so nah wie möglich an die Leitlösungen heranbringen.
Um die Optimierungsprobleme zu lösen, werden wir Punkt 8 überspringen und uns auf die Hauptidee des Algorithmus konzentrieren, indem wir versuchen, eine Abwandlung der Tabu-Suche zu implementieren, wobei wir, wenn möglich, die Punkte 1-7 beibehalten. Der ursprüngliche Algorithmus arbeitet mit diskreten Entscheidungen und versucht, den kürzesten Weg zwischen den Knotenpunkten zu finden. Um es an Probleme in einem kontinuierlichen Suchraum anzupassen, ist es notwendig, die machbaren Regionen für jeden zu optimierenden Parameter irgendwie zu diskretisieren. Das Problem ist, dass wir nicht jede mögliche Lösung kennzeichnen können, da die Anzahl der Kennzeichnungen kolossal wäre, was die Lösung fast unmöglich macht.
Anstelle einer Tabu-Liste werden wir für jeden Parameter das Konzept einer „weißen Liste“ und einer „schwarzen Liste“ einführen, die ihre Bereiche in Sektoren unterteilen (eine bestimmte Anzahl von Sektoren für jeden optimierten Parameter). Auf diese Weise können wir ein Häkchen in die weiße Liste setzen, wenn die Lösung erfolgreich ist, und ein Häkchen in die schwarze Liste setzen, wenn die Lösung im Vergleich zum vorherigen Schritt nicht besser ist. In Bereichen mit vielversprechenden Lösungen werden Punkte gesammelt, die eine gründlichere Erkundung des Gebiets und eine Verfeinerung der Lösung ermöglichen. Allerdings kann ein erfolgreicher Sektor auch extrem erfolglose Entscheidungen enthalten, in diesem Fall wird der Sektor auf die schwarze Liste gesetzt. Dies bedeutet, dass ein und derselbe Sektor sowohl Kennzeichen der weißen als auch der schwarzen Liste enthalten kann.
Die Auswahl der Sektoren für die Erstellung der nächsten Lösung sollte mit einer Wahrscheinlichkeit erfolgen, die proportional zur Anzahl der Kennzeichnungen in der weißen Liste ist. Nach der Generierung einer neuen Lösung wird der entsprechende Sektor mit der schwarzen Liste abgeglichen und die Wahrscheinlichkeit proportional zu den Markierungen der schwarzen Liste als Bruchteil der Summe der Markierungen der weißen Liste berechnet. Wenn die Wahrscheinlichkeit erfüllt ist, wählen wir einen anderen zufällig ausgewählten Sektor.
Unter Berücksichtigung der Merkmale der Oberfläche der zu optimierenden Funktion erzeugt der Algorithmus dynamisch Wahrscheinlichkeiten für die Erkundung aller verfügbaren Bereiche im Suchraum, ohne sich auf einen bestimmten Sektor zu beschränken. Selbst wenn ein Algorithmus nahe an der globalen optimalen Lösung landet, kann er seine Ergebnisse nicht unbegrenzt verbessern. Dies wiederum führt zu einem Anstieg der Markierungen auf der schwarzen Liste für diesen Sektor, was den Algorithmus zwingt, den Sektor zu wechseln und die Suche in anderen Bereichen des Hyperraums fortzusetzen.
Auf diese Weise soll eine breitere Streuung bei der Verfeinerung der gefundenen Lösungen und eine umfassende Untersuchung der Probleme gewährleistet werden. Dies sollte auch die Anzahl der externen Parameter des Algorithmus minimieren und ihm selbstanpassende Eigenschaften an die zu untersuchende Problemfunktion verleihen.
Lassen Sie uns die wichtigsten Punkte der Idee einer modifizierten Implementierung der klassischen Tabu-Suche hervorheben:
1. Diskretisierung. Die Unterteilung des Suchraums in Sektoren ermöglicht eine effizientere Erkundung von Bereichen.
2. Weiße und schwarze Listen. Erfolgreiche und erfolglose Entscheidungen werden getrennt erfasst, was eine dynamische Verfolgung der Branchenaussichten ermöglicht.
3. Dynamische Studie. Der Algorithmus generiert Wahrscheinlichkeiten für die Erkundung aller verfügbaren Bereiche, um zu vermeiden, dass man in ineffizienten Sektoren stecken bleibt.
4. Anpassungsfähigkeit. Der Algorithmus reagiert auf die Anhäufung von Markierungen auf der schwarzen Liste, was ihn zwingt, die Suchrichtung zu ändern und für Diversifizierung zu sorgen.
Unsere Version des Algorithmus kombiniert also Elemente von Tabu-Suche und evolutionären Algorithmen. Er verwendet einen Speichermechanismus in Form von schwarzen und weißen Listen, um die Suche auf vielversprechende Bereiche des Lösungsraums zu lenken und Bereiche zu vermeiden, die zu einer schlechteren Lösung geführt haben.
Der Übersichtlichkeit halber stellen wir die weiße und die schwarze Liste der Sektoren für jede Koordinate schematisch dar. Nehmen wir zum Beispiel drei Koordinaten, von denen jede in 4 Sektoren unterteilt ist. Weiße und schwarze Listen werden für jede Koordinate getrennt eingestellt.
So weist beispielsweise die Koordinate „0“ des Sektors „3)“ in der weißen Liste fünf „Häkchen“ auf, was die größte Anzahl aller Sektoren dieser Koordinate ist. Dies bedeutet, dass in der nächsten Iteration der Sektor mit der höchsten Wahrscheinlichkeit ausgewählt wird. Andererseits stehen gerade in diesem Sektor sechs „Kennzeichnungen“ auf der schwarzen Liste, was die Wahrscheinlichkeit erhöht, dass er bei der Entwicklung einer neuen Lösung ersetzt wird, obwohl er als der vielversprechendste gilt. So kann es vorkommen, dass ein Sektor mit weniger Potenzial bei der Auswahl der Sektoren eine geringere Wahrscheinlichkeit hat, durch einen anderen Sektor ersetzt zu werden (dies ist auf den ersten Blick nicht ersichtlich).
Wie man sieht, findet während der Erkundung des Suchraums eine ständige Neugewichtung der Wahrscheinlichkeiten statt, wodurch die Merkmale der Oberfläche berücksichtigt werden können. Diese Richtung scheint sehr vielversprechend zu sein, da sie wenig von den externen Parametern des Algorithmus abhängt, was ihn wirklich selbstanpassend macht.
0: |0)____VVV_____|1)____VV______|2)_____V______|3)____VVVVV____| 1: |0)_____VV_____|1)_____V______|2)____VVV_____|3)_____VVV_____| 2: |0)______V_____|1)____VVV_____|2)_____V______|3)_____VVV_____| 0: |0)_____ХХХ____|1)_____ХХ_____|2)_____XX_____|3)____XXXXXX___| 1: |0)______X_____|1)_____XXX____|2)____XXXXX___|3)______X______| 2: |0)_____XX_____|1)_____XXXX___|2)______X_____|3)____XXXXX____|
Jetzt können wir einen Pseudocode für eine modifizierte Version des Algorithmus schreiben, den wir als TSm bezeichnen:
1. Initialisierung der Population:
Für jeden Agenten in der Population:
Setzte zufällige Koordinaten innerhalb des angegebenen Bereichs.
Lege den Ausgangswert der vorherigen Fitness als den kleinstmöglichen Wert fest.
2. Die Hauptschleife des Algorithmus:
Wiederhole den Vorgang, bis die Abbruchbedingung erreicht ist:
a) Wenn dies die erste Iteration ist:
Initialisiere die Population.
b) Andernfalls:
Generiere neue Koordinaten für Agenten:
Für jeden Agenten und jede Koordinate:
Kopiere mit einer bestimmten Wahrscheinlichkeit die Koordinate der besten bekannten Lösung.
Andernfalls:
Wähle einen Sektor aus der weißen Liste des Agenten aus.
Erzeuge eine neue Koordinate in diesem Sektor.
Wenn der ausgewählte Sektor auf der schwarzen Liste steht, wähle einen zufälligen Sektor aus und erstelle darin eine Koordinate.
Prüfe, dass die neue Koordinate nicht über den zulässigen Bereich hinausgeht.
c) Bewerte die Eignung jedes Agenten mit neuen Koordinaten.
d) Aktualisiere die schwarzen und weißen Listen:
Für jeden Agenten:
Vergleich die aktuelle Eignung mit der vorherigen.
Wenn sich die Eignung verbessert hat, erhöhe den Zähler in der weißen Liste für den entsprechenden Sektor.
Wenn sie sich verschlechtert hat, erhöhe den Zähler in der schwarzen Liste.
Speicher die aktuelle Fitness als die vorherige für die nächste Iteration.
e) Aktualisiere die beste, gefundene Lösung, wenn ein Agent mit besserer Eignung gefunden wird.
3. Nach dem Ende der Schleife wird die beste, gefundene Lösung zurückgegeben.
Beginnen wir nun mit dem Schreiben des Codes. Beschreiben wir zwei Strukturen: S_TSmSector und S_TSmAgent werden verwendet, um mit Sektoren und Agenten in der Suchstrategie zu arbeiten.
1. S_TSmSector - die Struktur enthält ein Array mit den ganzen Zahlen von sector [], in dem die „Häkchen“ für den entsprechenden Sektor gespeichert werden (in Wirklichkeit handelt es sich um ein Array von Zählwerten).
2. S_TSmAgent - diese Struktur ist komplexer. Sie beschreibt den Suchagenten im Algorithmus und umfasst:
- blacklist [] - Array von schwarzen Listen nach Sektoren für jede Koordinate.
- whitelist [] - Array von weißen Listen nach Sektoren für jede Koordinate.
- fPrev - der Wert der vorherigen Fitness des Agenten.
Die Methode Init initialisiert die Instanz S_TSmAgent. Parameter:
- coords - Anzahl der Koordinaten.
- sectorsPerCord - Anzahl der Sektoren für jede Koordinate.
Logik:
1. Größenänderung der Arrays der schwarzen und der weißen Listen auf die Anzahl der Koordinaten.
2. Initialisierung der einzelnen Sektoren in einer Schleife über alle Koordinaten:
- Größenänderung des Arrays sector der schwarze Liste auf die aktuelle Koordinate.
- Dasselbe gilt für die weiße Liste.
- Initialisieren von allen Elementen der weißen und schwarzen Liste mit Nullen (dies sind Zähler, die später um eins erhöht werden).
3. fPrev-Initialisierung - Setze den Wert von fPrev auf -DBL_MAX, was den kleinstmöglichen Wert darstellt. Dies wird verwendet, um anzuzeigen, dass der Agent noch keine Fitness erworben hat.
Der Code erstellt eine Agentenstruktur, die schwarze und weiße Listen für Sektoren verschiedener Dimensionen des Suchraums verwalten kann, wobei es notwendig ist, den Überblick über die erlaubten und verbotenen Sektoren zu behalten, die die Agenten besuchen dürfen.
//—————————————————————————————————————————————————————————————————————————————— struct S_TSmSector { int sector []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— struct S_TSmAgent { S_TSmSector blacklist []; //black list by sectors of each coordinate S_TSmSector whitelist []; //white list by sectors of each coordinate double fPrev; //previous fitness void Init (int coords, int sectorsPerCord) { ArrayResize (blacklist, coords); ArrayResize (whitelist, coords); for (int i = 0; i < coords; i++) { ArrayResize (blacklist [i].sector, sectorsPerCord); ArrayResize (whitelist [i].sector, sectorsPerCord); ArrayInitialize (blacklist [i].sector, 0); ArrayInitialize (whitelist [i].sector, 0); } fPrev = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Beschreibung der Klasse C_AO_TSm, die von der Basisklasse C_AO ebgeleitet wurde.
1. Der Konstruktor setzt Anfangswerte für Variablen:
- popSize - Die Populationsgröße beträgt 50.
- sectorsPerCoord - Anzahl der Sektoren pro Koordinate ist 100.
- bestProbab - die Wahrscheinlichkeit, die beste Lösung zu wählen, beträgt 0,8.
- Es erstellt und initialisiert das Array params mit drei Parametern, die den oben genannten Variablen entsprechen.
2. Die Methode SetParams setzt die Werte von Parametern aus dem Array params zurück auf die entsprechenden Klassenvariablen.
3. Die Methode Init initialisiert den Algorithmus mit den angegebenen Bereichen und Suchschritten.
4. Moving() - die Methode ist für das Verschieben von Agenten im Suchraum zuständig, während Revision() aktuelle Lösungen mit Hilfe der Tabu-Suche-Logik überprüft und aktualisiert.
5. Mitglieder der Klasse:
- S_Agent agents [] - Array von Agenten, die Lösungen für das Problem im Suchprozess darstellen.
6. Private Methoden:
- InitializePopulation() - die Methode zur Initialisierung einer Population von Agenten.
- UpdateLists() - die Methode zur Aktualisierung der schwarzen und weißen Listen der Sektoren für Agenten.
- GenerateNewCoordinates() - die Methode zur Erzeugung neuer Koordinaten während der Suche.
- GetSectorIndex() - die Methode zur Ermittlung eines Sektorindexes auf der Grundlage von Koordinaten und Abmessungen.
- ChooseSectorFromWhiteList() - die Methode zur Auswahl eines Sektors aus der weißen Liste für einen bestimmten Bearbeiter und eine bestimmte Dimension.
- GenerateCoordInSector() - die Methode zur Erzeugung einer Koordinate in einem bestimmten Sektor.
- IsInBlackList() - die Methode zum Testen der Leistung der Wahrscheinlichkeit der Auswahl eines anderen Sektors mit Auswirkungen auf die Auswahl der weißen und schwarzen Listen.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_TSm : public C_AO { public: //-------------------------------------------------------------------- C_AO_TSm () { ao_name = "TSm"; ao_desc = "Tabu Search M"; ao_link = "https://www.mql5.com/en/articles/15654"; popSize = 50; sectorsPerCoord = 100; bestProbab = 0.8; ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "sectorsPerCoord"; params [1].val = sectorsPerCoord; params [2].name = "bestProbab"; params [2].val = bestProbab; } void SetParams () { popSize = (int)params [0].val; sectorsPerCoord = (int)params [1].val; bestProbab = params [2].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- int sectorsPerCoord; double bestProbab; S_TSmAgent agents []; private: //------------------------------------------------------------------- void InitializePopulation (); void UpdateLists (); void GenerateNewCoordinates (); int GetSectorIndex (double coord, int dimension); int ChooseSectorFromWhiteList (int agentIndex, int dimension); double GenerateCoordInSector (int sectorIndex, int dimension); bool IsInBlackList (int agentIndex, int dimension, int sectorIndex); }; //——————————————————————————————————————————————————————————————————————————————
Es ist an der Zeit, die Methode Init der Klasse C_AO_TSm zu betrachten, die für die Initialisierung des Algorithmus Tabu-Suche verantwortlich ist. Schlüsseln wir sie Stück für Stück auf:
1. Die Methode ruft zunächst StandardInit auf, indem sie die Arrays mit den Minimal- und Maximalwerten und den Schritten an sie übergibt. Dies ist eine Standardinitialisierung, die die Algorithmusparameter einrichtet. Als Nächstes wird die Größe des Agenten-Arrays anhand von popSize angepasst und die Anzahl der Agenten in der Population festgelegt. Als Nächstes folgt eine Schleife, die jeden Agenten im Array der Agenten durchläuft. Die Methode Init wird für jeden Agenten aufgerufen. Die Methode initialisiert ihre Parameter, darunter Koordinaten (coords) und die Anzahl der Sektoren pro Koordinate (sectorsPerCoord).
2. Wenn alle Initialisierungsschritte erfolgreich sind, gibt die Methode true zurück und zeigt damit die erfolgreiche Initialisierung des Algorithmus an.
Die Methode Init ist der Schlüssel zur Vorbereitung des Tabu-Suche-Algorithmus auf die Arbeit. Er legt die Suchbereiche fest, initialisiert die Agentengruppe und bereitet sie auf die weitere Lösungssuche vor. Tritt in irgendeiner Phase der Initialisierung ein Fehler auf, bricht die Methode ab und gibt false zurück.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSm::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agents, popSize); for (int i = 0; i < popSize; i++) agents [i].Init (coords, sectorsPerCoord); return true; } //——————————————————————————————————————————————————————————————————————————————
Betrachten wir nun die Methode Moving der Klasse C_AO_TSm. Die Logik der Methode:
- if (!revision) - hier wird die logische Variable revision geprüft. Wenn sie falsch ist (die Initialisierung wurde noch nicht durchgeführt), wird der nächste Codeblock ausgeführt.
- InitializePopulation() - ist verantwortlich für die Initialisierung der Agentenpopulation.
Bei der zweiten und den folgenden Iterationen des Algorithmus wird die Methode GenerateNewCoordinates() aufgerufen. Die Methode erzeugt neue Koordinaten (neue Lösungen) für Agenten im Suchprozess.
Die Methode Moving verwaltet bewegliche Agenten im Algorithmus Tabu-Suche. Sie prüft zunächst, ob die Population initialisiert wurde. Ist dies nicht der Fall, wird die Population initialisiert, andernfalls erzeugt die Methode neue Koordinaten für die Agenten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::Moving () { //---------------------------------------------------------------------------- if (!revision) { InitializePopulation (); revision = true; return; } //---------------------------------------------------------------------------- GenerateNewCoordinates (); } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision ist für die Aktualisierung der aktuell besten Lösung während Tabu-Suche zuständig. Sie geht alle Lösungen in der Population durch, vergleicht ihre Punktzahlen mit dem aktuell besten Wert und aktualisiert die entsprechenden Variablen, wenn er eine bessere Lösung findet. Am Ende der Methode werden die weißen und schwarzen Listen aktualisiert, was für die weitere Ausführung des Algorithmus erforderlich ist.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::Revision () { //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c); } } //---------------------------------------------------------------------------- UpdateLists (); } //——————————————————————————————————————————————————————————————————————————————
Die nächste Methode InitializePopulation ist für die Initialisierung der Population der Tabu-Suche-Agenten zuständig. Es generiert Zufallswerte für jede Agentenkoordinate in vorgegebenen Bereichen und legt auch den Anfangswert für die vorherige Punktzahl jedes Agenten fest. Dies ist für weitere Iterationen des Algorithmus erforderlich, bei denen die Bewertung und Aktualisierung der Lösungen erfolgt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::InitializePopulation () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } agents [i].fPrev = -DBL_MAX; } } //——————————————————————————————————————————————————————————————————————————————
Als Nächstes folgt die Methode UpdateLists der Klasse C_AO_TSm. Die Logik der Methode:
- Die äußere Schleife durchläuft alle Agenten in der Population, wobei popSize die Populationsgröße ist.
- Die innere Schleife durchläuft alle Koordinaten der einzelnen Agenten.
- Für jede c-Koordinate des Agenten a [i] wird der Sektorindex mit Hilfe der Methode GetSectorIndex berechnet. Dies ist notwendig, um die Werte für die weitere Analyse bestimmten Sektoren zuzuordnen.
- Wenn die aktuelle Punktzahl a [i].f des Agenten seine vorherige Punktzahl agents [i].fPrev übersteigt, bedeutet dies, dass der Agent seine Entscheidung verbessert hat. In diesem Fall wird der Zähler der weißen Liste für den betreffenden Sektor erhöht.
- Ist die aktuelle Punktzahl niedriger als die vorherige, bedeutet dies, dass der Agent seine Entscheidung verschlechtert hat, und der Zähler der schwarzen Liste für den entsprechenden Sektor wird erhöht.
- Nachdem alle Koordinaten abgearbeitet wurden, wird die vorherige Schätzung des Agenten auf den aktuellen Wert aktualisiert, damit sie in der nächsten Iteration mit dem neuen Wert verglichen werden kann.
Die Methode UpdateLists ist für die Aktualisierung der Listen (weiß und schwarz) für jeden Agenten in der Population auf der Grundlage seiner aktuellen und früheren Punktzahlen verantwortlich. So kann Tabu-Suche verfolgen, welche Sektoren erfolgreich waren (weiße Liste) und welche nicht (schwarze Liste). So hilft die Methode bei der weiteren Steuerung der Lösungssuche, indem sie das erneute Aufsuchen ineffizienter Bereiche des Lösungsraums vermeidet.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::UpdateLists () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { int sectorIndex = GetSectorIndex (a [i].c [c], c); if (a [i].f > agents [i].fPrev) { agents [i].whitelist [c].sector [sectorIndex]++; } else if (a [i].f < agents [i].fPrev) { agents [i].blacklist [c].sector [sectorIndex]++; } } agents [i].fPrev = a [i].f; } } //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns nun die Methode GenerateNewCoordinates der Klasse C_AO_TSm an. Die Logik der Methode:
- Die äußere Schleife durchläuft alle Agenten in der Population, wobei popSize die Populationsgröße ist.
- Die innere Schleife durchläuft alle Koordinaten der einzelnen Agenten.
- Zunächst wird die Wahrscheinlichkeit mit der RNDprobab-Methode überprüft. Wenn die Wahrscheinlichkeit erfüllt ist, erhält der Agent eine Koordinate aus der besten globalen Lösung cB [c].
- Ist die Wahrscheinlichkeit nicht erfüllt, wird mit der Methode ChooseSectorFromWhiteList() ein Sektor aus der weißen Liste ausgewählt.
- Dann wird mit der Methode GenerateCoordInSector() eine neue Koordinate in diesem Sektor erzeugt.
- Befindet sich der ausgewählte Sektor in der schwarzen Liste, wird mit u.RNDminusOne() ein neuer Sektor nach dem Zufallsprinzip ausgewählt und eine neue Koordinate darin erzeugt.
- Prüft, ob die neue Koordinate innerhalb der angegebenen Grenzen und mit dem erforderlichen Schritt liegt.
Die Methode GenerateNewCoordinates ist für die Erzeugung neuer Koordinaten für jeden Agenten in der Population zuständig. Es verwendet einen probabilistischen Ansatz, um zwischen den besten bekannten Koordinaten und der zufälligen Generierung in Sektoren auf der Grundlage von weißen und schwarzen Listen zu wählen. Die Methode stellt auch die Gültigkeit der Koordinaten sicher, indem sie sie auf die Einhaltung der festgelegten Grenzen überprüft.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::GenerateNewCoordinates () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < bestProbab) { a [i].c [c] = cB [c]; } else { int sectorIndex = ChooseSectorFromWhiteList (i, c); double newCoord = GenerateCoordInSector (sectorIndex, c); if (IsInBlackList (i, c, sectorIndex)) { sectorIndex = u.RNDminusOne (sectorsPerCoord); newCoord = GenerateCoordInSector (sectorIndex, c); } newCoord = u.SeInDiSp (newCoord, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newCoord; } } } } //——————————————————————————————————————————————————————————————————————————————
Analysieren wir nun den Code der Funktion GetSectorIndex, die den Sektorindex für eine bestimmte Koordinate in der angegebenen Dimension angibt. Die Funktionslogik:
- Wenn der maximale und der minimale Wert eines Bereichs für eine bestimmte Dimension gleich sind, bedeutet dies, dass der Bereich keine Länge hat. In diesem Fall gibt die Funktion sofort 0 zurück, da es keine Möglichkeit gibt, den Bereich in Sektoren zu unterteilen.
- Anschließend wird die Länge eines Sektors sL berechnet, indem die Länge des Bereichs durch die Anzahl der Sektoren sectorsPerCoord geteilt wird.
- Der Sektorindex ind wird anhand einer Gleichung berechnet, die bestimmt, in welche Branche eine bestimmte Koordinate fällt. Zunächst wird der Mindestwert des Bereichs von der Koordinate abgezogen, dann wird das Ergebnis durch die Länge des Sektors geteilt und der resultierende Wert auf die nächste Ganzzahl abgerundet.
- Ist die Koordinate gleich dem Maximalwert des Bereichs, gibt die Funktion den Index des letzten Sektors zurück.
- Weitere Kontrollen stellen sicher, dass der Index die zulässigen Werte nicht überschreitet. Wenn der Index größer oder gleich der Anzahl der Sektoren ist, wird der letzte Sektor zurückgegeben. Wenn der Index kleiner als 0 ist, wird 0 zurückgegeben.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_TSm::GetSectorIndex (double coord, int dimension) { if (rangeMax [dimension] == rangeMin [dimension]) return 0; double sL = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord; int ind = (int)MathFloor ((coord - rangeMin [dimension]) / sL); // Special handling for max value if (coord == rangeMax [dimension]) return sectorsPerCoord - 1; if (ind >= sectorsPerCoord) return sectorsPerCoord - 1; if (ind < 0) return 0; return ind; } //——————————————————————————————————————————————————————————————————————————————
Kommen wir nun zur Methode ChooseSectorFromWhiteList, die einen Sektor aus der „weißen Liste“ der Sektoren für einen bestimmten Agenten und eine bestimmte Dimension auswählt. Die Methode gibt den Index des ausgewählten Sektors zurück. Die Logik der Methode:
- Die Variable totalCount wird mit Null initialisiert. Sie wird verwendet, um die Gesamtzahl der „Häkchen“ in den Sektoren der weißen Liste zu zählen.
- Wenn totalCount gleich Null ist, bedeutet dies, dass die Sektoren noch keine „Häkchen“ enthalten und alle Sektoren gleich sind. In diesem Fall wählt die Methode einen zufälligen Sektor aus allen verfügbaren Sektoren aus und gibt ihn zurück.
- Anschließend wird die Anzahl der „Häkchen“ in der Schleife kumulativ gezählt. Wenn randomValue kleiner oder gleich dem aktuellen kumulativen Wert ist, gibt die Methode den Index des aktuellen Sektors s zurück. Auf diese Weise kann ein Sektor proportional zu seinem Gewicht auf der weißen Liste ausgewählt werden.
Die Methode ChooseSectorFromWhiteList ermöglicht die Auswahl eines Sektors aus der Whitelist für einen Agenten auf der Grundlage einer Wahrscheinlichkeitsverteilung, die eine Roulette-Auswahl simuliert.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_TSm::ChooseSectorFromWhiteList (int agentIndex, int dimension) { int totalCount = 0; for (int s = 0; s < sectorsPerCoord; s++) { totalCount += agents [agentIndex].whitelist [dimension].sector [s]; } if (totalCount == 0) { int randomSector = u.RNDminusOne (sectorsPerCoord); return randomSector; } int randomValue = u.RNDminusOne (totalCount); int cumulativeCount = 0; for (int s = 0; s < sectorsPerCoord; s++) { cumulativeCount += agents [agentIndex].whitelist [dimension].sector [s]; if (randomValue <= cumulativeCount) { return s; } } return sectorsPerCoord - 1; } //——————————————————————————————————————————————————————————————————————————————
Analysieren wir nun die Methode GenerateCoordInSector, die eine zufällige Koordinate in einem bestimmten Sektor für eine bestimmte Dimension erzeugt. Die Logik der Methode:
- Die Sektorgröße für eine bestimmte Dimension wird berechnet.
- sectorStart wird berechnet als der Mindestwert des Bereichs für eine bestimmte Dimension plus einem Offset, der dem Sektorindex multipliziert mit der Sektorgröße entspricht. sectorEnd ist definiert als sectorStart plus sectorSize. Damit werden die Grenzen des Sektors festgelegt.
- Als Nächstes wird die Funktion RNDfromCI aufgerufen. Die Funktion erzeugt einen Zufallswert von sectorStart bis sectorEnd. Dieser Wert steht für eine Koordinate, die innerhalb des angegebenen Sektors erzeugt wurde.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_TSm::GenerateCoordInSector (int sectorIndex, int dimension) { double sectorSize = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord; double sectorStart = rangeMin [dimension] + sectorIndex * sectorSize; double sectorEnd = sectorStart + sectorSize; double newCoord = u.RNDfromCI (sectorStart, sectorEnd); return newCoord; } //——————————————————————————————————————————————————————————————————————————————
Analysieren Sie abschließend die Methode IsInBlackList, die prüft, ob der Agent auf der „schwarzen Liste“ für einen bestimmten Sektor und eine bestimmte Dimension steht. Parameter:
- agentIndex - der Index des Agenten, für den die Prüfung durchgeführt wird.
- Dimension - der Index der Dimension.
- sectorIndex - der Index des zu prüfenden Sektors.
Die Methode liefert true, wenn der Agent auf der schwarzen Liste steht und die Wahrscheinlichkeit für einen Wechsel des Sektors erfüllt ist, wobei die „Leistungen“ des Sektors gemäß der weißen Liste berücksichtigt werden.
- blackCount und whiteCount ermitteln die Anzahl der Einträge in den schwarzen bzw. weißen Listen für den angegebenen Bearbeiter, die Dimension und den Sektor.
- Die Gesamtzahl der Einträge totalCount wird als Summe der schwarzen und weißen Einträge berechnet.
- Wenn die Gesamtzahl der Datensätze Null ist, gibt die Methode sofort false zurück, was bedeutet, dass der Agent nicht auf die schwarze Liste gesetzt werden kann, da es keine schwarzen oder weißen Einträge gibt.
- Anschließend wird die Wahrscheinlichkeit berechnet, dass ein bestimmter Sektor auf die schwarze Liste gesetzt wird. Dazu wird die Anzahl der schwarzen Einträge durch die Gesamtzahl der Einträge geteilt.
- Die Methode RNDprobab() erzeugt eine Zufallszahl zwischen 0 und 1. Ist diese Zufallszahl kleiner als die berechnete Wahrscheinlichkeit der schwarzen Liste blackProbability, gibt die Methode true zurück.
Die Methode IsInBlackList berücksichtigt sowohl schwarze als auch weiße Einträge, um die Wahrscheinlichkeit zu bestimmen, dass ein Sektor auf der schwarzen Liste steht und geändert werden muss. Je größer die Anzahl der Einträge in der schwarzen Liste im Vergleich zu den Einträgen in der weißen Liste ist, desto höher ist die Wahrscheinlichkeit, dass der Sektor in Zukunft in einen anderen zufälligen Sektor wechselt.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSm::IsInBlackList (int agentIndex, int dimension, int sectorIndex) { int blackCount = agents [agentIndex].blacklist [dimension].sector [sectorIndex]; int whiteCount = agents [agentIndex].whitelist [dimension].sector [sectorIndex]; int totalCount = blackCount + whiteCount; if (totalCount == 0) return false; double blackProbability = (double)blackCount / totalCount; return u.RNDprobab () < blackProbability; } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Ergebnisse des TSm-Tests:
TSm|Tabu Search M|50.0|100.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8779456463913048
25 Hilly's; Func runs: 10000; result: 0.6143121517195806
500 Hilly's; Func runs: 10000; result: 0.2910412462428753
=============================
5 Forest's; Func runs: 10000; result: 0.9288481105123887
25 Forest's; Func runs: 10000; result: 0.5184350456698835
500 Forest's; Func runs: 10000; result: 0.19054478009120634
=============================
5 Megacity's; Func runs: 10000; result: 0.6107692307692308
25 Megacity's; Func runs: 10000; result: 0.3821538461538462
500 Megacity's; Func runs: 10000; result: 0.1215692307692319
=============================
All score: 4.53562 (50.40%)
Wie wir sehen können, funktioniert der Algorithmus recht gut. Sowohl bei den Testfunktionen als auch bei der Visualisierung gibt es gute Ergebnisse. Natürlich gibt es eine Streuung bei den Funktionen mit kleinen Dimensionen, aber wie Sie festgestellt haben, sind viele Algorithmen von diesem Phänomen betroffen. Beachten Sie die gute Fähigkeit des Algorithmus, die Mehrheit der signifikanten Oberflächenbereiche der untersuchten Funktion hervorzuheben.
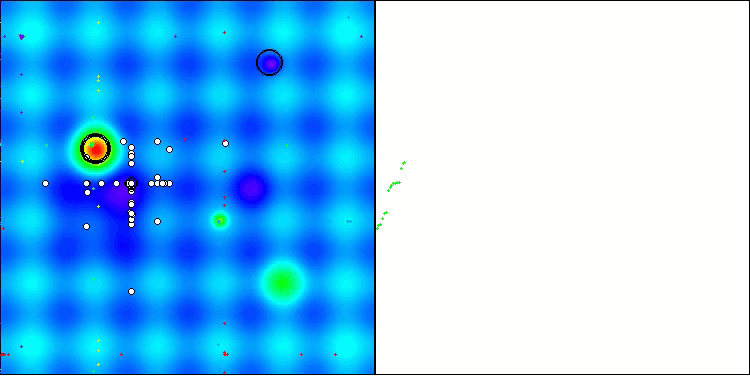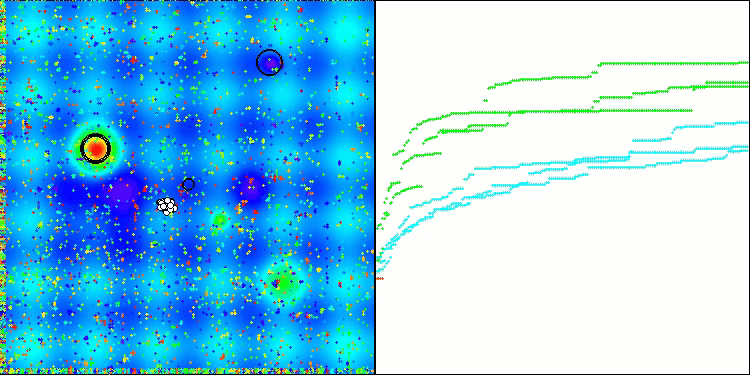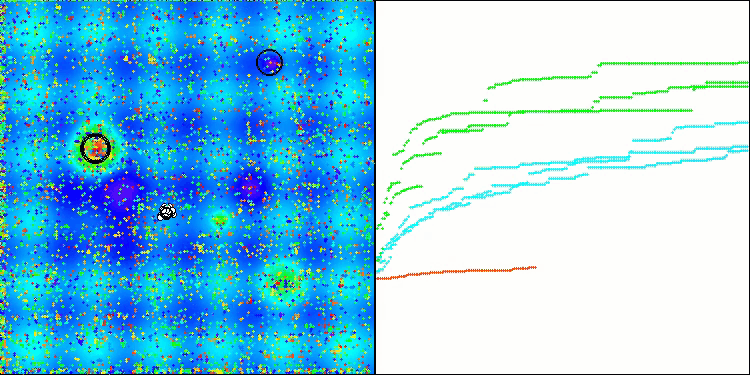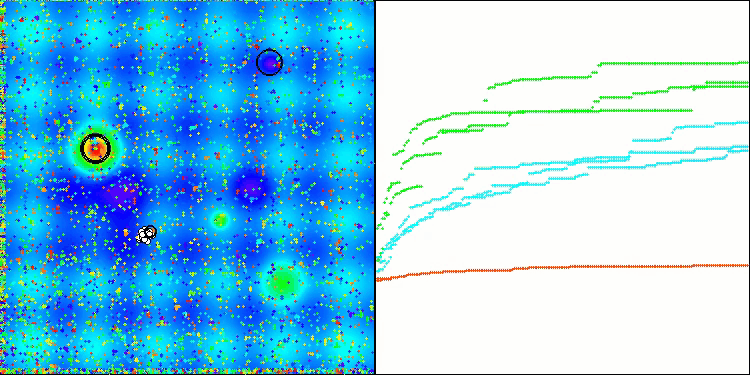
TSm mit der Testfunktion Hilly
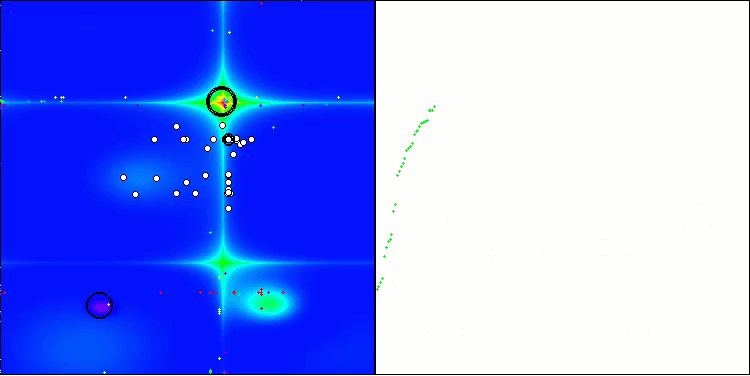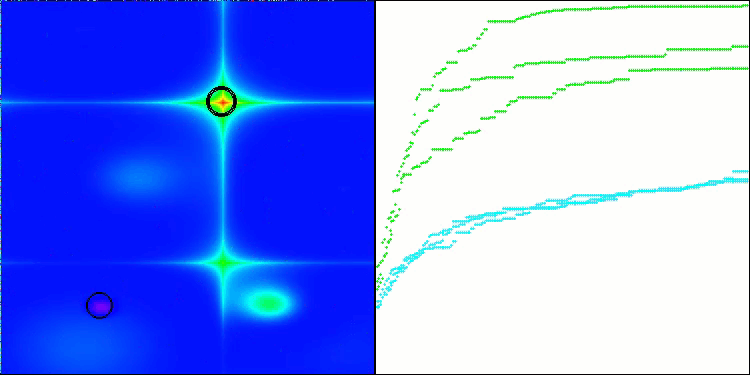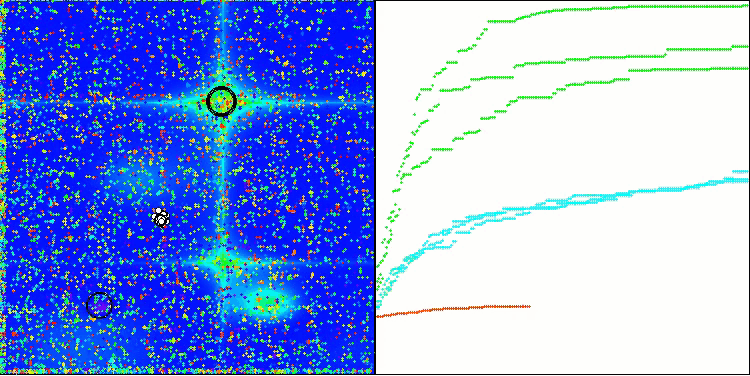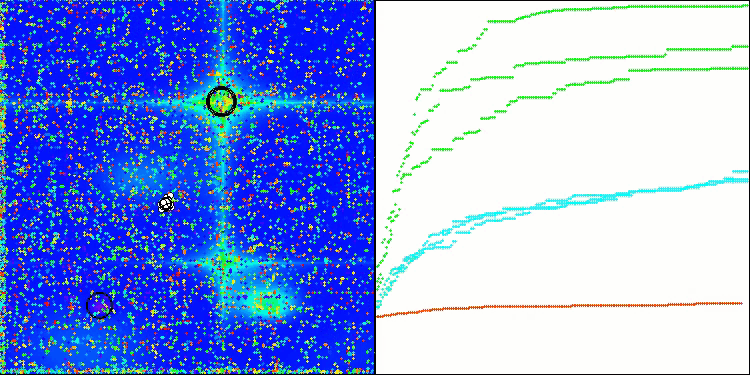
TSm mit der Testfunktion Forest
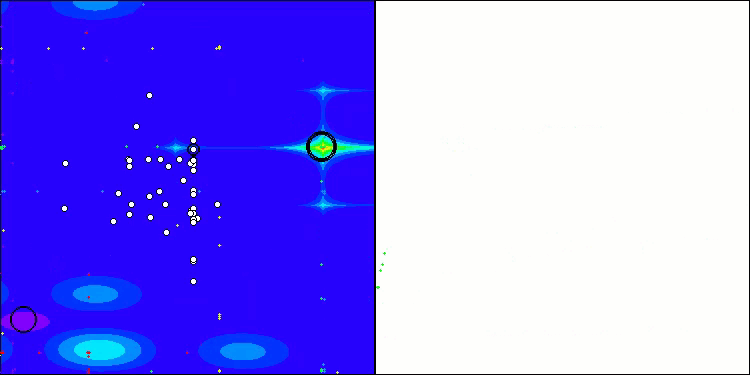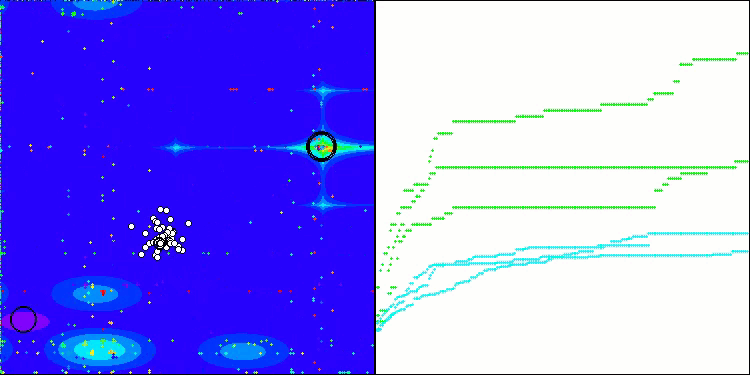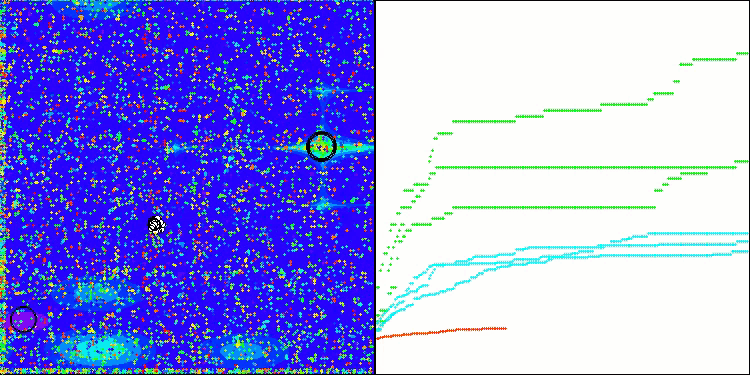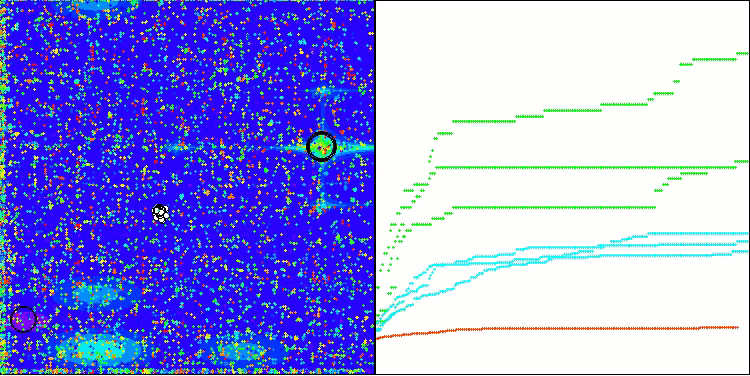
TSm mit der Testfunktion Megacity
Auf der Grundlage der Testergebnisse rangiert der Algorithmus in der Bewertungstabelle auf Platz 18. Dies ist ein überdurchschnittliches Ergebnis.
# | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Сode Lock Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 8 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 9 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 10 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 11 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 12 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 13 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 14 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 15 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 16 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 17 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 18 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 19 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 20 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 21 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 22 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 23 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 24 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 25 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 26 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 27 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 28 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 29 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 30 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 31 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 32 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 33 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 34 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 35 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 36 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 37 | AAA | Künstlicher Algenalgorithmus (AAA) | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 38 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 39 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 40 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 41 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 42 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 43 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 44 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 45 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
Zusammenfassung
Betrachtet man die Ergebnisse der Arbeit des Algorithmus mit Testfunktionen verschiedener Dimensionen, so ist festzustellen, dass der Algorithmus bei der glatten Hilly-Funktion größere Schwierigkeiten hat, mit großdimensionalen Problemen fertig zu werden. In anderen Tests zeigt der Algorithmus durchweg gute Ergebnisse.
Die vorgeschlagene Modifikation des bekannten Tabu-Suche-Algorithmus kann im Gegensatz zur ursprünglichen Version für alle allgemeinen Optimierungsprobleme in kontinuierlichen Suchräumen verwendet werden, einschließlich glatter und diskreter Probleme. Der Algorithmus kann als leistungsfähige Grundlage für die Anwendung der zugrunde liegenden Idee in anderen Algorithmen dienen. Um die Genauigkeit der Konvergenz zu verbessern, können wir die in den zuvor besprochenen Algorithmen angewandten Methoden verwenden, aber in diesem Stadium präsentiere ich die Änderung „wie sie ist“.
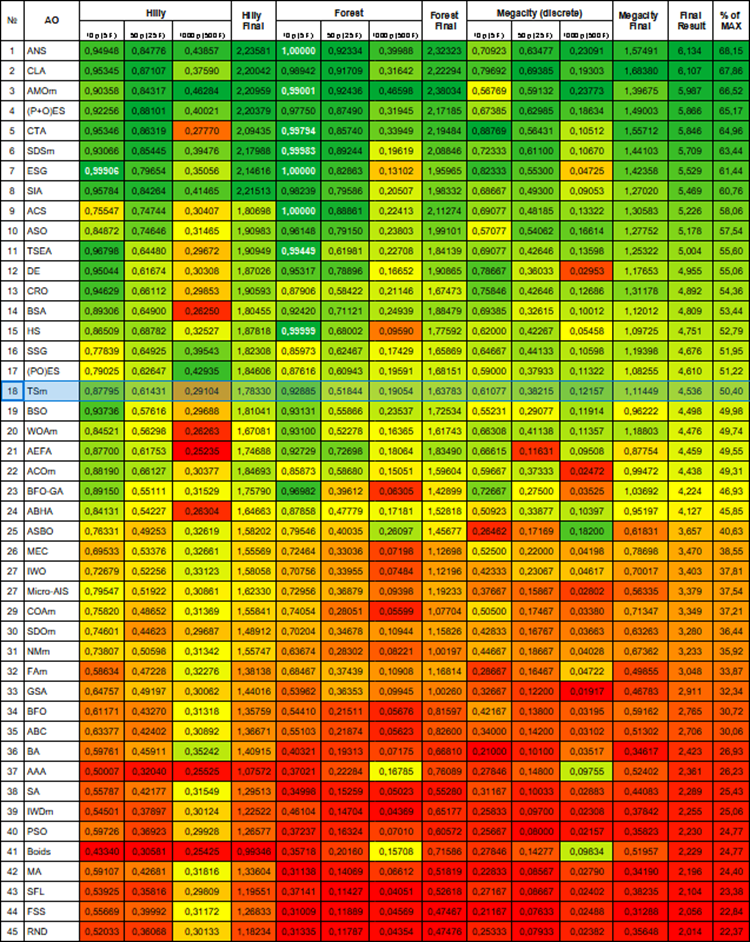
Abbildung 1. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
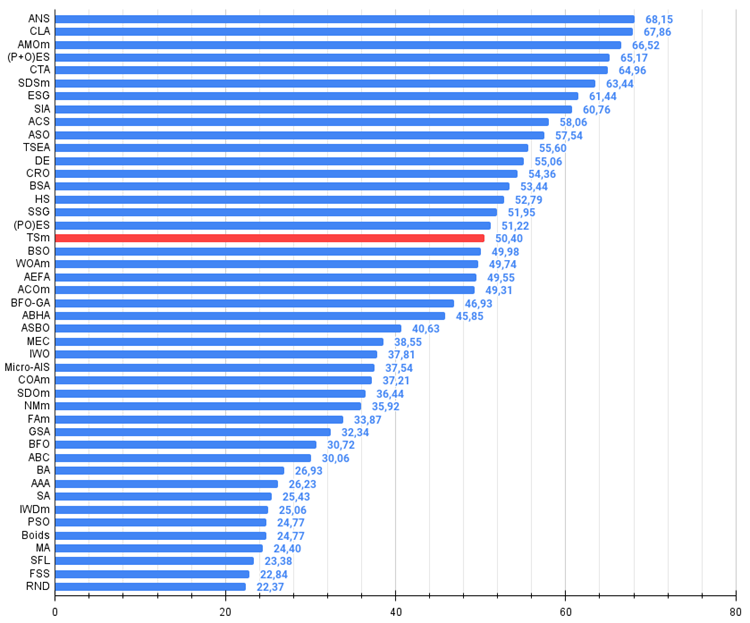
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
Vor- und Nachteile von TSm:
Vorteile:
- Eine vielversprechende Idee für weitere Verbesserungen und die Verwendung als Grundlage für neue Algorithmen.
- Gute Skalierbarkeit.
- Eine geringe Anzahl von intuitiven Parametern (nur zwei, außer der Bevölkerungsgröße).
Nachteile
- Die Konvergenzgenauigkeit hätte besser sein können.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15654
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronales Netz in der Praxis: Das erste Neuron
Neuronales Netz in der Praxis: Das erste Neuron
 Implementierung eines Schnellfeuer-Handelsstrategie-Algorithmus mit parabolischem SAR und einfachem gleitenden Durchschnitt (SMA) in MQL5
Implementierung eines Schnellfeuer-Handelsstrategie-Algorithmus mit parabolischem SAR und einfachem gleitenden Durchschnitt (SMA) in MQL5
 MQL5 beherrschen, vom Anfänger zum Profi (Teil V): Grundlegende Operatoren für die Ablaufkontrolle
MQL5 beherrschen, vom Anfänger zum Profi (Teil V): Grundlegende Operatoren für die Ablaufkontrolle
 Neuronale Netze im Handel: Hierarchische Vektortransformer (HiVT)
Neuronale Netze im Handel: Hierarchische Vektortransformer (HiVT)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.