Сode Lock Algorithmus (CLA)

Inhalt

1. Einführung
2. Implementierung des Algorithmus
3. Die Testergebnisse

1. Einführung

Zahlenschlösser, auch digitales Schloss oder Kombinations-Schloss genannt, sind Sicherheitsmechanismen, mit denen der Zugang zu Räumen, Tresoren, Schränken und anderen Objekten kontrolliert werden kann. Sie unterscheiden sich von gewöhnlichen Schlössern dadurch, dass sie nicht mit einem Schlüssel, sondern mit einer bestimmten Zahlenkombination geöffnet werden.

Zahlenschlösser sind in der Regel mit einer Tastatur, speziellen Zylindern oder anderen Drehmechanismen ausgestattet, die es dem Nutzer ermöglichen, eine Codefolge einzugeben. Sobald die richtige Kombination eingegeben wird, aktiviert das Zahlenschloss einen Mechanismus, der das Schloss entriegelt und es dem Nutzer ermöglicht, eine Tür zu öffnen oder auf den Inhalt eines Tresors zuzugreifen. Der Nutzer kann seine eigenen Codes einstellen oder den mitgelieferten Code zum Öffnen des Schlosses verwenden.

Vorteile des Zahlenschloss‘:

• Sicherheit. Zahlenschlösser können ein hohes Maß an Sicherheit bieten, insbesondere wenn die Codes regelmäßig geändert werden.
• Bequemlichkeit. Keine Schlüssel müssen mitgeführt werden, was die Verwendung von Zahlenschlösser sehr bequem macht.
• Die Möglichkeit, mehrere Codes einzustellen. Bei einigen Modellen können verschiedene Codes für unterschiedliche Nutzer oder für unterschiedliche Zeitintervalle eingestellt werden.

Zahlenschlösser werden in einer Vielzahl von Bereichen eingesetzt, z. B. in der Haussicherheit, in Geschäftsgebäuden, Hotels, Schulen, Büros und anderen Einrichtungen, in denen eine Zugangskontrolle erforderlich ist. Die Verwendung von Zahlenschlösser im Rahmen von Optimierungsalgorithmen kann eine interessante Idee sein. Eine mögliche Anwendung von Zahlenschlösser in Optimierungsalgorithmen könnte darin bestehen, ein System zu schaffen, das die Prinzipien von Zahlenschlösser zur Lösung von Optimierungsproblemen nutzt, z. B. zur Suche nach optimalen Parameterwerten bei Problemen des maschinellen Lernens oder zur Lösung anderer Optimierungsprobleme.

Das Funktionsprinzip des Zahlenschlösser, das auf der Eingabe der richtigen Zahlenkombination zum Entsperren beruht, kann mit den Mechanismen von Optimierungsalgorithmen verglichen werden, die versuchen, die optimale Lösung zu finden, indem sie iterativ die Parameter ändern und ihre Effizienz bewerten.

Man kann sich zum Beispiel einen Optimierungsalgorithmus vorstellen, der die Analogie des Zahlenschloss‘ wie folgt verwendet:

1. Kombination als Parameter. Die zu optimierenden Parameter können als eine „Kombination“ von Eingaben dargestellt werden.
2. Überprüfung der Gültigkeit der Kombination. Der Algorithmus kann die Werte der Parameter ändern und ihre Effizienz bewerten, ähnlich wie ein Nutzer verschiedene Kombinationen in ein Zahlenschloss eingibt, um ihre Gültigkeit zu überprüfen.
3. Optimale Lösung als Entsperrung. Wenn der Algorithmus optimale Parameterwerte findet, kann dies als „Freischaltung“ der optimalen Lösung betrachtet werden.

So inspirierten mich Zahlenschlösser dazu, einen Optimierungsalgorithmus zu entwickeln, mit dem sich optimale Lösungen für verschiedene Probleme finden lassen, darunter maschinelles Lernen und die Entwicklung von Handelssystemen.

2. Implementierung des Algorithmus

Stellen wir uns eine Population von Agenten als eine Population von Schlössern vor, wobei jedes Schloss eine Lösung für ein Problem darstellt. Dann können wir einen ungefähren Pseudocode für den Zahlenschloss-Algorithmus skizzieren:

1. Initialisierung:
      Erstelle ein Array von Zahlenschlösser der Größe popSize. Jedes Zahlenschloss (code lock) hat coords Sätze von Zahlenscheiben (disks), und jeder Satz hat lockDiscs Zahlenscheiben.
2. Auswahl einer Kombination von Schlössern:
      Wenn dies der erste Schritt ist, initialisiere jede Scheibe von jedem Satz von jedem Zahlenschloss mit einer Zufallszahl zwischen 0 und 9.
      Andernfalls, für jedes Zahlenschloss:
         - Wenn eine Zufallszahl kleiner als copyProb ist, wird ein Satz von Zahlenscheiben aus einem zufällig ausgewählten Zahlenschloss kopiert.
         - Andernfalls für jeden Satz von Zahlenscheiben:
            - Wenn eine Zufallszahl kleiner als rotateProb ist, wird die Scheibe auf eine Zufallszahl von 0 bis 9 gesetzt.
            - Andernfalls kopiere die Scheibe von einem zufällig ausgewählten Schloss.
3. Bewertung der Qualität der Zahlenkombinationen:
      Aktualisiere die Qualität der Kombinationen der einzelnen Schlösser.   
      Finde das Schloss mit der besten Kombinationsqualität und aktualisiere ggf. die global beste Lösung.
      Kopiere alle Schließungen in den gemeinsamen Schließkorb.
      Sortiere den Korb mit den Schlössern nach Fitness.
4. Wiederhole die Schritte 2 und 3 für die angegebene Anzahl von Epochen oder bis das Stoppkriterium erreicht ist.

Das Konzept ist recht spannend, aber einige Aspekte werfen noch Fragen auf. Insbesondere ist nicht ganz klar, wie der Kombinationscode im Schloss eine Lösung für ein Problem darstellen kann. Zum besseren Verständnis wäre es hilfreich, eine Illustration zu haben.

Stellen wir uns also vor, dass wir die Lösung für ein Problem, bei dem wir einen oder mehrere Parameter optimieren müssen, in Form eines Zahlenschloss darstellen. In diesem Fall kann jeder Parameter als Zahlenkombination dargestellt werden, wobei sich jede Zahl auf einer eigenen Scheibe befindet. Es können beliebig viele Zahlenscheiben vorhanden sein. Die Zahl wird als externer Parameter des Algorithmus angegeben. So wird jeder Parameter durch einen Satz von Scheiben mit digitalen Etiketten dargestellt.

Wenn zum Beispiel ein Aufgabenparameter einen Satz von 9 Scheiben mit Nummern von 0 bis 9 hat, kann die Kombination von 000000000 bis 999999999 reichen. Wir skalieren die resultierende Zahl in den Bereich von „min“ bis „max“ des entsprechenden Parameters. Wenn wir also z. B. drei optimierte Parameter haben, dann hat unser Zahlenschloss 3 x 9 = 27 digitale Scheiben. Abbildung 1 veranschaulicht den Kodierungsmechanismus für einen Parameter.

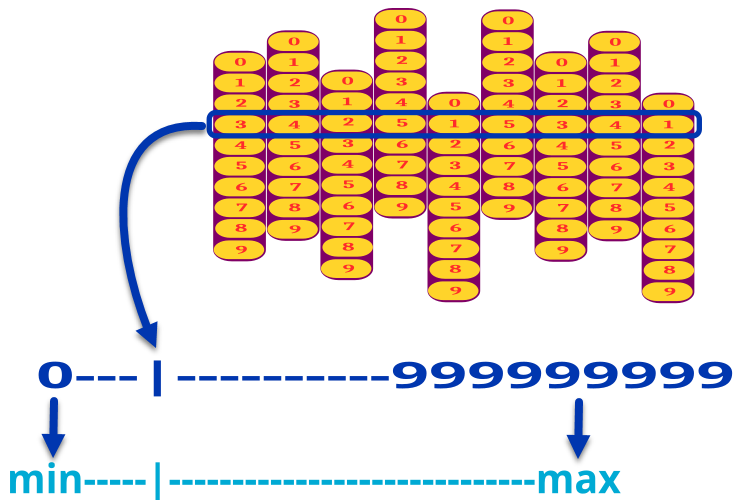
Abbildung 1. Dekodierung eines Aufgabenparameters aus einem digitalen Code in einen realen Wert

Die Operatoren in Optimierungsalgorithmen, wie Kreuzen und Mutation, werden in den CLA-Optimierungsalgorithmus mit Hilfe der Zahlenschloss-Idee integriert.

1. Kreuzen. Das Kreuzen in genetischen Algorithmen dient dazu, das genetische Material zweier Elternteile zu kombinieren, um Nachkommen zu erzeugen.

• Im Zusammenhang mit Zahlenschlösser können wir uns ein Kreuzen als eine Kombination von Scheibenwerten aus verschiedenen Schlössern vorstellen, um eine neue Kombination von kodierten Aufgabenparametern zu schaffen.
• Dieser Prozess bietet dem Algorithmus kombinatorische Möglichkeiten, neue Parameterkombinationen auszuprobieren, ähnlich wie ein Nutzer verschiedene Kombinationen in einem Zahlenschloss ausprobieren kann und dennoch die erfolgreichsten Zahlenkombinationen für verschiedene Schlösser verwendet.

2. Mutation. Bei genetischen Algorithmen ist Mutation die zufällige Veränderung des genetischen Materials, um Vielfalt in einer Population zu schaffen.

• Im Zusammenhang mit Zahlenschlösser kann Mutation als zufälliges Drehen der Scheiben in eine beliebige Zahlenposition interpretiert werden, um die Kombination im Zahlenschloss zu ändern.
• Dieser Prozess hilft dem Algorithmus, neue Parameterkombinationen im gesamten Lösungsraum zu erkunden und zu vermeiden, dass er in lokalen Optima stecken bleibt.

Im Allgemeinen kann die Integration von Kreuzen und Mutieren in den Optimierungsalgorithmus die Vielfalt der Lösungen erhöhen, die Konvergenz zur optimalen Lösung beschleunigen und eine vorzeitige Konvergenz vermeiden helfen. Dieser Ansatz kann bei Optimierungsproblemen mit großen Suchräumen und komplexen Zielfunktionen nützlich sein. In der Tat bleibt uns nichts anderes übrig, als die Scheiben zu drehen, indem wir die Analogie zu den genetischen Operatoren nutzen.

Um das Problem zu lösen, müssen wir die richtige Zahlenkombination auf dem Zahlenschloss wählen. Wir müssen die Scheiben drehen, um die richtige Codekombination zu finden, mit der wir das Schloss öffnen können. Im Gegensatz zu genetischen Algorithmen, bei denen durch „Rotation“ des binären Codewerts in den Genen die Wahrscheinlichkeit, einen Wert zu erhalten, 50/50 ist (entweder 0 oder 1), können wir beim Algorithmus für die Schlüsselkombination Wahrscheinlichkeitsverteilungen in der Strategie der Scheibenrotation verwenden. Lassen Sie uns einige Optionen in Betracht ziehen.

Wir können eine Gauß-Verteilung verwenden, bei der die Kombinationsparameter mutiert werden und jeder Parameter einen Zufallswert annimmt, der aus einer Normalverteilung (Gauß) ausgewählt wird. Dadurch können die Parameter nach dem Zufallsprinzip verändert werden, wobei ihr aktueller Wert bis zu einem gewissen Grad erhalten bleibt.

Die Verwendung einer Gauß-Verteilung für die Mutation kann nützlich sein, da sie die Kontrolle über den Grad der Parameteränderungen ermöglicht. Die Parameter können um kleine Werte in der Nähe der aktuellen verändert werden, was dazu beiträgt, die guten Eigenschaften der aktuellen Lösung zu bewahren, während der Zufallscharakter der Mutation dem Algorithmus erlaubt, neue Bereiche des Suchraums zu erkunden.

Die Verwendung einer Gauß-Verteilung für die Mutation kann also dazu beitragen, ein Gleichgewicht zwischen der Suche nach neuen Lösungen und der Beibehaltung der guten Eigenschaften der aktuellen Lösungen herzustellen, was die effiziente Suche nach der optimalen Lösung in komplexen Parameterräumen erleichtert.

Wir können auch eine Potenzgesetzverteilung für den Mutationsprozess verwenden. Im Gegensatz zur Gauß-Verteilung hat die Potenzgesetz-Verteilung schwerere Schwänze, was bedeutet, dass große Parameteränderungen wahrscheinlicher sind, was in Fällen nützlich sein kann, in denen eine radikalere Erkundung des Parameterraums erforderlich ist. Eine Leistungsverteilung kann dem Algorithmus helfen, aus lokalen Fallen „herauszuspringen“.

Wir können auch versuchen, eine dritte Option zu verwenden - die Gleichverteilung, die eine gleiche Wahrscheinlichkeit für die Wahl einer beliebigen Zahl auf der Sperrscheibe schafft.

Jetzt können wir vom theoretischen Teil zum Schreiben von Code und zur praktischen Forschung übergehen.

In dem CLA-Algorithmus des Agenten, der die Problemlösung darstellt, beschreiben wir die Sperre mit Hilfe der Struktur S_CLA_Agent. Hier sind seine wichtigsten Bestandteile:

• f ist eine Agententauglichkeit. Er wird mit -DBL_MAX initialisiert, was den kleinstmöglichen Wert für den Typ double bedeutet.
• struct S_Lock ist eine verschachtelte Struktur, die das Array der Schlösser enthält. Dieses Array wird verwendet, um die Zahlenkombination eines einzelnen zu optimierenden Auftragsparameters zu speichern.
• S_Lock code [] ist das Array der Struktur S_Lock. Diese gesamte Anordnung ist eine „Sperre“.
• void Init (int coords, int lockDiscs) ist eine Initialisierungsfunktion. Sie akzeptiert zwei Parameter: coords definiert die Anzahl der Parametersätze, und lockDiscs die Anzahl der Zahlenscheiben (disks) in jedem Satz. Innerhalb dieser Funktion wird das Array code initialisiert.

Insgesamt stellt diese Struktur einen Agenten des CLA-Optimierungsalgorithmus dar. Jeder Agent hat seine eigene Beschreibung der Fitness und der Zahlenkombination, die während der Ausführung des Algorithmus optimiert wird.

//——————————————————————————————————————————————————————————————————————————————
struct S_CLA_Agent
{
    double f;  //fitness

    struct S_Lock
    {
        int lock [];
    };

    S_Lock code [];


    void Init (int coords, int lockDiscs)
    {
      f = -DBL_MAX;

      ArrayResize (code, coords);

      for (int i = 0; i < coords; i++)
      {
        ArrayResize (code [i].lock, lockDiscs);
      }
    }
};
//——————————————————————————————————————————————————————————————————————————————

Nun beschreiben wir die Klasse C_AO_CLA, die von der Klasse C_AO abgeleitet ist. Hauptbestandteile der Klasse:

• C_AO_CLA () - Klassenkonstruktor, der das Klassenobjekt initialisiert. Solche Parameter wie popSize, lockDiscs, copyProb, rotateProb und params werden im Konstruktor initialisiert.
• SetParams () setzt die Algorithmusparameter auf der Grundlage der Werte im Array params.
• Init () ist eine Initialisierungsfunktion, die die Suchbereiche und die Anzahl der Epochen als Parameter annimmt.
• Moving () und Revision () sind die Funktionen, die zur Ausführung der Hauptlogik im Algorithmus verwendet werden.
• lockDiscs, copyProb und rotateProb sind die Variablen, die zum Speichern der Algorithmusparameter verwendet werden.
• S_CLA_Agent agent [] ist ein Array von Agenten. Jeder Agent ist ein Objekt der Struktur S_CLA_Agent.
• maxLockNumber, S_CLA_Agent parents [] und S_CLA_Agent parTemp [] sind private Variablen und Arrays, die innerhalb der Klasse verwendet werden.
• ArrayToNumber () und LockToDouble () sind private Methoden, mit denen ein Array einer Zahlenkombination in eine Zahl und ein Schloss in eine Gleitkommazahl umgewandelt werden kann.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CLA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CLA () { }
  C_AO_CLA ()
  {
    ao_name = "CLA";
    ao_desc = "Code Lock Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14878";

    popSize     = 100;   //population size

    lockDiscs   = 8;     //lock discs
    copyProb    = 0.8;   //copying probability
    rotateProb  = 0.03;  //rotate disc probability

    ArrayResize (params, 4);

    params [0].name = "popSize";     params [0].val = popSize;

    params [1].name = "lockDiscs";   params [1].val = lockDiscs;
    params [2].name = "copyProb";    params [2].val = copyProb;
    params [3].name = "rotateProb";  params [3].val = rotateProb;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;

    lockDiscs  = (int)params [1].val;
    copyProb   = params      [2].val;
    rotateProb = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    lockDiscs;    //lock discs
  double copyProb;     //copying probability
  double rotateProb;   //rotate disc probability

  S_CLA_Agent agent [];

  private: //-------------------------------------------------------------------
  int maxLockNumber; //max lock number

  S_CLA_Agent parents [];
  S_CLA_Agent parTemp [];

  int    ArrayToNumber (int &arr []);
  double LockToDouble  (int lockNum, int coordPos);
};
//——————————————————————————————————————————————————————————————————————————————

In der Klasse C_AO_CLA definieren wir die Methode Init. Diese Methode initialisiert den Algorithmus mit den angegebenen Suchbereichen und der Anzahl der Epochen. Beschreibung der einzelnen Schritte:

1. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - Aufruf der Funktion StandardInit mit den angegebenen Suchbereichen. Wenn die Initialisierung fehlschlägt, gibt die Funktion „false“ zurück.

2. ArrayResize (agent, popSize); - passt die Größe des Arrays „agent“ an die Populationsgröße popSize an.

3. for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs); - die Schleife initialisiert jeden Agenten in der Population mit der angegebenen Anzahl von Koordinaten coords und Zahlenscheiben lockDiscs.

4. ArrayResize (parents, popSize * 2); ArrayResize (parTemp, popSize * 2); - Ändern der Größe der Arrays parents und parTemp auf zwei Populationsgrößen.

5. for (int i = 0; i < popSize * 2; i++) { parents [i].Init (coords, lockDiscs); parTemp [i].Init (coords, lockDiscs); } - die Schleife initialisiert jedes Elternteil und temporäre Elternteil in den Arrays parents und parTemp.

6. maxLockNumber = 0; for (int i = 0; i < lockDiscs; i++) { maxLockNumber += 9 * (int)pow (10, i); } - die Schleife berechnet die maximale Zahl in der Zahlenkombinationen maxLockNumber anhand der Anzahl der Schlossscheibe (lockDiscs).

7. return true; - wenn alle vorherigen Operationen erfolgreich waren, gibt die Funktion „true“ zurück.

Die Funktion initialisiert Agenten und Eltern im CLA-Code-Sperr-Optimierungsalgorithmus und legt die maximale Anzahl von Zahlenkombinationen auf der Grundlage der Anzahl von Schlossscheiben fest.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_CLA::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs);

  ArrayResize (parents, popSize * 2);
  ArrayResize (parTemp, popSize * 2);

  for (int i = 0; i < popSize * 2; i++)
  {
    parents [i].Init (coords, lockDiscs);
    parTemp [i].Init (coords, lockDiscs);
  }

  maxLockNumber = 0;
  for (int i = 0; i < lockDiscs; i++)
  {
    maxLockNumber += 9 * (int)pow (10, i);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Auswahl von digitalen Kombinationen in Schlössern wird in der Methode Moving der Klasse C_AO_CLA beschrieben. Das Verfahren ist wie folgt:

• val = 0.0; code = 0; pos = 0; - Initialisierung der Variablen, die in der Methode verwendet werden sollen.
• if (!revision) {...} - der Codeblock wird ausgeführt, wenn revision „false“ ist. Innerhalb dieses Codeblocks werden die Agenten und Eltern mit Zufallswerten initialisiert. 
• Dann werden die Werte des Codes und val für jeden Agenten und jedes Elternteil berechnet und zur Aktualisierung der Koordinaten des Agenten verwendet. Danach wird die Revision auf „true“ gesetzt und die Funktion ist abgeschlossen.
• for (int i = 0; i < popSize; i++) {...} - der Codeblock wird ausgeführt, wenn revision „true“ ist. Die Agenten werden innerhalb des Codeblocks aktualisiert. Wenn eine Zufallszahl kleiner als copyProb ist, wird der Sperrcode eines der Elternteile auf den Agenten übertragen. Andernfalls wird der Sperrcode des Agenten entweder mit einem Zufallswert oder dem Zahlenschlüssel eines der Elternteile aktualisiert. 
• Anschließend werden die Werte von code und val für jeden Agenten berechnet. Diese Werte werden zur Aktualisierung der Koordinaten des Agenten verwendet.

Die Funktion wird zur Aktualisierung der Agenten im CLA-Optimierungsalgorithmus verwendet.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CLA::Moving ()
{
  double val  = 0.0;
  int    code = 0;
  int    pos  = 0;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int l = 0; l < lockDiscs; l++)
        {
          agent [i].code [c].lock [l] = u.RNDminusOne (10);
        }

        code = ArrayToNumber (agent [i].code [c].lock);
        val  = LockToDouble  (code, c);
        a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < popSize * 2; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int l = 0; l < lockDiscs; l++)
        {
          parents [i].code [c].lock [l] = u.RNDminusOne (10);
        }
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < copyProb)
      {
        int pos = u.RNDminusOne (popSize);
        ArrayCopy (agent [i].code [c].lock, parents [pos].code [c].lock, 0, 0, WHOLE_ARRAY);
      }
      else
      {
        for (int l = 0; l < lockDiscs; l++)
        {
          if (u.RNDprobab () < rotateProb)
          {
            //pos = u.RNDminusOne (popSize);
            //agent [i].code [c].lock [l] = (int)round (u.GaussDistribution (agent [i].codePrev [c].lock [l], 0, 9, 8));
            //agent [i].code [c].lock [l] = (int)round (u.PowerDistribution (agent [i].codePrev [c].lock [l], 0, 9, 20));
            agent [i].code [c].lock [l] = u.RNDminusOne (10);
          }
          else
          {
            pos = u.RNDminusOne (popSize);
            agent [i].code [c].lock [l] = parents [pos].code [c].lock [l];
          }
        }
      }

      code = ArrayToNumber (agent [i].code [c].lock);
      val  = LockToDouble  (code, c);
      a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision in der Klasse C_AO_CLA ist im Allgemeinen für die Aktualisierung der globalen Lösung gedacht. Die Methode geht folgendermaßen vor:

• ind = -1; - Initialisierung der Variable „ind“, die dazu dient, den Index des Agenten mit der besten Fitness zu verfolgen.
• for (int i = 0; i < popSize; i++) {...} - die Schleife durchläuft jeden Agenten in der Population und prüft, ob die Fitness des Agenten den aktuellen fB-Bestwert überschreitet. Ist dies der Fall, so wird fB aktualisiert und ind auf den aktuellen Index gesetzt.
• if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); - wenn der Agent mit der besten Fitness gefunden wurde, werden seine Koordinaten nach cB kopiert.
• for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; } - die Schleife aktualisiert die Fitness der einzelnen Agenten auf der Grundlage der aktuellen Werte im Array a.
• for (int i = 0; i < popSize; i++) { parents [i + popSize] = agent [i]; } - die Schleife kopiert jeden Agenten in das Eltern-Array, beginnend mit der Position popSize, also der zweiten Hälfte der Elternpopulation.
• u.Sorting (parents, parTemp, popSize * 2); - der String sortiert das Array parents unter Verwendung des Arrays parTemp als Zwischenspeicher.

Im Allgemeinen wird diese Funktion zur Aktualisierung der Fitness der Schlüssel von Agenten und Eltern im CLA-Algorithmus verwendet. Dabei wird der beste Fitnesswert aktualisiert und die Elternpopulation nach ihrer Fitness sortiert.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CLA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    parents [i + popSize] = agent [i];
  }

  u.Sorting (parents, parTemp, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode ArrayToNumber wandelt die Zeichen einer Schlüsselkombination in eine Zahl um. Methodische Maßnahmen:

• result = 0; - Initialisierung der Variablen, die zur Speicherung des Ergebnisses verwendet werden soll.
• for (int i = 0; i < ArraySize (arr); i++) {...} - die Schleife durchläuft jedes Element des Arrays arr. Für jedes Element von arr[i] multipliziert es das aktuelle Ergebnis mit 10 und addiert arr[i].
• return result; - die Zeichenfolge gibt das endgültigen Ergebnis zurück.

Im Allgemeinen wandelt diese Methode eine Reihe von Ganzzahlen in eine einzige Ganzzahl um, indem jedes Element der Reihe als eine Ziffer in der Dezimaldarstellung der Zahl interpretiert wird.

Zum Beispiel die Werte des Eingabe-Arrays arr (Codekombination): |0|3|1|5|7|0|. Wir müssen alle Nullen auf der linken Seite der Kombination weglassen und die Zahl ab dem Wert 3 bilden. Das Ergebnis ist die Nummer 31570. Wenn alle Zellen des Feldes in der Kombination Nullen enthalten, ist die endgültige Zahl 0.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_CLA::ArrayToNumber (int &arr [])
{
  int result = 0;
  for (int i = 0; i < ArraySize (arr); i++)
  {
    result = result * 10 + arr [i];
  }
  return result;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode LockToDouble in der Klasse C_AO_CLA wandelt die Nummer der Codekombination in den Maßstab des optimierten Parameters um. Diese Funktion ist folgendermaßen aufgebaut:

• LockToDouble (int lockNum, int coordPos) - die Methode benötigt zwei Parameter: lockNum ist die Schlossnummer coordPos und die Koordinatenposition im Koordinatenfeld (optimierter Parameter).
• return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]); - die Zeichenkette gibt den Wert zurück, den man durch Skalierung von lockNum aus dem Bereich von [0, maxLockNumber] bis [rangeMin [coordPos], rangeMax [coordPos]].
  

Im Allgemeinen wird diese Methode verwendet, um die Schlossnummer in eine Gleitkommazahl umzuwandeln, die auf einem bestimmten Bereich basiert. Mit anderen Worten: Die Schlossnummern werden in die Werte der optimierten Aufgabenparameter umgerechnet.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_CLA::LockToDouble (int lockNum, int coordPos)
{
  return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]);
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Die Ergebnisse des CLA-Optimierungsalgorithmus für die Testfunktionen sehen hervorragend aus. Das Erreichen von 67,86 % des höchstmöglichen Wertes ist ein hervorragendes Ergebnis. Dies beweist die hohe Leistungsfähigkeit des CLA-Algorithmus bei der Optimierung komplexer Funktionen.

Diese Ergebnisse zeigen, dass der CLA-Algorithmus sehr effektiv ist und erfolgreich auf verschiedene Probleme angewendet werden kann, bei denen eine Optimierung mehrdimensionaler Funktionen erforderlich ist. Seine Skalierbarkeit und seine Fähigkeit, komplexe Probleme zu bewältigen, machen es zu einem vielversprechenden Werkzeug für die Lösung eines breiten Spektrums von Optimierungsproblemen.

CLA|Code Lock Algorithm|100.0|8.0|0.8|0.03|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534490932631814
25 Hilly's; Func runs: 10000; result: 0.8710742215971827
500 Hilly's; Func runs: 10000; result: 0.375900385878165
=============================
5 Forest's; Func runs: 10000; result: 0.9894215656296362
25 Forest's; Func runs: 10000; result: 0.917091907561472
500 Forest's; Func runs: 10000; result: 0.3164221021938828
=============================
5 Megacity's; Func runs: 10000; result: 0.7969230769230768
25 Megacity's; Func runs: 10000; result: 0.693846153846154
500 Megacity's; Func runs: 10000; result: 0.19303076923077062
=============================
All score: 6.10716 (67.86%)

Bei der Visualisierung des Algorithmusbetriebs auf Testfunktionen ist bei Funktionen kleiner Dimension eine Streuung der Ergebnisse festzustellen, die jedoch mit zunehmender Anzahl der Aufgabenparameter verschwindet. Darüber hinaus ist das Potenzial des Algorithmus für große Probleme (1000 Parameter) an der Form der Konvergenzkurve (rote Linie) erkennbar. Die Linie wächst mit der Beschleunigung. Wenn wir die Begrenzung der Anzahl der Durchläufe der Fitnessfunktion (unsere Testregeln) aufheben, wird sich der Algorithmus weiterhin dem globalen Optimum nähern.

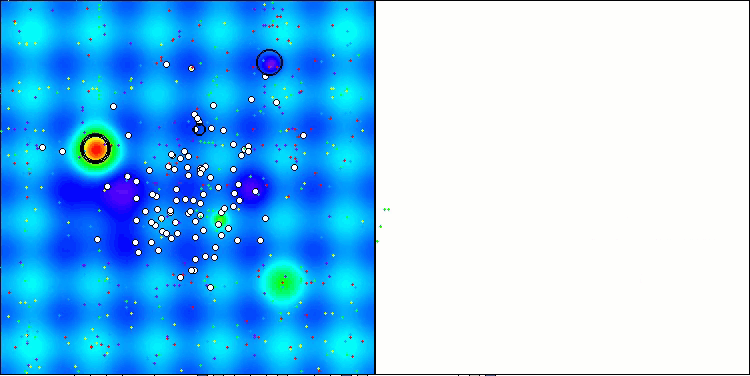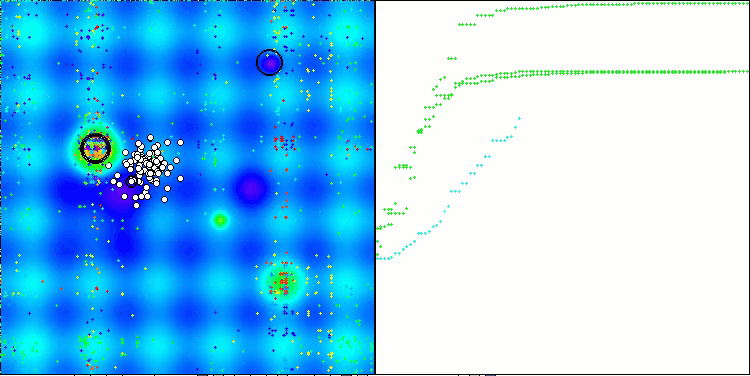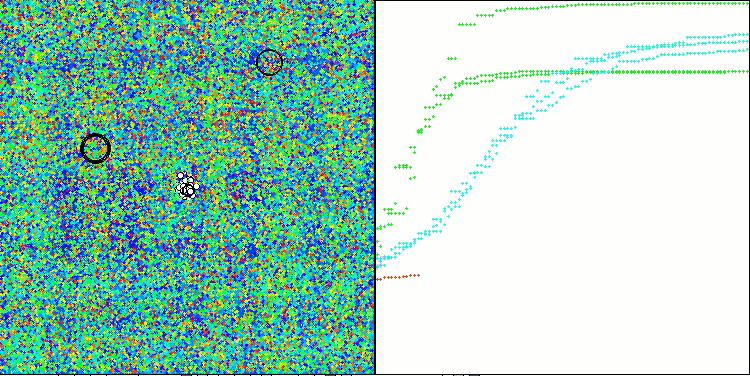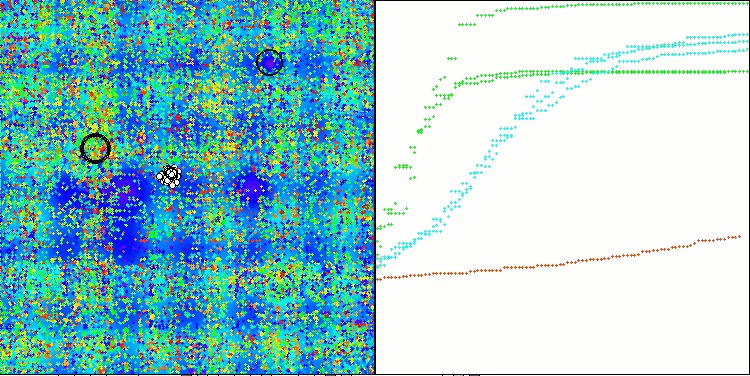
  CLA mit der Testfunktion Hilly

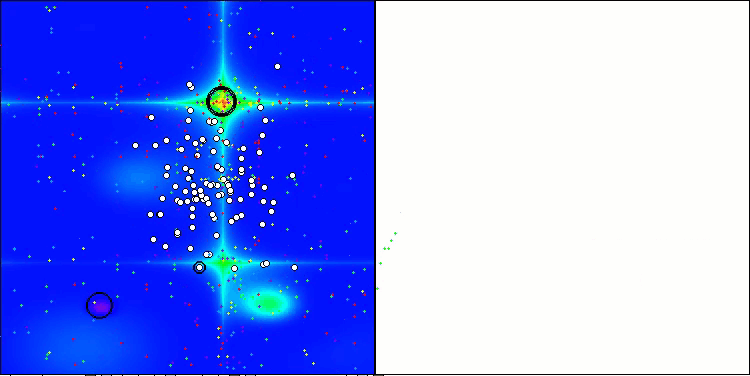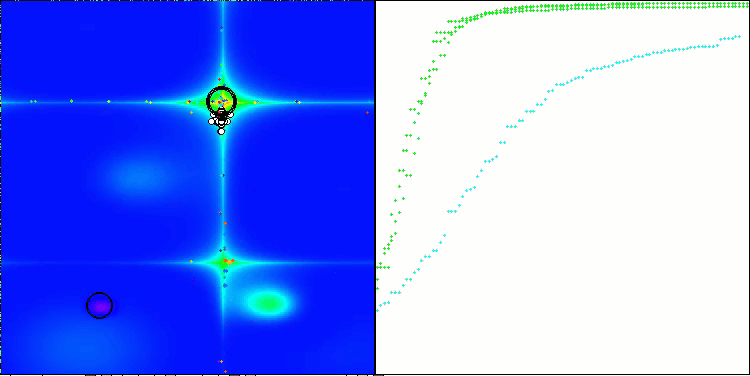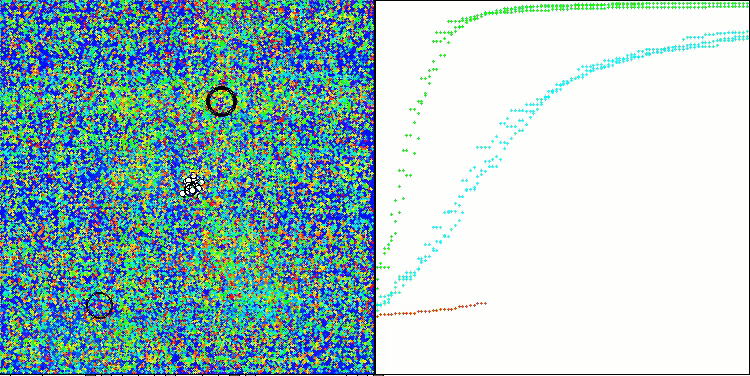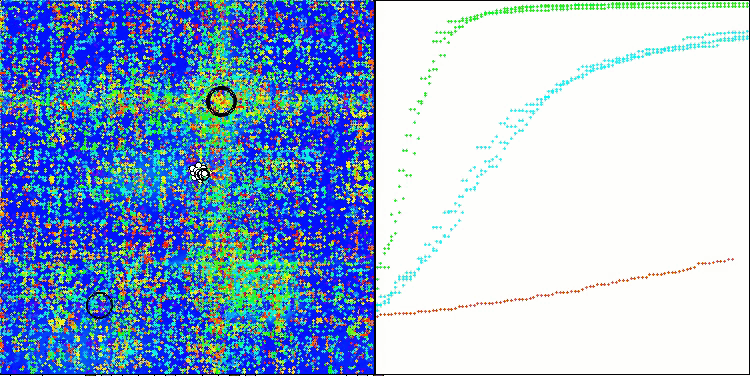
  GAV mit der Testfunktion Forest

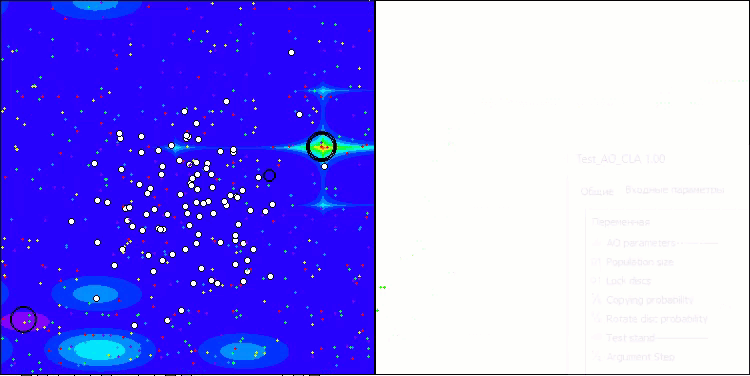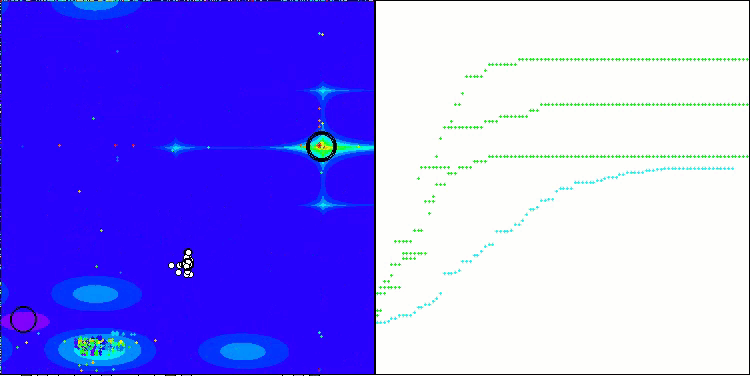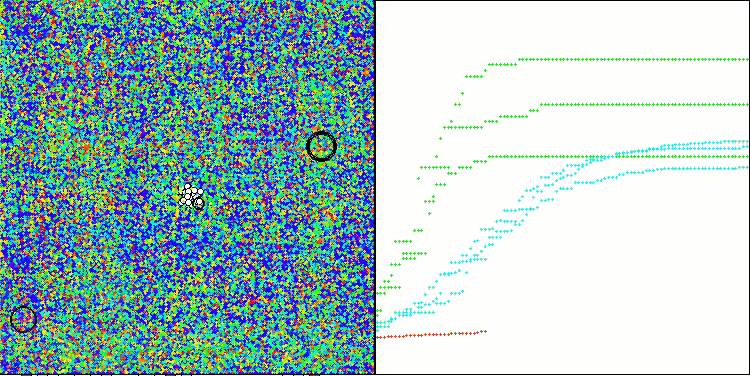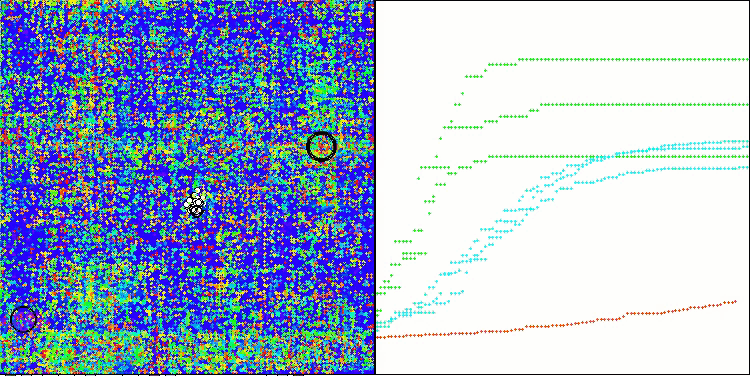
  CLA mit der Testfunktion Megacity

Der Zahlenschloss-Algorithmus belegte den zweiten Platz in der Rangliste. Bei der Funktion „sharp Forest“ mit 10 Parametern konnte CLA sogar den Tabellenführer BGA überholen. Die Farbe der Ergebniszellen für alle Testfunktionen ist grün (Vergleich mit allen Algorithmen in der Tabelle), was auf eine sehr einheitliche Leistung bei verschiedenen Aufgabentypen hinweist, ohne erkennbare Fehler bei einzelnen Tests. 

#	AO	Beschreibung	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binärer genetischer Algorithmus	0,99989	0,99518	0,42835	2,42341	0,96153	0,96181	0,32027	2,24360	0,91385	0,95908	0,24220	2,11512	6,782	75,36
2	CLA	Zahlenschloss-Algorithmus	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	(P+O)ES	(P+O) Entwicklungsstrategien	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
4	CTA	Kometenschweif-Algorithmus	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
5	SDSm	stochastische Diffusionssuche M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
6	ESG	Entwicklung der sozialen Gruppen	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
7	SIA	Simuliertes isotropes Abkühlen	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
8	TSEA	Schildkrötenpanzer-Evolutionsalgorithmus	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
9	DE	differentielle Evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
10	BSA	Vogelschwarm-Algorithmus	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
11	HS	Harmoniesuche	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
12	SSG	Setzen, Säen und Wachsen	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
13	(PO)ES	(PO) Entwicklungsstrategien	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
14	BSO	Brainstorming-Optimierung	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
15	WOAm	Wal-Optimierungsalgorithmus M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
16	ACOm	Ameisen-Kolonie-Optimierung M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
17	BFO-GA	Optimierung der bakteriellen Futtersuche - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
18	MEC	Evolutionäre Berechnung des Geistes	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
19	IWO	Optimierung mit invasiven Unkräutern	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
20	Micro-AIS	Künstliches Mikro-Immunsystem	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
21	COAm	Kuckuck-Optimierungsalgorithmus M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
22	SDOm	Optimierung der Spiraldynamik M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
23	NMm	Nelder-Mead-Verfahren M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
24	FAm	Firefly-Algorithmus M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
25	GSA	Algorithmus für die Schwerkraftsuche	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
26	BFO	Optimierung der bakteriellen Futtersuche	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
27	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
28	BA	Fledermaus-Algorithmus	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
29	SA	simuliertes Abkühlen	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
30	IWDm	intelligente Wassertropfen M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
31	PSO	Partikelschwarmoptimierung	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
32	Gebote	Boids-Algorithmus	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
33	MA	Affen-Algorithmus	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
34	SFL	schlurfender Froschsprung	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
35	FSS	Fischschulsuche	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
36	RND	zufällig	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
37	GWO	Grauer-Wolf-Optimierung	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
38	CSS	Suche geladener Systeme	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
39	EM	elektromagnetismusähnlicher Algorithmus	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

Zusammenfassung

Der binäre genetische Algorithmus (BGA) spielte eine gewisse Rolle bei der Entwicklung des CLA-Algorithmus. Mein Ziel war es, einen schnelleren Algorithmus zu entwickeln. Ich hatte die Idee, die binäre Kodierung durch eine dezimale zu ersetzen. Der Mechanismus des Zahlenschloss‘ diente als Prototyp für die Entwicklung des Algorithmus. Dies erwies sich als eine erfolgreiche Lösung. CLA arbeitet schneller als BGA und konkurriert gleichzeitig erfolgreich mit ihm in Bezug auf die Effizienz. Darüber hinaus ermöglicht die Dezimalkodierung die Verwendung verschiedener Arten von Verteilungen bei der Erzeugung einer Zahlenkombination, was für einige Aufgaben nützlich sein kann (im Code sind die Potenz- und Normalverteilungen auskommentiert und können bei Bedarf verwendet werden). Experimente haben gezeigt, dass die Verwendung einer einfachen Gleichverteilung in diesem Fall effektiver ist.

Zusammenfassend lässt sich sagen, dass der CLA-Algorithmus von Zahlenschlössern bei allen Testfunktionen hervorragende Ergebnisse, Stabilität und Effizienz zeigte. Dies zeigt die hohe Skalierbarkeit des Algorithmus und seine Fähigkeit, komplexe Probleme zu bewältigen, und unterstreicht die Flexibilität und den vielversprechenden Charakter des CLA-Algorithmus in verschiedenen Optimierungsszenarien.

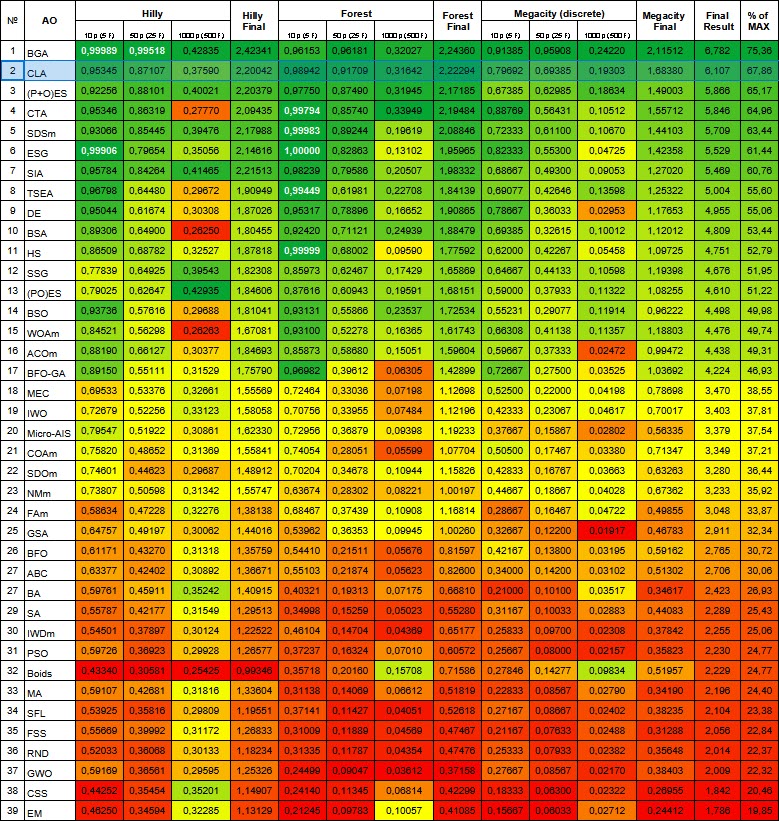
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

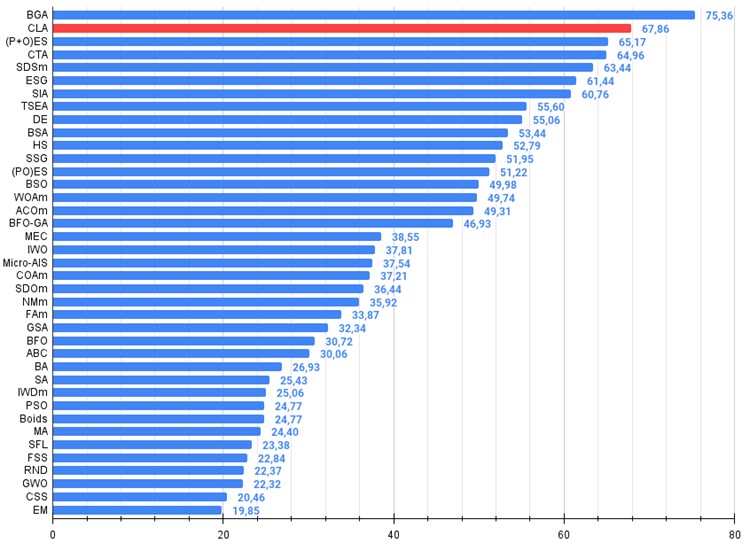
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)

GAV Pro und Kontra:

Vorteile:

1. Ausgezeichnete Konvergenz bei verschiedenen Arten von Funktionen.
2. Einfache Umsetzung.

Nachteile

1. Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
   

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355