Schildkrötenpanzer-Evolutionsalgorithmus (TSEA)

Inhalt

1. Einführung
2. Implementierung des Algorithmus
3Testergebnisse

1. Einführung

Die Schildkröte ist eine der ältesten und erstaunlichsten Schöpfungen der Natur. Sie trägt eine Muschel - ein Symbol für Widerstandsfähigkeit, Schutz und Überleben. Dieser majestätische Schild, der sich im Laufe des Lebens der Schildkröte bildet, verkörpert nicht nur physischen Schutz, sondern symbolisiert auch ihre kontinuierliche Entwicklung und die Überwindung von Hindernissen. 

Das Muster auf der Muschel zeugt von der Einzigartigkeit ihres Entwicklungsweges und symbolisiert die Harmonie zwischen der Zeit und der Kreatur selbst. Die Schale wächst von einem zentralen Punkt aus, der Nabelschnur genannt wird. Der bestehenden Schale werden neue Schichten hinzugefügt, sodass unterschiedliche Muster entstehen. Jedes Segment des Musters steht für ein anderes Jahr oder eine andere Jahreszeit des Wachstums der Schildkröte. Schicht für Schicht, Jahr für Jahr, reift der Panzer zusammen mit der Schildkröte. Er nimmt neue Muster an und bildet einzigartige Cluster, die die Lebenserfahrungen und das Wachstum des Tieres widerspiegeln.

Der Panzer der Schildkröte besteht aus zwei Hauptteilen: dem oberen Teil, dem Carapax, und dem unteren Teil, dem Plastron. Das Wachstum des Panzers einer Schildkröte ist eine Folge der Metamorphose. Die Muster auf dem Panzer einer Schildkröte sind das Ergebnis eines komplexen Zusammenspiels vieler Faktoren, darunter Genetik, Umwelt und das Wachstum des Panzers selbst.

Der Schildkrötenpanzer besteht aus biologischem Gewebe und Karbonatstoffen, wie Kalzium und Magnesium. Die Karbonatstruktur des Panzers verleiht ihm Festigkeit und schützt die inneren Organe der Schildkröte. Der Panzer junger Schildkröten besteht aus weichen Knorpelplatten, die sich mit der Zeit verhärten und zu Knochen werden. Der Panzer wächst durch die regelmäßige Ablagerung neuer Schichten von Knochengewebe unter der Haut der Schildkröte. Dieser Prozess ermöglicht es, dass der Panzer mit dem Wachstum der Schildkröte an Größe zunimmt, und kann dazu führen, dass im Laufe der Zeit neue Muster entstehen oder sich bestehende Muster verändern.

Die Muster auf dem Panzer der Schildkröte sind nicht zufällig. Sie entstehen durch bestimmte biologische Prozesse und können aufgrund ihrer Form, Farbe und Lage in verschiedene Gruppen oder „Cluster“ eingeteilt werden. So haben einige Schildkröten sternförmige Muster, während andere Muster haben, die an Leopardenfell erinnern. Wenn der Panzer einer Schildkröte wächst, können sich die Muster auf dem Panzer verändern und weiterentwickeln. Dies kann zu einer Änderung des Clusters führen, zu dem das Muster gehört. So kann beispielsweise ein Muster, das ursprünglich als „Stern“ klassifiziert wurde, im Laufe der Zeit komplexer werden.

Es ist wichtig zu wissen, dass jede Schildkröte einzigartige Muster auf ihrem Panzer hat, die ihr helfen, sich an ihre Umgebung anzupassen und wichtige Funktionen zu erfüllen, wie z. B. sich zu tarnen oder Partner für die Fortpflanzung anzulocken.

Die Muster auf dem Schildkrötenpanzer inspirierten mich dazu, einen originellen Optimierungsalgorithmus zu entwickeln, und die Entwicklung des Schildkrötenpanzers wurde zu einer Metapher für den Prozess des Zusammenführens und Clusterns von Daten und bestimmte die Schaffung eines neuen Tools, das sich auf der Grundlage von Erfahrung und Wissen anpassen und weiterentwickeln kann.

2. Implementierung des Algorithmus

Die Idee hinter dem Schildkrötenpanzer-Evolutionsalgorithmus ist es, das Wachstum des Panzers durch die allmähliche Bildung neuer keratinisierter Hautbereiche zu emulieren, die Lösungen für das Optimierungsproblem darstellen. Bei diesem Modell werden die besten Lösungen härter und befinden sich näher an der Außenfläche, während die weniger erfolgreichen Lösungen weicher bleiben und sich im Inneren befinden.

Die Schale ist in diesem Zusammenhang in Cluster unterteilt, die auf ihrer Oberfläche ein Muster bilden, und ihre Schichten werden durch vertikale Unterteilung in Cluster simuliert. Der Prozess der Nachahmung des Wachstums der Schale im Algorithmus umfasst sowohl die Bewegung nach oben (nach außen) und nach unten (nach innen) als auch die Ausdehnung. Ein einzigartiges Merkmal dieses Optimierungsalgorithmus ist die Erhaltung weniger erfolgreicher Lösungen, was sich in einem Wachstum der Schale nach innen äußert. Die innere Schicht der Schale ist die einzige, die sich in beide Richtungen ausdehnt, während die anderen Schichten sich nur nach außen ausdehnen, wobei die schlechtesten Lösungen durch neue ersetzt werden. Jeder vertikale Cluster (Layer) hat eine begrenzte Kapazität für Lösungen; wenn die maximale Anzahl nicht erreicht wird, werden einfach Lösungen hinzugefügt, andernfalls wird die Lösung nach dem beschriebenen Prinzip ersetzt.

Abbildung 1 zeigt deutlich die Gruppierung der Lösungen nach ihrer Qualität und dem Abstand zwischen ihnen. Zum besseren Verständnis wird ein hypothetisches Beispiel mit einem eindimensionalen Lösungsraum verwendet. Anhand dieses Diagramms lässt sich die Bildung von Clustern in Abhängigkeit von der Qualität und der Nähe der Lösungen zueinander deutlich erkennen.

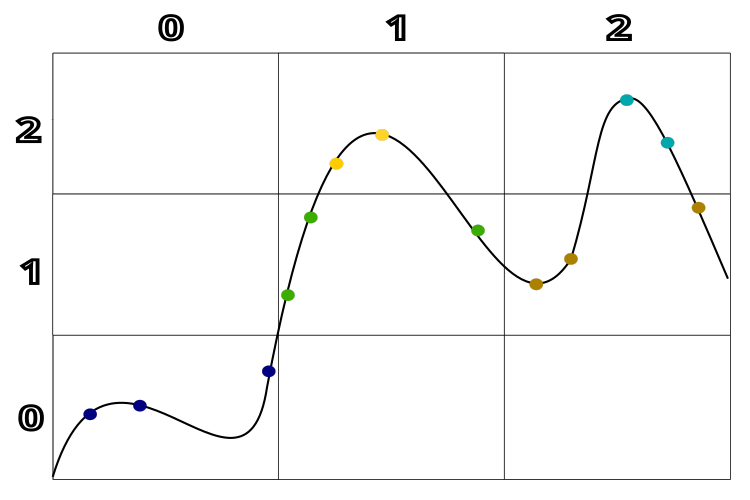
Abbildung 1. Clustering nach Lösungsqualität und Abstand zwischen Lösungen im TSEA-Algorithmus

Lassen Sie uns einen Pseudocode für den TSEA-Algorithmus schreiben:

1. Generiere zufällige Individuen für die Population.
2. Berechne FF.
3. Ursprüngliche vertikale Clusterung der Population.
4. Die ursprüngliche K-Means-Population wird horizontal geclustert.
5. Setze die Population in eine Schale.
6. Erzeuge eine neue Population auf der Grundlage der Daten in der Shell:
     6.1. Mit einer Wahrscheinlichkeit von 0,8:
          Wähle einen Cluster vertikal aus.
          Wähle den besten Agenten in der Zelle oder einen beliebigen Agenten in der Zelle mit einer Wahrscheinlichkeit von 0,5.
          Verwende den ausgewählten Agenten in der Zelle oder verwende die beste globale Lösung mit einer Wahrscheinlichkeit von 0,6.
          Erstelle eine neue Agentenkoordinate unter Verwendung der Energieverteilung.
     6.2 Oder:
          Wähle einen Cluster vertikal aus.
          Wähle zwei Cluster vertikal aus und wähle einen Agenten nach dem Zufallsprinzip aus diesen Clustern aus.
          Erstelle eine neue Koordinate als Durchschnittswert der Koordinaten der ausgewählten Agenten.
7.   Berechne FF.
8.   Vertikale Clusterbildung der Population.
9.   Definiere die Zugehörigkeit der Agenten zu den Clustern der K-NN-Schale (die Methode der nächsten N Nachbarn).
10. Führe alle 50 Epochen ein vertikales Clustering der Schale durch.
11. Setze die Population in eine Schale.
12. Wiederhole den Vorgang ab 6.

Wählen des Cluster vertikal nach dem quadratischen Gesetz aus (Abb. 2), das die höhere Wahrscheinlichkeit bestimmt für den letzten (besten) Cluster auf der Liste ausgewählt zu werden, im Vergleich zum 0. (schlechtesten) Cluster.

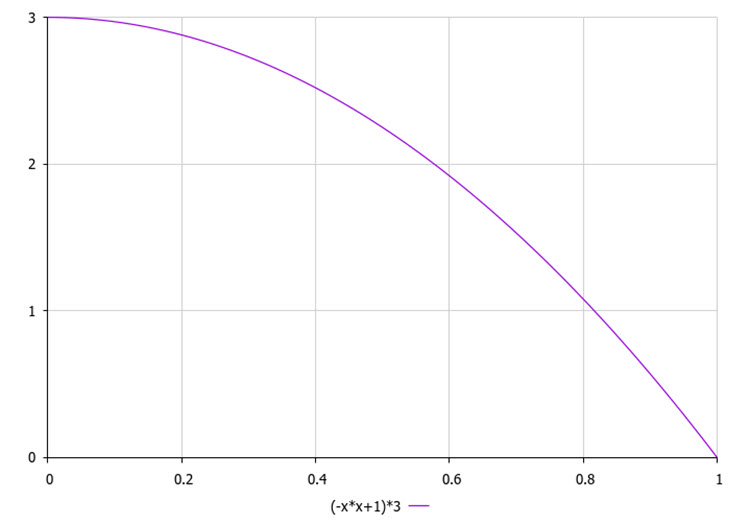
Abbildung 2. Das Wahrscheinlichkeitsgesetz für die vertikale Auswahl eines Clusters (nach Qualität), wobei 3 die Anzahl der Cluster ist

Die Logik der Erstellung neuer Abschnitte der Schale (Agenten - Lösungen für das Optimierungsproblem) ist also wie folgt:

1. Auswahl der Schalenschicht (vertikaler Cluster). Die Wahrscheinlichkeit, dass die oberste, härtere Schicht gewählt wird, ist höher als die unteren, weniger harten Schichten.
2. Auswahl von Panzerteilen aus horizontalen Clustern in der ausgewählten Ebene.
3. „Verschmelzen“ der ausgewählten Abschnitte.

Die Wahrscheinlichkeit des „Verschmelzens“ (Aushärtung) ist bei den oberen Schichten höher als bei den unteren.

Jetzt, da wir den Pseudocode und das Gesetz der Agentenauswahl in der Elternpopulation haben, ist die Aufgabe zu 99 % erfüllt. Natürlich mache ich nur Spaß. Wir müssen ja noch den Code schreiben.

Wir beschreiben den Optimierungsagenten des TSEA-Algorithmus als die Struktur S_TSEA_Agent. Wir benötigen Cluster-Etiketten in vertikaler und horizontaler Richtung.

1. Die Struktur enthält folgende Felder:

• c[] - Array zum Speichern der Koordinaten des Agenten
• f - Variable zur Speicherung der Agentenbewertung (Fitness)
• label - Bezeichnung der Cluster-Mitgliedschaft
• labelClustV - vertikale Clusterbildung
• minDist - Mindestabstand zum nächstgelegenen Schwerpunkt

2. Init ist eine Methode der Struktur S_TSEA_Agent, die die Felder der Struktur initialisiert. Sie übernimmt das Integer-Argument „coords“, das zur Größenänderung des Arrays „c“ mit der Funktion ArrayResize verwendet wird.
3. f = -DBL_MAX - setzt den Anfangswert der Variablen „f“ gleich dem kleinstmöglichen Wert einer „double“-Zahl.
4. label = -1 und labelClustV = -1 - Initialisierung der Clustermitgliedslabels auf -1.
5. minDist = DBL_MAX - setzt den Anfangswert der Variablen „minDist“ gleich dem kleinstmöglichen Wert eines „double“-Wertes.

Dieser Code stellt die grundlegende Datenstruktur für Agenten im TSEA-Optimierungsalgorithmus dar und initialisiert deren Felder, wenn ein neuer Agent erstellt wird. Auf diese Weise können die Agenten Informationen über ihren aktuellen Zustand speichern und diese während der Ausführung des Algorithmus aktualisieren.

//——————————————————————————————————————————————————————————————————————————————
struct S_TSEA_Agent
{
    double c     [];     //coordinates
    double f;            //fitness
    int    label;        //cluster membership label
    int    labelClustV;  //clusters vertically
    double minDist;      //minimum distance to the nearest centroid

    void Init (int coords)
    {
      ArrayResize (c,     coords);
      f           = -DBL_MAX;
      label       = -1;
      labelClustV = -1;
      minDist     = DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Wir müssen den Schildkrötenpanzer beschreiben, der ein zweidimensionales Feld ist, in dem Fitness-Cluster vertikal und Standort-Cluster horizontal angeordnet sind. Jede Zelle des zweidimensionalen Arrays enthält einen Wert zwischen 0 und dem in den externen Parametern des Algorithmus angegebenen Höchstwert.

Beschreibe den horizontalen Cluster mit der Struktur S_TSEA_horizontal, die die Felder enthält:

• indBest - Index des besten Agenten in der Zelle
  
• agent[] - Array von S_TSEA_Agent-Strukturen, die zum Speichern von Agenten verwendet werden

Wir können den vertikalen Cluster mit Hilfe der Struktur S_TSEA_horizontal beschreiben, die die Felder enthält:

• cell[] - Array von S_TSEA_horizontal Strukturen.
  

Der Code gibt uns also die Möglichkeit, den Schildkrötenpanzer in zwei Richtungen eines zweidimensionalen Feldes zu beschreiben. Wir können in jeder Zelle des Arrays Optimierungsagenten speichern. Im Wesentlichen handelt es sich bei der Schale um eine speziell strukturierte Elternpopulation, auf die bei der Erstellung von Kind-Agenten bequem zugegriffen werden kann.

//——————————————————————————————————————————————————————————————————————————————
struct S_TSEA_horizontal
{
    int indBest;
    S_TSEA_Agent agent [];
};

struct S_TSEA_vertical
{
    S_TSEA_horizontal cell [];
};

//——————————————————————————————————————————————————————————————————————————————

Um das Clustering durchzuführen, wendet der TSEA-Algorithmus gemäß dem angegebenen Pseudocode zwei Clustering-Methoden an: K-Means und K-NN. Wir haben K-Means bereits in dem Artikel über den BSO-Algorithmus betrachtet. Erinnern wir uns daran, wie die Clusterstruktur aussieht:

• centroid[] - Array zum Speichern der Koordinaten des Zellschwerpunkts
• f - Variable zur Speicherung der Punktzahl (Fitness) des Schwerpunkts
• count - Anzahl der Agenten im Cluster
• agentList[] - Liste der Agenten im Cluster
• Init - Methode der S_Cluster-Struktur, die die Felder der Struktur initialisiert
  

//——————————————————————————————————————————————————————————————————————————————
struct S_Cluster
{
    double centroid [];  //cluster centroid
    double f;            //centroid fitness
    int    count;        //number of points in the cluster

    void Init (int coords)
    {
      ArrayResize (centroid, coords);
      f     = -DBL_MAX;
      count = 0;
      ArrayResize (ideasList, 0, 100);
    }
};
//——————————————————————————————————————————————————————————————————————————————

Um die Zugehörigkeit eines untergeordneten Agenten zu dem entsprechenden Cluster zu bestimmen, verwenden wir die K-NN-Methode (die Methode der k-nächsten Nachbarn).

Zusätzlich zur K-Means-Methode enthält die Klasse C_TSEA_clusters die folgenden Methoden:

1. Die Methode VectorDistance:

• Die Methode berechnet den euklidischen Abstand zwischen den Vektoren „v1“ und „v2“, die durch Arrays von „double“-Zahlen dargestellt werden.
• Sie verwendet die Gleichung des euklidischen Abstands: .
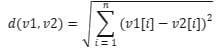• Der berechnete Abstand wird zurückgegeben.

2. Die Struktur DistanceIndex:

• Die Struktur stellt ein Paar von Werten dar: „distance“ und „index“.
• Die Struktur wird verwendet, um Abstand von einem Punkt zu anderen Punkten und deren Indizes zu speichern.

3. Die Methode BubbleSort:

• Die Methode sortiert ein Array von Objekten des Typs DistanceIndex mit Hilfe der Bubble-Sort-Methode in aufsteigender Reihenfolge nach Entfernung.
• Eine temporäre „temp“-Variable wird zum Austausch von Array-Elementen verwendet.

4. Die KNN-Methode setzt den Algorithmus der k-nächsten Nachbarn zur Klassifizierung eines „Punktes“ ein:

• Es berechnet die Abstände zwischen dem „Punkt“ und allen Punkten im „Daten“-Array, sortiert diese Abstände und bestimmt, ob der Punkt zu einem der n_Cluster gehört - Cluster auf der Grundlage von k-nächsten Nachbarn.
• Das Array „votes“ wird verwendet, um die Stimmen jedes Clusters zu berechnen.
• Der Index des Clusters mit der höchsten Stimmenzahl wird zurückgegeben.

//——————————————————————————————————————————————————————————————————————————————
class C_TSEA_clusters
{
  public:

  double VectorDistance (double &v1 [], double &v2 [])
  {
    double distance = 0.0;
    for (int i = 0; i < ArraySize (v1); i++)
    {
      distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]);
    }
    return MathSqrt (distance);
  }

  struct DistanceIndex
  {
      double distance;
      int index;
  };

  void BubbleSort (DistanceIndex &arr [], int start, int end)
  {
    for (int i = start; i < end; i++)
    {
      for (int j = start; j < end - i; j++)
      {
        if (arr [j].distance > arr [j + 1].distance)
        {
          DistanceIndex temp = arr [j];
          arr [j] = arr [j + 1];
          arr [j + 1] = temp;
        }
      }
    }
  }

  int KNN (S_TSEA_Agent &data [], S_TSEA_Agent &point, int k_neighbors, int n_clusters)
  {
    int n = ArraySize (data);
    DistanceIndex distances_indices [];

    // Calculate the distances from a point to all other points
    for (int i = 0; i < n; i++)
    {
      DistanceIndex dist;
      dist.distance = VectorDistance (point.c, data [i].c);
      dist.index = i;
      ArrayResize (distances_indices, n);
      distances_indices [i] = dist;
    }

    // Sort the distances
    BubbleSort (distances_indices, 0, n - 1);

    // Define the cluster for the point
    int votes [];
    ArrayResize (votes, n_clusters);
    ArrayInitialize (votes, 0);

    for (int j = 0; j < k_neighbors; j++)
    {
      int label = data [distances_indices [j].index].label;

      if (label != -1 && label < n_clusters)
      {
        votes [label]++;
      }
    }

    int max_votes = 0;
    int max_votes_cluster = -1;

    for (int j = 0; j < n_clusters; j++)
    {
      if (votes [j] > max_votes)
      {
        max_votes = votes [j];
        max_votes_cluster = j;
      }
    }

    return max_votes_cluster;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Fahren wir nun mit der Beschreibung der Klasse C_AO_TSEA fort, die von der Basisklasse C_AO abgeleitet ist. Die Klasse implementiert den „Turtle Shell Evolution Algorithm“ (TSEA) Algorithmus. Felder und Methoden der Klasse:

1. C_AO_TSEA - der Konstruktor initialisiert die Klassenfelder. Er enthält den Namen des Algorithmus, seine Beschreibung und einen Link zu dem Artikel über den Algorithmus. Sie legt auch die Parameter des Algorithmus fest, wie z. B. die Größe der Population, die Anzahl der vertikalen und horizontalen Cluster, die Anzahl der nächsten Nachbarn und die maximale Anzahl von Agenten in einer Zelle.

2. SetParams - die Methode setzt die Algorithmusparameter auf der Grundlage der Werte des Arrays „params“.

3. Init - die Methode initialisiert den Algorithmus. Er akzeptiert minimale und maximale Suchbereiche, Suchschritte und die Anzahl der Epochen.

4. Die Methoden „Moving“ und „Revision“ sind die Hauptmethoden des TSEA-Algorithmus, die seine grundlegende Logik umsetzen.

5. Die Felder vClusters, hClusters, neighbNumb und maxAgentsInCell sind die Algorithmusparameter, die im Konstruktor festgelegt werden und mit der Methode SetParams geändert werden können.

6. Die Arrays der Agenten, Zellen und Cluster sind die vom Algorithmus verwendeten Datenstrukturen. Sie enthalten Informationen über die Agenten, Zellen bzw. Cluster.

7. Das Objekt „km“ der Klasse C_TSEA_clusters wird für die Durchführung von Clustering-Operationen verwendet.

8. Die privaten Felder minFval, stepF, epochs und epochsNow sind interne Variablen. Sie sind nicht für den Zugriff von außerhalb der Klasse bestimmt.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_TSEA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_TSEA () { }
  C_AO_TSEA ()
  {
    ao_name = "TSEA";
    ao_desc = "Turtle Shell Evolution Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14789";

    popSize         = 100; //population size

    vClusters       = 3;   //number of vertical clusters
    hClusters       = 10;  //number of horizontal clusters
    neighbNumb      = 5;   //number of nearest neighbors
    maxAgentsInCell = 3;   //max agents in cell

    ArrayResize (params, 5);

    params [0].name = "popSize";          params [0].val  = popSize;

    params [1].name = "vClusters";        params [1].val  = vClusters;
    params [2].name = "hClusters";        params [2].val  = hClusters;
    params [3].name = "neighbNumb";       params [3].val  = neighbNumb;
    params [4].name = "maxAgentsInCell";  params [4].val  = maxAgentsInCell;
  }

  void SetParams ()
  {
    popSize         = (int)params [0].val;

    vClusters       = (int)params [1].val;
    hClusters       = (int)params [2].val;
    neighbNumb      = (int)params [3].val;
    maxAgentsInCell = (int)params [4].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    vClusters;      //number of vertical clusters
  int    hClusters;      //number of horizontal clusters
  int    neighbNumb;     //number of nearest neighbors
  int    maxAgentsInCell;

  S_TSEA_Agent    agent   [];
  S_TSEA_vertical cell    [];

  S_Cluster      clusters [];
  C_TSEA_clusters km;

  private: //-------------------------------------------------------------------
  double minFval;
  double stepF;

  int    epochs;
  int    epochsNow;
};
//——————————————————————————————————————————————————————————————————————————————

Die Methode Init der Klasse C_AO_TSEA initialisiert den TSEA-Algorithmus. Eine ausführliche Beschreibung ihrer Arbeit finden Sie weiter unten:

1. StandardInit (rangeMinP, rangeMaxP, rangeStepP) - die Methode wird zur Standardinitialisierung des Algorithmus aufgerufen. Er akzeptiert minimale und maximale Suchbereiche und Suchschritte. Wenn die Initialisierung fehlschlägt, gibt die Methode „false“ zurück.

2. ArrayResize (agent, popSize) passt die Größe des Arrays „agent“ an die Größe der Population „popSize“ an. Die Methode Init(coords) wird dann für jeden Agenten aufgerufen, um ihn zu initialisieren.

3. ArrayResize (clusters, hClusters) passt die Größe des Arrays „clusters“ an die Anzahl der horizontalen Cluster von hClusters an. Die Methode Init(coords) wird als Nächstes für jeden Cluster aufgerufen, um ihn zu initialisieren.

4. ArrayResize (cell, vClusters) ändert die Größe des Arrays „cell“ auf die Anzahl der vertikalen vClusters-Cluster. Das Array cell[i].cell und das Array der Agenten in jeder Zelle werden dann für jede Zelle initialisiert.

5. "minFval = DBL_MAX", "stepF = 0.0", "epochs = epochsP", "epochsNow = 0". Initialisierung der internen Variablen des Algorithmus.

6. Am Ende gibt die Methode „true“ zurück und zeigt damit an, dass die Initialisierung erfolgreich war.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSEA::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (clusters, hClusters);
  for (int i = 0; i < hClusters; i++) clusters [i].Init (coords);

  ArrayResize (cell, vClusters);

  for (int i = 0; i < vClusters; i++)
  {
    ArrayResize (cell [i].cell, hClusters);

    for (int c = 0; c < hClusters; c++) ArrayResize (cell [i].cell [c].agent, 0, maxAgentsInCell);
  }

  minFval   = DBL_MAX;
  stepF     = 0.0;
  epochs    = epochsP;
  epochsNow = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving der Klasse C_AO_TSEA implementiert die grundlegende Logik der Agentenbewegung im TSEA-Algorithmus. Kurze Beschreibung der wichtigsten Schritte:

1. Initialisierung der Population:

• Wenn dies die erste Iteration ist (Revision == false), werden zufällige Individuen in die Population aufgenommen.
• Andernfalls wird die Grundgesamtheit auf der Grundlage bestehender Entscheidungen aktualisiert.

2. Aktualisierung der Population:

• Für jeden Cluster wird die beste Lösung gefunden (vClusters х hClusters).
• Neue Lösungen werden wie folgt gebildet:
• Die beste Lösung wird mit einer Wahrscheinlichkeit von 0,5 aus einem zufälligen Cluster mit einer gewissen Bias kopiert.
• Mit einer Wahrscheinlichkeit von 0,2 wird eine neue Lösung als Mittelwert zwischen zwei Zufallslösungen aus verschiedenen Clustern gebildet
• Neue Lösungskoordinaten werden mit Hilfe einer Potenzgesetzverteilung erzeugt, um die Nähe zu den besten Lösungen zu erhalten.

3. Aktualisierung der Agenten (Individuen) in der Population

Mit dieser Methode wird die Grundidee der Schildkrötenpanzer-Evolution umgesetzt, bei der die besten Lösungen „härter“ werden und sich näher an der Außenfläche befinden, während die weniger erfolgreichen Lösungen „weicher“ bleiben und sich im Inneren befinden. Das Clustern von Lösungen und das Zurückhalten weniger erfolgreicher Varianten gewährleistet die Flexibilität und Anpassungsfähigkeit des Algorithmus.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSEA::Moving ()
{
  epochsNow++;

  //----------------------------------------------------------------------------
  //1. Generate random individuals for the population
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  int    vPos = 0;
  int    hPos = 0;
  int    pos  = 0;
  int    size = 0;
  double val  = 0.0;
  double rnd  = 0.0;
  double min  = 0.0;
  double max  = 0.0;

  for (int v = 0; v < vClusters; v++)
  {
    for (int h = 0; h < hClusters; h++)
    {
      size = ArraySize (cell [v].cell [h].agent);

      if (size > 0)
      {
        max = -DBL_MAX;
        pos = -1;

        for (int c = 0; c < size; c++)
        {
          if (cell [v].cell [h].agent [c].f > max)
          {
            max = cell [v].cell [h].agent [c].f;
            pos = c;
            cell [v].cell [h].indBest = c;
          }
        }
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    if (u.RNDprobab () < 0.8)
    {
      while (true)
      {
        rnd = u.RNDprobab ();
        rnd = (-rnd * rnd + 1.0) * vClusters;

        vPos = (int)rnd;
        if (vPos > vClusters - 1) vPos = vClusters - 1;

        hPos = u.RNDminusOne (hClusters);

        size = ArraySize (cell [vPos].cell [hPos].agent);

        if (size > 0) break;
      }

      pos = u.RNDminusOne (size);

      if (u.RNDprobab () < 0.5) pos = cell [vPos].cell [hPos].indBest;

      for (int c = 0; c < coords; c++)
      {
        if (u.RNDprobab () < 0.6) val = cell [vPos].cell [hPos].agent [pos].c [c];
        else                      val = cB [c];

        double dist = (rangeMax [c] - rangeMin [c]) * 0.1;
        min = val - dist; if (min < rangeMin [c]) min = rangeMin [c];
        max = val + dist; if (max > rangeMax [c]) max = rangeMax [c];

        val = u.PowerDistribution (val, min, max, 30);

        a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }
    else
    {
      int size2 = 0;
      int hPos2 = 0;
      int pos2  = 0;

      while (true)
      {
        rnd = u.RNDprobab ();
        rnd = (-rnd * rnd + 1.0) * vClusters;

        vPos = (int)rnd;
        if (vPos > vClusters - 1) vPos = vClusters - 1;

        hPos = u.RNDminusOne (hClusters);
        size = ArraySize (cell [vPos].cell [hPos].agent);

        hPos2 = u.RNDminusOne (hClusters);
        size2 = ArraySize (cell [vPos].cell [hPos2].agent);

        if (size > 0 && size2 > 0) break;
      }

      pos  = u.RNDminusOne (size);
      pos2 = u.RNDminusOne (size2);

      for (int c = 0; c < coords; c++)
      {
        val = (cell [vPos].cell [hPos ].agent [pos ].c [c] +
               cell [vPos].cell [hPos2].agent [pos2].c [c]) * 0.5;

        a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision der Klasse C_AO_TSEA implementiert die Phase der Umverteilung der Schildkrötenpanzerabschnitte im TSEA-Algorithmus.

Er ist für die Überarbeitung (Aktualisierung) der Agentenpopulation und die Aktualisierung der besten globalen Lösung zuständig.

Die wichtigsten Schritte in diesem Teil des Algorithmus sind:

1. Berechnung der „Fitness“ jedes Agenten und Ermittlung der besten Lösung „fB“.
2. Einteilung der Agenten in vertikale „labelClustV“-Cluster auf der Grundlage ihrer Fitness.
3. Handelt es sich um die erste Iteration (Revision == false), dann wird das Clustering der Agenten mit dem K-Means-Algorithmus initialisiert.
4. Wenn es sich nicht um die erste Iteration handelt, wird Folgendes durchgeführt:

- Alle Agenten werden in einem einzigen Array „Daten“ zusammengefasst.
- Für jeden Agenten in der Population wird sein horizontales „Label“-Cluster mithilfe des Algorithmus K-Nächste Nachbarn bestimmt.
- Die „Zellstruktur“, in der die in Cluster unterteilten Agenten gespeichert sind, wird alle 50 Epochen aktualisiert.

5. Platzierung jedes Mittels in der entsprechenden Zelle. Wenn die Zelle bereits gefüllt ist, ersetzt der Agent denjenigen mit der niedrigsten (oder höchsten, wenn die Zelle auf der untersten Ebene liegt) Fitness in der Zelle.

Der Hauptgedanke dieser Phase besteht darin, die Struktur der Schale beizubehalten, bei der die besten Lösungen näher an der Außenfläche liegen, während die weniger erfolgreichen im Inneren angesiedelt sind. Die Gruppierung der Agenten und die dynamische Aktualisierung der Schalenstruktur gewährleisten die Flexibilität und Anpassungsfähigkeit des Algorithmus.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSEA::Revision ()
{
  //get fitness--------------------------------------------------
  int pos = -1;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;

    if (a [i].f > fB)
    {
      fB = a [i].f;
      pos = i;
    }

    if (a [i].f < minFval) minFval = a [i].f;
  }

  if (pos != -1) ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY);

  stepF = (fB - minFval) / vClusters;

  //Vertical layout of the child population-----------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (agent [i].f == fB) agent [i].labelClustV = vClusters - 1;
    else
    {
      agent [i].labelClustV = int((agent [i].f - minFval) / stepF);
      if (agent [i].labelClustV > vClusters - 1) agent [i].labelClustV = vClusters - 1;
    }
  }

  //----------------------------------------------------------------------------
  if (!revision)
  {
    km.KMeansPlusPlusInit (agent, popSize, clusters);
    km.KMeans             (agent, popSize, clusters);

    revision = true;
  }
  //----------------------------------------------------------------------------
  else
  {
    static S_TSEA_Agent data [];
    ArrayResize (data, 0, 1000);
    int size = 0;

    for (int v = 0; v < vClusters; v++)
    {
      for (int h = 0; h < hClusters; h++)
      {
        for (int c = 0; c < ArraySize (cell [v].cell [h].agent); c++)
        {
          size++;
          ArrayResize (data, size);

          data [size - 1] = cell [v].cell [h].agent [c];
        }
      }
    }

    for (int i = 0; i < popSize; i++)
    {
      agent [i].label = km.KNN (data, agent [i], neighbNumb, hClusters);
    }
    
    if (epochsNow % 50 == 0)
    {
      for (int v = 0; v < vClusters; v++)
      {
        for (int h = 0; h < hClusters; h++)
        {
          ArrayResize (cell [v].cell [h].agent, 0);
        }
      }

      for (int i = 0; i < ArraySize (data); i++)
      {
        if (data [i].f == fB) data [i].labelClustV = vClusters - 1;
        else
        {
          data [i].labelClustV = int((data [i].f - minFval) / stepF);
          if (data [i].labelClustV > vClusters - 1) data [i].labelClustV = vClusters - 1;
        }

        int v = data [i].labelClustV;
        int h = data [i].label;

        int size = ArraySize (cell [v].cell [h].agent) + 1;
        ArrayResize (cell [v].cell [h].agent, size);

        cell [v].cell [h].agent [size - 1] = data [i];
      }
    }
  }

  //Place the population in the shell------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int v = agent [i].labelClustV;
    int h = agent [i].label;

    int size = ArraySize (cell [v].cell [h].agent);
    int pos    = 0;
    int posMin = 0;
    int posMax = 0;

    if (size >= maxAgentsInCell)
    {
      double minF =  DBL_MAX;
      double maxF = -DBL_MAX;

      for (int c = 0; c < maxAgentsInCell; c++)
      {
        if (cell [v].cell [h].agent [c].f < minF)
        {
          minF = cell [v].cell [h].agent [c].f;
          posMin = c;
        }
        if (cell [v].cell [h].agent [c].f > maxF)
        {
          maxF = cell [v].cell [h].agent [c].f;
          posMax = c;
        }
      }

      if (v == 0)
      {
        if (agent [i].f < minF)
        {
          pos = posMin;
        }
        else
        {
          pos = posMax;
        }
      }
      else  pos = posMin;
    }
    else
    {
      ArrayResize (cell [v].cell [h].agent, size + 1);
      pos = size;
    }

    cell [v].cell [h].agent [pos] = agent [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

TSEA-Ergebnisse:

TSEA|Turtle Shell Evolution Algorithm|100.0|3.0|10.0|5.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.811921100517765
25 Hilly's; Func runs: 10000; result: 0.5537631430428238
500 Hilly's; Func runs: 10000; result: 0.2813575513298344
=============================
5 Forest's; Func runs: 10000; result: 0.9564485273109922
25 Forest's; Func runs: 10000; result: 0.481362270824773
500 Forest's; Func runs: 10000; result: 0.181400891410298
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.3633846153846153
500 Megacity's; Func runs: 10000; result: 0.11670769230769343
=============================
All score: 4.41404 (49.04%)

Die Gesamtpunktzahl für alle Testfunktionen beträgt 4,41404, was 49,04 % der theoretischen optimalen Lösung entspricht.

Die Visualisierung des Prüfstandsbetriebs zeigt die gute Konvergenz des Algorithmus. Für alle Testfunktionen gibt es eine Streuung der Trajektorien auf dem Konvergenzdiagramm. Mit zunehmender Anzahl von Freiheitsgraden nimmt diese Streuung jedoch ab. Die Verwendung von Clustern im Algorithmus sowie die Beibehaltung einer konstanten Anzahl von Agenten in jeder Zelle ermöglichen es dem Algorithmus, wichtige Bereiche der Fitnessfunktion effektiv zu untersuchen.

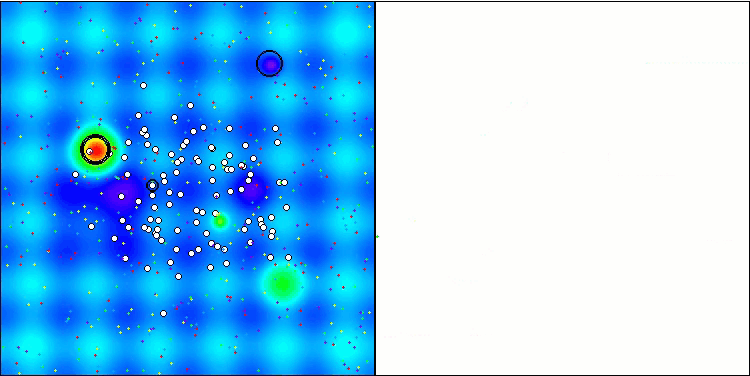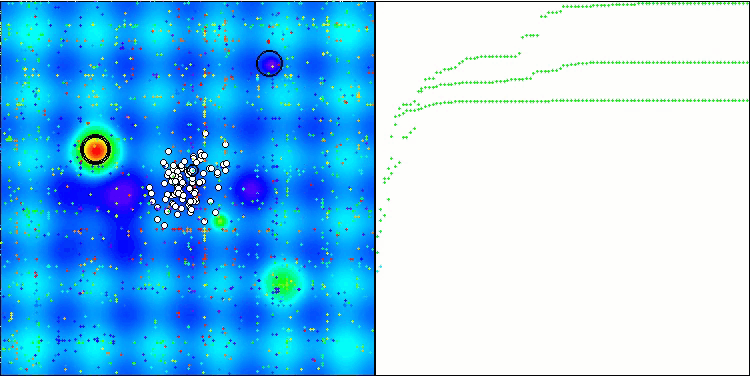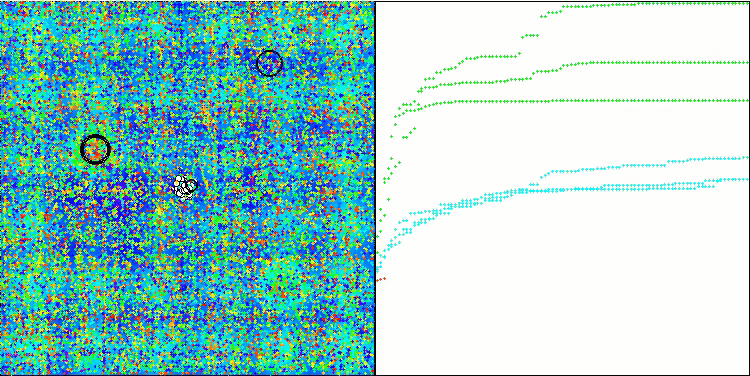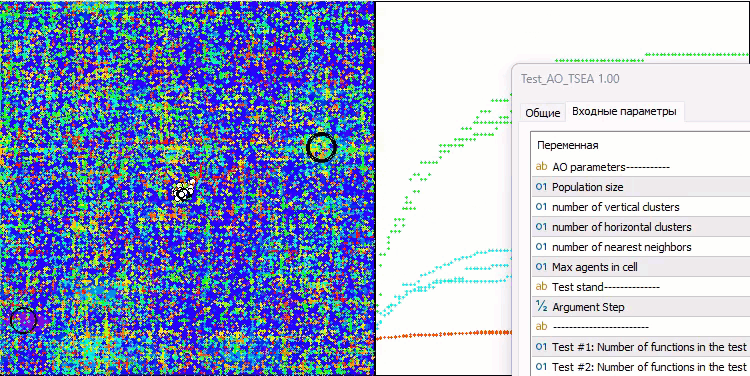
  TSEA mit der Testfunktion Hilly

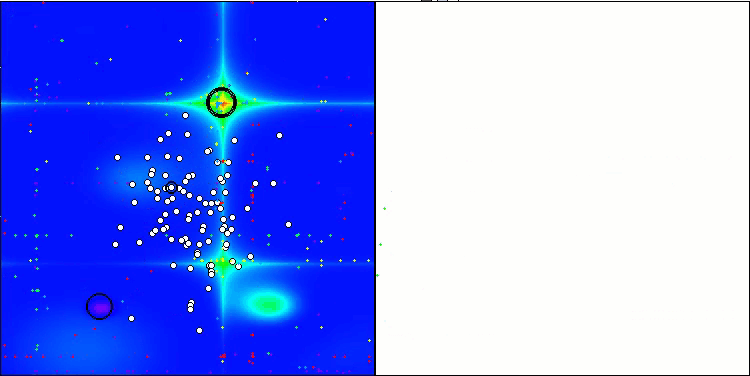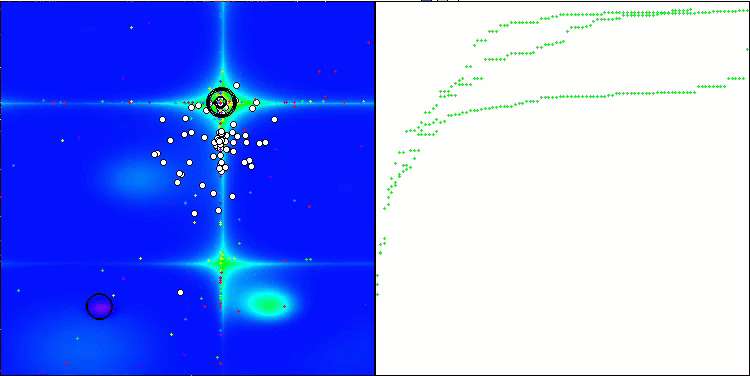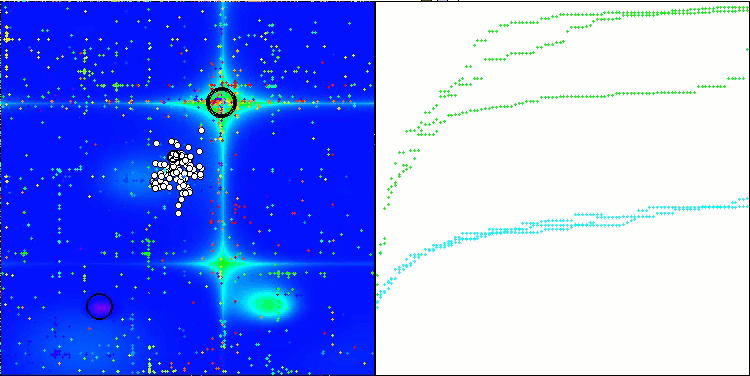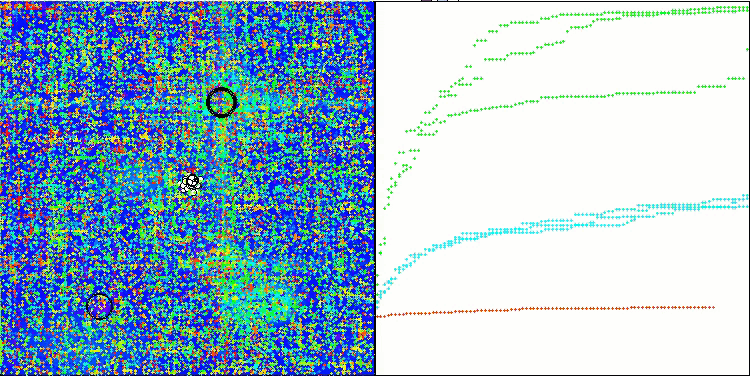
  TSEA mit der Testfunktion Forest

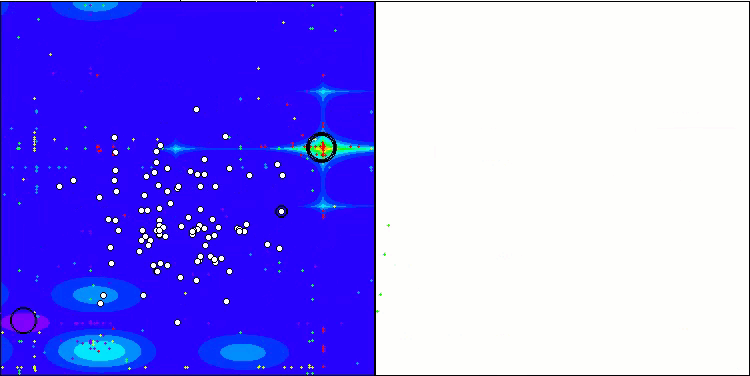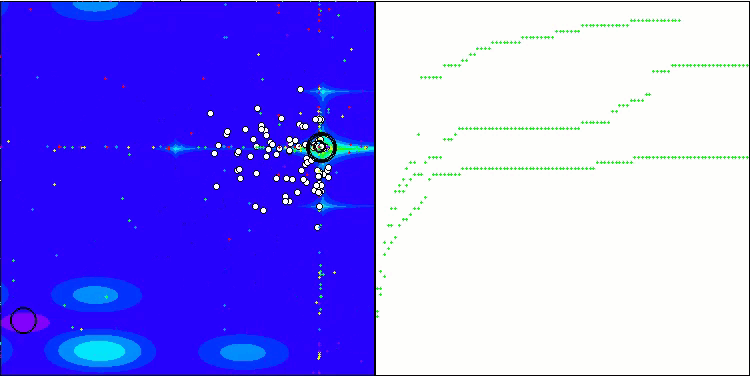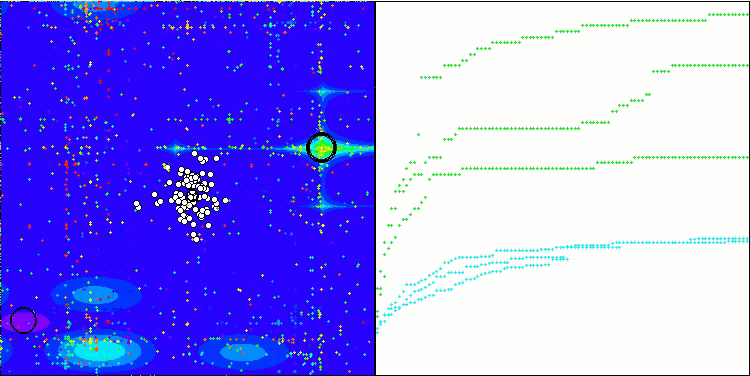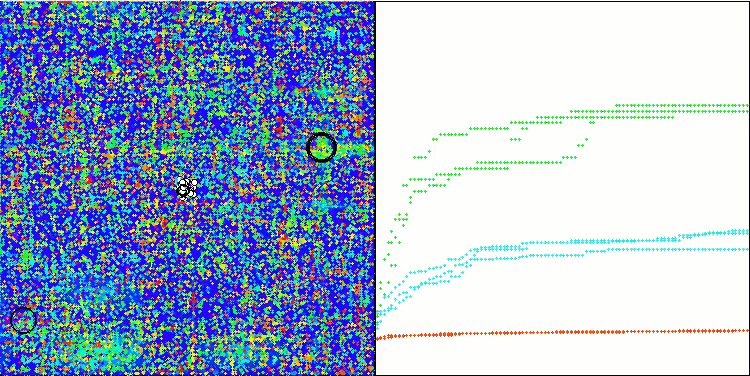
  TSEA mit der Testfunktion Megacity

Nach Prüfung der Testfunktionen belegt der Algorithmus einen würdigen 6. Platz an der Spitze der abschließenden Bewertungstabelle.

#	AO	Beschreibung	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binärer genetischer Algorithmus	0.99992	0.99484	0.50483	2.49959	1.00000	0.99975	0.32054	2.32029	0.90667	0.96400	0.23035	2.10102	6.921	76.90
2	(P+O)ES	(P+O) Entwicklungsstrategien	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
3	SDSm	stochastische Diffusionssuche M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
4	ESG	Entwicklung der sozialen Gruppen	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
5	SIA	Simuliertes isotropes Abkühlen	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
6	TSEA	Schildkrötenpanzer-Evolutionsalgorithmus	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
7	DE	differentielle Evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
8	BSA	Vogelschwarm-Algorithmus	0.90857	0.73661	0.25767	1.90285	0.90437	0.81619	0.16401	1.88457	0.61692	0.54154	0.10951	1.26797	5.055	56.17
9	HS	Harmoniesuche	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
10	SSG	Setzen, Säen und Wachsen	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
11	(PO)ES	(PO) Entwicklungsstrategien	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
12	BSO	Brainstorming-Optimierung	0.91301	0.56222	0.30047	1.77570	0.97162	0.57162	0.23449	1,77772	0.60462	0.27138	0.12011	0.99611	4.550	50.55
13	WOAm	Wal-Optimierungsalgorithmus M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
14	ACOm	Ameisen-Kolonie-Optimierung M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
15	BFO-GA	Optimierung der bakteriellen Futtersuche - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
16	MEC	Evolutionäre Berechnung des Geistes	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
17	IWO	Optimierung mit invasiven Unkräutern	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
18	Micro-AIS	Künstliches Mikro-Immunsystem	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
19	COAm	Kuckuck-Optimierungsalgorithmus M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
20	SDOm	Optimierung der Spiraldynamik M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
21	NMm	Nelder-Mead-Verfahren M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
22	FAm	Firefly-Algorithmus M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
23	GSA	Algorithmus für die Schwerkraftsuche	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
24	BFO	Optimierung der bakteriellen Futtersuche	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
25	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
26	BA	Fledermaus-Algorithmus	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
27	SA	simuliertes Abkühlen	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
28	IWDm	intelligente Wassertropfen M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
29	PSO	Partikelschwarmoptimierung	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
30	Gebote	Boids-Algorithmus	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
31	MA	Affen-Algorithmus	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
32	SFL	schlurfender Froschsprung	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
33	FSS	Fischschulsuche	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
34	RND	zufällig	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
35	GWO	Grauer-Wolf-Optimierung	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
36	CSS	Suche geladener Systeme	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
37	EM	elektromagnetismusähnlicher Algorithmus	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

Zusammenfassung

Die Idee eines Optimierungsalgorithmus, der auf dem Wachstum des Panzers einer Schildkröte basiert, erwies sich als sehr interessant. Selbst solche langsamen Tiere können als Inspiration und Beispiel für „technische“ Lösungen dienen, die die Natur in großen Mengen bereitstellt. Auf der Grundlage der TSEA-Tests (Turtle Shell Evolution Algorithm) ist es uns gelungen, die Hauptmerkmale des Algorithmus zu definieren.

Die Beibehaltung weniger erfolgreicher Lösungen ist ein einzigartiges Merkmal des Algorithmus. Dies zeigt sich darin, dass weniger erfolgreiche Varianten in der inneren Schicht der Schale erhalten bleiben. Dieser Ansatz ermöglicht es, die Vielfalt in der Population zu erhalten und eine vorzeitige Konvergenz zu lokalen Optima zu verhindern. Es ist wichtig, daran zu denken, dass ein lokales Minimum, das die schlechteste Lösung zu sein scheint, nahe am globalen Optimum liegen kann, sodass es sinnvoll ist, seine Umgebung weiter zu untersuchen. Auch wenn der Algorithmus solche Gebiete weniger intensiv erkundet als vielversprechendere Standorte, bleiben sie dennoch im Fokus der Aufmerksamkeit.

Die Aufteilung der Lösungen in vertikale Cluster, die die Schichten der Schale simulieren, und horizontale Cluster, die die charakteristischen Muster auf der Oberfläche simulieren, ermöglicht es uns, Bereiche des Lösungsraums recht effizient zu isolieren und separat zu untersuchen. Gleichzeitig bleibt das Muster auf der Schale beweglich und kann sich verändern und an die Oberfläche der Fitnessfunktion anpassen.

Die Schichtung der Schale ermöglicht die Bildung neuer Lösungen innerhalb jeder Schicht. Die oberen harten Schichten interagieren nicht mit den unteren weichen Schichten und umgekehrt. Dies ähnelt dem Prozess des Panzerwachstums bei einer lebenden Schildkröte, allerdings mit dem Unterschied, dass der harte Teil aus der unteren Schicht durch periodische Umschichtung in die oberen Schichten wandern kann. Dies ist vergleichbar mit dem Abstreifen der alten Schale und der Bildung einer neuen, stärkeren und besseren Schale.

Der Algorithmus zeigt eine gute Leistung bei Problemen mit einer unterschiedlichen Anzahl von Dimensionen (Skalierbarkeit), was auf seine Flexibilität hindeutet.

Insgesamt ist TSEA ein interessanter Ansatz, der evolutionäre Algorithmen und Clustering-Mechanismen kombiniert. Ich bin jedoch zuversichtlich, dass das Potenzial des Algorithmus noch lange nicht ausgeschöpft ist. An dieser Stelle wurden nur einige der vielen verschiedenen Möglichkeiten zur Schaffung neuer Lösungen aus der großen Vielfalt, die zuvor in den Artikeln besprochen wurden, verwendet. Der Algorithmus bleibt in meinem Fokus und ist offen für weitere Verbesserungen. Vielleicht dient sie als Grundlage für neue Änderungen, ähnlich wie bei PSO und anderen bekannten Algorithmen.

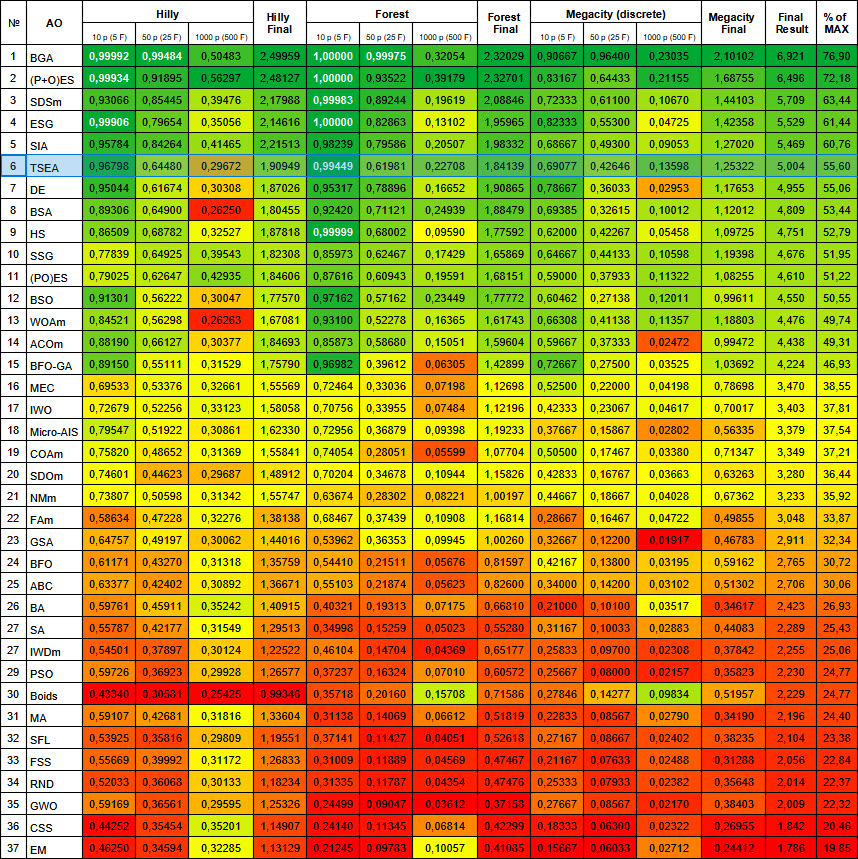
Abbildung 3. Farbliche Abstufung der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben

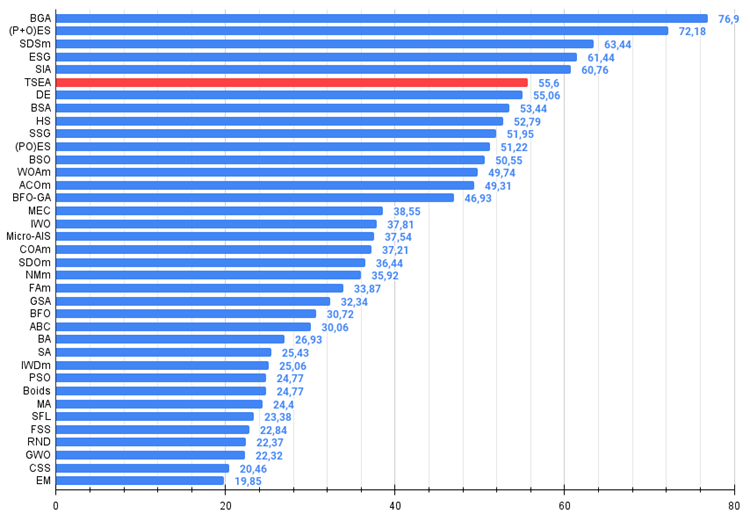
Abbildung 4. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)

TSEA Pro und Kontra:

Vorteile:

1. Gute Konvergenz bei verschiedenen Arten von Funktionen
2. Geringe Anzahl von externen Parametern
   

Nachteile

1. Große Streuung der Ergebnisse bei niedrigdimensionalen Funktionen
   
2. Hohe Belastung der Computerressourcen

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

CodeBase: https://www.mql5.com/ru/code/49355