
Population optimization algorithms: Grey Wolf Optimizer (GWO)
Contents
1. Introduction2. Algorithm description
3. Test functions
4. Test results
1. Introduction
The gray wolf algorithm is a metaheuristic stochastic swarm intelligence algorithm developed in 2014. Its idea is based on the gray wolf pack hunting model. There are four types of wolves: alpha, beta, delta and omega. Alpha has the most "weight" in decision making and managing the pack. Next come the beta and the delta, which obey the alpha and have power over the rest of the wolves. The omega wolf always obeys the rest of the dominant wolves.
In the wolf hierarchy mathematical model, the alpha-α-wolf is considered the dominant wolf in the pack, and his orders should be carried out by the members of the pack. Beta-β-subordinate wolves assist the alpha in decision making and are considered the best candidates for the role of alpha. Delta wolves δ should obey alpha and beta, but they dominate omega. Omega ω wolves are considered the scapegoats of the pack and the least important individuals. They are only allowed to eat at the end. Alpha is considered the most favorable solution.
The second and third best solutions are beta and delta, respectively. The rest of the solutions are considered omega. It is assumed that the fittest wolves (alpha, beta and delta), that is, those closest to the prey, will be approached by the rest of the wolves. After each approach, it is determined who is alpha, beta and delta at this stage, and then the wolves are rearranged again. The formation takes place until the wolves gather in a pack, which will be the optimal direction for an attack with a minimum distance.
During the algorithm, 3 main stages are performed, in which the wolves search for prey, surround and attack it. The search reveals alpha, beta and delta - the wolves that are closest to the prey. The rest, obeying the dominant ones, may begin to surround the prey or continue to randomly move in search of the best option.
2. Algorithm description
The hierarchy in the pack is schematically displayed in Figure 1. Alpha plays a dominant role.

Fig. 1. Social hierarchy in a pack of wolves
Mathematical model and algorithm
Social hierarchy:
- The best solution in the form of an alpha wolf (α).
- The second best solution as a beta wolf (β).
- The third best solution as a delta wolf (δ).
- Other possible solutions as omega volves (ω).
Encircling prey: when there are already the best alpha, beta and delta solutions, the further actions depend on the omega.
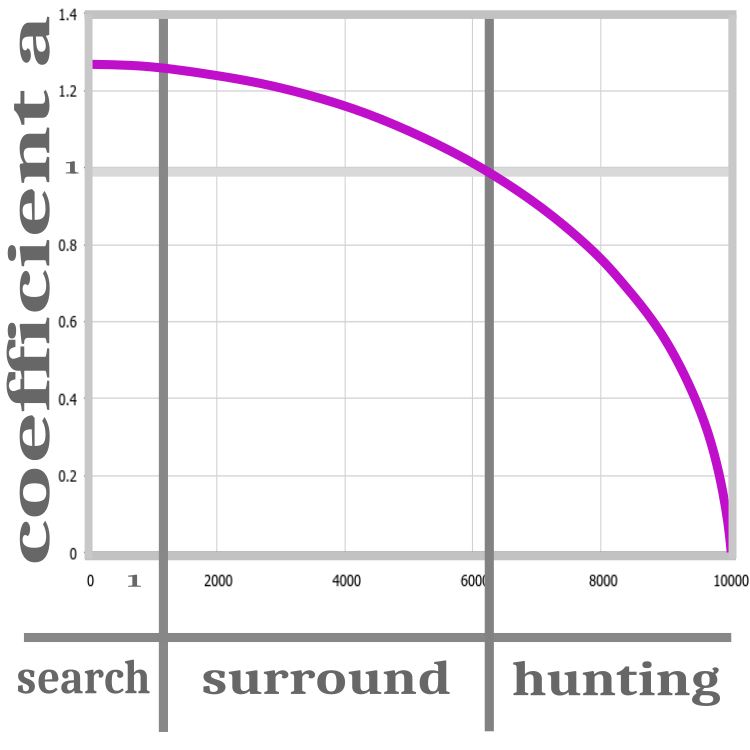
Fig 2. Hunting stages: search, encircling, attack.
All iterations of the algorithm are represented by three stages: search, encircling and hunting. The canonical version of the algorithm features the а calculated ratio introduced to improve the convergence of the algorithm. The ratio decreases to zero at each iteration. As long as the ratio exceeds 1, the initialization of the wolves is in progress. At this stage, the position of the prey is completely unknown, so the wolves should be distributed randomly.
After the "search" stage, the value of the fitness function is determined, and only after that it is possible to proceed to the "encircling" stage. At this stage, the a ratio is greater than 1. This means that alpha, beta and delta are moving away from their previous positions, thus allowing the position of the estimated prey to be refined. When the а ratio becomes equal to 1, the "attack" stage starts, while the ratio tends to 0 before the end of the iterations. This causes the wolves to approach the prey, suggesting that the best position has already been found. Although, if at this stage one of the wolves finds a better solution, then the position of the prey and the hierarchy of the wolves will be updated, but the ratio will still tend to 0. The process of changing a is represented by a non-linear function. The stages are schematically shown in Figure 2.
The behavior of omega wolves is unchanged throughout all epochs and consists in following the geometric center between the positions of the currently dominant individuals. In Figure 3, alpha, beta and delta deviate from their previous position in a random direction with a radius that is given by the coefficients, and omegas move to the center between them but with some degree of probability deviating from it within the radius. The radii determine the а ratio, which, as we remember, changes causing the radii to decrease proportionally.
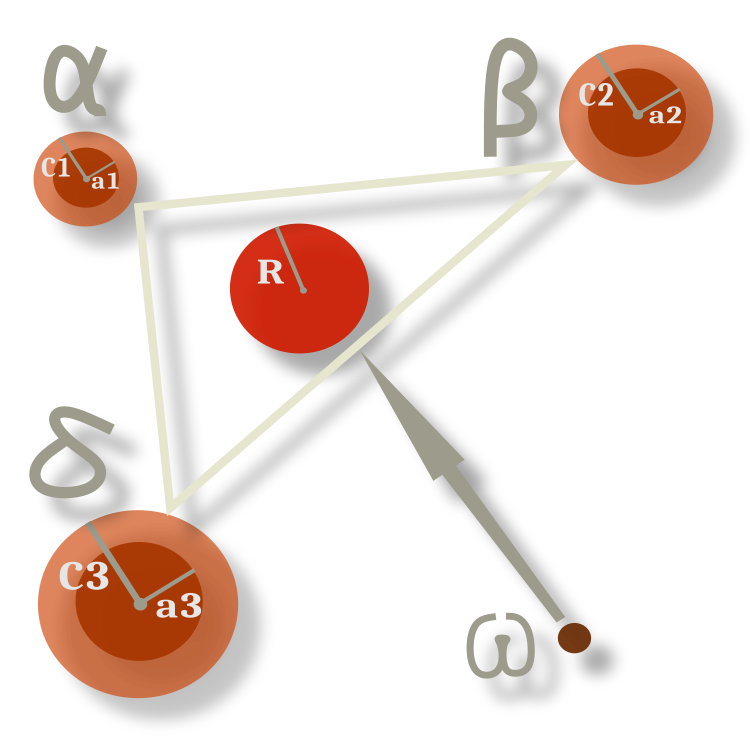
Fig. 3. Diagram of the omega movement in relation to alpha, beta and delta
The pseudocode of the GWO algorithm is as follows:
1) Randomly initialize the gray wolf population.
2) Calculate the fitness of each member of the population.
3) Pack leaders:
-α = member with the best fitness value
-β = second best member (in terms of fitness)
-δ = third best member (in terms of fitness value)
Update the position of all omega wolves according to the equations depending on α, β, δ
4) Calculate the fitness of each member of the population.
5) repeat step 3.
Let's move on to the algorithm code. The only addition I made to the original version is the ability to set the number of leading wolves in the pack. Now you can set any number of leaders, up to the entire pack. This may be useful for specific tasks.
We start, as usual, with the elementary unit of the algorithm - the wolf, which is a solution to the problem. This is a structure that includes an array of coordinates and a prey value (fitness functions). The structure is the same for leaders and minor members of the pack. This simplifies the algorithm and allows us to use the same structures in the loop operations. Moreover, during all iterations, the roles of the wolves change many times. The roles are uniquely determined by the position in the array after sorting. The leaders are at the beginning of the array.
//—————————————————————————————————————————————————————————————————————————————— struct S_Wolf { double c []; //coordinates double p; //prey }; //——————————————————————————————————————————————————————————————————————————————
The wolf pack is represented by a compact and understandable class. Here we declare the ranges and step of the parameters to be optimized, the best production position, the best solution value and auxiliary functions.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_GWO //wolfpack { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Wolf wolves []; //wolves of the pack public: double cB []; //best prey coordinates public: double pB; //best prey public: void InitPack (const int coordinatesP, //number of opt. parameters const int wolvesNumberP, //wolves number const int alphaNumberP, //alpha beta delta number const int epochCountP); //epochs number public: void TasksForWolves (int epochNow); public: void RevisionAlphaStatus (); //============================================================================ private: void ReturnToRange (S_Wolf &wolf); private: void SortingWolves (); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: int coordinates; //coordinates number private: int wolvesNumber; //the number of all wolves private: int alphaNumber; //Alpha beta delta number of all wolves private: int epochCount; private: S_Wolf wolvesT []; //temporary, for sorting private: int ind []; //array for indexes when sorting private: double val []; //array for sorting private: bool searching; //searching flag }; //——————————————————————————————————————————————————————————————————————————————
Traditionally, the class declaration is followed by the initialization. Here we reset to the minimum 'double' value of the wolves' fitness and distribute the size of the arrays.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_GWO::InitPack (const int coordinatesP, //number of opt. parameters const int wolvesNumberP, //wolves number const int alphaNumberP, //alpha beta delta number const int epochCountP) //epochs number { MathSrand (GetTickCount ()); searching = false; pB = -DBL_MAX; coordinates = coordinatesP; wolvesNumber = wolvesNumberP; alphaNumber = alphaNumberP; epochCount = epochCountP; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (ind, wolvesNumber); ArrayResize (val, wolvesNumber); ArrayResize (wolves, wolvesNumber); ArrayResize (wolvesT, wolvesNumber); for (int i = 0; i < wolvesNumber; i++) { ArrayResize (wolves [i].c, coordinates); ArrayResize (wolvesT [i].c, coordinates); wolves [i].p = -DBL_MAX; wolvesT [i].p = -DBL_MAX; } } //——————————————————————————————————————————————————————————————————————————————
The first public method called at each iteration is the most difficult to understand and the most voluminous. Here is the main logic of the algorithm. In fact, the performance of the algorithm is provided by a probabilistic mechanism strictly described by equations. Let's consider this method step by step. On the first iteration, when the position of the intended prey is unknown, after checking the flag, we send the wolves in a random direction simply by generating values from the max and min of the optimized parameters.
//---------------------------------------------------------------------------- //space has not been explored yet, then send the wolf in a random direction if (!searching) { for (int w = 0; w < wolvesNumber; w++) { for (int c = 0; c < coordinates; c++) { wolves [w].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); wolves [w].c [c] = SeInDiSp (wolves [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } searching = true; return; }
In the canonical version of the algorithm description, there are equations that operate vectors. However, they are much clearer in the form of code. The calculation of omega wolves goes is performed prior to the calculation of alpha, beta and delta wolves because we need to use the previous leader values.
The main component that provides three stages of hunting (search, encirclement and attack) is the a ratio. It represents a non-linear dependence on the current iteration and the total number of iterations, and tends to 0.The next components of the equation are Ai and Сi:
- Ai = 2.0 * a * r1 - a;
- Ci = 2.0 * r2;
In the expression
//---------------------------------------------------------------------------- double a = sqrt (2.0 * (1.0 - (epochNow / epochCount))); double r1 = 0.0; double r2 = 0.0; double Ai = 0.0; double Ci = 0.0; double Xn = 0.0; double min = 0.0; double max = 1.0; //omega----------------------------------------------------------------------- for (int w = alphaNumber; w < wolvesNumber; w++) { Xn = 0.0; for (int c = 0; c < coordinates; c++) { for (int abd = 0; abd < alphaNumber; abd++) { r1 = RNDfromCI (min, max); r2 = RNDfromCI (min, max); Ai = 2.0 * a * r1 - a; Ci = 2.0 * r2; Xn += wolves [abd].c [c] - Ai * (Ci * wolves [abd].c [c] - wolves [w].c [c]); } wolves [w].c [c] = Xn /= (double)alphaNumber; } ReturnToRange (wolves [w]); }
Here is the calculation of the leaders. The a, Ai and Ci ratios per each coordinate are calculated for them. The only difference is that the position of the leaders changes in relation to the best prey coordinates at the current moment and their own positions. The leaders circle around the prey, moving in and out, and control the minor wolves in the attack.
//alpha, beta, delta---------------------------------------------------------- for (int w = 0; w < alphaNumber; w++) { for (int c = 0; c < coordinates; c++) { r1 = RNDfromCI (min, max); r2 = RNDfromCI (min, max); Ai = 2.0 * a * r1 - a; Ci = 2.0 * r2; wolves [w].c [c] = cB [c] - Ai * (Ci * cB [c] - wolves [w].c [c]); } ReturnToRange (wolves [w]); }
This is the second public method called on each iteration. The status of the leaders in the pack is updated here. In fact, the wolves are sorted by fitness value. If better prey coordinates are found than those stored throughout the swarm, then we update the values.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_GWO::RevisionAlphaStatus () { SortingWolves (); if (wolves [0].p > pB) { pB = wolves [0].p; ArrayCopy (cB, wolves [0].c, 0, 0, WHOLE_ARRAY); } } //——————————————————————————————————————————————————————————————————————————————
3. Test functions
You already know the Skin, Forest and Megacity functions. These test functions satisfy all the complexity criteria for testing optimization algorithms. However, there is one feature that was not taken into account. It should be implemented to increase the test objectivity. The requirements are as follows:
- The global extremum should not be on the borders of the range. If the algorithm does not have an out-of-range check, then situations are possible when the algorithm will show excellent results. This is due to the fact that the values will be located on the borders due to an internal defect.
- The global extremum should not be in the center of the range coordinates. In this case, the algorithm, generating values averaged in a range, is taken into account.
- The global minimum should be located in the center of coordinates. This is necessary in order to deliberately exclude the situations described in the p. 2.
- The calculation of the results of the test function should take into account the case, in which randomly generated numbers over the entire domain of the function (when the function is multivariable) will give an average result of about 50% of the maximum, although in fact these results were obtained by chance.
Taking into account these requirements, the boundaries of the test functions were revised, and the centers of the range were shifted to the minimums of the function values. Let me summarize once again. Doing this was necessary in order to obtain the greatest plausibility and objectivity of the results of the test optimization algorithms. Therefore, on new test functions, the optimization algorithm based on random number generation showed a naturally low overall result. The updated rating table is located at the end of the article.
Skin function. A smooth function that has several local extrema that can confuse the optimization algorithm as it can get stuck in one of them. The only global extremum is characterized by weakly changing values in the vicinity. This function clearly shows the ability of the algorithm to be divided into areas under study, rather than focusing on a single one. In particular, the bee colony (ABC) algorithm behaves this way.
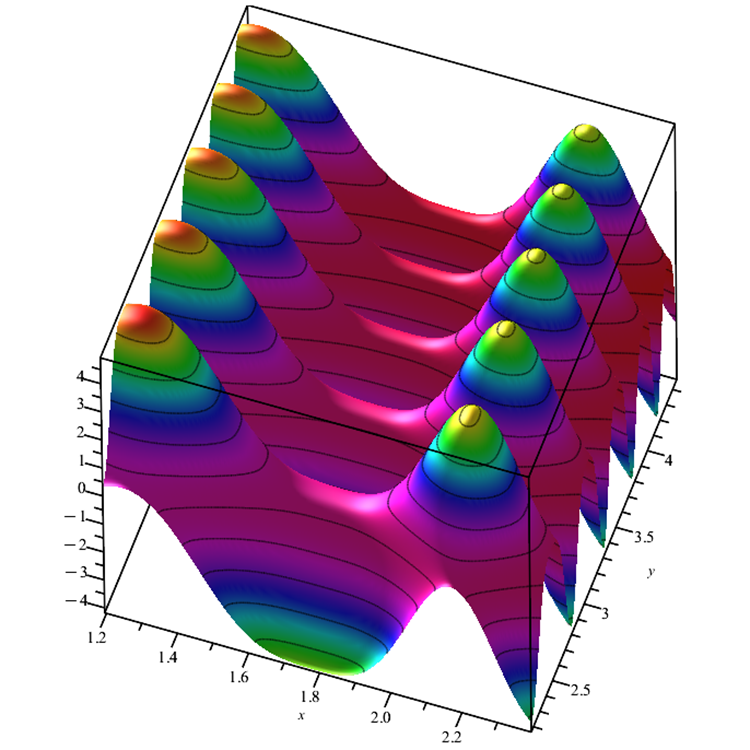
Fig. 4. Skin test function
Forest function. A function with several smooth and several non-differentiable extrema. This is a worthy test of optimization algorithms for the ability to find a "needle in a haystack". Finding a single global maximum point is a very difficult task, especially if the function contains many variables. The ant colony algorithm (ACO) distinguished itself in this task by the characteristic behavior, which paves paths to the goal in an incredible way.
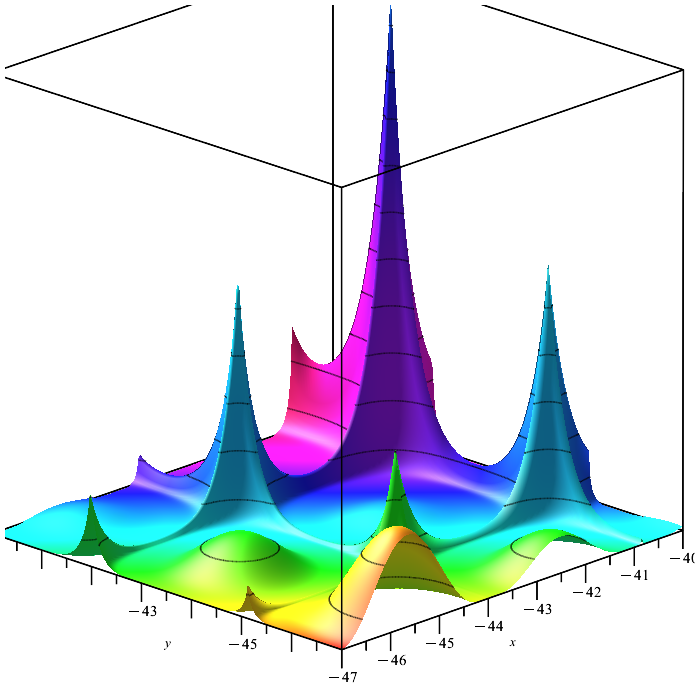
Figure 5 Forest test function
Megacity function. The function is a discrete optimization problem with one global and several local extrema. Extremely complex surface to study provides a good test of algorithms that require a gradient. An additional complexity is added by a completely even "floor", which is also a minimum, which does not give any information about the possible direction towards the global maximum.
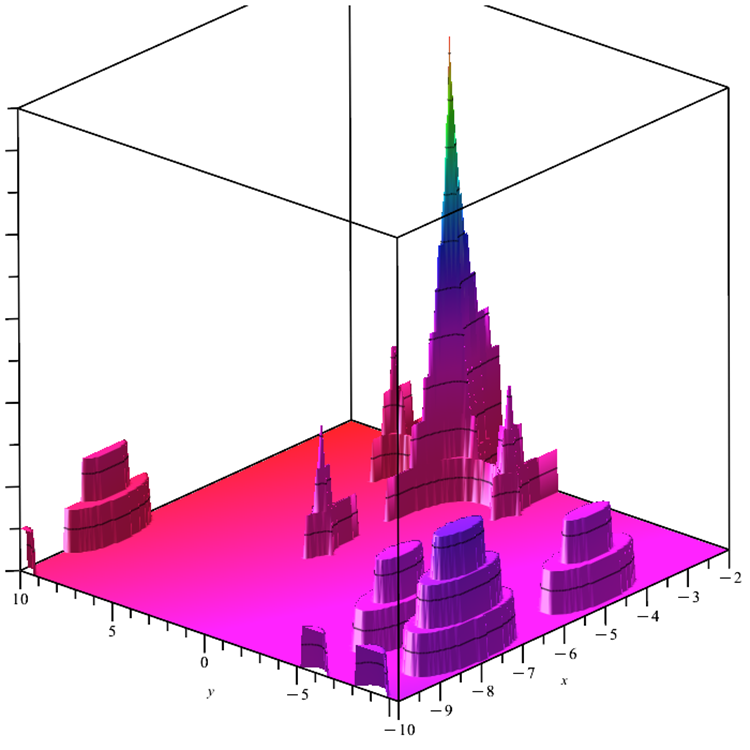
Figure 6 Megacity test function
Checks of incoming arguments for out-of-range values have been added to the code of test functions. In the previous versions of the functions, optimization algorithms could unfairly obtain function values larger than the function actually has within the range of its definition.
4. Test results
Due to the changes made to the test functions, the test stand has also been updated. On the right side of the stand screen, you can still see the convergence graphs of the optimization algorithms. The green line stands for the results of convergence on functions with two variables. The blue line stands for the functions with 40 variables. The red one means functions with 1000 variables. The larger black circle indicates the position of the global maximum of the function. The smaller black circle indicates the position of the current optimization algorithm solution value. The crosshair of white lines indicates the geometric center of the test functions and corresponds to the global minimum. This has been introduced for a better visual perception of the behavior of the tested algorithms. White dots indicate averaged intermediate solutions. Colored small dots indicate pairs of coordinates of the corresponding dimension. The color indicates the ordinal position of the dimension of the test function.
The updated results of testing the optimization algorithms discussed in previous articles on the new stand can be seen in the updated table. For more visual clarity, the line about the speed of convergence has been removed from the table - it can be visually determined on the animation of the stand. Added the column with the algorithm description.
ACOm (Ant Colony Optimization) test results:
2022.11.28 12:17:00.468 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:17:06.382 Test_AO_ACO (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.844203223078298
2022.11.28 12:17:06.382 Test_AO_ACO (EURUSD,M1) Score: 0.98229
2022.11.28 12:17:14.191 Test_AO_ACO (EURUSD,M1) 20 Skin's; Func runs 10000 result: 4.043383610736287
2022.11.28 12:17:14.191 Test_AO_ACO (EURUSD,M1) Score: 0.79108
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.2580170651681026
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) Score: 0.12602
2022.11.28 12:17:55.578 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:18:01.491 Test_AO_ACO (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.7678766100234538
2022.11.28 12:18:01.491 Test_AO_ACO (EURUSD,M1) Score: 1.00000
2022.11.28 12:18:09.508 Test_AO_ACO (EURUSD,M1) 20 Forest's; Func runs 10000 result: 1.0974381500585855
2022.11.28 12:18:09.508 Test_AO_ACO (EURUSD,M1) Score: 0.62077
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.20367726028454042
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) Score: 0.11521
2022.11.28 12:18:53.348 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:18:59.303 Test_AO_ACO (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 4.6
2022.11.28 12:18:59.303 Test_AO_ACO (EURUSD,M1) Score: 0.38333
2022.11.28 12:19:07.598 Test_AO_ACO (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 5.28
2022.11.28 12:19:07.598 Test_AO_ACO (EURUSD,M1) Score: 0.44000
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.2852
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) Score: 0.02377
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) =============================
2022.11.28 12:19:53.172 Test_AO_ACO (EURUSD,M1) All score for C_AO_ACOm: 0.4980520084646583
(Artificial Bee Colony) test results:
2022.11.28 12:35:47.181 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:35:52.581 Test_AO_ABCm (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.918379986612587
2022.11.28 12:35:52.581 Test_AO_ABCm (EURUSD,M1) Score: 1.00000
2022.11.28 12:35:59.454 Test_AO_ABCm (EURUSD,M1) 20 Skin's; Func runs 10000 result: 3.4073825805846374
2022.11.28 12:35:59.454 Test_AO_ABCm (EURUSD,M1) Score: 0.63922
2022.11.28 12:36:32.428 Test_AO_ABCm (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.0684464927353337
2022.11.28 12:36:32.428 Test_AO_ABCm (EURUSD,M1) Score: 0.08076
2022.11.28 12:36:32.428 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:36:38.086 Test_AO_ABCm (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.766245456669898
2022.11.28 12:36:38.086 Test_AO_ABCm (EURUSD,M1) Score: 0.99908
2022.11.28 12:36:45.326 Test_AO_ABCm (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.35556125136004335
2022.11.28 12:36:45.326 Test_AO_ABCm (EURUSD,M1) Score: 0.20112
2022.11.28 12:37:22.301 Test_AO_ABCm (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.06691711149962026
2022.11.28 12:37:22.301 Test_AO_ABCm (EURUSD,M1) Score: 0.03785
2022.11.28 12:37:22.301 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:37:28.047 Test_AO_ABCm (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.11.28 12:37:28.047 Test_AO_ABCm (EURUSD,M1) Score: 1.00000
2022.11.28 12:37:35.689 Test_AO_ABCm (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 1.9600000000000002
2022.11.28 12:37:35.689 Test_AO_ABCm (EURUSD,M1) Score: 0.16333
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.33880000000000005
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) Score: 0.02823
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.28 12:38:11.609 Test_AO_ABCm (EURUSD,M1) All score for C_AO_ABCm: 0.4610669021761763
ABC (Artificial Bee Colony) test results:
2022.11.28 12:29:51.177 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:29:56.785 Test_AO_ABC (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.890679983950205
2022.11.28 12:29:56.785 Test_AO_ABC (EURUSD,M1) Score: 0.99339
2022.11.28 12:30:03.880 Test_AO_ABC (EURUSD,M1) 20 Skin's; Func runs 10000 result: 3.8035430744604133
2022.11.28 12:30:03.880 Test_AO_ABC (EURUSD,M1) Score: 0.73381
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.195840100227333
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) Score: 0.11118
2022.11.28 12:30:37.089 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:30:42.811 Test_AO_ABC (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.7667070507449298
2022.11.28 12:30:42.811 Test_AO_ABC (EURUSD,M1) Score: 0.99934
2022.11.28 12:30:50.108 Test_AO_ABC (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.3789854806095275
2022.11.28 12:30:50.108 Test_AO_ABC (EURUSD,M1) Score: 0.21437
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.07451308481273813
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) Score: 0.04215
2022.11.28 12:31:25.900 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:31:31.510 Test_AO_ABC (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 10.2
2022.11.28 12:31:31.510 Test_AO_ABC (EURUSD,M1) Score: 0.85000
2022.11.28 12:31:38.855 Test_AO_ABC (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 2.02
2022.11.28 12:31:38.855 Test_AO_ABC (EURUSD,M1) Score: 0.16833
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.37559999999999993
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) Score: 0.03130
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) =============================
2022.11.28 12:32:14.623 Test_AO_ABC (EURUSD,M1) All score for C_AO_ABC: 0.46043003186219245
PSO (Particle Swarm Optimization) test results
2022.11.28 12:01:03.967 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:01:09.723 Test_AO_PSO (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.90276049713715
2022.11.28 12:01:09.723 Test_AO_PSO (EURUSD,M1) Score: 0.99627
2022.11.28 12:01:17.064 Test_AO_PSO (EURUSD,M1) 20 Skin's; Func runs 10000 result: 2.3250668562024566
2022.11.28 12:01:17.064 Test_AO_PSO (EURUSD,M1) Score: 0.38080
2022.11.28 12:01:52.880 Test_AO_PSO (EURUSD,M1) 500 Skin's; Func runs 10000 result: 0.943331687769892
2022.11.28 12:01:52.881 Test_AO_PSO (EURUSD,M1) Score: 0.05089
2022.11.28 12:01:52.881 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:01:58.492 Test_AO_PSO (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.6577769478566602
2022.11.28 12:01:58.492 Test_AO_PSO (EURUSD,M1) Score: 0.93772
2022.11.28 12:02:06.105 Test_AO_PSO (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.25704414127018393
2022.11.28 12:02:06.105 Test_AO_PSO (EURUSD,M1) Score: 0.14540
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.08584805450831333
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) Score: 0.04856
2022.11.28 12:02:44.566 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:02:50.268 Test_AO_PSO (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.11.28 12:02:50.268 Test_AO_PSO (EURUSD,M1) Score: 1.00000
2022.11.28 12:02:57.649 Test_AO_PSO (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 1.1199999999999999
2022.11.28 12:02:57.649 Test_AO_PSO (EURUSD,M1) Score: 0.09333
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.268
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) Score: 0.02233
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) =============================
2022.11.28 12:03:34.895 Test_AO_PSO (EURUSD,M1) All score for C_AO_PSO: 0.40836715689743186
RND (Random) test results:
2022.11.28 16:45:15.976 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:45:21.569 Test_AO_RND (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.915522750114194
2022.11.28 16:45:21.569 Test_AO_RND (EURUSD,M1) Score: 0.99932
2022.11.28 16:45:28.607 Test_AO_RND (EURUSD,M1) 20 Skin's; Func runs 10000 result: 2.584546688199847
2022.11.28 16:45:28.607 Test_AO_RND (EURUSD,M1) Score: 0.44276
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.0161336237263792
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) Score: 0.06827
2022.11.28 16:46:02.695 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:46:09.622 Test_AO_RND (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.4695680943894533
2022.11.28 16:46:09.622 Test_AO_RND (EURUSD,M1) Score: 0.83126
2022.11.28 16:46:17.675 Test_AO_RND (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.20373533112604475
2022.11.28 16:46:17.675 Test_AO_RND (EURUSD,M1) Score: 0.11524
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.0538909816827325
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) Score: 0.03048
2022.11.28 16:46:54.544 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:47:00.219 Test_AO_RND (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 10.0
2022.11.28 16:47:00.219 Test_AO_RND (EURUSD,M1) Score: 0.83333
2022.11.28 16:47:08.145 Test_AO_RND (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 1.08
2022.11.28 16:47:08.145 Test_AO_RND (EURUSD,M1) Score: 0.09000
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.28840000000000005
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) Score: 0.02403
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) =============================
2022.11.28 16:47:49.875 Test_AO_RND (EURUSD,M1) All score for C_AO_RND: 0.38163317904126015
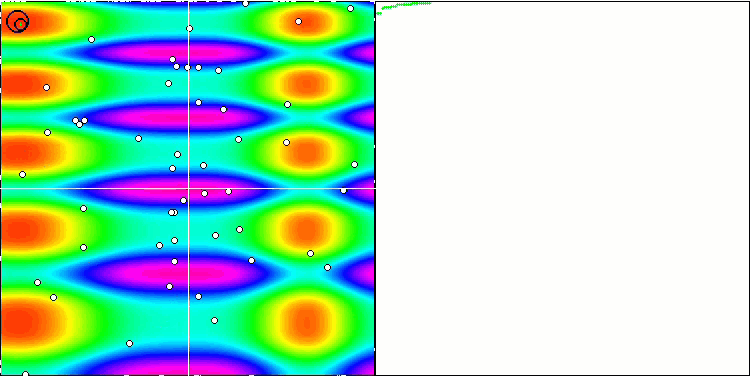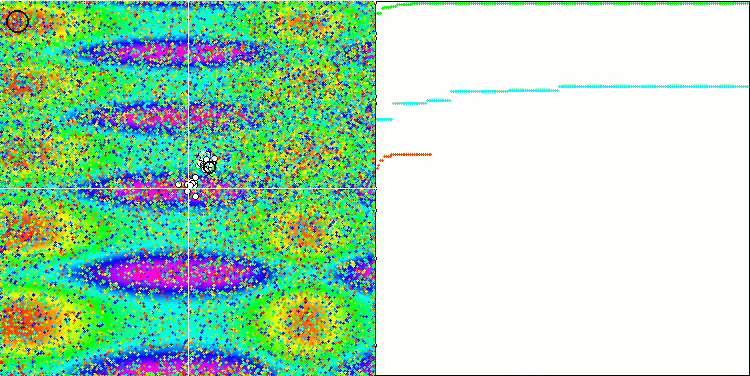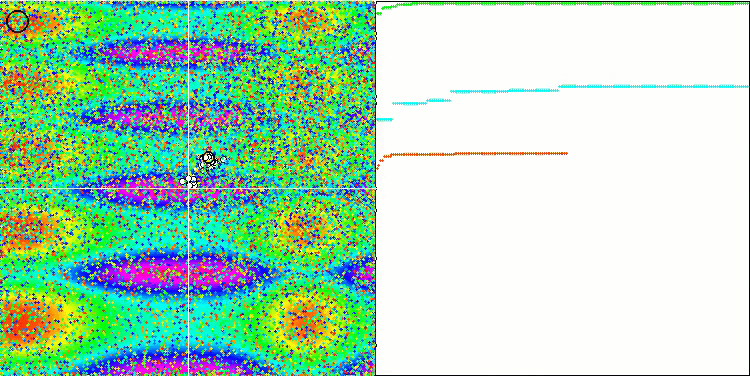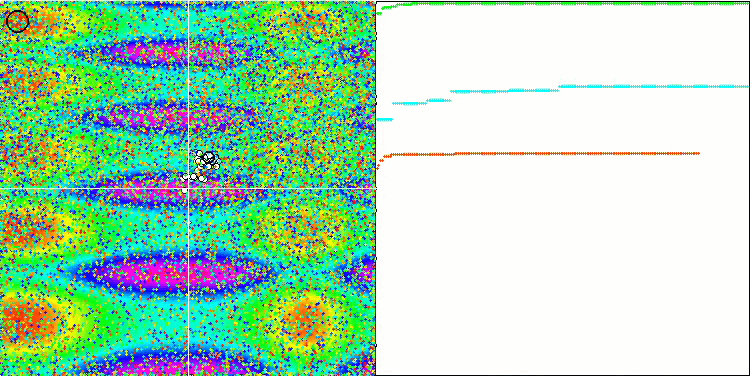
GWO on the Skin test function
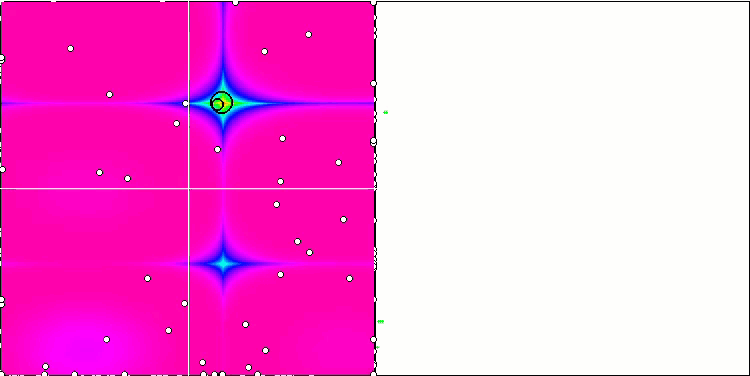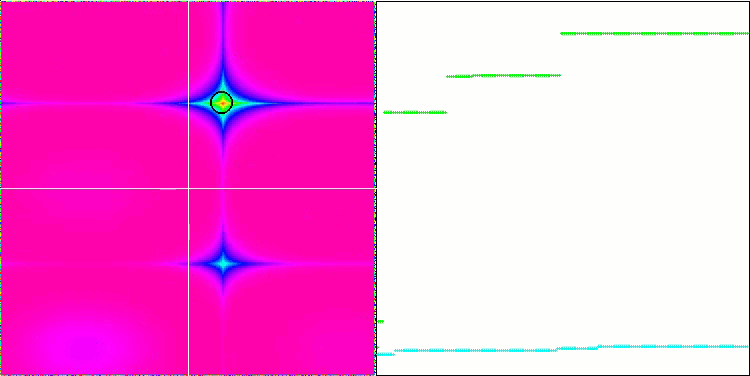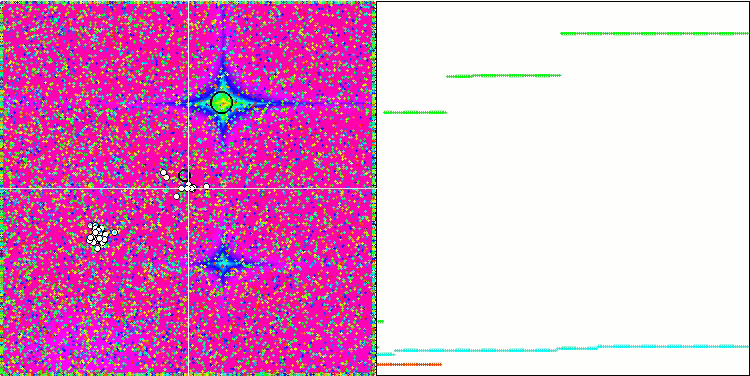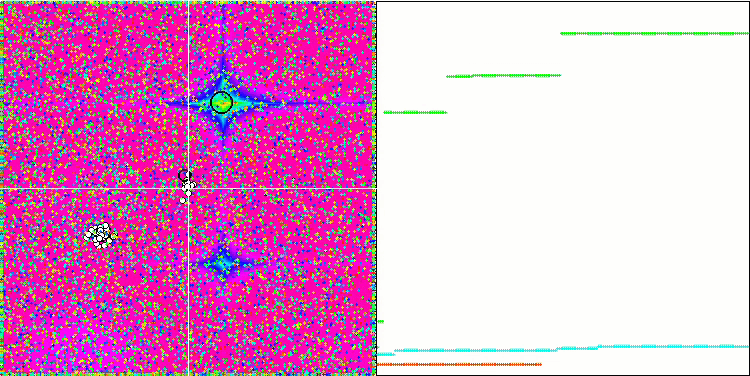
GWO on the Forest test function
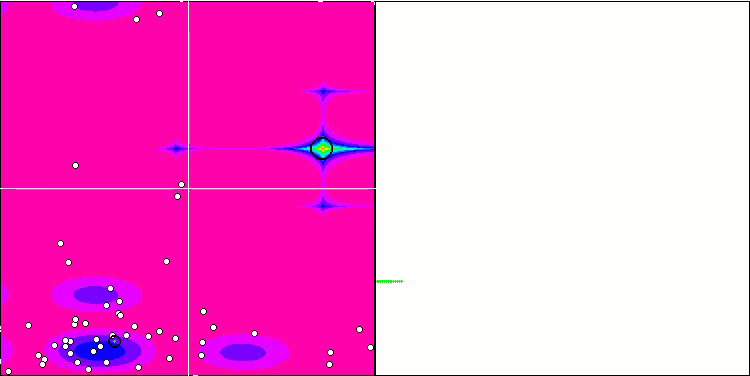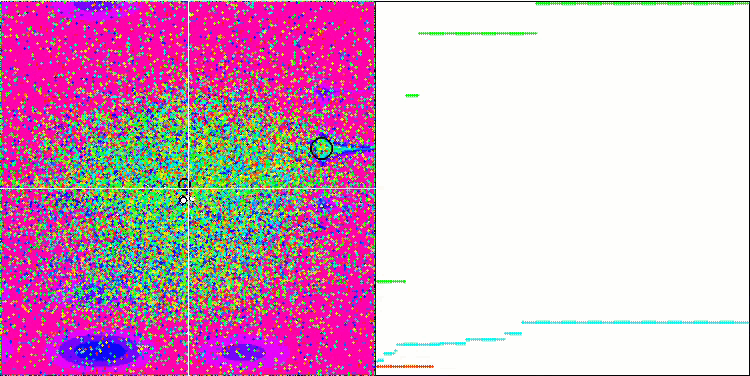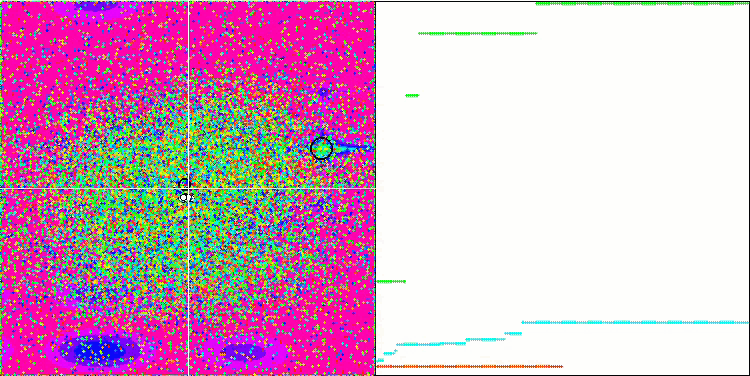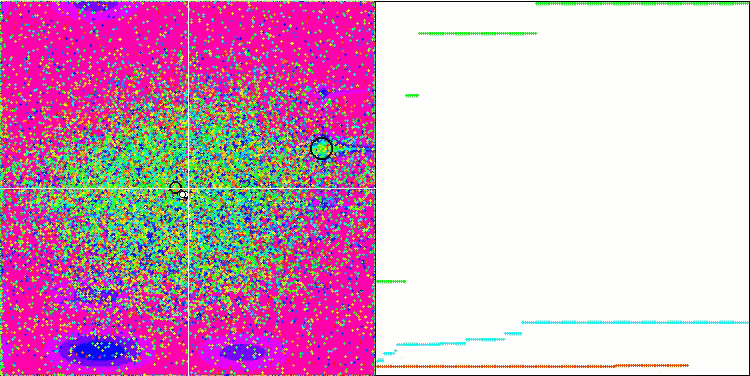
GWO on the Megacity test function
GWO test results.
2022.11.28 13:24:09.370 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:24:14.895 Test_AO_GWO (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.914175888065222
2022.11.28 13:24:14.895 Test_AO_GWO (EURUSD,M1) Score: 0.99900
2022.11.28 13:24:22.175 Test_AO_GWO (EURUSD,M1) 20 Skin's; Func runs 10000 result: 2.7419092435309405
2022.11.28 13:24:22.175 Test_AO_GWO (EURUSD,M1) Score: 0.48033
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.5227848592798188
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) Score: 0.18924
2022.11.28 13:25:01.381 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:25:06.924 Test_AO_GWO (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.4822580151819842
2022.11.28 13:25:06.924 Test_AO_GWO (EURUSD,M1) Score: 0.83844
2022.11.28 13:25:14.551 Test_AO_GWO (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.15477395149266915
2022.11.28 13:25:14.551 Test_AO_GWO (EURUSD,M1) Score: 0.08755
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.04517298232457319
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) Score: 0.02555
2022.11.28 13:25:56.900 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:26:02.305 Test_AO_GWO (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.11.28 13:26:02.305 Test_AO_GWO (EURUSD,M1) Score: 1.00000
2022.11.28 13:26:09.475 Test_AO_GWO (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 1.2
2022.11.28 13:26:09.475 Test_AO_GWO (EURUSD,M1) Score: 0.10000
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.2624
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) Score: 0.02187
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) =============================
2022.11.28 13:26:48.980 Test_AO_GWO (EURUSD,M1) All score for C_AO_GWO: 0.41577484361261224
The Gray Wolves Optimization Algorithm (GWO) is one of the recent bio-inspired optimization algorithms based on the simulated hunting of a pack of gray wolves. On average, the algorithm has proven itself quite efficient on various types of functions, both in terms of the accuracy of finding an extremum and in terms of the speed of convergence. In some tests, it has turned out to be the best. The main performance indicators of the "Gray Wolves" optimization algorithm are better than those of the particle swarm optimization algorithm, which is believed to be "conventional" in the class of bio-inspired optimization algorithms.
At the same time, the computational complexity of the Gray Wolves optimization algorithm is comparable to the particle swarm optimization algorithm. Due to numerous advantages of the GWO optimization algorithm, many works on its modification have appeared in a short time since the algorithm was first published. The only drawback of the algorithm is the low accuracy of the found coordinates of the Forest sharp-maximum function.
The low accuracy of the found extremum manifested itself in all dimensions of the Forest function, and the results are the worst among all participants in the table. The algorithm proved to be efficient on the smooth Skin function, especially in case of the larger dimension Skin function. GWO is also third in the table to achieve a 100% hit in the global maximum on the Megacity function.
| AO | Description | Skin | Forest | Megacity (discrete) | Final result | ||||||
| 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | |||
| ant colony optimization | 0.98229 | 0.79108 | 0.12602 | 1.00000 | 0.62077 | 0.11521 | 0.38333 | 0.44000 | 0.02377 | 0.49805222 | |
| artificial bee colony M | 1.00000 | 0.63922 | 0.08076 | 0.99908 | 0.20112 | 0.03785 | 1.00000 | 0.16333 | 0.02823 | 0.46106556 | |
| artificial bee colony | 0.99339 | 0.73381 | 0.11118 | 0.99934 | 0.21437 | 0.04215 | 0.85000 | 0.16833 | 0.03130 | 0.46043000 | |
| grey wolf optimizer | 0.99900 | 0.48033 | 0.18924 | 0.83844 | 0.08755 | 0.02555 | 1.00000 | 0.10000 | 0.02187 | 0.41577556 | |
| particle swarm optimisation | 0.99627 | 0.38080 | 0.05089 | 0.93772 | 0.14540 | 0.04856 | 1.00000 | 0.09333 | 0.02233 | 0.40836667 | |
| random | 0.99932 | 0.44276 | 0.06827 | 0.83126 | 0.11524 | 0.03048 | 0.83333 | 0.09000 | 0.02403 | 0.38163222 | |
Conclusions:
Pros:
1. High speed.
2. High convergence for smooth functions with a large number of variables.
Cons:
1. Not universal.
2. Getting stuck in local extremes.
3. Low scalability on discrete and non-differentiable functions.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/11785
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Will there be optimisation by the poor trader's flock method? ))
Those articles about metaheuristic optimization techniques are awesome! You are doing a great job Andrey, it's mind blowing how much experience you have to share with us, thank you!
@METAQUOTES please consider implement those metaheuristic optimization targets to the optimizer! It would be great for the software.
Something easy that user can set inside OnTester() as:
Cheers from Brazil