Artificial Showering Algorithm (ASHA)
18
0
Inhalt
Einführung
Da die Datenmengen in der heutigen Welt schnell wachsen und die Aufgaben immer komplexer und energieintensiver werden, ist der Bedarf an effektiven Optimierungsmethoden dringender denn je. Metaheuristische Algorithmen mit hoher Konvergenz und Verarbeitungsgeschwindigkeit eröffnen neue Horizonte für die Lösung einer Vielzahl von Problemen in unterschiedlichen Bereichen, von den Finanzmärkten bis zur wissenschaftlichen Forschung.
Die Geschwindigkeit der Datenverarbeitung und die Qualität der daraus resultierenden Lösungen spielen eine entscheidende Rolle für die erfolgreiche Umsetzung von Projekten. Unter strengen Zeitvorgaben, bei denen jeder Augenblick entscheidend sein kann, ermöglichen metaheuristische Algorithmen Ergebnisse, die bisher unerreichbar schienen. Sie ermöglichen nicht nur eine schnelle Verarbeitung großer Informationsmengen, sondern helfen auch, im Vergleich zu traditionellen numerischen Methoden bessere Lösungen zu finden.
Die Einsparung von Ressourcen ist ein weiterer wichtiger Aspekt, der bei der Optimierung zu berücksichtigen ist. Unter den Bedingungen begrenzter Rechenleistung benötigen solche Algorithmen weniger Zeit und Speicherplatz, was besonders beim Cloud Computing von Vorteil ist. Die Anpassungsfähigkeit von Algorithmen an veränderte Bedingungen und die Fähigkeit, schnell auf neue Daten zu reagieren, machen sie nahezu ideal für dynamische Systeme. So können wir die Relevanz der Lösungen erhalten und die Effizienz der Problemlösung unter realen Bedingungen verbessern.
Der Vergleich verschiedener Algorithmen anhand ihrer Eigenschaften, wie Konvergenzrate, Lösungsqualität und Resistenz gegen das Verharren in lokalen Extremen, ermöglicht die Auswahl der qualitativ besten, was wiederum die Innovation und die Entwicklung völlig neuer, oft von der Natur inspirierter Methoden fördert und einen wichtigen Schritt im Bereich der Optimierung darstellt.
Der Artificial Showering Algorithm (ASHA) ist eine neue metaheuristische Methode, die für die Lösung allgemeiner Optimierungsprobleme entwickelt wurde. Der Algorithmus basiert auf der Modellierung des Fließens und der Akkumulation von Wasser, das durch von Menschen gesteuerte Geräte auf einem idealen Feld verteilt wird. ASHA simuliert die Wasserverteilung (Duschen) über ein Feld, wobei das Wasser die Ressourceneinheiten und das Feld den Suchraum darstellt. Der Algorithmus nutzt die Prinzipien des Fließens und der Akkumulation, um optimale Lösungen für Probleme ohne Zwänge zu finden. Der Artificial Showering Algorithm (ASHA) wurde von einer Gruppe von Autoren entwickelt: Ali J., M. Saeed, N.A. Chaudhry, M. Luqman und M. F. Tabassum und wurde 2015 veröffentlicht.
Implementierung des Algorithmus
Die Methode basiert auf den folgenden Punkten:
- Ideales Einsatzgebiet. Der Suchraum ist ein ideales Feld, in dem das Wasser ohne Widerstand fließt und die Versickerung nur am tiefsten Punkt erfolgt.
- Keine externen Faktoren. Es gibt keine Verdunstung, keinen Regen, keinen Fließen von Wasser.
- Verfügbarkeit von Sprühgeräten. Jeder Teil des Suchraums befindet sich in Reichweite von Sprühgeräten, die sich oberhalb des Feldes befinden.
- Konstante Wassermenge. Es gibt einen Wasserüberschuss, dessen Menge in dem geschlossenen System während aller Iterationen konstant bleibt.
- Wasserbewegung. Jede Wassereinheit hat eine wahrscheinliche Tendenz, sich bergab zu bewegen.
ASHA (Artificial Showering Algorithm) Beschreibung Schritt für Schritt.
Parameter des Algorithmus:
- f - Zielfunktion, die minimiert werden soll
- R*n - n-dimensionaler Suchraum
- K - aktuelle Position im Iterationszähler
- m - Anzahl der Wassereinheiten (Suchagenten)
- F - Wasserdurchflussmenge
- δ - Widerstandsgrad (Versickerungsschwelle)
- ρ₀ - Anfangswahrscheinlichkeit
- β - Änderungsrate der Wahrscheinlichkeit
- M - maximale Anzahl von Iterationen
Schritte des Algorithmus:
1. Initialisierung:
Wir setzen den Anfangswert ρ = ρ₀.
Dann erzeugen wir m Wassereinheiten und platzieren sie zufällig im Suchraum R*n
2. Bewertung der Landschaft: Für jede Wassereinheit berechnen wir den Wert der Zielfunktion f an ihrer aktuellen Position
3. Hauptschleife (m-mal wiederholen): für jede Wassereinheit i (1 ≤ i ≤ m):
a) Wähle eine Zufallszahl r_i ∈ (0, 1)
b) Wenn r_i < ρ:
Wähle eine zufällige x_lower Position unterhalb der aktuellen Position
Erzeuge einen Zufallsvektor s ∈ (0, 1)*n
Berechne einer neuen Position:
x_new = x_old + F × (s ∘ (x_lower x_old))
wobei ∘ die elementweise Multiplikation bezeichnet
Wenn x_new auf einer niedrigeren Ebene liegt als x_old:
Eine neue Position akzeptieren
Andernfalls:
Erzeuge eine Zufallszahl r ∈ (0, 1)
Suche nach der niedrigsten Position x_lowest unter allen Wassereinheiten
Berechne die neue Position:
x_new = x_old + F × r × (x_lowest x_old)
c) Kontrolle der Infiltration:
Wenn eine Einheit Wasser den Widerstandswert von δ überwunden hat:
Erstelle eine neue Wassereinheit an einer zufälligen Position
d) Vergleich mit der niedrigsten Position:
Suche nach der Wassereinheit mit dem niedrigsten Wert der Zielfunktion
Wenn die aktuelle Wassereinheit einen niedrigeren Wert hat, vertausche aus.
e) Aktualisierungswahrscheinlichkeit ρ = max((M - K) / (β × M), ρ₀)
4. Fertigstellung:
Suche nach der Wassereinheit mit dem kleinsten Wert der Zielfunktion
Wir geben seine Position als die beste gefundene Lösung zurück
Erklärungen zum Algorithmus:
1. Der Algorithmus simuliert den Prozess einer Oberflächendusche, wobei jede Wassereinheit einen Suchagenten darstellt.
2. Der Suchraum wird als eine Landschaft betrachtet, in der niedrigere Werte der Zielfunktion niedrigeren Punkten des Geländes entsprechen.
3. Die Wassereinheiten neigen dazu, zu den unteren Punkten der Landschaft zu „fließen“, was der Suche nach dem Minimum der Zielfunktion entspricht.
4. Der Parameter ρ steuert das Gleichgewicht zwischen der Erkundung des Raums (große ρ-Werte) und der Ausnutzung der gefundenen Lösungen (kleine ρ-Werte).
5. Der Infiltrationsmechanismus verhindert, dass man in lokalen Minima stecken bleibt, indem neue Wassereinheiten an zufälligen Positionen geschaffen werden.
6. Der Vergleich und Austausch mit der niedrigsten Position gewährleistet, dass die beste gefundene Lösung erhalten bleibt.
7. Durch die dynamische Aktualisierung von ρ kann der Algorithmus mit zunehmender Zahl der Iterationen allmählich von der Erkundung zur Ausbeutung übergehen.
Der Algorithmus verwendet eine Analogie des Wasserflusses für die Optimierung, bei der das Wasser (die Suchagenten) versucht, die niedrigsten Punkte in der Landschaft (Minima der Zielfunktion) zu finden.
Die Hauptvorteile dieses Algorithmus sind nach Ansicht der Autoren folgende:
- Die Fähigkeit, dank der zufälligen Bewegung des Wassers einen großen Lösungsraum zu erkunden.
- Fähigkeit zur Vermeidung lokaler Minima durch den Infiltrationsmechanismus.
- Adaptives Verhalten aufgrund der dynamischen Änderung der ρ-Wahrscheinlichkeit.
Betrachten wir alle vom Algorithmus verwendeten Gleichungen im Detail.
1. Gleichung für die Aktualisierung der Position im Falle der Wahrscheinlichkeitserfüllung „ρ“: x_new = x_old + F × (s ∘ (x_lower - x_old)), wobei:
- x_new - neue Position der Wassereinheit
- x_old - aktuelle Position der Wassereinheit
- F - Wasserdurchsatz (Algorithmusparameter)
- s - Zufallsvektor im Bereich (0, 1)
- x_lower - zufällig ausgewählte Position unterhalb der aktuellen Position
- ∘ - Operator für die elementweise Multiplikation
Die Gleichung simuliert die Bewegung von Wasser einen Hang hinunter. Der Zufallsvektor s fügt der Bewegung ein Element der Zufälligkeit hinzu, während F die Schrittgröße steuert.
2. Alternative Formel, bei Ausfall von der Wahrscheinlichkeit ρ, Positionsaktualisierung: x_neu = x_alt + F × r × (x_niedrigst - x_alt), wobei:
- r - Zufallszahl im Bereich (0, 1)
- x_lowest - Position mit dem niedrigsten Wert der Zielfunktion
Die Gleichung wird verwendet, wenn die Grundformel nicht zu einer Verbesserung führt. Sie lenkt eine Wassereinheit auf das globale Minimum.
Aus diesen Gleichungen ist ersichtlich, dass Wasser immer dazu neigt, sich zu Positionen hinzubewegen, die niedriger sind als seine aktuelle Position. Wenn der Algorithmus nur bis zu diesem Schritt implementiert wird, bleibt er unweigerlich in lokalen Extremen stecken.
3. Wahrscheinlichkeitsaktualisierungsgleichung, ρ = max ((M - K) / (β × M), ρ₀), wobei:
- ρ - aktuelle Wahrscheinlichkeit der Wasserbewegung
- M - maximale Anzahl von Iterationen
- K - aktuelle Iterationsnummer
- β - Änderungsrate der Wahrscheinlichkeit
- ρ₀ - Anfangswahrscheinlichkeit
Diese Gleichung verringert allmählich die Wahrscheinlichkeit, dass sich das Wasser in Richtung zufällig ausgewählter niedrigerer Positionen bewegt, und erhöht die Wahrscheinlichkeit, dass es sich in Richtung des globalen Minimums bewegt. So kann der Algorithmus von der Erkundung des Raums zur Verfeinerung der gefundenen Lösungen übergehen.
4. Infiltrationsbedingung, wenn f (x_current) < δ, wird eine neue Wassereinheit geschaffen, wobei:
- f (x_aktuell) - Wert der Zielfunktion an der aktuellen Position
- δ - Widerstandsgrad (Versickerungsschwelle)
Unter dieser Bedingung können neue Wassereinheiten an zufälligen Positionen angelegt werden, wenn die aktuelle Wassereinheit einen ausreichend niedrigen Punkt erreicht. Damit soll vermieden werden, dass man in lokalen Minima stecken bleibt.
5. Vergleich der Positionen, wenn f (x_i) < f (x_lowest), tausche x_i and x_lowest, wobei:
- f (x_i) - Wert der Zielfunktion für die i-te Wassereinheit
- f (x_lowest) - kleinster gefundener Wert der Zielfunktion
Die obigen Gleichungen bilden die Grundlage für den ASHA-Algorithmus.
- Die Gleichung zur Positionsaktualisierung simuliert die Bewegung von Wasser einen Hang hinunter. Ein Zufallselement (s oder r) bringt Abwechslung in die Suche, indem es die Erkundung verschiedener Bereiche des Lösungsraums ermöglicht.
- Eine alternative Positionsaktualisierungsgleichung wird mit steigender Wahrscheinlichkeit bei jeder neuen Iteration verwendet, um sicherzustellen, dass der Verfeinerungsgrad der globalen Lösung über alle Iterationen hinweg zunimmt.
- Die Formel für die Wahrscheinlichkeitsaktualisierung ρ sorgt für ein Gleichgewicht zwischen Erkundung und Ausbeutung. Zu Beginn des Algorithmus ist die Wahrscheinlichkeit, sich zu zufällig ausgewählten niedrigeren Positionen in der Landschaft zu bewegen, hoch, was eine breite Erkundung des Raums fördert. Mit fortschreitender Iteration sinkt die Wahrscheinlichkeit, was zu einer gründlicheren Erkundung vielversprechender Bereiche führt.
- Die Infiltrationsbedingung erlaubt es dem Algorithmus, die Suche von neuen zufälligen Positionen aus „neu zu starten“, wenn eine ausreichend gute Lösung gefunden wurde. Auf diese Weise lässt sich vermeiden, dass man in lokalen Minima stecken bleibt.
- Durch den Vergleich der Positionen wird sichergestellt, dass sich der Algorithmus stets an die beste gefundene Lösung „erinnert“ und diese zur Steuerung der weiteren Suche verwendet.
Die Idee ist also, dass der Algorithmus zunächst versucht, eine bessere Position zu finden, indem er sich zu einem zufälligen unteren Punkt bewegt. Gelingt dies nicht, wird versucht, die global beste gefundene Position anzusteuern. Dadurch wird ein Gleichgewicht zwischen lokaler Suche und globaler Erkundung des Lösungsraums geschaffen.
Das Prinzip der Infiltration im ASHA-Algorithmus mag auf den ersten Blick nicht offensichtlich sein. Lassen Sie uns gemeinsam einen genaueren Blick darauf werfen:
- Wir haben den Parameter δ (Delta), der als Widerstandsniveau oder Infiltrationsschwelle bezeichnet wird.
- Bei jeder Iteration wird für jede Wassereinheit geprüft, ob sie „zu gut“ geworden ist, d.h. ob sie unter den Wert von δ gefallen ist.
- Wenn der Wert der Zielfunktion für eine gegebene Wassereinheit kleiner als δ wird, wird das Wasser als „versickert“ oder „infiltriert“ in den Boden betrachtet.
- In diesem Fall „schaffen“ wir eine neue Wassereinheit, indem wir sie an einer zufälligen Position im Suchraum platzieren.
Formal kann dies wie folgt geschrieben werden: wenn f (x_i) < δ, x_i = random_position (), wobei f (x_i) ein Wert der Zielfunktion für die i-te Feldeinheit und x_i die Position der i-ten Wassereinheit ist.
Die Idee hinter diesem Mechanismus ist es, zu vermeiden, dass alle Wassereinheiten in einem einzigen lokalen Minimum stecken bleiben; zu versuchen, den Suchraum weiter zu erforschen, selbst nachdem man eine gute Lösung gefunden hat; und potenziell noch bessere Lösungen in unerforschten Gebieten zu finden.
Es ist wichtig, den richtigen Wert δ zu wählen. Ist δ zu klein, kann es sein, dass gar kein Versickern stattfindet; ist δ zu groß, kann es sein, dass der Algorithmus ständig „neu startet“, ohne Zeit zu haben, die optimale Lösung zu finden. Darüber hinaus kann die Bestimmung des geeigneten Wertes von δ eine nicht triviale Aufgabe sein, insbesondere dann, wenn wir den Wertebereich der Zielfunktion nicht im Voraus kennen und diesen Parameter nicht als externen Parameter festlegen können. Deshalb habe ich für jeden Tropfen einen Zähler für die Anzahl der Versuche „zu versickern“ eingeführt, und in dem externen Parameter ist es notwendig, seinen Höchstwert festzulegen. Bei jedem neuen Versuch steigt die Wahrscheinlichkeit des „Versickerns“ nach einem quadratischen Gesetz, d. h. mit der Beschleunigung. Auf diese Weise verbleibt kein Tropfen zu lange an einer Stelle, was dazu beiträgt, dass man nicht in lokalen Extremen stecken bleibt.
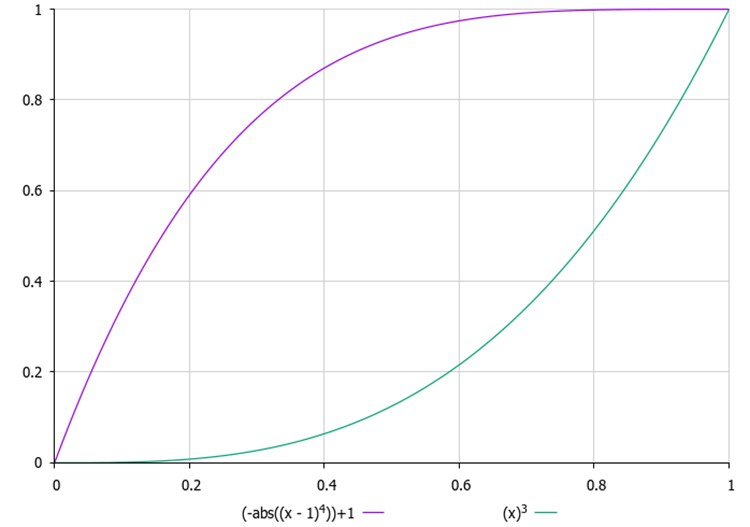
Abbildung 1. Beispiele für die Veränderung der Infiltrationswahrscheinlichkeit in Abhängigkeit von der Anzahl der Versuche
Bei der Verwendung der Koordinaten des tiefsten Punktes wird in der Regel folgender Ansatz gewählt:
- Die Wassereinheit mit dem kleinsten Wert der Zielfunktion wird gefunden (nennen wir sie x_lowest).
- Bei der Aktualisierung der Position werden alle Koordinaten dieses niedrigsten Punktes verwendet: x_neu = x_alt + F × r × (x_niedrigst - x_alt). Hier sind x_new, x_old und x_lowest Vektoren, die alle Koordinaten enthalten.
- Diese Vektorgleichung gilt für alle Koordinaten gleichzeitig. Das heißt, die neue Position wird von dem niedrigsten Punkt in allen Dimensionen des Suchraums „angezogen“.
Dieser Ansatz ermöglicht es uns, die Suche auf den vielversprechendsten Bereich des Lösungsraums zu lenken, wobei alle Dimensionen gleichzeitig berücksichtigt werden.
Für diesen Algorithmus (und ggf. für nachfolgende Algorithmen) ist es notwendig, die Standardstruktur zu erweitern, um zusätzliche Informationen über den Optimierungsagenten zu speichern. Die neu eingegebenen Felder werden grün hervorgehoben.
Erinnern wir uns daran, wie die Standardstruktur S_AO_Agent des Optimierungsagenten, auf den das Nutzerprogramm zugreift, aussieht. Mit Ergänzungen sieht es so aus:
1. Die Felder der Struktur:
- c [] - Array der aktuellen Koordinaten des Agenten im Suchraum.
- cP [] - Array mit den vorherigen Koordinaten des Agenten.
- cB [] - Array der besten Koordinaten, die der Agent über die gesamte Zeit gefunden hat.
- f - Wert der Fitnessfunktion für die aktuellen Agentenkoordinaten, um zu beurteilen, wie gut der Agent die Aufgabe bewältigt.
- fP - Wert der Fitnessfunktion für die vorherigen Koordinaten, um Veränderungen in der Leistung des Agenten zu verfolgen.
- fB - Wert der Fitnessfunktion für die besten Koordinaten unter Beibehaltung des besten vom Agenten erzielten Ergebnisses.
- cnt - Zähler zur Erfassung der Anzahl der Iterationen.
2. Init () - Die Initialisierungsmethode nimmt die Anzahl der für den Agenten benötigten Koordinaten und führt folgende Aktionen durch:
- Sie ändert die Größe des Arrays c auf coords und weist Speicher zum Speichern der aktuellen Koordinaten zu.
- Sie ändert in ähnlicher Weise die Größe des cP-Arrays zur Speicherung der vorherigen Koordinaten und die Größe des Arrays cB zur Speicherung der besten Koordinaten.
- Sie initialisiert den aktuellen Wert der Fitnessfunktion auf den kleinstmöglichen Wert und ermöglicht es dem Agenten, ihn bei der ersten Auswertung zu aktualisieren.
- Sie initialisiert den vorherigen und besten Wert der Fitnessfunktion auf ähnliche Weise.
- Sie initialisiert den Zählerwert auf Null.
Die Struktur S_AO_Agent ermöglicht die Speicherung von Informationen über den aktuellen Zustand des Agenten, seine Leistung und seine Änderungshistorie. Die an der Struktur vorgenommenen Änderungen werden sich nicht auf die bereits auf ihrer Grundlage geschriebenen Optimierungsalgorithmen auswirken, sondern werden die Konstruktion neuer Algorithmen in der Zukunft vereinfachen.
//—————————————————————————————————————————————————————————————————————————————— struct S_AO_Agent { double c []; //coordinates double cP []; //previous coordinates double cB []; //best coordinates double f; //fitness double fP; //previous fitness double fB; //best fitness int cnt; //counter void Init (int coords) { ArrayResize (c, coords); ArrayResize (cP, coords); ArrayResize (cB, coords); f = -DBL_MAX; fP = -DBL_MAX; fB = -DBL_MAX; cnt = 0; } }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_AO_ASHA wird von der Basisklasse C_AO abgeleitet und ist eine Implementierung des ASHA-Optimierungsalgorithmus. Analysieren wir seine Struktur und die Funktionsweise:
- F, δ, β und ρ0 - spezifische Parameter, die zuvor beschrieben wurden, bestimmen sein Verhalten.
- params - Array von Strukturen zur Speicherung der Algorithmusparameter. Jedes Array-Element enthält den Namen des Parameters und seinen Wert.
Die Methode SetParams () wird verwendet, um die Werte der Algorithmusparameter aus dem Array params zu setzen.
Die Methode Init () initialisiert den Algorithmus, indem sie die minimalen und maximalen Suchgrenzen, den Suchschritt und die Anzahl der Epochen als Eingabe erhält.
Die Methoden Moving () und Revision () sind dafür zuständig, Agenten im Suchraum zu bewegen, den Zustand der Agenten und ihre Positionen anhand von Optimierungskriterien zu überprüfen und zu aktualisieren.
Private Felder:
- S_AO_Agent aT [] - Array für temporäre Populationen, die für die Sortierung der Population verwendet werden.
- epochs - Gesamtzahl der für die Optimierung verwendeten Epochen.
- epochNow - aktuelle Epoche, in der sich der Algorithmus befindet.
Die Klasse C_AO_ASHA enthält die Parameter, Methoden und Strukturen, die zur Steuerung des Optimierungsprozesses und der Interaktion der Agenten erforderlich sind.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASHA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASHA () { } C_AO_ASHA () { ao_name = "ASHA"; ao_desc = "Artificial Showering Algorithm"; ao_link = "https://www.mql5.com/en/articles/15980"; popSize = 100; //population size F = 0.3; //water flow velocity δ = 2; //resistance level(infiltration threshold) β = 0.8; //parameter that controls the rate of change in probability ρ0 = 0.1; //initial probability ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "F"; params [1].val = F; params [2].name = "δ"; params [2].val = δ; params [3].name = "β"; params [3].val = β; params [4].name = "ρ0"; params [4].val = ρ0; } void SetParams () { popSize = (int)params [0].val; F = params [1].val; δ = (int)params [2].val; β = params [3].val; ρ0 = params [4].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double F; //water flow velocity int δ; //resistance level(infiltration threshold) double β; //parameter that controls the rate of change in probability double ρ0; //initial probability private: //------------------------------------------------------------------- S_AO_Agent aT []; int epochs; int epochNow; }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init ist für die Initialisierung des Optimierungsalgorithmus zuständig. Die Logik der Methode:
1. Standard-Initialisierungsprüfung: Die Methode ruft StandardInit auf, das grundlegende Prüfungen und die Initialisierung der Parameter durchführt.
2. Installation der Zähler:
- epochs wird gleich dem übergebenen Wert epochsP (die Gesamtzahl der Iterationen, die der Algorithmus durchführen soll) gesetzt.
- epochNow auf Null initialisiert ist, beginnt der Algorithmus gerade erst mit der Ausführung und hat noch keine einzige Epoche durchgeführt.
3. Reservierung von Speicherplatz für eine temporäre Population von Agenten.
4. Wenn alle Initialisierungsschritte erfolgreich sind, gibt die Methode true zurück und zeigt damit die erfolgreiche Initialisierung des Algorithmus an.
Der Init ist der Schlüssel zur Vorbereitung des Algorithmus auf die Arbeit. Er prüft die Gültigkeit der Eingaben, setzt die notwendigen Werte zur Steuerung des Optimierungsprozesses und weist den Agenten Speicherplatz zu. Nach einer erfolgreichen Initialisierung kann der Algorithmus weitere Operationen wie das Verschieben und Überarbeiten von Agenten durchführen.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASHA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (aT, popSize); return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving implementiert die Logik der Bewegung von Agenten im Suchraum innerhalb des ASHA-Algorithmus. Analysieren wir sie Schritt für Schritt:
1. Die Methode erhöht den aktuellen Epochenzähler, sodass wir die Anzahl der durchgeführten Iterationen verfolgen können.
2. Initiale Initialisierung (wenn keine Revision erforderlich ist): für jeden Agenten i und Koordinate c:
- Erzeugt die Methode die Anfangspositionen für alle Agenten innerhalb der gegebenen Bereiche mit u.RNDfromCI und wendet Diskretisierung an.
- Danach wird revision auf true gesetzt, und die Methode wird beendet.
3. In der Hauptschleife der Agentenbewegung werden für jeden Agenten i die folgenden Aktionen durchgeführt:
- inf - Wahrscheinlichkeit, die mit Hilfe von u.Scale berechnet wird, um einen Wert zu erhalten, der vom Agentenzähler cnt abhängt. Dieser Wert wird dann mit der vierten Potenz erhöht, um die Wirkung zu verstärken.
- Es wird eine Zufallszahl rnd für die Entscheidungsfindung generiert.
4. Schleife durch die Koordinaten, für jede Koordinate c werden die folgenden Aktionen durchgeführt:
- Es wird der Index ind erstellt, um einen anderen Agenten mit einer niedrigeren Position im Suchraum auszuwählen, der zur Aktualisierung der Koordinaten verwendet wird.
- Wenn i < 1, dann: wenn rnd < inf, dann werden die Koordinaten des aktuellen Agenten unter Verwendung einer Normalverteilung um die besten Koordinaten cB mit Hilfe von u.GaussDistribution aktualisiert.
- Wenn i >= 1, dann: Wenn rnd < inf, dann werden die Koordinaten des aktuellen Agenten in gleicher Weise im Verhältnis zu den Koordinaten eines anderen Agenten a[ind].cB aktualisiert.
- Andernfalls: der alte Wert von xOld bleibt erhalten. Wenn die erzeugte Zufallszahl kleiner als ρ ist:
- xNew wird auf der Grundlage des besten Wertes eines anderen Agenten xLower aktualisiert.
- Andernfalls: xNew wird auf der Grundlage des global besten Wertes xLowest aktualisiert.
- Dann wird dem aktuellen Agenten der neue Wert xNew zugewiesen.
5. Koordinatenanpassung: Schließlich wird jeder neue Koordinatenwert mit u.SeInDiSp so angepasst, dass er in die angegebenen Bereiche und Schritte passt.
Die Methode Moving ermöglicht sowohl die Initialisierung der Agentenpositionen als auch deren Aktualisierung während der Optimierung auf der Grundlage ihres aktuellen Zustands und der Interaktion mit anderen Agenten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASHA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double xOld = 0.0; double xNew = 0.0; double xLower = 0.0; double xLowest = 0.0; double ρ = MathMax (β * (epochs - epochNow) / epochs, ρ0); double inf = 0.0; int ind = 0; double rnd = 0.0; for (int i = 0; i < popSize; i++) { inf = u.Scale (a [i].cnt, 0, δ, 0, 1); inf = inf * inf * inf * inf; rnd = u.RNDprobab (); for (int c = 0; c < coords; c++) { ind = (int)u.RNDintInRange (0, i - 1); if (i < 1) { if (rnd < inf) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); } } else { if (rnd < inf) { a [i].c [c] = u.GaussDistribution (a [ind].cB [c], rangeMin [c], rangeMax [c], 8); } else { xOld = a [i].c [c]; if (u.RNDprobab () < ρ) { xLower = a [ind].cB [c]; xNew = xOld + F * (u.RNDprobab () * (xLower - xOld)); } else { xLowest = cB [c]; xNew = xOld + F * (u.RNDprobab () * (xLowest - xOld)); } a [i].c [c] = xNew; } } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision ist für die Aktualisierung der Informationen über die besten Lösungen (Agenten) in der Population sowie für die Verfolgung ihrer Fitness zuständig. Die einzelnen Schritte werden im Folgenden beschrieben:
1. Die Variable ind wird mit -1 initialisiert. Sie wird verwendet, um den Index des Agenten mit dem besten Fitnessfunktionswert von f zu speichern.
2. Schleife über die Agenten: Die Methode durchläuft alle Agenten in der Population popSize in einer Schleife:
- Wenn der Wert der Fitnessfunktion f des aktuellen Agenten seinen aktuell besten Wert von fB übersteigt, wird fB aktualisiert und der Agentenindex in der Variablen ind gespeichert.
- Wenn der Wert der Fitnessfunktion f des aktuellen Agenten seinen lokal besten Wert von fB übersteigt, wird auch der lokal beste Wert von fB für den Agenten aktualisiert.
- Die Koordinaten c des Agenten werden nach cB kopiert, das sind seine besten bekannten Koordinaten.
- Der Zähler cnt wird auf 0 zurückgesetzt. Andernfalls, wenn sich der Wert der Fitnessfunktion nicht verbessert hat, wird der Zähler cnt inkrementiert.
3. Kopieren der besten Koordinaten: Wenn der Agent mit dem besten Funktionswert (ind ist ungleich -1) gefunden wurde, dann werden seine Koordinaten in die globale Variable von cB kopiert.
4. Sortieren der Agenten: Am Ende wird u.Sorting_fB aufgerufen, um die Agenten nach ihren lokal besten Werten von fB zu sortieren.
Die Revisionsmethode spielt eine zentrale Rolle in dem Algorithmus, da sie die Leistung der Agenten überwacht und ihre besten bekannten Lösungen aktualisiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASHA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); a [i].cnt = 0; } else { a [i].cnt++; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Die Testergebnisse des ASHA-Algorithmus zeigten eine durchschnittliche Leistung: =============================
5 Hilly's; Func runs: 10000; result: 0.8968571984324711
25 Hilly's; Func runs: 10000; result: 0.40433437407600525
500 Hilly's; Func runs: 10000; result: 0.25617375427148387
=============================
5 Forest's; Func runs: 10000; result: 0.8036024134603961
25 Forest's; Func runs: 10000; result: 0.35525531625936474
500 Forest's; Func runs: 10000; result: 0.1916000538491299
=============================
5 Megacity's; Func runs: 10000; result: 0.4769230769230769
25 Megacity's; Func runs: 10000; result: 0.1812307692307692
500 Megacity's; Func runs: 10000; result: 0.09773846153846236
=============================
All score: 3.66372 (40.71%)
Wenn man die Arbeit von ASHA während der Tests beobachtet, ist es schwierig, charakteristische Merkmale dieses Algorithmus zu erkennen. Einzelne Studien über vielversprechende Bereiche des Suchraums werden nicht entdeckt.
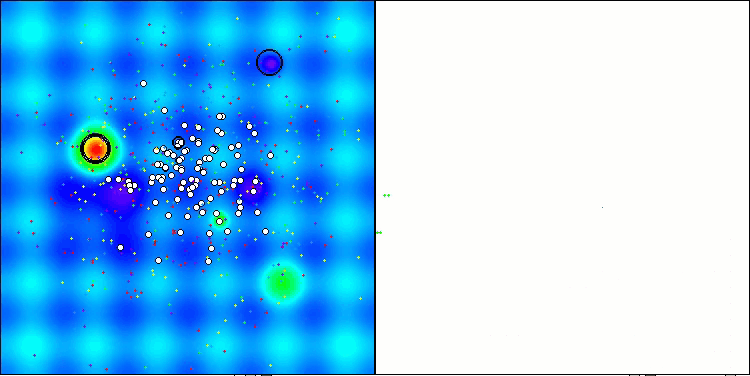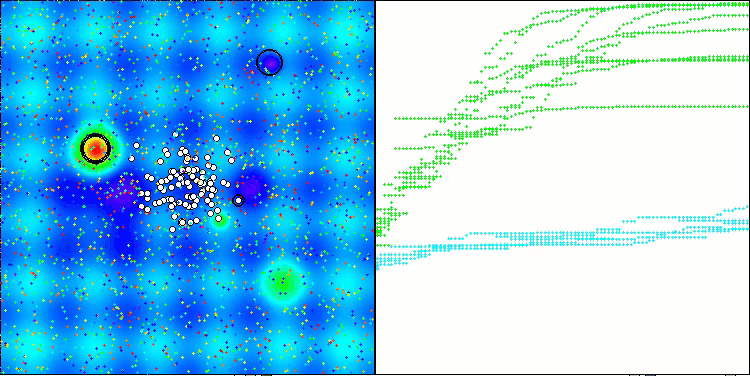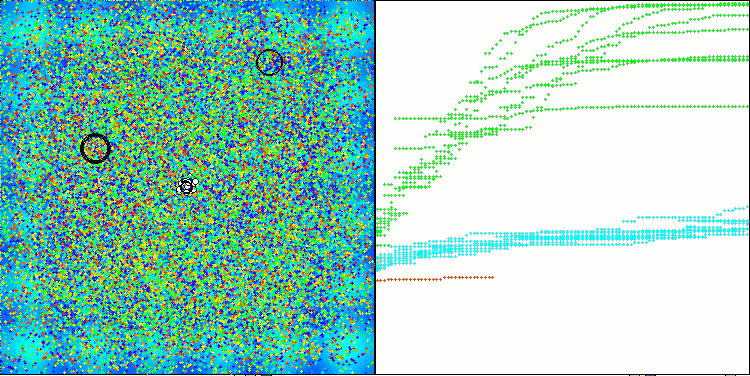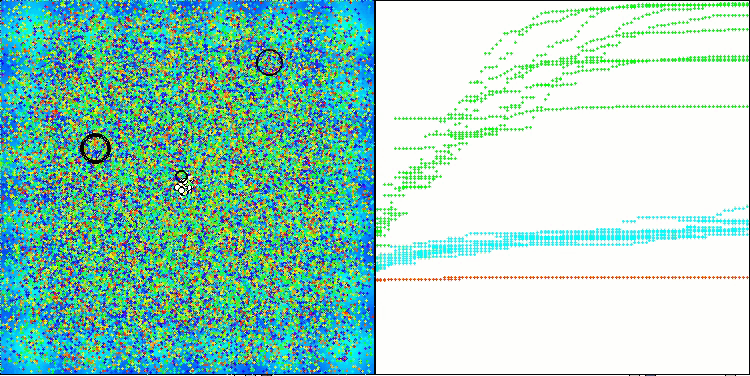
ASHA mit der Testfunktion Hilly
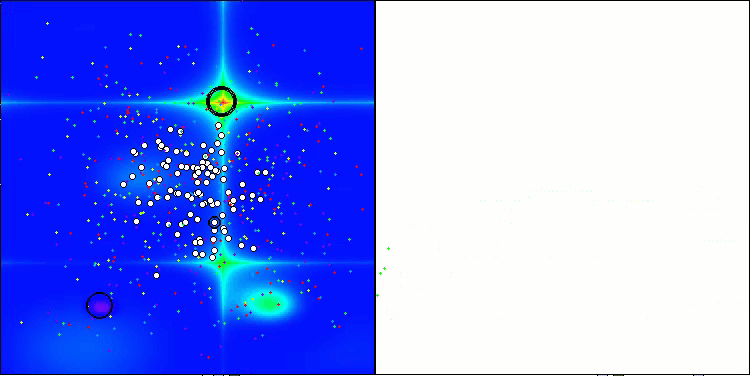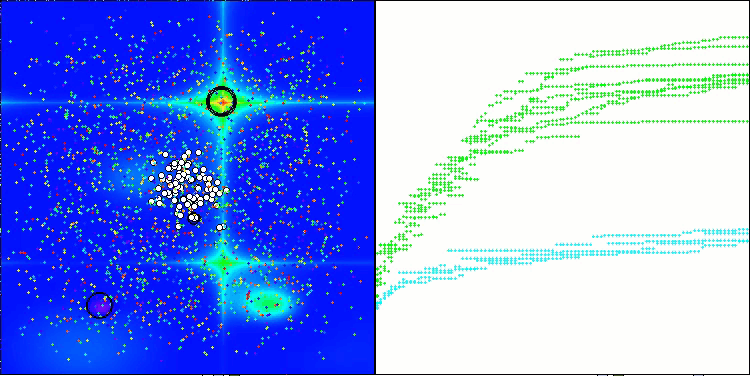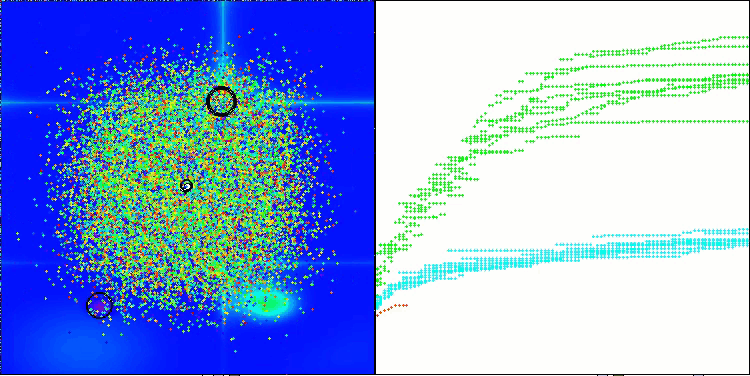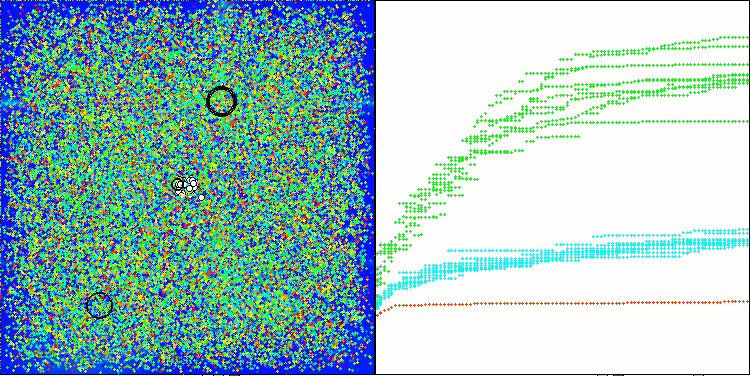
ASHA mit der Testfunktion Forest
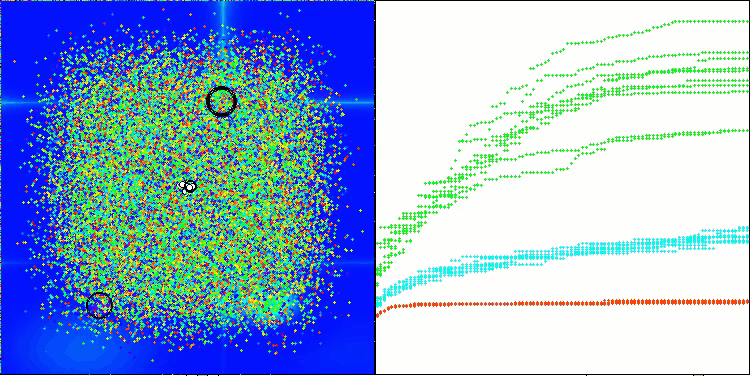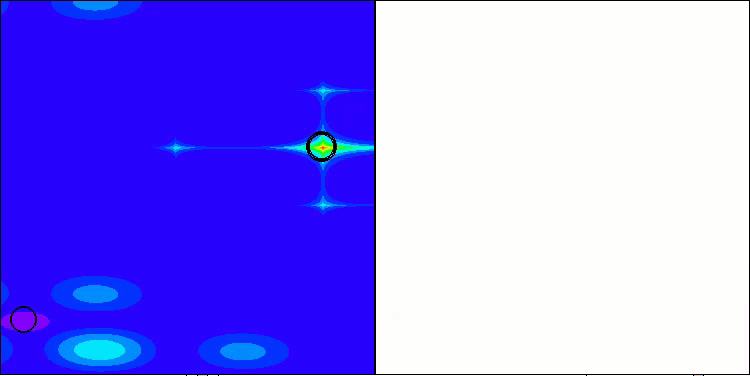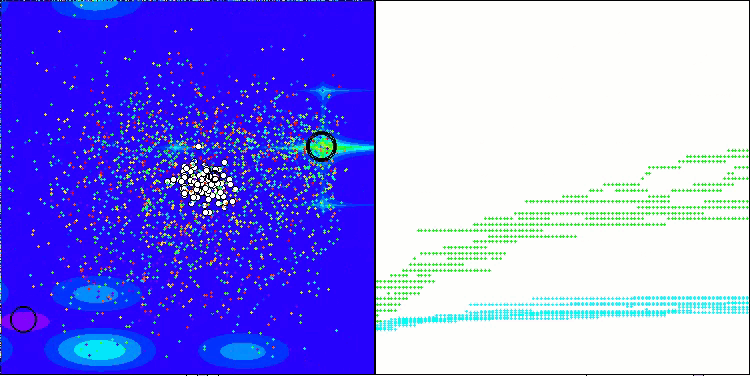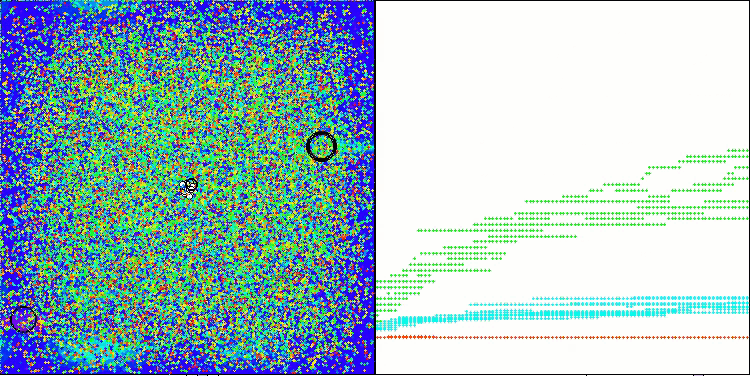
ASHA mit der Testfunktion Megacity
Auf der Grundlage der Testergebnisse belegte der ASHA-Algorithmus in der Bewertungstabelle den 28.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Сode Lock Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 12 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 20 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 21 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 22 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 23 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 24 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 25 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 26 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 27 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 28 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 29 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 30 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 31 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 32 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 33 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 34 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 35 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 36 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 37 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 38 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 39 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 40 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 41 | AAA | Künstlicher Algenalgorithmus (AAA) | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 42 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 43 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 44 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 45 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
Zusammenfassung
Die Idee des Algorithmus gefiel mir, aber bei der Umsetzung und den Tests hatte ich das Gefühl, dass dem Algorithmus etwas fehlte. Der Algorithmus gehört zwar nicht zu den schwächsten, aber bei weitem nicht zu den besten. Dies bietet den Forschern die Möglichkeit, weiter damit zu arbeiten, vor allem wegen seiner Einfachheit, denn die Idee selbst ist meiner Meinung nach sehr vielversprechend. Außerdem haben die Autoren die Infiltrationsrate nicht näher erläutert, sodass sie auf verschiedene Weise interpretiert werden kann, die nur durch die Phantasie des Forschers begrenzt ist.
Die wichtigste Schlussfolgerung, die aus diesem Artikel gezogen werden kann, ist, dass nicht jede einfache Idee so effektiv wie eine komplexere ist. Die Effizienz eines Optimierungsalgorithmus ist eine komplexe Angelegenheit, bei der Kompromisse eingegangen werden müssen. Ich hoffe, dass dieser Algorithmus eine weitere Seite im großen Buch des Wissens über die Feinheiten und Tricks der Kunst, die besten Lösungen zu finden, werden wird.
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
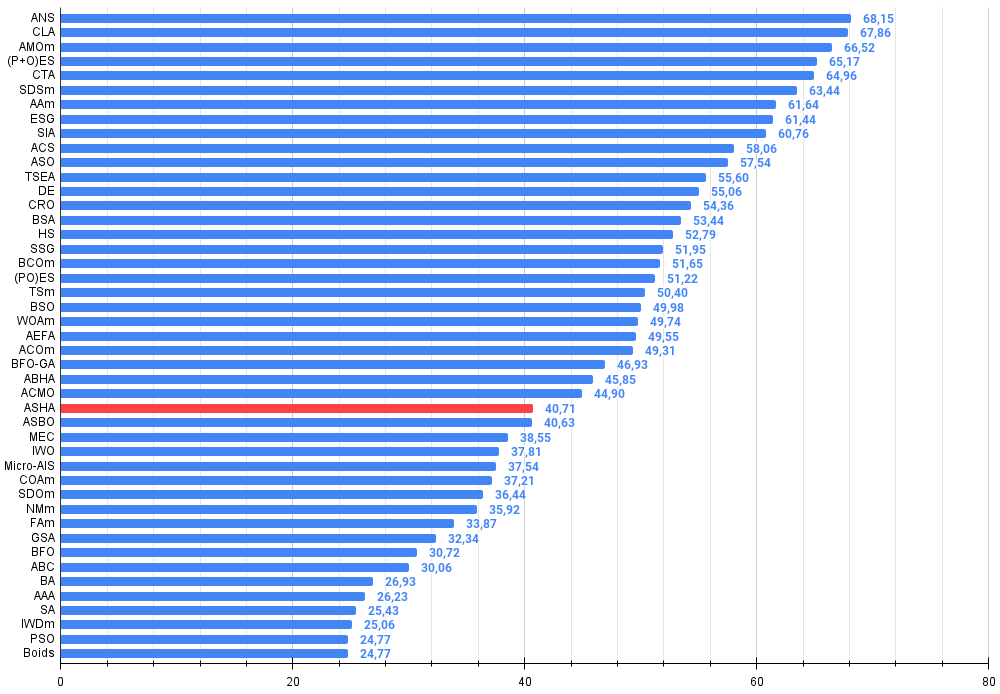
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
ASHA Pro und Kontra:
Vorteile:
- Schnell.
- Einfache Umsetzung.
Nachteile
- Geringe Konvergenzgenauigkeit.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15980
Finden von nutzerdefinierten Währungspaar-Mustern in Python mit MetaTrader 5
Von der Grundstufe bis zur Mittelstufe: Prioritätsfolge der Operatoren
Eine alternative Log-datei mit der Verwendung der HTML und CSS
Hochfrequenz-Arbitrage-Handelssystem in Python mit MetaTrader 5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.