Algorithmus zur chemischen Reaktionsoptimierung (CRO) (Teil II): Zusammenstellung und Ergebnisse

Inhalt

1. Einführung
2. Implementierung des Algorithmus
3. Testergebnisse

1. Einführung

Im zweiten Teil unseres Artikels tauchen wir weiter in die faszinierende Welt der chemischen Reaktionsoptimierung (CRO) ein. Ausgehend vom Konzept der „Moleküle“ und „Elementarreaktionen“ machten wir uns mit den zugrundeliegenden Algorithmusprinzipien vertraut und überlegten, wie diese Konzepte zur Lösung komplexer Optimierungsprobleme eingesetzt werden. Wir lernten auch die Schlüsselpunkte der Energieerhaltung innerhalb von CRO und die Algorithmusfunktionen kennen, wie Zerlegung, Synthese, intramolekulare und intermolekulare ineffiziente Kollisionen, die eine wichtige Rolle bei der Erkundung des Suchraums und der Suche nach optimalen Lösungen spielen.

Nachdem wir nun die grundlegenden Konzepte und Funktionsprinzipien der chemischen Operatoren des Algorithmus zur Optimierung chemischer Reaktionen behandelt haben, ist es nun an der Zeit, sich mit dem allgemeinen Aufbau des Algorithmus und seiner praktischen Anwendung zu befassen. Hier werden wir uns auf die Ergebnisse des Algorithmus bei verschiedenen Testfunktionen konzentrieren, um seine Effizienz und sein Potenzial bei der Lösung realer Probleme zu analysieren. Wir werden seine Leistung, Konvergenz und die Fähigkeit, globale Optima zu finden, untersuchen, um seine Anwendbarkeit zu bewerten und die Ergebnisse des CRO-Algorithmus mit anderen Optimierungsmethoden zu vergleichen und seine Vor- und Nachteile zu ermitteln.

2. Implementierung des Algorithmus

Fahren wir mit dem Schreiben des Algorithmus-Codes fort, indem wir die Vorlage verwenden, die Ihnen bereits für alle Algorithmen vertraut ist und die Standardfunktionen Init, Moving und Revision enthält. Da wir die Struktur bereits deklariert und die wichtigsten Operatoren chemischer Reaktionen implementiert haben, können wir nun die Algorithmusklasse schreiben, die alle Komponenten miteinander verbindet.

Wir benötigen einen Pseudocode, um den Algorithmus zu implementieren:

Wenn das Revisions-Flag zurückgesetzt wird - Initialisierung:
    Für jedes Molekül i von 0 bis popSize:
        Für jede Koordinate c von 0 bis coords
            Erzeuge einen Zufallswert für die Struktur eines Moleküls zwischen rangeMin und rangeMax
            Begrenze den Wert einer Struktur auf einen bestimmten Bereich
    Speichere die Struktur im Array a
Exit
Berechnung der kinetischen Energie:
    minKE = Höchstwert für den Typ double
Für jedes Molekül i von 0 bis popSize:
        Wenn die Fitness des Moleküls geringer ist als minKE:
            minKE = Fitness des Moleküls
    Für jedes Molekül i von 0 bis popSize:
        Berechne die kinetische Energie eines Moleküls KE als Skalierung der Fitness aus dem Bereich von minKE bis fB (beste globale Lösung) in den Bereich von 0,0 bis 1,0
molCNT = 0
Noch kein Stopp:
    Wenn die Zufallszahl kleiner ist als moleColl:
        Wähle zwei zufällige Moleküle M1 und M2
        Wenn KE der beiden Moleküle größer oder gleich β ist:
            Führe eine Synthese der Moleküle M1 und M2 durch.
        Ansonsten:
            Führe ein zwischenmolekulare, unwirksame Kollision zwischen M1 und M2 durch
    Ansonsten:
        Wähle ein zufälliges Molekül M
        Wenn NumHit des Moleküls größer ist als α:
            Zerlege das Molekül M
        Ansonsten:
            Führe eine Kollision des Moleküls M durch
Kopiere die Molekularstrukturen von Mfilial nach a
Berechne die Fitness der Individuen der Population a
Kopiere die Molekularstrukturen von a nach Mfilial
Initialisierung: ind = -1
Für jedes Molekül i von 0 bis popSize:
    Wenn die Fitness des Moleküls fB übersteigt:
        fB = Fitness des Moleküls
        ind = i
Wenn ind ungleich -1 ist:
    Kopiere die Struktur des Moleküls nach cB
Molekül-Update:
    Wenn es keine „Revision“ gibt:
        Für jedes Molekül i von 0 bis popSize:
            Aktualisiere die Fitness des Moleküls in Mparent
        Setze „Revision“ auf true
Exit
Für jedes Molekül i von 0 bis popSize:
    Aktualisiere die Fitness des Moleküls in Mfilial
    Je nach Art des Moleküls (Synthese, intermolekulare unwirksame Kollision, Zerlegung, Kollision):
        Führen Sie die entsprechenden Nachbehandlungen durch

Nachdem wir nun den Pseudocode und die chemischen Operatoren, die im ersten Teil des Artikels beschrieben wurden, haben, können wir mit der Implementierung des CRO-Algorithmus in Code beginnen.

Wir deklarieren die Klasse C_AO_CRO, die von der Basisklasse C_AO abgeleitet wird und eine Implementierung des Algorithmus der chemischen Reaktionsoptimierung (CRO) ist.

1. Öffentliche Felder:

• popSize - Größe der Population.
• moleColl, alpha, beta, molecPerturb - Algorithmusparameter.
• params - Array zur Speicherung der Algorithmusparameter.
• Mparent[], Mfilial[] - Objekte der Struktur S_CRO_Agent, zur Repräsentation der Moleküle.

2. Die verfügbaren Optionen sind:

• C_AO_CRO() - Klassenkonstruktor, der die Klassenfelder initialisiert.
• SetParams() - Methode zur Einstellung der Algorithmusparameter.
• Init() - Methode zur Initialisierung des Algorithmus. Die Methode akzeptiert minimale und maximale Suchbereiche, Suchschritte und die Anzahl der Epochen.
• Moving() und Revision() - Methoden, die die grundlegenden Operationen des Algorithmus implementieren.

3. Private Felder und Methoden:

• Synthesis(), InterMolInefColl(), Decomposition(), InefCollision() - Methoden, die verschiedene Arten von Reaktionen implementieren.
• PostSynthesis(), PostInterMolInefColl(), PostDecomposition(), PostInefCollision() - Methoden, die Aktionen nach entsprechenden Reaktionen durchführen.
• N() - Methode zur Änderung einer Komponente (Koordinate) der Struktur eines Moleküls.

Diese Klasse ist eine vollständige Implementierung des Algorithmus der chemischen Reaktionsoptimierung (CRO) und enthält alle dafür erforderlichen Daten und Methoden.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CRO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CRO () { }
  C_AO_CRO ()
  {
    ao_name = "CRO";
    ao_desc = "Chemical Reaction Optimisation";
    ao_link = "https://www.mql5.com/en/articles/15041";

    popSize      = 50;   //population size

    moleColl     = 0.9;
    alpha        = 200;
    beta         = 0.01;
    molecPerturb = 0.5;

    ArrayResize (params, 5);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "moleColl";     params [1].val = moleColl;
    params [2].name = "alpha";        params [2].val = alpha;
    params [3].name = "beta";         params [3].val = beta;
    params [4].name = "molecPerturb"; params [4].val = molecPerturb;

  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;

    moleColl     = params      [1].val;
    alpha        = (int)params [2].val;
    beta         = params      [3].val;
    molecPerturb = params      [4].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  S_CRO_Agent Mparent [];
  S_CRO_Agent Mfilial [];


  //----------------------------------------------------------------------------
  double moleColl;
  int    alpha;
  double beta;
  double molecPerturb;

  private: //-------------------------------------------------------------------
  bool Synthesis            (int index1, int index2, int &molCNT);
  bool InterMolInefColl     (int index1, int index2, int &molCNT);
  bool Decomposition        (int index,  int &molCNT);
  bool InefCollision        (int index,  int &molCNT);

  void PostSynthesis        (S_CRO_Agent &mol);
  void PostInterMolInefColl (S_CRO_Agent &mol);
  void PostDecomposition    (S_CRO_Agent &mol);
  void PostInefCollision    (S_CRO_Agent &mol);

  void N                    (double &coord, int coordPos);
};
//——————————————————————————————————————————————————————————————————————————————

Die Methode Init der Klasse C_AO_CRO dient der Initialisierung von Klassenvariablen auf der Grundlage der übergebenen Parameter. Bei dieser Methode geschieht Folgendes:

1. Die Methode ruft die Funktion StandardInit auf, die den minimalen und maximalen Suchbereich sowie den Suchschritt übernimmt. Wenn StandardInit false zurückgibt, gibt die Init-Methode ebenfalls false zurück und beendet ihre Arbeit.

2. Die Methode passt dann die Größe der Arrays Mparent und Mfilial an popSize an, was die Größe der Population darstellt.

3. Anschließend wird für jedes Element in den Arrays Mparent und Mfilial die Methode Init mit dem Parameter coords aufgerufen. Diese Methode initialisiert die Felder jedes Agenten in der Population.

4. Am Ende gibt die Methode true zurück und zeigt damit an, dass die Initialisierung erfolgreich abgeschlossen wurde.

Diese Methode führt die anfängliche Einrichtung des Algorithmus für die chemische Reaktionsoptimierung (CRO) mit gegebenen Parametern durch und bereitet ihn auf die Durchführung der Optimierung vor.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_CRO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (Mparent, popSize);
  ArrayResize (Mfilial, popSize);

  for (int i = 0; i < popSize; i++)
  {
    Mparent [i].Init (coords);
    Mfilial [i].Init (coords);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving der Klasse C_AO_CRO dient dazu, chemische Operatoren aufzurufen, die Änderungen an den Strukturen der Moleküle vornehmen und so die Moleküle während der Optimierung bewegen. Die Methode geht folgendermaßen vor:

1. Wenn revision gleich false ist, werden die Strukturen für jedes Molekül in der Population Mparent mit Zufallswerten in einem bestimmten Bereich zwischen rangeMin und rangeMax initialisiert. Diese Werte werden dann in das Array a kopiert.

2. Wenn revision ungleich false ist, wird der Mindestwert der Funktion f unter allen Molekülen in der Population Mparent berechnet. Der KE-Wert wird dann für jedes Molekül auf der Grundlage der Skalierung seines Funktionswertes f, des Minimalwertes f durch die Population der Elternmoleküle und der besten globalen Lösung fB im Bereich von 0,0 bis 1,0 berechnet.

3. Anschließend geschieht Folgendes, bis einer der chemischen Operatoren den Wert „false“ zurückgibt (was bedeutet, dass in der Tochterpopulation kein Platz mehr für Tochtermoleküle vorhanden ist):

• Ist die Zufallszahl kleiner als moleColl, so werden zwei zufällige Moleküle M1 und M2 ausgewählt. Wenn KE beider Moleküle größer oder gleich beta ist, wird die Synthese durchgeführt (d. h. die Synthese wird für Moleküle durchgeführt, die nicht kleiner sind als der in den Parametern angegebene relative Fitnesswert; zu diesem Zweck wurden die Fitnesswerte der Moleküle zuvor auf den Bereich von 0,0 bis 1,0 skaliert). Andernfalls kommt es zu einem intermolekularen unwirksamen Zusammenstoß.

• Wenn die Zufallszahl größer oder gleich moleColl ist, wird ein Zufallsmolekül M ausgewählt. Wenn NumHit des Moleküls alpha überschreitet (wenn das Molekül mehr Kollisionen erfahren hat, als in den Algorithmusparametern angegeben, dann „zerfällt“ das Molekül), wird die Zerlegung durchgeführt. Andernfalls kommt es zu einer Kollision.

4. Am Ende der Methode werden die Strukturen aller Moleküle in Mfilial in das Populations-Array a kopiert.

Diese Methode ist für die Aktualisierung der molekularen Strukturen im Algorithmus der chemischen Reaktionsoptimierung (CRO) entsprechend dem aktuellen Zustand des Systems und den gegebenen Parametern verantwortlich. Die Methode implementiert die grundlegenden Operationen des CRO-Algorithmus, wie Synthese, intermolekulare ineffiziente Kollision, Zerlegung und Kollision.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CRO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Mparent [i].structure [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Random structure in the range from rangeMin to rangeMax
        Mparent [i].structure [c] = u.SeInDiSp  (Mparent [i].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = Mparent [i].structure [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  double minKE = DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (Mparent [i].f < minKE) minKE = Mparent [i].f;
  }
  for (int i = 0; i < popSize; i++)
  {
    Mparent [i].KE = u.Scale (Mparent [i].f, minKE, fB, 0.0, 1.0);
  }

  //----------------------------------------------------------------------------
  int molCNT = 0;

  while (!IsStopped ())
  {
    if (u.RNDprobab () < moleColl)
    {
      // Select two random molecules M1 and M2
      int index1 = u.RNDminusOne (popSize);
      int index2 = u.RNDminusOne (popSize);

      // If KE ≤ β:
      if (Mparent [index1].KE >= beta && Mparent [index2].KE >= beta)
      {
        // Perform Synthesis
        if (!Synthesis (index1, index2, molCNT)) break;
      }
      else
      {
        // Perform Intermolecular Inefficient Collision
        if (!InterMolInefColl (index1, index2, molCNT)) break;
      }
    }
    else
    {
      // Select a random molecule M
      int index = u.RNDminusOne (popSize);

      // If NumHit > α:
      if (Mparent [index].NumHit > alpha)
      {
        // Perform Decomposition
        if (!Decomposition (index, molCNT)) break;
      }
      else
      {
        // Perform Collision
        if (!InefCollision (index, molCNT)) break;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    ArrayCopy (a [i].c, Mfilial [i].structure);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision der Klasse C_AO_CRO wird verwendet, um die beste globale Lösung zu aktualisieren und die Zustände der Moleküle in der Elternpopulation zu aktualisieren, indem chemische Post-Operatoren durchgeführt werden. Aktionen, die mit dieser Methode durchgeführt werden:

1. Aktualisiere die globale Lösung. In der for-Schleife durchläuft die Methode alle Moleküle. Wenn der Wert der Funktion f des aktuellen Moleküls den aktuellen besten Wert fB überschreitet, wird fB aktualisiert und das Koordinatenfeld des aktuellen Moleküls in das Feld cB kopiert.

2. Wenn revision gleich false ist, wird für jedes Molekül in der Population Mparent der f-Wert gleich dem f-Wert aus dem Array a gesetzt. Dann wird Revision auf true gesetzt und die Methode beendet. In diesem Stadium ist es wichtig, die Fitnesswerte der Elternmoleküle zu erhalten, damit in den folgenden Epochen chemische Operatoren, die von der kinetischen Energie abhängen (der Wert der Fitnessfunktion ist auf den Bereich von 0,0 bis 1,0 normiert), eingesetzt werden können.

3. Wenn revision ungleich false ist, dann wird für jedes Molekül in der Population Mfilial f gleich f aus dem Array a gesetzt. Dann wird je nach Reaktionstyp des Moleküls rType (Reaktion, an der das Molekül beteiligt war) die entsprechende Methode PostSynthesis, PostInterMolInefColl, PostDecomposition, PostInefCollision aufgerufen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CRO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Mparent [i].f = a [i].f;
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      Mfilial [i].f = a [i].f;
    }

    switch (Mfilial [i].rType)
    {
      case synthesis:
        PostSynthesis        (Mfilial [i]);
        break;
      case interMolecularInefColl:
        PostInterMolInefColl (Mfilial [i]);
        break;
      case decomposition:
        PostDecomposition    (Mfilial [i]);
        break;
      case inefCollision:
        PostInefCollision    (Mfilial [i]);
        break;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Der CRO-Algorithmus wurde mit den Funktionen „Hilly“, „Forest“ und „Megacity“ getestet. Es wurden jeweils zehn Funktionsläufe für jeden Landschaftstyp (5, 25 und 500 Funktionen) durchgeführt und die Optimierungsergebnisse ermittelt.

CRO|Chemical Reaction Optimisation|50.0|0.9|200.0|0.01|0.5|
=============================
5 Hilly's; Func runs: 10000; result: 0.9462894520167225
25 Hilly's; Func runs: 10000; result: 0.6611186250435438
500 Hilly's; Func runs: 10000; result: 0.2985263035668822
=============================
5 Forest's; Func runs: 10000; result: 0.8790568514481787
25 Forest's; Func runs: 10000; result: 0.584216839762206
500 Forest's; Func runs: 10000; result: 0.2114595696419046
=============================
5 Megacity's; Func runs: 10000; result: 0.7584615384615384
25 Megacity's; Func runs: 10000; result: 0.4264615384615384
500 Megacity's; Func runs: 10000; result: 0.12686153846153955
=============================
All score: 4.89245 (54.36%)

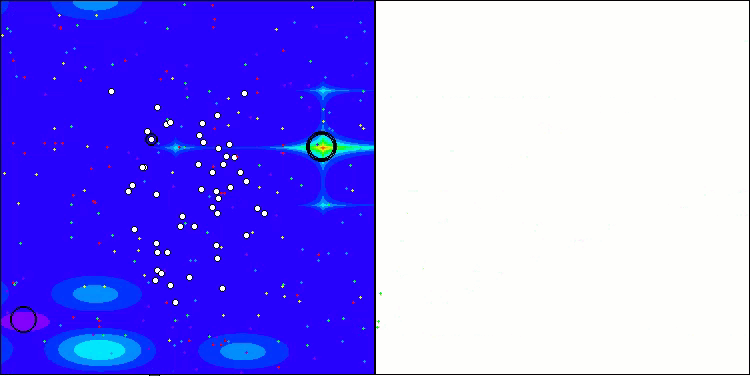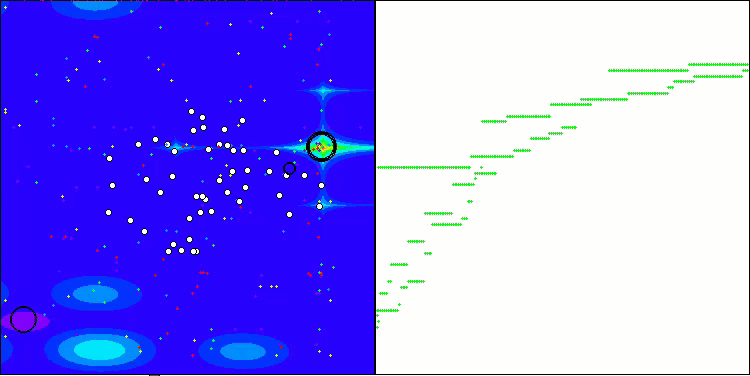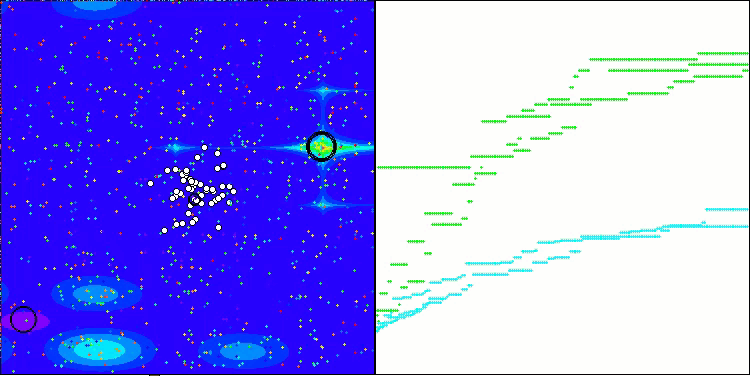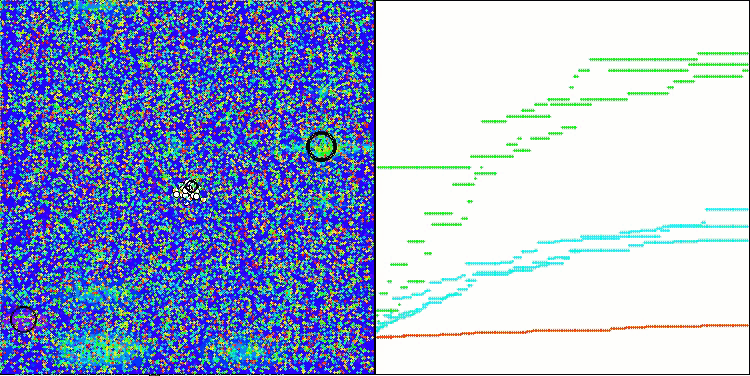
Die Visualisierung der Tests mit dem CRO-Algorithmus zeigt interessante Merkmale des Algorithmus auf. Obwohl CRO manchmal stecken bleiben kann, wie die langen flachen Abschnitte des Konvergenzdiagramms zeigen, zeigt es immer noch ordentliche Gesamtergebnisse.

Einer der auffälligsten Aspekte der CRO-Arbeit ist die Bewegung der „Moleküle“ im Suchgebiet. Auf den ersten Blick erscheint diese Bewegung chaotisch und ähnelt der Brownschen Bewegung. Trotz der äußeren Zufälligkeit gelingt es den „Molekülen“ jedoch, eine Zone des globalen Optimums zu finden. Dies zeigt, wie komplex und anspruchsvoll der CRO-Algorithmus ist, der die Prinzipien chemischer Reaktionen zur Lösung von Optimierungsproblemen nutzt.

Insgesamt ist der CRO-Algorithmus ein leistungsstarkes Optimierungsinstrument, das trotz einiger Schwierigkeiten eine Vielzahl von Aufgaben bewältigen kann. Seine einzigartigen Eigenschaften und seine Fähigkeit, globale Optima zu finden, machen es zu einem wertvollen Werkzeug im Bereich der Optimierung.

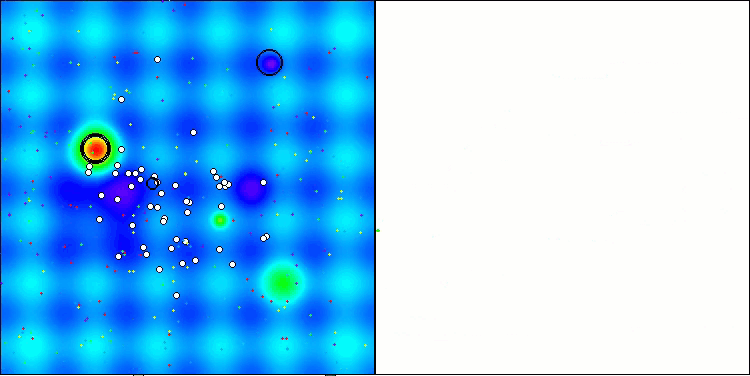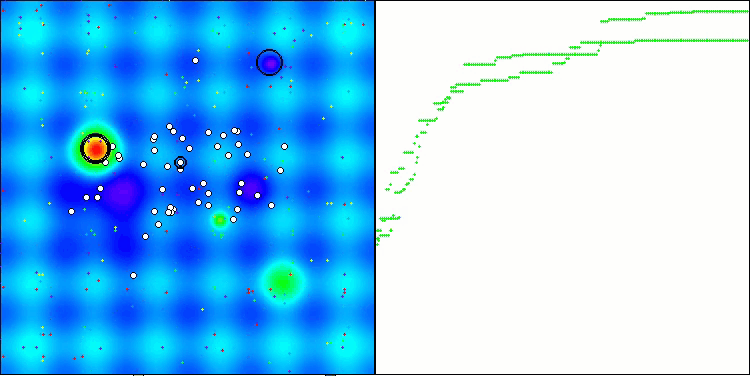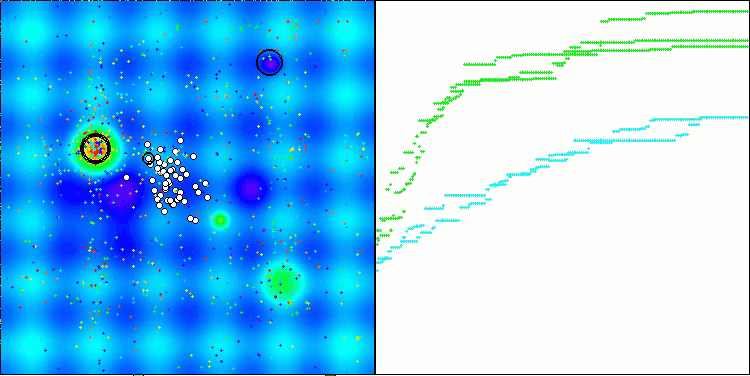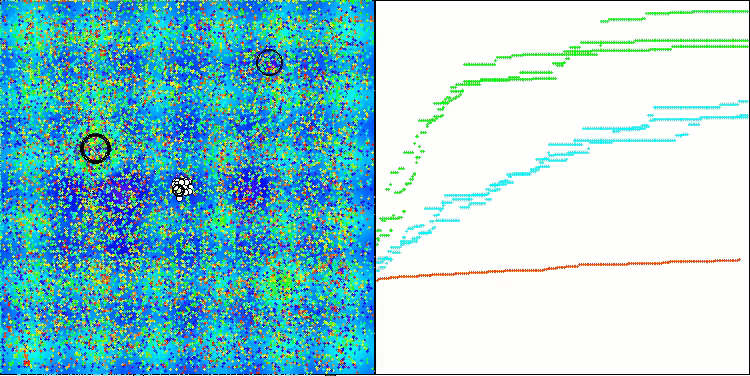
  CRO mit der Testfunktion Hilly

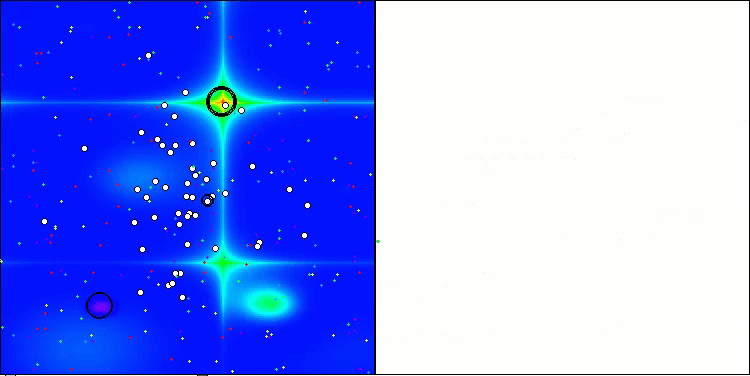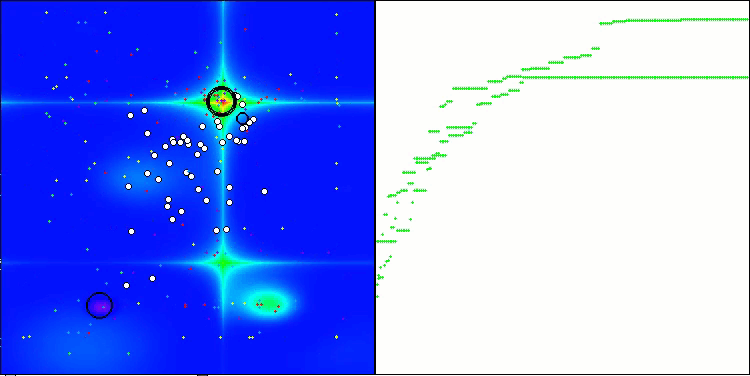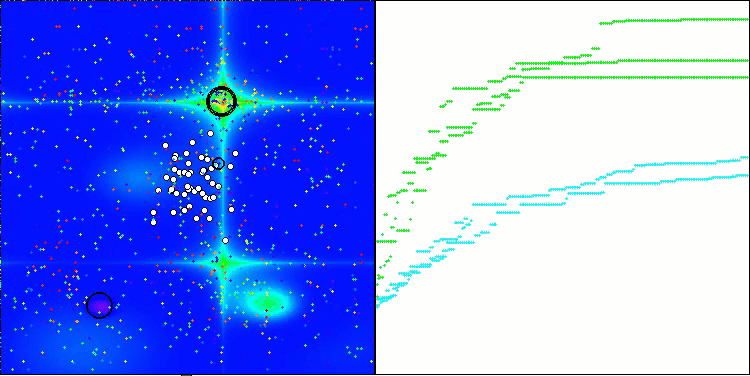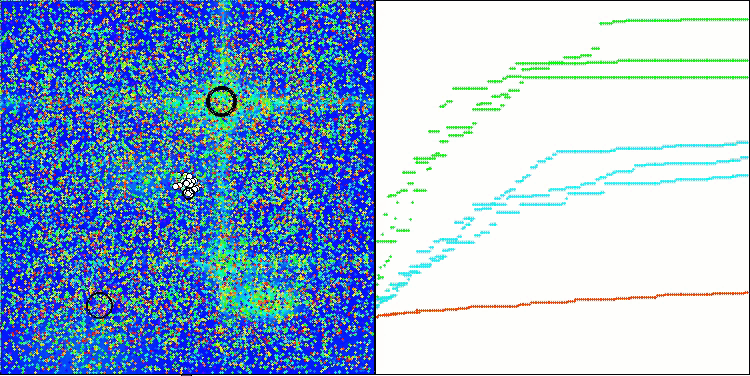
  CRO mit der Testfunktion Forest

  CRO mit der Testfunktion Megacity.

#	AO	Beschreibung	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binärer genetischer Algorithmus	0.99989	0.99518	0.42835	2.42341	0.96153	0.96181	0.32027	2.24360	0.91385	0.95908	0.24220	2.11512	6.782	75.36
2	CLA	Zahlenschloss-Algorithmus	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	(P+O)ES	(P+O) Entwicklungsstrategien	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
4	CTA	Kometenschweif-Algorithmus	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
5	SDSm	stochastische Diffusionssuche M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
6	ESG	Entwicklung der sozialen Gruppen	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
7	SIA	Simuliertes isotropes Abkühlen	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
8	ACS	künstliche, kooperative Suche	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
9	TSEA	Schildkrötenpanzer-Evolutionsalgorithmus	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
10	DE	differentielle Evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
11	CRO	Optimierung chemischer Reaktionen	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
12	BSA	Vogelschwarm-Algorithmus	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
13	HS	Harmoniesuche	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
14	SSG	Setzen, Säen und Wachsen	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
15	(PO)ES	(PO) Entwicklungsstrategien	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
16	BSO	Brainstorming-Optimierung	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
17	WOAm	Wal-Optimierungsalgorithmus M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
18	ACOm	Ameisen-Kolonie-Optimierung M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
19	BFO-GA	Optimierung der bakteriellen Futtersuche - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
20	MEC	Evolutionäre Berechnung des Geistes	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
21	IWO	Optimierung mit invasiven Unkräutern	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
22	Micro-AIS	Künstliches Mikro-Immunsystem	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
23	COAm	Kuckuck-Optimierungsalgorithmus M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
24	SDOm	Optimierung der Spiraldynamik M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
25	NMm	Nelder-Mead-Verfahren M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
26	FAm	Firefly-Algorithmus M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
27	GSA	Algorithmus für die Schwerkraftsuche	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
28	BFO	Optimierung der bakteriellen Futtersuche	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
29	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
30	BA	Fledermaus-Algorithmus	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
31	SA	simuliertes Abkühlen	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
32	IWDm	intelligente Wassertropfen M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
33	PSO	Partikelschwarmoptimierung	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
34	Gebote	Boids-Algorithmus	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
35	MA	Affen-Algorithmus	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
36	SFL	schlurfender Froschsprung	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
37	FSS	Fischschulsuche	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
38	RND	zufällig	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
39	GWO	Grauer-Wolf-Optimierung	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
40	CSS	Suche geladener Systeme	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
41	EM	elektromagnetismusähnlicher Algorithmus	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

Zusammenfassung

Aus der Tabelle und den Ergebnissen lassen sich die folgenden Schlussfolgerungen über die Leistung des CRO-Algorithmus ziehen:

1. CRO zeigt hervorragende Ergebnisse bei der Testfunktion Hilly. Bei 5 Parametern betrug das Ergebnis etwa 0,95, bei 25 Parametern etwa 0,66 und bei 500 Parametern etwa 0,30. Dies zeigt, dass CRO bei glatten Funktionen wirksam ist, insbesondere bei weniger Parametern.

2. Auch bei der Testfunktion Forest zeigt CRO gute Ergebnisse. Bei 5 Parametern betrug das Ergebnis etwa 0,88, bei 25 Parametern etwa 0,58 und bei 500 Parametern etwa 0,21. Dies deutet darauf hin, dass CRO auch bei Funktionen mit „scharfen“ Extremen wirksam ist, aber Schwierigkeiten hat, Punktoptima zu finden.

3. Bei der Megacity-Testfunktion zeigt CRO weiterhin gute Leistungen. Bei 5 Parametern betrug das Ergebnis etwa 0,76, bei 25 Parametern etwa 0,43 und bei 500 Parametern etwa 0,13. Dies deutet darauf hin, dass CRO bei dieser diskreten Funktion wirksam ist, denn seine Ergebnisse sind im Vergleich zu anderen Algorithmen, auch zu den höheren in der Tabelle, einheitlich „grün“.

Aus der Tabelle geht hervor, dass der CRO-Algorithmus im Vergleich zu anderen Algorithmen gute Ergebnisse erzielt. Insbesondere bei den Funktionen „Hilly“, „Forest“ und „Megacity“ erweist sich CRO als wettbewerbsfähig, vor allem mit weniger Parametern.

MegacityDer CRO-Algorithmus belegte den 11. Platz in der Rangliste. Anhand der Farbabstufung in der nachstehenden Tabelle (wobei dunkelgrün für bessere Ergebnisse steht) lässt sich sagen, dass CRO im Allgemeinen eine gute und stabile Leistung zeigt (stabile und gleichmäßige Färbung). Bei der Funktion Hilly mit 1000 Parametern sehen die Ergebnisse etwas schwächer aus.

Der CRO-Algorithmus hat sich als vielversprechender Optimierungsansatz erwiesen. Er verwendet zwei Agentenpopulationen (in meiner Implementierung), die miteinander interagieren, um für Vielfalt zu sorgen und zu vermeiden, dass sie in lokalen Optima stecken bleiben. Eine der Besonderheiten des Algorithmus ist die Verwendung spezieller Operatoren, die chemischen Reaktionen, Zerlegungen, Synthesen und anderen ähneln.

Im Allgemeinen ist der CRO-Algorithmus eine vielversprechende Optimierungsmethode, die sich durch ihre Originalität und ihre Fähigkeit auszeichnet, bei verschiedenen Optimierungsproblemen gute Ergebnisse zu erzielen.

Die Wahl des Optimierungsalgorithmus sollte auf der Grundlage der spezifischen Aufgabenstellung und der Leistungsanforderungen erfolgen; unsere Rangliste hilft dabei. Durch die Überarbeitung der ursprünglichen Version des CRO-Algorithmus, um von der C_AO-Klasse zu erben, die ich für Populationsalgorithmen übernommen habe, kann dieser interessante Algorithmus auf Optimierungsprobleme im Allgemeinen angewendet werden.

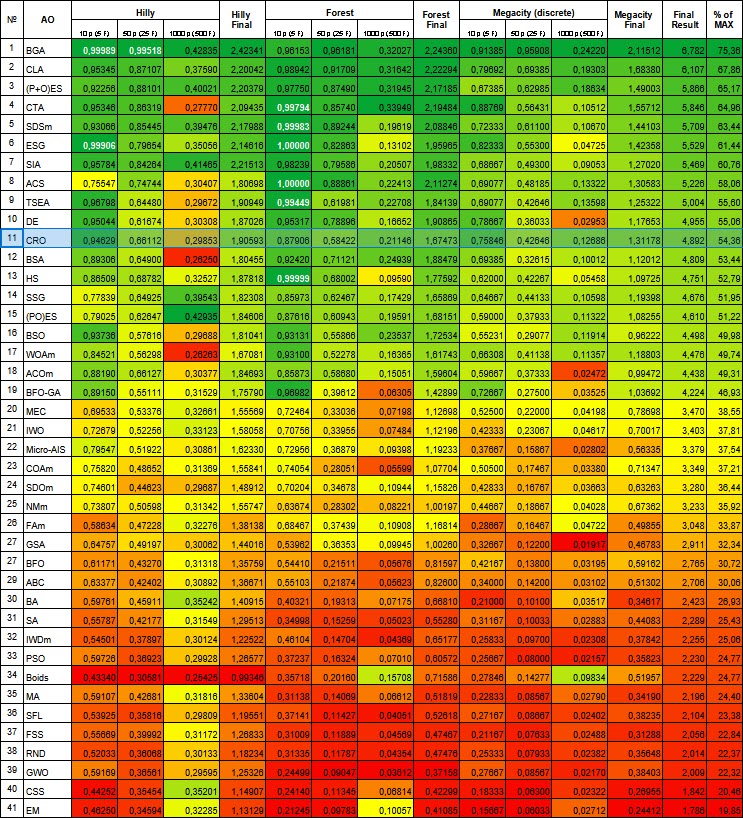
Abbildung 1. Die farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

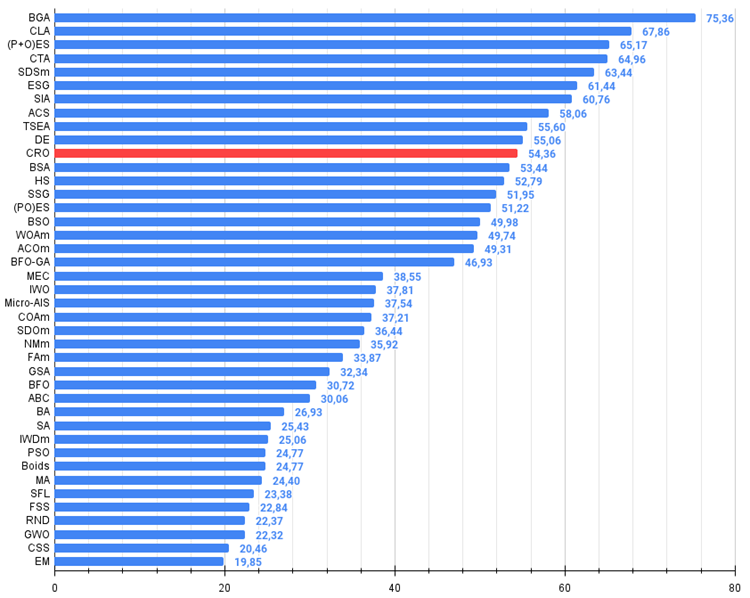
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)

CRO allgemeine Vor- und Nachteile:

Vorteile:

1. Gute Konvergenz bei verschiedenen Arten von Funktionen.
2. Trotz seiner komplexen Architektur sehr schnell.
3. Gute Skalierbarkeit.
   

Nachteile

1. Bleibt manchmal in lokalen Extremen stecken.
   

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355