Optimierung mit der bakteriellen Chemotaxis (BCO)

Inhalt

1. Einführung
2. Implementierung des Algorithmus
3. Testergebnisse

Einführung

Im Bereich der Optimierung lassen sich viele Forscher und Entwickler von biologischen Prozessen in der Natur inspirieren, z. B. von der Evolution, sozialen Interaktionen oder dem Verhalten von Lebewesen bei der Nahrungssuche. Dies führt zur Entwicklung völlig neuer, innovativer Optimierungsmethoden. Studien haben gezeigt, dass diese Methoden die klassischen heuristischen und gradientenbasierten Ansätze häufig übertreffen, insbesondere bei der Lösung multimodaler, nicht differenzierbarer und diskreter Probleme. Eine solche Methode ist der Chemotaxis-Algorithmus, der erstmals von Bremermann und Kollegen vorgeschlagen wurde. Wir haben bereits den Algorithmus zur Optimierung der bakteriellen Futtersuche (BFO) erörtert. Er simuliert die Reaktion von Bakterien auf Chemoattraktoren in Konzentrationsgradienten. Bremermann analysierte die Chemotaxis in dreidimensionalen Gradienten und wandte sie zum Training neuronaler Netze an. Obwohl dieser Algorithmus auf den Prinzipien der bakteriellen Chemotaxis basiert, haben neue biologische Entdeckungen es ermöglicht, ein detaillierteres Modell des Prozesses zu erstellen.

In diesem Artikel werden wir versuchen, dieses Modell als neue Optimierungsstrategie zu betrachten. Die wichtigsten Unterschiede zwischen dem neuen Modell und dem traditionellen Chemotaxis-Algorithmus sind folgende:

1. Die Bakterien im neuen Modell verwenden Informationen über Konzentrationswerte.
2. Sie bewegen sich nicht weiter in eine Richtung, wenn die Konzentration des chemischen Attraktor steigt.

Bakterien sind Einzeller, eine der einfachsten Lebensformen auf der Erde. Trotz ihrer Einfachheit sind sie in der Lage, Informationen über die Umwelt zu erhalten, sich in ihr zurechtzufinden und diese Informationen effektiv zum Überleben zu nutzen. Die Reaktion von Bakterien auf Umweltveränderungen war in den letzten Jahrzehnten Gegenstand intensiver Forschung, die auch die Aufmerksamkeit von Wissenschaftlern auf dem Gebiet der Optimierung auf sich gezogen hat. Optimierungsalgorithmen können als Systeme betrachtet werden, die Informationen über die funktionale Landschaft sammeln und diese nutzen, um ein Optimum zu erreichen. Die Einfachheit der Idee der bakteriellen Chemotaxis macht sie zu einem attraktiven Ausgangspunkt für die Entwicklung dieser Art von Algorithmen.

In verschiedenen Studien wurde festgestellt, dass Bakterien untereinander Informationen austauschen, obwohl nicht viel über die Mechanismen dieser Kommunikation bekannt ist. In der Regel werden Bakterien als Individuen behandelt, und soziale Interaktionen werden in den Modellen nicht berücksichtigt. Damit unterscheiden sie sich von Interaktionsmodellen, die das Verhalten sozialer Insekten (wie Ameisen, Bienen, Wespen oder Termiten) beschreiben, die als Systeme mit kollektiver Intelligenz agieren, was verschiedene Möglichkeiten zur Lösung unterschiedlicher Probleme eröffnet.

Ein weiterer wichtiger Aspekt der Chemotaxis ist die Adaptation. Bakterien sind in der Lage, ihre Empfindlichkeit gegenüber konstanten chemischen Bedingungen zu ändern, sodass sie wirksam auf Veränderungen in der Umwelt reagieren können. Diese Eigenschaft macht sie nicht nur widerstandsfähig, sondern auch äußerst effizient bei der Suche nach Ressourcen.

In dieser Studie konzentrierten sich die Autoren auf mikroskopische Modelle, die die Chemotaxis einzelner Bakterien berücksichtigen, im Gegensatz zu makroskopischen Modellen, die die Bewegung von Kolonien analysieren. Der Algorithmus wurde von S. D. entwickelt. Müller und P. Koumatsakas, und seine Hauptideen wurden 2002 vorgestellt und veröffentlicht.

Implementierung des Algorithmus

Die Idee des bakteriellen Chemotaxis-Optimierungsalgorithmus (BCO) ist es, biologische Prinzipien, die im bakteriellen Verhalten beobachtet werden, zur Lösung von Optimierungsproblemen zu nutzen. Der Algorithmus modelliert, wie Bakterien auf chemische Gradienten in ihrer Umgebung reagieren, und ermöglicht es ihnen so, günstigere Lebensbedingungen zu finden. Die wichtigsten Ideen des Algorithmus:

1. Der Algorithmus beschreibt die Bewegung der Bakterien als eine Abfolge von geradlinigen Bahnen, die durch momentane Wendungen verbunden sind. Jede Bewegung ist durch Geschwindigkeit, Richtung und Dauer gekennzeichnet.
2. Die Drehrichtung des Bakteriums wird durch eine Wahrscheinlichkeitsverteilung bestimmt, sodass zufällige Bewegungsänderungen berücksichtigt werden können.
3. Der Algorithmus verwendet Informationen über die Gradienten der Funktion, um das Bakterium zu einer optimalen Lösung zu führen und die Anzahl der zum Erreichen des Ziels erforderlichen Iterationen zu minimieren.

Der detaillierte Pseudocode des bakteriellen Chemotaxis-Optimierungsalgorithmus (BCO) beschreibt die wichtigsten Schritte des Algorithmus, einschließlich der Initialisierung, der Hauptoptimierungsschleife mit Bewegungs- und Revisionsschritten sowie der Hilfsfunktionen.

Initialisierung.

1. Festlegen der Parameter:

• popSize - Größe der Population (Anzahl der Bakterien)
• hs - Anzahl der Schritte zur Berechnung der durchschnittlichen Veränderung
• T0 - Anfangstemperatur
• b - Parameter
• tau_c - Parameter
• v - Geschwindigkeit

2. Erstellen des Bakterien-Arrays mit der Größe popSize

3. Für jedes bacterium i von 0 bis popSize-1:

• Initialisierung von fPrev auf -DBL_MAX
• Erstellen des Arrays fHistory mit der Größe hs und gefüllt mit Nullen

Grundlegende Optimierungsschleife. Wiederholung des Vorgangs, bis der Stopp erreicht ist:

Die Bewegungsphase für jedes bacterium i von 0 bis popSize - 1:

1. Abfrage des aktuellen Werts der Zielfunktion f_tr

2. Abrufen des vorherigen Werts der Zielfunktion f_pr aus bacterium [i].fPrev

3. Wenn f_tr <= f_pr: T = T0

    Andernfalls: Berechnung von b_corr = CalculateCorrectedB (f_tr, f_pr, i)

• T = T0 * exp (b_corr * (f_tr - f_pr))

4. Erzeugen von „tau“ aus einer Exponentialverteilung mit dem Parameter T.

5. Berechnung von new_angles [] für die Dimensionen coords - 1: für jeden Winkel j von 0 bis coords - 2:

• theta = CalculateRotationAngle ()
• mu = 62 * (1 - cos (theta)) * π / 180
• sigma = 26 * (1 - cos (theta)) * π / 180
• new_angles [j] = Zufallszahl aus der Gaußschen Verteilung mit den Parametern (mu, mu-π, mu+π)

6. Berechnen einer neuen Position:

• l = v * tau
• CalculateNewPosition (l, new_angles, new_position, current_position)

7. Aktualisieren der Position eines Bakteriums unter Berücksichtigung der Werte innerhalb von rangeMin und rangeMax

8. Aktualisieren von bacterium [i].fPrev mit dem Wert von f_tr

Revisions-Phase.

1. Aktualisieren der global besten Lösung cB mit dem Fitnesswert fB

2. Für jedes bacterium i von 0 bis popSize - 1. Aktualisieren der Historie der Werte der Zielfunktion fHistory:

• Alle Werte um eine Position nach links verschieben.
• Den aktuellen Wert der Zielfunktion an das Ende der Historie anhängen.

Hilfsfunktionen:

CalculateCorrectedB (f_tr, f_pr, bacteriumIndex)

1. Berechnung von delta_f_tr = f_tr - f_pr

2. Berechnung von delta_f_pr = durchschnittliche Veränderung über die letzten hs-Schritte

3. Wenn |delta_f_pr| < epsilon: Rückgabe von b

   Andernfalls: Rückgabe von b * (1 / (|delta_f_tr / delta_f_pr| + 1) + 1 / (|f_pr| + 1))

CalculateRotationAngle ()

1. Berechnen von cos_theta = exp (-tau_c / T0)

2. Rückgabe von arccos (cos_theta)

CalculateNewPosition (l, angles, new_position, current_position)

1. Berechnung der neuen Position [0] unter Berücksichtigung aller Winkel

2. Für jede Koordinate i von 1 bis coords - 1:

   Berechnung von new_position [i] unter Berücksichtigung der entsprechenden Winkel

3. Anwendung einer zufälligen Richtung (1 oder -1) auf jede Koordinate

GenerateFromExponentialDistribution (T)

Rückgabe -T * ln (Zufallszahl zwischen 0 und 1)

Gehen wir nun zum Schreiben des Algorithmus-Codes über. Um Bakterien als Lösung für ein Optimierungsproblem darzustellen, beschreiben wir die Struktur S_BCO_Bacterium.

1. Die Felder der Struktur:

• fPrev - vorheriger Wert der Zielfunktion.
  
• fHistory [] - Array mit der Historie der Zielfunktionswerte.
  

2. Init - Die Initialisierungsmethode führt die folgenden Aktionen durch:

• fHistory-Array wird auf die Größe von historySize angepasst.
• alle Elemente des Arrays fHistory werden mit 0,0 initialisiert.
• fPrev - der vorherige Wert der Zielfunktion wird auf den kleinstmöglichen Wert gesetzt.

Ein Bakterium in Form einer Struktur, die es ermöglicht, Änderungen der Werte der Zielfunktion über eine bestimmte Anzahl von Iterationen (Einzelbewegungen) zu verfolgen.

//——————————————————————————————————————————————————————————————————————————————
struct S_BCO_Bacterium
{
    double fPrev;        // previous value of the objective function
    double fHistory [];  // history of objective function values

    void Init (int coords, int historySize)
    {
      ArrayResize     (fHistory, historySize);
      ArrayInitialize (fHistory, 0.0);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Beschreiben Sie die Algorithmusklasse C_AO_BCO. Lassen Sie uns das Stück für Stück aufschlüsseln.

1. Die externen Parameter des Algorithmus werden im Konstruktor initialisiert.

2. Die Methode SetParams aktualisiert die Parameterwerte aus dem Array params.

3. Die Methoden Moving und Revision sind für das Verschieben von Bakterien und die Revision ihrer Positionen zuständig.

4. Die Klasse definiert mehrere private Methoden, die für verschiedene Berechnungen im Zusammenhang mit dem Algorithmus verwendet werden. „CalculateAverageDeltaFpr“, „CalculateNewAngles“, „CalculateNewPosition“, „GenerateFromExponentialDistribution“, „CalculateCorrectedB“, „CalculateRotationAngle“, „RNDdir“, bacterium - Array von Bakterien (Population). Parameter der Klasse:

• hs - Anzahl der Schritte zur Berechnung der durchschnittlichen Veränderung.
• T0 - Anfangstemperatur.
• b - Parameter.
• tau_c - Parameter.
• v - Geschwindigkeit.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BCO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BCO () { }
  C_AO_BCO ()
  {
    ao_name = "BCO";
    ao_desc = "Bacterial Chemotaxis Optimization";
    ao_link = "https://www.mql5.com/en/articles/15711";

    popSize = 50;     // population size (number of bacteria)
    hs      = 10;     // number of steps to calculate average change
    T0      = 1.0;    // initial temperature
    b       = 0.5;    // parameter b
    tau_c   = 1.0;    // parameter tau_c
    v       = 1.0;    // velocity

    ArrayResize (params, 6);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "hs";      params [1].val = hs;
    params [2].name = "T0";      params [2].val = T0;
    params [3].name = "b";       params [3].val = b;
    params [4].name = "tau_c";   params [4].val = tau_c;
    params [5].name = "v";       params [5].val = v;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    hs      = (int)params [1].val;
    T0      = params      [2].val;
    b       = params      [3].val;
    tau_c   = params      [4].val;
    v       = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    hs;
  double T0;
  double b;
  double tau_c;
  double v;

  S_BCO_Bacterium bacterium [];

  private: //-------------------------------------------------------------------
  double CalculateAverageDeltaFpr            (int bacteriumIndex);
  void   CalculateNewAngles                  (double &angles []);
  void   CalculateNewPosition                (double l, const double &angles [], double &new_position [], const double &current_position []);
  double GenerateFromExponentialDistribution (double T);
  double CalculateCorrectedB                 (double f_tr, double f_pr, int bacteriumIndex);
  double CalculateRotationAngle              ();
  int    RNDdir                              ();
};

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving der Klasse C_AO_BCO ist für die Bewegung der Bakterien im Suchraum zuständig. Schauen wir uns einmal an, wie sie funktioniert:

1. Wenn revision false ist, bedeutet dies, dass die Bakterien eine Ausgangsposition haben.

• Für jedes Bakterium a[i] werden zufällige Koordinaten innerhalb eines bestimmten Bereichs erzeugt.
• Die Funktion u.RNDfromCI generiert einen Zufallswert, während u.SeInDiSp diesen unter Berücksichtigung der angegebenen Stufe anpasst.

2. Grundlegende Bewegungsschleife, wenn revision wahr ist. Die Methode setzt die grundlegende Logik der bakteriellen Bewegung um. Festlegung der Temperatur T:

• Wenn der aktuelle Wert der Funktion f_tr besser oder gleich dem vorherigen f_pr ist, wird die Anfangstemperatur T0 verwendet.
• Andernfalls wird die Temperatur mit der Funktion CalculateCorrectedB angepasst, die die Differenz zwischen dem aktuellen und dem vorherigen Wert der Fitnessfunktion berücksichtigt. 
• Erzeugung der Bewegungszeit Tau: Es wird eine Exponentialverteilung zur Erzeugung der Bewegungszeit verwendet.
• Die neuen Bewegungswinkel und die neue Position werden auf der Grundlage der Bewegungslänge l und der neuen Winkel berechnet.
• Die neue Position wird unter Berücksichtigung des angegebenen Bereichs und Schrittes eingestellt.
• Am Ende der Schleife wird der vorherige Wert der Fitnessfunktion für jedes Bakterium aktualisiert.

Die Methode Moving implementiert die grundlegende Logik der Bewegung von Bakterien im Suchraum und passt ihr Verhalten in Abhängigkeit von den Ergebnissen früherer Iterationen an. Sie verwendet Zufallselemente und adaptive Mechanismen, um die optimale Lösung zu finden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    double f_tr = a [i].f;
    double f_pr = bacterium [i].fPrev;

    double T;
    
    if (f_tr <= f_pr)
    {
      T = T0;
    }
    else
    {
      double b_corr = CalculateCorrectedB (f_tr, f_pr, i);
      
      T = T0 * exp (b_corr * (f_tr - f_pr));
    }

    double tau = GenerateFromExponentialDistribution (T);

    double new_angles [];
    ArrayResize (new_angles, coords - 1);
    CalculateNewAngles (new_angles);

    double l = v * tau;
    double new_position [];
    ArrayResize (new_position, coords);
    CalculateNewPosition (l, new_angles, new_position, a [i].c);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.SeInDiSp (new_position [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision der Klasse C_AO_BCO ist für die Aktualisierung der Informationen über die besten gefundenen Lösungen und den Verlauf der Fitnessfunktionswerte für jedes Bakterium zuständig.

1. Die Variable ind wird mit dem Wert -1 initialisiert. Er wird verwendet, um den Index des Bakteriums zu speichern, das den besten Funktionswert aufweist.

2. Suche nach dem besten Funktionswert:

• Die Methode geht durch alle Bakterien in der Population popSize und sucht dasjenige, dessen Funktionswert f größer ist als der aktuell beste Wert von fB.
• Wird ein Bakterium mit einem höheren Funktionswert gefunden, so wird fB aktualisiert und der Index dieses Bakteriums in ind gespeichert.

3. Wenn eine Bakterie mit dem Index ind (ist ungleich -1), dann werden die Koordinaten dieser Bakterie in das Array cB kopiert, das die Koordinaten der aktuell besten Lösung darstellt.

4. Für jedes Bakterium wird der Verlauf der Funktionswerte aktualisiert. Die Methode iteriert über jedes Element fHistory und verschiebt die Werte um eine Position nach links, um Platz für den neuen Wert zu schaffen. Am Ende jeder Iteration erhält das letzte Element des Arrays fHistory den aktuellen Fitnesswert a [i].f für jedes Bakterium.

Die Methode Revision erfüllt also zwei Hauptfunktionen:

• Aktualisieren des besten Fitnessfunktionswertes und der entsprechenden Koordinaten.
• Aktualisieren des Verlaufs der Fitnessfunktionswerte für jedes Bakterium, sodass Änderungen ihres Zustands im Verlauf ihrer Bewegungsgeschichte verfolgt werden können. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1)
  {
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 1; j < hs; j++)
    {
      bacterium [i].fHistory [j - 1] = bacterium [i].fHistory [j];
    }

    bacterium [i].fHistory [hs - 1] = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode CalculateAverageDeltaFpr der Klasse C_AO_BCO dient der Berechnung der durchschnittlichen Änderungen der Fitnessfunktionswerte (Deltas) für ein bestimmtes Bakterium zwischen seinen beiden benachbarten Positionen auf der Grundlage der Historie der Fitnesswerte.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateAverageDeltaFpr (int bacteriumIndex)
{
  double sum = 0;

  for (int i = 1; i < hs; i++)
  {
    sum += bacterium [bacteriumIndex].fHistory [i] - bacterium [bacteriumIndex].fHistory [i - 1];
  }

  return sum / (hs - 1);
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode CalculateNewAngles der Klasse C_AO_BCO dient der Berechnung neuer Winkel auf der Grundlage einer Logik, die sich auf die Drehung und Verteilung bezieht, und führt die folgenden Aktionen aus:

• Iterieren über das Array für neue Winkel und Berechnen eines neuen Wertes für jeden Winkel.
• Verwendung von Parametern, die vom Kosinus des Winkels abhängen, um Werte zu erzeugen, die eine Gaußsche Verteilung verwenden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewAngles (double &angles [])
{
  for (int i = 0; i < coords - 1; i++)
  {
    double theta = CalculateRotationAngle ();
    double mu    = 62 * (1 - MathCos (theta)) * M_PI / 180.0;
    double sigma = 26 * (1 - MathCos (theta)) * M_PI / 180.0;

    angles [i] = u.GaussDistribution (mu, mu - M_PI, mu + M_PI, 8);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode CalculateNewPosition der Klasse C_AO_BCO dient der Berechnung neuer Positionskoordinaten auf der Grundlage der aktuellen Koordinaten, Winkel und des Parameters l. 

1. Die Eingabeparameter der Methode:

• l - Verhältnis, das die Veränderung der Position beeinflusst.
• angles [] - Array von Winkeln, die zur Berechnung der neuen Position verwendet werden.
• new_position [] - Array, in das die neuen Koordinaten eingesetzt werden.
• current_position [] - Array der aktuellen Koordinaten.

2. Die erste Koordinate new_position [0] wird als Summe aus der aktuellen Koordinate current_position [0] und einem Produkt aus l und der Differenz zwischen rangeMax [0] und rangeMin [0] berechnet.

3. Dann wird die erste Koordinate mit den Kosinus der Winkel aus dem Array angles multipliziert, beginnend mit der ersten bis zur vorletzten.

4. Das Ergebnis wird mit dem von der Funktion RNDdir () zurückgegebenen Wert multipliziert, der eine Zufallsrichtung von „-1“ oder „1“ erzeugt.

5. Für jede folgende Koordinate new_position [i], wobei i von 1 bis coords - 2 reicht, wird eine neue Position auf der Grundlage der aktuellen Position und des Sinus des entsprechenden Winkels berechnet.

6. Jede neue Koordinate wird ebenfalls mit den Kosinus der Winkel multipliziert, beginnend mit dem aktuellen Index i bis zum vorletzten Winkel.

7. Zufallsrichtung für die übrigen Koordinaten, das Ergebnis wird ebenfalls mit dem von RNDdir () zurückgegebenen Wert multipliziert.

8. Behandlung der letzten Koordinate: Wenn die Anzahl der Koordinaten größer als 1 ist, wird für die letzte Koordinate new_position [coords - 1] eine neue Position auf der Grundlage der aktuellen Position und des Sinus des letzten Winkels berechnet.

Die Methode CalculateNewPosition führt also die folgenden Aktionen durch:

• Berechnung der neuen Koordinaten auf der Grundlage der aktuellen Koordinaten und Winkel.
• Berücksichtigung des Einflusses der Zufallsrichtung auf jede Koordinate.
• Verwendung trigonometrischer Funktionen (Sinus und Kosinus) zur Berechnung von Winkeln.

Mit dieser Methode wird die Bewegung von Bakterien im Raum simuliert, wobei ihre aktuelle Position und die vorgegebenen Winkel berücksichtigt werden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewPosition (double l, const double &angles [], double &new_position [], const double &current_position [])
{
  new_position [0] = current_position [0] + l * (rangeMax [0] - rangeMin [0]);
 
  for (int k = 0; k < coords - 1; k++)
  {
    new_position [0] *= MathCos (angles [k]);
  }
 
  new_position [0] *= RNDdir ();

  for (int i = 1; i < coords - 1; i++)
  {
    new_position [i] = current_position [i] + l * MathSin (angles [i - 1]) * (rangeMax [0] - rangeMin [0]);
    
    for (int k = i; k < coords - 1; k++)
    {
      new_position [i] *= MathCos (angles [k]);
    }
    
    new_position [i] *= RNDdir ();
  }

  if (coords > 1)
  {
    new_position [coords - 1] = current_position [coords - 1] + l * MathSin (angles [coords - 2]);
  }
 
}
//——————————————————————————————————————————————————————————————————————————————

Im Folgenden wird kurz die Methode RNDdir der Klasse C_AO_BCO beschrieben, mit der eine Zufallsrichtung erzeugt wird, die einen von zwei Werten annehmen kann: -1 oder 1.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BCO::RNDdir ()
{
  if (u.RNDbool () < 0.5) return -1;
 
  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

Werfen wir einen kurzen Blick auf die Methoden der Klasse C_AO_BCO.

Die Methode GenerateFromExponentialDistribution führt aus:

• Generierung einer Zufallszahl unter Verwendung der Exponentialverteilung mit dem Parameter T.
• Dann wird eine Zufallszahl aus dem Bereich (0, 1) verwendet, ihr Logarithmus berechnet und mit -T multipliziert.
• Wir erhalten eine Zufallszahl, die nach dem Exponentialgesetz verteilt ist.

 Die Methode CalculateCorrectedB führt aus:

• Berechnung des angepassten Wertes b auf der Grundlage der Differenz zwischen f_tr und f_pr (aktuelle und vorherige Fitness).
• Berechnung der Differenz zwischen f_tr und f_pr, Ermittlung des Durchschnittswerts für die Bakterien und Rückgabe des angepassten Werts b.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::GenerateFromExponentialDistribution (double T)
{
  return -T * MathLog (u.RNDprobab ());
}

double C_AO_BCO::CalculateCorrectedB (double f_tr, double f_pr, int bacteriumIndex)
{
  double delta_f_tr = f_tr - f_pr;
  double delta_f_pr = CalculateAverageDeltaFpr (bacteriumIndex);

  if (MathAbs (delta_f_pr) < DBL_EPSILON)
  {
    return b;
  }
  else
  {
    return b * (1 / (MathAbs (delta_f_tr / delta_f_pr) + 1) + 1 / (MathAbs (f_pr) + 1));
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode CalculateRotationAngle der Klasse C_AO_BCO kommt zuletzt. Die Methode berechnet den Drehwinkel auf der Grundlage der angegebenen Parameter und gibt den Wert in Radiant zurück.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateRotationAngle ()
{
  double cos_theta = MathExp (-tau_c / T0);
  return MathArccos (cos_theta);
}
//——————————————————————————————————————————————————————————————————————————————

Testen wir die Originalversion des Algorithmus und sehen wir uns die Ergebnisse an:

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|1.0|0.5|1.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.42924491510564006
25 Hilly's; Func runs: 10000; result: 0.282259866768426
500 Hilly's; Func runs: 10000; result: 0.2515386629014219
=============================
5 Forest's; Func runs: 10000; result: 0.2476662231845009
25 Forest's; Func runs: 10000; result: 0.17824381036550777
500 Forest's; Func runs: 10000; result: 0.15324081202657283
=============================
5 Megacity's; Func runs: 10000; result: 0.2430769230769231
25 Megacity's; Func runs: 10000; result: 0.11415384615384619
500 Megacity's; Func runs: 10000; result: 0.09444615384615461
=============================
All score: 1.99387 (22.15%)

Die erzielten Ergebnisse sind so schwach, dass es keinen Sinn macht, sie in die Bewertungstabelle aufzunehmen. Beim Entwurf des Algorithmus und beim Schreiben des Codes auf der Grundlage der Textbeschreibung des Autors musste ich einige Gleichungen anpassen: einige von ihnen machten mathematisch keinen Sinn (z. B. die Division einer Zahl durch einen Vektor), während andere entweder in extrem kleine oder extrem große Werte ausarteten, die mit den Dimensionen des Problems nicht vergleichbar waren. Dabei druckte ich die Ergebnisse der Funktionen für jede der vorgestellten Gleichungen aus und analysierte sie. Der Algorithmus kann also nicht in der Form funktionieren, in der er von den Autoren beschrieben wird.

Darüber hinaus können Operationen mit Winkeln, bei denen die Normalverteilung verwendet wird, erheblich vereinfacht werden, da die physikalische Bedeutung dieser Operationen darauf beruht, dass man bei jeder Koordinate einfach ein neues Inkrement vom aktuellen Standort des Bakteriums aus setzen kann. Also beschloss ich, meine eigene Implementierung der bakteriellen Chemotaxis zu entwickeln, wobei ich mich so nah wie möglich an die grundlegenden Konzepte und Ideen des Algorithmus hielt.

Hier ist der Pseudocode für meine Version des Algorithmus:

Initialisierung:
1. Erstellen einer Bakterien-Population mit der Größe popSize.
2. Für jedes Bakterium i:
    Initialisierung der Historie der Werte der Zielfunktion f_history [i] der Größe hs
    Anfangswert setzen f_prev [i] = -DBL_MAX

Hauptschleife:
Bis zum Erreichen der Stopp-Bedingung:

1. Wenn dies die erste Iteration ist:
   Für jedes Bakterium i:
     Zufällige Initialisierung der Position x [i] im Suchraum
     x [i].[j] ∈ [x_min [j], x_max [j]] für jede Koordinate j

2. Andernfalls:
   Für jedes Bakterium i:
     a. Berechnen der durchschnittlichen Änderung der Zielfunktion:
        delta_ave [i] = (1 / (hs - 1)) * sum (f_history [i].[k] - f_history [i].[k-1] for k in 1..hs-1) + epsilon
     
     b. Berechnen der relativen Veränderung der Fitness:
        delta [i] = 1 - |f (x [i]) - f_prev [i]| / delta_ave [i]
        delta [i] = max (delta [i], 0.0001)
     
     c. Für jede Koordinate j:
        Mit einer Wahrscheinlichkeit von 0,5:
          dist [j] = (x_max [j] - x_min [j]) * delta [i]
          x [i].[j] = N (x [i].[j], x [i].[j] - dist [j], x [i].[j] + dist [j])
          Beschränkung von x [i].[j] auf innerhalb [x_min [j], x_max [j]]
        Andernfalls:
          x [i].[j] = x_best [j]
     
     d. Aktualisieren von f_prev [i] = f (x [i])

3. Bewerten der Zielfunktion f (x [i]) für jedes Bakterium

4. Aktualisieren der besten gefundenen Lösung:
   Wenn i existiert: f (x [i]) > f (x_best), dann x_best = x [i]

5. Aktualisieren der Historie der Zielfunktionswerte für jedes Bakterium:
   Werte in f_history [i] verschieben
   Einen neuen Wert hinzufügen: f_history [i].[hs - 1] = f (x [i])

Beendigung:
Rückgabe der besten gefundenen Lösung x_best

wobei:

• x [i] - Position des i-ten Bakteriums
• f (x) - Zielfunktion
• hs - Größe der Historie
• epsilon - eine kleine Konstante, die eine Division durch Null verhindert
• N (μ, a, b) - abgeschnittene Normalverteilung mit Mittelwert μ und den Grenzen [a, b]

Mein modifizierter Pseudocode spiegelt also die grundlegende Struktur und Logik des BCO-Algorithmus wider. Konzentrieren wir uns auf die wichtigsten Punkte:

• Der Algorithmus verwendet eine Population von Bakterien, die jeweils eine potenzielle Lösung darstellen.
• Bei jeder Iteration bewegen sich die Bakterien durch den Suchraum und nutzen dabei Informationen über ihre früheren Ergebnisse.
• Die Bewegung basiert auf der relativen Änderung der Zielfunktion, die es dem Algorithmus ermöglicht, sich an die Optimierungslandschaft anzupassen.
• Der Algorithmus speichert eine Historie der Zielfunktionswerte für jedes Bakterium, die zur Berechnung der durchschnittlichen Veränderung verwendet wird.
• Es besteht eine gewisse Wahrscheinlichkeit, dass sich das Bakterium auf die beste bekannte Lösung zubewegt, anstatt ein neues Gebiet zu erkunden (analog zur Vererbung von Merkmalen in der Genetik).
  
• Nach jedem Zug werden die neuen Positionen bewertet und die beste gefundene Lösung aktualisiert.

Die BCOm-Version kombiniert Elemente der lokalen Suche (Bewegung einzelner Bakterien) und der globalen Suche (Austausch von Informationen über die beste bekannte Lösung).

Schauen wir uns die wichtigsten Unterschiede zwischen den beiden Versionen des Algorithmus an. Erstens wurde der Mechanismus der bakteriellen Bewegung vereinfacht. Das komplexe System mit Drehwinkeln und Temperatur habe ich aufgegeben. Zweitens stützt sich die neue Version weniger auf die Änderungshistorie, um das Verhalten der Bakterien anzupassen, sondern verwendet einen einfacheren Ansatz zur Aktualisierung der Positionen. Anstelle einer Kombination aus Exponential- und Normalverteilung verwendet der neue Algorithmus die Normalverteilung zur Aktualisierung der Koordinaten. Das Ergebnis der Änderungen war eine Reduzierung der Anzahl der Parameter auf einen (ohne die Populationsgröße), die das Verhalten des Algorithmus steuern, was die Konfiguration des Optimierungsprozesses veränderte und die Verwaltung vereinfachte.

Insgesamt geht der neue Pseudocode von einfacheren Berechnungen bei jedem Optimierungsschritt aus, was sich auch positiv auf die Geschwindigkeit der Aufgabenausführung des Algorithmus auswirken dürfte (die ursprüngliche Version führte mehrere Berechnungen des Sinus und Kosinus der Drehwinkel für jede Koordinate jedes Bakteriums durch). Ich verfolge einen etwas anderen Ansatz, indem ich zwischen der Erkundung eines neuen Lösungsraums und der Nutzung bereits gefundener guter Lösungen abwäge.

Diese Änderungen in der Logik führten zu einem einfacheren und vermutlich (in Erwartung der Testergebnisse) effizienteren Algorithmus. Kommen wir nun zum Schreiben des Codes.

Die Struktur S_BCO_Bacterium, die jedes Bakterium darstellt, bleibt unverändert. Es dient der Speicherung von Informationen über das Bakterium und seine Geschichte der Zielfunktionswerte.

In der Methode Init der Klasse C_AO_BCOm, die für die Initialisierung der Algorithmus-Parameter zuständig ist, fügen wir eine Definition der Entfernung der akzeptablen Bewegung entlang jeder Koordinate hinzu.

So ist die Methode Init der Klasse C_AO_BCOm für die Initialisierung der Parameter des Optimierungsalgorithmus zuständig. Es prüft die Standardinitialisierungsbedingungen, erstellt die erforderlichen Arrays und füllt sie mit Werten.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCOm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  ArrayResize (allowedDispl, coords);
  for (int c = 0; c < coords; c++) allowedDispl [c] = rangeMax [c] - rangeMin [c];

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Schauen wir uns die Methode Moving der Klasse C_AO_BCOm an, die für die Bewegung der Bakterien im Suchraum verantwortlich ist. Lassen Sie uns das Stück für Stück aufschlüsseln.

1. Bei der ersten Iteration haben sich die Aktionen der Methode nicht geändert: Initialisierung der Bakterienkoordinaten mit zufälligen Werten in einem bestimmten Bereich.

2. Der grundlegende Algorithmus für die Bewegung besteht darin, Variablen zu deklarieren, um Werte wie Δ, ΔAve und dist sowie für jedes Individuum der Population zu speichern:

• Der Durchschnittswert ΔAve wird mit der Funktion CalculateAverageDeltaFpr (i) berechnet.
• Die relative Veränderung Δ, die zur Bestimmung des Grades der Veränderung der Position der Bakterien dient, wird berechnet.
• Wenn Δ zu klein ist, wird es auf 0,0001 gesetzt.

3. Ändern der Koordinaten:

• Für jede Koordinate wird eine Zufallswahrscheinlichkeit (50 %) geprüft.
• Wenn die Bedingung erfüllt ist, wird dist in Abhängigkeit von allowedDispl [c] und Δ berechnet.
• Der neue Wert x wird mit der Funktion GaussDistribution unter Berücksichtigung der Grenzen xMin und xMax berechnet.
• Wenn x außerhalb des Bereichs liegt, wird es mit RNDfromCI korrigiert.
• Schließlich wird der neue Koordinatenwert unter Berücksichtigung des rangeStep gespeichert.

4. Der vorherige Wert f der Fitnessfunktion wird für jedes Individuum im Bakterium-Array gespeichert. a und Bakterium-Arrays werden verwendet. Die Funktionen RNDfromCI, SeInDiSp und GaussDistribution sind für die Erzeugung von Zufallszahlen und Verteilungen sowie für die Normalisierung von Koordinatenwerten zuständig.

Die Funktion Moving () ist also für die Initialisierung und Aktualisierung der Position der Individuen in der Population innerhalb des Algorithmus verantwortlich. Es verwendet zufällige Wahrscheinlichkeiten und Verteilungen, um die Bewegung von Bakterien zu kontrollieren. Der Hauptunterschied zur ursprünglichen Version besteht jedoch in einer einfacheren und effizienteren Implementierung des Gradienten der Fitnessfunktion. Wenn der Unterschied im Wohlbefinden der Bakterien auf der aktuellen Stufe im Vergleich zur vorherigen Stufe abnimmt, beschleunigt sich ihre Bewegung. Umgekehrt verlangsamen sich die Bakterien, wenn sie sich in einer günstigen äußeren Umgebung befinden. Dies widerspricht dem natürlichen Verhalten von Bakterien, die in einer aggressiven Umgebung depressiv werden und sich in einen Ruhezustand begeben.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double x    = 0.0;
  double xMin = 0.0;
  double xMax = 0.0;
  double Δ    = 0.0;
  double ΔAve = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    ΔAve = CalculateAverageDeltaFpr (i) + DBL_EPSILON;

    Δ = fabs (a [i].f - bacterium [i].fPrev) / ΔAve;

    Δ = 1.0 - Δ;

    if (Δ < 0.0001) Δ = 0.0001;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < 0.5)
      {
        dist = allowedDispl [c] * Δ;

        x    = a [i].c [c];
        xMin = x - dist;
        xMax = x + dist;

        x = u.GaussDistribution (x, xMin, xMax, 8);

        if (x > rangeMax [c]) x = u.RNDfromCI (xMin, rangeMax [c]);
        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], xMax);

        a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else a [i].c [c] = cB [c];
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision () in der Klasse C_AO_BCOm, die für die Aktualisierung der Informationen über die Grundgesamtheit und den Verlauf der Werte der Zielfunktion zuständig ist, wurde nicht geändert.

Testergebnisse

Schauen wir uns nun die Leistung der neuen Version des BCOm-Algorithmus an:

BCO|Bakterielle Chemotaxis-Optimierung|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.759526049526603
25 Hilly's; Func runs: 10000; result: 0.6226756163411526
500 Hilly's; Func runs: 10000; result: 0.31483373090540534
=============================
5 Forest's; Func runs: 10000; result: 0.8937814268120954
25 Forest's; Func runs: 10000; result: 0.6133909133246214
500 Forest's; Func runs: 10000; result: 0.22541842289630293
=============================
5 Megacity's; Func runs: 10000; result: 0.653846153846154
25 Megacity's; Func runs: 10000; result: 0.42092307692307684
500 Megacity's; Func runs: 10000; result: 0.14435384615384755
=============================
All score: 4.64875 (51.65%)

Wahrscheinlich haben die gesammelten Erfahrungen und ein kritischer Blick auf die verfügbaren Informationen über die ursprüngliche Version ihre Arbeit getan, und die neue Version des Algorithmus erwies sich in der praktischen Anwendung als leistungsfähiger als das Original.

In der Visualisierung des BCOm-Algorithmus können wir die gute Ausarbeitung signifikanter Abschnitte des Hyperraums sehen, was auf eine hohe Fähigkeit zur Untersuchung der Oberfläche der optimierten Funktion hinweist.

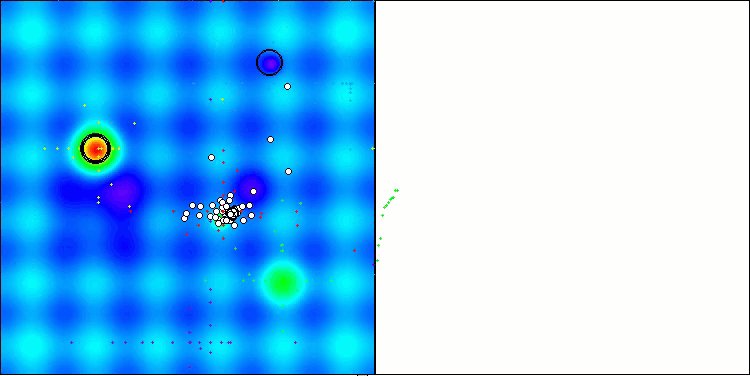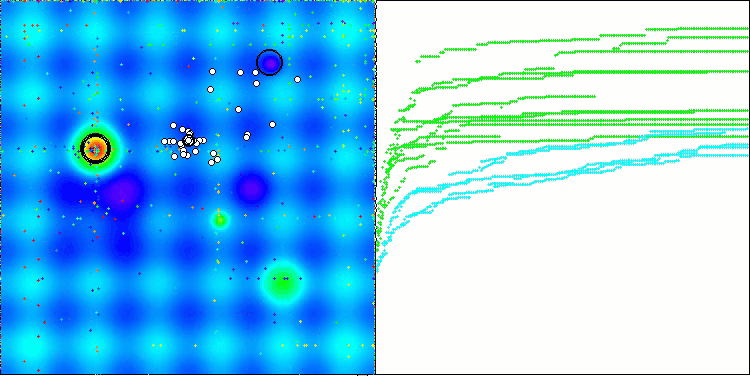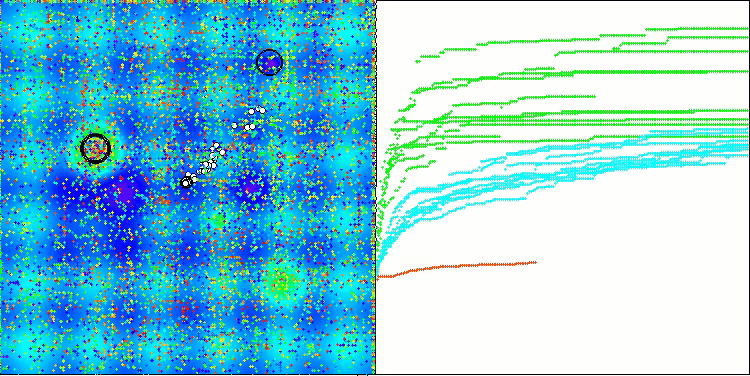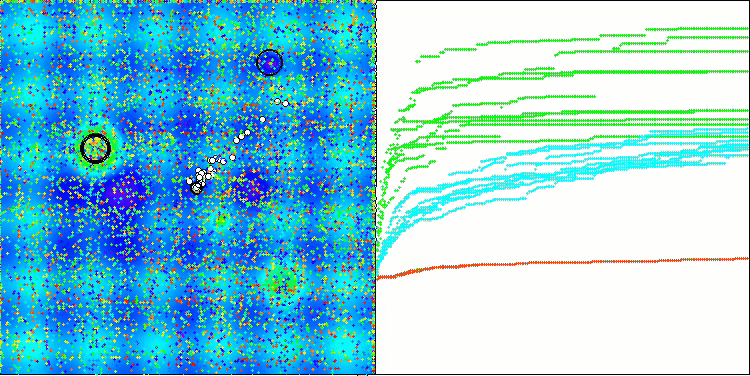
BCOm mit der Testfunktion Hilly

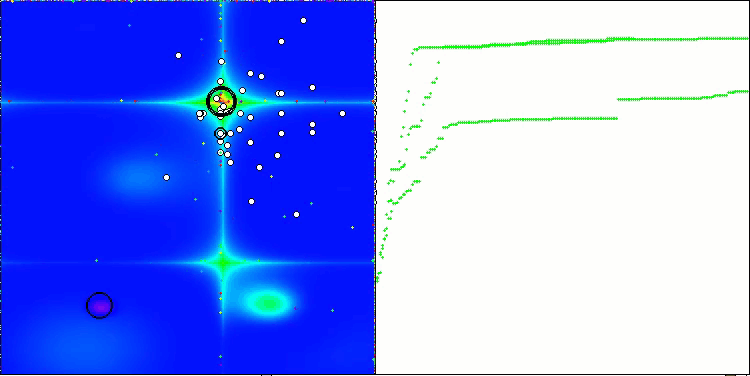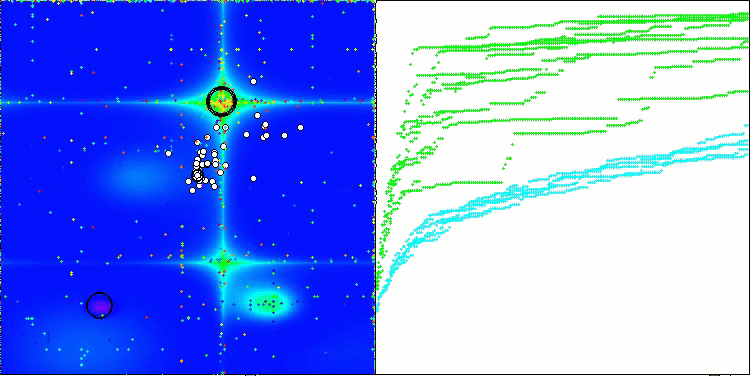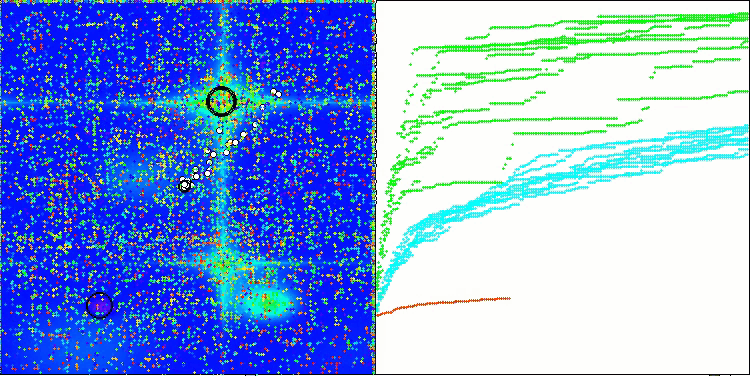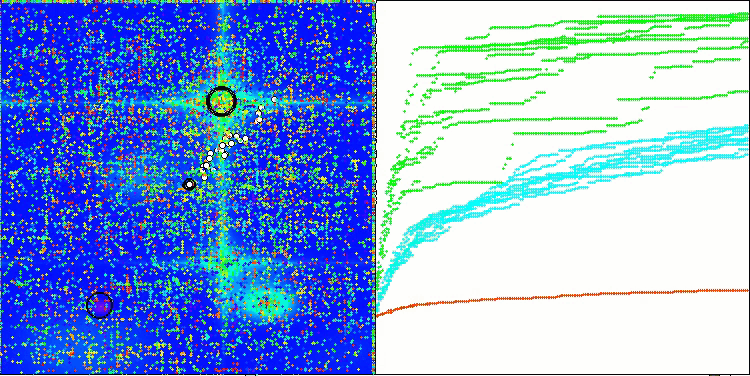
BCOm mit der Testfunktion Forest

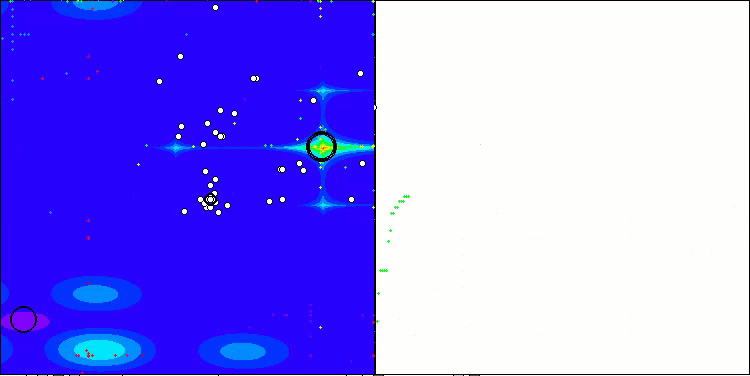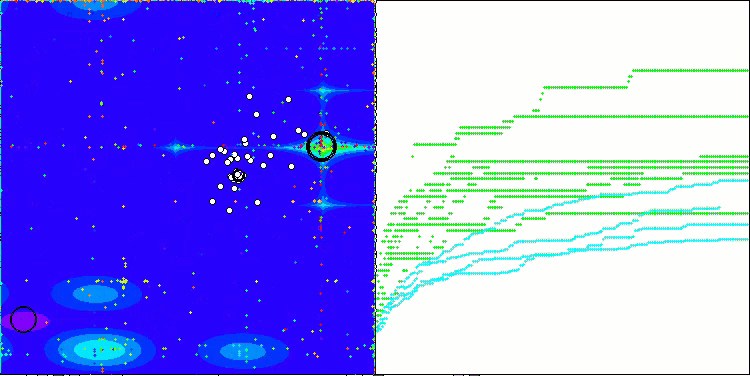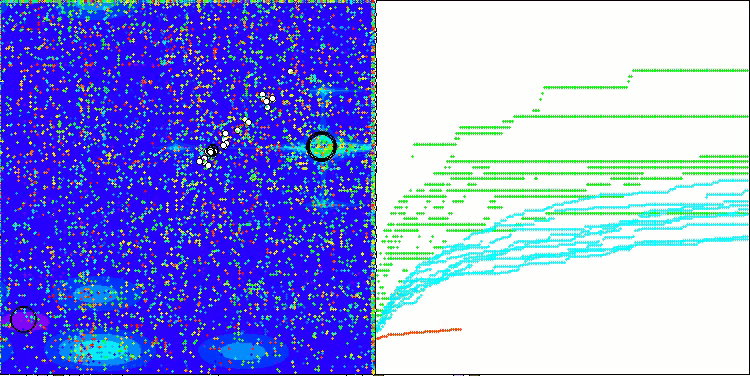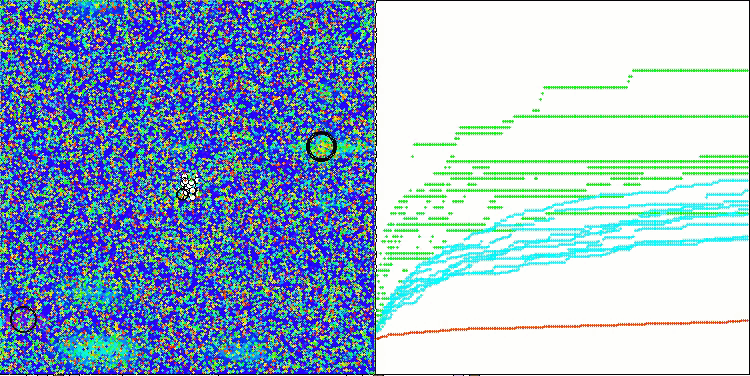
BCOm mit der Testfunktion Megacity

Aufgrund der Testergebnisse belegte der Algorithmus einen stabilen 17. Platz in der Gesamtwertung der Optimierungsalgorithmen.

#	AO	Beschreibung	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	Suche über die gesamte Nachbarschaft	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	Сode Lock Algorithmus	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	Optimierung der Tiermigration M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5.987	66,52
4	(P+O)ES	(P+O) Entwicklungsstrategien	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	Kometenschweif-Algorithmus	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastische Diffusionssuche M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	Entwicklung der sozialen Gruppen	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	Simuliertes isotropes Abkühlen	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	künstliche, kooperative Suche	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	Anarchische Gesellschaftsoptimierung	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5.178	57,54
11	TSEA	Schildkrötenpanzer-Evolutionsalgorithmus	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	differentielle Evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	Optimierung chemischer Reaktionen	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	Vogelschwarm-Algorithmus	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	Harmoniesuche	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	Setzen, Säen und Wachsen	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	BCOm	Optimierung mit der bakteriellen Chemotaxis M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
18	(PO)ES	(PO) Entwicklungsstrategien	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
19	TSm	Tabu-Suche M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
20	BSO	Brainstorming-Optimierung	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
21	WOAm	Wal-Optimierungsalgorithmus M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
22	AEFA	Algorithmus für künstliche elektrische Felder	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
23	ACOm	Ameisen-Kolonie-Optimierung M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
24	BFO-GA	Optimierung der bakteriellen Futtersuche - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
25	ABHA	Algorithmus für künstliche Bienenstöcke	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
26	ASBO	Optimierung des adaptiven Sozialverhaltens	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
27	MEC	Evolutionäre Berechnung des Geistes	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
28	IWO	Optimierung mit invasiven Unkräutern	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
29	Micro-AIS	Künstliches Mikro-Immunsystem	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
30	COAm	Kuckuck-Optimierungsalgorithmus M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
31	SDOm	Optimierung der Spiraldynamik M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
32	NMm	Nelder-Mead-Verfahren M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
33	FAm	Firefly-Algorithmus M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
34	GSA	Algorithmus für die Schwerkraftsuche	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
35	BFO	Optimierung der bakteriellen Futtersuche	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
36	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
37	BA	Fledermaus-Algorithmus	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
38	AAA	Künstlicher Algenalgorithmus (AAA)	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
39	SA	simuliertes Abkühlen	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
40	IWDm	intelligente Wassertropfen M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
41	PSO	Partikelschwarmoptimierung	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
42	Gebote	Boids-Algorithmus	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
43	MA	Affen-Algorithmus	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
44	SFL	schlurfender Froschsprung	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
45	FSS	Fischschulsuche	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84

Zusammenfassung

Wir haben die ursprüngliche und die modifizierte Version des BCO-Algorithmus besprochen. Die ursprüngliche Version, die aus offenen Quellen erstellt wurde, erwies sich als überladen mit schweren trigonometrischen Berechnungen und hatte schwache Sucheigenschaften sowie mathematische „Ausrutscher“. Es war notwendig, den gesamten Algorithmus zu überdenken und eine tiefgreifende Analyse der Suchstrategie durchzuführen und eine neue, modifizierte Version zu erstellen. Änderungen an der Algorithmuslogik führten zu einfacheren Berechnungen bei jedem Optimierungsschritt, was sich positiv auf die Geschwindigkeit der Codeausführung auswirkte. Der neue Algorithmus wägt außerdem zwischen der Erkundung eines neuen Lösungsraums und der Nutzung bereits gefundener guter Lösungen ab.

Obwohl der neue Ansatz dem natürlichen Verhalten von Bakterien etwas zuwiderläuft, hat er sich in der Praxis als äußerst effizient erwiesen. Die Visualisierung der Funktionsweise des Algorithmus zeigte, dass er in der Lage ist, wichtige Bereiche des Hyperraums zu erforschen, was auch auf seine verbesserten Forschungsmöglichkeiten hinweist. Infolgedessen erwies sich die neue Version des Algorithmus als leistungsfähiger und effizienter als das Original.

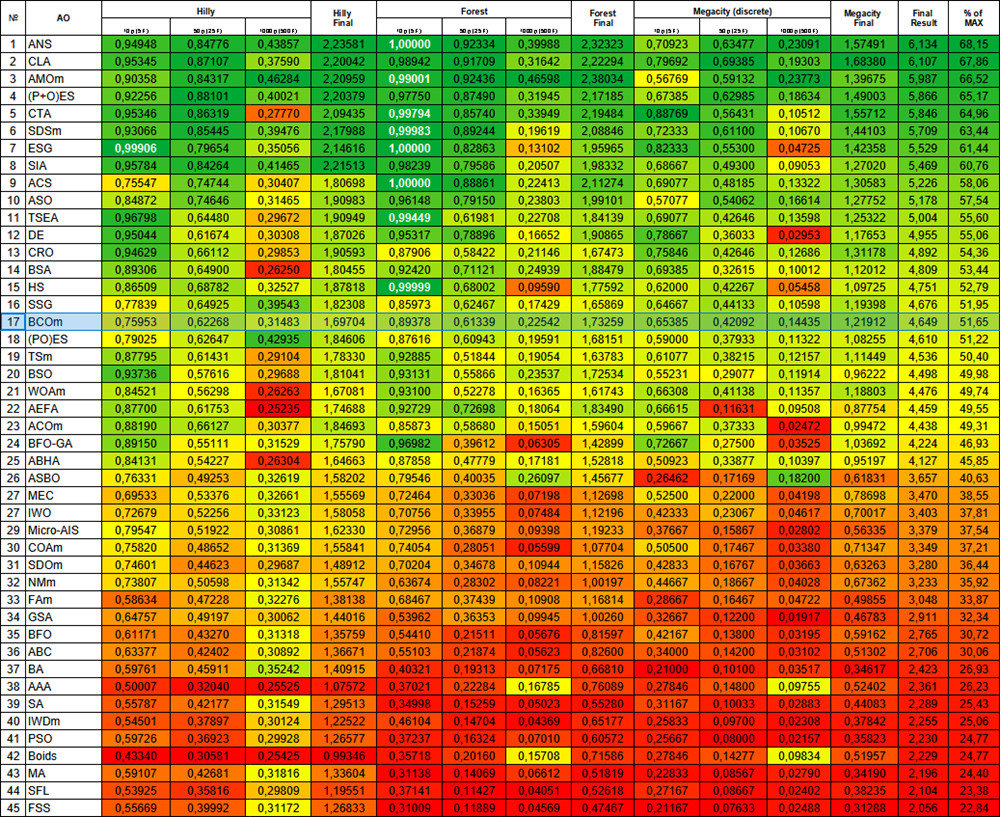
Abbildung 1. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

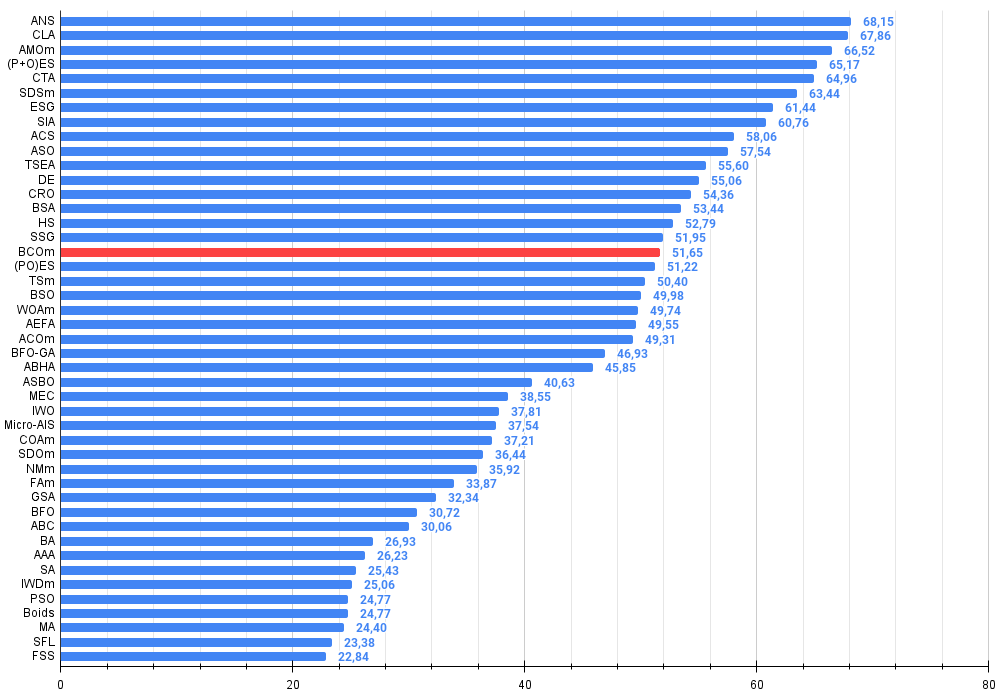
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)

Vor- und Nachteile von BCOm:

Vorteile:

1. Schnell.
2. Selbstanpassend.
   
3. Gute Skalierbarkeit.
4. Nur ein externer Parameter.
   

Nachteile

1. Große Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
   

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355