Algorithmus für die künstliche, kooperative Suche (Artificial Cooperative Search, ACS)
111
0
Inhalt
1. Einführung
2. Implementierung des Algorithmus
3. Testergebnisse
1. Einführung
Die Natur ist eine unerschöpfliche Quelle der Inspiration für Wissenschaftler und Ingenieure, die nach innovativen Lösungen suchen. Eines dieser bemerkenswerten Phänomene ist der Mutualismus - eine für beide Seiten vorteilhafte biologische Interaktion zwischen verschiedenen Arten. Lebewesen, die an mutualistischen Beziehungen beteiligt sind, streben danach, aus dieser Interaktion gegenseitigen Nutzen zu ziehen, um die Entwicklung und Vielfalt der Population zu fördern. Um dies zu verstehen, werde ich einige Beispiele für wechselseitige (symbiotische) Beziehungen zwischen lebenden Organismen anführen, bei denen sie sich gegenseitig Vorteile verschaffen:
1. Blühende Pflanzen und Bestäuber:
- Pflanzen produzieren Nektar und andere Belohnungen, um Bestäuber wie Insekten, Vögel und Fledermäuse anzulocken.
- Die Bestäuber wiederum übertragen den Pollen von einer Blüte zur anderen, was die Fortpflanzung der Pflanze fördert.
2. Pilze und Pflanzenwurzeln (Mykorrhiza):
- Pilze dringen in die Wurzeln von Pflanzen ein und nehmen von ihnen organische Verbindungen (Produkte der Photosynthese) auf.
- Die Pilze wiederum erweitern die Aufnahmefläche der Wurzeln und erhöhen so die Verfügbarkeit von Wasser und Mineralien für die Pflanzen.
3. Termiten und symbiotische Bakterien:
- Termiten enthalten in ihren Eingeweiden symbiotische Bakterien, die ihnen bei der Verdauung von Zellulose, dem Hauptbestandteil von Holz, helfen.
- Die Bakterien erhalten Nährstoffe von den Termiten, und die Termiten erhalten die Fähigkeit, die Fasern zu verdauen.
Diese Beispiele zeigen, wie lebende Organismen interagieren, um sich gegenseitig Vorteile zu verschaffen und ihre Überlebenschancen zu erhöhen.
Der ACS-Algorithmus orientiert sich auch am Migrationsverhalten eusozialer Superorganismen, die sich eine gemeinsame Umgebung teilen. Im Folgenden werden einige Beispiele für ein solches Wanderungsverhalten eusozialer Superorganismen aufgeführt:
1. Ameisenkolonien:
- Während einer Koloniewanderung nehmen die Ameisen Larven, Puppen und andere wichtige Elemente des Nestes mit sich.
2. Bienenfamilien:
- Beim Schwärmen können Bienenvölker vorübergehend aus ihrem Bienenstock auswandern, um an einem anderen Ort ein neues Volk zu gründen.
- Während der Wanderung eines Schwarms nehmen die Bienen Königinnen, Larven und die notwendigen Honigvorräte mit, um ein neues Nest anzulegen.
Ein gemeinsames Merkmal dieser Beispiele ist, dass eusoziale Superorganismen wie Ameisen, Termiten, Bienen und Wespen in der Lage sind, ihre Kolonien als Reaktion auf Umweltveränderungen oder Ressourcenknappheit kollektiv umzusiedeln. Diese Wanderungsfähigkeit ermöglicht es ihnen, sich an veränderte Bedingungen anzupassen und sichert das Überleben des gesamten Superorganismus. Die mutualistische und kooperative biologische Interaktion zweier eusozialer Superorganismen, die in derselben Umgebung leben, diente als Inspiration für den ACS-Algorithmus. Bei diesem Algorithmus entspricht das Konzept des Lebensraums dem Konzept des Suchraums in Bezug auf das entsprechende Optimierungsproblem.
Konzeptionell betrachtet der ACS-Algorithmus zufällige Lösungen für das entsprechende Problem als künstliche Superorganismen, die zu produktiveren Nahrungsgebieten wandern. Die beiden Haupt-Superorganismen, die als α und β bezeichnet werden, enthalten künstliche Sub-Superorganismen, die der Größe der Bevölkerung entsprechen. Die Populationsgröße entspricht der Anzahl der Individuen in diesen Sub-Superorganismen. Im Prozess der Ko-Evolution interagieren die Superorganismen α und β als Räuber und Beute und nutzen zwei dynamische Populationen, um den Suchraum effizient zu erkunden und das globale Optimum für numerische Optimierungsprobleme zu finden.
Der ACS-Algorithmus wurde von Pinar Civicioglu im Jahr 2013 vorgeschlagen. Es beginnt mit zwei Basispopulationen, die Kandidatenlösungen innerhalb der Vertrauensregion enthalten. Der Algorithmus erzeugt dann zwei neue Populationen, Räuber und Beute, indem er Werte aus den ursprünglichen Populationen α und β mit Hilfe von Zufallsschritten und einer binären Matrix abbildet. Darüber hinaus wird die fünfte Population auf der Grundlage der Werte der Raubtier- und der Beutepopulation berechnet. Bei diesem Verfahren werden die Ausgangspopulationen für eine bestimmte Anzahl von Iterationen aktualisiert, wobei die beste Lösung aus diesen beiden Populationen ausgewählt wird.
Die Migration und Evolution zweier künstlicher Superorganismen, die auf biologische Weise miteinander interagieren, um das globale Extremum der Zielfunktion zu erreichen, und der Prozess, der dem kooperativen Verhalten in der Natur ähnelt, sind der Schlüssel zur hohen Leistung von ACS bei numerischen Optimierungsproblemen. Dieser einzigartige Ansatz für biologisch motivierte Interaktionen zwischen Populationen ermöglicht dem ACS-Algorithmus eine beeindruckende Konvergenzgeschwindigkeit und hohe Lösungsgenauigkeit. Aufgrund seiner Fähigkeit, schnell und genau optimale Lösungen zu finden, hat sich ACS als leistungsfähiges Werkzeug für die Lösung eines breiten Spektrums numerischer Optimierungsprobleme erwiesen.
In diesem Artikel werde ich das Konzept des ACS-Algorithmus im Detail beschreiben und seine bemerkenswerten Fähigkeiten demonstrieren. Die Leser werden ein tiefes Verständnis dafür gewinnen, wie biologische Inspiration erfolgreich in fortschrittliche Optimierungsalgorithmen implementiert werden kann, die in der Lage sind, komplexe Probleme mit hoher Effizienz zu lösen.
2. Implementierung des Algorithmus
Der Algorithmus der Künstlichen Kooperativen Suche (ACS) funktioniert wie folgt:
1. Initialisierung. Es werden die Populationsgröße „popSize“, die Anzahl der Variablen „N“, die unteren „XLow“ und oberen „XHi“ Variablengrenzen sowie die Wahrscheinlichkeit der biologischen Interaktion „Probab“ festgelegt. Anschließend werden die Ausgangspositionen der Populationen „A“ und „B“ generiert und ihre Fitnesswerte „YA“ und „YB“ berechnet.
2. Schleife nach Iterationen. Die folgenden Schritte werden bei jeder Iteration durchgeführt:
- Auswahl. Es wird festgelegt, welche Gruppe von Agenten aus den Populationen A oder B in der aktuellen Iteration als „Raubtier“ verwendet wird.
- Das Mischen der „Beute“. Die Positionen der Agenten in der Auswahlmenge werden neu verteilt.
- Mutation. Die Positionen der Agenten werden mit einem zufällig generierten R-Skalierungsfaktor aktualisiert. Die „Raubtiere“ mutieren anhand der Informationen über die Entscheidungsvektoren der „Beute“.
- Füllen der binären Matrix M. Die binäre Matrix M wird erstellt, um zu bestimmen, welche Variablen in der aktuellen Iteration aktualisiert werden.
- Aktualisierung der Agentenpositionen. Die Positionen der Agenten werden unter Berücksichtigung der Werte in der M-Matrix aktualisiert. Ist der Wert in M gleich 1, so wird die entsprechende Agentenvariable aktualisiert.
- Kontrolle der Grenzen. Liegt die aktualisierte Position des Agenten außerhalb der angegebenen Grenzen, wird sie angepasst.
- Aktualisierung der Auswahl. In diesem Stadium werden die besten Lösungen für die nächste Iteration des Algorithmus gespeichert.
- Aktualisierung der global besten Lösung. Wenn eine bessere Lösung gefunden wird, wird sie gespeichert.
3. Rückgabe des Ergebnisses. Am Ende des Algorithmus werden die global beste Lösung und ihr Fitnesswert zurückgegeben.
Der Algorithmus verfügt über einige einzigartige Operatoren wie den „Beute“-Mischungsoperator und den Mutationsoperator, die die Verwendung der binären Matrix M beinhalten.
Die M-Matrix ist ein zweidimensionales Feld mit „popSize“-Zeilen (die Anzahl der Kandidaten in der Grundgesamtheit) und „N“-Spalten (die Anzahl der Variablen in jedem Kandidaten). Jedes Element der Matrix kann entweder 0 oder 1 sein. Die M-Matrix wird verwendet, um zu bestimmen, welche Kandidaten für die weitere Erneuerung der Population ausgewählt werden. Die Werte 0 und 1 in der Matrix geben an, ob der entsprechende Kandidat auf der Grundlage der zufälligen Rand-Werte und der Probab-Interaktionswahrscheinlichkeit zur Aktualisierung ausgewählt wird.
Die M-Matrix trägt dazu bei, die Auswahl der Kandidaten für die Erneuerung der Population zu regeln. Die M-Matrix spielt also eine Schlüsselrolle bei der Populationsentwicklung und der Suche nach der optimalen Lösung in ACS.
Schauen wir uns die einzelnen Schritte des ACS-Algorithmus in Pseudocode an:
1. Initialisierung:
- Die folgenden Parameter werden eingestellt:
- popSize - Größe der Bevölkerung
- N - Anzahl der Variablen
- MaxIter - maximale Anzahl von Iterationen
- XLow - unterer Grenzwert für Variablen
- XHi - Obergrenze für Variablen
- Probab - Wahrscheinlichkeit einer biologischen Interaktion
- Rand - Funktion, die gleichmäßig verteilte Zahlen im Bereich (0, 1) liefert
- GlobMax wird durch den negativen DBL_MAX initialisiert.
2. Hauptschleife:
- Für jedes Element der Grundgesamtheit (I = 1 bis popSize):
- Für jede Variable (J = 1 bis N):
- Die Anfangswerte A(I,J) und B(I,J) im Bereich [XLow(J), XHi(J)] werden berechnet
- Die Anfangswerte der Zielfunktion YA(I) = Fx(A(I,:)) und YB(I) = Fx(B(I,:)) werden berechnet
- Die Hauptschleife mit (Iter = 1 bis MaxIter) Iterationen beginnt
3. Auswahl:
- Wir wählen nach dem Zufallsprinzip, ob A oder B als Räuber eingesetzt werden soll:
- Wenn Rand < 0,5, Predator= A, Ypred = YA, Key = 1
- Andernfalls: Predator = B, Ypred = YB, Key = 2
- Wir wählen nach dem Zufallsprinzip, ob A oder B als Beute eingesetzt wird:
- Wenn Rand < 0,5, Beute = A
- Andernfalls: Beute = B
- Die Beute wird zufällig gemischt
- Der R-Parameter wird berechnet:
- Wenn Rand < 0,5, R = 4 * Rand * (Rand - Rand)
- Andernfalls ist R = 1/exp(4 * Rand)
- Die Binärmatrix M von popSize x N, gefüllt mit Einsen, wird erstellt
- Einige Elemente der Matrix M werden zufällig mit der Wahrscheinlichkeit Probab auf 0 gesetzt
- Wenn Rand < Probab ist, werden einige Elemente der Matrix M zufällig auf 0 oder 1 gesetzt
- Für jede Zeile der Matrix M wird, wenn die Summe der Elemente N ist, ein Element zufällig ausgewählt und auf 0 gesetzt
4. Mutation:
- Der neue Wert X = Räuber + R * (Beute - Räuber) wird berechnet
- Für jedes Element der Grundgesamtheit (I = 1 bis popSize) und jede Variable (J = 1 bis N):
- Ist das entsprechende Element der M-Matrix größer als 0, so ist X(I,J) = Predator(I,J)
- Liegt X(I,J) außerhalb des Bereichs [XLow(J), XHi(J)], so wird X(I,J) auf einen Zufallswert in diesem Bereich gesetzt
5. Aktualisierung der Auswahl:
- Für jedes Element der Grundgesamtheit (I = 1 bis popSize):
- Wenn Fx(X(I,:)) < Ypred(i), dann Predator(I,:) = X(I,:) und Ypred(I) = Fx(X(I,:))
- Wenn Schlüssel = 1, dann A = Räuber und YA = Ypred, andernfalls B = Räuber und YB = Ypred
- Ybest = min(Ypred)
- Ibest = Index der Predator-Zeile, die Ybest entspricht
- Wenn Ybest > GlobMax, dann GlobMax = Ybest und GlobMax = Predator(Ibest,:)
6. Geben Sie das Ergebnis zurück:
- Rückgabe GlobMax und GlobMaxX Vektor
Fahren wir mit der Beschreibung der Implementierung des ACS-Algorithmus fort. Wir verwenden die einfachste Struktur „S_D “, um die Grundgesamtheit zu beschreiben (von denen es im Algorithmus fünf gibt):
- c [] ist ein Array zur Speicherung von Koordinaten (optimierte Parameter der Aufgabe)
- Init (int coords) - die Methode ändert die Größe des Arrays c auf die in coords angegebene Größe (Anzahl der Koordinaten) unter Verwendung der Funktion ArrayResize
Im Allgemeinen wird diese Struktur verwendet, um ein Objekt zu erstellen, das eine Reihe von reellen Zahlen enthält. Die Methode Init wird verwendet, um die Größe des Arrays zu ändern.
//—————————————————————————————————————————————————————————————————————————————— struct S_D { void Init (int coords) { ArrayResize (c, coords); } double c []; }; //——————————————————————————————————————————————————————————————————————————————
Um die Matrix M zu beschreiben, legen wir die Struktur S_C an, die sich von der Struktur des Feldtyps S_D unterscheidet:
- c[] - das Array zur Speicherung der Matrixsymbole „0“ und „1
- Init (int coords) - die Methode ändert die Größe des Arrays c auf die in coords angegebene Größe unter Verwendung der Funktion ArrayResize
//—————————————————————————————————————————————————————————————————————————————— struct S_C { void Init (int coords) { ArrayResize (c, coords); } char c []; }; //——————————————————————————————————————————————————————————————————————————————
Der Algorithmus wird als Klasse C_AO_ACS beschrieben, die von der Basisklasse C_AO abgeleitet ist und die folgenden Felder enthält:
- ~C_AO_ACS () { } - Klassen-Destruktor, der aufgerufen wird, wenn das Klassenobjekt gelöscht wird. In diesem Fall ist der Destruktor leer.
- C_AO_ACS () - Klassen-Konstruktor, der die Datenelemente der Klasse initialisiert, die Größe des Arrays params ändert und den Algorithmusparametern Standardwerte zuweist.
- SetParams () - Methode setzt die Werte popSize und bioProbab basierend auf den Werten im Array params.
- Init () - die Methode nimmt mehrere Argumente entgegen und gibt einen booleschen Wert zurück.
- Moving () und Revision () sind Methoden, die die Hauptlogik des Algorithmus enthalten.
- bioProbab - das Datenelement, das die Wahrscheinlichkeit einer biologischen Interaktion speichert.
- S_D A [], S_D B [], S_D Predator [], S_D Prey [], S_C M [], double YA [], double YB [], double Ypred [], int Key, int phase - sind private Datenmitglieder der Klasse.
- ArrayShuffle () - private Methode, die die Array-Elemente mischt.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ACS () { } C_AO_ACS () { ao_name = "ACS"; ao_desc = "Artificial Cooperative Search"; ao_link = "https://www.mql5.com/ru/articles/15004"; popSize = 1; //population size bioProbab = 0.9; //biological interaction probability ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bioProbab"; params [1].val = bioProbab; } void SetParams () { popSize = (int)params [0].val; bioProbab = params [1].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double bioProbab; //biological interaction probability private: //------------------------------------------------------------------- S_D A []; S_D B []; S_D Predator []; S_D Prey []; S_C M []; double YA []; double YB []; double Ypred []; int Key; int phase; void ArrayShuffle (double &arr []); }; //——————————————————————————————————————————————————————————————————————————————
Als Nächstes wird die Methode Init der Klasse C_AO_ACS vorgestellt. Die Methode initialisiert das Klassenobjekt:
- Init () - Deklaration der Methode. Sie benötigt vier Argumente: minimaler Suchbereich „rangeMinP“, maximaler Suchbereich „rangeMaxP“, Suchschritt „rangeStepP“ und die Anzahl der Epochen „epochsP“, die standardmäßig 0 ist.
- if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - Aufruf der Funktion StandardInit, die die Standardinitialisierung der Basisklasse durchführt. Wenn StandardInit false zurückgibt, wird die Methode Init sofort beendet und gibt false zurück.
- In der Schleife for (int i = 0; i < popSize; i++) wird jedes Element der Arrays A, B, Predator, Prey und M mit der Methode Init initialisiert.
- ArrayResize (YA, popSize) und ähnliche Zeilen ändern die Größe der Arrays YA, YB und Ypred auf popSize.
- ArrayInitialize (YA, -DBL_MAX) und ähnliche Zeilen initialisieren alle Elemente der Arrays YA, YB und Ypred mit dem Wert-DBL_MAX.
- In der verschachtelten for-Schleife wird jedes c-Element jedes Objekts in den Arrays A und B mit einem Zufallswert im angegebenen Bereich initialisiert.
- phase = 0 setzt „phase“ auf 0.
Die Logik des ursprünglichen Algorithmus unterteilt nicht in Phasen. Ich musste Phasen hinzufügen, um den Algorithmus in dem Stil zu implementieren, den ich für alle Bevölkerungsalgorithmen übernommen habe. Dies war notwendig, weil das ACS eine Vorausberechnung der Agentenfitness für die Populationen А und B verwendet. Eine Phasenteilung wurde hinzugefügt, um diese Operationen in den Methoden nacheinander durchzuführen.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ACS::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (A, popSize); ArrayResize (B, popSize); ArrayResize (Predator, popSize); ArrayResize (Prey, popSize); ArrayResize (M, popSize); for (int i = 0; i < popSize; i++) { A [i].Init (coords); B [i].Init (coords); Predator [i].Init (coords); Prey [i].Init (coords); M [i].Init (coords); } ArrayResize (YA, popSize); ArrayResize (YB, popSize); ArrayResize (Ypred, popSize); ArrayInitialize (YA, -DBL_MAX); ArrayInitialize (YB, -DBL_MAX); ArrayInitialize (Ypred, -DBL_MAX); // Initialization for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab(); B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab(); } } phase = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_ACS implementiert die grundlegende Logik des Verschiebens von Individuen im Algorithmus. Diese Methode führt mehrere Operationen durch, darunter das Kopieren von Arrays, Auswahl, Permutation, Mutation und Crossover.
- if (phase == 0) - Individuen aus der Population A werden in dieser Phase kopiert.
- if (phase == 1) - in dieser Phase geben wir die Fitness der Individuen der Population А zurück und kopieren Individuen aus der PopulationB.
- if (phase == 2) - in dieser Phase geben wir die Fitness der Individuen der Population B zurück und die gesamte weitere Algorithmuslogik wird danach ausgeführt.
- Auswahl - der Block führt eine Auswahl durch. Abhängig von einer Zufallszahl werden die Felder A oder B in das Feld Predator kopiert, während die entsprechenden Werte in das Feld Ypred kopiert werden.
- Permutation von Prey - hier wird eine Permutation der Elemente des Prey-Arrays durchgeführt.
- R - eine Variable wird deklariert, die dann je nach Zufallszahl mit einem von zwei möglichen Werten initialisiert wird.
- Auffüllen der Binärmatrix M mit Einsen - hier wird die Binärmatrix M mit Einsen aufgefüllt.
- Zusätzliche Operationen mit der Matrix M - der Block führt zusätzliche Operationen mit der Matrix M durch, einschließlich der Änderung einiger ihrer Elemente auf 0 oder 1, abhängig von der Zufallszahl und der bioProbab-Wahrscheinlichkeit der biologischen Interaktion.
- Mutation - der Block führt eine Mutation durch, bei der die a-Array-Elemente auf der Grundlage der Predator- und Prey-Array-Elemente sowie des R-Werts geändert werden.
- Crossover - der Block führt eine Crossover-Operation durch, bei der einige Elemente des Arrays a durch die Elemente des Arrays Predator ersetzt werden.
- Boundary Control - der Block führt eine Boundary Control durch, bei der die Elemente eines Arrays, die außerhalb des angegebenen Bereichs der optimierten Parameter liegen, durch zufällige Werte innerhalb dieses Bereichs ersetzt werden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::Moving () { //---------------------------------------------------------------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 1) { for (int i = 0; i < popSize; i++) YA [i] = a [i].f; for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) YB [i] = a [i].f; phase++; } //---------------------------------------------------------------------------- // Selection if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { ArrayCopy (Predator [i].c, A [i].c); } ArrayCopy (Ypred, YA); Key = 1; } else { for (int i = 0; i < popSize; i++) { ArrayCopy (Predator [i].c, B [i].c); } ArrayCopy (Ypred, YB); Key = 2; } if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { ArrayCopy (Prey [i].c, A [i].c); } } else { for (int i = 0; i < popSize; i++) { ArrayCopy (Prey [i].c, B [i].c); } } // Permutation of Prey for (int i = 0; i < popSize; i++) { ArrayShuffle (Prey [i].c); } double R; if (u.RNDprobab () < 0.5) { R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0); } else R = 1 / MathExp (4 * MathRand () / 32767.0); // Fill binary matrix M with 1s for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = 1; } } // Additional operations with matrix M for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } else { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { int sum = 0; for (int c = 0; c < coords; c++) sum += M [i].c [c]; if (sum == coords) { int j = MathRand () % coords; M [i].c [j] = 0; } } // Mutation for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]); // Crossover if (M [i].c [j] > 0) { a [i].c [j] = Predator [i].c [j]; } // Boundary control if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j]) { a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Revisionsmethode der Klasse C_AO_ACS. Die Methode führt eine Reihe von Operationen durch: Sortieren und Rückwärtskopieren von Arrays sowie Aktualisieren des besten Werts der globalen Lösung.
- if (phase < 3) return - die Grundlogik der Methode wird erst dann ausgeführt, wenn alle drei Phasen der Vorbereitung der Populationen für die weitere Interaktion abgeschlossen sind.
- Aktualisierung der Auswahl - der Block aktualisiert die Auswahl der Personen. Für jedes Individuum der Reihe a wird geprüft, ob sein f-Fitnesswert den entsprechenden Wert in der Reihe Ypred übersteigt.
- if (Key == 1) und else - in diesen Blöcken werden je nach dem Wert von Key die Elemente des Arrays Predator aus dem Array A oder B kopiert, während die entsprechenden Werte von Ypred aus dem Array YA oder YB kopiert werden.
- ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY) - das Array Ypred mit den Fitnesswerten wird sortiert und dann umgekehrt, sodass die Werte in absteigender Reihenfolge sind.
- Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred) - hier ist Ybest ein Höchstwert in Ypred, während Ibest ein Index dieses Höchstwertes ist.
- if (Ybest > fB) - wenn Ybest den aktuellen fB-Wert überschreitet, wird fB aktualisiert, während die entsprechenden Array-Elemente a und cB aus dem Predator-Array kopiert werden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::Revision () { if (phase < 3) return; // Selection update for (int i = 0; i < popSize; i++) { double d = a [i].f; if (d > Ypred [i]) { ArrayCopy (Predator [i].c, a [i].c); Ypred [i] = d; } } if (Key == 1) { for (int i = 0; i < popSize; i++) { ArrayCopy (A [i].c, Predator [i].c); } ArrayCopy (YA, Ypred); } else { for (int i = 0; i < popSize; i++) { ArrayCopy (B [i].c, Predator [i].c); } ArrayCopy (YB, Ypred); } ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY); double Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred); if (Ybest > fB) { fB = Ybest; ArrayCopy (a [Ibest].c, Predator [Ibest].c); ArrayCopy (cB, Predator [Ibest].c); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode ArrayShuffle der Klasse C_AO_ACS führt ein zufälliges Mischen der Elemente im Array durch.
- for (int i = n - 1; i > 0; i--) - Die Schleife durchläuft das Array arr in umgekehrter Reihenfolge, beginnend mit dem letzten Element.
- j = MathRand () % (i + 1) - hier ist j eine Zufallszahl von 0 bis i.
- tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp - in diesen Zeilen werden die Elemente von arr[i] und arr[j] vertauscht.
Infolgedessen werden die Elemente des Arrays arr nach dem Zufallsprinzip gemischt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::ArrayShuffle (double &arr []) { int n = ArraySize (arr); for (int i = n - 1; i > 0; i--) { int j = MathRand () % (i + 1); double tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp; } } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Die Originalität des Algorithmus wird durch die durchgeführten Tests bestätigt. Dieser Algorithmus ist einzigartig in seiner Fähigkeit, hervorragende Ergebnisse zu erzielen, wenn die Population reduziert ist. Mit zunehmender Anzahl von Iterationen kann der Algorithmus eine 100%ige Konvergenz bei einzelnen Testfunktionen erreichen, was ihn von anderen Algorithmen unterscheidet, bei denen eine Erhöhung der Anzahl von Durchläufen der Fitnessfunktionen noch keine Konvergenz ermöglicht. Diese Eigenschaft zeichnet sich dadurch aus, dass sie nicht in lokalen „Fallen“ stecken bleiben kann.
Sehen wir uns an, wie sich die Ergebnisse des Algorithmus in Abhängigkeit von der Bevölkerungsgröße verändern. Ich verwende in der Regel einen Durchschnitt von 50 Personen in einer Population. Beim Testen zeigte sich jedoch, dass dieser Algorithmus bereits bei niedrigeren Populationsgrößen annehmbare Ergebnisse liefert.
Bei 10 Individuen in der Population und einer Anzahl von 10.000 Starts der Fitnessfunktion erreicht der Algorithmus ein Ergebnis von 49,97 %.
ACS|Artificial Cooperative Search|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8213829114300768
25 Hilly's; Func runs: 10000; result: 0.5418951009344799
500 Hilly's; Func runs: 10000; result: 0.2811381329747021
=============================
5 Forest's; Func runs: 10000; result: 0.9750514085798038
25 Forest's; Func runs: 10000; result: 0.5078176955906151
500 Forest's; Func runs: 10000; result: 0.20112458337102135
=============================
5 Megacity's; Func runs: 10000; result: 0.736923076923077
25 Megacity's; Func runs: 10000; result: 0.31446153846153846
500 Megacity's; Func runs: 10000; result: 0.11721538461538572
=============================
All score: 4.49701 (49.97%)
Bei 3 Individuen in der Population und einer Anzahl von 10.000 Starts der Fitnessfunktion erreicht der Algorithmus ein Ergebnis von 55,23 %.
ACS|Artificial Cooperative Search|3.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8275253778390631
25 Hilly's; Func runs: 10000; result: 0.6349216357701294
500 Hilly's; Func runs: 10000; result: 0.29382093872076825
=============================
5 Forest's; Func runs: 10000; result: 0.9998874875962974
25 Forest's; Func runs: 10000; result: 0.6985911632646721
500 Forest's; Func runs: 10000; result: 0.2132502183011688
=============================
5 Megacity's; Func runs: 10000; result: 0.7507692307692307
25 Megacity's; Func runs: 10000; result: 0.4270769230769231
500 Megacity's; Func runs: 10000; result: 0.1252615384615397
=============================
All score: 4.97110 (55.23%)
Bei 1 Individuum in der Population und einer Anzahl von 10.000 Starts der Fitnessfunktion erreicht der Algorithmus ein Ergebnis von 58,06 %.
ACS|Artificial Cooperative Search|1.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7554725186591347
25 Hilly's; Func runs: 10000; result: 0.7474431551529281
500 Hilly's; Func runs: 10000; result: 0.3040669213089683
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999993218
25 Forest's; Func runs: 10000; result: 0.888607840003743
500 Forest's; Func runs: 10000; result: 0.2241289484506152
=============================
5 Megacity's; Func runs: 10000; result: 0.6907692307692308
25 Megacity's; Func runs: 10000; result: 0.4818461538461539
500 Megacity's; Func runs: 10000; result: 0.1332153846153859
=============================
All score: 5.22555 (58.06%)
Sie können sich fragen, wie Interaktion in einer Population mit nur einem Individuum stattfindet. Wie Sie sich vielleicht erinnern, verwendet der Algorithmus fünf Populationen, und zwischen den Individuen in diesen Populationen finden Interaktionen statt. Trotz der sehr geringen Anzahl von Individuen bewahrt der Algorithmus die Vielfalt der Populationen und hat keinen „Flaschenhalseffekt“.
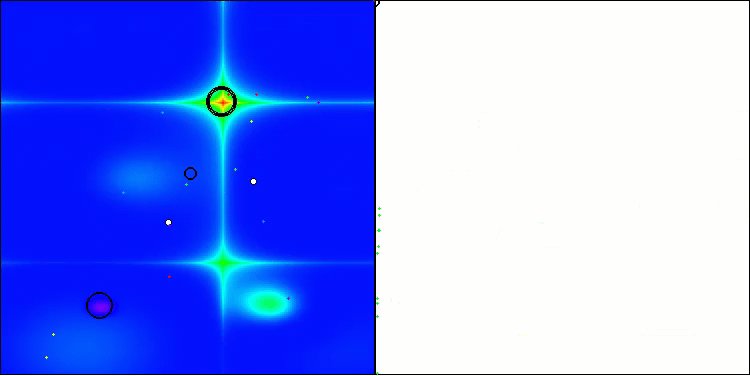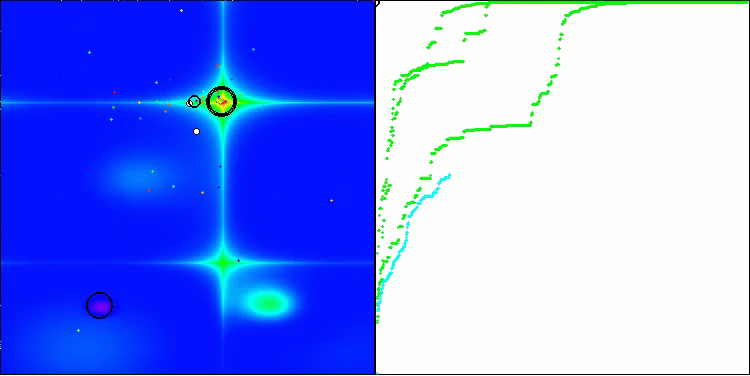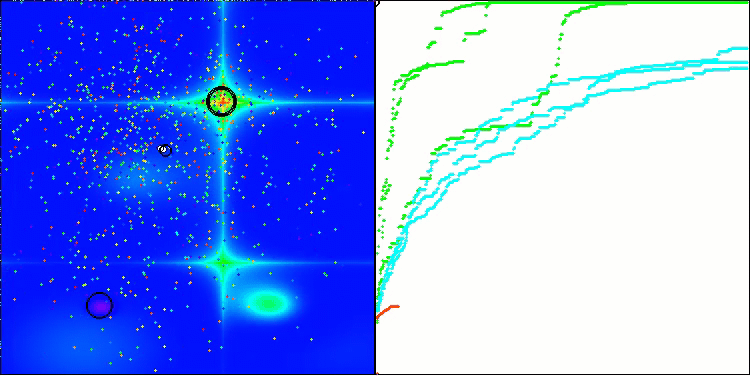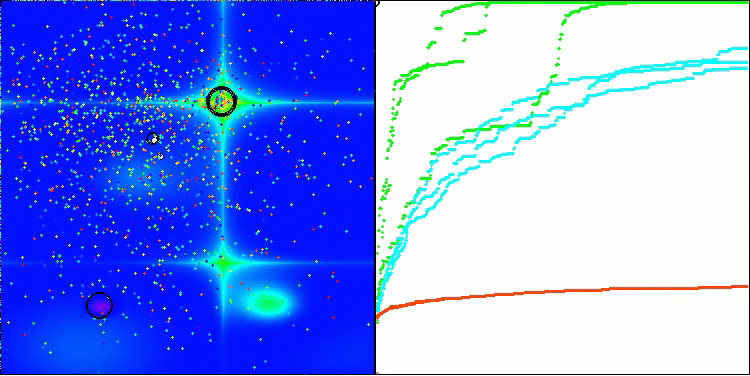
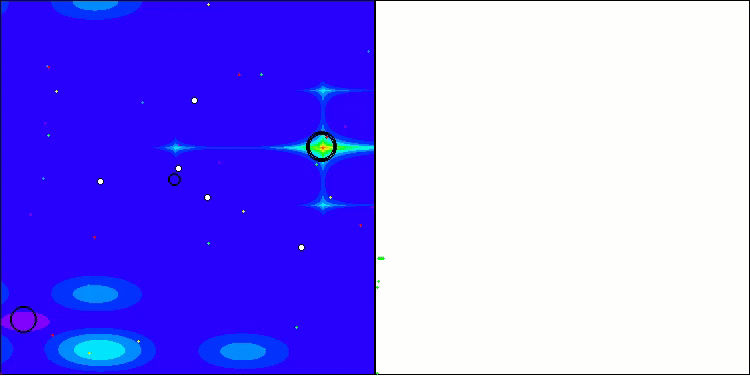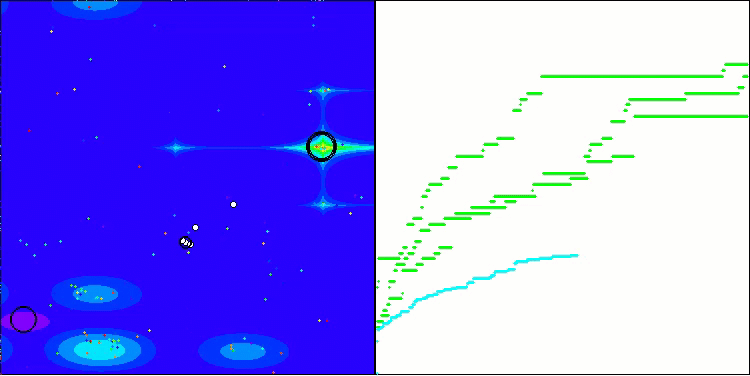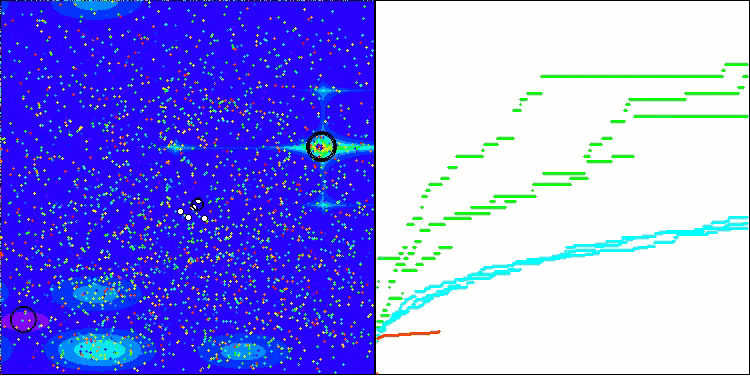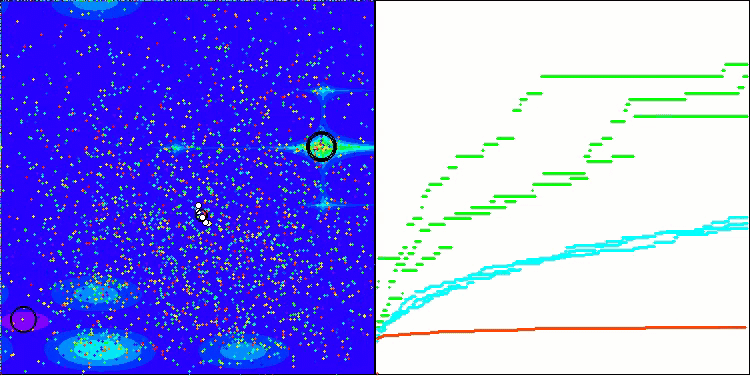
In der Visualisierung ist zu erkennen, dass es keinen Clustereffekt gibt und dass sich die Agenten scheinbar chaotisch verhalten. Agenten betreten Bereiche des Suchraums auch dann, wenn es keine vielversprechenden Richtungen gibt. Dieses Merkmal ist deutlich in den Merkmalen Forest und Megacity zu erkennen, die große, flache Gebiete mit geringen Geländeunterschieden aufweisen.
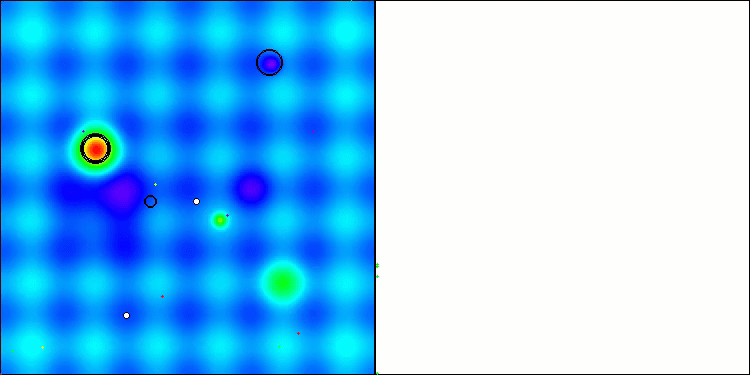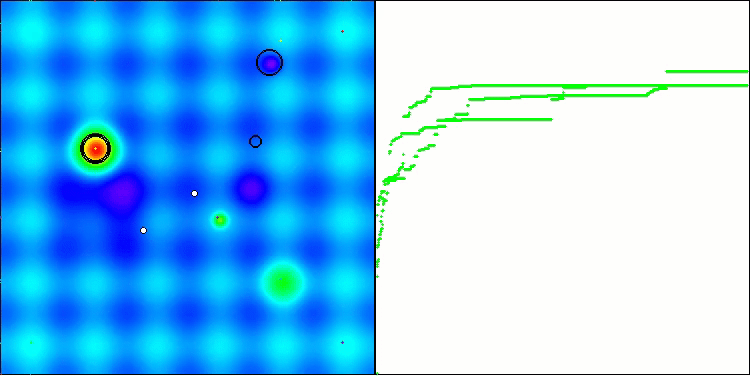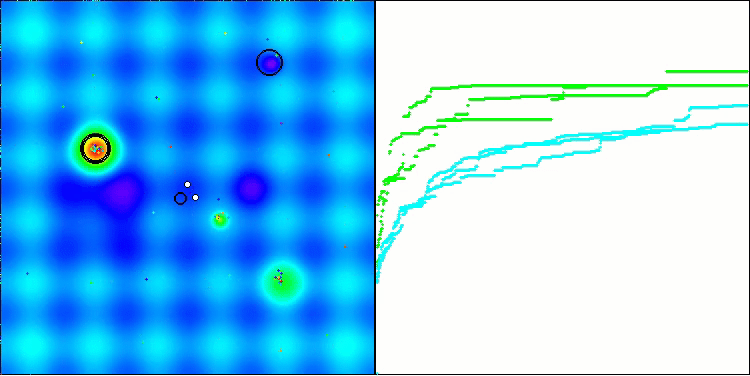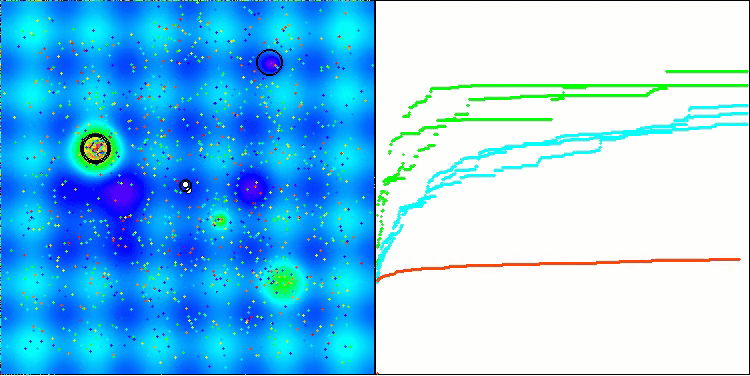
ACS mit der Testfunktion Hilly.
ACS mit der Testfunktion Forest
ACS mit der Testfunktion Megacity
Aufgrund der Testergebnisse belegte der Algorithmus den 8. Platz. ACS zeichnete sich besonders in den Funktionen Forest und Megacity aus.
# | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binärer genetischer Algorithmus | 0.99989 | 0.99518 | 0.42835 | 2.42341 | 0.96153 | 0.96181 | 0.32027 | 2.24360 | 0.91385 | 0.95908 | 0.24220 | 2.11512 | 6.782 | 75.36 |
| 2 | CLA | Zahlenschloss-Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 10 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 11 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 12 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 13 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 14 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 15 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 16 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 17 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 18 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 19 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 20 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 21 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 22 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 23 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 24 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 25 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 26 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 27 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 28 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 29 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 30 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 31 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 32 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 33 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 34 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 35 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 36 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 37 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 38 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 39 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 40 | EM | elektromagnetismusähnlicher Algorithmus | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Zusammenfassung
Der Algorithmus der künstlichen kooperativen Suche (Artificial Cooperative Search, ACS) hat sich als interessanter Optimierungsansatz erwiesen, der sich in der Verwendung mehrerer Populationen von Agenten manifestiert, die miteinander interagieren und so für Vielfalt und Resistenz gegenüber dem Verharren in lokalen Optima sorgen, sowie in der Verwendung spezieller Operatoren, wie dem Mischen der „Beute“ und der Mutation unter Verwendung einer binären Matrix. Letzteres verleiht dem Algorithmus Originalität und die Fähigkeit, mit einer sehr kleinen Populationsgröße (bis zu 1 Individuum in jeder der fünf Populationen) hohe Ergebnisse zu erzielen. Der originelle Ansatz und die Fähigkeit, mit kleinen Populationen zu arbeiten (was die Resistenz gegen die Degeneration der Kolonien unterstreicht), machen ACS zu einem wirklich vielversprechenden Optimierungsalgorithmus.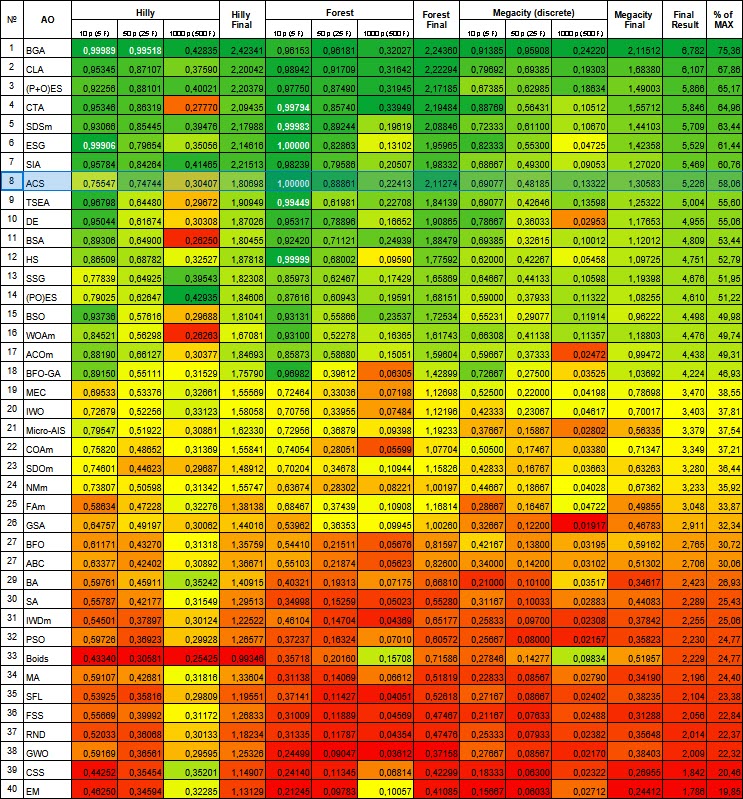 
Abbildung 1. Die farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
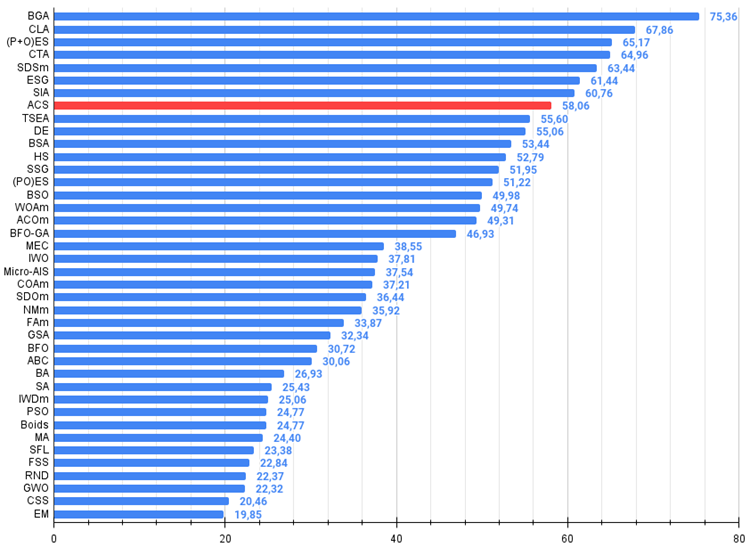
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von ACS:
Vorteile:
- Geringe Anzahl von externen Parametern (nur einer).
- Gute Konvergenz bei verschiedenen Arten von Funktionen.
Nachteile
- Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15004
Beispiel für stochastische Optimierung und optimale Kontrolle
Neuronale Netze leicht gemacht (Teil 90): Frequenzinterpolation von Zeitreihen (FITS)
Erstellen eines Handelsadministrator-Panels in MQL5 (Teil II): Verbesserte Reaktionsfähigkeit und schnelle Nachrichtenübermittlung
Nachrichtenhandel leicht gemacht (Teil 2): Risikomanagement
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.