
Chaos Game Optimization (CGO)
Inhalt
Einführung
Optimierungsalgorithmen spielen eine strategische Rolle bei der Lösung komplexer Probleme nicht nur in verschiedenen Bereichen der modernen Wissenschaft, sondern auch im Handel. Mit der rasanten Entwicklung der Technik werden diese Aufgaben immer komplexer, und die Suche nach der besten Lösung wird immer energieaufwändiger. Daher steigen die Anforderungen an Optimierungsalgorithmen, ihre Effektivität und hohe betriebliche Effizienz. Eine der neuesten und vielversprechendsten Methoden ist der Chaos Game Optimization (CGO) Algorithmus, der von Siamak Talatahari und Mehdi Azizi im Jahr 2020 entwickelt wurde. Dieser Algorithmus basiert auf den Prinzipien der Chaostheorie und verwendet chaotische Sequenzen, um Lösungen zu erzeugen und zu verbessern.
Die Hauptidee des Algorithmus besteht darin, chaotische Sequenzen zu verwenden, um globale Optima in komplexen, mehrdimensionalen Räumen zu finden. Chaotische Sequenzen verfügen über bestimmte Eigenschaften, die es ihnen theoretisch ermöglichen, lokale Fallstricke zu vermeiden und qualitativ hochwertige Lösungen zu finden. In diesem Artikel werden wir die grundlegenden Prinzipien und Stufen des Chaos Game Optimization Algorithmus untersuchen, ihn in Code implementieren, Standardtests mit Testfunktionen durchführen und Schlussfolgerungen über seine Leistung ziehen.
Implementierung des Algorithmus
Stellen Sie sich eine Gruppe von Forschern vor, von denen jeder versucht, ein Extremum in einem mehrdimensionalen Labyrinth zu finden. Zu Beginn der Reise sind die Suchenden wahllos im Labyrinth verstreut und finden ihre erste Zuflucht innerhalb streng definierter räumlicher Grenzen. Dies ist ihr Ausgangspunkt. Jeder Suchende handelt nicht allein – er beobachtet seine Mitmenschen und wählt zu einem bestimmten Zeitpunkt eine zufällige Gruppe von Mitmenschen aus, berechnet den Mittelpunkt ihres Standorts, als ob er einen Gleichgewichtspunkt zwischen ihren Positionen finden würde.
Es ist die kollektive Weisheit, die sich aus der Erfahrung der Gruppe ergibt. Und dann beginnt der wahre Zauber des Chaos. Der Suchende kann einen von vier Wegen für seinen nächsten Schritt wählen. Jeder Pfad ist eine spezielle Bewegungsgleichung, bei der drei Schlüsselpunkte miteinander verwoben sind: die aktuelle Position des Suchenden, der beste von der gesamten Gruppe gefundene Ort und das Zentrum der ausgewählten Untergruppe. Diese Punkte werden gemischt, und die Stärke ihres Einflusses auf die weitere Bewegung wird durch das Verhältnis α – den Leiter des Chaos – bestimmt.
Der Quotient α selbst nimmt verschiedene Inkarnationen an, und jeder Suchende kann, den Regeln folgend, entweder von seiner Position aus losstürmen und zur goldenen Mitte zwischen dem besten Ergebnis und dem Zentrum der Gruppe eilen oder vom besten Punkt aus starten und den Raum um ihn herum erkunden, und er kann auch vom Zentrum der Gruppe losstürmen oder einen völlig zufälligen Sprung ins Ungewisse machen.
Am Ende jeder dieser Aktionen findet ein Vergleich der Ergebnisse statt. Findet einer der Suchenden einen Ort, der besser ist als der bisherige Rekord, wird er zum neuen Leuchtturm für die gesamte Gruppe bei ihrer weiteren Suche.
Das ist die wahre Schönheit des Algorithmus – seine Fähigkeit, Chaos in Ordnung zu verwandeln, Zufälligkeit in zielgerichtete Bewegung, Ungewissheit in Fortschritt, und jeder Schritt, jede Bewegung ist der Suche nach Lösungen zwischen dem Bekannten und dem Unbekannten, zwischen Stabilität und Risiko, zwischen Ordnung und Chaos untergeordnet.
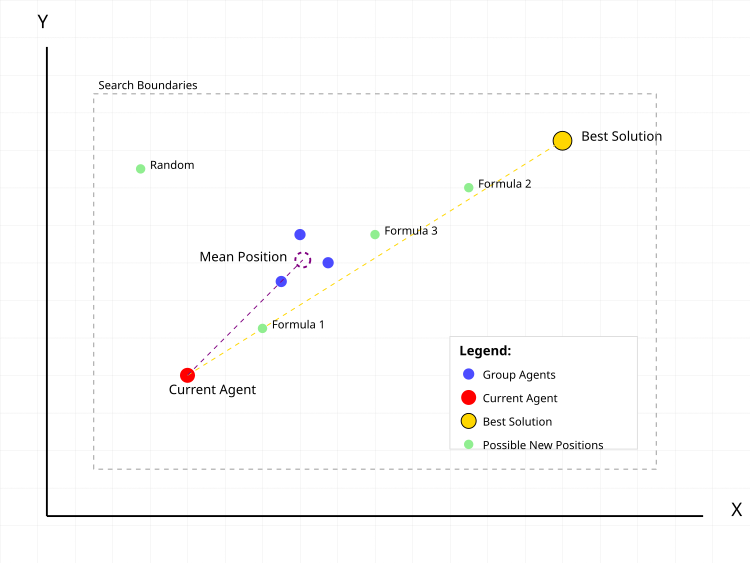
Abbildung 1. Typische Aktionen eines Suchagenten im CGO-Algorithmus
In Abbildung 1 ist der rote Punkt der aktuelle Agent, für den die neue Position berechnet wird. Die blauen Punkte sind eine Gruppe von zufällig ausgewählten Agenten in der Population in einer zufällig ausgewählten Anzahl. Der lila gepunktete Kreis ist die mittlere Position der Gruppe. Der goldene Punkt ist die beste gefundene Lösung. Grüne Punkte sind mögliche neue Positionen des Agenten nach verschiedenen Formeln:- Formel 1: aktuell + α(β×beste - γ×Durchschnitt)
- Formel 2: beste + α(β×Durchschnitt - γ×aktuell)
- Formel 3: Durchschnitt + α(β×beste - γ×aktuell)
- Random: zufällige Position
Die gestrichelten Linien zeigen die Vektoren des Einflusses der besten Lösung und der durchschnittlichen Position der Gruppe auf die Bewegung des aktuellen Agenten. Das grau gestrichelte Rechteck zeigt die Grenzen des Suchgebiets.
Beginnen wir mit dem Schreiben des Pseudocodes für den Algorithmus.
- Populationsgröße festlegen (Standard ist 50 Agenten)
- Definieren der Suchgrenzen für jede Koordinate:
- Mindestwerte (rangeMin)
- Höchstwerte (rangeMax)
- Schrittweite (rangeStep)
- Für jeden Agenten in der Population:
- Erzeuge zufällige Anfangskoordinaten innerhalb der vorgegebenen Grenzen.
- Runde die Koordinaten unter Berücksichtigung der Stufe.
- Berechne die Werte der Zielfunktion.
- Bestimme die beste Ausgangslösung unter allen Agenten.
- Für jeden Agenten in der Population:
- Untergruppengröße = Zufallszahl zwischen 1 und der Grundgesamtheit
- Wähle eine zufällige Auswahl von Agenten in einer Untergruppe.
- für jede Koordinate: average_coordinate = sum_of_group_coordinates / group_size
- α (alpha) = Wählen eine der Methoden nach dem Zufallsprinzip:
- Methode 1: Zufallszahl von 0 bis 1
- Methode 2: 2 × random(0,1) - 1 [Abruf einer Zahl von -1 bis 1]
- Methode 3: Ir × random(0,1) + 1
- Methode 4: Ir × random(0,1) + (1-Ir) mit Ir = zufällig 0 oder 1
- β (beta) = zufällig 1 oder 2
- γ (gamma) = zufällig 1 oder 2
- Formel 1: new_position = aktuell + α(β×beste - γ×Durchschnitt)
- Formel 2: new_position = beste + α(β×Durchschnitt - γ×aktuell)
- Formel 3: new_position = Durchschnitt + α(β×beste - γ×aktuell)
- Formel 4: new_position = zufällige Position innerhalb der Suchgrenzen
- für jede Koordinate:
- Berechne einen neuen Wert anhand der Gleichung
- Prüfe für eine Suche außerhalb der Grenzen
- Passe bei seiner Überschreitung den jew. Grenzwert an den nächstliegenden Grenzwert an.
- Runde den Wert unter Berücksichtigung des Schrittweite.
- Für jeden Agenten:
- wenn der Wert der Zielfunktion des Agenten besser ist als der derzeit beste Wert:
- Aktualisiere den Bestwert.
- Speichere die Koordinaten der neuen besten Lösung.
- wenn der Wert der Zielfunktion des Agenten besser ist als der derzeit beste Wert:
- Wiederhole die Schritte 2-3, bis die Stoppbedingung erfüllt ist:
- Erreichen der maximalen Anzahl von Iterationen
- oder Finden einer Lösung mit der erforderlichen Qualität
- oder eines anderen Haltbarkeitskriteriums
Kommen wir nun zur Implementierung des Algorithmus selbst. Die Klasse C_AO_CGO implementiert den CGO-Algorithmus und ist von der Klasse C_AO abgeleitet, wobei sie die Eigenschaften und Methoden der Basisklasse erbt.
Methoden:
- SetParams () – setzt den Wert popSize basierend auf den Daten des params-Arrays. Dies ist wichtig, um den Algorithmus vor seiner Verwendung abzustimmen.
- Init () – Initialisierungsmethode, die die minimalen und maximalen Werte des Bereichs, die Schrittweite und die Anzahl der Epochen akzeptiert. Er dient dazu, den Algorithmus für den Start vorzubereiten, indem die Suchgrenzen und andere Parameter festgelegt werden.
- Moving () beschreibt die Schritte, die mit der Bewegung von Individuen während der Optimierung verbunden sind. Seine Umsetzung liefert die Logik der alternativen Lösungen und deren Verbesserung.
- Revision () ist für die Überarbeitung der aktuellen Lösungen für die aktuelle Population sowie für die global beste Lösung zuständig.
Private Methoden:
- GetAlpha (), um den Alpha-Parameter zu erhalten, der zur Steuerung der Suchstrategie verwendet wird, sowie seine „Intensität“ und „Vielfalt“.
- GenerateNewSolution () zur Erzeugung einer neuen Lösung auf der Grundlage des Index (seedIndex) und des Gruppenmittelwertes (meanGroup).
class C_AO_CGO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CGO () { } C_AO_CGO () { ao_name = "CGO"; ao_desc = "Chaos Game Optimization"; ao_link = "https://www.mql5.com/en/articles/17047"; popSize = 25; ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); private: //------------------------------------------------------------------- double GetAlpha (); void GenerateNewSolution (int seedIndex, double &meanGroup []); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_CGO ist für die Initialisierung der Parameter des Optimierungsalgorithmus zuständig, bevor dieser gestartet wird. Er nimmt die folgenden Argumente entgegen: Arrays mit den Minimal- und Maximalwerten für jede Suchvariable, die Schrittgröße für jede Variable und die Anzahl der Epochen (Iterationen) des Algorithmus.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CGO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) // number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; return true; } //——————————————————————————————————————————————————————————————————————————————
Die Moving-Methode implementiert die Hauptlogik der Bewegung von Individuen der Lösungspopulation im CGO-Algorithmus. Das Hauptziel dieser Methode ist die Aktualisierung von Entscheidungen in einer Population auf der Grundlage von Regeln, einschließlich der Generierung neuer Entscheidungen und der Mittelung der Ergebnisse. Schauen wir uns die wichtigsten Bestandteile genauer an.
Der erste Teil, die Initialisierung beim ersten Aufruf (wenn „revision“ gleich „false“ ist):
- Die äußere Schleife wird über alle Elemente der Grundgesamtheit (popSize) und für jedes Element (Individuum i) durchlaufen:
- Es wird die innere Schleife durch Koordinaten (coords) gestartet:
- Es wird ein Zufallswert für jede Koordinate mit der Methode u.RNDfromCI (), die einen Zufallswert innerhalb des angegebenen Bereichs liefert.
- Dieser Wert wird dann mit u.SeInDiSp() angepasst, wodurch sichergestellt wird, dass der Wert innerhalb des Bereichs bleibt und auf die nächste Stufe gerundet wird.
- Es wird das Flag „revision“ für den nächsten Methodenaufruf auf „true“ gesetzt und die Methode beendet.
- Für jedes Individuum der Population:
- Erzeuge eine zufällige Gruppengröße randGroupSize von 1 bis popSize.
- Erstelle das Array meanGroup, um den Mittelwert der Koordinaten zu speichern. Die Größe des Arrays entspricht der Anzahl der Koordinaten und wird auf coords gesetzt.
- Fülle das Array randIndices mit zufälligen Indizes (Individuen), die zur Bildung der Gruppe verwendet werden sollen.
- Bei jeder Iteration werden zufällige Indizes zu randIndices hinzugefügt, wobei die Indizes zufällig ausgewählt werden.
- Dann werden für jede Gruppe die Koordinatenwerte für jedes Individuum aus zufällig ausgewählten Indizes summiert und das Ergebnis in meanGroup gespeichert.
- Nach der Summierung wird der Wert in meanGroup durch die Anzahl der Personen in der Gruppe geteilt, um den Mittelwert zu erhalten.
- Erzeugen einer neuen Lösung für „i“ Individuum auf der Grundlage des Gruppenmittelwerts unter Verwendung der Methode GenerateNewSolution().
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { int randGroupSize = u.RNDminusOne (popSize) + 1; double meanGroup []; ArrayResize (meanGroup, coords); ArrayInitialize (meanGroup, 0); int randIndices []; ArrayResize (randIndices, randGroupSize); for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize); for (int j = 0; j < randGroupSize; j++) { for (int c = 0; c < coords; c++) { meanGroup [c] += a [randIndices [j]].c [c]; } } for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize; GenerateNewSolution (i, meanGroup); } } //——————————————————————————————————————————————————————————————————————————————
Bei der Revisionsmethode werden die besten Lösungen in der Population aktualisiert. Es durchläuft alle Individuen in der Population in einer Schleife und prüft für jedes Individuum, ob sein Fitnessfunktionswert „f“ größer ist als der aktuell beste Wert fB. Wenn ja, wird fB mit dem neuen Wert von „f“ aktualisiert und die c-Koordinaten des aktuellen Individuums werden in das Array cB kopiert. So findet und aktualisiert die Revisionsmethode die beste bekannte Lösung in der Population auf der Grundlage der Werte der Fitnessfunktion.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode GetAlpha erzeugt einen zufälligen Alphawert auf der Grundlage zufälliger Auswahlbedingungen und gibt ihn zurück.
- Ir – Zufallswert gleich 0 oder 1.
- Es gibt vier mögliche Fälle (aufgeführt in „Fall“), von denen jeder einen Wert „alpha“ unter Verwendung der entsprechenden Gleichung erzeugt:
- Fall 0: Erzeugt einen Wert zwischen 0 und 1.
- Fall 1: Erzeugt einen Wert von -1 bis 1.
- Fall 2: Erzeugt einen Wert von 1 bis 2 durch Multiplikation mit „Ir“ (0 oder 1).
- Fall 3: Erzeugt einen Wert, der von „Ir“ abhängt und einen Bereich von 0 bis 1 oder 1 hat, je nach dem Wert von „Ir“.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CGO::GetAlpha () { int Ir = u.RNDminusOne (2); switch (u.RNDminusOne (4)) { case 0: return u.RNDfromCI (0, 1); case 1: return 2 * u.RNDfromCI (0, 1) - 1; case 2: return Ir * u.RNDfromCI (0, 1) + 1; case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir); } return 0; } //——————————————————————————————————————————————————————————————————————————————
Die Methode GenerateNewSolution ist für die Generierung einer neuen Lösung für einen bestimmten Agenten in der Population verantwortlich, basierend auf verschiedenen Zufallsparametern.
Initialisierung der Parameter:- alpha ist der Wert, den man durch den Aufruf der Methode GetAlpha () erhält, um die neue Position zu beeinflussen.
- beta und gamma sind Zufallswerte (1 oder 2).
- Formel – eine von vier möglichen Gleichungen wird zufällig ausgewählt, nach der die neue Position berechnet wird.
- newPos – eine Variable zum Speichern der neuen Position unter Verwendung der gewählten Gleichung.
- Das hängt von der Bedeutung des Begriffs „Formel“ ab:
- Fall 0: Eine neue Position wird berechnet als die aktuelle Position des Agenten plus eine Kombination von Koordinaten aus cB (der besten Lösung in der Population) und meanGroup.
- Fall 1: Eine neue Position wird anhand der Koordinate aus cB und dem Mittelwert von meanGroup berechnet.
- Fall 2: Eine neue Position wird durch den Durchschnittswert und die Koordinate des aktuellen Agenten bestimmt.
- Fall 3: Eine neue Position wird zufällig innerhalb des angegebenen Bereichs (rangeMin [c] und rangeMax [c]) festgelegt.
- a [seedIndex].c [c] – die entsprechende Agentenkoordinate wird mit der Methode u.SeInDiSp() aktualisiert, die die Mindest- und Höchstwerte sowie die Schritte berücksichtigt, um sicherzustellen, dass der neue Wert innerhalb der zulässigen Grenzen liegt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Nach der Durchführung von Tests habe ich versucht, die Konvergenz des Algorithmus zu verbessern, und beschlossen, einen Zusatz zur Grundversion des CGO-Algorithmus zu machen. Der Hauptunterschied besteht zu Beginn der Bearbeitung jeder Koordinate, bevor die grundlegenden Bewegungsgleichungen angewendet werden:
double rnd = u.RNDprobab(); // Get a random number from 0.0 to 1.0 rnd *= rnd; // Squate it int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1); // Scale to index a[seedIndex].c [c] = a[ind].c [c]; // Copy the coordinate from another agent with the received index
Die Koordinate wird von einem zufällig ausgewählten Agenten kopiert, und der Agent wird nicht gleichmäßig, sondern mit einer quadratischen Wahrscheinlichkeitsverteilung (rnd *= rnd) ausgewählt. Dies führt zu einer Verzerrung, einem „bias“ bei der Auswahl von Agenten mit kleineren Indizes (bessere Lösungen haben eine höhere Wahrscheinlichkeit, ausgewählt zu werden). Wir quadrieren die Zufallszahl, wodurch eine ungleichmäßige Verteilung entsteht, skalieren sie auf den Bereich der Populationsindizes und kopieren sie dann, bevor wir die grundlegenden Bewegungsgleichungen anwenden. Meine Bemühungen, die Konvergenz in vielversprechenden Bereichen zu beschleunigen, haben leider nicht die erwartete Wirkung gezeigt.
Wahrscheinlich nimmt die Diversität in der Population infolge der vorzeitigen Konvergenz durch den Verstärkungseffekt schnell ab, was bei diesem Algorithmus dazu führt, dass er in einem noch größeren Ausmaß stecken bleibt; es ist möglich, dass die Logik des Algorithmus selbst dies verhindert. Nachstehend finden Sie den Abschnitt des Codes, an dem die Änderungen vorgenommen wurden. Darüber hinaus unternahm ich mehrere weitere Versuche, ihn zu verbessern, doch es wurden keine nennenswerten Fortschritte erzielt, und ich beschloss, bei der ursprünglichen Version des Algorithmus zu bleiben.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double rnd = u.RNDprobab (); rnd *= rnd; int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); a [seedIndex].c [c] = a [ind].c [c]; double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Wie Sie aus den nachstehenden Testergebnissen ersehen können, ist der Gesamtprozentsatz, den der Algorithmus erzielt, recht bescheiden. Wenn Sie jedoch genau hinsehen, können Sie eine interessante Eigenschaft dieses Algorithmus feststellen, die ich im Folgenden beschreiben werde.
CGO|Chaos Game Optimization|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.5725597668122144
25 Hilly's; Func runs: 10000; result: 0.3715760642098293
500 Hilly's; Func runs: 10000; result: 0.32017971142744234
=============================
5 Forest's; Func runs: 10000; result: 0.6117551660766816
25 Forest's; Func runs: 10000; result: 0.619308424855028
500 Forest's; Func runs: 10000; result: 0.6216109945434442
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2192307692307692
500 Megacity's; Func runs: 10000; result: 0.19028461538461647
=============================
All score: 3.90189 (43.35%)
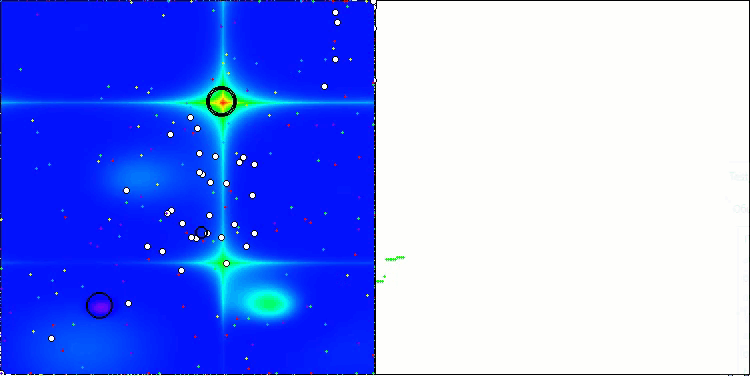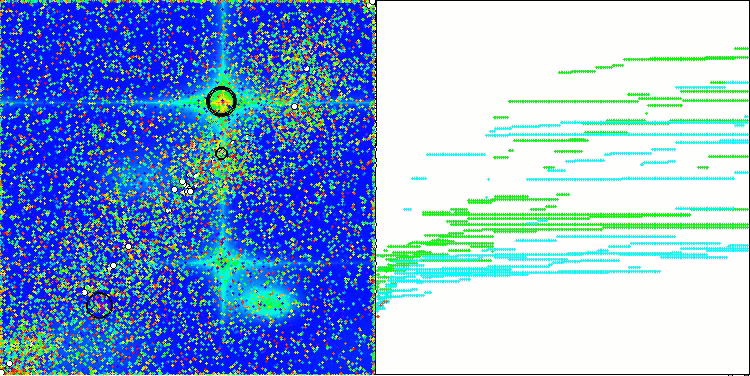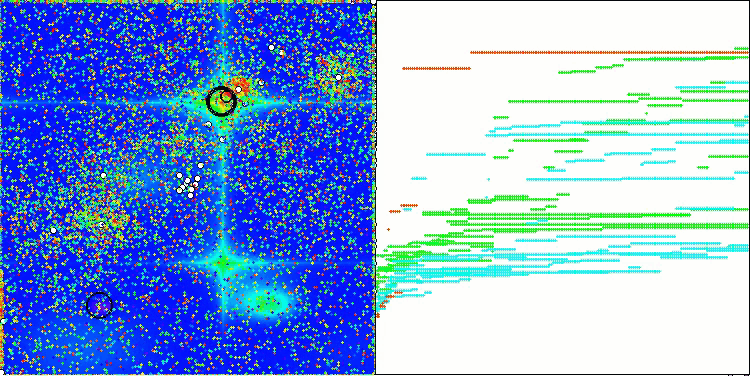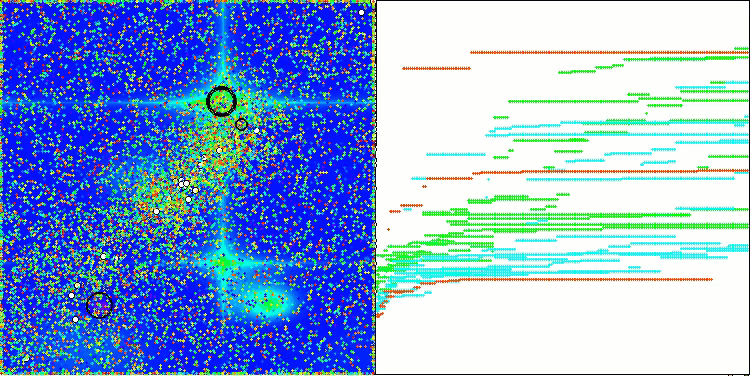
Die Visualisierung der Funktionsweise des Algorithmus auf Testfunktionen zeigt deutlich die Bildung von Strukturen bei der Gruppierung von Agenten, und diese Strukturen sind für verschiedene Aufgaben unterschiedlich. Aber die allgemeine Natur des Algorithmusbetriebs ist die riesige Bandbreite der Optimierungsergebnisse.

CGO mit der Testfunktion Hilly
CGO mit der Testfunktion Forest
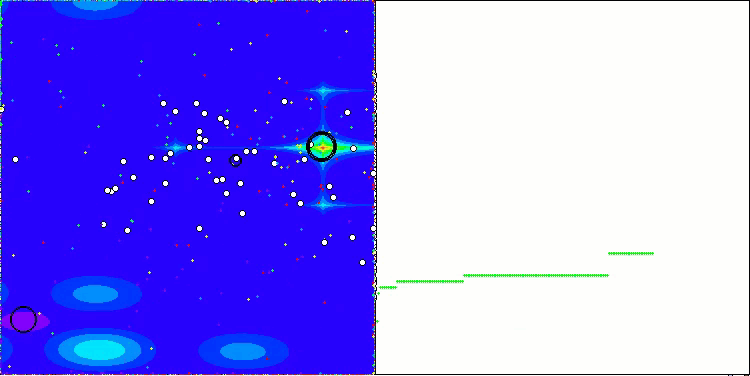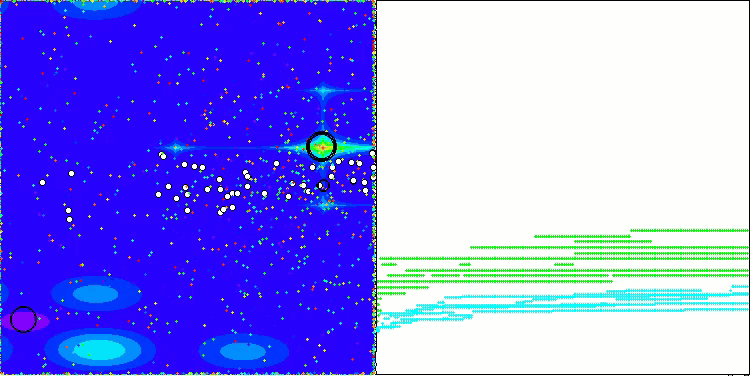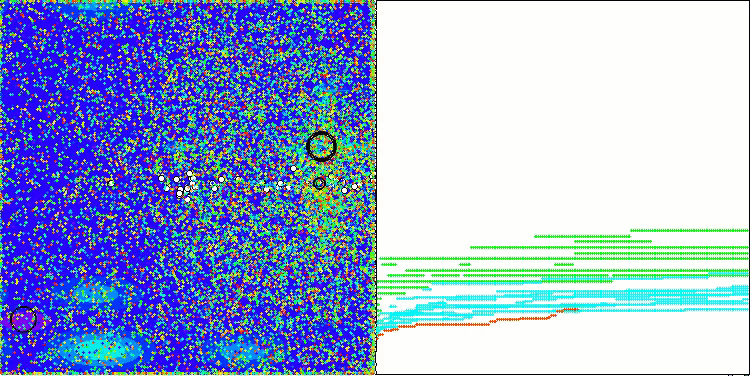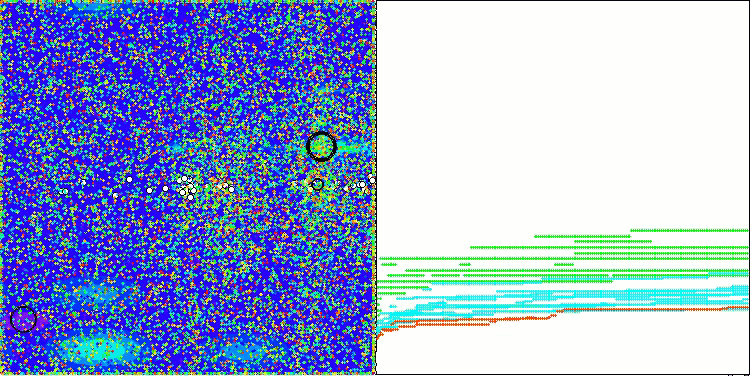
CGO mit der Testfunktion Megacity
Aufgrund der Testergebnisse belegt der CGO-Algorithmus Platz 38 in der Rangliste der populationsbasierten Optimierungsalgorithmen.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 15 | RFO | Optimierung des Royal Flush (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BIO | Optimierung der Blutvererbung (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 21 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 22 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 23 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 24 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 25 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 26 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 27 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 28 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 29 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 30 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 31 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 32 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 33 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 34 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 35 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 36 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 37 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 38 | CGO | Chaos Game Optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 39 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 40 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 41 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 42 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 43 | CSA | Kreis-Such-Algorithmus | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 44 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 45 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Nach der Analyse der Ergebnisse des CGO-Algorithmus bin ich zu einigen wichtigen Schlussfolgerungen gekommen. Der Algorithmus der Chaos Game Optimization zeigt ein sehr interessantes Verhalten. Insgesamt ist seine Effizienz als unterdurchschnittlich einzustufen, was durch das Gesamtergebnis von 43,35 % bestätigt wird. Am bemerkenswertesten ist jedoch sein Verhalten bei der Skalierung des Problems; CGO zeigt gerade bei mehrdimensionalen Problemen – Tests mit einer Dimension von 1000 Variablen – eine hohe Effizienz. Dies ist eine untypische Eigenschaft für die meisten metaheuristischen Algorithmen, die in der Regel unter dem „Fluch der Dimensionen“ leiden und mit zunehmender Anzahl von Variablen an Effizienz verlieren. Im Gegenteil, CGO übertrifft seine Ergebnisse bei 10- und 50-dimensionalen Problemen manchmal sogar, wenn es mit 1000-dimensionalen Problemen arbeitet. Besonders deutlich wird dies bei der Forest-Testfunktion, die ein globales Extremum an einem „scharfen“ Punkt aufweist.
Ich glaube, dass dieses Phänomen auf die Natur des Algorithmus selbst zurückzuführen ist. Die chaotische Natur von CGO und die Vielfalt der Bewegungsgleichungen schaffen einen effizienten Mechanismus zur Erkundung hochdimensionaler Räume. Vier verschiedene Positionsaktualisierungsstrategien, eine zufällige Auswahl zwischen ihnen und ein unvorhersehbares α-Verhältnis ermöglichen es dem Algorithmus, Probleme in komplexen mehrdimensionalen Landschaften zu lösen. Besonders gut schnitt der Algorithmus bei Funktionen vom Typ Forest ab, mit Ergebnissen von 0,61-0,62, die deutlich über seinem Durchschnitt liegen.
Wenn ich den Entwurf des Algorithmus analysiere, sehe ich, dass seine Stärke in hohen Dimensionen mit der koordinatenweisen Verarbeitung zusammenhängt. Anstatt mit dem gesamten Lösungsvektor zu arbeiten, aktualisiert CGO jede Koordinate unabhängig, was bei zunehmender Dimensionalität von Vorteil ist. Darüber hinaus gewährleistet die Verwendung von Zufallsgruppen und deren Durchschnittspositionen einen effizienten Informationsaustausch zwischen den Agenten auch in hochdimensionalen Räumen.
Ich habe versucht, die Oberfläche der Funktion Forrest in verschiedenen Winkeln zu drehen, um sicherzugehen, dass die interessanten Ergebnisse, die ich erhielt, nicht nur auf die spezifischen Merkmale der Algorithmuslogik und der entsprechenden Testfunktion zurückzuführen sind. Dies war notwendig, um die Möglichkeit auszuschließen, versehentlich auf ein globales Extremum zu stoßen. Experimente mit Funktionsrotation haben nur bestätigt, dass solche Ergebnisse nicht zufällig sind. In Anbetracht dieser Besonderheit im Umgang von CGO mit Funktionen mit scharfen Extremen empfehle ich, bei Verwendung dieses Algorithmus mehrere Optimierungsläufe durchzuführen. Diese Empfehlung ist für diesen Algorithmus besonders wichtig.
Insgesamt ist CGO trotz seiner durchschnittlichen Gesamtleistung aufgrund seiner einzigartigen Fähigkeit, die Effizienz bei zunehmender Problemgröße beizubehalten und sogar zu verbessern, ein außerordentlich interessanter Algorithmus für weitere Untersuchungen und Anwendungen auf komplexe Optimierungsprobleme.
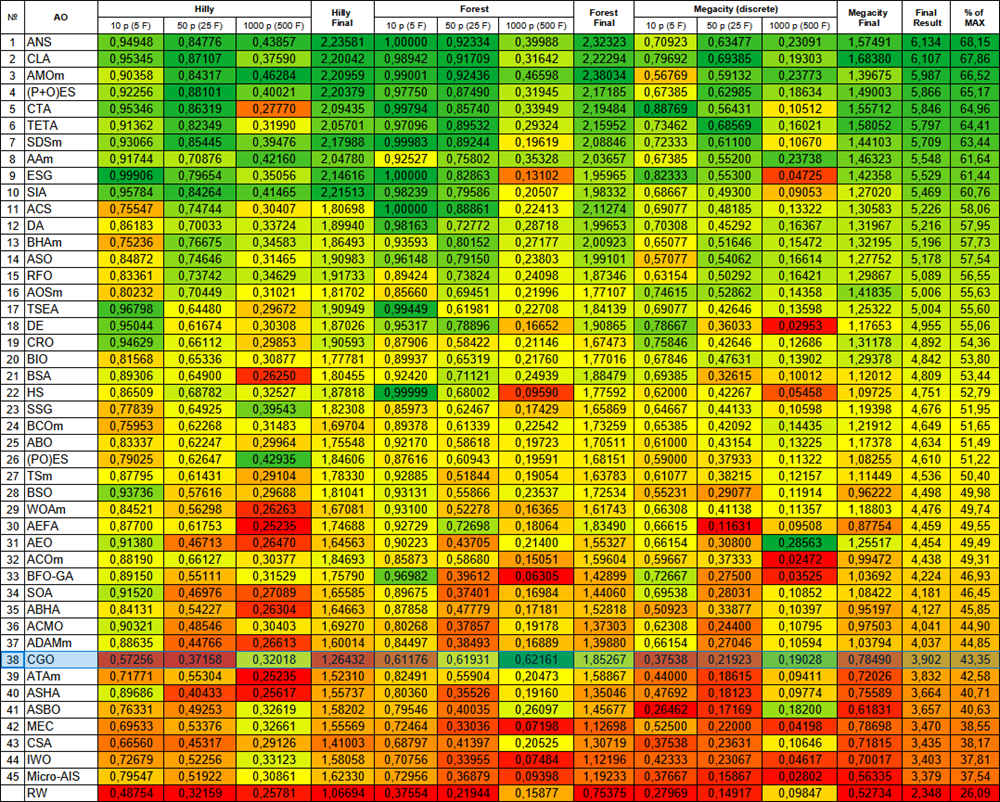
Abbildung 2. Farbabstufung der Algorithmen nach den entsprechenden Tests
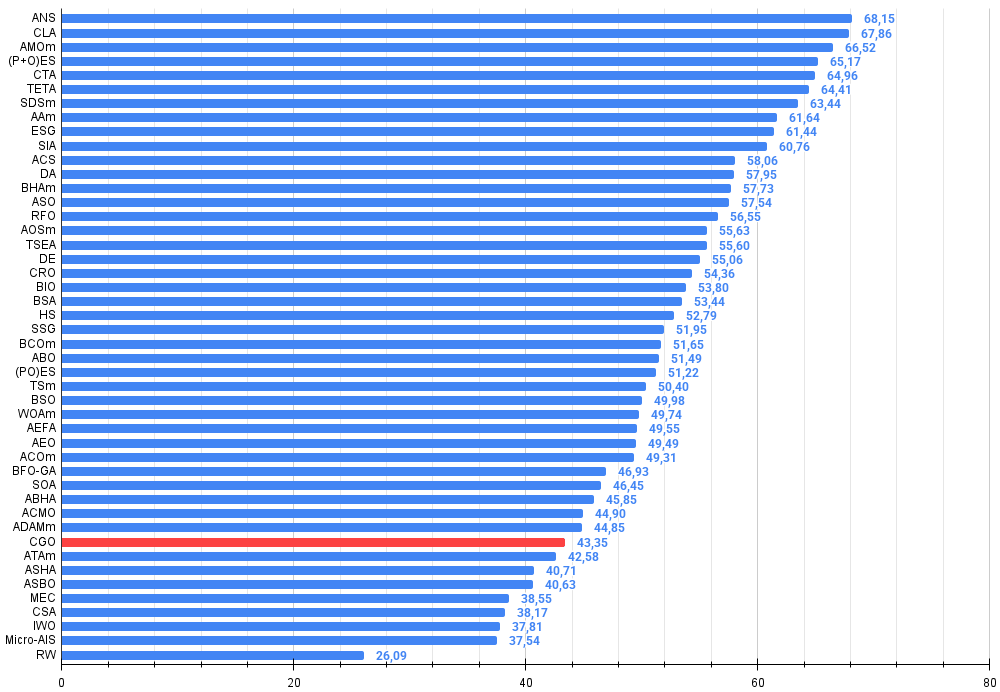
Abbildung 3. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von CGO:
Vorteile:
- Keine externen Parameter
- Gute Konvergenz bei hoch- und mitteldimensionalen Funktionen
Nachteile:
- Bleibt bei niedrigdimensionalen Problemen an lokalen Extremen hängen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Elternklasse der Populationsoptimierung Algorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_CGO.mq5 | Skript | CGO-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17047
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Structs (II)
Von der Grundstufe bis zur Mittelstufe: Structs (II)
 Marktsimulation (Teil 07): Sockets (I)
Marktsimulation (Teil 07): Sockets (I)
 Marktsimulation (Teil 08): Sockets (II)
Marktsimulation (Teil 08): Sockets (II)
 Biologisches Neuron zur Vorhersage von Finanzzeitreihen
Biologisches Neuron zur Vorhersage von Finanzzeitreihen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.