
Population ADAM (Adaptive Moment Estimation)
Inhalt
Einführung
In der Welt des maschinellen Lernens, in der die Daten schnell wachsen und die Algorithmen immer komplexer werden, spielt die Optimierung eine Schlüsselrolle, um gute Ergebnisse zu erzielen. Unter den vielen Methoden, die versuchen, dieses Problem zu lösen, zeichnet sich der ADAM-Algorithmus (Adaptive Moment Estimation) durch seine Eleganz und Effizienz aus.
Im Jahr 2014 schlugen zwei herausragende Köpfe, D. P. Kingma und J. Ba, den ADAM-Algorithmus vor, der die besten Eigenschaften seiner Vorgänger, wie AdaGrad und RMSProp, vereint. Der Algorithmus wurde speziell für die Optimierung der Gewichte von neuronalen Netzen unter Verwendung der Gradienten der Aktivierungsfunktionen der Neuronen entwickelt. Es basiert auf adaptiven Schätzungen des ersten und zweiten Moments und ist daher einfach zu implementieren und sehr recheneffizient. Der Algorithmus benötigt nur minimale Speicherressourcen und ist nicht von der diagonalen Neuskalierung der Gradienten abhängig, was ihn besonders für Probleme mit großen Datenmengen und Parametern geeignet macht.
ADAM funktioniert auch gut bei nicht stationären Zielen und in Situationen, in denen die Gradienten verrauscht oder spärlich sind. Die Hyperparameter des Algorithmus sind einfach zu interpretieren und erfordern in der Regel keine komplexe Abstimmung.
Trotz seiner Effizienz im Bereich der neuronalen Netze ist ADAM jedoch auf die Verwendung von analytischen Gradienten beschränkt, was den Anwendungsbereich einschränkt. In diesem Artikel schlagen wir einen innovativen Ansatz zur Modifizierung des ADAM-Algorithmus vor, indem wir ihn in einen populationsbasierten Optimierungsalgorithmus umwandeln, der mit numerischen Gradienten umgehen kann. Diese Modifikation erweitert nicht nur den Anwendungsbereich von ADAM über neuronale Netze hinaus, sondern eröffnet auch neue Möglichkeiten zur Lösung eines breiten Spektrums von Optimierungsproblemen im Allgemeinen.
Unsere Forschung zielt darauf ab, einen Allzweckoptimierer zu entwickeln, der die Vorteile des ursprünglichen ADAM beibehält, aber auch in Umgebungen effektiv arbeiten kann, in denen keine analytischen Gradienten verfügbar sind. Dadurch kann das modifizierte ADAM in Bereichen wie der globalen Optimierung und der Mehrzieloptimierung eingesetzt werden, was sein Potenzial und seinen praktischen Wert erheblich erweitert.
Implementierung des Algorithmus
Der ADAM-Algorithmus wird häufig als stochastische gradientenbasierte Optimierungsmethode eingestuft. Es ist jedoch wichtig zu beachten, dass ADAM selbst keine internen stochastischen Elemente in seiner Kernlogik enthält. Die mit ADAM verbundene Stochastik entsteht durch die Art und Weise, wie die Daten aufbereitet und in den Algorithmus eingespeist werden, und nicht durch dessen interne Mechanik. Es ist wichtig, zwischen der Stochastik bei der Datenaufbereitung und dem Determinismus des Optimierungsalgorithmus selbst zu unterscheiden.
Der ADAM-Algorithmus selbst ist vollständig deterministisch. Bei gleichen Eingabedaten und Ausgangsbedingungen führt sie immer zu den gleichen Ergebnissen. Die Parameter in ADAM werden auf der Grundlage klar definierter Gleichungen aktualisiert, die keine Zufallselemente enthalten.
Diese Unterscheidung zwischen der deterministischen Natur des ADAM-Algorithmus und der stochastischen Natur der Datenaufbereitung ist wichtig für das richtige Verständnis seiner Funktionsweise und seines Änderungspotenzials. Die Anerkennung dieser Tatsache eröffnet Möglichkeiten, ADAM an Probleme anzupassen, bei denen eine stochastische Datenaufbereitung nicht anwendbar oder wünschenswert ist, wobei die leistungsstarken Optimierungseigenschaften erhalten bleiben.
Schauen wir uns den Pseudocode mit den Gleichungen an:
1. Initialisierung:
m₀ = 0 (Initialisierung des ersten Moments)
v₀ = 0 (Initialisierung des zweiten Moments)
t = 0 („step“-Zähler)
2. Bei jedem „step“ t:
t = t + 1
gₜ = ∇ₜf(θₜ₋₁) (Berechnung des Gradienten)
3. Aktualisierung der ersten und zweiten angepassten Momente:
mₜ = β₁ · mₜ₋₁ + (1 - β₁) · gₜ
vₜ = β₂ · vₜ₋₁ + (1 - β₂) · gₜ²
m̂ₜ = mₜ / (1 - β₁ᵗ)
v̂ₜ = vₜ / (1 - β₂ᵗ)
4. Aktualisierung der Parameter:
θₜ = θₜ₋₁ - α · m̂ₜ / (√v̂ₜ + ε)
wobei:
θₜ - Modellparameter bei „step“ t
f(θ) - Zielfunktion
α - Lernrate (normalerweise α = 0,001)
β₁, β₂ - Dämpfungsverhältnisse für die Momente (normalerweise β₁ = 0,9, β₂ = 0,999)
ε - kleine Konstante, um eine Division durch Null zu verhindern (normalerweise 10⁻⁸)
mₜ, vₜ - Schätzungen des ersten und zweiten Moments des Gradienten
m̂ₜ, v̂ₜ - bereinigte Momentschätzungen
Diese Gleichungen erfassen das Wesen des ADAM-Algorithmus und zeigen, wie er die Lernrate für jeden Parameter auf der Grundlage von Schätzungen der ersten und zweiten Momente der Gradienten adaptiv anpasst. Wie wir sehen können, gibt es überhaupt keine Stochastik in dem Algorithmus. In der Regel ist der ADAM-Algorithmus in seinen zahlreichen Software-Implementierungen fest mit der Architektur neuronaler Netze verwoben. In diesem Artikel werden wir jedoch ein wenig zaubern: Wir werden sie nicht nur zu einer unabhängigen und autarken Einheit machen, sondern sie auch in eine Population und eine wirklich stochastische Methode verwandeln.
Zunächst muss ADAM in einem Populationsformat implementiert werden, wobei die ursprünglichen Gleichungen beibehalten werden, während ein Zufallselement nur in der Phase der anfänglichen Initialisierung der zu optimierenden Parameter hinzugefügt wird. Aber das ist erst der Anfang! Wir werden dann Zufälligkeit in die Dynamik des Verhaltens dieser Gradientenmethode einführen und sehen, zu welchen Ergebnissen dies führen kann.
Definieren wir die Struktur S_Gradients, die Gradienten und zwei Momentvektoren (den ersten und den zweiten) speichern wird. Die Methode Init(int coords) legt die Größe der Arrays fest und initialisiert sie auf Null.
//—————————————————————————————————————————————————————————————————————————————— // Structure for storing gradients and moments struct S_Gradients { double g []; // Gradients double m []; // Vectors of the first moment double v []; // Vectors of the second moment // Method for initializing gradients void Init (int coords) { ArrayResize (g, coords); ArrayResize (m, coords); ArrayResize (v, coords); ArrayInitialize (g, 0.0); // Initialize gradients to zeros ArrayInitialize (m, 0.0); // Initialize the first moment with zeros ArrayInitialize (v, 0.0); // Initialize the second moment with zeros } }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_AO_ADAM implementiert den ADAM-Optimierungsalgorithmus. Hauptfunktionen der Klasse:
- Der Konstruktor initialisiert Algorithmusparameter wie Populationsgröße, Lern- und Abklingraten.
- SetParams() setzt die Werte der Parameter aus dem Array params, sodass sie nach der Initialisierung geändert werden können.
- Init() bereitet den Algorithmus auf die Arbeit vor, indem es Parameterbereiche und die Anzahl der Epochen annimmt.
- Moving() und Revision() dienen der Durchführung von Optimierungsschritten, der Aktualisierung von Modellparametern und der Überprüfung des Zustands des Algorithmus.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAM : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAM () { } // Class constructor C_AO_ADAM () { ao_name = "ADAM"; // Algorithm name ao_desc = "Adaptive Moment Estimation"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 50; // Population size alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 1e-8; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha"; params [1].val = alpha; params [2].name = "beta1"; params [2].val = beta1; params [3].name = "beta2"; params [3].val = beta2; params [4].name = "epsilon"; params [4].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size alpha = params [1].val; // Set the learning ratio beta1 = params [2].val; // Set beta1 beta2 = params [3].val; // Set beta2 epsilon = params [4].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_ADAM führt die Initialisierung des Algorithmus durch:
- Sie ruft StandardInit() auf, um die Standardparametereinstellungen zu erhalten. Ist dies fehlgeschlagen, wird false zurückgegeben.
- Sie setzt step und den Iterationszähler t zurück.
- Sie ändert die Größe des Gradienten-Arrays grad entsprechend der Populationsgröße popSize.
- Sie initialisiert die Gradienten für jedes Individuum in der Population anhand der Koordinaten.
Wenn alle Operationen erfolgreich waren, gibt die Methode true zurück.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_ADAM implementiert den Optimierungsschritte im ADAM-Algorithmus:
1. „step“ prüfen, wenn „step“ kleiner als 2 ist:
- Der vorherige Wert der Funktion und der Koordinaten wird für jedes Individuum der Population gespeichert.
- Neue Zufallskoordinaten werden innerhalb des angegebenen Bereichs erzeugt und auf akzeptable Werte eingestellt.
- Der „step“-Zähler wird inkrementiert und die Methode wird beendet.
2. Berechnung der Gradienten: Wenn step 2 oder mehr beträgt, wird die Veränderung des Wertes der Zielfunktion und der Koordinaten für jedes Individuum berechnet.
- Um eine Division durch Null zu verhindern, wird ein kleiner Wert Epsilon hinzugefügt. Darüber hinaus ist dieser Wert ein externer Parameter des Algorithmus, der die Sucheigenschaften beeinflusst.
- Die Steigung wird für jeden Parameter berechnet.
3. Aktualisierung der Parameter für jede Person:
- Frühere Werte der Funktion und der Koordinaten werden beibehalten.
- Die verzerrten Schätzungen der ersten und zweiten Momente des Gradienten werden aktualisiert.
- Es werden bereinigte Momentschätzungen berechnet und die Koordinaten mit Hilfe der ADAM-Gleichung aktualisiert.
- Die Koordinaten werden angepasst, um sicherzustellen, dass sie innerhalb akzeptabler Grenzen bleiben.
4. Der Iterationszähler t wird inkrementiert.
Die Methode ist also dafür verantwortlich, die Positionen der Individuen während der Optimierung mit Hilfe von adaptiven Gradientenmomenten zu aktualisieren. Die ersten beiden Schritte des Algorithmus sind notwendig, um den Gradienten der Veränderung des Werts der Fitnessfunktion zu berechnen, da der Gradient numerisch berechnet wird, ohne die analytische Gleichung des zu lösenden Optimierungsproblems zu kennen. Für die Berechnung sind mindestens zwei Punkte erforderlich, und die in den beiden vorangegangenen Schritten erhaltenen Lösungen können in den nachfolgenden Schritten verwendet werden.
Die Logik des ADAM-Algorithmus legt keine bestimmte Methode zur Berechnung des Gradienten nahe. Der Gradient kann entweder analytisch oder numerisch berechnet werden, und seine Berechnung erfolgt außerhalb des Algorithmus selbst. Die Abstraktion des Algorithmus von der Art und Weise, wie er verwendet wird, ist sehr wichtig, um die Rolle der einzelnen Komponenten im Gesamtprojekt des maschinellen Lernens zu verstehen. Dies ermöglicht eine bessere Bewertung der Auswirkungen der einzelnen Elemente auf das Endergebnis und erleichtert die Anpassung des Algorithmus an verschiedene Aufgaben.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision der Klasse C_AO_ADAM führt die folgenden Aktionen durch:
- Sie initialisiert den Index des besten Individuums ind mit -1.
- Sie durchläuft alle Individuen in der Population, und wenn der Wert der Funktion des aktuellen Individuums größer ist als der beste gefundene Wert fB, aktualisiert sie die beste globale Lösung und speichert den Index des besten Individuums.
- Wenn ein bestes Individuum gefunden wurde, kopiert es seine Koordinaten in das Array cB.
So findet und speichert die Methode die Koordinaten des besten Individuums auf der Grundlage der Werte der Fitnessfunktion.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual } //——————————————————————————————————————————————————————————————————————————————
Wie wir sehen können, ist der ADAM-Algorithmus nun populationsbasiert, und wenn wir den Parameter für die externe Populationsgröße auf 1 setzen, verhält sich der Algorithmus vollständig wie ein regulärer ADAM-Algorithmus ohne Population. Jetzt können wir den Algorithmus an unseren Testfunktionen testen. Schauen wir uns die Ergebnisse an:
ADAM|Adaptive Moment Estimation|50.0|0.001|0.9|0.999|0.00000001|
=============================
5 Hilly's; Func runs: 10000; result: 0.3857584301959297
25 Hilly's; Func runs: 10000; result: 0.29733109680042824
500 Hilly's; Func runs: 10000; result: 0.25390478702062613
=============================
5 Forest's; Func runs: 10000; result: 0.30772687797850234
25 Forest's; Func runs: 10000; result: 0.1982664040653052
500 Forest's; Func runs: 10000; result: 0.15554626746207786
=============================
5 Megacity's; Func runs: 10000; result: 0.18153846153846154
25 Megacity's; Func runs: 10000; result: 0.12430769230769231
500 Megacity's; Func runs: 10000; result: 0.09503076923077
=============================
All score: 1.99941 (22.22%)
Die Ergebnisse sind leider nicht die besten, aber das eröffnet Möglichkeiten für potenzielles Wachstum und gibt uns Raum für Verbesserungen, insbesondere für die Einführung einer echten stochastischen Komponente in den Algorithmus.
In der obigen Implementierung des ADAM-Populationsalgorithmus stellt jeder Agent einen separaten „Thread“ der Ausführung der ursprünglichen Logik der Autoren dar, wie Schlangen, die über die Hügel des Suchraums kriechen und aufgrund der anfänglichen zufälligen Initialisierung über das Feld verteilt sind. Diese Schlangen interagieren nicht miteinander und tauschen keine Informationen über die besten Lösungen aus. Da es sich um einen gradientenbasierten Algorithmus handelt, ist es wichtig, dass er die Änderungen des Oberflächenniveaus an möglichst nahe beieinander liegenden Punkten berücksichtigt. Wird der numerische Differenzierungsschritt verkleinert, kann es zu einer langsamen Konvergenz kommen, während eine Vergrößerung des Schritts zu großen Sprüngen im Raum führt, was es schwierig macht, Informationen über die Oberfläche zwischen den Punkten zu erhalten.
Um diese Probleme zu lösen, werden wir einen Teil der Population zu hybriden Individuen machen, die aus Elementen der Entscheidungen anderer Agenten bestehen werden. Die Idee ist folgende: Wir sortieren die Population nach der Fitness der Individuen, und am Ende der Liste (wo sich die schwächsten Individuen befinden) schaffen wir Hybride. Für solche Individuen werden Lösungen generiert, indem ein neuer Punkt im Raum gebildet wird, der auf Elementen der Lösungen von besser angepassten Individuen basiert. Je höher die Fitness eines Individuums ist, desto größer ist die Wahrscheinlichkeit, dass es Informationen über seine Position an Hybriden weitergibt.
Ein Teil der Individuen in der Population stellt also Lösungen nach der ursprünglichen Logik des Algorithmus dar, der andere Teil sind so genannte Hybride, die eine Kombination von Elementen der Lösungen aus der Population sind. Die entstehende Hybride wird nicht einfach aus Teilen anderer Individuen kopiert; jeder dieser Teile variiert gemäß einer Wahrscheinlichkeitsverteilung nach dem Potenzgesetz. Wir nennen den Grad dieses Gesetzes „Hybridstabilität“: Je höher der Grad, desto weniger verändert sich der Hybrid und desto mehr ähnelt er den Elementen der besten Lösungen in der Population.
Kommen wir nun zu der aktualisierten Version des Algorithmus. Bei der Klasse C_AO_ADAMm wurden mehrere Änderungen an der Klasse C_AO_ADAM vorgenommen, die sich theoretisch positiv auf deren Funktionalität und Verhalten auswirken können. Hier sind die wichtigsten Änderungen:
1. Neue Parameter:
- hybridsPercentage - bestimmt den Prozentsatz der Hybriden in der Population.
- hybridsResistance - regelt die Widerstandsfähigkeit von Hybriden gegen Veränderungen.
2. Im Konstruktor der Klasse C_AO_ADAMm werden die neuen Parameter hybridsPercentage und hybridsResistance initialisiert. Ihre Werte werden dem Array params hinzugefügt.
3. SetParams enthält Zeichenketten für die Einstellung neuer Parameter hybridsPercentage und hybridsResistance, die es uns ermöglichen, ihre Werte dynamisch zu ändern.
Wird der Parameter für den Hybridanteil auf „1“ gesetzt, wird die ADAM-Logik effektiv deaktiviert. Wird dieser Wert auf „0“ gesetzt, so hat der Algorithmus keine kombinatorischen Eigenschaften. So habe ich nach einigen Versuchen den optimalen Wert „0,5“ gefunden, der sich als der beste herausstellte.
Der zweite Parameter ist für die Widerstandsfähigkeit von Hybriden gegenüber Veränderungen verantwortlich. Wenn niedrige Werte eingestellt werden, verändern sich die Hybriden nach der Vererbung von Merkmalen erheblich und können den gesamten Bereich der akzeptablen Werte der optimierten Parameter abdecken. Gleichzeitig tendiert die Variabilität von Hybriden bei zu hohen Werten, z. B. „20“ oder mehr, gegen „0“, und sie werden nur zu Trägern der besten Eigenschaften der Elterntiere. Auch für diesen Parameter wurde versuchsweise der optimale Wert von „10“ ermittelt.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAMm : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAMm () { } // Class constructor C_AO_ADAMm () { ao_name = "ADAMm"; // Algorithm name ao_desc = "Adaptive Moment Estimation M"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 100; // Population size hybridsPercentage = 0.5; // Percentage of hybrids in the population hybridsResistance = 10; // Resistance of hybrids to changes alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 0.1; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "hybridsPercentage"; params [1].val = hybridsPercentage; params [2].name = "hybridsResistance"; params [2].val = hybridsResistance; params [3].name = "alpha"; params [3].val = alpha; params [4].name = "beta1"; params [4].val = beta1; params [5].name = "beta2"; params [5].val = beta2; params [6].name = "epsilon"; params [6].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size hybridsPercentage = params [1].val; // Set the percentage of hybrids in the population hybridsResistance = params [2].val; // Set hybrids' resistance to change alpha = params [3].val; // Set the learning ratio beta1 = params [4].val; // Set beta1 beta2 = params [5].val; // Set beta2 epsilon = params [6].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double hybridsPercentage; // Percentage of hybrids in the population double hybridsResistance; // Resistance of hybrids to changes double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter int hybridsNumber; // Number of hybrids in the population }; //——————————————————————————————————————————————————————————————————————————————
In der Methode Init der Klasse C_AO_ADAMm gibt es folgende Änderungen im Vergleich zu der ähnlichen Methode in der vorherigen Klasse:
- Die Anzahl der Hybriden in einer Population wird auf der Grundlage des prozentualen Anteils hybridsPercentage berechnet. Dieser neue Wert von hybridsNumber wird verwendet, um die Zusammensetzung der Population zu kontrollieren.
- Es wurde eine Prüfung hinzugefügt, die sicherstellt, dass die Anzahl der Hybriden nicht größer als popSize ist. Dies verhindert Fehler im Zusammenhang mit einem Array-Überlauf.
Diese Änderungen machen Init anpassungsfähiger an die hybriden Merkmale des Algorithmus und gewährleisten eine korrekte Verwaltung des Zustands und der Initialisierung der Individuen in der Population.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAMm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter hybridsNumber = int(popSize * hybridsPercentage); // Calculation of the number of hybrids in the population if (hybridsNumber > popSize) hybridsNumber = popSize; // Correction ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
Auch bei der Methode „Moving“ gibt es einige Änderungen im Vergleich zur vorherigen Version dieser Methode.
Aktualisierung der Parameter mit Hilfe des ADAM-Algorithmus. Die Bedingungen für die Behandlung von Hybriden wurden diesem Block hinzugefügt. Wenn der individuelle Index i größer oder gleich popSize - hybridsNumber ist, werden neue Koordinaten unter Verwendung einer Zufallsverteilung und des Parameters hybridsResistance erzeugt. Dadurch können Hybriden kleine Abweichungen in den vererbten Merkmalen von ihren Eltern aufweisen (eine Art Analogie zur Merkmalsmutation). Andernfalls werden für Individuen, die keine Hybride sind, die verzerrten Schätzungen des ersten und zweiten Moments aktualisiert und dann die bereinigten Schätzungen berechnet.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates double cNew; for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; if (i >= popSize - hybridsNumber) { double pr = u.RNDprobab (); pr *= pr; int ind = (int)u.Scale (pr, 0, 1, 0, popSize - 1); cNew = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], hybridsResistance); } else { // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates //a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); cNew = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); } // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (cNew, rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision weist im Vergleich zur vorherigen Version dieser Methode folgende Änderungen auf.
Vorbereitung eines Arrays für die Sortierung: Erstellen des temporären Arrays aT in der Größe der Population und dann der Aufruf der Sortiermethode u.Sorting(). Ein sortiertes Populations-Array ermöglicht die Vererbung von Merkmalen durch Hybriden mit einer höheren Wahrscheinlichkeit von besser angepassten Individuen. Die temporäre Populationsgruppe hätte in die Klassenfelder verschoben werden können, aber in diesem Fall wurde dies aus Gründen der Übersichtlichkeit getan.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual //---------------------------------------------------------------------------- S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Betrachten wir nun die Ergebnisse der modifizierten Version der wirklich stochastischen Population ADAMm:
ADAMm|Adaptive Moment-Schätzung M|100.0|0.5|10.0|0.001|0.9|0.999|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8863499654810468
25 Hilly's; Func runs: 10000; result: 0.4476644542595641
500 Hilly's; Func runs: 10000; result: 0.2661291031673467
=============================
5 Forest's; Func runs: 10000; result: 0.8449728914068644
25 Forest's; Func runs: 10000; result: 0.3849320103361983
500 Forest's; Func runs: 10000; result: 0.16889385703816007
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.2704615384615384
500 Megacity's; Func runs: 10000; result: 0.10593846153846247
=============================
All score: 4.03688 (44.85%)
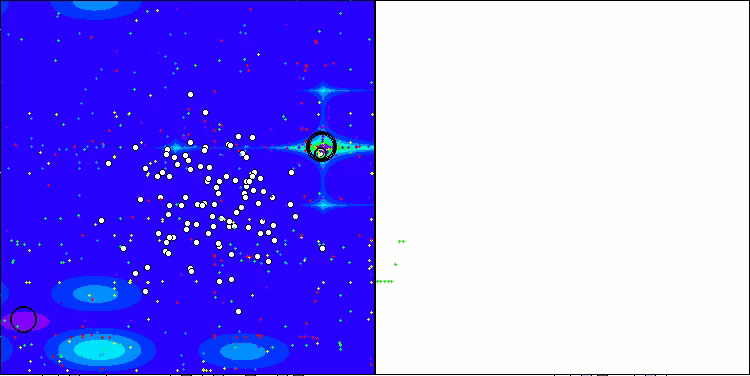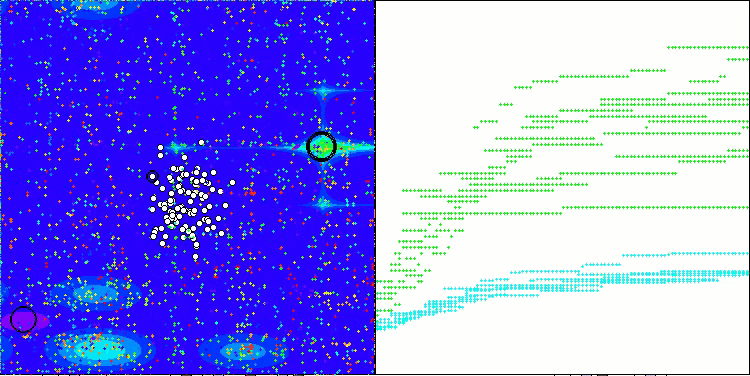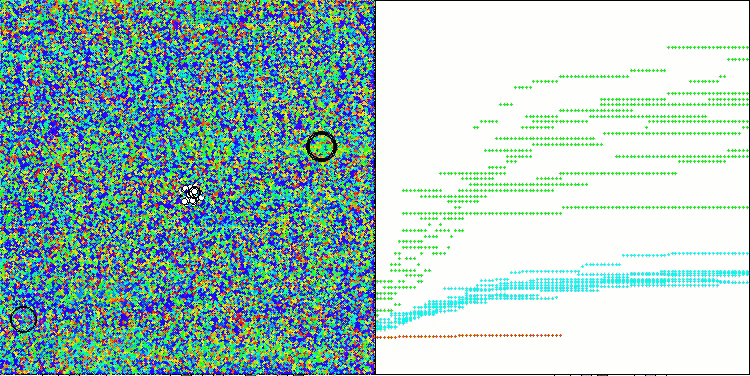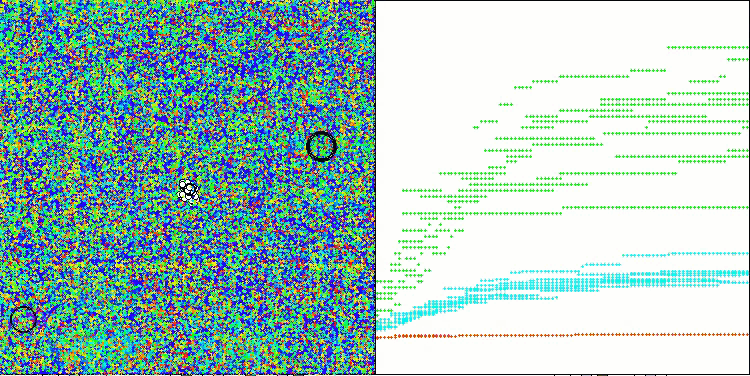
Die erzielten Ergebnisse haben sich deutlich verbessert. Unten sehen Sie eine Visualisierung eines einfachen ADAM-Populationsalgorithmus, die die eigentümliche Bewegung einzelner „Schlangen“ zeigt, die in alle Richtungen kriechen, während sie den Suchraum erkunden. Es werden auch Visualisierungen der stochastischen Population ADAMm vorgestellt, die eine aktivere Bewegung der Suchagenten in Richtung des globalen Optimums zeigen, aber in diesem Fall geht das charakteristische „Schlangen“-Aussehen verloren.
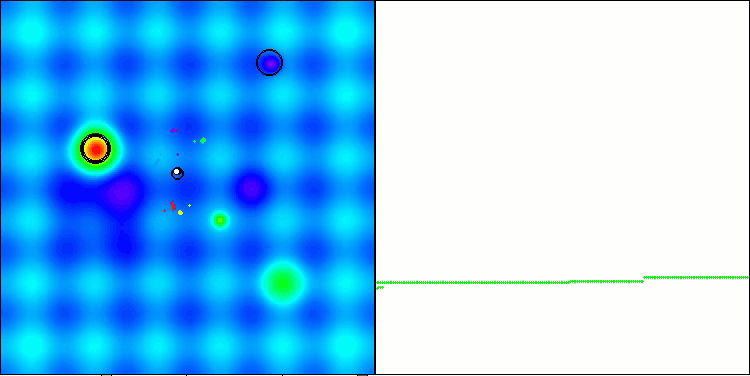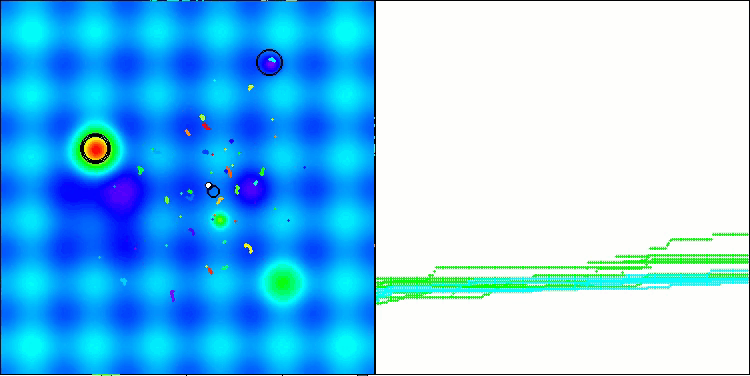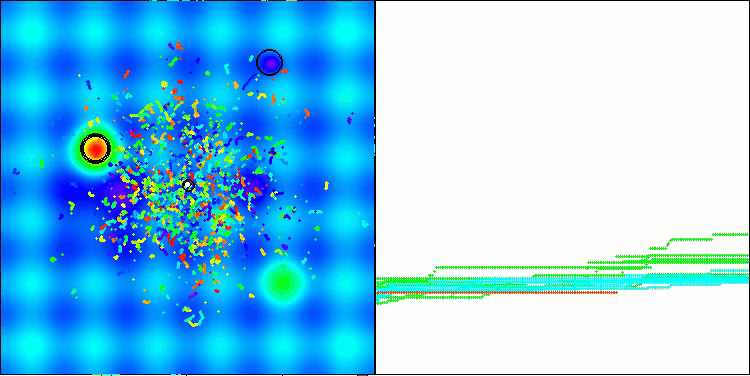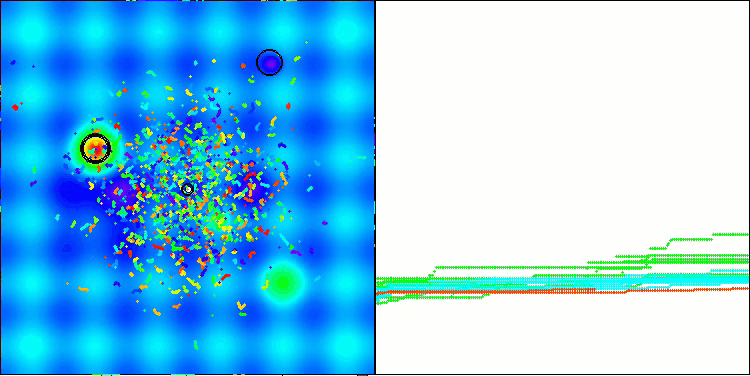
ADAM mit der Testfunktion Hilly
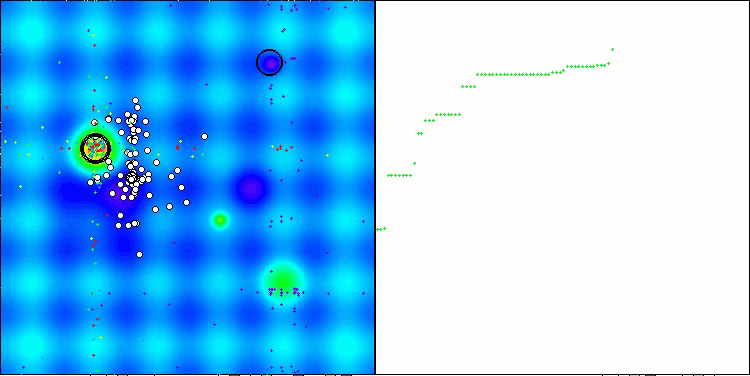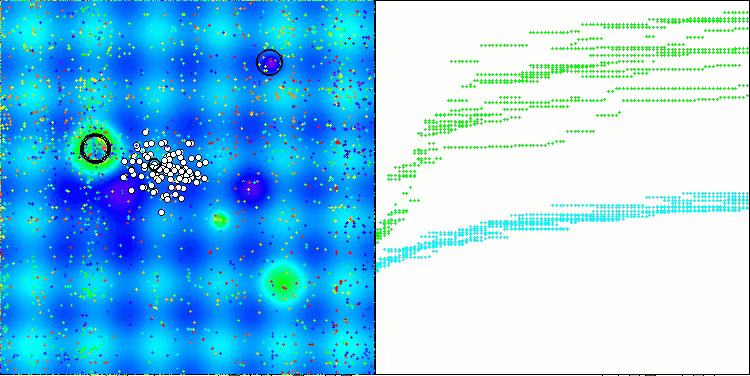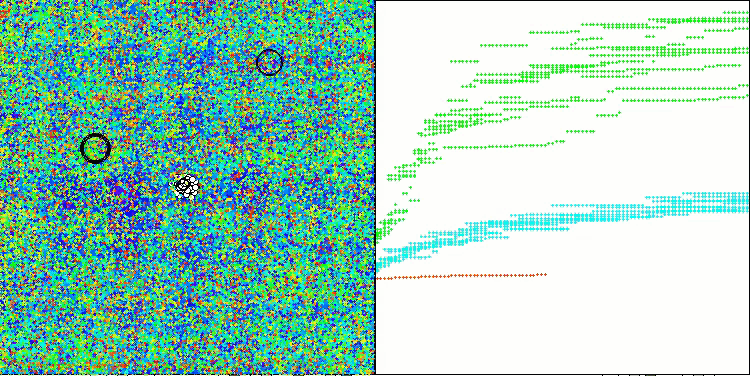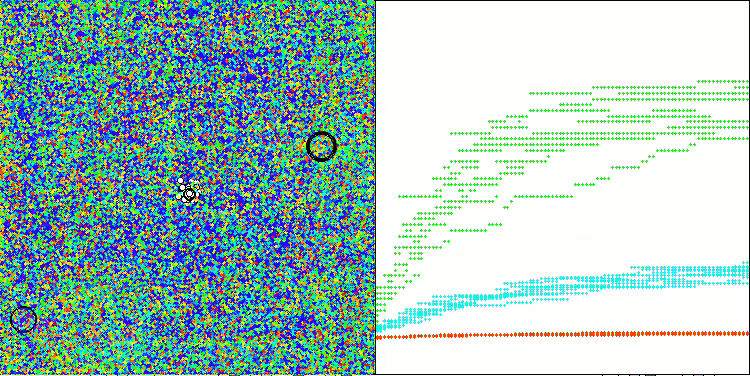
ADAMm mit der Testfunktion Hilly
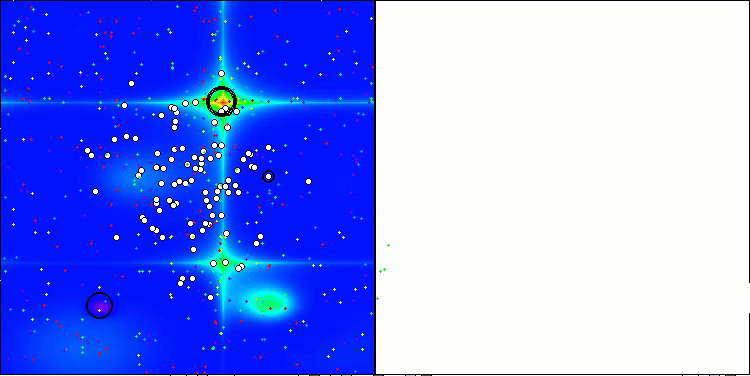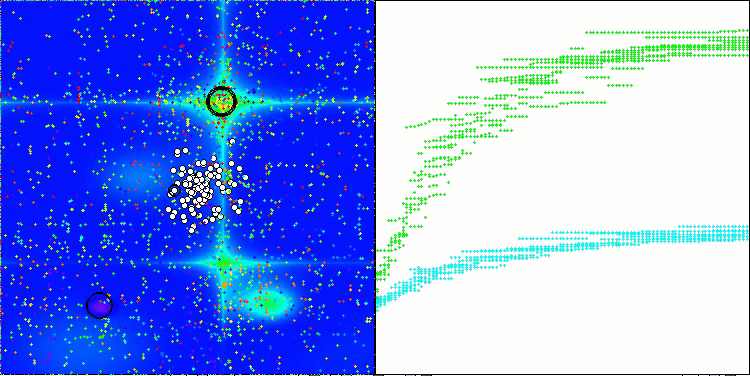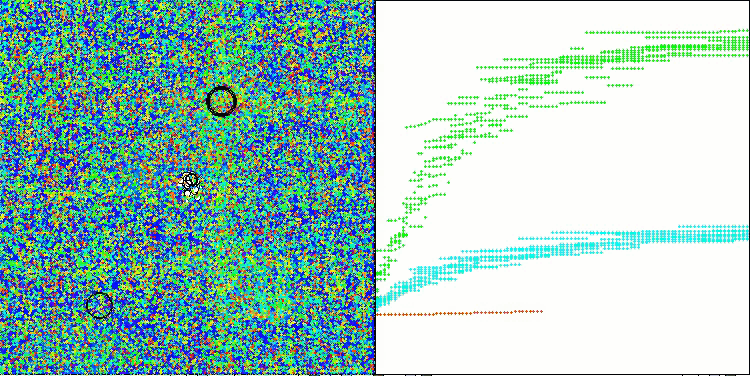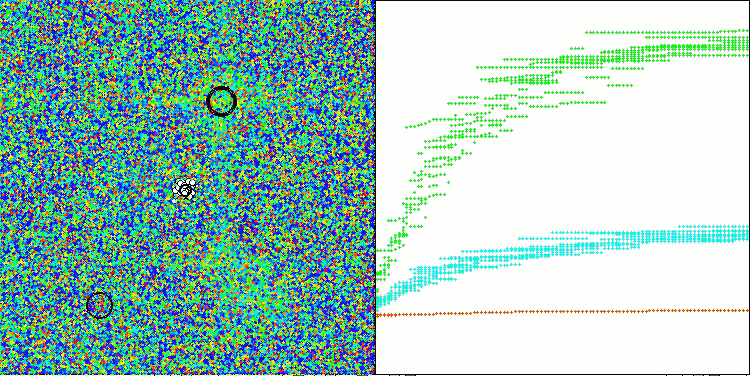
ADAMm mit der Testfunktion Forest
ADAMm mit der Testfunktion Megacity
Auf der Grundlage der Testergebnisse belegt die stochastische Populationsversion von ADAM Platz 32 in der Rangliste, was ein recht gutes Ergebnis ist. Die ursprüngliche Version konnte aufgrund ihrer schlechten Ergebnisse nicht in die Tabelle aufgenommen werden.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 12 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 30 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 31 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 32 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 33 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 34 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 35 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 36 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 37 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 38 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 39 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 40 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 41 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 42 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 43 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 44 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 45 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
Zusammenfassung
Der Artikel stellt einen Versuch dar, die bekannte Gradientenmethode ADAM, die traditionell in neuronalen Netzen verwendet wird, an die Lösung allgemeiner Optimierungsprobleme anzupassen. Dieser Versuch war erfolgreich, denn die daraus resultierende, wirklich stochastische Population ADAMm ist in der Lage, mit den leistungsfähigsten Algorithmen für globale Optimierungsprobleme zu konkurrieren. Der Artikel zeigt, dass deterministische Ansätze zur Suche nach optimalen Lösungen in mehrdimensionalen Suchräumen oft nicht so effektiv sind wie stochastische Methoden, und dass nur zusätzliche Zufallselemente die Suchmöglichkeiten jedes Optimierungsalgorithmus erweitern können.
Es ist jedoch anzumerken, dass netzintegrierte Gradientenverfahren wie das herkömmliche ADAM beim Training neuronaler Netze nach wie vor praktisch konkurrenzlos sind, da sie den exakten Gradientenwert bei der Backpropagation verwenden. Beim Training neuronaler Netze mit komplexeren Bewertungskriterien als der Fehlerminimierungsfunktion können Gradientenmethoden jedoch auf Schwierigkeiten stoßen und in lokalen Optima steckenbleiben, wie viele Autoren von Artikeln über maschinelles Lernen feststellen.
Der hier vorgestellte Ansatz kann bei der klassischen Verwendung integrierter Methoden in neuronalen Netzen nützlich sein, da er eine ausgezeichnete Genauigkeit und Konvergenzgeschwindigkeit beibehält, die analytische Form der Aktivierungsfunktion der Neuronen verwendet und die Fähigkeit, Störungen während der Ausbildung neuronaler Netze zu widerstehen, erheblich verbessert. Dies wird den Einsatz klassischer Methoden bei Aufgaben mit sehr komplexen Metriken und Kriterien während des Trainings ermöglichen. Ich hoffe, dass diese Arbeit Forschern und Praktikern helfen wird, Optimierungsprobleme im Allgemeinen und Methoden des maschinellen Lernens im Besonderen aus einer neuen Perspektive zu betrachten.
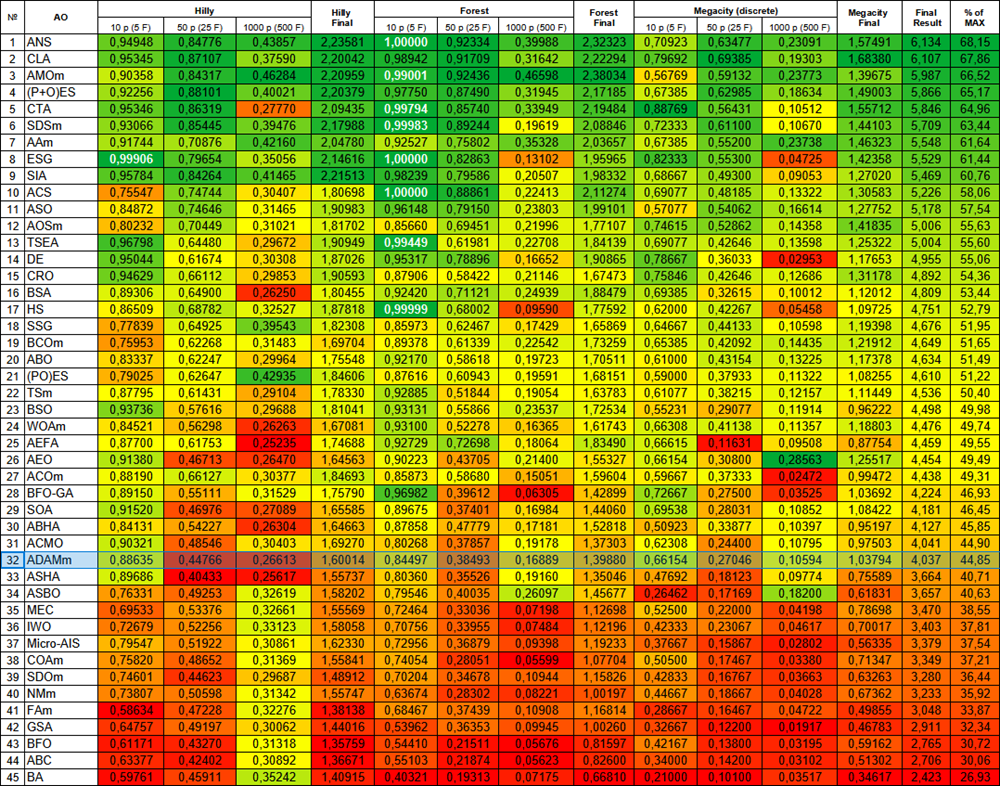
Abbildung 1. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
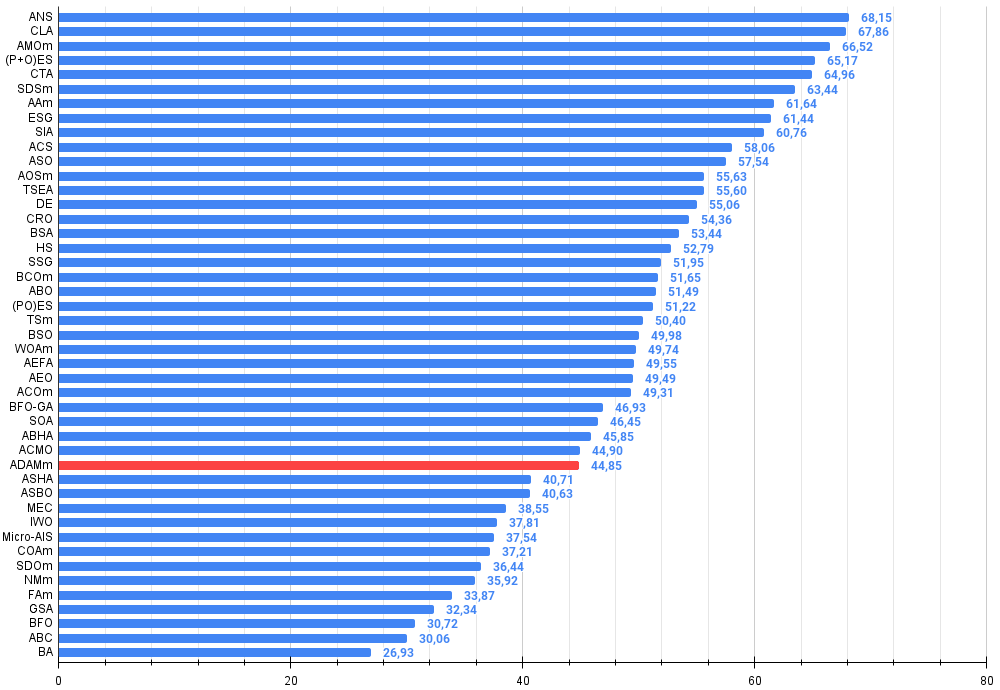
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
Vor- und Nachteile von ADAMm:
Vorteile:
- Gute Ergebnisse bei niedrigdimensionalen Problemen.
- Geringe Streuung der Ergebnisse.
Nachteile
- Viele externe Parameter.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Aufzählung von Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek der Testfunktionen |
| 5 | Utilities.mqh | Include | Bibliothek der Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_ADAM.mq5 | Skript | ADAM- und ADAMm-Testverfahren |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16443
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Templates und Typename (II)
Von der Grundstufe bis zur Mittelstufe: Templates und Typename (II)
 MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 61): Verwendung von ADX- und CCI-Mustern mit überwachtem Lernen
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 61): Verwendung von ADX- und CCI-Mustern mit überwachtem Lernen
 MQL5-Handelswerkzeuge (Teil 1): Aufbau eines interaktiven visuellen Handelsassistenten für schwebende Aufträge
MQL5-Handelswerkzeuge (Teil 1): Aufbau eines interaktiven visuellen Handelsassistenten für schwebende Aufträge
 Die Grenzen des maschinellen Lernens überwinden (Teil 1): Mangel an interoperablen Metriken
Die Grenzen des maschinellen Lernens überwinden (Teil 1): Mangel an interoperablen Metriken
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.