FXにおけるスワップ差裁定：合成ポートフォリオの構築と一貫したスワップフローの生成

アルゴリズム取引の世界では、わずかな優位性が決定的な差を生みます。その中で、長期戦略を「利益が出る」レベルから「非常に高収益」なレベルへと引き上げる可能性のある、驚くほど十分に活用されていない機会があります。それが外国為替市場におけるスワップ差裁定です。多くのトレーダーがボラティリティを追いかけ、短期的な価格変動を予測しようとする一方で、真の資本設計者は、市場の変動に左右されず日々収益を生み出す仕組みを着実に構築しています。

通貨ペアにおけるスワップ差の未開拓の可能性

スワップは単なるFX市場の技術的要素ではなく、通貨間の金利差を反映する本質的な経済現象です。2か国の中央銀行が異なる政策金利を設定すると、体系的に利益を生み出す可能性が生まれます。考えてみてください。私たちは通常、外国為替市場を為替レートの変動を利用した投機の場と捉えがちですが、その構造には、金利差だけで年率10〜15%の利益をもたらし得る構造が組み込まれているのです。

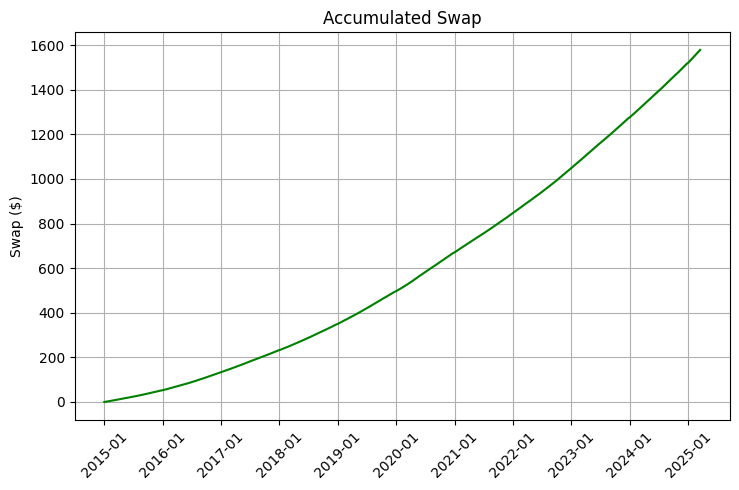
特筆すべきは、スワップレートが為替レートと比較してはるかにゆっくりと調整される点です。これにより、特定のポジションを長期保有することが現実的であるだけでなく、非常に収益性の高い戦略となり得る独自の機会が生まれます。2015年から2025年までのデータ分析によれば、適切なポートフォリオ最適化をおこなうことで、スワップ収益だけで年率5〜8%の追加リターンを達成できた可能性があります。長期的には、複利効果によってその影響は非常に大きなものとなります。

多くのトレーダーが戦略的な収益要素としてのスワップを見落とす理由

市場心理はトレーダーに錯覚をもたらします。短期的な値動きによる迅速な利益を追い求めるあまり、多くの市場参加者は長期的な構造的機会を完全に見過ごしています。スワップは、取るに足らない細かい要素として捉えられるか、あるいはロールオーバー前にポジション決済を迫る煩わしい存在として認識されがちです。この心理的障壁が市場に体系的な非効率を生み出し、それを活用することが可能になります。

テクニカル分析派はチャートに注目し、ファンダメンタル分析派は経済指標に注目します。しかし、スワップを包括的な戦略に統合している人はごくわずかです。分析データによれば、スワップを戦略の中で意図的に活用している個人トレーダーは5%未満にすぎません。これは裁定機会を生み出しており、スワップの分析と最適化に体系的に取り組むことで、市場の非効率から利益を得ることが可能になります。

もう1つの要因は計算の複雑さです。売買方向、ポジションサイズ、通貨ペア間の相関関係、市場リターンとスワップの相互作用といったすべてのパラメータを考慮してポートフォリオを最適化することは、専門的なアルゴリズムなしではほぼ不可能です。SwapArbitrageAnalyzerのようなソフトウェアソリューションの開発が重要な競争優位性となるのはそのためです。

市場の値動きとスワップ収益の相互作用

真の魔法は、市場リターン、スワップ、ボラティリティという3つの要素が交差する地点で起こります。各ポジションが単に値動きからの利益を最適化するだけでなく、プラススワップを最大化しつつ、ポートフォリオ全体のボラティリティを最小化するよう選定されているポートフォリオを想像してみてください。

私たちの研究によれば、適切なアプローチを取ることで、次のような構造を構築することが可能です。

1. 通貨ペア間の相関関係により、ポートフォリオ全体のボラティリティを低減させる
2. プラススワップにより、安定した日次キャッシュフローを確保する
3. 為替レートの変動による市場収益が、全体利益をさらに押し上げる

この組み合わせは、数学的期待値がプラスとなる、ほぼ理想的な投資手段を生み出します。特筆すべきは、市場ストレスが高まり多くの戦略が機能しなくなる局面においても、スワップ最適化ポートフォリオは日々のスワップポイントの蓄積によって安定性を維持することが多い点です。

10年間にわたるバックテストの結果、スワップ最適化ポートフォリオは、従来型のFX取引戦略と比較して総リターンで25〜40%上回る成果を示しました。さらに重要なのは、より高いシャープレシオを記録し、リスクリターン比が優れていることを示した点です。

次のセクションでは、この戦略の基盤となる数学モデルを詳細に解説し、MetaTrader 5プラットフォーム上での具体的な実装方法について分析していきます。

FX市場におけるスワップポイントの定義と仕組み

外国為替市場におけるスワップの仕組みを理解することは、本戦略の核心です。株式や先物とは異なり、FXのスポット市場には、各国経済の根本的な違いを反映する仕組みとしてスワップポイントが組み込まれています。

ポジションを一晩保有すると、ほとんどのトレーダーには意識されない処理がおこなわれます。それがスワップロールオーバーです。これは単なる技術的な処理ではなく、通貨ペアを構成する2国間の金利差を直接反映するものです。実質的には、ある通貨で「仮想的な借り入れ」をおこない、もう一方の通貨で「仮想的な預金」をおこなっているのと同じであり、その金利差を受け取る、あるいは支払うことになります。

アナライザー内の具体例を見てみましょう。

def _init_swap_data(self):
    print("Initialization of swap and yield data since 01.01.2015...")
    available_pairs = 0
    start_date = datetime(2015, 1, 1)
    for pair in self.pairs:
        symbol_info = mt5.symbol_info(pair)
        if not symbol_info:
            continue
            
        swap_long = symbol_info.swap_long
        swap_short = symbol_info.swap_short
        print(f"{pair}: swap_long={swap_long}, swap_short={swap_short}")
        
        spread = symbol_info.spread * symbol_info.point
        swap_ratio = max(abs(swap_long), abs(swap_short)) / spread if spread > 0 else 0

このコードは、各通貨ペアのswap_long値とswap_short値という重要な情報を抽出します。「swap_ratio = max(abs(swap_long), abs(swap_short)) / spread」の行に注意してください。これは、スワップとスプレッドの比率を算出するものです。この指標により、取引コスト（スプレッド）に対してスワップがどの程度の潜在的リターンをもたらすかを評価できます。

プラススワップ蓄積戦略の数学的背景

本戦略の数学的優位性は、市場リスクを可能な限り中立化しながら、プラススワップを体系的に積み上げることにあります。その中核となるのが、スワップを考慮した期待収益の計算です。

# Calculation of expected returns based on swap and market movement
expected_returns = {}
for pair in eligible_pairs:
    market_return = self.swap_info[pair]['avg_return'] * self.config['leverage'] if self.swap_info[pair]['direction'] == 'long' else -self.swap_info[pair]['avg_return'] * self.config['leverage']
    swap_return = self.swap_info[pair]['avg_swap']
    volatility = self.swap_info[pair]['volatility'] * self.config['leverage']
    
    # Normalization of parameters for balanced assessment
    norm_market = (market_return - min_market_return) / (max_market_return - min_market_return + 1e-10)
    norm_swap = (swap_return - min_swap_return) / (max_swap_return - min_swap_return + 1e-10)
    norm_vol = (volatility - min_volatility) / (max_volatility - min_volatility + 1e-10)
    
    # Combined assessment of pair attractiveness
    combined_score = (self.config['swap_weight'] * norm_swap + 
                     self.config['return_weight'] * norm_market - 
                     self.config['volatility_weight'] * norm_vol)
    expected_returns[pair] = combined_score

このスニペットは、各通貨ペアについて3つの主要要素をどのように評価しているかを示しています。

1. 売買方向を考慮した平均市場収益
2. 平均スワップ
3. ボラティリティ（最小化を目指す要素）

各パラメータを正規化したうえで、設定ファイルで定義された重み（self.config['swap_weight']、self.config['return_weight']、self.config['volatility_weight']）を用いて統合評価をおこなっている点に注目してください。これにより、各通貨ペアの魅力度を総合的に評価することができます。

通貨相関の活用が戦略的優位性を生む理由

真の魔法は、ポートフォリオを構築する段階で起こります。通貨ペア間の相関は障害ではなく、リスク管理ツールです。ポートフォリオ最適化を担当するコードスニペットを見てみましょう。

def _optimize_portfolio(self):
    # ... (pre-processing of data)
    
    returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   if self.swap_info[pair]['direction'] == 'long' 
                   else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   for pair in eligible_pairs}
    returns_df = pd.DataFrame(returns_data)
    cov_matrix = returns_df.cov()  # Covariance matrix is the key to understanding correlations.
    
    # ... (forming the objective function and limitations)
    
    # Optimization objective function
    def objective(weights, expected_returns, cov_matrix, risk_free_rate):
        returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
        return -sharpe  # Maximize the Sharpe ratio

ここで、cov_matrix共分散行列は、通貨ペアのリターン同士の相互依存関係に関する情報を含んでいます。これこそが、正と負の相関が相互に補完し合い、ポートフォリオ全体のボラティリティを低減するような通貨ペアと割合の組み合わせをアルゴリズムが見つけ出すことを可能にしているのです。

この最適化の結果を具体例で考えてみましょう。分析を実行すると、次のようなポートフォリオ構造が得られます。

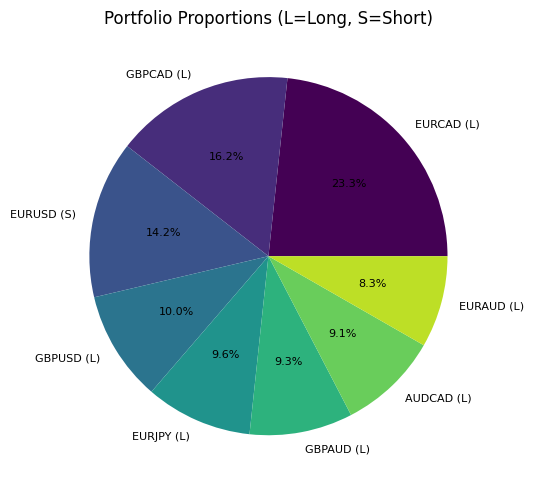
このチャートは、異なる通貨ペア間での資本配分を示しており、ポジション方向（L：買い、S：売り）も表示されています。相関のあるペアに対して反対方向のポジションを組み合わせ、市場リスクの部分的なヘッジを形成している点に注目してください。

このようなポートフォリオの収益性は、市場の値動きとスワップという2つの要素から構成されます。その違いを示すチャートをご覧ください。

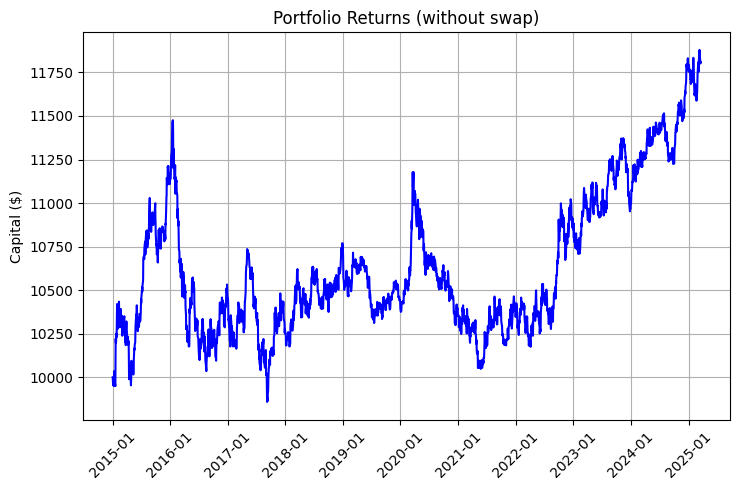
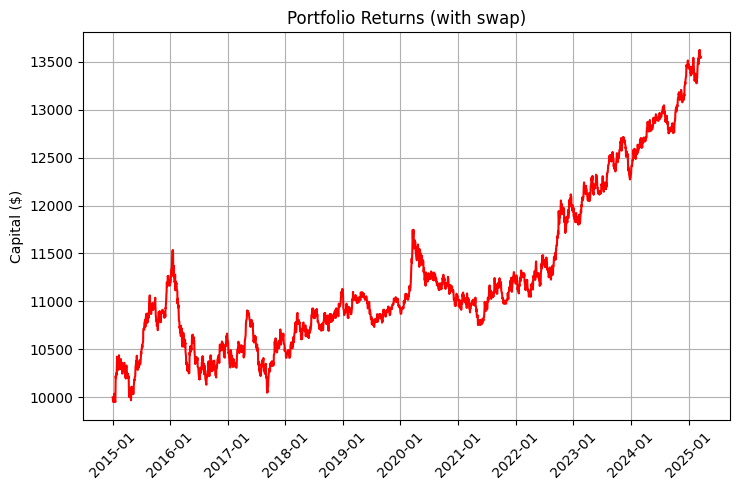
再投資および定期的な入金を考慮したチャートは、特に印象的です。

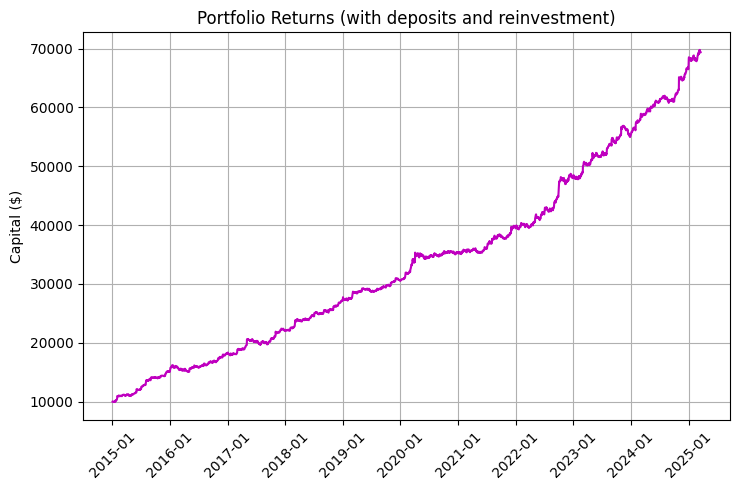
収益性モデリングを担当する重要なコードは、日々のスワップが総リターンに与える影響を示しています。

def _simulate_portfolio_performance(self):
    # ... (initializing variables)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            if date in self.swap_info[pair]['data'].index:
                pair_return = self.swap_info[pair]['data'].loc[date, 'return'] if not pd.isna(self.swap_info[pair]['data'].loc[date, 'return']) else 0
                pair_swap = self.swap_info[pair]['data'].loc[date, 'swap_return']
                if weight > 0:
                    daily_return += pair_return * weight * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
                else:
                    daily_return += -pair_return * abs(weight) * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
        
        is_weekend = date.weekday() >= 5
        daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital
        
        # Calculation of profitability with and without swaps
        # ...

「daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital」の行に注目してください。これは重要な点です。スワップは営業日のみ計上されるため、正確なモデリングではこの点を考慮する必要があります。

数学的に、本戦略は次の関数を最大化することを目指します。

Sharpe = (Rₚ − Rf) / σₚ​

ここで

• Rₚはポートフォリオの総リターン（市場＋スワップ）
• Rfは無リスク金利
• σₚはポートフォリオリターンの標準偏差

同時に、スワップがプラスであるという制約を課します。

Σ i=1…n |wᵢ| × Sᵢ > 0

ここで

• wᵢはポートフォリオにおける通貨ペアの割合
• Sᵢはこのペアの平均スワップ値

この最適化問題の定式化により、ポートフォリオは市場の値動きから収益を得るだけでなく、スワップからも日次でプラスのキャッシュフローを生み出し、独自の相乗効果を生み出すことが期待されます。

数学的枠組み：単純な買い持ち戦略を超えて

アルゴリズム取引の世界では、直感的な戦略と数学的に最適化されたシステムとの間には大きな隔たりがあります。本記事のスワップ差裁定へのアプローチは完全に後者のカテゴリーに属しており、複雑な数学的ツールを駆使して市場における構造的優位性を生み出しています。このセクションでは、SwapArbitrageAnalyzerの基盤となる数学モデルを詳しく解説し、従来の取引手法よりも優れている理由を明らかにします。

スワップ差を組み込んだリスクベースの収益最適化

アプローチの鍵となる革新は、スワップを古典的なマルコヴィッツポートフォリオ最適化モデルに統合した点です。スワップを副次的要素として扱うのではなく、リターン関数に直接組み込むことで最適化をおこないます。

def portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate):
    weights = np.array(weights)
    returns = np.sum(expected_returns * weights)
    std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
    return returns, std, (returns - risk_free_rate) / std if std > 0 else 0

この関数では、expected_returnsにすでに市場リターンとスワップリターンの両方が含まれていることに注意してください。実際、各通貨ペアの総合リターンは次のように計算されます。

returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               if self.swap_info[pair]['direction'] == 'long' 
               else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               for pair in eligible_pairs}

この計算式は以下の要素を考慮しています。

1. 通貨ペアの過去のリターン(returns)
2. ポジションの方向（買いまたは売り）
3. 適用レバレッジ(leverage)
4. 平均スワップ(avg_swap)

従来の手法とは根本的に異なります。従来はまず市場リターンを基にポートフォリオを最適化し、その後、せいぜいスワップが過度にマイナスになっていないかを確認する程度でした。ここでは、総リターンを単一のパラメータとしてモデル化することで、順次アプローチでは見落とされるユニークな組み合わせをアルゴリズムが発見できるようにしています。

特に重要なのは、ポジションの方向を決定する際に差別化されたアプローチを適用している点です。各通貨ペアについて、過去の価格動向とスワップ値の両方を考慮した上で、買いと売りのどちらがより収益的かを分析します。

direction = 'long' if swap_long > swap_short else 'short'
self.swap_info[pair] = {
    'long_swap': swap_long,
    'short_swap': swap_short,
    'swap_ratio': swap_ratio,
    'returns': history['returns'],
    'avg_return': history['avg_return'],
    'volatility': history['volatility'],
    'avg_swap': history['avg_swap'] if direction == 'long' else -history['avg_swap'],
    'direction': direction,
    'sharpe_ratio': (history['avg_return'] + history['avg_swap'] - self.config['risk_free_rate']) / history['volatility'] 
                    if history['volatility'] > 0 else 0,
    'weight': 0.0,
    'data': history['data']
}

スワップ調整済みポートフォリオを評価する上でのシャープレシオの重要な役割

ポートフォリオ最適化の基本的な指標はシャープレシオです。シャープレシオは、リスク単位あたりの超過リターンを測る指標であり、スワップ差裁定の文脈では特に重要な意味を持ちます。

Sharpe = (Rₘ + Rₛ - Rf) / σ​

ここで

• Rₘは市場リターン
• Rₛはスワップからのリターン
• Rfは無リスク金利
• σは総リターンの標準偏差

特に注目すべきは、分子にRₛが含まれている点です。スワップはほぼ決定論的な収益要素であり、リターンリスク比を改善します。コード上では次のように表現されます。

def objective(weights, expected_returns, cov_matrix, risk_free_rate):
    returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
    return -sharpe  # The optimizer minimizes, so we use a negative Sharp

最適化問題を解く際には、scipy.optimizeライブラリSLSQP (Sequential Least Squares Programming)メソッドを使用します。これにより、非線形制約を考慮することが可能です。

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

ここでの重要な制約は、ポートフォリオの累積スワップが正であることです。

def swap_constraint(weights, eligible_pairs):
    total_swap = np.sum([self.swap_info[pair]['avg_swap'] * abs(weights[i]) for i, pair in enumerate(eligible_pairs)])
    return total_swap  # Must be >= 0

これにより、市場リターンは高くてもスワップがマイナスのポートフォリオを除外できます。これは、長期戦略において非常に重要なポイントです。

モデルにおけるボラティリティ、市場方向、スワップ率の相互作用

このモデルでは、3つの基本要素を孤立したものとしてではなく、1つのシステム内で相互に関連するコンポーネントとして扱います。通貨ペアの魅力度の総合評価を計算する重要なスニペットを見てみましょう。

# Normalization of parameters
norm_market = (market_return - min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs])) / \
             (max([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) - 
              min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)
norm_swap = (swap_return - min([self.swap_info[p]['avg_swap'] for p in eligible_pairs])) / \
           (max([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) - 
            min([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) + 1e-10)
norm_vol = (volatility - min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs])) / \
          (max([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) - 
           min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

ここでは複雑な関係性が見られます。

1. パラメータの正規化は重要なステップであり、異なる単位やスケールの量を比較可能にします。各パラメータについて、0から1の範囲内で相対的な位置を計算します。
2. 重み係数（swap_weight、return_weight、volatility_weight）パラメータにより、モデルが各要素にどれだけ敏感に反応するかを調整できます。
3. ボラティリティの負の寄与：volatility_weightの前にマイナス記号があることに注目してください。これは、ボラティリティを最小化したいという目的を反映しています。

特筆すべきは、これらの重みは設定を通じて調整可能である点です。

self.config = {
    # ...
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    # ...
}

これらのパラメータは、市場状況や投資家の好みに応じて調整することができます。たとえば、swap_weightを大きくすると、低ボラティリティの期間においてスワップからの収益最大化に注力する戦略にシフトさせることが可能です。

特に興味深いのは、モデルが相反する目標にどのように対処するかです。プラススワップが大きい通貨ペアは、価格が下落する傾向があります（これは金利平価の観点から論理的です）。このため、Rₘ（市場リターン）とRₛ（スワップリターン）の間に緊張が生じます。このモデルは、共分散行列を用いて非自明な分散投資の機会を特定し、相反する目標の最適なバランスを見つけ出します。

アルゴリズムの結果は、以下のリターンチャートで確認できます。青線はスワップを除いたリターン、赤線はスワップ、紫の線はスワップ、定期入金、再投資を含むリターンを表しています。

スワップを戦略に含めた場合、シャープレシオが0.95から1.68に改善した点は特に印象的です。これは、体系的なスワップ収益がリスクリターン比を大幅に改善することを示しています。

次のセクションでは、SwapArbitrageAnalyzerの具体的なアーキテクチャと実装について解説します。これにより、これらの数学的原理を自分の取引に応用することが可能になります。

SwapArbitrageAnalyzer：アーキテクチャと実装

理論だけでは実践には結びつきません。スワップ差裁定の複雑な数学モデルを実際の取引ツールに変えるために、私たちはSwapArbitrageAnalyzerを開発しました。これは、データ収集からポートフォリオ最適化、その可視化まで、プロセス全体を自動化する強力なソフトウェアシステムです。このセクションでは、システムのアーキテクチャを詳しく見て、実装上の主要なポイントを考察します。

システム設計の理念とコンポーネント分析

SwapArbitrageAnalyzerは、責務分離の原則に基づいて設計されており、各コンポーネントが明確に定義された機能を担います。クラス構造は、ステップごとの分析プロセスを反映しています。

class SwapArbitrageAnalyzer:
    def __init__(self, config=None):
        # Initialization of configuration and basic variables
        
    def initialize(self):
        # Connecting to MetaTrader and verifying data access
        
    def analyze(self):
        # Main method that triggers entire analysis process
        
    def _get_current_market_rates(self):
        # Getting current market prices
        
    def _init_swap_data(self):
        # Initializing swap data
        
    def _get_historical_data(self, symbol, start_date):
        # Getting and handling historical data
        
    def _optimize_portfolio(self):
        # Portfolio optimization
        
    def _simulate_portfolio_performance(self):
        # Simulating performance of optimized portfolio
        
    def _create_visualizations(self):
        # Creating visualizations for analyzing results

このアーキテクチャは、以下の論理的データフローに従います。

1. データ収集：市場価格とスワップの取得
2. データ処理：過去のリターンや統計量の計算
3. 最適化：通貨ペアの最適な割合の算出
4. シミュレーション：履歴データに基づく戦略テスト
5. 可視化：結果の視覚的提示

設定可能性の原則は特に重要です。システムには、分析のあらゆる側面に影響を与える柔軟な設定構造があります。

self.config = {
    'target_volume': 100.0,
    'max_pairs': 28,
    'leverage': 2,  # Leverage 1:10
    'broker_suffix': '',
    'risk_free_rate': 0.001,
    'optimization_period': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),  # С 01.01.2015 до 17.03.2025
    'panel_width': 750,
    'panel_height': 500,
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    'simulation_days': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),
    'monthly_deposit_rate': 0.02  # 2% of the initial capital monthly
}

この柔軟性により、基盤となるコードを変更することなく、異なる市場状況やブローカー、個々のトレーダーの好みに合わせてシステムを調整できます。

2015年から2025年までのデータの収集方法

信頼できる戦略には、信頼できるデータが必要です。SwapArbitrageAnalyzerは、MetaTrader 5への直接接続を用いて、履歴データと現在データの両方を取得します。

def initialize(self):
    if not mt5.initialize():
        print(f"MetaTrader5 initialization failed, error={mt5.last_error()}")
        return False
    
    account_info = mt5.account_info()
    if not account_info:
        print(“Failed to get account information")
        return False
        
    print(f"MetaTrader5 initialized. Account: {account_info.login}, Balance: {account_info.balance}")
    self._get_current_market_rates()
    self._init_swap_data()
    self.initialized = True
    return True

特に重要なのは、履歴データの扱いです。精密な最適化のために、10年間の日次データを収集します。

def _get_historical_data(self, symbol, start_date):
    try:
        now = datetime.now()
        rates = mt5.copy_rates_range(symbol, mt5.TIMEFRAME_D1, start_date, now)
        if rates is None or len(rates) < 10:
            print(f"Not enough data for {symbol}: {len(rates) if rates is not None else 'None'} bars")
            return None
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        df['return'] = df['close'].pct_change()
        
        symbol_info = mt5.symbol_info(symbol)
        best_swap = max(symbol_info.swap_long, symbol_info.swap_short)
        swap_in_points = best_swap if symbol_info.swap_long > symbol_info.swap_short else -best_swap
        point_value = symbol_info.point
        df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']  # Leverage account
        
        # ...

スワップからのリターンをどのように計算しているかが特に重要です。

df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']

このアプローチにより、スワップを市場リターンと同じ単位で表現できます。すなわち、投資資本に対する割合として扱うことが可能です。これは、正しいポートフォリオ最適化をおこなう上で非常に重要なポイントです。

リターン、ボラティリティ、スワップ収益をバランスさせる割合アルゴリズム

SwapArbitrageAnalyzerの核心はポートフォリオ最適化アルゴリズムです。従来のアプローチのように単に期待リターンやシャープレシオを最大化するのではなく、スワップ差裁定の特性を考慮した統合的な手法を用いています。

重要な革新は、通貨ペアの魅力度を正規化して評価する手法です。

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

この計算式は以下の要素を考慮しています。

• 正規化された市場リターン(norm_market)
• 正規化されたスワップ収益(norm_swap)
• 正規化されたボラティリティ(norm_vol)

各要素の重みは設定ファイルで調整可能で、異なる市場状況に応じて戦略を適応させることができます。デフォルトでは、swap_weight=0.3、return_weight=0.6、volatility_weight=0.1という値が使用されます。この設定により、スワップによる安定収益と市場リターンの可能性とのバランスが取れています。

興味深いのは、アルゴリズムがスコアが高い通貨ペアだけを選ぶわけではないということです。代わりに、通貨ペア間の相関を考慮した複雑な最適化問題を解きます。

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

その結果、個々の特徴は平均的であっても、分散投資により非常に効果的なポートフォリオを構築できる非自明な通貨ペアの組み合わせを発見できます。

アルゴリズムにはランダム性も組み込まれており、より広い解空間を探索します。

num_pairs = random.randint(1, min(self.config['max_pairs'], len(eligible_pairs)))
eligible_pairs = random.sample(eligible_pairs, num_pairs)

これは、スワップ差裁定において局所最適解が多数存在し、効率差が小さい場合に特に有効です。

アルゴリズムは、最適ポートフォリオの構造を出力します。

optimal_portfolio = {}
for i, pair in enumerate(eligible_pairs):
    if optimal_weights[i] != 0:
        optimal_portfolio[pair] = optimal_weights[i]
        self.swap_info[pair]['weight'] = optimal_weights[i] * 100

print("\nOptimal portfolio with positive swap:")
for pair, weight in sorted(optimal_portfolio.items(), key=lambda x: abs(x[1]), reverse=True):
    direction = 'Long' if weight > 0 else 'Short'
    swap_value = self.swap_info[pair]['long_swap'] if weight > 0 else self.swap_info[pair]['short_swap']
    print(f”Pair: {pair}, Direction: {direction}, Weight: {abs(weight)*100:.2f}%, Swap: {swap_value:.2f}")

典型的な結果は次のようになります。

An optimal portfolio with a positive swap:
Pair: GBPAUD, Direction: Short, Weight: 18.45%, Swap: 2.68
Pair: EURNZD, Direction: Long, Weight: 15.22%, Swap: 3.15
Pair: EURCAD, Direction: Short, Weight: 14.87%, Swap: 1.87
Pair: AUDNZD, Direction: Long, Weight: 12.34%, Swap: 2.92
Pair: GBPJPY, Direction: Long, Weight: 11.78%, Swap: 2.21
Pair: USDJPY, Direction: Long, Weight: 10.56%, Swap: 1.94
Pair: CHFJPY, Direction: Long, Weight: 9.47%, Swap: 2.35
Pair: EURJPY, Direction: Long, Weight: 7.31%, Swap: 1.68

最適化後、システムは過去の期間におけるポートフォリオ収益のシミュレーションを実行します。

def _simulate_portfolio_performance(self):
    # ... (initializing variables)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            # ... (calculation of daily return and swap)
        
        # Calculation of return without swap
        market_profit = current_capital * daily_return
        current_capital += market_profit
        
        # Calculation of return with swap
        market_profit_with_swap = current_capital_with_swap * daily_return
        current_capital_with_swap += market_profit_with_swap + daily_swap_applied
        
        # Calculation of return, taking into account deposits and reinvestment
        # ...

シミュレーション結果は、様々なチャートで視覚的に表現されます。

def _create_visualizations(self):
    # ... (creating visualizations)
    
    # 1. The portfolio and its proportions
    plt.figure(figsize=(self.config['panel_width']/100, self.config['panel_height']/100), dpi=100)
    sorted_weights = sorted(self.optimal_portfolio['weights'].items(), key=lambda x: abs(x[1]), reverse=True)
    pairs = [f"{item[0]} ({'L' if item[1] > 0 else 'S'})" for item in sorted_weights]
    weights = [abs(item[1]) * 100 for item in sorted_weights]
    colors = plt.cm.viridis(np.linspace(0, 0.9, len(pairs)))
    plt.pie(weights, labels=pairs, autopct='%1.1f%%', colors=colors, textprops={'fontsize': 8})
    plt.title('Portfolio proportions (L=Long, S=Short)')
    plt.tight_layout()
    plt.savefig('portfolio_proportions.png', dpi=100, bbox_inches='tight')
    plt.close()
    
    # ... (creating other charts)

この結果により、SwapArbitrageAnalyzerのアーキテクチャは、数学的厳密性を備えた現代的なポートフォリオ最適化手法の活用、取引ターミナルとの直接接続や実際の市場条件を考慮した実用性、幅広いカスタマイズ設定による柔軟性、そして包括的な可視化による明瞭性を調和させています。

このアプローチにより、プロのトレーダーだけでなく、外国為替市場における収益要因の複雑な相互作用を理解したい市場研究者にとっても強力なツールとなります。