
Otimização com neuroboids — Neuroboids Optimization AlgorithmN 2 (NOA2)
Conteúdo
Introdução
À medida que me aprofundava cada vez mais nos algoritmos de otimização ao longo dos anos, fui frequentemente inspirado por duas ideias paralelas: a auto-organização de enxames biológicos e as capacidades de aprendizado adaptativo das redes neurais. A síntese dessas duas abordagens me levou a desenvolver um algoritmo de abordagem híbrida que une a inteligência espacial dos Boids de Craig Reynolds com o aprendizado adaptativo proporcionado pelas redes neurais.
Meu ponto de partida foi a observação de que os algoritmos tradicionais de enxame, embora eficientes para explorar espaços de busca complexos por meio do comportamento coletivo, geralmente não são capazes de aprender com o histórico de suas próprias explorações. Por outro lado, as redes neurais são excelentes em aprender padrões complexos, mas podem ter dificuldades em realizar uma exploração espacial eficaz quando aplicadas diretamente a problemas de otimização. A pergunta que motivou minha pesquisa era, ao mesmo tempo, simples e profunda: e se cada agente do enxame pudesse aprender a melhorar suas estratégias de movimento com o uso de uma rede neural dedicada?
O algoritmo resultante utiliza agentes que seguem as regras clássicas de coesão, separação e alinhamento dos boids, permitindo que eles se auto-organizem e explorem o espaço de busca de maneira eficiente. No entanto, ao contrário das implementações tradicionais de boid, cada agente é equipado com uma rede neural multicamada que aprende continuamente com a própria experiência do agente, adaptando suas estratégias de movimento de acordo com as características específicas do terreno de adaptabilidade. Esse nível de controle neural vai moldando gradualmente o comportamento dos boids, que evoluem de estratégias voltadas à diversificação nas primeiras iterações para um movimento mais focado na intensificação à medida que regiões promissoras são identificadas.
O que mais me fascinava durante o desenvolvimento era observar como as redes neurais desenvolviam estratégias distintas, dependendo da posição no espaço de busca. Agentes próximos a regiões promissoras desenvolviam padrões neurais que intensificavam a exploração local, enquanto agentes em áreas esparsas mantinham um comportamento voltado à diversificação. Essa especialização emergente surgiu naturalmente dos processos individuais de aprendizado, criando um enxame com comportamento heterogêneo e dependente do contexto, sem necessidade de coordenação global explícita.
Neste artigo, apresentarei a arquitetura, os detalhes da implementação e a análise de desempenho do algoritmo NOA2, além de uma demonstração de seu potencial em diversas funções de benchmark.
Implementação do algoritmo
Talvez eu esteja me repetindo, mas a ideia central do algoritmo de neuroboids é unir duas grandes abordagens: a inteligência coletiva dos algoritmos de enxame e o aprendizado adaptativo das redes neurais.
No algoritmo tradicional de boids (boids), proposto por Craig Reynolds, os agentes seguem três regras simples: coesão (movimento em direção ao centro do grupo), separação (evitar colisões) e alinhamento (ajustar a velocidade com base nos vizinhos). Essas regras resultam em um comportamento coletivo realista, semelhante ao das aves em voo em bando. Os neuroboids expandem esse conceito, equipando cada agente com uma rede neural individual que aprende com a própria experiência do agente durante a exploração do espaço de busca. Essa rede neural executa duas funções principais:
- Controle adaptativo de movimento ajusta a velocidade do agente com base no estado atual e no histórico de movimentação.
- Modificação das regras padrão dos boids ajusta dinamicamente a influência das regras de coesão, separação e alinhamento conforme o contexto.
Como resultado, temos um algoritmo híbrido onde cada agente mantém o comportamento social necessário para explorar o espaço com eficiência, mas também se adapta individualmente ao terreno da função de adaptabilidade por meio do aprendizado. Isso gera um equilíbrio autorregulado entre diversificação (exploration) e intensificação (exploitation).
As principais vantagens dessa abordagem estão na capacidade dos agentes de aprenderem sozinhos estratégias ótimas de movimentação, o que permite que o algoritmo se adapte automaticamente a diferentes tipos de terrenos de otimização, mantendo a exploração do espaço por meio do comportamento coletivo, mesmo sem um controle centralizado. Uma analogia simples ajuda a visualizar: imagine um bando de aves voando no céu. Elas se movem de forma coordenada, isto ]e, ninguém colide, permanecem unidas e seguem na mesma direção. Esse comportamento pode ser descrito com três regras simples: mantenha-se próximo dos seus vizinhos (não se afaste do grupo), evite colisões (respeite a distância) e siga na mesma direção (mantenha o curso comum).
Essa é a base do chamado algoritmo de "boids" (de "bird-oid", "semelhante a pássaro"). Cada pássaro no bando não apenas segue essas regras, mas também é capaz de aprender com a própria experiência. A ave lembra quais ações levaram ao sucesso (por exemplo, encontrar mais alimento) e quais não. Com o tempo, ela se torna mais inteligente e toma decisões melhores sobre como voar. Essa é justamente a essência do algoritmo de neuroboids: combinar regras simples de movimentação coletiva com a capacidade de cada participante aprender com sua própria vivência. O "neuro" no nome destaca exatamente essa capacidade de aprendizado. Esse tipo de abordagem é especialmente interessante porque combina a força da exploração coletiva (ninguém deixa passar uma área importante) com as vantagens do aprendizado individual (cada um se torna mais eficiente em sua própria região de busca).
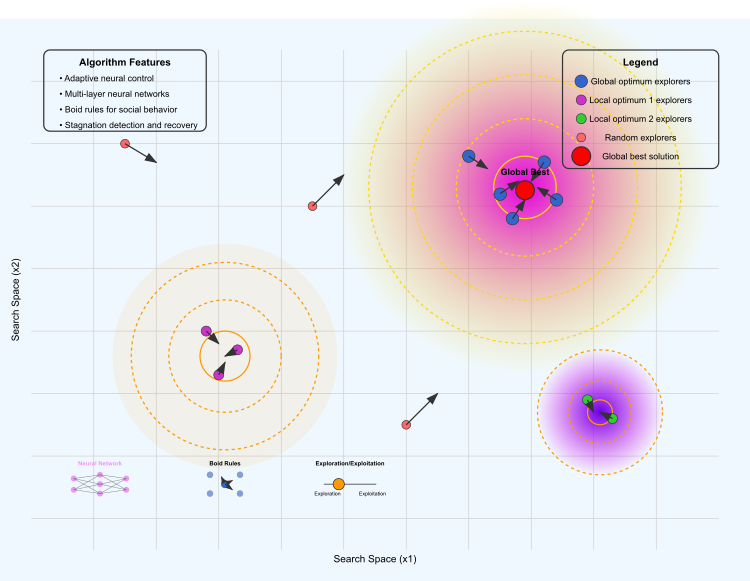
Figura 1. Ilustração do funcionamento do algoritmo NOA2
A ilustração mostra os seguintes elementos principais: o terreno de otimização, onde a área amarelo-violeta representa o ótimo global, as áreas laranja e violeta representam ótimos locais, e as linhas de contorno indicam a "elevação" do terreno da função de adaptabilidade.
Diferentes grupos de agentes: os azuis exploram a área do ótimo global, os violetas estão concentrados ao redor do primeiro ótimo local, os verdes exploram o segundo ótimo local e os vermelhos realizam uma exploração aleatória do espaço. As setas indicam a direção do movimento dos boids. O ponto vermelho marca a melhor solução encontrada até o momento.
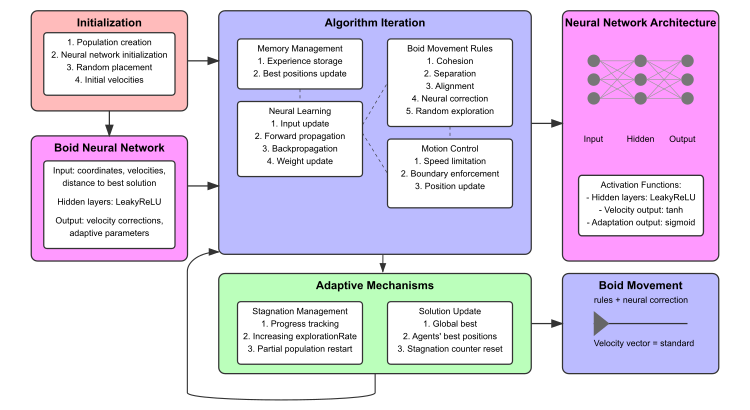
Figura 2. Diagrama de funcionamento do algoritmo NOA2
O diagrama inclui: o bloco de inicialização (vermelho), a Rede Neural do boid (rosa), as iterações do algoritmo com sub-blocos (azul), os mecanismos adaptativos (verde), visualização da arquitetura da rede neural com exemplos de conexões. Na parte inferior, são mostrados diagramas em miniatura no formato de estrutura da rede neural, visualizações das regras de movimento dos boids e o equilíbrio entre diversificação e intensificação.
Com a ideia principal compreendida, podemos passar à descrição do pseudocódigo do algoritmo.
INICIALIZAÇÃO:
- Defina os parâmetros de busca e crie uma população de agentes.
- Para cada agente: inicialize uma posição aleatória, uma velocidade pequena, a rede neural (camadas de entrada → ocultas → saída) e uma memória de experiências vazia.
- Defina a melhor adaptabilidade global como menos infinito e zere o contador de estagnação.
LAÇO PRINCIPAL:
Para cada iteração:
AVALIAÇÃO:
- Calcule a adaptabilidade de todos os agentes.
- Atualize as melhores posições pessoais e global.
- Salve as experiências nos buffers de memória.
CONTROLE DE ESTAGNAÇÃO:
- Se não houver melhora: aumente a diversificação, reinicie periodicamente os agentes mais fracos.
- Caso contrário: reduza gradualmente o nível de diversificação.
PROCESSAMENTO NEURAL:
- Para cada agente:
- Propagação para frente: dados de entrada (posição, velocidade, distância até a melhor posição, adaptabilidade) → camadas ocultas → saídas.
- Se houver experiência suficiente acumulada e for detectada melhoria: atualize os pesos neurais.
ATUALIZAÇÃO DO MOVIMENTO:
- Para cada agente:
- Calcule as forças padrão dos boids (coesão, separação, alinhamento).
- Aplique forças modificadas neuralmente e correções diretas da rede neural.
- Adicione um componente de diversificação aleatória com certa probabilidade.
- Imponha limites à velocidade e respeite as fronteiras.
- Atualize a posição com base na velocidade final.
CÁLCULOS DE SUPORTE:
- Cálculo da massa: normalize os valores de adaptabilidade para atribuir uma massa a cada agente.
- Coesão: mova-se em direção ao centro de massa ponderado dos agentes vizinhos.
- Separação: evite aglomeração com os vizinhos.
- Alinhamento: ajuste a velocidade de acordo com os agentes mais próximos.
- Atualização neural: propagação reversa simplificada com base na melhoria de adaptabilidade.
RETORNO: melhor posição global e adaptabilidade.
Agora está tudo pronto para escrever o código do algoritmo. Vamos definir a estrutura "S_NeuroBoids_Agent", que representará um agente neuroboid baseado em arquitetura neural para execução de tarefas de otimização. Nesta implementação, o agente possui os seguintes componentes e funções principais:
Coordenadas e velocidades:
- x[] — coordenadas atuais do agente.
- dx[] — velocidades atuais do agente.
- inputs[] — valores de entrada para os neurônios (coordenadas, velocidades, distância até a melhor posição conhecida, etc.).
- outputs[] — valores de saída da rede neural (correções de velocidade e parâmetros de adaptação).
- weights[] — pesos das conexões da rede neural.
- biases[] — vieses dos neurônios.
- memory[] — vetor para armazenar posições anteriores e seus respectivos valores de adaptabilidade.
- memory_size — tamanho máximo da memória.
- memory_index — índice atual da memória.
- best_local_fitness — melhor adaptabilidade local do agente.
- m — massa do agente.
- cB[] — coordenadas da melhor posição encontrada pelo agente.
- fB — valor da função de adaptabilidade da melhor posição.
Inicialização (Init) — todos os vetores e variáveis são inicializados com zeros ou valores aleatórios. Os tamanhos dos vetores são definidos, e os pesos e vieses são iniciados com pequenos valores aleatórios.
Funções de ativação — Tanh, ReLU, Sigmoid: diferentes funções de ativação aplicadas na rede neural.
Atualização dos dados de entrada (UpdateInputs) — preenche o vetor de entradas com as coordenadas atuais, velocidades, distância até a melhor posição conhecida e o valor atual de adaptabilidade.
Propagação para frente (ForwardPass) — calcula as saídas da rede neural com base nas entradas, pesos e vieses, aplicando as funções de ativação correspondentes.
Aprendizado baseado na experiência (Learn) — atualiza os pesos e vieses com base nas experiências acumuladas, caso a experiência atual seja melhor do que as anteriores.
Memorização da experiência (MemorizeExperience) — armazena as coordenadas e o valor de adaptabilidade atual do agente na memória.
Atualização da melhor posição (UpdateBestPosition) — se o valor atual de adaptabilidade for superior ao anteriormente registrado, atualiza a melhor posição encontrada.
//—————————————————————————————————————————————————————————————————————————————— // Структура нейро-боидного агента //—————————————————————————————————————————————————————————————————————————————— struct S_NeuroBoids_Agent { double x []; // текущие координаты double dx []; // текущие скорости double inputs []; // входы нейрона double outputs []; // выходы нейрона double weights []; // веса нейрона double biases []; // смещения нейрона double memory []; // память предыдущих позиций и их фитнесов int memory_size; // размер памяти для накопления опыта int memory_index; // текущий индекс в памяти double best_local_fitness; // лучший локальный фитнес агента double m; // масса бойда double cB []; // координаты лучшей позиции double fB; // значение фитнес-функции // Инициализация агента void Init (int coords, int neuron_size) { ArrayResize (x, coords); ArrayResize (dx, coords); ArrayInitialize (x, 0.0); ArrayInitialize (dx, 0.0); // Инициализируем структуру лучшей позиции ArrayResize (cB, coords); ArrayInitialize (cB, 0.0); fB = -DBL_MAX; // Входы: координаты, скорости, расстояние до лучшего и т.д. int input_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness ArrayResize (inputs, input_size); ArrayInitialize (inputs, 0.0); // Выходы: коррекция скоростей и адаптивные факторы для правил стаи int output_size = coords + 3; // dx_correction + 3 адаптивных параметра ArrayResize (outputs, output_size); ArrayInitialize (outputs, 0.0); // Веса и смещения для каждого выхода ArrayResize (weights, input_size * output_size); ArrayInitialize (weights, 0.0); ArrayResize (biases, output_size); ArrayInitialize (biases, 0.0); // Инициализация весов и смещений малыми случайными значениями for (int i = 0; i < ArraySize (weights); i++) { weights [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0); } for (int i = 0; i < ArraySize (biases); i++) { biases [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0); } // Инициализация памяти для накопления опыта memory_size = 10; ArrayResize (memory, memory_size * (coords + 1)); // координаты + фитнес ArrayInitialize (memory, 0.0); memory_index = 0; best_local_fitness = -DBL_MAX; // Инициализация массы m = 0.5; } // Функция активации - гиперболический тангенс double Tanh (double input_val) { return MathTanh (input_val); } // Функция активации ReLU double ReLU (double input_val) { return (input_val > 0.0) ? input_val : 0.0; } // Функция активации Sigmoid double Sigmoid (double input_val) { return 1.0 / (1.0 + MathExp (-input_val)); } // Обновление входов нейронной сети - исправленная версия void UpdateInputs (double &global_best [], double current_fitness, int coords_count) { int input_index = 0; // Координаты for (int c = 0; c < coords_count; c++) { inputs [input_index++] = x [c]; } // Скорости for (int c = 0; c < coords_count; c++) { inputs [input_index++] = dx [c]; } // Расстояние до лучшего глобального решения double dist_to_best = 0; for (int c = 0; c < coords_count; c++) { dist_to_best += MathPow (x [c] - global_best [c], 2); } dist_to_best = MathSqrt (dist_to_best); inputs [input_index++] = dist_to_best; // Текущая фитнес-функция inputs [input_index++] = current_fitness; } // Прямое распространение по сети void ForwardPass (int coords_count) { int input_size = ArraySize (inputs); int output_size = ArraySize (outputs); // Для каждого выхода вычисляем взвешенную сумму входов + смещение for (int o = 0; o < output_size; o++) { double sum = biases [o]; for (int i = 0; i < input_size; i++) { sum += inputs [i] * weights [o * input_size + i]; } // Применяем разные функции активации в зависимости от выхода if (o < coords_count) // Для коррекции скорости используем гиперболический тангенс { outputs [o] = Tanh (sum); } else // Для адаптивных параметров используем сигмоиду { outputs [o] = Sigmoid (sum); } } } // Обучение на основе накопленного опыта void Learn (double learning_rate, int coords_count) { if (memory_index < memory_size) return; // Недостаточно опыта // Находим лучший опыт в памяти int best_index = 0; double best_fitness = memory [coords_count]; // Первая фитнес-функция в памяти for (int i = 1; i < memory_size; i++) { double fitness = memory [i * (coords_count + 1) + coords_count]; if (fitness > best_fitness) { best_fitness = fitness; best_index = i; } } // Если текущий опыт не лучше предыдущего, не обновляем веса if (best_fitness <= best_local_fitness) return; best_local_fitness = best_fitness; // Простой метод обновления весов int input_size = ArraySize (inputs); int output_size = ArraySize (outputs); // Простая форма градиентного обновления for (int o = 0; o < output_size; o++) { for (int i = 0; i < input_size; i++) { int weight_index = o * input_size + i; if (weight_index < ArraySize (weights)) { weights [weight_index] += learning_rate * outputs [o] * inputs [i]; } } // Обновляем смещения biases [o] += learning_rate * outputs [o]; } } // Запоминаем текущий опыт (координаты и фитнес) void MemorizeExperience (double fitness, int coords_count) { int offset = memory_index * (coords_count + 1); // Запоминаем координаты for (int c = 0; c < coords_count; c++) { memory [offset + c] = x [c]; } // Запоминаем фитнес-функцию memory [offset + coords_count] = fitness; // Обновляем индекс памяти memory_index = (memory_index + 1) % memory_size; } // Обновление лучшей позиции агента void UpdateBestPosition (double current_fitness, int coords_count) { if (current_fitness > fB) { fB = current_fitness; ArrayCopy (cB, x, 0, 0, WHOLE_ARRAY); } } };
A classe "C_AO_NOA2" representa a implementação do algoritmo NOA2 e herda da classe base "C_AO". Vamos analisar a estrutura e os principais aspectos dessa classe com mais detalhes.
Parâmetros principais:- popSize — tamanho da população de agentes (boids).
- cohesionWeight, cohesionDist — peso e distância para a regra de coesão.
- separationWeight, separationDist — peso e distância para a regra de separação.
- alignmentWeight, alignmentDist — peso e distância para a regra de alinhamento.
- maxSpeed e minSpeed — velocidades máxima e mínima dos agentes.
- learningRate — taxa de aprendizado da rede neural.
- neuralInfluence — influência da rede neural sobre o movimento dos agentes.
- explorationRate — probabilidade de diversificação aleatória no espaço de soluções.
- m_stagnationCounter e m_prevBestFitness — contador de estagnação e melhor valor anterior de adaptabilidade.
- SetParams() — método que define os parâmetros do algoritmo com base nos valores armazenados no vetor "params".
- Init() — inicialização que define os parâmetros de faixa de valores dos agentes e configura as condições iniciais de operação do algoritmo.
- Moving() — responsável pelo movimento dos agentes com base nas diferentes regras de interação.
- Revision() — utilizado para revisar o estado dos agentes durante a execução do algoritmo.
Agentes: S_NeuroBoids_Agent agent[] — vetor de agentes que representam os boids da população.
Métodos privados (para uso interno da classe):
- CalculateMass() — calcula a massa dos agentes.
- Cohesion() — implementa a regra de coesão.
- Separation() — implementa a regra de separação.
- Alignment() — implementa a regra de alinhamento.
- LimitSpeed() — limita a velocidade do agente.
- KeepWithinBounds() — mantém os agentes dentro dos limites definidos.
- Distance() — calcula a distância entre dois agentes.
- ApplyNeuralControl() — aplica o controle neural ao agente.
- AdaptiveExploration() — implementa a diversificação adaptativa.
//—————————————————————————————————————————————————————————————————————————————— // Класс нейро-боидного алгоритма оптимизации, наследуемый от C_AO //—————————————————————————————————————————————————————————————————————————————— class C_AO_NOA2 : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_NOA2 () { } C_AO_NOA2 () { ao_name = "NOA2"; ao_desc = "Neuroboids Optimization Algorithm 2 (joo)"; ao_link = "https://www.mql5.com/ru/articles/17497"; popSize = 50; // размер популяции cohesionWeight = 0.6; // вес сближения cohesionDist = 0.001; // дистанция сближения separationWeight = 0.005; // вес разделения separationDist = 0.03; // дистанция разделения alignmentWeight = 0.1; // вес выравнивания alignmentDist = 0.1; // дистанция выравнивания maxSpeed = 0.001; // максимальная скорость minSpeed = 0.0001; // минимальная скорость learningRate = 0.01; // скорость обучения нейронной сети neuralInfluence = 0.3; // влияние нейронной сети на движение explorationRate = 0.1; // вероятность случайного исследования ArrayResize (params, 12); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "cohesionWeight"; params [1].val = cohesionWeight; params [2].name = "cohesionDist"; params [2].val = cohesionDist; params [3].name = "separationWeight"; params [3].val = separationWeight; params [4].name = "separationDist"; params [4].val = separationDist; params [5].name = "alignmentWeight"; params [5].val = alignmentWeight; params [6].name = "alignmentDist"; params [6].val = alignmentDist; params [7].name = "maxSpeed"; params [7].val = maxSpeed; params [8].name = "minSpeed"; params [8].val = minSpeed; params [9].name = "learningRate"; params [9].val = learningRate; params [10].name = "neuralInfluence"; params [10].val = neuralInfluence; params [11].name = "explorationRate"; params [11].val = explorationRate; // Инициализация счетчика стагнации и предыдущего лучшего значения фитнеса m_stagnationCounter = 0; m_prevBestFitness = -DBL_MAX; } void SetParams () { popSize = (int)params [0].val; cohesionWeight = params [1].val; cohesionDist = params [2].val; separationWeight = params [3].val; separationDist = params [4].val; alignmentWeight = params [5].val; alignmentDist = params [6].val; maxSpeed = params [7].val; minSpeed = params [8].val; learningRate = params [9].val; neuralInfluence = params [10].val; explorationRate = params [11].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double cohesionWeight; // вес сближения double cohesionDist; // дистанция сближения double separationWeight; // вес разделения double separationDist; // дистанция разделения double alignmentWeight; // вес выравнивания double alignmentDist; // дистанция выравнивания double minSpeed; // минимальная скорость double maxSpeed; // максимальная скорость double learningRate; // скорость обучения нейронной сети double neuralInfluence; // влияние нейронной сети на движение double explorationRate; // вероятность случайного исследования int m_stagnationCounter; // счетчик стагнации double m_prevBestFitness; // предыдущее лучшее значение фитнеса S_NeuroBoids_Agent agent []; // агенты (боиды) private: //------------------------------------------------------------------- double distanceMax; // максимальная дистанция double speedMax []; // максимальные скорости по измерениям int neuron_size; // размер нейрона (количество входов) void CalculateMass (); // расчет масс агентов void Cohesion (S_NeuroBoids_Agent &boid, int pos); // правило сближения void Separation (S_NeuroBoids_Agent &boid, int pos); // правило разделения void Alignment (S_NeuroBoids_Agent &boid, int pos); // правило выравнивания void LimitSpeed (S_NeuroBoids_Agent &boid); // ограничение скорости void KeepWithinBounds (S_NeuroBoids_Agent &boid); // удержание в границах double Distance (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2); // расчет дистанции void ApplyNeuralControl (S_NeuroBoids_Agent &boid, int pos); // применение нейронного управления void AdaptiveExploration (); // адаптивное исследование }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" é responsável pela inicialização dos parâmetros do algoritmo e dos agentes, começando sua execução com a chamada de "StandardInit", à qual são passados os vetores de valores mínimos e máximos do intervalo e os passos de busca. Caso a inicialização padrão falhe, o método retorna imediatamente "false". Define-se o tamanho do neurônio que será utilizado na rede neural dos agentes.
Nesse caso, o tamanho é calculado como o número de coordenadas multiplicado por 2, com a adição de dois valores extras: "dist_to_best" e "current_fitness". O tamanho do vetor de agentes é então ajustado conforme o valor definido para a população "popSize". Em seguida, para cada agente, é chamado o método "Init", que inicializa seus parâmetros, incluindo a configuração da rede neural.
Cálculo da distância e velocidade máximas:
- A variável "distanceMax" é inicializada com zero.
- Para cada coordenada, calcula-se o valor máximo da velocidade com base na diferença entre os valores máximo e mínimo do intervalo.
- Também é calculada a distância máxima, como a raiz quadrada da soma dos quadrados das velocidades máximas.
O contador de estagnação (m_stagnationCounter) é reiniciado em zero, e a variável que armazena o melhor valor anterior de adaptabilidade (m_prevBestFitness) é definida como o menor valor possível. O método também define diversas variáveis globais, como os pesos de coesão, separação e alinhamento, as velocidades máximas e mínimas, a taxa de aprendizado, a influência da rede neural e a probabilidade de diversificação. Se todas as etapas forem concluídas com sucesso, o método retorna "true", confirmando que a inicialização foi realizada corretamente.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_NOA2::Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Определение размера нейрона neuron_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness // Инициализация агентов ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) { agent [i].Init (coords, neuron_size); } distanceMax = 0; ArrayResize (speedMax, coords); for (int c = 0; c < coords; c++) { speedMax [c] = rangeMax [c] - rangeMin [c]; distanceMax += MathPow (speedMax [c], 2); } distanceMax = MathSqrt (distanceMax); // Сброс счетчика стагнации и предыдущего лучшего значения фитнеса m_stagnationCounter = 0; m_prevBestFitness = -DBL_MAX; GlobalVariableSet ("#reset", 1.0); GlobalVariableSet ("1cohesionWeight", params [1].val); GlobalVariableSet ("2cohesionDist", params [2].val); GlobalVariableSet ("3separationWeight", params [3].val); GlobalVariableSet ("4separationDist", params [4].val); GlobalVariableSet ("5alignmentWeight", params [5].val); GlobalVariableSet ("6alignmentDist", params [6].val); GlobalVariableSet ("7maxSpeed", params [7].val); GlobalVariableSet ("8minSpeed", params [8].val); GlobalVariableSet ("9learningRate", params [9].val); GlobalVariableSet ("10neuralInfluence", params [10].val); GlobalVariableSet ("11explorationRate", params [11].val); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" é responsável pelo deslocamento dos agentes no ambiente, com base nos dados obtidos e na interação entre eles. Primeiramente, o método verifica o valor da variável global "#reset"; se ela for igual a 1.0, ocorre a redefinição dos parâmetros (a variável "revision" é configurada como "false" e, em seguida, retorna para "0.0"). A partir das variáveis globais, são extraídos os valores de diferentes parâmetros, como pesos de coesão, separação e alinhamento, velocidades mínima e máxima, taxa de aprendizado, influência neural e coeficiente de diversificação. Esses parâmetros podem ser ajustados para alterar o comportamento dos agentes.
Se a variável "revision" for igual a "false", ocorre a inicialização das posições "x" e das velocidades "dx" dos agentes. Para cada coordenada, são atribuídos valores aleatórios dentro do intervalo definido, enquanto as velocidades recebem pequenos valores aleatórios. Em cada coordenada também é armazenado o estado do agente, com base em sua posição atual. O método "AdaptiveExploration()" é então chamado para realizar a busca adaptativa, que pode modificar o comportamento dos agentes conforme o estado de estagnação.
Ciclo principal de movimento dos agentes (para cada um):
- O agente armazena sua experiência atual.
- A melhor posição encontrada pelo agente é atualizada.
- Os dados de entrada da rede neural do agente são atualizados.
- É realizada a propagação para frente dos dados através da rede neural.
- Os agentes treinam com base na experiência acumulada.
Aplicação das regras e movimento: inicia-se novamente o laço sobre os agentes, e para cada um são aplicadas as regras padrão do algoritmo dos boids:
- Coesão (Cohesion): os agentes tendem a se aproximar uns dos outros.
- Separação (Separation): os agentes evitam aproximação excessiva para não colidirem.
- Alinhamento (Alignment): os agentes procuram mover-se na mesma direção que seus vizinhos.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA2::Moving () { double reset = GlobalVariableGet ("#reset"); if (reset == 1.0) { revision = false; GlobalVariableSet ("#reset", 0.0); } // Получение параметров из глобальных переменных для интерактивной настройки cohesionWeight = GlobalVariableGet ("1cohesionWeight"); cohesionDist = GlobalVariableGet ("2cohesionDist"); separationWeight = GlobalVariableGet ("3separationWeight"); separationDist = GlobalVariableGet ("4separationDist"); alignmentWeight = GlobalVariableGet ("5alignmentWeight"); alignmentDist = GlobalVariableGet ("6alignmentDist"); maxSpeed = GlobalVariableGet ("7maxSpeed"); minSpeed = GlobalVariableGet ("8minSpeed"); learningRate = GlobalVariableGet ("9learningRate"); neuralInfluence = GlobalVariableGet ("10neuralInfluence"); explorationRate = GlobalVariableGet ("11explorationRate"); // Инициализация начальных позиций и скоростей if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001; a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Адаптивное исследование в зависимости от стагнации AdaptiveExploration (); //---------------------------------------------------------------------------- // Основной цикл движения боидов for (int i = 0; i < popSize; i++) { // Запоминаем текущий опыт agent [i].MemorizeExperience (a [i].f, coords); // Обновляем лучшую позицию агента agent [i].UpdateBestPosition (a [i].f, coords); // Обновляем входы нейронной сети agent [i].UpdateInputs (cB, a [i].f, coords); // Прямое распространение по нейронной сети agent [i].ForwardPass (coords); // Обучение на основе накопленного опыта agent [i].Learn (learningRate, coords); } // Расчет масс CalculateMass (); // Применение правил и движение for (int i = 0; i < popSize; i++) { // Стандартные правила алгоритма боидов Cohesion (agent [i], i); Separation (agent [i], i); Alignment (agent [i], i); // Применение нейронного управления ApplyNeuralControl (agent [i], i); // Ограничение скорости и удержание в границах LimitSpeed (agent [i]); KeepWithinBounds (agent [i]); // Обновление позиций for (int c = 0; c < coords; c++) { agent [i].x [c] += agent [i].dx [c]; a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateMass" realiza o cálculo da "massa" dos agentes com base em sua adaptabilidade (produtividade) e normaliza esses valores. As variáveis "maxMass" e "minMass" são inicializadas com os valores -DBL_MAX e DBL_MAX, respectivamente. Essas variáveis são utilizadas para encontrar os maiores e menores valores de adaptabilidade entre toda a população de agentes. O método verifica se há pelo menos um agente, confirmando que "popSize" (tamanho da população) é maior que zero. Se não houver agentes, o método encerra a execução. No primeiro laço, percorrem-se todos os agentes (de 0 até popSize), e para cada um é verificado se sua adaptabilidade (valor a[i].f) é maior que o valor atual de "maxMass" ou menor que "minMass".
Como resultado desse laço, são determinados os valores máximo e mínimo de adaptabilidade entre todos os agentes. No segundo laço, novamente são percorridos todos os agentes, e para cada um é calculada sua "massa" (variável "m") utilizando a função "u.Scale", que normaliza os valores de adaptabilidade.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA2::CalculateMass () { double maxMass = -DBL_MAX; double minMass = DBL_MAX; // Проверка на наличие данных перед вычислениями if (popSize <= 0) return; for (int i = 0; i < popSize; i++) { if (a [i].f > maxMass) maxMass = a [i].f; if (a [i].f < minMass) minMass = a [i].f; } for (int i = 0; i < popSize; i++) { agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.1, 1.0); } } //——————————————————————————————————————————————————————————————————————————————
O método "ApplyNeuralControl" é responsável por aplicar o controle baseado nas saídas da rede neural ao agente do tipo "boid". O método percorre todas as coordenadas do agente "coords". Para cada coordenada "c", verifica-se se o índice atual está dentro dos limites do vetor de saídas "boid.outputs". Caso o índice seja válido, a velocidade "dx[c]" do agente é ajustada com base no valor correspondente das saídas da rede neural, multiplicado pela influência da rede "neuralInfluence".
O tamanho do vetor "boid.outputs" é extraído para simplificar as verificações subsequentes. Para os coeficientes de coesão, separação e alinhamento — "cohesion_factor", "separation_factor" e "alignment_factor" — o método verifica se os índices correspondentes estão dentro dos limites do vetor de saídas. Se algum índice estiver fora dos limites, é atribuído o valor padrão 0.5. Esses coeficientes são utilizados para ajustar os pesos básicos de acordo com o impacto da rede neural. Eles influenciam o comportamento dos agentes, modificando os pesos de coesão, separação e alinhamento:
- local_cohesion define o peso de coesão.
- local_separation define o peso de separação.
- local_alignment define o peso de alinhamento.
O método também verifica se é necessário realizar diversificação aleatória, utilizando a probabilidade definida em "explorationRate", se a condição for satisfeita, é escolhida uma coordenada aleatória "c" para ser perturbada. O tamanho da perturbação "perturbation_size" é calculado com base na massa do agente (que representa sua adaptabilidade) e na faixa de valores possíveis dessa coordenada. Isso permite controlar a intensidade da variação aleatória de acordo com a massa do agente. À velocidade "dx[c]" é então adicionado um deslocamento aleatório, selecionado dentro do intervalo de –"perturbation_size" até +"perturbation_size". O método "ApplyNeuralControl" integra os resultados do processamento da rede neural ao controle de movimento dos agentes. Ele ajusta suas velocidades com base nos dados calculados e também considera a necessidade de diversificação aleatória quando apropriado.
//—————————————————————————————————————————————————————————————————————————————— // Применение нейронного управления к боиду void C_AO_NOA2::ApplyNeuralControl (S_NeuroBoids_Agent &boid, int pos) { // Используем выходы нейронной сети для коррекции скорости for (int c = 0; c < coords; c++) { // Проверяем, что индекс не выходит за границы массива if (c < ArraySize (boid.outputs)) { // Применяем нейронную коррекцию скорости с заданным влиянием boid.dx [c] += boid.outputs [c] * neuralInfluence; } } // Используем выходы нейронной сети для адаптации параметров стаи // Проверяем, что индексы не выходят за границы массива int output_size = ArraySize (boid.outputs); double cohesion_factor = (coords < output_size) ? boid.outputs [coords] : 0.5; double separation_factor = (coords + 1 < output_size) ? boid.outputs [coords + 1] : 0.5; double alignment_factor = (coords + 2 < output_size) ? boid.outputs [coords + 2] : 0.5; // Масштабируем базовые веса с учетом нейронной адаптации // Эти переменные локальные и не изменяют глобальные параметры double local_cohesion = cohesionWeight * (0.5 + cohesion_factor); double local_separation = separationWeight * (0.5 + separation_factor); double local_alignment = alignmentWeight * (0.5 + alignment_factor); // Случайное исследование с заданной вероятностью if (u.RNDprobab () < explorationRate) { // Выбираем случайную координату для возмущения int c = (int)u.RNDfromCI (0, coords - 1); // Адаптивный размер возмущения в зависимости от массы (фитнеса) double perturbation_size = (1.0 - boid.m) * (rangeMax [c] - rangeMin [c]) * 0.01; // Добавляем случайное возмущение boid.dx [c] += u.RNDfromCI (-perturbation_size, perturbation_size); } } //——————————————————————————————————————————————————————————————————————————————
O método "AdaptiveExploration" da classe "C_AO_NOA2" implementa a diversificação adaptativa conforme o estágio de estagnação do processo de otimização. O método inicia verificando se o valor da função objetivo "fB" mudou em relação ao valor anterior armazenado em "m_prevBestFitness". Se a diferença entre eles for menor que 0.000001, considera-se que não houve progresso, e o contador de estagnação "m_stagnationCounter" é incrementado. Caso contrário, a estagnação é encerrada, o contador é zerado, e o valor atual "fB" é armazenado como o novo melhor.
Se o número de ocorrências de estagnação exceder 20, a probabilidade de diversificação aleatória "explorationRate" é aumentada, mas limitada a 0.5, para evitar um nível excessivo de variação aleatória. A cada 50 iterações de estagnação ocorre um reinício parcial: 70% dos agentes da população são reiniciados com novos valores aleatórios dentro dos limites definidos por "rangeMin" e "rangeMax". Os agentes de melhor desempenho mantêm suas posições e não são alterados. Após o reinício, o contador de estagnação é zerado.
Se houver progresso e o número de parâmetros "params" for maior que 11, a probabilidade de diversificação "explorationRate" é definida a partir do vetor de parâmetros. Caso o número de parâmetros seja menor, é atribuído o valor padrão de 0.1.
//—————————————————————————————————————————————————————————————————————————————— // Адаптивное исследование в зависимости от стагнации void C_AO_NOA2::AdaptiveExploration () { // Определяем, есть ли прогресс в поиске if (MathAbs (fB - m_prevBestFitness) < 0.000001) { m_stagnationCounter++; } else { m_stagnationCounter = 0; m_prevBestFitness = fB; } // Увеличиваем исследование при стагнации if (m_stagnationCounter > 20) { // Увеличиваем вероятность случайного исследования explorationRate = MathMin (0.5, explorationRate * 1.5); // Каждые 50 итераций стагнации выполняем частичный рестарт if (m_stagnationCounter % 50 == 0) { // Перезапускаем 70% популяции, оставляя лучших агентов int restart_count = (int)(popSize * 0.7); for (int i = popSize - restart_count; i < popSize; i++) { for (int c = 0; c < coords; c++) { agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001; } } // Сбрасываем счетчик стагнации m_stagnationCounter = 0; } } else { // При хорошем прогрессе используем обычный уровень исследования if (11 < ArraySize (params)) { explorationRate = params [11].val; } else { explorationRate = 0.1; // значение по умолчанию } } } //——————————————————————————————————————————————————————————————————————————————
O método "Cohesion" da classe "C_AO_NOA2" é responsável por implementar o comportamento de convergência ("cohesion") no modelo de agentes do tipo boid. São declaradas as seguintes variáveis:
- centerX — vetor utilizado para armazenar as coordenadas do centro de massa dos agentes vizinhos. O tamanho do vetor corresponde ao número de coordenadas "coords".
- numNeighbors — contador de vizinhos que rastreia a quantidade de agentes localizados dentro do raio definido (levando em conta suas massas).
- sumMass — soma das massas dos agentes vizinhos, usada para normalizar as coordenadas do centro de massa.
O primeiro laço (de 0 até popSize) soma as massas de todos os agentes da população, excluindo o boid atual (agente com índice "pos"). O segundo laço percorre todos os agentes e verifica se eles estão dentro da distância máxima multiplicada pelo coeficiente "cohesionDist" em relação ao boid atual. Se a distância até o agente for menor que o limite especificado, as coordenadas desse agente (ponderadas por sua massa) são adicionadas a "centerX", e o contador "numNeighbors" é incrementado.
Após calcular a soma das coordenadas e das massas dos vizinhos, o método verifica se há vizinhos (ou seja, numNeighbors > 0) e se a soma das massas (sumMass > 0.0) é positiva, e se essas condições forem satisfeitas, as coordenadas do centro de massa são normalizadas (dividindo-se pela soma das massas). Em seguida, a velocidade "dx" do boid é ajustada na direção do centro de massa, aplicando o peso definido em "cohesionWeight", isso significa que o boid se moverá em direção ao centro de massa de seus vizinhos, levando em consideração a influência de suas respectivas massas.
O método "Cohesion" calcula o centro de massa e ajusta a velocidade do boid atual de forma que ele "converja" para esse ponto central. Esse comportamento é um dos elementos fundamentais na simulação do movimento coletivo em grupo ou bando. Os parâmetros "cohesionDist" e "cohesionWeight" determinam, respectivamente, a distância dentro da qual esse comportamento atua e a intensidade da influência do centro de massa sobre o deslocamento dos boids.
//—————————————————————————————————————————————————————————————————————————————— // Найти центр масс других боидов и скорректировать скорость в направлении центра масс void C_AO_NOA2::Cohesion (S_NeuroBoids_Agent &boid, int pos) { double centerX []; ArrayResize (centerX, coords); ArrayInitialize (centerX, 0.0); int numNeighbors = 0; double sumMass = 0; for (int i = 0; i < popSize; i++) { if (pos != i) sumMass += agent [i].m; } for (int i = 0; i < popSize; i++) { if (pos != i) { if (Distance (boid, agent [i]) < distanceMax * cohesionDist) { for (int c = 0; c < coords; c++) { centerX [c] += agent [i].x [c] * agent [i].m; } numNeighbors++; } } } if (numNeighbors > 0 && sumMass > 0.0) { for (int c = 0; c < coords; c++) { centerX [c] /= sumMass; boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight; } } } //——————————————————————————————————————————————————————————————————————————————
O método "Separation" da classe "C_AO_NOA2" implementa o comportamento de repulsão ("separation") entre os agentes do modelo, cuja função é evitar colisões entre o boid atual e seus vizinhos, "moveX" (assim como em "cohesionDist") é usada como vetor de deslocamento, armazenando as forças de afastamento aplicadas para empurrar o boid para longe de outros agentes próximos.
O tamanho do vetor corresponde ao número de coordenadas "coords". O vetor "moveX" é inicializado com zeros para evitar o acúmulo de valores residuais, em seguida, todos os agentes da população são percorridos (de 0 até popSize). Depois, é verificado se o agente está próximo do boid atual. Essa verificação é feita com a função "Distance", e, caso a distância entre o boid e o agente seja menor que o valor máximo permitido (multiplicado pelo coeficiente "separationDist"), para cada coordenada é subtraída a posição do agente da posição do boid atual, criando um vetor que aponta na direção oposta, ou seja, afastando o boid do agente vizinho.
Após a conclusão do laço sobre os agentes, a velocidade atual "dx" do boid é incrementada pelo vetor de deslocamento "moveX", multiplicado pelo coeficiente "separationWeight". Isso permite controlar a intensidade da força de repulsão: quanto maior o valor de "separationWeight", mais fortemente o boid evita colisões.
O método "Separation" implementa o comportamento que faz com que o boid se afaste de seus vizinhos mais próximos, prevenindo colisões. Esse aspecto é fundamental na simulação do comportamento coletivo, pois mantém um "espaço pessoal" para cada agente e favorece interações mais naturais entre eles. Parâmetros como "separationDist" e "separationWeight" permitem ajustar, de forma flexível, tanto o raio de ação quanto a intensidade do efeito de repulsão, respectivamente.
//—————————————————————————————————————————————————————————————————————————————— // Отталкивание от других боидов, чтобы избежать столкновений void C_AO_NOA2::Separation (S_NeuroBoids_Agent &boid, int pos) { double moveX []; ArrayResize (moveX, coords); ArrayInitialize (moveX, 0.0); for (int i = 0; i < popSize; i++) { if (pos != i) { if (Distance (boid, agent [i]) < distanceMax * separationDist) { for (int c = 0; c < coords; c++) { moveX [c] += boid.x [c] - agent [i].x [c]; } } } } for (int c = 0; c < coords; c++) { boid.dx [c] += moveX [c] * separationWeight; } } //——————————————————————————————————————————————————————————————————————————————
O método "Alignment" da classe "C_AO_NOA2" implementa o comportamento de alinhamento ("alignment") entre os agentes do modelo. Esse comportamento leva os boids a ajustar suas velocidades em relação às de seus vizinhos, promovendo um movimento mais harmônico e coordenado no grupo, "avgDX" (um vetor) é usada para armazenar o vetor médio de velocidade dos agentes vizinhos. O tamanho do vetor é igual ao número de coordenadas "coords", e "numNeighbors" é o contador que registra quantos vizinhos se encontram dentro da distância especificada.
O laço percorre todos os agentes da população. Dentro dele, verifica-se se o agente atual não é o próprio boid sendo analisado. Se a distância até outro agente for menor que o valor máximo multiplicado pelo coeficiente "alignmentDist", a velocidade "dx" desse agente é somada ao vetor "avgDX". O contador "numNeighbors" é então incrementado em 1. Após o término do laço, caso sejam encontrados vizinhos (ou seja, numNeighbors > 0), a velocidade média (avgDX) é calculada dividindo o vetor somado pelo número de vizinhos. Em seguida, a velocidade atual "dx" do boid é ajustada em direção à velocidade média de seus vizinhos, levando em conta o coeficiente "alignmentWeight".
O método "Alignment" permite que o boid adapte sua velocidade de acordo com as velocidades de seus vizinhos. Esse comportamento ajuda os grupos de boids a se moverem de forma mais coordenada e reduz a probabilidade de conflitos ou mudanças bruscas de direção. Parâmetros como "alignmentDist" e "alignmentWeight" definem, respectivamente, o raio de ação do efeito de alinhamento e o grau de influência da velocidade média dos vizinhos sobre a velocidade do boid atual.//—————————————————————————————————————————————————————————————————————————————— // Выравнивание скорости с другими боидами void C_AO_NOA2::Alignment (S_NeuroBoids_Agent &boid, int pos) { double avgDX []; ArrayResize (avgDX, coords); ArrayInitialize (avgDX, 0.0); int numNeighbors = 0; for (int i = 0; i < popSize; i++) { if (pos != i) { if (Distance (boid, agent [i]) < distanceMax * alignmentDist) { for (int c = 0; c < coords; c++) { avgDX [c] += agent [i].dx [c]; } numNeighbors++; } } } if (numNeighbors > 0) { for (int c = 0; c < coords; c++) { avgDX [c] /= numNeighbors; boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight; } } } //——————————————————————————————————————————————————————————————————————————————
O método "LimitSpeed" da classe "C_AO_NOA2" tem como finalidade controlar a velocidade dos agentes (boids) no modelo, garantindo que suas velocidades permaneçam dentro de um intervalo permitido, "speed" é utilizada para armazenar a velocidade atual do boid, calculada como o comprimento do vetor de velocidade. O laço que percorre as coordenadas (coords) computa o quadrado da velocidade em cada coordenada (somando boid.dx[c] * boid.dx[c]) e acumula o resultado. Isso permite calcular o quadrado do comprimento do vetor de velocidade. Em seguida, o valor da velocidade (ou magnitude real) é obtido pela função "MathSqrt", que calcula a raiz quadrada da soma dos quadrados. Se a velocidade for maior que um pequeno valor limite (1e-10), o programa continua a execução. Caso a velocidade atual seja menor que a velocidade mínima permitida (definida como speedMax[0] * minSpeed), o vetor de velocidade "boid.dx" é normalizado (dividido por sua magnitude atual) e escalonado até o valor mínimo permitido.
Se a velocidade atual for maior que a velocidade máxima permitida (speedMax[0] * maxSpeed), de modo análogo, o vetor de velocidade é normalizado e ajustado para o valor máximo de velocidade, já se a velocidade for praticamente nula (zero ou muito próxima de zero), cada coordenada do vetor de velocidade é substituída por um pequeno valor aleatório gerado pela função "u.RNDfromCI(-1.0, 1.0)", multiplicado pela velocidade máxima.
O método "LimitSpeed" garante que a velocidade dos boids permaneça dentro dos limites aceitáveis, evitando movimentos excessivamente lentos ou rápidos. Esse comportamento contribui para uma simulação mais realista dos agentes, impedindo desvios extremos de velocidade que poderiam causar deslocamentos artificiais ou instáveis. Os parâmetros "minSpeed" e "maxSpeed" podem ser ajustados para controlar o comportamento e a dinâmica dos agentes conforme as necessidades do modelo de simulação.
//—————————————————————————————————————————————————————————————————————————————— // Ограничение скорости void C_AO_NOA2::LimitSpeed (S_NeuroBoids_Agent &boid) { double speed = 0; for (int c = 0; c < coords; c++) { speed += boid.dx [c] * boid.dx [c]; } speed = MathSqrt (speed); // Если скорость не нулевая (предотвращаем деление на ноль) if (speed > 1e-10) { // Если скорость слишком мала, увеличиваем её if (speed < speedMax [0] * minSpeed) { for (int c = 0; c < coords; c++) { boid.dx [c] = boid.dx [c] / speed * speedMax [c] * minSpeed; } } // Если скорость слишком велика, уменьшаем её else if (speed > speedMax [0] * maxSpeed) { for (int c = 0; c < coords; c++) { boid.dx [c] = boid.dx [c] / speed * speedMax [c] * maxSpeed; } } } else { // Если скорость почти нулевая, задаем небольшую случайную скорость for (int c = 0; c < coords; c++) { boid.dx [c] = u.RNDfromCI (-1.0, 1.0) * speedMax [c] * minSpeed; } } } //——————————————————————————————————————————————————————————————————————————————
O método "KeepWithinBounds" da classe "C_AO_NOA2" tem a função de manter o agente (boid) dentro dos limites definidos. Caso o boid se aproxime demais das bordas da área, esse método altera sua direção e aplica um pequeno impulso que o empurra de volta para dentro dos limites. O método começa com um laço que percorre todas as coordenadas, permitindo que ele funcione em espaços multidimensionais.
Para cada coordenada, é verificado se a posição do boid (boid.x[c]) está abaixo do limite mínimo (rangeMin[c]); se estiver, a direção de sua velocidade (boid.dx[c]) é invertida com a instrução "boid.dx[c] = -1.0". Isso faz com que o boid se mova na direção oposta. Em seguida, adiciona-se um pequeno impulso afastando-o da borda: (rangeMax[c] - rangeMin[c]) * 0.001, o que ajuda a empurrar o boid de volta para dentro da região de busca.
É feita uma verificação análoga para o limite máximo (rangeMax[c]): se a posição do boid ultrapassar esse limite, sua velocidade também é invertida e ajustada, mas com a subtração de um pequeno valor, de forma semelhante ao caso anterior.
O método "KeepWithinBounds" limita de maneira eficaz o movimento dos boids dentro da região estabelecida, evitando que ultrapassem os limites e garantindo que retornem gradualmente ao interior do espaço definido.
//—————————————————————————————————————————————————————————————————————————————— // Удержание боида в границах. Если он оказывается слишком близко к краю, // подталкиваем его обратно и меняем направление. void C_AO_NOA2::KeepWithinBounds (S_NeuroBoids_Agent &boid) { for (int c = 0; c < coords; c++) { if (boid.x [c] < rangeMin [c]) { boid.dx [c] *= -1.0; // Добавляем небольшой толчок от границы boid.dx [c] += (rangeMax [c] - rangeMin [c]) * 0.001; } if (boid.x [c] > rangeMax [c]) { boid.dx [c] *= -1.0; // Добавляем небольшой толчок от границы boid.dx [c] -= (rangeMax [c] - rangeMin [c]) * 0.001; } } } //——————————————————————————————————————————————————————————————————————————————
O método "Distance" da classe "C_AO_NOA2" é utilizado para calcular a distância entre dois agentes (boids) em um espaço multidimensional. Ele emprega a fórmula da distância euclidiana, sendo "dist" a variável onde é acumulada a soma dos quadrados das diferenças entre as coordenadas dos dois boids.
O método inicia um laço que percorre todas as coordenadas, permitindo calcular a distância em espaços de qualquer dimensão. Para cada coordenada "c", é calculado o quadrado da diferença entre as respectivas coordenadas dos dois boids: boid1.x[c] - boid2.x[c].
Os resultados ((boid1.x[c] - boid2.x[c])²) são somados à variável "dist". Após o término do laço, a variável "dist" conterá a soma dos quadrados das diferenças das coordenadas. Para obter a distância real, o método utiliza "MathSqrt" para calcular a raiz quadrada dessa soma, seguindo a fórmula padrão da distância euclidiana.
//—————————————————————————————————————————————————————————————————————————————— // Расчет расстояния между двумя боидами double C_AO_NOA2::Distance (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2) { double dist = 0; for (int c = 0; c < coords; c++) { dist += MathPow (boid1.x [c] - boid2.x [c], 2); } return MathSqrt (dist); } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" da classe "C_AO_NOA2" é responsável por atualizar as informações sobre a melhor solução encontrada durante o processo de otimização. Esse processo envolve a atualização do valor da função de adaptabilidade, bem como das coordenadas correspondentes a esse valor. O método também monitora o progresso e ajusta os parâmetros do algoritmo quando há melhorias significativas. Ele percorre toda a população, representada pelo vetor "a", que contém "popSize" (número de agentes).
Dentro do laço, cada agente é verificado para determinar se seu valor de adaptabilidade (a[i].f) é maior que o melhor valor atual (fB). Se o agente apresentar um valor de adaptabilidade superior, o melhor valor global da função de adaptabilidade é atualizado, atribuindo-se a "fB" o novo valor "a[i].f". Em seguida, as coordenadas da melhor solução também são atualizadas. Para cada coordenada "c", o vetor "cB" (que contém as coordenadas da melhor solução) recebe os valores correspondentes do agente atual. O contador de estagnação (m_stagnationCounter) é redefinido para zero, pois foi identificada uma melhoria na solução.
O método utiliza a variável "hasProgress" para determinar se houve progresso. Isso é feito calculando a diferença absoluta entre o valor atual e o anterior da melhor adaptabilidade (MathAbs(fB - m_prevBestFitness)); se essa diferença for maior que 0.000001, considera-se que houve progresso. Caso o progresso seja confirmado, a variável "m_prevBestFitness" é atualizada para o novo valor "fB".
Além disso, ocorre uma adaptação da taxa de diversificação "explorationRate": ela é reduzida quando uma melhoria é encontrada, levando em conta um dos parâmetros do vetor "params" e o valor atual de "explorationRate".
//—————————————————————————————————————————————————————————————————————————————— // Обновление лучшего найденного решения void C_AO_NOA2::Revision () { // Обновляем лучшие координаты и значение фитнес-функции for (int i = 0; i < popSize; i++) { // Обновление глобального лучшего решения if (a [i].f > fB) { fB = a [i].f; for (int c = 0; c < coords; c++) { cB [c] = a [i].c [c]; } // Сбрасываем счетчик стагнации при нахождении лучшего решения m_stagnationCounter = 0; } } // Проверка наличия прогресса для адаптации параметров алгоритма bool hasProgress = MathAbs (fB - m_prevBestFitness) > 0.000001; if (hasProgress) { m_prevBestFitness = fB; explorationRate = MathMax (params [11].val * 0.5, explorationRate * 0.9); } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Os resultados dos testes foram relativamente modestos.NOA2|Neuroboids Optimization Algorithm 2 (joo)|50.0|0.6|0.001|0.005|0.03|0.1|0.1|0.1|0.01|0.01|0.3|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.47680799582735267
25 Hilly's; Func runs: 10000; result: 0.30763714006051013
500 Hilly's; Func runs: 10000; result: 0.2544737238936433
=============================
5 Forest's; Func runs: 10000; result: 0.3238017030688524
25 Forest's; Func runs: 10000; result: 0.20976876473929068
500 Forest's; Func runs: 10000; result: 0.15740101965732595
=============================
5 Megacity's; Func runs: 10000; result: 0.27076923076923076
25 Megacity's; Func runs: 10000; result: 0.14676923076923082
500 Megacity's; Func runs: 10000; result: 0.09729230769230844
=============================
All score: 2.24472 (24.94%)
Na visualização, é possível observar as capacidades limitadas de busca do algoritmo. A possibilidade de modificar parâmetros externos por meio de variáveis globais permite realizar experimentos com o comportamento dos boids, revelando padrões interessantes de movimentação. Abaixo estão representadas algumas visualizações de comportamentos possíveis.
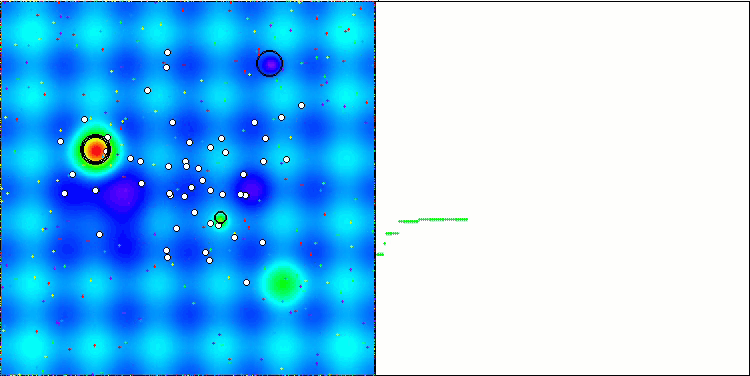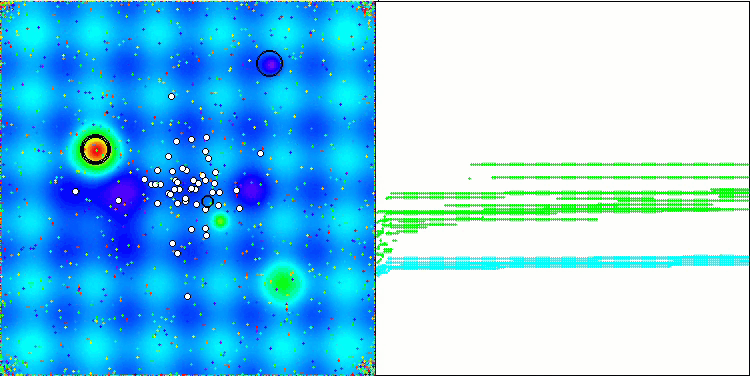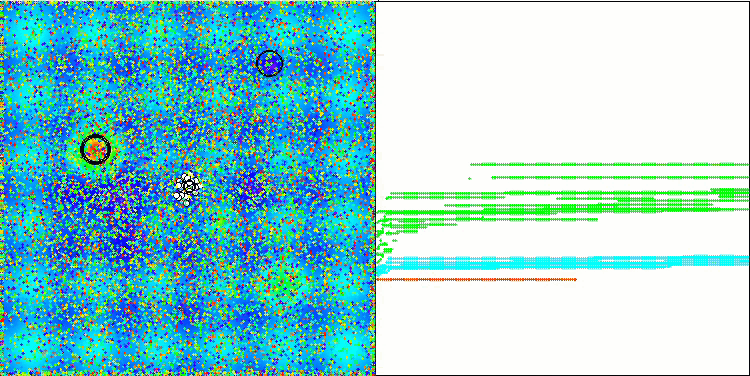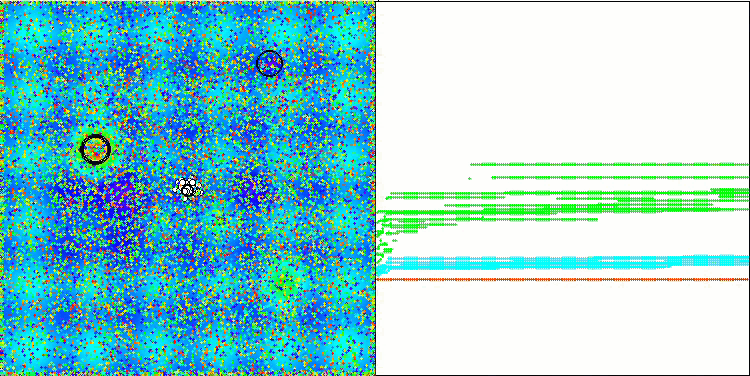
NOA2 na função de teste Hilly
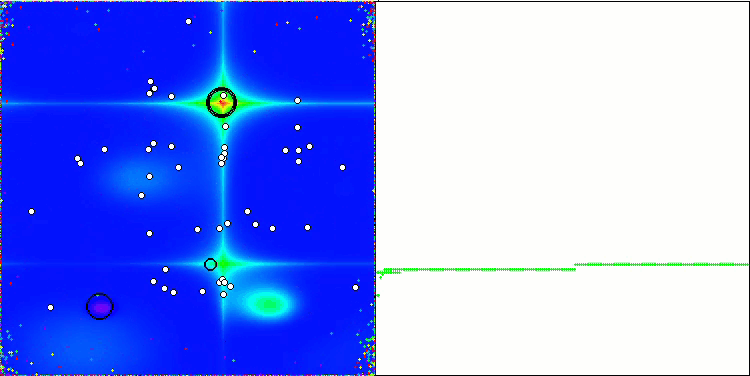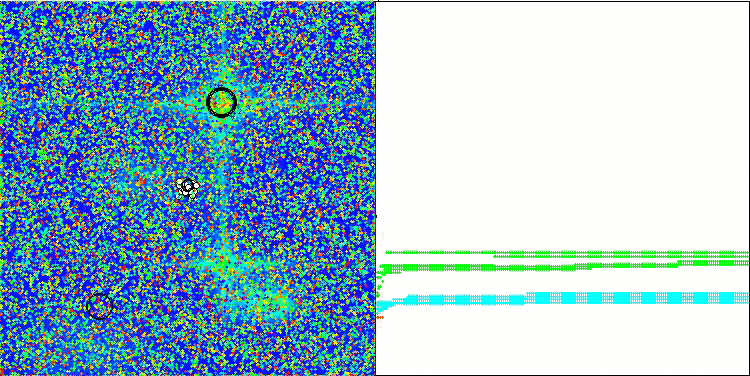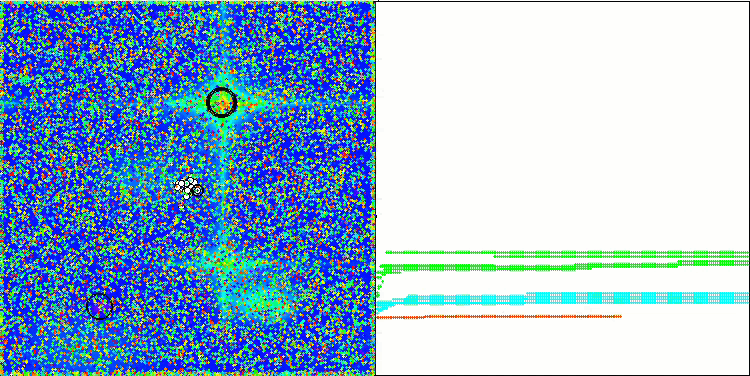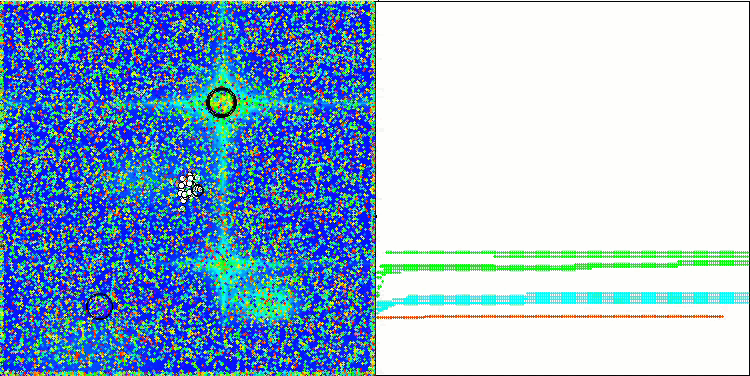
NOA2 na função de teste Forest
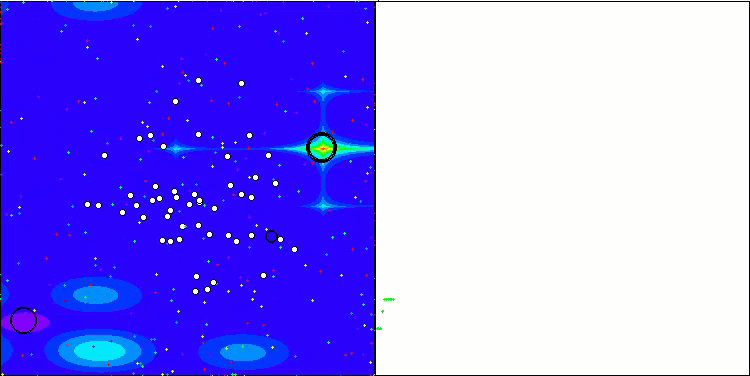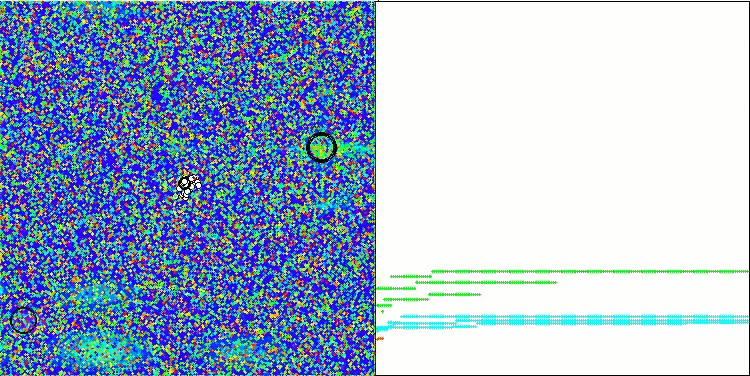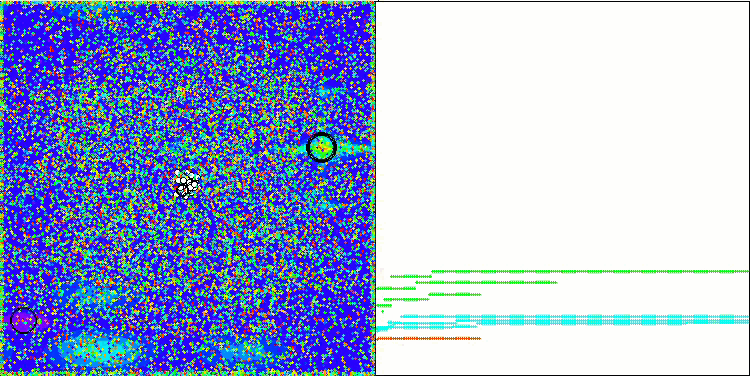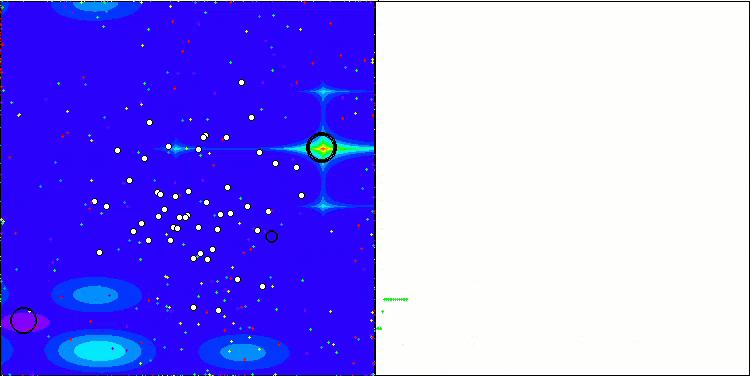
NOA2 na função de teste Megacity
Com base nos testes realizados, o algoritmo NOA2, em sua versão básica, é apresentado apenas para fins de familiarização na nossa tabela comparativa de algoritmos populacionais de otimização.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 43 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 44 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 45 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| NOA2 | neuroboids optimization algorithm 2(joo) | 0,47681 | 0,30764 | 0,25447 | 1,03892 | 0,32380 | 0,20977 | 0,15740 | 0,69097 | 0,27077 | 0,14677 | 0,09729 | 0,51483 | 2,245 | 24,94 | |
Considerações finais
O algoritmo de otimização neuroboid (NOA2), desenvolvido por mim, representa uma abordagem híbrida que combina os princípios da inteligência de enxame (algoritmo de boids) com o controle baseado em redes neurais. A ideia central é o uso de uma rede neural para o controle adaptativo dos parâmetros de comportamento dos agentes boids. Na implementação atual, é utilizada uma rede neural simples de camada única, sem camadas ocultas. Ela é composta por uma camada de entrada, que recebe as coordenadas atuais, velocidades, distância até a melhor solução e o valor da função de adaptabilidade, e uma camada de saída, que define as correções de velocidade e os parâmetros adaptativos das regras de comportamento do grupo de boids.
Nesta versão, não há camadas intermediárias. O número de entradas é definido como (coords * 2 + 2), onde "coords" representa o número de dimensões do espaço de busca. As saídas incluem uma correção para cada coordenada e três parâmetros adicionais destinados à adaptação das regras do enxame. O algoritmo possui um grande número de parâmetros ajustáveis, o que torna difícil encontrar a combinação ideal e testei diversas variações, mas ainda não encontrei um conjunto que proporcionasse resultados consistentemente superiores nas funções de teste.
No estado atual, o algoritmo serve claramente como uma demonstração conceitual e, de modo geral, representa um experimento interessante na área de métodos híbridos de otimização, mas não apresenta desempenho suficiente para ser considerado competitivo. O NOA2 obteve uma pontuação mínima nos testes realizados e deve ser visto principalmente como uma ilustração de como pode ser feita a hibridização de algoritmos. Para pesquisadores e desenvolvedores interessados, o código do NOA2 pode servir como ponto de partida para experimentos com diferentes configurações e parâmetros, bem como para o desenvolvimento de algoritmos híbridos de otimização mais avançados que combinem os pontos fortes dos métodos populacionais e das técnicas de aprendizado de máquina.
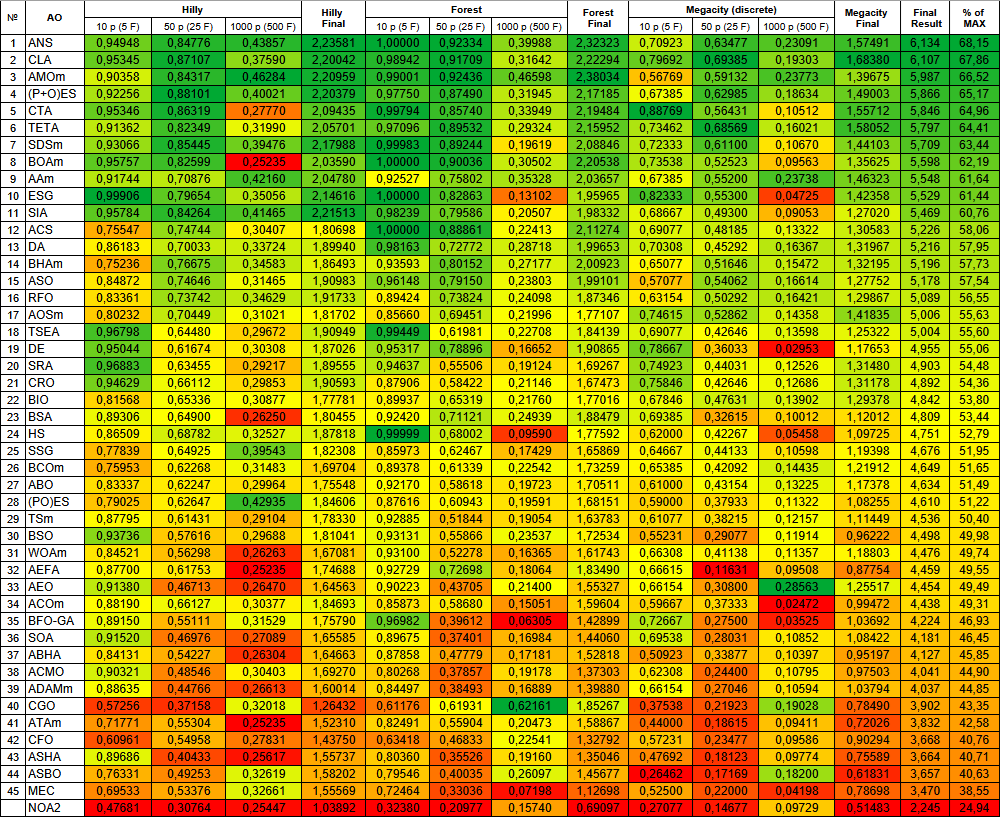
Figura 3. Gradação de cores dos algoritmos de acordo com os testes correspondentes
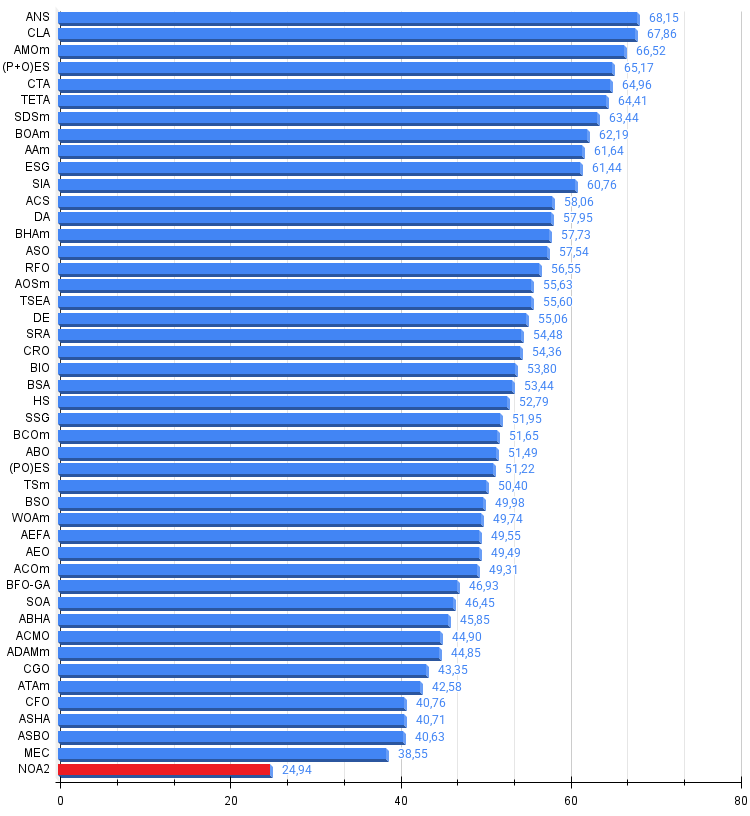
Figura 4. Histograma dos resultados dos testes dos algoritmos (em escala de 0 a 100, quanto maior melhor, onde 100 é o resultado teórico máximo possível, no arquivo compactado há um script para calcular a tabela de classificação)
Vantagens e desvantagens do algoritmo NOA2:
Vantagens:
- Uma ideia interessante em termos de concepção e implementação.
Desvantagens:
- Resultados fracos.
O artigo inclui um arquivo com as versões mais recentes dos códigos dos algoritmos. O autor não assume responsabilidade pela precisão absoluta das descrições dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e considerações apresentadas neste texto baseiam-se exclusivamente nos resultados experimentais obtidos.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do ambiente de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente unificado de testes para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_NOA2.mq5 | Script | Ambiente de teste específico para o NOA2 |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17497
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Negociando com o Calendário Econômico do MQL5 (Parte 5): Aprimorando o Painel com Controles Responsivos e Botões de Filtro
Negociando com o Calendário Econômico do MQL5 (Parte 5): Aprimorando o Painel com Controles Responsivos e Botões de Filtro
 Desenvolvimento de estratégias de trading de tendência baseadas em aprendizado de máquina
Desenvolvimento de estratégias de trading de tendência baseadas em aprendizado de máquina
 Como publicar código no CodeBase: Guia prático
Como publicar código no CodeBase: Guia prático
 Reimaginando Estratégias Clássicas (Parte 12): Estratégia de Breakout EURUSD
Reimaginando Estratégias Clássicas (Parte 12): Estratégia de Breakout EURUSD
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso