MetaTrader 5 / Tester
Русский Español Português
preview
Neuroboids Optimization Algorithm 2 (NOA2)

Neuroboids Optimization Algorithm 2 (NOA2)

MetaTrader 5 — Tester |
159 0
Andrey Dik
Andrey Dik

Contents

  1. Introduction
  2. Implementation of the algorithm
  3. Test results


Introduction

As I delved deeper into optimization algorithms over the years, I was often drawn by two parallel inspirations: the self-organization of biological swarms and the adaptive learning capabilities of neural networks. The synthesis of these two paradigms led me to develop a hybrid approach algorithm that combines the spatial intelligence of Craig Reynolds' Boids with the adaptive learning capabilities of neural networks.

My journey began with the observation that traditional swarm algorithms, while suitable for exploring complex search spaces through collective behavior, often lack the ability to learn from the history of their explorations. Conversely, neural networks are excellent at learning complex patterns, but may struggle to effectively explore spatial patterns when directly applied to optimization problems. The question that motivated my research was deceptively simple: what if each agent in a swarm could learn to improve its movement strategies using a dedicated neural network?

The resulting algorithm uses agents that follow the classical boid rules of cohesion, separation, and alignment, allowing them to self-organize and efficiently explore the search space. However, unlike traditional boid implementations, each agent is equipped with a multi-layer neural network that continuously learns from the agent's experience, adapting its movement strategies to the specific characteristics of the fitness landscape. This level of neural control gradually influences the behavior of the boids, shifting from strategies that dominate exploration in early iterations to exploitation-oriented movement as promising regions are identified.

What I found most fascinating during development was observing how neural networks evolved different strategies depending on their position in the search space. Agents near promising regions developed neural patterns that enhanced local exploitation, while agents in sparse regions supported exploratory behavior. This emergent specialization arose naturally from individual learning processes, creating a swarm with heterogeneous, context-dependent behavior, without apparent global coordination.

In this article, I will present the architecture, implementation details, and performance analysis of the NOA2 algorithm, as well as demonstrate its capabilities on various benchmark functions. 


Implementation of the algorithm

As I have already mentioned, the main idea of the neuroboids algorithm is to combine two paradigms: the collective intelligence of swarm algorithms and the adaptive learning of neural networks.

In the traditional boids algorithm, proposed by Craig Reynolds, agents follow three simple rules: convergence (moving toward the center of the group), separation (avoiding collisions), and alignment (matching speed with neighbors). These rules create realistic group behavior, similar to the behavior of birds in flocks. Neuroboids extend this concept by equipping each agent with an individual neural network that learns from the agent's experience exploring the search space. This neural network performs two key functions:

  1. Adaptive motion control adjusts the agent's speed based on its current state and movement history.
  2. Modification of the standard rules of boids dynamically adjusts the influence of convergence, separation, and alignment rules depending on the context.

The result is a hybrid algorithm where each agent retains the social behavior necessary for efficient exploration of the space, but at the same time individually adapts to the fitness function landscape through learning. This creates a self-regulating balance between exploration and exploitation.

The key advantages of this approach are the independent learning of agents in optimal movement strategies, as a result of which the algorithm automatically adapts to different types of optimization landscapes, while preserving the exploration of space, thanks to collective behavior without centralized control. Let me give you a simple analogy: imagine a flock of birds flying in the sky. They move in a coordinated manner: no one collides, they stick together and fly in the same direction. This behavior can be described by three simple rules: stay close to your neighbors (do not break away from the flock), do not collide with your neighbors (keep your distance), and fly in the same direction (maintain a common course).

This is the basis of the so-called boid ("bird-oid") algorithm. Each bird in the flock not only follows these rules, but also learns from its own experience. The bird remembers which actions led to success (for example, finding more food) and which did not. Over time, the bird becomes smarter and makes better decisions about how to fly. This is the essence of the neuroboids algorithm: combining simple rules of group movement with the ability of each participant to learn from their own experience. The "neuro" in the name indicates the ability to learn. This approach is particularly interesting because it combines the power of collective research (no one misses an important area) with the benefits of individual learning (everyone becomes the best in their field of research).

NOA2-illustration

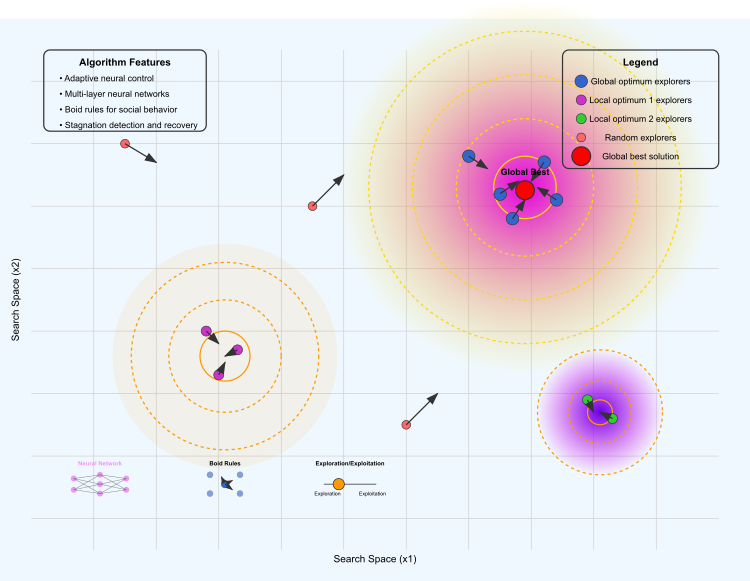
Figure 1. NOA2 algorithm operation  

The illustration shows the following key elements: the optimization landscape, where the yellow-purple area represents the global optimum, the orange and purple areas represent local optimums, and the contour lines show the "height" of the fitness function landscape. 

Different groups of agents: blue ones explore the area of the global optimum, purple ones are concentrated around the first local optimum, green ones explore the second local optimum, and red ones perform random exploration of the space. The arrows show the direction of movement of the boids. The red dot marks the current best solution found.

NOA2-diagram

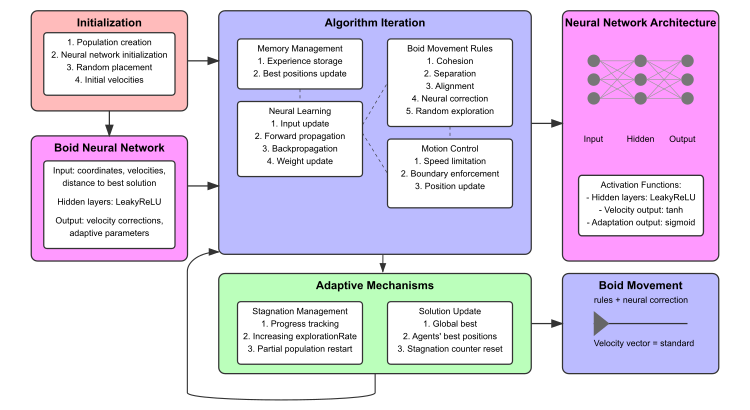
Figure 2. NOA2 algorithm operation  

The diagram includes: initialization block (red), boid neural network (pink), algorithm iterations with subblocks (blue), adaptive mechanisms (green), visualization of the neural network architecture with connection examples. The bottom section shows miniature diagrams of the neural network structure, visualization of the rules of boids' movement, and the balance between exploration and exploitation.

Having understood the basic concept, we can proceed to describing the pseudocode of the algorithm.

INITIALIZATION:

  • Set search parameters and create a population of agents.
  • For each agent: initialize a random position, a low speed, a neural network (input → hidden → output layers), and an empty experience memory.
  • Set global best fitness to negative infinity and the stagnation counter to zero.

MAIN LOOP:

  • For each iteration:

    ESTIMATION:

    • Calculate the fitness for all agents.
    • Update your personal and global best positions.
    • Save experiments in memory buffers.

    STAGNATION MANAGEMENT:

    • If there is no improvement: increase research, restart weak agents from time to time.
    • Otherwise: gradually reduce the level of research.

    NEURAL PROCESSING:

    • For each agent:
      • Forward pass: inputs (position, speed, distance to best, fitness) → hidden layers → outputs.
      • If enough experience has been collected and an improvement has been detected: update the neural weights.

    MOVEMENT UPDATE:

    • For each agent:
      • Calculate standard boid forces (cohesion, separation, alignment).
      • Apply neurally modified forces and direct neural corrections.
      • Add a random trial component with probability.
      • Enforce speed limits and respect the boundaries.
      • Update position based on final speed.

SUPPORTING CALCULATIONS:

  • Mass calculation: normalize the fitness values to assign a mass to each agent.
  • Cohesion: move towards the weighted center of mass of nearby agents.
  • Separation: avoid crowding with neighbors.
  • Alignment: coordinate speed with nearby agents.
  • Neural update: simplified backpropagation based on fitness enhancement.

RETURN: global best position and fitness.

Now everything is ready for writing the algorithm code. Assign the S_NeuroBoids_Agent structure, which will represent a neuro-boid agent based on neural network architecture for performing optimization tasks. In this implementation, the agent has the following key components and functions:

Coordinates and speeds:

  • x [] — current agent coordinates.
  • dx [] — current agent speeds.
Neural network:
  • inputs [] — input values for neurons (coordinates, speeds, distance to the best known position, etc.).
  • outputs [] — output values of the neural network (speed correction and adaptation parameters).
  • weights [] — weights of connections in the neural network.
  • biases [] — biases for neurons.
Memory:
  • memory [] — array for storing previous positions and their fitness values.
  • memory_size — maximum size of memory for storage.
  • memory_index — current index in memory.
Fitness and weight:
  • best_local_fitness — best local fitness agent.
  • m — agent mass.
  • cB [] — coordinates of the best position found by the agent.
  • fB — fitness function value for the best position.

Initialization (Init) — all arrays and variables are initialized to zeros or random values. The array sizes are set, and the influences (weights and biases) are initialized to small random values.

Activation functions — Tanh, ReLU, Sigmoid: various activation functions used in neural networks.

Update input data (UpdateInputs) fills the input array with the current coordinates, speeds, distance to the best known position, and the current fitness value.

Forward pass (ForwardPass) computes the outputs of a neural network based on inputs, weights, and biases using activation functions.

Experiential learning (Learn) updates weights and biases based on accumulated experience if the current experience is better than the previous ones.

Memorizing experience (MemorizeExperience) saves the current coordinates and agent fitness to memory.

Best position update (UpdateBestPosition) — update the best position if the current fitness value is better than the previously found one.

//——————————————————————————————————————————————————————————————————————————————
// Neuro-boid agent structure
//——————————————————————————————————————————————————————————————————————————————
struct S_NeuroBoids_Agent
{
    double x       [];            // current coordinates
    double dx      [];            // current speeds
    double inputs  [];            // neuron inputs
    double outputs [];            // neuron outputs
    double weights [];            // neuron weights
    double biases  [];            // neuron biases
    double memory  [];            // memory of previous positions and their fitnesses
    int    memory_size;           // memory size for accumulating experience
    int    memory_index;          // current index in memory
    double best_local_fitness;    // best local agent fitness
    double m;                     // boid mass
    double cB [];                 // best position coordinates
    double fB;                    // fitness function value

    // Agent initialization
    void Init (int coords, int neuron_size)
    {
      ArrayResize (x, coords);
      ArrayResize (dx, coords);
      ArrayInitialize (x, 0.0);
      ArrayInitialize (dx, 0.0);

      // Initialize the best position structure
      ArrayResize     (cB, coords);
      ArrayInitialize (cB, 0.0);
      fB = -DBL_MAX;

      // Inputs: coordinates, speeds, distance to best, etc.
      int input_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness
      ArrayResize (inputs, input_size);
      ArrayInitialize (inputs, 0.0);

      // Outputs: Speed correction and adaptive factors for flock rules
      int output_size = coords + 3; // dx_correction + 3 adaptive parameters
      ArrayResize (outputs, output_size);
      ArrayInitialize (outputs, 0.0);

      // Weights and biases for each output
      ArrayResize (weights, input_size * output_size);
      ArrayInitialize (weights, 0.0);
      ArrayResize (biases, output_size);
      ArrayInitialize (biases, 0.0);

      // Initialize weights and biases with small random values
      for (int i = 0; i < ArraySize (weights); i++)
      {
        weights [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0);
      }

      for (int i = 0; i < ArraySize (biases); i++)
      {
        biases [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0);
      }

      // Initialize memory for accumulating experience
      memory_size = 10;
      ArrayResize (memory, memory_size * (coords + 1)); // coordinates + fitness
      ArrayInitialize (memory, 0.0);
      memory_index = 0;
      best_local_fitness = -DBL_MAX;

      // Initialize mass
      m = 0.5;
    }

    // Activation function - hyperbolic tangent
    double Tanh (double input_val)
    {
      return MathTanh (input_val);
    }

    // ReLU activation function
    double ReLU (double input_val)
    {
      return (input_val > 0.0) ? input_val : 0.0;
    }

    // Sigmoid activation function
    double Sigmoid (double input_val)
    {
      return 1.0 / (1.0 + MathExp (-input_val));
    }

    // Updating neural network inputs - Corrected version
    void UpdateInputs (double &global_best [], double current_fitness, int coords_count)
    {
      int input_index = 0;

      // Coordinates
      for (int c = 0; c < coords_count; c++)
      {
        inputs [input_index++] = x [c];
      }

      // Speeds
      for (int c = 0; c < coords_count; c++)
      {
        inputs [input_index++] = dx [c];
      }

      // Distance to the best global solution
      double dist_to_best = 0;
      for (int c = 0; c < coords_count; c++)
      {
        dist_to_best += MathPow (x [c] - global_best [c], 2);
      }
      dist_to_best = MathSqrt (dist_to_best);
      inputs [input_index++] = dist_to_best;

      // Current fitness function
      inputs [input_index++] = current_fitness;
    }

    // Direct distribution over the network
    void ForwardPass (int coords_count)
    {
      int input_size = ArraySize (inputs);
      int output_size = ArraySize (outputs);

      // For each output, calculate the weighted sum of the inputs + bias
      for (int o = 0; o < output_size; o++)
      {
        double sum = biases [o];

        for (int i = 0; i < input_size; i++)
        {
          sum += inputs [i] * weights [o * input_size + i];
        }

        // Apply different activation functions depending on the output
        if (o < coords_count) // Use the hyperbolic tangent to correct the speed
        {
          outputs [o] = Tanh (sum);
        }
        else // Use sigmoid for adaptive parameters
        {
          outputs [o] = Sigmoid (sum);
        }
      }
    }

    // Learning from accumulated experience
    void Learn (double learning_rate, int coords_count)
    {
      if (memory_index < memory_size) return; // Insufficient experience

      // Find the best experience in memory
      int best_index = 0;
      double best_fitness = memory [coords_count]; // The first fitness function in memory

      for (int i = 1; i < memory_size; i++)
      {
        double fitness = memory [i * (coords_count + 1) + coords_count];
        if (fitness > best_fitness)
        {
          best_fitness = fitness;
          best_index = i;
        }
      }

      // If the current experience is not better than the previous one, do not update the weights
      if (best_fitness <= best_local_fitness) return;

      best_local_fitness = best_fitness;

      // Simple method for updating weights
      int input_size = ArraySize (inputs);
      int output_size = ArraySize (outputs);

      // Simple form of gradient update
      for (int o = 0; o < output_size; o++)
      {
        for (int i = 0; i < input_size; i++)
        {
          int weight_index = o * input_size + i;
          if (weight_index < ArraySize (weights))
          {
            weights [weight_index] += learning_rate * outputs [o] * inputs [i];
          }
        }

        // Update offsets
        biases [o] += learning_rate * outputs [o];
      }
    }

    // Save current experience (coordinates and fitness)
    void MemorizeExperience (double fitness, int coords_count)
    {
      int offset = memory_index * (coords_count + 1);

      // Save the coordinates
      for (int c = 0; c < coords_count; c++)
      {
        memory [offset + c] = x [c];
      }

      // Save the fitness function
      memory [offset + coords_count] = fitness;

      // Update the memory index
      memory_index = (memory_index + 1) % memory_size;
    }

    // Update the agent's best position
    void UpdateBestPosition (double current_fitness, int coords_count)
    {
      if (current_fitness > fB)
      {
        fB = current_fitness;
        ArrayCopy (cB, x, 0, 0, WHOLE_ARRAY);
      }
    }
};

The C_AO_NOA2 class is an implementation of the NOA2 algorithm and inherits from the C_AO base class. Let's take a closer look at the structure and key aspects of the class.

Main parameters:
  • popSize — agent (boid) population.
  • cohesionWeight, cohesionDist — weight and distance for the cohesion rule.
  • separationWeight, separationDist — weight and distance for the separation rule.
  • alignmentWeight, alignmentDist — weight and distance for the alignment rule.
  • maxSpeed and minSpeed — maximum and minimum agent speeds.
  • learningRate — learning rate for the neural network.
  • neuralInfluence — influence of a neural network on the movement of agents.
  • explorationRate — probability of random exploration of the solution space.
  • m_stagnationCounter and m_prevBestFitness — stagnation counter and the previous best fitness value.
Class methods:
  • SetParams () — method that sets the algorithm parameters based on the values stored in the "params" array.
  • Init () — initialization, takes parameters to define value ranges for agents. The method sets up the initial conditions for the algorithm to operate.
  • Moving () — responsible for the movement of agents based on various interaction rules.
  • Revision () — used to revise the state of agents during the algorithm execution.

Agents: S_NeuroBoids_Agent agent [] — array of agents representing boids in the population.

Private methods (for use within the class):

  • CalculateMass () — mass of agents.
  • Cohesion () — cohesion rule.
  • Separation () — separation rule.
  • Alignment () — alignment rule.
  • LimitSpeed () — limits the agent speed.
  • KeepWithinBounds () — keep agents within the given boundaries.
  • Distance () — calculate the distance between two agents.
  • ApplyNeuralControl () — apply neural network control to the agent.
  • AdaptiveExploration() — implement adaptive exploration.
//——————————————————————————————————————————————————————————————————————————————
// Class of neuron-like optimization algorithm inherited from C_AO
//——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA2 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA2 () { }
  C_AO_NOA2 ()
  {
    ao_name = "NOA2";
    ao_desc = "Neuroboids Optimization Algorithm 2 (joo)";
    ao_link = "https://www.mql5.com/en/articles/17497";

    popSize          = 50;     // population size

    cohesionWeight   = 0.6;    // cohesion weight
    cohesionDist     = 0.001;  // cohesion distance

    separationWeight = 0.005;  // separation weight
    separationDist   = 0.03;   // separation distance

    alignmentWeight  = 0.1;    // alignment weight
    alignmentDist    = 0.1;    // alignment distance

    maxSpeed         = 0.001;  // maximum speed
    minSpeed         = 0.0001; // minimum speed 

    learningRate     = 0.01;   // neural network learning speed
    neuralInfluence  = 0.3;    // influence of the neural network on movement
    explorationRate  = 0.1;    // random exploration probability

    ArrayResize (params, 12);

    params [0].name  = "popSize";          params [0].val = popSize;

    params [1].name  = "cohesionWeight";   params [1].val  = cohesionWeight;
    params [2].name  = "cohesionDist";     params [2].val  = cohesionDist;

    params [3].name  = "separationWeight"; params [3].val  = separationWeight;
    params [4].name  = "separationDist";   params [4].val  = separationDist;

    params [5].name  = "alignmentWeight";  params [5].val  = alignmentWeight;
    params [6].name  = "alignmentDist";    params [6].val  = alignmentDist;

    params [7].name  = "maxSpeed";         params [7].val  = maxSpeed;
    params [8].name  = "minSpeed";         params [8].val  = minSpeed;

    params [9].name  = "learningRate";     params [9].val  = learningRate;
    params [10].name = "neuralInfluence";  params [10].val = neuralInfluence;
    params [11].name = "explorationRate";  params [11].val = explorationRate;

    // Initialize the stagnation counter and the previous best fitness value
    m_stagnationCounter = 0;
    m_prevBestFitness   = -DBL_MAX;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;

    learningRate     = params [9].val;
    neuralInfluence  = params [10].val;
    explorationRate  = params [11].val;
  }

  bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0);
  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double cohesionWeight;     // cohesion weight
  double cohesionDist;       // cohesion distance

  double separationWeight;   // separation weight
  double separationDist;     // separation distance

  double alignmentWeight;    // alignment weight
  double alignmentDist;      // alignment distance

  double minSpeed;           // minimum speed
  double maxSpeed;           // maximum speed

  double learningRate;       // neural network learning speed
  double neuralInfluence;    // influence of the neural network on movement
  double explorationRate;    // random exploration probability

  int m_stagnationCounter;   // stagnation counter
  double m_prevBestFitness;  // previous best fitness value

  S_NeuroBoids_Agent agent []; // agents (boids)

  private: //-------------------------------------------------------------------
  double distanceMax;     // maximum distance
  double speedMax [];     // maximum speeds by measurements

  int neuron_size;        // neuron size (number of inputs)

  void   CalculateMass       ();                                  // calculation of agent masses 
  void   Cohesion            (S_NeuroBoids_Agent &boid, int pos); // cohesion rule
  void   Separation          (S_NeuroBoids_Agent &boid, int pos); // separation rule
  void   Alignment           (S_NeuroBoids_Agent &boid, int pos); // alignment rule
  void   LimitSpeed          (S_NeuroBoids_Agent &boid);          // speed limit
  void   KeepWithinBounds    (S_NeuroBoids_Agent &boid);          // keep within bounds
  double Distance            (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2); // calculate distance
  void   ApplyNeuralControl  (S_NeuroBoids_Agent &boid, int pos); // apply neural control
  void   AdaptiveExploration ();                                  // adaptive research
};
//——————————————————————————————————————————————————————————————————————————————

The Init method is responsible for initializing the parameters of the algorithm and agents and begins its work by calling StandardInit, passing it arrays of the minimum and maximum values of the range and search steps. If standard initialization fails, the method immediately returns 'false'. The size of the neuron that will be used in the agent neural network is set.

In this case, the size is calculated as the number of coordinates multiplied by 2, and two additional values - dist_to_best and current_fitness - are added. The size of the agent array is changed in accordance with the specified popSize. Then, for each agent, the Init method is called, which initializes its parameters, including the neural network.

Calculate maximum distance and speed:

  • The distanceMax variable is initialized to zero.
  • For each coordinate, the maximum speed value is calculated based on the difference between the maximum and minimum range values.
  • The maximum distance is also calculated as the square root of the sum of the squares of the maximum speeds.

The stagnation counter (m_stagnationCounter) is reset to zero, and the variable storing the previous best fitness value (m_prevBestFitness) is set to the minimum possible value. The method sets various global variables, such as coherence, separation and alignment weights, maximum and minimum speeds, learning rate, neural network influence and exploration probability. If all steps are successful, the method returns 'true', which confirms successful initialization.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA2::Init (const double &rangeMinP  [],  // minimum search range
                      const double &rangeMaxP  [],  // maximum search range
                      const double &rangeStepP [],  // search step
                      const int    epochsP)         // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  // Determine the size of a neuron
  neuron_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness

  // Initialize the agents
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init (coords, neuron_size);
  }

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += MathPow (speedMax [c], 2);
  }

  distanceMax = MathSqrt (distanceMax);

  // Reset the stagnation counter and the previous best fitness value
  m_stagnationCounter = 0;
  m_prevBestFitness   = -DBL_MAX;

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);

  GlobalVariableSet ("9learningRate",     params [9].val);
  GlobalVariableSet ("10neuralInfluence", params [10].val);
  GlobalVariableSet ("11explorationRate", params [11].val);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method is responsible for the movement of agents in the environment based on the received data and the interaction between them. First, the method checks the value of the #reset global variable. If it is equal to 1.0, the parameters are reset (the 'revision' variable is set to 'false', and then returns to 0.0). The values of various parameters such as the cohesion, separation and alignment weights, the minimum and maximum speeds, the learning rate, the neural network influence and the exploration ratio are extracted from the global variables. These parameters can be configured to change the behavior of agents.

If the 'revision' variable is 'false', the x positions and dx speeds of the agents are initialized. For each coordinate, random values from a given range are applied, and speeds are set to small random values. Each coordinate also stores the agent's state based on its current position. The AdaptiveExploration () method is called for adaptive exploration, which can change the behavior of agents depending on the stagnation state.

The main loop of agent movement (for each):

  • Save the agent's current experience.
  • Update the best position the agent found.
  • Update the input data of the agent's neural network.
  • Perform direct propagation of data through the neural network.
  • Agents are trained based on accumulated experience.
Mass calculation: call the CalculateMass () method to evaluate interactions between agents given their mass.

    Applying rules and movement: the loop through agents begins again, and the standard rules of the boid algorithm are applied to each one:

    • Cohesion: agents strive to be closer to each other.
    • Separation: agents avoid getting close to each other to avoid collisions.
    • Alignment: agents try to move in the same direction as their neighbors.
    The ApplyNeuralControl () method is called for neural network based control. The speed of agents is limited using LimitSpeed() and it is ensured that agents stay within the boundaries of the given area using KeepWithinBounds (). The agents' positions are updated at each coordinate, adding the current speed to the current position and state. 

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA2::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  // Get parameters from global variables for interactive configuration
  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  learningRate     = GlobalVariableGet ("9learningRate");
  neuralInfluence  = GlobalVariableGet ("10neuralInfluence");
  explorationRate  = GlobalVariableGet ("11explorationRate");

  // Initialization of initial positions and speeds
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  // Adaptive research depending on stagnation
  AdaptiveExploration ();

  //----------------------------------------------------------------------------
  // Main loop of boid movement
  for (int i = 0; i < popSize; i++)
  {
    // Save the current experience
    agent [i].MemorizeExperience (a [i].f, coords);

    // Update the agent's best position
    agent [i].UpdateBestPosition (a [i].f, coords);

    // Update the neural network inputs
    agent [i].UpdateInputs (cB, a [i].f, coords);

    // Forward propagation through the neural network
    agent [i].ForwardPass (coords);

    // Learning from accumulated experience
    agent [i].Learn (learningRate, coords);
  }

  // Calculate masses
  CalculateMass ();

  // Application of rules and movement
  for (int i = 0; i < popSize; i++)
  {
    // Standard rules of the boid algorithm
    Cohesion (agent [i], i);
    Separation (agent [i], i);
    Alignment (agent [i], i);

    // Apply neural control
    ApplyNeuralControl (agent [i], i);

    // Speed limit and keeping within bounds
    LimitSpeed (agent [i]);
    KeepWithinBounds (agent [i]);

    // Update positions
    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The CalculateMass method calculates the "mass" of agents based on their fitness (productivity) and normalizes these values. The maxMass and minMass variables are initialized to -DBL_MAX and DBL_MAX, respectively. These variables will be used to find the highest and lowest fitness values among the entire population of agents. The method checks whether there is at least one agent by checking that "popSize" (population size) is greater than zero. If there are no agents, the method terminates. In the first loop, all agents are iterated over (from 0 to popSize), and for each one it is checked whether its fitness (the value of a[i].f) is greater than the current maxMass or less than minMass.

    As a result of this loop, the maximum and minimum fitness values among all agents will be determined. In the second loop, all agents are again iterated over, and for each one, its "mass" (m variable) is calculated using the u.Scale function, which normalizes the fitness values. 

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA2::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass = DBL_MAX;

  // Check for data presence before calculations
  if (popSize <= 0) return;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.1, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The ApplyNeuralControl method is responsible for applying control based on the neural network outputs to the "boid" type agent. The method iterates over all the agent's 'coords' coordinates. For each c coordinate, it is checked that the current index does not go beyond the bounds of the boid.outputs output array. If the index is correct, the dx[c] agent speed is adjusted based on the corresponding value from the neural network outputs multiplied by its neuralInfluence.

    The size of the boid.outputs array is retrieved to simplify further checks. Check whether the corresponding indices are within the output array for the cohesion_factor, separation_factor, alignment_factor cohesion, separation and alignment ratios. If the index is out of bounds, the default value of 0.5 is assigned. These ratios are used to scale the base weights to account for the neural network influence. They influence the behavior of agents by changing the weights for convergence, separation, and alignment:

    • local_cohesion sets the cohesion weight.
    • local_separation sets the separation weight.
    • local_alignment sets the alignment weight.

    The method checks whether a random exploration should be performed using the given xplorationRate probability. If the condition is met, a random c coordinate is selected for the perturbation. The perturbation_size is calculated based on the agent mass (which is a measure of its fitness) and the range of possible values for that coordinate. This allows the magnitude of random variation to be controlled, regardless of the agent mass. A random perturbation chosen from the range from perturbation_size to perturbation_size is added to the dx[c] speed. The ApplyNeuralControl method integrates the neural network operation results into agent movement management. It adjusts their speed based on data, and the method also takes into account the need for random exploration.

    //——————————————————————————————————————————————————————————————————————————————
// Apply neural control to a boid
void C_AO_NOA2::ApplyNeuralControl (S_NeuroBoids_Agent &boid, int pos)
{
  // Use the neural network outputs to correct the speed
  for (int c = 0; c < coords; c++)
  {
    // Make sure the index is not outside the array bounds 
    if (c < ArraySize (boid.outputs))
    {
      // Apply neural speed correction with a given influence
      boid.dx [c] += boid.outputs [c] * neuralInfluence;
    }
  }

  // Use the neural network outputs to adapt the flock parameters
  // Check that the indices do not go beyond the array bounds
  int output_size = ArraySize (boid.outputs);

  double cohesion_factor   = (coords < output_size) ? boid.outputs [coords] : 0.5;
  double separation_factor = (coords + 1 < output_size) ? boid.outputs [coords + 1] : 0.5;
  double alignment_factor  = (coords + 2 < output_size) ? boid.outputs [coords + 2] : 0.5;

  // Scale the base weights considering neural adaptation
  // These variables are local and do not change global parameters
  double local_cohesion   = cohesionWeight * (0.5 + cohesion_factor);
  double local_separation = separationWeight * (0.5 + separation_factor);
  double local_alignment  = alignmentWeight * (0.5 + alignment_factor);

  // Random study with a given probability
  if (u.RNDprobab () < explorationRate)
  {
    // Select a random coordinate for perturbation
    int c = (int)u.RNDfromCI (0, coords - 1);

    // Adaptive perturbation size depending on mass (fitness)
    double perturbation_size = (1.0 - boid.m) * (rangeMax [c] - rangeMin [c]) * 0.01;

    // Add random perturbation
    boid.dx [c] += u.RNDfromCI (-perturbation_size, perturbation_size);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The AdaptiveExploration method of the C_AO_NOA2 class implements adaptive exploration depending on the stage of stagnation in the optimization process. The method starts by checking whether the fB objective function value has changed compared to the m_prevBestFitness previous best value. If the difference between them is less than 0.000001, it is considered that there is no progress and the m_stagnationCounter is increased. Otherwise, stagnation is terminated, the counter is reset, and the current fB value is stored as the new best.

    If the amount of stagnation exceeds 20, the chance of random exploration (explorationRate) increases, but it is capped at 0.5 to prevent too high a chance of random changes. Every 50 stagnation iterations, a partial restart occurs: 70% of the agents in the population are restarted with new random values within the specified rangeMin and rangeMax ranges. At the same time, the remaining top agents with their current positions remain unchanged. After a restart, the stagnation counter is reset.

    If there is progress and the number of "params" parameters is greater than 11, the exploration probability "explorationRate" is set from the parameters array. If there are fewer parameters, the default value of 0.1 is set.

    //——————————————————————————————————————————————————————————————————————————————
// Adaptive research depending on stagnation
void C_AO_NOA2::AdaptiveExploration ()
{
  // Determine if there is progress in the search
  if (MathAbs (fB - m_prevBestFitness) < 0.000001)
  {
    m_stagnationCounter++;
  }
  else
  {
    m_stagnationCounter = 0;
    m_prevBestFitness = fB;
  }

  // Increase research during stagnation
  if (m_stagnationCounter > 20)
  {
    // Increase the probability of random exploration
    explorationRate = MathMin (0.5, explorationRate * 1.5);

    // Perform a partial restart every 50 stagnation iterations
    if (m_stagnationCounter % 50 == 0)
    {
      // Restart 70% of the population leaving the best agents
      int restart_count = (int)(popSize * 0.7);

      for (int i = popSize - restart_count; i < popSize; i++)
      {
        for (int c = 0; c < coords; c++)
        {
          agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
          agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;
        }
      }

      // Reset the stagnation counter
      m_stagnationCounter = 0;
    }
  }
  else
  {
    // If progress is good enough, use the normal research level 
    if (11 < ArraySize (params))
    {
      explorationRate = params [11].val;
    }
    else
    {
      explorationRate = 0.1; // default value
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The Cohesion method of the C_AO_NOA2 class is responsible for implementing the "cohesion" behavior for the agent-based model of boids. Variable declaration:

    • centerX — array will be used to store the coordinates of the center of mass of neighboring agents. The size of the array corresponds to the number of 'coords' coordinates.
    • numNeighbors — neighbor counter keeps track of the number of agents within the given distance (taking into account mass).
    • sumMass — sum of the masses of neighboring agents is used to normalize the coordinates of the center of mass.

    The first loop (from 0 to popSize) sums the masses of all agents in the population, excluding the current boid (agent) at "pos" index. The second loop goes through all agents and checks if they are within the maximum distance multiplied by the cohesionDist factor from the current boid. If the distance to an agent is less than the specified maximum, the coordinates of that agent (taking into account its mass) are added to centerX, and the numNeighbors counter is incremented.

    After the coordinate sums and masses of the neighbors have been calculated, it is checked whether there are neighbors (i.e. numNeighbors > 0) and the sum of masses (sumMass > 0.0), and if neighbors are found, the coordinates of the center of mass are normalized (by dividing by the sum of masses). Then the current dx speed of the boid is increased towards the center of mass with the given cohesionWeight weight, this means that the boid will move towards the center of mass of its neighbors, taking into account their masses.

    The Cohesion method calculates the center of mass and adjusts the current boid speed so that it "converges" toward this center. This behavior is one of the key aspects of simulating flock or group behavior. Parameters, such as cohesionDist and cohesionWeight allow us to control the distance, at which this behavior takes effect, and the degree, to which the center of mass influences the movement of boids. 

    //——————————————————————————————————————————————————————————————————————————————
// Find the center of mass of other boids and adjust the speed towards the center of mass
void C_AO_NOA2::Cohesion (S_NeuroBoids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int numNeighbors = 0;
  double sumMass = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i) sumMass += agent [i].m;
  }

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c] * agent [i].m;
        }

        numNeighbors++;
      }
    }
  }

  if (numNeighbors > 0 && sumMass > 0.0)
  {
    for (int c = 0; c < coords; c++)
    {
      centerX [c] /= sumMass;
      boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The Separation method of the C_AO_NOA2 class implements the separation behavior for the model agents, which is intended to prevent collisions between the boid and neighboring agents. moveX parameters, such as the cohesionDist array, will be used to store the displacement vectors to push the boid away from other agents.

    The size of the array corresponds to the number of 'coords' coordinates. The moveX array is initialized to zero to avoid the accumulation of random values, then all agents in the population are iterated over (from 0 to popSize). Then we check whether the agent is close to the current boid. This is done using the Distance function, and if the distance between the boid and the agent is less than the specified maximum (multiplied by the separationDist factor), then for each coordinate the agent coordinates are subtracted from the current boid coordinates to effectively create a vector pointing towards the current boid (i.e. pushing away from the agent).

    After completing the loop through agents, the current dx speed of the boid is increased by the calculated moveX displacement vector multiplied by the separationWeight ratio. This allows us to control the repulsion force: the higher the separationWeight value, the more the boid will avoid collisions.

    The Separation method implements a behavior that causes the boid to bounce off its nearest neighbors, preventing collisions. This is an important aspect in simulating flock behavior, which helps maintain personal space for each agent and promotes more natural interactions between them. The parameters, such as separationDist and separationWeight, allow us to flexibly adjust the radius and strength of the repulsion effect, respectively.

    //——————————————————————————————————————————————————————————————————————————————
// Pushing away from other boids to avoid collisions
void C_AO_NOA2::Separation (S_NeuroBoids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The Alignment method of the C_AO_NOA2 class implements the alignment behavior for agents in the model. This behavior causes boids to coordinate their speeds with neighboring agents to create a more harmonious and coordinated group movement, avgDX is an array that will be used to store the average speed vector of neighboring agents. The array size corresponds to the number of coords coordinates, numNeighbors is a counter that tracks the number of neighbors within a given distance.

    The loop iterates through all agents in the population. Inside the loop, it is checked whether the current agent is the very same boid. If the distance to another agent is less than the given maximum multiplied by the alignmentDist factor, the current dx speed of that agent is added to avgDX. The numNeighbors counter is incremented by 1. After the loop completes, if neighbors were found (i.e. numNeighbors > 0), then the average speed (avgDX) is calculated by dividing the summed speed vector by the number of neighbors. Then the current dx speed of the boid is adjusted towards the average speed of its neighbors, taking into account the alignmentWeight ratio. 

    The Alignment method allows a boid to adapt its speed to the speeds of its neighbors. This behavior helps groups of boids move more cohesively and reduces the likelihood of conflicts or abrupt changes in direction. The parameters, such as alignmentDist and alignmentWeight, set the radius of the alignment effect and the degree to which the average speed of neighbors influences the speed of the current boid, respectively.  
    //——————————————————————————————————————————————————————————————————————————————
// Align speed with other boids
void C_AO_NOA2::Alignment (S_NeuroBoids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

  if (numNeighbors > 0)
  {
    for (int c = 0; c < coords; c++)
    {
      avgDX [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The LimitSpeed method of the C_AO_NOA2 class is designed to control the speed of agents (boids) in the model to ensure that the speeds of the boids are within a given range, "speed" is a variable for storing the current speed of the boids, which will be calculated as the length of the speed vector. The coordinates loop (coords) calculates the square of the speed for each coordinate (by adding boid.dx[c] * boid.dx[c]) and sums them up. This allows us to calculate the square of the length of the speed vector. The length (or actual speed) is then obtained using the MathSqrt function, which calculates the square root of the sum of squares. If the speed is greater than a small value (1e-10), the program continues executing, if the current speed is less than the minimum allowed speed (defined as speedMax[0] * minSpeed), then the boid.dx speed vector is normalized (divided by its current length) and increased to a value equal to the minimum allowed value.

    If the current speed is greater than the maximum allowed speed (speedMax[0] * maxSpeed), then similarly, the speed vector is normalized and set to the value of the maximum speed, and if the speed is almost zero (zero or very close to zero), each coordinate of the speed vector is replaced by a small random value obtained using the u.RNDfromCI(-1.0, 1.0) function multiplied by the maximum speed.

    The LimitSpeed method ensures that the speed of boids is maintained within acceptable limits, preventing them from moving too slowly or too quickly. This behavior allows for more realistic agent simulations because it does not allow for significant variations in speed that could lead to unnatural movement. The minSpeed and maxSpeed parameters can be configured to adjust the agents' behavior and speed depending on the simulation tasks.

    //——————————————————————————————————————————————————————————————————————————————
// Speed limit
void C_AO_NOA2::LimitSpeed (S_NeuroBoids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = MathSqrt (speed);

  // If the speed is not zero (prevent division by zero)
  if (speed > 1e-10)
  {
    // If the speed is too low, increase it
    if (speed < speedMax [0] * minSpeed)
    {
      for (int c = 0; c < coords; c++)
      {
        boid.dx [c] = boid.dx [c] / speed * speedMax [c] * minSpeed;
      }
    }
    // If the speed is too high, reduce it
    else
      if (speed > speedMax [0] * maxSpeed)
      {
        for (int c = 0; c < coords; c++)
        {
          boid.dx [c] = boid.dx [c] / speed * speedMax [c] * maxSpeed;
        }
      }
  }
  else
  {
    // If the speed is almost zero, set a small random speed
    for (int c = 0; c < coords; c++)
    {
      boid.dx [c] = u.RNDfromCI (-1.0, 1.0) * speedMax [c] * minSpeed;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The KeepWithinBounds method of the C_AO_NOA2 class is designed to keep the agent (boid) within the specified boundaries. If a boid gets too close to the edges of the region, this method changes its direction and provides a certain push back into the boundaries. The method starts with a loop over all coordinates, which allows working with multidimensional space.

    For each coordinate, check if the boid position (boid.x[c]) is below the minimum bound (rangeMin[c]), if so, the velocity direction (boid.dx[c]) is inverted using "boid.dx[c] *= -1.0". This means that the boid will move in the opposite direction. Then a small push from the boundary is added: (rangeMax[c] - rangeMin[c]) * 0.001, which helps push the boid back into the area.

    A similar check is performed for the maximum bound (rangeMax[c]): if the boid position goes beyond the maximum, its speed is also inverted and adjusted, but by subtracting some value similar to the previous case.

    The KeepWithinBounds method effectively restricts the movements of boids within a given area, preventing them from flying out of bounds and ensuring they return within. 

    //——————————————————————————————————————————————————————————————————————————————
// Keep the boid within the boundaries. If it gets too close to the edge,
// push it back and change direction.
void C_AO_NOA2::KeepWithinBounds (S_NeuroBoids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    if (boid.x [c] < rangeMin [c])
    {
      boid.dx [c] *= -1.0;
      // Add a small push from the border
      boid.dx [c] += (rangeMax [c] - rangeMin [c]) * 0.001;
    }
    if (boid.x [c] > rangeMax [c])
    {
      boid.dx [c] *= -1.0;
      // Add a small push from the border
      boid.dx [c] -= (rangeMax [c] - rangeMin [c]) * 0.001;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The Distance method of the C_AO_NOA2 class is designed to calculate the distance between two agents (boids) in a multidimensional space. It uses an equation to calculate the Euclidean distance, 'dist' is a variable that will store the sum of the squared differences between the coordinates of two boids.

    The method starts a loop that goes through all coordinates, which allows calculating the distance in a space of any dimension. For each c coordinate, the square of the difference between the corresponding coordinates of both boids is calculated: boid1.x[c] - boid2.x[c].

    Results ((boid1.x[c] - boid2.x[c])^2) are added to the 'dist' variable. After the loop completes, the 'dist' variable will contain the sum of the squares of the differences in the coordinates. To get the actual distance, the method uses MathSqrt to calculate the square root of the sum of squares, which corresponds to the Euclidean distance equation.

    //——————————————————————————————————————————————————————————————————————————————
// Calculate the distance between two boids
double C_AO_NOA2::Distance (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += MathPow (boid1.x [c] - boid2.x [c], 2);
  }

  return MathSqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

    The Revision method of the C_AO_NOA2 class is responsible for updating information about the best solution found during the optimization. This process involves updating the value of the fitness function as well as the coordinates corresponding to that value. The method also monitors progress and adapts the algorithm parameters if there are significant improvements. The method runs through the entire population, represented by the a array, which contains popSize (the number of agents).

    Inside the loop, each agent is checked to see if its fitness value (a[i].f) is greater than the current best value (fB). If the current agent shows the best fitness value, the global best value of the fitness function is updated, assigning fB a new value of a[i].f, and then the coordinates of the best solution are updated. For each c coordinate, the cB array (containing the coordinates of the best solution) is updated with the values of the current agent. The stagnation counter (m_stagnationCounter) is reset to zero because an improvement in the solution was found.

    The method uses the hasProgress variable to determine whether progress has been made. This is done by calculating the absolute difference between the current and previous best values of the fitness function (MathAbs(fB - m_prevBestFitness)), and if this difference is greater than 0.000001, the progress is considered to be evident. If there is progress, m_prevBestFitness is updated to the current best fB value.
    The explorationRate exploration speed is also adapted: it is reduced if an improvement is found, taking into account some parameter from the params array and the current value of explorationRate.

    //——————————————————————————————————————————————————————————————————————————————
// Update the best solution found
void C_AO_NOA2::Revision ()
{
  // Update the best coordinates and fitness function value
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      for (int c = 0; c < coords; c++)
      {
        cB [c] = a [i].c [c];
      }

      // Reset the stagnation counter when a better solution is found
      m_stagnationCounter = 0;
    }
  }

  // Check for progress to adapt the algorithm parameters
  bool hasProgress = MathAbs (fB - m_prevBestFitness) > 0.000001;
  if (hasProgress)
  {
    m_prevBestFitness = fB;
    explorationRate = MathMax (params [11].val * 0.5, explorationRate * 0.9);
  }
}
//——————————————————————————————————————————————————————————————————————————————


    Test results

    The test results are quite weak.

    NOA2|Neuroboids Optimization Algorithm 2 (joo)|50.0|0.6|0.001|0.005|0.03|0.1|0.1|0.1|0.01|0.01|0.3|0.1|
    =============================
    5 Hilly's; Func runs: 10000; result: 0.47680799582735267
    25 Hilly's; Func runs: 10000; result: 0.30763714006051013
    500 Hilly's; Func runs: 10000; result: 0.2544737238936433
    =============================
    5 Forest's; Func runs: 10000; result: 0.3238017030688524
    25 Forest's; Func runs: 10000; result: 0.20976876473929068
    500 Forest's; Func runs: 10000; result: 0.15740101965732595
    =============================
    5 Megacity's; Func runs: 10000; result: 0.27076923076923076
    25 Megacity's; Func runs: 10000; result: 0.14676923076923082
    500 Megacity's; Func runs: 10000; result: 0.09729230769230844
    =============================
    All score: 2.24472 (24.94%)

    The visualization shows modest search capabilities. The ability to change external parameters of the algorithm using global variables allows experimenting with the behavior of boids, revealing interesting behavior patterns. Below are visualizations of some of the many possible behavior patterns.

    Hilly

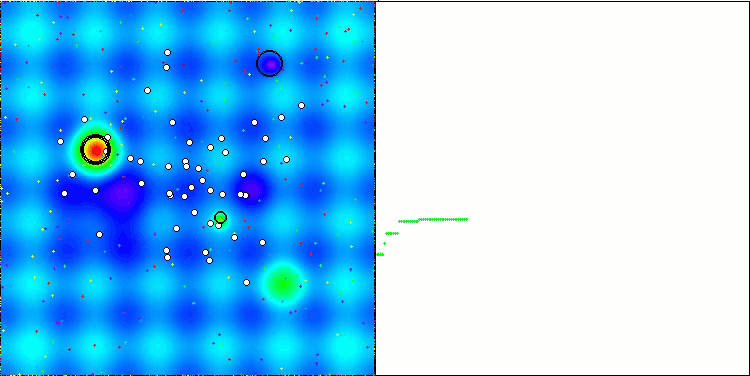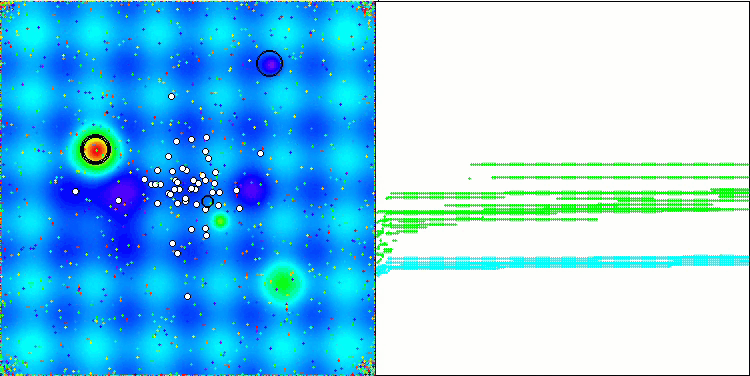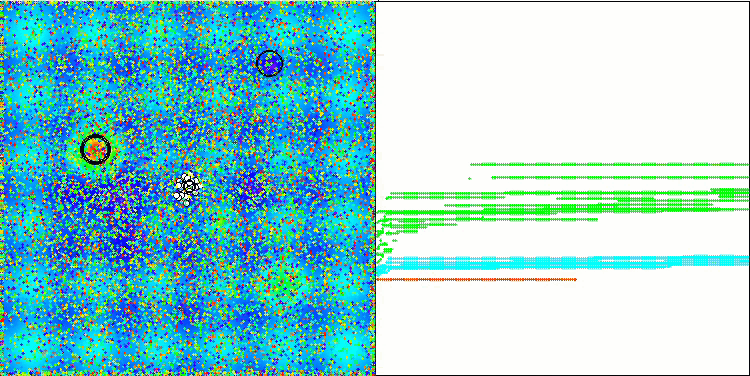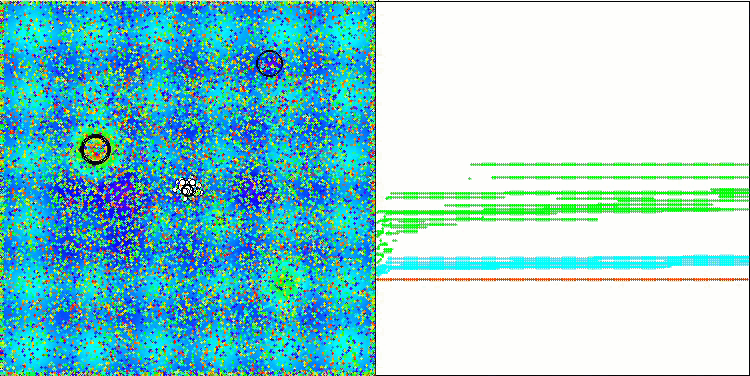
    NOA2 on the Hilly test function

    Forest

    NOA2 on the Forest test function

    Megacity

    NOA2 on the Megacity test function

    Based on the test results, the NOA2 algorithm in its basic version is included in our ranking table of population optimization algorithms for information only.

    # AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
    10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
    1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA code lock algorithm (joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm animal migration ptimization M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O) evolution strategies 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA comet tail algorithm (joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA time evolution travel algorithm (joo) 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm stochastic diffusion search M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 BOAm billiards optimization algorithm M 0.95757 0.82599 0.25235 2.03590 1.00000 0.90036 0.30502 2.20538 0.73538 0.52523 0.09563 1.35625 5.598 62.19
    9 AAm archery algorithm M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    10 ESG evolution of social groups (joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    11 SIA simulated isotropic annealing (joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    12 ACS artificial cooperative search 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    13 DA dialectical algorithm 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    14 BHAm black hole algorithm M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    15 ASO anarchy society optimization 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    16 RFO royal flush optimization (joo) 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    17 AOSm atomic orbital search M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    18 TSEA turtle shell evolution algorithm (joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    19 DE differential evolution 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    20 SRA successful restaurateur algorithm (joo) 0.96883 0.63455 0.29217 1.89555 0.94637 0.55506 0.19124 1.69267 0.74923 0.44031 0.12526 1.31480 4.903 54.48
    21 CRO chemical reaction optimization 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    22 BIO blood inheritance optimization (joo) 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    23 BSA bird swarm algorithm 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    24 HS harmony search 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    25 SSG saplings sowing and growing 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    26 BCOm bacterial chemotaxis optimization M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    27 ABO african buffalo optimization 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    28 (PO)ES (PO) evolution strategies 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    29 TSm tabu search M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    30 BSO brain storm optimization 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    31 WOAm wale optimization algorithm M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    32 AEFA artificial electric field algorithm 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    33 AEO artificial ecosystem-based optimization algorithm 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    34 ACOm ant colony optimization M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    35 BFO-GA bacterial foraging optimization - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    36 SOA simple optimization algorithm 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    37 ABHA artificial bee hive algorithm 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    38 ACMO atmospheric cloud model optimization 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    39 ADAMm adaptive moment estimation M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    40 CGO chaos game optimization 0.57256 0.37158 0.32018 1.26432 0.61176 0.61931 0.62161 1.85267 0.37538 0.21923 0.19028 0.78490 3.902 43.35
    41 ATAm artificial tribe algorithm M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    42 CFO central force optimization 0.60961 0.54958 0.27831 1.43750 0.63418 0.46833 0.22541 1.32792 0.57231 0.23477 0.09586 0.90294 3.668 40.76
    43 ASHA artificial showering algorithm 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    44 ASBO adaptive social behavior optimization 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    45 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    NOA2 neuroboids optimization algorithm 2(joo) 0.47681 0.30764 0.25447 1.03892 0.32380 0.20977 0.15740 0.69097 0.27077 0.14677 0.09729 0.51483 2.245 24.94


    Summary

    The neuroboid optimization algorithm (NOA2) I developed is a hybrid approach that combines the principles of swarm intelligence (the boid algorithm) with neural control. The key idea is to use a neural network to adaptively control the behavioral parameters of boid agents. The current implementation uses a simple single-layer neural network without hidden layers. It consists of an input layer that receives current coordinates, speeds, distance to the best solution, and fitness function value, as well as an output layer that defines speed corrections and adaptive parameters for the boid flock behavior rules.

    This version does not have intermediate layers. The number of inputs is defined as (coords * 2 + 2), where "coords" is the number of dimensions of the search space. The outputs include a correction for each coordinate and three additional parameters for adapting the flock rules. The algorithm has a large number of configurable parameters, which makes it difficult to find the best ones. I tried various combinations, but I still did not find the ideal combination that would demonstrate the best results on the test functions.

    In its current form, the algorithm clearly serves as a proof of concept and is overall an interesting experiment in the field of hybrid optimization methods, but it does not demonstrate sufficient performance. It scores minimally in the tests conducted and can only be considered as an illustration of the approach to algorithm hybridization. For interested researchers and developers, the NOA2 code can serve as a starting point for experimenting with different configurations and parameters, and for creating more advanced hybrid optimization algorithms that leverage the advantages of both population-based and machine learning methods.

    Tab

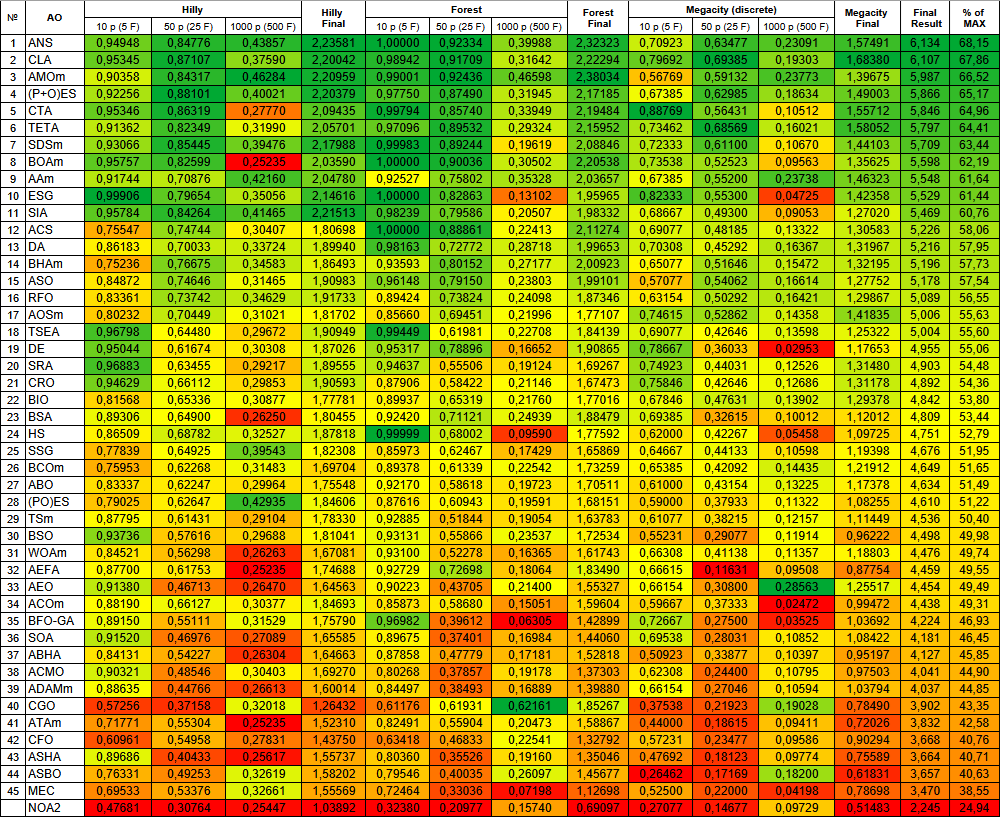
    Figure 3. Color gradation of algorithms according to the corresponding tests

    chart

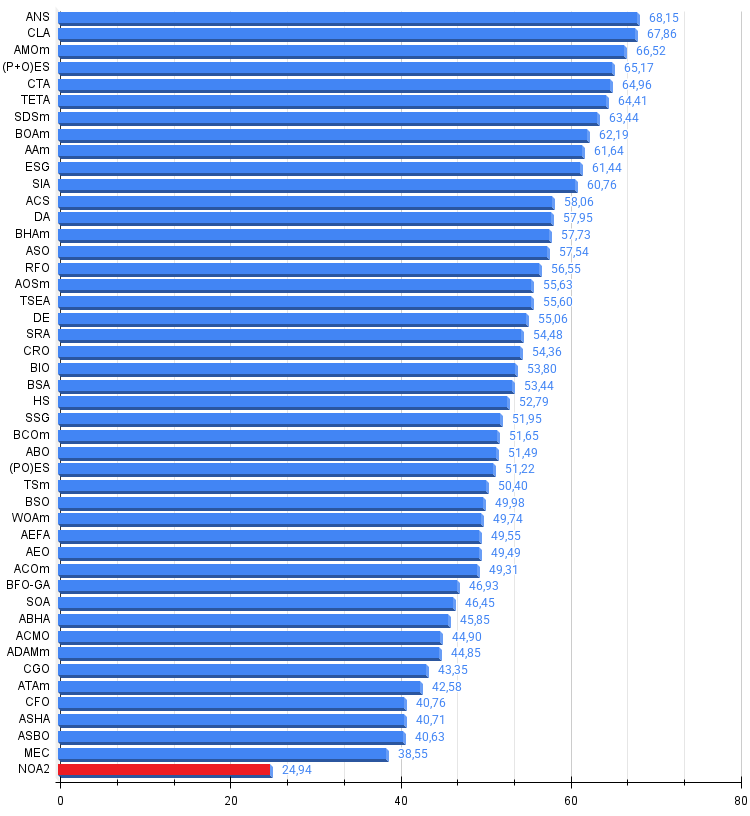
    Figure 4. Histogram of algorithm testing results (scale from 0 to 100, the higher the better, where 100 is the maximum possible theoretical result, in the archive there is a script for calculating the rating table)

    NOA2 pros and cons:

    Pros:

    1. Interesting idea.

    Cons:

    1. Weak results.

    The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.


    Programs used in the article

    # Name Type Description
    1 #C_AO.mqh
    		 Include
    		 Parent class of population optimization algorithms
    2 #C_AO_enum.mqh
    		 Include
    		 Enumeration of population optimization algorithms
    3 TestFunctions.mqh
    		 Include
    		 Library of test functions
    4 TestStandFunctions.mqh
    		 Include
    		 Test stand function library
    5 Utilities.mqh
    		 Include
    		 Library of auxiliary functions
    6 CalculationTestResults.mqh
    		 Include
    		 Script for calculating results in the comparison table
    7 Testing AOs.mq5
    		 Script The unified test stand for all population optimization algorithms
    8 Simple use of population optimization algorithms.mq5
    		 Script
    		 A simple example of using population optimization algorithms without visualization
    9 Test_AO_NOA2.mq5
    		 Script NOA2 test stand

    Translated from Russian by MetaQuotes Ltd.
    Original article: https://www.mql5.com/ru/articles/17497

    Attached files |
    Download ZIP
    NOA2.zip (186.45 KB)

    Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

    This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

    Other articles by this author

    Go to discussion
    Graph Theory: Traversal Breadth-First Search (BFS) Applied in Trading Graph Theory: Traversal Breadth-First Search (BFS) Applied in Trading
    Breadth First Search (BFS) uses level-order traversal to model market structure as a directed graph of price swings evolving through time. By analyzing historical bars or sessions layer by layer, BFS prioritizes recent price behavior while still respecting deeper market memory.
    Formulating Dynamic Multi-Pair EA (Part 6): Adaptive Spread Sensitivity for High-Frequency Symbol Switching Formulating Dynamic Multi-Pair EA (Part 6): Adaptive Spread Sensitivity for High-Frequency Symbol Switching
    In this part, we will focus on designing an intelligent execution layer that continuously monitors and evaluates real-time spread conditions across multiple symbols. The EA dynamically adapts its symbol selection by enabling or disabling trading based on spread efficiency rather than fixed rules. This approach allows high-frequency multi-pair systems to prioritize cost-effective symbols.
    Market Simulation (Part 10): Sockets (IV) Market Simulation (Part 10): Sockets (IV)
    In this article, we'll look at what you need to do to start using Excel to manage MetaTrader 5, but in a very interesting way. To do this, we will use an Excel add-in to avoid using built-in VBA. If you don't know what add-in is meant, read this article and learn how to program in Python directly in Excel.
    Tracking Account Dynamics: Balance, Equity, and Floating P/L Visualization in MQL5 Tracking Account Dynamics: Balance, Equity, and Floating P/L Visualization in MQL5
    Create a custom MT5 indicator that processes the entire deal history and plots starting balance, balance, equity, and floating P/L as continuous curves. It updates per bar, aggregates positions across symbols, and avoids external dependencies through local caching. Use it to inspect equity–balance divergence, realized vs. unrealized results, and the timing of risk deployment.