MetaTrader 5 / 测试者
English Русский Español Português
preview
混沌博弈优化（CGO）

混沌博弈优化（CGO）

MetaTrader 5 — 测试者 |
30 0
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法实现
  3. 测试结果


概述

在现代科学的各个领域以及交易中，当解决复杂问题时优化算法均发挥着战略性的作用。随着科技的飞速发展，这些任务正变得愈发复杂，而寻找最优解决方案的过程也日益耗费大量能源。因此，对优化算法的有效性及其高运行效率的要求也在不断提高。其中一种最新且极具前景的方法是CGO算法，该算法由Siamak Talatahari和Mehdi Azizi于2020年开发。此算法基于混沌理论原理，利用混沌序列生成并改进解决方案。

该算法的主要思路是利用混沌序列在复杂的多维空间中寻找全局最优解。混沌序列具有某些特性，理论上可使它们避开局部陷阱，找到高质量的解决方案。在本文中，我们将探讨混沌博弈优化算法的基本原理和阶段，用代码实现该算法，在测试函数上进行标准测试，并得出关于其性能的结论。


算法实现

想象一群研究人员，他们各自试图在多维迷宫中寻找极值。在旅程开始时，我们的探索者们随机散布在整个迷宫中，并在严格界定的空间范围内找到他们的第一个避难所。这就是他们的起点。每个探索者并非独自行动——他观察同伴，并在任何给定时刻，随机选择一组同伴，计算他们所在位置的中心点，仿佛在他们的位置之间找到一个平衡点。

这是群体经验的集体智慧。然后，混沌的真正魔力便开始了。探索者可以选择四条路径中的一条作为下一步。每条路径都是一种特殊的运动方程，其中交织着三个关键点：探索者当前的位置、整个群体找到的最优位置以及所选子群体的中心。这些点相互混合，它们对进一步运动的影响程度由α比率决定——这是混沌的引导者。

α比率本身有多种表现形式，每个探索者遵循规则，既可以从自己的位置出发，冲向最优结果与群体中心之间的黄金分割点，也可以从最优点出发，探索其周围的空间，还可以从群体中心出发，或者完全随机地跃入未知领域。

此类行动每次结束时，都会对结果进行比较。如果某个探索者找到了比之前记录更好的位置，那么它将成为整个群体在进一步搜索中的新灯塔。

这就是该算法的真正魅力所在——它能够将混沌转化为秩序，将随机性转化为有目的的运动，将不确定性转化为进步，每一步、每一次移动都服从于在已知与未知、稳定与风险、秩序与混沌之间寻找解决方案。

CGO图解

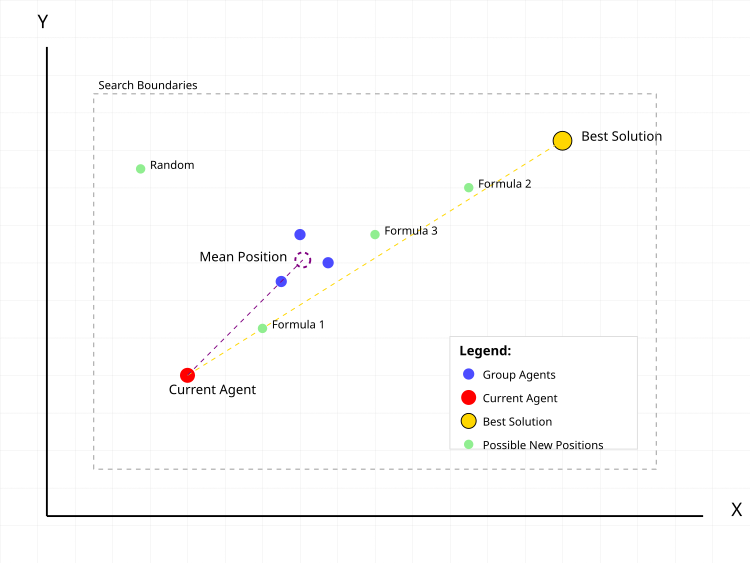
图例1. CGO算法中搜索智能体的典型行为

在图例1中，红色圆点代表当前要计算新位置的智能体。蓝色圆点是从种群中随机选取的一组智能体，数量随机。紫色虚线圆圈表示该组的中间位置。金色圆点代表已找到的最优解。绿色圆点表示根据不同公式计算得出的智能体可能的新位置：
  • 公式1：当前位置 + α(β×最优位置 - γ×平均位置)
  • 公式2：最优位置 + α(β×平均位置 - γ×当前位置)
  • 公式3：平均位置 + α(β×最优位置 - γ×当前位置)
  • 随机：随机位置

    虚线表示最优解和群体平均位置对当前智能体移动的影响向量。灰色虚线矩形表示搜索区域的边界。

    让我们开始编写该算法的伪代码。

  1. 算法初始化：
    • 设定种群规模（默认50个智能体）
    • 为每个坐标定义搜索边界：
      • 最小值（rangeMin）
      • 最大值（rangeMax）
      • 变化步长（rangeStep）
    • 对于种群中的每个个体：
      • 在给定边界内生成随机初始坐标
      • 根据步长对坐标进行取整
      • 计算目标函数值
    • 确定所有智能体中的最优初始解
  2. 主优化循环：
    • 对于种群中的每个个体： 
    a) 随机选择一个智能体子组：
    • 子组规模 = 1到种群规模之间的随机数
    • 随机将智能体选入子组
    b) 计算所选子组的平均位置：
    • 对于每个坐标：平均坐标 = 组坐标之和 / 组规模
    c) 生成运动公式所需的比率：
    • α（阿尔法）= 随机选择以下方法之一：
      • 方法1：0到1之间的随机数
      • 方法2：2 × random(0,1) - 1 [得到-1到1之间的数]
      • 方法3：Ir × random(0,1) + 1
      • 方法4：Ir × random(0,1) + (1-Ir)，其中Ir = 随机0或1
    • β（贝塔）= 随机1或2
    • γ（伽马）= 随机1或2
    d) 随机选择四种运动公式之一：
    • 公式1：新位置 = 当前位置 + α(β×最优位置 - γ×平均位置)
    • 公式2：新位置 = 最优位置 + α(β×平均位置 - γ×当前位置)
    • 公式3：新位置 = 平均位置 + α(β×最优位置 - γ×当前位置)
    • 公式4：新位置 = 在搜索边界内的随机位置
    e) 应用所选方程：
    • 对于每个坐标：
      • 使用方程计算新值
      • 检查是否超出搜索边界
      • 如果超出边界，则调整到最近的边界值
      • 根据变化步长对值进行取整
    f) 计算新位置的目标函数值
  3. 更新最优解：
    • 对于每个智能体：
      • 如果智能体的目标函数值优于当前最优值：
        • 更新最优值
        • 保存新最优解的坐标
  4. 重复：
    • 重复步骤2-3，直到满足停止条件：
      • 达到最大迭代次数
      • 或找到所需质量的解
      • 或其他停止准则

    5. 让我们继续实现算法本身。C_AO_CGO类实现了CGO算法，它继承自C_AO类，并继承了基类的属性和方法。 

    方法：

    • SetParams() —— 根据参数数组（params）中的数据设置种群规模（popSize）的值。在算法使用前对其进行调优时，这一点至关重要。
    • Init() —— 初始化方法，接受最小和最大范围值、步长以及迭代次数（epochs）。其目的是通过设置搜索边界和其他参数，为算法的启动做好准备。
    • Moving() —— 描述优化过程中个体移动的相关步骤。其实现提供了替代解的逻辑及其改进方式。
    • Revision() —— 负责修订当前种群中的当前解，以及全局最优解。

    私有方法：

    • GetAlpha() —— 用于获取用于控制搜索策略及其“强度”和“多样性”的α参数。
    • GenerateNewSolution() —— 根据索引（seedIndex）和群体均值（meanGroup）生成新解。 
    class C_AO_CGO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CGO () { }
  C_AO_CGO ()
  {
    ao_name = "CGO";
    ao_desc = "Chaos Game Optimization";
    ao_link = "https://www.mql5.com/en/articles/17047";

    popSize = 25;

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving ();
  void Revision ();

  private: //-------------------------------------------------------------------
  double GetAlpha ();
  void   GenerateNewSolution (int seedIndex, double &meanGroup []);
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CGO类的Init方法负责在启动优化算法之前初始化其参数。该方法接受以下参数：包含每个搜索变量最小值和最大值的数组、每个变量的步长，以及算法的迭代次数。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CGO::Init (const double &rangeMinP  [], // minimum values
                     const double &rangeMaxP  [], // maximum values
                     const double &rangeStepP [], // step change
                     const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    在CGO算法中，Moving方法实现了对解群体中个体移动的主要逻辑。该方法的主要目标是根据规则更新群体中的决策，包括生成新的决策以及对结果取平均值。下面我们详细看看它的主要部分。

    第一部分，首次调用时的初始化 （如果“revision”等于“false”）：

    • 外层循环遍历群体中的所有元素（群体规模为popSize），对于每个元素（即第i个个体）：
      • 内层循环从坐标（coords）开始：
      • 使用u.RNDfromCI()方法为每个坐标生成一个随机值，该方法返回给定范围内的随机值。
      • 然后使用u.SeInDiSp()方法对这个值进行调整，确保该值保持在范围内，并将其四舍五入到最近的增量值。
      • 将“revision”标识设置为“true”，以便下次调用该方法时使用，然后退出该方法。
      第二部分，群体更新（如果“revision”设置为“true”）：
      • 对于群体中的每个个体：
        • 从1到popSize生成一个随机的组规模randGroupSize。
        • 创建meanGroup数组，用于存储坐标的平均值，其大小与坐标数量相对应，并初始化为coords。
        • 用随机索引（个体）填充randIndices数组，这些索引将用于分组。
        • 在每次迭代中，随机选择的索引，并将添加到randIndices中。
        • 然后，对于每个组，将随机选择的索引对应的每个个体的坐标值相加，并将结果存储在meanGroup中。
        • 求和后，将meanGroup中的值除以组中个体的数量，得到平均值。
        • 使用GenerateNewSolution()方法，根据组平均值为第i个个体生成一个新解。
      //——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int randGroupSize = u.RNDminusOne (popSize) + 1;
    double meanGroup [];
    ArrayResize (meanGroup, coords);
    ArrayInitialize (meanGroup, 0);

    int randIndices [];
    ArrayResize (randIndices, randGroupSize);

    for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize);

    for (int j = 0; j < randGroupSize; j++)
    {
      for (int c = 0; c < coords; c++)
      {
        meanGroup [c] += a [randIndices [j]].c [c];
      }
    }
    for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize;

    GenerateNewSolution (i, meanGroup);
  }
}
//——————————————————————————————————————————————————————————————————————————————

      Revision方法用于更新群体中的最优解。该方法会遍历群体中的所有个体，对于每个个体，检查其适应度函数值“f”是否大于当前的最佳值fB。如果是，则用“f”的新值更新fB，并将当前个体的c个坐标复制到cB数组中。因此，修订方法根据适应度函数的值，找出并更新群体中已知的最优解。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      GetAlpha方法根据随机选择条件生成并返回一个随机的α值。

      • Ir —— 等于0或1的随机值。
      • 有四种可能的情况（列于“case”中），每种情况都使用相应的公式生成一个“α”值：
        • 情况0：生成一个0到1之间的值。
        • 情况1：生成一个1到1之间的值。
        • 情况2：通过将某个值乘以“Ir”（0或1），生成一个1到2之间的值。
        • 情况3：生成一个取决于“Ir”的值，其范围根据“Ir”的值不同，为0到1之间或固定为1。
      请注意，用于生成“α”值的表达式本可以采用更简单的形式，但此处使用的是与算法作者对应的公式原始形式。
        //——————————————————————————————————————————————————————————————————————————————
double C_AO_CGO::GetAlpha ()
{
  int Ir = u.RNDminusOne (2);

  switch (u.RNDminusOne (4))
  {
    case 0: return u.RNDfromCI (0, 1);
    case 1: return 2 * u.RNDfromCI (0, 1) - 1;
    case 2: return Ir * u.RNDfromCI (0, 1) + 1;
    case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir);
  }
  return 0;
}
//——————————————————————————————————————————————————————————————————————————————

        GenerateNewSolution方法负责根据各种随机参数，为群体中的给定个体生成一个新解。

        参数初始化：
        • 通过调用GetAlpha()方法获取α的值，影响新位置。
        • β和γ是随机值（取值为1或2）。
        选择公式：
        • formula —— 根据该公式计算新位置，从四种可能的公式中随机选择一种。
        按坐标循环：针对每个坐标（从0到coords）：
        • newPos —— 使用所选公式存储新位置的变量。
        • 根据“formula”的含义：
          • 情况0：新位置计算为个体当前位置加上cB（群体中的最优解）和meanGroup的坐标组合值。
          • 情况1：新位置使用cB的坐标和meanGroup的平均值计算得出。
          • 情况2：新位置由平均值和当前个体的坐标确定。
          • 情况3：新位置在给定范围内（rangeMin[c]和rangeMax[c]）随机设置。
        新位置修正：
        • a[seedIndex].c[c] —— 使用u.SeInDiSp()方法更新相应个体的坐标，该方法考虑了最小值、最大值和步长，以确保新值在允许的范围内。
        //——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup [])
{
  double alpha = GetAlpha ();
  int    beta  = u.RNDminusOne (2) + 1;
  int    gamma = u.RNDminusOne (2) + 1;

  int formula = u.RNDminusOne (4);

  for (int c = 0; c < coords; c++)
  {
    double newPos = 0;

    switch (formula)
    {
      case 0:
        newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]);
        break;

      case 1:
        newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]);
        break;

      case 2:
        newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]);
        break;

      case 3:
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        break;
    }

    a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

        在完成测试后，我尝试改进算法的收敛性，并决定在基础版CGO算法的基础上做出一项补充改进。主要区别在于，在处理每个坐标时、应用基础移动公式之前，新增了以下操作：

        double rnd = u.RNDprobab();                             // Get a random number from 0.0 to 1.0
rnd *= rnd;                                             // Squate it
int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1);  // Scale to index
a[seedIndex].c [c] = a[ind].c [c];                      // Copy the coordinate from another agent with the received index

        在处理每个坐标时，会从随机选中的个体中复制该坐标值，且个体并非均匀选取，而是遵循二次概率分布（rnd *= rnd）。这样会形成一种"偏向性"，即更倾向于选择索引较小的个体（因为更优的解被选中的概率更高）。我们对随机数进行平方运算以生成非均匀分布，将其缩放至群体索引范围后，再在应用基础移动公式前复制该坐标值。试图通过聚焦于加速有潜力区域的收敛，但遗憾的是，并未达到预期效果。

        这可能是由于强化效应导致的过早收敛，使得群体多样性迅速降低，而该算法在这种情况下更容易陷入局部最优；又或许算法本身的逻辑机制对此产生了抑制作用。以下是修改后的代码段。此外，我还进行了多次其他改进尝试，但均未取得显著进展，因此最终决定沿用算法的原始版本。

        //——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup [])
{
  double alpha = GetAlpha ();
  int    beta  = u.RNDminusOne (2) + 1;
  int    gamma = u.RNDminusOne (2) + 1;

  int formula = u.RNDminusOne (4);

  for (int c = 0; c < coords; c++)
  {
    double rnd = u.RNDprobab ();
    rnd *= rnd;
    int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);
    a [seedIndex].c [c] = a [ind].c [c];

    double newPos = 0;

    switch (formula)
    {
      case 0:
        newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]);
        break;

      case 1:
        newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]);
        break;

      case 2:
        newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]);
        break;

      case 3:
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        break;
    }

    a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————


        测试结果

        由以下测试结果可见，该算法带来的整体提升幅度相当有限，然而，如果仔细观察，您会发现该算法存在一个颇具趣味的特性，其描述如下。

        CGO|Chaos Game Optimization|50.0|
        =============================
        5 Hilly's; Func runs: 10000; result: 0.5725597668122144
        25 Hilly's; Func runs: 10000; result: 0.3715760642098293
        500 Hilly's; Func runs: 10000; result: 0.32017971142744234
        =============================
        5 Forest's; Func runs: 10000; result: 0.6117551660766816
        25 Forest's; Func runs: 10000; result: 0.619308424855028
        500 Forest's; Func runs: 10000; result: 0.6216109945434442
        =============================
        5 Megacity's; Func runs: 10000; result: 0.3753846153846153
        25 Megacity's; Func runs: 10000; result: 0.2192307692307692
        500 Megacity's; Func runs: 10000; result: 0.19028461538461647
        =============================
        总分：3.90189 (43.35%)

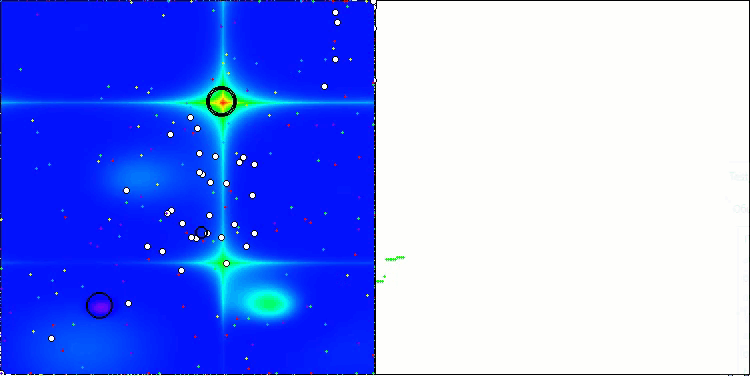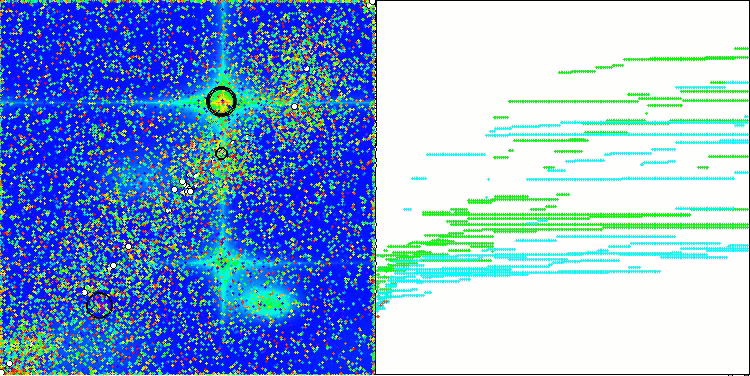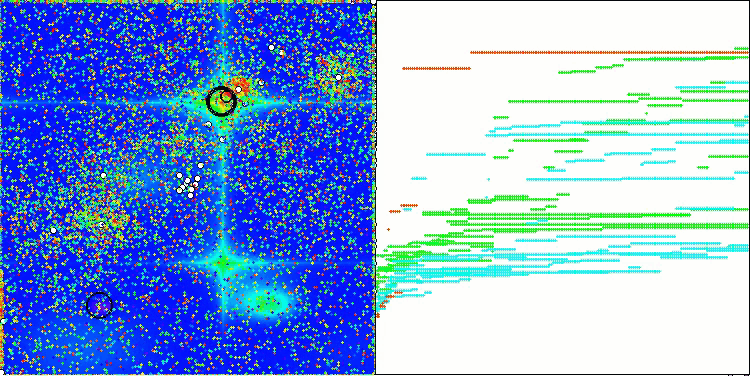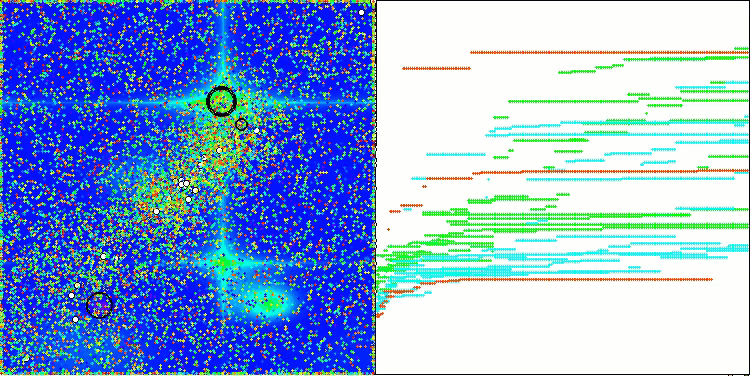
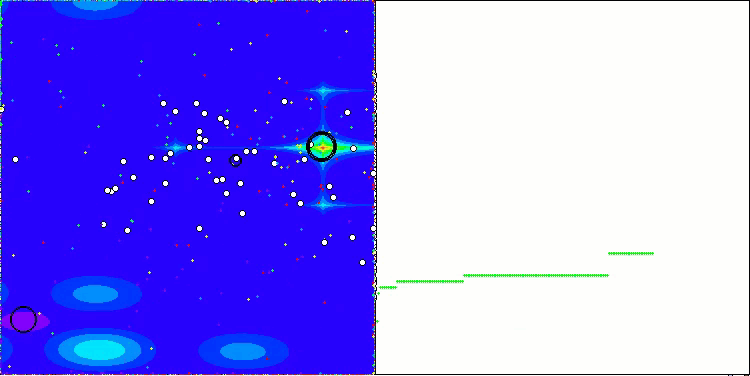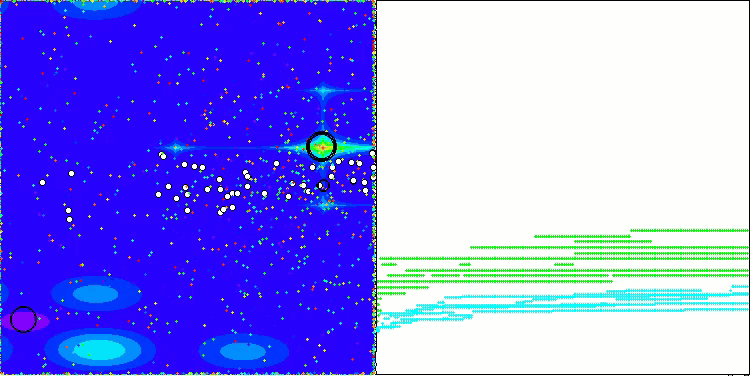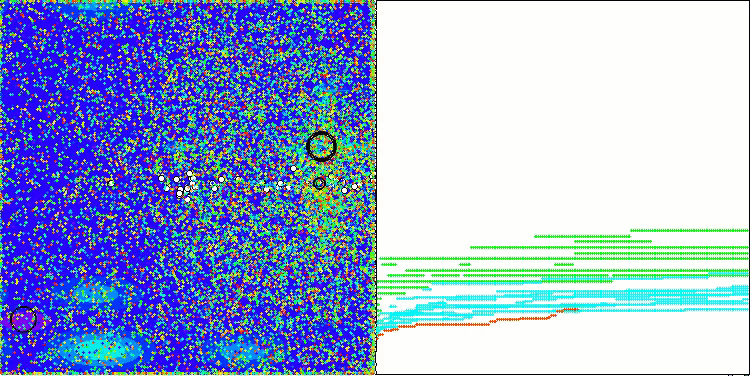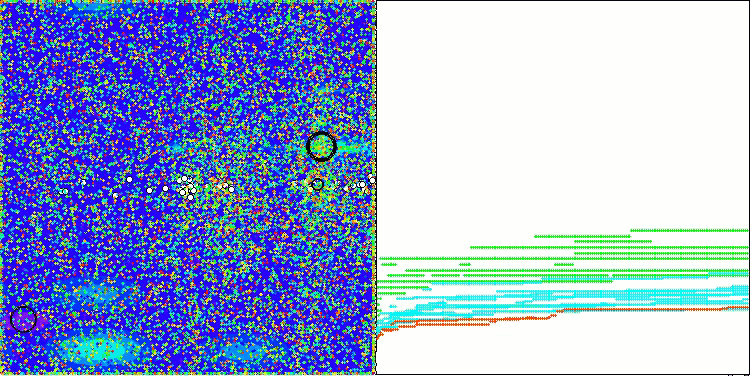
        通过测试函数可视化算法运行过程，可以清晰地观察到个体群体中形成了特定结构，且这些结构会因任务不同而呈现差异。不过该算法运行的普遍特征在于，其优化结果存在极大的波动范围。

        Hilly值

        CGO在Hilly测试函数上

        Forest值

        CGO在Forest测试函数上

        Megacity值

        CGO在Megacity测试函数上

        根据测试结果，CGO算法在群体智能优化算法排行榜中位列第38位。

        # AO 描述 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
        10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
        1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
        2 CLA 密码锁算法（joo） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
        3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
        4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
        5 CTA 彗星尾算法（joo） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
        6 TETA 时间演化旅行算法（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
        7 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
        8 AAm 射箭算法M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
        9 ESG 社会群体的进化（joo） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
        10 SIA 模拟各向同性退火（joo） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
        11 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
        12 DA 辩证算法 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
        13 BHAm 黑洞算法M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
        14 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
        15 RFO 皇家同花顺优化（joo） 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
        16 AOSm 原子轨道搜索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
        17 TSEA 龟壳演化算法（joo） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
        18 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
        19 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
        20 BIO 血液遗传优化算法（joo） 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
        21 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
        22 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
        23 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
        24 BCOm 细菌趋化性优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
        25 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
        26 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
        27 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
        28 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
        29 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
        30 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
        31 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
        32 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
        33 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
        34 SOA 简单优化算法 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
        35 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
        36 ACMO 大气云模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
        37 ADAMm 群体自适应矩估计M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
        38 CGO 混沌博弈优化 0.57256 0.37158 0.32018 1.26432 0.61176 0.61931 0.62161 1.85267 0.37538 0.21923 0.19028 0.78490 3.902 43.35
        39 ATAm 人工部落算法M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
        40 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
        41 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
        42 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
        43 CSA 圆搜索算法 0.66560 0.45317 0.29126 1.41003 0.68797 0.41397 0.20525 1.30719 0.37538 0.23631 0.10646 0.71815 3.435 38.17
        44 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
        45 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54

        		RW 随机游走 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


        总结

        在分析CGO算法的测试结果后，我得出了若干重要结论。该算法展现出极为有趣的行为特征。尽管其整体效率仅为43.35%，可归为中下水平。但是，其最显著的特点在于问题规模扩展性：CGO在处理1000维变量等高维问题时表现出色。这一特性与多数元启发式算法形成鲜明对比，其他算法通常受"维度灾难"困扰，随着变量数量增加效率骤降。而CGO在处理1000维问题时，其表现甚至有时优于处理10维和50维问题的情况。这种特性在Forest测试函数中尤为明显，该函数的全局极值点呈现"尖锐"特征。

        我认为这种现象源于该算法的本质特性。CGO的混沌本质与多样化的运动方程，共同构建了高效探索高维空间的机制。其四种不同的位置更新策略、策略间的随机选择机制，以及不可预测的α系数，使算法能够在复杂的多维地形中解决问题。该算法在Forest类函数上的表现尤为突出，取得0.61-0.62的优异成绩，显著高于其平均水平。

        通过分析算法设计，我发现其高维优势与坐标逐维处理机制密切相关。CGO不直接操作完整解向量，而是独立更新每个坐标，这种特性使其在维度增加时仍能保持优势。此外，随机分组及其平均位置的使用，确保了即使在超维空间中个体间仍能高效交换信息。

        为验证测试结果的可靠性，我通过旋转Forest函数曲面至不同角度进行实验。排除算法逻辑与特定测试函数特征偶然契合的可能性。旋转实验进一步证实，这些结果并非随机现象。鉴于CGO在处理尖锐极值函数时展现的特殊性质，我建议使用该算法时进行多次优化运行。这一建议对该算法尤为重要。

        总体而言，尽管CGO的整体性能处于中等水平，但其随问题规模扩大仍能保持甚至提升效率的独特能力，使其成为值得深入研究并应用于复杂优化问题的极具潜力的算法。

        标签

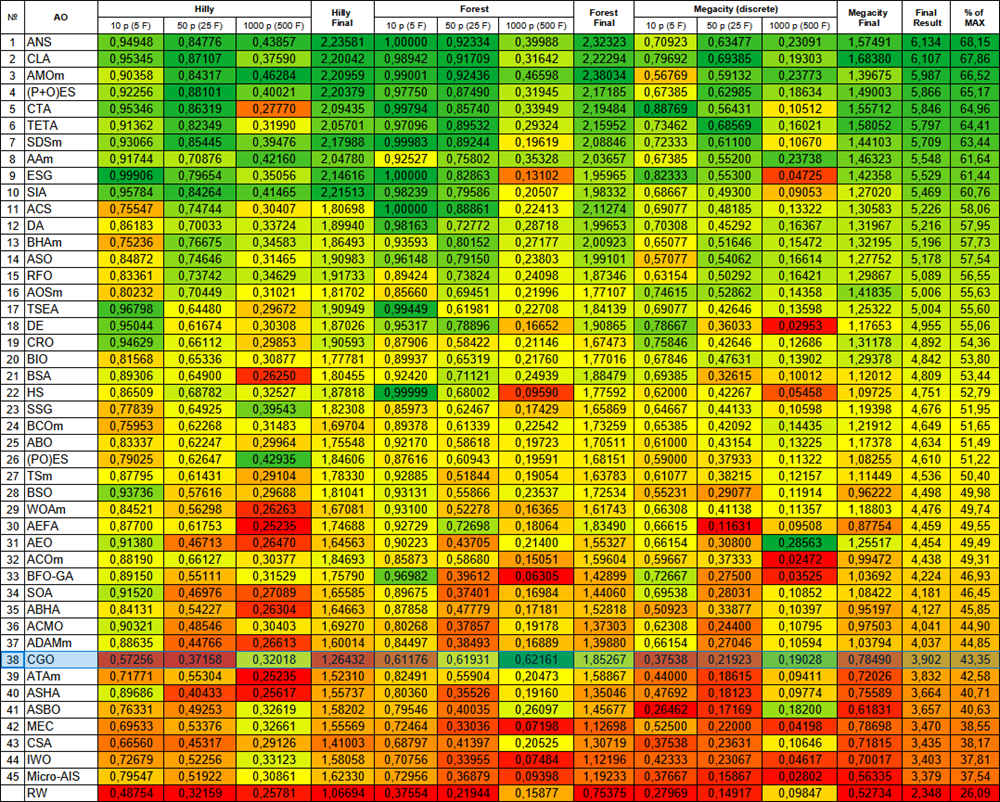
        图例2. 算法在相应测试中的颜色渐变表示

        图表

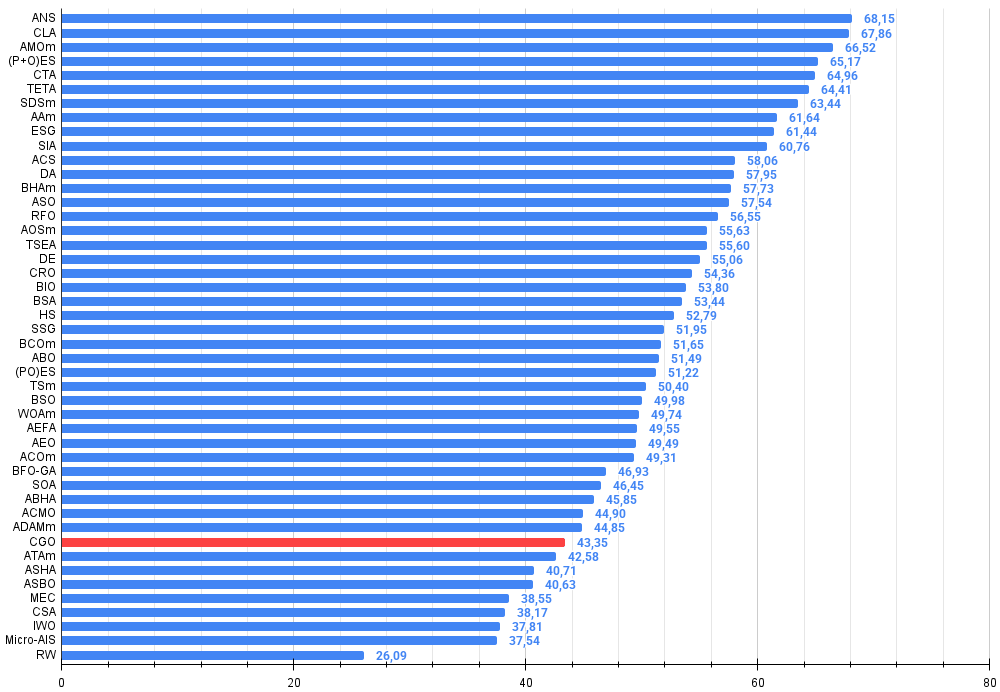
        图例3. 算法测试结果的直方图（评分范围为0到100，越高越好，其中100为理论上的最高可能得分，档案中附有计算排名表的脚本）

        CGO的优缺点：

        优点：

        1. 无外部参数。
        2. 在高维和中维函数上具有良好的收敛性。

        缺点：

        1. 在低维问题上易陷入局部最优。

        文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。


        文中所用的程序

        # 名称 类型 描述
        1 #C_AO.mqh
        		 库
        		 种群优化父类
        算法
        2 #C_AO_enum.mqh
        		 库
        		 种群优化算法的枚举说明
        3 TestFunctions.mqh
        		 库
        		 测试函数库
        4
        		 TestStandFunctions.mqh
        		 库
        		 测试台函数库
        5
        		 Utilities.mqh
        		 库
        		 辅助函数库
        6
        		 CalculationTestResults.mqh
        		 库
        		 用于计算比较表结果的脚本
        7
        		 Testing AOs.mq5
        		 脚本 面向所有种群优化算法的统一测试平台
        8
        		 Simple use of population optimization algorithms.mq5
        		 脚本
        		 种群优化算法非可视化简易使用案例
        9
        		 Test_AO_CGO.mq5
        		 脚本 CGO测试台

        本文由MetaQuotes Ltd译自俄文
        原文地址： https://www.mql5.com/ru/articles/17047

        附加的文件 |
        下载ZIP
        CGO.zip (168.66 KB)

        注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

        本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

        该作者的其他文章

        前往讨论
        交易策略 交易策略
        各种交易策略的分类都是任意的，下面这种分类强调从交易的基本概念上分类。
        从基础到中级：结构（一） 从基础到中级：结构（一）
        今天，我们将开始以更简单、更实用、更舒适的方式研究结构。结构是编程的基础之一，无论它们是否结构化。我知道很多人认为结构只是数据的集合，但我向你保证，它们不仅仅是结构。接下来，我们将以最富启发性的方式开始探索这个全新的宇宙。
        新手在交易中的10个基本错误 新手在交易中的10个基本错误
        新手在交易中会犯的10个基本错误: 在市场刚开始时交易, 获利时不适当地仓促, 在损失的时候追加投资, 从最好的仓位开始平仓, 翻本心理, 最优越的仓位, 用永远买进的规则进行交易, 在第一天就平掉获利的仓位,当发出建一个相反的仓位警示时平仓, 犹豫。
        交易中的神经网络：针对金融市场的多模态、扩增工具型智代（FinAgent） 交易中的神经网络：针对金融市场的多模态、扩增工具型智代（FinAgent）
        我们邀请您来探索 FinAgent，一个多模态金融交易智代框架，设计用来分析反映市场动态和历史交易形态的各种数据。