
Chaos Game Optimization (CGO)
Contents
Introduction
Optimization algorithms play a strategic role in solving complex problems not only in various areas of modern science, but also in trading. With the rapid development of technology, these tasks are becoming even more complex, and the search for the best solution is becoming increasingly energy-intensive. Therefore, the requirements for optimization algorithms, their effectiveness and high operational efficiency are increasing. One of the newest and most promising methods is the Chaos Game Optimization (CGO) algorithm, developed by Siamak Talatahari and Mehdi Azizi in 2020. This algorithm is based on the principles of chaos theory and uses chaotic sequences to generate and improve solutions.
The main idea of the algorithm is to use chaotic sequences to find global optima in complex multidimensional spaces. Chaotic sequences possess certain properties that, theoretically, allow them to avoid local pitfalls and find high-quality solutions. In this article, we will examine the basic principles and stages of the Chaos Game Optimization algorithm, implement it in code, conduct standard tests on test functions, and draw conclusions about its performance.
Implementation of the algorithm
Imagine a group of researchers, each trying to find an extremum in a multidimensional labyrinth. At the beginning of the journey, our seekers are scattered randomly throughout the labyrinth and find their first refuge within strictly defined boundaries of space. This is their starting point. Each seeker does not act alone - he observes his peers, and at any given moment, he selects a random group of peers, calculates the center of their location, as if finding a point of balance between their positions.
It is the collective wisdom, averaged over the group's experience. And then the real magic of chaos begins. The seeker can choose one of four paths for his next step. Each path is a special equation of movement, where three key points are intertwined: seeker's current position, the best place found by the whole group, and the center of the selected subgroup. These points are mixed, and the strength of their influence on further movement is determined by the α ratio – the conductor of chaos.
The α ratio itself takes on different incarnations, and each seeker, following the rules, can either push off from his position, rushing towards the golden mean between the best result and the center of the group, or start from the best point, exploring the space around it, and can also push off from the center of the group, or make a completely random leap into the unknown.
At the end of each such action, a comparison of the results takes place. If one of the seekers finds a place better than the previous record, it becomes a new beacon for the entire group in their further search.
This is the true beauty of the algorithm - its ability to transform chaos into order, randomness into purposeful movement, uncertainty into progress, and every step, every movement is subordinated to the search for solutions between the known and the unknown, between stability and risk, between order and chaos.
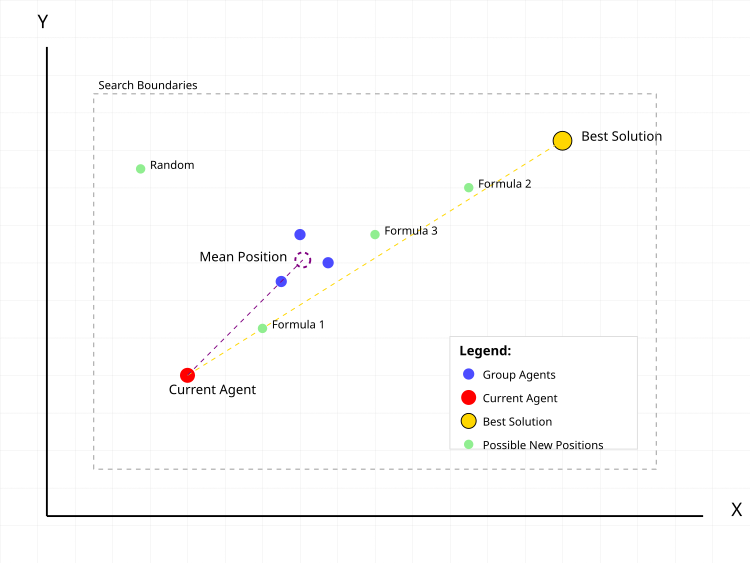
Figure 1. Typical actions of a search agent in the CGO algorithm
In Figure 1, the red dot is the current agent the new position is calculated for. Blue dots are a group of randomly selected agents in the population in a randomly selected number. The purple dotted circle is the middle position of the group. The golden dot is the best solution found. Green dots are possible new positions of the agent according to different formulas:- Formula 1: current + α(β×best - γ×average)
- Formula 2: best + α(β×average - γ×current)
- Formula 3: average + α(β×best - γ×current)
- Random: random position
The dotted lines show the vectors of influence of the best solution and the average position of the group on the movement of the current agent. The grey dotted rectangle indicates the boundaries of the search area.
Let's start writing the pseudocode of the algorithm.
- Set population size (the default is 50 agents)
- Define search boundaries for each coordinate:
- minimum values (rangeMin)
- maximum values (rangeMax)
- change step (rangeStep)
- For each agent in the population:
- generate random initial coordinates within the given boundaries
- round coordinates taking into account the step
- calculate the value of the objective function
- Determine the best initial solution among all agents
- For each agent in the population:
- subgroup size = random number between 1 and population size
- randomly select agents into a subgroup
- for each coordinate: average_coordinate = sum_of_group_coordinates / group_size
- α (alpha) = choose one of the methods at random:
- method 1: random number from 0 to 1
- method 2: 2 × random(0,1) - 1 [get number from -1 to 1]
- method 3: Ir × random(0,1) + 1
- method 4: Ir × random(0,1) + (1-Ir) where Ir = random 0 or 1
- β (beta) = random 1 or 2
- γ (gamma) = random 1 or 2
- Formula 1: new_position = current + α(β×best - γ×average)
- Formula 2: new_position = best + α(β×average - γ×current)
- Formula 3: new_position = average + α(β×best - γ×current)
- Formula 4: new_position = random position within search boundaries
- for each coordinate:
- calculate a new value using the equation
- check for search out of bounds
- if the limits have been exceeded, adjust to the nearest limit
- round the value taking into account the step of change
- For each agent:
- if the value of the agent objective function is better than the current best:
- update best value
- save the coordinates of the new best solution
- if the value of the agent objective function is better than the current best:
- Repeat steps 2-3 until the stop condition is met:
- reached maximum number of iterations
- or found a solution of the required quality
- or another stop criterion
Let's move on to the implementation of the algorithm itself. The C_AO_CGO class implements the CGO algorithm and is derived from the C_AO class, inheriting the properties and methods of the base class.
Methods:
- SetParams () — set the popSize value based on the data in the params array. This is important to tune the algorithm before using it.
- Init () — initialization method that accepts the minimum and maximum range values, the step size, and the number of epochs. Its purpose is to prepare the algorithm for launch by setting the search boundaries and other parameters.
- Moving () describes the steps associated with the movement of individuals during the optimization. Its implementation provides the logic of alternative solutions and their improvement.
- Revision () is responsible for revising the current solutions for the current population, as well as the globally best solution.
Private methods:
- GetAlpha () for receiving the alpha parameter used to control the search strategy, as well as its "intensity" and "diversity".
- GenerateNewSolution () for generating a new solution based on the index (seedIndex) and the group mean (meanGroup).
class C_AO_CGO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CGO () { } C_AO_CGO () { ao_name = "CGO"; ao_desc = "Chaos Game Optimization"; ao_link = "https://www.mql5.com/en/articles/17047"; popSize = 25; ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); private: //------------------------------------------------------------------- double GetAlpha (); void GenerateNewSolution (int seedIndex, double &meanGroup []); }; //——————————————————————————————————————————————————————————————————————————————
The Init method of the C_AO_CGO class is responsible for initializing the parameters of the optimization algorithm before it is launched. It takes the following arguments: arrays containing the minimum and maximum values for each search variable, the step size for each variable, and the number of epochs (iterations) of the algorithm.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CGO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) // number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; return true; } //——————————————————————————————————————————————————————————————————————————————
The Moving method implements the main logic of moving individuals of the solution population in the CGO algorithm. The main goal of this method is to update decisions in a population based on rules, including generating new decisions and averaging the results. Let's take a closer look at its main parts.
The first part, initialization on first call (if "revision" is equal to 'false'):
- The outer loop is run over all elements of the population (popSize) and for each element (i individual):
- The inner loop is started by coordinates (coords):
- Generate a random value for each coordinate using the u.RNDfromCI () method, which returns a random value within the given range.
- This value is then adjusted using u.SeInDiSp(), which ensures that the value stays within range and rounds it to the nearest increment.
- Set the "revision" flag to 'true' for the next method call and exit the method.
- For each individual in the population:
- Generate a random randGroupSize group size from 1 to popSize.
- Create the meanGroup array to store the mean value of coordinates, the size of which corresponds to the number of coordinates and set to coords.
- Populate the randIndices array with random indices (individuals) that will be used to form the group.
- At each iteration, random indices are added to randIndices, with the indices chosen randomly.
- Then, for each group, the coordinate values for each individual from randomly selected indices are summed and the result is stored in meanGroup.
- After summation, the value in meanGroup is divided by the number of individuals in the group to obtain the mean.
- Generate a new solution for "i" individual based on the group mean using the GenerateNewSolution() method.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { int randGroupSize = u.RNDminusOne (popSize) + 1; double meanGroup []; ArrayResize (meanGroup, coords); ArrayInitialize (meanGroup, 0); int randIndices []; ArrayResize (randIndices, randGroupSize); for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize); for (int j = 0; j < randGroupSize; j++) { for (int c = 0; c < coords; c++) { meanGroup [c] += a [randIndices [j]].c [c]; } } for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize; GenerateNewSolution (i, meanGroup); } } //——————————————————————————————————————————————————————————————————————————————
The Revision method updates the best solutions in the population. It loops through all individuals in the population and, for each individual, checks if its fitness function value of "f" is greater than the current best value fB. If so, it updates fB with the new value of "f" and copies the c coordinates of the current individual to the cB array. Thus, the Revision method finds and updates the best known solution in the population based on the values of the fitness function.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
The GetAlpha method generates and returns a random alpha value based on random selection conditions.
- Ir — random value equal to 0 or 1.
- There are four possible cases (listed in "case"), each of which generates an "alpha" value using the corresponding equation:
- Case 0: Generates a value from 0 to 1.
- Case 1: Generates a value from -1 to 1.
- Case 2: Generates a value from 1 to 2 by multiplying it by "Ir" (0 or 1).
- Case 3: Generates a value that depends on "Ir" and has a range from 0 to 1, or 1, depending on the value of "Ir".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CGO::GetAlpha () { int Ir = u.RNDminusOne (2); switch (u.RNDminusOne (4)) { case 0: return u.RNDfromCI (0, 1); case 1: return 2 * u.RNDfromCI (0, 1) - 1; case 2: return Ir * u.RNDfromCI (0, 1) + 1; case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir); } return 0; } //——————————————————————————————————————————————————————————————————————————————
The GenerateNewSolution method is responsible for generating a new solution for a given agent in the population, based on various random parameters.
Initialization of parameters:- alpha is the value obtained by calling the GetAlpha () method used to influence the new position.
- beta and gamma are random values (1 or 2).
- formula — one of four possible equations is randomly selected, according to which the new position will be calculated.
- newPos — a variable to store the new position using the selected equation.
- Depending on the meaning of "formula":
- Case 0: a new position is calculated as the current position of the agent plus a combination of coordinates from cB (the best solution in the population) and meanGroup.
- Case 1: a new position is calculated using the coordinate from cB and the mean value of meanGroup.
- Case 2: a new position is determined by the average value and the coordinate of the current agent.
- Case 3: a new position is set randomly within the given range (rangeMin [c] and rangeMax [c]).
- a [seedIndex].c [c] — the corresponding agent coordinate is updated using the u.SeInDiSp() method, which takes into account the minimum values, maximum values and steps to ensure that the new value is within the allowed limits.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
After conducting tests, I attempted to improve the convergence of the algorithm and decided to make an addition compared to the basic version of the CGO algorithm. The main difference is at the beginning of handling each coordinate, before applying the basic movement equations:
double rnd = u.RNDprobab(); // Get a random number from 0.0 to 1.0 rnd *= rnd; // Squate it int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1); // Scale to index a[seedIndex].c [c] = a[ind].c [c]; // Copy the coordinate from another agent with the received index
The coordinate is copied from a randomly selected agent, and the agent is not selected uniformly, but with a quadratic probability distribution (rnd *= rnd). This creates a "bias" towards selecting agents with smaller indices (better solutions have a higher probability of being selected). We square the random number, thereby creating a non-uniform distribution, scale it to the range of population indices, and then copy it before applying the basic movement equations. My focus on trying to accelerate convergence in promising areas, unfortunately, did not produce the expected effect.
Probably, as a result of premature convergence, due to the strengthening effect, diversity in the population quickly decreases, which in this algorithm leads to being stuck at an even greater extent; it is possible that the logic of the algorithm itself prevents this. Below is the section of code where the changes have been made. In addition, I made several more attempts to improve it, however, no noticeable progress was achieved, and I decided to stay with the original version of the algorithm.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double rnd = u.RNDprobab (); rnd *= rnd; int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); a [seedIndex].c [c] = a [ind].c [c]; double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Test results
As you can see from the test results below, the overall percentage gained by the algorithm is quite modest, however, if you look closely, you can notice an interesting feature of this algorithm, which I will describe below.
CGO|Chaos Game Optimization|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.5725597668122144
25 Hilly's; Func runs: 10000; result: 0.3715760642098293
500 Hilly's; Func runs: 10000; result: 0.32017971142744234
=============================
5 Forest's; Func runs: 10000; result: 0.6117551660766816
25 Forest's; Func runs: 10000; result: 0.619308424855028
500 Forest's; Func runs: 10000; result: 0.6216109945434442
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2192307692307692
500 Megacity's; Func runs: 10000; result: 0.19028461538461647
=============================
All score: 3.90189 (43.35%)
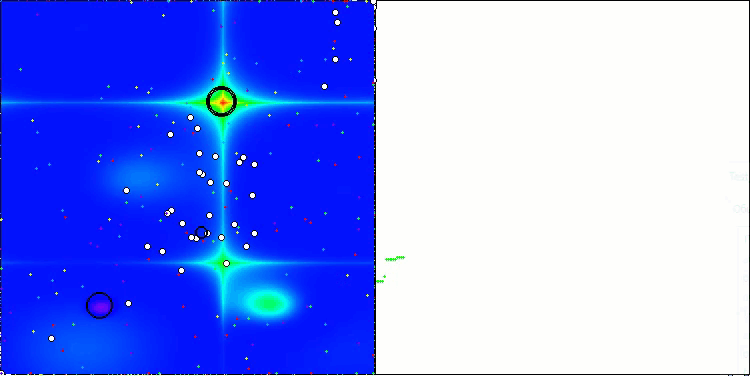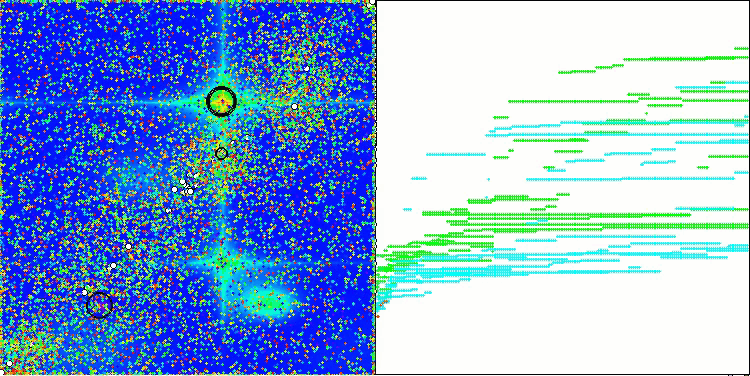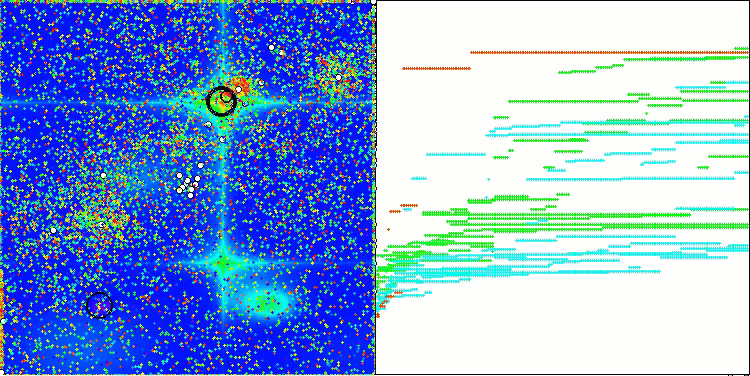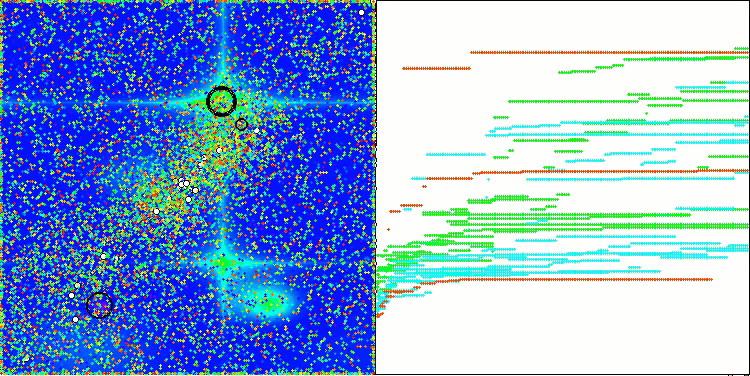
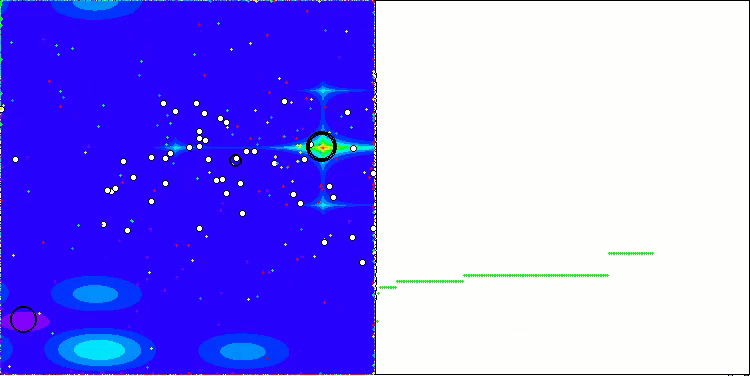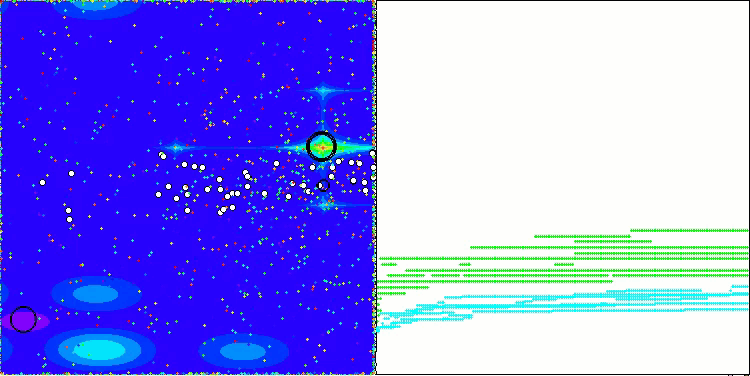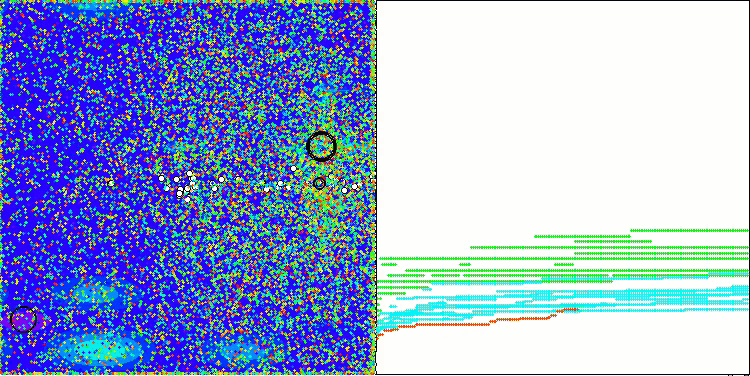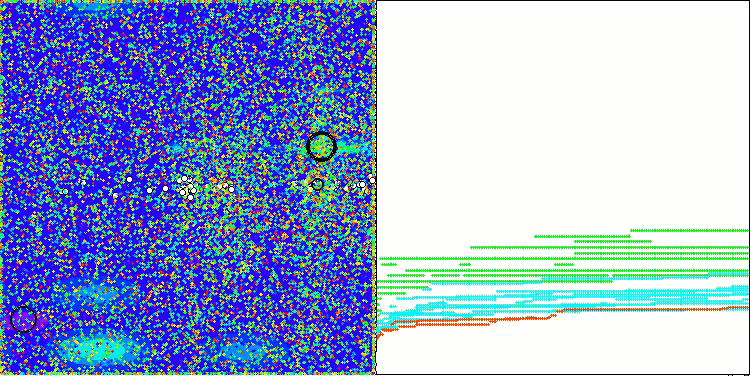
The visualization of the algorithm operation on test functions clearly shows the formation of structures in the grouping of agents, and these structures are different for different tasks. But the general nature of the algorithm operation is the huge range of optimization results.

CGO on the Hilly test function
CGO on the Forest test function
CGO on the Megacity test function
Based on the test results, the CGO algorithm occupies 38th position in the ranking table of population-based optimization algorithms.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 15 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BIO | blood inheritance optimization (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 21 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 22 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 23 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 24 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 25 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 26 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 27 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 28 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 29 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 30 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 31 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 32 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 33 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 34 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 35 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 36 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 37 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 38 | CGO | chaos game optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 39 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 40 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 41 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 42 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 43 | CSA | circle search algorithm | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 44 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 45 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| RW | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Summary
After analyzing the results of the CGO algorithm, I came to some important conclusions. The Chaos Game Optimization algorithm exhibits very interesting behavior. Overall, its efficiency can be rated as below average, which is confirmed by the overall result of 43.35%. However, its most notable behavior is when scaling the problem; CGO shows high efficiency precisely on multidimensional problems — tests with a dimension of 1000 variables. This is an atypical property for most metaheuristic algorithms, which typically suffer from the "curse of dimensionality" and lose efficiency as the number of variables increases. CGO, on the contrary, sometimes even outperforms its results on 10- and 50-dimensional problems when working with 1000-dimensional problems. This is especially evident in the Forest test function, which has a global extremum at one "sharp" point.
I believe that this phenomenon is due to the very nature of the algorithm. The chaotic nature of CGO and the diversity of motion equations create an efficient mechanism for exploring high-dimensional spaces. Four different position update strategies, random choice between them, and an unpredictable α ratio allow the algorithm to solve problems on complex multidimensional landscapes. The algorithm performed particularly well on Forest-type functions, with results of 0.61–0.62, which is significantly higher than its average.
Analyzing the design of the algorithm, I see that its strength in high dimensions is related to coordinate-wise processing. Instead of working with the full solution vector, CGO updates each coordinate independently, which gives it an advantage as the dimensionality increases. Furthermore, the use of random groups and their average positions ensures efficient information exchange between agents even in high-dimensional spaces.
I tried rotating the Forest function surface at different angles to make sure that the interesting results I got were not a coincidence of the specific features of the algorithm logic and the corresponding test function. This was necessary in order to exclude the possibility of accidentally hitting a global extremum. Experiments with function rotation only confirmed that such results are not random. Given this peculiarity of CGO's handling of functions with sharp extremes, I recommend running multiple optimization runs if using this algorithm. This recommendation is particularly relevant for this algorithm.
Overall, despite its average overall performance, CGO's unique ability to maintain and even improve efficiency as the problem size increases makes it an exceptionally interesting algorithm for further study and application to complex optimization problems.
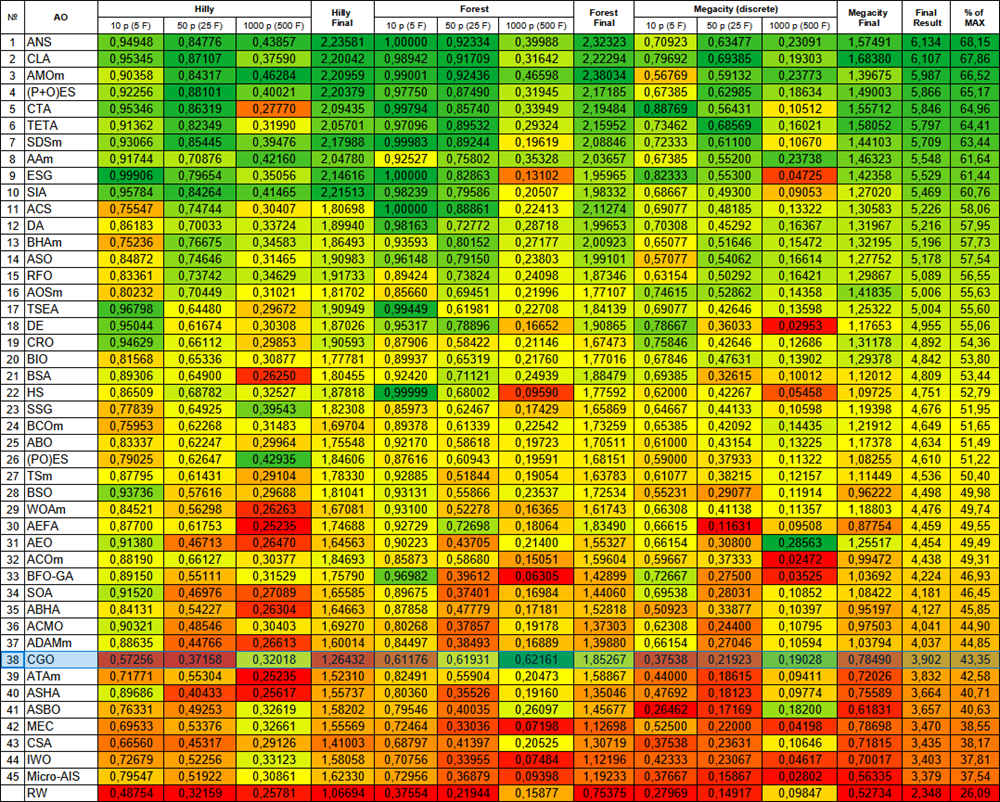
Figure 2. Color gradation of algorithms according to the corresponding tests
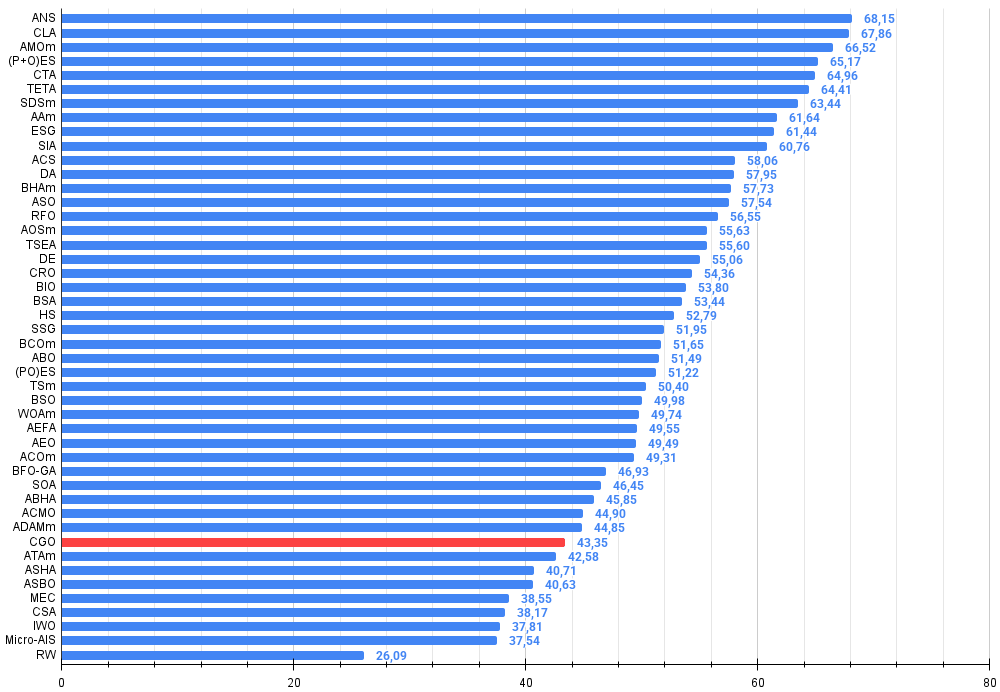
Figure 3. Histogram of algorithm testing results (scale from 0 to 100, the higher the better, where 100 is the maximum possible theoretical result, in the archive there is a script for calculating the rating table)
CGO pros and cons:
Pros:
- No external parameters
- Good convergence on high and medium dimensional functions
Disadvantages:
- Gets stuck at local extremes on low-dimensional problems.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Parent class of population optimization algorithms |
| 2 | #C_AO_enum.mqh | Include | Enumeration of population optimization algorithms |
| 3 | TestFunctions.mqh | Include | Library of test functions |
| 4 | TestStandFunctions.mqh | Include | Test stand function library |
| 5 | Utilities.mqh | Include | Library of auxiliary functions |
| 6 | CalculationTestResults.mqh | Include | Script for calculating results in the comparison table |
| 7 | Testing AOs.mq5 | Script | The unified test stand for all population optimization algorithms |
| 8 | Simple use of population optimization algorithms.mq5 | Script | A simple example of using population optimization algorithms without visualization |
| 9 | Test_AO_CGO.mq5 | Script | CGO test stand |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/17047
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Automating Trading Strategies in MQL5 (Part 45): Inverse Fair Value Gap (IFVG)
Automating Trading Strategies in MQL5 (Part 45): Inverse Fair Value Gap (IFVG)
 From Novice to Expert: Developing a Geographic Market Awareness with MQL5 Visualization
From Novice to Expert: Developing a Geographic Market Awareness with MQL5 Visualization
 The View and Controller components for tables in the MQL5 MVC paradigm: Containers
The View and Controller components for tables in the MQL5 MVC paradigm: Containers
 Reimagining Classic Strategies (Part 19): Deep Dive Into Moving Average Crossovers
Reimagining Classic Strategies (Part 19): Deep Dive Into Moving Average Crossovers
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use