
Otimização com Jogo do Caos — Chaos Game Optimization (CGO)
Conteúdo
Introdução
Os algoritmos de otimização desempenham um papel estratégico não apenas na solução de problemas complexos em várias áreas da ciência moderna, mas também no trading. Com o rápido avanço das tecnologias, esses problemas se tornam cada vez mais difíceis e a busca pela melhor solução exige mais recursos, aumentando as demandas sobre os algoritmos de otimização, especialmente no que se refere à eficácia aliada à eficiência. Um dos métodos mais recentes e promissores é o algoritmo Chaos Game Optimization (CGO), desenvolvido por Siamak Talatahari e Mehdi Azizi em 2020. Ele se baseia nos princípios da teoria do caos e utiliza sequências caóticas para gerar e aprimorar soluções.
A ideia central do algoritmo é utilizar sequências caóticas para encontrar ótimos globais em espaços multidimensionais complexos. As sequências caóticas possuem propriedades específicas que, em tese, possibilitam evitar armadilhas locais e encontrar soluções de qualidade. Neste artigo, destrincharemos os princípios e as etapas do algoritmo Chaos Game Optimization, o implementaremos em código e realizaremos testes padrões em funções de benchmark, tirando considerações finais sobre seu desempenho.
Implementação do algoritmo
Imagine um grupo de exploradores, cada um tentando encontrar um extremo em um labirinto multidimensional. No início do percurso, esses exploradores são espalhados aleatoriamente pelo labirinto e estabelecem seu primeiro ponto de referência dentro de limites bem definidos do espaço. Essa é sua posição inicial. Cada explorador não age sozinho, ele observa seus companheiros e, a cada instante, escolhe aleatoriamente um grupo de aliados, calcula o centro de suas posições, como se estivesse encontrando um ponto de equilíbrio entre eles.
Esse é o conhecimento coletivo, uma sabedoria construída a partir da média da experiência do grupo. E então começa a verdadeira magia do caos. O explorador pode escolher um entre quatro caminhos para dar o próximo passo. Cada caminho é uma fórmula particular de movimento, na qual se entrelaçam três pontos principais: a posição atual do explorador, o melhor ponto encontrado por todo o grupo e o centro do subgrupo escolhido. Esses pontos se combinam e a intensidade da influência de cada um sobre o deslocamento é determinada pelo coeficiente α, o condutor do caos.
Por si só, o coeficiente α assume diferentes formas, e cada explorador, seguindo as regras, pode se afastar de sua posição atual em direção ao ponto médio entre o melhor resultado e o centro do grupo; partir da melhor posição encontrada, explorando o espaço ao redor dela; se deslocar a partir do centro do grupo; ou realizar um salto totalmente aleatório para o desconhecido.
Ao final de cada etapa, os resultados são comparados. Se algum explorador encontrar um ponto melhor que o recorde anterior, ele se tornará o novo farol para toda a equipe em sua busca.
É justamente aí que reside a verdadeira beleza do algoritmo, em sua capacidade de transformar o caos em ordem, a aleatoriedade em movimento direcionado, a incerteza em progresso. Cada passo, cada deslocamento, está subordinado à busca de soluções entre o conhecido e o inexplorado, entre a estabilidade e o risco, entre a ordem e o caos.
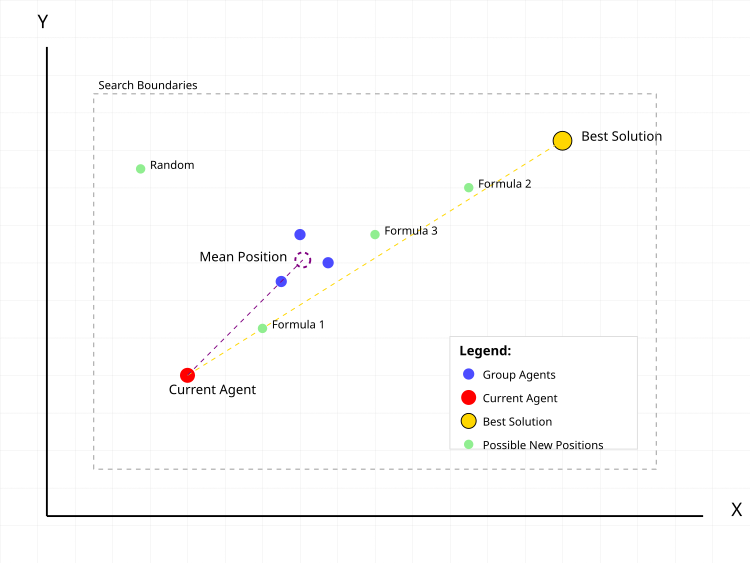
Figura 1. Ações típicas do agente de busca no algoritmo CGO
Na figura 1, o ponto vermelho representa o agente atual, para o qual é calculada a nova posição. Os pontos azuis representam o grupo de agentes escolhidos aleatoriamente da população, em uma quantidade também aleatória. A circunferência tracejada em roxo mostra a posição média do grupo. O ponto dourado representa a melhor solução encontrada até o momento. Os pontos verdes são as possíveis novas posições do agente, calculadas segundo diferentes fórmulas:- Formula 1: atual + α(β×melhor - γ×média)
- Formula 2: melhor + α(β×média - γ×atual)
- Formula 3: média + α(β×melhor - γ×atual)
- Random: posição aleatória
As linhas tracejadas representam os vetores de influência da melhor solução e da posição média do grupo sobre o movimento do agente atual. O retângulo tracejado em cinza indica os limites da área de busca.
Passemos agora à escrita do pseudocódigo do algoritmo.
- Definir o tamanho da população (por padrão 50 agentes)
- Definir os limites de busca para cada coordenada:
- valores mínimos (rangeMin)
- valores máximos (rangeMax)
- passo de variação (rangeStep)
- Para cada agente na população:
- gerar coordenadas iniciais aleatórias dentro dos limites definidos
- arredondar as coordenadas de acordo com o passo
- calcular o valor da função objetivo
- Determinar a melhor solução inicial entre todos os agentes
- Para cada agente na população:
- tamanho do subgrupo = número aleatório entre 1 e o tamanho da população
- escolher aleatoriamente os agentes do subgrupo
- para cada coordenada: média_coord = soma_coord_grupo / tamanho_grupo
- α (alfa) = escolher aleatoriamente um dos métodos:
- método 1: número aleatório de 0 a 1
- método 2: 2 × aleatório(0,1) - 1 [resulta em número de -1 a 1]
- método 3: Ir × aleatório(0,1) + 1
- método 4: Ir × aleatório(0,1) + (1-Ir) onde Ir = aleatório 0 ou 1
- β (beta) = aleatório 1 ou 2
- γ (gama) = aleatório 1 ou 2
- Fórmula 1: nova_posição = atual + α(β×melhor - γ×média)
- Fórmula 2: nova_posição = melhor + α(β×média - γ×atual)
- Fórmula 3: nova_posição = média + α(β×melhor - γ×atual)
- Fórmula 4: nova_posição = posição aleatória dentro dos limites de busca
- para cada coordenada:
- calcular o novo valor segundo a fórmula
- verificar se saiu dos limites de busca
- se saiu, ajustar para a borda mais próxima
- arredondar o valor de acordo com o passo de variação
- Para cada agente:
- se o valor da função objetivo do agente for melhor que o melhor atual:
- atualizar o melhor valor
- salvar as coordenadas da nova melhor solução
- se o valor da função objetivo do agente for melhor que o melhor atual:
- Repetir os passos 2-3 até que a condição de parada seja atingida:
- atingido o número máximo de iterações
- ou encontrada solução com a qualidade exigida
- ou outro critério de parada definido
Agora passamos para a implementação do algoritmo. A classe "C_AO_CGO" implementa o algoritmo CGO e é derivada da classe "C_AO", herdando as propriedades e métodos da classe base.
Métodos:
- SetParams () — define o valor de "popSize" com base nos dados do array de parâmetros "params". Isso é importante para configurar o algoritmo antes de utilizá-lo.
- Init () — método de inicialização, recebe os valores mínimo e máximo do intervalo, o passo de variação e a quantidade de épocas. Seu objetivo é preparar o algoritmo para a execução, estabelecendo os limites de busca e outros parâmetros.
- Moving () — descreve os passos relacionados ao movimento dos indivíduos durante a otimização. Sua implementação garante a lógica de alternativas de solução e seu aprimoramento.
- Revision () — responsável pela revisão tanto das soluções atuais da população quanto da melhor solução global.
Métodos privados:
- GetAlpha () — usado para obter o parâmetro alpha, que controla a estratégia, a "intensidade" e a "diversidade" da busca.
- GenerateNewSolution () — usado para gerar uma nova solução com base no índice (seedIndex) e no valor médio do grupo (meanGroup).
class C_AO_CGO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CGO () { } C_AO_CGO () { ao_name = "CGO"; ao_desc = "Chaos Game Optimization"; ao_link = "https://www.mql5.com/en/articles/17047"; popSize = 25; ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); private: //------------------------------------------------------------------- double GetAlpha (); void GenerateNewSolution (int seedIndex, double &meanGroup []); }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" da classe "C_AO_CGO" é responsável por inicializar os parâmetros do algoritmo de otimização antes de sua execução. Ele recebe os seguintes argumentos: arrays contendo os valores mínimos e máximos de cada variável de busca, o passo de variação para cada variável e o número de épocas (iterações) do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CGO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) // number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" executa a lógica principal de deslocamento dos indivíduos da população de soluções no algoritmo CGO. O objetivo central desse método é atualizar as soluções da população com base nas regras, incluindo a geração de novas soluções e o cálculo da média dos resultados. Vamos detalhar suas principais etapas.
A primeira parte é a inicialização durante a primeira chamada (quando a variável "revision" é igual a "false"):
- É iniciado um laço externo para percorrer todos os elementos da população (popSize) e, para cada elemento (indivíduo i):
- É iniciado um laço interno para percorrer as coordenadas (coords):
- Um valor aleatório é gerado para cada coordenada usando o método u.RNDfromCI(), que retorna um valor dentro do intervalo definido.
- Esse valor é então ajustado pelo método u.SeInDiSp(), garantindo que ele permaneça dentro dos limites e seja arredondado ao passo mais próximo.
- Em seguida, a flag "revision" é definida como "true" para a próxima chamada do método, e ocorre a saída do método.
- Para cada indivíduo da população:
- É gerado um tamanho de grupo aleatório "randGroupSize", variando de "1" até "popSize".
- É criado um array "meanGroup" para armazenar os valores médios das coordenadas, com tamanho correspondente ao número de coordenadas definido em "coords".
- É preenchido o array "randIndices", que contém índices aleatórios (indivíduos) selecionados para formar o grupo.
- A cada iteração, são adicionados índices aleatórios em "randIndices", escolhidos de forma aleatória.
- Em seguida, para cada grupo, são somados os valores das coordenadas de cada indivíduo selecionado aleatoriamente, e o resultado é armazenado em "meanGroup".
- Após o somatório, o valor em "meanGroup" é dividido pelo número de indivíduos do grupo para calcular a média.
- Um novo indivíduo para a posição "i" é então gerado com base nesse valor médio de grupo, utilizando o método "GenerateNewSolution()".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { int randGroupSize = u.RNDminusOne (popSize) + 1; double meanGroup []; ArrayResize (meanGroup, coords); ArrayInitialize (meanGroup, 0); int randIndices []; ArrayResize (randIndices, randGroupSize); for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize); for (int j = 0; j < randGroupSize; j++) { for (int c = 0; c < coords; c++) { meanGroup [c] += a [randIndices [j]].c [c]; } } for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize; GenerateNewSolution (i, meanGroup); } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" realiza a atualização das melhores soluções na população. Procorre todos os indivíduos em um laço e, para cada um, verifica se seu valor de função de adaptabilidade "f" é melhor que o valor atual "fB", e se for, atualiza "fB" com o novo valor de "f" e copia as coordenadas do indivíduo atual para o array "cB". Assim, o método "Revision" identifica e atualiza a melhor solução conhecida na população com base nos valores da função de adaptabilidade.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
O método "GetAlpha" gera e retorna um valor aleatório para "alpha", dependendo de condições aleatórias de escolha.
- Ir — valor aleatório que pode ser "0" ou "1".
- Existem quatro possíveis casos (listados em "case"), em cada um dos quais o valor de "alpha" é calculado segundo uma fórmula correspondente:
- Caso 0: Gera um valor entre 0 e 1.
- Caso 1: Gera um valor entre -1 e 1.
- Caso 2: Gera um valor entre 1 e 2, multiplicado por "Ir" (0 ou 1).
- Caso 3: Gera um valor que depende de "Ir" e pode variar de 0 a 1 ou ser igual a 1, dependendo de seu valor.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CGO::GetAlpha () { int Ir = u.RNDminusOne (2); switch (u.RNDminusOne (4)) { case 0: return u.RNDfromCI (0, 1); case 1: return 2 * u.RNDfromCI (0, 1) - 1; case 2: return Ir * u.RNDfromCI (0, 1) + 1; case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir); } return 0; } //——————————————————————————————————————————————————————————————————————————————
O método "GenerateNewSolution" é responsável por gerar uma nova solução para um agente específico da população, com base em diferentes parâmetros aleatórios.
Inicialização dos parâmetros:- alpha — valor obtido pela chamada do método "GetAlpha()", utilizado para influenciar a nova posição.
- beta e gamma — valores aleatórios (1 ou 2).
- formula — uma das quatro equações possíveis é selecionada aleatoriamente para calcular a nova posição.
- newPos — variável para armazenar a nova posição com base na fórmula escolhida.
- Em dependendo do valor de "formula":
- Caso 0: a nova posição é calculada como a posição atual do agente somada a uma combinação das coordenadas de "cB" (melhor solução da população) e "meanGroup".
- Caso 1: a nova posição é calculada utilizando a coordenada de "cB" e o valor médio de "meanGroup".
- Caso 2: a nova posição é definida a partir do valor médio e da coordenada atual do agente.
- Caso 3: a nova posição é definida aleatoriamente dentro do intervalo especificado (rangeMin[c] e rangeMax[c]).
- a[seedIndex].c[c] — a coordenada correspondente do agente é atualizada utilizando o método "u.SeInDiSp()", que considera valores mínimos, máximos e passos, garantindo que o novo valor permaneça dentro dos limites permitidos.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Após os testes realizados, busquei melhorar a convergência do algoritmo e decidi introduzir uma modificação em relação à versão básica do CGO. A principal diferença está no início do processamento de cada coordenada, antes da aplicação das fórmulas principais de movimento:
double rnd = u.RNDprobab(); // Get a random number from 0.0 to 1.0 rnd *= rnd; // Squate it int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1); // Scale to index a[seedIndex].c [c] = a[ind].c [c]; // Copy the coordinate from another agent with the received index
Ocorre a cópia de uma coordenada de um agente escolhido aleatoriamente, porém a seleção do agente não é uniforme, mas sim feita com uma distribuição quadrática de probabilidade (rnd *= rnd). Isso cria um "bias" em direção à escolha de agentes com índices menores (as melhores soluções têm maior probabilidade de serem selecionadas). O número aleatório é elevado ao quadrado, criando assim uma distribuição não uniforme, escalado para o intervalo de índices da população, e em seguida é feita a cópia antes da aplicação das fórmulas principais de movimento. Minha intenção era acelerar a convergência em regiões promissoras, mas, infelizmente, isso não trouxe o efeito esperado.
Provavelmente, devido à convergência prematura, o aumento do efeito reduz rapidamente a diversidade da população, o que neste algoritmo resulta em maior risco de estagnação. É possível que a própria lógica do algoritmo dificulte essa adaptação. Abaixo está o trecho de código onde foram feitas as alterações, além disso, realizei outras tentativas de aprimoramento, mas nenhum progresso significativo foi alcançado, e decidi manter a versão original do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double rnd = u.RNDprobab (); rnd *= rnd; int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); a [seedIndex].c [c] = a [ind].c [c]; double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Como pode ser observado nos resultados dos testes, a porcentagem geral obtida pelo algoritmo é relativamente modesta, porém, analisando com mais atenção, é possível perceber uma característica interessante desse algoritmo, que descrevo a seguir.
CGO|Chaos Game Optimization|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.5725597668122144
25 Hilly's; Func runs: 10000; result: 0.3715760642098293
500 Hilly's; Func runs: 10000; result: 0.32017971142744234
=============================
5 Forest's; Func runs: 10000; result: 0.6117551660766816
25 Forest's; Func runs: 10000; result: 0.619308424855028
500 Forest's; Func runs: 10000; result: 0.6216109945434442
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2192307692307692
500 Megacity's; Func runs: 10000; result: 0.19028461538461647
=============================
All score: 3.90189 (43.35%)
Na visualização do funcionamento do algoritmo em funções de teste, nota-se claramente a formação de estruturas no agrupamento dos agentes, sendo que essas estruturas variam conforme o problema. Mas o ponto em comum no comportamento do algoritmo está na enorme dispersão dos resultados de otimização.

CGO na função de teste Hilly
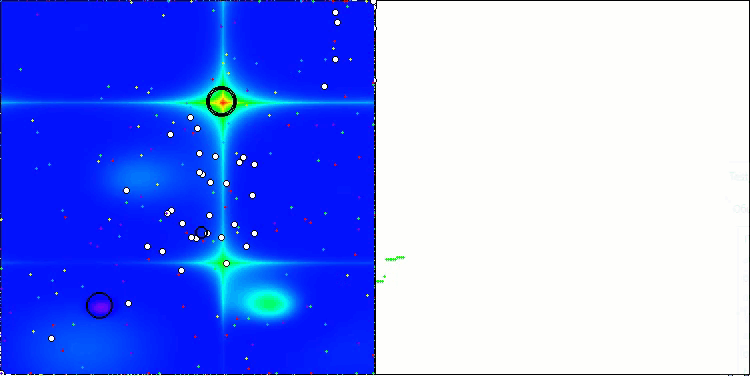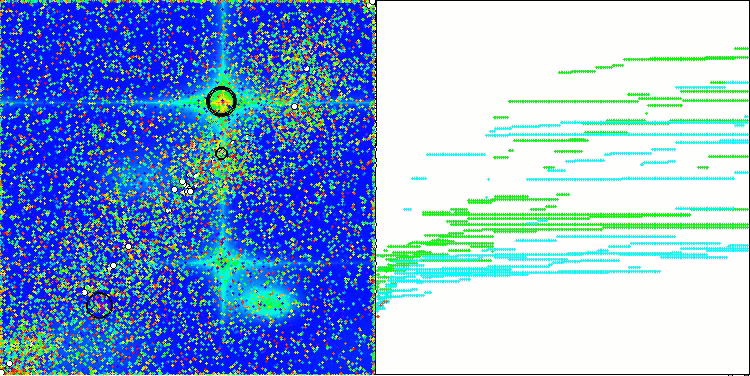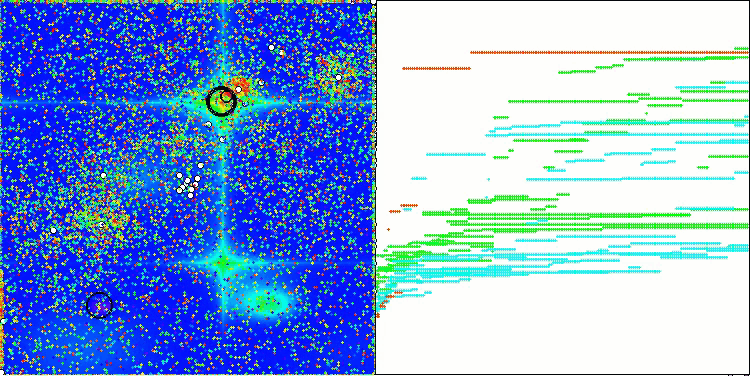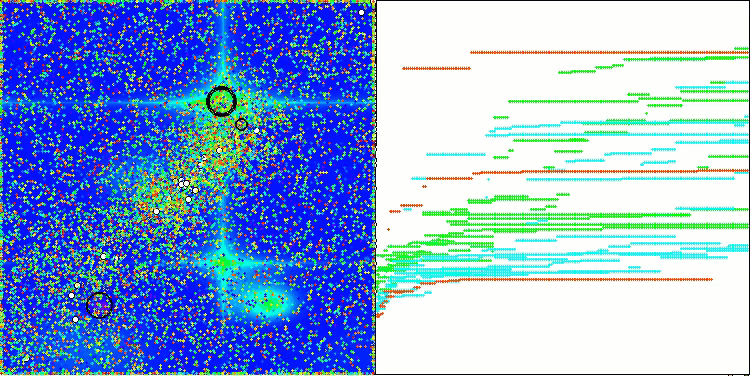
CGO na função de teste Forest
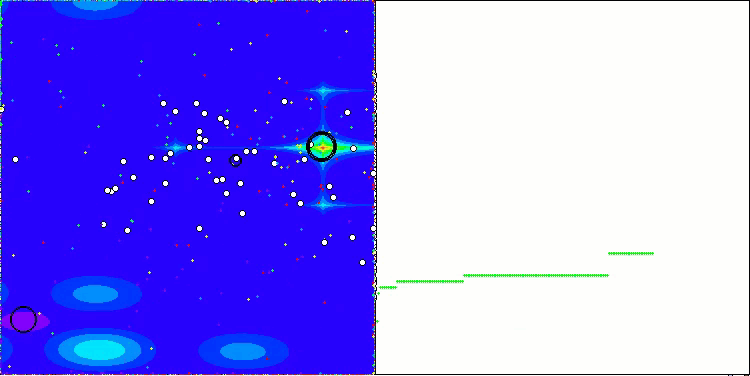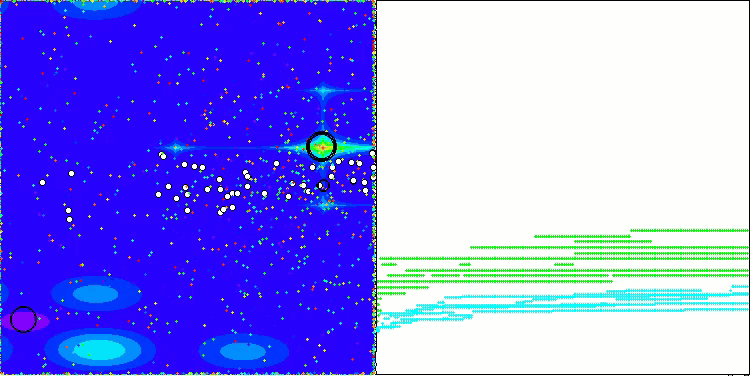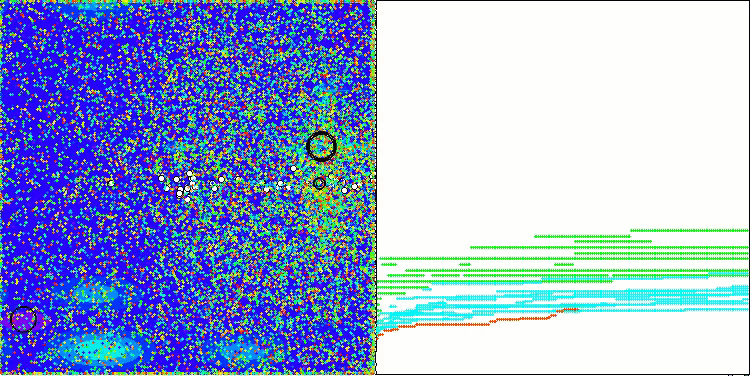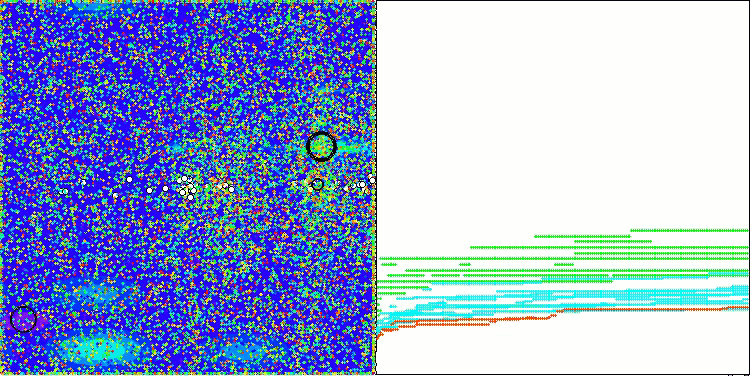
CGO na função de teste Forest
Com base nos testes, o algoritmo CGO ocupa a 38ª posição no ranking dos algoritmos populacionais de otimização.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 15 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BIO | blood inheritance optimization (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 21 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 22 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 23 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 24 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 25 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 26 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 27 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 28 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 29 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 30 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 31 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 32 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 33 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 34 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 35 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 36 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 37 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 38 | CGO | chaos game optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 39 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 40 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 41 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 42 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 43 | CSA | circle search algorithm | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 44 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 45 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| RW | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Considerações finais
Após analisar os resultados do algoritmo CGO, cheguei a conclusões importantes. O Chaos Game Optimization demonstra um comportamento extremamente interessante. De forma geral, sua eficiência pode ser avaliada como abaixo da média, o que é confirmado pelo resultado global de 43,35%. Porém, o mais notável é seu desempenho em problemas de alta dimensionalidade, pois o CGO mostra grande eficiência justamente em tarefas com 1000 variáveis. Essa é uma característica atípica para a maioria dos algoritmos meta-heurísticos, que geralmente sofrem com a "maldição da dimensionalidade" e perdem eficiência conforme o número de variáveis aumenta. O CGO, ao contrário, às vezes até supera seus próprios resultados em tarefas de 10 e 50 dimensões quando aplicado a problemas de 1000 dimensões. Isso se evidencia de maneira especial na função de teste Forest, que possui um extremo global concentrado em um único ponto "agudo".
Acredito que esse fenômeno seja explicado pela própria natureza do algoritmo. A base caótica do CGO e a variedade de fórmulas de movimento criam um mecanismo eficiente para a exploração de espaços de alta dimensionalidade. As quatro diferentes estratégias de atualização de posições, a escolha aleatória entre elas e o coeficiente α imprevisível permitem que o algoritmo enfrente tarefas em paisagens multidimensionais complexas. Ele se destacou especialmente em funções do tipo Forest, com resultados entre 0.61–0.62, bem acima de sua média geral.
Analisando a estrutura do algoritmo, vejo que sua força em altas dimensões está relacionada ao processamento por coordenadas. Em vez de trabalhar com o vetor de solução completo, o CGO atualiza cada coordenada de forma independente, o que lhe dá vantagem à medida que a dimensionalidade cresce. Além disso, o uso de grupos aleatórios e de suas posições médias garante um intercâmbio eficiente de informações entre os agentes, mesmo em espaços de grande dimensionalidade.
Experimentei girar a superfície da função Forest em diferentes ângulos para verificar se os resultados interessantes obtidos não eram apenas coincidência entre a lógica do algoritmo e as características da função de teste. Isso foi necessário para eliminar a possibilidade de acerto ocasional no extremo global. Os experimentos com rotação apenas confirmaram que os resultados não foram fruto do acaso. Considerando essa particularidade do CGO em funções com extremos agudos, recomendo realizar múltiplas execuções de otimização ao utilizar esse algoritmo. Essa recomendação é especialmente válida para o CGO.
De forma geral, apesar de seus resultados médios, a capacidade única do CGO de manter e até melhorar sua eficiência em tarefas de maior dimensionalidade faz dele um algoritmo extremamente interessante para estudos futuros e aplicação em problemas complexos de otimização.
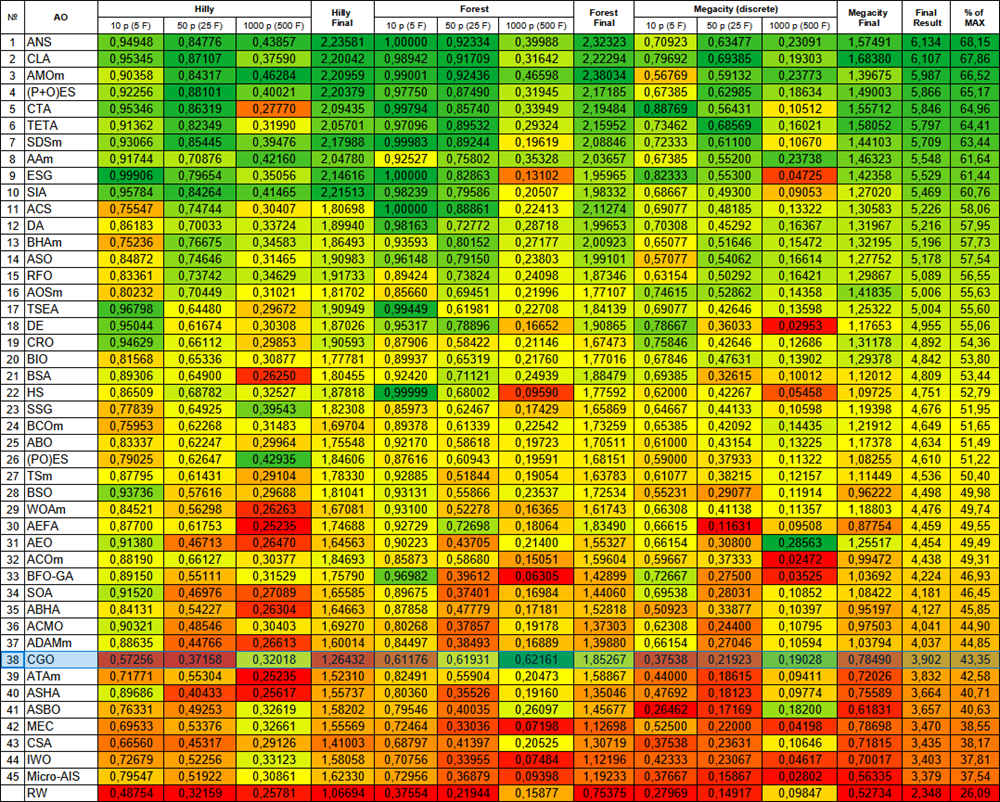
Figura 2. Gradação de cores dos algoritmos nos testes correspondentes
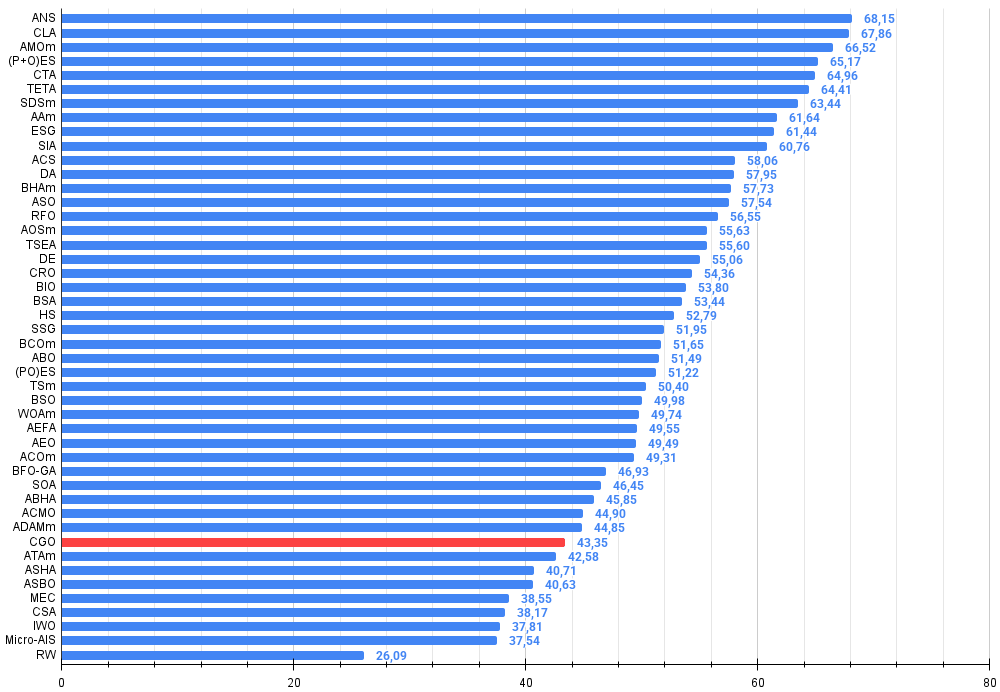
Figura 3. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo está o script para cálculo da tabela de classificação)
Prós e contras do algoritmo CGO:
Prós:
- Não possui parâmetros externos
- Boa convergência em funções de média e alta dimensionalidade
Contras:
- Tende a ficar preso em extremos locais em tarefas de baixa dimensionalidade.
Um arquivo compactado com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, já que muitos deles foram modificados para ampliar suas capacidades de busca. As conclusões e observações apresentadas nos artigos baseiam-se nos resultados obtidos nos experimentos.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do banco de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de testes unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_CGO.mq5 | Script | Banco de testes para o CGO |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17047
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Desenvolvendo um EA multimoeda (Parte 24): Conectando uma nova estratégia (I)
Desenvolvendo um EA multimoeda (Parte 24): Conectando uma nova estratégia (I)
 Desenvolvimento do Kit de Ferramentas de Análise de Price Action (Parte 1): Projetor de Gráficos
Desenvolvimento do Kit de Ferramentas de Análise de Price Action (Parte 1): Projetor de Gráficos
 Solicitação no Connexus (Parte 6): Criando uma Requisição e Resposta HTTP
Solicitação no Connexus (Parte 6): Criando uma Requisição e Resposta HTTP
 Simulação de mercado: Position View (VIII)
Simulação de mercado: Position View (VIII)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso