
Оптимизация хаотичной игрой — Chaos Game Optimization (CGO)
Содержание
Введение
Алгоритмы оптимизации играют стратегическую роль в решении сложных задач не только в различных областях современной науки, но и в трейдинге. С быстрым развитием технологий эти задачи становятся еще более сложными, а поиск лучшего решения — все более энергозатратным, поэтому возрастают и требования к алгоритмам оптимизации, их результативности при высокой экономичности работы. Одним из новейших и перспективных методов стал алгоритм Chaos Game Optimization (CGO), разработанный Сиамаком Талатахари и Мехди Азизи в 2020 году. Этот алгоритм основан на принципах теории хаоса и использует хаотические последовательности для генерации и улучшения решений.
Основная идея алгоритма заключается в использовании хаотических последовательностей для поиска глобальных оптимумов в сложных многомерных пространствах. Хаотические последовательности обладают определенными свойствами, которые, теоретически, позволяют им избегать локальных ловушек и находить качественные решения. В данной статье разберем основные принципы и этапы алгоритма Chaos Game Optimization, реализуем его в коде и проведем уже стандартные испытания на тестовых функциях, сделаем выводы о его работе.
Реализация алгоритма
Представьте себе группу из исследователей, каждый из которых пытается найти экстремум в многомерном лабиринте. В начале пути наши искатели разбрасываются по лабиринту случайным образом и находят свое первое пристанище в строго определенных границах пространства. Это их точка отсчета. Каждый искатель не действует в одиночку — он наблюдает за своими товарищами, и в каждый момент времени выбирает случайную группу соратников, вычисляет центр их расположения, словно находя точку равновесия между их позициями.
Это коллективная мудрость, усредненная опытом группы. А дальше начинается настоящая магия хаоса. Искатель может выбрать один из четырех путей для своего следующего шага. Каждый путь — это особая формула движения, где переплетаются три ключевые точки: его текущая позиция, лучшее найденное место всей группой и центр выбранной подгруппы. Эти точки смешиваются, и силу их влияния на дальнейшее перемещение определяет коэффициент α – проводник хаоса.
Коэффициент α сам по себе принимает разные воплощения, и каждый искатель, следуя правилам, может либо оттолкнуться от своей позиции, устремляясь к золотой середине между лучшим результатом и центром группы, либо начать от лучшей точки, исследуя пространство вокруг нее, а также может оттолкнуться от центра группы, или совершить совершенно случайный прыжок в неизведанное.
В конце каждого такого действа происходит сравнение результатов. Если кто-то из искателей находит место лучше прежнего рекорда, оно становится новым маяком для всей группы в их дальнейшем поиске.
В этом и заключается истинная красота алгоритма — в его способности превращать хаос в порядок, случайность в целенаправленное движение, неопределенность в прогресс и каждый шаг, каждое движение подчинено поиску решений между известным и неизведанным, между стабильностью и риском, между порядком и хаосом.
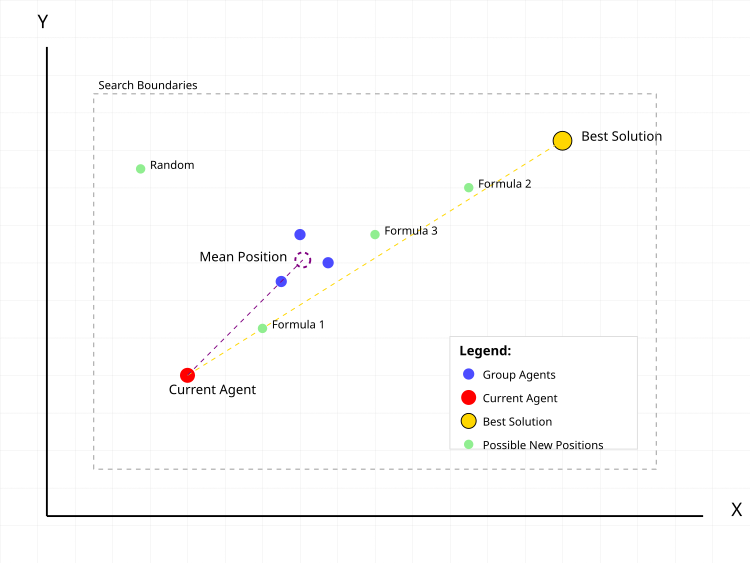
Рисунок 1. Типичные действия поискового агента в алгоритме CGO
На рисунке 1 красная точка — текущий агент, для которого вычисляется новая позиция. Синие точки — группа случайно выбранных агентов в популяции в случайно выбранном количестве. Фиолетовая пунктирная окружность — средняя позиция группы. Золотая точка — лучшее найденное решение. Зеленые точки — возможные новые позиции агента по разным формулам:- Formula 1: текущая + α(β×лучшая - γ×средняя)
- Formula 2: лучшая + α(β×средняя - γ×текущая)
- Formula 3: средняя + α(β×лучшая - γ×текущая)
- Random: случайная позиция
Пунктирные линии показывают векторы влияния лучшего решения и средней позиции группы на движение текущего агента. Серый пунктирный прямоугольник обозначает границы области поиска.
Приступим к написанию псевдокода алгоритма.
- Задать размер популяции (по умолчанию 50 агентов)
- Определить границы поиска для каждой координаты:
- минимальные значения (rangeMin)
- максимальные значения (rangeMax)
- шаг изменения (rangeStep)
- Для каждого агента в популяции:
- сгенерировать случайные начальные координаты в заданных границах
- округлить координаты с учетом шага
- вычислить значение целевой функции
- Определить лучшее начальное решение среди всех агентов
- Для каждого агента в популяции:
- размер подгруппы = случайное число от 1 до размера популяции
- случайно выбрать агентов в подгруппу
- для каждой координаты: средняя_координата = сумма_координат_группы / размер_группы
- α (альфа) = выбрать случайно один из способов:
- способ 1: случайное число от 0 до 1
- способ 2: 2 × случайное(0,1) - 1 [получаем число от -1 до 1]
- способ 3: Ir × случайное(0,1) + 1
- способ 4: Ir × случайное(0,1) + (1-Ir) где Ir = случайно 0 или 1
- β (бета) = случайно 1 или 2
- γ (гамма) = случайно 1 или 2
- Формула 1: новая_позиция = текущая + α(β×лучшая - γ×средняя)
- Формула 2: новая_позиция = лучшая + α(β×средняя - γ×текущая)
- Формула 3: новая_позиция = средняя + α(β×лучшая - γ×текущая)
- Формула 4: новая_позиция = случайная позиция в границах поиска
- для каждой координаты:
- вычислить новое значение по формуле
- проверить выход за границы поиска
- если вышли за границы, скорректировать до ближайшей границы
- округлить значение с учетом шага изменения
- Для каждого агента:
- если значение целевой функции агента лучше текущего лучшего:
- обновить лучшее значение
- сохранить координаты нового лучшего решения
- если значение целевой функции агента лучше текущего лучшего:
- Повторять шаги 2-3 пока не выполнится условие остановки:
- достигнуто максимальное число итераций
- или найдено решение требуемого качества
- или другой критерий остановки
Переходим к самой реализации алгоритма. Класс "C_AO_CGO" реализует алгоритм CGO и является производным от класса "C_AO", в нем наследуются свойства и методы базового класса.
Методы:
- SetParams () — устанавливает значение "popSize" на основе данных в массиве параметров "params". Это важно для настройки алгоритма перед его использованием.
- Init () — метод инициализации, принимает минимальные и максимальные значения диапазона, шаг изменения и количество эпох. Его цель — подготовить алгоритм к запуску, задавая границы поиска и другие параметры.
- Moving () — описывает шаги, связанные с движением особей в процессе оптимизации. Его реализация обеспечивает логику альтернативных решений и их улучшение.
- Revision () — отвечает за пересмотр текущих по популяции и глобально лучшего решения.
Приватные методы:
- GetAlpha () — для получения параметра alpha, который используется для контроля стратегии, "интенсивности" и "разнообразия" поиска.
- GenerateNewSolution () — для генерации нового решения на основе индекса (seedIndex) и среднего значения группы (meanGroup).
class C_AO_CGO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CGO () { } C_AO_CGO () { ao_name = "CGO"; ao_desc = "Chaos Game Optimization"; ao_link = "https://www.mql5.com/ru/articles/17047"; popSize = 25; ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); private: //------------------------------------------------------------------- double GetAlpha (); void GenerateNewSolution (int seedIndex, double &meanGroup []); }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_CGO" отвечает за инициализацию параметров алгоритма оптимизации перед его запуском. Он принимает следующие аргументы: массивы, содержащий минимальные и максимальные значения для каждой переменной поиска, шаг изменения для каждой переменной, количество эпох (итераций) алгоритма.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CGO::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" выполняет основную логику перемещения особей популяции решений в алгоритме CGO. Основная цель этого метода — обновить решения в популяции на основе правил, включая генерацию новых решений и усреднение результатов. Давайте подробно рассмотрим его основные части.
Первая часть, инициализация при первом вызове (если переменная "revision" равна "false"):
- Запускается внешний цикл по всем элементам популяции (popSize) и для каждого элемента (индивидуума i):
- Запускается внутренний цикл по координатам (coords):
- Генерируется случайное значение для каждой координаты с помощью метода u.RNDfromCI (), который возвращает случайное значение в заданном диапазоне.
- Это значение затем корректируется с помощью u.SeInDiSp (), что гарантирует, что значение остаётся в пределах диапазона, и округляет его к ближайшему шагу.
- Устанавливается флаг "revision" в "true" для следующего вызова метода и выходим из метода.
- Для каждого индивидуума популяции:
- Генерируется случайный размер группы "randGroupSize" от "1" до "popSize".
- Создается массив "meanGroup" для хранения среднего значения координат, размер которого соответствует количеству координат, устанавливается в "coords".
- Заполняется массив "randIndices", содержащий случайные индексы (индивидов), которые будут использованы для формирования группы.
- На каждой итерации добавляются случайные индексы в "randIndices", при этом индексы выбираются случайным образом.
- Затем для каждой группы суммируются значения координат для каждого индивидуума из случайно выбранных индексов, и результат сохраняется в "meanGroup".
- После суммирования, значение в "meanGroup" делится на количество индивидов в группе для получения среднего значения.
- Генерируется новое решение для индивидуума "i" на основе среднего значения группы с помощью метода "GenerateNewSolution ()".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { int randGroupSize = u.RNDminusOne (popSize) + 1; double meanGroup []; ArrayResize (meanGroup, coords); ArrayInitialize (meanGroup, 0); int randIndices []; ArrayResize (randIndices, randGroupSize); for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize); for (int j = 0; j < randGroupSize; j++) { for (int c = 0; c < coords; c++) { meanGroup [c] += a [randIndices [j]].c [c]; } } for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize; GenerateNewSolution (i, meanGroup); } } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" выполняет обновление лучших решений в популяции. Проходит по всем индивидам в популяции циклом и для каждого индивидуума проверяет, если его значение функции приспособленности "f" больше текущего лучшего значения "fB", и если это так, обновляет "fB" новым значением "f" и копирует координаты c текущего индивидуума в массив "cB". Таким образом, метод "Revision" находит и обновляет лучшее известное решение в популяции на основе значений функции приспособленности.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "GetAlpha" генерирует и возвращает случайное значение "alpha" в зависимости от случайных условий выбора.
- Ir — случайное значение, равное "0" или "1".
- Существует четыре возможных случая (имеющихся в "case"), в каждом из которых генерируется значение "alpha" по соответствующей формуле:
- Случай 0: Генерирует значение от 0 до 1.
- Случай 1: Генерирует значение от -1 до 1.
- Случай 2: Генерирует значение от 1 до 2, умножая его на "Ir" (0 или 1).
- Случай 3: Генерирует значение, которое зависит от "Ir" и имеет диапазон от 0 до 1, либо 1, в зависимости от значения "Ir".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CGO::GetAlpha () { int Ir = u.RNDminusOne (2); switch (u.RNDminusOne (4)) { case 0: return u.RNDfromCI (0, 1); case 1: return 2 * u.RNDfromCI (0, 1) - 1; case 2: return Ir * u.RNDfromCI (0, 1) + 1; case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir); } return 0; } //——————————————————————————————————————————————————————————————————————————————
Метод "GenerateNewSolution" отвечает за генерацию нового решения для заданного агента в популяции, основываясь на различных случайных параметрах.
Инициализация параметров:- alpha — значение, полученное вызовом метода "GetAlpha ()", используемое для влияния на новое положение.
- beta и gamma — случайные значения (1 или 2).
- formula — случайно выбирается одно из четырех возможных уравнений, по которым будет рассчитано новое положение.
- newPos — переменная для хранения нового положения с использованием выбранной формулы.
- В зависимости от значения "formula":
- Случай 0: новое положение рассчитывается как текущее положение агента с добавлением комбинации координат из "cB" (лучшее решение по популяции) и "meanGroup".
- Случай 1: новое положение рассчитывается с использованием координаты из "cB" и среднего значения "meanGroup".
- Случай 2: новое положение определяется по среднему значению и координате текущего агента.
- Случай 3: новое положение задается случайным образом в пределах заданного диапазона (rangeMin [c] и rangeMax [c]).
- a [seedIndex].c [c] — соответсвующая координата агента обновляется с использованием метода "u.SeInDiSp ()", который учитывает минимальные значения, максимальные значения и шаги, чтобы гарантировать, что новое значение находится в допустимых пределах.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
После проведенных испытаний я предпринял попытку улучшения сходимости алгоритма и решил сделать дополнение по сравнению с базовой версией алгоритма CGO. Основное отличие находится в начале обработки каждой координаты, перед применением основных формул движения:
double rnd = u.RNDprobab(); // Получаем случайное число от 0.0 до 1.0 rnd *= rnd; // Возводим его в квадрат int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1); // Масштабируем в индекс a[seedIndex].c [c] = a[ind].c [c]; // Копируем координату из другого агента с полученным индексом
Происходит копирование координаты из случайно выбранного агента, и выбор агента происходит не равномерно, а с квадратичным распределением вероятности (rnd *= rnd). Это создает "bias" в сторону выбора агентов с меньшими индексами (лучшие решения имеют большую вероятность быть выбранными). Случайное число возводим в квадрат, тем самым создаем неравномерное распределение, масштабируем в диапазон индексов популяции и затем копируем, до применения основных формул движения. Моя нацеленность на попытку ускорить конвергенцию в перспективных областях, к сожалению не принесла ожидаемого эффекта.
Вероятно, в следствие преждевременной конвергенции, за счет усиления эффекта быстро уменьшается разнообразие в популяции, что в данном алгоритме приводит еще к большему застреванию, возможно, что сама логика алгоритма препятствует этому. Ниже представлен участок кода, где были внесены изменения, кроме того, я предпринял еще несколько попыток улучшения, однако, заметного прогресса не было достигнуто, и я решил остаться при оригинальной версии алгоритма.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double rnd = u.RNDprobab (); rnd *= rnd; int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); a [seedIndex].c [c] = a [ind].c [c]; double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Как можно заметить ниже из результатов тестирования, что общее количество процентов, набранное алгоритмом, достаточно скромное, однако, если внимательно присмотреться, можно заметить интересную особенность этого алгоритма, которую я опишу ниже.
CGO|Chaos Game Optimization|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.5725597668122144
25 Hilly's; Func runs: 10000; result: 0.3715760642098293
500 Hilly's; Func runs: 10000; result: 0.32017971142744234
=============================
5 Forest's; Func runs: 10000; result: 0.6117551660766816
25 Forest's; Func runs: 10000; result: 0.619308424855028
500 Forest's; Func runs: 10000; result: 0.6216109945434442
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2192307692307692
500 Megacity's; Func runs: 10000; result: 0.19028461538461647
=============================
All score: 3.90189 (43.35%)
На визуализации работы алгоритма на тестовых функциях хорошо прослеживается формирование структур в группировании агентов, причем эти структуры разные на различных задачах. Но общее в характере работы алгоритма заключается в огромном разбросе результатов оптимизации.

CGO на тестовой функции Hilly
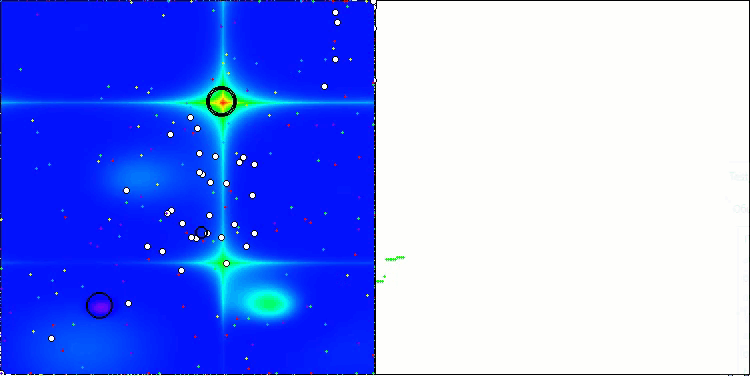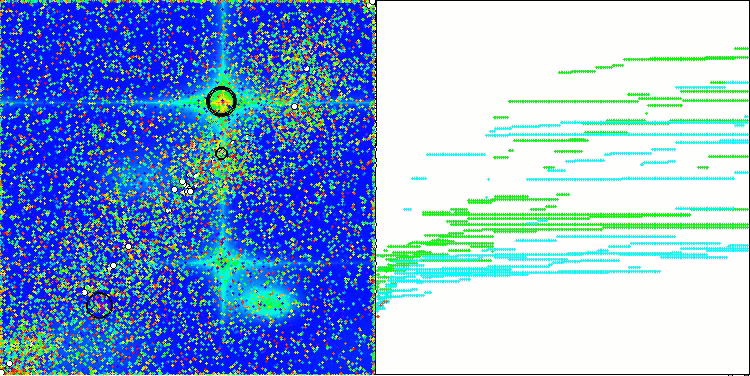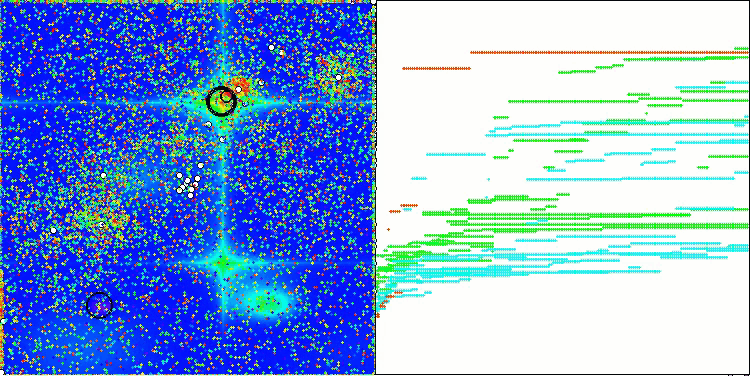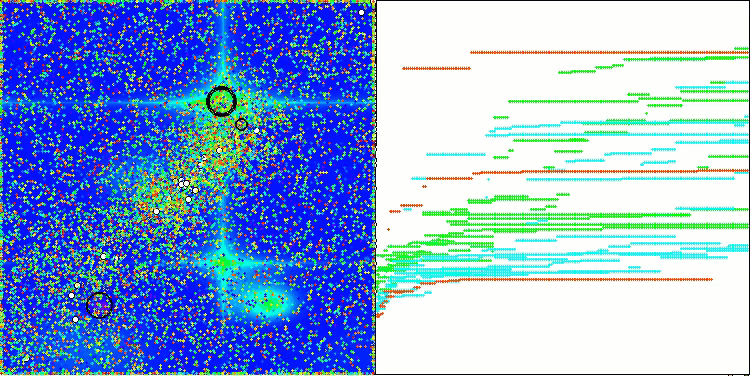
CGO на тестовой функции Forest
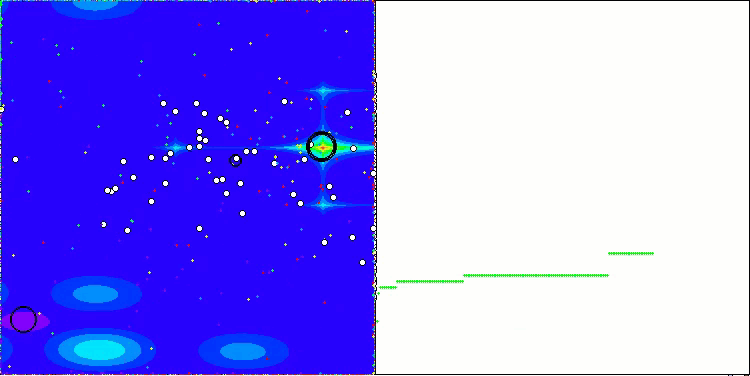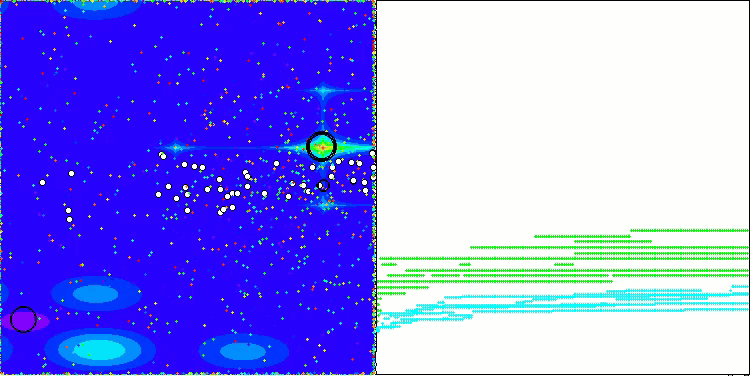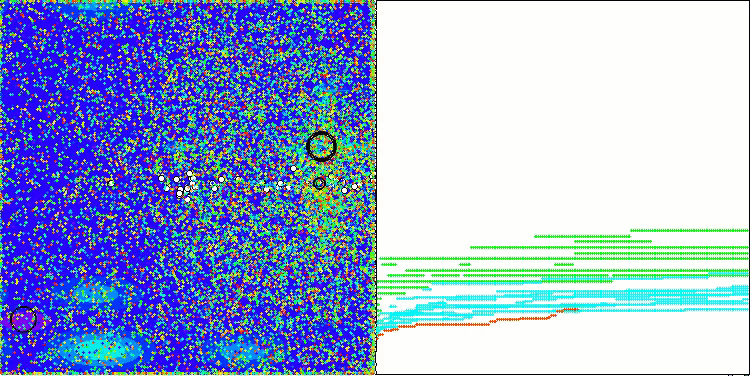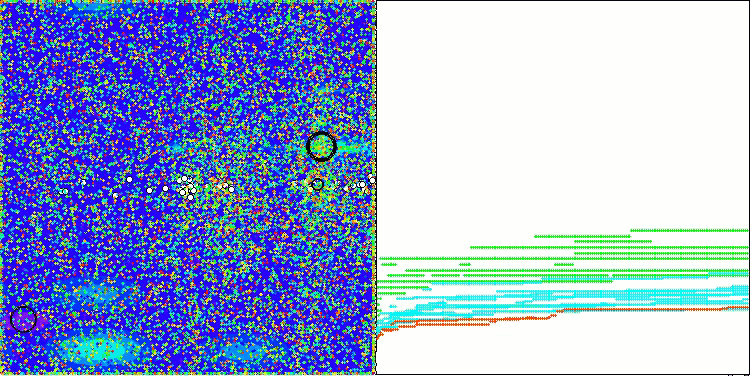
CGO на тестовой функции Megacity
По итогам тестирования алгоритм CGO занимает 38-ю позицию в рейтинговой таблице популяционных алгоритмов оптимизации.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 16 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 18 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 19 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 20 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 21 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 22 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 23 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 24 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 25 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 26 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 27 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 28 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 29 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 30 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 31 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 32 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 33 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 34 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 35 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 36 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 37 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 38 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 39 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 40 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 41 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 42 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 43 | CSA | circle search algorithm | 0,66560 | 0,45317 | 0,29126 | 1,41003 | 0,68797 | 0,41397 | 0,20525 | 1,30719 | 0,37538 | 0,23631 | 0,10646 | 0,71815 | 3,435 | 38,17 |
| 44 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 45 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Проанализировав результаты работы алгоритма CGO, я пришёл к важным выводам. Алгоритм Chaos Game Optimization демонстрирует крайне интересное поведение. В целом, его эффективность можно оценить как ниже среднего, что подтверждается общим результатом в 43.35%. Однако наиболее примечательным является его поведение при масштабировании задачи, CGO показывает высокую эффективность именно на многомерных задачах — тестах с размерностью в 1000 переменных. Это нетипичное свойство для большинства метаэвристических алгоритмов, которые обычно страдают от "проклятия размерности" и теряют эффективность при увеличении числа переменных. CGO же, напротив, иногда даже превосходит свои результаты на 10-и и 50-и мерных задачах при работе с 1000-мерными задачами. Особенно ярко это проявляется на тестовой функции Forest, имеющей глобальный экстремум в одной "острой" точке.
Я полагаю, что этот феномен обусловлен самой природой алгоритма. Хаотическая основа CGO и разнообразие формул движения создают эффективный механизм исследования высокоразмерных пространств. Четыре различные стратегии обновления позиций, случайный выбор между ними и непредсказуемый коэффициент α, позволяют алгоритму решать задачи на сложных многомерных ландшафтах. Особенно хорошо алгоритм проявил себя на функциях типа Forest с результатами 0.61-0.62, что значительно выше его средних показателей.
Анализируя устройство алгоритма, я вижу, что его сила в высокой размерности связана с покоординатной обработкой. Вместо того, чтобы работать с полным вектором решения, CGO обновляет каждую координату независимо, что даёт ему преимущество при увеличении размерности. Кроме того, использование случайных групп и их средних позиций обеспечивает эффективный обмен информацией между агентами даже в высокоразмерных пространствах.
Я попробовал поворачивать поверхность функции Forest под различными углами, чтобы убедиться, что полученные интересные результаты не являются случайным совпадением особенностей логики алгоритма и соответствующей ему тестовой функции. Это было необходимо для того, чтобы исключить возможность случайного попадания в глобальный экстремум. Эксперименты с поворотом функции лишь подтвердили, что такие результаты неслучайны. Учитывая эту особенность работы CGO с функциями с острыми экстремумами, я рекомендую проводить многократные запуски оптимизации, если используется этот алгоритм. Данная рекомендация является особенно актуальной именно для этого алгоритма.
В целом, несмотря на средние общие показатели, уникальная способность CGO сохранять и даже повышать эффективность при увеличении размерности задачи делает его исключительно интересным алгоритмом для дальнейшего изучения и применения в сложных оптимизационных задачах.
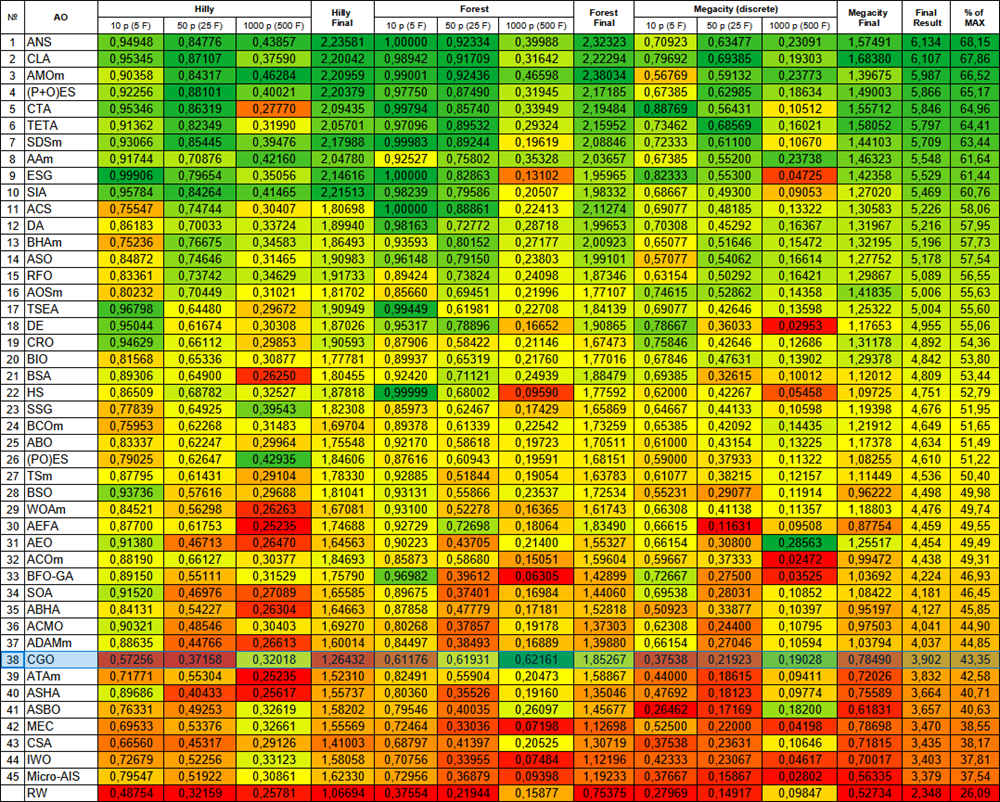
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
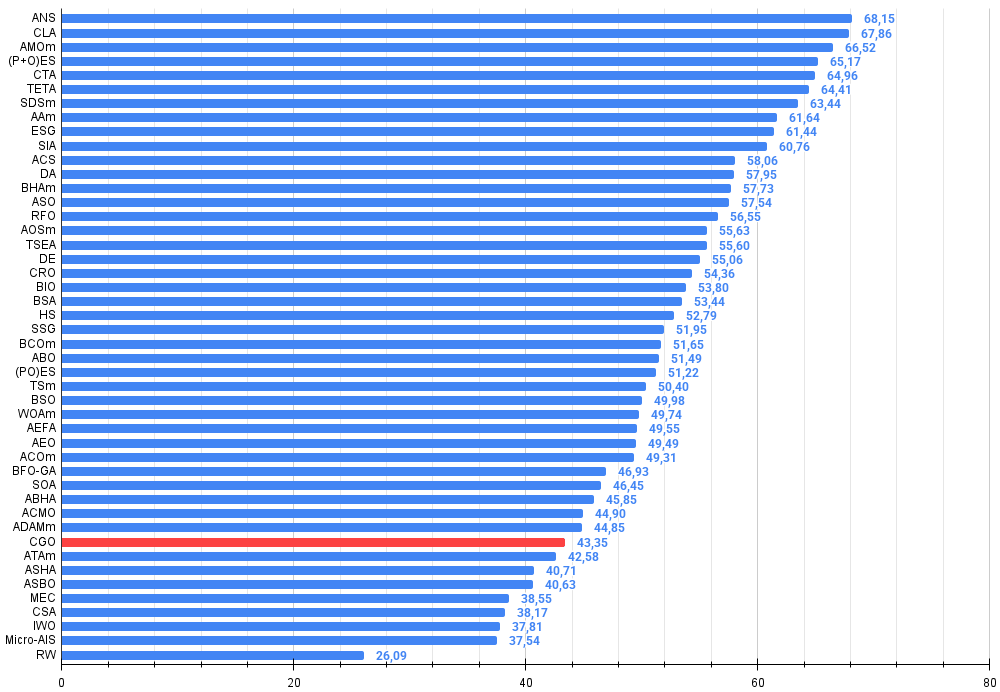
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма CGO:
Плюсы:
- Отсутствуют внешние параметры
- Хорошая сходимость на функциях высокой и средней размерности
Минусы:
- Застревает в локальных экстремумах на задачах малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_CGO.mq5 | Скрипт | Испытательный стенд для CGO |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Анализ всех вариантов движения цены на квантовом компьютере IBM
Анализ всех вариантов движения цены на квантовом компьютере IBM
 От начального до среднего уровня: Массивы и строки (III)
От начального до среднего уровня: Массивы и строки (III)
 Разрабатываем мультивалютный советник (Часть 24): Подключаем новую стратегию (I)
Разрабатываем мультивалютный советник (Часть 24): Подключаем новую стратегию (I)
 Объединение стратегий фундаментального и технического анализа на языке MQL5 для начинающих
Объединение стратегий фундаментального и технического анализа на языке MQL5 для начинающих
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования