
Algoritmo de Partenogênese Cíclica — Cyclic Parthenogenesis Algorithm (CPA)
Conteúdo
Introdução
Algoritmos de otimização inspirados em fenômenos naturais continuam a desempenhar um papel importante na solução de tarefas complexas de otimização. Algoritmos baseados no comportamento de insetos sociais, como formigas, abelhas e pulgões, despertam interesse especial. Em artigos anteriores já analisamos alguns deles: ACOm, ABHA. Neste artigo, apresentamos um novo algoritmo metaheurístico de otimização — o Algoritmo de Partenogênese Cíclica (Cyclic Parthenogenesis Algorithm, CPA), que imita a estratégia reprodutiva única dos pulgões (aphids).
Os pulgões demonstram uma notável adaptabilidade devido ao seu ciclo de vida incomum, que inclui reprodução assexuada (partenogênese) e sexual. Em condições favoráveis, os pulgões se reproduzem por partenogênese, o que permite o rápido crescimento populacional. Quando as condições se deterioram, eles passam à reprodução sexual, o que promove a diversidade genética e aumenta as chances de sobrevivência em ambientes mutáveis.
O CPA modela matematicamente esses mecanismos biológicos, criando um equilíbrio entre intensificação das soluções encontradas (via partenogênese) e diversificação em novas regiões do espaço de busca (via reprodução sexual). O algoritmo também imita o comportamento social dos pulgões, estruturando as soluções em colônias e implementando um mecanismo de migração entre elas, o que promove o intercâmbio de informações.
Essas características tornam o CPA especialmente eficaz na resolução de problemas de otimização multidimensionais, onde é necessário equilibrar a busca local e global. Neste artigo, vamos explorar detalhadamente os princípios de funcionamento do algoritmo, seu modelo matemático e sua implementação prática. O algoritmo de partenogênese cíclica foi proposto por Ali Kaveh e Zolghadr. E foi publicado pela primeira vez em 2019.Implementação do algoritmo
Imagine que você está observando uma colônia de pulgões no jardim. Essas pequenas criaturas utilizam duas formas de reprodução e se adaptam de forma extremamente eficiente ao ambiente. O algoritmo CPA (Cyclic Parthenogenesis Algorithm) imita exatamente esse comportamento para resolver tarefas complexas de otimização. Como isso funciona? Na organização inicial, são criados vários grupos (colônias) de soluções, em cada um dos quais há indivíduos "fêmeas" e "machos".
O algoritmo propõe duas formas de gerar novas soluções:- A primeira forma é a "Reprodução autônoma", onde as melhores soluções criam cópias de si mesmas com pequenas modificações.
- A segunda forma é a tradicional, chamada de "Reprodução em pares", na qual duas soluções diferentes se combinam, criando uma nova.
Às vezes, a melhor solução de uma colônia "voa" para outra. O algoritmo verifica constantemente quais soluções têm melhor desempenho, armazena os melhores achados e, no decorrer da busca, combina as variantes de sucesso. Tudo isso com o objetivo de encontrar a solução mais ideal. A principal característica do algoritmo é sua capacidade de equilibrar o uso de boas soluções já encontradas com a busca por variantes totalmente novas, assim como os pulgões se adaptam às mudanças no ambiente.
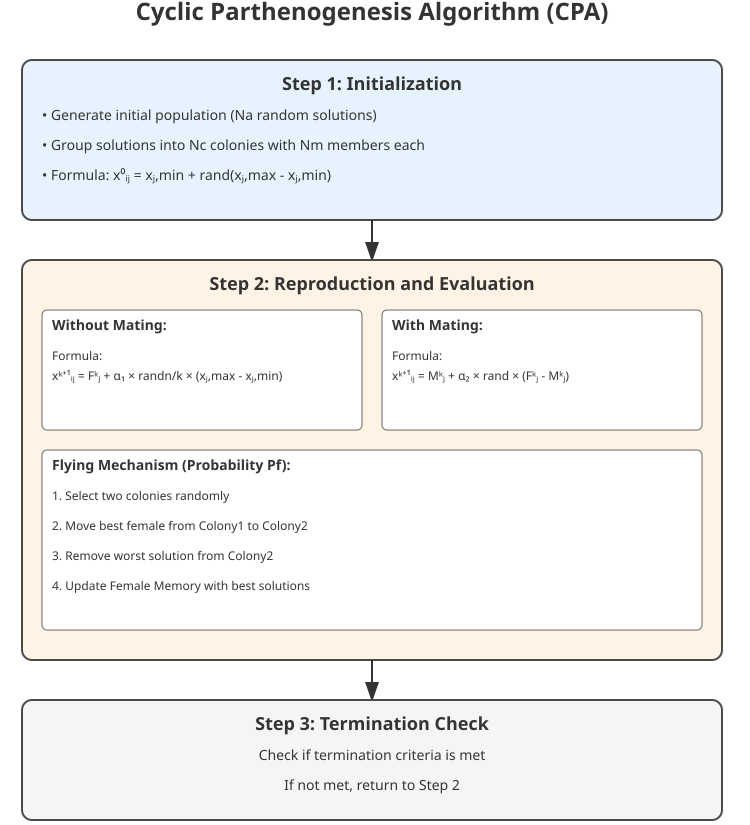
Figura 1. Esquema de funcionamento do algoritmo CPA, fórmulas principais
Vamos passar à representação visual do algoritmo CPA, onde os principais elementos na ilustração são as colônias; os quadrados rosa indicam indivíduos fêmeas (soluções), os azuis — indivíduos machos (soluções), e a linha pontilhada — o caminho de voo entre colônias. A ilustração demonstra a estrutura das colônias, os mecanismos de reprodução, o processo de voo entre colônias e a interação entre os indivíduos dentro das colônias. Isso ajuda a entender melhor os princípios de funcionamento do algoritmo por meio de uma metáfora visual com pulgões reais (aphids).
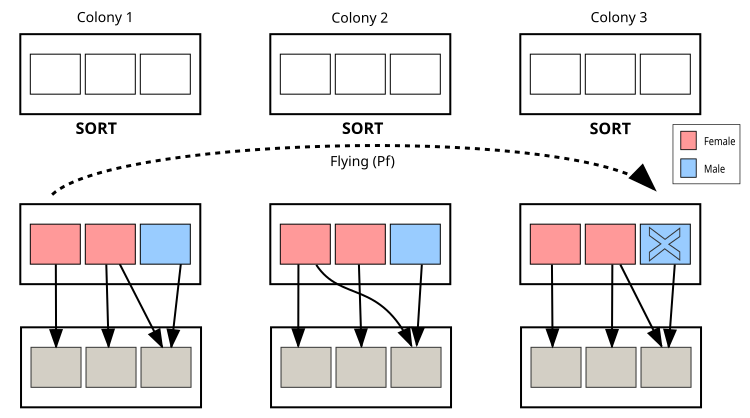
Figura 2. Colônias de pulgões e sua interação no algoritmo CPA
Agora que já entendemos um pouco mais sobre a descrição do algoritmo, vamos escrever o pseudocódigo:
Inicialização:
Criar uma população com Na indivíduos
Dividir a população em Nc colônias
Em cada colônia:
Definir a quantidade de indivíduos do sexo feminino (Fr * Nm)
Definir a quantidade de indivíduos do sexo masculino (os restantes)
Definir os parâmetros iniciais:
alpha1 (coeficiente de partenogênese)
alpha2 (coeficiente de acasalamento)
Pf (probabilidade de voo)
Ciclo principal (para cada época):
Para cada colônia:
Para indivíduos do sexo feminino:
Atualizar a posição usando partenogênese:
nova_posição = posição_atual + alpha1 * k * N(0,1) * (max_range - min_range)
onde k = (total_epochs - current_epoch) / total_epochs
N(0,1) — distribuição normal
Para indivíduos do sexo masculino:
Escolher um indivíduo fêmea aleatório da mesma colônia
Atualizar a posição por acasalamento:
nova_posição = posição_atual + alpha2 * random[0,1] * (posição_fêmea - posição_atual)
Revisão das posições:
Atualizar a melhor solução encontrada
Salvar as posições atuais
Ordenar os indivíduos em cada colônia conforme o valor da função objetivo
Migração (com probabilidade Pf):
Selecionar duas colônias aleatórias
Comparar suas melhores soluções
Mover a melhor solução para a colônia com pior desempenho
Reordenar os indivíduos na colônia
Tudo está pronto para escrever o código do algoritmo, vamos em frente. Vamos escrever a classe "C_AO_CPA", que herda da classe "C_AO". Esta classe implementa todo o algoritmo, com uma breve descrição de seus componentes:
Construtor C_AO_CPA:
- Define parâmetros como tamanho da população, número de colônias, proporção de fêmeas, probabilidade de voo e coeficientes de escala para partenogênese e acasalamento.
- Reserva o array de parâmetros e o preenche com valores.
Método SetParams define os valores dos parâmetros a partir do array "params", convertendo-os para os tipos apropriados.
Métodos Init, Moving e Revision:
- Init — usado para iniciar o algoritmo com os intervalos e número de épocas definidos.
- Moving e Revision — métodos que implementam a lógica de movimentação e revisão dentro do algoritmo.
Membros da classe são definidos com variáveis para armazenar os parâmetros do algoritmo, como número de colônias, proporção de fêmeas e machos, e também parâmetros de controle do processo.
Membros privados incluem variáveis para acompanhar a época atual, número de membros por colônia e um array temporário de agentes.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the Cyclic Parthenogenesis Algorithm (CPA) // Inherited from the optimization base class class C_AO_CPA : public C_AO { public: C_AO_CPA (void) { ao_name = "CPA"; ao_desc = "Cyclic Parthenogenesis Algorithm"; ao_link = "https://www.mql5.com/en/articles/16877"; popSize = 50; // total population size Na Nc = 10; // number of colonies Fr = 0.2; // ratio of female individuals Pf = 0.9; // probability of flight between colonies alpha1 = 0.3; // scaling factor for parthenogenesis alpha2 = 0.9; // scaling factor for pairing ArrayResize (params, 6); // Setting algorithm parameters params [0].name = "popSize"; params [0].val = popSize; params [1].name = "Nc"; params [1].val = Nc; params [2].name = "Fr"; params [2].val = Fr; params [3].name = "Pf"; params [3].val = Pf; params [4].name = "alpha1_init"; params [4].val = alpha1; params [5].name = "alpha2_init"; params [5].val = alpha2; } void SetParams () { popSize = (int)params [0].val; Nc = (int)params [1].val; Fr = params [2].val; Pf = params [3].val; alpha1 = params [4].val; alpha2 = params [5].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // function for moving individuals void Revision (); // function for reviewing and updating positions //---------------------------------------------------------------------------- int Nc; // number of colonies double Fr; // ratio of female individuals double Pf; // probability of flight between colonies private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch int Nm; // number of individuals in each colony double alpha1; // scaling factor for parthenogenesis double alpha2; // scaling factor for pairing int fNumber; // number of females in the colony int mNumber; // number of males in the colony S_AO_Agent aT []; // temporary colony for sorting void SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count); // agent sorting function }; //——————————————————————————————————————————————————————————————————————————————
Implementação do método "Init" da classe "C_AO_CPA", e sua funcionalidade:
Parâmetros do método:
- rangeMinP, rangeMaxP, rangeStepP — arrays que definem os valores mínimos e máximos do intervalo, além do passo da busca.
- epochsP — número de épocas (por padrão, 0).
- O método chama primeiro "StandardInit" para executar a inicialização padrão com os intervalos passados. Se a inicialização falhar, o método retorna "false".
- Define o número de épocas (epochs) e a época atual (epochNow).
- Calcula o número de membros por colônia (Nm) com base no tamanho da população e no número de colônias.
- Define o número de fêmeas (fNumber) na colônia, garantindo que seja no mínimo 1. O número de machos (mNumber) é calculado como a diferença entre o total de membros e o número de fêmeas.
- Reserva o array "aT" para armazenar os agentes temporários da colônia.
- O método retorna "true" se a inicialização for bem-sucedida.
Esse método configura os parâmetros e a estrutura para o funcionamento do algoritmo, garantindo uma inicialização adequada antes do início da execução.
//—————————————————————————————————————————————————————————————————————————————— // Initialization of the algorithm with the given search parameters bool C_AO_CPA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Calculating the colony size and the number of individuals of each gender Nm = popSize / Nc; fNumber = int(Nm * Fr); if (fNumber < 1) fNumber = 1; mNumber = Nm - fNumber; ArrayResize (aT, Nm); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" da classe "C_AO_CPA" realiza o deslocamento dos agentes no espaço de soluções, adaptando suas coordenadas com base em regras definidas e fatores aleatórios. Vamos analisar isso passo a passo:
Aumento da época. O método começa incrementando o valor atual da época (epochNow), o que indica que foi executado mais um passo no processo de otimização ou evolução.
Primeira etapa (caso a revisão não seja necessária) — se o campo "revision" estiver definido como "false", as coordenadas de cada agente na população (popSize) são inicializadas:
- Cada agente (a[i]) recebe novas coordenadas em cada dimensão (coords) usando a função "RNDfromCI", que gera valores aleatórios dentro do intervalo definido [rangeMin[c], rangeMax[c]].
- Em seguida, as coordenadas são modificadas com a função "SeInDiSp", que ajusta os valores de acordo com o passo de discretização (rangeStep[c]).
- O sinalizador "revision" é então definido como "true", e o método termina sua execução.
- A variável "k" é calculada como a razão entre o número de épocas restantes e o total de épocas. Isso permite reduzir gradualmente a amplitude dos deslocamentos dos agentes à medida que a otimização se aproxima do fim.
- As colônias (col) e funções (fNumber) são percorridas para atualizar as coordenadas de cada agente. Para os primeiros "fNumber" agentes em cada colônia, essa atualização se baseia nas suas coordenadas anteriores (cP), com adição de um valor aleatório gerado com distribuição normal (GaussDistribution). Esse valor é escalonado dentro do intervalo entre "rangeMin" e "rangeMax".
- Para os demais agentes (de m = fNumber até Nm), as coordenadas também são atualizadas, mas agora utilizando as coordenadas de um dos melhores agentes da mesma colônia, escolhido aleatoriamente. Valores aleatórios são somados às coordenadas de cada agente com base no parâmetro "alpha2".
- O objetivo geral desse método é deslocar os agentes no espaço de soluções com base em sua posição anterior, adicionando um elemento de aleatoriedade para explorar a região, aumentando as chances de encontrar o ótimo global.
- Parâmetros como "alpha1" e "alpha2" ajudam a controlar o grau de adaptação e a intensidade da aleatoriedade.
Assim, o método "Moving", no contexto do algoritmo de otimização, é essencial para o deslocamento dos agentes no espaço de soluções, levando em consideração tanto suas próprias posições anteriores quanto as posições de outros agentes.
//—————————————————————————————————————————————————————————————————————————————— // The main function for moving individuals in the search space void C_AO_CPA::Moving () { epochNow++; //---------------------------------------------------------------------------- // Initial random initialization of positions if this is the first iteration if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a random position in a given range a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Calculate the search power decay rate over time double k = (epochs - epochNow)/(double)epochs; int ind = 0; int indF = 0; // Handling each colony for (int col = 0; col < Nc; col++) { // Updating the positions of female individuals (parthenogenesis) for (int f = 0; f < fNumber; f++) { ind = col * Nm + f; for (int c = 0; c < coords; c++) { // Parthenogenetic position update using normal distribution a [ind].c [c] = a [ind].cP [c] + alpha1 * k * u.GaussDistribution (0.0, -1.0, 1.0, 8) * (rangeMax [c] - rangeMin [c]); } } // Update positions of males (mating) for (int m = fNumber; m < Nm; m++) { ind = col * Nm + m; // Select a random female for mating indF = u.RNDintInRange (ind, col * Nm + fNumber - 1); for (int c = 0; c < coords; c++) { // Update position based on the selected female a [ind].c [c] = a [ind].cP [c] + alpha2 * u.RNDprobab () * (a [indF].cP [c] - a [ind].cP [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" da classe "C_AO_CPA" é responsável por atualizar o estado dos agentes na população com base em seus valores da função "f". Vamos analisar isso em mais detalhes:
Inicialização — o método começa inicializando a variável "ind" com o valor "-1", que será usada para armazenar o índice do agente com o melhor valor da função "f".
Busca pelo melhor agente — no primeiro laço "for", todos os agentes da população (popSize) são percorridos, e se o valor da função "f" do agente atual (a[i].f) for maior que o valor atual "fB", então:
- "fB" é atualizado com o valor de "a[i].f".
- O índice do melhor agente é salvo na variável "ind".
- Após o fim do laço, se foi encontrado um agente com melhor valor (ind ≠ -1), suas coordenadas (c) são copiadas para o array "cB".
Cópia das coordenadas atuais. No segundo laço "for", as coordenadas atuais (c) de cada agente são copiadas para suas coordenadas anteriores (cP). Isso permite manter o estado anterior dos agentes para análise posterior.
Ordenação dos agentes. O terceiro laço "for" percorre todas as colônias (Nc) e, para cada colônia, é chamado o método "SortFromTo", que ordena os agentes dentro da colônia de acordo com seus valores da função "f". O índice de início da ordenação é calculado como (ind = col * Nm).
Atualização probabilística. O método verifica se um valor aleatório gerado pela função "u.RNDprobab()" é menor que o valor limite "Pf":
- Se a condição for satisfeita, dois índices de colônias aleatórios (indCol_1 e indCol_2) são escolhidos, garantindo que não sejam iguais.
- Comparam-se os valores da função "f" dos agentes líderes nessas colônias. Se o valor da primeira colônia for menor do que o da segunda, os índices são trocados.
- As coordenadas do primeiro agente da primeira colônia são então copiadas para o último agente da segunda colônia.
- Depois disso, "SortFromTo" é chamado novamente para atualizar a ordem dos agentes na segunda colônia.
Lógica geral:
O método "Revision" serve para atualizar o estado dos agentes, armazenar informações sobre o melhor agente e permitir o intercâmbio de informação entre colônias.
//—————————————————————————————————————————————————————————————————————————————— // Function for revising positions and exchanging information between colonies void C_AO_CPA::Revision () { // Find and update the best solution int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Save the current positions for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY); } // Sort individuals in each colony by the target function value for (int col = 0; col < Nc; col++) { ind = col * Nm; SortFromTo (a, aT, ind, Nm); } // Mechanism of flight (migration) between colonies if (u.RNDprobab () < Pf) { int indCol_1 = 0; int indCol_2 = 0; // Select two random different colonies indCol_1 = u.RNDminusOne (Nc); do indCol_2 = u.RNDminusOne (Nc); while (indCol_1 == indCol_2); // Ensure that the best solution is in the first colony if (a [indCol_1 * Nm].f < a [indCol_2 * Nm].f) { int temp = indCol_1; indCol_1 = indCol_2; indCol_2 = temp; } // Copy the best solution to the worst colony ArrayCopy (a [indCol_2 * Nm + Nm - 1].cP, a [indCol_1 * Nm].cP, 0, 0, WHOLE_ARRAY); // Re-sort the colony after migration SortFromTo (a, aT, indCol_2 * Nm, Nm); } } //——————————————————————————————————————————————————————————————————————————————
O método "SortFromTo" da classe "C_AO_CPA" é destinado à ordenação do array de agentes com base nos valores da função "f". Vamos ver em detalhes:
Inicialização das variáveis:
- O método recebe três parâmetros, que são: o array de agentes "p", um array temporário "pTemp", o índice de início da ordenação "from" e a quantidade de elementos a serem ordenados "count".
- As variáveis "cnt", "t0" e "t1" são usadas para contar as trocas e armazenar temporariamente os valores.
- Os arrays "ind" e "val" são criados para armazenar os índices e os valores da função de adaptabilidade "f", respectivamente.
Preenchimento dos arrays de índices e valores. No primeiro laço "for", os arrays "ind" e "val" são preenchidos:
- ind[i] recebe o índice do agente no array original, começando a partir de "from".
- val[i] recebe o valor da função "f" para o agente correspondente.
Ordenação. O laço principal "while" é executado enquanto houver trocas (ou seja, cnt > 0). O laço interno "for" percorre o array "val" comparando valores adjacentes:
- Se o valor atual for menor que o próximo (val[i] < val[i + 1]), os índices no array "ind" e os valores no array "val" são trocados.
- O contador "cnt" é incrementado para indicar que ocorreu uma troca.
- Esse processo continua até que uma iteração completa ocorra sem nenhuma troca.
Cópia dos valores ordenados:
- Após a conclusão da ordenação, no primeiro laço "for" os agentes ordenados são copiados do array temporário "pTemp" de volta para o array original "p", começando do índice "from".
- O segundo laço "for" atualiza o array original "p", substituindo-o pelos valores ordenados.
//—————————————————————————————————————————————————————————————————————————————— // Auxiliary function for sorting agents by the value of the objective function void C_AO_CPA::SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count) { int cnt = 1; int t0 = 0; double t1 = 0.0; int ind []; double val []; ArrayResize (ind, count); ArrayResize (val, count); // Copy values for sorting for (int i = 0; i < count; i++) { ind [i] = i + from; val [i] = p [i + from].f; } // Bubble sort in descending order while (cnt > 0) { cnt = 0; for (int i = 0; i < count - 1; i++) { if (val [i] < val [i + 1]) { // Exchange of indices t0 = ind [i + 1]; ind [i + 1] = ind [i]; ind [i] = t0; // Exchange values t1 = val [i + 1]; val [i + 1] = val [i]; val [i] = t1; cnt++; } } } // Apply the sorting results for (int i = 0; i < count; i++) pTemp [i] = p [ind [i]]; for (int i = from; i < from + count; i++) p [i] = pTemp [i - from]; } //——————————————————————————————————————————————————————————————————————————————
Depois de escrever e analisar detalhadamente o código do algoritmo, passamos aos resultados dos testes do algoritmo CPA.
Resultados dos testes
Ao implementar a lógica interessante e peculiar do algoritmo, nem me passou pela cabeça que ele não figuraria nas primeiras posições da tabela de classificação, por isso houve certa decepção ao examinar detalhadamente os resultados dos testes do algoritmo CPA. Com base nos testes, o algoritmo alcançou no máximo 34,76% do resultado possível.
CPA|Cyclic Parthenogenesis Algorithm|50.0|10.0|0.2|0.9|0.3|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7166412833856777
25 Hilly's; Func runs: 10000; result: 0.4001377868508138
500 Hilly's; Func runs: 10000; result: 0.25502012607456315
=============================
5 Forest's; Func runs: 10000; result: 0.6217765628284961
25 Forest's; Func runs: 10000; result: 0.3365148812759322
500 Forest's; Func runs: 10000; result: 0.192638189788532
=============================
5 Megacity's; Func runs: 10000; result: 0.34307692307692306
25 Megacity's; Func runs: 10000; result: 0.16769230769230772
500 Megacity's; Func runs: 10000; result: 0.09455384615384692
=============================
All score: 3.12805 (34.76%)
A visualização demonstra o comportamento característico do algoritmo, com o deslocamento dos pulgões virtuais no espaço de busca, o que se torna particularmente visível em problemas de alta dimensionalidade — é possível, até visualmente, distinguir as colônias e o movimento das criaturas virtuais dentro delas.
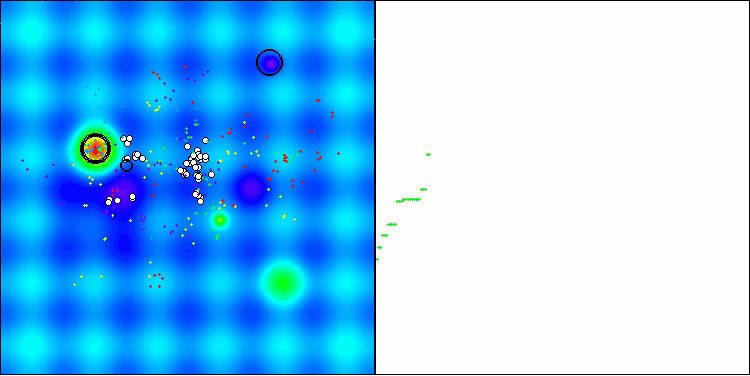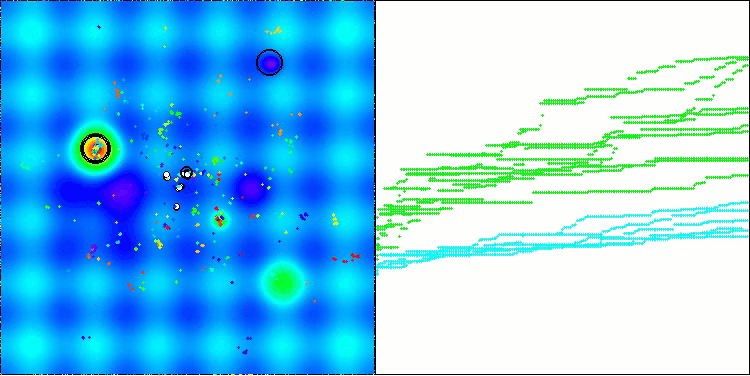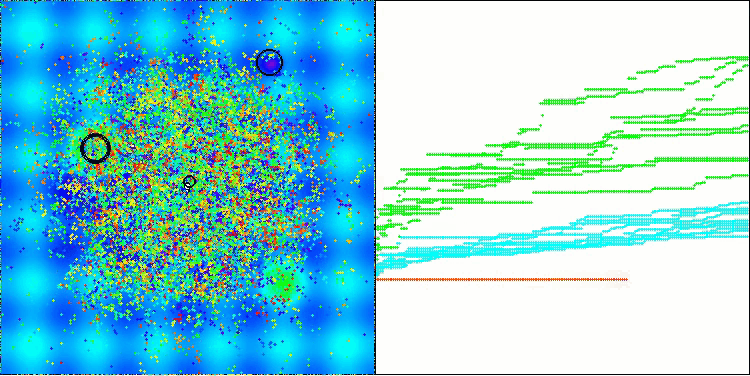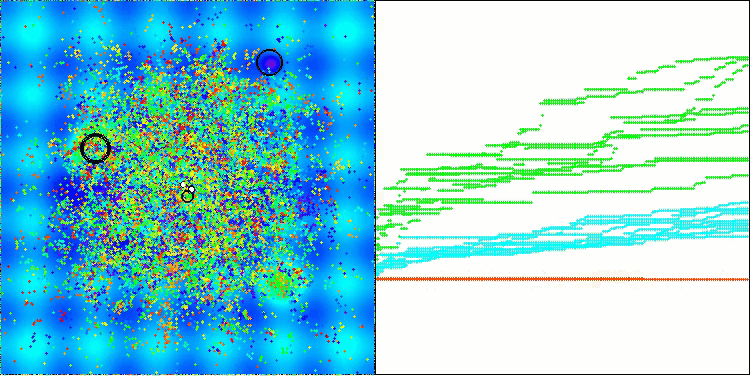
CPA na função de teste Hilly
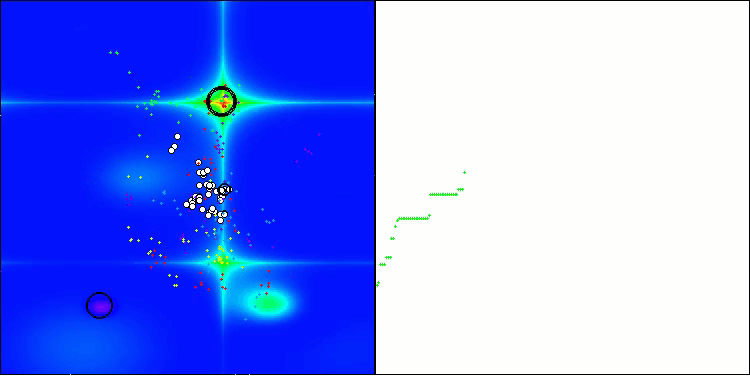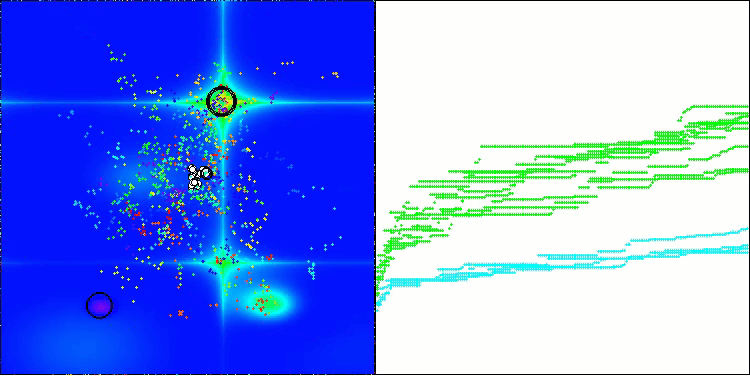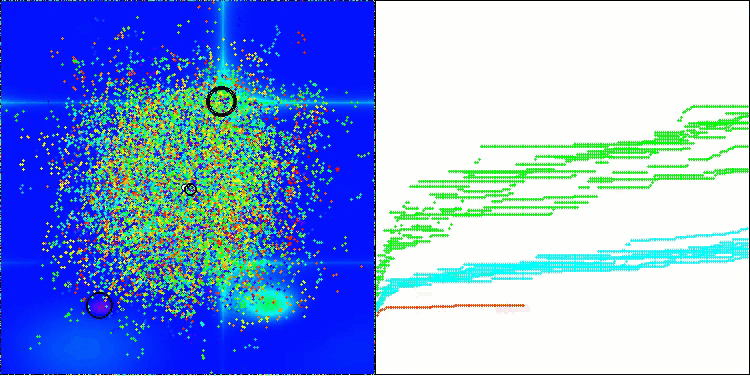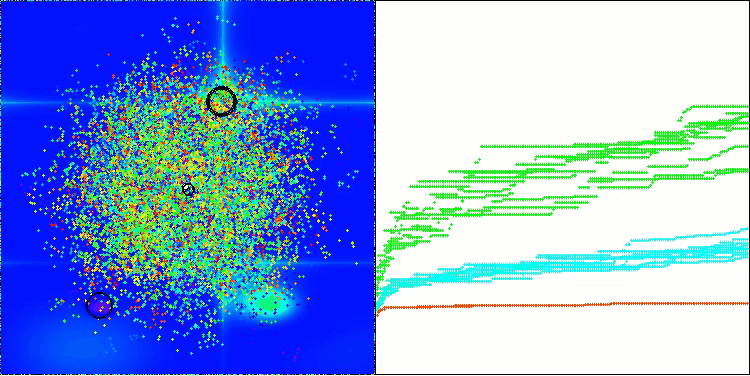
CPA na função de teste Forest

CPA na função de teste Megacity
Após os testes, o algoritmo CPA ficou em 44º lugar na tabela de classificação e entrou no grupo dos 45 melhores algoritmos populacionais de otimização.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 13 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | BBBC | big bang-big crunch algorithm | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1.08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 44 | CPA | cyclic parthenogenesis algorithm | 0.71664 | 0.40014 | 0.25502 | 1.37180 | 0.62178 | 0.33651 | 0.19264 | 1.15093 | 0.34308 | 0.16769 | 0.09455 | 0.60532 | 3.128 | 34.76 |
| 45 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| RW | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Considerações finais
O trabalho de implementação e testes do algoritmo CPA permitiu observações e conclusões interessantes. O algoritmo é um método populacional de otimização baseado no comportamento dos pulgões e, embora a ideia em si pareça promissora, os resultados dos testes mostraram uma eficácia relativamente baixa em comparação com outros algoritmos populacionais.
A ideia central do algoritmo é o uso de dois tipos de reprodução (com e sem acasalamento) e a divisão da população em colônias com possibilidade de migração entre elas. A metáfora biológica aqui é bastante elegante: os pulgões realmente utilizam tanto partenogênese quanto reprodução sexual, adaptando-se às condições do ambiente. No entanto, a implementação matemática desses conceitos não se mostrou tão eficaz quanto se esperava.
Os pontos fracos do algoritmo se manifestam em vários aspectos. Em primeiro lugar, a divisão dos indivíduos da população em fêmeas e machos não garante diversidade e qualidade suficientes nas soluções. Em segundo, a separação em colônias, embora tenha como objetivo explorar diferentes regiões do espaço de busca, na prática frequentemente leva à convergência prematura para ótimos locais. O mecanismo de voo entre colônias, que deveria mitigar esse efeito, acaba sendo pouco eficaz.
A configuração dos parâmetros do algoritmo também representa um desafio não trivial. Parâmetros como o tamanho das colônias (Nm), a proporção de indivíduos fêmeas (Fr), a probabilidade de voo (Pf) e os coeficientes de escala (alpha1, alpha2) afetam diretamente o desempenho do algoritmo, e encontrar seus valores ideais é complicado. Tentativas de melhorar o algoritmo introduzindo parâmetros adaptativos trouxeram algumas melhorias, mas não conseguiram elevar substancialmente sua eficácia. Isso leva à reflexão de que o problema pode ser mais profundo e estar relacionado à própria estrutura do algoritmo.
Mesmo assim, o trabalho com esse algoritmo foi útil sob vários pontos de vista. Primeiro, ofereceu uma boa experiência na análise e implementação de um algoritmo bioinspirado. Segundo, o processo de depuração e otimização ajudou a entender melhor a importância do equilíbrio entre diversificação do espaço de busca e intensificação das soluções encontradas nos algoritmos metaheurísticos. Terceiro, é um bom exemplo de como uma analogia biológica elegante nem sempre se traduz em um algoritmo de otimização eficiente.
Em conclusão, vale ressaltar que mesmo algoritmos menos bem-sucedidos contribuem para o avanço da área de otimização metaheurística, trazendo novas ideias e abordagens que podem ser aproveitadas no desenvolvimento de métodos mais eficazes. O CPA, apesar de suas limitações, apresenta uma abordagem interessante para equilibrar diferentes estratégias de busca de soluções e pode servir como ponto de partida para pesquisas futuras nessa direção.
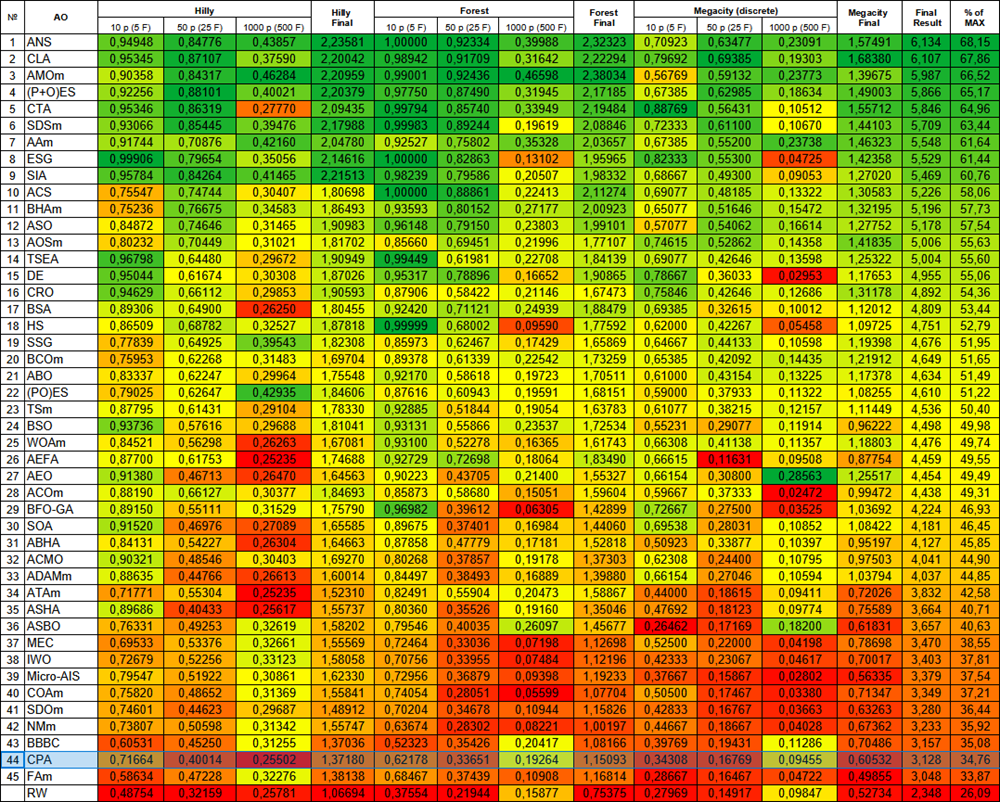
Figura 3. Gradação de cores dos algoritmos conforme os testes correspondentes
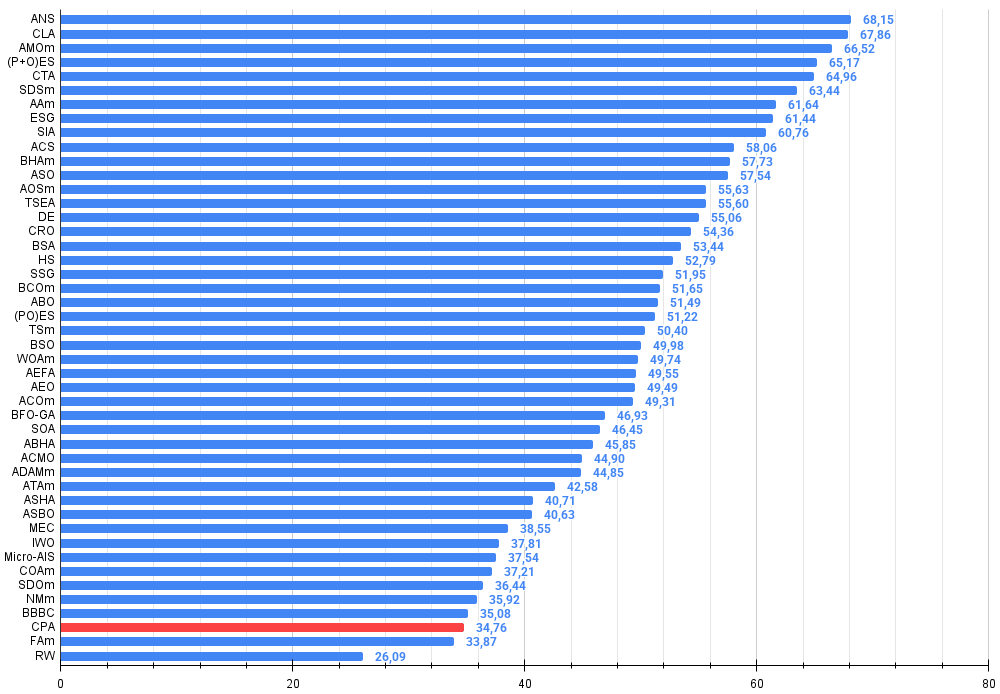
Figura 3. Histograma dos resultados de testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo está o script para cálculo da tabela de classificação)
Prós e contras do algoritmo CPA:
Prós:
- Ideia interessante.
- Implementação relativamente simples.
- Apresenta desempenho razoável em tarefas de alta dimensionalidade.
Contras:
- Muitos parâmetros externos.
- Baixa velocidade e precisão de convergência.
Um arquivo com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela exatidão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar a capacidade de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe pai dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do ambiente de teste |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados para tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente de teste unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso de algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_CPA.mq5 | Script | Ambiente de teste para o CPA |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16877
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais em trading: Aprendizado contextual com memória (MacroHFT)
Redes neurais em trading: Aprendizado contextual com memória (MacroHFT)
 Dados de mercado sem intermediários: conectando MetaTrader 5 à MOEX via ISS API
Dados de mercado sem intermediários: conectando MetaTrader 5 à MOEX via ISS API
 Do básico ao intermediário: Objetos (IV)
Do básico ao intermediário: Objetos (IV)
 Sistemas neurossimbólicos no algotrading: Unindo regras simbólicas e redes neurais
Sistemas neurossimbólicos no algotrading: Unindo regras simbólicas e redes neurais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso