
Algoritmo de Partenogénesis Cíclica - Cyclic Parthenogenesis Algorithm (CPA)
Contenido
Introducción
Los algoritmos de optimización inspirados en fenómenos naturales siguen jugando un papel importante en la resolución de problemas complejos de optimización. Los algoritmos basados en el comportamiento de insectos sociales como hormigas, abejas y pulgones, resultan especialmente interesantes. En artículos anteriores ya hemos examinado algunas de ellos, como el ACOm, o el ABHA. Este artículo presenta un nuevo algoritmo metaheurístico de optimización, el Algoritmo de Partenogénesis Cíclica (CPA), que imita la singular estrategia reproductiva de los pulgones.
Los pulgones muestran una notable capacidad de adaptación debido a su inusual ciclo vital, que incluye tanto la reproducción asexual (partenogénesis) como la reproducción sexual. En condiciones favorables, los pulgones se reproducen mediante partenogénesis, lo cual permite una rápida expansión de la población. Cuando las condiciones empeoran, recurren a la reproducción sexual, que favorece la diversidad genética y aumenta las posibilidades de supervivencia en un entorno cambiante.
El CPA modela matemáticamente estos mecanismos biológicos, creando un equilibrio entre la explotación de las soluciones encontradas (mediante la partenogénesis) y la exploración de nuevas áreas del espacio de búsqueda (mediante la reproducción sexual). El algoritmo también imita el comportamiento social de los pulgones organizando las decisiones en una colonia y aplicando un mecanismo de migración entre ellos, lo cual facilita el intercambio de información.
Las características enumeradas deberían demostrar que el CPA resulta especialmente eficaz para los problemas de optimización multidimensional en los que se requiere un equilibrio entre la búsqueda local y la global. En este artículo, detallaremos los principios del algoritmo, su modelo matemático y su aplicación práctica. El algoritmo de partenogénesis cíclica fue propuesto por Ali Kaveh y Zolghadr, y se publicó por primera vez en 2019.Implementación del algoritmo
Imagine que está observando una colonia de pulgones en un jardín. Estas diminutas criaturas tienen dos métodos de reproducción y son muy eficientes adaptándose a su entorno. El algoritmo CPA (Cyclic Parthenogenesis Algorithm) imita exactamente este comportamiento para resolver problemas complejos de optimización. ¿Cómo funciona? En la organización inicial, se crean varios grupos (colonias) de soluciones, cada uno con individuos "hembras" y "machos".
El algoritmo propone dos formas de crear nuevas soluciones:- El primer método es la "reproducción autónoma", en el que las mejores soluciones crean sus propias copias con pequeñas modificaciones.
- El segundo es el tradicional: la "reproducción por pares", en la que dos soluciones diferentes se combinan para crear una nueva.
A veces, la mejor solución de una colonia "vuela" a otra. El algoritmo comprueba constantemente qué soluciones funcionan mejor, almacena los mejores hallazgos y combina las opciones acertadas en una continuación de la búsqueda. Y todo ello para encontrar la mejor solución posible. La principal característica del algoritmo es que encuentra un equilibrio entre el uso de buenas soluciones ya encontradas y la búsqueda de opciones completamente nuevas, de manera similar a como los pulgones se adaptan a los cambios del entorno.
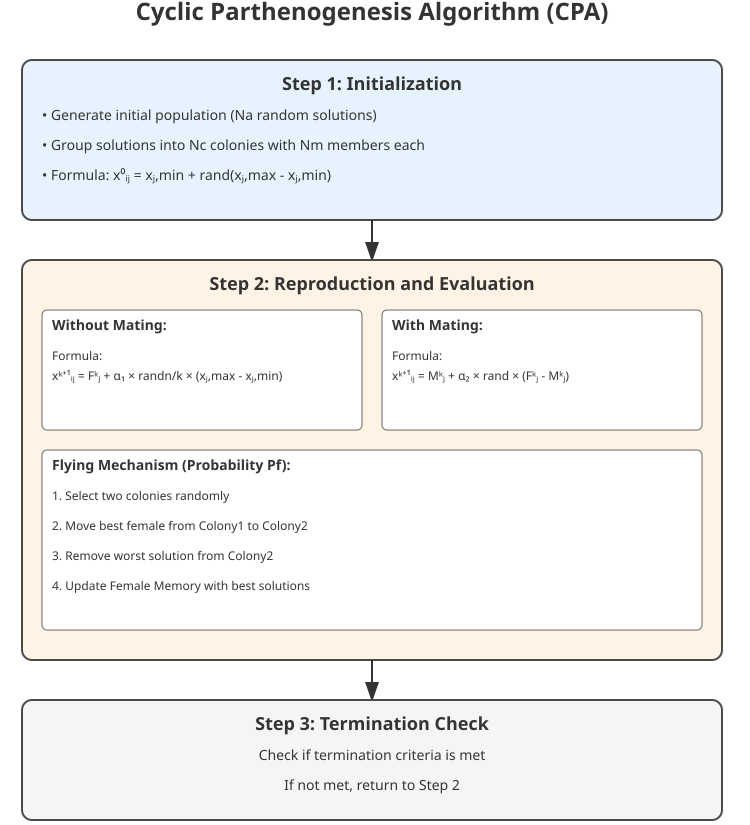
Figura 1. Esquema del algoritmo CPA, fórmulas básicas
Vamos a pasar ahora a la representación visual del algoritmo CPA, en la que los elementos principales de la ilustración son las colonias, los cuadrados rosas marcan los individuos femeninos (soluciones), los azules los masculinos (soluciones) y la línea de puntos muestra la trayectoria de vuelo entre colonias. La ilustración muestra la estructura de las colonias, los mecanismos de reproducción, el proceso de vuelo entre colonias y la interacción de los individuos dentro de las mismas. Esto nos ayudará a comprender mejor los principios del algoritmo mediante una metáfora visual con pulgones reales.
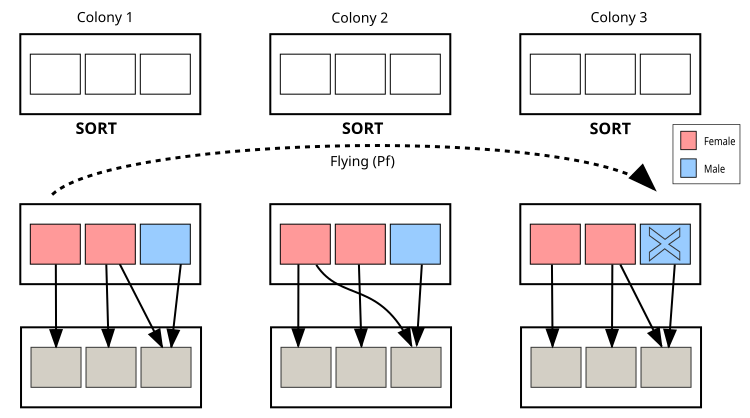
Figura 2. Colonias de pulgones y sus interacciones en el algoritmo CPA
Ahora que entendemos un poco la descripción del algoritmo, vamos a escribir el pseudocódigo:
Inicialización:
Creamos una población de Na individuos
Dividimos la población en Nc colonias
En todas las colonias:
Determinamos el número de individuos hembra (Fr * Nm)
Determinamos el número de individuos macho (resto)
Configuramos los parámetros iniciales:
alfa1 (coeficiente de partenogénesis)
alfa2 (coeficiente de apareamiento)
Pf (probabilidad de vuelo)
Ciclo básico (para cada época):
Para cada colonia:
Para los individuos hembra:
La posición se actualiza mediante partenogénesis:
nueva_posición = posición_actual + alfa1 * k * N(0,1) * (max_range - min_range)
donde k = (total_epochs - current_epoch) / total_epochs
N(0,1) - distribución normal
Para los individuos macho:
Seleccionamos una hembra al azar de la misma colonia
Actualizamos la posición mediante el apareamiento:
nueva_posición = posición_actual + alpha2 * random[0,1] * (posición_hembra - posición_actual)
Revisión de la posición:
Actualizamos la mejor solución encontrada
Guardamos posiciones actuales
Clasificamos los individuos de cada colonia según el valor de la función objetivo.
Migración (con probabilidad Pf):
Seleccionamos dos colonias al azar
Comparamos sus mejores soluciones
Trasladamos la mejor solución a la peor colonia
Reordenamos los individuos de la colonia
Todo está preparado para escribir el código del algoritmo, sigamos adelante. Vamos a escribir la clase "C_AO_CPA", que heredará de la clase "C_AO". Esta clase implementará el algoritmo completo. Aquí vemos una breve descripción de sus componentes:
Constructor C_AO_CPA:
- Establece parámetros como el tamaño de la población, el número de colonias, la proporción de hembras, la probabilidad de vuelo y los coeficientes de escala para la partenogénesis y el apareamiento.
- Reserva un array de parámetros y lo rellena con valores.
El método SetParams establece los valores de los parámetros del array "params", convirtiéndolos a los tipos correspondientes.
Métodos Init, Moving y Revision:
- Init — se ha diseñado para inicializar el algoritmo con los rangos y número de épocas especificados.
- Moving y Revision — los métodos implementan la lógica del desplazamiento y la revisión dentro del algoritmo.
Los miembros de la clase están definidos por variables para almacenar los parámetros del algoritmo como el número de colonias, la proporción de hembras y machos y los parámetros para controlar el proceso.
Los miembros privados incluyen las variables para rastrear la época actual, el número de miembros en la colonia, y un array temporal de agentes.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the Cyclic Parthenogenesis Algorithm (CPA) // Inherited from the optimization base class class C_AO_CPA : public C_AO { public: C_AO_CPA (void) { ao_name = "CPA"; ao_desc = "Cyclic Parthenogenesis Algorithm"; ao_link = "https://www.mql5.com/es/articles/16877"; popSize = 50; // total population size Na Nc = 10; // number of colonies Fr = 0.2; // ratio of female individuals Pf = 0.9; // probability of flight between colonies alpha1 = 0.3; // scaling factor for parthenogenesis alpha2 = 0.9; // scaling factor for pairing ArrayResize (params, 6); // Setting algorithm parameters params [0].name = "popSize"; params [0].val = popSize; params [1].name = "Nc"; params [1].val = Nc; params [2].name = "Fr"; params [2].val = Fr; params [3].name = "Pf"; params [3].val = Pf; params [4].name = "alpha1_init"; params [4].val = alpha1; params [5].name = "alpha2_init"; params [5].val = alpha2; } void SetParams () { popSize = (int)params [0].val; Nc = (int)params [1].val; Fr = params [2].val; Pf = params [3].val; alpha1 = params [4].val; alpha2 = params [5].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // function for moving individuals void Revision (); // function for reviewing and updating positions //---------------------------------------------------------------------------- int Nc; // number of colonies double Fr; // ratio of female individuals double Pf; // probability of flight between colonies private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch int Nm; // number of individuals in each colony double alpha1; // scaling factor for parthenogenesis double alpha2; // scaling factor for pairing int fNumber; // number of females in the colony int mNumber; // number of males in the colony S_AO_Agent aT []; // temporary colony for sorting void SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count); // agent sorting function }; //——————————————————————————————————————————————————————————————————————————————
Implementación del método "Init" de la clase "C_AO_CPA", su funcionalidad:
Parámetros del método:
- rangeMinP, rangeMaxP, rangeStepP - arrays que definen los valores mínimo y máximo del rango, así como el paso de búsqueda.
- epochsP - número de épocas (por defecto es igual a 0).
- El método llama primero a "StandardInit" para efectuar la inicialización estándar con los rangos transmitidos. Si la inicialización falla, el método retornará "false".
- Establece el número de épocas (epochs) y la época actual (epochNow).
- Calcula el número de miembros por colonia (Nm) según el tamaño de la población y del número de colonias.
- Determina el número de hembras (fNumber) de la colonia, asegurándose de que no sea inferior a 1. El número de hombres (fNumber) se calcula como la diferencia entre el número total de miembros y el número de hembras.
- Reserva el array "aT" para almacenar agentes de colonias temporales.
- El método retornará "true" si la inicialización se ha realizado correctamente.
Este método establece los parámetros y la estructura para que el algoritmo se ejecute, asegurándose de que esté correctamente inicializado antes de empezar a ejecutarse.
//—————————————————————————————————————————————————————————————————————————————— // Initialization of the algorithm with the given search parameters bool C_AO_CPA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Calculating the colony size and the number of individuals of each gender Nm = popSize / Nc; fNumber = int(Nm * Fr); if (fNumber < 1) fNumber = 1; mNumber = Nm - fNumber; ArrayResize (aT, Nm); return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" de la clase "C_AO_CPA" desplaza los agentes en el espacio de decisiones adaptando sus coordenadas en base a ciertas reglas y factores aleatorios. Veámoslo paso a paso:
Aumento de la época. El método comienza aumentando el valor de la época actual (epochNow), lo cual indica que se ha invocado otro paso en el proceso de optimización o evolución.
Primer paso (si no se requiere revisión): si el campo "revision" se establece en "false", se inicializarán las coordenadas de cada agente de la población (popSize):
- Cada agente (a[i]) obtiene nuevas coordenadas en cada dimensión (coords) utilizando la función "RNDfromCI", que genera valores aleatorios en un rango dado [rangeMin[c], rangeMax[c]].
- A continuación, la coordinación se modifica usando la función "SeInDiSp", que ofrece una corrección de los valores según el paso de muestreo (rangeStep[c]).
- La bandera "revision" se pone en "true" y el método finaliza la ejecución.
- La variable "k" se calcula como la relación entre el número restante de épocas y el número total de épocas. Esto permite reducir gradualmente la dispersión del movimiento de los agentes conforme se acerca el final de la optimización.
- Luego se buscan colonias (col) y las características (fNumber); para actualizar las coordenadas de cada agente para los primeros agentes "fNumber" en una colonia, esta actualización se basa en sus coordenadas previas (cP), con la adición de un valor aleatorio generado usando una distribución normal (GaussDistribution). Este valor se escala entre "rangeMin" y "rangeMax".
- Para el resto de agentes (m desde fNumber hasta Nm), también se actualizan las coordenadas, pero ahora se utilizan las coordenadas seleccionadas aleatoriamente de uno de los mejores agentes de la misma colonia. Luego se añaden valores aleatorios a las coordenadas de cada agente, teniendo en cuenta el parámetro "alpha2".
- El objetivo general de este método consiste en mover a los agentes en el espacio de decisiones usando como base su posición anterior e inyectar un elemento de aleatoriedad para explorar la vecindad y mejorar la posibilidad de encontrar un óptimo global.
- Parámetros como "alpha1" y "alpha2" ayudan a controlar el nivel de adaptación y aleatoriedad.
Así, el método Moving en el contexto de un algoritmo de optimización resulta esencial para mover a los agentes a través del espacio de decisiones, considerando tanto sus propias posiciones previas como las de otros agentes.
//—————————————————————————————————————————————————————————————————————————————— // The main function for moving individuals in the search space void C_AO_CPA::Moving () { epochNow++; //---------------------------------------------------------------------------- // Initial random initialization of positions if this is the first iteration if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a random position in a given range a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Calculate the search power decay rate over time double k = (epochs - epochNow)/(double)epochs; int ind = 0; int indF = 0; // Handling each colony for (int col = 0; col < Nc; col++) { // Updating the positions of female individuals (parthenogenesis) for (int f = 0; f < fNumber; f++) { ind = col * Nm + f; for (int c = 0; c < coords; c++) { // Parthenogenetic position update using normal distribution a [ind].c [c] = a [ind].cP [c] + alpha1 * k * u.GaussDistribution (0.0, -1.0, 1.0, 8) * (rangeMax [c] - rangeMin [c]); } } // Update positions of males (mating) for (int m = fNumber; m < Nm; m++) { ind = col * Nm + m; // Select a random female for mating indF = u.RNDintInRange (ind, col * Nm + fNumber - 1); for (int c = 0; c < coords; c++) { // Update position based on the selected female a [ind].c [c] = a [ind].cP [c] + alpha2 * u.RNDprobab () * (a [indF].cP [c] - a [ind].cP [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" de la clase "C_AO_CPA" es el encargado de actualizar el estado de los agentes de la población según los valores de su función f, veámoslo con más detalle:
Inicialización: el método comienza inicializando la variable "ind" con el valor "-1", que se utilizará para almacenar el índice del agente con el mejor valor de la función "f".
Búsqueda del mejor agente: el primer ciclo "for" busca todos los agentes de la población (popSize) y si el valor de la función "f" del agente actual (a[i].f) es mayor que el mejor valor actual "fB", entonces:
- Se actualiza "fB" al valor "a[i].f".
- Se almacena el índice del mejor agente en la variable "ind".
- Una vez finalizado el ciclo, si se ha encontrado el agente con el mejor valor (ind != -1), sus coordenadas (c) se copiarán en el array "cB".
Copiando las coordenadas actuales. El segundo ciclo "for" copia las coordenadas actuales (c) de cada agente en sus coordenadas anteriores (cP). Esto permite almacenar el estado anterior de los agentes para posteriores análisis.
Agentes clasificadores. El tercer ciclo "for" itera por todas las colonias (Nc), y para cada colonia, se llama al método "SortFromTo", que clasifica los agentes dentro de la colonia según sus valores de la función "f". El índice para la clasificación se calcula como (ind = col * Nm).
Actualización probabilística. El método comprueba si el valor aleatorio generado por "u.RNDprobab()" es menor que el valor umbral "Pf":
- Si se cumple la condición, se seleccionarán dos índices de colonia aleatorios (indCol_1 e indCol_2), comprobando que no sean iguales entre sí.
- Después se comparan los valores de la función f de los agentes en estas colonias. Si el valor de la función en la primera colonia es menor que en la segunda, se intercambiarán los índices.
- A continuación, las coordenadas del primer agente de la primera colonia se copian en las coordenadas del último agente de la segunda colonia.
- Luego se vuelve a llamar a "SortFromTo" para actualizar el orden de los agentes en la segunda colonia.
Lógica general:
El método "Revision" sirve para actualizar el estado de los agentes, almacenando información sobre el mejor agente y permitiendo compartir información entre colonias.
//—————————————————————————————————————————————————————————————————————————————— // Function for revising positions and exchanging information between colonies void C_AO_CPA::Revision () { // Find and update the best solution int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Save the current positions for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY); } // Sort individuals in each colony by the target function value for (int col = 0; col < Nc; col++) { ind = col * Nm; SortFromTo (a, aT, ind, Nm); } // Mechanism of flight (migration) between colonies if (u.RNDprobab () < Pf) { int indCol_1 = 0; int indCol_2 = 0; // Select two random different colonies indCol_1 = u.RNDminusOne (Nc); do indCol_2 = u.RNDminusOne (Nc); while (indCol_1 == indCol_2); // Ensure that the best solution is in the first colony if (a [indCol_1 * Nm].f < a [indCol_2 * Nm].f) { int temp = indCol_1; indCol_1 = indCol_2; indCol_2 = temp; } // Copy the best solution to the worst colony ArrayCopy (a [indCol_2 * Nm + Nm - 1].cP, a [indCol_1 * Nm].cP, 0, 0, WHOLE_ARRAY); // Re-sort the colony after migration SortFromTo (a, aT, indCol_2 * Nm, Nm); } } //——————————————————————————————————————————————————————————————————————————————
El método "SortFromTo" de la clase "C_AO_CPA" está diseñado para clasificar el array de agentes usando como base sus valores de la función "f"; vamos a verlo con detalle:
Inicialización de variables:
- El método admite tres parámetros: un array de agentes "p", un array temporal "pTemp", el índice de inicio de la clasificación "from" y el número de elementos a clasificar "count".
- Las variables "cnt", "t0" y "t1" se usan para llevar la cuenta del número de intercambios y almacenar temporalmente los valores.
- Los arrays "ind" y "val" se crean para almacenar los índices y valores de la función de aptitud "f" respectivamente.
Rellenado de los arrays de índices y valores. En el primer ciclo "for", se rellenan los arrays "ind" y "val":
- ind[i] obtiene el índice del agente en el array de origen, empezando por "from".
- val[i] obtiene el valor de la función "f" para el agente correspondiente.
Clasificación. El ciclo principal "while" se ejecuta mientras haya intercambios (es decir, que cnt > 0). El ciclo interno "for" itera por el array "val" y compara los valores vecinos:
- Si el actual es menor que el siguiente (val[i] < val[i + 1]), se intercambiarán los índices del array "ind" y los valores del array "val" .
- El contador "cnt" aumenta para indicar que se ha producido un intercambio.
- Este proceso continuará hasta que se completa una iteración completa sin intercambios.
Copiado de los valores clasificados:
- Una vez finalizada la clasificación, el primer ciclo "for" copia los agentes clasificados del array temporal "pTemp" de nuevo al array original "p", comenzando en el índice "from".
- El segundo ciclo "for" actualiza el array original "p", sustituyéndolo por los valores clasificados.
//—————————————————————————————————————————————————————————————————————————————— // Auxiliary function for sorting agents by the value of the objective function void C_AO_CPA::SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count) { int cnt = 1; int t0 = 0; double t1 = 0.0; int ind []; double val []; ArrayResize (ind, count); ArrayResize (val, count); // Copy values for sorting for (int i = 0; i < count; i++) { ind [i] = i + from; val [i] = p [i + from].f; } // Bubble sort in descending order while (cnt > 0) { cnt = 0; for (int i = 0; i < count - 1; i++) { if (val [i] < val [i + 1]) { // Exchange of indices t0 = ind [i + 1]; ind [i + 1] = ind [i]; ind [i] = t0; // Exchange values t1 = val [i + 1]; val [i + 1] = val [i]; val [i] = t1; cnt++; } } } // Apply the sorting results for (int i = 0; i < count; i++) pTemp [i] = p [ind [i]]; for (int i = from; i < from + count; i++) p [i] = pTemp [i - from]; } //——————————————————————————————————————————————————————————————————————————————
Después de escribir y analizar detalladamente el código del algoritmo, vamos a pasar a los resultados de las pruebas del algoritmo CPA.
Resultados de las pruebas
Al implementar la peculiar lógica del algoritmo, ni siquiera me permití pensar que no llegaría a las primeras líneas de la tabla de clasificación, y la verdad es que experimenté cierta decepción al ver los resultados detallados de las pruebas del algoritmo CPA. Al final de la prueba, el algoritmo ha obtenido como máximo el 34,76% de la puntuación máxima posible.
CPA|Cyclic Parthenogenesis Algorithm|50.0|10.0|0.2|0.9|0.3|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7166412833856777
25 Hilly's; Func runs: 10000; result: 0.4001377868508138
500 Hilly's; Func runs: 10000; result: 0.25502012607456315
=============================
5 Forest's; Func runs: 10000; result: 0.6217765628284961
25 Forest's; Func runs: 10000; result: 0.3365148812759322
500 Forest's; Func runs: 10000; result: 0.192638189788532
=============================
5 Megacity's; Func runs: 10000; result: 0.34307692307692306
25 Megacity's; Func runs: 10000; result: 0.16769230769230772
500 Megacity's; Func runs: 10000; result: 0.09455384615384692
=============================
All score: 3.12805 (34.76%)
La visualización muestra el movimiento de los pulgones virtuales en el espacio de búsqueda característico del algoritmo, especialmente en dimensionalidades altas del problema, incluso podemos identificar a ojo colonias individuales y el movimiento de las criaturas virtuales en ellas.
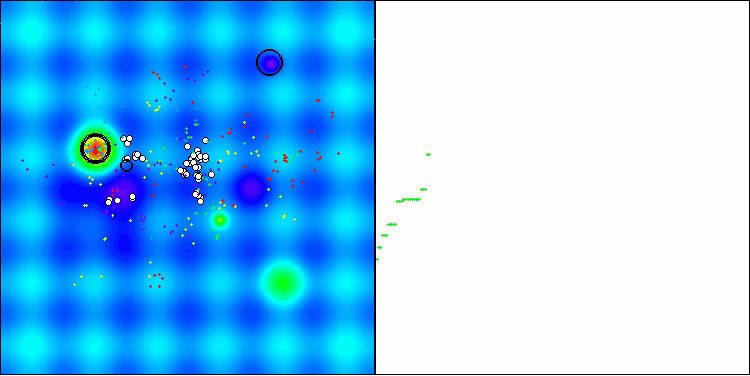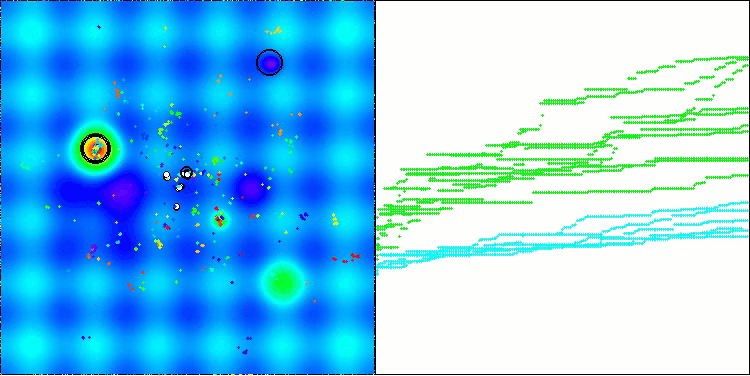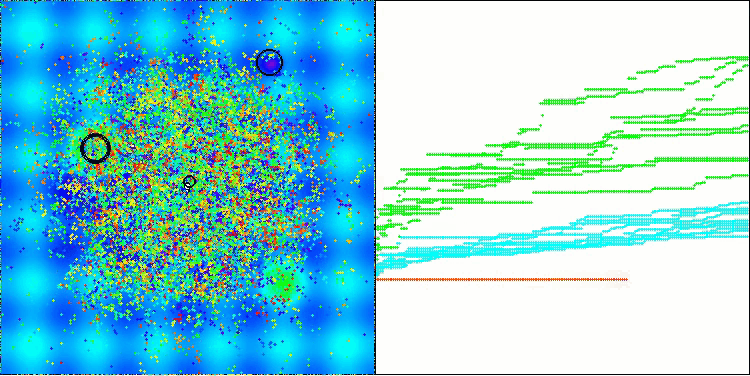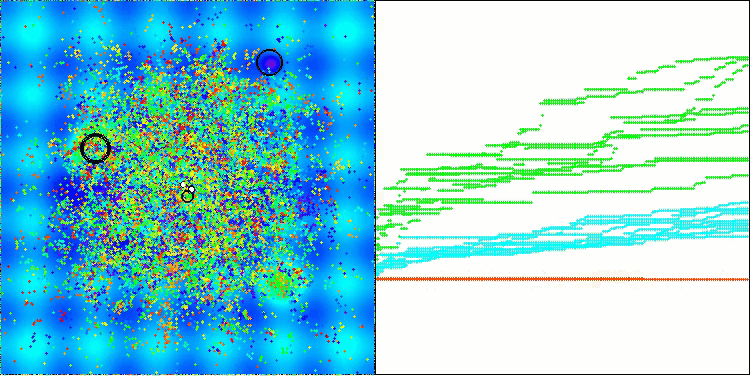
CPA en la función de prueba Hilly
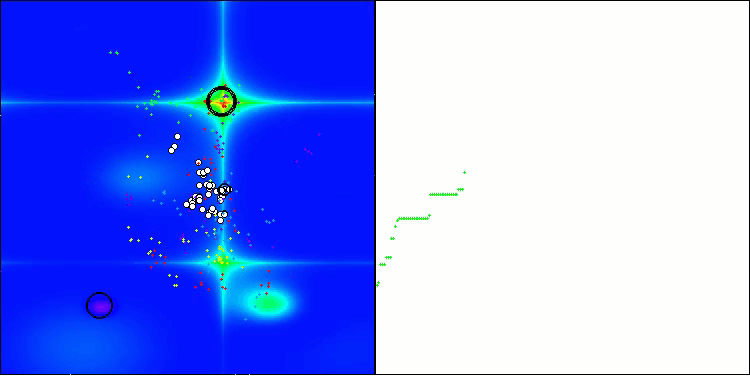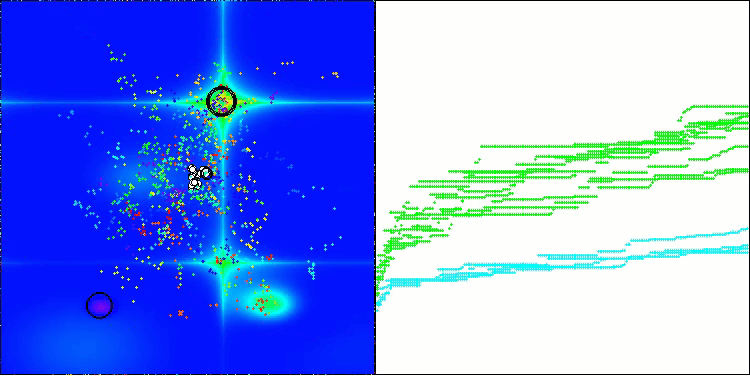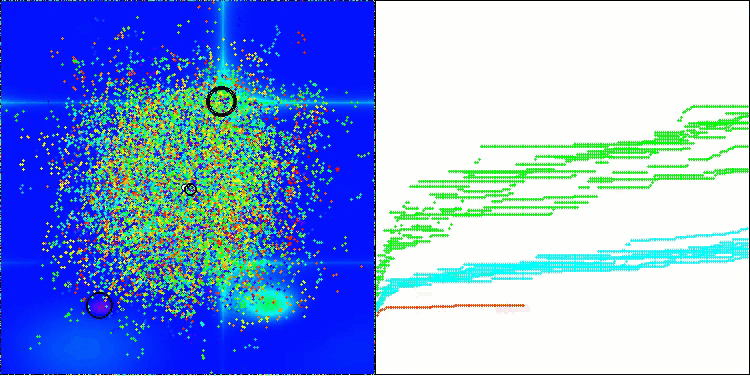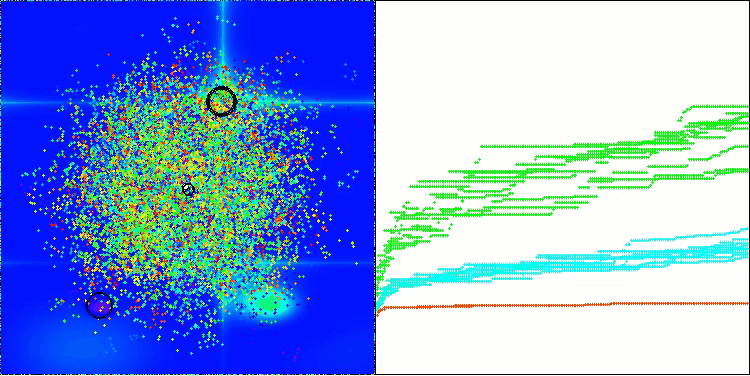
CPA en la función de prueba Forest

CPA en la función de prueba Megacity
Tras las pruebas, el algoritmo CPA se ha situado en el puesto 44 de la tabla de clasificación, entrando en el grupo de los 45 mejores algoritmos de optimización de la población.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 13 | AOSm | búsqueda de orbitales atómicos M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | BBC | big bang-big crunch algorithm | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1,08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 44 | CPA | cyclic parthenogenesis algorithm | 0.71664 | 0.40014 | 0.25502 | 1.37180 | 0.62178 | 0.33651 | 0.19264 | 1.15093 | 0.34308 | 0.16769 | 0.09455 | 0.60532 | 3.128 | 34.76 |
| 45 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
El trabajo en la aplicación y las pruebas del algoritmo CPA ha dado lugar a algunas observaciones y conclusiones interesantes. El algoritmo es un método de optimización poblacional basado en el comportamiento de los pulgones y, aunque la idea en sí parece prometedora, los resultados de las pruebas muestran un rendimiento relativamente pobre en comparación con otros algoritmos poblacionales.
La idea básica del algoritmo consiste en utilizar dos tipos de reproducción (con y sin apareamiento) y dividir la población en colonias con posibilidad de migración entre ellas. La metáfora biológica es bastante elegante: los pulgones recurren tanto a la partenogénesis como a la reproducción sexual para adaptarse a las condiciones del entorno. Sin embargo, la realización matemática de estos conceptos no ha sido todo lo eficaz que habríamos querido.
Los puntos débiles del algoritmo se manifiestan en varios aspectos. En primer lugar, dividir a los individuos de la población en hembras y machos no ofrece la suficiente diversidad y calidad en las soluciones. En segundo lugar, la partición de colonias, aunque pretende facilitar la exploración de distintas regiones del espacio de búsqueda, en la práctica suele provocar una convergencia prematura a óptimos locales. El mecanismo de vuelo entre colonias, que debería contrarrestar este efecto, resulta ser insuficientemente.
Ajustar los parámetros del algoritmo tampoco es una tarea sencilla. Parámetros como el tamaño de la colonia (Nm), la proporción de hembras (Fr), la probabilidad de vuelo (Pf) y los factores de escala (alfa1, alfa2) influyen significativamente en el rendimiento del algoritmo y encontrar sus valores óptimos resulta complicado. Los intentos de mejorar el algoritmo introduciendo parámetros adaptativos ha dado lugar a ciertas mejoras, pero no han conseguido mejorar drásticamente su eficacia. Esto sugiere que el problema puede ser más profundo y estar relacionado con la estructura del propio algoritmo.
No obstante, los trabajos sobre este algoritmo han sido útiles desde varias perspectivas. En primer lugar, nos han proporcionado una buena experiencia en el análisis y la aplicación de un algoritmo inspirado en la biología. En segundo lugar, el proceso de depuración y optimización nos ha ayudado a comprender mejor la importancia de equilibrar la exploración del espacio de búsqueda con la explotación de las soluciones encontradas en los algoritmos metaheurísticos. En tercer lugar, supone un buen ejemplo de cómo una bella analogía biológica no siempre se traduce en un algoritmo de optimización eficaz.
Como conclusión, debemos señalar que incluso los algoritmos no tan exitosos contribuyen al campo de la optimización metaheurística aportando nuevas ideas y enfoques que pueden utilizarse para desarrollar métodos más eficientes. El CPA, a pesar de sus limitaciones, demuestra un enfoque interesante para posibilitar el equilibrio entre diferentes estrategias de búsqueda de soluciones y puede servir como punto de partida para futuras investigaciones en esta dirección.
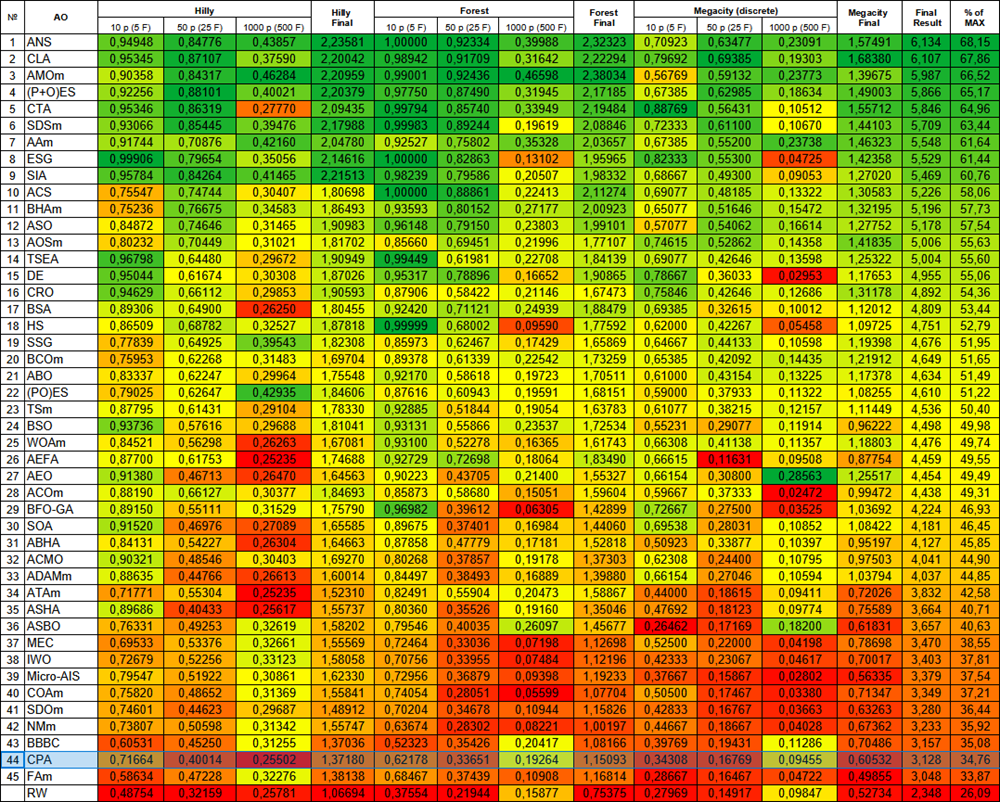
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas
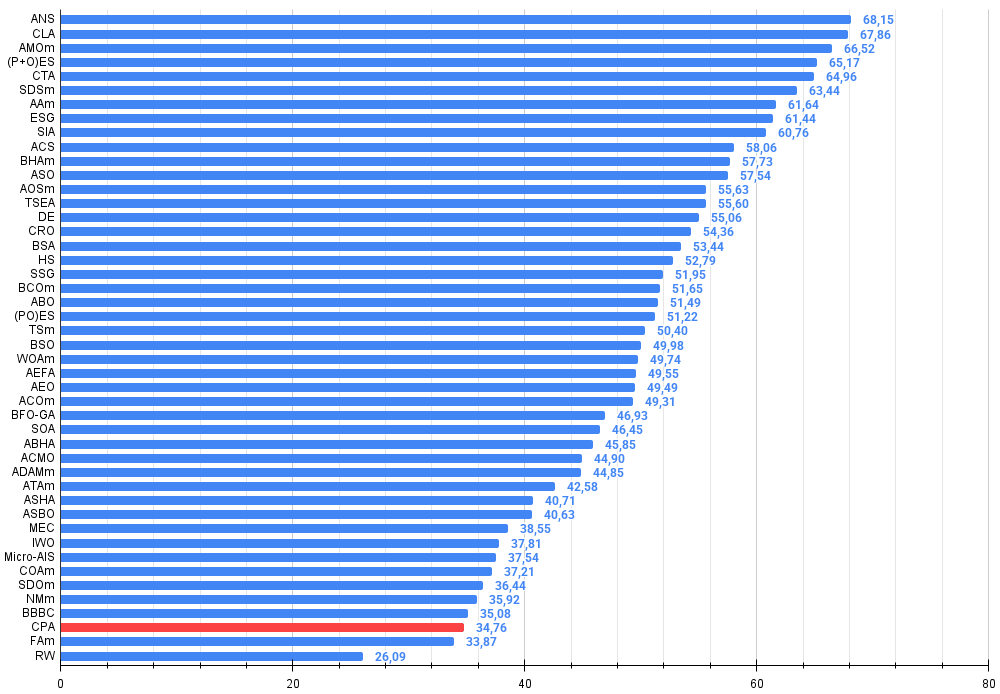
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo CPA:
Ventajas:
- Supone una idea interesante.
- Aplicación bastante sencilla.
- Funciona bien en problemas de gran escala.
Desventajas:
- Muchos parámetros externos.
- La baja velocidad y precisión de convergencia.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_CPA.mq5 | Script | Banco de pruebas para el CPA |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16877
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Cómo empezar a trabajar con MQL5 Algo Forge
Cómo empezar a trabajar con MQL5 Algo Forge
 Redes neuronales en el trading: Sistema multiagente con validación conceptual (Final)
Redes neuronales en el trading: Sistema multiagente con validación conceptual (Final)
 Redes neuronales en el trading: Aprendizaje contextual aumentado por memoria (MacroHFT)
Redes neuronales en el trading: Aprendizaje contextual aumentado por memoria (MacroHFT)
 Desarrollamos un asesor experto multidivisas (Parte 21): Preparación para un experimento importante y optimización del código
Desarrollamos un asesor experto multidivisas (Parte 21): Preparación para un experimento importante y optimización del código
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso