Cyclic Parthenogenesis Algorithm (CPA)
405
0
Contents
Introduction
Optimization algorithms inspired by natural phenomena continue to play an important role in solving complex optimization problems. Of particular interest are algorithms based on the behavior of social insects such as ants, bees, and aphids. We have already discussed a number of similar algorithms like ACOm and ABHA. This article presents the Cyclic Parthenogenesis Algorithm (CPA), which mimics the unique reproductive strategy of aphids.
Aphids exhibit remarkable adaptability due to their unusual life cycle, which includes both asexual (parthenogenesis) and sexual reproduction. Under favorable conditions, aphids reproduce parthenogenetically, which allows for rapid population growth. When conditions worsen, they switch to sexual reproduction, which promotes genetic diversity and increases the chances of survival in a changing environment.
CPA mathematically simulates these biological mechanisms, creating a balance between the exploitation of found solutions (through parthenogenesis) and the exploration of new areas of the search space (through sexual reproduction). The algorithm also mimics the social behavior of aphids, organizing decisions within the colony and implementing a migration mechanism between them, which facilitates the exchange of information.
The features listed above should make CPA particularly efficient for solving multidimensional optimization problems where a balance between local and global search is required. In this article, we will examine in detail the principles of the algorithm, its mathematical model, and practical implementation. The algorithm of cyclic parthenogenesis was proposed by Ali Kaveh and Zolghadr. It was first published in 2019.Implementation of the algorithm
Imagine you are observing a colony of aphids in your garden. These tiny creatures use two methods of reproduction and adapt to their environment very effectively. The Cyclic Parthenogenesis Algorithm (CPA) simulates exactly this behavior to solve complex optimization problems. How it works? During the initial organization, several groups (colonies) of solutions are created, each of which contains "female" and "male" individuals.
The algorithm proposes two ways to create new solutions:- The first method is "Self-Replication", where the best solutions create copies of themselves with minor modifications.
- The second method is traditional "Paired Reproduction", where two different solutions are combined to create a new one.
Sometimes, the best solution from one colony "flies" to another. The algorithm constantly checks which solutions work best, saves the best findings, and combines successful options as the search continues. And all this in order to find the most optimal solution. The key feature of the algorithm is that it finds a balance between using already found good solutions and searching for completely new options, similar to how aphids adapt to changes in the environment.
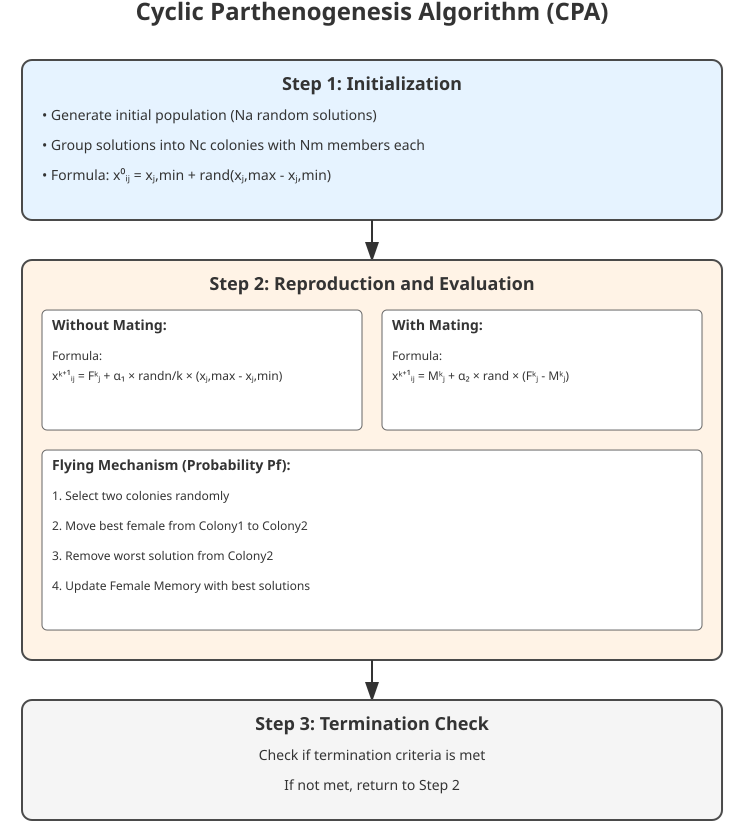
Figure 1. CPA algorithm operation structure, basic equations
Let's move on to a visual representation of the CPA algorithm, where the main elements in the illustration are colonies, pink squares indicate female individuals (solutions), blue squares indicate male individuals (solutions), and the dotted line indicates the flight path between colonies. The illustration demonstrates the structure of colonies, the mechanisms of reproduction, the flight between colonies, and the interaction of individuals within colonies. This will help to better understand the principles of the algorithm through a visual metaphor with real aphids.
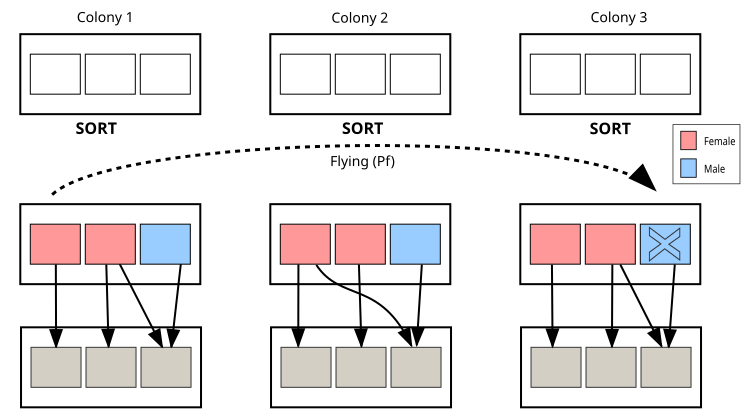
Figure 2. Aphid colonies and their interactions in the CPA algorithm
Now that we have become a little more familiar with the algorithm's description, let's move on to writing pseudocode:
Initialization:
Create a population of Na individuals
Divide the population into Nc colonies
In each colony:
Determine the number of female individuals (Fr * Nm)
Determine the number of males (the rest)
Set initial parameters:
alpha1 (parthenogenesis ratio)
alpha2 (mating ratio)
Pf (flight probability)
Main cycle (for each epoch):
For each colony:
For females:
Update position using parthenogenesis:
new_position = current_position + alpha1 * k * N(0,1) * (max_range - min_range)
where k = (total_epochs - current_epoch) / total_epochs
N(0,1) - normal distribution
For males:
Select a random female from the same colony
Update position via pairing:
new_position = current_position + alpha2 * random[0,1] * (female_position - current_position)
Revision of positions:
Update the best solution found
Save the current positions
Sort individuals in each colony by the value of the objective function
Migration (with Pf probability):
Select two random colonies
Compare their best solutions
Move the best solution to the worst colony
Re-sort individuals in the colony
Everything is ready for writing the algorithm code, let's move on. Let's write the C_AO_CPA class that inherits from the C_AO class. This class implements the entire algorithm, a brief description of its components:
C_AO_CPA constructor:
- Sets parameters such as population size, colony number, female ratio, flight probability, and scaling factors for parthenogenesis and mating.
- Reserves an array of parameters and fills it with values.
SetParams method sets the values of the parameters from the "params" array converting them to the appropriate types.
Init, Moving and Revision methods:
- Init is intended to initialize the algorithm with specified ranges and number of epochs.
- Moving and Revision — methods implement the logic of moving and revising within the algorithm.
Class members are defined by variables to store algorithm parameters such as the number of colonies, the ratio of females to males, and parameters to control the process.
Private members include variables to track the current epoch, the number of members in the colony, and a temporary array of agents.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the Cyclic Parthenogenesis Algorithm (CPA) // Inherited from the optimization base class class C_AO_CPA : public C_AO { public: C_AO_CPA (void) { ao_name = "CPA"; ao_desc = "Cyclic Parthenogenesis Algorithm"; ao_link = "https://www.mql5.com/en/articles/16877"; popSize = 50; // total population size Na Nc = 10; // number of colonies Fr = 0.2; // ratio of female individuals Pf = 0.9; // probability of flight between colonies alpha1 = 0.3; // scaling factor for parthenogenesis alpha2 = 0.9; // scaling factor for pairing ArrayResize (params, 6); // Setting algorithm parameters params [0].name = "popSize"; params [0].val = popSize; params [1].name = "Nc"; params [1].val = Nc; params [2].name = "Fr"; params [2].val = Fr; params [3].name = "Pf"; params [3].val = Pf; params [4].name = "alpha1_init"; params [4].val = alpha1; params [5].name = "alpha2_init"; params [5].val = alpha2; } void SetParams () { popSize = (int)params [0].val; Nc = (int)params [1].val; Fr = params [2].val; Pf = params [3].val; alpha1 = params [4].val; alpha2 = params [5].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // function for moving individuals void Revision (); // function for reviewing and updating positions //---------------------------------------------------------------------------- int Nc; // number of colonies double Fr; // ratio of female individuals double Pf; // probability of flight between colonies private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch int Nm; // number of individuals in each colony double alpha1; // scaling factor for parthenogenesis double alpha2; // scaling factor for pairing int fNumber; // number of females in the colony int mNumber; // number of males in the colony S_AO_Agent aT []; // temporary colony for sorting void SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count); // agent sorting function }; //——————————————————————————————————————————————————————————————————————————————
Implementing the Init method of the C_AO_CPA class, its functionality:
Method parameters:
- rangeMinP, rangeMaxP, rangeStepP - arrays defining the minimum and maximum values of the range, as well as the search step.
- epochsP — number of epochs (default 0).
- The method first calls StandardInit to perform standard initialization with the passed ranges. If initialization fails, the method returns "false".
- Sets the number of epochs and the current epoch (epochNow).
- Calculates the number of members in a colony (Nm) based on the population size and the number of colonies.
- Determines the number of females (fNumber) in the colony, ensuring that it is not less than 1. The number of males (mNumber) is calculated as the difference between the total number of members and the number of females.
- Reserves the "aT" array to store temporary colony agents.
- The method returns "true" if initialization is successful.
This method sets up the parameters and structure for the algorithm to operate on, ensuring proper initialization before it begins executing.
//—————————————————————————————————————————————————————————————————————————————— // Initialization of the algorithm with the given search parameters bool C_AO_CPA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Calculating the colony size and the number of individuals of each gender Nm = popSize / Nc; fNumber = int(Nm * Fr); if (fNumber < 1) fNumber = 1; mNumber = Nm - fNumber; ArrayResize (aT, Nm); return true; } //——————————————————————————————————————————————————————————————————————————————
The Movingmethod of the C_AO_CPA class moves agents in the solution space adapting their coordinates based on certain rules and random factors. Let's take a look at it step by step:
Epoch increase. The method starts by incrementing the current epoch (epochNow), which indicates that another step in the optimization or evolution process has been called.
First stage (if revision is not required) - if the "revision" field is set to "false", the coordinates of each agent in the population (popSize) are initialized:
- Each (a[i]) agent gets new coordinates in each dimension (coords) using the RNDfromCI function, which generates random values in the given range [rangeMin[c], rangeMax[c]].
- The coordination is then modified using the SeInDiSp function, which provides a correction of the values according to the discretization step (rangeStep[c]).
- The "revision" flag is set to "true" and the method terminates.
- The k variable is calculated as the ratio of the remaining number of epochs to the total number of epochs. This allows the agents' range of movement to be gradually narrowed as the optimization nears completion.
- The colonies (col) and functions (fNumber) are iterated over to update the coordinates of each agent for the first fNumber agents in the colony based on their previous coordinates (cP) with the addition of a random value generated using a normal distribution (GaussDistribution). This value is scaled between rangeMin and rangeMax.
- For the remaining agents (m from fNumber to Nm), the coordinates are also updated, but now randomly selected coordinates of one of the best agents in the same colony are used. Random values are added to the coordinates of each agent, taking into account the alpha2 parameter.
- The overall goal of this method is to move agents in the solution space based on their previous position and injecting an element of randomness into the exploration of the area to improve the possibility of finding a global optimum.
- Parameters, such as alpha1 and alpha2, help control the level of adaptation and randomness.
Thus, the Moving method in the context of the optimization algorithm is important for moving agents across the solution space, taking into account both their own previous positions and the positions of other agents.
//—————————————————————————————————————————————————————————————————————————————— // The main function for moving individuals in the search space void C_AO_CPA::Moving () { epochNow++; //---------------------------------------------------------------------------- // Initial random initialization of positions if this is the first iteration if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a random position in a given range a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Calculate the search power decay rate over time double k = (epochs - epochNow)/(double)epochs; int ind = 0; int indF = 0; // Handling each colony for (int col = 0; col < Nc; col++) { // Updating the positions of female individuals (parthenogenesis) for (int f = 0; f < fNumber; f++) { ind = col * Nm + f; for (int c = 0; c < coords; c++) { // Parthenogenetic position update using normal distribution a [ind].c [c] = a [ind].cP [c] + alpha1 * k * u.GaussDistribution (0.0, -1.0, 1.0, 8) * (rangeMax [c] - rangeMin [c]); } } // Update positions of males (mating) for (int m = fNumber; m < Nm; m++) { ind = col * Nm + m; // Select a random female for mating indF = u.RNDintInRange (ind, col * Nm + fNumber - 1); for (int c = 0; c < coords; c++) { // Update position based on the selected female a [ind].c [c] = a [ind].cP [c] + alpha2 * u.RNDprobab () * (a [indF].cP [c] - a [ind].cP [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
The Revision method of the C_AO_CPA class is responsible for updating the state of agents in the population based on their values of the f function. Let's take a closer look:
Initialization — the method starts by initializing the "ind" variable with the value of "-1", which will be used to store the index of the agent with the best value of the f function.
Finding the best agent — in the first "for" loop, all agents in the population (popSize) are iterated over, and if the value of the f function of the current (a[i].f) agent is greater than the current fB best value, then:
- fB is updated by a[i].f.
- The index of the best agent is stored in the "ind" variable.
- After the loop is completed, if an agent with a better value (ind != -1) was found, its coordinates (c) are copied into the cB array.
Copying current coordinates. The second "for" loop copies the current coordinates (c) of each agent to their previous coordinates (cP). This allows the previous state of agents to be saved for further analysis.
Sorting agents. The third "for" loop iterates through all colonies (Nc), and for each colony the SortFromTo method is called, which sorts the agents within the colony by their values of the f function. The sorting index is calculated as (ind = col * Nm).
Probabilistic update. The method checks if the random value generated by the u.RNDprobab() function is less than the threshold value of Pf:
- If the condition is met, two random colony indices (indCol_1 and indCol_2) are selected, ensuring that they are not equal to each other.
- The values of the f function of agents in these colonies are compared. If the function value in the first colony is less than in the second, the indices are swapped.
- Then the coordinates of the first agent in the first colony are copied to the coordinates of the last agent in the second colony.
- After this, SortFromTo is called again to update the order of agents in the second colony.
General logic:
The Revision method is used to update the state of agents, storing information about the best agent and providing the ability to exchange information between colonies.
//—————————————————————————————————————————————————————————————————————————————— // Function for revising positions and exchanging information between colonies void C_AO_CPA::Revision () { // Find and update the best solution int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Save the current positions for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY); } // Sort individuals in each colony by the target function value for (int col = 0; col < Nc; col++) { ind = col * Nm; SortFromTo (a, aT, ind, Nm); } // Mechanism of flight (migration) between colonies if (u.RNDprobab () < Pf) { int indCol_1 = 0; int indCol_2 = 0; // Select two random different colonies indCol_1 = u.RNDminusOne (Nc); do indCol_2 = u.RNDminusOne (Nc); while (indCol_1 == indCol_2); // Ensure that the best solution is in the first colony if (a [indCol_1 * Nm].f < a [indCol_2 * Nm].f) { int temp = indCol_1; indCol_1 = indCol_2; indCol_2 = temp; } // Copy the best solution to the worst colony ArrayCopy (a [indCol_2 * Nm + Nm - 1].cP, a [indCol_1 * Nm].cP, 0, 0, WHOLE_ARRAY); // Re-sort the colony after migration SortFromTo (a, aT, indCol_2 * Nm, Nm); } } //——————————————————————————————————————————————————————————————————————————————
The SortFromTo method of the C_AO_CPA class is designed to sort an array of agents based on their values of the f function. Let's take a closer look:
Initialization of variables:
- The method takes three parameters: p array of agents, pTemp temporary array, "from" sorting start index and "count" number of elements for sorting.
- The variables cnt, t0 and t1 are used to track the number of exchanges and temporarily store values.
- The ind and val arrays are created to store the indices and values of the f fitness function respectively.
Filling arrays of indices and values. In the first "for" loop, the ind and val arrays are filled:
- ind[i] gets the index of the agent in the source array, starting from "from".
- val[i] gets the value of the f function for the corresponding agent.
Sorting. The main "while" loop is executed as long as there are exchanges (i.e. cnt > 0). The inner "for" loop iterates through the val array and compares adjacent values:
- If the current one is less than the next one (val[i] < val[i + 1]), the indices in the ind array and the values in the val array are exchanged.
- The cnt counter is incremented to indicate that the exchange has occurred.
- This process continues until a complete iteration is performed without exchanges.
Copying sorted values:
- After sorting is complete, the first "for" loop copies the sorted agents from the temporary pTemp array back to the original p array, starting from the "from" index.
- The second "for" loop updates the original p array, replacing it with the sorted values.
//—————————————————————————————————————————————————————————————————————————————— // Auxiliary function for sorting agents by the value of the objective function void C_AO_CPA::SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count) { int cnt = 1; int t0 = 0; double t1 = 0.0; int ind []; double val []; ArrayResize (ind, count); ArrayResize (val, count); // Copy values for sorting for (int i = 0; i < count; i++) { ind [i] = i + from; val [i] = p [i + from].f; } // Bubble sort in descending order while (cnt > 0) { cnt = 0; for (int i = 0; i < count - 1; i++) { if (val [i] < val [i + 1]) { // Exchange of indices t0 = ind [i + 1]; ind [i + 1] = ind [i]; ind [i] = t0; // Exchange values t1 = val [i + 1]; val [i + 1] = val [i]; val [i] = t1; cnt++; } } } // Apply the sorting results for (int i = 0; i < count; i++) pTemp [i] = p [ind [i]]; for (int i = from; i < from + count; i++) p [i] = pTemp [i - from]; } //——————————————————————————————————————————————————————————————————————————————
After writing and thoroughly analyzing the algorithm code, we will move on to the results of testing the CPA algorithm.
Test results
When implementing the interesting and unique logic of the algorithm, I did not even consider that it would not make it to the top of the ranking table, and there was some disappointment when examining the results of the CPA algorithm testing in detail. Based on the testing results, the algorithm scored at most 34.76% of the maximum possible result.
CPA|Cyclic Parthenogenesis Algorithm|50.0|10.0|0.2|0.9|0.3|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7166412833856777
25 Hilly's; Func runs: 10000; result: 0.4001377868508138
500 Hilly's; Func runs: 10000; result: 0.25502012607456315
=============================
5 Forest's; Func runs: 10000; result: 0.6217765628284961
25 Forest's; Func runs: 10000; result: 0.3365148812759322
500 Forest's; Func runs: 10000; result: 0.192638189788532
=============================
5 Megacity's; Func runs: 10000; result: 0.34307692307692306
25 Megacity's; Func runs: 10000; result: 0.16769230769230772
500 Megacity's; Func runs: 10000; result: 0.09455384615384692
=============================
All score: 3.12805 (34.76%)
The visualization demonstrates the algorithm's characteristic movement of virtual aphids in the search space. This is especially noticeable for high-dimensional problems; individual colonies and the movement of virtual creatures within them can even be identified by eye.
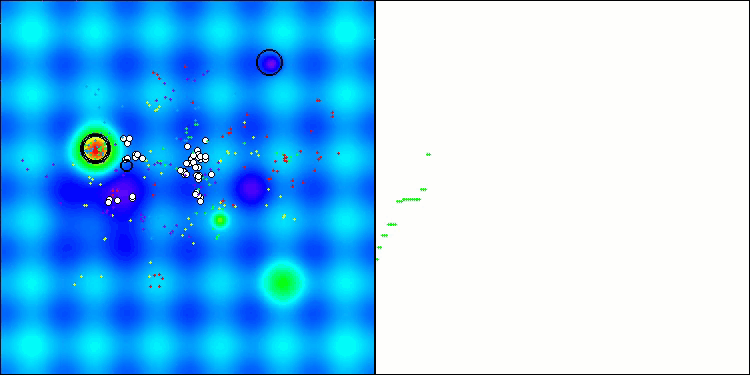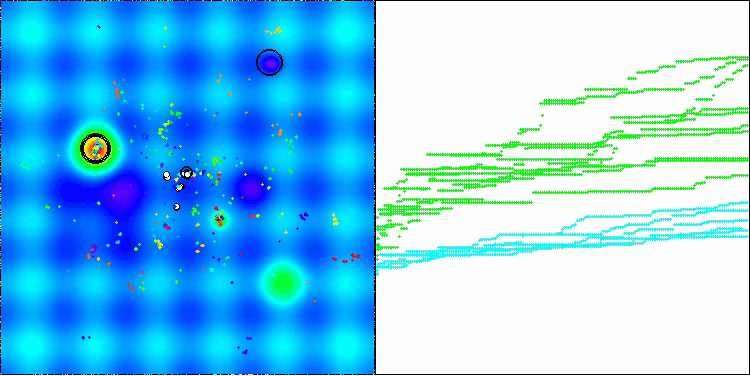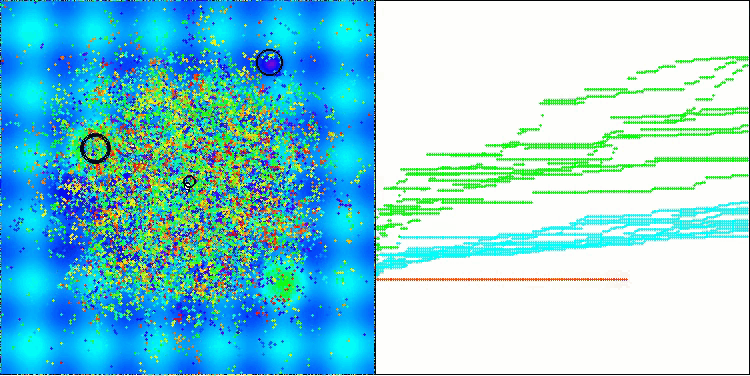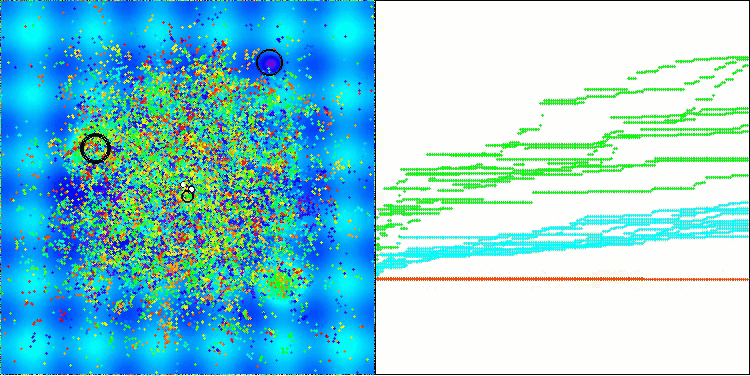
CPA on the Hilly test function
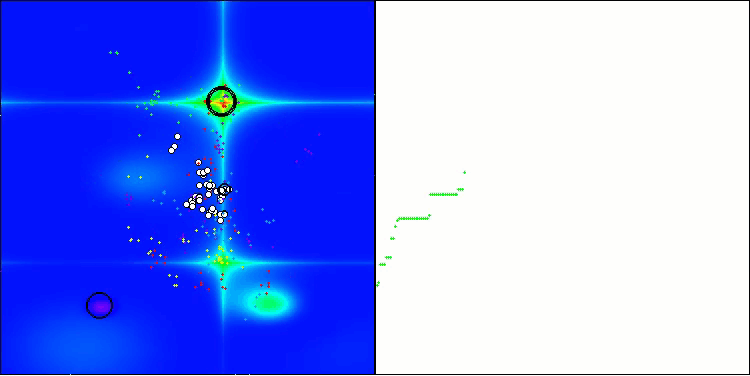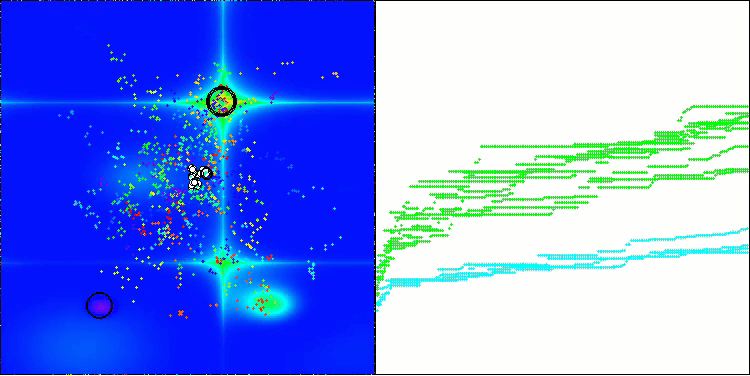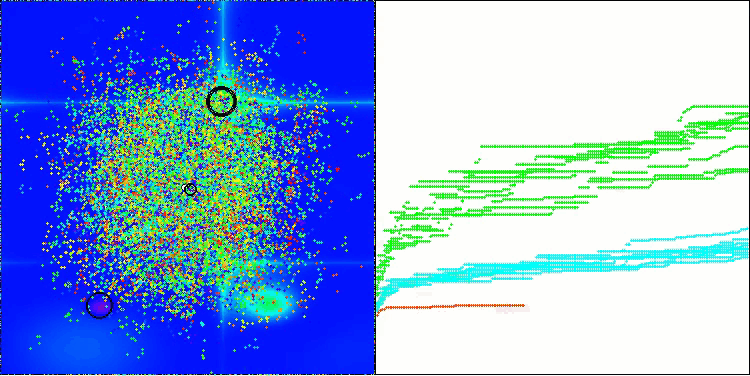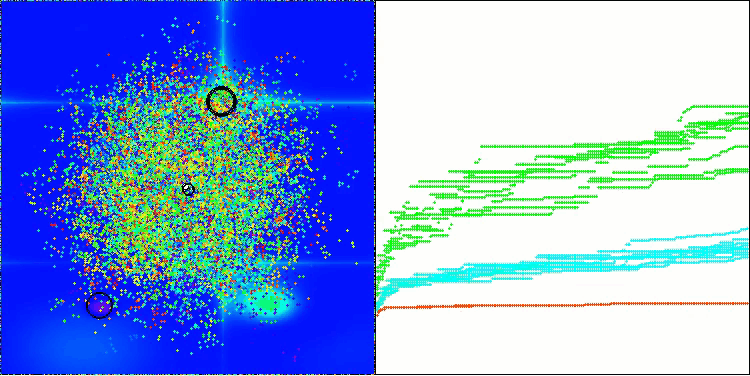
CPA on the Forest test function
CPA on the Megacity test function
After testing, the CPA algorithm ranked 44th in the ranking table and entered the group of 45 best population optimization algorithms.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 13 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | BBBC | big bang-big crunch algorithm | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1.08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 44 | CPA | cyclic parthenogenesis algorithm | 0.71664 | 0.40014 | 0.25502 | 1.37180 | 0.62178 | 0.33651 | 0.19264 | 1.15093 | 0.34308 | 0.16769 | 0.09455 | 0.60532 | 3.128 | 34.76 |
| 45 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| RW | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Summary
Work on the implementation and testing of the CPA algorithm allowed us to make interesting observations and conclusions. The algorithm is a population-based optimization method based on aphid behavior, and while the idea itself appears promising, test results show relatively low performance compared to other population-based algorithms.
The main idea of the algorithm is to use two types of reproduction (with and without mating) and to divide the population into colonies with the possibility of migration between them. The biological metaphor here is quite elegant: aphids actually use both parthenogenesis and sexual reproduction, adapting to environmental conditions. However, the mathematical implementation of these concepts turned out to be not as effective as desired.
The algorithm's weaknesses manifest themselves in several aspects. Firstly, dividing individuals in a population into females and males does not provide sufficient diversity and quality of solutions. Secondly, division into colonies, although intended to facilitate exploration of different regions of the search space, in practice often leads to premature convergence to local optima. The efficiency of the intercolony flight mechanism that should counteract this effect turned out to be low.
Tuning the algorithm parameters is also a non-trivial task. Parameters, such as colony size (Nm), proportion of females (Fr), flight probability (Pf) and scaling factors (alpha1, alpha2), significantly affect the performance of the algorithm and finding their optimal values is difficult. Attempts to improve the algorithm by introducing adaptive parameters resulted in some improvements, but failed to significantly increase its efficiency. This suggests that the problem may be more fundamental and related to the structure of the algorithm itself.
However, working on this algorithm was useful in several ways. Firstly, it provided good experience in analyzing and implementing a bioinspired algorithm. Secondly, the process of debugging and optimization helped to better understand the importance of the balance between exploration of the search space and exploitation of the found solutions in metaheuristic algorithms. Third, this is a good example of how a beautiful biological analogy does not always translate into an effective optimization algorithm.
In conclusion, it is worth noting that even the least successful algorithms contribute to the development of the field of metaheuristic optimization by providing new ideas and approaches that can be used in the development of more efficient methods. Despite its limitations, CPA demonstrates an interesting approach to balancing between different solution search strategies and can serve as a starting point for further research in this direction.
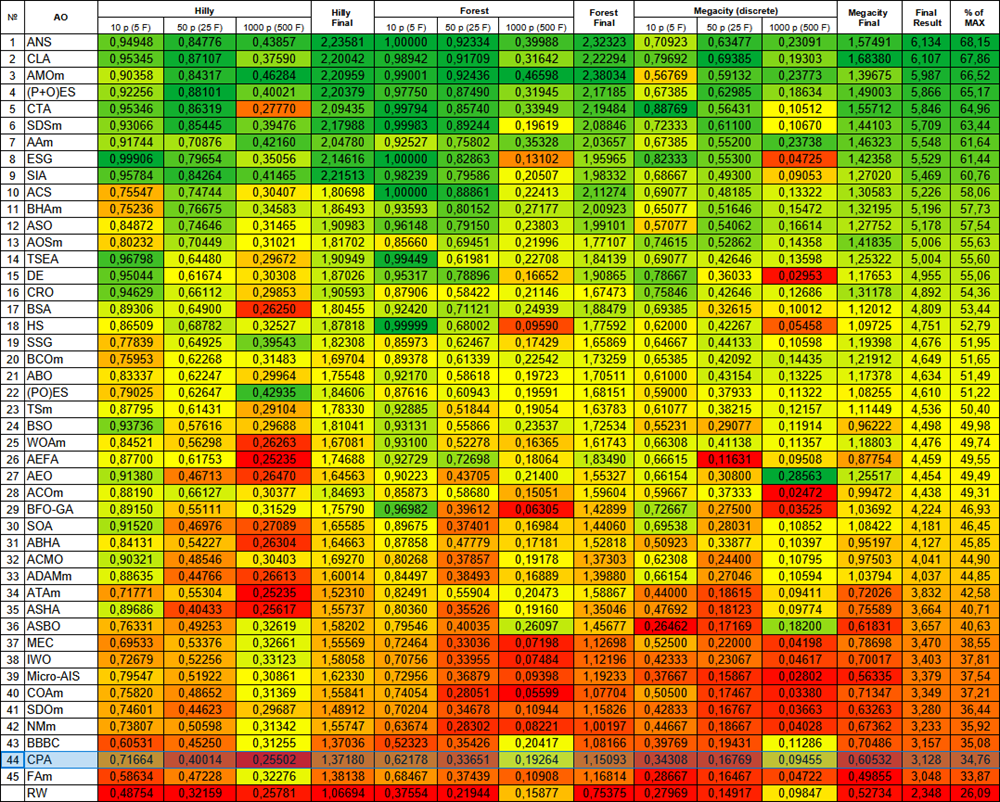
Figure 3. Color gradation of algorithms according to the corresponding tests
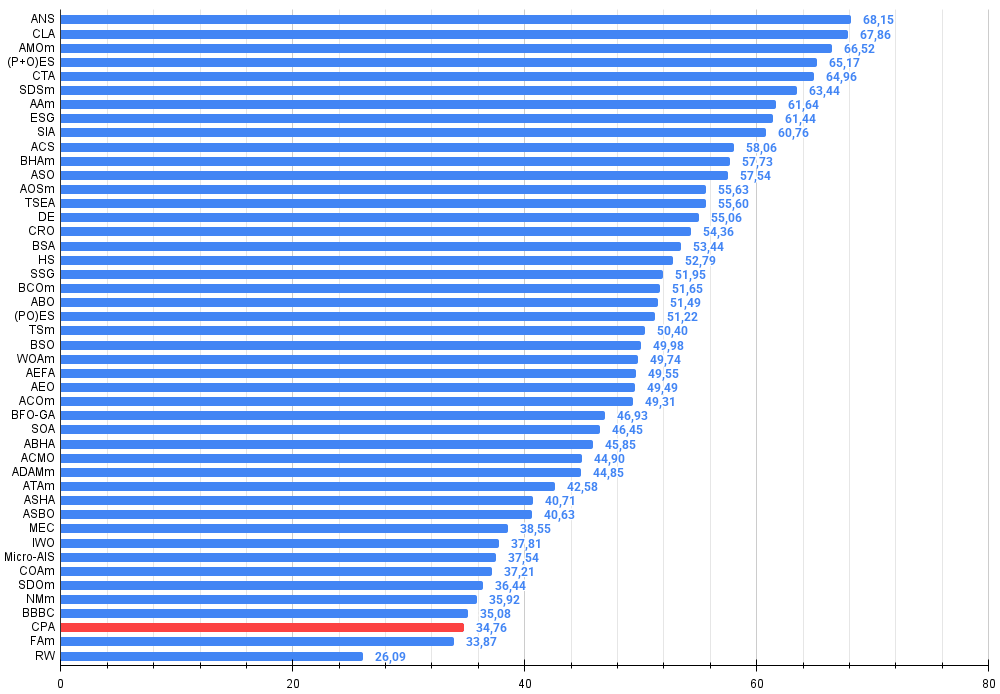
Figure 4. Histogram of algorithm testing results (scale from 0 to 100, the higher the better, where 100 is the maximum possible theoretical result, in the archive there is a script for calculating the rating table)
CPA pros and cons:
Pros:
- Interesting idea.
- Quite a simple implementation.
- Works well on large-scale problems.
Disadvantages:
- Many external parameters.
- Low speed and convergence accuracy.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Parent class of population optimization algorithms |
| 2 | #C_AO_enum.mqh | Include | Enumeration of population optimization algorithms |
| 3 | TestFunctions.mqh | Include | Library of test functions |
| 4 | TestStandFunctions.mqh | Include | Test stand function library |
| 5 | Utilities.mqh | Include | Library of auxiliary functions |
| 6 | CalculationTestResults.mqh | Include | Script for calculating results in the comparison table |
| 7 | Testing AOs.mq5 | Script | The unified test stand for all population optimization algorithms |
| 8 | Simple use of population optimization algorithms.mq5 | Script | A simple example of using population optimization algorithms without visualization |
| 9 | Test_AO_CPA.mq5 | Script | CPA test stand |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/16877
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
Features of Custom Indicators Creation
Automating Trading Strategies in MQL5 (Part 34): Trendline Breakout System with R-Squared Goodness of Fit
Features of Experts Advisors
Statistical Arbitrage Through Cointegrated Stocks (Part 5): Screening
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use