MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
循环孤雌生殖算法（CPA）

循环孤雌生殖算法（CPA）

MetaTrader 5 — 测试者 |
248 0
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法实现
  3. 测试结果


概述

受自然现象启发的优化算法仍在解决复杂优化问题中扮演重要角色。其中基于社会性昆虫（如蚂蚁、蜜蜂、蚜虫）行为的算法尤为引人关注。此前我们已讨论过ACOm与ABHA等类似算法，本文则提出循环孤雌生殖算法（CPA），它模拟蚜虫独特的生殖策略。

蚜虫因兼具无性（孤雌生殖）与有性生殖而表现出惊人适应性。当环境良好时，以孤雌生殖快速扩增种群。当环境恶化时，会转为有性生殖，促进遗传多样性以提高存活机会。

CPA 在数学上模拟这些生物机制，平衡对已发现解的利用（孤雌生殖）与对搜索空间新区域的探索（有性生殖）。该算法还模仿蚜虫的社会行为，在群体内组织决策并实施群体间迁移机制，实现信息交换。

上述特性使 CPA 在需要平衡局部与全局搜索的多维优化问题中尤为高效。本文将详细探讨其原理、数学模型及实际应用。该算法由Ali Kaveh与Zolghadr提出。于2019年首次发表。


算法实现

想象您在花园中观察蚜虫群体。这些微小生物使用两种生殖方式，对环境适应极为有效。CPA正是模拟这种行为以解决复杂优化问题。其如何工作？在初始阶段创建若干群体（集群），每个群体包含“雌”与“雄”个体。

算法提供两种生成新解的方式：
    • 第一种方式是“自体复制”，通过最优解产生自身副本并附带微小的修改。
    • 第二种方式是“配对繁殖”，通过两个不同解组合生成新解。

    有时，某群体的最优解会“迁飞”至另一群体。算法持续评估哪些解最优，保存最优发现，并在搜索过程中结合成功选项。目的是最终找到最优点。其关键在于平衡利用已发现的优良解与搜索全新选项，正如蚜虫对环境变化的适应。

    CPA

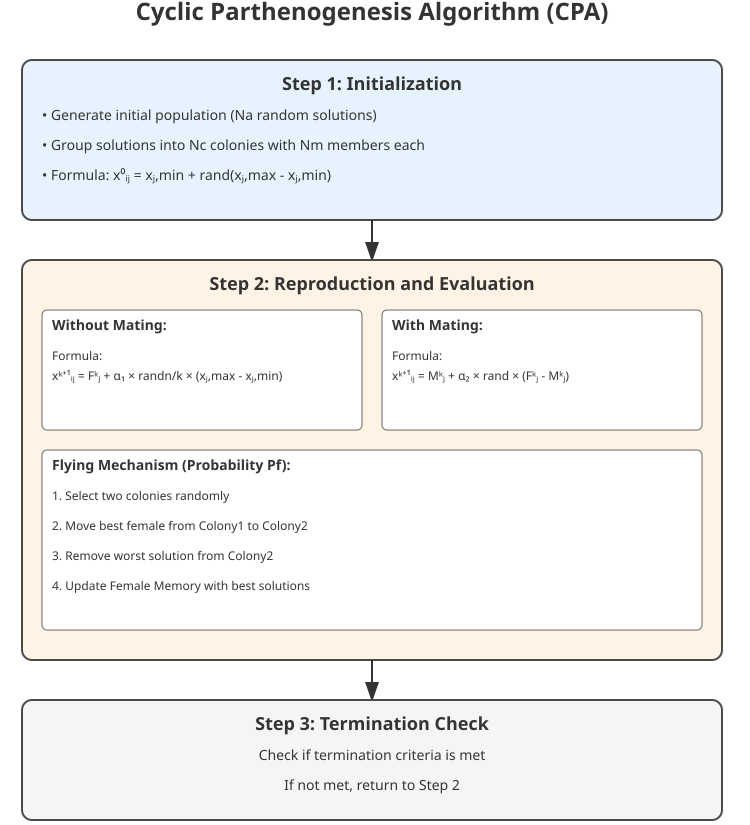
    图例1. CPA算法操作结构、基础方程

    让我们来看一下CPA算法的可视化表示，图中主要元素包括群体，粉色方块表示雌性个体（解），蓝色方块表示雄性个体（解），虚线表示群体间的飞行路径。该图展示了群体的结构、繁殖机制、群体间的飞行以及群体内个体的相互作用。这将通过与蚜虫真实行为的可视化类比，帮助更好地理解该算法的原理。

    CPA算法图示

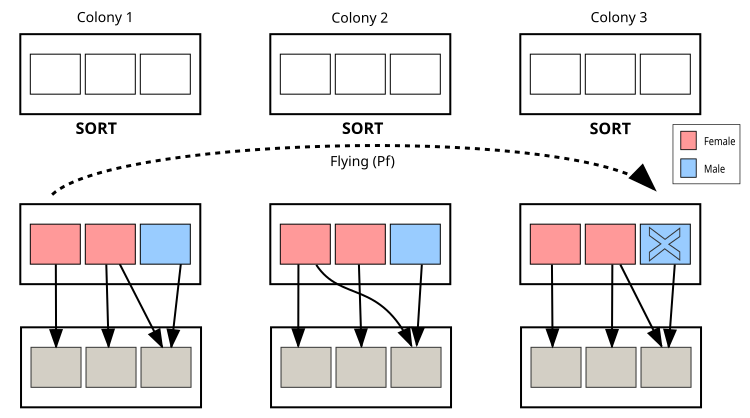
    图例2. CPA算法中的蚜虫群体及其相互作用

    现在我们已经对算法描述有了更深入地了解，让我们继续编写伪代码：

    初始化：
    创建包含Na个个体的种群
    将种群划分为Nc个群体

    在每个群体中：
    确定雌性个体的数量（Fr * Nm）
    确定雄性个体的数量（其余个体）

    设置初始参数：
    alpha1（孤雌生殖比例）
    alpha2（交配比例）
    Pf（飞行概率）

    主循环（针对每个时期）：
    在每个群体中：
    针对雌性个体：

    通过孤雌生殖更新位置：
    新位置 = 当前位置 + alpha1 * k * N(0,1) * （最大范围 - 最小范围）
    其中，k = （总时期数 - 当前时期数）/ 总时期数
    N(0,1)——正态分布

    针对雄性个体：
    从同一群体中随机选择一个雌性个体
    通过配对更新位置：
    新位置 = 当前位置 + alpha2 * 随机数[0,1] * （雌性个体位置 - 当前位置）

    位置修订：
    更新找到的最优解
    保存当前位置
    根据目标函数值对每个群体中的个体进行排序

    迁移（根据Pf概率）：
    随机选择两个群体
    比较它们的最优解
    将最优解移动到最差的群体中
    重新对群体中的个体进行排序

    一切准备就绪，可以编写算法代码了，继续。让我们编写继承自C_AO类的C_AO_CPA类。该类实现了整个算法，以下是其组件的简要描述：

    C_AO_CPA构造函数：

    • 设置参数，如种群大小、群体数量、雌性比例、飞行概率以及孤雌生殖和交配的缩放因子。
    • 预留一个参数数组并给其赋值。

    SetParams方法从“params”数组中设置参数值，并将它们转换为适当的类型。 

    Init、Moving和Revision方法：

    • Init用于使用指定的范围和时期数初始化算法。
    • Moving和Revision方法实现了算法内部的移动和修订逻辑。

    类成员由存储算法参数的变量定义，如群体数量、雌雄比例以及控制过程的参数。

    私有成员包括跟踪当前时期、群体成员数量以及临时智能体数组的变量。

    //——————————————————————————————————————————————————————————————————————————————
// Class implementing the Cyclic Parthenogenesis Algorithm (CPA)
// Inherited from the optimization base class
class C_AO_CPA : public C_AO
{
  public:
  C_AO_CPA (void)
  {
    ao_name = "CPA";
    ao_desc = "Cyclic Parthenogenesis Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16877";

    popSize = 50;       // total population size Na

    Nc      = 10;       // number of colonies
    Fr      = 0.2;      // ratio of female individuals
    Pf      = 0.9;      // probability of flight between colonies
    alpha1  = 0.3;      // scaling factor for parthenogenesis
    alpha2  = 0.9;      // scaling factor for pairing

    ArrayResize (params, 6);

    // Setting algorithm parameters
    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "Nc";          params [1].val = Nc;
    params [2].name = "Fr";          params [2].val = Fr;
    params [3].name = "Pf";          params [3].val = Pf;
    params [4].name = "alpha1_init"; params [4].val = alpha1;
    params [5].name = "alpha2_init"; params [5].val = alpha2;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;

    Nc      = (int)params [1].val;
    Fr      = params      [2].val;
    Pf      = params      [3].val;
    alpha1  = params      [4].val;
    alpha2  = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   ();         // function for moving individuals
  void Revision ();         // function for reviewing and updating positions

  //----------------------------------------------------------------------------
  int    Nc;                // number of colonies
  double Fr;                // ratio of female individuals
  double Pf;                // probability of flight between colonies

  private: //-------------------------------------------------------------------
  int    epochs;            // total number of epochs
  int    epochNow;          // current epoch
  int    Nm;                // number of individuals in each colony
  double alpha1;            // scaling factor for parthenogenesis
  double alpha2;            // scaling factor for pairing
  int    fNumber;           // number of females in the colony
  int    mNumber;           // number of males in the colony

  S_AO_Agent aT [];         // temporary colony for sorting
  void SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count); // agent sorting function
};
//——————————————————————————————————————————————————————————————————————————————

    实现C_AO_CPA类的Init方法，其功能如下：

    方法参数：

    • rangeMinP、rangeMaxP、rangeStepP——分别定义搜索范围的最小值、最大值以及搜索步长的数组。
    • epochsP——迭代次数（默认值为 0）。
    方法逻辑：
    • 该方法首先调用StandardInit方法，使用传入的范围进行标准初始化。若初始化失败，该方法会返回"false"。
    • 设置总迭代数和当前迭代数（epochNow）。
    • 根据种群大小和群体数量计算群体中的成员数量（Nm）。
    • 确定群体中的雌性个体数量（fNumber），确保其不小于1。通过总成员数与雌性个体数的差值计算雄性个体数量（mNumber）。
    • 预留“aT”数组以存储临时群体智能体。
    返回值：
    • 如果初始化成功，该方法返回“true”。

      此方法为算法的运行设置参数和结构，确保在算法开始执行前进行正确的初始化。

      //——————————————————————————————————————————————————————————————————————————————
// Initialization of the algorithm with the given search parameters
bool C_AO_CPA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;
  // Calculating the colony size and the number of individuals of each gender
  Nm       = popSize / Nc;
  fNumber  = int(Nm * Fr); if (fNumber < 1) fNumber = 1;
  mNumber  = Nm - fNumber;

  ArrayResize (aT, Nm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      C_AO_CPA类的Moving方法会根据特定规则和随机因素，在解空间中移动智能体，调整其坐标。让我们逐步了解一下：

      迭代数递增。该方法首先将当前迭代数（epochNow）递增，这表示优化或进化过程又前进了一步。

      第一阶段（如果无需修订） ——如果“revision”字段设置为“false”，则对种群（popSize）中的每个智能体的坐标进行初始化：

      • 每个智能体（a[i]）使用RNDfromCI函数在各个维度（coords）上获取新坐标，该函数会在给定范围[rangeMin[c], rangeMax[c]]内生成随机值。
      • 然后，使用SeInDiSp函数对坐标进行修改，该函数会根据离散化步长（rangeStep[c]）对值进行校正。
      • 将“revision”标识设置为“true”，之后方法终止。
        第二阶段（如果需要修订）——如果“revision”设置为“true”，则根据智能体之前的坐标和一些随机成分来调整坐标：
        • 计算变量k，即剩余时期数与总时期数的比值。这样，随着优化接近完成，智能体的移动范围会逐渐缩小。
        • 遍历群体（col）和雌性代理数量（fNumber），根据群体中前fNumber个智能体之前的坐标（cP），加上使用正态分布生成的随机值，来更新这些智能体的坐标。该值在rangeMin和rangeMax之间进行缩放。
        • 对于剩余的智能体（从fNumber到Nm的m），也更新其坐标，但这次是根据同一群体中某个最优智能体而随机选择的坐标。在考虑alpha2参数的情况下，向每个智能体的坐标添加随机值。
        行为逻辑：
        • 该方法的总体目标是根据智能体之前的坐标，在解空间中移动智能体，并为区域探索注入随机性元素，以提高找到全局最优解的可能性。
        • alpha1和alpha2等参数有助于控制适应程度和随机性。

          因此，在优化算法的上下文中，Moving方法对于让智能体在解空间中移动至关重要，它同时考虑了智能体自身的先前位置和其他智能体的位置。

          //——————————————————————————————————————————————————————————————————————————————
// The main function for moving individuals in the search space
void C_AO_CPA::Moving ()
{
  epochNow++;
  //----------------------------------------------------------------------------
  // Initial random initialization of positions if this is the first iteration
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate a random position in a given range
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Calculate the search power decay rate over time
  double k    = (epochs - epochNow)/(double)epochs;
  int    ind  = 0;
  int    indF = 0;

  // Handling each colony
  for (int col = 0; col < Nc; col++)
  {
    // Updating the positions of female individuals (parthenogenesis)
    for (int f = 0; f < fNumber; f++)
    {
      ind = col * Nm + f;

      for (int c = 0; c < coords; c++)
      {
        // Parthenogenetic position update using normal distribution
        a [ind].c [c] = a [ind].cP [c] + alpha1 * k * u.GaussDistribution (0.0, -1.0, 1.0, 8) * (rangeMax [c] - rangeMin [c]);
      }
    }

    // Update positions of males (mating)
    for (int m = fNumber; m < Nm; m++)
    {
      ind = col * Nm + m;

      // Select a random female for mating
      indF = u.RNDintInRange (ind, col * Nm + fNumber - 1);

      for (int c = 0; c < coords; c++)
      {
        // Update position based on the selected female
        a [ind].c [c] = a [ind].cP [c] + alpha2 * u.RNDprobab () * (a [indF].cP [c] - a [ind].cP [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

          C_AO_CPA类的Revision方法负责根据智能体的f函数值更新种群中智能体的状态。让我们来详细了解一下：

          初始化——该方法首先将“ind”变量初始化为“-1”，该变量将用于存储f函数值最佳的智能体的索引。

          寻找最佳智能体——在第一个“for”循环中，遍历种群（popSize）中的所有智能体，如果当前智能体（a[i].f）的f函数值大于当前的最优fB值，则：

          • 用a[i].f更新fB。
          • 将最优智能体的索引存储在“ind”变量中。
          • 循环完成后，如果找到了f函数值更优的智能体（ind != -1），则将其坐标（c）复制到cB数组中。

          复制当前坐标。第二个“for”循环将每个智能体的当前坐标（c）复制到其先前的坐标（cP）中。这样，就可以保存智能体的先前状态，以便进一步分析。

          对智能体进行排序。第三个“for”循环遍历所有群体（Nc），并对每个群体调用SortFromTo方法，该方法根据代理的f函数值对群体内的代理进行排序。排序索引计算为（ind = col * Nm）。

          概率性更新。该方法检查由u.RNDprobab()函数生成的随机值是否小于阈值Pf：

          • 如果满足条件，则选择两个不同的随机群体索引（indCol_1和indCol_2）。
          • 比较这两个群体中智能体的f函数值。如果第一个群体中的函数值小于第二个群体中的函数值，则交换这两个索引。
          • 然后，将第一个群体中第一个智能体的坐标复制到第二个群体中最后一个智能体的坐标。
          • 之后，再次调用SortFromTo以更新第二个群体中智能体的顺序。

          总体逻辑：

          Revision方法用于更新智能体的状态，存储有关最优智能体的信息，并提供群体之间交换信息的能力。

          //——————————————————————————————————————————————————————————————————————————————
// Function for revising positions and exchanging information between colonies
void C_AO_CPA::Revision ()
{
  // Find and update the best solution
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  // Save the current positions
  for (int i = 0; i < popSize; i++)
  {
    ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY);
  }

  // Sort individuals in each colony by the target function value
  for (int col = 0; col < Nc; col++)
  {
    ind = col * Nm;
    SortFromTo (a, aT, ind, Nm);
  }

  // Mechanism of flight (migration) between colonies
  if (u.RNDprobab () < Pf)
  {
    int indCol_1 = 0;
    int indCol_2 = 0;

    // Select two random different colonies
    indCol_1 = u.RNDminusOne (Nc);
    do indCol_2 = u.RNDminusOne (Nc);
    while (indCol_1 == indCol_2);

    // Ensure that the best solution is in the first colony 
    if (a [indCol_1 * Nm].f < a [indCol_2 * Nm].f)
    {
      int temp = indCol_1;
      indCol_1 = indCol_2;
      indCol_2 = temp;
    }

    // Copy the best solution to the worst colony
    ArrayCopy (a [indCol_2 * Nm + Nm - 1].cP, a [indCol_1 * Nm].cP, 0, 0, WHOLE_ARRAY);

    // Re-sort the colony after migration
    SortFromTo (a, aT, indCol_2 * Nm, Nm);
  }
}
//——————————————————————————————————————————————————————————————————————————————

          C_AO_CPA类的SortFromTo方法旨在根据代理的f函数值对代理数组进行排序。让我们来详细了解一下：

          变量初始化：

          • 该方法接受三个参数：代理数组p、临时数组pTemp、“from”排序起始索引以及用于排序的元素数量“count”。
          • 变量cnt、t0和t1用于跟踪交换次数并临时存储值。
          • 创建数组ind和val，分别用于存储f适应度函数的索引和值。

          填充索引和值数组。在第一个“for”循环中，填充ind和val数组：

          • ind[i]获取源数组中从“from”开始的智能体索引。
          • val[i]获取相应智能体的f函数值。

          排序。只要存在交换（即cnt > 0），就会执行主“while”循环。内部“for”循环遍历val数组并比较相邻值：

          • 如果当前值小于下一个值（val[i] < val[i + 1]），则交换ind数组中的索引和val数组中的值。
          • cnt计数器递增，以表示发生了交换。
          • 此过程持续进行，直到完成一次没有交换的迭代。

          复制排序后的值：

          • 排序完成后，第一个“for”循环将排序后的智能体从临时数组pTemp复制回原始数组p，从“from”索引开始。
          • 第二个“for”循环更新原始数组p，用排序后的值替换它。
          //——————————————————————————————————————————————————————————————————————————————
// Auxiliary function for sorting agents by the value of the objective function
void C_AO_CPA::SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count)
{
  int    cnt = 1;
  int    t0  = 0;
  double t1  = 0.0;
  int    ind [];
  double val [];
  ArrayResize (ind, count);
  ArrayResize (val, count);

  // Copy values for sorting
  for (int i = 0; i < count; i++)
  {
    ind [i] = i + from;
    val [i] = p [i + from].f;
  }

  // Bubble sort in descending order
  while (cnt > 0)
  {
    cnt = 0;
    for (int i = 0; i < count - 1; i++)
    {
      if (val [i] < val [i + 1])
      {
        // Exchange of indices
        t0 = ind [i + 1];
        ind [i + 1] = ind [i];
        ind [i] = t0;

        // Exchange values
        t1 = val [i + 1];
        val [i + 1] = val [i];
        val [i] = t1;

        cnt++;
      }
    }
  }

  // Apply the sorting results
  for (int i = 0;    i < count; i++)        pTemp [i] = p [ind [i]];
  for (int i = from; i < from + count; i++) p     [i] = pTemp  [i - from];
}
//——————————————————————————————————————————————————————————————————————————————

          在编写并深入分析算法代码之后，我们将转向CPA算法的测试结果。


          测试结果

          在实现该算法有趣且独特的逻辑时，我甚至都没想过它无法在排名表中名列前茅，而在仔细审视CPA算法的测试结果时，我感到有些失望。根据测试结果，该算法最多达到最大可能结果的 34.76%。

          CPA|Cyclic Parthenogenesis Algorithm|50.0|10.0|0.2|0.9|0.3|0.9|
          =============================
          5 Hilly's; Func runs: 10000; result: 0.7166412833856777
          25 Hilly's; Func runs: 10000; result: 0.4001377868508138
          500 Hilly's; Func runs: 10000; result: 0.25502012607456315
          =============================
          5 Forest's; Func runs: 10000; result: 0.6217765628284961
          25 Forest's; Func runs: 10000; result: 0.3365148812759322
          500 Forest's; Func runs: 10000; result: 0.192638189788532
          =============================
          5 Megacity's; Func runs: 10000; result: 0.34307692307692306
          25 Megacity's; Func runs: 10000; result: 0.16769230769230772
          500 Megacity's; Func runs: 10000; result: 0.09455384615384692
          =============================
          总分：3.12805 (34.76%)

          该图展示了算法中虚拟蚜虫在搜索空间内的典型移动特征。对于高维问题而言，这一点尤为明显；甚至用肉眼就能分辨出各个群体以及群体内虚拟生物的移动情况。

          Hilly值

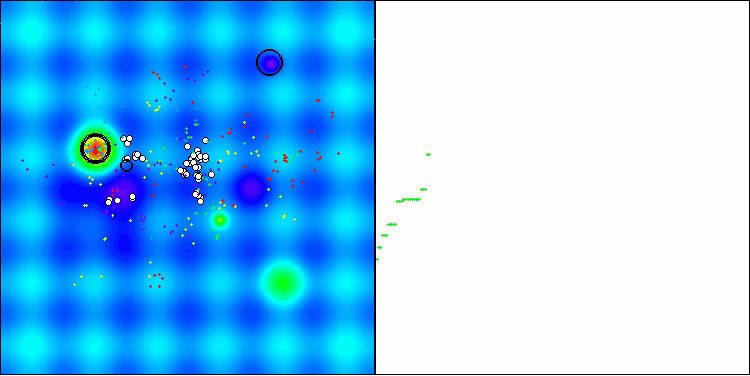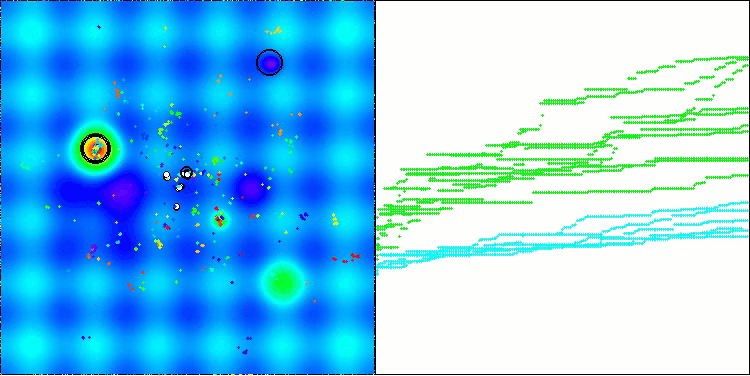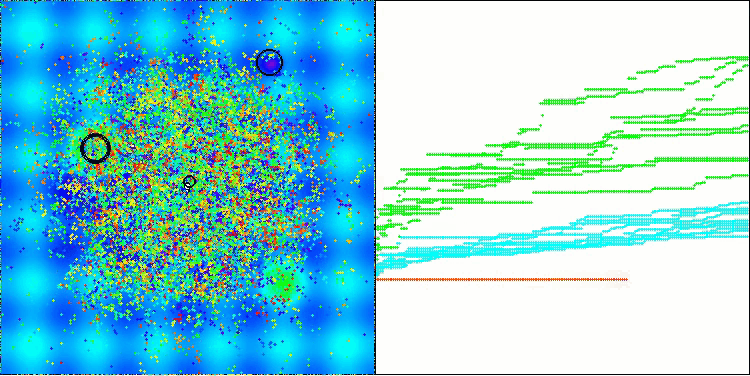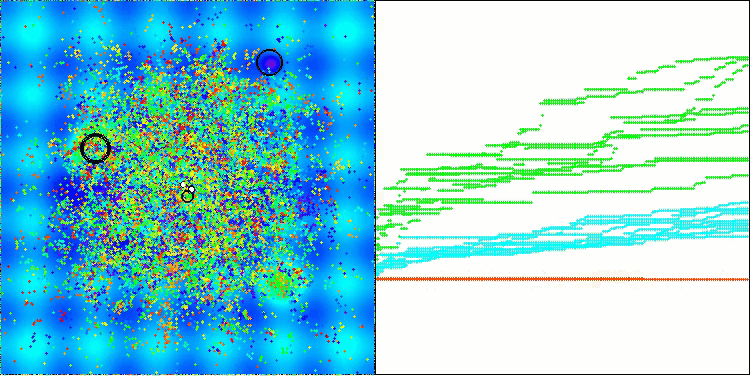
            CPA在Hilly测试函数上

          Forest值

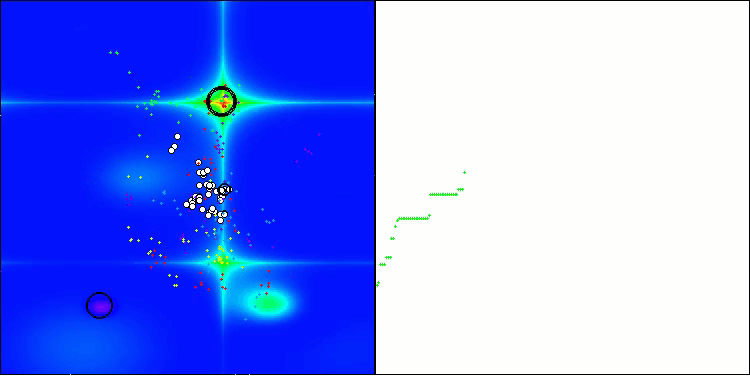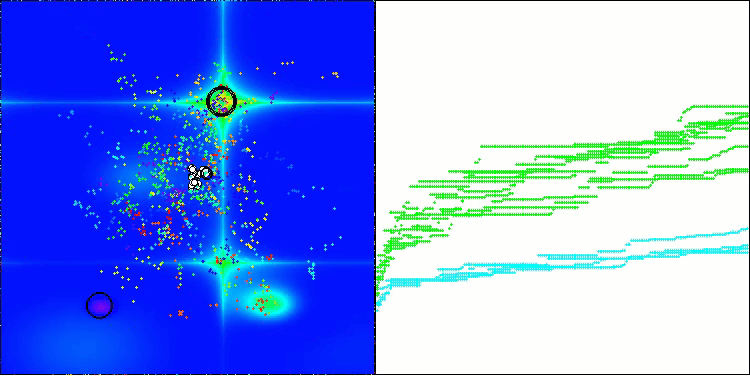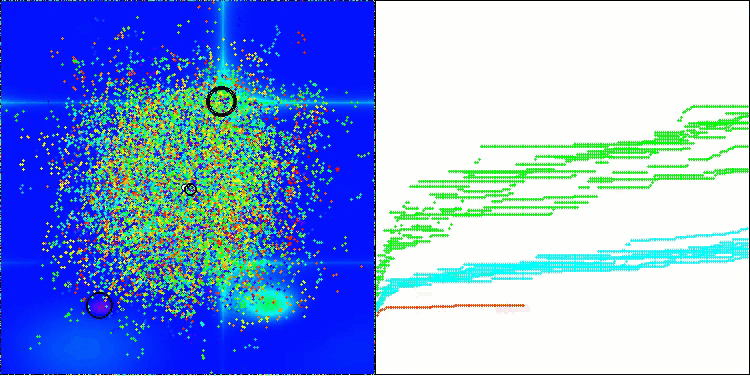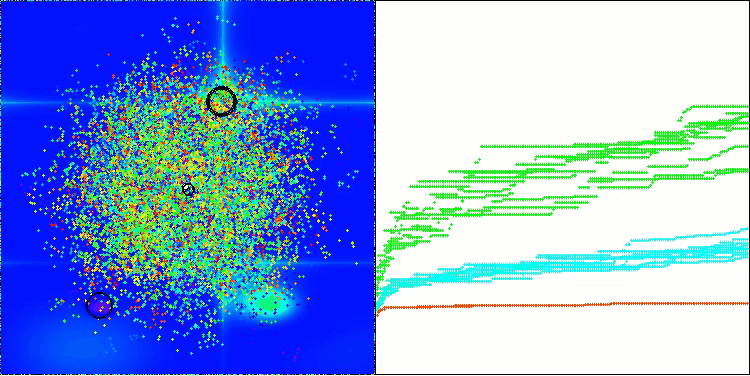
            CPA在Forest测试函数上

          Megacity值

            CPA在Megacity测试函数上

          测试结束后，CPA算法在排名表中位列第44名，跻身45种最优群体优化算法之列。

          # AO 描述 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
          10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
          1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
          2 CLA 密码锁算法（joo） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
          3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
          4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
          5 CTA 彗星尾算法（joo） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
          6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
          7 AAm 射箭算法M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
          8 ESG 社会群体的进化（joo） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
          9 SIA 模拟各向同性退火（joo） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
          10 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
          11 BHAm 黑洞算法M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
          12 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
          13 AOSm 原子轨道搜索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
          14 TSEA 龟壳演化算法（joo） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
          15 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
          16 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
          17 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
          18 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
          19 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
          20 BCOm 细菌趋化性优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
          21 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
          22 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
          23 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
          24 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
          25 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
          26 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
          27 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
          28 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
          29 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
          30 SOA 简单优化算法 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
          31 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
          32 ACMO 大气云模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
          33 ADAMm 群体自适应矩估计M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
          34 ATAm 人工部落算法M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
          35 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
          36 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
          37 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
          38 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
          39 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
          40 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
          41 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
          42 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
          43 BBBC 大爆炸-大坍缩算法 0.60531 0.45250 0.31255 1.37036 0.52323 0.35426 0.20417 1.08166 0.39769 0.19431 0.11286 0.70486 3.157 35.08
          44 CPA 循环孤雌生殖算法 0.71664 0.40014 0.25502 1.37180 0.62178 0.33651 0.19264 1.15093 0.34308 0.16769 0.09455 0.60532 3.128 34.76
          45 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
          RW 随机游走 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09




          总结

          基于CPA算法实现与测试工作，我们得以做出一些有趣的观察并得出相应的结论。该算法是一种基于蚜虫行为的群体优化方法，尽管这一想法本身看似颇具潜力，但测试结果表明，与其他群体优化算法相比，其性能相对较低。

          该算法的主要思路是采用两种繁殖方式（有性繁殖和无性繁殖），并将种群划分为多个群体，群体间存在迁移的可能性。这里的生物学隐喻相当巧妙：蚜虫实际上既采用孤雌生殖（无性繁殖）又采用有性生殖，以适应环境条件。然而，这些概念在数学层面的实现效果却并不尽如人意。

          该算法的弊端体现在多个方面。首先，将种群中的个体划分为雌性和雄性，并不能提供足够多样化的解决方案以及高质量的解。其次，划分群体虽然旨在促进对搜索空间不同区域的探索，但在实践中，却常常导致过早收敛至局部最优解。本应抵消这一影响的群体间迁移机制，其效率却很低。

          调整算法参数也并非易事。诸如群体规模（Nm）、雌性比例（Fr）、迁移概率（Pf）以及缩放因子（alpha1、alpha2）等参数，均会显著影响算法的性能，而找到它们的最优值十分困难。尝试通过引入自适应参数来改进算法，虽取得了一些进展，但并未显著提升其效率。这表明，问题可能更加基本，与算法本身的结构有关。

          然而，研究该算法在多个方面仍颇具价值。首先，它为分析和实现生物启发式算法提供了宝贵的经验。其次，调试和优化过程有助于我们更深入地理解在元启发式算法中，搜索空间探索与已发现解的利用之间保持平衡的重要性。第三，这是一个很好的例证，说明完美的生物学行为，并不总能转化为有效的优化算法。 

          总之，值得注意的是，即便是最不成功的算法，也能通过提供可应用于开发更高效方法的新思路和新途径，为元启发式优化领域的发展做出贡献。尽管CPA算法存在局限性，但它展示了一种在不同解搜索策略之间实现平衡的有趣方法，并可作为该方向进一步研究的起点。

          标签

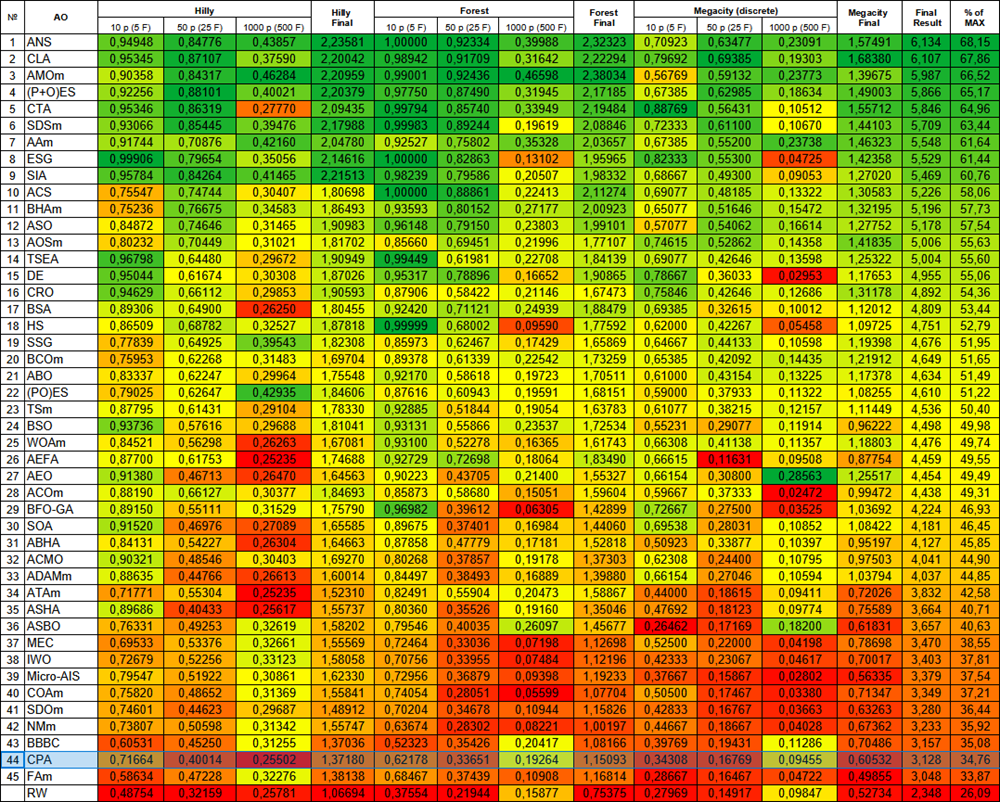
          图例3. 算法在相应测试中的颜色渐变表示

          图表

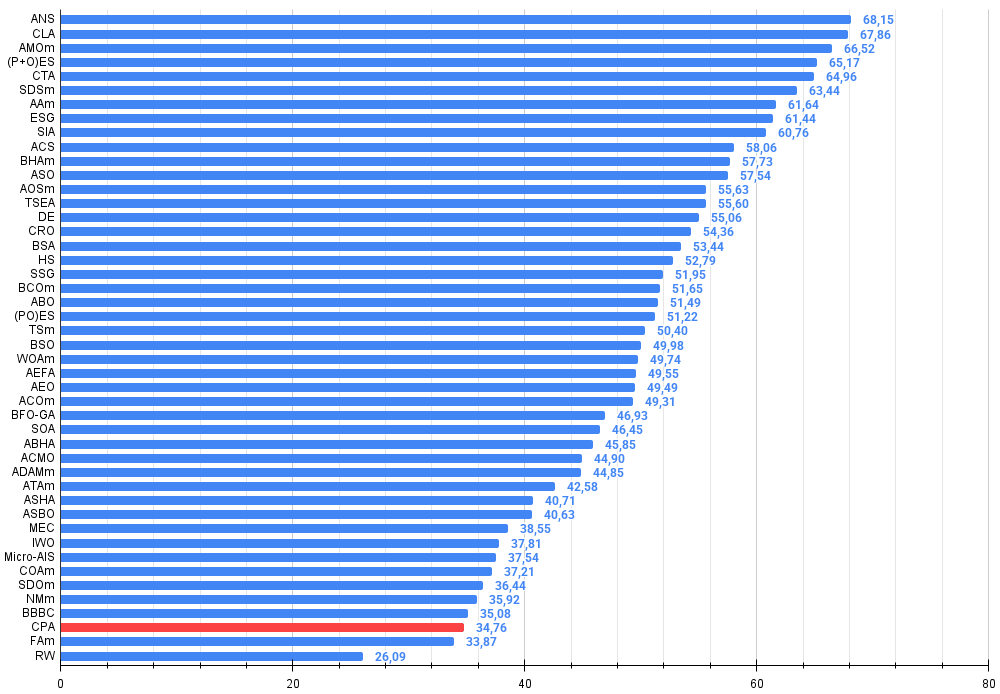
          图例4. 算法测试结果的直方图（评分范围为0到100，越高越好，其中100为理论上的最高可能得分，档案中附有计算排名表的脚本）

          CPA的优缺点：

          优点：

          1. 这是个有趣的理念。
          2. 实现起来相当简单。
          3. 在大规模问题中表现优异。

          缺点：

          1. 许多外部参数。
          2. 低速和低收敛精度。

          文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

          文中所用的程序

          # 名称 类型 描述
          1 #C_AO.mqh
          		 库
          		 种群优化算法的基类
          2 #C_AO_enum.mqh
          		 库
          		 种群优化算法的枚举说明
          3 TestFunctions.mqh
          		 库
          		 测试函数库
          4
          		 TestStandFunctions.mqh
          		 库
          		 测试台函数库
          5
          		 Utilities.mqh
          		 库
          		 辅助函数库
          6
          		 CalculationTestResults.mqh
          		 库
          		 用于计算比较表结果的脚本
          7
          		 Testing AOs.mq5
          		 脚本 面向所有种群优化算法的统一测试平台
          8
          		 Simple use of population optimization algorithms.mq5
          		 脚本
          		 种群优化算法非可视化简易使用案例
          9
          		 Test_AO_CPA.mq5
          		 脚本 CPA测试

          本文由MetaQuotes Ltd译自俄文
          原文地址： https://www.mql5.com/ru/articles/16877

          附加的文件 |
          下载ZIP
          CPA.zip (153.67 KB)

          注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

          本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

          该作者的其他文章

          前往讨论
          黑洞算法（BHA） 黑洞算法（BHA）
          黑洞算法（BHA）利用黑洞引力原理来优化解。在本文中，我们将考察 BHA 如何在避免局部极端情况的同时，吸引最佳解，以及为什么该算法已成为解决复杂问题的强大工具。学习简单的思路如何在优化世界带来令人印象深刻的结果。
          开发回放系统（第 76 部分）：新 Chart Trade（三） 开发回放系统（第 76 部分）：新 Chart Trade（三）
          在本文中，我们将看看上一篇文章中缺少的 DispatchMessage 代码是如何工作的。我们还会介绍下一篇文章的主题。因此，在继续下一个主题之前，了解这段代码的工作原理非常重要。此处提供的内容仅用于教育目的。在任何情况下，除了学习和掌握所提出的概念外，都不应出于任何目的使用此应用程序。
          从基础到中级：定义（一） 从基础到中级：定义（一）
          在这篇文章中，我们将做一些许多人会觉得奇怪和完全脱离上下文的事情，但如果使用得当，这将使你的学习更加有趣：我们将能够根据这里显示的内容构建非常有趣的东西。这将使您更好地理解 MQL5 语言的语法。此处提供的材料仅用于教育目的。它不应以任何方式被视为最终应用程序。其目的不是探索所提出的概念。
          构建MQL5自优化智能交易系统（EA）（第四部分）：动态头寸规模调整 构建MQL5自优化智能交易系统（EA）（第四部分）：动态头寸规模调整
          成功运用算法交易需要持续的跨学科学习。然而，无限的可能性可能会耗费数年努力，却无法取得切实成果。为解决这一问题，我们提出一个循序渐进增加复杂性的框架，让交易者能够迭代优化策略，而非将无限时间投入不确定的结果中。