母集団最適化アルゴリズム：モンキーアルゴリズム(MA)

内容：

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

モンキーアルゴリズム（MA、Monkey Algorithm）は、メタヒューリスティクス探索アルゴリズムの1つです。本稿では、アルゴリズムの主要な構成要素について説明し、上昇（上向きの動き）、局所的ジャンプ、 大局的ジャンプの解決策を紹介します。このアルゴリズムは2007年にR. ZhaoとW. Tangによって提案されました。このアルゴリズムは、餌を求めて山を移動し、飛び越える猿の行動をシミュレートしています。山が高ければ高いほど、その頂上には食べ物がたくさんあることから生まれたと推測されています。

猿が探索する領域は適応度関数の地形なので、一番高い山が問題の解に相当します（大域最大化の問題を考慮）。現在の位置から、それぞれの猿は山の頂上まで移動していきます。上昇の過程は、目標関数の値を徐々に向上させるように設計されています。そして、猿はより高い山を見つけるために、ランダムな方向に局所的なジャンプを繰り返し、上昇の動きを繰り返します。ある一定回数の上昇と局所的ジャンプをおこなった後、猿は初期位置の周辺の地形を十分に探索したと考えるようになります。

探索空間の新しい領域を探索するために、猿は長い大局的ジャンプをおこないます。以上の手順をアルゴリズムパラメータで指定された回数だけ繰り返します。問題の解は、与えられた猿の集団が見つけた頂点のうち、最も高いものであると宣言されます。しかし、MAは上昇の過程で局所最適解を探索するため、多大な計算時間を費やしてしまいます。大局的ジャンプ処理により、アルゴリズムの収束速度を速めることができます。この過程の目的は、猿が局所的検索に陥らないように、新しい検索機会を見つけさせることです。このアルゴリズムには、構造が簡単で、比較的信頼性が高く、局所最適解をよく探索できるなどの利点があります。

MAは、非線形性、非微分性、高次元を特徴とする多くの複雑な最適化問題を解くことができる新しいタイプの進化的アルゴリズムです。他のアルゴリズムとの違いは、MAが費やした時間が、主に局所最適解を見つけるための上昇過程の使用によるものであることです。次のセクションでは、アルゴリズムの主な構成要素、提示された解決策、初期化、上昇、観察、ジャンプについて説明します。

2.アルゴリズム

モンキーアルゴリズムを理解しやすくするために、まず擬似コードから始めるのが合理的です。

モンキーアルゴリズムの擬似コードは次の通りです。

1.探索空間上に猿をランダムに配置します。
2.猿の位置の高さを測定します。
3.局所的ジャンプを一定回数おこないます。
4.ステップ3で得られた新しい頂点が上位であれば、この場所から局所的ジャンプをおこなうべきです。
5.局所的ジャンプの回数の限界を超え、新しい頂点が見つからない場合は、 大局的ジャンプをおこないます。
6.ステップ5以降、ステップ3を繰り返します。
7.停止基準を満たすまで、ステップ2から繰り返します。

擬似コードの各ポイントをより詳しく分析してみましょう。

1.最適化の最初の段階では、猿にとって探索空間は未知数です。餌の位置はどの場所でも同じ確率で決まるので、動物は未開の地にランダムに配置されます。

2.猿の位置の高さを測定する過程は、適応度関数のタスクの履行です。

3.局所的ジャンプをおこなう場合、アルゴリズムパラメータで指定された数の制限があります。つまり、猿は食品分野で局所的に小さなジャンプをすることで、現在の位置を向上させようとしているのです。新しく見つけた餌の供給源の方が良い場合は、ステップ4に進みます。

4.新しい餌が見つかったので、局所的ジャンプ回数がリセットされます。今度は、ここから新たな餌の供給源を探すことになります。

5.局地的ジャンプをしてもより良い餌の供給源を発見できない場合、猿は現在の領域を十分に探索したと判断し、より遠くの新しい場所を探す時期に来ていると判断します。この時点で、さらなるジャンプの方向性について疑問が生じます。このアルゴリズムのアイデアは、すべての猿の座標の中心を使用することで、何らかのコミュニケーション、つまり群れの中の猿同士のコミュニケーションを提供することです。猿は大声で叫ぶことができ、優れた空間聴覚を持っているので、親族の位置を正確に把握することができるのです。同時に、親族の位置を知ることで（親族は餌のない場所にはいない）、餌の最適な新位置をおおよそ計算できるため、この方向にジャンプすることが必要です。

オリジナルのアルゴリズムでは、猿はすべての猿の座標の中心と自分の現在位置を通る線に沿って 大局的ジャンプをおこないます。ジャンプの方向は、座標の中心に向かっても、中心から反対方向に向かってもよくなります。中心から反対方向へのジャンプは、すべての猿の近似座標で餌を見つけるという論理そのものに反するもので、これはアルゴリズムを使った私の実験でも確認できました。実際、これは50％の確率で大域最適からの距離が存在することになります。

練習の結果、ジャンプしない、あるいは逆方向にジャンプするよりも、座標の中心を越えてジャンプした方が得策であることがわかりました。一見すると、このような論理で必然的にそうなるのですが、すべての猿が一点に集中することは起こりません。実際、局所的ジャンプの限界を超えた猿は、中心より遠くジャンプすることで、集団内のすべての猿の位置を回転させます。このアルゴリズムに従う高等類人猿を精神的に想像すると、群れ自体がより豊かな食物源に向かって移動していくうちに、何匹かの群れが、群れの幾何学的な中心を時々飛び越えるのが見えるでしょう。この「群れ移動」の効果は、アルゴリズムのアニメーションで視覚的にはっきりと確認することができます（オリジナルのアルゴリズムではこの効果はなく、結果は悪化しています）。

6.大局的ジャンプをした猿は、新しい場所での餌源の位置を特定し始めます。停止基準が満たされるまで、このプロセスは継続されます。

アルゴリズムの全貌は、1つの図に簡単に収まります。図1では、猿の動きを数字付きの丸で表しています。それぞれの数字が、猿の新しい位置となります。小さな黄色の丸は、局所的ジャンプの失敗を表しています。6は、局所的ジャンプの限界を超え、新たな最適の位置が見つかっていない位置を示します。数字のない円は、群れの残りの位置を表しています。群れの幾何学的な中心は、座標(x,y)を持つ小さな円で示されます。

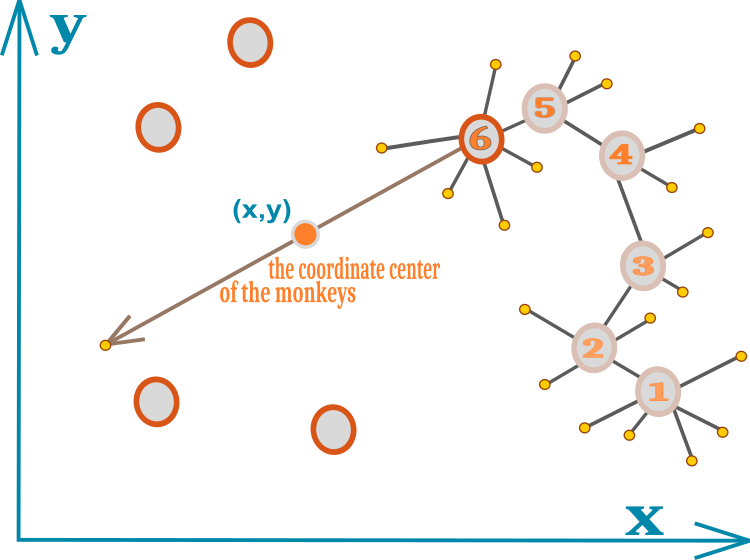
図1：群れの中の猿の動きを模式的に表現したもの

MAコードを見てみましょう。

群れ内の猿をS_Monkey構造体で記述すると便利です。この構造体には，現在の座標を表す c []配列，最良の食べ物座標を表す cB []配列（局所的ジャンプが発生するのは，この座標の位置から），h と hB（それぞれ現在の点の高さの値と最高点の値）． lCNT（位置を改善しようとする回数を制限する局所的ジャンプカウンタ）が含まれます。

//——————————————————————————————————————————————————————————————————————————————
struct S_Monkey
{
  double c  []; //coordinates
  double cB []; //best coordinates
  double h;     //height of the mountain
  double hB;    //best height of the mountain
  int    lCNT;  //local search counter
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_MAモンキーアルゴリズムクラスは、先に説明したアルゴリズムと何ら変わりません。猿の群れは、クラス内でm[]構造体の配列として表現されます。メソッドやメンバーのクラス内の宣言は、コード量としては少ないです。アルゴリズムが簡潔なので、他の多くの最適化アルゴリズムとは異なり、ここでは並び替えがありません。最適化されたパラメータの最大値、最小値、ステップを設定するための配列と、アルゴリズムの外部パラメータを渡すための定数変数が必要です。それでは、MAの主要なロジックを含むメソッドの解説に移りましょう。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MA
{
  //----------------------------------------------------------------------------
  public: S_Monkey m       []; //monkeys
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double hB;           //best height of the mountain

  public: void Init (const int    coordNumberP,     //coordinates number
                     const int    monkeysNumberP,   //monkeys number
                     const double bCoefficientP,    //local search coefficient
                     const double vCoefficientP,    //jump coefficient
                     const int    jumpsNumberP);    //jumps number

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordNumber;       //coordinates number
  private: int    monkeysNumber;     //monkeys number

  private: double b [];              //local search coefficient
  private: double v [];              //jump coefficient
  private: double bCoefficient;      //local search coefficient
  private: double vCoefficient;      //jump coefficient
  private: double jumpsNumber;       //jumps number
  private: double cc [];             //coordinate center

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

public Init()メソッドは、アルゴリズムを初期化するためのメソッドです。ここでは、配列の大きさを設定します。猿が見つけた最良の領域の品質を、可能な限り最小の「double」値で初期化し、MA構造配列の対応する変数についても同様の処理をおこなうことにします。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Init (const int    coordNumberP,    //coordinates number
                    const int    monkeysNumberP,  //monkeys number
                    const double bCoefficientP,   //local search coefficient
                    const double vCoefficientP,   //jump coefficient
                    const int    jumpsNumberP)    //jumps number
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  coordNumber   = coordNumberP;
  monkeysNumber = monkeysNumberP;
  bCoefficient  = bCoefficientP;
  vCoefficient  = vCoefficientP;
  jumpsNumber   = jumpsNumberP;

  ArrayResize (rangeMax,  coordNumber);
  ArrayResize (rangeMin,  coordNumber);
  ArrayResize (rangeStep, coordNumber);
  ArrayResize (b,         coordNumber);
  ArrayResize (v,         coordNumber);
  ArrayResize (cc,        coordNumber);

  ArrayResize (m, monkeysNumber);

  for (int i = 0; i < monkeysNumber; i++)
  {
    ArrayResize (m [i].c,  coordNumber);
    ArrayResize (m [i].cB, coordNumber);
    m [i].h    = -DBL_MAX;
    m [i].hB   = -DBL_MAX;
    m [i].lCNT = 0;
  }

  ArrayResize (cB, coordNumber);
}
//——————————————————————————————————————————————————————————————————————————————

最初のpublicメソッドであるMoving()は、各反復で実行する必要があり、モンキージャンプのロジックを実装しています。最初の反復では、「revision」フラグが「false」である場合、学習空間の座標範囲のランダムな値でエージェントを初期化する必要があり、これは群れの生息地内での猿のランダムな位置に相当します。大局的ジャンプや局所的ジャンプの係数の計算など、多重に繰り返される演算を減らすために、対応する座標の値（それぞれの座標は独自の次元を持つことができる）をv []配列とb []配列に格納します。各猿の局所的ジャンプのカウンタを0にリセットしてみましょう。 

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    for (int c = 0; c < coordNumber; c++)
    {
      m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      m [monk].c [c] = SeInDiSp  (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      m [monk].h     = -DBL_MAX;
      m [monk].hB    = -DBL_MAX;
      m [monk].lCNT  = 0;
    }
  }

  for (int c = 0; c < coordNumber; c++)
  {
    v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient;
    b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient;
  }

  revision = true;
}

すべての猿の座標中心を計算するには、座標数に対応した次元の配列cc []を使用します。ここでのアイディアは、猿の座標を足して、できた合計を個体数で割るというものです。したがって、座標の中心は、座標の算術平均となります。

//calculate the coordinate center of the monkeys----------------------------
for (int c = 0; c < coordNumber; c++)
{
  cc [c] = 0.0;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    cc [c] += m [monk].cB [c];
  }

  cc [c] /= monkeysNumber;
}

擬似コードによると、局所ジャンプの限界に達しない場合、猿はその場所から全方向に等確率でジャンプします。局所ジャンプの円の半径は，b[]配列の座標の次元に応じて再計算される局所ジャンプの係数で調節されます。

//local jump--------------------------------------------------------------
if (m [monk].lCNT < jumpsNumber) //local jump
{
  for (int c = 0; c < coordNumber; c++)
  {
    m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]);      
    m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

MAロジックの非常に重要な部分に移りましょう。アルゴリズムの性能は、 大局的ジャンプの実装に大きく依存します。この問題は、著者によって様々な角度からアプローチされ、様々な解決策が提示されています。研究によると、局所的ジャンプはアルゴリズムの収束にほとんど影響を与えないそうです。局所的な極値から「ジャンプ」するアルゴリズムの能力を決定するのは、 大局的ジャンプです。私の大局的ジャンプの実験では、この特殊なアルゴリズムで結果を向上させる有効なアプローチは1つしかありませんでした。

上では、座標の中心に向かってジャンプすることが望ましいと述べましたが、終点が中心より後ろにあり、中心と現在の座標の間にないことが望ましいとされています。このアプローチは、カッコウ最適化アルゴリズム(COA)についての記事で詳しく説明したレヴィフライトの式を適用しています。

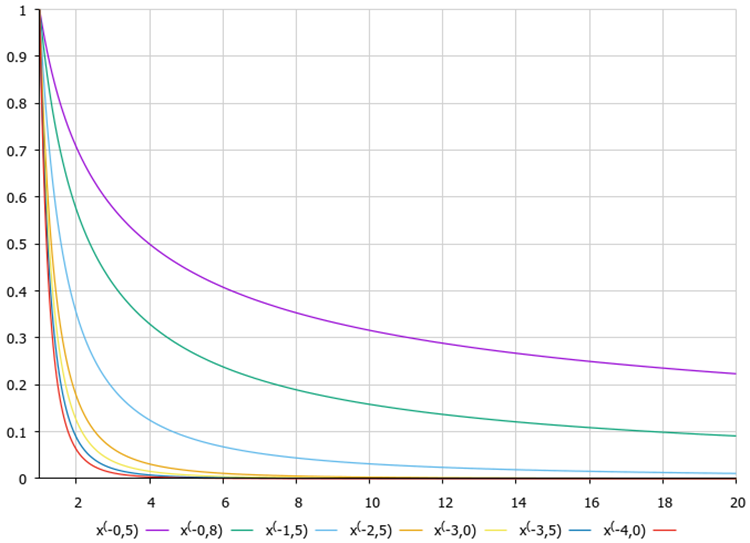
図2：方程式の度合いに応じたレヴィフライト関数のグラフ

モンキー座標は、以下の式で算出されます。

m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0)；

ここで

cc [c]：座標の中心の座標

v [c]：探索空間の次元に合わせて再計算されたジャンプ半径の係数

r2：1から20の範囲内の数値

この操作でレヴィフライトを適用することで、猿が座標の中心付近に当たる確率を高く、中心から遠く離れた場所にある確率を低くすることを実現しています。このように、研究と探索のバランスをとりながら、新しい餌の発掘をおこなっています。受信した座標が許容範囲の下限を超えている場合は、許容範囲の上限に対応する距離に座標を転送します。上限を超えている場合も同様です。座標計算の最後に、得られた値が境界線と研究ステップに適合しているかどうかを確認します。

//global jump-------------------------------------------------------------
for (int c = 0; c < coordNumber; c++)
{
  r1 = RNDfromCI (0.0, 1.0);
  r1 = r1 > 0.5 ? 1.0 : -1.0;
  r2 = RNDfromCI (1.0, 20.0);

  m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
          
  if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]);
  if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]);
          
  m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
}

局所的/大局的ジャンプをした後、ジャンプカウンタを1つ増やします。

m [monk].lCNT++;

Revision()は、適応度関数が計算された後、各反復で呼び出される2番目のpublicメソッドです。このメソッドは、より良い解が見つかった場合、 大局的解を更新します。局所的ジャンプと 大局的ジャンプの後の結果の処理ロジックは、それぞれ異なります。局所的ジャンプの場合は、現在位置が改善されたかどうかを確認して更新する必要があります（次の反復では、この新しい場所からジャンプがおこなわれます）が、 大局的ジャンプの場合は、改善の確認はありません。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Revision ()
{
  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    if (m [monk].h > hB)
    {
      hB = m [monk].h;
      ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY);
    }

    if (m [monk].lCNT <= jumpsNumber) //local jump
    {
      if (m [monk].h > m [monk].hB)
      {
        m [monk].hB = m [monk].h;
        ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
        m [monk].lCNT = 0;
      }
    }
    else //global jump
    {
      m [monk].hB = m [monk].h;
      ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
      m [monk].lCNT = 0;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

このアルゴリズムのアプローチは、粒子群(PSO)など、同様の検索戦略ロジックを持つ群知能アルゴリズム群に類似していることに気づくことができます。

3.テスト結果

MAテストスタンドの結果：

2023.02.22 19:36:21.841 Test_AO_MA (EURUSD,M1) C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:36:26.877 Test_AO_MA (EURUSD,M1) 5 Rastrigin's; Func runs 10000 result：64.89788419898215
2023.02.22 19:36:26.878 Test_AO_MA (EURUSD,M1) Score：0.80412
2023.02.22 19:36:36.734 Test_AO_MA (EURUSD,M1) 25 Rastrigin's; Func runs 10000 result：55.57339368461394
2023.02.22 19:36:36.734 Test_AO_MA (EURUSD,M1) Score：0.68859
2023.02.22 19:37:34.865 Test_AO_MA (EURUSD,M1) 500 Rastrigin's; Func runs 10000 result：41.41612351844293
2023.02.22 19:37:34.865 Test_AO_MA (EURUSD,M1) Score：0.51317
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:37:39.165 Test_AO_MA (EURUSD,M1) 5 Forest's; Func runs 10000 result：0.4307085210424681
2023.02.22 19:37:39.165 Test_AO_MA (EURUSD,M1) Score：0.24363
2023.02.22 19:37:49.599 Test_AO_MA (EURUSD,M1) 25 Forest's; Func runs 10000 result：0.19875891413613866
2023.02.22 19:37:49.599 Test_AO_MA (EURUSD,M1) Score：0.11243
2023.02.22 19:38:47.793 Test_AO_MA (EURUSD,M1) 500 Forest's; Func runs 10000 result：0.06286212143582881
2023.02.22 19:38:47.793 Test_AO_MA (EURUSD,M1) Score：0.03556
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:38:53.947 Test_AO_MA (EURUSD,M1) 5 Megacity's; Func runs 10000 result：2.8
2023.02.22 19:38:53.947 Test_AO_MA (EURUSD,M1) Score：0.23333
2023.02.22 19:39:03.336 Test_AO_MA (EURUSD,M1) 25 Megacity's; Func runs 10000 result：0.96
2023.02.22 19:39:03.336 Test_AO_MA (EURUSD,M1) Score：0.08000
2023.02.22 19:40:02.068 Test_AO_MA (EURUSD,M1) 500 Megacity's; Func runs 10000 result：0.34120000000000006
2023.02.22 19:40:02.068 Test_AO_MA (EURUSD,M1) Score：0.02843

テスト関数でのアルゴリズムの可視化に注目すると、動作にパターンがなく、RNDアルゴリズムと非常に似ていることがわかります。極値にエージェントが集中することがあり、アルゴリズムによる解の洗練を試みていることがわかりますが、明らかなピンチはありません。

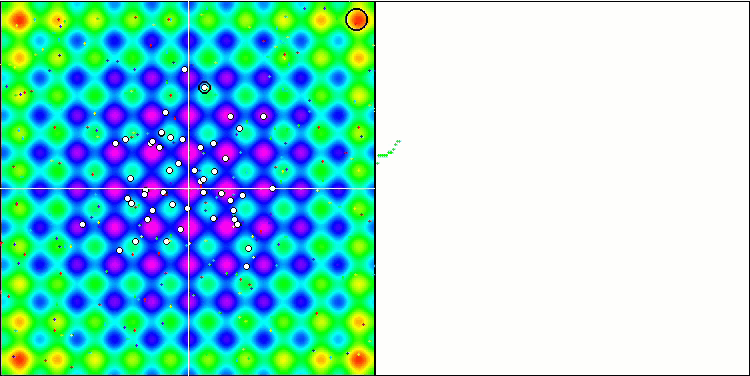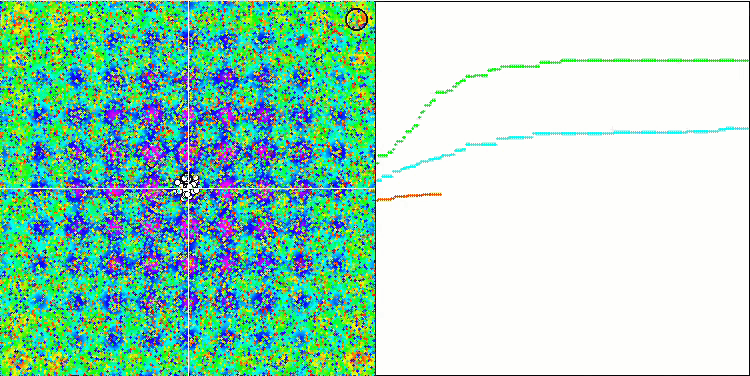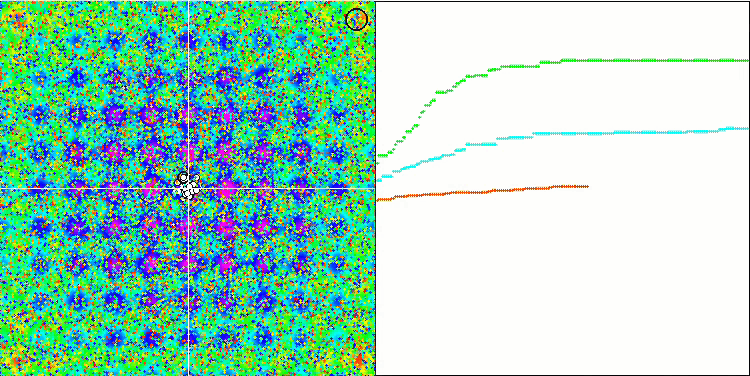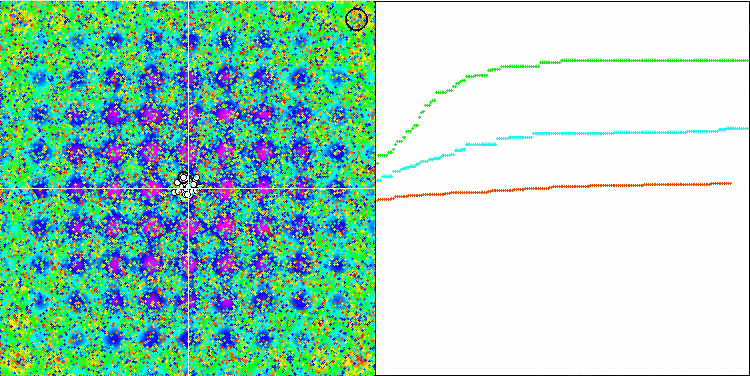
  Rastriginテスト関数のMA

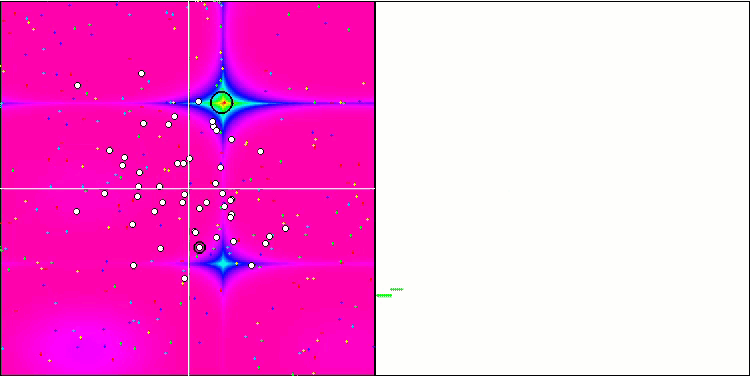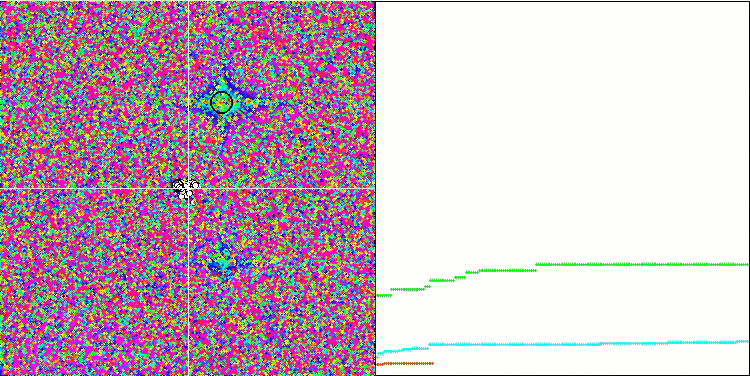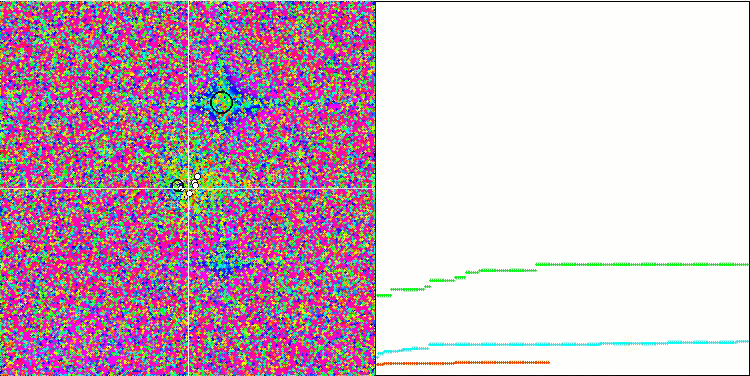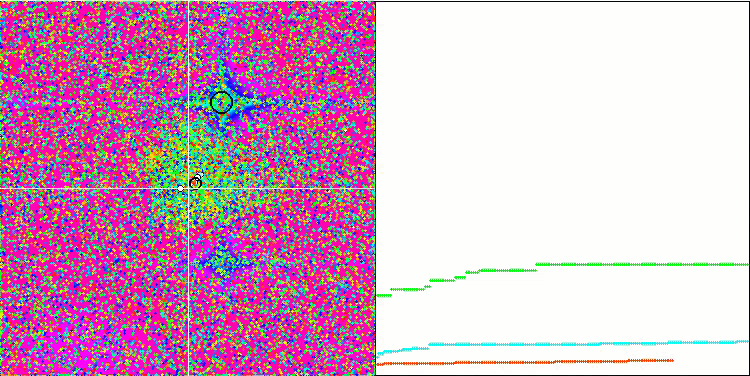
  Forestテスト関数のMA

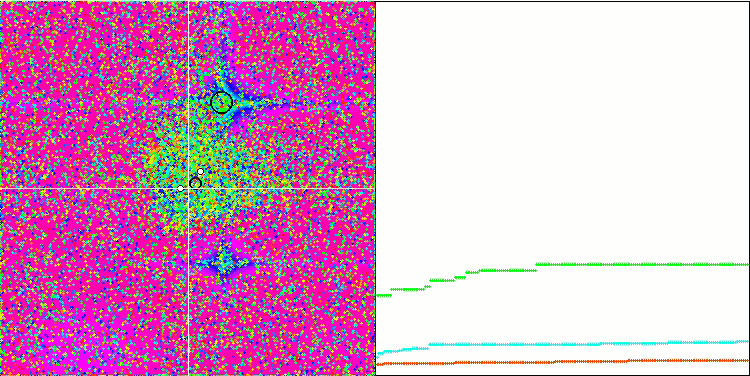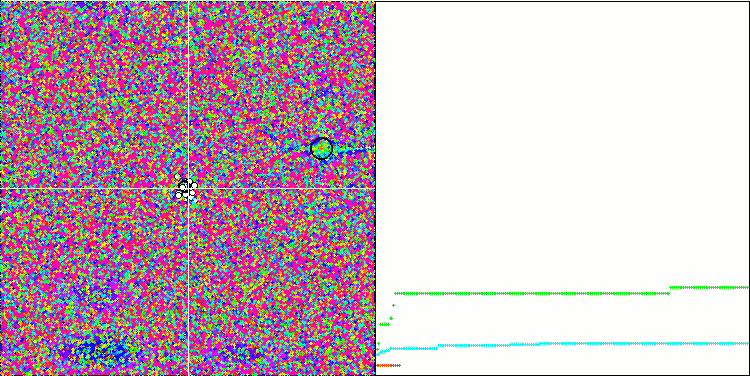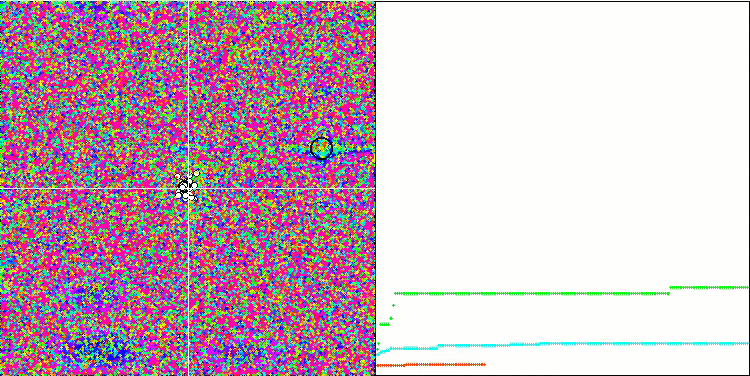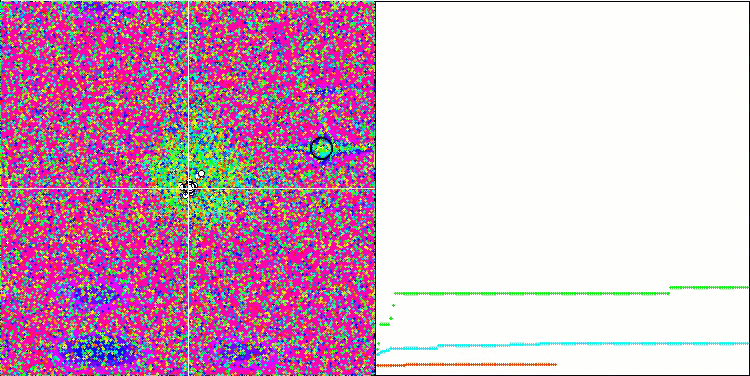
  Megacityテスト関数のMA

では、テスト結果の分析に移りましょう。採点結果によると、MAアルゴリズムはGSAとFSSの間で最下位に位置しています。アルゴリズムのテストは、結果のスコアがベストとワーストの相対値である比較分析原理に基づいているため、あるテストでは優れた結果を示し、他のテストでは悪い結果を示すアルゴリズムが出現すると、他のテスト参加者のパラメータが変化することがあります。

しかし、MAの結果によって、表中の他のテスト参加者の結果が再計算されることはありませんでした。MAには、相対的な結果がゼロで評価が高いアルゴリズム（例えばGSA）がありますが、最悪となるテスト結果は1つもありません。したがって、アルゴリズムの挙動はやや控えめで、探索能力の表現も十分とは言えませんが、安定した結果を示しており、最適化アルゴリズムとしては好ましい資質です。

AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity(discrete)			Megacity最終	最終結果
		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）
HS	ハーモニー検索	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.000
ACOm	蟻コロニー最適化M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	侵入雑草最適化	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	カッコウ最適化アルゴリズムM	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	ホタルアルゴリズムM	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	コウモリアルゴリズム	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	人工蜂コロニー	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	細菌採餌の最適化	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	重力探索法	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
MA	モンキーアルゴリズム	0.33300	0.35107	0.17340	0.85747	0.03684	0.07891	0.11546	0.23121	0.05838	0.00383	0.25809	0.32030	14.848
FSS	魚群検索	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	粒子群最適化	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	ランダム	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

まとめ

古典的なMAアルゴリズムは、基本的に上昇過程を利用して局所最適解を求めるものです。上昇ステップは、局所解の近似精度に決定的な役割を果たします。局所ジャンプの上昇ステップを小さくすればするほど解の精度は高くなりますが、大域的な最適値を求めるにはより多くの反復が必要になります。反復回数を減らして計算時間を短縮するために、多くの研究者は、最適化の初期段階でABC、COA、IWOなどの他の最適化手法を使用し、大域解を絞り込むためにMAを使用することを推奨しています。このやり方には賛成できません。MAには発展性があるため、さらなる実験や研究の対象として適していますが、MAではなく、今回紹介したアルゴリズムをすぐに使用する方が便利だと思います。 

モンキーアルゴリズムは、自然界にそのルーツを持つ集団ベースのアルゴリズムです。他の多くのメタヒューリスティクスアルゴリズムと同様に、このアルゴリズムも進化型であり、非線形性、非微分性、探索空間の高次元化など、多くの最適化問題を高い収束率で解くことができます。また、このアルゴリズムは、少ないパラメータで制御できるため、実装がかなり容易であることも利点です。結果は安定しているものの、収束率が低いためにかなりの回数の反復を必要であり、計算量の多い問題の解決にモンキーアルゴリズムを推奨することはできません。同じ作業をより短い時間（反復回数）でおこなうアルゴリズムは、他にもたくさんあります。

何度も実験しましたが、古典的なバージョンのアルゴリズムは、評価表の下から3行目より上に行くことができず、極値で立ち往生し、離散関数では極めて貧弱に動作しました。特に記事にするほどの思いはなかったので、改善するように心がけました。そのうちの1つは、 大局的ジャンプの確率バイアスを利用し、 大局的ジャンプの原理そのものを見直すことで、収束指標に一定の改善が見られ、結果の安定性が高まりました。MA研究者の多くがアルゴリズムの近代化の必要性を指摘しているため、このアルゴリズムには多くの改良が加えられています。MAというアルゴリズム自体が優れているわけではなく、むしろ粒子群(PSO)をアレンジしたものなので、MAのあらゆる改良を検討するのは本意ではありませんでした。その結果、この記事で紹介したアルゴリズムの最終版には、「m」（修正）マークが追加されませんでした。

アルゴリズムテスト結果のヒストグラムは以下の通りです。

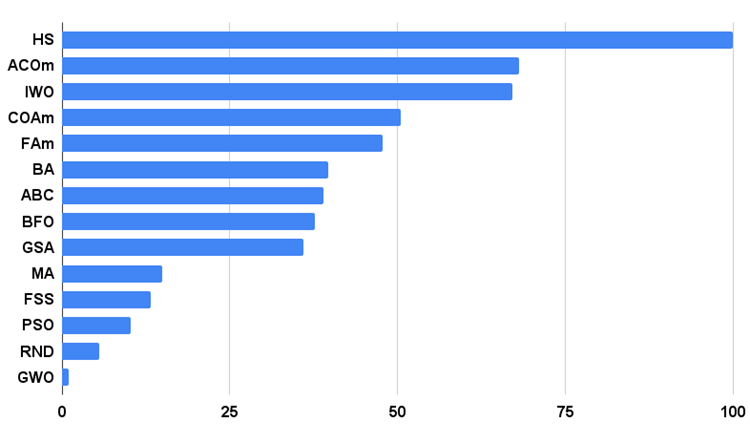
図3：アルゴリズムのテスト結果のヒストグラム

MAの長所と短所：

長所：
1.簡単に実装できる
2.収束率が低いにもかかわらず、良好なスケーラビリティを実現する
3.離散関数に対して良好な性能を発揮する
4.外部パラメータの数が少ない

短所：
1.収束率が低い
2.検索に大量の反復を必要とする
3.総合効率が低い

各記事には、過去の記事のアルゴリズムコードを最新版に更新したアーカイブが用意されています。本記事は、著者の蓄積された経験に基づくものであり、個人的な意見を述べたものです。結論や判断は、実験に基づくものです。