MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
母集団最適化アルゴリズム：ボイドアルゴリズム

母集団最適化アルゴリズム：ボイドアルゴリズム

MetaTrader 5 — 例 | 20 8月 2024, 12:25
145 0
Andrey Dik
Andrey Dik

内容

1.  はじめに
2.  アルゴリズムの説明
3.  テスト結果


1. はじめに

自然界の動物たちの群れ行動を観察していると、その連携のとれた効果的な相互作用に思わず感心してしまいます。まるで目に見えない力に支配されているかのように、彼らは同期してひとつの生命体として再編成し、障害を乗り越え、最適な道を見つけ出します。シンプルな相互作用のルールに基づく、この魅力的な動きのハーモニーは、多くのメタヒューリスティクス最適化アルゴリズムの創造にインスピレーションを与えてきた。

鳥の群れの複雑な移動ルートを研究することで、科学者たちは鳥が群知能アルゴリズムに似た原理に従っていることを発見しました。このように、魚の群れは生きた細胞のように、セル・オートマトンに基づく最適化手法を思わせる脈動構造を形成します。有蹄類の群れ行動、危険に対する協調反応、ムクドリの群れの同期された飛行などは、共同行動を調整する動物の驚くべき能力を表しています。

このような自然界の魅力的な例は、物流ルートの計画から効率的な制御システムの設計まで、複雑な問題を解決できる強力な最適化ツールにインスピレーションを与えています。

ボイドアルゴリズム（birdとoidの略、類似性）とは、1986年にクレイグ・レイノルズによって作られた、動物、特に鳥の群れの行動をモデル化したコンピュータアルゴリズムです。このアルゴリズムは、群れの自然な行動を模倣するように設計されており、各個体は単純なルールに従って動き、やがて集団行動が出現します。それは以下の3つのルールに基づいています。

1. 分離：各オブジェクト（「ボイド」）は、近くのオブジェクトとの衝突の可能性を最小限にしようとします。
2. 整列：各オブジェクトは、その移動方向が近くのオブジェクトの平均的な移動方向となるように努力します。
3. 結束：各オブジェクトは、その位置を近くのオブジェクトの平均位置に近づけようと努力します。

この3つのシンプルなルールによって、鳥の群れや昆虫の大群の複雑な行動をモデル化することができます。ボイドアルゴリズムは、鳥の群れ、昆虫の群れ、魚の群れのアニメーションを作成するために、コンピュータグラフィックスで広く使用されています。

オリジナルのボイドアルゴリズムには、いくつかの目的と用途がありました。

1. リアルなアニメーションの作成：ボイドアルゴリズムは、動物の群れのリアルなアニメーションを作成することを可能にし、コンピュータグラフィックスとアニメーションの発展に重要な方向性を与えました。
2. 行動モデリング：ボイドは、各個人の単純なルールに基づいて複雑な集団行動をシミュレートすることができます。これは、動物行動研究、ロボット工学、交通管理など、さまざまな分野で応用されています。

ボイドアルゴリズムは、粒子群最適化(PSO)や群衆行動モデリングアルゴリズムなど、他のアルゴリズムの開発に影響を与えました。

ボイドアルゴリズムは、集団行動をモデル化するための一般的なツールであり、科学技術のさまざまな分野で研究開発の対象となり続けています。

下のアニメーションでは、同じボイドの行動を見ることができます。ボイドはコンパクトなグループに集まったり、バラバラに飛んだり、隣のグループと速度を同期させたりすることができます。アニメーションを録画する際、アルゴリズムの設定はその場で変更され、対応する設定がボイドの挙動に与える影響を見ることができました。

ボイド

ボイドアルゴリズムの視覚化

config

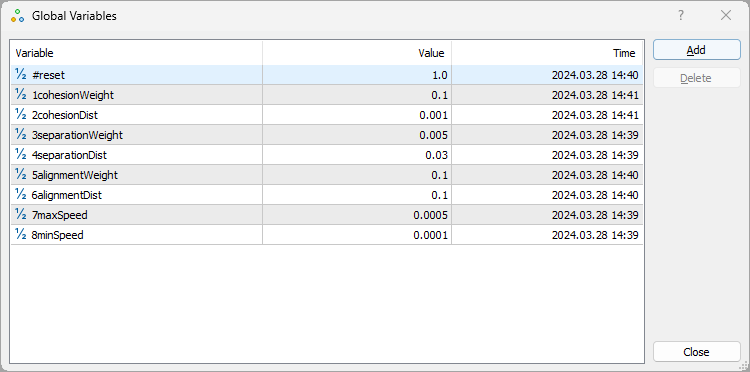
F3キーを押して呼び出されるボイドアルゴリズム設定ウィンドウ：パラメータ#resetにより、値1を適用してアルゴリズムを再開できる


2. アルゴリズム

クレイグ・レイノルズが開発したボイドアルゴリズムは、もともと鳥の群れや昆虫の群れなど、動物のあらゆる群れ行動をモデル化するために設計されました。しかし、その柔軟性と適応性により、このアルゴリズムは最適化や探索を含む様々な分野で応用されています。最適化と探索の文脈では、ボイドアルゴリズムは、エージェントグループの協調行動に関する問題を解くのに使用することができます。例えば、未知の領域を探索する大群の行動をモデル化するのに使用することができます。

しかし、ボイドアルゴリズム自体が、伝統的な意味での検索アルゴリズムではないことは注目に値します。これは、例えば勾配降下アルゴリズムや遺伝的アルゴリズムがそうであるように、与えられた解の可能な空間から最適解を見つけるようには設計されていません。その代わりに、ボイドアルゴリズムは、単純なルールのセットに基づいてエージェントのグループの行動をモデル化することで、グループレベルでの複雑で協調的な行動をモデル化することができます。

ボイドアルゴリズムは、関数の極値の分散探索に適応できます。この文脈では、それぞれのボイドは、可能な解の空間を移動する探索エージェントを表しています。各エージェントは、単に他の「ボイド」に従うのではなく、現在位置での関数の値を使用して、その動きを調整したり、集団内の他のボイドの適応度を考慮に入れたりすることができます。

クレイグ・レイノルズが群れ行動をシミュレートするボイドアルゴリズムを開発したことで、群知能の概念が生まれました。群知能は、分散型自己組織化システムの集団行動を記述するもので、PSOアルゴリズムを含みます。

群知能システムは通常、複数のエージェント（ボイド）が互いに、また環境と局所的に相互作用することで構成されます。行動学的なアイデアは一般的に自然から、特に生物学的システムから生まれます。それぞれのボイドは非常にシンプルなルールに従っています。中央集権的な行動制御システムはありませんが、局所的でややランダムな相互作用の結果、個々のボイドの制御を超えた知能的な集団行動が生まれます。

ボイドアルゴリズムには非常に多くの外部パラメータがあり、そのひとつひとつがボイドの動きの性質に大きく影響します。これらのパラメータを見てみましょう。

  1. cohesionWeight：凝集重量は、群れのメンバーが互いに引き合う力を決定します
  2. cohesionDist ：凝集距離は、群れのメンバーが互いに引き寄せられ始める距離を決定します
  3. separationWeight：分離重量は、群れのメンバーがどれだけ強く反発しあうかを決定します
  4. separationDist：分離距離は、群れのメンバーが互いに反発し始める距離を決定します
  5. alignmentWeight ：整列の重みは、群れのメンバーが互いの移動方向に対してどれだけ強く整列するかを決定します
  6. alignmentDist：整列距離は、群れのメンバー間の距離を決定します。群れのメンバーは、この距離で互いの移動方向に整列し始めます
  7. minSpeed：ボイドの停止を防ぐための最低速度
  8. maxSpeed ：ボイドの最大速度

これらのパラメータを調整し、望ましい群れの行動を得るために一連の実験をおこなうことが重要です。提案された値から始めて、群れの行動にどのような影響を与えるか、徐々に調整することができます。ボイドアルゴリズムには、絶対的な意味での「正しい」パラメータ値や「最良の」パラメータ値は存在しないことに注意してください。すべては特定のタスクとシナリオによります。

次にボイドアルゴリズムのコードを書きましょう。各エージェントを記述するために、S_Boids_Agent構造体を定義します。ここで何が起こっているのかを見てみましょう。


1. この構造体には以下のフィールドが含まれます。

  • x[]：現在のエージェント座標を格納する配列
  • dx[]：現在のエージェントスピードの配列
  • m：エージェントの質量

2. Init：S_Boids_Agent構造体フィールドを初期化する構造体メソッドこれは、ArrayResize関数を使用してxおよびdx配列のサイズを変更するために使用されるcoords整数引数を取ります。

このコードは、ボイドアルゴリズムにおけるエージェントの基本的なデータ構造を表し、新しいエージェントが作成されたときにそのフィールドを初期化します。これにより、各エージェントは独自の座標と速度を持つことができ、これはボイドアルゴリズムの重要な側面です。mフィールドは、ボイドを移動させる際の適応度関数表面を考慮するために私が主導して追加したもので、質量が適応度値となります。

//——————————————————————————————————————————————————————————————————————————————
struct S_Boids_Agent
{
    double x  [];
    double dx [];
    double m;

    void Init (int coords)
    {
      ArrayResize (x,  coords);
      ArrayResize (dx, coords);
    }
};
//——————————————————————————————————————————————————————————————————————————————

ボイドアルゴリズムのC_AO_Boidsクラスを定義しましょう。このクラスはC_AO母集団アルゴリズムの基本クラスを継承し、以下のフィールドとメソッドを含んでいます。

1. publicフィールド

  • ao_name：最適化アルゴリズム名
  • ao_desc：最適化アルゴリズムの説明
  • popSize：母集団のサイズ
  • params：アルゴリズムのパラメータの配列
  • cohesionWeight：凝集度
  • cohesionDist：凝集距離
  • separationWeight：分離重量
  • separationDist：分離距離
  • alignmentWeight：整列の重み
  • alignmentDist：整列距離
  • maxSpeed：最高速度
  • minSpeed：最低速度
  • agent：エージェントのベクトル

2. オプション

  • C_AO_Boids：クラスフィールドを初期化するクラスコンストラクタ
  • SetParams：アルゴリズムのパラメータを設定するメソッド
  • Init：アルゴリズムを初期化するメソッド（最小検索範囲と最大検索範囲、検索ステップ、エポック数を受ける）
  • Moving：エージェントを移動させるメソッド
  • Revision：エージェントの改訂メソッド

3. privateフィールド

  • distanceMax：探索空間におけるユークリッド距離の最大値
  • speedMax：最高速度
//——————————————————————————————————————————————————————————————————————————————
class C_AO_Boids : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_Boids () { }
  C_AO_Boids ()
  {
    ao_name = "Boids";
    ao_desc = "Boids Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/14576";

    popSize          = 50;   //population size

    cohesionWeight   = 0.6;
    cohesionDist     = 0.001;

    separationWeight = 0.005;
    separationDist   = 0.03;

    alignmentWeight  = 0.1;
    alignmentDist    = 0.1;

    maxSpeed         = 0.001;
    minSpeed         = 0.0001;

    ArrayResize (params, 9);

    params [0].name = "popSize";          params [0].val = popSize;

    params [1].name = "cohesionWeight";   params [1].val = cohesionWeight;
    params [2].name = "cohesionDist";     params [2].val = cohesionDist;


    params [3].name = "separationWeight"; params [3].val = separationWeight;
    params [4].name = "separationDist";   params [4].val = separationDist;

    params [5].name = "alignmentWeight";  params [5].val = alignmentWeight;
    params [6].name = "alignmentDist";    params [6].val = alignmentDist;

    params [7].name = "maxSpeed";         params [7].val = maxSpeed;
    params [8].name = "minSpeed";         params [8].val = minSpeed;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double cohesionWeight;   //cohesion weight
  double cohesionDist;     //cohesion distance

  double separationWeight; //separation weight
  double separationDist;   //separation distance

  double alignmentWeight;  //alignment weight
  double alignmentDist;    //alignment distance

  double minSpeed;         //minimum velocity
  double maxSpeed;         //maximum velocity

  S_Boids_Agent agent [];

  private: //-------------------------------------------------------------------
  double distanceMax;
  double speedMax [];

  void   CalculateMass    ();
  void   Cohesion         (S_Boids_Agent &boid, int pos);
  void   Separation       (S_Boids_Agent &boid, int pos);
  void   Alignment        (S_Boids_Agent &boid, int pos);
  void   LimitSpeed       (S_Boids_Agent &boid);
  void   KeepWithinBounds (S_Boids_Agent &boid);
  double Distance         (S_Boids_Agent &boid1, S_Boids_Agent &boid2);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのInitメソッドは、渡されたパラメータに基づいてクラス変数を初期化するために使用されます。このメソッドは、StandardInitメソッドを使用して標準的な初期化をおこない、最小検索範囲と最大検索範囲、検索ステップを受け取ります。

標準の初期化が成功した場合、このメソッドはエージェントをpopSizeサイズにリサイズします。Initメソッドは、agentの各要素に対してcoordsパラメータを指定して呼び出されます。

そして、この方法は、エージェントの動きを決定するためにボイドアルゴリズムで使用される最大距離と最大速度を計算します。

次に、この方法は、ボイドアルゴリズムのさまざまなパラメータ（凝集度、凝集距離、分離度、分離距離、整列度、整列距離、最高速度、最低速度など）のグローバル変数を設定します。

このメソッドは、初期化に成功すればtrueを返し、そうでなければfalseを返します。

このメソッドは、与えられたパラメータでボイド最適化アルゴリズムの初期設定をおこない、最適化を実行する準備をします。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_Boids::Init (const double &rangeMinP  [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += pow (speedMax [c], 2);
  }

  distanceMax = sqrt (distanceMax);

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);


  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのMovingメソッドは、最適化中にエージェントを移動させるために使用されます。このメソッドは次をおこないます。

  1. グローバル変数resetの値を確認します。1.0の場合、revisionフラグはfalseに設定されます。グローバル変数resetの値が0.0に設定され、メソッドは終了します。
  2. アルゴリズムパラメータの値はグローバル変数から抽出されます。
  3. revisionフラグがfalseの場合、エージェントの座標と速度は、指定された範囲のランダムな値で初期化されます。その後revisionフラグがtrueにセットされ、メソッドは終了します。
  4. revisionフラグがfalseでない場合、各エージェントに対して以下のアクションが実行されます。
    • CalculateMass、Cohesion、Separation、Alignment、LimitSpeed、KeepWithinBoundsメソッドがエージェントの速度を更新するために呼び出されます。
    • エージェントの座標は、その速度に基づいて更新されます。
    • エージェント座標はa配列の対応する要素にコピーされます。
/——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    CalculateMass    ();
    Cohesion         (agent [i], i);
    Separation       (agent [i], i);
    Alignment        (agent [i], i);
    LimitSpeed       (agent [i]);
    KeepWithinBounds (agent [i]);

    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのCalculateMassメソッドは、ボイドアルゴリズムにおける各エージェントの「質量」を計算するために使用されます。このメソッドで起こることは以下の通りです。

  1. 変数maxMassとminMassは、全エージェント間の適応度関数の最大値と最小値を格納するために初期化されます。
  2. 集団内の各エージェントについて、そのa[i].f適応度関数が現在の最大値maxMassよりも大きく、現在の最小値minMassよりも小さいかどうかが確認されます。条件が満たされれば、対応する最大値と最小値が更新されます。
  3. すべてのエージェントがテストされた後、各エージェントの質量は、最小値と最大値に対する適応度関数のスケール値として計算されます。

このメソッドは、ボイドアルゴリズムにおける各エージェントの質量の計算を提供します。これにより、ボイドが移動する地形の「表面」を考慮に入れることができます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.0, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのCohesionメソッドは、ボイドアルゴリズムにおける「凝集」動作を実装するために使用されます。この行動により、エージェントは隣人の「重心」に向かって移動します。このメソッドは以下のタスクを実行します。

  1. centerX配列は重心の座標を格納するために初期化され、numNeighbors変数は近傍の数を数えます。
  2. 母集団内の各エージェントについて、それが自分自身でないかどうか（エージェントは自分自身を隣人とみなすべきではないため）と、ある距離（distanceMax * cohesionDistとして定義）内に位置しているかどうかが確認されます。両方の条件が満たされた場合、エージェント座標がcenterXに追加され、numNeighborsが1インクリメントされます。
  3. 少なくとも1つの近傍が見つかった場合は、centerX座標を近傍の数で割って、近傍の重心の座標を求めます。次に、エージェントboid.dxの速度は、cohesionWeight凝集重量を考慮して、質量中心に向かって調整されます。

このメソッドは、エージェントがグループとして一緒に移動するのを助ける、ボイドアルゴリズムの「結束」動作を実装しています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Cohesion (S_Boids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize     (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int    numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c];
        }

        numNeighbors++;
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    centerX [c] /= numNeighbors;
    boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのSeparationメソッドは、ボイドアルゴリズムにおける「分離」動作を実装するために使用されます。この行動により、エージェントは衝突を避けるために、近すぎる隣人とは反対方向に移動します。このメソッドで起こることは以下の通りです。

  1. moveX配列は、エージェント座標の変更を格納するために初期化されます。
  2. 母集団内の各エージェントについて、それが自分自身でないかどうか（エージェントは自分自身を隣人とみなすべきではないため）と、ある距離（distanceMax * separationDist として定義）内に位置しているかどうかが確認されます。両方の条件が満たされた場合、現在のエージェントとその隣のエージェントの座標の差がmoveXに追加されます。
  3. すべての隣接が確認された後、boid.dxエージェントの速度は、separationWeight分離重量を考慮して、moveXと反対方向に調整されます。

この方法は、ボイドアルゴリズムの「分離」動作を実装しており、エージェント同士の衝突を回避するのに役立ちます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Separation (S_Boids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize     (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのAlignmentメソッドは、ボイドアルゴリズムにおける「整列」動作を実装するために使用されます。この行動により、エージェントは隣人と同じ方向に移動します。このメソッドでは以下がおこなわれます。

  1. 配列avgDXは近隣の平均速度を格納するために初期化され、変数numNeighborsは近隣の数をカウントするために初期化されます。
  2. 母集団内の各エージェントについて、それが自分自身でないかどうか（エージェントは自分自身を隣人とみなすべきではないため）と、ある距離（distanceMax * alignmentDistとして定義）内に位置しているかどうかが確認されます。両方の条件が満たされた場合、その隣人のスピードがavgDXに加算され、numNeighborsが1増加します。
  3. 少なくとも1つの近傍が見つかった場合、avgDXの速度を近傍の数で割って平均速度を求めます。その後、「boid.dx」エージェントの速度は、「alignmentWeight」整列ウェイトを考慮して、平均速度に向けて調整されます。

このメソッドは、エージェントが同じ方向に一緒に移動するのを助ける、ボイドアルゴリズムの「整列」動作を実装しています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Alignment (S_Boids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize     (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

    for (int c = 0; c < coords; c++)
    {
      avgDX   [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのLimitSpeedメソッドは、ボイドアルゴリズムでエージェントの速度を制限するために使用されます。この動作は、エージェントが無限にスピードを上げることを防ぐもので、実際の動物にとっては不自然なものです。このメソッドは次をおこないます。

  1. speed変数はエージェントの現在の速度を格納するために初期化され、d変数はデータを一時的に格納するために初期化されます。
  2. エージェントの現在の速度は、各座標の速度に基づいて計算されます。
  3. 各エージェント座標に対して以下のアクションが実行されます。
    • dは、レンジの最大値と最小値の差に最低速度係数を掛けた値として計算されます。 
    • boid.dxエージェントの速度は、speedMax可能な最大速度とmaxSpeed最大速度係数に従って調整されます。
    • エージェント速度の絶対値がdより小さい場合、エージェント速度はdに等しく設定される（符号は維持される）。

このメソッドは、エージェントの移動速度を制御し、ボイドが停止するのを防ぐのに役立つ、ボイドアルゴリズムの「速度制限」動作を実装しています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::LimitSpeed (S_Boids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = sqrt (speed);

  double d = 0;

  for (int c = 0; c < coords; c++)
  {
    d = (rangeMax [c] - rangeMin [c]) * minSpeed;

    boid.dx [c] = (boid.dx [c] / speed) * speedMax [c] * maxSpeed;

    if (fabs (boid.dx [c]) < d)
    {
      if (boid.dx [c] < 0.0) boid.dx [c] = -d;
      else                   boid.dx [c] =  d;
    }

  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのKeepWithinBoundsメソッドは、ボイドアルゴリズムで指定された境界内でのエージェントの動きを制限するために使用されます。この動作は、エージェントが指定された境界を超えることを防ぎます。

  1. 各エージェント座標について、それが指定された境界（rangeMinとrangeMaxとして定義される）の外側にあるかどうかが確認されます。
  2. エージェント座標がrangeMinより小さい場合、rangeMaxに設定され、エージェントは境界の反対側に移動します。
  3. エージェント座標がrangeMaxより大きい場合、rangeMinと等しく設定され、エージェントは境界の反対側に移動します。

このメソッドは、ボイドアルゴリズムに「境界制約」を与え、エージェントが与えられた境界内にとどまるのを助けます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::KeepWithinBounds (S_Boids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    double margin     = 0; //(rangeMax [c] - rangeMin [c])* 0.00001;
    double turnFactor = (rangeMax [c] - rangeMin [c]) * 0.0001;

    /*
    if (boid.x [c] < rangeMin [c] + margin)
    {
      boid.dx [c] += turnFactor;
    }
    if (boid.x [c] > rangeMax [c] - margin)
    {
      boid.dx [c] -= turnFactor;
    }
    */
    if (boid.x [c] < rangeMin [c]) 
    {
      //boid.x [c] = rangeMax [c];
      boid.dx [c] *= -1;
      
    }
    if (boid.x [c] > rangeMax [c])
    {
      //boid.x [c] = rangeMin [c];
      boid.dx [c] *= -1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのDistanceメソッドは、ボイドアルゴリズムで2つのエージェント間のユークリッド距離を計算するために使用されます。

  1. dist変数は距離を格納するために初期化されます。
  2. 各エージェント座標について、その座標間の差の二乗が計算され、distに加算されます。
  3. 最後に、このメソッドはエージェント間のユークリッド距離に相当するdistの平方根を返します。

このメソッドは、ボイドアルゴリズムにおけるエージェント間の距離の計算を提供し、エージェント間の相互作用を決定するために使用されます。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_Boids::Distance (S_Boids_Agent &boid1, S_Boids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += pow (boid1.x [c] - boid1.x [c], 2);
  }

  return sqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BoidsクラスのRevisionメソッドは、ボイドアルゴリズムの最適解を更新するために使用されます。

  1. 変数indは-1で初期化されます。この変数は、最適解を持つエージェントのインデックスを格納するために使用されます。
  2. 集団内の各エージェントについて、その適合度関数a[i].fが現在の最適解fBより小さいかどうかが確認されます。a[i].fが現在の最適解fBより小さい場合、indはエージェントのインデックスに設定されます。
  3. より良い解を持つエージェントが見つかった場合（indが-1でない）、最適解fBと最適座標cBはこのエージェントの値で更新されます。

このメソッドは、ボイドアルゴリズムにおける最適解の更新を提供し、アルゴリズムが解空間の最も有望な領域に集中するのを助けます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. テスト結果

様々な関数集合に対するボイドアルゴリズムの結果について、もう少し詳しく述べたいと思います。ボイドの全テスト関数にわたる総合得点は2.22889点で、これは可能な最高得点の24.77%にあたります。この結果は、アルゴリズムの効率が低いことを示しています。このことから、ボイドアルゴリズムは、様々な関数に関する最適化問題を解く可能性は低いと結論づけることができます。

Boids|50.0|0.05|0.002|0.01|0.01|0.0001|0.01|0.001|0.0001|
=============================
5 Hilly's; Func runs:100000; result:0.43339505349362384
25 Hilly's; Func runs:100000; result:0.3058074706767012
500 Hilly's; Func runs:100000; result:0.2542539219446322
=============================
5 Forest's; Func runs:100000; result:0.35717696198531945
25 Forest's; Func runs:100000; result:0.20160005990319796
500 Forest's; Func runs:100000; result:0.15708435238635948
=============================
5 Megacity's; Func runs:100000; result:0.2784615384615384
25 Megacity's; Func runs:100000; result:0.14276923076923081
500 Megacity's; Func runs:100000; result:0.09833846153846236
=============================
All score:2.22889 (24.77%)

ボイドアルゴリズムは、群知能システムの同胞であるPSOアルゴリズムに次いで、ランキング表の28位を獲得しました。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA バイナリ遺伝的アルゴリズム 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O）進化戦略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG 社会集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA 鳥群アルゴリズム 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 WOAm 鯨最適化アルゴリズム M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
12 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
13 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
14 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
15 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
16 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
17 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
18 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
19 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
20 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
21 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
22 BFO 細菌採餌の最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
23 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
24 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
25 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
26 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
27 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
28 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
29 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
30 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
31 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
32 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
33 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
34 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
35 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


まとめ

テスト関数の結果が弱いにもかかわらず、1000個の変数を持つForest関数とMegacity関数の結果が非常にまともで、表の上半分のアルゴリズムの結果に対応していることは注目に値します。これは、ボイドアルゴリズムが、より大きな数の変数を扱う場合により効率的であることを示しているのかもしれません。全体として、これらの結果は、ボイドアルゴリズムにこれ以上の可能性を期待するのは難しいことを示しています。

表

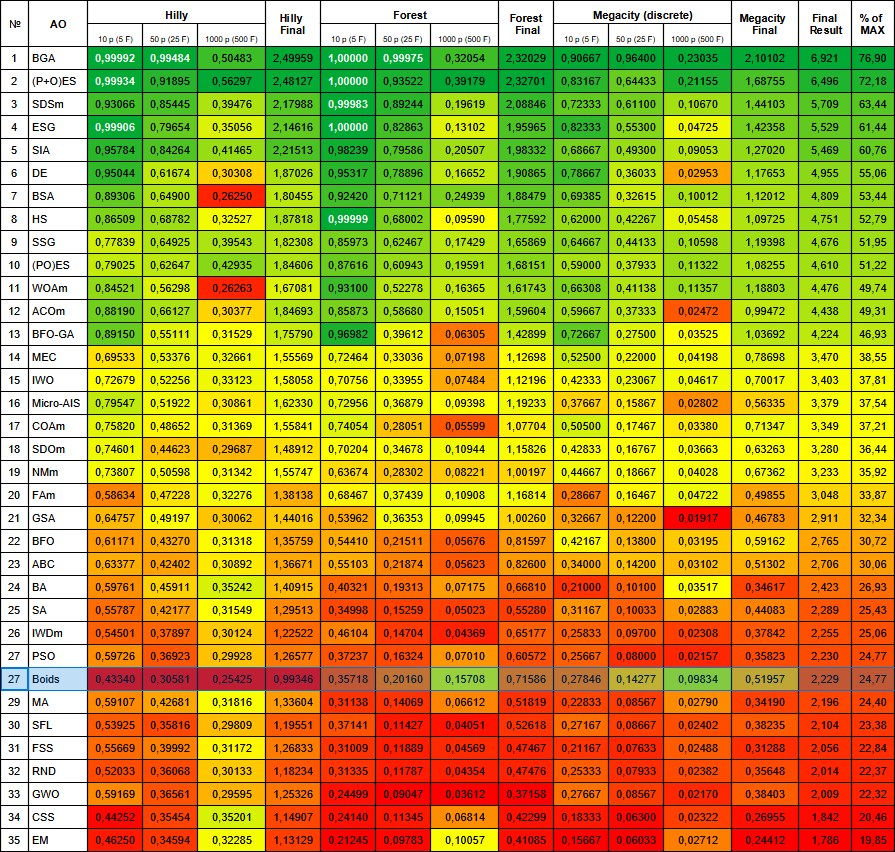
図1：関連テストに応じたアルゴリズムのカラーグラデーション0.99以上の結果は白で強調表示

チャート

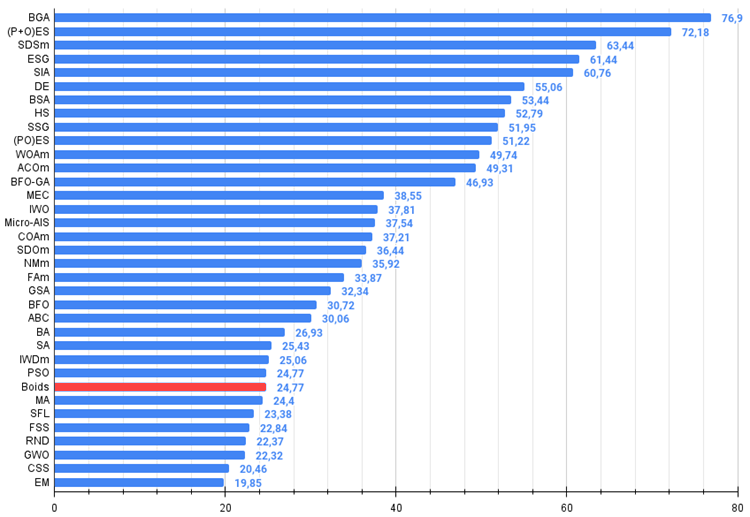
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている)

ボイドの長所と短所

長所

  1. リアルな群れ行動シミュレーション

短所

  1. 収束性が低い
  2. 計算量が多い
  3. Hillyのような滑らかな関数ではスケーラビリティが低い（高次元タスクの問題）

この記事には、現在のコードバージョンのアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14576

添付されたファイル |
ZIPをダウンロード
Boids.zip (28.61 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
古典的な戦略をPythonで再構築する：MAクロスオーバー 古典的な戦略をPythonで再構築する：MAクロスオーバー
この記事では、古典的な移動平均クロスオーバー戦略を再検討し、その現在の有効性を評価します。開始以来の経過時間を考慮して、AI がこの伝統的な取引戦略にもたらす可能性のある機能強化について検討します。AI技術を取り入れることで、高度な予測能力を活用し、取引のエントリとエグジットのポイントを最適化し、さまざまな市場環境に適応し、従来のアプローチと比較して全体的なパフォーマンスを向上させる可能性があることを目指します。
多通貨エキスパートアドバイザーの開発（第6回）：インスタンスグループ選択の自動化 多通貨エキスパートアドバイザーの開発（第6回）：インスタンスグループ選択の自動化
取引戦略を最適化した後、パラメータのセットを受け取ります。これらを使用して、1つのEAに複数の取引戦略のインスタンスを作成することができます。以前は手動でおこないましたが、ここでは、このプロセスの自動化を試みます。
Candlestick Trend Constraintモデルの構築（第5回）：通知システム（パート3） Candlestick Trend Constraintモデルの構築（第5回）：通知システム（パート3）
本稿ではWhatsAppとMetaTrader 5を統合して通知する方法を紹介します。理解を容易にするためにフローチャートを掲載し、統合におけるセキュリティ対策の重要性について説明します。指標の主な目的は、自動化によって分析を簡素化することであり、特定の条件が満たされたときにユーザーに警告するための通知方法を含むべきです。詳しくは本稿で説明します。
PythonとMQL5でロボットを開発する（第1回）：データ前処理 PythonとMQL5でロボットを開発する（第1回）：データ前処理
機械学習に基づく自動売買ロボットの開発の詳細なガイドです。連載第1回は、データと特徴量の収集と準備についてです。プロジェクトは、Pythonプログラミング言語とライブラリ、およびMetaTrader 5プラットフォームを使用して実装されます。