Otimização por Quimiotaxia Bacteriana (BCO)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

Na área de otimização, muitos pesquisadores e desenvolvedores se inspiram em processos biológicos observados na natureza, como a evolução, interações sociais ou o comportamento de organismos vivos na busca por alimento. Isso leva ao desenvolvimento de novos e inovadores métodos de otimização. Pesquisas demonstraram que esses métodos geralmente superam abordagens heurísticas clássicas e técnicas baseadas em gradientes, especialmente na resolução de problemas multimodais, não diferenciáveis e discretos. Um desses métodos é o algoritmo de quimiotaxia, inicialmente proposto por Bremermann e seus colegas. Já analisamos anteriormente o algoritmo de otimização por busca alimentar bacteriana (BFO), que modela a reação das bactérias aos quimioatraentes em gradientes de concentração. Bremermann realizou uma análise da quimiotaxia em gradientes tridimensionais e aplicou esse conceito no treinamento de redes neurais. Embora esse algoritmo tenha sido fundamentado nos princípios da quimiotaxia bacteriana, descobertas biológicas mais recentes possibilitaram a criação de um modelo mais detalhado desse processo.

Neste artigo, exploramos essa nova abordagem como uma estratégia de otimização. As principais diferenças entre o novo modelo e o algoritmo tradicional de quimiotaxia são as seguintes:

1. No novo modelo, as bactérias utilizam informações sobre os valores de concentração.
2. Elas não continuam se movendo na mesma direção quando há um aumento na concentração de quimioatraentes.

As bactérias são organismos unicelulares, uma das formas de vida mais simples da Terra. Apesar dessa simplicidade, elas são capazes de captar informações do ambiente, se orientar nele e utilizar essas informações de forma eficiente para sobreviver. A resposta das bactérias às mudanças ambientais tem sido objeto de intensas pesquisas nas últimas décadas, atraindo também o interesse de cientistas da área de otimização. Os algoritmos de otimização podem ser vistos como sistemas que coletam informações sobre a paisagem funcional e as utilizam para alcançar o ótimo. A simplicidade do conceito de quimiotaxia bacteriana torna esse tipo de algoritmo um ponto de partida atrativo.

Em diversos estudos, foi estabelecido que as bactérias trocam informações entre si, embora os mecanismos exatos dessa comunicação ainda não sejam totalmente compreendidos. Normalmente, as bactérias são tratadas como indivíduos, e a interação social não é considerada nos modelos. Isso as diferencia dos modelos de interação que descrevem o comportamento de insetos sociais (como formigas, abelhas, vespas ou cupins), que operam como sistemas de inteligência coletiva, abrindo novas possibilidades para a resolução de diferentes problemas.

A adaptação é outro aspecto fundamental da quimiotaxia. As bactérias podem modificar sua sensibilidade a condições químicas constantes, o que lhes permite reagir eficientemente às mudanças no ambiente. Essa capacidade as torna não apenas resistentes, mas também altamente eficazes na busca por recursos.

Neste estudo, os autores se concentraram em modelos microscópicos que consideram a quimiotaxia de bactérias individuais, ao invés dos modelos macroscópicos, que analisam o movimento de colônias. O algoritmo em questão foi desenvolvido por S. D. Müller e P. Koumoutsakos, e suas principais ideias foram apresentadas e publicadas em 2002.

Implementação do algoritmo

A ideia central do algoritmo de otimização por quimiotaxia bacteriana (BCO) é utilizar princípios biológicos observados no comportamento das bactérias para resolver problemas de otimização. Ele modela a forma como as bactérias respondem a gradientes de substâncias químicas no ambiente, permitindo-lhes encontrar condições mais favoráveis para sua sobrevivência. As principais ideias do algoritmo são as seguintes:

1. O algoritmo descreve o movimento das bactérias como uma sequência de trajetórias retilíneas conectadas por mudanças instantâneas de direção. Cada movimento é caracterizado por velocidade, direção e duração.
2. A direção da mudança de trajetória da bactéria é determinada por uma distribuição probabilística, permitindo incorporar variações aleatórias no deslocamento.
3. O algoritmo utiliza informações sobre os gradientes da função para guiar a bactéria em direção à solução ótima, minimizando o número de iterações necessárias para alcançar o objetivo.

O pseudocódigo detalhado do algoritmo de otimização por quimiotaxia bacteriana (BCO) descreve as principais etapas do algoritmo, incluindo a inicialização, o ciclo principal de otimização com as fases de movimento e revisão, além de funções auxiliares.

Inicialização.

1. Definir parâmetros:

• popSize: tamanho da população (quantidade de bactérias)
• hs: número de passos para calcular a média da variação
• T0: temperatura inicial
• b: parâmetro
• tau_c: parâmetro
• v: velocidade

2. Criar um array de bactérias com tamanho popSize

3. Para cada bactéria i de 0 a popSize - 1:

• Inicializar fPrev com o valor -DBL_MAX
• Criar um array fHistory de tamanho hs e preenchê-lo com zeros

Ciclo principal de otimização. Repetir até que a condição de parada seja atendida:

Fase de movimento para cada bactéria i de 0 a popSize - 1:

1. Obter o valor atual da função objetivo f_tr

2. Obter o valor anterior da função objetivo f_pr a partir de bacterium[i].fPrev

3. Se f_tr <= f_pr: T = T0

    Caso contrário: calcular b_corr = CalculateCorrectedB (f_tr, f_pr, i)

• T = T0 * exp (b_corr * (f_tr - f_pr))

4. Gerar tau a partir de uma distribuição exponencial com parâmetro T.

5. Calcular novos ângulos new_angles[] para coords - 1 dimensões: para cada ângulo j de 0 a coords - 2:

• theta = CalculateRotationAngle ()
• mu = 62 * (1 - cos(theta)) * π / 180
• sigma = 26 * (1 - cos(theta)) * π / 180
• new_angles[j] = número aleatório de uma distribuição gaussiana com parâmetros (mu, mu-π, mu+π)

6. Calcular a nova posição:

• l = v * tau
• CalculateNewPosition (l, new_angles, new_position, current_position)

7. Atualizar a posição da bactéria, limitando os valores dentro de rangeMin e rangeMax

8. Atualizar bacterium[i].fPrev com o valor f_tr

Fase de revisão.

1. Atualizar a melhor solução global cB com o valor de aptidão fB

2. Para cada bactéria i de 0 a popSize - 1, atualizar o histórico de valores da função objetivo fHistory:

• Deslocar todos os valores uma posição para a esquerda
• Adicionar o valor atual da função objetivo ao final do histórico

Funções auxiliares:

CalculateCorrectedB (f_tr, f_pr, bacteriumIndex)

1. Calcular delta_f_tr = f_tr - f_pr

2. Calcular delta_f_pr = variação média nos últimos hs passos

3. Se |delta_f_pr| < epsilon: Retornar b

   Caso contrário: Retornar b * (1 / (|delta_f_tr / delta_f_pr| + 1) + 1 / (|f_pr| + 1))

CalculateRotationAngle ()

1. Calcular cos_theta = exp (-tau_c / T0)

2. Retornar arccos (cos_theta)

CalculateNewPosition (l, angles, new_position, current_position)

1. Calcular new_position[0] considerando todos os ângulos

2. Para cada coordenada i de 1 a coords - 1:

   Calcular new_position[i] considerando os ângulos correspondentes

3. Aplicar uma direção aleatória (1 ou -1) a cada coordenada

GenerateFromExponentialDistribution (T)

Retornar -T * ln (número aleatório entre 0 e 1)

Agora passamos à implementação do código do algoritmo. Para representar a bactéria como uma solução do problema de otimização, descreveremos a estrutura "S_BCO_Bacterium".

1. Campos da estrutura:

• fPrev - valor anterior da função objetivo.
  
• fHistory[] - array do histórico de valores da função objetivo.
  

2. Init - o método de inicialização executa as seguintes ações:

• O tamanho do array "fHistory" é ajustado para "historySize".
• Todos os elementos do array "fHistory" são inicializados com o valor "0.0".
• O valor de fPrev é definido como o menor valor possível da função objetivo.

A bactéria é representada como uma estrutura que permite rastrear a variação dos valores da função objetivo ao longo de um número determinado de iterações (movimentos individuais).

//——————————————————————————————————————————————————————————————————————————————
struct S_BCO_Bacterium
{
    double fPrev;        // previous value of the objective function
    double fHistory [];  // history of objective function values

    void Init (int coords, int historySize)
    {
      ArrayResize     (fHistory, historySize);
      ArrayInitialize (fHistory, 0.0);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Agora descreveremos a classe do algoritmo "C_AO_BCO". Vamos analisá-la por partes.

1. No construtor, os parâmetros externos do algoritmo são inicializados.

2. O método "SetParams" atualiza os valores dos parâmetros a partir do array "params".

3. Os métodos "Moving" e "Revision" são responsáveis pelo movimento das bactérias e pela revisão de suas posições.

4. A classe contém vários métodos privados utilizados para diferentes cálculos relacionados ao algoritmo, como "CalculateAverageDeltaFpr", "CalculateNewAngles", "CalculateNewPosition", "GenerateFromExponentialDistribution", "CalculateCorrectedB", "CalculateRotationAngle" e "RNDdir". Além disso, há o array bacterium, que representa a população de bactérias. Os parâmetros da classe incluem:

• hs - número de passos para calcular a média da variação.
• T0 - temperatura inicial.
• b - parâmetro.
• tau_c - parâmetro.
• v - velocidade.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BCO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BCO () { }
  C_AO_BCO ()
  {
    ao_name = "BCO";
    ao_desc = "Bacterial Chemotaxis Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15711";

    popSize = 50;     // population size (number of bacteria)
    hs      = 10;     // number of steps to calculate average change
    T0      = 1.0;    // initial temperature
    b       = 0.5;    // parameter b
    tau_c   = 1.0;    // parameter tau_c
    v       = 1.0;    // velocity

    ArrayResize (params, 6);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "hs";      params [1].val = hs;
    params [2].name = "T0";      params [2].val = T0;
    params [3].name = "b";       params [3].val = b;
    params [4].name = "tau_c";   params [4].val = tau_c;
    params [5].name = "v";       params [5].val = v;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    hs      = (int)params [1].val;
    T0      = params      [2].val;
    b       = params      [3].val;
    tau_c   = params      [4].val;
    v       = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    hs;
  double T0;
  double b;
  double tau_c;
  double v;

  S_BCO_Bacterium bacterium [];

  private: //-------------------------------------------------------------------
  double CalculateAverageDeltaFpr            (int bacteriumIndex);
  void   CalculateNewAngles                  (double &angles []);
  void   CalculateNewPosition                (double l, const double &angles [], double &new_position [], const double &current_position []);
  double GenerateFromExponentialDistribution (double T);
  double CalculateCorrectedB                 (double f_tr, double f_pr, int bacteriumIndex);
  double CalculateRotationAngle              ();
  int    RNDdir                              ();
};

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" da classe "C_AO_BCO" é responsável pelo deslocamento das bactérias no espaço de busca. Vamos analisar seu funcionamento:

1. Se "revision" for "false", significa que as bactérias estão em suas posições iniciais.

• Para cada bactéria "a[i]", são geradas coordenadas aleatórias dentro do intervalo definido.
• A função "u.RNDfromCI" gera um valor aleatório, e "u.SeInDiSp" o ajusta de acordo com o passo especificado.

2. O ciclo principal de movimentação, caso "revision" seja "true". Esse método executa a lógica principal do deslocamento das bactérias. Definição da temperatura "T":

• Se o valor atual da função "f_tr" for melhor ou igual ao anterior "f_pr", a temperatura inicial "T0" é utilizada.
• Caso contrário, a temperatura é ajustada pela função "CalculateCorrectedB", que considera a diferença entre os valores atual e anterior da função de aptidão. 
• Geração do tempo de deslocamento "tau": um tempo de deslocamento é gerado utilizando uma distribuição exponencial.
• Os novos ângulos de deslocamento e a nova posição são calculados com base no comprimento do deslocamento "l" e nos novos ângulos.
• A nova posição é ajustada conforme o intervalo e o passo definidos.
• Ao final do ciclo, o valor anterior da função de aptidão de cada bactéria é atualizado.

O método "Moving" implementa a lógica principal do deslocamento das bactérias no espaço de busca, adaptando seu comportamento com base nos resultados das iterações anteriores. Ele incorpora elementos aleatórios e mecanismos adaptativos na busca pela solução ótima.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    double f_tr = a [i].f;
    double f_pr = bacterium [i].fPrev;

    double T;
    
    if (f_tr <= f_pr)
    {
      T = T0;
    }
    else
    {
      double b_corr = CalculateCorrectedB (f_tr, f_pr, i);
      
      T = T0 * exp (b_corr * (f_tr - f_pr));
    }

    double tau = GenerateFromExponentialDistribution (T);

    double new_angles [];
    ArrayResize (new_angles, coords - 1);
    CalculateNewAngles (new_angles);

    double l = v * tau;
    double new_position [];
    ArrayResize (new_position, coords);
    CalculateNewPosition (l, new_angles, new_position, a [i].c);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.SeInDiSp (new_position [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" da classe "C_AO_BCO" é responsável por atualizar as informações sobre as melhores soluções encontradas e o histórico de valores da função de aptidão para cada bactéria.

1. A variável "ind" é inicializada com o valor "-1". Ela será utilizada para armazenar o índice da bactéria que apresentar o melhor valor da função.

2. Busca do melhor valor da função:

• O método percorre todas as bactérias da população "popSize" e procura aquela cujo valor da função "f" seja superior ao valor atual "fB".
• Se uma bactéria com um valor de função superior for encontrada, o valor "fB" é atualizado e o respectivo índice é armazenado em "ind".

3. Se uma bactéria com índice "ind" foi encontrada (ou seja, "ind" não é igual a "-1"), suas coordenadas são copiadas para o array "cB", que representa a melhor solução encontrada até o momento.

4. O histórico de valores da função é atualizado para cada bactéria. O método percorre cada elemento do array "fHistory", deslocando os valores uma posição para a esquerda para liberar espaço para um novo valor. Ao final de cada iteração, o último elemento do array "fHistory" recebe o valor atual de aptidão "a[i].f" de cada bactéria.

Dessa forma, o método "Revision" executa duas funções principais:

• Atualiza o melhor valor da função de aptidão e suas respectivas coordenadas.
• Atualiza o histórico de valores da função de aptidão para cada bactéria, permitindo rastrear mudanças no desempenho ao longo de suas movimentações. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1)
  {
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 1; j < hs; j++)
    {
      bacterium [i].fHistory [j - 1] = bacterium [i].fHistory [j];
    }

    bacterium [i].fHistory [hs - 1] = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "CalculateAverageDeltaFpr" da classe "C_AO_BCO" é utilizado para calcular a variação média dos valores da função de aptidão (delta) para uma bactéria específica entre suas posições consecutivas, com base no histórico de valores.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateAverageDeltaFpr (int bacteriumIndex)
{
  double sum = 0;

  for (int i = 1; i < hs; i++)
  {
    sum += bacterium [bacteriumIndex].fHistory [i] - bacterium [bacteriumIndex].fHistory [i - 1];
  }

  return sum / (hs - 1);
}
//——————————————————————————————————————————————————————————————————————————————

O método "CalculateNewAngles" da classe "C_AO_BCO" calcula novos ângulos com base na lógica relacionada à rotação e distribuição, executando as seguintes etapas:

• Percorre o array de novos ângulos e, para cada ângulo, calcula um novo valor.
• Utiliza parâmetros dependentes do cosseno do ângulo para gerar valores baseados em uma distribuição gaussiana.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewAngles (double &angles [])
{
  for (int i = 0; i < coords - 1; i++)
  {
    double theta = CalculateRotationAngle ();
    double mu    = 62 * (1 - MathCos (theta)) * M_PI / 180.0;
    double sigma = 26 * (1 - MathCos (theta)) * M_PI / 180.0;

    angles [i] = u.GaussDistribution (mu, mu - M_PI, mu + M_PI, 8);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "CalculateNewPosition" da classe "C_AO_BCO" é responsável por calcular novas coordenadas de posição com base nas coordenadas atuais, nos ângulos e no parâmetro "l". 

1. Parâmetros de entrada do método:

• l - coeficiente que influencia a alteração da posição.
• angles[] - array de ângulos utilizado para calcular a nova posição.
• new_position[] - array onde serão armazenadas as novas coordenadas.
• current_position[] - array das coordenadas atuais.

2. A primeira coordenada "new_position[0]" é calculada somando a coordenada atual "current_position[0]" ao produto de "l" pela diferença entre "rangeMax[0]" e "rangeMin[0]".

3. Em seguida, a primeira coordenada é multiplicada pelos cossenos dos ângulos do array "angles", do primeiro até o penúltimo.

4. O resultado é multiplicado pelo valor retornado pela função "RNDdir()", que gera uma direção aleatória "-1" ou "1".

5. Para cada coordenada seguinte "new_position[i]", onde "i" varia de "1" até "coords - 2", a nova posição é calculada com base na posição atual e no seno do ângulo correspondente.

6. Cada nova coordenada também é multiplicada pelos cossenos dos ângulos, do índice atual "i" até o penúltimo.

7. A direção aleatória é aplicada às demais coordenadas, e o resultado também é multiplicado pelo valor retornado por "RNDdir()".

8. Para a última coordenada, caso o número de coordenadas seja maior que 1, a nova posição "new_position[coords - 1]" é calculada com base na posição atual e no seno do último ângulo.

Dessa forma, o método "CalculateNewPosition" realiza as seguintes ações:

• Calcula novas coordenadas com base nas coordenadas atuais e nos ângulos.
• Considera a influência da direção aleatória em cada coordenada.
• Aplica funções trigonométricas (seno e cosseno) para levar em conta os ângulos.

Esse método é utilizado para modelar o deslocamento das bactérias no espaço, levando em consideração sua posição atual e os ângulos definidos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewPosition (double l, const double &angles [], double &new_position [], const double &current_position [])
{
  new_position [0] = current_position [0] + l * (rangeMax [0] - rangeMin [0]);
 
  for (int k = 0; k < coords - 1; k++)
  {
    new_position [0] *= MathCos (angles [k]);
  }
 
  new_position [0] *= RNDdir ();

  for (int i = 1; i < coords - 1; i++)
  {
    new_position [i] = current_position [i] + l * MathSin (angles [i - 1]) * (rangeMax [0] - rangeMin [0]);
    
    for (int k = i; k < coords - 1; k++)
    {
      new_position [i] *= MathCos (angles [k]);
    }
    
    new_position [i] *= RNDdir ();
  }

  if (coords > 1)
  {
    new_position [coords - 1] = current_position [coords - 1] + l * MathSin (angles [coords - 2]);
  }
 
}
//——————————————————————————————————————————————————————————————————————————————

Agora, descreveremos brevemente o método "RNDdir" da classe "C_AO_BCO", que gera uma direção aleatória assumindo um dos dois valores possíveis: -1 ou 1.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BCO::RNDdir ()
{
  if (u.RNDbool () < 0.5) return -1;
 
  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

Segue uma visão geral dos métodos da classe "C_AO_BCO":

O método "GenerateFromExponentialDistribution" executa:

• A geração de um número aleatório segundo uma distribuição exponencial com parâmetro "T".
• Em seguida, utiliza um número aleatório no intervalo (0,1), calcula seu logaritmo e multiplica por "-T".
• Assim, obtém-se um número aleatório distribuído de acordo com a lei exponencial.

 O método "CalculateCorrectedB" realiza:

• O cálculo do valor corrigido de "b" com base na diferença entre "f_tr" e "f_pr" (os valores atual e anterior da função de aptidão).
• Calcula a diferença entre "f_tr" e "f_pr", obtém a média para a bactéria e, dependendo desse valor, retorna o valor corrigido de "b".

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::GenerateFromExponentialDistribution (double T)
{
  return -T * MathLog (u.RNDprobab ());
}

double C_AO_BCO::CalculateCorrectedB (double f_tr, double f_pr, int bacteriumIndex)
{
  double delta_f_tr = f_tr - f_pr;
  double delta_f_pr = CalculateAverageDeltaFpr (bacteriumIndex);

  if (MathAbs (delta_f_pr) < DBL_EPSILON)
  {
    return b;
  }
  else
  {
    return b * (1 / (MathAbs (delta_f_tr / delta_f_pr) + 1) + 1 / (MathAbs (f_pr) + 1));
  }
}
//——————————————————————————————————————————————————————————————————————————————

O último método a ser abordado é "CalculateRotationAngle" da classe "C_AO_BCO". Esse método calcula o ângulo de rotação com base nos parâmetros fornecidos e retorna o valor em radianos.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateRotationAngle ()
{
  double cos_theta = MathExp (-tau_c / T0);
  return MathArccos (cos_theta);
}
//——————————————————————————————————————————————————————————————————————————————

Agora, testamos a versão original do algoritmo e analisamos os resultados:

BCO|Otimização da quimiotaxia bacteriana|50.0|10.0|1.0|0.5|1.0|1.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.42924491510564006
25 Hilly's; Func runs: 10000; result: 0.282259866768426
500 Hilly's; Func runs: 10000; result: 0.2515386629014219
=============================
5 Forest's; Func runs: 10000; result: 0.2476662231845009
25 Forest's; Func runs: 10000; result: 0.17824381036550777
500 Forest's; Func runs: 10000; result: 0.15324081202657283
=============================
5 Megacity's; Func runs: 10000; result: 0.2430769230769231
25 Megacity's; Func runs: 10000; result: 0.11415384615384619
500 Megacity's; Func runs: 10000; result: 0.09444615384615461
=============================
All score: 1.99387 (22.15%)

Os resultados obtidos são tão fracos que não faz sentido incluí-los na tabela de classificações. Durante a implementação do algoritmo e a escrita do código com base na descrição textual dos autores, precisei corrigir algumas fórmulas. Algumas não faziam sentido matemático (por exemplo, a divisão de um número por um vetor), enquanto outras resultavam em valores extremamente pequenos ou extremamente grandes, incompatíveis com as dimensões do problema. Durante esse processo, imprimi os resultados das funções para cada uma das fórmulas apresentadas e analisei seu comportamento. Dessa forma, o algoritmo não pode funcionar corretamente conforme descrito pelos autores.

Além disso, as operações com ângulos, nas quais é utilizado o modelo de distribuição normal, podem ser significativamente simplificadas. O significado físico dessas operações pode ser reduzido ao fato de que, em cada coordenada, basta aplicar uma nova variação a partir da posição atual da bactéria. Portanto, decidi desenvolver minha própria implementação da quimiotaxia bacteriana, buscando manter ao máximo os conceitos e ideias centrais do algoritmo original.

Agora, apresento o pseudocódigo da minha versão do algoritmo:

Inicialização:
1. Criar uma população com popSize bactérias.
2. Para cada bactéria i:
    Inicializar o histórico de valores da função objetivo f_history[i] com tamanho hs e valores nulos.
    Definir o valor inicial f_prev[i] = -DBL_MAX.

Ciclo principal:
Enquanto a condição de parada não for atendida:

1. Se for a primeira iteração:
   Para cada bactéria i:
     Inicializar aleatoriamente a posição x[i] no espaço de busca.
     x[i][j] ∈ [x_min[j], x_max[j]] para cada coordenada j.

2. Caso contrário:
   Para cada bactéria i:
     a. Calcular a variação média da função objetivo:
        delta_ave[i] = (1 / (hs - 1)) * sum(f_history[i][k] - f_history[i][k-1] para k em 1..hs-1) + epsilon.
     
     b. Calcular a variação relativa da aptidão:
        delta[i] = 1 - |f(x[i]) - f_prev[i]| / delta_ave[i].
        delta[i] = max(delta[i], 0.0001).
     
     c. Para cada coordenada j:
        Com probabilidade 0.5:
          dist[j] = (x_max[j] - x_min[j]) * delta[i].
          x[i][j] = N(x[i][j], x[i][j] - dist[j], x[i][j] + dist[j]).
          Limitar x[i][j] ao intervalo [x_min[j], x_max[j]].
        Caso contrário:
          x[i][j] = x_best[j].
     
     d. Atualizar f_prev[i] = f(x[i]).

3. Avaliar a função objetivo f(x[i]) para cada bactéria.

4. Atualizar a melhor solução encontrada:
   Se existir um i tal que f(x[i]) > f(x_best), então x_best = x[i].

5. Atualizar o histórico de valores da função objetivo para cada bactéria:
   Deslocar os valores em f_history[i].
   Adicionar o novo valor: f_history[i][hs - 1] = f(x[i]).

Conclusão:
Retornar a melhor solução encontrada x_best.

Onde:

• x[i] - posição da i-ésima bactéria.
• f(x) - função objetivo.
• hs - tamanho do histórico.
• epsilon - pequena constante para evitar divisão por zero.
• N(μ, a, b) - distribuição normal truncada com média μ e limites [a, b].

Dessa forma, meu pseudocódigo modificado reflete a estrutura e a lógica central do algoritmo BCO. Vamos destacar os principais pontos:

• O algoritmo utiliza uma população de bactérias, onde cada uma representa uma solução potencial.
• Em cada iteração, as bactérias se deslocam no espaço de busca utilizando informações sobre seus resultados anteriores.
• O movimento é baseado na variação relativa da função objetivo, permitindo que o algoritmo se adapte ao cenário de otimização.
• O algoritmo mantém um histórico dos valores da função objetivo para cada bactéria, usado no cálculo da variação média.
• Com certa probabilidade, a bactéria se move em direção à melhor solução conhecida, em vez de explorar uma nova região (um conceito análogo à herança de características na genética).
  
• Após cada deslocamento, as novas posições são avaliadas e a melhor solução encontrada é atualizada.

A versão BCOm combina elementos de busca local (movimento de bactérias individuais) e busca global (compartilhamento de informações através da melhor solução conhecida).

Agora, vejamos as principais diferenças entre as duas versões do algoritmo. Primeiramente, o mecanismo de movimento das bactérias foi simplificado, eliminando a complexa estrutura baseada em ângulos de rotação e temperatura. Em segundo lugar, a nova versão depende menos do histórico de mudanças para ajustar o comportamento das bactérias, adotando uma abordagem mais direta na atualização de suas posições. Em vez de utilizar uma combinação de distribuições exponencial e normal, o novo algoritmo utiliza apenas a distribuição normal. Como consequência dessas mudanças, o número de parâmetros necessários para controlar o comportamento do algoritmo foi reduzido a um único parâmetro (além do tamanho da população), o que simplifica a configuração e o gerenciamento do processo de otimização.

No geral, o novo pseudocódigo propõe cálculos mais simples em cada etapa da otimização, o que deve impactar positivamente na velocidade de execução do algoritmo. Na versão original, eram realizados cálculos repetidos de seno e cosseno dos ângulos de rotação para cada coordenada de cada bactéria. Minha abordagem equilibra de forma diferente a exploração de novas regiões do espaço de soluções e a utilização das melhores soluções já encontradas.

Essas mudanças na lógica resultaram em um algoritmo mais simples e, presumivelmente (até que os testes sejam concluídos), mais eficiente. Agora passamos para a implementação do código.

A estrutura "S_BCO_Bacterium", que representa cada bactéria, permanecerá inalterada. Ela é responsável por armazenar informações sobre a bactéria e o histórico de valores da função objetivo.

No método "Init" da classe "C_AO_BCOm", que lida com a inicialização dos parâmetros do algoritmo, será adicionada a definição da distância permitida para o deslocamento em cada coordenada.

Dessa forma, o método "Init" da classe "C_AO_BCOm" é responsável por configurar os parâmetros do algoritmo de otimização. Ele verifica as condições padrão de inicialização, cria os arrays necessários e os preenche com valores apropriados.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCOm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  ArrayResize (allowedDispl, coords);
  for (int c = 0; c < coords; c++) allowedDispl [c] = rangeMax [c] - rangeMin [c];

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Agora, analisamos o método "Moving" da classe "C_AO_BCOm", que gerencia o deslocamento das bactérias no espaço de busca. Vamos analisá-la por partes.

1. Na primeira iteração, as ações do método permanecem inalteradas: as coordenadas das bactérias são inicializadas com valores aleatórios dentro do intervalo definido.

2. No algoritmo principal de movimentação, são declaradas variáveis para armazenar valores como "Δ", "ΔAve" e "dist", e, para cada indivíduo da população:

• O valor médio "ΔAve" é calculado utilizando a função "CalculateAverageDeltaFpr(i)".
• O valor relativo "Δ" é computado e utilizado para determinar a intensidade da alteração da posição das bactérias.
• Se "Δ" for muito pequeno, ele é ajustado para 0.0001.

3. Alteração das coordenadas:

• Para cada coordenada, uma probabilidade aleatória de 50% é avaliada.
• Se a condição for atendida, a distância "dist" é calculada com base em "allowedDispl[c]" e "Δ".
• O novo valor de "x" é determinado utilizando a função "GaussDistribution", considerando os limites "xMin" e "xMax".
• Se "x" ultrapassar os limites do intervalo, ele é ajustado com a função "RNDfromCI".
• Finalmente, o novo valor da coordenada é armazenado considerando o passo "rangeStep".

4. O valor anterior da função de aptidão "f" é armazenado para cada indivíduo no array "bacterium". São utilizados os arrays "a" e "bacterium". As funções "RNDfromCI", "SeInDiSp" e "GaussDistribution" são responsáveis pela geração de números aleatórios e distribuições, além da normalização dos valores das coordenadas.

Dessa forma, a função "Moving()" é responsável pela inicialização e atualização das posições dos indivíduos na população dentro do algoritmo. Esta função utiliza probabilidades e distribuições aleatórias para controlar a movimentação das bactérias. No entanto, a principal diferença em relação à versão original é a implementação mais simples e eficiente do gradiente da função de aptidão. Quando a diferença na adaptação da bactéria diminui em relação ao passo anterior, sua movimentação acelera. Por outro lado, ao encontrar um ambiente favorável, a bactéria desacelera. Isso contradiz o comportamento natural das bactérias, que tendem a entrar em estado de anabiose quando se deparam com um ambiente hostil.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double x    = 0.0;
  double xMin = 0.0;
  double xMax = 0.0;
  double Δ    = 0.0;
  double ΔAve = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    ΔAve = CalculateAverageDeltaFpr (i) + DBL_EPSILON;

    Δ = fabs (a [i].f - bacterium [i].fPrev) / ΔAve;

    Δ = 1.0 - Δ;

    if (Δ < 0.0001) Δ = 0.0001;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < 0.5)
      {
        dist = allowedDispl [c] * Δ;

        x    = a [i].c [c];
        xMin = x - dist;
        xMax = x + dist;

        x = u.GaussDistribution (x, xMin, xMax, 8);

        if (x > rangeMax [c]) x = u.RNDfromCI (xMin, rangeMax [c]);
        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], xMax);

        a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else a [i].c [c] = cB [c];
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision()" da classe "C_AO_BCOm", responsável por atualizar as informações da população e o histórico de valores da função objetivo, permaneceu inalterado.

Resultados dos testes

Agora analisamos o desempenho da nova versão do algoritmo BCOm:

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.759526049526603
25 Hilly's; Func runs: 10000; result: 0.6226756163411526
500 Hilly's; Func runs: 10000; result: 0.31483373090540534
=============================
5 Forest's; Func runs: 10000; result: 0.8937814268120954
25 Forest's; Func runs: 10000; result: 0.6133909133246214
500 Forest's; Func runs: 10000; result: 0.22541842289630293
=============================
5 Megacity's; Func runs: 10000; result: 0.653846153846154
25 Megacity's; Func runs: 10000; result: 0.42092307692307684
500 Megacity's; Func runs: 10000; result: 0.14435384615384755
=============================
All score: 4.64875 (51.65%)

Provavelmente, a experiência acumulada e a análise crítica das informações disponíveis sobre a versão original foram determinantes para que a nova versão do algoritmo demonstrasse um desempenho mais robusto na prática do que a versão original.

Ao visualizar o funcionamento do algoritmo BCOm, é possível observar uma boa exploração das regiões significativas do hiperespaço, o que indica uma alta capacidade de investigação da superfície da função a ser otimizada.

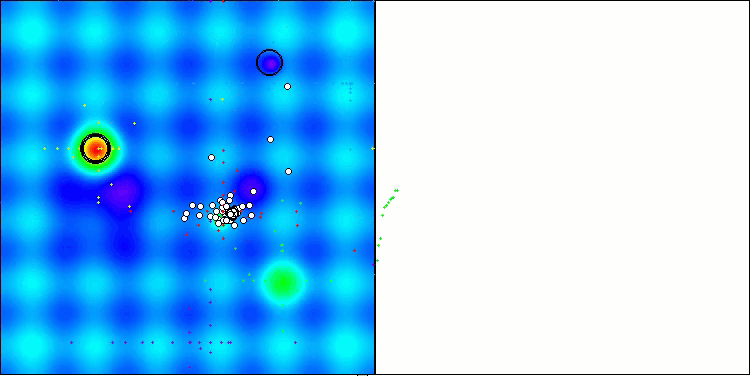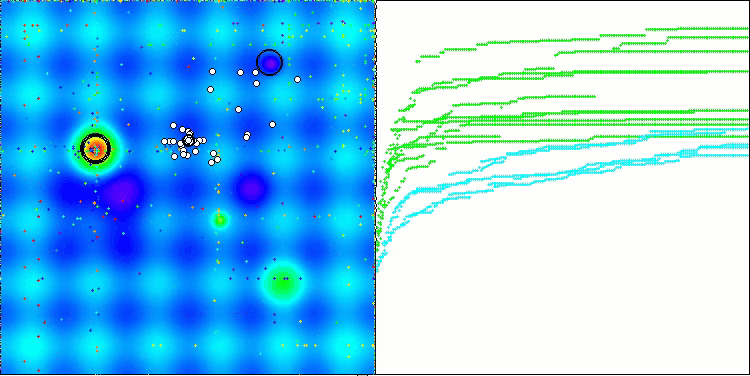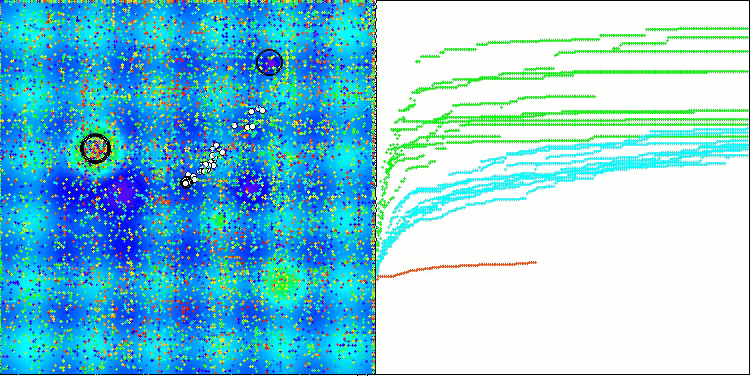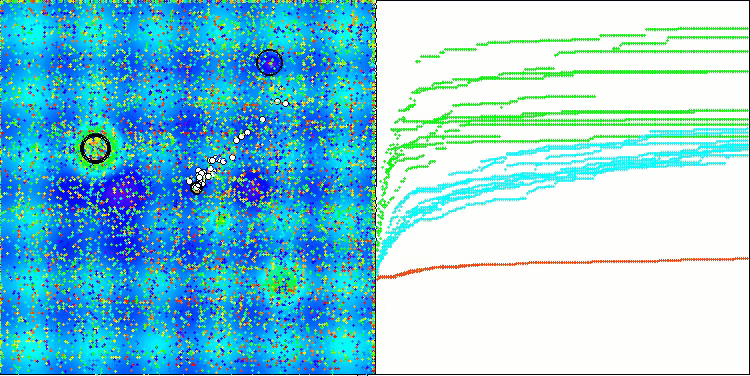
BCOm na função de teste Hilly

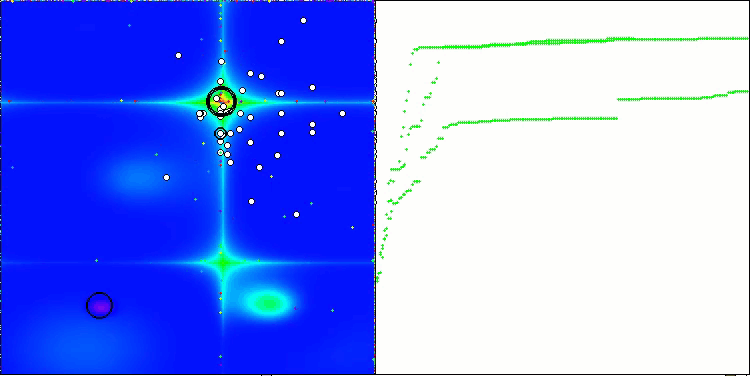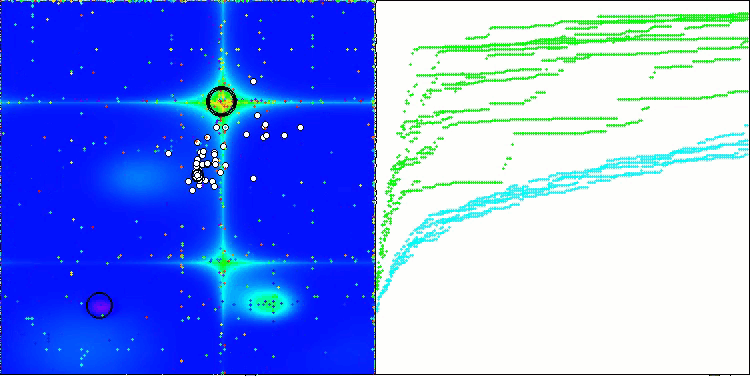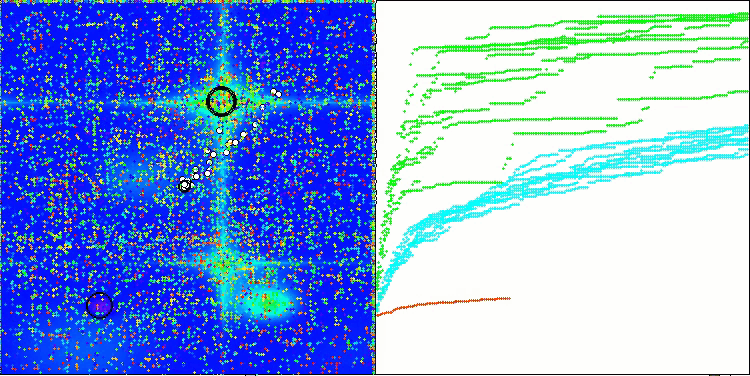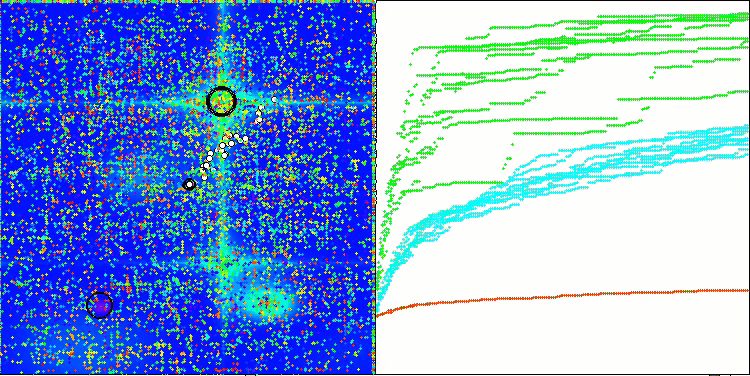
BCOm na função de teste Forest

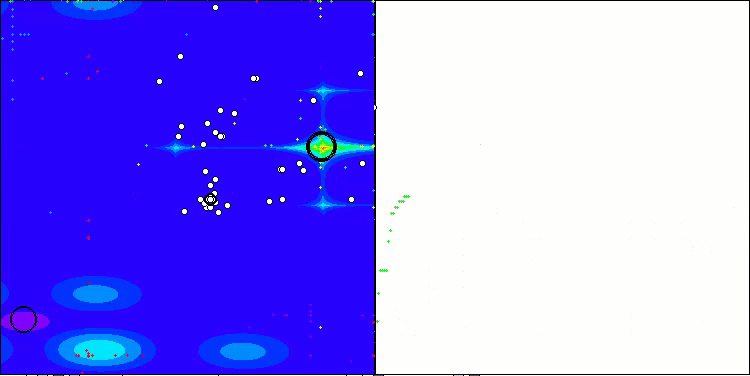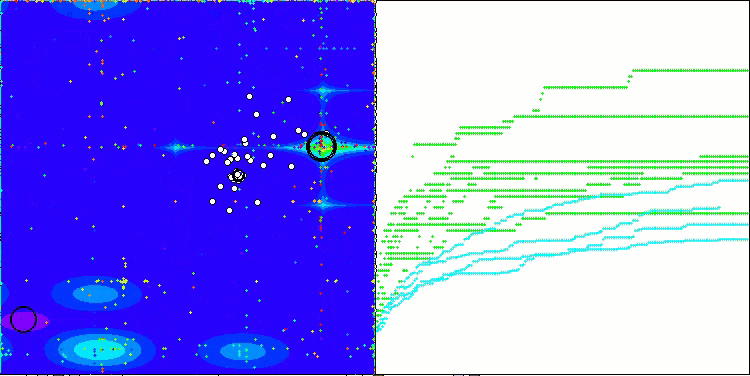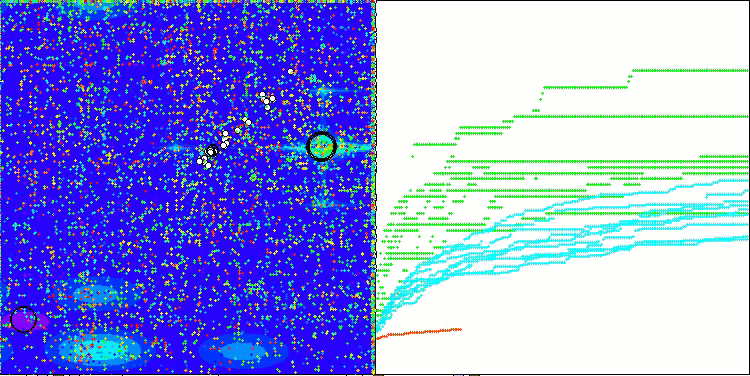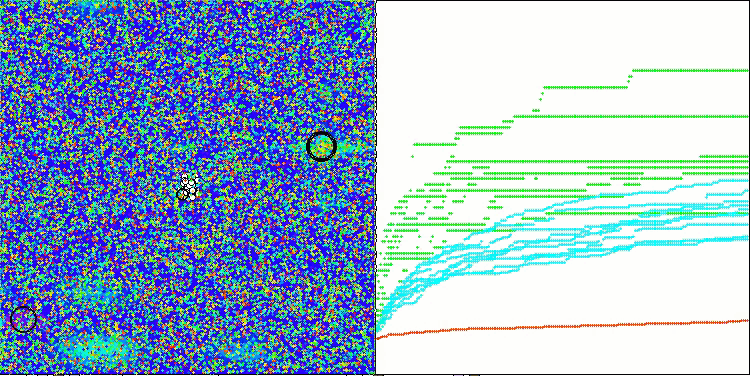
BCOm na função de teste Megacity

Nos testes, o algoritmo conquistou uma posição estável em 17º lugar no ranking geral dos algoritmos de otimização.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration optimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
8	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
9	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
10	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
11	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
12	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
13	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
14	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
15	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
16	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
17	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
18	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
19	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
20	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
21	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
22	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
23	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
24	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
25	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
26	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
27	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
28	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
29	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
30	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
31	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
32	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
33	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
34	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
35	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
36	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
37	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
38	AAA	algae adaptive algorithm	0,50007	0,32040	0,25525	1,07572	0,37021	0,22284	0,16785	0,76089	0,27846	0,14800	0,09755	0,52402	2,361	26,23
39	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
40	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
41	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
42	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
43	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
44	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
45	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84

Considerações finais

Foram apresentadas as versões original e modificada (BCOm) do algoritmo BCO. A versão original, reconstruída com base em informações de fontes abertas, apresentou cálculos trigonométricos complexos, além de propriedades de busca fracas e falhas matemáticas. Por isso, foi necessário repensar completamente o algoritmo, realizar uma análise aprofundada da estratégia de busca e criar uma nova versão modificada. As mudanças na lógica do algoritmo resultaram em cálculos mais simples a cada etapa da otimização, o que impactou positivamente a velocidade de execução do código. O novo algoritmo também equilibra de maneira diferente a exploração de novos espaços de soluções e a utilização de soluções já encontradas.

Embora essa abordagem atualizada contrarie um pouco o comportamento natural das bactérias, ela demonstrou alta eficiência na prática. A visualização de seu funcionamento mostrou sua capacidade de explorar profundamente regiões significativas do hiperespaço, evidenciando seu aprimoramento na capacidade de busca. Como resultado, a nova versão do algoritmo mostrou-se mais poderosa e eficaz que a original.

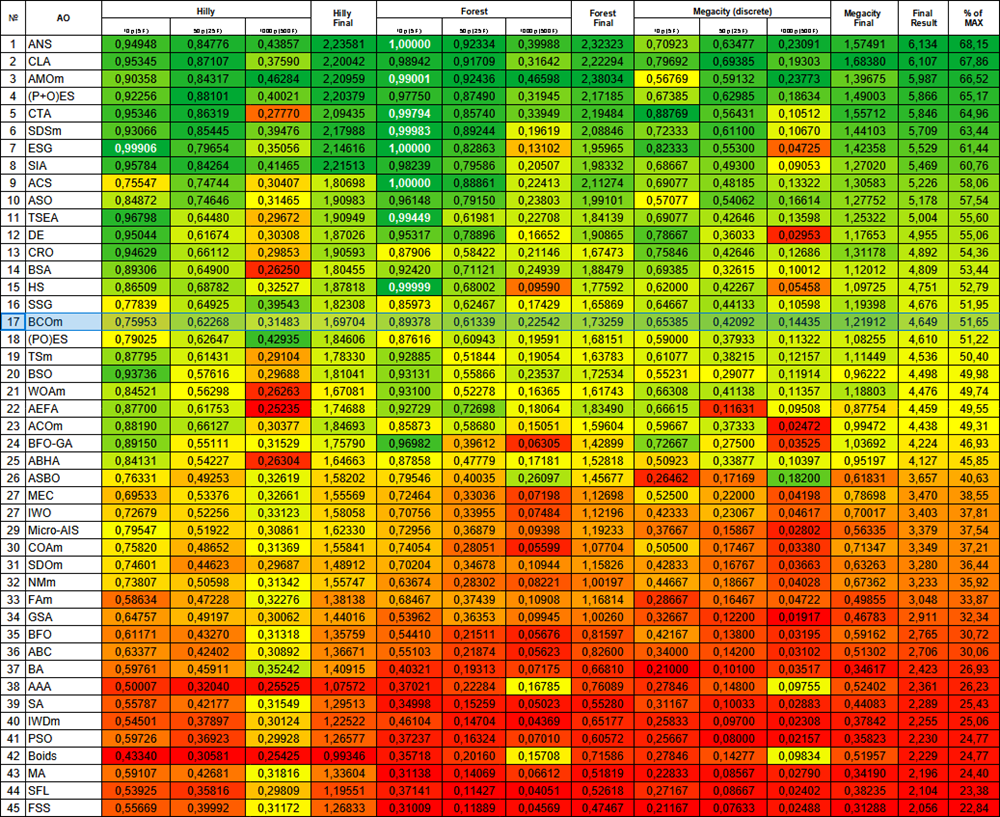
Figura 1. Graduação de cores dos algoritmos para os respectivos testes. Os resultados destacados em branco são maiores ou iguais a  0.99

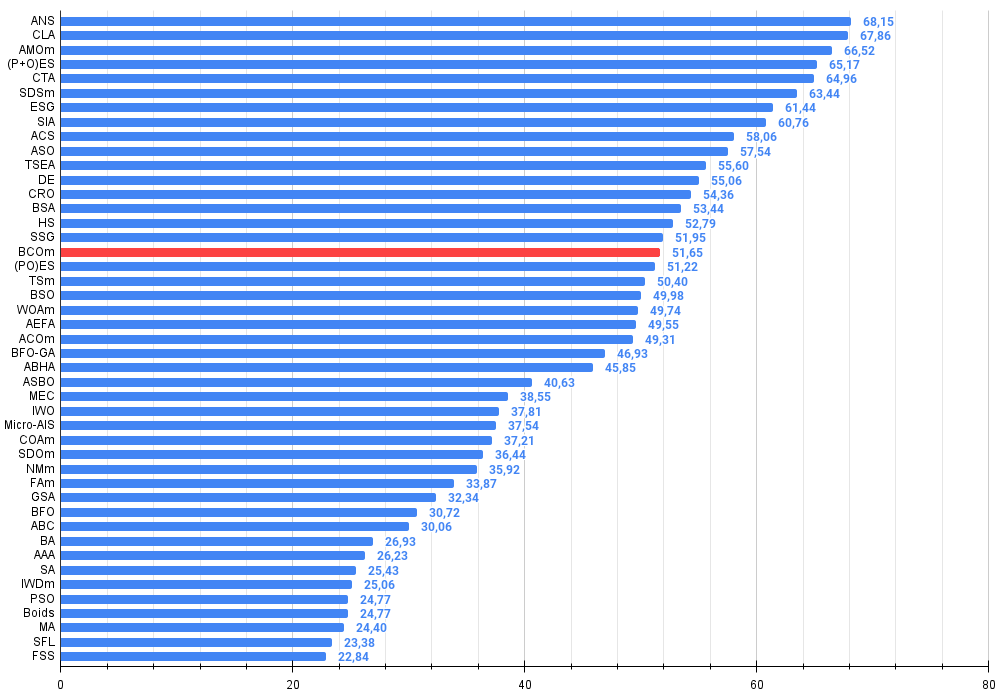
Figura 2. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível, e o arquivo contém um script para cálculo da tabela de classificação)

Prós e contras do algoritmo BCOm:

Prós:

1. Rápido.
2. Auto-adaptável.
   
3. Boa escalabilidade.
4. Apenas um parâmetro externo.
   

Contras:

1. Alta dispersão de resultados em funções de pequena dimensionalidade.
   

O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/pt/code/49355