母集団最適化アルゴリズム：Shuffled Frog-Leaping (SFL) アルゴリズム

MetaTrader 5 — 例 | 22 2月 2024, 10:32

203

Andrey Dik

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

Shuffled Frog Leaping Algorithm (SFL)は、М.Eusuffらによって2003年に提案されました。このアルゴリズムは、Memeticアルゴリズムと粒子群アルゴリズムの原理を組み合わせたもので、その設計は、採食過程におけるカエルの集団の行動にヒントを得たものです。

SFLアルゴリズムは、もともと組合せ最適化問題を解くためのメタヒューリスティクス手法として開発されました。これは数学的関数の使用と、情報に基づいたヒューリスティックな探索に基づいています。

SFLアルゴリズムは、ミームプレックスと呼ばれるカエルの複数の相互作用する仮想集団で構成されます。仮想のカエルはミームの宿主またはキャリアとして機能し、ミームは文化的進化の単位を表します。各ミームプレックスは、粒子群最適化に似た手法を用いて、独立した局所探索をおこないますが、局所探索に重点が置かれています。

大域的探索をサポートするため、シャッフル複合進化アルゴリズムに似た方法で、仮想カエルは定期的にシャッフルされ、新しいミームプレックスに再編成されます。さらに、改良された情報がランダムに生成されるように、ランダムな仮想カエルが生成され、集団の中で入れ替わります。

Shuffled Frog-Leapingは、複雑な最適化問題を解くのに有効な方法です。様々な応用領域で最適解を得ることができます。この記事では、このアルゴリズムの基本原理と応用、そして利点と限界について見ていきます。

2.アルゴリズム

ミーム学とは、ミームの概念に基づいた進化的情報伝達モデルのアプローチです。遺伝子の類似体であるミームは、模倣、学習、その他の手段を通じて人々の間に広まる文化的情報の単位として機能します。ミームの概念とミーム学の基礎は、1976年に、C.R.ドーキンスによって開発されました。ミームは、先人、親、教育者、本、文化的成果物などから、垂直的に伝達されます。人から人へ、文化から文化へのミームの水平伝播も可能です。ミームは純粋な情報であるにもかかわらず、その機能は人間の行動に大きな変化をもたらします。

ミームアルゴリズム（Mアルゴリズム）は、ミームの概念とネオダーウィンの進化原理に基づくハイブリッド集団メタヒューリスティック検索エンジン最適化アルゴリズムと定義されます。Mアルゴリズムの文脈では、ミームとは局所最適化アルゴリズムの実装であり、各反復で、あるいは一定の反復回数後に現在の解を改良します。Mアルゴリズムは、母集団ベースの大域的探索アルゴリズムと、1つ以上の古典的または母集団ベースの局所最適化アルゴリズムのハイブリッドとみなすことができます。当初、遺伝的アルゴリズムの効率を高めるための選択肢の1つとして、Mアルゴリズムが提案されました。

Mアルゴリズムの効率は、その自由パラメータの値に大きく依存します。多くの研究が、使用するミームの選択がこれらのアルゴリズムの効率に非常に大きな影響を与えることを示しています。そのため、この問題はMアルゴリズムに関する研究の中心的な位置を占めています。

ミームは、遺伝子の進化と人間の文化の進化の類似性を示唆する画期的なアイデアの1つです。ドーキンスによれば、ミームとは文化交流の単位であり、文化における遺伝子に相当します。ミームとは、ジェスチャーであったり、言葉であったり、アイデアであったりします。模倣学習によって人から人へと伝達できる文化情報の単位はすべてミームです。

遺伝的アルゴリズムとは異なり、memeticアルゴリズムは文化的進化の過程を模倣します。モスカートのアプローチは、ミームの進化になぞらえています。Memeticアルゴリズムは、局所探索、協調、競争、探索終了基準の段階から構成されます。ミームクラスは、遺伝的アルゴリズムに個人の個別学習を組み込み、可能な解決策の空間構造に関する情報を使用するという、共通のアイデアによって統合された幅広いアルゴリズムのクラスです。母集団探索と局所探索のバランスをとる問題は、探索空間の広範な探索と集中的な探索のバランスを保つ一般的な問題とみなすことができます。

ミームアルゴリズムには、大まかに以下の要素が含まれます。

1.局所検索：これを実装するには、焼きなまし法(Simulated Annealing)とSimulated Liftingのアルゴリズムを使うことができます。
2.協力：個体間の情報交換は、遺伝的アルゴリズムにおける2点交差演算子の使用と同様の手順でおこなうことができます。
3.競争：淘汰は遺伝的アルゴリズムと同様で、通常、集団の中で最も適合した個体を選択し、適合していない個体をそこから除外します。
4.検索終了基準：ミームアルゴリズムでは、反復回数のカウントや結果の改善の評価に加え、個体の多様性を推定することも含まれます。

ミームアルゴリズムは、個体の個別学習と可能解空間の構造に関する情報の利用という共通の考え方によって統合されたアルゴリズムの幅広いクラスです。

ミームは遺伝子と同様、複製子、つまり自己複製が可能な物体です。ミームにとって、生存と繁殖は、ミームを広める宿主の存在に依存します。ミームは変化し、新しいミームを形成し、人々の心という資源をめぐる争いに参加することができます。

ミームはしばしば複合体（ミームプレックス）にまとめられ、キャリアの争奪戦を盛り上げる。ミームプレックスは、生物の遺伝暗号を構成する遺伝子の共生的集合体に類似しています。ミームプレックスの例は宗教です。ミームプレックスは、個人や社会の行動形成に大きな影響を与えます。

Shuffled Frog-Leapingアルゴリズムに直接移りましょう。アルゴリズムの主なアイデアは、大域的リーダーGを持つカエルの集団全体をミームに分割することです。各ミーム（グループ）にはリーダーLがいます（図1）。

カエル1

図1：大域的リーダー(G)を持つカエルの集団が、局所的リーダー(L)を持つミームに分かれます。

それぞれのミームの中で、カエルはその局所的リーダーの方向に動く傾向があります。1匹のカエルの地位が上がれば、リーダーシップは更新されます。ミームは探索空間で分離されておらず、重複している可能性があります。したがって、あるミームの領域にいるカエルは、別のミームに属する可能性があります。これにより、カエルは探索空間における位置の変化に応じて、あるミームから別のミームへと空間的に移動することができるダイナミックな環境が作り出されます。

大域的な条件付き最適化問題についえ考えます。そこでは、適応度関数は最大化の対象となります。SFLアルゴリズムには以下の基本ステップがあります。

1.0 アルゴリズムを初期化する
1.1 ランダムな座標を持つカエルの初期集団を作成する
1.2 それぞれのカエルの適応度を決定する
1.3 ミームプレックス（亜個体群）を作成し、ミームプレックス間にカエルを分布する

2.0 最適解探索のサイクル
2.1 各ミームプレックスについて：
    2.1.1 一番良いカエルを決定する
    2.1.2 残りのカエルをミームプレックスで一番良いカエルに向かわせる
2.2 カエルを動かしても適応度が向上しない場合：
    2.2.1 大域的に一番良いカエルに向かって動かす
    2.2.2 それでも適応度が向上しない場合は、カエルをフィールド上のランダムな場所に動かす

3.0 カエルの適応度を測定する
3.1 個体群内のそれぞれのカエルの適応度を測定する
3.2 各ミームプレックスおよび母集団全体において一番良いカエルに関する情報を更新する

4.0 大域的に一番良いカエルを決定し、ミームプレックスを更新する
4.1 全個体群に対して大域的に一番良いカエルを決定する
4.2 最終サイクルの場合：
    4.2.1 ミームプレックスサイクルカウンタをリセットする
    4.2.2 カエルのランダムインデックスを生成する
    4.2.3 新しいインデックスを使ってカエルをミームプレックスにコピーする
    4.2.4 各ミームプレックスで一番良いカエルを決定する
    4.2.5 カエルの適応度とステップをリセットする
4.3 これが最終サイクルでない場合：
    4.3.1 母集団のカエルの適応度と座標を、対応するミームプレックスのカエルにコピーする
    4.3.2 各ミームプレックスで一番良いカエルを決定する
    4.3.3 それぞれのカエルの適応度に応じて、次のジャンプの方向を決める

このように、SFLアルゴリズムの基本は、各ミームプレックス内での局所探索と、最適なミームプレックスエージェントの位置に関する情報を交換することによる大域探索の組み合わせです。
このアルゴリズムはSFLアルゴリズムを改良したもので、局所探索の段階でエージェントは対応するミームプレックスの最良のエージェントの方向に正確に移動するのではなく、ランダムに摂動された方向に移動します。人工免疫システムアルゴリズムを含む）多くの集団アルゴリズムとの逐次および並列ハイブリダイゼーションが知られています。

カエル2

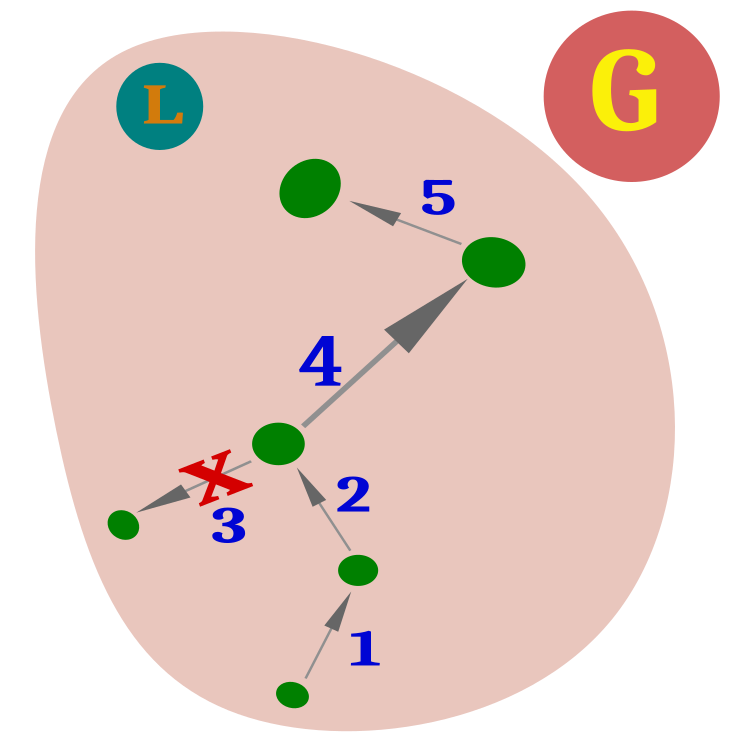
図2：カエルのジャンプ：前の移動が失敗した場合、次のジャンプは同じ場所からおこなわれる

SFL最適化アルゴリズムの論理単位はカエルです。これは、探索空間におけるエージェントを表すS_Frog構造体によって記述することができます。

S_Frog構造体は以下のフィールドを含みます。

c：カエルの現在位置を表す座標の配列
cPrev：カエルの前の位置の座標の配列
f：カエルの現在位置に対する適応度関数
fPrev：カエルの前の位置に対する適応度関数
frogStep：カエルがいるステップの番号

//——————————————————————————————————————————————————————————————————————————————
struct S_Frog
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
    frogStep = 0;
  }
  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
  int    frogStep; //frog step
};
//——————————————————————————————————————————————————————————————————————————————

S_Memeplex構造体は、アルゴリズムにおけるmemeplexを記述します。以下のフィールドが含まれます。

frogs：ミームプレックスを構成するカエルの配列
fBest：ミームプレックス内のすべてのカエルの中での適応度関数の最高値
cBest：ミームプレックスにおける適応度関数のベスト値に対応する座標の配列

//——————————————————————————————————————————————————————————————————————————————
struct S_Memeplex
{
  S_Frog frogs [];
  double fBest;     //best fitness
  double cBest [];  //best coordinates
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_SFLクラスは、アルゴリズムの初期化、カエルの移動、母集団の修正などのメソッドを提供します。また、値の変換や乱数生成のための補助メソッドも含まれています。

以下のフィールドを含むSFLアルゴリズムクラスを書きましょう。

cB：最適な座標を格納する配列
fB：最適な座標に対する適応度関数の値を格納する変数
frogs：個体群内のすべてのカエルを格納する配列
mems：ミームプレックス（カエルのグループ）を格納する配列
rangeMax：各探索座標の最大値を格納する配列
rangeMin：各探索座標の最小値を格納する配列
rangeStep：各座標の探索ステップを格納する配列

publicクラスのメソッド：

Init：アルゴリズムのパラメータを初期化するメソッド
coordinatesNumberP：検索座標の数
populationSizeP：個体数（カエルの数）
numbMemsP：ミームプレックス（カエルのグループ）の数
numbCyclesP：ミームプレックスのサイクル数
frogStepsToLocalMaxP：局所的最大値までのカエルステップ数
movConstantP：カエルの変位定数（検索ステップ）

Moving：探索空間におけるカエルの移動を実装するメソッド
Revision：カエルの個体数の修正を実装し、最適な座標を更新するメソッド
SeInDiSp：ある範囲から別の範囲へ、指定されたステップで値を変換する補助メソッド
RNDfromCI：与えられた間隔で乱数を生成する補助メソッド

privateクラスのフィールドの説明：

coordinatesNumber：検索座標の数
frogsNumber：個体群内のカエルの数
numbMems：ミームプレックス（カエルのグループ）の数
numbCycles：ミームプレックスのサイクル数
frogStepsToLocalMax：局所的最大値までのカエルステップ数
movConstant：カエルの変位定数（検索ステップ）
memsFrogs：各ミームプレックス内のカエルの数
numbCyclesCNT：サイクルカウンタ
vect：ベクトルを格納する配列
indexes：インデックスを格納する配列
revision：母集団修正の必要性を示すフラグ

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SFL
{
  //----------------------------------------------------------------------------
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates
  public: S_Frog frogs     []; //all frogs
  public: S_Memeplex mems  []; //memeplexes

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search


  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    numbMemsP,            //number of memeplexes
                     const int    numbCyclesP,          //number of cycles in the memeplex
                     const int    frogStepsToLocalMaxP, //frog steps to the local maximum
                     const double movConstantP);        //movement step (0.0 .. 1.0)

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber;   //coordinates number
  private: int    frogsNumber;         //frogs number
  private: int    numbMems;            //number of memeplexes
  private: int    numbCycles;          //number of cycles in the memeplex
  private: int    frogStepsToLocalMax; //frog steps to the local maximum
  private: double movConstant;         //movement step (0.0 .. 1.0)
  private: int    memsFrogs;           //number of frogs in the memplex
  private: int    numbCyclesCNT;       //cycle counter

  private: double vect    [];          //vector
  private: int    indexes [];          //indexes
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

アルゴリズムを初期化するために、いくつかのパラメータを持つInit初期化メソッドを使用します。

coordinatesNumberP：座標の数
populationSizeP：母集団のサイズ
numbMemsP：ミームプレックスの数
numbCyclesP：ミームプレックスのサイクル数
frogStepsToLocalMaxP：局所的最大値までのカエルのステップ数
movConstantP：移動ステップ（0.0から1.0まで）

まず、このメソッドは乱数発生器をリセットし、変数fB(-DBL_MAX)とrevision(false)の初期値を設定します。
次に、このメソッドは、必要な次元のrangeMax、rangeMin、rangeStep、vect、indexes、cB、frogs、mems各配列を作成します。
このメソッドは、座標の数を渡すInitメソッドを使用して、frogs配列の各カエルと、mems配列の各ミームプレックスの各カエルを初期化します。
次に、このメソッドは、各ミームプレックスのfBest変数の初期値を-DBL_MAXに設定し、各メミームプレックスのcBest配列を必要なサイズで作成します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SFL::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    numbMemsP,            //number of memeplexes
                     const int    numbCyclesP,          //number of cycles in the memeplex
                     const int    frogStepsToLocalMaxP, //frog steps to the local maximum
                     const double movConstantP)         //movement step (0.0 .. 1.0)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber   = coordinatesNumberP;
  frogsNumber         = populationSizeP;
  numbMems            = numbMemsP;
  numbCycles          = numbCyclesP;
  frogStepsToLocalMax = frogStepsToLocalMaxP;
  movConstant         = movConstantP;
  memsFrogs           = frogsNumber / numbMems;

  numbCyclesCNT       = 0;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);
  ArrayResize (indexes,   frogsNumber);

  ArrayResize (cB, coordinatesNumber);

  ArrayResize (frogs, frogsNumber);
  for (int i = 0; i < frogsNumber; i++)
  {
    frogs [i].Init (coordinatesNumber);
  }

  ArrayResize (mems, numbMems);
  for (int i = 0; i < numbMems; i++)
  {
    ArrayResize (mems [i].frogs, memsFrogs);
    for (int frgs = 0; frgs < memsFrogs; frgs++)
    {
      mems [i].frogs [frgs].Init (coordinatesNumber);
    }

    mems [i].fBest = -DBL_MAX;
    ArrayResize (mems [i].cBest, coordinatesNumber);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Moving メソッドは、カエルを探索空間内を移動させるように設計されています。このメソッドはかなり大きいので、部分的に分析することにします。

コードの冒頭で、revision変数の値を確認します。falseの場合、以下のコードブロックが実行されます。

- 関数の最良推定値を表すfB変数の初期値を設定します。この場合、-DBL_MAX値（負の無限大）が割り当てられます。
- 各カエルが初期化されるサイクルを開始します。それぞれのカエルに：
- 各c座標のサイクルを開始します。
- 与えられた範囲内の乱数を返すRNDfromCI関数を使用して、c座標の乱数値を生成します。
- c座標値はSeInDiSp関数を使って範囲に変換され、あるステップで範囲内の値をシフトさせることができます。
- カエルのf関数の値を-DBL_MAXに設定します。
- カエルのfPrev関数の前の値を-DBL_MAXに設定します。
-frogStepを0に設定します。

- 各c座標のサイクルを開始します。
- movConstantの範囲の最大値と最小値の差の積であるvect[c]を計算します。
- revision 変数にtrueを設定し、初期化が完了したことを示します。
- numbCyclesCNT変数を0に設定します。

したがって、このコードではカエルを初期化し、関数とその他のパラメータの初期値を設定し、さらに各c座標のvect[c]値を計算します。

if (!revision)
{
  fB = -DBL_MAX;

  for (int frgs = 0; frgs < frogsNumber; frgs++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      frogs [frgs].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      frogs [frgs].c [c] = SeInDiSp (frogs [frgs].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      frogs [frgs].f        = -DBL_MAX;
      frogs [frgs].fPrev    = -DBL_MAX;
      frogs [frgs].frogStep = 0;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = (rangeMax [c] - rangeMin [c]) * movConstant;
  }

  revision      = true;
  numbCyclesCNT = 0;
}

revision フラグがtrueの場合、アルゴリズムがカエルを動かす段階に入ったことを意味します。メソッド変数についてはすでに熟知しているので、詳細は割愛します。コードのこの部分は、各カエルの個々のステップに従って、カエルのジャンプを実装しています。最初のステップで、カエルは局所的リーダーに向かって跳び、カエルの位置が改善された場合は試行がカウントされ、そうでない場合はステップカウンタが増加します。言い換えれば、アルゴリズムの外部パラメータに従って、局所的リーダーに向かって跳ねるために一定の試行回数が割り当てられます。

リーダーであるカエルには、ミームプレックスの他のカエルとは異なる動きの原理が使われています。リーダーは、自分の陣地の狭い範囲内でランダムな方向に跳ねるだけです。

リーダーとは異なり、他のすべてのカエルは次の式に従ってリーダーに向かって跳寝ます。

coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);

この式は、カエルの新しい座標が、rndランダム成分を導入しながら、すべての座標のユークリッド距離で正規化された距離だけリーダーに向かって移動することによって得られることを示しています。

else
{
  int cnt = 0;
  double eDistance = 0.0; //euclidean distance
  double coordDiff = 0.0; //the difference in coordinates

  for  (int m = 0; m < numbMems; m++)
  {
    for (int frgs = 0; frgs < memsFrogs; frgs++)
    {
      //2.1 move the frogs towards the best one in the memeplex-----------------
      if (mems [m].frogs [frgs].frogStep < frogStepsToLocalMax)
      {
        if (mems [m].frogs [frgs].fPrev != -DBL_MAX && mems [m].fBest != -DBL_MAX)
        {
          if (mems [m].frogs [frgs].fPrev == mems [m].fBest)
          {
            for (int c = 0; c < coordinatesNumber; c++)
            {
              rnd = RNDfromCI (-1.0, 1.0);
              rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd;
              coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * 0.2;
              mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
            }
          }
          else
          {
            eDistance = 0.0;
            coordDiff = 0.0;

            //calculate Euclidean distance----------------------------------
            for (int c = 0; c < coordinatesNumber; c++)
            {
              coordDiff  = mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c];
              coordDiff *= coordDiff;
              eDistance += coordDiff;
            }

            eDistance = sqrt (eDistance);

            for (int c = 0; c < coordinatesNumber; c++)
            {
              rnd = RNDfromCI (-1.0, 1.0);
              coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);
              mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
            }
          }
        }
        else
        {
          for (int c = 0; c < coordinatesNumber; c++)
          {
            rnd = RNDfromCI (-1.0, 1.0);
            rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd;
            coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c];
            mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
      }
      else
      {
        //2.2 move towards global if the move is worse than the previous one-----
        if (mems [m].frogs [frgs].frogStep /*==*/ >= frogStepsToLocalMax)
        {
          eDistance = 0.0;
          coordDiff = 0.0;

          //calculate Euclidean distance------------------------------------
          for (int c = 0; c < coordinatesNumber; c++)
          {
            coordDiff  = cB [c] - mems [m].frogs [frgs].cPrev [c];
            coordDiff *= coordDiff;
            eDistance += coordDiff;
          }

          eDistance = sqrt (eDistance);

          for (int c = 0; c < coordinatesNumber; c++)
          {
            rnd = RNDfromCI (-1.0, 1.0);
            coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((cB [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);
            mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
        //2.3 move randomly across the field --------------------------------
        else
        {
          for (int c = 0; c < coordinatesNumber; c++)
          {
            rnd = RNDfromCI (-1.0, 1.0);

            coord    = RNDfromCI (rangeMin [c], rangeMax [c]);
            mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
      }

      frogs [cnt] = mems [m].frogs [frgs];
      cnt++;
    }
  }


  //--------------------------------------------------------------------------
  numbCyclesCNT++;
}

Revisionメソッドは、アルゴリズムの各反復で大域的リーダーを決定し、局所的リーダーを決定するように設計されています。各ミームプレックス内のカエルの移動に割り当てられるサイクル数がなくなったら、シャッフルをおこないます。つまり、カエルをランダムにミームプレックスに割り当て直し、それによってミームプレックス間で情報を交換します。この方法では、対応するリープステップ、つまりカエルが次の反復で移動する方向（局所的リーダーまたは大域的リーダーに向かって、あるいは探索空間のランダムな方向）も考慮します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SFL::Revision ()
{
  //4.1 determine the globally best one by population-------------------------------
  for (int i = 0; i < frogsNumber; i++)
  {
    if (frogs [i].f > fB)
    {
      fB = frogs [i].f;
      ArrayCopy (cB, frogs [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  int cnt = 0;

  //if the last loop=========================================================
  if (numbCyclesCNT >= numbCycles)
  {
    //4.2.0 reset the memeplex cycle counter-----------------------------------
    numbCyclesCNT = 0;

    //4.2.1 generate random indices--------------------------------------
    for (int i = 0; i < frogsNumber; i++) indexes [i] = i;

    Shuffle (indexes, frogsNumber);

    //4.2.2 copy to memeplexes accidentally------------------------------------
    for  (int m = 0; m < numbMems; m++)
    {
      mems [m].fBest = -DBL_MAX;

      for (int frgs = 0; frgs < memsFrogs; frgs++)
      {
        mems [m].frogs [frgs] = frogs [indexes [cnt]];
        cnt++;

        //4.2.3 determine the best one in each memeplex---------------------------
        if (mems [m].frogs [frgs].f > mems [m].fBest)
        {
          mems [m].fBest = mems [m].frogs [frgs].f;
          ArrayCopy (mems [m].cBest, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY);
        }

        //4.2.4 reset frogs' fitness and step------------------------
        mems [m].frogs [frgs].f        = -DBL_MAX;
        mems [m].frogs [frgs].fPrev    = -DBL_MAX;
        mems [m].frogs [frgs].frogStep = 0;
      }
    }
  }
  //if NOT the last cycle======================================================
  else
  {
    for  (int m = 0; m < numbMems; m++)
    {
      for (int frgs = 0; frgs < memsFrogs; frgs++)
      {
        mems [m].frogs [frgs].frogStep++;

        //4.3.1 copy the fitness and coordinates of frogs from the population to the
        //corresponding frog memeplexes
        mems [m].frogs [frgs].f = frogs [cnt].f;
        ArrayCopy (mems [m].frogs [frgs].c, frogs [cnt].c, 0, 0, WHOLE_ARRAY);

        //4.3.2 determine the best one in each memeplex---------------------------
        if (frogs [cnt].f > mems [m].fBest)
        {
          mems [m].fBest = frogs [cnt].f;
          ArrayCopy (mems [m].cBest, frogs [cnt].c, 0, 0, WHOLE_ARRAY);
        }

        //4.3.3 determine the direction of the next jump------------------------
        if (mems [m].frogs [frgs].frogStep <= frogStepsToLocalMax)
        {
          if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev)
          {
            mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f;
            ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY);
            mems [m].frogs [frgs].frogStep = 0;
          }
        }
        else
        {
          if (mems [m].frogs [frgs].frogStep >= frogStepsToLocalMax + 1)
          {
            if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev)
            {
              mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f;
              ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY);
              mems [m].frogs [frgs].frogStep = 0;
            }
          }
          else
          {
            mems [m].frogs [frgs].f        = -DBL_MAX;
            mems [m].frogs [frgs].fPrev    = -DBL_MAX;
            mems [m].frogs [frgs].frogStep = 0;
          }
        }

        cnt++;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

SFL最適化アルゴリズムでは、ミームプレックス間でカエルをランダムに混ぜる必要があります。ランダムシャッフリング問題は、そのアルゴリズム解が自明でないため興味深い問題ですが、ロナルド・フィッシャーとフランク・イエーツが効果的で高速なアルゴリズムを提供しています。以前は、その必要性がなかったため、同様のコンセプトは使用していませんでした。コンピュータサイエンス、特に遺伝的アルゴリズム、暗号、統計の分野で広く使われています。

フィッシャー-イエーツアルゴリズムの主な利点：
1.導入の容易さ：フィッシャー-イエーツアルゴリズムは、どんなプログラミング言語でも簡単に実装できます。複雑な数学的計算や特別なライブラリを必要としません。
2.効率：フィッシャー-イエーツアルゴリズムは線形時間で実行されます。言い換えれば、実行時間は並べ替えが必要な要素の数に依存します。そのため、大規模なデータセットに対して非常に効率的です。
3.ランダム性：フィッシャー-イエーツアルゴリズムは、非常にランダムな順列を保証します。これは、ランダムテスト、暗号化、シミュレーションなど多くの用途で重要です。
4.入力の独立性：フィッシャー-イエーツアルゴリズムは、データの構造や特性を知らなくても、どのようなデータ集合にも適用できます。そのため、さまざまな作業に使える万能ツールとなっています。
5.疑似ランダム性：フィッシャー-イエーツアルゴリズムは、ランダム性（必ずしも真のランダム性ではない）が要求される多くのアプリケーションで使用できる擬似ランダム順列を生成します。

一般的に、フィッシャー-イエーツアルゴリズムはシンプルで効率的、かつ汎用性が高くなります。ランダム性とデータの並べ替えを含む多くの問題に役立つツールです。

//——————————————————————————————————————————————————————————————————————————————
void Shuffle (int & arr [], int size)
{
  int index, temp;
  for (int i = size - 1; i > 0; i--)
  {
    index = MathRand () % (i + 1);
    temp = arr [i];
    arr [i] = arr [index];
    arr [index] = temp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

SFLテストスタンドの結果：

C_AO_SFL:50;25;15;5;0.7
=============================
5 Rastrigin's; Func runs 10000 result:66.52578871476199
Score:0.82429
25Rastrigin's;Funcruns10000result：52.38937199890908
Score:0.64913
500 Rastrigin's; Func runs 10000 result:44.5591163558836
Score:0.55211
=============================
5 Forest's; Func runs 10000 result:0.5762718670482314
Score:0.32597
25 Forest's; Func runs 10000 result:0.16329693292687839
Score:0.09237
500 Forest's; Func runs 10000 result:0.04968320483668511
Score:0.02810
=============================
5 Megacity's; Func runs 10000 result:3.1599999999999997
Score:0.26333
25 Megacity's; Func runs 10000 result:1.016
Score:0.08467
500 Megacity's; Func runs 10000 result:0.3004
Score:0.02503
=============================
All score:2.84501

SFLアルゴリズムのアニメーションを観察すると、その逆が予想されていたにもかかわらず、個々のミームによるクラスタリングやグループ化は検出されません。最適化エージェント（点）はフィールド全体に無秩序に分布し、粒子の動きにはパターンがありません。アルゴリズムの収束の質の低さはすぐに目につき、収束グラフ上の長い滑らかな部分によって決定される局所極値で立ち往生することで明らかになります。しかし、最適化されたパラメータの数が増えると、「ステップ」は減少します。

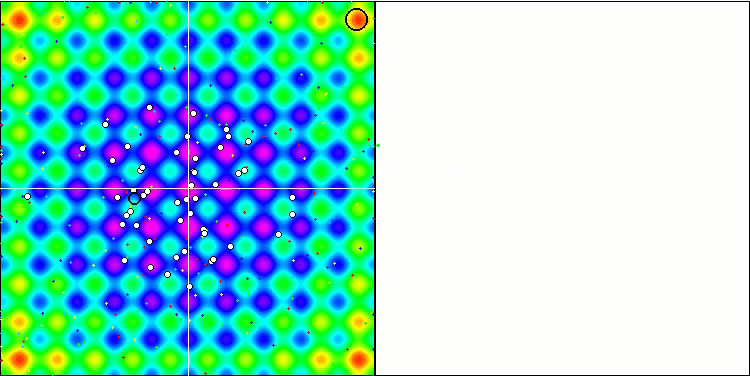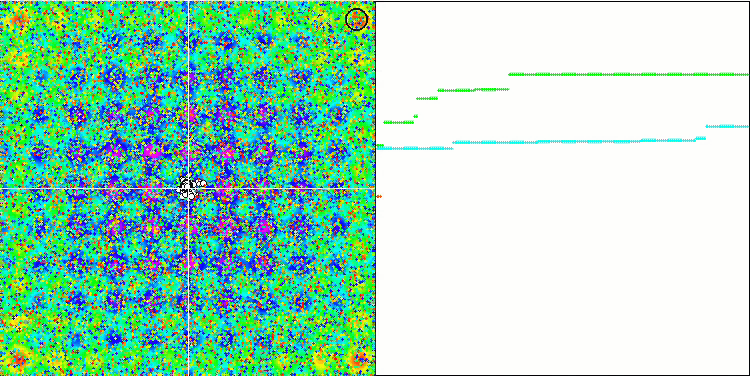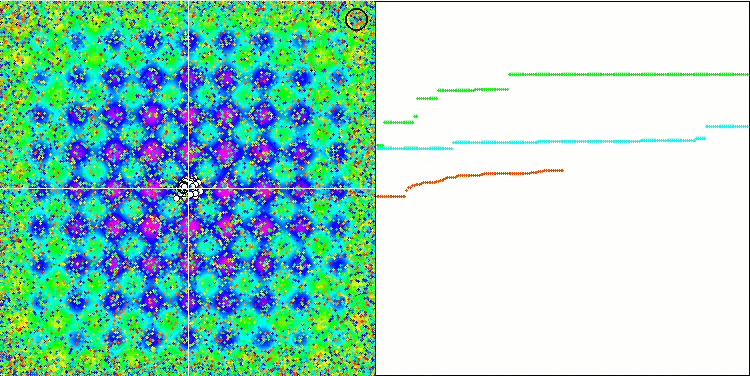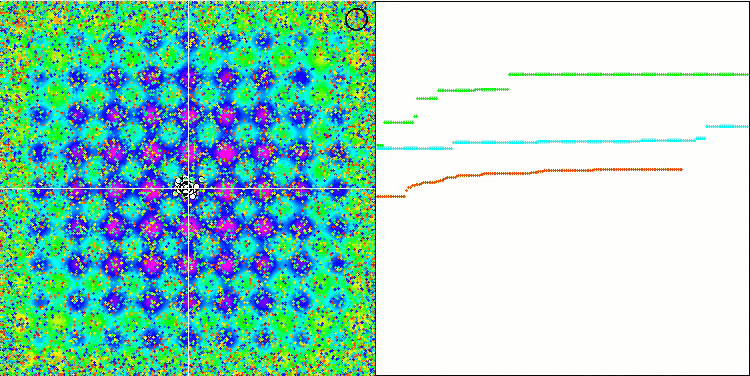
Rastriginテスト関数のSFL

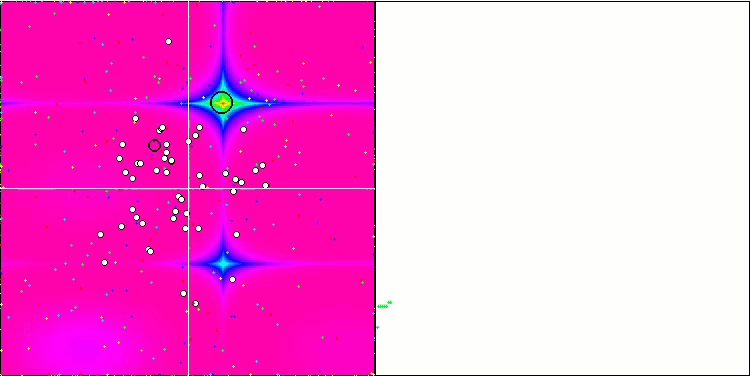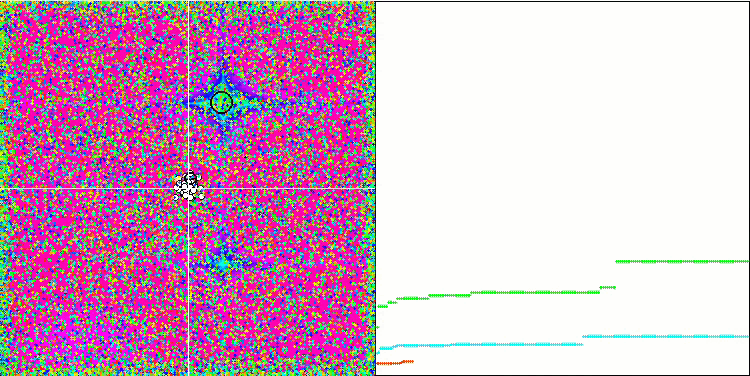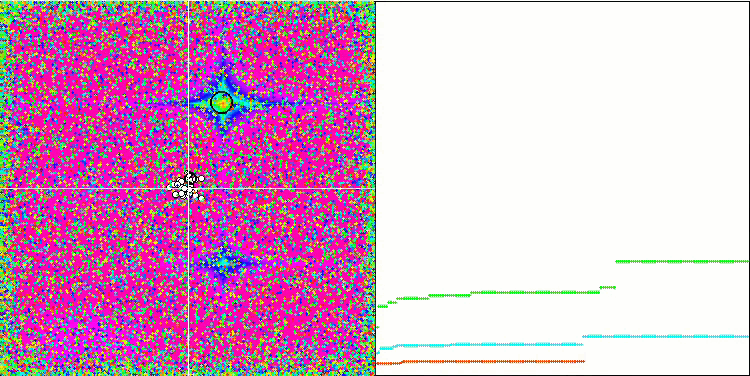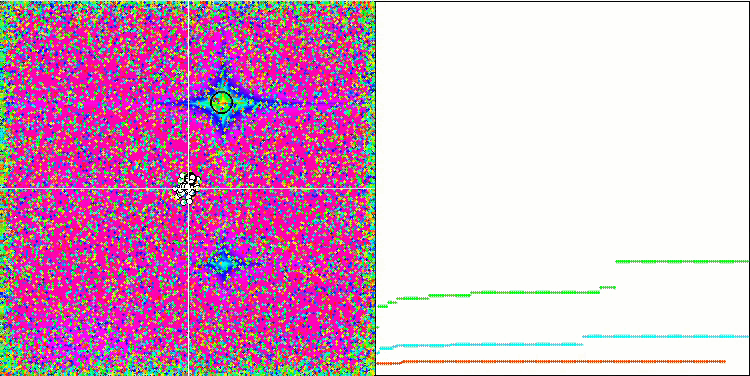
Forestテスト関数のSFL

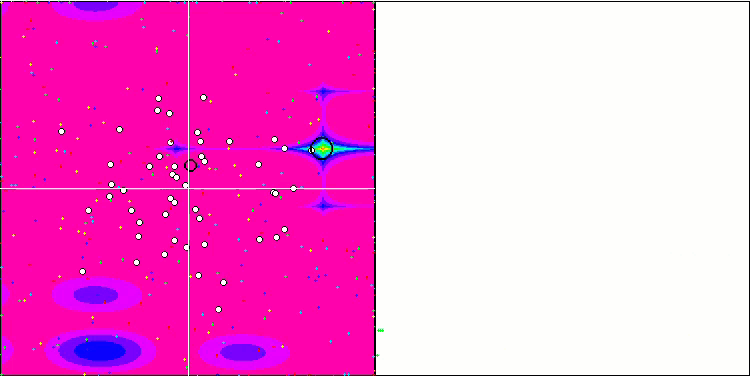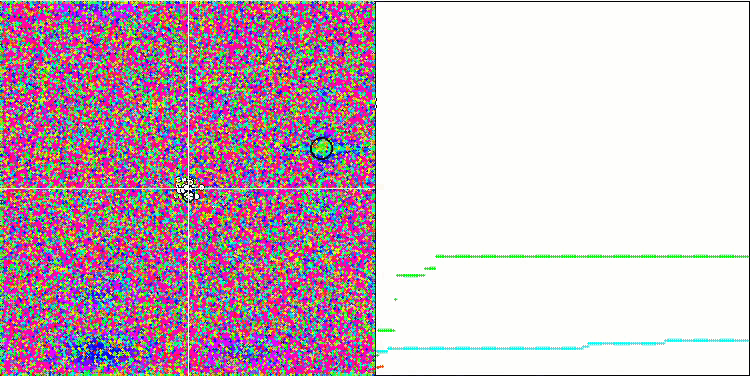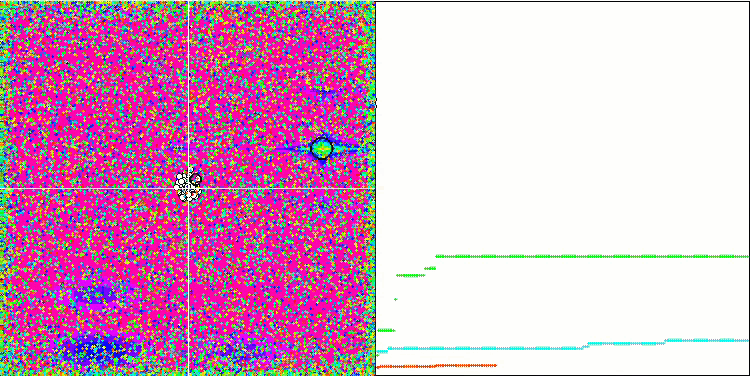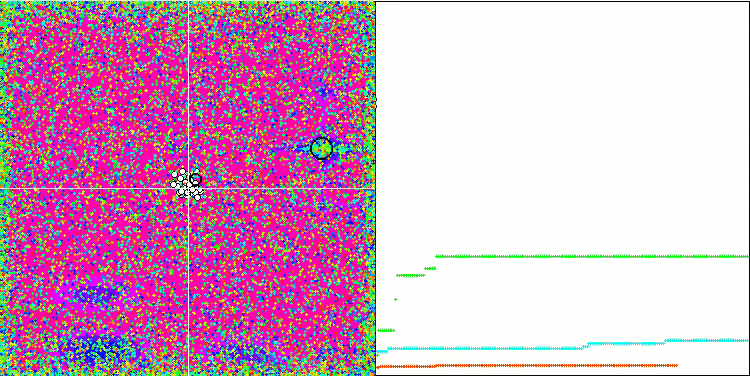
Megacityテスト関数のSFL

そろそろ結論を出す時期です。結果表によると、SFLアルゴリズムは最適化の点で平均以下の結果を示しています。SFLは滑らかなRastrigin関数に対していくらか有利ではあるが、滑らかな関数に対して好ましいアルゴリズムとして推奨するには不十分です。ForestとMegacityの曲げ関数では、SFLは滑らかな関数に比べて悪い結果を示しました。これは、最適化された機能を持つ平坦な区間では、跳ねるカエルはその位置を改善せず、地形に「引っかかる」ことなく、常に元の場所に戻ってしまうという事実から説明できます。

AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果
AO	詳細	10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）	Rastrigin最終	10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）	Forest最終	10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）	Megacity最終	最終結果
SSG	苗木の播種と育成	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100.000
HS	ハーモニー検索	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
ACOm	蟻コロニー最適化M	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
IWO	侵入雑草最適化	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
COAm	カッコウ最適化アルゴリズムM	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
FAm	ホタルアルゴリズムM	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
ABC	人工蜂コロニー	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
GSA	重力探索法	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
BA	コウモリアルゴリズム	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
BFO	細菌採餌の最適化	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
ゆうようびせいぶつぐん	電磁気学的アルゴリズム	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
SFL	Shuffled Frog-Leaping	0.40072	0.23739	0.26548	0.90360	0.20153	0.04147	0.02652	0.26952	0.27273	0.05535	0.06639	0.39446	15.203
MA	モンキーアルゴリズム	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
FSS	魚群検索	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
PSO	粒子群最適化	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
RND	ランダム	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

まとめ

SFLはむしろ、他の最適化アルゴリズムの「上部構造」であり、ミームプレックス内のエージェントを動かすためのロジックとして使用できます。SFLはもともと、既存のアルゴリズムの最適化品質を向上させる技術として考案されました。単独の最適化アルゴリズムとしては、SFLは先に述べた集団アルゴリズムの中で平均以下の結果を示しています。SFLは、アルゴリズム内の論理ステップを組み合わせて、探索と利用の両方を強化する実験に大きな可能性を秘めています。SFLは非常に柔軟で適応性が高いため、特定の最適化問題での使用に適しています。

アルゴリズムのテスト結果のヒストグラムを以下に示します（0から100までのスケールで、多ければ多いほど良くなります。アーカイブには、この記事で説明した方法で評価表を計算するスクリプトがある）。

チャート

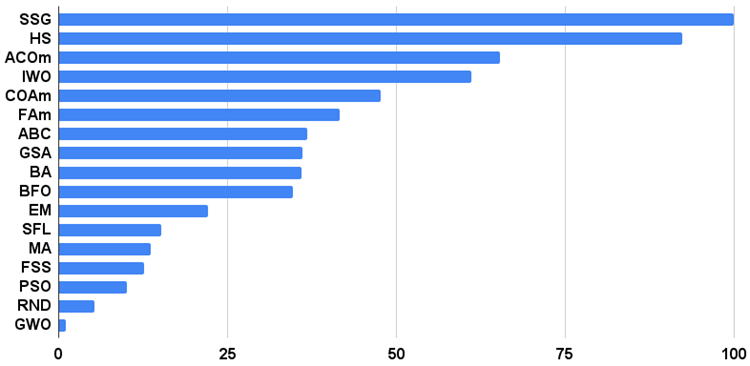
図3：テストアルゴリズムの最終結果のヒストグラム

Shuffled Frog-Leaping (SFL)アルゴリズムの長所と短所：

長所：
1.少数の外部パラメータ
2.アルゴリズムアーキテクチャの独創性、ミームで他の最適化アルゴリズムを使用する能力

短所：
1.計算量が多い
2.滑らかで離散的な関数に関する悪い結果
3.水平に平らな「パッド」を持つ関数でスタックする

各記事には、過去の記事のアルゴリズムコードを最新版に更新したアーカイブが用意されています。本記事は、著者の蓄積された経験に基づくものであり、個人的な意見を述べたものです。結論や判断は、実験に基づくものです。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13366

添付されたファイル |

ZIPをダウンロード

17_The_world_of_AO_SFL.zip (143.2 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (11)

fxsaber | 20 9月 2023 において 00:33

Stanislav Korotky #:

文字列検索（！）でループを使うことに "はまった "のだが、大きなプログラムでは超非効率的になる可能性がある。

iniファイルには文字列パラメーターだけでなく、他のタイプのパラメーターも含まれている（テキストで表現されているが）。

ファクトリーでのシングルトンは問題ない。関数オブジェクトでのシングルトン - この場合は例の操作性のためだけですが - 多重性を実装できます。

私は初期化の段階で文字列解決を使います。ミリ秒もかからないと思います。正直なところ、潜在的な問題は感じなかった。

Dmitry Fedoseev | 20 9月 2023 において 06:16

fxsaber #:

素晴らしい仕事をしてくれた作者に感謝するとともに、ありがたく使わせてもらう機会を与えてくれたことに感謝する！

ちょっとコードを見ている。そして、この美しさをこのような恐怖に置き換えた。

このゲインは何だ？本当に恐ろしい。何かあればすみません))

Dmitry Fedoseev | 20 9月 2023 において 06:32

Stanislav Korotky #:

語句の語句の語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句語句そこには著者のバリエーションがある。もうひとつ、こんなものもある：

Functions.mqhファイル：

このようなスクリプトで使用します：

申し訳ないが、私はもちろん間違っている：

static FunctionInstance *pointers[] = {C_Function::fabric<C_Skin>(), C_Function::fabric<C_Forest>(), C_Function::fabric<C_Megacity>(), C_Function::fabric<C_Rastrigin>(), C_Function::fabric<C_Universe>()};

各タイプのオブジェクトを作成しないのですか？

......では、どのように、1つのタイプは、プログラムの全体の時間の間に使用されます。

fxsaber | 20 9月 2023 において 07:25

Dmitry Fedoseev #:

ゲインは？というか、本当にひどい。何かあったら謝ります)))

難しい質問だね。分からないよ。

Stanislav Korotky | 20 9月 2023 において 19:46

Dmitry Fedoseev #:

申し訳ないが、私はもちろん間違っている：

各タイプのオブジェクトが作成されないのですか？

......それなら、プログラムの間、一つの型しか使われないことになります。

この行でファクトリーが作られる。ファクトリーは（開始時に）すべてのクラスに予約されています。ファクトリーは明示的にcreateを呼び出すことで、動作するオブジェクトを作成します。

エキスパートアドバイザー(EA)に指標を追加するための既製のテンプレート（第3部）：トレンド指標

この参考記事では、トレンド指標カテゴリから標準的な指標を取り上げます。パラメータの宣言と設定、指標の初期化と解除、EAの指標バッファからのデータとシグナルの受信など、EAで指標を使用するためのすぐに使えるテンプレートを作成します。

ニューラルネットワークが簡単に（第58回）：Decision Transformer (DT)

強化学習の手法を引き続き検討します。この記事では、一連の行動を構築するパラダイムでエージェントの方策を考慮する、少し異なるアルゴリズムに焦点を当てます。

ソフトウェア開発とMQL5におけるデザインパターン（第１回）：生成パターン

繰り返し発生する問題の多くを解決するためには、使用できる方法があります。これらの方法の使い方を理解すれば、ソフトウェアを効果的に作成し、DRY (Do not Repeat Yourself)の概念を適用するのに非常に役立ちます。この文脈では、デザインパターンのトピックが非常に役に立ちます。なぜなら、デザインパターンは、よく説明され、繰り返される問題に対する解決策を提供するパターンだからです。

データサイエンスと機械学習(第15回)：SVM、すべてのトレーダーのツールボックスの必須ツール

取引の未来を形作るサポートベクターマシン(SVM)の不可欠な役割をご覧ください。この包括的なガイドブックでは、SVMがどのように取引戦略を向上させ、意思決定を強化し、金融市場における新たな機会を解き放つことができるかを探求しています。実際のアプリケーション、ステップバイステップのチュートリアル、専門家の洞察でSVMの世界に飛び込みましょう。現代の複雑な取引をナビゲートするのに不可欠なツールを装備してください。SVMはすべてのトレーダーのツールボックスの必需品です。