MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
preview
母集団最適化アルゴリズム：魚群検索(FSS)

母集団最適化アルゴリズム：魚群検索(FSS)

MetaTrader 5 — 例 | 6 2月 2023, 11:19
178 0
Andrey Dik
Andrey Dik

内容

1.はじめに
2.アルゴリズムの説明
3.テスト結果


1.はじめに

魚の集合体とは、ある場所に集まっている魚の集まりの総称です。魚の集合体には、構造化されているものとされていないものがあります。例えば、食物や営巣地など、局所的な資源の近くにランダムに集まった種や大きさが混在する集団は非構造化集合体です。

さらに、その集合体が相互作用的、社会的に集まってくる場合は、大群と呼ばれることがあります。その多くはライフサイクルの同じ時期にあり、互いに活発に接触し群れのメンバーにとって有益な生物学的に活発で組織的な活動を常に示すことができます。
個体での生活とは対照的な群れでの生活には、外敵から身を守れるという利点と、餌を得るための競争が激しくなるという妥協点があります。

自然界で魚が群れを作るにはいくつかの方法があります。原則として、同種の個体だけで構成される大きな群れが好まれます。外見が目立つ、あるいは何らかの違いがある群れのメンバーは、捕食者の格好の標的になります。魚が同じ個体の群れを好むのはこのためです。こうすることで、群れ全体の均質性が保たれます。

群れは、魚が同じスピードで同じ方向に同期して泳ぐと、かなりしっかりと編成されます。これは、同じ種類、年齢、サイズの魚が一定の距離を保って移動しているために起こります。魚の群れは、まるで集団の知性と共通の心を持っているかのように、複雑な手順を成し遂げることができます。
特に移動や摂食のあり方など、群れの形成の繊細な部分はまだ十分に理解されていないのが現状です。

より良い方向性、狩りの同期化、捕食者を惑わせる、捕まるリスクの提言など、群れ行動を説明するための仮説は数多く提唱されています。群れをなす魚は、近い距離から互いの行動を制御する情報を共有しているようです。ある魚の摂食行動が、他の魚の活発な餌探しをすぐに刺激するのです。群れで泳ぐ魚は、互いに衝突しないように形を変えながら、しばしば急速な上昇と下降を繰り返し、軸の周りを回転します。このような動きには、非常に高速な応答システムが必要です。群れをなして生活するということで、魚には隣人との位置関係のわずかな変化に瞬時に対応できる感覚器官があることが示唆されます。

より全体的な像を把握するために、このような挙動の数理モデル化が使用されています。最も一般的な数理モデルは、群れ内の個々の動物が3つの基本的なルールに従うと仮定しています。

  1. 隣の個体と同じ方向に移動する
  2. 隣の個体の近くに留まる
  3. 隣の個体との衝突を避ける


群れをなす魚がどのように泳ぐ方向を選択するのかという疑問は、いまだ解決されていません。移動の際には、群れのほとんどのメンバーが行き先を知っているように思えます。群れのメンバー全部が食べ物の有無を等しく認識しているとしても、他の親族よりも大胆な行動をとるリーダーがいます。この群れでの振る舞いをきっかけに、多くの研究者が数理モデルだけでなく、様々な最適化問題を解くためのアルゴリズムモデルも作成しました。


2.アルゴリズムの説明

魚群検索(FSS)は、メタヒューリスティックアルゴリズムのクラスに属する群知能アルゴリズムのサブファミリーです。2008年にBastos FilhoとLima Netoによって提案され、2009年に初めて出版されました。FSSでは、単純なエージェントを魚と呼び、それぞれの魚は探索中に達成した「成功」を表す重みを持ちます。重みの値や変動は、個体や集団の動きに影響を与えます。内蔵された摂食と協調行動のメカニズムにより、群れは重みを増やすために正の勾配の方向に動き、局地的および大域的に最高のスポットを見つけるように強制されます。FSSは、多峰性探索空間における連続最適化問題のために開発されました。また、このことをきっかけに、他の研究者も、二項問題における最適化や多目的最適化など、他の問題を解決するための選択肢を提案するようになりました。

FSSアルゴリズムでは、条件付きの水槽の中で魚が泳いでいると想像すると簡略化され、その壁が学習された関数定義の領域の境界となります。魚の重みは、餌（解）を見つけることに成功したかどうかの指標になります。それに、魚の記憶の役割も担っています。重みの存在はこのアルゴリズムの主な考え方であり、粒子の群れとの違いです。このFSSアルゴリズムの特徴により、粒子の群れのように大域的に最適解を見つけて固定化する必要はありません。

FSSアルゴリズムの演算子は、2つのグループに分けられます。
- 摂食演算子はエリア探査の成功を公式化する
- 遊泳演算子は魚の個体や群れ全体の回遊アルゴリズムを実行する

摂食演算子は、魚の重みを計算したものです。基本的な考え方は、魚が「食べて」「重みを増す」ために、正の勾配に向かって「泳ぐ」ように仕向けることです。重みがより大きい魚は、探索プロセス全体に対して大きな影響を与えるため、魚群塊の中心は反復処理によって探索空間のより良い場所に移動することになります。ある反復における重みの増分は、適応度関数の値の正規化された差に比例します。

fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);

ここで

  • weight - 魚の重み
  • delta_fitness - 適応度関数値間の差
  • max_delta_fitness - すべての魚の適応度関数の差の最大値

浮遊演算子は、動作の種類によって3つに分けられます。

- individual（個体の遊泳）

- instinctive-collective（本能的集団遊泳）

- collective-volitional（意志的集団遊泳）

個体の遊泳は、魚の現在位置の近傍での局所的探索として解釈できます。各個体の動きベクトルはランダムに指示され、異なる値を持ちます。

fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;

ここで

  • new_position - 対応する座標における新しい位置
  • current_position - 対応する座標における現在の位置
  • step_ind - 個体の移動ステップ（以下で計算）

initial_step_ind * (rangeMax [d] - rangeMin [d]);

ここで

  • initial_step_ind - 個体の移動のためのアルゴリズムパラメータ
  • rangeMaxとrangeMin - 最適化された引数値の範囲
  • r - 乱数 [-1.0;1.0]

模式的に、個体の遊泳を図1に示します。

個体

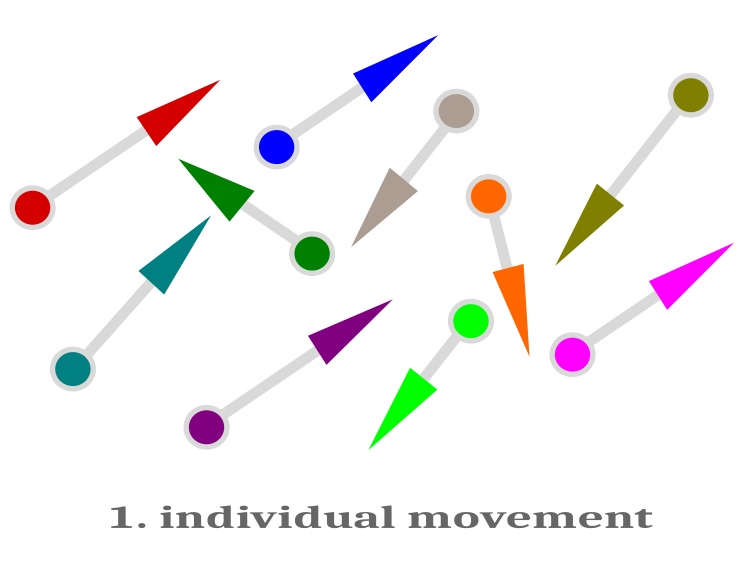
図1：個体の遊泳 - それぞれの魚の移動ベクトルはランダムな方向を向いており、異なるスカラー値を持つ

個体の遊泳後、適応度関数を測定します。その結果、魚の位置が改善されなかった場合は、この魚は移動しなかったと判断し、そのままの状態を維持します。適応度関数を向上させた魚だけが、新しい位置に移動します。

個体の遊泳が終わると、本能的な集団移動演算子が実行されます。まず、図2を見てみましょう。

collect

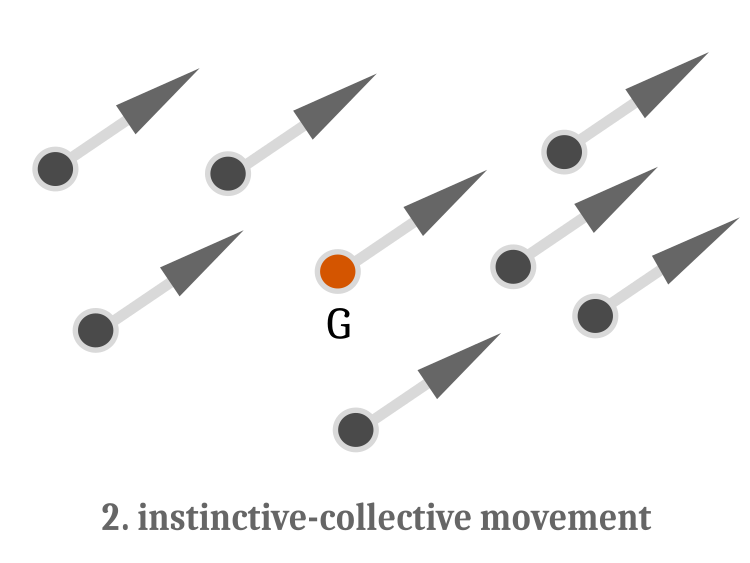
図2：本能的集団遊泳 - すべての魚で重心Gに対する方向と大きさのベクトルが同じであることが動きの特徴

本能的集団移動は、直前の反復における各魚の適応度関数の変化を考慮して、魚群の全体的な位置を修正する役割を担っています。新しい座標は次のように計算されます。

fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];

ここで

  • new_position - 対応する座標における魚の新しい位置
  • current_position - 対応する座標における現在の位置
  • collective_instinct - 対応する座標に沿った移動量（以下で計算）

collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

ここで

  • delta_position - 個体遊泳の段階で得られた、現在の座標と以前の位置の差
  • delta_fitness - 現在位置と個体遊泳における前回位置の適応度関数の変化

本能的集団遊泳が、魚群の新しい場所への群れの同期移動を形式化して新しい餌の場所の検索を提供する一方、個体移動は局所的に状況を改善することを可能にするものです。

次に、意志的集団遊泳について考えてみましょう。これは2種類に分けられます。

- 重心から - 群全体としての位置が以前と比較して改善されていない場合、魚は餌をさらに探すことを象徴するように横に広がる（図3）。

- 改善された場合重心に移動。魚は重心に移動し、輪を絞り、獲物を襲うことを象徴。アルゴリズム的には、最適化問題の解を洗練させることを意味する（図4）。

col vol out

図3：意志的集団遊泳 - 方向ベクトルは、重心Gから向けられる

col vol in

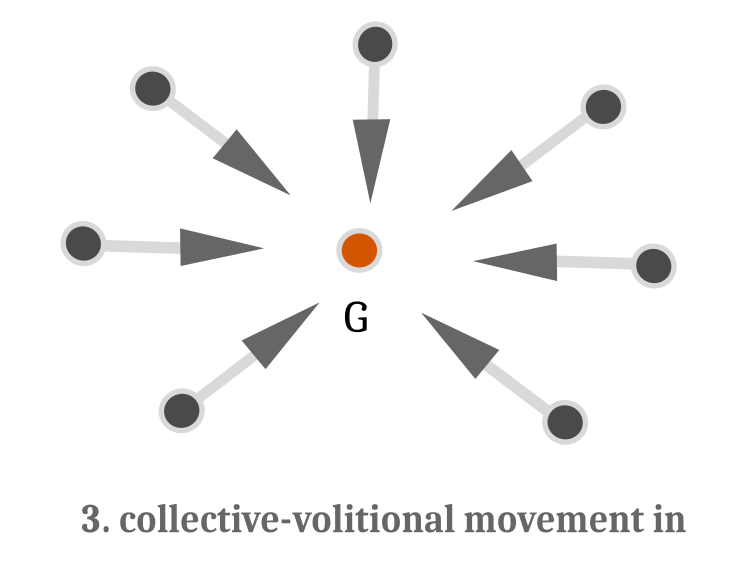
図4：意志的集団遊泳 - 方向ベクトルは重心Gに向けられる


意志的集団遊泳の計算のために、重心の概念を導入しています。ここから、意志的集団遊泳の方程式は、次のようになります。

fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);

ここで

  • pos - current_positionと同じ
  • search_operator - 直前の移動で位置が改善された場合は1、そうでない場合は-1

  • step_vol [d] - 集団移動ステップ（以下で計算）

step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);

ここで

  • initial_step_vol - 集団移動のためのアルゴリズムパラメータ

  • barycenter [d] - 重心の位置（以下で計算）

barycenter [d] += fishes [f].weight * fishes [f].current_position [d];

上のように魚の重みの合計に座標を乗じ、下のように魚群の重みの合計で割ります。

barycenter [d] /= current_total_weight;

アルゴリズムの擬似コードは次のようになります。

1）乱数で魚の位置を初期化する

2）個体移動

3）適応度関数を計算する

4）それぞれの魚の重みを再定義する

5）本能的集団移動

6）意志的集団移動

7）重みの合計を再計算する

8）適応度関数を計算する

9）停止条件が満たされるまで、2）から繰り返す。

スキーマFSS

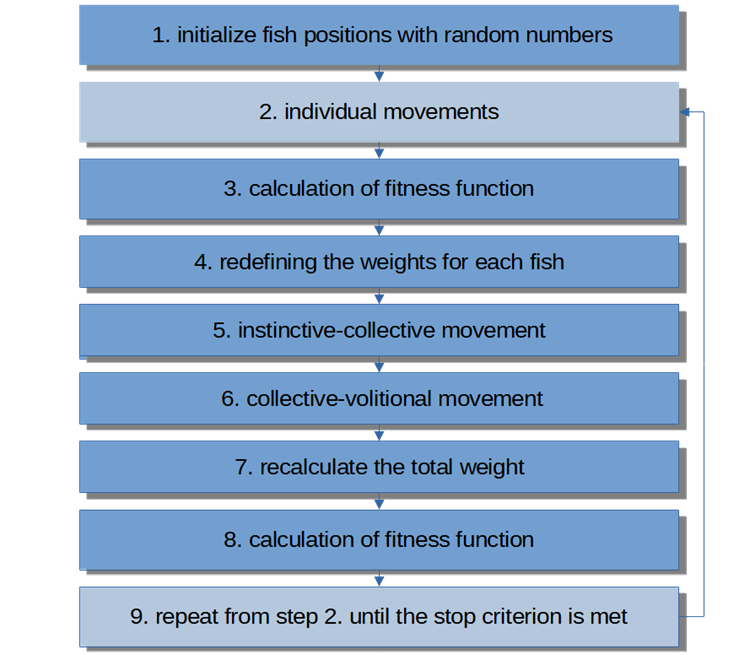
図5：FSSアルゴリズムのブロック図

それでは、コードの記述に入ります。

ご推察の通り、アルゴリズムの最も単純な論理単位は、魚を記述する構造体です。魚は何回か初期化する必要があります。構造体が比較的大きいので、特別なInit()メソッドで「ゼロにする」ことが望ましくなります。これによってコードを少し最適化することができます。この構造体には、現在位置、新しい位置、前回の移動からの座標の差の配列が含まれます。重みはデフォルトで1000標準単位に相当しますが、任意の値を設定することができます。また、魚は、現在の適応関数の値、以前の適応度関数の値、およびそれらの差によって特徴付けられます。Init()メソッドでは、適応度関数が可能な限り小さなdouble値で初期化されます。魚はまだ移動していないので、適応度の差は0です。

//——————————————————————————————————————————————————————————————————————————————
struct S_Fish
{
  void Init (int dimensions)
  {
    ArrayResize (current_position, dimensions);
    ArrayResize (new_position,     dimensions);
    ArrayResize (delta_position,   dimensions);
    weight        = 1000.0;
    fitness       = -DBL_MAX;
    delta_fitness = 0.0;
  }

  double current_position [];
  double new_position     [];
  double delta_position   [];
  double weight;
  double fitness;
  double new_fitness;
  double delta_fitness;
};
//——————————————————————————————————————————————————————————————————————————————

自然群落モデルを数学的に表現した魚の群れ、C_AO_FSSクラスを宣言してみましょう。珍しいことは1つもありません。また、ユーザープログラムとの対話に必要なpublicメソッドとして、魚の座標や群れでの相互作用を考慮するために必要な最適化関数の値の範囲と配列の2つを用意します。

初期化クラスInit()のpublicメソッドでは、変数を元の値に戻すことと配列のためのメモリを確保することが必要です。特にinit変数とswimmingRegime変数に注意してください。擬似コードによると、適応度関数の計算は2回おこなわれます。1回目は個体移動の後、2回目は2種類の集団移動の後です。これは、私たちが採用したアルゴリズムとアプリケーションのリンク方式、つまり、各反復がfirst_method -> calculation_fitness_functions -> second_methodという順序を特徴とすることと矛盾しています。これを修正し、正統派アルゴリズムの動作シーケンスを変更するために、これら2つの変数を適用します。init変数はアルゴリズムの最初でfalseであるべきです。これは、アルゴリズムの全ロジックが座標の現在値と前回値の差と適応度関数を用いているため、魚を初期化して適応度関数を計算し、再度移動をおこなう必要があることを示すフラグです。それがなければ、値の差は出なかったと思います。2つ目の重要なフラグはswimmingRegimeです。これにより、魚の移動を表現するメソッドの呼び出し順を、私たちの構造体に合うように再定義することができます。1の値は「個体」遊泳の呼び出しに対応し、そうでない場合は上で検討した集団移動のシーケンスを使用します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Init (const int    dimensionsP,
                     const int    fishSchSizeP,
                     const double initial_step_indP,
                     const double initial_step_volP)
{
  MathSrand (GetTickCount ());
  init = false;
  swimmingRegime = 1;

  dimensions     = dimensionsP;

  ArrayResize (rangeMax,  dimensions);
  ArrayResize (rangeMin,  dimensions);
  ArrayResize (rangeStep, dimensions);

  num_of_individuos = fishSchSizeP;

  ArrayResize (fishes, num_of_individuos);

  for (int i = 0; i < num_of_individuos; i++)
  {
    fishes [i].Init (dimensions);
  }

  global_best = -DBL_MAX;
  ArrayResize (global_best_position, dimensions);

  total_weight     = num_of_individuos;

  initial_step_ind = initial_step_indP;
  ArrayResize (step_ind, dimensions);

  initial_step_vol = initial_step_volP;
  ArrayResize (step_vol, dimensions);

  ArrayResize (collective_instinct, dimensions);
  ArrayResize (barycenter, dimensions);
}
//——————————————————————————————————————————————————————————————————————————————

各反復で最初に呼ばれるpublicメソッドSwimming()で、個体移動と集団移動の呼び出しの順序を決定します。このメソッドが初めて呼ばれた場合、2つのアルゴリズムパラメータ（initial_step_indとinitial_step_vol）によって、個体と集団の移動ステップが、対応する座標に沿って可能な範囲の一部として初期化されます。それぞれ0.01と0.001に設定することを推奨する著者もいますが、この値では良い結果は得られなかったので、0.1と0.8を使用します。また、アルゴリズムの初回実行時には、魚の位置座標の現在値を、最適化されたパラメータの範囲内の乱数で初期化します。swimmingRegimeフラグに従って、後続のメソッド呼び出し時に適切な移動タイプが呼び出されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Swimming (int i)
{
  //----------------------------------------------------------------------------
  if (!init)
  {
    global_best    = -DBL_MAX;
    swimmingRegime = 1;

    for (int d = 0; d < dimensions; d++)
    {
      step_ind [d] = initial_step_ind * (rangeMax [d] - rangeMin [d]);
      step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      fishes [f].Init (dimensions);

      for (int d = 0; d < dimensions; d++)
      {
        fishes [f].new_position [d] = RNDfromCI (rangeMin [d], rangeMax [d]);
        fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
      }
    }
  }
  //----------------------------------------------------------------------------
  else
  {
    switch (swimmingRegime)
    {
    case 1:
      apply_individual_movement ();            //individual movement
      break;
    default:
      apply_instintive_collective_movement (); //instinctively-collective movement
      apply_collective_volitive_movement ();   //collective-volitional movement
      update_total_weight ();                  //recalculate the total weight
      break;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

反復ごとに呼び出される2つ目のpublicメソッドRegrouping()は、主に泳法の呼び出し順序（個体遊泳、本能的集団遊泳、意志的集団遊泳）を決定することを目的としています。呼び出しの順番を確保するためのメソッドの追加機能は、値1および2を取るswimmingRegimeフラグによって提供されます。これは、古典版での魚の移動メソッドの呼び出し順序を、私が採用した構造体に合わせて、first_open_method -> _fitness_function_calculation -> second_open_methodと定義し直すために必要です。Initフラグによって、アルゴリズムが最初の反復にあることがわかった場合、適応度関数の計算後にメソッドが呼ばれることを想定しているので、座標の現在位置と適応度関数の値を保存して、後にそれらの差を計算できるようにします。Initフラグが2回目以降の繰り返しであることを示している場合、個体移動の後に、適応度関数の現在値と前回値の差、および現在位置と前回位置の座標の差を求める必要があります。この差は、位置が改善されたという前提で計算されます。そうでない場合は移動しなかったとみなし、魚の重みの値を初期状態に戻し、動作と適応度関数の差を0に等しくします。最適解に達した場合は、直ちに updates_optimal_solution()メソッドを呼び出して更新するとともに、apply_feeding()メソッドで魚の摂食を適用します。swimmingRegimeフラグが1でない場合、本能的集団移動と意志的集団移動が適用されました。実行後、swimmingRegimeを1に設定します。次は個体移動です。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::Regrouping ()
{
  //----------------------------------------------------------------------------
  if (swimmingRegime == 1
  {
    if (!init)
    {
      for (int f = 0; f < num_of_individuos; f++)
      {
        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
        ArrayInitialize (fishes [f].delta_position, 0.0);

        fishes [f].fitness = fishes [f].new_fitness;
        fishes [f].delta_fitness = 0.0;
      }

      init = true;
      return;
    }

    for (int f = 0; f < num_of_individuos; f++)
    {
      //remember the best position for the fish
      if (fishes [f].new_fitness > fishes [f].fitness)
      {
        fishes [f].delta_fitness = fishes [f].new_fitness - fishes [f].fitness; //fabs
        fishes [f].fitness = fishes [f].new_fitness;

        for (int d = 0; d < dimensions; d++)
        {
          fishes [f].delta_position [d] = fishes [f].new_position [d] - fishes [f].current_position [d];
        }

        ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY);
      }
      else
      {
        ArrayInitialize (fishes [f].delta_position, 0.0);
        fishes [f].delta_fitness = 0.0;
      }
    }

    swimmingRegime = 2;
    updates_optimal_solution ();
    apply_feeding ();
    return;
  }

  //----------------------------------------------------------------------------
  swimmingRegime = 1;
  updates_optimal_solution ();
}
//——————————————————————————————————————————————————————————————————————————————

以下の単純なprivateメソッドは、アルゴリズムの最良の結果に到達した場合に更新するために使用されます。そのためには、単にそれぞれの魚の適応度関数値を大域的なものと比較すればよいのです。改善があれば保存します。

//——————————————————————————————————————————————————————————————————————————————
// update the best overall solution
void C_AO_FSS::updates_optimal_solution ()
{
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].fitness > global_best)
    {
      global_best = fishes [f].fitness;
      ArrayCopy (global_best_position, fishes [f].current_position, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

個体遊泳を提供するprivateメソッドの方程式については、すでに検討済みです。それぞれの魚の現在の座標に-1.0から1.0までの乱数をかけたステップを追加し、プラス方向とマイナス方向に増分を与えるというシンプルなものです。最適化されたパラメータ値が範囲を超えた場合、その座標に境界値が設定されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_individual_movement ()
{
  // move the fish to new places-----------------------------------------------
  double r = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (-1.0, 1.0);

      fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

摂食メソッドは、理解に困難をきたさないと思います。実は、魚の重みは、その魚自身の適応度関数の差と、魚の群れ全体の差の最大値の商として決定されます。ただし、すべての魚の最大差が0になることもあります。古典版アルゴリズムの説明では、魚の重みは常に正でなければならないとされています。一般的には、適応度関数が正の値をとる場合のみを考慮するのが普通ですが、私はこの要件に実用的な意味を見い出せませんでした。魚の重みは負の値も取り得るので、適応度関数の最大差（それぞれの魚の重みを正規化する値）がすべての魚の中でゼロであれば、魚の重みは1に等しいとします。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_feeding ()
{
  double max_delta_fitness = -DBL_MAX;

  //find the maximum weight among fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (fishes [f].delta_fitness > max_delta_fitness) max_delta_fitness = fishes [f].delta_fitness;
  }

  //feed the fish
  for (int f = 0; f < num_of_individuos; f++)
  {
    if (max_delta_fitness != 0.0)
    {
      fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);
    }
    else fishes [f].weight = 1;
  }
}
//——————————————————————————————————————————————————————————————————————————————

本能的・集団的移動のprivateメソッドは、各魚の座標を集団的本能の値だけ増加させて変更します。この集団的本能は、今回の反復と前回の反復における位置の差に、前回の移動で達成した適合度関数の差を乗じたものにほかなりません。ここでは、最適化されたパラメータの境界を越える場合の境界の値を割り当てています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_instintive_collective_movement ()
{
  double sum_delta_fitness = 0.0;
  for (int f = 0; f < num_of_individuos; f++)
  {
    sum_delta_fitness += fishes [f].delta_fitness;
  }

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;

      if (sum_delta_fitness != 0.0)
      {
        collective_instinct [d] /= sum_delta_fitness;
      }

      fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

以下は、魚の群れの重心と現在の重みの合計を計算する、意志的集団遊泳のprivateメソッドです。魚の群れの重みの合計が増加した場合、魚は重心に向かって移動し始め、そうでない場合は中心から遠ざかります。この式については、先ほど詳しく説明しました。魚の群れの重みの合計は、後述する特殊なメソッドで更新されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::apply_collective_volitive_movement ()
{
  //----------------------------------------------------------------------------
  double current_total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    current_total_weight += fishes [f].weight;
  }

  ArrayInitialize (barycenter, 0.0);

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      barycenter [d] += fishes [f].weight * fishes [f].current_position [d];
    }
  }

  for (int d = 0; d < dimensions; d++)
  {
    barycenter [d] /= current_total_weight;
  }

  //----------------------------------------------------------------------------
  double search_operator = current_total_weight > total_weight ? 1.0 : -1.0;
  double r   = 0.0;
  double pos = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    for (int d = 0; d < dimensions; d++)
    {
      r = RNDfromCI (0.0, 1.0);
      pos = fishes [f].current_position [d];

      fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);
      fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

実は、これは魚の重みの合計を更新するメソッドそのものです。すべてがシンプルです。一匹一匹の重みを測って、合計していきます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FSS::update_total_weight ()
{
  total_weight = 0.0;

  for (int f = 0; f < num_of_individuos; f++)
  {
    total_weight += fishes [f].weight;
  }
}
//——————————————————————————————————————————————————————————————————————————————


3.テスト結果

では、最後に最も興味深い部分である結果に移りましょう。このアルゴリズムには、全体最適を考慮する必要がないこと、重心や本能的・意思的移動の概念を導入し、全体として位置が改善されたかどうかによって、群れの中心からの収束や散乱を意味するなど、興味深いトリックが盛り込まれています。これらのことから、研究した関数に対するアルゴリズムの本来の挙動に期待が持てるようになりました。

一般に、空間の探索領域における行動には独創性があり、すなわち、蜂アルゴリズムで観察されたものと同様に、空間の別々の部分に魚の分散が見られますが、FSSの方程式と動作原理を詳細に検討すると、群れが別々のグループに分散することを意味するものではありません。総じて、PSOアルゴリズムをわずかに上回る程度で、成績は芳しくはありませんでした。

個別のテストに目を向けると、FSSはまだいくつかのテストで優秀な成績を収めています。特に、滑らかなSkin関数では、FSSアルゴリズムがオオカミアルゴリズムよりも優れていることが判明し、良好（最高ではない）な結果を示しましたが、これは容易に説明できるものです。このアルゴリズムでは、対象となる関数の表面の勾配を座標ごとに増分で考え、各反復における適合度関数の変化を利用します。Skin関数は滑らかであるため、表面の変化によく「くっつく」アルゴリズムです。

Forest関数に関しては、このアルゴリズムは平均を下回る結果を示しました。テスト関数を滑らかに変化させることで、ある程度は空間のナビゲーションをおこなうことができましたが、最大値を見つけることはできませんでした。Megacityを考えると、FSSの欠点はより顕著になります。個々のエージェントの現在の位置の近傍で研究対象の関数が変化しない場合、アルゴリズムは本当にそれを「嫌がり」、新しい潜在的なより良い場所を特定するためのロングジャンプをすることができなません。そのため、近傍に増分がない極値では動けなくなります。

Megacityテストは、どの最適化アルゴリズムにとっても非常に難しく、比較表の他の参加者は、一般にFSSにあまり差をつけていませんが、それでも、離散的な問題に対するアルゴリズムの弱い能力を認識する必要があります。いくつかのテストでは、ランダム検索が最も良い結果を示しました。アニメーションで見る限り、アルゴリズムの動作に「クラスタリング」は見られません。前回の記事で紹介した最適化アルゴリズム「結晶化」を覚えていらっしゃるでしょうか。

以下は、FSSアルゴリズムの結果です。

2022.12.08 13:14:06.033    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    1 Skin's; Func runs 10000 result:4.892861444841324
2022.12.08 13:14:08.388    Test_AO_FSS (EURUSD,M1)    Score:0.99391
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    20 Skin's; Func runs 10000 result:3.11410005347766
2022.12.08 13:14:12.557    Test_AO_FSS (EURUSD,M1)    Score:0.56920
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    500 Skin's; Func runs 10000 result:1.20519552002827
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    Score:0.11341
2022.12.08 13:14:47.176    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    1 Forest's; Func runs 10000 result:1.5057381856551146
2022.12.08 13:14:49.498    Test_AO_FSS (EURUSD,M1)    Score:0.85172
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    20 Forest's; Func runs 10000 result:0.21468156279781656
2022.12.08 13:14:53.825    Test_AO_FSS (EURUSD,M1)    Score:0.12143
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    500 Forest's; Func runs 10000 result:0.056970068652984526
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    Score:0.03223
2022.12.08 13:15:31.235    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    1 Megacity's; Func runs 10000 result:11.0
2022.12.08 13:15:34.066    Test_AO_FSS (EURUSD,M1)    Score:0.91667
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    20 Megacity's; Func runs 10000 result:1.03
2022.12.08 13:15:38.467    Test_AO_FSS (EURUSD,M1)    Score:0.08583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    500 Megacity's; Func runs 10000 result:0.31
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    Score:0.02583
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    =============================
2022.12.08 13:16:16.589    Test_AO_FSS (EURUSD,M1)    All score for C_AO_FSS:0.4122477188979048

Skin

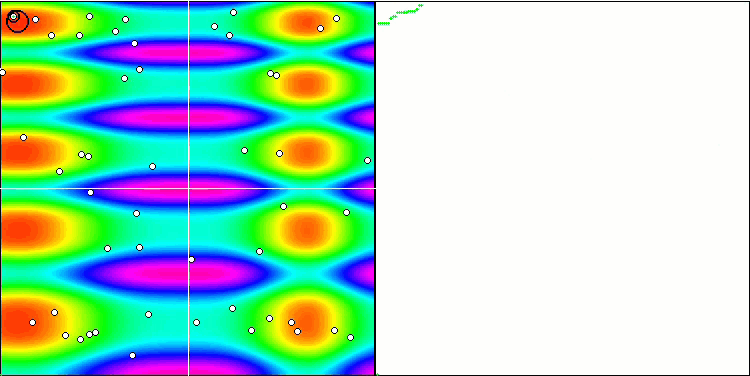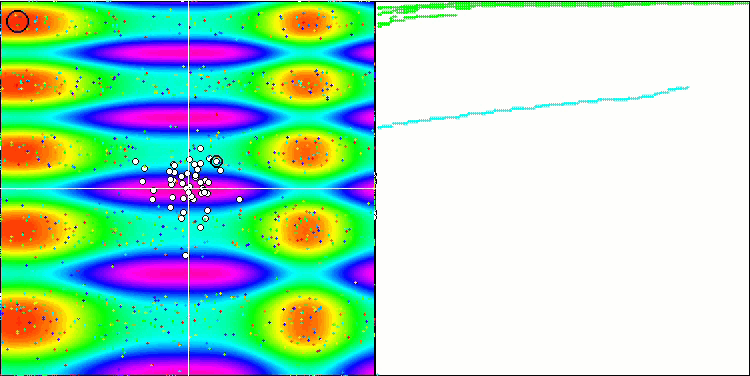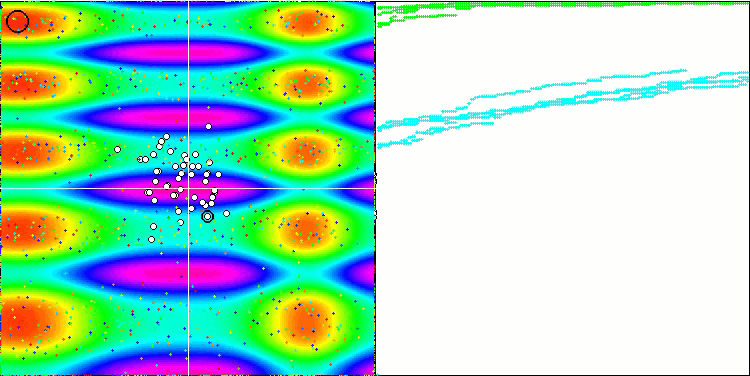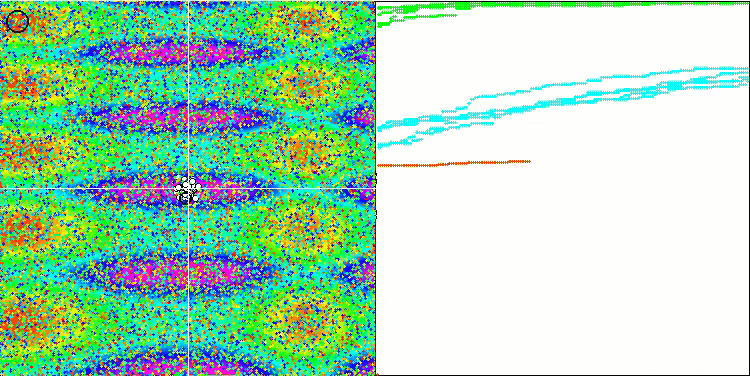
  Skinテスト関数のFSS

Forest

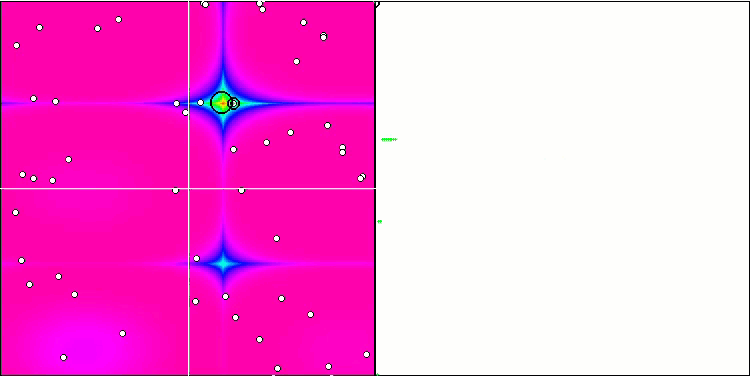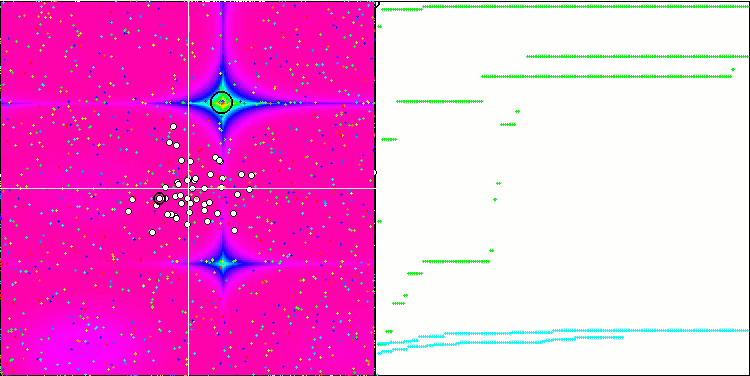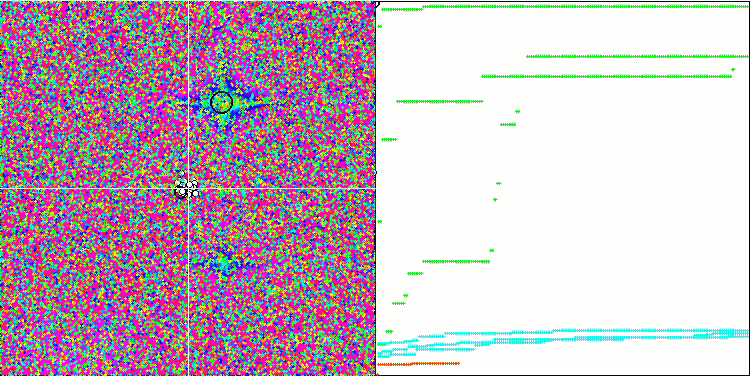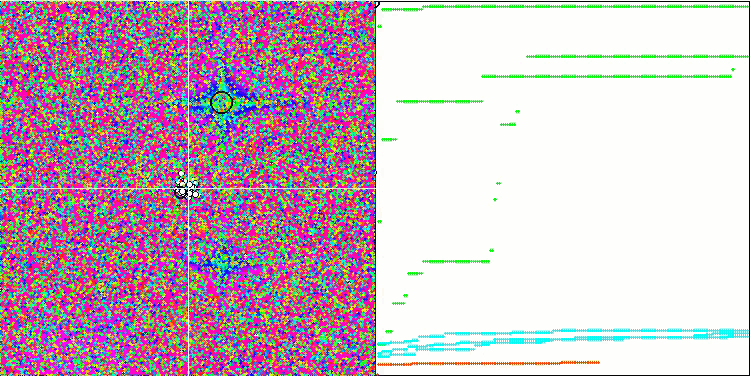
  Forestテスト関数のFSS

Megacity

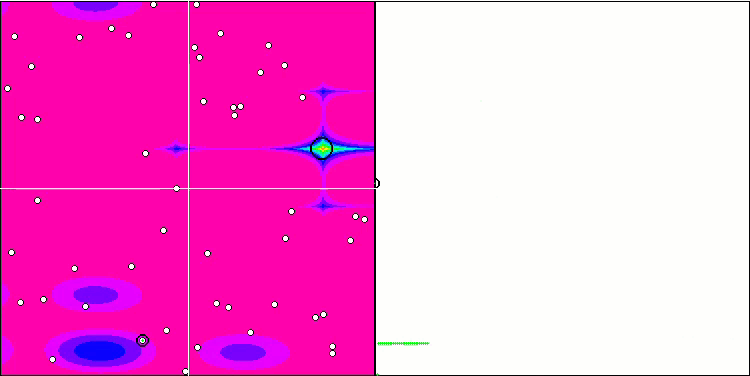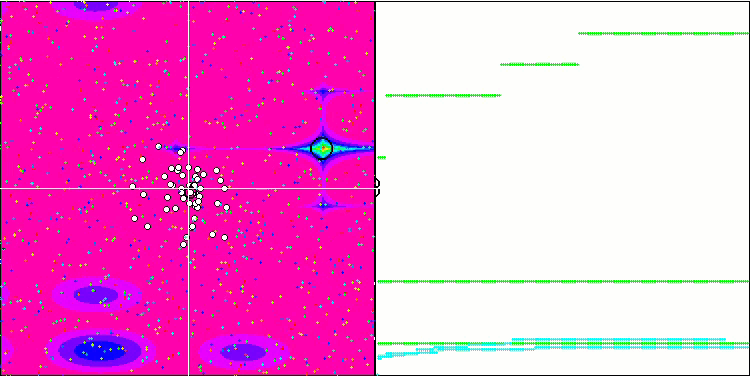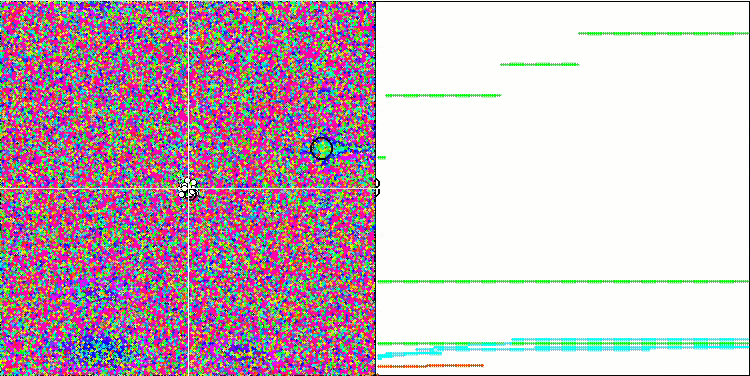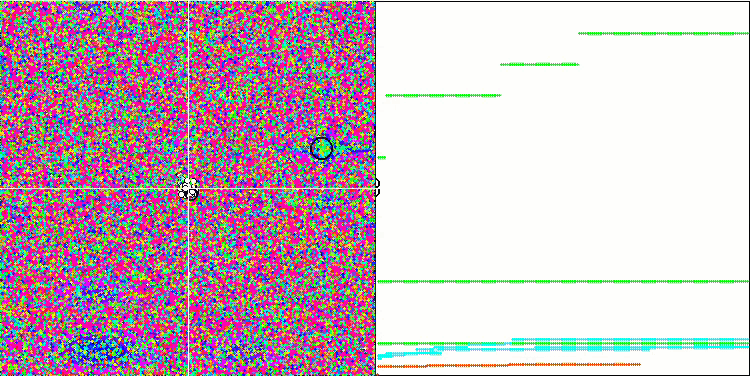
  Megacityテスト関数のFSS

こちらが最終的な表です。各テスト関数に対するアルゴリズムを個別に評価する際の利便性を高めるために列を追加しているのが特徴で、これにより、特定のタスクに対する各アルゴリズムの適用性をより公平に論じることができるようになりました。

AO

詳細

Skin

Skin最終

Forest

Forest最終

Megacity (discrete)

Megacity最終

最終結果

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

COAm

カッコウ最適化アルゴリズム

1.00000

0.85911

0.14316

0.66742

0.99283

0.28787

0.04551

0.44207

1.00000

0.24917

0.03537

0.42818

0.51255778

ACOm

蟻コロニー最適化

0.98229

0.79108

0.12602

0.63313

1.00000

0.62077

0.11521

0.57866

0.38333

0.44000

0.02377

0.28237

0.49805222

ABCm

人工蜂コロニーM

1.00000

0.63922

0.08076

0.57333

0.99908

0.20112

0.03785

0.41268

1.00000

0.16333

0.02823

0.39719

0.46106556

ABC

人工蜂コロニー

0.99339

0.73381

0.11118

0.61279

0.99934

0.21437

0.04215

0.41862

0.85000

0.16833

0.03130

0.34988

0.46043000

GWO

灰色オオカミオプティマイザ

0.99900

0.48033

0.18924

0.55619

0.83844

0.08755

0.02555

0.31718

1.00000

0.10000

0.02187

0.37396

0.41577556

FSS

魚群検索

0.99391

0.5692

0.11341

0.55884

0.85172

0.12143

0.03223

0.33513

0.91667

0.08583

0.02583

0.34278

0.41224778

PSO

粒子群最適化

0.99627

0.38080

0.05089

0.47599

0.93772

0.14540

0.04856

0.37723

1.00000

0.09333

0.02233

0.37189

0.40836667

RND

ランダム

0.99932

0.44276

0.06827

0.50345

0.83126

0.11524

0.03048

0.32566

0.83333

0.09000

0.02403

0.31579

0.38163222


確率的（ランダム）なヒューリスティック手法は、正確な解を保証するものではありませんが、原則として、実用に十分近い解を許容時間内に見つけることが可能です。しかし、実際には、優れた収束能力を発揮できるアルゴリズムもあります。ただし、FSSの場合では違います。一般に、魚群探索アルゴリズムは、粒子の群れに基づくアルゴリズムの特殊なケースです。そのため、メリットとデメリットの両方を受け継いでいます。アルゴリズムの特徴としては、粒子群では見られない魚の群れ（群）の分割が挙げられます。このアルゴリズムは滑らかな関数に比較的よく対応しますが、多変数を持つ関数にFSSがうまく対応できるかどうかは定かでありません。

賛成：
1.滑らかな関数をかなりうまく処理することができる。
2.魚の群れが別々のグループに分けられることで、アルゴリズムが他の潜在的に優れた極所をさらに探索することが可能になる。

反対：
1.個々のテストの結果の大きなばらつきは、アルゴリズムが不安定であることを示している。
2.離散関数と切れ目のある関数に対する収束が非常に弱い。離散関数の場合はほとんど適用できない。
3.拡張性が弱い。


MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11841

添付されたファイル |
ZIPをダウンロード
7_The_world_of_AO_yFSSa.zip (64.26 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
DoEasy - コントロール（第29部）：ScrollBar補助コントロール DoEasy - コントロール（第29部）：ScrollBar補助コントロール
この記事では、ScrollBar補助コントロール要素とその派生オブジェクト（垂直および水平のスクロールバー）の開発を開始します。スクロールバーは、フォームのコンテンツがコンテナを超えた場合にスクロールするために使用されます。スクロールバーは通常フォームの下部と右側にあります。下部の水平のものはコンテンツを左右にスクロールし、垂直のものは上下にスクロールします。
MQL5クックブック - サービス MQL5クックブック - サービス
この記事では、チャートへの結合を必要としないMQL5プログラムである「サービス」の多彩な機能について説明しています。また、他のMQL5プログラムとのサービスの違いをハイライトし、開発者がサービスで作業する際の微妙な違いを強調しています。例として、読者にはサービスとして実装できる幅広い機能をカバーするさまざまなタスクが提供されます。
MQL5の圏論（第1回） MQL5の圏論（第1回）
圏論は数学の一分野であり、多様な広がりを見せていますが、MQLコミュニティではまだ比較的知られていない分野です。この連載では、その概念のいくつかを紹介して考察することで、コメントや議論を呼び起こし、トレーダーの戦略開発におけるこの注目すべき分野の利用を促進することを目的としたオープンなライブラリを確立することを目指しています。
母集団最適化アルゴリズム：カッコウ最適化アルゴリズム(COA) 母集団最適化アルゴリズム：カッコウ最適化アルゴリズム(COA)
次に考察するのは、レヴィフライトを使ったカッコウ検索最適化アルゴリズムです。これは最新の最適化アルゴリズムの1つで、リーダーボードの新しいリーダーです。