取引におけるニューラルネットワーク：点群解析（PointNet）

はじめに

点群は、メッシュに伴う組み合わせの不整合や複雑さを回避できる、シンプルで統一された構造です。点群には標準的なデータ形式が存在しないため、多くの研究者は、これらのデータセットをディープネットワークに入力する前に、一般的な3Dボクセルグリッドや画像集合に変換しています。しかしこの変換処理は、データを不必要に大きくし、量子化アーティファクトを生じさせる可能性があり、データ本来の不変性を損なうことがあります。

このような理由から、一部の研究者は3次元形状の別の表現方法として、点群を直接用いる手法に注目しています。このような生のデータを扱うモデルでは、点群が単なる点の集合であり、その要素の順序に不変であるという特性を考慮する必要があります。したがって、モデルの計算にはある種の対称性が求められます。

そのような解決策の一例が、論文「PointNet:Deep Learning on Point Sets for 3D Classification and Segmentation」で提案されています。この研究で紹介されたPointNetは、点群を直接入力として受け取り、データセット全体に対するクラスラベルや、各点に対するセグメンテーションラベルを出力する統一的なアーキテクチャです。

このモデルの基本構造は非常にシンプルです。初期段階では、各点が同一かつ独立に処理されます。標準設定では、各点は3次元座標(x, y, z)のみで表されますが、法線やその他の局所的・大域的特徴量を追加することで、より高次元な表現を可能にすることもできます。

PointNetアプローチの重要な点は、対称関数であるMaxPoolingを利用している点です。本質的には、ネットワークは点群内の重要かつ有益な要素を選択し、その選択理由を表現する最適化関数を学習します。そして出力層の全結合層では、学習された最適値を形状全体の大域的記述子へと集約します。

この入力形式は、各点が個別に変換されるため、剛体変換やアフィン変換との相性も良好です。その結果、その著者はPointNetで処理する前にデータを正規化するための、データ依存型の空間変換モジュールを導入しており、これによって手法の精度と効率がさらに向上しています。

1.PointNetアルゴリズム

PointNetの著者は、順序のない点集合を直接入力データとして扱うディープラーニングフレームワークを開発しました。点群は、3次元点の集合{Pi|i=1,…,n}として表されます。ここで、各点Piはその座標(x, y, z)に加え、色などの属性を含む追加の特徴チャネルを持つベクトルです。

このモデルにおける入力データはユークリッド空間内の点の部分集合であり、以下の3つの主要な特性を備えています。

• 非順序：画像のピクセル配列とは異なり、点群は順序が定義されていない要素の集合です。つまり、N個の3次元の点からなるセットを扱うモデルは、入力のN!通りの順列に対して不変でなければなりません。
• 点同士の相互作用：点は距離尺度を持つ空間に存在しており、孤立しているわけではありません。隣接する点同士は意味のある局所構造を形成しうるため、モデルは近傍点からの局所的なパターンや、複数の局所構造間の組み合わせ的な相互作用を捉える必要があります。
• 変換に対する不変性：点集合は幾何学的構造体であり、その表現は特定の変換（たとえば回転や平行移動）に対して不変であることが望まれます。つまり、点群全体を一括で回転・移動しても、そのカテゴリやセグメンテーションは変わるべきではありません。

PointNetのアーキテクチャは、分類モデルとセグメンテーションモデルの大部分の構造を共有しており、以下の3つの主要モジュールから構成されています。

• 最大プーリング層：すべての点から情報を集約するための対称関数として機能します。
• 局所的および大域的特徴量の統合構造：個々の点の特徴と全体の形状を関連づけます。
• 2つのアライメントネットワーク：生の入力点と、そこから得られた特徴表現をそれぞれ正規化（整列）します。

入力データの順序に対する不変性を確保するため、著者は以下の3つの戦略を検討しました。

1. 入力データを正規の順序にソートする
2. RNNに入力するシーケンスとして扱い、すべての順列を訓練セットに含める
3. 順序に依存しない対称関数を用いて各点の情報を集約する（対称関数はn個のベクトルを入力として受け取り、入力の順序に依存しない新しいベクトルを出力します）

一見するとソートは簡単な解決策のように思えますが、多次元空間では摂動（ノイズや小さな変化）に対して安定な順序付けをおこなうことは困難です。そのため、ソートによって順序の問題を完全に解決することはできません。これにより、入力と出力の間で一貫した対応をモデルが学習することが難しくなります。実験的には、ソート済みの点集合にMLPを直接適用しても、未ソートの生データよりわずかに性能が向上する程度で、十分な精度は得られませんでした。

RNNは短いシーケンス（数十個の点）に対しては順序の揺らぎに対してある程度の頑健性を示しますが、数千個の点にスケールすることは困難です。論文の実験でも、RNNベースのモデルがPointNetに比べて優れていないことが示されています。

PointNetの中核となる考え方は、点集合上で定義された任意の関数を、集合内の各点に変換を施し、対称関数を適用することで近似するというものです。

著者は、非常にシンプルな基本モジュールを経験的に提案しています。まず、関数hをMLPによって近似し、関数gは単変数関数と最大プーリング関数で構成されます。実験によってこのアプローチの有効性が確認されており、複数のh関数を組み合わせることで、入力データセットの様々な特性を捉えるためのf関数を学習できます。

この基本モジュールはシンプルでありながら強力であり、さまざまな応用において高い性能を発揮します。

この主要モジュールの出力として、ベクトル[f1,…,fK]が形成され、これは入力点群全体を表すグローバルシグネチャとして機能します。この大域的特徴量を用いることで、SVMやMLPといった分類器による分類タスクの学習が可能になります。しかし、点単位のセグメンテーションには、局所的知識と全体的知識の組み合わせが必要です。著者は、このニーズに対しシンプルかつ効果的な手法を提案しています。

PointNetの著者は、点群全体の大域的特徴量ベクトルを計算した後、そのベクトルを各点の特徴量ベクトルと連結し、個々の点にフィードバックします。これにより、各点は局所的情報と全体的情報の両方を反映した特徴を持つようになり、新たな点単位の特徴量が抽出可能になります。

この修正により、PointNetは局所的な幾何構造と全体的な意味情報の両方に基づいて、点ごとのスコアを予測できるようになります。たとえば、各点の法線ベクトルを正確に予測できることから、モデルが局所的近傍の情報をうまく統合できていることが確認されています。実験結果は、このモデルが形状の部分セグメンテーションやシーンのセグメンテーションタスクにおいて最先端の性能を達成したことを示しています。

点群に対するセマンティックラベリングは、剛体変換（例：回転や平行移動）を受けても不変であるべきです。したがって、著者らは学習された点集合の表現もこのような変換に対して不変性を持つことを期待しています。

この要件への自然な対応策は、特徴量抽出の前に点群全体を標準空間に揃えることです。点群という入力形式の利点を活かし、この目的は比較的容易に達成できます。具体的には、T-net（変換ネットワーク）と呼ばれる小さなネットワークによってアフィン変換行列を予測し、それを入力点座標に直接適用します。このT-netは、PointNetの本体に似た構造を持ち、点ごとに独立した特徴量抽出モジュール、最大プーリングによる統合、全結合層の基本要素から成り立っています。

このアイデアは、空間的整列だけでなく、特徴空間の整列にも拡張可能です。すなわち、点レベルの特徴量ベクトルに対して追加のアライメントネットワークを挿入し、異なる入力点群からの特徴量を整列させるための特徴量変換行列を予測します。ただし、特徴量空間での変換行列は、空間的な変換行列よりもはるかに高次元であり、最適化が難しくなります。そこで、著者はSoftmax損失関数に正則化項を導入し、変換行列が直交行列に近くなるよう制約を加えています。これにより、変換の安定性と一般化能力が向上します。

ここで、Aはミニネットワークによって予測される特徴量アライメント行列です。

直交変換は、入力段階で情報の損失を伴わないため、理想的な変換とされています。PointNetの著者は、この正則化項を導入することで、最適化がより安定し、モデル性能が向上することを確認しました。

著者によるPointNet法の視覚化を以下に示します。

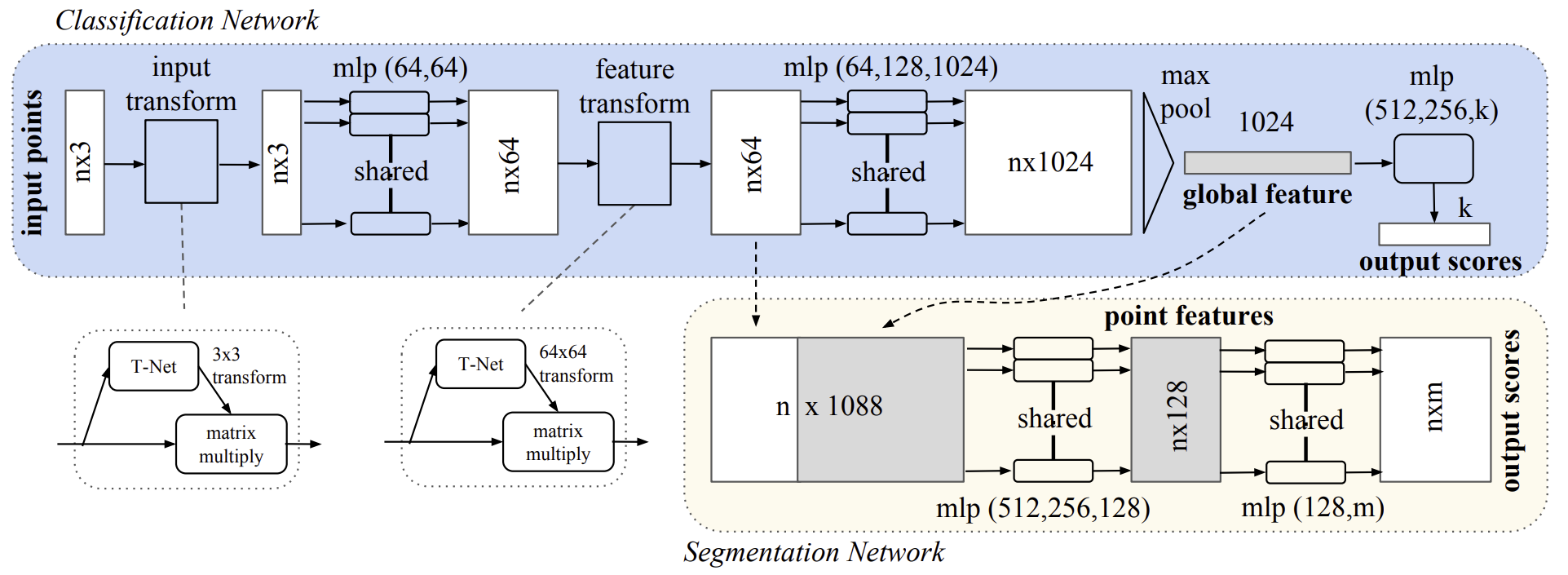
2.MQL5での実装

前のセクションでは、PointNetで提案されたアプローチの理論的基礎を検討しました。次に、この記事の実践的な部分に進み、MQL5を使用して提案されたアプローチの独自のバージョンを実装します。

2.1PointNetクラスの作成

PointNetアルゴリズムをコードに実装するには、全結合層CNeuronBaseOCLから基本機能を継承した新しいクラスCNeuronPointNetOCLを作成します。以下に新しいクラスの構造を示します。

class CNeuronPointNetOCL   :  public CNeuronBaseOCL
  {
protected:
   CNeuronPointNetOCL   *cTNet1;
   CNeuronBaseOCL       *cTurned1;
   CNeuronConvOCL       cPreNet[2];
   CNeuronBatchNormOCL  cPreNetNorm[2];
   CNeuronPointNetOCL   *cTNet2;
   CNeuronBaseOCL       *cTurned2;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronTransposeOCL  cTranspose;
   CNeuronProofOCL      cMaxPool;
   CNeuronBaseOCL       cFinalMLP[2];
   //---
   virtual bool         OrthoganalLoss(CNeuronBaseOCL *NeuronOCL, bool add = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNetOCL(void) {};
                    ~CNeuronPointNetOCL(void);
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNetOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

クラス構造内の多数のネストされたオブジェクトを観察することにすでに慣れているはずです。しかし、このケースには独自のニュアンスがあります。まず、静的オブジェクトの他に、動的オブジェクトもいくつかあります。クラスデストラクタでは、それらをデバイスのメモリから削除する必要があります。

CNeuronPointNetOCL::~CNeuronPointNetOCL(void)
  {
   if(!!cTNet1)
      delete cTNet1;
   if(!!cTNet2)
      delete cTNet2;
   if(!!cTurned1)
      delete cTurned1;
   if(!!cTurned2)
      delete cTurned2;
  }

ただし、クラスコンストラクタではこれらのオブジェクトを作成しないため、空のままにしておくことができます。

2番目のニュアンスは、ネストされた動的オブジェクトのうち2つが、作成しているクラスCNeuronPointNetOCLのインスタンスであるということです。つまり、それらはネストされたオブジェクト内にネストされます。

これら両方のニュアンスは、入力データと機能を特定の標準空間に合わせるという著者のアプローチに由来しています。これについては、クラスメソッドの実装中にさらに詳しく説明します。

クラスオブジェクトの新しいインスタンスの初期化は、通常どおり、Initメソッドで実装されます。このメソッドのパラメータには、作成されたオブジェクトのアーキテクチャを定義する主要な定数が含まれます。

この場合、アルゴリズムは点群分類用に設計されています。基本的な考え方は、PointNetアプローチを使用して環境状態エンコーダを構築することです。このエンコーダは、現在の環境状態を特定のタイプにマッピングする確率分布を返します。次に、Actor方策は、特定の環境状態タイプを、特定の状態で最大の収益性をもたらす可能性のある一連の取引パラメータにマッピングします。このことから、クラスアーキテクチャの主なパラメータが明らかになります。

• window：解析対象の点群内の単一点のパラメータウィンドウのサイズ
• units_count：点群内の点の数
• output：結果テンソルのサイズ
• use_tnets：入力データと特徴を標準空間に投影するためのモデルを作成するかどうか

outputパラメータは、結果バッファの合計サイズを指定します。以前使用した結果ウィンドウパラメータと混同しないでください。この場合、出力は分析された環境状態の記述子になると予想されます。結果テンソルのサイズは、可能な環境状態分類タイプの数に論理的に対応します。 

bool CNeuronPointNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                              uint window, uint units_count, uint output, bool use_tnets,
                              ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, output, optimization_type, batch))
      return false;

メソッドの本体では、通常どおり、最初に親クラスの同じ名前のメソッドを呼び出します。このメソッドでは、受信したパラメータの最低限必要な検証と継承されたオブジェクトの初期化が既に実装されています。同時に、メソッド操作の実行結果を確認します。

次に、ネストされたオブジェクトの初期化に進みます。最初に、ソースデータと機能を標準空間に投影するための内部モデルを作成する必要があるかどうかを確認します。

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNet1)
        {
         cTNet1 = new CNeuronPointNetOCL();
         if(!cTNet1)
            return false;
        }
      if(!cTNet1.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

投影モデルを作成する必要がある場合は、まずモデルオブジェクトへのポインタの有効性を確認し、必要に応じてCNeuronPointNetOCLクラスの新しいオブジェクトをインスタンス化します。これに続いて初期化に進みます。

投影行列生成オブジェクトのソースデータのサイズは、メインクラスが外部プログラムから受信したソースデータのサイズと一致することに注意してください。ただし、結果バッファのサイズは、ソースデータウィンドウの2乗に等しくなります。これは、このモデルの出力が、ソースデータを標準空間に投影するための正方行列になることが予想されるためです。さらに、ソースデータと特徴量の投影行列を作成する必要があることを示すパラメータを明示的にfalseに設定します。これにより、制御されていない再帰オブジェクトの作成が防止されます。さらに、ソースデータの変換モデルを別のソースデータの変換モデル内に埋め込むことは非論理的です。 

最後に、修正されたデータを記録するオブジェクトへのポインタを検証し、必要に応じてオブジェクトの新しいインスタンスを作成します。

      if(!cTurned1)
        {
         cTurned1 = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurned1.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;

そして、この内部層を初期化します。そのサイズは元のデータのテンソルに対応します。

特徴量投影モデルに対しても同様の操作を実行します。唯一の違いは、内部層の寸法にあります。

      if(!cTNet2)
        {
         cTNet2 = new CNeuronPointNetOCL();
         if(!cTNet2)
            return false;
        }
      if(!cTNet2.Init(0, 2, OpenCL, 64, units_count, 64 * 64, false, optimization, iBatch))
         return false;
      if(!cTurned2)
        {
         cTurned2 = new CNeuronBaseOCL();
         if(!cTurned2)
            return false;
        }
      if(!cTurned2.Init(0, 3, OpenCL, 64 * units_count, optimization, iBatch))
         return false;
     }

次に、点特徴量の一次抽出のMLPを形成します。この段階で、PointNetの著者は点特徴量の独立した抽出を提案しています。したがって、全結合層を、分析対象データのウィンドウのサイズに等しいステップサイズを持つ畳み込み層に置き換えます。この場合、それらは1つの点を表すベクトルのサイズに等しくなります。

//--- Init PreNet
   if(!cPreNet[0].Init(0, 0, OpenCL, window, window, 64, units_count, optimization, iBatch))
      return false;
   cPreNet[0].SetActivationFunction(None);
   if(!cPreNetNorm[0].Init(0, 1, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cPreNetNorm[0].SetActivationFunction(LReLU);
   if(!cPreNet[1].Init(0, 2, OpenCL, 64, 64, 64, units_count, optimization, iBatch))
      return false;
   cPreNet[1].SetActivationFunction(None);
   if(!cPreNetNorm[1].Init(0, 3, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cPreNetNorm[1].SetActivationFunction(None);

畳み込み層の間にバッチ正規化層を挿入し、活性化関数を適用します。この場合、手法の著者が提案した寸法の各タイプの2つの層を使用します。

同様に、高次の特徴量抽出のために3層パーセプトロンを追加します。

//--- Init Feature Net
   if(!cFeatureNet[0].Init(0, 4, OpenCL, 64, 64, 64, units_count, optimization, iBatch))
      return false;
   cFeatureNet[0].SetActivationFunction(None);
   if(!cFeatureNetNorm[0].Init(0, 5, OpenCL, 64 * units_count, iBatch, optimization))
      return false;
   cFeatureNet[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 6, OpenCL, 64, 64, 128, units_count, optimization, iBatch))
      return false;
   cFeatureNet[1].SetActivationFunction(None);
   if(!cFeatureNetNorm[1].Init(0, 7, OpenCL, 128 * units_count, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 8, OpenCL, 128, 128, 512, units_count, optimization, iBatch))
      return false;
   cFeatureNet[2].SetActivationFunction(None);
   if(!cFeatureNetNorm[2].Init(0, 9, OpenCL, 512 * units_count, iBatch, optimization))
      return false;
   cFeatureNetNorm[2].SetActivationFunction(None);

本質的には、最後の2つのブロックのアーキテクチャは同一です。異なるのは、層の数とサイズのみです。論理的には、それらを1つのブロックに結合することができます。ただし、この場合、それらは、それらの間の標準空間に特徴量変換ブロックを挿入できるようにするためだけに分離されています。

点特徴量の抽出に続く次の段階では、PointNetアルゴリズムで指定されたMaxPooling関数を適用します。この関数は、解析された点群全体から各特徴量ベクトル要素の最大値を選択します。その結果、点群は、分析されたクラウド内のすべての点の対応する要素の最大値を含む特徴量ベクトルによって表されます。

私たちのツールキットにはすでにCNeuronProofOCLクラスがあり、これは同様の機能を実行しますが、次元が異なります。したがって、まず得られた点特徴量行列を転置します。

   if(!cTranspose.Init(0, 10, OpenCL, units_count, 512, optimization, iBatch))
      return false;

そして、最大値のベクトルを形成します。

   if(!cMaxPool.Init(512, 11, OpenCL, units_count, units_count, 512, optimization, iBatch))
      return false;

解析された点群の得られた記述子は、3層MLPによって処理されます。ただし、この場合は、ちょっとした工夫をして、内部の全結合層を2つだけ宣言することにしました。3番目の層では、親クラスから必要な機能をすべて継承しているため、作成されたオブジェクト自体を使用します。

//--- Init Final MLP
   if(!cFinalMLP[0].Init(256, 12, OpenCL, 512, optimization, iBatch))
      return false;
   cFinalMLP[0].SetActivationFunction(LReLU);
   if(!cFinalMLP[1].Init(output, 13, OpenCL, 256, optimization, iBatch))
      return false;
   cFinalMLP[1].SetActivationFunction(LReLU);

クラスオブジェクト初期化メソッドの最後に、活性化関数を明示的に指定し、操作の論理結果を呼び出し元プログラムに返します。

   SetActivationFunction(None);
//---
   return true;
  }

新しいクラスの初期化メソッドの実装が完了したら、PointNetのフィードフォワードパスアルゴリズムの構築に進みます。これは、feedForwardメソッドで実行されます。前と同様に、このメソッドのパラメータでは、ソースデータオブジェクトへのポインタを受け取ります。

bool CNeuronPointNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- PreNet
   if(!cTNet1)
     {
      if(!cPreNet[0].FeedForward(NeuronOCL))
         return false;
     }

メソッドの本体では、元のデータを標準空間に投影する必要性に応じて、アルゴリズムの分岐がすぐにわかります。オブジェクトを初期化するときに、データ投影を実行する必要があることを示すフラグを内部変数に保存したことに注意してください。ただし、データ投影が必要かどうかを確認するには、対応するオブジェクトへのポインタの検証を使用できます。これは、投影モデルは必要な場合にのみ作成されるためです。デフォルトでは存在しません。

したがって、元データの投影行列を生成するためのモデルオブジェクトへの有効なポインタがない場合、取得した元データオブジェクトへのポインタを、事前特徴量抽出ブロックの最初の畳み込み層のフィードフォワードメソッドに渡すだけです。

データを標準空間に投影する必要がある場合は、受信したデータをモデルのフィードフォワードパスメソッドに渡して、データ変換行列を生成します。

   else
     {
      if(!cTurned1)
         return false;
      if(!cTNet1.FeedForward(NeuronOCL))
         return false;

投影モデルの出力では、正方形のデータ変換行列が得られます。したがって、結果テンソルのサイズによってデータウィンドウの次元を決定できます。

      int window = (int)MathSqrt(cTNet1.Neurons());

次に、行列乗算を使用して、元の点群を標準空間に投影します。

      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNet1.getOutput(), cTurned1.getOutput(), NeuronOCL.Neurons() / window,
                                                                                                window, window))
         return false;

次に、標準空間内の初期点の投影が、主要な特徴量抽出ブロックの最初の層に入力されます。

      if(!cPreNet[0].FeedForward(cTurned1.AsObject()))
         return false;
     }

この段階では、元のデータを標準空間に投影する必要があるかどうかに関係なく、主要な特徴量抽出ブロックの最初の層のフィードフォワードパスはすでに実行されています。次に、指定されたブロックのすべての層のフィードフォワードパスメソッドを順番に呼び出します。

   if(!cPreNetNorm[0].FeedForward(cPreNet[0].AsObject()))
      return false;
   if(!cPreNet[1].FeedForward(cPreNetNorm[0].AsObject()))
      return false;
   if(!cPreNetNorm[1].FeedForward(cPreNet[1].AsObject()))
      return false;

次に、点の特徴を標準空間に投影する必要があるかどうかという問題に直面します。ここでのアルゴリズムは初期点の投影に似ています。

//--- Feature Net
   if(!cTNet2)
     {
      if(!cFeatureNet[0].FeedForward(cPreNetNorm[1].AsObject()))
         return false;
     }
   else
     {
      if(!cTurned2)
         return false;
      if(!cTNet2.FeedForward(cPreNetNorm[1].AsObject()))
         return false;
      int window = (int)MathSqrt(cTNet2.Neurons());
      if(IsStopped() ||
         !MatMul(cPreNetNorm[1].getOutput(), cTNet2.getOutput(), cTurned2.getOutput(),
                                     cPreNetNorm[1].Neurons() / window, window, window))
         return false;
      if(!cFeatureNet[0].FeedForward(cTurned2.AsObject()))
         return false;
     }

その後、分析された初期データの点群の点の特徴を抽出する操作を完了します。

   if(!cFeatureNetNorm[0].FeedForward(cFeatureNet[0].AsObject()))
      return false;
   uint total = cFeatureNet.Size();
   for(uint i = 1; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(cFeatureNetNorm[i - 1].AsObject()))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
     }

次のステップでは、結果の特徴量テンソルを転置します。次に、分析された点群の記述子ベクトルを形成します。

   if(!cTranspose.FeedForward(cFeatureNetNorm[total - 1].AsObject()))
      return false;
   if(!cMaxPool.FeedForward(cTranspose.AsObject()))
      return false;

次に、PointNet分類アルゴリズムに従って、受信したデータをMLPで処理する必要があります。ここでは、2つの内部全結合層に対してフィードフォワードパス操作を実行します。

   if(!cFinalMLP[0].FeedForward(cMaxPool.AsObject()))
      return false;
   if(!cFinalMLP[1].FeedForward(cFinalMLP[0].AsObject()))
      return false;

次に、親クラスの同様のメソッドを呼び出して、内部層へのポインタを渡します。

   if(!CNeuronBaseOCL::feedForward(cFinalMLP[1].AsObject()))
      return false;
//---
   return true;
  }

この場合、親クラスは全結合層であることに注意してください。したがって、親クラスのフィードフォワードパスメソッドを呼び出すと、全結合層のフィードフォワードパスが実行されます。唯一の違いは、今回はネストされた層のオブジェクトではなく、親クラスから継承したオブジェクトを使用することです。

フィードフォワードパスメソッドのすべての操作が正常に完了すると、実行された操作を示すブール値が呼び出し元プログラムに返されます。

この時点で、フィードフォワード法に関する作業は終了し、誤差勾配分布とモデルパラメータ調整の2つの部分に分かれているバックプロパゲーションパスメソッドに移ります。

何度も述べたように、誤差勾配分布は、情報の流れが逆になることを除いて、フィードフォワードパスとまったく同じアルゴリズムに従います。ただし、この場合は、特別なニュアンスがあります。データ投影行列の場合、PointNet法の著者は、投影行列が直交行列に可能な限り近くなることを保証する正規化手法を導入しました。これらの正規化操作はフィードフォワードパスアルゴリズムには影響せず、モデルパラメータの最適化にのみ関係します。さらに、これらの操作を実行するには、OpenCLプログラム内で追加の計算が必要になります。

まず、提案された正規化式を調べてみましょう。

著者は、直交行列をその転置コピーで乗算すると単位行列になるという特性を活用していることは明らかです。

分解すると、行列をその転置コピーで乗算するということは、結果の行列の各要素が2つの対応する行のドット積を表すことを意味します。直交行列の場合、行とそれ自身のドット積は1になります。それ以外の場合、2つの異なる行のドット積は0になります。

ただし、バックプロパゲーションパス内での正規化を扱っていることに注意することが重要です。つまり、誤差を計算するだけでなく、各要素の誤差勾配も計算する必要があります。

このアルゴリズムをOpenCLプログラム内に実装するには、OrthogonalLossという名前のカーネルを作成します。このカーネルのパラメータには、2つのデータバッファへのポインタが含まれます。1つには元の行列が含まれ、もう1つは対応する誤差勾配を格納するために使用されます。さらに、勾配値を上書きするか、以前保存した値で累積するかを指定するためのフラグを導入します。

__kernel void OrthoganalLoss(__global const float *data,
                             __global float *grad,
                             const int add
                            )
  {
   const size_t r = get_global_id(0);
   const size_t c = get_local_id(1);
   const size_t cols = get_local_size(1);

この場合、行列の次元は指定しません。しかし、ここではすべてが非常にシンプルです。行列の行数と列数に応じて、2次元タスク空間でカーネルを実行する予定です。

カーネル本体では、タスク空間の両方の次元で現在のスレッドを即座に識別します。

ここで扱うのは正方行列であることも覚えておく価値があります。したがって、行列の完全なサイズを理解するには、1つの次元のスレッド数を決定するだけで済みます。

ベクトル乗算演算を複数のスレッドに分散するために、元の行列の行内にローカルワークグループを作成します。また、スレッド間のデータ交換のプロセスを整理するために、OpenCLコンテキストのローカルメモリ内の配列を使用します。

   __local float Temp[LOCAL_ARRAY_SIZE];
   uint ls = min((uint)cols, (uint)LOCAL_ARRAY_SIZE);

次に、ソースデータバッファ内の必要なオブジェクトへのオフセット定数を定義します。

   const int shift1 = r * cols + c;
   const int shift2 = c * cols + r;

対応する要素の値をデータバッファからロードします。

   float value1 = data[shift1];
   float value2 = (shift1==shift2 ? value1 : data[shift2]);

グローバルメモリのアクセスを最小限に抑えるために、対角要素の再読み取りは避けることに注意してください。

ここでは、取得した値の有効性をすぐに確認し、無効な数値をゼロ値に置き換えます。

   if(isinf(value1) || isnan(value1))
      value1 = 0;
   if(isinf(value2) || isnan(value2))
      value2 = 0;

その後、結果の有効性を必須チェックしながら積を計算します。

   float v2 = value1 * value2;
   if(isinf(v2) || isnan(v2))
      v2 = 0;

次のステップは、ワークグループスレッドの強制的な同期を使用して、ローカル配列の個々の要素で取得された値の並列合計のループを構成することです。

   for(int i = 0; i < cols; i += ls)
     {
      //---
      if(i <= c && (i + ls) > c)
         Temp[c - i] = (i == 0 ? 0 : Temp[c - i]) + v2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

次に、ローカル配列の要素の取得された値を合計するループを作成します。

   uint count = min(ls, (uint)cols);
   do
     {
      count = (count + 1) / 2;
      if(c < ls)
         Temp[c] += (c < count && (c + count) < cols ? Temp[c + count] : 0);
      if(c + count < ls)
         Temp[c + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

ワークグループスレッドの同期にも特別な注意を払います。

ローカル配列の最初の要素で実行された演算の結果として、行列の分析された2つの行の積の値が得られます。これで誤差値を計算できます。

   const float sum = Temp[0];
   float loss = -pow((float)(r == c) - sum, 2.0f);

しかし、これは作業の一部に過ぎません。次に、元の行列の各要素の誤差勾配を決定する必要があります。まず、ベクトル積のレベルで誤差勾配を計算します。

   float g = (2 * (sum - (float)(r == c))) * loss;

次に、現在のスレッド値の積の最初の要素に誤差勾配を伝播します。

   g = value2 * g;

得られた誤差勾配の値が有効であることを必ず確認してください。

   if(isinf(g) || isnan(g))
      g = 0;

その後、それをグローバル誤差勾配バッファの対応する要素に保存します。

   if(add == 1)
      grad[shift1] += g;
   else
      grad[shift1] = g;
  }

ここでは、誤差勾配値を追加するか上書きするかを決定するフラグをチェックし、それに応じて対応する操作を実行する必要があります。

カーネル内では、積の要素の1つに対してのみ誤差勾配を計算することに注意することが重要です。積の2番目の要素の勾配は別のスレッドで計算され、行列の行と列のインデックスが入れ替わります。

このカーネルはCNeuronPointNetOCL::OrthogonalLossメソッドを使用して実行キューに配置されます。そのアルゴリズムは、OpenCLプログラムカーネルを実行キューに配置するという基本原則に完全に準拠しており、以前の記事で詳しく説明されています。このメソッドのコードを独自に確認することをお勧めします。添付ファイルに記載しております。

ここで、誤差勾配分布メソッド「calcInputGradients」の背後にあるアルゴリズムを詳しく見てみましょう。以前と同様に、このメソッドは、前の層のオブジェクトへのポインタをパラメータとして受け取ります。この場合、このオブジェクトは生データレベルでの誤差勾配の受信者として機能します。

bool CNeuronPointNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

メソッド本体では、受け取ったポインタの妥当性を即座に確認します。そうでなければ、それ以上の操作は意味がありません。

次に、誤差勾配を点群の記述子解釈パーセプトロンに渡します。

   if(!CNeuronBaseOCL::calcInputGradients(cFinalMLP[1].AsObject()))
      return false;
   if(!cFinalMLP[0].calcHiddenGradients(cFinalMLP[1].AsObject()))
      return false;

誤差勾配をMaxPooling層を通じて伝播し、対応する点の特徴に転置します。

   if(!cMaxPool.calcHiddenGradients(cFinalMLP[0].AsObject()))
      return false;
   if(!cTranspose.calcHiddenGradients(cMaxPool.AsObject()))
      return false;

次に、もちろん逆の順序で、点の特徴量抽出層を通じて誤差勾配を伝播します。

   uint total = cFeatureNet.Size();
   for(uint i = total - 1; i > 0; i--)
     {
      if(!cFeatureNet[i].calcHiddenGradients(cFeatureNetNorm[i].AsObject()))
         return false;
      if(!cFeatureNetNorm[i - 1].calcHiddenGradients(cFeatureNet[i].AsObject()))
         return false;
     }
   if(!cFeatureNet[0].calcHiddenGradients(cFeatureNetNorm[0].AsObject()))
      return false;

ここまではすべてごく普通の処理です。しかし、私たちは点の特徴量を正準空間へ射影する段階に到達しました。もちろん、これが必要ない場合は、単に誤差勾配を一次特徴量抽出ブロックへ渡すだけです。

   if(!cTNet2)
     {
      if(!cPreNetNorm[1].calcHiddenGradients(cFeatureNet[0].AsObject()))
         return false;
     }

これを実装する必要がある場合、アルゴリズムはより複雑になります。まず、誤差勾配をデータ投影レベルまで伝播します。

   else
     {
      if(!cTurned2)
         return false;
      if(!cTurned2.calcHiddenGradients(cFeatureNet[0].AsObject()))
         return false;

その後、点の特徴量と投影行列の間で誤差勾配を分配します。数ステップ先を見てみると、誤差勾配も投影行列生成モデルを通じて点特徴量レベルに伝播されることがわかります。後で重要なデータが上書きされるのを防ぐため、この段階では誤差勾配を予備特徴量抽出ブロックの最終層に渡さず、最後から2番目の層に渡します。

念のため、予備的な特徴量抽出ブロックの最後の層はバッチ正規化層です。その前の層は、個々の点から独立した特徴量抽出を行う畳み込み層です。どちらの層も同じサイズの誤差勾配バッファを持っているため、バッファ境界を超えるリスクなしに、安全にバッファを置き換えることができます。

      int window = (int)MathSqrt(cTNet2.Neurons());
      if(IsStopped() ||
         !MatMulGrad(cPreNetNorm[1].getOutput(), cPreNet[1].getGradient(), cTNet2.getOutput(), 
                     cTNet2.getGradient(), cTurned2.getGradient(), cPreNetNorm[1].Neurons() / window,
                                                                                       window, window))
         return false;

誤差勾配を2つのデータスレッドに分割した後、投影行列レベルで正規化誤差勾配を追加します。

      if(!OrthoganalLoss(cTNet2.AsObject(), true))
         return false;

次に、誤差勾配を投影行列生成ブロックを通じて伝播します。

      if(!cPreNetNorm[1].calcHiddenGradients((CObject*)cTNet2))
         return false;

そして、2つの情報スレッドからの誤差勾配を合計します。

      if(!SumAndNormilize(cPreNetNorm[1].getGradient(), cPreNet[1].getGradient(), cPreNetNorm[1].getGradient(),
                                                                                         1, false, 0, 0, 0, 1))
         return false;
     }

そして、誤差勾配をプライマリ特徴量抽出ブロックを通じて元のデータ投影のレベルまで伝播することができます。

   if(!cPreNet[1].calcHiddenGradients(cPreNetNorm[1].AsObject()))
      return false;
   if(!cPreNetNorm[0].calcHiddenGradients(cPreNet[1].AsObject()))
      return false;
   if(!cPreNet[0].calcHiddenGradients(cPreNetNorm[0].AsObject()))
      return false;

ここでは、特徴量投影による誤差勾配分布に似たアルゴリズムを適用します。アルゴリズムの最も単純なバージョンは、データ投影行列を使用しないバージョンです。誤差勾配を前の層のバッファに渡すだけです。

   if(!cTNet1)
     {
      if(!NeuronOCL.calcHiddenGradients(cPreNet[0].AsObject()))
         return false;
     }

しかし、データを投影する必要がある場合は、まず誤差勾配を投影レベルに伝播します。

      if(!cTurned1)
         return false;
      if(!cTurned1.calcHiddenGradients(cPreNet[0].AsObject()))
         return false;

そして、結果への影響に応じて、誤差勾配を2つのスレッドに分散します。

      int window = (int)MathSqrt(cTNet1.Neurons());
      if(IsStopped() ||
         !MatMulGrad(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cTNet1.getOutput(), cTNet1.getGradient(),
                     cTurned1.getGradient(), NeuronOCL.Neurons() / window, window, window))
         return false;

結果として得られる誤差勾配に正規化値を追加します。

      if(!OrthoganalLoss(cTNet1, true))
         return false;

ここで、誤差勾配の上書きに関する問題に直面します。この段階では、データを保存するための空きバッファが存在しません。誤差勾配を2方向に分配した際、それを直ちに前段の層のバッファに書き込みました。しかし、これから誤差勾配を投影行列生成ブロックに伝播する必要があり、この操作によって勾配の値が上書きされ、すでに保存されていたデータが失われてしまいます。データの損失を防ぐには、勾配の値を適切なデータバッファにコピーする必要があります。では、そのようなバッファはどこにあるのでしょうか。クラスの初期化時に、中間データを保存するための専用バッファは作成していません。しかし注意深く確認すると、「データ投影記録層」が存在することに気づきます。この層のサイズは、元のデータテンソルのサイズと一致しています。さらに、この層に格納されている誤差勾配はすでに2つの計算パスに分配済みであり、今後の処理で使用されることはありません。

同時に、このバッファサイズの一致は、別の手法の可能性を示唆しています。データをそのままコピーするのではなく、バッファポインタを入れ替えるという方法です。ポインタのスワップは、完全なデータコピーに比べて遥かに低コストであり、バッファサイズにも依存しません。

      CBufferFloat *temp = NeuronOCL.getGradient();
      NeuronOCL.SetGradient(cTurned1.getGradient(), false);
      cTurned1.SetGradient(temp, false);

データバッファへのポインタを並べ替えた後、データ投影行列からの誤差勾配を前の層のレベルに渡すことができます。

      if(!NeuronOCL.calcHiddenGradients(cTNet1.AsObject()))
         return false;
      if(!SumAndNormilize(NeuronOCL.getGradient(), cTurned1.getGradient(), NeuronOCL.getGradient(),
                                                                            1, false, 0, 0, 0, 1))
         return false; 
     }
//---
   return true;
  }

メソッド操作の最後に、2つの情報スレッドからの誤差勾配を合計し、メソッド操作の論理結果を呼び出し元プログラムに返します。

訓練可能なモデルパラメータの更新は、updateInputWeightsメソッドによって処理されます。いつものように、そのアルゴリズムは単純です。訓練可能なパラメータを含む内部オブジェクトの同じ名前のメソッドを順番に呼び出します。同時に、その機能はMLPベースの点群記述子評価の3番目の層として使用されるため、親クラスの対応するメソッドを確実に呼び出すようにします。この記事では、このメソッドの実装については詳しく説明しません。添付ファイルでコードを個別に確認することをお勧めします。

これで、CNeuronPointNetOCLクラスメソッドを構築するためのアルゴリズムの考察は終了です。この記事の添付ファイルには、このクラスの完全なコードとそのすべてのメソッドが記載されています。

2.2モデルアーキテクチャ

MQL5を用いてPointNetベースのアプローチを実装した後、私たちはモデルのアーキテクチャに新しいオブジェクトを統合します。前述のように、新しいクラスCNeuronPointNetOCLは、CreateEncoderDescriptionsメソッドで定義されている環境状態エンコーダモデルに組み込まれています。

アルゴリズムのほぼすべてを単一のブロック内に実装している点は特に重要です。これにより、簡潔かつコンパクトな高レベルアーキテクチャを持つモデルの構築が可能になります。ここで「高レベルアーキテクチャ」という表現を強調したいと思います。CNeuronPointNetOCLブロックというシンプルな名前とは裏腹に、実際には非常に複雑で多層的なニューラルネットワーク構造がこの中にカプセル化されています。

従来どおり、モデルへの入力は未処理の生データで構成されており、互換性を保つためにバッチ正規化層を通じて正規化されます。

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

その後、すぐにそれらを新しいPointNetブロックに渡します。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNetOCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

ここで注目すべきは、CNeuronPointNetOCLブロックの出力で活性化関数を指定していないことです。この手順は、点群識別ブロックのアーキテクチャを拡張する機能をユーザーに提供するために意図的に実行されます。ただし、この実験では、得られた結果を確率値の領域に変換するために、Softmax層のみを追加します。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

これで、新しい環境状態エンコーダモデルのアーキテクチャが完成しました。

また、ActorモデルとCriticモデルのアーキテクチャも簡素化されたことに触れておくべきでしょう。これらのモデルでは、マルチヘッドクロスアテンションブロックを単純なデータ連結層に置き換えました。とはいえ、これらの具体的な変更内容については、添付ファイルをご確認いただくことをお勧めします。

次に、モデルのトレーニングプログラムについて少し説明します。モデルアーキテクチャの変更はソースデータおよび結果の構造には影響しないため、環境とのインタラクションに使用していた既存のプログラムや、オフライン学習用に収集したデータを引き続き使用可能です。ただし、以前に収集したデータセットには、選択された環境状態に対するクラスラベルが含まれていません。これらのラベルを新たに作成するには追加のコストが発生します。そこで、私たちは別のアプローチを取り、Actor方策の訓練過程において環境状態エンコーダを同時に訓練することにしました。その結果、環境状態エンコーダを個別に訓練するEA「StudyEncoder.mq5」は不要となり、削除しました。代わりに、ActorおよびCriticの訓練用EA「Study.mq5」に対して小規模な修正を加え、環境状態エンコーダの訓練機能を追加しています。これらの修正内容も、ぜひ添付ファイルでご確認ください。

この記事で紹介したクラスとそのすべてのメソッドの完全なコード、および本稿作成に使用した全プログラムのアルゴリズムは、添付ファイルに含まれています。これより、作業の最終段階である、結果のテストおよび評価フェーズに進みます。

3.テスト

本記事では、点群形式の生データ処理に対応する新しいPointNet法を紹介し、著者らが提案したアプローチをMQL5を用いて実装しました。ここでは、これらのアプローチが実際のタスク解決にどれほど有効かを検証します。そのために、EURUSDの実際の履歴データを使用して、記事内で解説した各モデルを訓練します。実験には2023年の履歴データを訓練データセットとして使用し、2024年1月のデータをテストに用います。どちらのケースでも、H1時間枠とすべての分析対象インジケーターに対してデフォルトパラメータを使用します。

基本的に、これまでの複数の記事において、モデルの訓練およびテストパラメータは変更せずに一貫して使用しています。そのため、初期訓練は既存の収集済みデータセットを使用しておこなわれます。

また、環境状態エンコーダーの訓練は、Actor方策の訓練と同時に実施されます。ご存知の通り、Actor方策の訓練は反復的におこなわれ、訓練データセットは定期的に更新されます。この手法により、データセットが現在のActor方策の行動空間に常に適合し、整合性を保った状態で訓練が継続できます。これにより、より精緻なモデルのチューニングが可能となります。

数回の訓練イテレーションを経て、訓練データおよびテストデータの両方において利益を生み出すActor方策の獲得に成功しました。以下にそのテスト結果を示します。

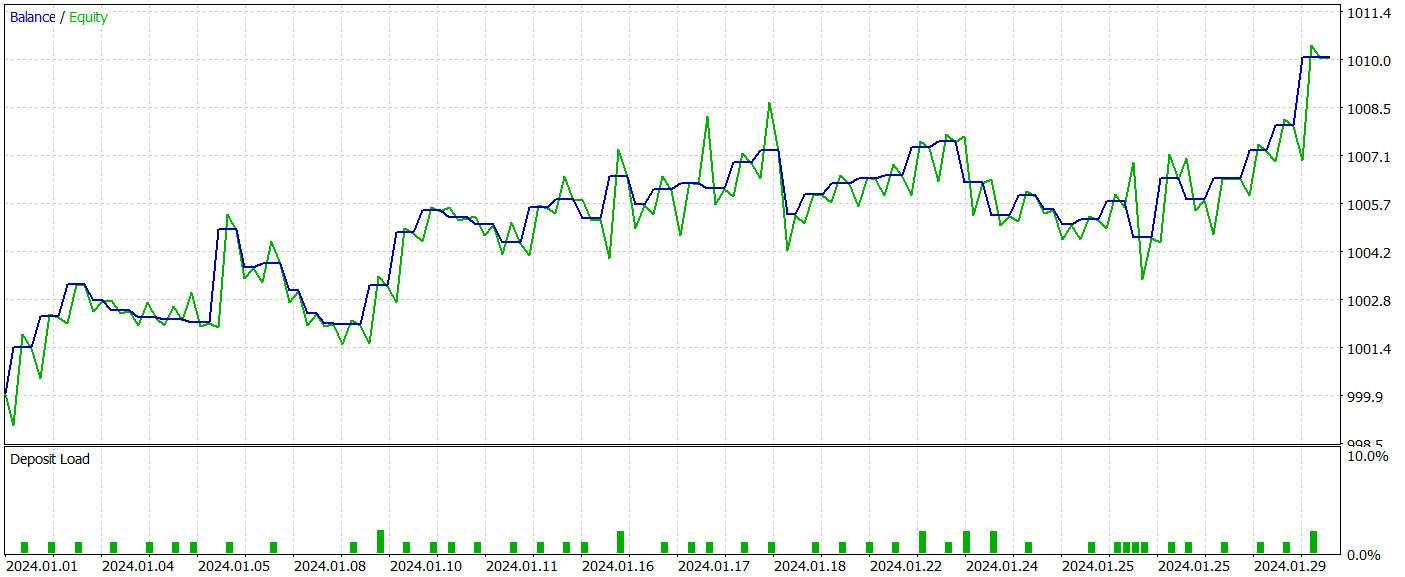
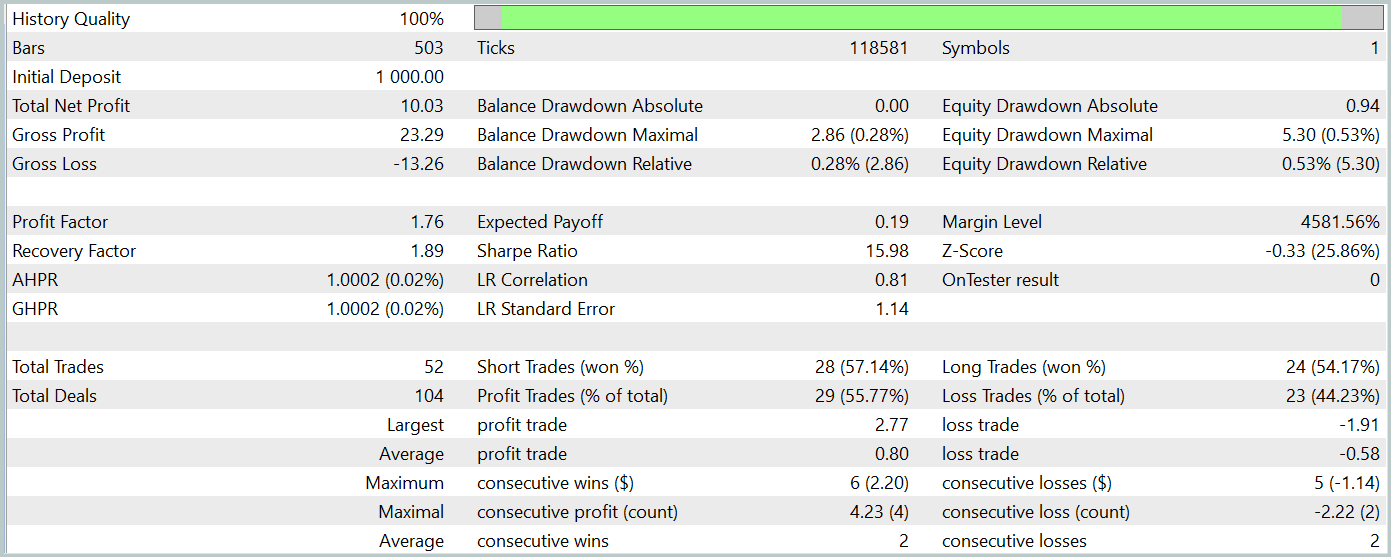
テスト期間中、モデルは52件の取引を実行し、そのうち55.77%が利益で終了しました。ロングポジションとショートポジションの比率が（それぞれ24件と28件で）ほぼ均衡している点は注目に値します。最大利益および平均利益の取引は、いずれも対応する損失取引を上回っており、プロフィットファクターは1.76に達しました。バランスカーブは明確な上昇傾向を示しています。ただし、テスト期間が短く、取引回数も比較的少ないため、学習されたポリシーの長期的な安定性については結論を出すには時期尚早です。

まとめると、実装したアプローチは有望ではあるものの、さらなる検証が必要です。

結論

本記事では、点群データを直接入力として処理可能な統合アーキテクチャ「PointNet」という新しい手法を紹介しました。PointNetを取引に応用することで、価格パターンのような複雑な多次元データを他の形式に変換することなく効果的に分析できるようになり、市場動向のより正確な予測や意思決定アルゴリズムの改善につながる新たな可能性が開かれます。このような分析は、金融市場における取引戦略の効率向上に寄与する可能性を秘めています。

記事の実践部分では、提案されたアプローチの構想をMQL5上で実装し、実際の過去データを用いてモデルを訓練し、MetaTrader 5のストラテジーテスターにて、学習済みのポリシーを活用したEAのテストをおこないました。その結果、有望な成果が得られました。ただし、本記事で紹介したすべてのプログラムはあくまで情報提供を目的としており、提案手法の可能性を示すためのデモンストレーションとして作成されたものです。実運用にあたっては、十分な精度向上とあらゆる状況下での包括的かつ徹底的な検証が必要となります。

参考文献

PointNet:DeepLearningonPointSetsfor3DClassificationandSegmentation

本連載の他の記事

記事で使用されているプログラム

#	ファイル名	種類	詳細
1	Research.mq5	EA	事例収集のためのEA
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	Test.mq5	EA	モデルテストEA
5	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ