Bacterial Chemotaxis Optimization (BCO)

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

Introduction

In the field of optimization, many researchers and developers draw inspiration from biological processes occurring in nature, such as evolution, social interactions, or the behavior of living organisms in search of food. This leads to the development of completely new innovative optimization methods. Studies have shown that these methods often outperform classical heuristic and gradient-based approaches, especially when solving multi-modal, non-differentiable and discrete problems. One such method is the chemotaxis algorithm, first proposed by Bremermann and colleagues. We have already discussed the algorithm for optimizing bacterial foraging (BFO). It simulates the response of bacteria to chemoattractants in concentration gradients. Bremermann analyzed chemotaxis in three-dimensional gradients and applied it to train neural networks. Although this algorithm is based on the principles of bacterial chemotaxis, new biological discoveries have made it possible to create a more detailed model of the process.

In this article, we will try to consider this model as a new optimization strategy. The main differences between the new model and the traditional chemotaxis algorithm are as follows:

1. Bacteria in the new model use information about concentration values.
2. They do not continue to move in one direction as chemoattractant concentrations increase.

Bacteria are single-celled organisms, one of the simplest forms of life on Earth. Despite their simplicity, they are able to receive information about the environment, navigate it and effectively use this information for survival. The response of bacteria to environmental changes has been the subject of intensive research in recent decades, which has also attracted the attention of scientists working in the field of optimization. Optimization algorithms can be viewed as systems that collect information about the functional landscape and use it to achieve an optimum. The simplicity of the idea of bacterial chemotaxis makes it an attractive starting point for building these types of algorithms.

Various studies have found that bacteria exchange information with each other, although not much is known about the mechanisms of this communication. Typically, bacteria are treated as individuals and social interactions are not taken into account in models. This distinguishes them from interaction models describing the behavior of social insects (such as ants, bees, wasps, or termites), which act as systems with collective intelligence, which opens up different possibilities for solving various problems.

Adaptation is another important aspect of chemotaxis. Bacteria are able to change their sensitivity to constant chemical conditions, allowing them to respond effectively to changes in the environment. This quality makes them not only hardy, but also highly efficient in finding resources.

In this study, the authors focused on microscopic models that account for the chemotaxis of individual bacteria, as opposed to macroscopic models that analyze the movement of colonies. The algorithm was developed by S. D. Müller and P. Koumatsakas, and its main ideas were presented and published in 2002.

Implementation of the algorithm

The idea of the bacterial chemotaxis optimization algorithm (BCO) is to use biological principles observed in bacterial behavior to solve optimization problems. The algorithm models how bacteria respond to chemical gradients in their environment, allowing them to find more favorable conditions to live in. The main ideas of the algorithm:

1. The algorithm describes the movement of bacteria as a sequence of straight-line trajectories connected by instantaneous turns. Each movement is characterized by speed, direction and duration.
2. The direction of the bacteria's rotation is determined by a probability distribution, which allows for random changes in movement to be taken into account.
3. The algorithm uses information about the gradients of the function to guide the bacterium toward an optimal solution, minimizing the number of iterations needed to reach the goal.

The detailed pseudocode of the bacterial chemotaxis optimization (BCO) algorithm describes the main steps of the algorithm, including initialization, the main optimization loop with movement and revision steps, and auxiliary functions.

Initialization.

1. Set the parameters:

• popSize - population size (number of bacteria)
• hs - number of steps to calculate the average change
• T0 - initial temperature
• b - parameter
• tau_c - parameter
• v - speed

2. Create a bacteria array of popSize

3. For each i bacterium from 0 to popSize-1:

• Initialize fPrev to -DBL_MAX
• Create the fHistory array of hs size and fill it with zeros

Basic optimization loop. Repeat until stop condition is reached:

The movement stage for each i bacterium from 0 to popSize - 1:

1. Get the current value of the target f_tr function

2. Get the previous value of the f_pr target function from bacterium [i].fPrev

3. If f_tr <= f_pr: T = T0

    Otherwise: calculate b_corr = CalculateCorrectedB (f_tr, f_pr, i)

• T = T0 * exp (b_corr * (f_tr - f_pr))

4. Generate 'tau' from an exponential distribution with T parameter.

5. Calculate new_angles [] for coords - 1 dimensions: for each j angle from 0 to coords - 2:

• theta = CalculateRotationAngle ()
• mu = 62 * (1 - cos (theta)) * π / 180
• sigma = 26 * (1 - cos (theta)) * π / 180
• new_angles [j] = random number from Gaussian distribution with parameters (mu, mu-π, mu+π)

6. Calculate a new position:

• l = v * tau
• CalculateNewPosition (l, new_angles, new_position, current_position)

7. Update a bacterium position constraining the values within rangeMin and rangeMax

8. Update bacterium [i].fPrev with the value of f_tr

Revision stage.

1. Update the cB global best solution with the fB fitness value

2. For each i bacterium from 0 to popSize - 1. Update the history of the values of the fHistory target function:

• Shift all values one position to the left
• Add the current value of the target function to the end of the history

Auxiliary functions:

CalculateCorrectedB (f_tr, f_pr, bacteriumIndex)

1. Calculate delta_f_tr = f_tr - f_pr

2. Calculate delta_f_pr = average change over the last hs steps

3. If |delta_f_pr| < epsilon: Return b

   Otherwise: Return b * (1 / (|delta_f_tr / delta_f_pr| + 1) + 1 / (|f_pr| + 1))

CalculateRotationAngle ()

1. Calculate cos_theta = exp (-tau_c / T0)

2. Return arccos (cos_theta)

CalculateNewPosition (l, angles, new_position, current_position)

1. Calculate new_position [0] considering all angles

2. For each i coordinate from 1 to coords - 1:

   Calculate new_position [i] given the corresponding angles

3. Apply a random direction (1 or -1) to each coordinate

GenerateFromExponentialDistribution (T)

Return -T * ln (random number between 0 and 1)

Let's move on to writing the algorithm code. To represent bacteria as a solution to an optimization problem, describe the S_BCO_Bacterium structure.

1. Structure fields:

• fPrev - previous value of the objective function.
  
• fHistory [] - array of target function values history.
  

2. Init - initialization method performs the following actions:

• fHistory array is resized to historySize.
• all elements of the fHistory array are initialized with 0.0.
• fPrev - the previous value of the objective function is set to the minimum possible value.

A bacterium in the form of a structure that provides for tracking changes in the values of the objective function over a given number of iterations (individual movements).

//——————————————————————————————————————————————————————————————————————————————
struct S_BCO_Bacterium
{
    double fPrev;        // previous value of the objective function
    double fHistory [];  // history of objective function values

    void Init (int coords, int historySize)
    {
      ArrayResize     (fHistory, historySize);
      ArrayInitialize (fHistory, 0.0);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Describe the C_AO_BCO algorithm class. Let's break it down piece by piece.

1. External parameters of the algorithm are initialized in the constructor.

2. SetParams method updates the parameter values from the params array.

3. The Moving and Revision methods are responsible for the movement of bacteria and the revision of their positions.

4. The class defines several private methods used for various calculations related to the algorithm. "CalculateAverageDeltaFpr", "CalculateNewAngles", "CalculateNewPosition", "GenerateFromExponentialDistribution", "CalculateCorrectedB", "CalculateRotationAngle", "RNDdir", bacterium - array of bacteria (population). Class parameters:

• hs - number of steps for calculating the average change.
• T0 - initial temperature.
• b - parameter.
• tau_c - parameter.
• v - speed.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BCO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BCO () { }
  C_AO_BCO ()
  {
    ao_name = "BCO";
    ao_desc = "Bacterial Chemotaxis Optimization";
    ao_link = "https://www.mql5.com/en/articles/15711";

    popSize = 50;     // population size (number of bacteria)
    hs      = 10;     // number of steps to calculate average change
    T0      = 1.0;    // initial temperature
    b       = 0.5;    // parameter b
    tau_c   = 1.0;    // parameter tau_c
    v       = 1.0;    // velocity

    ArrayResize (params, 6);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "hs";      params [1].val = hs;
    params [2].name = "T0";      params [2].val = T0;
    params [3].name = "b";       params [3].val = b;
    params [4].name = "tau_c";   params [4].val = tau_c;
    params [5].name = "v";       params [5].val = v;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    hs      = (int)params [1].val;
    T0      = params      [2].val;
    b       = params      [3].val;
    tau_c   = params      [4].val;
    v       = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    hs;
  double T0;
  double b;
  double tau_c;
  double v;

  S_BCO_Bacterium bacterium [];

  private: //-------------------------------------------------------------------
  double CalculateAverageDeltaFpr            (int bacteriumIndex);
  void   CalculateNewAngles                  (double &angles []);
  void   CalculateNewPosition                (double l, const double &angles [], double &new_position [], const double &current_position []);
  double GenerateFromExponentialDistribution (double T);
  double CalculateCorrectedB                 (double f_tr, double f_pr, int bacteriumIndex);
  double CalculateRotationAngle              ();
  int    RNDdir                              ();
};

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method of the C_AO_BCO class is responsible for the movement of bacteria in the search space. Let's take a look at how it works:

1. If revision is false, this means that the bacteria have an initial position.

• For each a [i] bacterium, random coordinates are generated within a given range.
• The u.RNDfromCI function generates a random value, while u.SeInDiSp adjusts it taking into account the specified step.

2. Basic movement loop if revision is true. The method implements the basic logic of bacterial movement. Defining the T temperature:

• If the current value of the f_tr function is better or equal to the previous f_pr, the initial temperature T0 is used.
• Otherwise, the temperature is adjusted using the CalculateCorrectedB function, which takes into account the difference between the current and previous value of the fitness function. 
• Generation of the tau movement time: exponential distribution to generate movement time is used.
• New movement angles and new position are calculated based on the l movement length and new angles.
• The new position is adjusted taking into account the specified range and step.
• At the end of the loop, the previous value of the fitness function for each bacterium is updated.

The Moving method implements the basic logic of moving bacteria in the search space, adapting their behavior depending on the results of previous iterations. It uses random elements and adaptive mechanisms to find the optimal solution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    double f_tr = a [i].f;
    double f_pr = bacterium [i].fPrev;

    double T;
    
    if (f_tr <= f_pr)
    {
      T = T0;
    }
    else
    {
      double b_corr = CalculateCorrectedB (f_tr, f_pr, i);
      
      T = T0 * exp (b_corr * (f_tr - f_pr));
    }

    double tau = GenerateFromExponentialDistribution (T);

    double new_angles [];
    ArrayResize (new_angles, coords - 1);
    CalculateNewAngles (new_angles);

    double l = v * tau;
    double new_position [];
    ArrayResize (new_position, coords);
    CalculateNewPosition (l, new_angles, new_position, a [i].c);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.SeInDiSp (new_position [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method of the C_AO_BCO class is responsible for updating information about the best solutions found and the history of fitness function values for each bacterium.

1. The ind variable is initialized with the value of -1. It will be used to store the index of the bacterium that was found to have the best function value.

2. Finding the best function value:

• The method goes through all bacteria in the popSize population and looks for the one whose function value f is greater than the current best value of fB.
• If a bacterium with a higher function value is found, then fB is updated and the index of this bacterium is saved to ind.

3. If a bacterium with the ind index ('ind' is not equal to -1), then the coordinates of this bacterium are copied into the cB array, which represents the coordinates of the current best solution.

4. For each bacterium, the history of function values is updated. The method iterates over each fHistory element shifting the values one position to the left to make room for the new value. At the end of each iteration, the last element of the fHistory array gets the current fitness value a [i].f for each bacterium.

Thus, the Revision method performs two main functions:

• Updating the best fitness function value and the corresponding coordinates.
• Updating the history of fitness function values for each bacterium, allowing changes in their state to be tracked over the course of their movement history. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1)
  {
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 1; j < hs; j++)
    {
      bacterium [i].fHistory [j - 1] = bacterium [i].fHistory [j];
    }

    bacterium [i].fHistory [hs - 1] = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The CalculateAverageDeltaFpr method of the C_AO_BCO class is designed to calculate the average changes in fitness function values (deltas) for a particular bacterium between its two neighboring positions, based on the history of fitness values.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateAverageDeltaFpr (int bacteriumIndex)
{
  double sum = 0;

  for (int i = 1; i < hs; i++)
  {
    sum += bacterium [bacteriumIndex].fHistory [i] - bacterium [bacteriumIndex].fHistory [i - 1];
  }

  return sum / (hs - 1);
}
//——————————————————————————————————————————————————————————————————————————————

The CalculateNewAngles method of the C_AO_BCO class is designed to calculate new angles based on logic related to rotation and distribution, and performs the following actions:

• Iterating over the array for new angles and calculating a new value for each angle.
• Using parameters that depend on the cosine of the angle to generate values that use a Gaussian distribution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewAngles (double &angles [])
{
  for (int i = 0; i < coords - 1; i++)
  {
    double theta = CalculateRotationAngle ();
    double mu    = 62 * (1 - MathCos (theta)) * M_PI / 180.0;
    double sigma = 26 * (1 - MathCos (theta)) * M_PI / 180.0;

    angles [i] = u.GaussDistribution (mu, mu - M_PI, mu + M_PI, 8);
  }
}
//——————————————————————————————————————————————————————————————————————————————

The CalculateNewPosition method of the C_AO_BCO class is designed to calculate new position coordinates based on current coordinates, angles and the parameter l. 

1. Input parameters of the method:

• l - ratio that influences the change in position.
• angles [] - array of angles used to calculate the new position.
• new_position [] - array new coordinates are set into.
• current_position [] - array of current coordinates.

2. The first coordinate new_position [0] is calculated as the sum of the current coordinate current_position [0] and a product of l and the difference between rangeMax [0] and rangeMin [0].

3. Then the first coordinate is multiplied by the cosines of the angles from the angles array starting from the first to the second to last.

4. The result is multiplied by the value returned by the RNDdir () function, which generates a random direction of "-1" or "1".

5. For each subsequent coordinate new_position [i], where i from 1 to coords - 2, a new position is calculated based on the current position and the sine of the corresponding angle.

6. Each new coordinate is also multiplied by the cosines of the angles starting from the current index i up to the penultimate one.

7. Random direction for the remaining coordinates, the result is also multiplied by the value returned by RNDdir ().

8. Handling the last coordinate, if the number of coordinates is greater than 1, for the last coordinate new_position [coords - 1], a new position is calculated based on the current position and the sine of the last angle.

Thus, the CalculateNewPosition method performs the following actions:

• Calculating new coordinates based on current coordinates and angles.
• Taking into account the influence of random direction on each coordinate.
• Using trigonometric functions (sine and cosine) to account for angles.

Thus, the method is used to simulate the movement of bacteria in space, taking into account their current position and given angles.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewPosition (double l, const double &angles [], double &new_position [], const double &current_position [])
{
  new_position [0] = current_position [0] + l * (rangeMax [0] - rangeMin [0]);
 
  for (int k = 0; k < coords - 1; k++)
  {
    new_position [0] *= MathCos (angles [k]);
  }
 
  new_position [0] *= RNDdir ();

  for (int i = 1; i < coords - 1; i++)
  {
    new_position [i] = current_position [i] + l * MathSin (angles [i - 1]) * (rangeMax [0] - rangeMin [0]);
    
    for (int k = i; k < coords - 1; k++)
    {
      new_position [i] *= MathCos (angles [k]);
    }
    
    new_position [i] *= RNDdir ();
  }

  if (coords > 1)
  {
    new_position [coords - 1] = current_position [coords - 1] + l * MathSin (angles [coords - 2]);
  }
 
}
//——————————————————————————————————————————————————————————————————————————————

Next, we will briefly describe the RNDdir method of the C_AO_BCO class designed to generate a random direction that can take one of two values: -1 or 1.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BCO::RNDdir ()
{
  if (u.RNDbool () < 0.5) return -1;
 
  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

Let's take a quick look at the methods of the C_AO_BCO class.

The GenerateFromExponentialDistribution method performs:

• generation of a random number using exponential distribution with the T parameter.
• then it uses a random number from the range (0, 1), calculates its logarithm and multiplies it by -T.
• we get a random number distributed according to the exponential law.

 The CalculateCorrectedB method performs:

• calculation of the adjusted b value based on the difference between f_tr and f_pr (current and previous fitness).
• calculating the difference between f_tr and f_pr, getting the average value for the bacteria, and returning the adjusted b value.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::GenerateFromExponentialDistribution (double T)
{
  return -T * MathLog (u.RNDprobab ());
}

double C_AO_BCO::CalculateCorrectedB (double f_tr, double f_pr, int bacteriumIndex)
{
  double delta_f_tr = f_tr - f_pr;
  double delta_f_pr = CalculateAverageDeltaFpr (bacteriumIndex);

  if (MathAbs (delta_f_pr) < DBL_EPSILON)
  {
    return b;
  }
  else
  {
    return b * (1 / (MathAbs (delta_f_tr / delta_f_pr) + 1) + 1 / (MathAbs (f_pr) + 1));
  }
}
//——————————————————————————————————————————————————————————————————————————————

The CalculateRotationAngle method of the C_AO_BCO class comes last. The method calculates the rotation angle based on the given parameters and returns the value in radians.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateRotationAngle ()
{
  double cos_theta = MathExp (-tau_c / T0);
  return MathArccos (cos_theta);
}
//——————————————————————————————————————————————————————————————————————————————

Let's test the original version of the algorithm and have a look at the results:

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|1.0|0.5|1.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.42924491510564006
25 Hilly's; Func runs: 10000; result: 0.282259866768426
500 Hilly's; Func runs: 10000; result: 0.2515386629014219
=============================
5 Forest's; Func runs: 10000; result: 0.2476662231845009
25 Forest's; Func runs: 10000; result: 0.17824381036550777
500 Forest's; Func runs: 10000; result: 0.15324081202657283
=============================
5 Megacity's; Func runs: 10000; result: 0.2430769230769231
25 Megacity's; Func runs: 10000; result: 0.11415384615384619
500 Megacity's; Func runs: 10000; result: 0.09444615384615461
=============================
All score: 1.99387 (22.15%)

The results obtained are so weak that there is no point in including them in the rating table. When designing the algorithm and writing the code based on the author's text description, I had to adjust some equations: some of them did not make mathematical sense (for example, dividing a number by a vector), while others degenerated into either extremely small or extremely large values that were incomparable with the dimensions of the problem. In doing so, I printed out the results of the functions for each of the presented equations and analyzed them. Thus, the algorithm cannot function in the form, in which it is described by the authors.

In addition, operations with angles, in which the normal distribution is used, can be significantly simplified, since the physical meaning of these operations comes down to the fact that at each coordinate one can simply set a new increment from the current location of the bacterium. So I decided to develop my own implementation of bacterial chemotaxis, keeping as close as possible to the basic concepts and ideas of the algorithm.

Here is the pseudocode of my version of the algorithm:

Initialization:
1. Create a population of popSize bacteria
2. For each i bacterium:
    Initialize the history of values of the objective function f_history [i] of the hs size
    Set initial value f_prev [i] = -DBL_MAX

Main loop:
Until the stop condition is reached:

1. If this is the first iteration:
   For each i bacterium:
     Randomly initialize the x [i] position in the search space
     x [i].[j] ∈ [x_min [j], x_max [j]] for each j coordinate

2. Otherwise:
   For each i bacterium:
     a. Calculate the average change in the target function:
        delta_ave [i] = (1 / (hs - 1)) * sum (f_history [i].[k] - f_history [i].[k-1] for k in 1..hs-1) + epsilon
     
     b. Calculate the relative change in fitness:
        delta [i] = 1 - |f (x [i]) - f_prev [i]| / delta_ave [i]
        delta [i] = max (delta [i], 0.0001)
     
     c. For each j coordinate:
        With the probability of 0.5:
          dist [j] = (x_max [j] - x_min [j]) * delta [i]
          x [i].[j] = N (x [i].[j], x [i].[j] - dist [j], x [i].[j] + dist [j])
          Limit x [i].[j] within [x_min [j], x_max [j]]
        Otherwise:
          x [i].[j] = x_best [j]
     
     d. Update f_prev [i] = f (x [i])

3. Evaluate the target function f (x [i]) for each bacterium

4. Update the best solution found:
   If i exists: f (x [i]) > f (x_best), then x_best = x [i]

5. Update the history of target function values for each bacterium:
   Shift values in f_history [i]
   Add a new value: f_history [i].[hs - 1] = f (x [i])

Completion:
Return the best solution found x_best

where;

• x [i] - position of the i th bacterium
• f (x) - target function
• hs - history size
• epsilon - a small constant to prevent division by zero
• N (μ, a, b) - truncated normal distribution with mean μ and bounds [a, b]

Thus, my modified pseudocode reflects the basic structure and logic of the BCO algorithm. Let's focus on the main points:

• The algorithm uses a population of bacteria, each representing a potential solution.
• At each iteration, bacteria move through the search space using information about their previous results.
• The movement is based on the relative change of the objective function, which allows the algorithm to adapt to the optimization landscape.
• The algorithm stores a history of the objective function values for each bacterium, which is used to calculate the average change.
• There is some probability that the bacterium will move towards the best known solution instead of exploring a new area (analogous to the inheritance of traits in genetics).
  
• After each move, new positions are evaluated and the best solution found is updated.

The BCOm version combines elements of local search (movement of individual bacteria) and global search (exchange of information via the best known solution).

Let's look at the main differences between the two versions of the algorithm. Firstly, the mechanism of bacterial movement has been simplified. I have abandoned the complex system with rotation angles and temperature. Second, the new version relies less on change history to adjust bacterial behavior, using a more straightforward approach to updating positions. Instead of a combination of exponential and normal distributions, the new algorithm uses the normal distribution to update coordinates. The result of the changes was a reduction in the number of parameters to one (not counting the population size) that control the behavior of the algorithm, which changed the way the optimization process was configured and simplified the management.

Overall, the new pseudocode assumes simpler calculations at each optimization step, which should also have a positive effect on the speed of the algorithm's task execution (the original version performed multiple calculations of the sine and cosine of the rotation angles for each coordinate of each bacterium). My approach is a little different, balancing between exploring a new solution space and exploiting good solutions that have already been found.

These changes in logic resulted in a simpler and, presumably (pending test results), more efficient algorithm. Let's move on to writing the code.

The S_BCO_Bacterium structure, representing each bacterium, is left unchanged. It is designed to store information about the bacterium and its history of objective function values.

In the Init method of the C_AO_BCOm class, responsible for initializing the algorithm parameters, we will add a definition of the distance of acceptable movement along each coordinate.

Thus, the Init method of the C_AO_BCOm class is responsible for initializing the parameters of the optimization algorithm. It checks the standard initialization conditions, creates the necessary arrays and fills them with values.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCOm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  ArrayResize (allowedDispl, coords);
  for (int c = 0; c < coords; c++) allowedDispl [c] = rangeMax [c] - rangeMin [c];

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Let's look at the Moving method of the C_AO_BCOm class responsible for the movement of bacteria in the search space. Let's break it down piece by piece.

1. At the first iteration, the method actions did not change: initialization of the bacteria coordinates with random values in a given range.

2. The basic algorithm for moving is to declare variables to store values, such as Δ, ΔAve and dist, as well as for each individual in the population:

• The average value ΔAve is calculated using the CalculateAverageDeltaFpr (i) function.
• The Δ relative change, used to determine the degree of change in the position of bacteria, is calculated.
• If Δ is too small, it is set to 0.0001.

3. Changing coordinates:

• A random probability (50%) is checked for each coordinate.
• If the condition is met, calculate dist depending on allowedDispl [c] and Δ.
• New value x is calculated using the function GaussDistribution considering xMin and xMax boundaries.
• If x is out of range, it is corrected using RNDfromCI.
• Finally, the new coordinate value is stored taking into account the rangeStep.

4. The previous value f of the fitness function is saved for each individual in the bacterium array. a and bacterium arrays are used. The RNDfromCI, SeInDiSp and GaussDistribution functions are responsible for generating random numbers and distributions, as well as for normalizing coordinate values.

Thus, the Moving () function is responsible for initializing and updating the position of individuals in the population within the algorithm. It uses random probabilities and distributions to control the movement of bacteria. However, the key difference from the original version is a simpler and more efficient way of implementing the gradient of the fitness function. When the difference in the bacteria's well-being at the current step decreases compared to the previous one, its movement accelerates. Conversely, when in a favorable external environment, the bacteria slow down. This contradicts the natural behavior of bacteria, which in an aggressive environment become depressed and go into suspended animation.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double x    = 0.0;
  double xMin = 0.0;
  double xMax = 0.0;
  double Δ    = 0.0;
  double ΔAve = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    ΔAve = CalculateAverageDeltaFpr (i) + DBL_EPSILON;

    Δ = fabs (a [i].f - bacterium [i].fPrev) / ΔAve;

    Δ = 1.0 - Δ;

    if (Δ < 0.0001) Δ = 0.0001;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < 0.5)
      {
        dist = allowedDispl [c] * Δ;

        x    = a [i].c [c];
        xMin = x - dist;
        xMax = x + dist;

        x = u.GaussDistribution (x, xMin, xMax, 8);

        if (x > rangeMax [c]) x = u.RNDfromCI (xMin, rangeMax [c]);
        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], xMax);

        a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else a [i].c [c] = cB [c];
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision () method in the C_AO_BCOm class, which is responsible for updating information about the population and the history of the values of the target function, has not changed.

Test results

Now let's see the performance of the new version of the BCOm algorithm:

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.759526049526603
25 Hilly's; Func runs: 10000; result: 0.6226756163411526
500 Hilly's; Func runs: 10000; result: 0.31483373090540534
=============================
5 Forest's; Func runs: 10000; result: 0.8937814268120954
25 Forest's; Func runs: 10000; result: 0.6133909133246214
500 Forest's; Func runs: 10000; result: 0.22541842289630293
=============================
5 Megacity's; Func runs: 10000; result: 0.653846153846154
25 Megacity's; Func runs: 10000; result: 0.42092307692307684
500 Megacity's; Func runs: 10000; result: 0.14435384615384755
=============================
All score: 4.64875 (51.65%)

Probably, the accumulated experience and a critical look at the available information about the original version did their job, and the new version of the algorithm proved to be more powerful in practical application than the original.

In the visualization of the BCOm algorithm, we can see the good elaboration of significant sections of hyperspace, which indicates a high ability to study the surface of the optimized function.

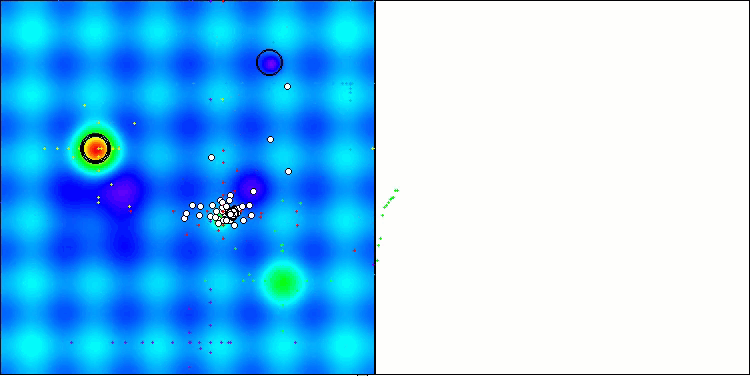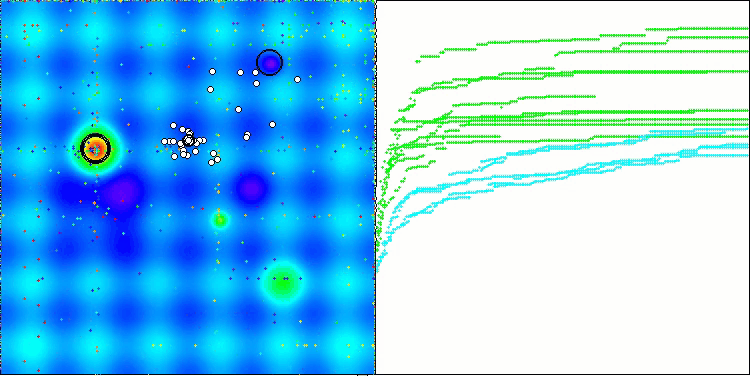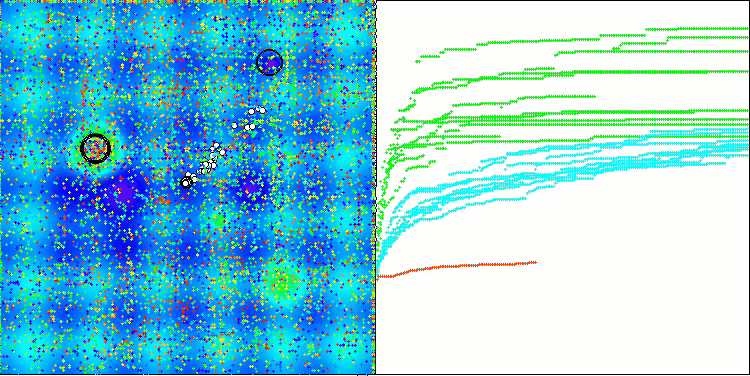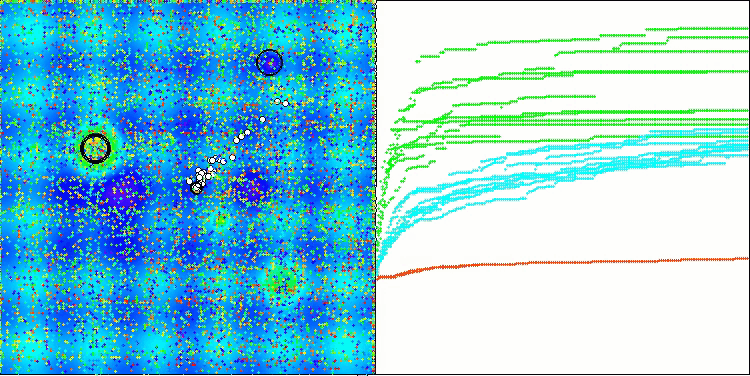
BCOm on the Hilly test function

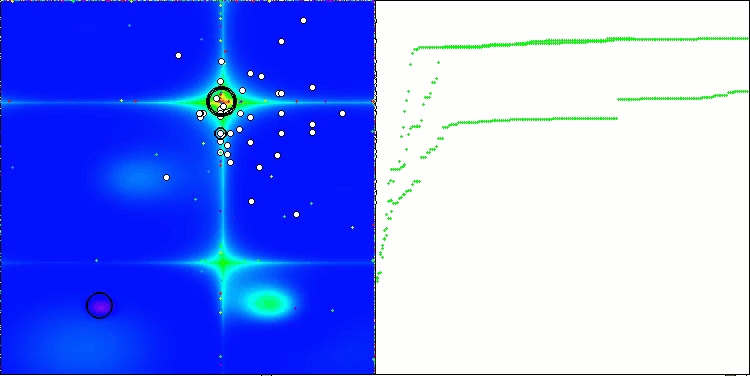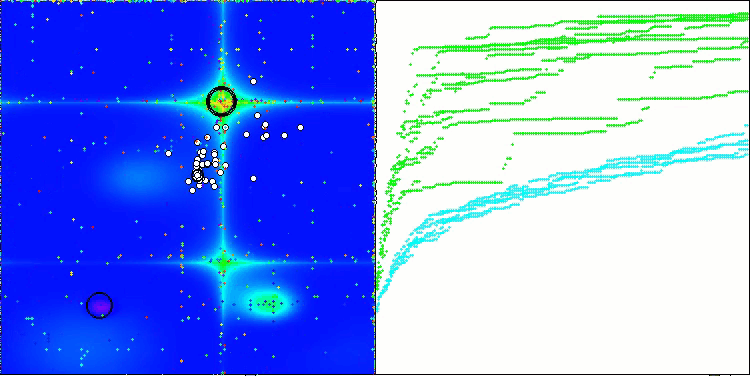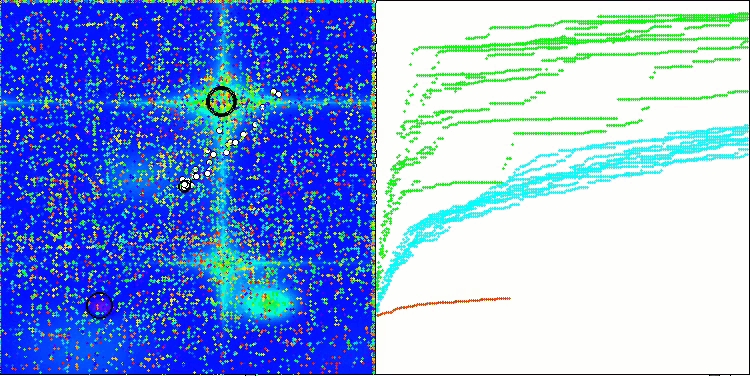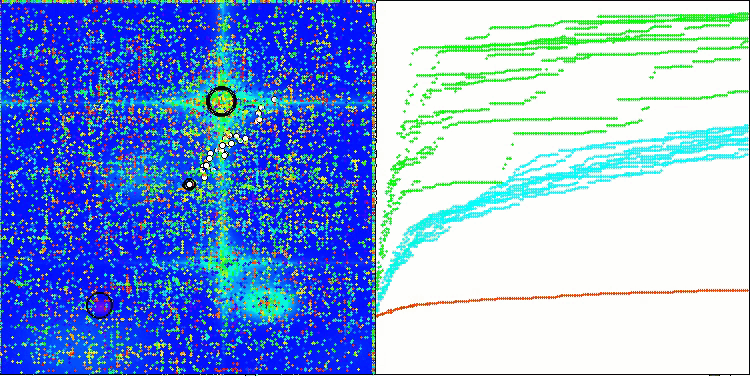
BCOm on the Forest test function

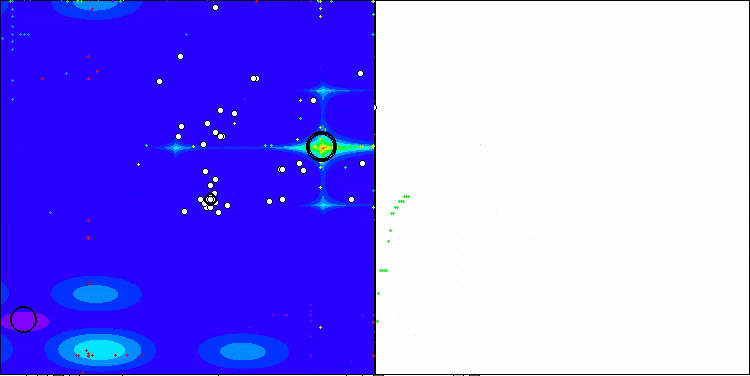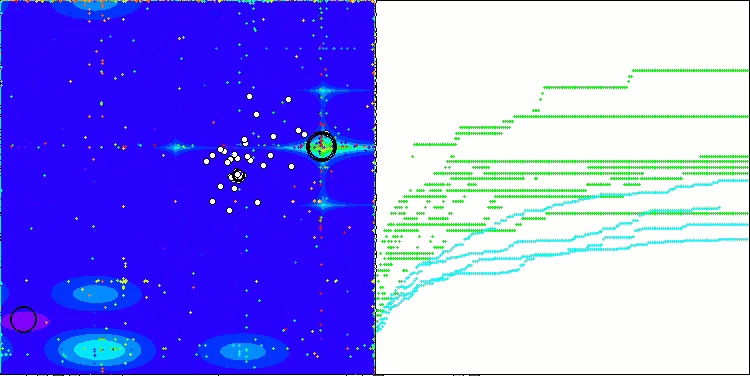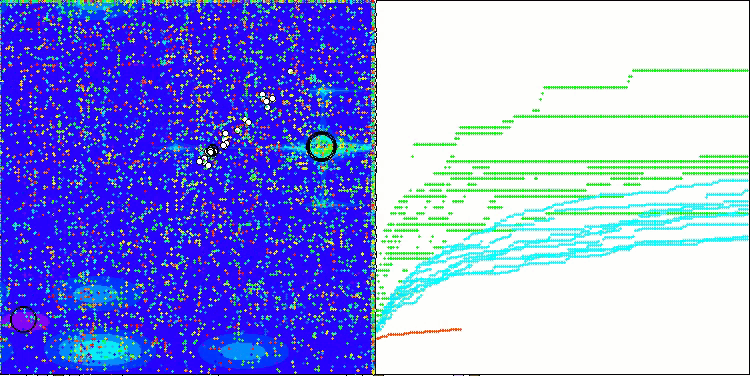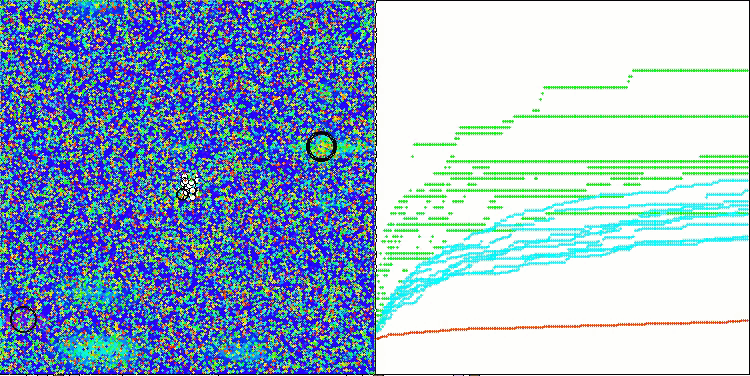
BCOm on the Megacity test function

Based on the test results, the algorithm took a stable 17 th place in the overall ranking of the optimization algorithms.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration ptimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	evolution of social groups	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	simulated isotropic annealing	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	turtle shell evolution algorithm	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	BCOm	bacterial chemotaxis optimization M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
18	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
19	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
20	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
21	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
22	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
23	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
24	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
25	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
26	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
27	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
28	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
29	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
30	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
31	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
32	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
33	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
34	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
35	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
36	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
37	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
38	AAA	algae adaptive algorithm	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
39	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
40	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
41	PSO	particle swarm optimisation	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
42	Boids	boids algorithm	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
43	MA	monkey algorithm	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
44	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
45	FSS	fish school search	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84

Summary

We have considered the original and modified versions of the BCO algorithm. The original version, recreated from open sources, turned out to be overloaded with heavy trigonometric calculations and had weak search properties, as well as mathematical "bloopers". It was necessary to rethink the entire algorithm and conduct a deep analysis of the search strategy and create a new modified version. Changes in the algorithm logic resulted in simpler calculations at each optimization step, which had a positive effect on the speed of code execution. The new algorithm also balances differently between exploring a new solution space and exploiting good solutions that have already been found.

Although the new approach is somewhat contrary to the natural behavior of bacteria, it has proven highly efficient in practical applications. Visualization of the algorithm operation showed its ability to deeply explore significant areas of hyperspace, which also indicates its improved research capabilities. As a result, the new version of the algorithm turned out to be more powerful and efficient compared to the original.

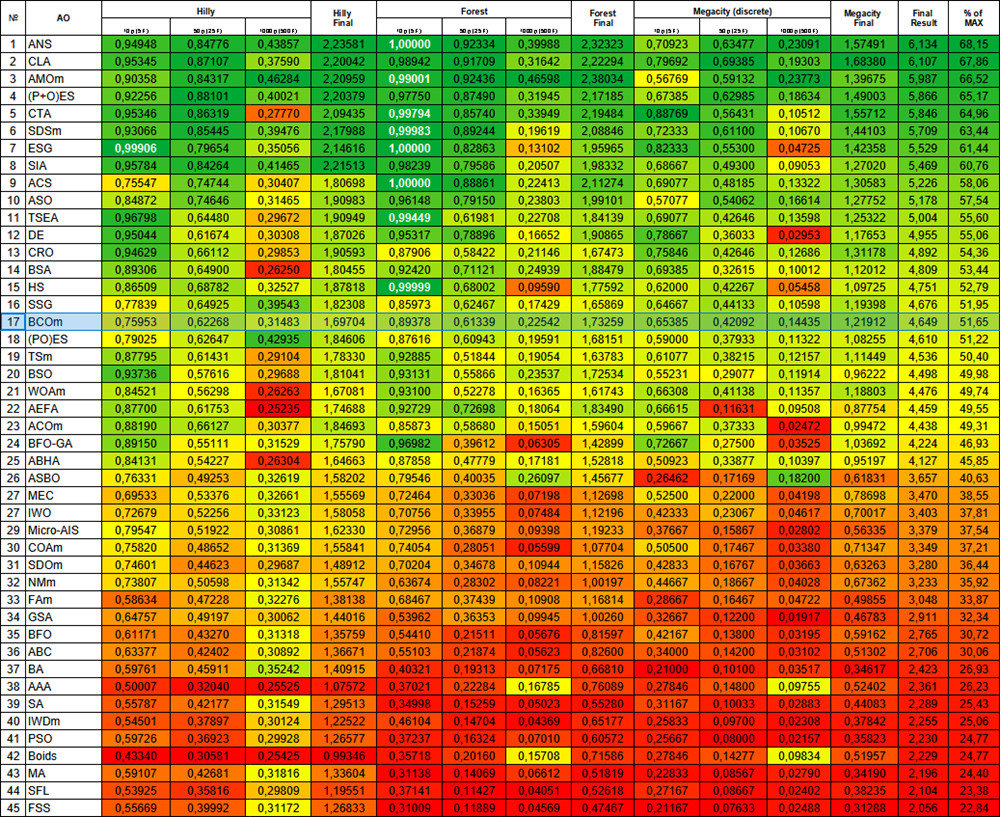
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

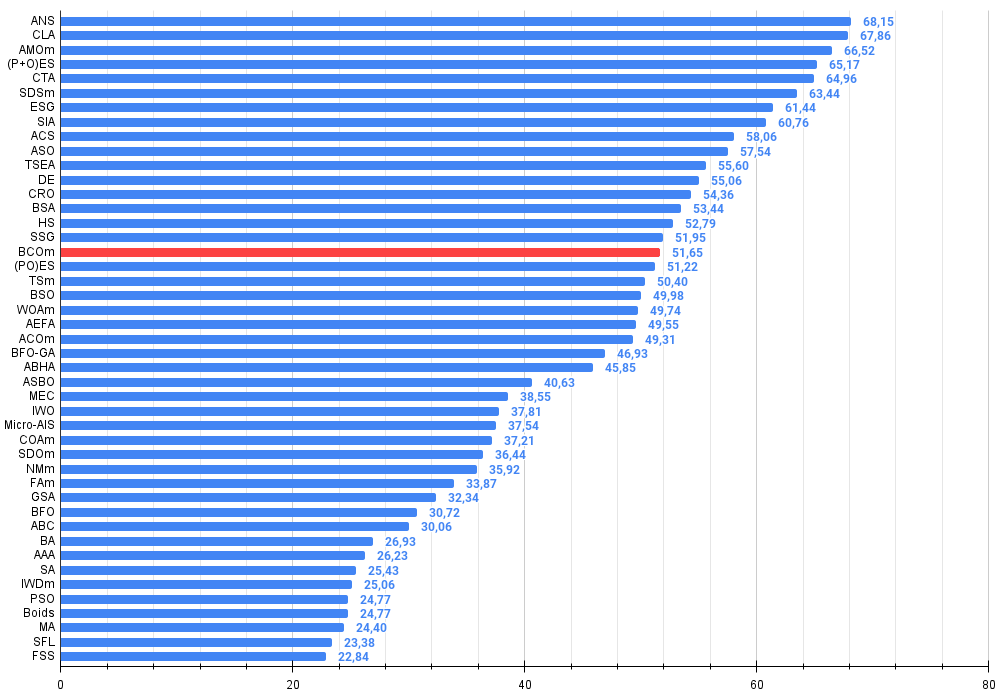
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

BCOm pros and cons:

Pros:

1. Fast.
2. Self-adapting.
   
3. Good scalability.
4. Just one external parameter.
   

Cons:

1. High scatter of results on low-dimensional functions.
   

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355