MetaTrader 5 / トレーディングシステム
English Русский Español Português
preview
取引におけるニューラルネットワーク：点群の階層的特徴量学習

取引におけるニューラルネットワーク：点群の階層的特徴量学習

MetaTrader 5 — トレーディングシステム | 6 5月 2025, 15:20
55 0
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

幾何学的な点の集合とは、ユークリッド空間内の点の集まりを指します。このようなデータは集合として扱われるため、要素の順序が変わっても不変である必要があります。また、距離メトリックは局所的な近傍を定義し、そこでは点密度などの属性が領域ごとに異なる場合があります。

前回の記事では、PointNet手法について説明しました。この手法の基本的な考え方は、各点に対して空間的なエンコーディングを学習し、その後、すべての個別表現を集約して点群全体の大域的な特徴量（シグネチャ）を得るというものです。ただし、PointNetは局所構造を捉えることができません。一方で、畳み込みニューラルネットワーク(CNN)の成功には、局所構造の活用が重要であることが示されています。CNNは規則的なグリッド上に配置されたデータを処理し、多段階の解像度階層を通じて、徐々により大きなスケールで対象物を捉えていきます。低い層では受容野が小さく、細かな情報を捉えますが、高い層ではより広い領域をカバーし、抽象度の高い特徴量を学習します。このように、階層的に局所パターンを抽象化できる点が、モデルの汎化能力を高めています。

同様のアプローチはPointNet++モデルでも採用されており、その詳細は論文「PointNet++:Deep Hierarchical Feature Learning on Point Sets in a Metric Space」で紹介されています。pointnet++の中心的なアイデアは、距離メトリックに基づき点群を重複する局所領域に分割し、局所的な特徴量を抽出することです。CNNと同様に、PointNet++は小さな領域からきめ細かな幾何構造を捉え、それらを統合してより高次の表現へと変換します。このプロセスは繰り返され、最終的に点群全体の特徴量表現が得られます。

pointnet++の設計において、著者らは、「点群の分割方法」と「局所的な特徴量学習を通じた抽象化」の2つの主要な課題に取り組みました。これらは密接に関係しており、点群をうまく分割するには、セグメント間で構造を共有できるようにする必要があり、これはCNNのような重みの共有にとって不可欠です。著者は、順序のない点集合を効率的に処理し、意味的特徴量を抽出するアーキテクチャとしてpointnetを局所学習ユニットとして選択しました。このアーキテクチャは入力データのノイズにも頑健です。PointNetは基本的な構成要素として、局所的な点やオブジェクトの集合を高次の表現へと抽象化します。このフレームワーク内で、PointNet++は入力データの入れ子構造に対してPointNetを再帰的に適用します。

残された課題の1つは、点群の重複領域の作成方法です。各領域はユークリッド空間内の近傍球として定義され、セントロイドの位置やスケールなどのパラメータによって特徴付けられます。点集合全体を均等にカバーするために、セントロイドは元の点群からFarthest Point Samplingアルゴリズムを用いて選ばれます。固定ストライドで空間を走査するボリューム畳み込みモデルと比較して、PointNet++における局所受容野は入力データと距離メトリックの両方に依存するため、より効率的になります。


1.PointNet++アルゴリズム

PointNetアーキテクチャは、単一のMaxPooling操作によって点集合全体を集約します。これに対し、PointNet++の著者は、複数の階層にわたって局所領域を段階的に抽象化する階層型アーキテクチャを導入しました。

提案された階層構造は、いくつかの事前に定義された抽象化レベルから構成されます。各レベルでは、点群が処理・抽象化され、より少ない要素を持つ新たなデータセットが生成されます。各抽象化レベルは、サンプリング層、グループ化層、PointNet層の3つの主要な層から構成されます。サンプリング層は、元の点群から点のサブセットを選択し、局所領域の重心を定義します。続くグループ化層では、各重心の周囲にある「近傍」の点を特定し、局所点集合を形成します。最後に、pointnet層がミニpointnetを適用し、局所パターンを特徴量ベクトルとしてエンコードします。

抽象化レベルは、サイズn×(d+c)の入力行列を受け取ります。ここでnは点の数、dは座標の次元、cは特徴量の次元です。出力はサイズn′×(d+c′)の行列です。ここで、n′はサブサンプルされた点の数、c′は局所文脈を表現する新たな特徴量ベクトルの次元です。

PointNet++の著者は、重心点のサブセットを選択するために反復的なFarthest Point Sampling (FPS)を提案しています。ランダムサンプリングと比較して、同数の重心点を維持しながら点群全体をより広くカバーできます。従来の畳み込みネットワークがデータ分布とは無関係にベクトル空間をスキャンするのに対し、このサンプリング戦略はデータに依存した受容野を自然に生成します。

グループ化層は、サイズN×(d+C)の点群とサイズN′×dの重心座標のセットを入力として受け取ります。出力は、サイズN′×K×(d+C)のグループ化された点集合で、各グループは局所領域に対応します。ここでKは、各重心の近傍にある点の数です。

kの値はグループによって異なりますが、後続のpointnet層は、柔軟な数の点から局所領域を表す固定長の特徴量ベクトルを生成できます。

畳み込みニューラルネットワーク(CNN)においては、ピクセルの局所近傍は、所定のマンハッタン距離（カーネルサイズ）内にある隣接ピクセルから構成されます。一方、点群では点が距離空間内に存在するため、近傍関係は距離メトリックによって決まります。

グループ化処理では、モデルはクエリ点の定義された半径内に存在するすべての点を識別します（Kはハイパーパラメータとして上限が設定されます）。

PointNet層では、入力はN′×K×(d+C)サイズの N′個の局所領域で構成されます。各局所領域は、最終的にその重心と、その近傍をエンコードした局所特徴量ベクトルに抽象化されます。出力されるテンソルのサイズはN′×(d+C)です。

各局所領域内の点の座標は、まず対応する重心を基準とした局所座標系に変換されます。

i=1,2,…,K、j=1,2,…,d、ただし重心の座標を表します。

PointNet++の著者らは、局所パターンを学習するための基本構成要素としてPointNetを用いています。相対座標と各点の特徴量を組み合わせることで、局所領域内の点同士の関係性を効果的に捉えることができます。

多くの点群データでは、領域によって点の密度が不均一であることがよくあります。このような非均質性は、点集合の特徴量学習において大きな問題となります。密にサンプリングされた領域で学習された特徴量は、疎な領域にはうまく一般化できない可能性があります。そのため、スパースな点群で訓練されたモデルは、きめ細かな局所構造を認識できなくなるおそれがあります。

理想的には、点群の処理は、高密度にサンプリングされた領域の細部まで捉えられるよう、可能な限り精密であるべきです。しかし、点の密度が低い領域では、データ不足により局所パターンが歪められる可能性があり、このような詳細な分析は非効率的です。このような場合には、より広い近傍を考慮して、大きなスケールの構造を検出する必要があります。これに対応するため、PointNet++では、点密度の変化を考慮して複数のスケールから特徴量を集約できるように設計された密度適応型PointNet層を提案しています。

PointNet++における各抽象化レベルでは、複数スケールの局所パターンを抽出し、局所の点密度に応じて賢く統合されます。論文では、2種類の密度適応層が提案されています。

マルチスケールなパターンを捉える基本的で効果的な手法として、異なるスケールの複数のグループ化層を適用し、それぞれに対応するPointNetモジュールを割り当てて各スケールで特徴量を抽出する方法があります。こうして得られたマルチスケール表現は、統一された特徴量ベクトルとして結合されます。

ネットワークは、マルチスケール特徴量を結合するための最適な戦略を学習します。この戦略は、各インスタンスに割り当てられた確率で入力点をランダムに削除（ドロップ）することで実現されます。

ただしこの方法は、各重心点に対して大きな近傍範囲において局所的なPointNet処理をおこなうため、計算コストが高くなります。こうした計算負荷を軽減しつつ、情報を適応的に集約する能力を維持するため、著者らは2つの特徴量ベクトルを連結する代替的な特徴量融合手法を提案しています。1つ目のベクトルは、現在の抽象化レベルにおいて、下位レベルLi-1の各サブ領域から集約された特徴量によって得られます。2つ目のベクトルは、局所領域内のすべての元の点に対して、単一のPointNetモジュールを直接適用することで得られます。

局所領域の密度が低い場合、1つ目のベクトルは、計算に使われたサブ領域の点数自体がさらに少なく、スパースサンプリングの影響を受けやすいため、2つ目のベクトルに比べて信頼性が下がる可能性があります。このような場合には、2つ目のベクトルに高い重みを与える必要があります。一方で、点密度が高い場合、1つ目のベクトルはより高い解像度で局所構造を再帰的に捉えることができるため、より精緻な情報を提供します。

この手法は、大規模な近傍に対して特徴量を最下位レベルで計算する必要がないため、計算効率にも優れています。

抽象化層では、元の点集合がサブサンプリングされます。しかし、セマンティックラベリングのようなセグメンテーションタスクでは、元のすべての点に対して特徴量を得ることが望まれます。その1つの解決策は、すべての抽象化レベルで元の全点を重心としてサンプリングすることですが、これは計算コストを著しく増加させます。もう1つの方法は、サブサンプルされた点から元の点に特徴量を伝播することです。

PointNet++の手法に関する著者による可視化が以下に示されています。


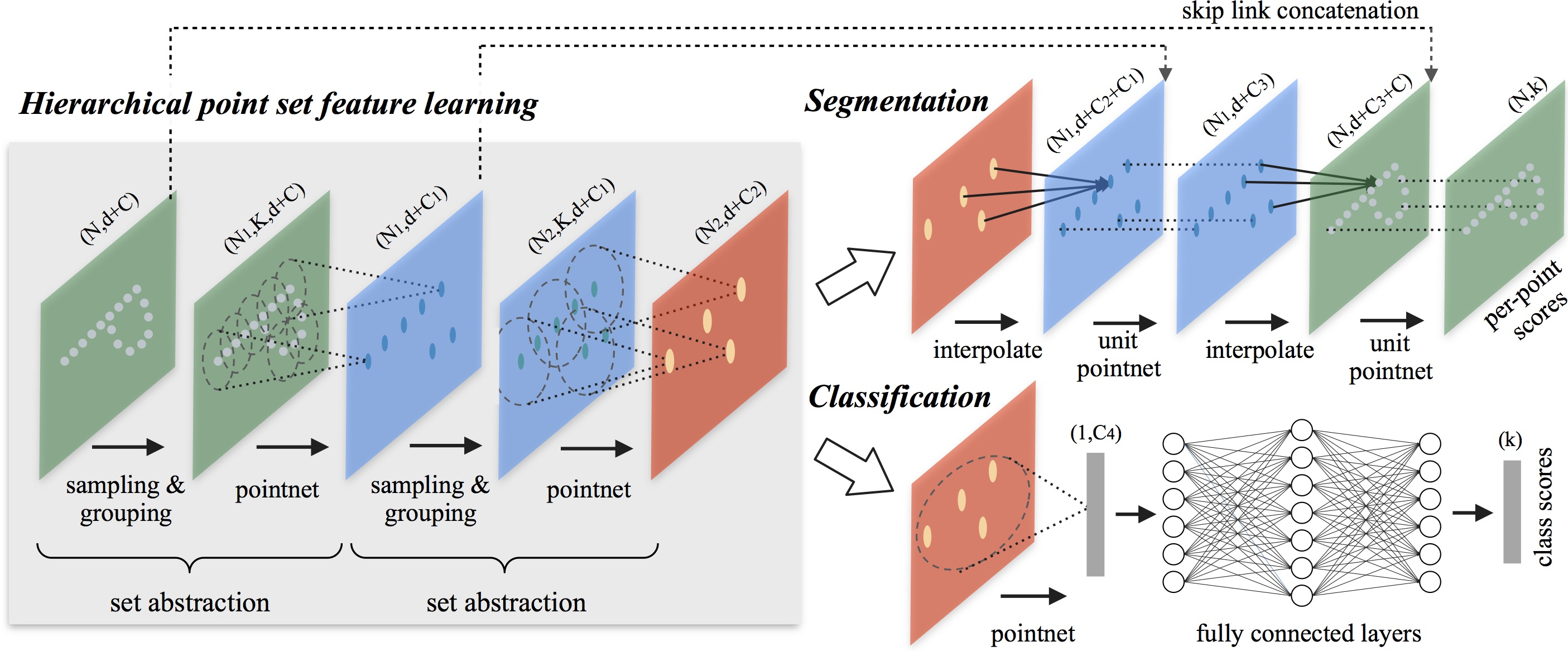
2.MQL5での実装

PointNet++法の理論的側面について確認した後は、本稿の実用的な部分に移り、MQL5を使用して、提案するアプローチのビジョンを実装します。なお、私たちの実装は、前述のオリジナル手法とは一部異なる点があります。ですが、まずは基本から順を追って説明していきます。

実装作業は、次の2つの主要なセクションに分かれます。最初に、先ほど説明したサンプリング層とグループ化層を統合した局所サブサンプリング層を作成します。次に、それらの個々のコンポーネントを組み合わせて、完全なPointNet++アルゴリズムとして構築する高レベルクラスを開発します。

2.1 OpenCLプログラムの拡張

局所サブサンプリングアルゴリズムは、CNeuronPointNet2Localクラスで実装されます。ただし、このクラスの作業に取りかかる前に、まずOpenCLプログラムの機能を拡張する必要があります。

はじめに作成するのは、CalcDistanceカーネルです。このカーネルは、解析対象となる点群内の各点同士の距離を計算します。

ここで重要なのは、距離が多次元の特徴量空間において計算される点です。各点は特徴量ベクトルとして表現され、カーネルの出力は対角要素がゼロのN×N行列となります。

このカーネルのパラメータには、2つのデータバッファ（1つは入力データ用、もう1つは計算結果格納用）へのポインタに加え、点の特徴量ベクトルの次元数を指定する定数が含まれます。

__kernel void CalcDistance(__global const float *data,
                           __global float *distance,
                           const int dimension
                          )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total = (int)get_local_size(1);

カーネル内では、タスク空間内のスレッドを識別します。

出力は正方行列となるため、適切なサイズの2次元タスク空間を定義します。これにより、各スレッドが結果行列の1つの要素のみを計算することが保証されます。

この時点で、私たちの実装はPointNet++の元のアルゴリズムから最初の逸脱をおこないます。局所領域の重心を反復的に決定することはせず、点群内のすべての点を重心として扱う方式を採用します。領域サイズに対する適応性を持たせるために、各点までの距離を正規化します。この距離の正規化には、スレッド間のデータ共有が必要です。そのため、結果行列の行に沿って局所ワークグループを構成することで、この通信を実現します。

ワークグループ内で効率的にデータを共有するために、ローカル配列を作成します。

   __local float Temp[LOCAL_ARRAY_SIZE];
   int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);

次に、データバッファ内の必要な要素へのオフセット定数を決定します。

   const int shift_main = main * dimension;
   const int shift_slave = slave * dimension;
   const int shift_dist = main * total + slave;

その後、多次元空間内の2つのオブジェクト間の距離を計算するためのループを作成します。

//--- calc distance
   float dist = 0;
   if(main != slave)
     {
      for(int d = 0; d < dimension; d++)
         dist += pow(data[shift_main + d] - data[shift_slave + d], 2.0f);
     }

計算は非対角要素に対してのみ実行されることに注意してください。これは、ある点からその点自体までの距離が「0」に等しいためです。したがって、無意味な計算にリソースを消費しないように、対角要素に対する計算はスキップされます。

次のステップは、ワークグループ内での最大距離を求めることです。まず、個々のブロックから得られた最大値をローカル配列に集めます。

//--- Look Max
   for(int i = 0; i < total; i += ls)
     {
      if(!isinf(dist) && !isnan(dist))
        {
         if(i <= slave && (i + ls) > slave)
            Temp[slave - i] = max((i == 0 ? 0 : Temp[slave - i]), dist);
        }
      else
         if(i == 0)
            Temp[slave] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

次に、配列内の最大値を見つけます。

   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(slave < count && (slave + count) < ls)
        {
         if(Temp[slave] < Temp[slave + count])
            Temp[slave] = Temp[slave + count];
         Temp[slave + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

分析点までの最大値を見つけたら、上で計算した距離をその値で割ります。その結果、点間のすべての距離は[0,1]の範囲で正規化されます。

//--- Normalize
   if(Temp[0] > 0)
      dist /= Temp[0];
   if(isinf(dist) || isnan(dist))
      dist = 1;
//--- result
   distance[shift_dist] = dist;
  }

計算された値は、グローバル結果バッファの対応する要素に保存されます。

もちろん、分析対象の2点間の最大距離は一様ではないことを認識しています。異なるスケール間で値を正規化することで、こうした違いは失われますが、まさにこの性質が受容野の適応を可能にするのです。

たとえば、分析対象の点が点群内の高密度領域にある場合、最も遠い点は通常、点群の境界付近に存在します。一方で、分析対象の点が点群の端に位置している場合、その最遠点は反対側の端にあることになります。この後者のケースでは、2点間の距離はより長くなり、その結果、受容野もより広くなります。

また、一般的に点群の内部の方が周縁部よりも点密度が高いと仮定します。したがって、点群の外縁部で受容野を広げることは、意味のある特徴量抽出をおこなうために合理的なアプローチです。

PointNet++の著者は、各点の重心に対する相対的な位置を計算し、これらの局所的な点群にミニPointNetを適用する手法を提案しています。しかし、この方法は一見シンプルに見えるものの、実装上の大きな課題を含んでいます。

すでに述べたとおり、各局所領域に含まれる点の数は一様ではなく、事前には分かりません。そのため、バッファの割り当てに関して問題が生じます。一つの解決策としては、各受容野ごとに最大点数を設定し、それに基づいて余裕を持ったバッファを確保する方法が考えられますが、このアプローチではメモリ消費が増大し、計算の複雑性も高まります。その結果、学習が困難になり、モデルの性能も低下する可能性があります。

その代わりに、私たちはよりシンプルで汎用性の高いアプローチを採用しました。それは、局所的な変位の計算を省略するというものです。点特徴量の学習には、従来のPointNetと同様に、すべての要素に対して単一の重み行列を適用します。ただし、受容野内でMaxPoolingを実行することは可能です。これを実現するために、新しいカーネルFeedForwardLocalMaxを作成しました。このカーネルは、点特徴量行列、正規化済み距離行列、結果格納用バッファの3つのバッファポインタを引数として受け取ります。さらに、受容野の半径を指定する定数も導入します。さらに、受容野半径の定数を導入します。

__kernel void FeedForwardLocalMax(__global const float *matrix_i,
                                  __global const float *distance,
                                  __global float *matrix_o,
                                  const float radius
                                 )
  {
   const size_t i = get_global_id(0);
   const size_t total = get_global_size(0);
   const size_t d = get_global_id(1);
   const size_t dimension = get_global_size(1);

カーネルの実行は、二次元のタスク空間で計画します。最初の次元では、点群内の要素の数を示し、2番目の次元では、1つの要素の特徴量の次元を示します。カーネル本体では、タスク空間の両方の次元で現在のスレッドを即座に識別します。この場合、各スレッドは独立して動作するため、ワークグループを作成してスレッド間でデータを交換する必要はありません。

次に、データバッファ内のオフセット定数を定義します。

   const int shift_dist = i * total;
   const int shift_out = i * dimension + d;

次に、最大値を決定するためのループを作成します。

   float result = -3.402823466e+38;
   for(int k = 0; k < total; k++)
     {
      if(distance[shift_dist + k] > radius)
         continue;
      int shift = k * dimension + d;
      result = max(result, matrix_i[shift]);
     }
   matrix_o[shift_out] = result;
  }

次の要素の値を確認する前に、まずそれが点群内の対応する点の受容野内にあるかどうかを確認することに注意してください。

ループの反復が完了すると、計算された値が結果バッファに保存されます。

同様に、誤差勾配を対応する要素に分配するバックプロパゲーションカーネルCalcInputGradientLocalMaxを実装します。フィードフォワードパスカーネルとバックプロパゲーションパスカーネルには多くの類似点があります。ぜひ独自に検討してみることをお勧めします。完全なカーネルコードは添付ファイルにあります。さて、メインプログラムの実装に進みます。

2.2 局所サブサンプリングクラス

OpenCL側の準備作業が完了したので、次は局所サブサンプリングクラスの開発に移ります。OpenCLカーネルを実装する際に、アルゴリズム設計の基本原則についてはすでに触れました。ただし、CNeuronPointNet2Localクラスの実装を進めていく中で、これらの原則をより詳細に検討し、コードでの実際の実装を検討していきます。以下に新しいクラスの構造を示します。

class CNeuronPointNet2Local   :  public CNeuronConvOCL
  {
protected:
   float                fRadius;
   uint                 iUnits;
   //---
   CBufferFloat         cDistance;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronBaseOCL       cLocalMaxPool;
   CNeuronConvOCL       cFinalMLP;
   //---
   virtual bool         CalcDistance(CNeuronBaseOCL *NeuronOCL);
   virtual bool         LocalMaxPool(void);
   virtual bool         LocalMaxPoolGrad(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNet2Local(void) {};
                    ~CNeuronPointNet2Local(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint window_out, float radius,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2LocalOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

上記の構造では、いくつかの内部ニューラル層オブジェクトと2つの変数を確認できます。その目的については、クラスメソッドの実装中に検討します。

また、オーバーライド可能なメソッドのよく知られたセットも見られます。さらに、以前に実装されたカーネルに対応する3つのメソッドがあります。

  • CalcDistance(CNeuronBaseOCL *NeuronOCL)
  • LocalMaxPool(void)
  • LocalMaxPoolGrad(void)

ご想像のとおり、これらのメソッドはカーネルの実行をキューに登録します。本アルゴリズムについては既に詳しく取り上げたため、本記事ではこれ以上掘り下げません。

また、このクラスが畳み込み層クラスCNeuronConvOCLを継承している点も注目に値します。これは本プロジェクトにおいては比較的珍しい設計であり、主にローカルグループ内で特徴を独立して処理する必要性によるものです。

クラスのすべての内部オブジェクトは静的に宣言されているため、クラスのコンストラクタとデストラクタを空のままにすることができます。新しいオブジェクトインスタンスの初期化は、Initメソッド内でおこなわれます。

bool CNeuronPointNet2Local::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                 uint window, uint units_count, uint window_out, float radius, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, 128, 128, window_out, 
                                        units_count, 1, optimization_type, batch))
      return false;

メソッドのパラメータでは、オブジェクトのアーキテクチャを定義する主要な定数を受け取ります。これらのパラメータは、畳み込み層で使用されるものと非常によく似ています。加えて、要素の受容野の半径を定義する追加パラメータradiusがあります。

メソッド本体では、まず親クラスの対応するメソッドを呼び出します。そこでは、必要なデータ検証や継承されたオブジェクトの初期化がすでに実装されています。ここで重要なのは、親クラスのメソッドに渡される値が、外部プログラムから受け取ったものとは若干異なるという点です。この差異は、親クラスのオブジェクトの使用方法に特有の事情によるものであり、この点についてはfeedForwardメソッドを実装する際に再度取り上げます。

親クラスのメソッドが正常に実行された後、受け取った定数の一部を保存し、残りは親クラス側の処理で既に保存されています。

   fRadius = MathMax(0.1f, radius);
   iUnits = units_count;

次に、内部オブジェクトの初期化に進みます。まず、解析された点群内のオブジェクト間の距離を記録するためのバッファを作成します。前述のとおり、これは正方行列となります。

   cDistance.BufferFree();
   if(!cDistance.BufferInit(iUnits * iUnits, 0) ||
      !cDistance.BufferCreate(OpenCL))
      return false;

点特徴量を抽出するには、pointnetアルゴリズムの特徴量抽出ブロックと同様に、3つの畳み込み層と3つのバッチ正規化層のブロックを作成します。ソースデータ投影ブロックは最上位クラスに存在すると想定しているため、作成しません。

   if(!cFeatureNet[0].Init(0, 0, OpenCL, window, window, 64, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[0].Init(0, 1, OpenCL, 64 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 2, OpenCL, 64, 64, 128, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[1].Init(0, 3, OpenCL, 128 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 4, OpenCL, 128, 128, 256, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[2].Init(0, 5, OpenCL, 256 * iUnits, iBatch, optimization))
      cFeatureNetNorm[2].SetActivationFunction(None);

次に、局所のMaxPooling結果を記録するための層を作成します。

   if(!cLocalMaxPool.Init(0, 6, OpenCL, cFeatureNetNorm[2].Neurons(), optimization, iBatch))
      return false;

結果として得られたMLPの1つの層を追加します。

   if(!cFinalMLP.Init(0, 7, OpenCL, 256, 256, 128, iUnits, 1, optimization, iBatch))
      return false;
   cFinalMLP.SetActivationFunction(LReLU);

継承した機能を第2層として利用する予定です。

なお、通常のPointNetとは異なり、出力で畳み込み層を使用します。これは、局所領域の記述子が独立して処理されるためです。

初期化メソッド操作の最後に、クラスに活性化関数がないことを示し、操作のブール結果を呼び出し元プログラムに返します。

   SetActivationFunction(None);
   return true;
  }

新しいオブジェクトの初期化作業が完了したら、feedForwardメソッドでフィードフォワードパスアルゴリズムの構築に進みます。このメソッドのパラメータでは、ソースデータオブジェクトへのポインタを受け取ります。

bool CNeuronPointNet2Local::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CalcDistance(NeuronOCL))
      return false;

前述のように、このクラスでは、データを正準空間(canonical space)に投影する予定はありません。この操作は、必要に応じて最上位レベルで実行されるものと想定されます。したがって、元のデータの要素間の距離をすぐに計算します。

次に、分析された要素の特徴量を計算するループを作成します。

   CNeuronBaseOCL *temp = NeuronOCL;
   uint total = cFeatureNet.Size();
   for(uint i = 0; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(temp))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
      temp = cFeatureNetNorm[i].AsObject();
     }

点の局所領域に対してMaxPooling操作を実行します。

   if(!LocalMaxPool())
      return false;

メソッド操作の最後に、すべての局所領域の記述子に独立した2層MLPを適用します。

   if(!cFinalMLP.FeedForward(cLocalMaxPool.AsObject()))
      return false;
   if(!CNeuronConvOCL::feedForward(cFinalMLP.AsObject()))
      return false;
//---
   return true;
  }

MLPの最初の層として、内部層cFinalMLPを使用します。第2層の操作は、親クラスから継承された機能を使用して実行されます。

各段階での作動プロセスの監視を忘れないでください。すべての操作が正常に完了したら、呼び出し元のプログラムに論理結果を返します。

バックプロパゲーションアルゴリズムは、calcInputGradientsメソッドとupdateInputWeightsメソッドに実装されています。calcInputGradientsメソッドは、最終結果への影響に応じて、すべての要素に誤差勾配を分散します。このアルゴリズムは、feedForwardメソッドと同じロジックに従いますが、操作を逆の順序で実行します。updateInputWeightsメソッドは、モデルの訓練可能なパラメータを更新します。ここでは、訓練可能なパラメータを含む内部オブジェクトの対応するメソッドを呼び出すだけです。どちらのメソッドも非常に簡単です。それぞれの実装を独自に調査してみることをお勧めします。このクラスとそのすべてのメソッドの完全なソースコードは添付ファイルにあります。

2.3PointNet++アルゴリズムの組み立て

作業の大部分は完了し、いよいよ実装の最終段階に差し掛かりました。このステップでは、各コンポーネントを統合し、ひとつのPointNet++アルゴリズムとしてまとめます。この統合処理は、CNeuronPointNet2OCLクラス内でおこなわれ、その構造体の概要は以下のとおりです。

class CNeuronPointNet2OCL   :  public CNeuronPointNetOCL
  {
protected:
   CNeuronPointNetOCL   *cTNetG;
   CNeuronBaseOCL       *cTurnedG;
   //---
   CNeuronPointNet2Local caLocalPointNet[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
public:
                     CNeuronPointNet2OCL(void) {};
                    ~CNeuronPointNet2OCL(void) ;
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2OCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

不思議なことに、このクラスではローカルデータの離散化用に2つの静的オブジェクトしか宣言されておらず、さらに2つの動的オブジェクトは、データの正準空間への射影が必要な場合にのみ初期化されます。このようなシンプルな設計は、ほとんどの機能がすでに実装されているバニラ版PointNetクラスを継承することで実現されています。

前述のように、動的オブジェクトは必要な場合にのみ初期化されます。したがって、コンストラクタは空のままにしておきます。ただし、デストラクタでは、動的オブジェクトへの有効なポインタをチェックし、必要に応じて削除します。

CNeuronPointNet2OCL::~CNeuronPointNet2OCL(void)
  {
   if(!!cTNetG)
      delete cTNetG;
   if(!!cTurnedG)
      delete cTurnedG;
  }

クラスオブジェクトの初期化は、通常どおり、Initメソッド内で実装されています。メソッドのパラメータでは、クラスのアーキテクチャを定義する主要な定数を受け取ります。これらの定数は、親クラスから完全に引き継がれています。

bool CNeuronPointNet2OCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                               uint window, uint units_count, uint output, bool use_tnets, 
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPointNetOCL::Init(numOutputs, myIndex, open_cl, 64, units_count, 
                                output, use_tnets, optimization_type, batch))
      return false;

メソッド本体では、すぐに親クラスの同様のメソッドを呼び出します。その後、元のデータの投影オブジェクトを正準空間に作成する必要があるかどうかを確認します。

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNetG)
        {
         cTNetG = new CNeuronPointNetOCL();
         if(!cTNetG)
            return false;
        }
      if(!cTNetG.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

必要に応じて、まず必要なオブジェクトを作成し、それらを初期化します。

      if(!cTurnedG)
        {
         cTurnedG = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurnedG.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;
     }

ユーザーが投影オブジェクトを作成する必要があると示していない場合は、オブジェクトへの現在のポインタがあるかどうかを確認します。そのようなポインタがある場合は、不要なオブジェクトを削除します。

   else
     {
      if(!!cTNetG)
         delete cTNetG;
      if(!!cTurnedG)
         delete cTurnedG;
     }

次に、異なる受信ウィンドウ半径を持つ2つの局所データサンプリングオブジェクトを初期化します。メソッドの実行を完了します。

   if(!caLocalPointNet[0].Init(0, 0, OpenCL, window, units_count, 64, 0.2f, optimization, iBatch))
      return false;
   if(!caLocalPointNet[1].Init(0, 0, OpenCL, 64, units_count, 64, 0.4f, optimization, iBatch))
      return false;
//---
   return true;
  }

まず小さな受容野ウィンドウから処理を開始し、徐々にそのサイズを拡大していく点に注意してください。ただし、受容野を完全にカバーするまでには広げません。これは、バニラ版PointNetクラスから継承された機能によって処理されるためです。

クラスオブジェクトの初期化メソッドの作業が完了した後は、feedForwardメソッド内で順伝播アルゴリズムの構築に移ります。

bool CNeuronPointNet2OCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- LocalNet
   if(!cTNetG)
     {
      if(!caLocalPointNet[0].FeedForward(NeuronOCL))
         return false;
     }

メソッドパラメータでは、ソースデータオブジェクトへのポインタを受け取ります。メソッド本体では、まず正準空間への投影が必要かどうかを確認します。ここでの手順は、標準のPointNetクラスで使用されるアプローチと似ています。データ投影が不要な場合は、受信したポインタをすぐに最初の局所離散化層のfeedForwardメソッドに渡します。

それ以外の場合は、まずデータの投影行列を生成します。

   else
     {
      if(!cTurnedG)
         return false;
      if(!cTNetG.FeedForward(NeuronOCL))
         return false;

その後、元のデータに投影行列を掛けて、元のデータの投影を実装します。

      int window = (int)MathSqrt(cTNetG.Neurons());
      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), 
                                    NeuronOCL.Neurons() / window, window, window))
         return false;

その後、取得した値をデータ離散化層のfeedForwardメソッドに渡します。

      if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject()))
         return false;
     }

次に、より大きな受容ウィンドウサイズで離散化を実行します。

   if(!caLocalPointNet[1].FeedForward(caLocalPointNet[0].AsObject()))
      return false;

最後の段階では、強化されたデータを親クラスのfeedForwardメソッドに渡し、分析された点群全体の記述子が決定されます。

   if(!CNeuronPointNetOCL::feedForward(caLocalPointNet[1].AsObject()))
      return false;
//---
   return true;
  }

ご覧のとおり、複雑な継承構造のおかげで、新しいクラスに対して簡潔なfeedForwardメソッドを構築することができました。逆伝播メソッドも同様の実装方針に従っているため、添付ファイルを参照しながら、ぜひご自身で確認してみてください。この記事で使用されているすべてのプログラムの完全なコードは添付ファイルに含まれています。これには、モデルの訓練スクリプトおよび環境との連携を実現するコード一式も含まれています。なお、これらのスクリプトは前回の記事から変更されることなく使用されています。また、モデルのアーキテクチャも大部分はそのまま保持されており、環境状態エンコーダでの唯一の変更点は、ある1つの層のタイプを変更しただけで、他のパラメータには一切手を加えていません。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNet2OCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

これにより、Actorの新しい方策訓練の結果を評価することがさらに興味深くなります。


3.テスト

これで、PointNet++の著者が提案したアプローチの実装が完了しました。次は、実際の過去データを使って、この実装の有効性を評価していきます。これまでと同様に、モデルは2023年通年のEURUSDの履歴データを用いて訓練されます。時間軸はH1を使用し、インジケーターのパラメータはすべてデフォルト設定のままです。訓練済みのモデルは、MetaTrader 5のストラテジーテスターを使ってテストされます。

前述の通り、新しいモデルは、以前のモデルと比べて1つの層のみが異なります。しかも、この新しい層は、以前の手法を改良したバージョンにすぎません。そのため、両モデルのパフォーマンスを比較することは、特に興味深い検証になります。公平な比較をおこなうために、前回の実験で使用したものと全く同じデータセットを使って両方のモデルを訓練します。

私は常に、モデルのパフォーマンスを最適化するには、訓練データセットを定期的に更新することが重要だと強調しています。データセットをActorの最新の方策に合わせておくことで、行動の評価精度が向上し、方策の改良につながるからです。しかし今回は、類似した2つのアプローチを比較し、階層的手法の有効性を検証する貴重な機会を逃すわけにはいきませんでした。前回の記事では、利益を生み出すActorの方策の訓練に成功しました。今回の新しいモデルも、少なくともそれと同等の性能を発揮すると期待されます。

訓練後、新しいモデルは収益性の高い方策をうまく学習し、訓練データとテストデータの両方でプラスのリターンを達成しました。以下に、新しいモデルのテスト結果を示します。

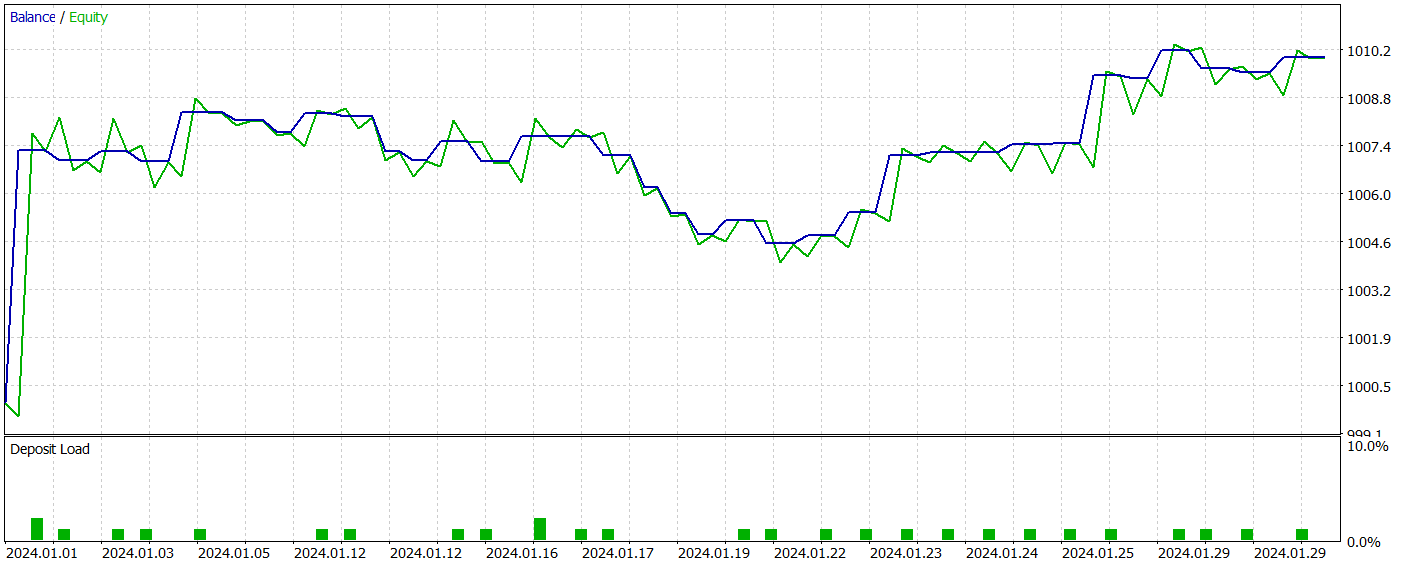
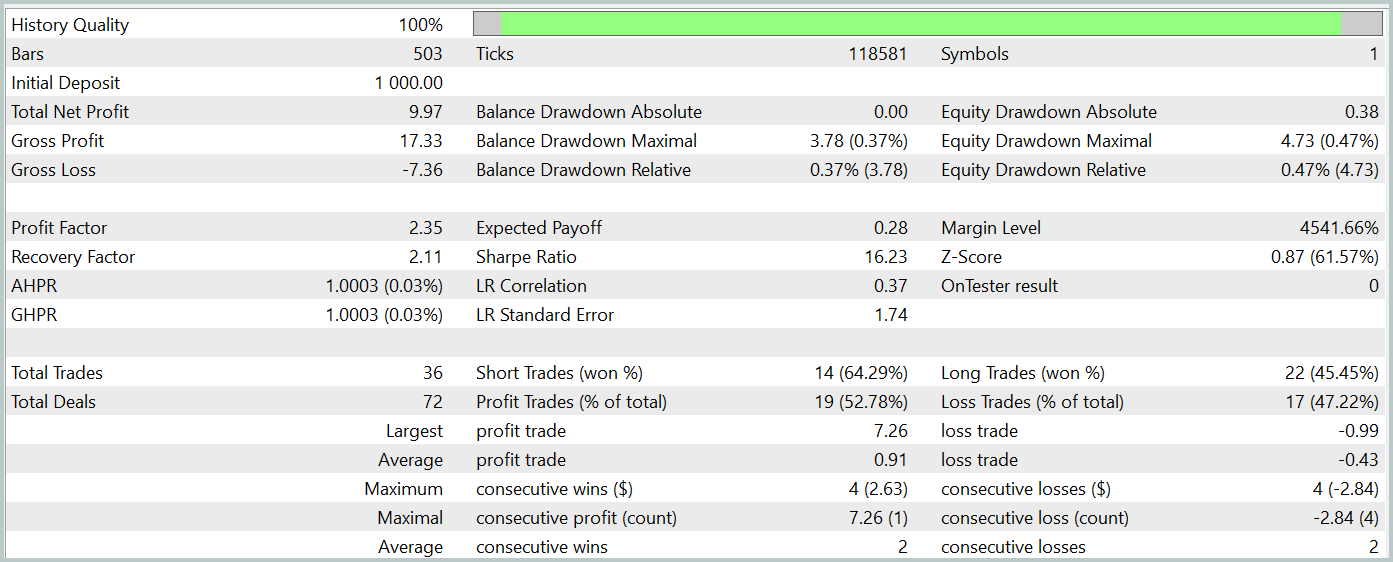
両モデルの結果を比較するのは、正直なところ非常に難しいと言わざるを得ません。テスト期間中、どちらのモデルもほぼ同等の利益を上げました。残高と有効証拠金におけるドローダウンの差異も、無視できる程度の誤差範囲に収まっています。ただし、新しいモデルの方が取引回数が少なく、その結果としてプロフィットファクターはわずかに向上しました。

とはいえ、両モデルの取引回数が少ないことから、長期的なパフォーマンスについて明確な結論を導くことは困難です。


結論

PointNet++法は、複雑な金融データにおける局所的および大域的なパターンを、多次元構造を考慮しながら効率的に分析する手法を提供します。点群処理における強化されたアプローチにより、予測精度および取引戦略の安定性が向上し、変動の激しい市場における、より情報に基づいた意思決定が可能となります。

本記事の実践セクションでは、PointNet++アプローチに対する独自の実装をおこないました。テストにおいて、このモデルはテストデータセット上で収益を生み出す能力を実証しました。ただし、ここで紹介したプログラムはあくまでデモンストレーションを目的としたものであり、手法の動作を説明するためのものにすぎない点にはご留意ください。


参照文献記事で使用されているプログラム
# ファイル名 種類 詳細
1 Research.mq5 EA 事例収集のためのEA
2 ResearchRealORL.mq5
 EA
 Real-ORL法による事例収集のためのEA
3 Study.mq5 EA モデル訓練EA
4 Test.mq5 EA モデルテストEA
5 Trajectory.mqh クラスライブラリ システム状態記述の構造体
6 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
7 NeuroNet.cl ライブラリ OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15789

添付されたファイル |
ZIPをダウンロード
MQL5.zip (1748.05 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
リプレイシステムの開発（第64回）：サービスの再生(V) リプレイシステムの開発（第64回）：サービスの再生(V)
この記事では、コード内の2つのエラーを修正する方法について説明します。ただし、初心者プログラマーの皆さんに、物事が必ずしも期待どおりに進むとは限らないことを理解してもらえるよう、できるだけわかりやすく解説したいと思います。いずれにせよ、これは学びの機会です。ここで提示されるコンテンツは、教育目的のみに使用されることを意図しています。ここで紹介する内容は教育目的のみに限定されており、提示された概念を探求すること以外の目的でこのアプリケーションを最終的な文書と見なすべきではありません。
リプレイシステムの開発（第63回）：サービスの再生(IV) リプレイシステムの開発（第63回）：サービスの再生(IV)
この記事では、1分足のティックシミュレーションに関する問題を最終的に解決し、実際のティックと共存できるようにします。これにより、将来的なトラブルを回避することが可能になります。ここで提示される資料は教育目的のみに使用されます。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。
取引におけるニューラルネットワーク：点群用Transformer (Pointformer) 取引におけるニューラルネットワーク：点群用Transformer (Pointformer)
この記事では、点群におけるオブジェクト検出問題を解決するためのアテンションを用いたアルゴリズムについて解説します。点群におけるオブジェクト検出は、多くの現実世界の応用において極めて重要です。
細菌走化性最適化(BCO) 細菌走化性最適化(BCO)
この記事では、細菌走化性最適化(BCO)アルゴリズムのオリジナルバージョンとその改良版を紹介します。新バージョン「BCOm」では、細菌の移動メカニズムを簡素化し、位置履歴への依78ytf存を軽減するとともに、計算負荷の大きかった元のバージョンに比べて、より単純な数学的手法を採用しています。この記事では両者の違いを詳しく検討し、とくにBCOmの特徴に焦点を当てます。また、テストを実施し、その結果をまとめます。