Misurazione delle informazioni degli indicatori

Introduzione

L'apprendimento automatico si basa su dati di addestramento per apprendere il comportamento generale del mercato e in ultima analisi, fare previsioni abbastanza accurate. L'algoritmo di apprendimento prescelto deve passare attraverso un campione accuratamente selezionato per estrarre informazioni significative. Il motivo per cui molti non riescono ad applicare con successo questi strumenti sofisticati è che la maggior parte delle informazioni significative è nascosta dalla rumorosità dei dati. A molti sviluppatori di strategie potrebbe non essere chiaro che i set di dati che utilizziamo potrebbero non essere appropriati per l'addestramento dei modelli.

Gli indicatori possono essere considerati come fornitori di informazioni sulle serie di prezzi sottostanti a cui sono applicati. Partendo da questa premessa, l'entropia può essere utilizzata per misurare la quantità di informazioni comunicate da un indicatore. Utilizzando i passaggi e gli strumenti documentati nel libro Testing and Tuning Market Trading Systems (TTMTS) scritto da Timothy Masters, dimostreremo come questi possano essere utilizzati per valutare la struttura dei dati degli indicatori.

Perché Misurare le Informazioni degli Indicatori

Spesso, quando si utilizzano strumenti di machine learning per lo sviluppo di strategie, si ricorre semplicemente a lanciare ogni sorta di dati agli algoritmi con la speranza di trarne qualcosa. In definitiva, il successo dipenderà dalla qualità dei predittori utilizzati nel modello e i predittori efficaci hanno solitamente determinate caratteristiche. Uno di questi è l’essere pieno di contenuti informativi significativi.

La quantità di informazioni nelle variabili utilizzate per l'addestramento del modello è importante, ma non è l'unico requisito per un addestramento efficace del modello. Pertanto, la misurazione del contenuto informativo può essere utilizzata per vagliare gli indicatori che altrimenti verrebbero utilizzati alla cieca durante il processo di addestramento.  È qui che viene applicato il concetto di entropia.

Entropia

L’Entropia è stata redatta su MQL5.com già diverse volte. Mi scuso con il lettore perché dovrà sopportare un’altra definizione, ma prometto che è essenziale per comprendere l'applicazione del concetto. Gli articoli precedenti hanno fornito la storia e la derivazione del calcolo dell'entropia, quindi per brevità inizieremo con l'equazione.

                                                        

H(X) indica l'entropia di X, X è una variabile discreta che rappresenta una variabile arbitraria, diciamo un messaggio. Il contenuto del messaggio può assumere solo un numero finito di valori. Questo viene rappresentato nell'equazione come x minuscola. La x minuscola sono i valori osservati dei messaggi, tali che, se tutti i possibili valori di x fossero enumerati in un insieme, N.

Consideriamo un esempio di dadi. I dadi, quando vengono lanciati, possono essere percepiti come fornitori di informazioni che determinano l'esito di un gioco. Il dado ha 6 facce uniche numerate da 1 a 6. La probabilità di osservare uno qualsiasi dei numeri rivolto verso l'alto è 1/6.

In questo esempio, la X maiuscola sarebbe il dado e la x minuscola potrebbe essere uno qualsiasi dei numeri disegnati sui lati del dado. Tutti i quali sono collocati nell'insieme N ={ 1,2,3,4,5,6}. Applicando la formula, l'entropia di questo dado è 0,7781.

                                                         

Consideriamo ora un altro dado, che presenta un difetto di fabbricazione. Ha due lati con lo stesso numero disegnato sopra. Per questo dado difettoso l'insieme N di valori possibili è {1,1,3,4,5,6}. Utilizzando nuovamente la formula si ottiene un valore medio di entropia pari a 0,6778 .

                                                 

Confrontando i valori notiamo che il contenuto informativo è diminuito. Analizzando entrambi i dadi, quando le probabilità di osservare ciascun valore possibile sono tutte uguali, l'equazione dell'entropia produce il suo massimo valore possibile. Pertanto, l'entropia raggiunge la sua media massima quando le probabilità di tutti i valori possibili sono uguali.

Se scartiamo il dado difettoso per un indicatore che produce numeri reali tradizionali come output. Quindi, X diventa l'indicatore e la x minuscola sarà l'intervallo di valori che l'indicatore può assumere. Prima di procedere oltre, abbiamo un problema perché l'equazione dell'entropia tratta esclusivamente con variabili discrete. È possibile trasformare l'equazione per lavorare con variabili continue, ma la sua applicazione sarebbe difficoltosa, quindi è più facile attenersi al campo dei numeri discreti.

Calcolo dell'entropia di un indicatore

Per applicare l'equazione dell'entropia a variabili continue dobbiamo discretizzare i valori dell'indicatore, dividendo l'intervallo dei valori in intervalli di uguale dimensione e contando il numero di valori che cade in ciascun intervallo. Con questo metodo, l'insieme originale che enumerava l'intervallo massimo di tutti i valori dell'indicatore viene sostituito da sottoinsiemi, ognuno dei quali rappresenta gli intervalli selezionati.

Quando si ha a che fare con variabili continue, la variazione delle probabilità dei possibili valori che la variabile può assumere diventa significativa, in quanto fornisce un aspetto importante all'applicazione dell'entropia agli indicatori.

Tornando al primo esempio dei dadi. Se dividiamo i valori finali dell'entropia di ciascuno per il log(N) per ogni rispettivo n. Il primo dado produce 1, mentre il dado difettoso dà come risultato 0,87. Dividendo il valore dell'entropia per il log del numero di valori che la variabile può assumere si ottiene una misura relativa all'entropia massima teorica della variabile. Si parla di entropia proporzionale o relativa.

Questo valore è utile per la nostra valutazione degli indicatori, in quanto indica quanto l'entropia dell'indicatore sia vicina alla sua media massima teorica. Più si avvicina a uno, il massimo, meglio è, e tutto ciò che si trova all'estremo opposto può suggerire un indicatore che non sarebbe un buon candidato per l'uso in qualsiasi tipo di apprendimento automatico. 

                                  

L'equazione finale che verrà applicata è mostrata sopra e il codice è implementato di seguito come script mql5 che è disponibile per il download come allegato alla fine dell'articolo. Utilizzando lo script saremo in grado di analizzare la maggior parte degli indicatori.

Uno script per calcolare l'entropia di un indicatore

Lo script viene invocato con i seguenti parametri impostabili dall'utente:

• TimeFrame - timeframe selezionato per analizzare i valori dell'indicatore.
• IndicatorType - Qui l'utente può selezionare uno degli indicatori incorporati per l'analisi. Per specificare un indicatore personalizzato, selezionare l'opzione Indicatore Custom e inserire il nome dell'indicatore nel valore del parametro successivo.
  
• CustomIndicatorName - Se l'opzione Custom indicator è stata selezionata per il parametro precedente, l'utente deve inserire qui il nome corretto dell'indicatore.
  
• UseDefaults - Se impostato su true, verranno utilizzati gli input predefiniti codificati nell'indicatore.
  
• IndicatorParameterTypes - si tratta di una stringa delimitata da virgole che elenca i tipi di dati dell'indicatore nel giusto ordine - Un esempio possibile di input, supponendo che l'indicatore da analizzare accetti 4 input di tipo double, integer, integer, string rispettivamente, l'utente deve semplicemente inserire "double, integer, integer, string", è supportata anche la forma abbreviata "d, i, i, s" dove d= double, i=integer e s=string. I valori dell'enum sono mappati al tipo integer.
  
• IndicatorParameterValues - Come l'input precedente, anche questo è un elenco di valori delimitato da virgole, ad esempio, utilizzando l'esempio precedente, "0.5,4,5,string_value". In caso di errore nella formattazione dei parametri sia di IndicatorParameterValues o IndicatorParameterTypes, verranno utilizzati i valori predefiniti dell'indicatore per qualsiasi valore specifico non decifrabile o mancante.
  Controllare la scheda expert per i messaggi di errore. Notare che non è necessario includere il nome dell'indicatore; se si considera un indicatore personalizzato (Custom), questo deve essere specificato da CustomIndicatorName.
• IndicatorBuffer - L'utente può stabilire quale buffer dell’indicatore analizzare.
  
• HistoryStart - La data di inizio del campione storico.
  
• HistorySize - Numero di barre da analizzare rispetto a HistoryStart.
  
• Intervals - Questo parametro indica il numero di intervalli che verranno creati per il processo di discretizzazione. L'autore del TTMTS specifica 20 intervalli per un campione di diverse migliaia, con 2 come valore minimo stabilito.  Ho aggiunto la mia idea su un valore appropriato da utilizzare qui, implementando la possibilità di variare il numero di intervalli in relazione alla dimensione del campione, in particolare 51 ogni 1000 campioni. Questa opzione è disponibile se l'utente inserisce un valore inferiore a 2. Quindi, per essere chiari, impostate Intervals su qualsiasi numero inferiore a 2 e il numero di intervalli utilizzati cambierà in base al numero di barre analizzate.
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Una nota sul valore selezionato per gli intervalli: Cambiando il numero di intervalli utilizzati nel calcolo, varierà il valore finale dell'entropia. Quando si conduce un'analisi, sarebbe opportuno avere una certa coerenza in modo da minimizzare gli effetti degli input indipendenti utilizzati. Nello script il calcolo dell'entropia relativa è incapsulato in una funzione definita nel file Entropy.mqh.

Lo script stampa semplicemente il valore dell’entropia risultante nella scheda expert. Eseguendo lo script per vari indicatori integrati e personalizzati si ottengono i risultati riportati di seguito. È interessante notare che William's Percent Range ha un'entropia relativa vicina alla perfezione. Il confronto con l'indicatore Market Facilitation Index mostra un risultato deludente.

Con questi risultati si possono compiere ulteriori passi per elaborare i dati e renderli adatti agli algoritmi di apprendimento automatico. Ciò comporta un'analisi rigorosa delle proprietà statistiche dell'indicatore. Lo studio della distribuzione dei valori degli indicatori rivelerà eventuali problemi di distorsione e valori anomali. Tutto ciò può degradare l'addestramento del modello.

A titolo di esempio, esaminiamo alcune proprietà statistiche di due indicatori analizzati in precedenza.

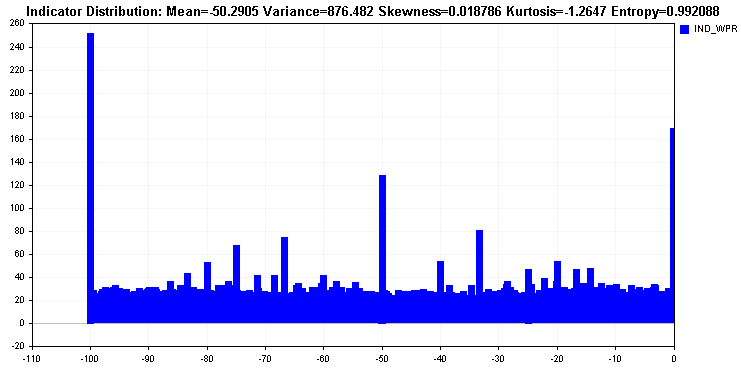
La distribuzione di Williams’s percent range rivela come quasi tutti i valori siano distribuiti sull'intero intervallo, oltre ad essere multi modale la distribuzione è abbastanza uniforme. Una tale distribuzione è ideale e si riflette nel valore dell'entropia.

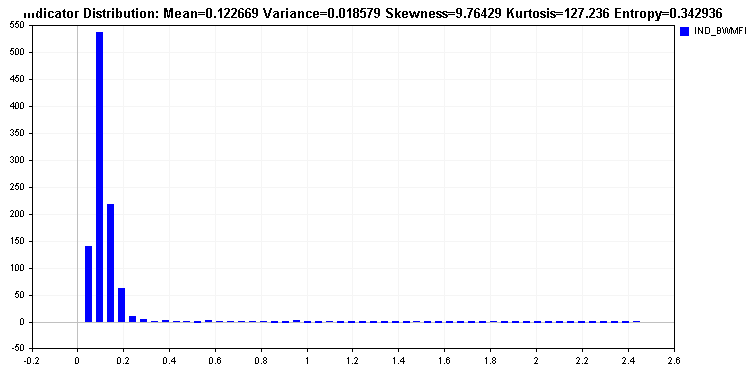
Questo è in contrasto con la distribuzione del Market Facilitation Index, che presenta una coda lunga. Un tale indicatore sarebbe problematico per la maggior parte degli algoritmi di apprendimento e richiede la trasformazione dei valori. La trasformazione dei valori dovrebbe portare a un miglioramento dell'entropia relativa dell'indicatore.

Migliorare il contenuto informativo di un indicatore

Va detto che le alterazioni che aumentano l'entropia dell'indicatore non devono essere viste come un modo per migliorare l'accuratezza dei segnali forniti dall'indicatore. L'aumento dell'entropia non trasformerà un indicatore inutile nel Santo Graal. Migliorare l'entropia significa elaborare i dati degli indicatori per utilizzarli efficacemente nei modelli predittivi.

Questa opzione dovrebbe essere presa in considerazione quando il valore dell'entropia è irrimediabilmente negativo, qualsiasi cosa ben al di sotto di 0,5 e più vicina allo zero. Le soglie superiori sono puramente arbitrarie. Spetta allo sviluppatore scegliere un valore minimo accettabile. L'obiettivo è produrre una distribuzione dei valori degli indicatori che sia il più possibile uniforme. La decisione di applicare una trasformazione deve basarsi su un'analisi condotta su un campione consistente e rappresentativo di valori dell'indicatore.

La trasformazione applicata non deve alterare il comportamento intrinseco dell'indicatore. L'indicatore trasformato deve avere una forma simile a quella dell'indicatore grezzo, ad esempio la posizione dei picchi e delle depressioni deve essere simile in entrambe le serie. In caso contrario, rischiamo di perdere informazioni potenzialmente utili.

Esistono numerosi metodi di trasformazione che mirano a differenti aspetti delle imperfezioni dei dati di prova. Prenderemo in considerazione solo alcune semplici trasformazioni che mirano a correggere difetti evidenti rivelati dall'analisi statistica di base. La preelaborazione è un vasto settore dell'apprendimento automatico. Chiunque speri di padroneggiare l'applicazione dei metodi di apprendimento automatico è invitato ad approfondire le proprie conoscenze in questo campo.

Per illustrare l'effetto di alcune trasformazioni, presentiamo uno script che ha la possibilità di applicare varie trasformazioni e di visualizzare la distribuzione dei dati analizzati. Lo script implementa 6 esempi di funzioni di trasformazione:

• la funzione di trasformazione in radice quadrata è appropriata per schiacciare i valori occasionali dell'indicatore che si discostano notevolmente dalla maggioranza.

• la trasformazione in radice cubica è un'altra funzione di schiacciamento che si applica meglio agli indicatori con valori negativi.

• mentre la trasformazione logaritmica comprime i valori in misura maggiore rispetto alle trasformazioni di compressione precedentemente menzionate.

• le trasformazioni tangente iperbolica e logistica devono essere applicate su valori di dati di scala adeguata per evitare problemi di produzione di numeri non validi (errori nan).

• la trasformazione estrema induce un'estrema uniformità in un insieme di dati. Dovrebbe essere applicata solo agli indicatori che producono per lo più valori unici con pochissimi dati simili.

Script per confrontare i valori trasformati degli indicatori

Rispetto allo script precedente, contiene gli stessi input dell'utente per specificare l'indicatore da analizzare. I nuovi input sono descritti di seguito:

• DisplayTime - lo script visualizza un grafico della distribuzione dell'indicatore. DisplayTime è un valore intero in secondi, che rappresenta il tempo in cui il grafico sarà visibile prima di essere rimosso.

• ApplyTransfrom - è un valore booleano che imposta la modalità dello script. Quando è false, lo script disegna la distribuzione e visualizza le statistiche di base del campione insieme all'entropia relativa. Se impostato su true, applica una trasformazione ai valori grezzi dell'indicatore e visualizza i valori dell’entropia relativa prima e dopo la trasformazione. La distribuzione dei campioni modificati può anche essere disegnata come una curva in rosso.

• Select_transform - è un'enumerazione che fornisce le trasformazioni descritte in precedenza che possono essere applicate per aumentare l'entropia dell'indicatore.

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Proseguendo con gli esempi, confrontiamo l'applicazione delle trasformate di radice quadrata e di radice cubica.

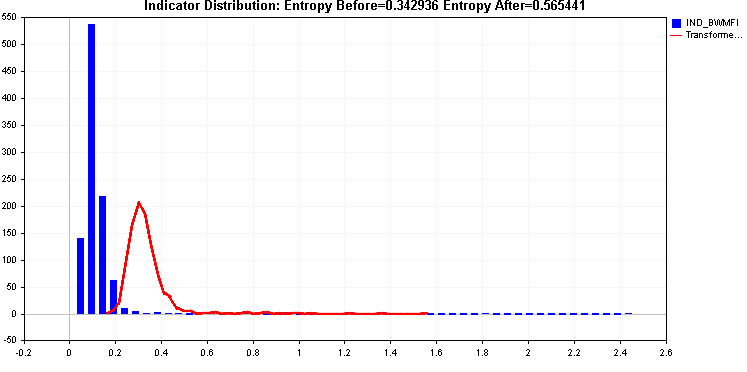
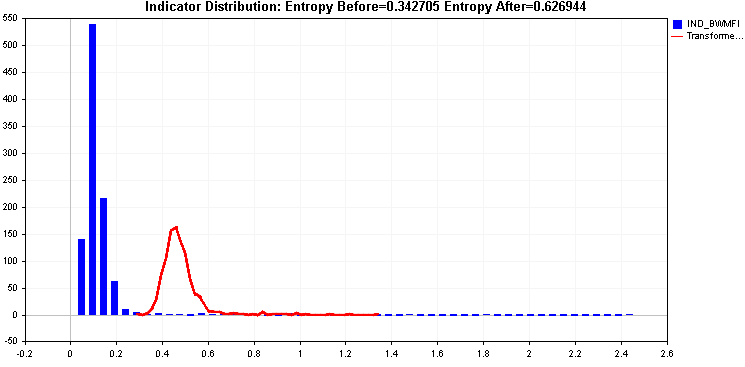
Entrambi forniscono un miglioramento dell'entropia, ma la coda destra potrebbe essere problematica e le due trasformazioni applicate finora non sono state in grado di gestirla efficacemente.

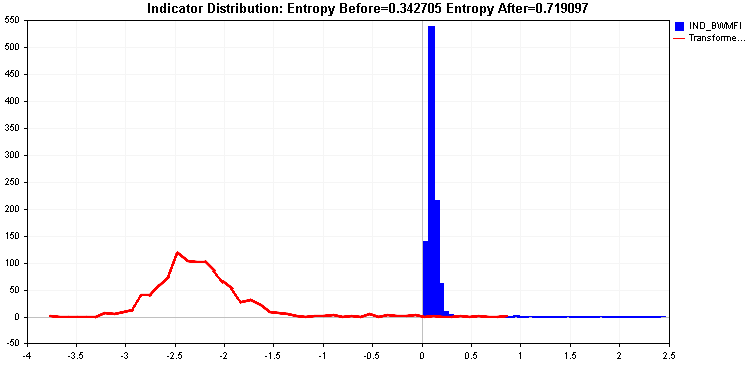
La trasformata log produce un valore di entropia ancora migliore. Le code sono comunque piuttosto significative. Come ultima risorsa, possiamo applicare la trasformazione estrema.

Conclusioni

Abbiamo esplorato il concetto di entropia per valutare la necessità di trasformare i valori degli indicatori prima di utilizzarli nell'addestramento dei modelli predittivi.

Il concetto è stato implementato in due script. In particolare EntropyIndicatorAnalyis che stampa l'entropia relativa di un campione nella scheda degli expert. L'altro script IndicatorAnalysis fa un ulteriore passo avanti, disegnando la distribuzione dei valori grezzi e trasformati degli indicatori e visualizzando i valori dell’entropia relativa prima e dopo.

Sebbene gli strumenti possano essere utili, va notato che non possono essere applicati a tutti i tipi di indicatori. In generale, gli indicatori a freccia che contengono valori vuoti non sono adatti per gli script qui descritti. In questi casi sarebbero necessarie altre tecniche di codifica.

Il tema della trasformazione dei dati è solo un sottoinsieme delle possibili fasi di preelaborazione che dovrebbero essere prese in considerazione quando si costruisce qualsiasi tipo di modello predittivo. L'uso di queste tecniche aiuterà a estrarre relazioni davvero uniche che potrebbero fornire il vantaggio necessario per battere i mercati.

Nome del File	Descrizione
Mql5/Include/Entropy.mqh	file include che contiene varie definizioni di funzioni utilizzate per calcolare l'entropia ed anche funzioni di utilità usate dagli script allegati.
Mql5/Scripts/IndicatorAnalysis.mq5	uno script che visualizza un grafico che mostra la distribuzione dei valori degli indicatori, insieme alla loro entropia.
Mql5/Scripts/EntropyIndicatorAnalysis	uno script che può essere utilizzato per calcolare l'entropia di un indicatore