Approccio brute force per la ricerca di pattern (Parte VI): Ottimizzazione ciclica

Contenuto

• Introduzione
• Routine
• Nuovo algoritmo di ottimizzazione
• Criterio di ottimizzazione più importante
• Ricerca automatica delle configurazioni di trading
• Conclusioni
• Link

Introduzione

Considerando il materiale dell'articolo precedente, posso dire che questa è solo una descrizione superficiale di tutte le funzioni che ho introdotto nel mio algoritmo. Esse riguardano non solo la completa automazione della creazione dell'EA, ma anche funzioni importanti come la completa automazione dell'ottimizzazione e della selezione dei risultati con il successivo utilizzo per il trading automatico, o la creazione di EA più avanzati che mostrerò poco più avanti.

Grazie alla simbiosi tra i terminali di trading, gli EA universali e l'algoritmo stesso, è possibile eliminare completamente lo sviluppo manuale o, nel peggiore dei casi, ridurre di un ordine di grandezza l'intensità del lavoro per eventuali miglioramenti, a condizione che si disponga delle capacità di calcolo necessarie. In questo articolo inizierò descrivendo gli aspetti più importanti di queste innovazioni.

Routine

Il fattore più importante per la creazione e le successive modifiche di tali soluzioni nel tempo è stato per me capire la possibilità di garantire la massima automazione delle azioni di routine. Le azioni di routine, in questo caso, comprendono tutto il lavoro umano non essenziale:

• Generazione di idee.
• Creare una teoria.
• Scrivere un codice secondo la teoria.
• Correzione del codice.
• Ottimizzazione costante dell’EA.
• Selezione costante dell’EA.
• Manutenzione dell’EA.
• Lavorare con i terminali.
• Esperimenti e pratica.
• Altro.

Come puoi vedere, la gamma di questa routine è piuttosto ampia. La tratto proprio come una routine, perché sono stato in grado di dimostrare che tutte queste cose possono essere automatizzate. Ho fornito un elenco generale. Non importa chi siate - un trader algoritmico, un programmatore o entrambi. Non importa se sapete programmare o meno. Anche se non lo fate, in ogni caso incontrerete almeno la metà di questo elenco. Non mi riferisco ai casi in cui si è acquistato un EA sul mercato, lo si è lanciato sul grafico e ci si è tranquillizzati premendo un solo pulsante. Questo, ovviamente, accade, anche se molto raramente.

Compreso tutto questo, per prima cosa ho dovuto automatizzare le cose più evidenti. Ho descritto concettualmente tutta questa ottimizzazione in un precedente articolo. Tuttavia, quando si fa una cosa del genere, si inizia a capire come migliorare il tutto, basandosi sulle funzionalità già implementate. Le idee principali a riguardo per me sono state le seguenti:

• Migliorare il meccanismo di ottimizzazione.
• Creazione di un meccanismo di unione degli EA (merging bots).
• Architettura corretta dei percorsi di interazione di tutti i componenti.

Naturalmente, si tratta di un'enumerazione piuttosto breve. Descriverò tutto in modo più dettagliato. Per miglioramento dell'ottimizzazione intendo un insieme di più fattori contemporaneamente. Tutto questo viene pensato all'interno del paradigma scelto per la costruzione dell'intero sistema:

• Accelerare l'ottimizzazione eliminando i tick.
• Accelerare l'ottimizzazione eliminando il controllo della curva dei profitti tra i punti di decisione del trading.
• Migliorare la qualità dell'ottimizzazione introducendo criteri di ottimizzazione personalizzati.
• Massimizzare l'efficienza del periodo di riferimento.

Sul Forum di questo sito web sono ancora in corso dibattiti sulla necessità dell'ottimizzazione e sui suoi benefici. In precedenza, avevo un atteggiamento piuttosto chiaro nei confronti di questa azione, in gran parte dovuto all'influenza di singoli utenti del forum e del sito web. Ora, questa opinione non mi disturba affatto. Per quanto riguarda l'ottimizzazione, tutto dipende se si sa utilizzarla correttamente e da quali sono gli obiettivi. Se usata correttamente, questa azione dà il risultato desiderato. In generale, si scopre che questa azione è estremamente utile.

A molti non piace l'ottimizzazione. Ci sono due ragioni oggettive per questo:

• Mancanza di comprensione delle basi (perché, cosa e come fare, come selezionare i risultati e tutto ciò che è correlato, incluso la mancanza di esperienza).
• Imperfezione degli algoritmi di ottimizzazione.

In realtà, entrambi i fattori si rafforzano a vicenda. A dire il vero, l'ottimizzatore di MetaTrader 5 è strutturalmente impeccabile, ma ha ancora bisogno di molti miglioramenti in termini di criteri di ottimizzazione e di possibili filtri. Finora, tutte queste funzionalità sono simili a una scatola di sabbia per bambini. Pochi pensano a come ottenere periodi di riferimento positivi e soprattutto, a come controllare questo processo. Ci ho pensato a lungo. In effetti, una buona parte del presente articolo sarà dedicata a questo argomento.

Nuovo algoritmo di ottimizzazione

Oltre ai criteri di valutazione di base conosciuti di qualsiasi backtest, possiamo individuare alcune caratteristiche combinate che possono contribuire a moltiplicare il valore di qualsiasi algoritmo per una selezione più efficiente dei risultati e la successiva applicazione delle impostazioni. Il vantaggio di queste caratteristiche è che possono accelerare il processo di ricerca delle impostazioni di lavoro. A tal scopo, ho creato una sorta di rapporto di verifica della strategia simile a quello di MetaTrader:

figura 1

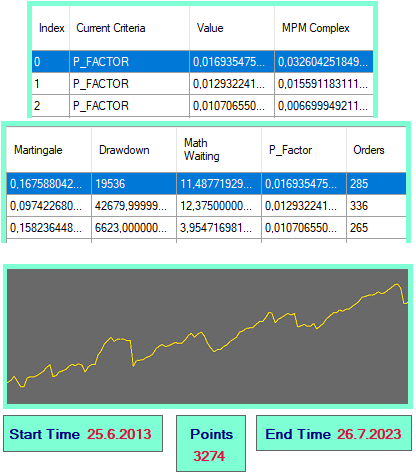
Con questo strumento, posso scegliere l'opzione che preferisco con un semplice clic. Facendo clic, viene generata un'impostazione con la quale posso immediatamente prendere e spostare nella cartella appropriata del terminale, in modo che gli EA universali possano leggerla e iniziare a operare con essa. Se voglio, posso anche fare clic sul pulsante per generare un EA e questo verrà costruito nel caso in cui mi serva un EA separato con le impostazioni programmate all'interno. È presente anche una curva dei profitti, che viene ridisegnata quando si seleziona l'opzione successiva dalla tabella.

Cerchiamo di capire cosa viene conteggiato nella tabella. Gli elementi principali per calcolare queste caratteristiche sono i seguenti dati:

1. Points: profitto dell'intero backtest in "_Point" dello strumento corrispondente.
2. Orders: il numero di ordini completamente aperti e chiusi (si susseguono in ordine rigoroso, secondo la regola "ci può essere solo un ordine aperto").
3. Drawdown: drawdown del saldo.

Sulla base di questi valori, vengono calcolate le seguenti caratteristiche dei trade:

• Attesa matematica: aspettativa matematica in punti.
• Fattore P: analogo al fattore di profitto normalizzato all'intervallo [-1 ... 0 ... 1] (criterio mio).
• Martingala: applicabilità della martingala (mio criterio).
• MPM Complex: un indicatore composito dei tre precedenti (mio criterio).

Vediamo ora come vengono calcolati questi criteri:

equazione 1

Come potete vedere, tutti i criteri che ho creato sono molto semplici e soprattutto, facili da capire. Poiché l'aumento di ciascuno dei criteri indica che il risultato del backtest è migliore in termini di teoria delle probabilità, diventa possibile moltiplicare questi criteri, come ho fatto per il criterio MPM Complex. Una metrica comune consente di ordinare in modo più efficace i risultati in base alla loro importanza. In caso di ottimizzazioni massicce, consentirà di mantenere più opzioni di alta qualità e di eliminare quelle di bassa qualità, rispettivamente.

Notare inoltre che in questi calcoli tutto avviene in punti. Questo ha un effetto positivo sul processo di ottimizzazione. Per i calcoli si utilizzano quantità primarie strettamente positive, che vengono sempre calcolate all'inizio. Tutto il resto viene calcolato in base ad essi. Penso che valga la pena elencare queste quantità primarie che non sono presenti nella tabella:

• Points Plus: somma in punti dei profitti di ogni ordine redditizio o nullo
• Points Minus: somma dei moduli in perdita di ogni ordine non redditizio, in punti
• Drawdown: drawdown per saldo (lo calcolo a modo mio)

La cosa più interessante è il modo in cui viene calcolato il drawdown. Nel nostro caso, si tratta del massimo drawdown relativo al saldo. Considerando che il mio algoritmo di test si rifiuta di monitorare la curva dei fondi, non è possibile calcolare altri tipi di drawdown. Tuttavia, credo che sarebbe utile mostrare come calcolo questo drawdown:

figura 2

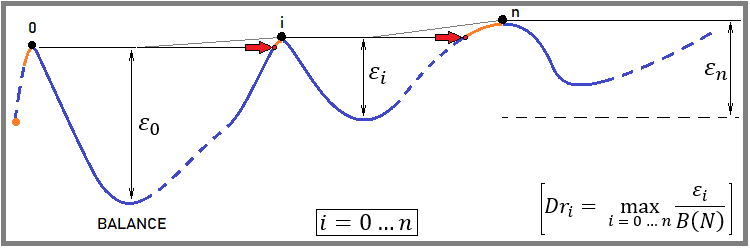
La definizione è molto semplice:

1. Calcolare il punto di partenza del backtest (l'inizio del conto alla rovescia del primo drawdown).
2. Se il trading inizia con un profitto, si sposta questo punto verso l'alto seguendo la crescita del saldo, finché non compare il primo valore negativo (che segna l'inizio del calcolo del drawdown).
3. Attendere che il saldo raggiunga il livello del punto di riferimento. Successivamente, impostarlo come nuovo punto di riferimento.
4. Torniamo all'ultima sezione della ricerca del drawdown e cerchiamo il punto più basso (l'importo del drawdown in questa sezione viene calcolato a partire da questo punto).
5. Ripetere l'intero processo per l'intero backtest o curva di trading.

L'ultimo ciclo rimarrà sempre incompiuto. Tuttavia, il suo drawdown verrà preso in considerazione nonostante il potenziale aumento se il test continua. Ma questo non è un aspetto particolarmente importante.

Criterio di ottimizzazione più importante

Parliamo ora del filtro più importante. In effetti, questo criterio è il più importante quando si selezionano i risultati dell'ottimizzazione. Questo criterio non è incluso nella funzionalità dell'ottimizzatore di MetaTrader 5, il che è un peccato. Pertanto, vorrei fornire del materiale teorico in modo che tutti possano riprodurre questo algoritmo nel proprio codice. In effetti, questo criterio è multifunzionale per qualsiasi tipo di trading e funziona assolutamente per qualsiasi curva di profitto, comprese le scommesse sportive, le criptovalute e qualsiasi altra cosa vi venga in mente. Il criterio è il seguente:

equazione 2

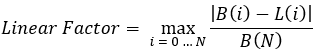
Vediamo cosa c'è dentro questa equazione:

• N - numero di posizioni di trading completamente aperte e chiuse nell'intero backtest o sezione di trading.
• B(i) - valore della linea del saldo dopo la corrispondente chiusura della posizione "i".
• L(i) - linea retta tracciata da zero all'ultimo punto del bilancio (saldo finale).

Per calcolare questo parametro è necessario eseguire due backtest. Il primo backtest calcolerà il saldo finale. In seguito, sarà possibile calcolare l'indicatore corrispondente salvando il valore di ogni punto di bilancio, in modo da non dover fare calcoli inutili. Tuttavia, questo calcolo può essere definito un backtest ripetuto. Questa equazione può essere utilizzata nei tester personalizzati, che possono essere integrati nei vostri EA.

È importante notare che questo indicatore nel suo complesso può essere modificato per una maggiore comprensione. Ad esempio, in questo modo:

equazione 3

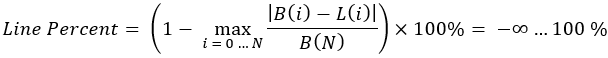
Questa equazione è più difficile in termini di percezione e comprensione. Dal punto di vista pratico, però, tale criterio è conveniente perché più è alto, più la nostra curva di bilancio assomiglia a una linea retta. Ho toccato questioni simili in articoli precedenti, ma non ne avevo spiegato il significato. Osserviamo innanzitutto la figura seguente:

figura 3

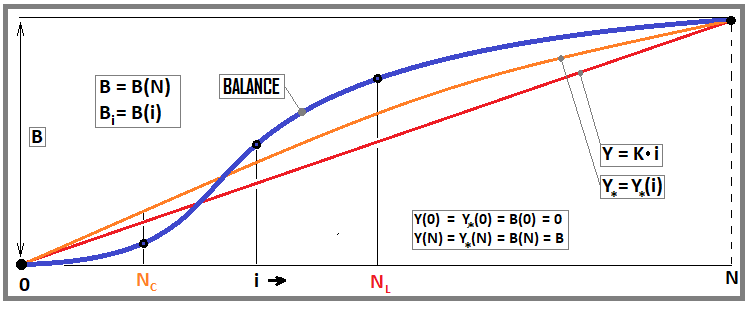
Questa figura mostra una linea di bilancio e due curve: una relativa alla nostra equazione (in rosso) e la seconda per il seguente criterio modificato (equazione 11). Lo mostrerò più avanti, ma ora concentriamoci sull'equazione.

Se immaginiamo il nostro backtest come una semplice array di punti con i saldi, possiamo rappresentarlo come un campione statistico e applicarvi le equazioni della teoria delle probabilità. Considereremo la linea retta come il modello a cui tendere e la stessa curva di profitto come il flusso di dati reale che tende al nostro modello.

È importante capire che il fattore di linearità indica l'affidabilità dell'intero insieme di criteri di trading disponibili. A sua volta, una maggiore affidabilità dei dati può indicare un possibile periodo di previsione più lungo e migliore (trading profittevole in futuro). Tecnicamente, inizialmente avrei dovuto iniziare a considerare queste cose tenendo conto delle variabili casuali, ma mi sembrava che una presentazione di questo tipo lo avrebbe reso più facile da capire.

Creiamo un’alternativa analoga del nostro fattore di linearità, tenendo conto di possibili spike casuali. Per fare ciò, dovremo introdurre una variabile casuale per noi conveniente e la sua media per il successivo calcolo della dispersione:

equazione 4

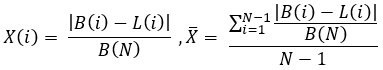
Per una migliore comprensione, va chiarito che abbiamo "N" posizioni completamente aperte e chiuse, che si susseguono rigorosamente una dopo l'altra. Ciò significa che abbiamo "N+1" punti che collegano questi segmenti della linea di bilancio. Il punto zero di tutte le linee è comune, quindi i suoi dati distorceranno i risultati nella direzione del miglioramento, proprio come l'ultimo punto. Pertanto, li escludiamo dai calcoli e ci rimangono "N-1" punti su cui eseguiremo i calcoli.

La scelta dell'espressione per convertire gli array dei valori delle due linee in una sola si è rivelata molto interessante. Notare la seguente frazione:

equazione 5

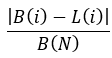
La cosa importante qui è che dividiamo tutto per il saldo finale in tutti i casi. In questo modo, riduciamo tutto a un valore relativo, che garantisce l'equivalenza delle caratteristiche calcolate per tutte le strategie testate, senza eccezioni. Non è una coincidenza che la stessa frazione sia presente nel primo e semplice criterio del fattore di linearità, poiché è realizzata sulla stessa considerazione. Ma completiamo la costruzione del nostro criterio alternativo. Per farlo, possiamo utilizzare un concetto ben noto come quello di dispersione:

equazione 6

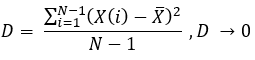
La dispersione non è altro che la media aritmetica dello scarto quadratico dalla media dell'intero campione. Ho immediatamente sostituito le nostre variabili casuali, le cui espressioni sono state definite in precedenza. Una curva ideale ha una deviazione media pari a zero e di conseguenza, anche la dispersione di un dato campione sarà pari a zero. Sulla base di questi dati, è facile intuire che questa dispersione, grazie alla sua struttura - la variabile casuale utilizzata o il campione (a scelta) - può essere utilizzata come fattore di linearità alternativo. Inoltre, entrambi i criteri possono essere utilizzati insieme per vincolare in modo più efficace i parametri del campione, anche se, ad essere onesto, utilizzo solo il primo criterio.

Esaminiamo un criterio simile e più conveniente, anch'esso basato su un nuovo fattore di linearità che abbiamo definito:

equazione 7

Come si può vedere, è identico a un criterio simile, costruito sulla base del primo (equazione 2). Tuttavia, questi due criteri sono ben lontani dal limite di ciò che si può pensare. Un fatto evidente che depone a favore di questa considerazione è che questo criterio è troppo idealizzato ed è più adatto a modelli ideali, e sarà estremamente difficile regolare un EA per ottenere una corrispondenza più o meno significativa. Penso che valga la pena elencare i fattori negativi che saranno evidenti qualche tempo dopo l'applicazione delle equazioni:

1. Riduzione critica del numero di trade (riduce l'affidabilità dei risultati)
2. Rifiuto del numero massimo di scenari efficienti (a seconda della strategia, la curva non tende sempre ad una linea retta)

Queste carenze sono molto critiche, poiché l'obiettivo non è quello di scartare strategie valide, ma, al contrario, di trovare criteri nuovi e migliori che siano privi di queste carenze. Questi svantaggi possono essere completamente o parzialmente neutralizzati introducendo più linee preferite contemporaneamente, ognuna delle quali può essere considerata un modello accettabile o preferibile. Per comprendere il nuovo criterio migliorato, privo di questi difetti, dovete solo comprendere la sostituzione corrispondente:

equazione 8

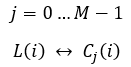
Quindi possiamo calcolare il fattore di adattamento per ogni curva dell'elenco:

equazione 9

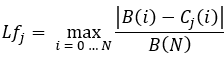
Allo stesso modo, possiamo calcolare un criterio alternativo che tenga conto degli spike casuali per ciascuna curva:

equazione 10

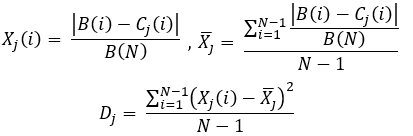
Quindi dovremo calcolare quanto segue:

equazione 11

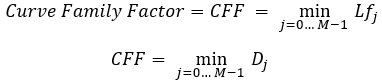
Qui introduco un criterio chiamato fattore di famiglia della curva. Infatti, con questa azione, troviamo contemporaneamente la curva più simile alla nostra curva di trading e troviamo immediatamente il fattore della sua corrispondenza. La curva con il fattore di corrispondenza minimo è la più vicina alla situazione reale. Prendiamo il suo valore come valore del criterio modificato e naturalmente, il calcolo può essere fatto in due modi, a seconda di quale delle due varianti ci piace di più.

Tutto questo è molto bello, ma qui, come molti hanno notato, ci sono delle sfumature legate alla selezione di questa famiglia di curve. Per descrivere correttamente una famiglia di questo tipo si possono seguire varie considerazioni, ma ecco le mie riflessioni:

• Tutte le curve non devono avere punti di flessione (ogni punto intermedio successivo deve essere strettamente superiore al precedente).
• La curva deve essere concava (la ripidità della curva può essere costante o può solo aumentare).
• La concavità della curva deve essere regolabile (ad esempio, la quantità di deflessione deve essere regolata utilizzando un valore relativo o una percentuale).
• Semplicità del modello di curva (è meglio basare il modello su modelli grafici inizialmente semplici e comprensibili).

Questa è solo la variante iniziale di questa famiglia di curve. È possibile effettuare variazioni più grandi tenendo conto di tutte le configurazioni desiderate, che possono salvarci dal perdere completamente impostazioni di qualità. Mi occuperò di questo compito in seguito, ma per ora mi limiterò a toccare solo la strategia originale della famiglia di curve concave. Sono stato in grado di creare una famiglia di questo tipo abbastanza facilmente utilizzando le mie conoscenze matematiche. Lasciate che vi mostri subito come si presenta questa famiglia di curve:

figura 4

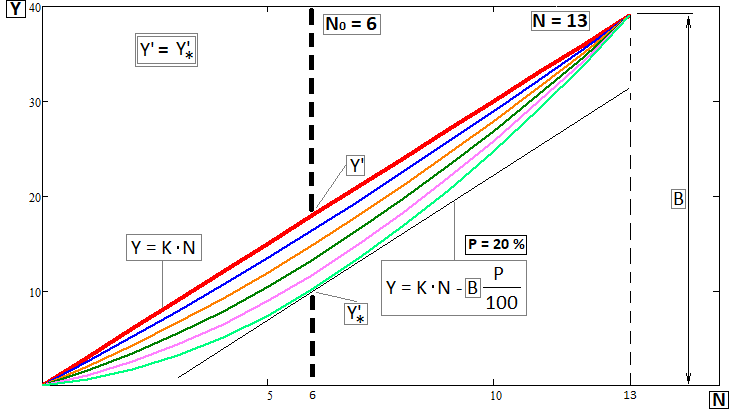
Per costruire questa famiglia, ho utilizzato l'astrazione di un'asta elastica che poggia su supporti verticali. Il grado di deflessione di tale asta dipende dal punto di applicazione della forza e dalla sua dimensione. È chiaro che questo assomiglia solo in parte a ciò che stiamo trattando qui, ma è alquanto sufficiente per sviluppare una sorta di modello visivamente simile. In questa situazione, ovviamente, occorre innanzitutto determinare la coordinata dell'estremo, che dovrebbe coincidere con uno dei punti del grafico del back test, dove l'asse X è rappresentato dagli indici di trade a partire da zero. Lo calcolo in questo modo:

equazione 12

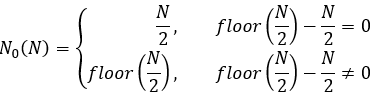
Esistono due casi: per "N" pari e per "N" dispari. Se "N" risulta essere pari, è impossibile dividerlo semplicemente per due, poiché l'indice deve essere un numero intero. A proposito, nell'ultima immagine ho rappresentato esattamente questo caso. In questo caso, il punto di applicazione della forza è un po' più vicino all'inizio. Naturalmente è possibile fare il contrario, un po' più vicino alla fine, ma ciò sarà significativo solo con un numero ridotto di operazioni, come illustrato nella figura. Con l'aumento del numero di trade, tutto questo non avrà un ruolo significativo per gli algoritmi di ottimizzazione.

Avendo impostato il valore di deflessione "P" in percentuale e “B” il saldo finale del backtest, avendo precedentemente determinato la coordinata dell'estremo, possiamo iniziare a calcolare in sequenza gli ulteriori componenti per costruire le espressioni per ciascuna delle famiglie di curve accettate. Poi ci serve la ripidità della linea retta che collega l'inizio e la fine del backtest:

equazione 13

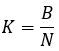
Un'altra caratteristica di queste curve è che l'angolo tangente a ciascuna di esse nei punti con ascissa "N0" è identico a "K". Nel costruire le equazioni, ho richiesto questa condizione al compito. Questo si può vedere anche graficamente nell'ultima figura (figura 4), dove sono presenti anche alcune equazioni e identità. Andiamo avanti. Ora dobbiamo calcolare il seguente valore:

equazione 14

 

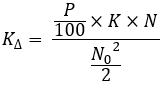
Tenere presente che "P" è impostato in modo diverso per ogni curva della famiglia. In senso stretto, si tratta di equazioni per la costruzione di una curva di una famiglia. Questi calcoli devono essere ripetuti per ogni curva della famiglia. Dobbiamo poi calcolare un altro importante rapporto:

equazione 15

Non è necessario approfondire il significato di queste strutture. Sono stati creati solo per semplificare il processo di costruzione delle curve. Resta da calcolare l'ultimo rapporto ausiliario:

equazione 16

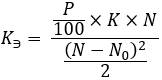
Ora, sulla base dei dati ottenuti, possiamo ricevere un'espressione matematica per calcolare i punti della curva costruita. Tuttavia, è necessario innanzitutto chiarire che la curva non è descritta da una singola equazione. A sinistra del punto "N0" abbiamo un'equazione, mentre un'altra funziona a destra. Per semplificare la comprensione, possiamo procedere come segue:

equazione 17

Ora possiamo vedere le equazioni finali:

equazioni 18

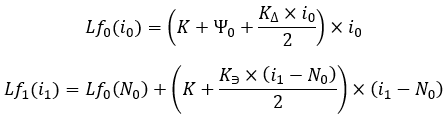
Possiamo anche mostrarlo come segue:

equazioni 19

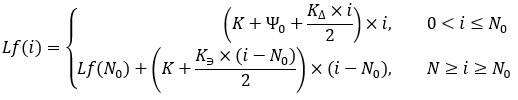
Tecnicamente, questa funzione deve essere utilizzata come funzione discreta e ausiliaria. Tuttavia, ci permette di calcolare valori frazionari in "i". Naturalmente, è improbabile avere qualsiasi beneficio nel contesto del nostro problema.

Dal momento che fornisco questo tipo di matematica, sono obbligato a fornire esempi di implementazione dell'algoritmo. Penso che tutti saranno interessati ad ottenere codice già pronto che sarà più facile adattare ai propri sistemi. Iniziamo definendo le principali variabili e i metodi che semplificheranno il calcolo delle quantità necessarie:

//+------------------------------------------------------------------+
//| Number of lines in the balance model                             |
//+------------------------------------------------------------------+
#define Lines 11 

//+------------------------------------------------------------------+
//| Initializing variables                                           |
//+------------------------------------------------------------------+
double MaxPercent = 10.0;
double BalanceMidK[,Lines];
double Deviations[Lines];
int Segments;
double K;

//+------------------------------------------------------------------+
//| Method for initializing required variables and arrays            |
//| Parameters: number of segments and initial balance               |
//+------------------------------------------------------------------+
void InitLines(int SegmentsInput, double BalanceInput) 
{
  Segments = SegmentsInput;
  K = BalanceInput / Segments;
  ArrayResize(BalanceMidK,Segments+1);
  ZeroStartBalances();
  ZeroDeviations();
  BuildBalances();
}

//+------------------------------------------------------------------+
//| Resetting variables for incrementing balances                    |
//+------------------------------------------------------------------+
void ZeroStartBalances()
{
  for (int i = 0; i < Lines; i++ ) 
  {
      for (int j = 0; j <= Segments; j++)
      {
          BalanceMidK[j,i] = 0.0;
      }
  }
}

//+------------------------------------------------------------------+
//| Reset deviations                                                 |
//+------------------------------------------------------------------+
void ZeroDeviations()
{
  for (int i = 0; i < Lines; i++)
  {
      Deviations[i] = -1.0;
  }
}

Il codice è progettato per essere riutilizzabile. Dopo il calcolo successivo, è possibile calcolare l'indicatore per una curva di bilancio diversa richiamando prima il metodo InitLines. È necessario indicare il saldo finale del backtest e il numero di operazioni, dopodiché è possibile iniziare a costruire le nostre curve sulla base di questi dati:

//+------------------------------------------------------------------+
//| Constructing all balances                                        |
//+------------------------------------------------------------------+
void BuildBalances()
{
   int N0 = MathFloor(Segments / 2.0) - Segments / 2.0 == 0 ? Segments / 2 : (int)MathFloor(Segments / 2.0);//calculate first required N0
   for (int i = 0; i < Lines; i++)
   {
       if (i==0)//very first and straight line 
       {
           for (int j = 0; j <= Segments; j++)
           {
               BalanceMidK[j,i] = K*j;
           }
       }
       else//build curved lines
       {
           double ThisP = i * (MaxPercent / 10.0);//calculate current line curvature percentage
           double KDelta = ( (ThisP /100.0) * K * Segments) / (MathPow(N0,2)/2.0 );//calculation first auxiliary ratio
           double Psi0 = -KDelta * N0;//calculation second auxiliary ratio
           double KDelta1 = ((ThisP / 100.0) * K * Segments) / (MathPow(Segments-N0, 2) / 2.0);//calculate last auxiliary ratio
           //this completes the calculation of auxiliary ratios for a specific line, it is time to construct it

           for (int j = 0; j <= N0; j++)//construct the first half of the curve 
           {
               BalanceMidK[j,i] = (K + Psi0 + (KDelta * j) / 2.0) * j;
           }
           for (int j = N0; j <= Segments; j++)//construct the second half of the curve 
           {
               BalanceMidK[j,i] = BalanceMidK[i, N0] + (K + (KDelta1 * (j-N0)) / 2.0) * (j-N0);
           }
       }
   }
}

Notare che "Lines" determina quante curve ci saranno nella nostra famiglia. La concavità aumenta gradualmente da zero (retta) e così via fino a MaxPercent, esattamente come mostrato nella figura corrispondente. È quindi possibile calcolare la deviazione per ciascuna curva e selezionare quella minima:

//+------------------------------------------------------------------+
//| Calculation of the minimum deviation from all lines              |
//| Parameters: initial balance passed via link                      |
//| Return: minimum deviation                                        |
//+------------------------------------------------------------------+
double CalculateMinDeviation(double &OriginalBalance[])
{
   //define maximum relative deviation for each curve 
   for (int i = 0; i < Lines; i++)
   {
       for (int j = 0; j <= Segments; j++)
       {
          double CurrentDeviation = OriginalBalance[Segments] ? MathAbs(OriginalBalance[j] - BalanceMidK[j, i]) / OriginalBalance[Segments] : -1.0;
          if (CurrentDeviation > Deviations[i])
          {
              Deviations[i] = CurrentDeviation;
          }           
       }
   }
    
   //determine curve with minimum deviation and deviation itself 
   double MinDeviation=0.0;
   for (int i = 0; i < Lines; i++)
   {
       if ( Deviations[i] != -1.0 && MinDeviation == 0.0)
       {
           MinDeviation = Deviations[i];
       }
       else if (Deviations[i] != -1.0 && Deviations[i] < MinDeviation)
       {
           MinDeviation = Deviations[i];
       }
   }
   return MinDeviation;
}

Ecco come dovremmo usarlo:

1. Definizione dell'array dei bilanci originali OriginalBalance.
2. Determina la lunghezza di SegmentsInput e il saldo finale di BalanceInput, oltre a chiamare il metodo InitLines.
3. Quindi si costruiscono le curve chiamando il metodo BuildBalances.
4. Poiché le curve sono tracciate, possiamo considerare il nostro criterio CalculateMinDeviation migliorato per la famiglia di curve.

Questo completa il calcolo del criterio. Penso che il calcolo del Fattore della Famiglia della Curva non creerà alcuna difficoltà. Non è necessario presentarlo qui.

Ricerca automatica delle configurazioni di trading 

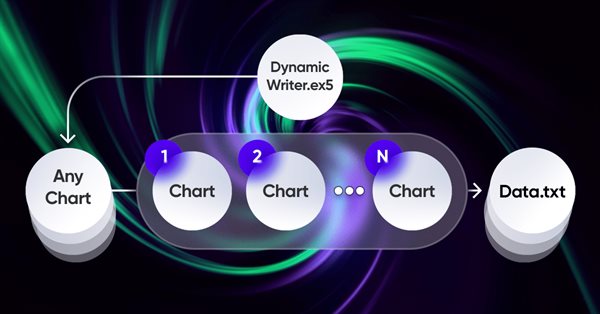
L'elemento più importante dell'intera idea è il sistema di interazione tra il terminale e il mio programma. Si tratta infatti di un ottimizzatore ciclico con criteri di ottimizzazione avanzati. Le più importanti sono state trattate nella sezione precedente. Affinché l'intero sistema funzioni, occorre innanzitutto una sorgente per le quotazioni, ovvero uno dei terminali MetaTrader 5. Come ho già mostrato nell'articolo precedente, le quotazioni vengono scritte in un file in un formato comodo per me. Per farlo si utilizza un EA, che a prima vista funziona in modo piuttosto strano:

.

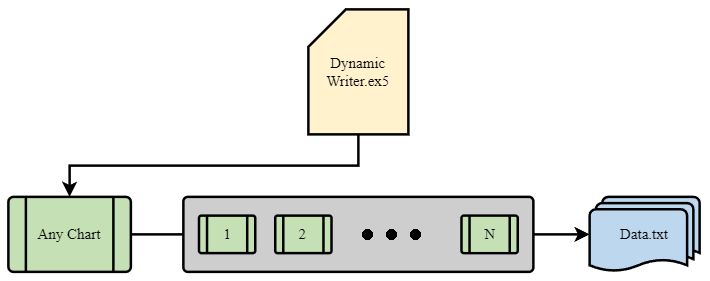
Ho trovato abbastanza interessante e utile l'esperienza di utilizzare il mio schema unico per il funzionamento dell’EA. Questa è solo una dimostrazione dei problemi che ho dovuto risolvere, ma tutto questo può essere utilizzato anche per gli EA di trading:

 

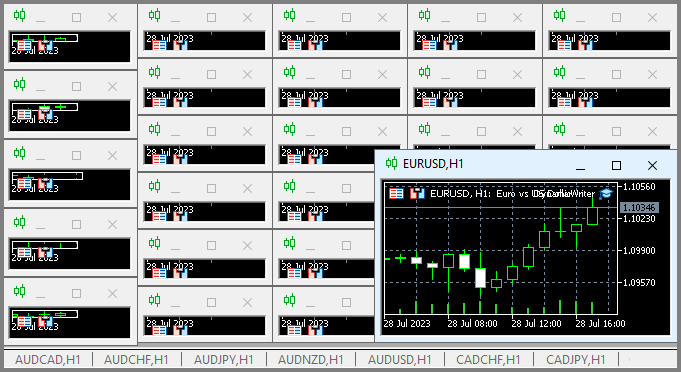
La peculiarità di questo schema è che possiamo scegliere qualsiasi grafico. Non verrà utilizzato come strumento di trading, per evitare la duplicazione dei dati, ma agirà solo come gestore di tick o timer. Il resto dei grafici rappresentano gli strumenti-periodi per i quali dobbiamo generare le quotazioni.

La scrittura delle quotazioni avviene sotto forma di una selezione casuale delle quotazioni utilizzando un generatore di numeri casuali. Se necessario, possiamo ottimizzare questo processo. La scrittura avviene dopo un certo periodo di tempo utilizzando questa funzione di base:

//+------------------------------------------------------------------+
//| Function to write data if present                                |
//| Write quotes to file                                             |
//+------------------------------------------------------------------+
void WriteDataIfPresent()
{
    // Declare array to store quotes 
    MqlRates rates[];
    ArraySetAsSeries(rates, false);

    // Select a random chart from those we added to the workspace 
    ChartData Chart = SelectAnyChart();
    
    // If the file name string is not empty 
    if (Chart.FileNameString != "")
    {
        // Copy quotes and calculate the real number of bars
        int copied = CopyRates(Chart.SymbolX, Chart.PeriodX, 1,
                        int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX))),
                        rates);
        
        // Calculate ideal number of bars
        int ideal = int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX)));
        
        // Calculate percentage of received data 
        double Percent = 100.0 * copied / ideal;
        
        // If the received data is not very different from the desired data, 
        // then we accept them and write them to a file
        if (Percent >= 95.0)
        {
            // Open file (create it if it does not exist, 
            // otherwise, erase all the data it contained)
            OpenAndWriteStart(rates, Chart, CommonE); 
            WriteAllBars(rates); // Write all data to file
            WriteEnd(rates); // Add to end
            CloseFile(); // Close and save data file
        }
        else 
        {
            // If there are much fewer quotes than required for calculation 
            Print("Not enough data"); 
        }
    }
}

La funzione WriteDataIfPresent scrive in un file le informazioni sulle quotazioni del grafico selezionato se i dati copiati corrispondono almeno al 95% del numero ideale di barre calcolato in base ai parametri specificati. Se i dati copiati sono inferiori al 95%, la funzione visualizza il messaggio "Dati insufficienti". Se un file con il nome indicato non esiste, la funzione lo crea.

Affinché questo codice funzioni, è necessario che sia descritto anche quanto segue:

//+------------------------------------------------------------------+
//| ChartData structure                                              |
//| Objective: Storing the necessary chart data                      |
//+------------------------------------------------------------------+
struct ChartData {
    string FileNameString;
    string SymbolX;
    ENUM_TIMEFRAMES PeriodX;
};

//+------------------------------------------------------------------+
//| Randomindex function                                             |
//| Objective: Get a random number with uniform distribution         |
//+------------------------------------------------------------------+
int Randomindex(int start, int end) {
    return start + int((double(MathRand())/32767.0)*double(end-start+1));
}

//+------------------------------------------------------------------+
//| SelectAnyChart function                                          |
//| Objective: View all charts except current one and select one of  |
//|       them to write quotes                                       |
//+------------------------------------------------------------------+
ChartData SelectAnyChart() {
    ChartData chosenChart;
    chosenChart.FileNameString = "";
    int chartCount = 0;
    long currentChartId, previousChartId = ChartFirst();

    // Calculate number of charts
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;  
        }
        previousChartId = currentChartId;
        
        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }

    int randomChartIndex = Randomindex(0, chartCount - 1);
    chartCount = 0;
    currentChartId = ChartFirst(); 
    previousChartId = currentChartId;
    
    // Select random chart
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;
        }
        
        previousChartId = currentChartId;
        
        // Fill in selected chart data
        if (chartCount == randomChartIndex) {
            chosenChart.SymbolX = ChartSymbol(currentChartId);
            chosenChart.PeriodX = ChartPeriod(currentChartId);
            chosenChart.FileNameString = "DataHistory" + " " + chosenChart.SymbolX + " " + IntegerToString(CorrectPeriod(chosenChart.PeriodX));
        }
        
        if (chartCount > randomChartIndex) {
            break;
        }

        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }
       
    return chosenChart;
}

Questo codice viene utilizzato per registrare e analizzare i dati storici del mercato finanziario (quotazioni) per diverse valute da vari grafici che possono essere aperti al momento nel terminale.

• La struttura ChartData è utilizzata per memorizzare i dati relativi ad ogni grafico, tra cui il nome del file, il simbolo (coppia di valute) e il timeframe. 
• La funzione "Randomindex(start, end)" genera un numero casuale tra "start" e "end". Viene utilizzato per selezionare a caso uno dei grafici disponibili.
• SelectAnyChart() esegue un'iterazione di tutti i grafici aperti e disponibili, escluso quello corrente, e ne seleziona uno a caso per l'elaborazione.

Le quotazioni generate vengono raccolte automaticamente dal programma, dopodiché vengono ricercate automaticamente le configurazioni profittevoli. L'automazione dell'intero processo è piuttosto complessa, ma ho provato a condensarla in un'immagine:

figura 5

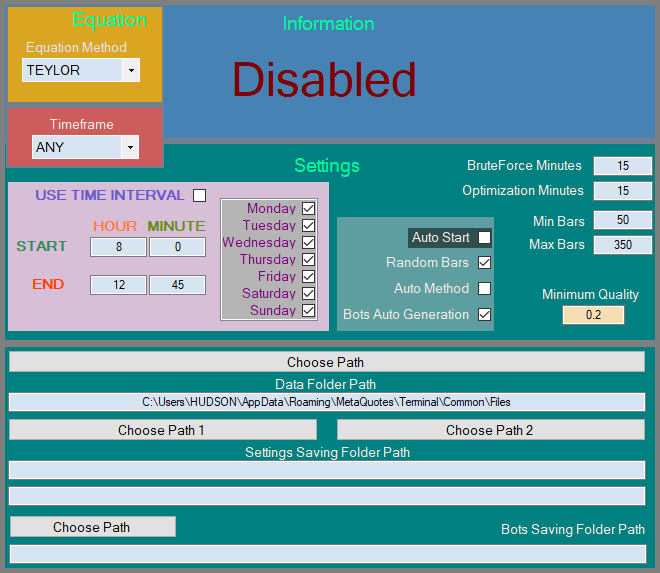
Questo algoritmo prevede tre stati:

1. Disattivato.
2. In attesa di quotazioni.
3. Attivo.

Se l'EA per la registrazione delle quotazioni non ha ancora generato un singolo file o se sono state eliminate tutte le quotazioni dalla cartella specificata, l'algoritmo attende semplicemente che compaiano e si ferma per un po'. Per quanto riguarda il nostro criterio migliorato, che ho implementato per voi in stile MQL5, è anche implementato sia per la brute force che per l'ottimizzazione:

figura 6

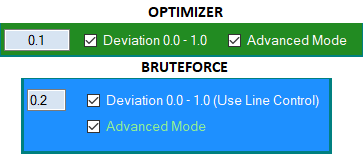
La modalità avanzata utilizza il fattore della famiglia di curve, mentre l'algoritmo standard utilizza solo il fattore di linearità. I restanti miglioramenti sono troppo estesi per essere inseriti in questo articolo. Nel prossimo articolo mostrerò il mio nuovo algoritmo per incollare gli advisor sulla base del modello universale multivaluta. Il modello viene lanciato su un solo grafico, ma elabora tutti i sistemi di trading accorpati senza richiedere che ogni EA venga lanciato sul proprio grafico. Alcune delle sue funzionalità sono state utilizzate in questo articolo.

Conclusioni

In questo articolo, abbiamo esaminato più in dettaglio nuove opportunità e idee nel campo dell'automazione del processo di sviluppo e ottimizzazione dei sistemi di trading. I risultati principali sono lo sviluppo di un nuovo algoritmo di ottimizzazione, la creazione di un meccanismo di sincronizzazione dei terminali e di un ottimizzatore automatico, nonché un importante criterio di ottimizzazione - il fattore di curva e la famiglia di curve. Questo ci permette di ridurre i tempi di sviluppo e di migliorare la qualità dei risultati ottenuti.

Un'importante aggiunta è anche la famiglia delle curve concave, che rappresentano un modello di bilancio più realistico nel contesto dei periodi di inversione a termine. Il calcolo del fattore di adattamento per ogni curva ci permette di selezionare accuratamente le impostazioni ottimali per il trading automatico.

Link

• Approccio brute force alla ricerca di pattern (Parte V): Una nuova prospettiva
  
• Approccio brute force alla ricerca di pattern (Parte IV): Funzionalità minima
• Approccio brute force alla ricerca di pattern (Parte III): Nuovi orizzonti
  
• Approccio brute force alla ricerca di pattern (Parte II): Immersione
  
• Approccio brute force alla ricerca di pattern