Modèles de régression de la bibliothèque Scikit-learn et leur export vers ONNX

ONNX(Open Neural Network Exchange) est un format de description et d'échange de modèles d'apprentissage automatique, qui permet de transférer des modèles entre différents modèles d'apprentissage automatique. Dans l'apprentissage profond et les réseaux neuronaux, des types de données comme float32 sont fréquemment utilisés. Ils sont largement appliqués car ils offrent généralement une précision et une efficacité acceptables pour la formation des modèles d'apprentissage profond.

Certains modèles classiques d'apprentissage automatique sont difficiles à représenter sous forme d’opérateurs ONNX. Des opérateurs ML (ai.onnx.ml) supplémentaires ont été introduits pour les mettre en œuvre dans ONNX. Il est intéressant de noter que selon la spécification ONNX, les opérateurs clés de cet ensemble (LinearRegressor, SVMRegressor, TreeEnsembleRegressor) peuvent accepter différents types de données d'entrée (tensor(float), tensor(double), tensor(int64), tensor(int32)), mais qu’ils renvoient toujours le type tensor(float) en sortie. Le paramétrage de ces opérateurs est également effectué à l'aide de nombres à virgule flottante, ce qui peut limiter la précision des calculs, en particulier si des nombres à double précision ont été utilisés pour définir les paramètres du modèle original.

Cela peut entraîner une perte de précision lors de la conversion de modèles ou de l'utilisation de différents types de données dans le processus de conversion et de traitement des données dans ONNX. Beaucoup dépend du convertisseur, comme nous le verrons plus loin ; certains modèles parviennent à contourner ces limitations et à assurer la portabilité totale des modèles ONNX, ce qui permet de travailler avec eux en double précision sans perdre en précision. Il est important de prendre en compte ces caractéristiques lorsque l'on travaille avec des modèles et leur représentation dans ONNX. En particulier dans les cas où la précision de la représentation des données est importante.

Scikit-learn est l'une des bibliothèques les plus populaires et les plus utilisées pour l'apprentissage automatique dans la communauté Python. Elle offre un large éventail d'algorithmes, une interface conviviale et une bonne documentation. L'article précédent, "Modèles de classification de la bibliothèque Scikit-learn et leur export vers ONNX", traitait des modèles de classification.

Dans cet article, nous allons explorer l'application des modèles de régression dans le package Scikit-learn, calculer leurs paramètres en double précision pour le jeu de données de test, tenter de les convertir au format ONNX pour la précision flottante et pour précision double, et utiliser les modèles obtenus dans des programmes MQL5. Nous comparerons également la précision des modèles originaux et de leurs versions ONNX pour la précision flottante et la précision double. Nous examinerons aussi la représentation ONNX des modèles de régression, ce qui permettra de mieux comprendre leur structure interne et leur fonctionnement.

Sommaire

• Si cela vous dérange, vous pouvez apporter votre contribution
  
  
• 1. Ensemble des Données de Test
  Le script d'affichage de l'ensemble des données de test
  
  
• 2. Modèles de régression
  2.0. Liste des Modèles de Régression Scikit-learn
  
  
• 2.1. Modèles de Régression Scikit-learn convertis en modèles ONNX float et double
  
  
• 2.1.1. sklearn.linear_model.ARDRegression
  2.1.1.1. Code de création de l'ARDRegression
  2.1.1.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.1.3. Représentation ONNX de ard_regression_float.onnx et ard_regression_double.onnx
  
  
• 2.1.2. sklearn.linear_model.BayesianRidge
  2.1.2.1. Code pour créer le modèle BayesianRidge et l'exporter vers ONNX pour float et double
  2.1.2.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.2.3. Représentation ONNX de bayesian_ridge_float.onnx et bayesian_ridge_double.onnx
  
  
• 2.1.3. sklearn.linear_model.ElasticNet
  2.1.3.1. Code pour créer le modèle ElasticNet et l'exporter vers ONNX pour float et double
  2.1.3.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.3.3. Représentation ONNX de elastic_net_float.onnx et elastic_net_double.onnx
  
  
• 2.1.4. sklearn.linear_model.ElasticNetCV
  2.1.4.1. Code pour créer le modèle ElasticNet et l'exporter vers ONNX pour float et double
  2.1.4.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.4.3. Représentation ONNX de elastic_net_cv_float.onnx et elastic_net_cv_double.onnx
  
  
• 2.1.5. sklearn.linear_model.HuberRegressor
  2.1.5.1. Code pour créer le modèle HuberRegressor et l'exporter vers ONNX pour float et double
  2.1.5.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.5.3. Représentation ONNX de huber_regressor_float.onnx et huber_regressor_double.onnx
  
  
• 2.1.6. sklearn.linear_model.Lars
  2.1.6.1. Code pour créer le modèle Lars et l'exporter vers ONNX pour float et double
  2.1.6.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.6.3. Représentation ONNX de lars_float.onnx et lars_double.onnx
  
  
• 2.1.7. sklearn.linear_model.LarsCV
  2.1.7.1. Code pour créer le modèle LarsCV et l'exporter vers ONNX pour float et double
  2.1.7.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.7.3. Représentation ONNX de lars_cv_float.onnx et lars_cv_double.onnx
  
  
• 2.1.8. sklearn.linear_model.Lasso
  2.1.8.1. Code pour créer le modèle Lasso et l'exporter vers ONNX pour float et double
  2.1.8.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.8.3. Représentation ONNX de lasso_float.onnx et lasso_double.onnx
  
  
• 2.1.9. sklearn.linear_model.LassoCV
  2.1.9.1. Code pour créer le modèle LassoCV et l'exporter vers ONNX pour float et double
  2.1.9.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.9.3. Représentation ONNX de lasso_cv_float.onnx et lasso_cv_double.onnx
  
  
• 2.1.10. sklearn.linear_model.LassoLars
  2.1.10.1. Code pour créer le modèle LassoLars et l'exporter vers ONNX pour float et double
  2.1.10.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.10.3. Représentation ONNX de lasso_lars_float.onnx et lasso_lars_double.onnx
  
  
• 2.1.11. sklearn.linear_model.LassoLarsCV
  2.1.11.1. Code pour créer le modèle LassoLarsCV et l'exporter vers ONNX pour float et double
  2.1.11.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.11.3. Représentation ONNX de lasso_lars_cv_float.onnx et lasso_lars_cv_double.onnx
  
  
• 2.1.12. sklearn.linear_model.LassoLarsIC
  2.1.12.1. Code pour créer le modèle LassoLarsIC et l'exporter vers ONNX pour float et double
  2.1.12.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.12.3. Représentation ONNX de lasso_lars_ic_float.onnx et lasso_lars_ic_double.onnx
  
  
• 2.1.13. sklearn.linear_model.LinearRegression
  2.1.13.1. Code pour créer le modèle LinearRegression et l'exporter vers ONNX pour float et double
  2.1.13.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.13.3. Représentation ONNX de linear_regression_float.onnx et linear_regression_double.onnx
  
  
• 2.1.14. sklearn.linear_model.Ridge
  2.1.14.1. Code pour créer le modèle Ridge et l'exporter vers ONNX pour float et double
  2.1.14.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.14.3. Représentation ONNX de ridge_float.onnx et ridge_double.onnx
  
  
• 2.1.15. sklearn.linear_model.RidgeCV
  2.1.15.1. Code pour créer le modèle RidgeCV et l'exporter vers ONNX pour float et double
  2.1.15.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.15.3. Représentation ONNX de ridge_cv_float.onnx et ridge_cv_double.onnx
  
  
• 2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
  2.1.16.1. Code pour créer le modèle OrthogonalMatchingPursuit et l'exporter vers ONNX pour float et double
  2.1.16.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.16.3. Représentation ONNX de l'orthogonal_matching_pursuit_float.onnx et de l'orthogonal_matching_pursuit_double.onnx
  
  
• 2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
  2.1.17.1. Code pour créer le modèle PassiveAggressiveRegressor et l'exporter vers ONNX pour float et double
  2.1.17.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.17.3. Représentation ONNX de passive_aggressive_regressor_float.onnx et passive_aggressive_regressor_double.onnx
  
  
• 2.1.18. sklearn.linear_model.QuantileRegressor
  2.1.18.1. Code pour créer le modèle QuantileRegressor et l'exporter vers ONNX pour float et double
  2.1.18.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.18.3. Représentation ONNX du quantile_regressor_float.onnx et du quantile_regressor_double.onnx
  
  
• 2.1.19. sklearn.linear_model.RANSACRegressor
  2.1.19.1. Code pour créer le modèle RANSACRegressor et l'exporter vers ONNX pour float et double
  2.1.19.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.19.3. Représentation ONNX du ransac_regressor_float.onnx et du ransac_regressor_double.onnx
  
  
• 2.1.20. sklearn.linear_model.TheilSenRegressor
  2.1.20.1. Code pour créer le modèle TheilSenRegressor et l'exporter vers ONNX pour float et double
  2.1.20.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.20.3. Représentation ONNX de theil_sen_regressor_float.onnx et theil_sen_regressor_double.onnx
  
  
• 2.1.21. sklearn.linear_model.LinearSVR
  2.1.21.1. Code pour créer le modèle LinearSVR et l'exporter vers ONNX pour float et double
  2.1.21.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.21.3. Représentation ONNX de linear_svr_float.onnx et linear_svr_double.onnx
  
  
• 2.1.22. sklearn.linear_model.MLPRegressor
  2.1.22.1. Code pour créer le modèle MLPRegressor et l'exporter vers ONNX pour float et double
  2.1.22.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.22.3. Représentation ONNX de mlp_regressor_float.onnx et mlp_regressor_double.onnx
  
  
• 2.1.23. sklearn.cross_decomposition.PLSRegression
  2.1.23.1. Code pour créer le modèle PLSRegression et l'exporter vers ONNX pour float et double
  2.1.23.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.23.3. Représentation ONNX de pls_regression_float.onnx et pls_regression_double.onnx
  
  
• 2.1.24. sklearn.linear_model.TweedieRegressor
  2.1.24.1. Code pour créer le modèle TweedieRegressor et l'exporter vers ONNX pour float et double
  2.1.24.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.24.3. Représentation ONNX de tweedie_regressor_float.onnx et tweedie_regressor_double.onnx
  
  
• 2.1.25. sklearn.linear_model.PoissonRegressor
  2.1.25.1. Code pour créer le modèle PoissonRegressor et l'exporter vers ONNX pour float et double
  2.1.25.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.25.3. Représentation ONNX du poisson_regressor_float.onnx et du poisson_regressor_double.onnx
  
  
• 2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
  2.1.26.1. Code pour créer le modèle RadiusNeighborsRegressor et l'exporter vers ONNX pour float et double
  2.1.26.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.26.3. Représentation ONNX du radius_neighbors_regressor_float.onnx et du radius_neighbors_regressor_double.onnx
  
  
• 2.1.27. sklearn.neighbors.KNeighborsRegressor
  2.1.27.1. Code pour créer le modèle KNeighborsRegressor et l'exporter vers ONNX pour float et double
  2.1.27.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.27.3. Représentation ONNX de kneighbors_regressor_float.onnx et kneighbors_regressor_double.onnx
  
  
• 2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
  2.1.28.1. Code pour créer le modèle GaussianProcessRegressor et l'exporter vers ONNX pour float et double
  2.1.28.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.28.3. Représentation ONNX du gaussian_process_regressor_float.onnx et du gaussian_process_regressor_double.onnx
  
  
• 2.1.29. sklearn.linear_model.GammaRegressor
  2.1.29.1. Code pour créer le modèle GammaRegressor et l'exporter vers ONNX pour float et double
  2.1.29.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.29.3. Représentation ONNX du gamma_regressor_float.onnx et du gamma_regressor_double.onnx
  
  
• 2.1.30. sklearn.linear_model.SGDRegressor
  2.1.30.1. Code pour créer le modèle SGDRegressor et l'exporter vers ONNX pour float et double
  2.1.30.2. Code MQL5 pour l'exécution des modèles ONNX
  2.1.30.3. Représentation ONNX de sgd_regressor_float.onnx et sgd_rgressor_double.onnx
  
  
  
• 2.2. Modèles de régression de la bibliothèque Scikit-learn qui sont convertis uniquement en modèles ONNX de précision flottante
  
  
• 2.2.1. sklearn.linear_model.AdaBoostRegressor
  2.2.1.1. Code pour créer le modèle AdaBoostRegressor et l'exporter vers ONNX pour float et double
  2.2.1.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.1.3. Représentation ONNX de adaboost_regressor_float.onnx et adaboost_regressor_double.onnx
  
  
• 2.2.2. sklearn.linear_model.BaggingRegressor
  2.2.2.1. Code pour créer le modèle BaggingRegressor et l'exporter vers ONNX pour float et double
  2.2.2.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.2.3. Représentation ONNX du bagging_regressor_float.onnx et du bagging_regressor_double.onnx
  
  
• 2.2.3. sklearn.linear_model.DecisionTreeRegressor 
  2.2.3.1. Code pour créer le modèle DecisionTreeRegressor et l'exporter vers ONNX pour float et double
  2.2.3.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.3.3. Représentation ONNX de decision_tree_regressor_float.onnx et decision_tree_regressor_double.onnx
  
  
• 2.2.4. sklearn.linear_model.ExtraTreeRegressor
  2.2.4.1. Code pour créer le modèle ExtraTreeRegressor et l'exporter vers ONNX pour float et double
  2.2.4.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.4.3. Représentation ONNX de l'extra_tree_regressor_float.onnx et de l'extra_tree_regressor_double.onnx
  
  
• 2.2.5. sklearn.ensemble.ExtraTreesRegressor
  2.2.5.1. Code pour créer le modèle ExtraTreesRegressor et l'exporter vers ONNX pour float et double
  2.2.5.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.5.3. Représentation ONNX des extra_trees_regressor_float.onnx et extra_trees_regressor_double.onnx
  
  
• 2.2.6. sklearn.svm.NuSVR
  2.2.6.1. Code pour créer le modèle NuSVR et l'exporter vers ONNX pour float et double
  2.2.6.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.6.3. Représentation ONNX de nu_svr_float.onnx et nu_svr_double.onnx
  
  
• 2.2.7. sklearn.ensemble.RandomForestRegressor
  2.2.7.1. Code pour créer le modèle RandomForestRegressor et l'exporter vers ONNX pour float et double
  2.2.7.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.7.3. Représentation ONNX de random_forest_regressor_float.onnx et random_forest_regressor_double.onnx
  
  
• 2.2.8. sklearn.ensemble.GradientBoostingRegressor
  2.2.8.1. Code pour créer le modèle GradientBoostingRegressor et l'exporter vers ONNX pour float et double
  2.2.8.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.8.3. Représentation ONNX du gradient_boosting_regressor_float.onnx et du gradient_boosting_regressor_double.onnx
  
  
• 2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
  2.2.9.1. Code pour créer le modèle HistGradientBoostingRegressor et l'exporter vers ONNX pour float et double
  2.2.9.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.9.3. Représentation ONNX de hist_gradient_boosting_regressor_float.onnx et hist_gradient_boosting_regressor_double.onnx
  
  
• 2.2.10. sklearn.svm.SVR
  2.2.10.1. Code pour créer le modèle SVR et l'exporter vers ONNX pour float et double
  2.2.10.2. Code MQL5 pour l'exécution des modèles ONNX
  2.2.10.3. Représentation ONNX de svr_float.onnx et svr_double.onnx
  
  
  
• 2.3. Modèles de Régression qui ont rencontré des problèmes lors de la conversion en ONNX
  
  
• 2.3.1. sklearn.dummy.DummyRegressor
  Code pour la création du DummyRegressor
  
  
• 2.3.2. sklearn.kernel_ridge.KernelRidge
  Code pour la création du KernelRidge
  
  
• 2.3.3. sklearn.isotonic.IsotonicRegression
  Code de création de IsotonicRegression
  
  
• 2.3.4. sklearn.cross_decomposition.PLSCanonical
  Code pour la création de PLSCanonical
  
  
• 2.3.5. sklearn.cross_decomposition.CCA
  Code de création de CCA
  
  
• Conclusion
  
  
• Résumé
  

Si cela vous dérange, vous pouvez apporter votre contribution

Sur le forum des développeurs du Runtime ONNX, l'un des utilisateurs a signalé une erreur "[ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Impossible de trouver une implémentation pour le nœud LinearRegressor:LinearRegressor(1)" lors de l'exécution d'un modèle via ONNX Runtime.

Bonjour à tous, j'obtiens cette erreur lorsque j'essaie de déduire un modèle de régression linéaire. Veuillez m'aider à résoudre ce problème.

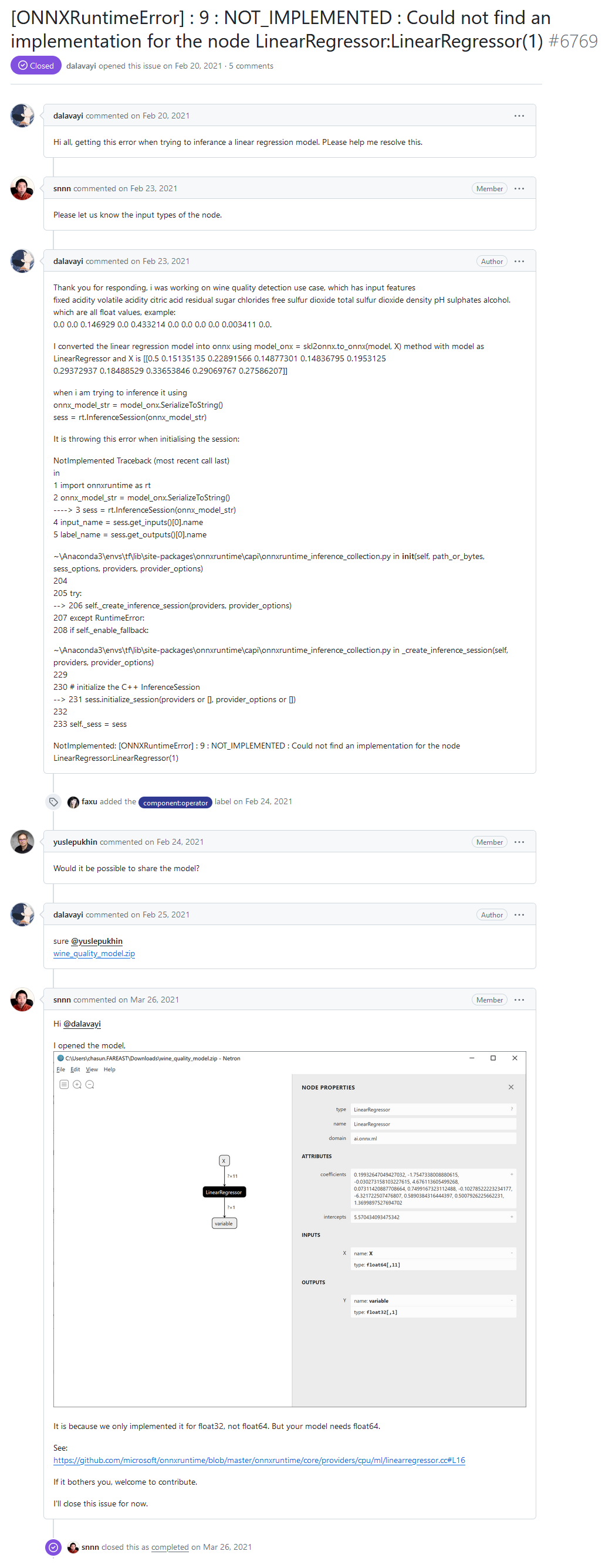
"NOT_IMPLEMENTED : Impossible de trouver une implémentation pour le nœud LinearRegressor:LinearRegressor(1)" dans le forum des développeurs du Runtime ONNX

Réponse du développeur :

C'est parce que nous ne l'avons implémenté que pour float32, pas pour float64. Mais votre modèle a besoin de float64.

Voir :
https://github.com/microsoft/onnxruntime/blob/master/onnxruntime/core/providers/cpu/ml/linearregressor.cc#L16

Si cela vous dérange, n'hésitez pas à y contribuer.

Dans le modèle ONNX de l'utilisateur, l'opérateur est appelé avec un type de données double (float64), et le message d'erreur apparaît parce que le Runtime ONNX ne supporte pas l'opérateur LinearRegressor() avec une double précision.

Selon la spécification de l'opérateur ai.onnx.ml.LinearRegressor, le type de données d'entrée double est possible (T: tensor(float), tensor(double), tensor(int64), tensor(int32)). Cependant, les développeurs ont intentionnellement choisi de ne pas l'implémenter.

La raison en est que la sortie renvoie toujours la valeur Y: tensor(float). De plus, les paramètres de calcul sont aussi des nombres flottants (coefficients : liste de float, intercepts : liste de float).

Par conséquent, lorsque les calculs sont effectués en double précision, cet opérateur réduit la précision à un flottant, et sa mise en œuvre dans les calculs en double précision a une valeur discutable.

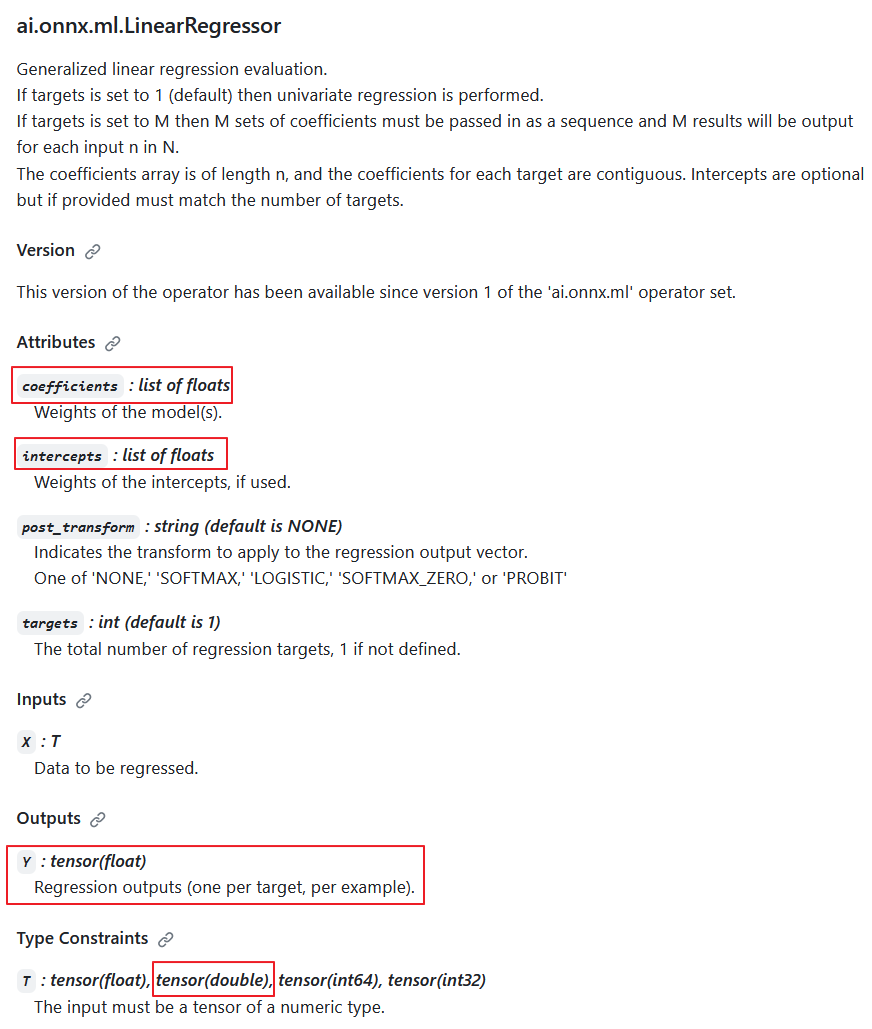
Description de l'opérateur ai.onnx.ml.LinearRegressor

Ainsi, la réduction de la précision à des valeurs flottantes dans les paramètres et la valeur de sortie empêche le ai.onnx.ml.LinearRegressor de fonctionner pleinement avec des nombres doubles (float64). C'est probablement pour cette raison que les développeurs du Runtime ONNX ont décidé de ne pas l'implémenter pour le type double

La méthode consistant à "ajouter le support du type double" a été démontrée par les développeurs dans les commentaires du code (surlignés en jaune).

Dans le Runtime ONNX, son calcul est effectué en utilisant la classe LinearRegressor (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.h).

Les paramètres de l'opérateur, coefficients_ et intercepts_, sont stockés sous forme de std::vector<float> :

#pragma once

#include "core/common/common.h"
#include "core/framework/op_kernel.h"
#include "core/util/math_cpuonly.h"
#include "ml_common.h"

namespace onnxruntime {
namespace ml {

class LinearRegressor final : public OpKernel {
 public:
  LinearRegressor(const OpKernelInfo& info);
  Status Compute(OpKernelContext* context) const override;

 private:
  int64_t num_targets_;
  std::vector<float> coefficients_;
  std::vector<float> intercepts_;
  bool use_intercepts_;
  POST_EVAL_TRANSFORM post_transform_;
};

}  // namespace ml
}  // namespace onnxruntime

L'implémentation de l'opérateur LinearRegressor (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.cc) :

// Copyright (c) Microsoft Corporation. All rights reserved.
// Licensed under the MIT License.

#include "core/providers/cpu/ml/linearregressor.h"
#include "core/common/narrow.h"
#include "core/providers/cpu/math/gemm.h"

namespace onnxruntime {
namespace ml {

ONNX_CPU_OPERATOR_ML_KERNEL(
    LinearRegressor,
    1,
    // KernelDefBuilder().TypeConstraint("T", std::vector<MLDataType>{
    //                                            DataTypeImpl::GetTensorType<float>(),
    //                                            DataTypeImpl::GetTensorType<double>()}),
    KernelDefBuilder().TypeConstraint("T", DataTypeImpl::GetTensorType<float>()),
    LinearRegressor);

LinearRegressor::LinearRegressor(const OpKernelInfo& info)
    : OpKernel(info),
      intercepts_(info.GetAttrsOrDefault<float>("intercepts")),
      post_transform_(MakeTransform(info.GetAttrOrDefault<std::string>("post_transform", "NONE"))) {
  ORT_ENFORCE(info.GetAttr<int64_t>("targets", &num_targets_).IsOK());
  ORT_ENFORCE(info.GetAttrs<float>("coefficients", coefficients_).IsOK());

  // use the intercepts_ if they're valid
  use_intercepts_ = intercepts_.size() == static_cast<size_t>(num_targets_);
}

// Use GEMM for the calculations, with broadcasting of intercepts
// https://github.com/onnx/onnx/blob/main/docs/Operators.md#Gemm
//
// X: [num_batches, num_features]
// coefficients_: [num_targets, num_features]
// intercepts_: optional [num_targets].
// Output: X * coefficients_^T + intercepts_: [num_batches, num_targets]
template <typename T>
static Status ComputeImpl(const Tensor& input, ptrdiff_t num_batches, ptrdiff_t num_features, ptrdiff_t num_targets,
                          const std::vector<float>& coefficients,
                          const std::vector<float>* intercepts, Tensor& output,
                          POST_EVAL_TRANSFORM post_transform,
                          concurrency::ThreadPool* threadpool) {
  const T* input_data = input.Data<T>();
  T* output_data = output.MutableData<T>();

  if (intercepts != nullptr) {
    TensorShape intercepts_shape({num_targets});
    onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans,
                                      num_batches, num_targets, num_features,
                                      1.f, input_data, coefficients.data(), 1.f,
                                      intercepts->data(), &intercepts_shape,
                                      output_data,
                                      threadpool);
  } else {
    onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans,
                                      num_batches, num_targets, num_features,
                                      1.f, input_data, coefficients.data(), 1.f,
                                      nullptr, nullptr,
                                      output_data,
                                      threadpool);
  }

  if (post_transform != POST_EVAL_TRANSFORM::NONE) {
    ml::batched_update_scores_inplace(gsl::make_span(output_data, SafeInt<size_t>(num_batches) * num_targets),
                                      num_batches, num_targets, post_transform, -1, false, threadpool);
  }
  return Status::OK();
}

Status LinearRegressor::Compute(OpKernelContext* ctx) const {
  Status status = Status::OK();

  const auto& X = *ctx->Input<Tensor>(0);
  const auto& input_shape = X.Shape();

  if (input_shape.NumDimensions() > 2) {
    return ORT_MAKE_STATUS(ONNXRUNTIME, INVALID_ARGUMENT, "Input shape had more than 2 dimension. Dims=",
                           input_shape.NumDimensions());
  }

  ptrdiff_t num_batches = input_shape.NumDimensions() <= 1 ? 1 : narrow<ptrdiff_t>(input_shape[0]);
  ptrdiff_t num_features = input_shape.NumDimensions() <= 1 ? narrow<ptrdiff_t>(input_shape.Size())
                                                            : narrow<ptrdiff_t>(input_shape[1]);
  Tensor& Y = *ctx->Output(0, {num_batches, num_targets_});
  concurrency::ThreadPool* tp = ctx->GetOperatorThreadPool();

  auto element_type = X.GetElementType();

  switch (element_type) {
    case ONNX_NAMESPACE::TensorProto_DataType_FLOAT: {
      status = ComputeImpl<float>(X, num_batches, num_features, narrow<ptrdiff_t>(num_targets_), coefficients_,
                                  use_intercepts_ ? &intercepts_ : nullptr,
                                  Y, post_transform_, tp);

      break;
    }
    case ONNX_NAMESPACE::TensorProto_DataType_DOUBLE: {
      // TODO: Add support for 'double' to the scoring functions in ml_common.h
      // once that is done we can just call ComputeImpl<double>...
      // Alternatively we could cast the input to float.
    }
    default:
      status = ORT_MAKE_STATUS(ONNXRUNTIME, FAIL, "Unsupported data type of ", element_type);
  }

  return status;
}

}  // namespace ml
}  // namespace onnxruntime

Il s'avère qu'il existe une option permettant d'utiliser des nombres doubles comme valeurs d'entrée et d'effectuer le calcul de l'opérateur avec des paramètres flottants. Une autre possibilité serait de réduire la précision des données d'entrée à des valeurs flottantes. Mais aucune de ces options ne peut être considérée comme une solution adéquate.

La spécification de l'opérateur ai.onnx.ml.LinearRegressor limite la possibilité d'un fonctionnement complet avec des nombres doubles puisque les paramètres et la valeur de sortie sont limités au type flottant.

Une situation similaire se produit avec d'autres opérateurs ML d'ONNX, tels que ai.onnx.ml.SVMRegressor et ai.onnx.ml.TreeEnsembleRegressor.

Par conséquent, tous les développeurs utilisant l'exécution de modèles ONNX en double précision sont confrontés à cette limitation de la spécification. Une solution pourrait consister à étendre la spécification ONNX (ou à ajouter des opérateurs similaires tels que LinearRegressor64, SVMRegressor64 et TreeEnsembleRegressor64 avec des paramètres et des valeurs de sortie en double). Mais à l'heure actuelle, cette question n'est pas résolue.

Tout dépend du convertisseur ONNX. Pour les modèles calculés en double, il peut être préférable de ne pas utiliser ces opérateurs (bien que cela ne soit pas toujours possible). Dans ce cas particulier, le convertisseur vers ONNX n'a pas fonctionné de manière optimale avec le modèle de l'utilisateur.

Comme nous le verrons plus loin, le convertisseur sklearn-onnx parvient à contourner la limitation de LinearRegressor : pour les modèles ONNX double, il utilise les opérateurs ONNX MatMul() et Add() à la place. Grâce à cette méthode, de nombreux modèles de régression de la bibliothèque Scikit-learn sont convertis avec succès en modèles ONNX calculés en double, tout en préservant la précision des modèles doubles originaux.

1. Ensemble des Données de Test

Pour exécuter les exemples, vous devrez installer Python (nous avons utilisé la version 3.10.8), des bibliothèques supplémentaires (pip install -U scikit-learn numpy matplotlib onnx onnxruntime skl2onnx), et spécifier le chemin vers Python dans MetaEditor (dans le menu Outils->Options->Compilateurs->Python).

Comme ensemble de données de test, nous utiliserons les valeurs générées de la fonction y = 4X + 10sin(X*0.5).

Pour afficher le graphique d'une telle fonction, ouvrez MetaEditor, créez un fichier nommé RegressionData.py, copiez le texte du script et exécutez-le en cliquant sur le bouton "Compiler".

Le script d'affichage de l'ensemble des données de test

# RegressionData.py
# The code plots the synthetic data, used for all regression models
# Copyright 2023, MetaQuotes Ltd.
# https://mql5.com

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

# set the figure size
plt.figure(figsize=(8,5))

# plot the initial data for regression
plt.scatter(X, y, label='Regression Data', marker='o')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Regression data')
plt.show()

Un graphique de la fonction sera ensuite affiché? Nous l’utiliserons pour tester les méthodes de régression.

Fig. 1. Fonction de test des modèles de régression

2. Modèles de Régression

L'objectif d'une tâche de régression est de trouver une fonction mathématique ou un modèle qui décrit au mieux la relation entre les caractéristiques et la variable cible afin de prédire les valeurs numériques des nouvelles données. Cela permet de faire des prévisions, d'optimiser les solutions et de prendre des décisions éclairées sur la base de ces données.

Considérons les principaux modèles de régression du paquet scikit-learn.

2.0. Liste des Modèles de Régression Scikit-learn

Pour afficher la liste des modèles de régression scikit-learn disponibles, vous pouvez utiliser le script suivant :

# ScikitLearnRegressors.py
# The script lists all the regression algorithms available inb scikit-learn
# Copyright 2023, MetaQuotes Ltd.
# https://mql5.com

# print Python version
from platform import python_version  
print("The Python version is ", python_version()) 

# print scikit-learn version
import sklearn
print('The scikit-learn version is {}.'.format(sklearn.__version__))

# print scikit-learn regression models
from sklearn.utils import all_estimators

regressors = all_estimators(type_filter='regressor')
for index, (name, RegressorClass) in enumerate(regressors, start=1):
    print(f"Regressor {index}: {name}")

Sortie :

The Python version is  3.10.8
The scikit-learn version is 1.3.2.
Regressor 1: ARDRegression
Regressor 2: AdaBoostRegressor
Regressor 3: BaggingRegressor
Regressor 4: BayesianRidge
Regressor 5: CCA
Regressor 6: DecisionTreeRegressor
Regressor 7: DummyRegressor
Regressor 8: ElasticNet
Regressor 9: ElasticNetCV
Regressor 10: ExtraTreeRegressor
Regressor 11: ExtraTreesRegressor
Regressor 12: GammaRegressor
Regressor 13: GaussianProcessRegressor
Regressor 14: GradientBoostingRegressor
Regressor 15: HistGradientBoostingRegressor
Regressor 16: HuberRegressor
Regressor 17: IsotonicRegression
Regressor 18: KNeighborsRegressor
Regressor 19: KernelRidge
Regressor 20: Lars
Regressor 21: LarsCV
Regressor 22: Lasso
Regressor 23: LassoCV
Regressor 24: LassoLars
Regressor 25: LassoLarsCV
Regressor 26: LassoLarsIC
Regressor 27: LinearRegression
Regressor 28: LinearSVR
Regressor 29: MLPRegressor
Regressor 30: MultiOutputRegressor
Regressor 31: MultiTaskElasticNet
Regressor 32: MultiTaskElasticNetCV
Regressor 33: MultiTaskLasso
Regressor 34: MultiTaskLassoCV
Regressor 35: NuSVR
Regressor 36: OrthogonalMatchingPursuit
Regressor 37: OrthogonalMatchingPursuitCV
Regressor 38: PLSCanonical
Regressor 39: PLSRegression
Regressor 40: PassiveAggressiveRegressor
Regressor 41: PoissonRegressor
Regressor 42: QuantileRegressor
Regressor 43: RANSACRegressor
Regressor 44: RadiusNeighborsRegressor
Regressor 45: RandomForestRegressor
Regressor 46: RegressorChain
Regressor 47: Ridge
Regressor 48: RidgeCV
Regressor 49: SGDRegressor
Regressor 50: SVR
Regressor 51: StackingRegressor
Regressor 52: TheilSenRegressor
Regressor 53: TransformedTargetRegressor
Regressor 54: TweedieRegressor
Regressor 55: VotingRegressor

Pour des raisons de commodité, les régresseurs sont mis en évidence dans des couleurs différentes. Les modèles qui nécessitent un modèle de régression de base sont surlignés en gris, alors que les autres modèles peuvent être utilisés indépendamment. Notez que les modèles exportés avec succès au format ONNX sont marqués en vert, les modèles qui rencontrent des erreurs lors de la conversion dans la version actuelle de scikit-learn 1.2.2 sont marqués en rouge. Les méthodes inadaptées à la tâche d'essai considérée sont surlignées en bleu.

L'analyse de la qualité de la régression utilise des mesures de régression, qui sont des fonctions des valeurs réelles et des valeurs prédites. Dans le langage MQL5, plusieurs métriques différentes sont disponibles. Elles sont détaillées dans l'article "Evaluation des modèles ONNX à l’aide de métriques de régression".

Dans cet article, 3 métriques seront utilisées pour comparer la qualité des différents modèles :

1. Le coefficient de détermination R-carré (R2) ;
2. L’Erreur Absolue Moyenne (EAM) ;
3. L’Erreur Quadratique Moyenne (EQM).

2.1. Modèles de régression Scikit-learn convertis en modèles ONNX float et double

Cette section présente les modèles de régression qui ont été convertis avec succès dans les formats ONNX en précision flottante et double.

Tous les modèles de régression examinés plus loin sont présentés sous la forme suivante :

1. Description du modèle, principe de fonctionnement, avantages et limites
2. Script Python pour créer le modèle, l'exporter vers des fichiers ONNX aux formats float et double, et exécuter les modèles obtenus en utilisant le Runtime ONNX en Python. Des métriques telles que R^2, MAE, MSE, calculées à l'aide de sklearn.metrics, sont utilisées pour évaluer la qualité des modèles originaux et ONNX.
   
3. Script MQL5 pour l'exécution de modèles ONNX (float et double) via le Runtime ONNX, avec des métriques calculées en utilisant RegressionMetric().
   
4. Représentation du modèle ONNX dans Netron pour les précisions float et double.

2.1.1. sklearn.linear_model.ARDRegression

L’ARDRegression (Automatic Relevance Determination Regression) est une méthode de régression conçue pour résoudre les problèmes de régression en déterminant automatiquement l'importance (la pertinence) des caractéristiques et en établissant leurs poids au cours du processus d'apprentissage du modèle.

L’ARDRegression permet de détecter et d'utiliser uniquement les caractéristiques les plus importantes pour construire un modèle de régression, ce qui peut s'avérer utile lorsqu'on a affaire à un grand nombre de caractéristiques.

Principe de fonctionnement de l'ARDRegression :

1. Régression Linéaire : L’ARDRegression est basé sur la régression linéaire, en supposant une relation linéaire entre les variables indépendantes (caractéristiques) et la variable cible.
2. Détermination Automatique de l'Importance des Caractéristiques : La principale caractéristique de l'ARDRegression est la détermination automatique des caractéristiques les plus importantes pour prédire la variable cible. Pour ce faire, on introduit des distributions préalables (régularisation) sur les poids, ce qui permet au modèle de fixer automatiquement des poids nuls pour les caractéristiques les moins significatives.
3. Estimation des Probabilités Postérieures : L’ARDRegression calcule les probabilités postérieures pour chaque caractéristique, ce qui permet de déterminer leur importance. Les caractéristiques dont la probabilité a posteriori est élevée sont considérées comme pertinentes et reçoivent des poids non nuls, tandis que les caractéristiques dont la probabilité a posteriori est faible reçoivent des poids nuls.
4. Réduction de la Dimensionnalité : Ainsi, l'ARDRegression peut conduire à une réduction de la dimensionnalité des données en supprimant les caractéristiques insignifiantes.

Avantages de l'ARDRegression :

• Détermination Automatique des Caractéristiques Importantes : La méthode identifie et utilise automatiquement les caractéristiques les plus importantes, ce qui peut améliorer les performances du modèle et réduire le risque de sur-ajustement.
• Résistance à la Multicolinéarité : L’ARDRegression gère bien la multicolinéarité, même lorsque les caractéristiques sont fortement corrélées.

Limites de l'ARDRegression :

• Nécessite la Sélection de Distributions Préalables : Le choix de distributions préalables appropriées peut nécessiter une expérimentation.
• Complexité de Calcul : L'apprentissage de l'ARDRegression peut être coûteux en termes de calcul, en particulier pour les grands ensembles de données.

L’ARDRegression est une méthode de régression qui détermine automatiquement l'importance des caractéristiques et établit leurs poids sur la base des probabilités a posteriori. Cette méthode est utile lorsque seules les caractéristiques significatives sont prises en compte pour construire un modèle de régression et qu'il est nécessaire de réduire la dimensionnalité des données.

2.1.1.1. Code pour créer le modèle ARDRegression et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.ARDRegression, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée flottantes et doubles. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# ARDRegression.py
# Le code démontre le processus d'entraînement du modèle ARDRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compte pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"

# crée un modèle ARDRegression
regression_model = ARDRegression()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)

print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)

print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Le script crée et entraîne le modèle sklearn.linear_model.ARDRegression (le modèle original est considéré en type double), puis exporte le modèle vers ONNX pour les types float et double (ard_regression_float.onnx et ard_regression_double.onnx) et compare la précision de leurs fonctionnements.

Il génère également les fichiers ARDRegression_plot_float.png et ARDRegression_plot_double.png, permettant une évaluation visuelle des résultats des modèles ONNX pour float et double (Fig. 2-3).

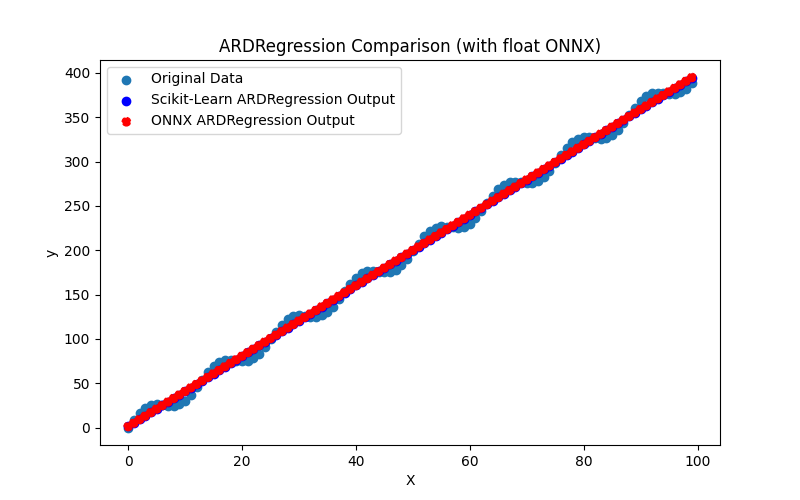
Fig. 2. Résultats de ARDRegression.py (float)

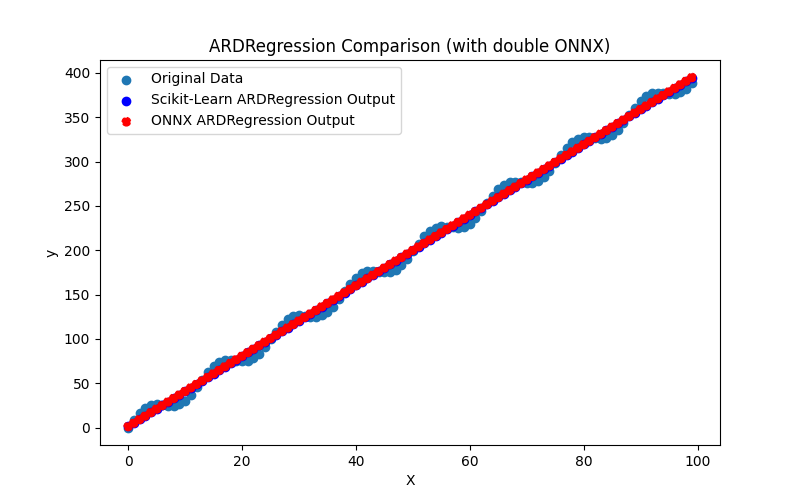
Fig. 3. Résultats de ARDRegression.py (double)

Visuellement, les modèles ONNX pour les flottants et les doubles sont identiques (Fig. 2-3), des informations détaillées peuvent être trouvées dans l'onglet Journal :

Python  ARDRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891289
Python  
Python  ARDRegression ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382627587808
Python  Mean Absolute Error: 6.347568283744705
Python  Mean Squared Error: 49.778160054267204
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  ARDRegression ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891289
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

Dans cet exemple, le modèle original a été considéré en double, puis il a été exporté dans les modèles ONNX ard_regression_float.onnx et ard_regression_double.onnx pour float et double, respectivement.

Si la précision du modèle est évaluée par l'Erreur Absolue Moyenne (MAE), la précision du modèle ONNX pour le flottant est de 6 décimales, alors que le modèle ONNX utilisant le type double a montré une rétention de précision jusqu'à 15 décimales, en ligne avec la précision du modèle original.

Les propriétés des modèles ONNX peuvent être visualisées dans MetaEditor (Fig. 4-5).

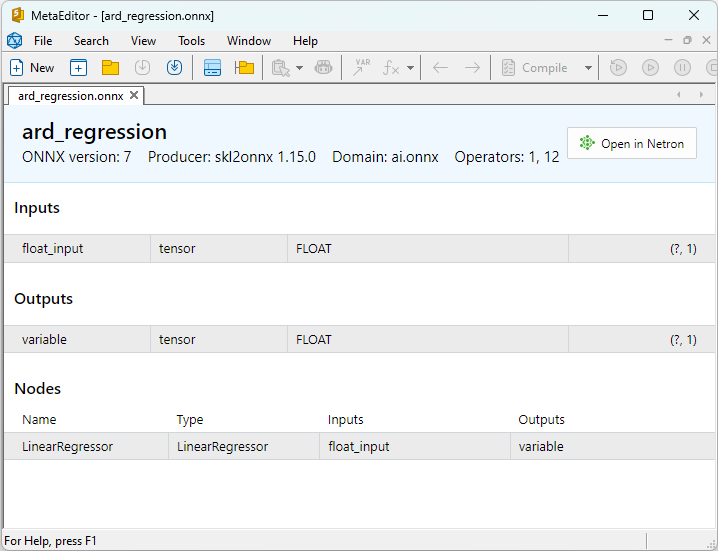
Fig. 4. Modèle ONNX ard_regression_float.onnx dans MetaEditor

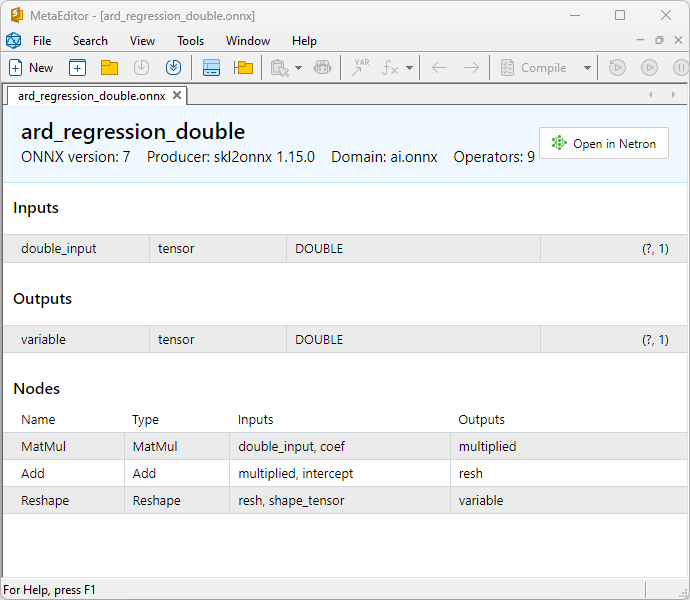
Fig. 5. Modèle ONNX ard_regression_double.onnx dans MetaEditor

Une comparaison entre les modèles ONNX flottants et doubles montre que dans ce cas, le calcul des modèles ONNX pour ARDRegression se fait différemment : pour les nombres flottants, l'opérateur LinearRegressor() d'ONNX-ML est utilisé, alors que pour les nombres doubles, les opérateurs ONNX MatMul(), Add(), et Reshape() sont utilisés.

L'implémentation du modèle dans ONNX dépend du convertisseur ; dans les exemples d'export vers ONNX, la fonction skl2onnx.convert_sklearn() de la bibliothèque skl2onnx sera utilisée.

2.1.1.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles ONNX ard_regression_float.onnx et ard_regression_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                ARDRegression.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ARDRegression"
#define   ONNXFilenameFloat  "ard_regression_float.onnx"
#define   ONNXFilenameDouble "ard_regression_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

ARDRegression (EURUSD,H1)       Testing ONNX float: ARDRegression (ard_regression_float.onnx)
ARDRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382627587808
ARDRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475682837447049
ARDRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781600542671896
ARDRegression (EURUSD,H1)       
ARDRegression (EURUSD,H1)       Testing ONNX double: ARDRegression (ard_regression_double.onnx)
ARDRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382628120845
ARDRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475680128537597
ARDRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781593489128795

Comparaison avec le modèle double original en Python :

Testing ONNX float: ARDRegression (ard_regression_float.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475682837447049
       
Testing ONNX double: ARDRegression (ard_regression_double.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475680128537597

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.1.3. Les représentations ONNX des modèles ard_regression_float.onnx et ard_regression_double.onnx

Netron (version web) est un outil de visualisation des modèles et d'analyse des graphes de calcul, qui peut être utilisé pour les modèles au format ONNX (Open Neural Network Exchange).

Netron présente les graphes des modèles et leur architecture sous une forme claire et interactive, permettant l'exploration de la structure et des paramètres des modèles d'apprentissage profond, y compris ceux créés à l'aide d'ONNX.

Les principales caractéristiques de Netron sont les suivantes

• Visualisation de graphiques : Netron affiche l'architecture du modèle sous forme de graphique, ce qui vous permet de voir les couches, les opérations et les connexions entre elles. Vous pouvez facilement comprendre la structure et le flux de données dans le modèle.
• Exploration interactive : Vous pouvez sélectionner des nœuds dans le graphique pour obtenir des informations supplémentaires sur chaque opérateur et sur ses paramètres.
• Prise en charge de différents formats : Netron prend en charge une variété de formats de modèles d'apprentissage profond, notamment ONNX, TensorFlow, PyTorch, CoreML, et d'autres.
• Capacité d'analyse des paramètres : Vous pouvez visualiser les paramètres et les poids du modèle, ce qui est utile pour comprendre les valeurs utilisées dans les différentes parties du modèle.

Netron est pratique pour les développeurs et les chercheurs dans le domaine de l'apprentissage automatique et de l'apprentissage profond, car il simplifie la visualisation et l'analyse des modèles, aidant à la compréhension et au débogage des réseaux neuronaux complexes.

Cet outil permet d'inspecter rapidement les modèles, d'explorer leur structure et leurs paramètres, ce qui facilite le travail avec les réseaux neuronaux profonds.

Pour plus de détails sur Netron, consultez les articles : Visualisez votre réseau neuronal avec Netron et Visualize Keras Neural Networks with Netron.

Vidéo sur Netron :

Le modèle ard_regression_float.onnx est présenté à la figure 6 :

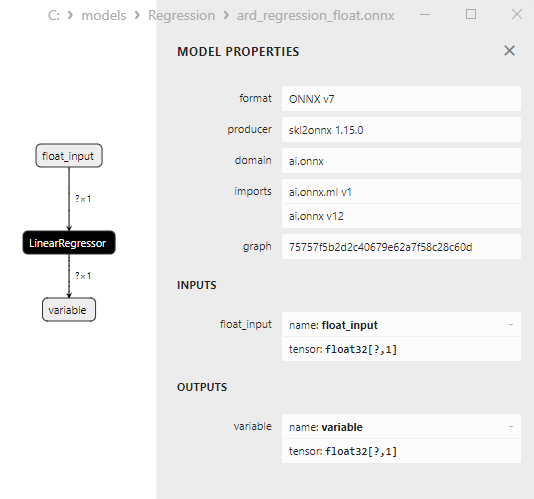
Fig. 6. Représentation du modèle ONNX ard_regression_float.onnx dans Netron

L'opérateur ONNX ai.onnx.ml LinearRegressor() fait partie de la norme ONNX, qui décrit un modèle pour les tâches de régression. Cet opérateur est utilisé pour la régression, il consiste à prédire des valeurs numériques (continues) sur la base de caractéristiques d'entrée.

Il prend en entrée les paramètres du modèle, tels que les poids et les biais, ainsi que les caractéristiques d'entrée, et exécute une régression linéaire. La régression linéaire estime les paramètres (poids) pour chaque caractéristique d'entrée et effectue ensuite une combinaison linéaire de ces caractéristiques avec les poids pour générer une prédiction.

Cet opérateur effectue les étapes suivantes :

1. Il prend les poids et les biais du modèle, ainsi que les caractéristiques d'entrée.
2. Pour chaque exemple de données d'entrée, il effectue une combinaison linéaire des poids avec les caractéristiques correspondantes.
3. Il ajoute le biais à la valeur obtenue.

Le résultat est la prédiction de la variable cible dans la tâche de régression.

Les paramètres de LinearRegressor() sont présentés à la figure 7.

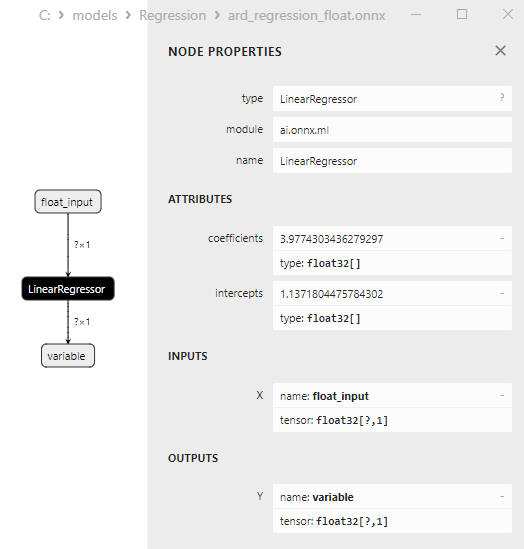
Fig. 7. Les propriétés de l'opérateur LinearRegressor() du modèle ard_regression_float.onnx dans Netron

Le modèle ONNX ard_regression_double.onnx est présenté à la Fig. 8 :

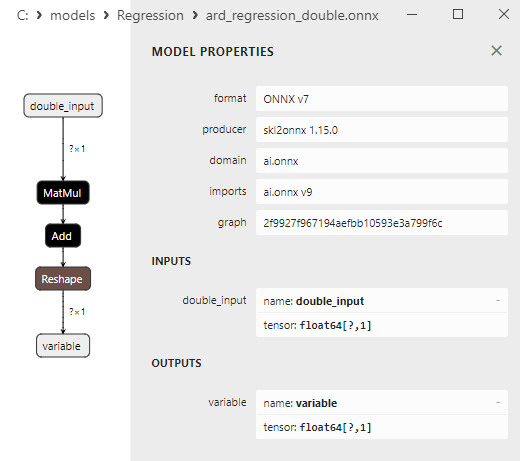
Fig. 8. Représentation ONNX du modèle ard_regression_double.onnx dans Netron

Les paramètres des opérateurs ONNX MatMul(), Add() et Reshape() sont présentés à la figure 9-11.

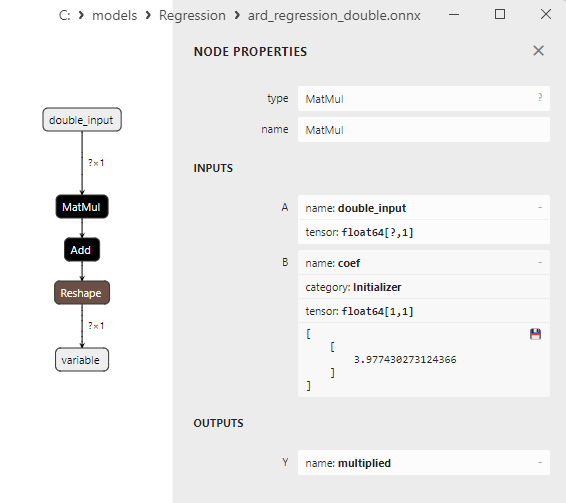
Fig. 9. Propriétés de l'opérateur MatMul dans le modèle ard_regression_double.onnx de Netron

L’opérateur ONNX MatMul (multiplication matricielle) effectue la multiplication de deux matrices.

Il prend deux entrées : deux matrices et renvoie leur produit matriciel.

Si vous avez deux matrices, A et B, le résultat de Matmul(A, B) est une matrice C, où chaque élément C[i][j] est calculé comme la somme des produits des éléments de la ligne i de la matrice A par les éléments de la colonne j de la matrice B.

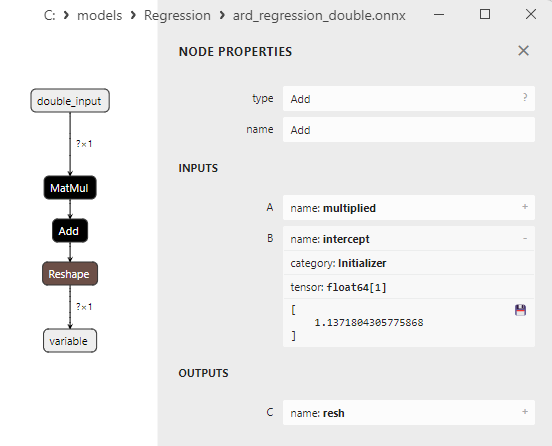
Fig. 10. Propriétés de l'opérateur Add dans le modèle ard_regression_double.onnx de Netron

L’opérateur ONNX Add() effectue l'addition par élément de deux tenseurs ou tableaux de même forme.

Il prend deux entrées et renvoie le résultat, où chaque élément du tenseur résultant est égal à la somme des éléments correspondants des tenseurs d'entrée.

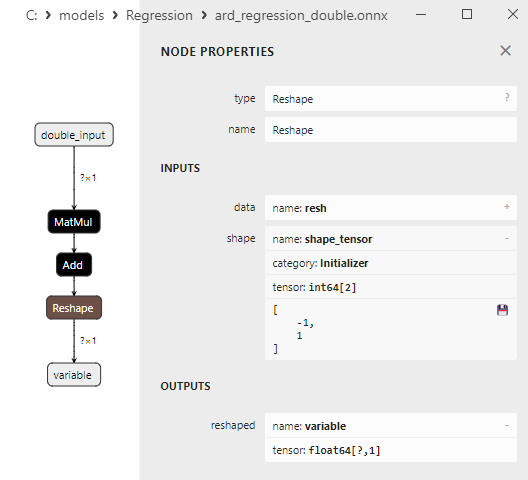
Fig. 11. Propriétés de l'opérateur Reshape dans le modèle ard_regression_double.onnx de Netron

L’opérateur ONNX Reshape(-1,1) est utilisé pour modifier la forme (ou la dimension) des données d'entrée. Dans cet opérateur, la valeur -1 pour la dimension indique que la taille de cette dimension doit être automatiquement calculée sur la base des autres dimensions afin de garantir la cohérence des données.

La valeur 1 dans la deuxième dimension indique qu'après la transformation de la forme, chaque élément aura une seule sous-dimension.

2.1.2. sklearn.linear_model.BayesianRidge

BayesianRidge est une méthode de régression qui utilise une approche bayésienne pour estimer les paramètres du modèle. Cette méthode permet de modéliser la distribution préalable des paramètres et de la mettre à jour en fonction des données pour obtenir la distribution postérieure des paramètres.

BayesianRidge est une méthode de régression bayésienne conçue pour prédire la variable dépendante en fonction d'une ou plusieurs variables indépendantes.

Principe de fonctionnement de BayesianRidge :

1. Distribution préalable des paramètres : Elle commence par la définition de la distribution préalable des paramètres du modèle. Cette distribution représente les connaissances préalables ou les hypothèses sur les paramètres du modèle avant l'examen des données. Dans le cas de BayesianRidge, des distributions préalables de forme gaussienne sont utilisées.
2. Mise à jour de la distribution des paramètres : Une fois que la distribution préalable des paramètres est définie, elle est mise à jour en fonction des données. Pour ce faire, on utilise la théorie bayésienne, dans laquelle la distribution postérieure des paramètres est calculée à partir des données. Un aspect essentiel est l'estimation des hyper-paramètres, qui influencent la forme de la distribution postérieure.
3. Prédiction : Après avoir estimé la distribution postérieure des paramètres, des prédictions peuvent être faites pour de nouvelles observations. Il en résulte une distribution des prévisions plutôt qu'une valeur ponctuelle unique, ce qui permet de prendre en compte l'incertitude des prévisions.

Avantages de BayesianRidge :

• Prise en compte de l'incertitude : BayesianRidge tient compte de l'incertitude des paramètres du modèle et des prévisions. Au lieu de prédictions ponctuelles, des intervalles de confiance sont fournis.
• Régularisation : La méthode de régression bayésienne peut être utile pour la régularisation du modèle, en aidant à prévenir l'ajustement excessif.
• Sélection automatique des caractéristiques : BayesianRidge peut déterminer automatiquement l'importance des caractéristiques en réduisant les poids des caractéristiques non significatives.

Limites de BayesianRidge :

• Complexité de calcul : La méthode nécessite des ressources de calcul pour estimer les paramètres et calculer la distribution postérieure.
• Niveau d'abstraction élevé : Une connaissance plus approfondie des statistiques bayésiennes peut être nécessaire pour comprendre et utiliser BayesianRidge.
• Ce n'est pas toujours le meilleur choix : La méthode BayesianRidge peut ne pas être la plus appropriée pour certaines tâches de régression, en particulier lorsqu'il s'agit de données limitées.

BayesianRidge est utile dans les tâches de régression où l'incertitude des paramètres et des prédictions est importante et dans les cas où la régularisation du modèle est nécessaire.

2.1.2.1. Code pour créer le modèle BayesianRidge et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.BayesianRidge, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# BayesianRidge.py
# Le code démontre le processus d'entraînement du modèle BayesianRidge, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"

# crée un modèle de régression bayésienne de type Ridge
regression_model = BayesianRidge()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')


# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  BayesianRidge Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891288
Python  
Python  BayesianRidge ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382627587808
Python  Mean Absolute Error: 6.347568283744705
Python  Mean Squared Error: 49.778160054267204
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  BayesianRidge ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891288
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

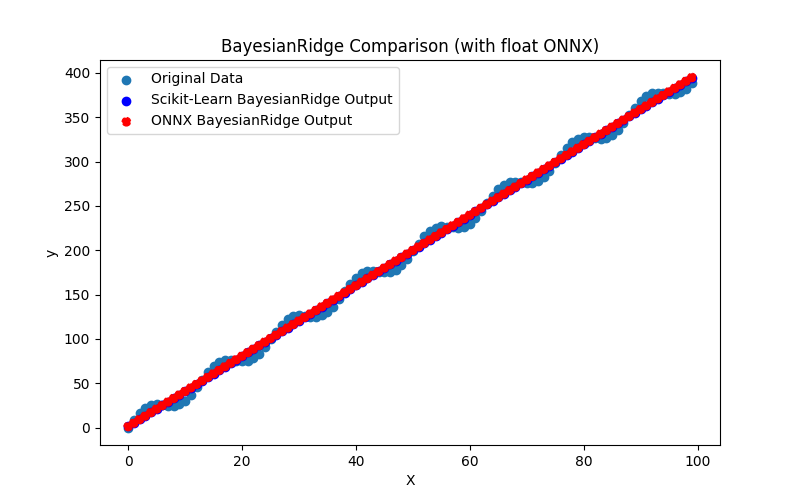
Fig. 12. Résultats de BayesianRidge.py (ONNX float)

2.1.2.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles ONNX bayesian_ridge_float.onnx et bayesian_ridge_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                BayesianRidge.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "BayesianRidge"
#define   ONNXFilenameFloat  "bayesian_ridge_float.onnx"
#define   ONNXFilenameDouble "bayesian_ridge_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

BayesianRidge (EURUSD,H1)       Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx)
BayesianRidge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382627587808
BayesianRidge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475682837447049
BayesianRidge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781600542671896
BayesianRidge (EURUSD,H1)       
BayesianRidge (EURUSD,H1)       Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx)
BayesianRidge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382628120845
BayesianRidge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475680128537624
BayesianRidge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781593489128866

Comparaison avec le modèle double original en Python :

Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475682837447049

Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475680128537624

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 13 décimales.

2.1.2.3. Représentation ONNX de bayesian_ridge_float.onnx et bayesian_ridge_double.onnx

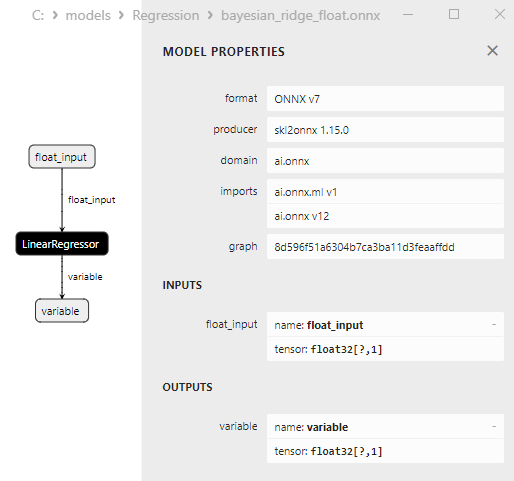
Fig. 13. Représentation ONNX du bayesian_ridge_float.onnx dans Netron

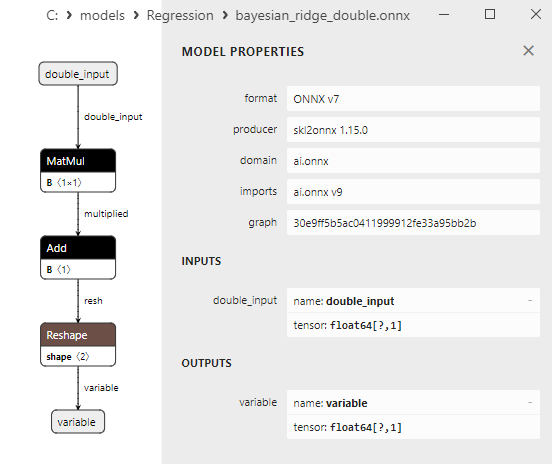
Fig. 14. Représentation ONNX de bayesian_ridge_double.onnx dans Netron

Note sur les méthodes ElasticNet et ElasticNetCV

ElasticNet et ElasticNetCV sont deux méthodes d'apprentissage automatique apparentées utilisées pour régulariser les modèles de régression, en particulier la régression linéaire. Ils partagent des fonctionnalités communes mais diffèrent dans leur mode d'utilisation et dans leur mode d'application.

    ElasticNet (Elastic Net Regression) :

• Principe de Fonctionnement : ElasticNet est une méthode de régression qui combine Lasso (régularisation L1) et Ridge (régularisation L2). Il ajoute deux composantes de régularisation à la fonction de perte : l'une pénalise le modèle pour les grandes valeurs absolues des coefficients (comme Lasso), et l'autre pénalise le modèle pour les grands carrés des coefficients (comme Ridge).
• ElasticNet est couramment utilisé en cas de multicolinéarité dans les données (lorsque les caractéristiques sont fortement corrélées) et lorsqu'une réduction de la dimensionnalité est nécessaire, ainsi que pour contrôler les valeurs des coefficients.

    ElasticNetCV (Elastic Net Cross-Validation) :

• Principe de Fonctionnement : ElasticNetCV est une extension d'ElasticNet qui consiste à sélectionner automatiquement les hyper-paramètres optimaux alpha (le coefficient de mélange entre les régularisations L1 et L2) et lambda (la force de régularisation) en utilisant la validation croisée. Il passe par différentes valeurs alpha et lambda, en choisissant la combinaison la plus performante lors de la validation croisée.
• Avantages : ElasticNetCV ajuste automatiquement les paramètres du modèle sur la base de la validation croisée, ce qui permet de sélectionner les valeurs optimales des hyper-paramètres sans qu'il soit nécessaire de procéder à un réglage manuel. Cela le rend plus pratique à utiliser et permet d'éviter l'ajustement excessif du modèle.

Ainsi, la principale différence entre ElasticNet et ElasticNetCV est qu'ElasticNet est la méthode de régression appliquée aux données, alors qu'ElasticNetCV est un outil qui trouve automatiquement les valeurs optimales des hyper-paramètres pour le modèle ElasticNet à l'aide de la validation croisée. ElasticNetCV est utile lorsque vous avez besoin de trouver les meilleurs paramètres du modèle et de rendre le processus de réglage plus automatisé.

2.1.3. sklearn.linear_model.ElasticNet

ElasticNet est une méthode de régression qui représente une combinaison des régularisations L1 (Lasso) et L2 (Ridge).

Cette méthode est utilisée pour la régression, qui consiste à prédire les valeurs numériques d'une variable cible sur la base d'un ensemble de caractéristiques. ElasticNet aide à contrôler le sur-ajustement et prend en compte les pénalités L1 et L2 sur les coefficients du modèle.

Principe de fonctionnement d'ElasticNet :

1. Données d'Entrée : Il commence par l'ensemble de données original où se trouvent les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Fonction Objective : ElasticNet minimise la fonction de perte qui comprend deux composantes : l'erreur quadratique moyenne (MSE) et deux régularisations : L1 (Lasso) et L2 (Ridge). Cela signifie que la fonction objective se présente comme suit :
   Fonction Objective = MSE + α * L1 + β * L2
   Où α et β sont des hyper-paramètres qui contrôlent les poids des régularisations L1 et L2, respectivement.
3. Recherche des Valeurs α et β Optimales : La méthode de validation croisée est généralement utilisée pour trouver les meilleures valeurs de α et β. Cela permet de sélectionner des valeurs qui établissent un équilibre entre la réduction de l'ajustement excessif et la préservation des caractéristiques essentielles.
4. Modèle d’Entraînement : ElasticNet entraîne le modèle en considérant les α et β optimaux en minimisant la fonction objective.
5. Prédiction : Une fois le modèle formé, ElasticNet peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages d'ElasticNet :

• Capacité de Sélection des Caractéristiques : ElasticNet peut sélectionner automatiquement les caractéristiques les plus importantes en fixant les poids à zéro pour les caractéristiques non significatives (comme Lasso).
• Contrôle du Sur-Ajustement : ElasticNet permet de contrôler le sur-ajustement grâce à la régularisation L1 et L2.
• Traitement de la Multicolinéarité : Cette méthode est utile en cas de multicolinéarité (forte corrélation entre les caractéristiques), car la régularisation L2 peut réduire l'influence des caractéristiques multicolinéaires.

Limites d'ElasticNet :

• Nécessite l'ajustement des hyper-paramètres α et β, ce qui peut être une tâche non triviale.
• En fonction du choix des paramètres, ElasticNet peut retenir trop ou trop peu de caractéristiques, ce qui affecte la qualité du modèle.

ElasticNet est une méthode de régression puissante qui peut s'avérer utile dans les tâches où la sélection des caractéristiques et le contrôle de l'ajustement excessif sont cruciaux.

2.1.3.1. Code pour créer le modèle ElasticNet et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.ElasticNet, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# ElasticNet.py
# Le code démontre le processus d'entraînement d'un modèle ElasticNet, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"

# crée un modèle ElasticNet
regression_model = ElasticNet()

# ajuste le modèle aux données
regression_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-carré (Coefficient de Détermination):", r2)
print("Erreur Absolue Moyenne :", mae)
print("Erreur Quadratique Moyenne :", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  ElasticNet Original model (double)
Python  R-squared (Coefficient of determination): 0.9962377031744798
Python  Mean Absolute Error: 6.344394662876524
Python  Mean Squared Error: 49.78556489812415
Python  
Python  ElasticNet ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962377032416807
Python  Mean Absolute Error: 6.344395027824294
Python  Mean Squared Error: 49.78556400887057
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  6
Python  float ONNX model precision:  5
Python  
Python  ElasticNet ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962377031744798
Python  Mean Absolute Error: 6.344394662876524
Python  Mean Squared Error: 49.78556489812415
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

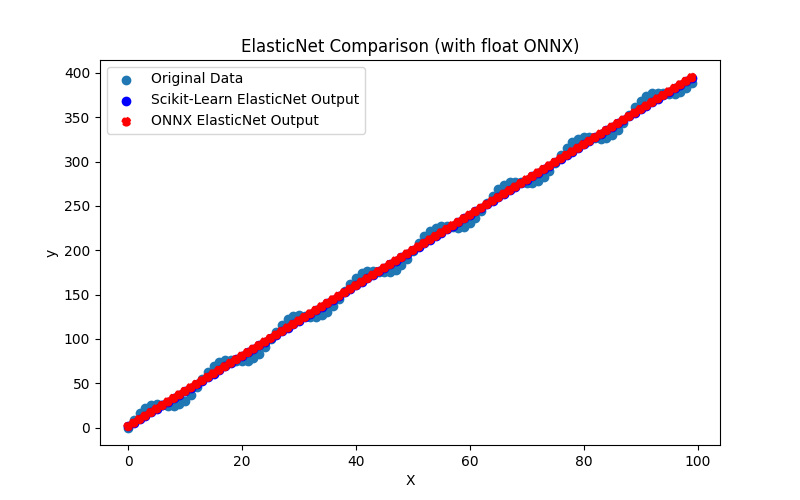
Fig. 15. Résultats de ElasticNet.py (ONNX float)

2.1.3.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles elastic_net_double.onnx et elastic_net_float.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                   ElasticNet.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ElasticNet"
#define   ONNXFilenameFloat  "elastic_net_float.onnx"
#define   ONNXFilenameDouble "elastic_net_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

ElasticNet (EURUSD,H1)  Testing ONNX float: ElasticNet (elastic_net_float.onnx)
ElasticNet (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9962377032416807
ElasticNet (EURUSD,H1)  MQL5:   Mean Absolute Error: 6.3443950278242944
ElasticNet (EURUSD,H1)  MQL5:   Mean Squared Error: 49.7855640088705869
ElasticNet (EURUSD,H1)  
ElasticNet (EURUSD,H1)  Testing ONNX double: ElasticNet (elastic_net_double.onnx)
ElasticNet (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9962377031744798
ElasticNet (EURUSD,H1)  MQL5:   Mean Absolute Error: 6.3443946628765220
ElasticNet (EURUSD,H1)  MQL5:   Mean Squared Error: 49.7855648981241217

Comparaison avec le modèle double original en Python :

Testing ONNX float: ElasticNet (elastic_net_float.onnx)
Python  Mean Absolute Error: 6.344394662876524
MQL5:   Mean Absolute Error: 6.3443950278242944
  
Testing ONNX double: ElasticNet (elastic_net_double.onnx)
Python  Mean Absolute Error: 6.344394662876524
MQL5:   Mean Absolute Error: 6.3443946628765220

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 14 décimales.

2.1.3.3. Représentation ONNX de elastic_net_float.onnx et elastic_net_double.onnx

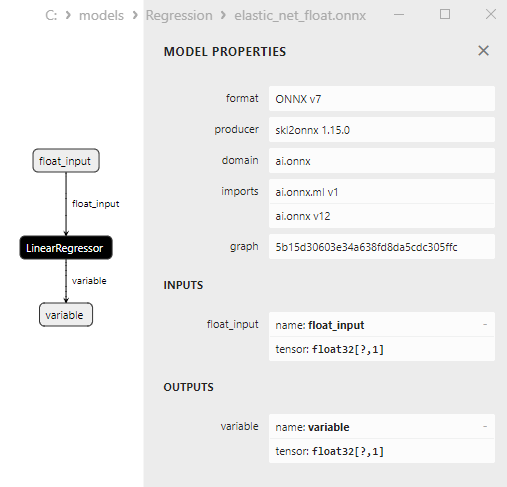
Fig. 16. Représentation ONNX de elastic_net_float.onnx dans Netron

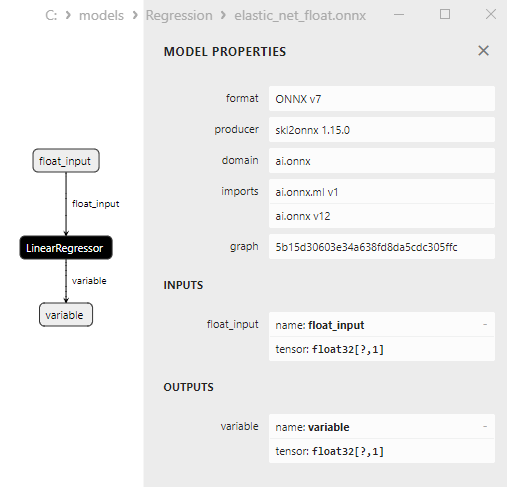
Fig. 17. Représentation ONNX de elastic_net_double.onnx dans Netron

2.1.4. sklearn.linear_model.ElasticNetCV

ElasticNetCV est une extension de la méthode ElasticNet conçue pour sélectionner automatiquement les valeurs optimales des hyper-paramètres α et β (régularisation L1 et L2) en utilisant la validation croisée.

Cela permet de trouver la meilleure combinaison de régularisations pour le modèle ElasticNet sans qu'il soit nécessaire de régler manuellement les paramètres.

Principe de fonctionnement d'ElasticNetCV :

1. Données d'Entrée : Il commence par l'ensemble de données original contenant des caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Définition de l’Intervalle α et β : L'utilisateur spécifie la plage de valeurs pour α et β à prendre en compte lors de l'optimisation. Ces valeurs sont généralement choisies sur une échelle logarithmique.
3. Fractionnement des Données : L'ensemble de données est divisé en plusieurs plis pour la validation croisée. Chaque pli est utilisé comme un ensemble de données de test, et les autres sont utilisés pour l’entraînement.
4. Validation Croisée : Pour chaque combinaison de α et β dans l’intervalle spécifié, une validation croisée est effectuée. Le modèle ElasticNet est entraîné sur les données d'entraînement, puis évalué sur les données de test.
5. Évaluation des Performances : L'erreur moyenne sur les ensembles de données de test dans la validation croisée est calculée pour chaque combinaison α et β.
6. Sélection des Paramètres Optimaux : Les valeurs de α et β correspondant à l'erreur moyenne minimale obtenue lors de la validation croisée sont déterminées.
7. Entraînement de Modèles avec des Paramètres Optimaux : Le modèle ElasticNetCV est formé en utilisant les valeurs optimales trouvées de α et β.
8. Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages d'ElasticNetCV :

• Sélection automatique des hyper-paramètres : ElasticNetCV trouve automatiquement les valeurs optimales de α et β, ce qui simplifie la mise au point du modèle.
• Prévention du Sur-Ajustement : La validation croisée permet de sélectionner un modèle ayant une bonne capacité de généralisation.
• Résistance au Bruit : Cette méthode est robuste face au bruit des données et permet d'identifier la meilleure combinaison de régularisations tout en tenant compte du bruit.

Limites d'ElasticNetCV :

• Complexité de Calcul : La validation croisée sur une large gamme de paramètres peut prendre beaucoup de temps.
• Les Paramètres Optimaux Dépendent du Choix de l’Intervalle : Les résultats peuvent dépendre du choix de la plage α et β. Il est donc important d'ajuster soigneusement cet intervalle.

ElasticNetCV est un outil puissant permettant de régler automatiquement la régularisation dans le modèle ElasticNet et d'améliorer ses performances.

2.1.4.1. Code pour créer le modèle ElasticNetCV et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.ElasticNetCV, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# ElasticNetCV.py
# Le code démontre le processus d'entraînement du modèle ElasticNetCV, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNetCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ElasticNetCV"
onnx_model_filename = data_path + "elastic_net_cv"

# crée un modèle ElasticNetCV
regression_model = ElasticNetCV()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  ElasticNetCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962137763338385
Python  Mean Absolute Error: 6.334487104423225
Python  Mean Squared Error: 50.10218299945999
Python  
Python  ElasticNetCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962137770260989
Python  Mean Absolute Error: 6.334486542922601
Python  Mean Squared Error: 50.10217383894468
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  ElasticNetCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962137763338385
Python  Mean Absolute Error: 6.334487104423225
Python  Mean Squared Error: 50.10218299945999
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

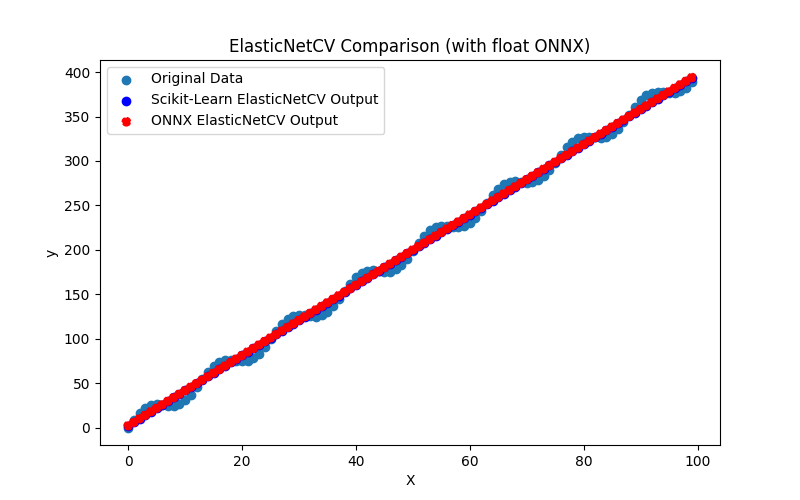
Fig. 18. Résultats de ElasticNetCV.py (ONNX float)

2.1.4.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles ONNX elastic_net_cv_float.onnx et elastic_net_cv_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                 ElasticNetCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ElasticNetCV"
#define   ONNXFilenameFloat  "elastic_net_cv_float.onnx"
#define   ONNXFilenameDouble "elastic_net_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

ElasticNetCV (EURUSD,H1)        Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx)
ElasticNetCV (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962137770260989
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3344865429226038
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Squared Error: 50.1021738389446938
ElasticNetCV (EURUSD,H1)        
ElasticNetCV (EURUSD,H1)        Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx)
ElasticNetCV (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962137763338385
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3344871044232205
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Squared Error: 50.1021829994599983

Comparaison avec le modèle double original en Python :

Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx)
Python  Mean Absolute Error: 6.334487104423225
MQL5:   Mean Absolute Error: 6.3344865429226038

Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx)
Python  Mean Absolute Error: 6.334487104423225
MQL5:   Mean Absolute Error: 6.3344871044232205

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 14 décimales.

2.1.4.3. Représentation ONNX de elastic_net_cv_float.onnx et elastic_net_cv_double.onnx

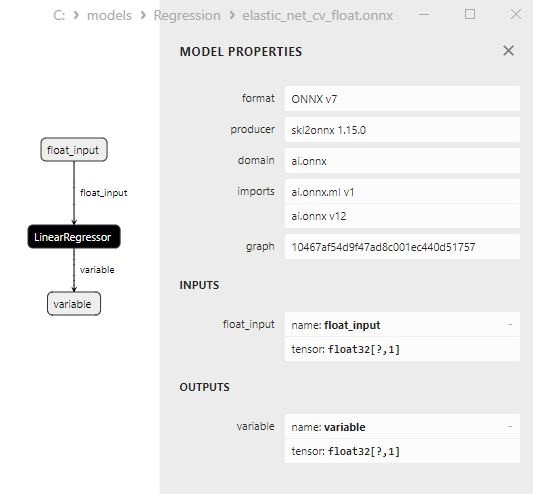
Fig. 19. Représentation ONNX de elastic_net_cv_float.onnx dans Netron

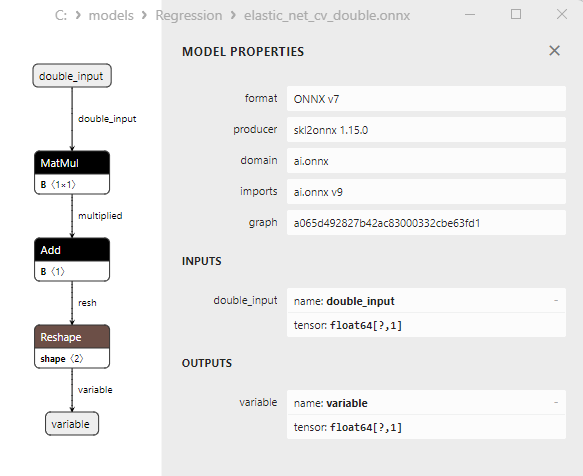
Fig. 20. Représentation ONNX de elastic_net_cv_double.onnx dans Netron

2.1.5. sklearn.linear_model.HuberRegressor

HuberRegressor - est une méthode d'apprentissage automatique utilisée pour les tâches de régression, qui est une modification de la méthode des Moindres Carrés Ordinaires (MCO) et qui est conçue pour résister aux valeurs aberrantes dans les données.

Contrairement à OLS, qui minimise le carré des erreurs, HuberRegressor minimise une combinaison d'erreurs au carré et d'erreurs absolues. Cela permet à la méthode de fonctionner de manière plus robuste en présence de valeurs aberrantes dans les données.

Principe de Fonctionnement de HuberRegressor :

1. Données d'Entrée : Il commence par l'ensemble de données original, qui contient des caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Fonction de Perte de Huber : HuberRegressor utilise la fonction de perte de Huber, qui combine une fonction de perte quadratique pour les petites erreurs et une fonction de perte linéaire pour les grandes erreurs. La méthode est ainsi plus résistante aux valeurs aberrantes.
3. Entraînement du Modèle : Le modèle est entraîné sur des données à l'aide de la fonction de perte de Huber. Pendant l'entraînement, il ajuste les poids (coefficients) de chaque caractéristique et le biais.
4. Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de HuberRegressor :

• Robustesse face aux valeurs aberrantes : HuberRegressor est plus résistant aux valeurs aberrantes des données que OLS, ce qui le rend utile dans les tâches où les données peuvent contenir des valeurs anormales.
• Estimation de l'Erreur : La fonction de perte de Huber contribue à l'estimation des erreurs de prédiction, ce qui peut être utile pour analyser les résultats du modèle.
• Niveau de Régularisation : HuberRegressor peut également intégrer un niveau de régularisation, qui peut réduire l'ajustement excessif.

Limites de HuberRegressor :

• Pas aussi précis que OLS en l'absence de valeurs aberrantes : Dans les cas où il n'y a pas de valeurs aberrantes dans les données, OLS peut fournir des résultats plus précis.
• Réglage des Paramètres : HuberRegressor a un paramètre qui définit le seuil de ce qui est considéré comme "grand" pour passer à la fonction de perte linéaire. Ce paramètre doit être ajusté.

HuberRegressor est très utile dans les tâches de régression où les données peuvent contenir des valeurs aberrantes et où un modèle robuste à ces anomalies est nécessaire.

2.1.5.1. Code pour créer le modèle HuberRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèlesklearn.linear_model.HuberRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# HuberRegressor.py
# Le code démontre le processus d'entraînement du modèle HuberRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"

# crée un modèle de Régresseur de Huber
huber_regressor_model = HuberRegressor()

# ajuste le modèle aux données
huber_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = huber_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-carré (Coefficient de Détermination) :", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE correspondant aux décimales : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  HuberRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9962363935647066
Python  Mean Absolute Error: 6.341633708569641
Python  Mean Squared Error: 49.80289464784336
Python  
Python  HuberRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962363944236795
Python  Mean Absolute Error: 6.341633300252807
Python  Mean Squared Error: 49.80288328126165
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  HuberRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962363935647066
Python  Mean Absolute Error: 6.341633708569641
Python  Mean Squared Error: 49.80289464784336
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

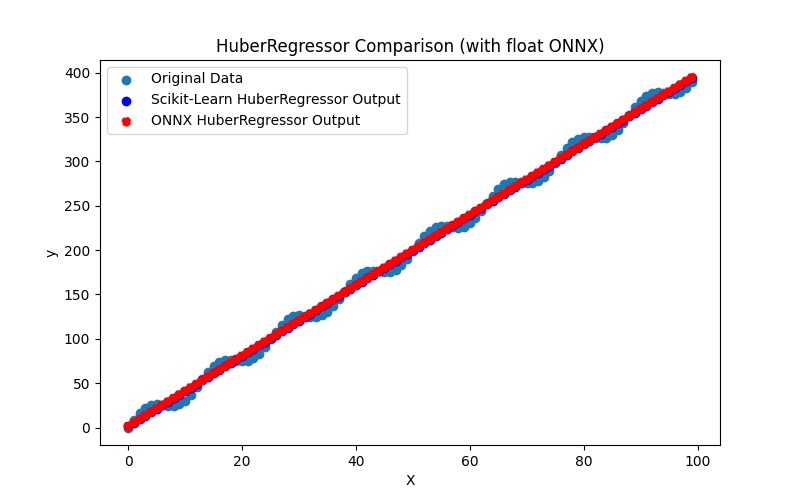
Fig. 21. Résultats de HuberRegressor.py (ONNX float)

2.1.5.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles ONNX huber_regressor_float.onnx et huber_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                               HuberRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "HuberRegressor"
#define   ONNXFilenameFloat  "huber_regressor_float.onnx"
#define   ONNXFilenameDouble "huber_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

HuberRegressor (EURUSD,H1)      Testing ONNX float: HuberRegressor (huber_regressor_float.onnx)
HuberRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962363944236795
HuberRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3416333002528074
HuberRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 49.8028832812616571
HuberRegressor (EURUSD,H1)      
HuberRegressor (EURUSD,H1)      Testing ONNX double: HuberRegressor (huber_regressor_double.onnx)
HuberRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962363935647066
HuberRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3416337085696410
HuberRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 49.8028946478433525

Comparaison avec le modèle double original en Python :

Testing ONNX float: HuberRegressor (huber_regressor_float.onnx)
Python  Mean Absolute Error: 6.341633708569641
MQL5:   Mean Absolute Error: 6.3416333002528074
      
Testing ONNX double: HuberRegressor (huber_regressor_double.onnx)
Python  Mean Absolute Error: 6.341633708569641
MQL5:   Mean Absolute Error: 6.3416337085696410

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.5.3. Représentation ONNX de huber_regressor_float.onnx et huber_regressor_double.onnx

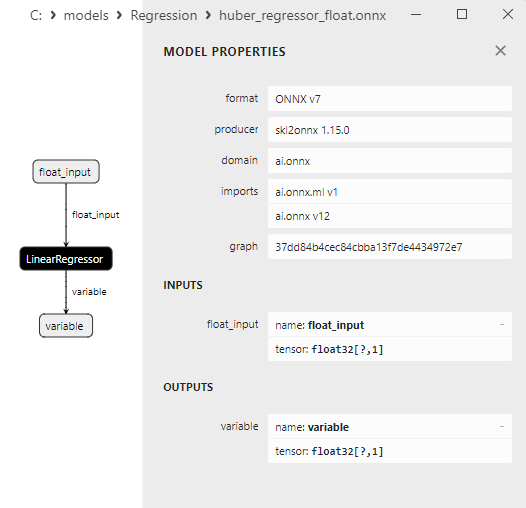
Fig. 22. Représentation ONNX de huber_regressor_float.onnx dans Netron

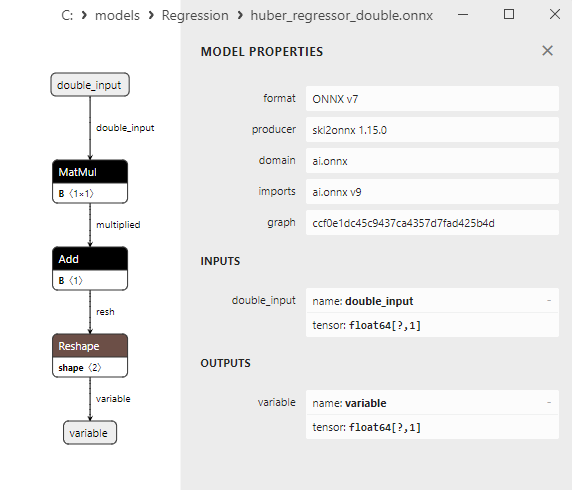
Fig. 23. Représentation ONNX de huber_regressor_double.onnx dans Netron

2.1.6. sklearn.linear_model.Lars

LARS (Least Angle Regression) est une méthode d'apprentissage automatique utilisée pour les tâches de régression. Il s'agit d'un algorithme qui construit un modèle de régression linéaire en sélectionnant des caractéristiques actives (variables) au cours du processus d'apprentissage.

LARS tente de trouver le moins de caractéristiques possibles qui fournissent la meilleure approximation de la variable cible.

Principe de Fonctionnement de LARS :

1. Données d'Entrée : Il commence par l'ensemble de données original, qui comprend des caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Initialisation : Il commence par un modèle nul, ce qui signifie qu'il n'y a pas de caractéristiques actives. Tous les coefficients sont fixés à zéro.
3. Sélection des Caractéristiques : A chaque étape, LARS sélectionne la caractéristique la plus corrélée avec les résidus du modèle. Cette caractéristique est ensuite ajoutée au modèle et son coefficient correspondant est ajusté par la méthode des moindres carrés.
4. Régression le long des caractéristiques actives : Après avoir ajouté la caractéristique au modèle, LARS met à jour les coefficients de toutes les caractéristiques actives pour tenir compte des changements dans le nouveau modèle.
5. Étapes Répétitives : Ce processus se poursuit jusqu'à ce que toutes les caractéristiques soient sélectionnées ou qu'un critère d'arrêt spécifié soit rempli.
6. Prédiction : Après l'apprentissage du modèle, il peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de LARS :

• Efficacité : LARS peut être une méthode efficace, en particulier lorsqu'il existe de nombreuses caractéristiques, mais que seules quelques-unes d'entre elles ont une incidence significative sur la variable cible.
• Interprétabilité : Étant donné que LARS vise à sélectionner uniquement les caractéristiques les plus informatives, le modèle reste relativement interprétable.

Limites de LARS :

• Modèle Linéaire : LARS construit un modèle linéaire, qui peut s'avérer insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Incapacité à gérer la multicolinéarité : Si les caractéristiques sont fortement corrélées, LARS peut rencontrer des problèmes de multicolinéarité.

LARS est utile dans les tâches de régression où la sélection des caractéristiques les plus informatives et la construction d'un modèle linéaire avec un nombre minimal de caractéristiques sont essentielles.

2.1.6.1. Code pour créer le modèle Lars et l'exporter vers ONNX pour les float et pour les double

Ce code crée le modèle sklearn.linear_model.Lars, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# Lars.py
# Le code démontre le processus d'entraînement du modèle Lars, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "Lars"
onnx_model_filename = data_path + "lars"

# crée un modèle Lars Regressor
lars_regressor_model = Lars()

# ajuste le modèle aux données
lars_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = lars_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-carré (Coefficient de Détermination) :", r2)
print("Erreur Absolue Moyenne :", mae)
print("Erreur Quadratique Moyenne :", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_double))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  Lars Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  
Python  Lars ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  Lars ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  15

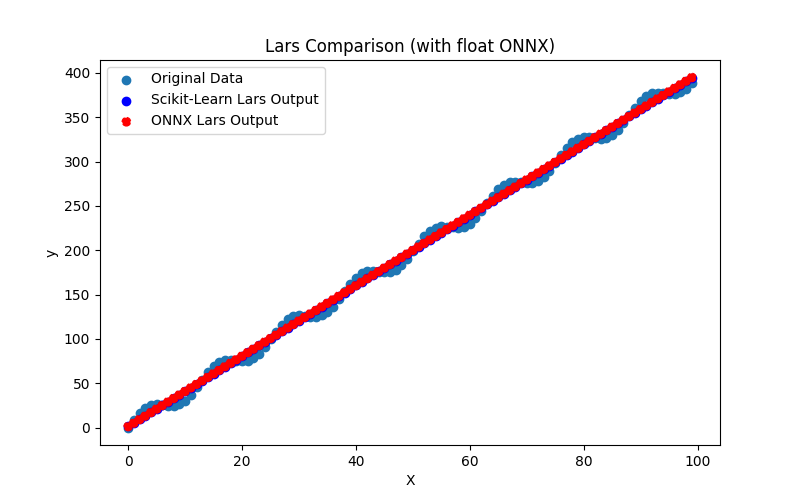
Fig. 24. Résultats de Lars.py (float ONNX)

2.1.6.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés lars_cv_float.onnx et lars_cv_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                         Lars.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "Lars"
#define   ONNXFilenameFloat  "lars_float.onnx"
#define   ONNXFilenameDouble "lars_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

Lars (EURUSD,H1)        Testing ONNX float: Lars (lars_float.onnx)
Lars (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
Lars (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3477377671679385
Lars (EURUSD,H1)        MQL5:   Mean Squared Error: 49.7781414740478638
Lars (EURUSD,H1)        
Lars (EURUSD,H1)        Testing ONNX double: Lars (lars_double.onnx)
Lars (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
Lars (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3477379263364302
Lars (EURUSD,H1)        MQL5:   Mean Squared Error: 49.7781401712817768

Comparaison avec le modèle double original en Python :

Testing ONNX float: Lars (lars_float.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477377671679385

Testing ONNX double: Lars (lars_double.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477379263364302

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 13 décimales.

2.1.6.3. Représentation ONNX de lars_float.onnx et lars_double.onnx

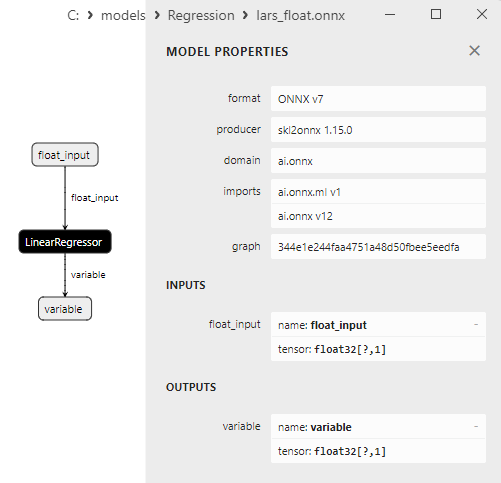
Fig. 25. Représentation ONNX de lars_float.onnx dans Netron

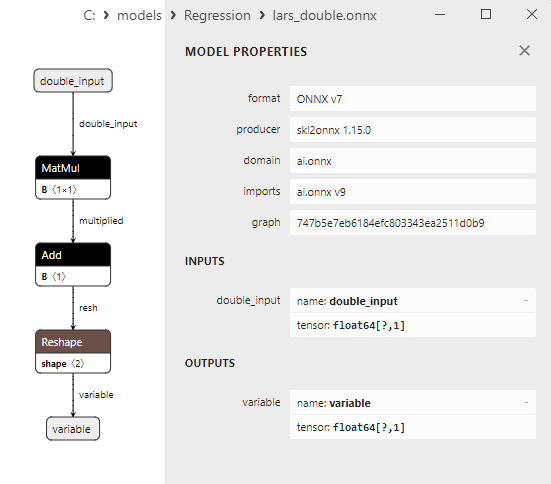
Fig. 26. Représentation ONNX de lars_double.onnx dans Netron

2.1.7. sklearn.linear_model.LarsCV

LarsCV est une variante de la méthode LARS (Least Angle Regression) qui sélectionne automatiquement le nombre optimal de caractéristiques à inclure dans le modèle à l'aide de la validation croisée.

Cette méthode permet de trouver un équilibre entre un modèle qui généralise efficacement les données et un modèle qui utilise un nombre minimal de caractéristiques.

Principe de Fonctionnement de LarsCV :

1. Données d'Entrée : Il commence par l'ensemble de données original, qui comprend des caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Initialisation : Il commence par un modèle nul, ce qui signifie qu'il n'y a pas de caractéristiques actives. Tous les coefficients sont fixés à zéro.
3. Validation Croisée : LarsCV effectue une validation croisée pour différentes quantités de caractéristiques incluses. Cela permet d'évaluer les performances du modèle avec différents ensembles de caractéristiques.
4. Sélection du nombre optimal de caractéristiques : LarsCV choisit le nombre de caractéristiques qui donne la meilleure performance du modèle, déterminée par validation croisée.
5. Entraînement du Modèle : Le modèle est formé en utilisant le nombre choisi de caractéristiques et leurs coefficients respectifs.
6. Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de LarsCV :

• Sélection Automatique des Caractéristiques : LarsCV choisit automatiquement le nombre optimal de caractéristiques, ce qui simplifie le processus de configuration du modèle.
• Interprétabilité : Tout comme LARS, LarsCV maintient une interprétabilité relativement élevée du modèle.
• Efficacité : La méthode peut être efficace, en particulier lorsque les ensembles de données comportent de nombreuses caractéristiques, mais que seules quelques-unes sont significatives.

Limites de LarsCV :

• Modèle Linéaire : LarsCV construit un modèle linéaire, qui peut s'avérer insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Incapacité à gérer la multicolinéarité : Si les caractéristiques sont fortement corrélées, LarsCV peut rencontrer des problèmes de multicolinéarité.

LarsCV est utile dans les tâches de régression où le choix automatique du meilleur ensemble de caractéristiques utilisées dans le modèle et le maintien de l'interprétabilité du modèle sont importants.

2.1.7.1. Code pour créer le modèle LarsCV et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LarsCV, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LarsCV.py
# Le code démontre le processus d'entraînement du modèle LarsCV, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"

# crée un modèle de Régresseur LarsCV
larscv_regressor_model = LarsCV()

# ajuste le modèle aux données
larscv_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = larscv_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Informations sur les tenseurs d'entrée dans ONNX :")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LarsCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  
Python  LarsCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382640824089
Python  Mean Absolute Error: 6.347737845846069
Python  Mean Squared Error: 49.778142539016564
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LarsCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  16

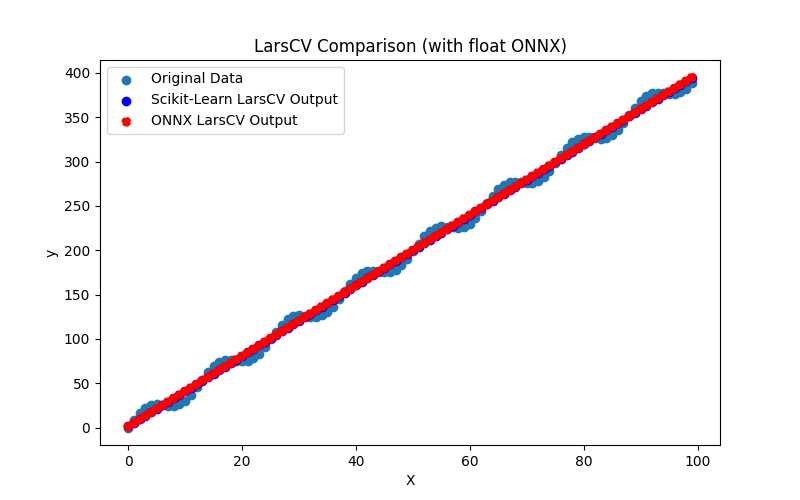
Fig. 27. Résultats de LarsCV.py (float ONNX)

2.1.7.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés lars_cv_float.onnx et lars_cv_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                       LarsCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LarsCV"
#define   ONNXFilenameFloat  "lars_cv_float.onnx"
#define   ONNXFilenameDouble "lars_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

LarsCV (EURUSD,H1)      Testing ONNX float: LarsCV (lars_cv_float.onnx)
LarsCV (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962382640824089
LarsCV (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3477378458460691
LarsCV (EURUSD,H1)      MQL5:   Mean Squared Error: 49.7781425390165566
LarsCV (EURUSD,H1)      
LarsCV (EURUSD,H1)      Testing ONNX double: LarsCV (lars_cv_double.onnx)
LarsCV (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962382642612767
LarsCV (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3477379221400145
LarsCV (EURUSD,H1)      MQL5:   Mean Squared Error: 49.7781401721031642

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: LarsCV (lars_cv_float.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477378458460691

Testing ONNX double: LarsCV (lars_cv_double.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477379221400145

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 16 décimales.

2.1.7.3. Représentation ONNX de lars_cv_float.onnx et lars_cv_double.onnx

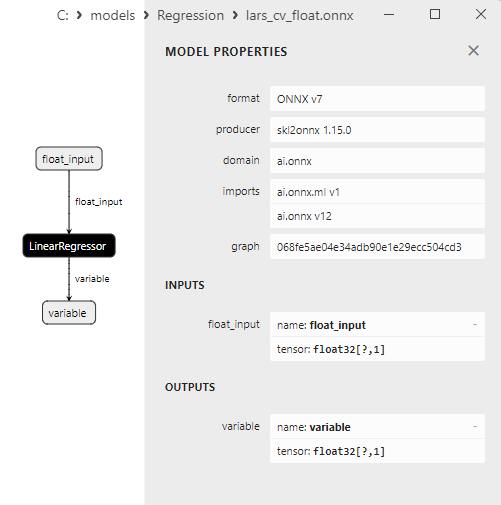
Fig. 28. Représentation ONNX de lars_cv_float.onnx dans Netron

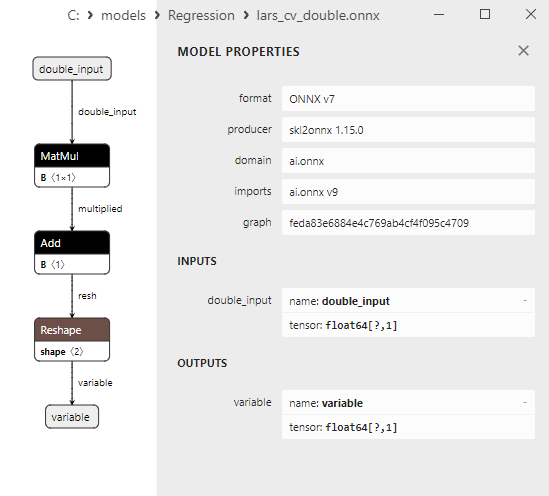
Fig. 29. Représentation ONNX de lars_cv_double.onnx dans Netron

2.1.8. sklearn.linear_model.Lasso

Lasso (Least Absolute Shrinkage and Selection Operator) est une méthode de régression utilisée pour sélectionner les caractéristiques les plus importantes et réduire la dimensionnalité du modèle.

Elle y parvient en ajoutant une pénalité pour la somme des valeurs absolues des coefficients (régularisation L1) dans le problème d'optimisation de la régression linéaire.

Principe de Fonctionnement du Lasso :

1. Données d'Entrée : Il commence par l'ensemble de données original, y compris les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Fonction Objective : La fonction objective du Lasso comprend la somme des carrés des erreurs de régression et une pénalité sur la somme des valeurs absolues des coefficients associés aux caractéristiques.
3. Optimisation : Le modèle Lasso est formé en minimisant la fonction objective, ce qui a pour effet de rendre certains coefficients nuls, excluant ainsi les caractéristiques correspondantes du modèle.
4. Sélection de la Valeur Optimale de la Pénalité : Lasso inclut un hyper-paramètre qui détermine l'intensité de la régularisation. Le choix de la valeur optimale de cet hyper-paramètre peut nécessiter une validation croisée.
5. Générer des Prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de Lasso :

• Sélection des Caractéristiques : Lasso sélectionne automatiquement les caractéristiques les plus importantes, en excluant les moins significatives du modèle. Cela permet de réduire la dimensionnalité des données et de simplifier le modèle.
• Régularisation : La pénalité sur la somme des valeurs absolues des coefficients permet d'éviter l'ajustement excessif du modèle et d'améliorer sa généralisation.
• Interprétabilité : Comme Lasso exclut certaines caractéristiques, le modèle reste relativement interprétable.

Limites de Lasso :

• Modèle Linéaire : Lasso construit un modèle linéaire, qui peut s'avérer insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Incapacité à gérer la multicolinéarité : Si les caractéristiques sont fortement corrélées, le Lasso peut rencontrer des problèmes de multicolinéarité.

Lasso est utile dans les tâches de régression où la sélection des caractéristiques les plus importantes et la réduction de la dimensionnalité du modèle tout en maintenant l'interprétabilité sont essentielles.

2.1.8.1. Code pour créer le modèle Lasso et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.Lasso, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# Lasso.py
# Le code démontre le processus d'entraînement du modèle Lasso, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "Lasso"
onnx_model_filename = data_path + "lasso"

# crée un modèle Lasso
lasso_model = Lasso()

# ajuste le modèle aux données
lasso_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = lasso_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Erreur Absolue Moyenne :", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  Lasso Original model (double)
Python  R-squared (Coefficient of determination): 0.9962381735682287
Python  Mean Absolute Error: 6.346393791922984
Python  Mean Squared Error: 49.77934029129379
Python  
Python  Lasso ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962381720269486
Python  Mean Absolute Error: 6.346395056911361
Python  Mean Squared Error: 49.77936068668213
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  Lasso ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962381735682287
Python  Mean Absolute Error: 6.346393791922984
Python  Mean Squared Error: 49.77934029129379
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

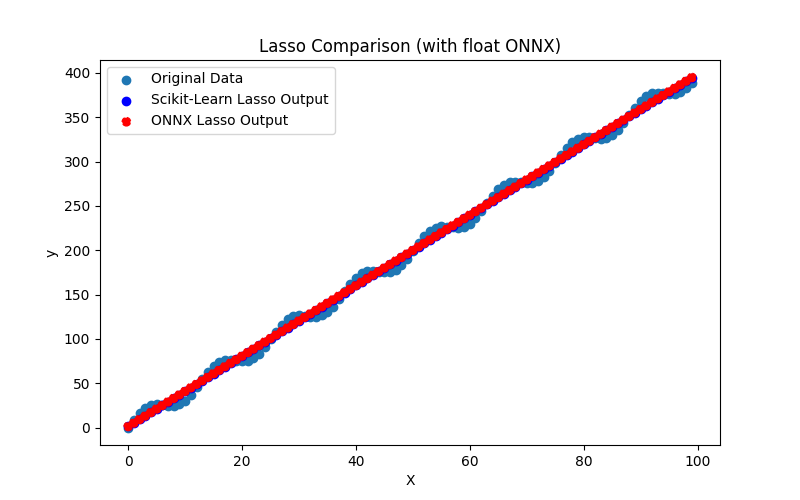
Fig. 30. Résultats de Lasso.py (ONNX float)

2.1.8.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés lasso_float.onnx et lasso_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                        Lasso.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "Lasso"
#define   ONNXFilenameFloat  "lasso_float.onnx"
#define   ONNXFilenameDouble "lasso_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

Lasso (EURUSD,H1)       Testing ONNX float: Lasso (lasso_float.onnx)
Lasso (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962381720269486
Lasso (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3463950569113612
Lasso (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7793606866821037
Lasso (EURUSD,H1)       
Lasso (EURUSD,H1)       Testing ONNX double: Lasso (lasso_double.onnx)
Lasso (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962381735682287
Lasso (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3463937919229840
Lasso (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7793402912937850

Comparaison avec le modèle double original en Python :

Testing ONNX float: Lasso (lasso_float.onnx)
Python  Mean Absolute Error: 6.346393791922984
MQL5:   Mean Absolute Error: 6.3463950569113612

Testing ONNX double: Lasso (lasso_double.onnx)
Python  Mean Absolute Error: 6.346393791922984
MQL5:   Mean Absolute Error: 6.3463937919229840

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 15 décimales.

2.1.8.3. Représentation ONNX de lasso_float.onnx et lasso_double.onnx

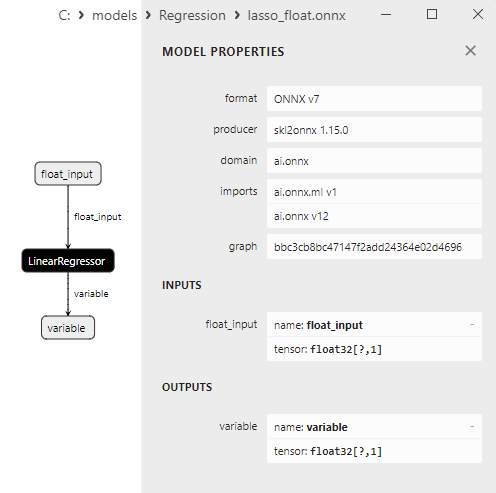
Fig. 31. Représentation ONNX de lasso_float.onnx dans Netron

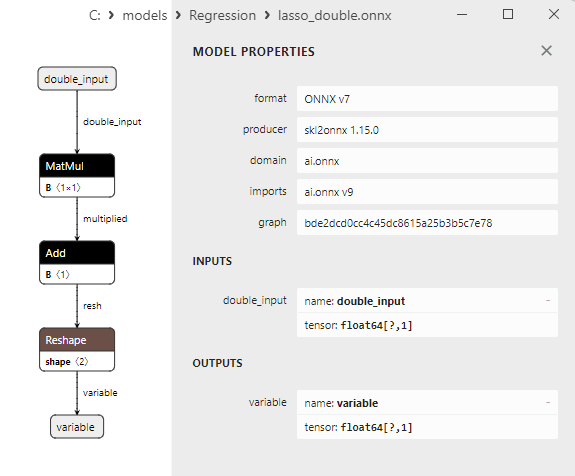
Fig. 32. Représentation ONNX de lasso_double.onnx dans Netron

2.1.9. sklearn.linear_model.LassoCV

LassoCV est une variante de la méthode Lasso (Least Absolute Shrinkage and Selection Operator) qui sélectionne automatiquement la valeur optimale de l'hyper-paramètre de régularisation (alpha) à l'aide de la validation croisée.

Cette méthode permet de trouver un équilibre entre la réduction de la dimensionnalité du modèle (sélection des caractéristiques importantes) et la prévention de l'ajustement excessif, ce qui la rend utile pour les tâches de régression.

Principe de fonctionnement de LassoCV :

1. Données d'Entrée : Il commence par l'ensemble de données original, y compris les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Initialisation : LassoCV initialise plusieurs valeurs différentes de l'hyper-paramètre de régularisation (alpha) qui couvrent une plage allant de faible à élevée.
3. Validation Croisée : Pour chaque valeur alpha, LassoCV effectue une validation croisée afin d'évaluer les performances du modèle. Des mesures telles que l'erreur quadratique moyenne (MSE) ou le coefficient de détermination (R^2) sont couramment utilisées.
4. Sélection de l'Alpha Optimal : LassoCV sélectionne la valeur alpha pour laquelle le modèle obtient la meilleure performance déterminée par validation croisée.
5. Entraînement du Modèle : Le modèle Lasso est formé en utilisant la valeur alpha choisie, en excluant les caractéristiques moins importantes et en appliquant la régularisation L1.
6. Générer des Prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de LassoCV :

• Sélection Automatique de l'Alpha : LassoCV sélectionne automatiquement la valeur alpha optimale à l'aide de la validation croisée, ce qui simplifie la mise au point du modèle.
• Sélection des Caractéristiques : LassoCV sélectionne automatiquement les caractéristiques les plus importantes, réduisant ainsi la dimensionnalité du modèle et simplifiant son interprétation.
• Régularisation : La méthode empêche le sur-ajustement du modèle grâce à la régularisation L1.

Limites de LassoCV :

• Modèle Linéaire : LassoCV construit un modèle linéaire, qui peut s'avérer insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Incapacité à gérer la multicolinéarité : Lorsque les caractéristiques sont fortement corrélées, le modèle LassoCV peut être confronté à des problèmes de multicolinéarité.

LassoCV est utile dans les tâches de régression où il est important de sélectionner les caractéristiques les plus importantes et de réduire la dimensionnalité du modèle tout en maintenant l'interprétabilité et en évitant le sur-ajustement.

2.1.9.1. Code pour créer le modèle LassoCV et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LassoCV, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LassoCV.py
# Le code démontre le processus d'entraînement du modèle LassoCV, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"

# crée un modèle de Régresseur LassoCV
lassocv_regressor_model = LassoCV()

# ajuste le modèle aux données
lassocv_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = lassocv_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LassoCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962241428413416
Python  Mean Absolute Error: 6.33567334453819
Python  Mean Squared Error: 49.96500551028169
Python  
Python  LassoCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.996224142876629
Python  Mean Absolute Error: 6.335673221332177
Python  Mean Squared Error: 49.96500504333324
Python  R^2 matching decimal places:  10
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  6
Python  float ONNX model precision:  6
Python  
Python  LassoCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962241428413416
Python  Mean Absolute Error: 6.33567334453819
Python  Mean Squared Error: 49.96500551028169
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  14

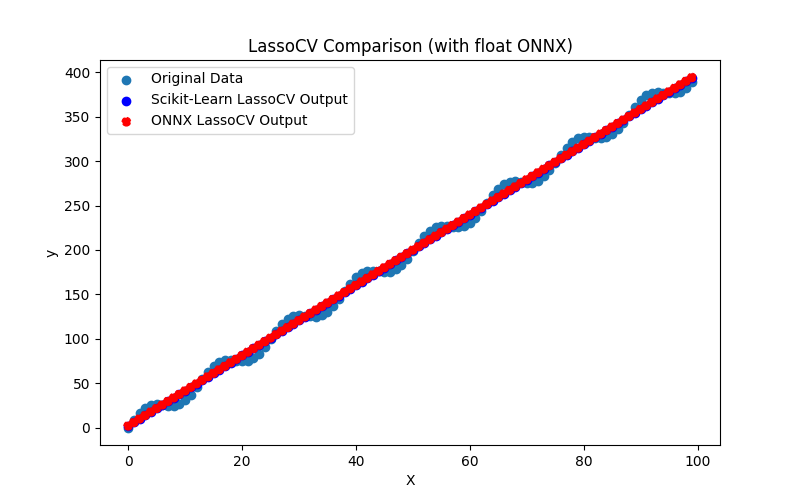
Fig. 33. Résultats de LassoCV.py (float ONNX)

2.1.9.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles lasso_cv_float.onnx et lasso_cv_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                      LassoCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoCV"
#define   ONNXFilenameFloat  "lasso_cv_float.onnx"
#define   ONNXFilenameDouble "lasso_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

2023.10.26 22:14:00.736 LassoCV (EURUSD,H1)     Testing ONNX float: LassoCV (lasso_cv_float.onnx)
2023.10.26 22:14:00.739 LassoCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962241428766290
2023.10.26 22:14:00.739 LassoCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3356732213321800
2023.10.26 22:14:00.739 LassoCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.9650050433332211
2023.10.26 22:14:00.748 LassoCV (EURUSD,H1)     
2023.10.26 22:14:00.748 LassoCV (EURUSD,H1)     Testing ONNX double: LassoCV (lasso_cv_double.onnx)
2023.10.26 22:14:00.753 LassoCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962241428413416
2023.10.26 22:14:00.753 LassoCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3356733445381899
2023.10.26 22:14:00.753 LassoCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.9650055102816992

Comparaison avec le modèle double original en Python :

Testing ONNX float: LassoCV (lasso_cv_float.onnx)
Python  Mean Absolute Error: 6.33567334453819
MQL5:   Mean Absolute Error: 6.3356732213321800
        
Testing ONNX double: LassoCV (lasso_cv_double.onnx)
Python  Mean Absolute Error: 6.33567334453819
MQL5:   Mean Absolute Error: 6.3356733445381899

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 13 décimales.

2.1.9.3. Représentation ONNX de lasso_cv_float.onnx et lasso_cv_double.onnx

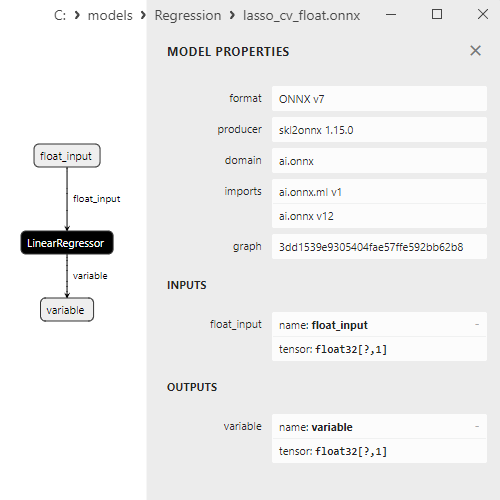
Fig. 34. Représentation ONNX de lasso_cv_float.onnx dans Netron

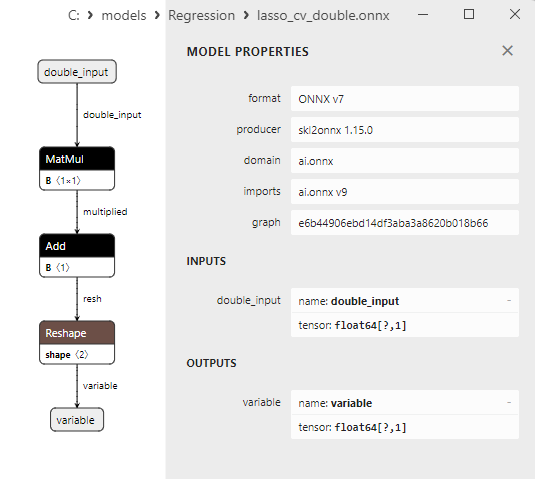
Fig. 35. Représentation ONNX de lasso_cv_double.onnx dans Netron

2.1.10. sklearn.linear_model.LassoLars

LassoLars est une combinaison de deux méthodes : Lasso (Least Absolute Shrinkage and Selection Operator) et LARS (Least Angle Regression).

Cette méthode est utilisée pour les tâches de régression et combine les avantages des deux algorithmes, permettant une sélection simultanée des caractéristiques et une réduction de la dimensionnalité du modèle.

Principe de Fonctionnement de LassoLars :

1. Données d'Entrée : Il commence par l'ensemble de données original, y compris les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Initialisation : LassoLars commence avec un modèle nul, ce qui signifie qu'il n'y a pas de caractéristiques actives. Tous les coefficients sont fixés à zéro.
3. Sélection Progressive des Caractéristiques : Comme la méthode LARS, LassoLars sélectionne, à chaque étape, la caractéristique la plus corrélée avec les résidus du modèle et l'ajoute au modèle. Le coefficient de cette caractéristique est ensuite ajusté en utilisant la méthode des moindres carrés.
4. Application de la Régularisation L1 : Parallèlement à la sélection progressive des caractéristiques, LassoLars applique la régularisation L1, en ajoutant une pénalité pour la somme des valeurs absolues des coefficients. Cela permet de modéliser des relations complexes et de choisir les caractéristiques les plus importantes.
5. Faire des Prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de LassoLars :

• Sélection des Caractéristiques : LassoLars sélectionne automatiquement les caractéristiques les plus importantes et réduit la dimensionnalité du modèle, ce qui permet d'éviter l'ajustement excessif et de simplifier l'interprétation.
• Interprétabilité : La méthode maintient l'interprétabilité du modèle, ce qui permet de déterminer facilement quelles caractéristiques sont incluses et comment elles influencent la variable cible.
• Régularisation : LassoLars applique la régularisation L1, empêchant l'ajustement excessif et améliorant la généralisation du modèle.

Limites de LassoLars :

• Modèle Linéaire : LassoLars construit un modèle linéaire, qui peut s'avérer insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Complexité de Calcul : La sélection des caractéristiques à chaque étape et l'application d'une régularisation peuvent nécessiter davantage de ressources informatiques qu'une simple régression linéaire.

LassoLars est utile dans les tâches de régression où il est important de choisir les caractéristiques les plus importantes, de réduire la dimensionnalité du modèle et de maintenir l'interprétabilité.

2.1.10.1. Code pour créer le modèle LassoLars et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LassoLars, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LassoLars.py
# Le code démontre le processus d'entraînement du modèle LassoLars, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"

# crée un modèle Régresseur LassoLars
lassolars_regressor_model = LassoLars(alpha=0.1)

# ajuste le modèle aux données
lassolars_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = lassolars_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LassoLars Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382633544077
Python  Mean Absolute Error: 6.3476035128950805
Python  Mean Squared Error: 49.778152172481896
Python  
Python  LassoLars ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382635045889
Python  Mean Absolute Error: 6.3476034814795375
Python  Mean Squared Error: 49.77815018516975
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LassoLars ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382633544077
Python  Mean Absolute Error: 6.3476035128950805
Python  Mean Squared Error: 49.778152172481896
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  16

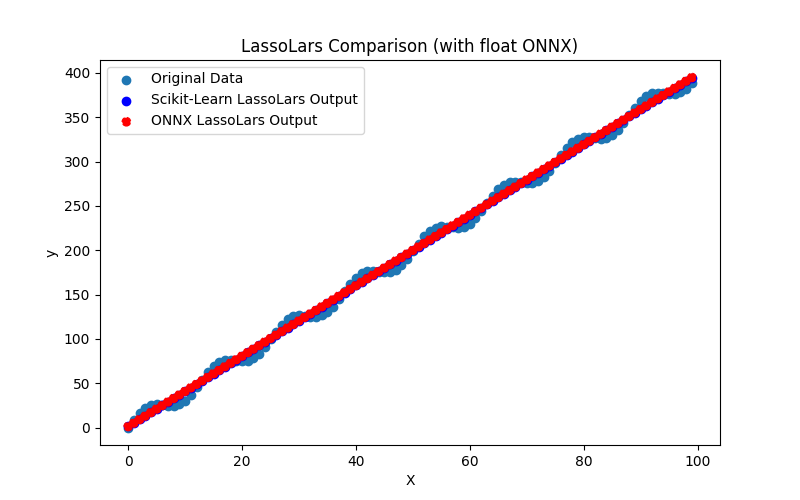
Fig. 36. Résultat de LassoLars.py (float)

2.1.10.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les fichiers sauvegardés lasso_lars_float.onnx et lasso_lars_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                    LassoLars.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoLars"
#define   ONNXFilenameFloat  "lasso_lars_float.onnx"
#define   ONNXFilenameDouble "lasso_lars_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

LassoLars (EURUSD,H1)   Testing ONNX float: LassoLars (lasso_lars_float.onnx)
LassoLars (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382635045889
LassoLars (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3476034814795375
LassoLars (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781501851697357
LassoLars (EURUSD,H1)   
LassoLars (EURUSD,H1)   Testing ONNX double: LassoLars (lasso_lars_double.onnx)
LassoLars (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382633544077
LassoLars (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3476035128950858
LassoLars (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781521724819029

Comparaison avec le modèle double original en Python :

Testing ONNX float: LassoLars (lasso_lars_float.onnx)
Python  Mean Absolute Error: 6.3476035128950805
MQL5:   Mean Absolute Error: 6.3476034814795375

Testing ONNX double: LassoLars (lasso_lars_double.onnx)
Python  Mean Absolute Error: 6.3476035128950805
MQL5:   Mean Absolute Error: 6.3476035128950858

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.10.3. Représentation ONNX de lasso_lars_float.onnx et lasso_lars_double.onnx

Fig. 37. Représentation ONNX de lasso_lars_float.onnx dans Netron

Fig. 38. Représentation ONNX de lasso_lars_double.onnx dans Netron

2.1.11. sklearn.linear_model.LassoLarsCV

LassoLarsCV est une méthode qui combine Lasso (Least Absolute Shrinkage and Selection Operator) et LARS (Least Angle Regression) avec une sélection automatique de l'hyper-paramètre de régularisation optimal (alpha) à l'aide de la validation croisée.

Cette méthode combine les avantages des deux algorithmes et permet de déterminer la valeur alpha optimale pour le modèle, en tenant compte de la sélection des caractéristiques et de la régularisation.

Principe de Fonctionnement de LassoLarsCV :

1. Données d'Entrée : Il commence par l'ensemble de données original, y compris les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Initialisation : LassoLarsCV commence par un modèle nul, dans lequel tous les coefficients sont fixés à 0.
3. Définition de l’Intervalle Alpha : Un intervalle de valeurs pour l'hyper-paramètre alpha est déterminé, et sera pris en compte lors du processus de sélection. En général, on utilise une échelle logarithmique des valeurs alpha.
4. Validation Croisée : Pour chaque valeur alpha de l'intervalle choisi, LassoLarsCV effectue une validation croisée afin d'évaluer les performances du modèle avec cette valeur alpha. On utilise généralement des mesures telles que l'erreur quadratique moyenne (MSE) ou le coefficient de détermination (R^2).
5. Sélection de l'Alpha Optimal : LassoLarsCV choisit la valeur alpha pour laquelle le modèle obtient les meilleures performances sur la base des résultats de la validation croisée.
6. Entraînement du Modèle : Le modèle LassoLars est entraîné en utilisant la valeur alpha sélectionnée, en excluant les caractéristiques moins importantes et en appliquant la régularisation L1.
7. Faire des Prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de LassoLarsCV :

• Sélection Automatique de l'Alpha : LassoLarsCV sélectionne automatiquement l'hyper-paramètre alpha optimal à l'aide de la validation croisée, ce qui simplifie la mise au point du modèle.
• Sélection des Caractéristiques : LassoLarsCV choisit automatiquement les caractéristiques les plus importantes et réduit la dimensionnalité du modèle.
• Régularisation : La méthode applique la régularisation L1, qui empêche l'ajustement excessif et améliore la généralisation du modèle.

Limites de LassoLarsCV :

• Modèle Linéaire : LassoLarsCV construit un modèle linéaire, qui peut s'avérer insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Complexité de Calcul : La sélection des caractéristiques à chaque étape et l'application d'une régularisation peuvent nécessiter davantage de ressources informatiques qu'une simple régression linéaire.

LassoLarsCV est utile dans les tâches de régression où il est essentiel de choisir les caractéristiques les plus importantes, de réduire la dimensionnalité du modèle, d'empêcher le sur-ajustement et d'ajuster automatiquement les hyper-paramètres du modèle.

2.1.11.1. Code pour créer le modèle LassoLarsCV et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LassoLarsCV, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LassoLarsCV.py
# Le code démontre le processus d'entraînement du modèle LassoLars, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"

# crée un modèle de Régresseur LassoLarsCV
lassolars_cv_regressor_model = LassoLarsCV(cv=5)

# ajuste le modèle aux données
lassolars_cv_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = lassolars_cv_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LassoLarsCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  
Python  LassoLarsCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382640824089
Python  Mean Absolute Error: 6.347737845846069
Python  Mean Squared Error: 49.778142539016564
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LassoLarsCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  16

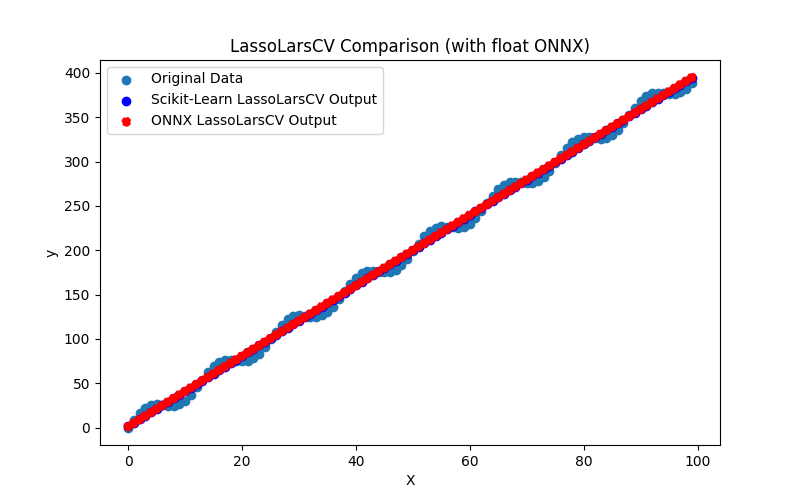
Fig. 39. Résultats de LassoLarsCV.py (ONNX float)

2.1.11.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles lasso_lars_cv_float.onnx et lasso_lars_cv_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                  LassoLarsCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoLarsCV"
#define   ONNXFilenameFloat  "lasso_lars_cv_float.onnx"
#define   ONNXFilenameDouble "lasso_lars_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

LassoLarsCV (EURUSD,H1) Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx)
LassoLarsCV (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382640824089
LassoLarsCV (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477378458460691
LassoLarsCV (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781425390165566
LassoLarsCV (EURUSD,H1) 
LassoLarsCV (EURUSD,H1) Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx)
LassoLarsCV (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382642612767
LassoLarsCV (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477379221400145
LassoLarsCV (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781401721031642

Comparaison avec le modèle double original en Python :

Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477378458460691
        
Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477379221400145

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 16 décimales.

2.1.11.3. Représentation ONNX de lasso_lars_cv_float.onnx et lasso_lars_cv_double.onnx

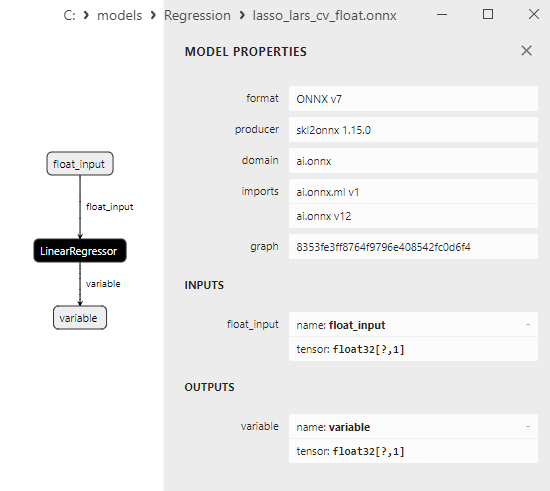
Fig. 40. Représentation ONNX de lasso_lars_cv_float.onnx dans Netron

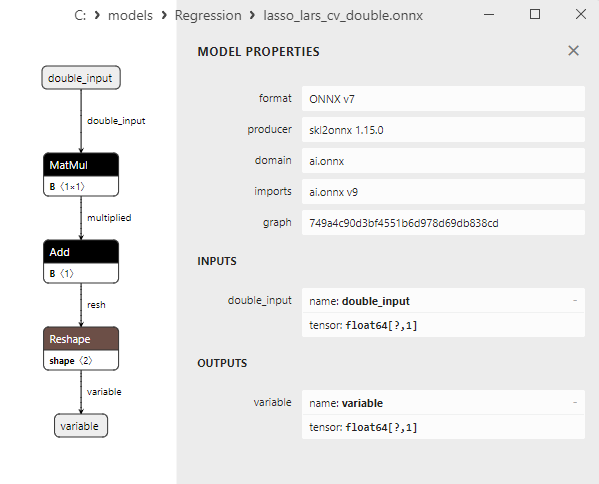
Fig. 41. Représentation ONNX de lasso_lars_cv_double.onnx dans Netron

2.1.12. sklearn.linear_model.LassoLarsIC

LassoLarsIC est une méthode de régression qui combine Lasso (Least Absolute Shrinkage and Selection Operator) et le Critère d'Information (IC) pour sélectionner automatiquement l'ensemble optimal de caractéristiques.

Il utilise des critères d'information tels que l'AIC (Critère d'Information d'Akaike) et le BIC (Critère d'Information Bayésien) pour déterminer les caractéristiques à inclure dans le modèle et applique la régularisation L1 pour estimer les coefficients du modèle.

Principe de Fonctionnement de LassoLarsIC :

1. Données d'Entrée : Il commence par l'ensemble de données original, y compris les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Initialisation : LassoLarsIC commence par un modèle nul, c'est-à-dire sans caractéristiques actives. Tous les coefficients sont fixés à zéro.
3. Sélection de Caractéristiques à l'aide du Critère d'Information : La méthode évalue le critère d'information (par exemple, AIC ou BIC) pour différents ensembles de caractéristiques, en partant d'un modèle vide et en incorporant progressivement des caractéristiques dans le modèle. Le critère d'information évalue la qualité du modèle, en tenant compte du compromis entre l'adaptation aux données et la complexité du modèle.
4. Sélection de l'Ensemble Optimal de Caractéristiques : LassoLarsIC choisit l'ensemble de caractéristiques pour lequel le critère d'information atteint la meilleure valeur. Cet ensemble de caractéristiques sera inclus dans le modèle.
5. Application de la Régularisation L1 : La régularisation L1 est appliquée aux caractéristiques sélectionnées, ce qui facilite l'estimation des coefficients du modèle.
6. Faire des Prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de LassoLarsIC :

• Sélection Automatique des Caractéristiques : LassoLarsIC choisit automatiquement l'ensemble de caractéristiques optimal, réduisant la dimensionnalité du modèle et évitant l'ajustement excessif.
• Critères d'Information : L'utilisation de critères d'information permet d'équilibrer la qualité et la complexité du modèle.
• Régularisation : La méthode applique la régularisation L1, qui empêche l'ajustement excessif et améliore la généralisation du modèle.

Limites de LassoLarsIC :

• Modèle Linéaire : LassoLarsIC construit un modèle linéaire, qui peut être insuffisant pour modéliser des relations non linéaires complexes.
• Sensibilité au Bruit : La méthode peut être sensible aux valeurs aberrantes des données.
• Complexité de Calcul : L'évaluation des critères d'information pour divers ensembles de caractéristiques pourrait nécessiter des ressources informatiques supplémentaires.

LassoLarsIC est utile dans les tâches de régression où la sélection automatique du meilleur ensemble de caractéristiques et la réduction de la dimensionnalité du modèle sur la base de critères d'information sont cruciales.

2.1.12.1. Code pour créer le modèle LassoLarsIC et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LassoLarsIC, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LassoLarsIC.py
# Le code démontre le processus d'entraînement du modèle LassoLarsIC, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"

# crée un modèle de Régresseur LassoLarsIC
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')

# ajuste le modèle aux données
lasso_lars_ic_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = lasso_lars_ic_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LassoLarsIC Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  
Python  LassoLarsIC ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LassoLarsIC ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  15

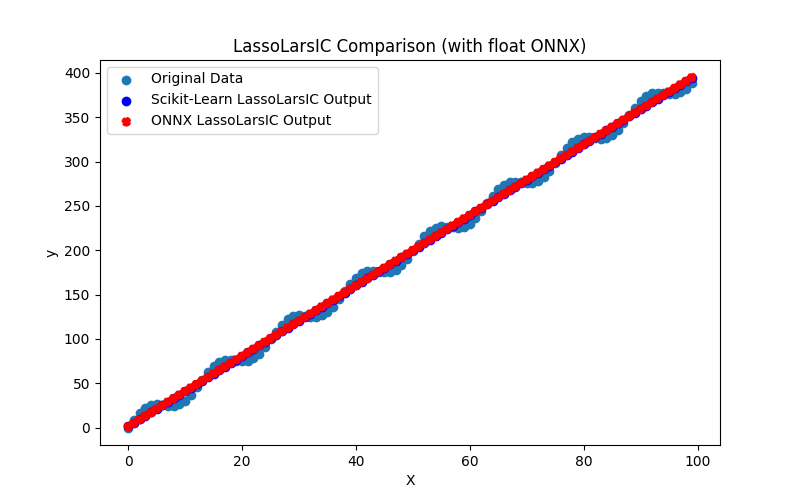
Fig. 42. Résultats de LassoLarsIC.py (ONNX float)

2.1.12.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles lasso_lars_ic_float.onnx et lasso_lars_ic_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                  LassoLarsIC.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoLarsIC"
#define   ONNXFilenameFloat  "lasso_lars_ic_float.onnx"
#define   ONNXFilenameDouble "lasso_lars_ic_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

LassoLarsIC (EURUSD,H1) Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx)
LassoLarsIC (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
LassoLarsIC (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477377671679385
LassoLarsIC (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781414740478638
LassoLarsIC (EURUSD,H1) 
LassoLarsIC (EURUSD,H1) Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx)
LassoLarsIC (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
LassoLarsIC (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477379263364302
LassoLarsIC (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781401712817768

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477377671679385
 
Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477379263364302

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 13 décimales.

2.1.12.3. Représentation ONNX de lasso_lars_ic_float.onnx et lasso_lars_ic_double.onnx

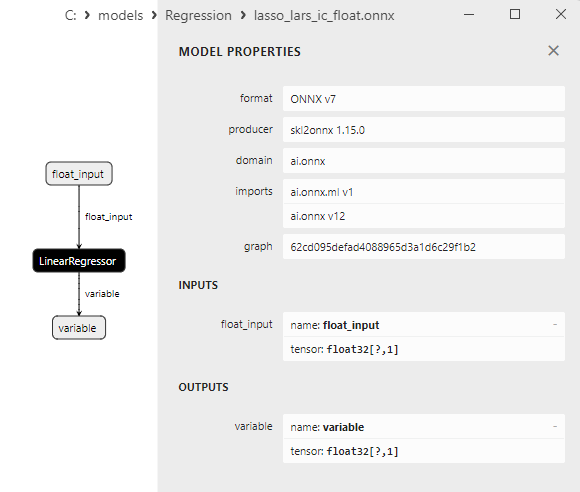
Fig. 43. Représentation ONNX de lasso_lars_ic_float.onnx dans Netron

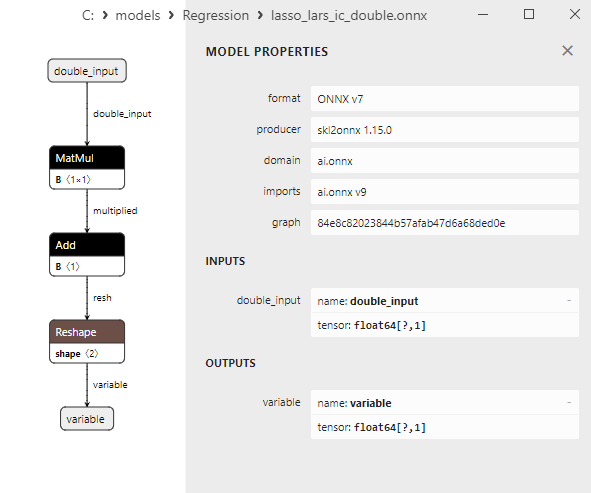
Fig. 44. Représentation ONNX de lasso_lars_ic_double.onnx dans Netron

2.1.13. sklearn.linear_model.LinearRegression

LinearRegression est l'une des méthodes les plus simples et les plus utilisées dans l'apprentissage automatique pour les tâches de régression.

Elle est utilisée pour construire des modèles linéaires qui prédisent des valeurs numériques (continues) de la variable cible sur la base d'une combinaison linéaire de caractéristiques d'entrée.

Principe de Fonctionnement de la Régression Linéaire :

1. Modèle Linéaire : Le LinearRegression suppose qu'il existe une relation linéaire entre les variables indépendantes (caractéristiques) et la variable cible. Cette relation peut être exprimée par l'équation de régression linéaire:y = β₀ + β₁x₁ + β₂x₂ + .... + βₚxₚ, où y est la variable cible, β₀ est le coefficient d'interception, β₁, β₂, ... βₚ sont les coefficients des caractéristiques et x₁, x₂, ... xₚ sont les valeurs des caractéristiques.
2. Estimation des Paramètres : L'objectif de la régression linéaire est d'estimer les coefficients β₀, β₁, β₂, ... βₚ, qui correspondent le mieux aux données. Pour cela, on utilise généralement la méthode des Moindres Carrés Ordinaires (Ordinary Least Squares - OLS), qui minimise la somme des différences quadratiques entre les valeurs réelles et les valeurs prédites.
3. Évaluation du Modèle : Diverses mesures telles que l'Erreur Quadratique Moyenne (Mean Squared Error, MSE), le Coefficient de Détermination (R²), entre autres, sont utilisées pour évaluer la qualité du modèle de régression linéaire.

Avantages de LinearRegression :

• Simplicité et Interprétabilité : La régression linéaire est une méthode simple et facile à interpréter, qui permet d'analyser l'influence de chaque caractéristique sur la variable cible.
• Vitesse Elevée d'Entraînement et de Prédiction : Le modèle de régression linéaire présente des vitesses d'apprentissage et de prédiction élevées, ce qui en fait un bon choix pour les grands ensembles de données.
• Applicabilité : LinearRegression peut être appliqué avec succès à diverses tâches de régression.

Limites de LinearRegression :

• Linéarité : Cette méthode suppose la linéarité de la relation entre les caractéristiques et la variable cible, ce qui peut s'avérer insuffisant pour modéliser des dépendances non linéaires complexes.
• Sensibilité aux Valeurs Aberrantes : LinearRegression est sensible aux valeurs aberrantes des données, qui peuvent affecter la qualité du modèle.

LinearRegression est une méthode de régression simple et largement utilisée qui construit un modèle linéaire pour prédire les valeurs numériques de la variable cible sur la base d'une combinaison linéaire de caractéristiques d'entrée. Elle est bien adaptée aux problèmes présentant une relation linéaire et lorsque l'interprétabilité du modèle est importante.

2.1.13.1. Code pour créer le modèle LinearRegression et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LinearRegression, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LinearRegression.py
# Le code démontre le processus d'apprentissage du modèle de régression linéaire, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"

# crée un modèle de régression linéaire
linear_model = LinearRegression()

# ajuste le modèle aux données
linear_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = linear_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LinearRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  
Python  LinearRegression ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LinearRegression ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

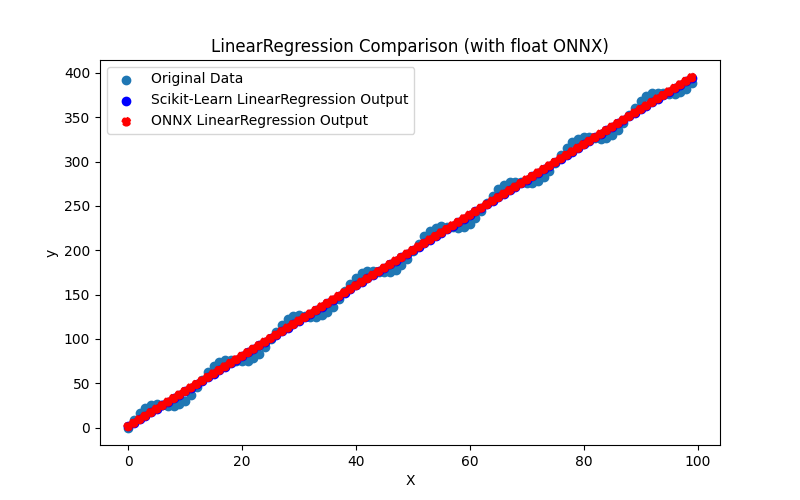
Fig. 45. Résultats de LinearRegression.py (ONNX float)

2.1.13.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les fichiers linear_regression_float.onnx et linear_regression_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                             LinearRegression.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LinearRegression"
#define   ONNXFilenameFloat  "linear_regression_float.onnx"
#define   ONNXFilenameDouble "linear_regression_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

LinearRegression (EURUSD,H1)    Testing ONNX float: LinearRegression (linear_regression_float.onnx)
LinearRegression (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
LinearRegression (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3477377671679385
LinearRegression (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7781414740478638
LinearRegression (EURUSD,H1)    
LinearRegression (EURUSD,H1)    Testing ONNX double: LinearRegression (linear_regression_double.onnx)
LinearRegression (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
LinearRegression (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3477379263364266
LinearRegression (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7781401712817768

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: LinearRegression (linear_regression_float.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477377671679385

Testing ONNX double: LinearRegression (linear_regression_double.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477379263364266

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.13.3. Représentation ONNX de linear_regression_float.onnx et linear_regression_double.onnx

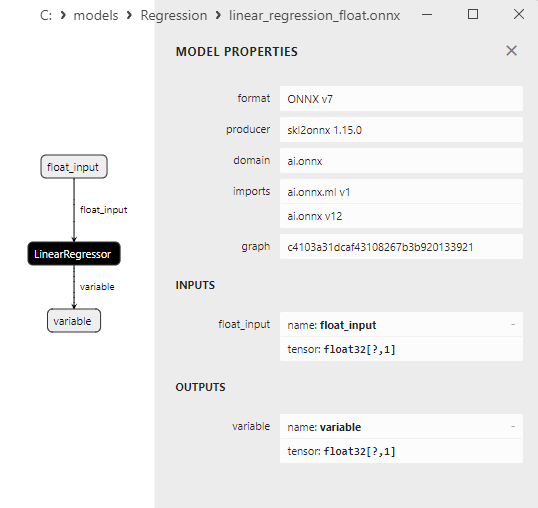
Fig. 46. Représentation ONNX de linear_regression_float.onnx dans Netron

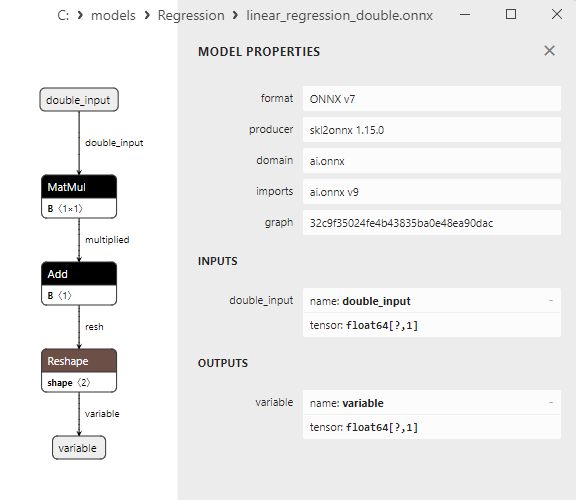
Fig. 47. Représentation ONNX de linear_regression_double.onnx dans Netron

Note sur les méthodes Ridge et RidgeCV

Ridge et RidgeCV sont deux méthodes apparentées d'apprentissage automatique utilisées pour la régularisation dans la régression Ridge. Elles ont des fonctionnalités similaires mais diffèrent dans leur utilisation et dans le réglage des paramètres.

Principe de Fonctionnement de Ridge (Ridge Regression) :

• Ridge est une méthode de régression impliquant une régularisation L2. Cela signifie qu'elle ajoute la somme des coefficients carrés (norme L2) à la fonction de perte minimisée par le modèle. Ce terme de régularisation supplémentaire permet de réduire l'ampleur des coefficients du modèle, évitant ainsi un sur-ajustement.
• Utilisation du paramètre alpha : Dans la méthode Ridge, le paramètre alpha (également connu sous le nom de force de régularisation) est prédéfini et n'est pas modifié automatiquement. Les utilisateurs doivent choisir une valeur alpha appropriée en fonction de leur connaissance des données et des expériences.

Principe de Fonctionnement de RidgeCV (Ridge Cross-Validation) :

• RidgeCV est une extension de la méthode Ridge, qui consiste à sélectionner automatiquement la valeur optimale du paramètre alpha à l'aide de la validation croisée. Au lieu de définir manuellement l'alpha, RidgeCV itère entre différentes valeurs d'alpha et choisit celle qui fournit les meilleures performances en validation croisée.
• Avantage du réglage automatique : Le principal avantage de RidgeCV est la détermination automatique de la valeur alpha optimale, sans qu'il soit nécessaire de procéder à un ajustement manuel. Cela rend le processus de réglage plus pratique et évite les erreurs potentielles dans la sélection de l'alpha.

La principale différence entre Ridge et RidgeCV est que Ridge demande aux utilisateurs de spécifier explicitement la valeur du paramètre alpha, alors que RidgeCV trouve automatiquement la valeur alpha optimale à l'aide de la validation croisée. RidgeCV est généralement un choix plus judicieux lorsque l'on traite un grand nombre de données et que l'on souhaite éviter un réglage manuel des paramètres.

2.1.14. sklearn.linear_model.Ridge

Ridge est une méthode de régression utilisée dans l'apprentissage automatique pour résoudre les problèmes de régression. Il fait partie de la famille des modèles linéaires et représente une régression linéaire régularisée.

La principale caractéristique de la régression Ridge est l'ajout d'une régularisation L2 à la méthode standard des moindres carrés ordinaires (MCO).

Comment Fonctionne la Régression Ridge :

1. Régression Linéaire : Comme la régression linéaire classique, la régression Ridge vise à trouver une relation linéaire entre les variables indépendantes (caractéristiques) et la variable cible.
2. Régularisation L2 : La principale distinction de la régression Ridge est l'ajout d'une régularisation L2 à la fonction de perte. Cela signifie qu'une pénalité pour les valeurs élevées des coefficients de régression est ajoutée à la somme des carrés des différences entre les valeurs réelles et les valeurs prédites.
3. Coefficients de pénalisation : La régularisation L2 impose une pénalité sur les valeurs des coefficients de régression. Par conséquent, certains coefficients tendent à être plus proches de 0, ce qui réduit l'ajustement excessif et améliore la stabilité du modèle.
4. Hyper-paramètre α : L'un des paramètres essentiels de la régression Ridge est l'hyper-paramètre α (alpha), qui détermine le degré de régularisation. Des valeurs α plus élevées conduisent à une régularisation plus forte, ce qui se traduit par des modèles plus simples avec des valeurs de coefficient plus faibles.

Avantages de la régression Ridge :

• Réduction de l'ajustement excessif : La régularisation L2 dans Ridge permet de réduire le sur-ajustement et de rendre le modèle plus robuste face au bruit des données.
• Traitement de la multicolinéarité : La régression Ridge permet de résoudre les problèmes de multicolinéarité, en particulier lorsque les caractéristiques sont fortement corrélées.
• La malédiction de la dimensionnalité : Ridge est utile dans les scénarios comportant de nombreuses caractéristiques, où les MCO peuvent être instables.

Limites de la régression Ridge :

• Il n'élimine pas les caractéristiques : La régression Ridge n'annule pas les coefficients des caractéristiques, mais les réduit, ce qui signifie que certaines caractéristiques peuvent subsister dans le modèle.
• Choix de la valeur optimale de α : La sélection de la valeur correcte de l'hyper-paramètre α peut nécessiter une validation croisée.

La régression Ridge est une méthode de régression qui introduit une régularisation L2 dans la régression linéaire standard afin de réduire l'ajustement excessif, d'améliorer la stabilité et de résoudre les problèmes de multicolinéarité. Cette méthode est utile lorsqu'il s'agit de trouver un équilibre entre la précision et la stabilité du modèle.

2.1.14.1. Code pour créer le modèle Ridge et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.Ridge, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# Ridge.py
# Le code démontre le processus d'entraînement du modèle Ridge, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "Ridge"
onnx_model_filename = data_path + "ridge"

# crée un modèle Ridge
regression_model = Ridge()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE correspondant aux décimales : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  Ridge Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382641178552
Python  Mean Absolute Error: 6.347684462929819
Python  Mean Squared Error: 49.77814206996523
Python  
Python  Ridge ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382634837793
Python  Mean Absolute Error: 6.347684915729416
Python  Mean Squared Error: 49.77815046053819
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  Ridge ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641178552
Python  Mean Absolute Error: 6.347684462929819
Python  Mean Squared Error: 49.77814206996523
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

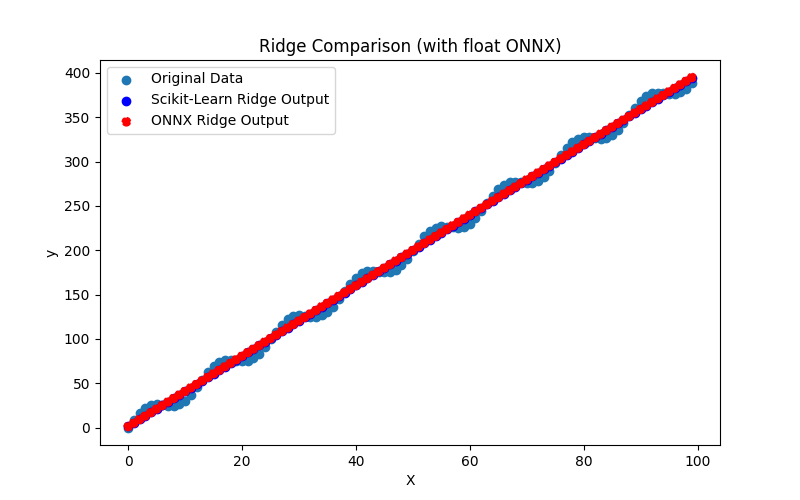
Fig. 49. Résultats du Ridge.py (ONNX float)

2.1.14.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles ridge_float.onnx et ridge_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                        Ridge.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "Ridge"
#define   ONNXFilenameFloat  "ridge_float.onnx"
#define   ONNXFilenameDouble "ridge_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

Ridge (EURUSD,H1)       Testing ONNX float: Ridge (ridge_float.onnx)
Ridge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382634837793
Ridge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3476849157294160
Ridge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781504605381784
Ridge (EURUSD,H1)       
Ridge (EURUSD,H1)       Testing ONNX double: Ridge (ridge_double.onnx)
Ridge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382641178552
Ridge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3476844629298235
Ridge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781420699652131

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: Ridge (ridge_float.onnx)
Python  Mean Absolute Error: 6.347684462929819
MQL5:   Mean Absolute Error: 6.3476849157294160
       
Testing ONNX double: Ridge (ridge_double.onnx)
Python  Mean Absolute Error: 6.347684462929819
MQL5:   Mean Absolute Error: 6.3476844629298235

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 13 décimales.

2.1.14.3. Représentation ONNX de ridge_float.onnx et ridge_double.onnx

Fig. 50. Représentation ONNX de ridge_float.onnx dans Netron

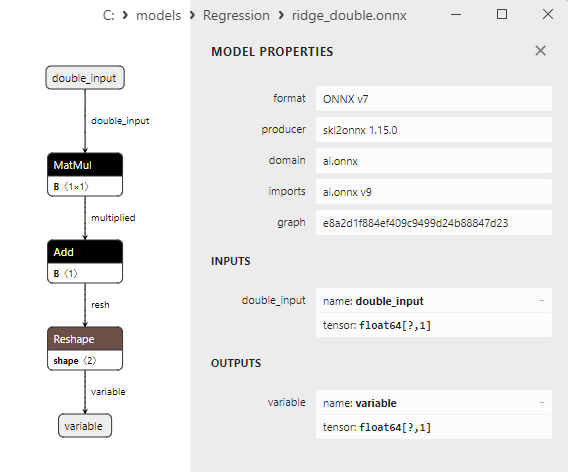
Fig. 51. Représentation ONNX de ridge_double.onnx dans Netron

2.1.15. sklearn.linear_model.RidgeCV

RidgeCV est une extension de la régression Ridge qui inclut la sélection automatique du meilleur hyper-paramètre α (alpha), qui détermine le degré de régularisation dans la régression Ridge. L'hyper-paramètre α contrôle l'équilibre entre la minimisation de la somme des erreurs quadratiques (comme dans la régression linéaire ordinaire) et la minimisation de la valeur des coefficients de régression (régularisation). RidgeCV sélectionne automatiquement la valeur optimale de α en fonction des paramètres et critères spécifiés.

Comment fonctionne RidgeCV :

1. Données d'Entrée : RidgeCV utilise des données d'entrée composées de caractéristiques (variables indépendantes) et de la variable cible (continue).
2. Choix de α : La régression Ridge nécessite la sélection de l'hyper-paramètre α, qui détermine le degré de régularisation. RidgeCV sélectionne automatiquement la valeur optimale de α dans l'intervalle donné.
3. Validation croisée : RidgeCV utilise la validation croisée, telle que la validation croisée k-fold, pour évaluer quelle valeur α fournit la meilleure généralisation du modèle sur des données indépendantes.
4. α Optimal: À l'issue du processus d'apprentissage, RidgeCV choisit la valeur α qui offre les meilleures performances en validation croisée et utilise cette valeur pour former le modèle de régression Ridge final.

Avantages de RidgeCV :

• Sélection automatique de α : RidgeCV permet de sélectionner automatiquement la valeur optimale de l'hyper-paramètre α, ce qui simplifie le processus de réglage du modèle.
• Équilibre entre régularisation et performance : Cette méthode permet de trouver l'équilibre optimal entre la régularisation (réduction de l'ajustement excessif) et la performance du modèle.

Limites de RidgeCV :

• Complexité de calcul : La validation croisée peut nécessiter des ressources de calcul importantes, en particulier lors de l'utilisation d'un large éventail de valeurs α.

RidgeCV est une méthode de régression Ridge avec sélection automatique de l'hyper-paramètre optimal α par validation croisée. Cette méthode rationalise le processus de sélection des hyper-paramètres et permet de trouver le meilleur équilibre entre la régularisation et la performance du modèle.

2.1.15.1. Code pour créer le modèle RidgeCV et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.RidgeCV, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# RidgeCV.py
# Le code démontre le processus d'entraînement du modèle RidgeCV, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"

# crée un modèle RidgeCV
regression_model = RidgeCV()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  RidgeCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382499160807
Python  Mean Absolute Error: 6.34720334999352
Python  Mean Squared Error: 49.77832999861571
Python  
Python  RidgeCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382499108485
Python  Mean Absolute Error: 6.3472036427935485
Python  Mean Squared Error: 49.77833006785168
Python  R^2 matching decimal places:  11
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  RidgeCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382499160807
Python  Mean Absolute Error: 6.34720334999352
Python  Mean Squared Error: 49.77832999861571
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  14

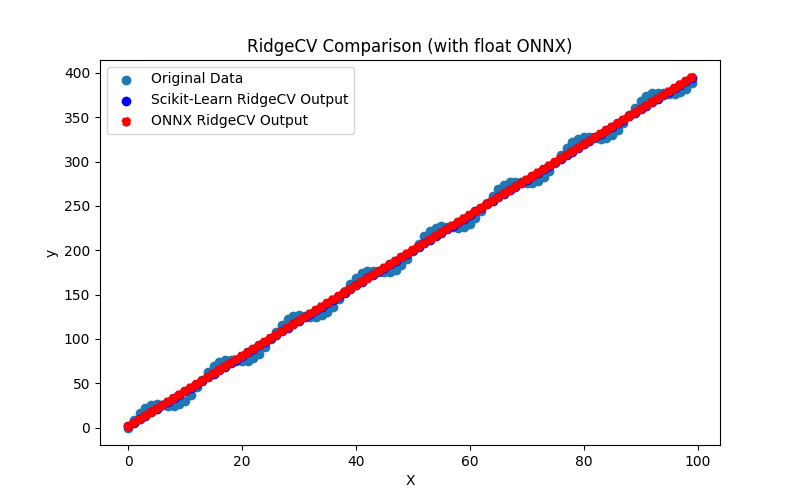
Fig. 52. Résultats de RidgeCV.py (ONNX float)

2.1.15.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles ridge_cv_float.onnx et ridge_cv_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                      RidgeCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RidgeCV"
#define   ONNXFilenameFloat  "ridge_cv_float.onnx"
#define   ONNXFilenameDouble "ridge_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

RidgeCV (EURUSD,H1)     Testing ONNX float: RidgeCV (ridge_cv_float.onnx)
RidgeCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382499108485
RidgeCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3472036427935485
RidgeCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7783300678516909
RidgeCV (EURUSD,H1)     
RidgeCV (EURUSD,H1)     Testing ONNX double: RidgeCV (ridge_cv_double.onnx)
RidgeCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382499160807
RidgeCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3472033499935216
RidgeCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7783299986157246

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: RidgeCV (ridge_cv_float.onnx)
Python  Mean Absolute Error: 6.34720334999352
MQL5:   Mean Absolute Error: 6.3472036427935485

Testing ONNX double: RidgeCV (ridge_cv_double.onnx)
Python  Mean Absolute Error: 6.34720334999352
MQL5:   Mean Absolute Error: 6.3472033499935216

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.15.3. Représentation ONNX de ridge_cv_float.onnx et ridge_cv_double.onnx

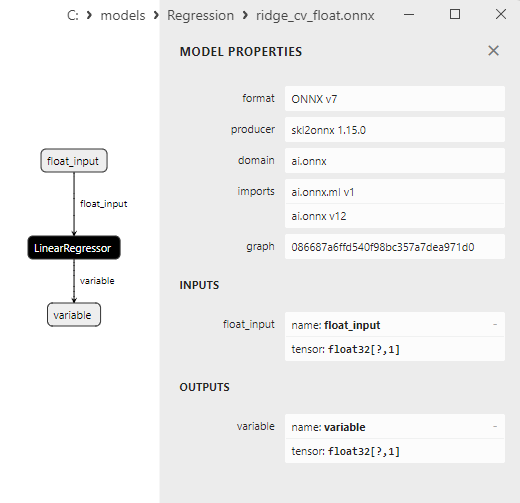
Fig. 53. Représentation ONNX de ridge_cv_float.onnx dans Netron

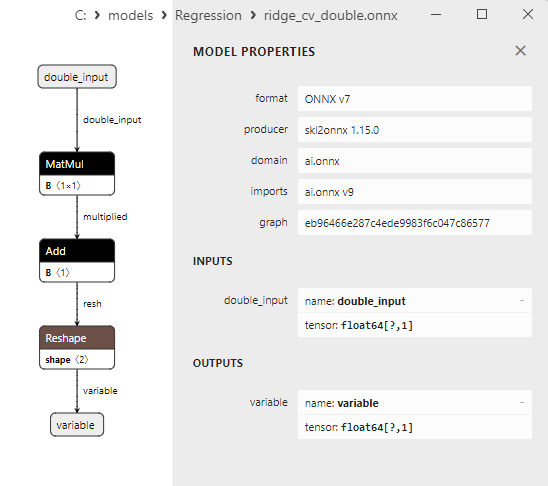
Fig. 54. Représentation ONNX de ridge_cv_double.onnx dans Netron

2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit

OrthogonalMatchingPursuit (OMP) est un algorithme utilisé pour résoudre les problèmes de sélection de caractéristiques et de régression linéaire.

Il s'agit d'une des méthodes permettant de sélectionner les caractéristiques les plus significatives, ce qui peut contribuer à réduire la dimensionnalité des données et à améliorer la capacité de généralisation du modèle.

Fonctionnement de l'OrthogonalMatchingPursuit :

1. Données d'Entrée : Elle commence par un ensemble de données contenant des caractéristiques (variables indépendantes) et des valeurs de la variable cible (continue).
2. Sélection du nombre de caractéristiques : L'une des premières étapes de l'utilisation de l'OrthogonalMatchingPursuit consiste à déterminer le nombre de caractéristiques à inclure dans le modèle. Ce nombre peut être prédéfini ou choisi en fonction de critères tels que le Critère d'Information d'Akaike (AIC) ou le critère d'erreur minimale.
3. Ajout itératif de fonctionnalités : L'algorithme part d'un modèle vide et ajoute itérativement les caractéristiques qui expliquent le mieux les résidus du modèle. À chaque itération, une nouvelle caractéristique est choisie pour être orthogonale aux caractéristiques précédemment sélectionnées. La caractéristique optimale est sélectionnée sur la base de sa corrélation avec les résidus du modèle.
4. Entraînement du modèle : Après avoir ajouté le nombre spécifié de caractéristiques, le modèle est entraîné sur les données en tenant compte uniquement des caractéristiques sélectionnées.
5. Générer des prédictions : Après l'entraînement, le modèle peut prédire les valeurs de la variable cible sur de nouvelles données.

Avantages de l’OrthogonalMatchingPursuit :

• Réduction de la dimensionnalité : L'OMP peut réduire la dimension des données en ne sélectionnant que les caractéristiques les plus informatives.
• Interprétabilité : Comme l'OMP ne sélectionne qu'un petit nombre de caractéristiques, les modèles créés à l'aide de cette méthode peuvent être plus faciles à interpréter.

Limites de l’OrthogonalMatchingPursuit :

• Sensibilité au nombre de caractéristiques sélectionnées : Le nombre de caractéristiques sélectionnées doit être correctement ajusté, et des choix incorrects peuvent conduire à un sur-ajustement ou à un sous-ajustement.
• Ne tient pas compte de la multicolinéarité : L'OMP peut ne pas tenir compte de la multicolinéarité entre les caractéristiques, ce qui pourrait avoir une incidence sur la sélection des caractéristiques optimales.
• Complexité de calcul : La méthode OMP est coûteuse en termes de calcul, en particulier pour les grands ensembles de données.

L’OrthogonalMatchingPursuit est un algorithme de sélection des caractéristiques et de régression linéaire, qui permet de sélectionner les caractéristiques les plus informatives pour le modèle. Cette méthode peut s'avérer précieuse pour réduire la dimensionnalité des données et améliorer l'interprétabilité des modèles.

2.1.16.1. Code pour créer le modèle OrthogonalMatchingPursuit et l'exporter vers ONNX pour les float et les double

Ce code crée le modèle sklearn.linear_model.OrthogonalMatchingPursuit, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# OrthogonalMatchingPursuit.py
# Le code démontre le processus d'entraînement du modèle OrthogonalMatchingPursuit, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"

# crée un modèle OrthogonalMatchingPursuit
regression_model = OrthogonalMatchingPursuit()

# ajuste le modèle aux données
regression_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  OrthogonalMatchingPursuit Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281784
Python  
Python  OrthogonalMatchingPursuit ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  OrthogonalMatchingPursuit ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281784
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  16

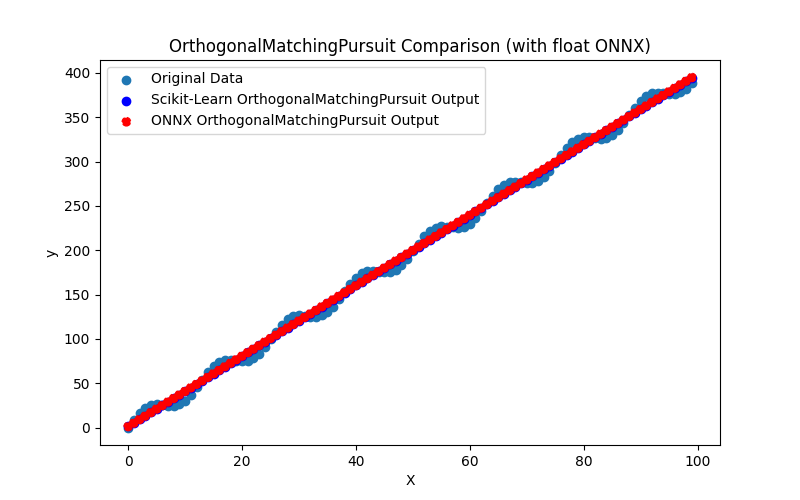
Fig. 55. Résultats de OrthogonalMatchingPursuit.py (ONNX float)

2.1.16.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles orthogonal_matching_pursuit_float.onnx et orthogonal_matching_pursuit_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                    OrthogonalMatchingPursuit.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "OrthogonalMatchingPursuit"
#define   ONNXFilenameFloat  "orthogonal_matching_pursuit_float.onnx"
#define   ONNXFilenameDouble "orthogonal_matching_pursuit_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

OrthogonalMatchingPursuit (EURUSD,H1)   Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx)
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3477377671679385
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781414740478638
OrthogonalMatchingPursuit (EURUSD,H1)   
OrthogonalMatchingPursuit (EURUSD,H1)   Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx)
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3477379263364275
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781401712817768

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477377671679385
        
Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477379263364275

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 16 décimales.

2.1.16.3. Représentation ONNX de l'orthogonal_matching_pursuit_float.onnx et de l'orthogonal_matching_pursuit_double.onnx

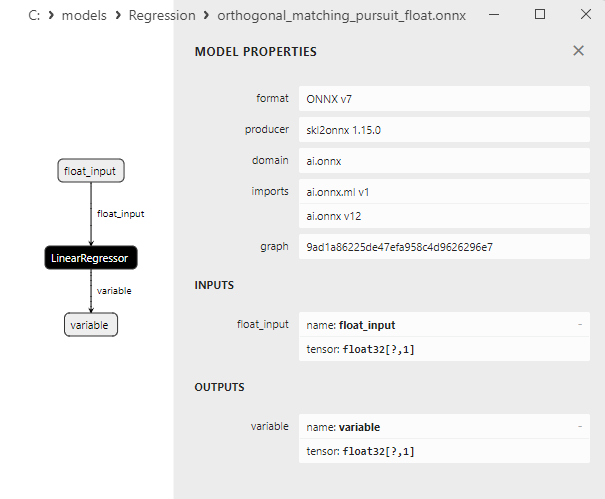
Fig. 56. Représentation ONNX de orthogonal_matching_pursuit_float.onnx dans Netron

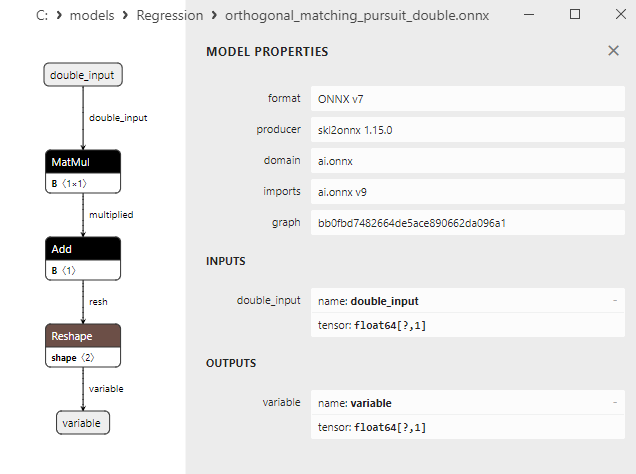
Fig. 57. Représentation ONNX de orthogonal_matching_pursuit_double.onnx dans Netron

2.1.17. sklearn.linear_model.PassiveAggressiveRegressor

PassiveAggressiveRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression.

Cette méthode est une variante de l'algorithme passif-agressif (PA) qui peut être utilisée pour former un modèle capable de prédire des valeurs continues de la variable cible.

Comment fonctionne PassiveAggressiveRegressor :

1. Données d'Entrée : Elle commence par un ensemble de données comprenant des caractéristiques (variables indépendantes) et des valeurs de la variable cible (continue).
2. Apprentissage supervisé : PassiveAggressiveRegressor est une méthode d'apprentissage supervisé entraînée sur des paires (X, y), où X représente les caractéristiques et y correspond aux valeurs de la variable cible.
3. Apprentissage adaptatif : L'idée principale qui sous-tend la méthode Passive-Agressive est l'approche de l'apprentissage adaptatif. Le modèle apprend en minimisant l'erreur de prédiction sur chaque exemple d'apprentissage. Il se met à jour en corrigeant les poids afin de réduire l'erreur de prédiction.
4. Paramètre C : PassiveAggressiveRegressor possède un hyper-paramètre C, qui contrôle la force d'adaptation du modèle aux erreurs. Une valeur C plus élevée signifie des mises à jour de poids plus agressives, tandis qu'une valeur C plus faible rend le modèle moins agressif.
5. Prédiction : Une fois entraîné, le modèle peut prédire les valeurs des variables cibles pour de nouvelles données.

Avantages du PassiveAggressiveRegressor :

• Capacité d'Adaptation : La méthode peut s'adapter aux changements de données et mettre à jour le modèle afin de minimiser les erreurs de prédiction.
• Efficacité pour les grands ensembles de données : PassiveAggressiveRegressor peut être une méthode efficace pour la régression, en particulier lorsqu'elle est entraînée sur des volumes de données importants.

Limites du PassiveAggressiveRegressor :

• Sensibilité au choix du paramètre C : Le choix de la valeur de C peut nécessiter des ajustements et de l'expérimentation.
• Des caractéristiques supplémentaires peuvent être nécessaires : Dans certains cas, des caractéristiques techniques supplémentaires peuvent être nécessaires à la réussite de l'apprentissage du modèle.

PassiveAggressiveRegressor est une méthode d'apprentissage automatique pour les tâches de régression qui apprend de manière adaptative en minimisant les erreurs de prédiction sur les données d'apprentissage. Cette méthode peut s'avérer utile pour traiter de grands ensembles de données et nécessite d'ajuster le paramètre C pour obtenir des performances optimales.

2.1.17.1. Code pour créer le modèle PassiveAggressiveRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.PassiveAggressiveRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# PassiveAggressiveRegressor.py
# Le code démontre le processus d'entraînement du modèle PassiveAggressiveRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"

# crée un modèle PassiveAggressiveRegressor
regression_model = PassiveAggressiveRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  PassiveAggressiveRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9894376841493092
Python  Mean Absolute Error: 9.64524669506544
Python  Mean Squared Error: 139.76857373191007
Python  
Python  PassiveAggressiveRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9894376801868329
Python  Mean Absolute Error: 9.645248834431873
Python  Mean Squared Error: 139.76862616640122
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  5
Python  
Python  PassiveAggressiveRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9894376841493092
Python  Mean Absolute Error: 9.64524669506544
Python  Mean Squared Error: 139.76857373191007
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  14

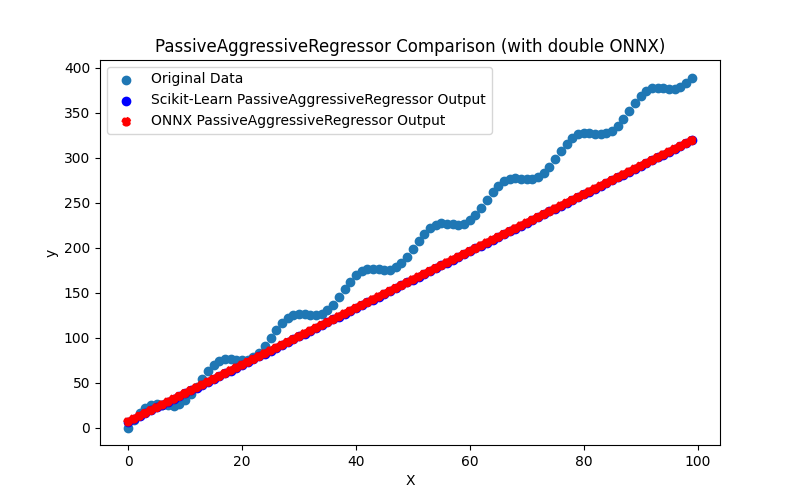
Fig. 58. Résultats de PassiveAggressiveRegressor.py (ONNX double)

2.1.17.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles enregistrés passive_aggressive_regressor_float.onnx et passive_aggressive_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                   PassiveAggressiveRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "PassiveAggressiveRegressor"
#define   ONNXFilenameFloat  "passive_aggressive_regressor_float.onnx"
#define   ONNXFilenameDouble "passive_aggressive_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

PassiveAggressiveRegressor (EURUSD,H1)  Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx)
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9894376801868329
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Absolute Error: 9.6452488344318716
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Squared Error: 139.7686261664012761
PassiveAggressiveRegressor (EURUSD,H1)  
PassiveAggressiveRegressor (EURUSD,H1)  Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx)
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9894376841493092
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Absolute Error: 9.6452466950654419
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Squared Error: 139.7685737319100667

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx)
Python  Mean Absolute Error: 9.64524669506544
MQL5:   Mean Absolute Error: 9.6452488344318716
        
Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx)
Python  Mean Absolute Error: 9.64524669506544
MQL5:   Mean Absolute Error: 9.6452466950654419

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 14 décimales.

2.1.17.3. Représentation ONNX de passive_aggressive_regressor_float.onnx et passive_aggressive_regressor_double.onnx

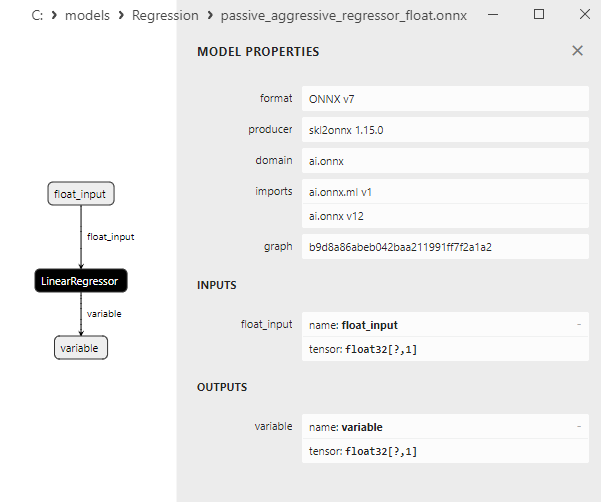
Fig. 59. Représentation ONNX de passive_aggressive_regressor_float.onnx dans Netron

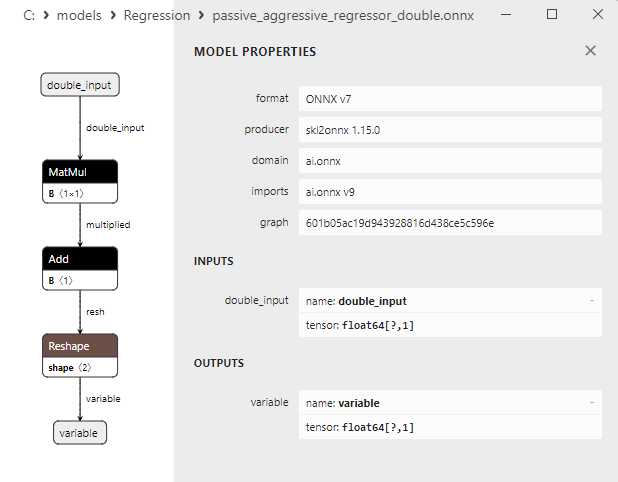
Fig. 60. Représentation ONNX de passive_aggressive_regressor_double.onnx dans Netron

2.1.18. sklearn.linear_model.QuantileRegressor

QuantileRegressor est une méthode d'apprentissage automatique utilisée pour estimer les quantiles (percentiles spécifiques) de la variable cible dans les tâches de régression.

Au lieu de prédire la valeur moyenne de la variable cible, comme c'est généralement le cas dans les tâches de régression, QuantileRegressor prédit les valeurs correspondant aux quantiles spécifiés, tels que la médiane (50e percentile) ou les 25e et 75e percentiles.

Comment fonctionne QuantileRegressor :

1. Données d'Entrée : Il commence par un ensemble de données contenant des caractéristiques (variables indépendantes) et la variable cible (continue).
2. Concentration sur le quantile : Au lieu de prédire les valeurs exactes de la variable cible, QuantileRegressor modélise la distribution conditionnelle de la variable cible et prédit les valeurs de certains quantiles de cette distribution.
3. Entraînement pour différents quantiles : L’entraînement d'un modèle QuantileRegressor implique la formation de modèles distincts pour chaque quantile souhaité. Chacun de ces modèles prédit une valeur correspondant à son quantile.
4. Paramètre du quantile : Le paramètre principal de cette méthode est le choix des quantiles souhaités pour lesquels vous voulez obtenir des prédictions. Par exemple, si vous avez besoin de prédictions pour la médiane, vous devrez entraîner le modèle sur le 50e centile.
5. Prédiction par quantile : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs correspondant aux quantiles spécifiés sur de nouvelles données.

Avantages de QuantileRegressor :

• Flexibilité : QuantileRegressor permet de prédire différents quantiles, ce qui peut s'avérer utile dans les tâches où différents centiles de la distribution sont importants.
• Robustesse face aux valeurs aberrantes : Une approche axée sur les quantiles peut être robuste face aux valeurs aberrantes, car elle ne tient pas compte de la moyenne, qui peut être fortement influencée par les valeurs extrêmes.

Limites de QuantileRegressor :

• Nécessité d'une sélection par quantile : Le choix des quantiles optimaux peut nécessiter une certaine connaissance de la tâche.
• Augmentation de la complexité des calculs : L'apprentissage de modèles distincts pour différents quantiles peut accroître la complexité de calcul de la tâche.

QuantileRegressor est une méthode d'apprentissage automatique conçue pour prédire les valeurs correspondant aux quantiles spécifiés de la variable cible. Cette méthode peut s'avérer utile dans les tâches où les différents centiles de la distribution sont intéressants et dans les cas où les données peuvent contenir des valeurs aberrantes.

2.1.18.1. Code pour créer le modèle QuantileRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.QuantileRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# QuantileRegressor.py
# Le code démontre le processus d'apprentissage du modèle QuantileRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"

# crée un modèle QuantileRegressor
regression_model = QuantileRegressor(solver='highs')

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  QuantileRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9959915738839231
Python  Mean Absolute Error: 6.3693091850025185
Python  Mean Squared Error: 53.0425343337143
Python  
Python  QuantileRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9959915739158818
Python  Mean Absolute Error: 6.3693091422201125
Python  Mean Squared Error: 53.042533910812814
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  7
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  7
Python  
Python  QuantileRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9959915738839231
Python  Mean Absolute Error: 6.3693091850025185
Python  Mean Squared Error: 53.0425343337143
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  13
Python  double ONNX model precision:  16

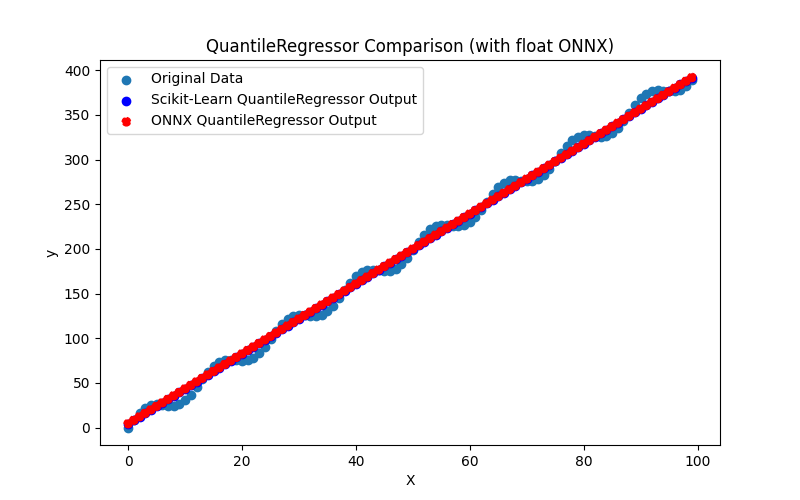
Fig. 61. Résultats de QuantileRegressor.py (ONNX float)

2.1.18.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les fichiers quantile_regressor_float.onnx et quantile_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                            QuantileRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "QuantileRegressor"
#define   ONNXFilenameFloat  "quantile_regressor_float.onnx"
#define   ONNXFilenameDouble "quantile_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

QuantileRegressor (EURUSD,H1)   Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx)
QuantileRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9959915739158818
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3693091422201169
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 53.0425339108128071
QuantileRegressor (EURUSD,H1)   
QuantileRegressor (EURUSD,H1)   Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx)
QuantileRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9959915738839231
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3693091850025185
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 53.0425343337142721

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx)
Python  Mean Absolute Error: 6.3693091850025185
MQL5:   Mean Absolute Error: 6.3693091422201169

Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx)
Python  Mean Absolute Error: 6.3693091850025185
MQL5:   Mean Absolute Error: 6.3693091850025185

Précision de la MAE ONNX float : 7 décimales, Précision de la MAE ONNX double : 16 décimales.

2.1.18.3. Représentation ONNX du quantile_regressor_float.onnx et du quantile_regressor_double.onnx

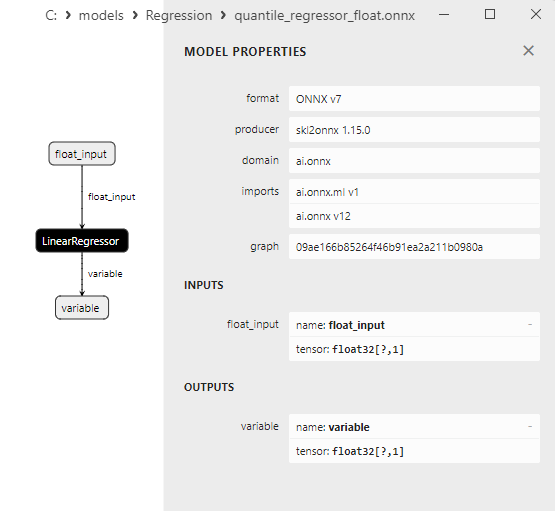
Fig. 62. Représentation ONNX du quantile_regressor_float.onnx dans Netron

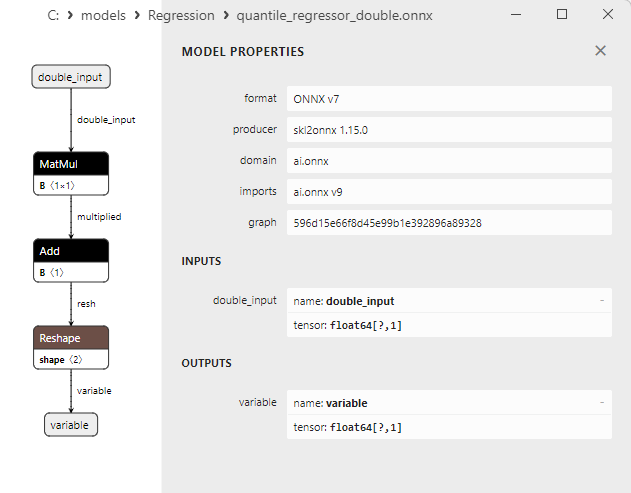
Fig. 63. Représentation ONNX du quantile_regressor_double.onnx dans Netron

2.1.19. sklearn.linear_model.RANSACRegressor

RANSACRegressor est une méthode d'apprentissage automatique utilisée pour résoudre les problèmes de régression à l'aide de la méthode RANSAC (Random Sample Consensus).

La méthode RANSAC est conçue pour traiter des données contenant des valeurs aberrantes ou des imperfections, ce qui permet d'obtenir un modèle de régression plus robuste en excluant l'influence des valeurs aberrantes.

Fonctionnement de RANSACRegressor :

1. Données d'Entrée : Il commence par un ensemble de données contenant des caractéristiques (variables indépendantes) et la variable cible (continue).
2. Sélection de sous-ensembles aléatoires : RANSAC commence par choisir des sous-ensembles aléatoires de données utilisés pour former le modèle de régression. Ces sous-ensembles sont appelés "hypothèses".
3. Adaptation du modèle aux hypothèses : Pour chaque hypothèse choisie, un modèle de régression est formé. Dans le cas de RANSACRegressor, la régression linéaire est généralement utilisée et le modèle est ajusté au sous-ensemble de données.
4. Évaluation des valeurs aberrantes : Après l'entraînement du modèle, son adaptation à toutes les données est évaluée. L'erreur entre les valeurs prédites et réelles est calculée pour chaque point de données.
5. Identification des valeurs aberrantes : Les points de données dont les erreurs dépassent un seuil spécifié sont considérés comme aberrants. Ces valeurs aberrantes peuvent influencer l'apprentissage du modèle et fausser les résultats.
6. Mise à jour du modèle : Tous les points de données qui ne sont pas considérés comme aberrants sont utilisés pour mettre à jour le modèle de régression. Ce processus peut être répété plusieurs fois avec différentes hypothèses aléatoires.
7. Modèle final : Après plusieurs itérations, RANSACRegressor sélectionne le meilleur modèle formé sur le sous-ensemble de données et le renvoie comme modèle de régression final.

Avantages de RANSACRegressor :

• Robustesse des valeurs aberrantes : RANSACRegressor est une méthode robuste contre les valeurs aberrantes, car elle les exclut de la formation.
• Régression robuste : Cette méthode permet de créer un modèle de régression plus fiable lorsque les données contiennent des valeurs aberrantes ou des imperfections.

Limites de RANSACRegressor :

• Sensibilité au seuil d'erreur : Le choix d'un seuil d'erreur pour déterminer quels points sont considérés comme aberrants peut nécessiter une expérimentation.
• Complexité de la sélection des hypothèses : Le choix de bonnes hypothèses au stade initial n'est pas toujours évident.

RANSACRegressor est une méthode d'apprentissage automatique utilisée pour les problèmes de régression basés sur la méthode RANSAC. Cette méthode permet de créer un modèle de régression plus robuste lorsque les données contiennent des valeurs aberrantes ou des imperfections en excluant leur influence sur le modèle.

2.1.19.1. Code pour créer le modèle RANSACRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.RANSACRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# RANSACRegressor.py
# Le code démontre le processus d'entraînement du modèle RANSACRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"

# crée un modèle RANSACRegressor
regression_model = RANSACRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  RANSACRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  
Python  RANSACRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  RANSACRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

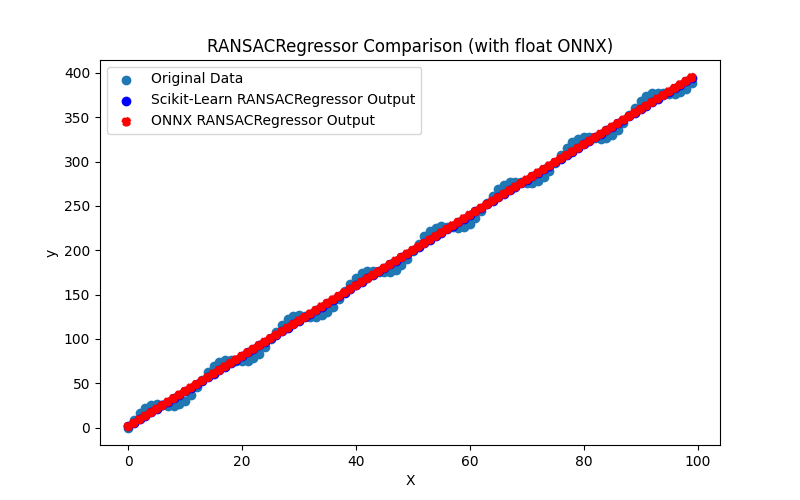
Fig. 64. Résultats de RANSACRegressor.py (ONNX float)

2.1.19.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles enregistrés ransac_regressor_float.onnx et ransac_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                              RANSACRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RANSACRegressor"
#define   ONNXFilenameFloat  "ransac_regressor_float.onnx"
#define   ONNXFilenameDouble "ransac_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

RANSACRegressor (EURUSD,H1)     Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx)
RANSACRegressor (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3477377671679385
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7781414740478638
RANSACRegressor (EURUSD,H1)     
RANSACRegressor (EURUSD,H1)     Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx)
RANSACRegressor (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3477379263364266
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7781401712817768

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477377671679385
     
Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477379263364266

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.19.3. Représentation ONNX du ransac_regressor_float.onnx et du ransac_regressor_double.onnx

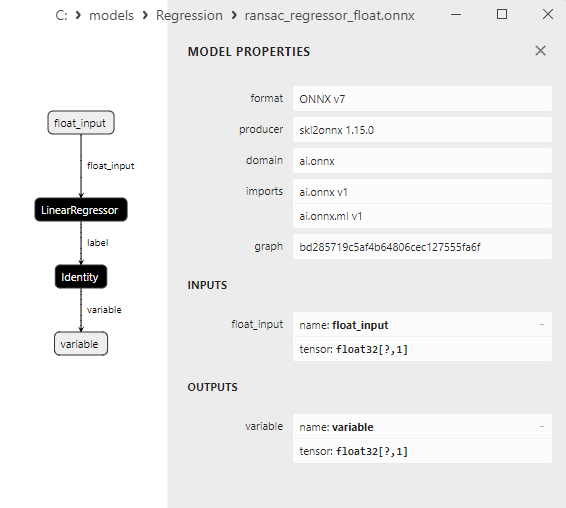
Fig. 65. Représentation ONNX de ransac_regressor_float.onnx dans Netron

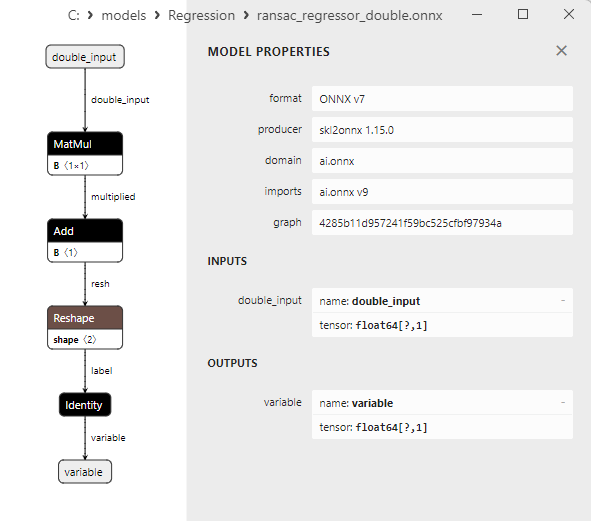
Fig. 66. Représentation ONNX de ransac_regressor_double.onnx dans Netron

2.1.20. sklearn.linear_model.TheilSenRegressor

La Régression de Theil-Sen (estimateur de Theil-Sen) est une méthode d'estimation de la régression utilisée pour approximer les relations linéaires entre les variables indépendantes et la variable cible.

Elle offre une estimation plus robuste que la régression linéaire ordinaire en présence de valeurs aberrantes et de bruit dans les données.

Comment fonctionne la régression Theil-Sen :

1. Sélection des points : Dans un premier temps, Theil-Sen sélectionne des paires aléatoires de points de données dans l'ensemble de données d'apprentissage.
2. Calcul de la pente : Pour chaque paire de points de données, la méthode calcule la pente de la ligne passant par ces points, créant ainsi un ensemble de pentes.
3. Pente médiane : La méthode permet ensuite de trouver la pente médiane dans l'ensemble des pentes. Cette pente médiane est utilisée comme estimation de la pente de la régression linéaire.
4. Écarts médians : Pour chaque point de données, la méthode calcule l'écart (différence entre la valeur réelle et la valeur prédite sur la base de la pente médiane) et trouve la médiane de ces écarts. On obtient ainsi une estimation du coefficient de l'ordonnée à l'origine de la régression linéaire.
5. Estimation finale : Les estimations finales des coefficients de pente et d'interception sont utilisées pour construire le modèle de régression linéaire.

Avantages de la régression Theil-Sen :

• Résilience des valeurs aberrantes : La régression Theil-Sen est plus résistante aux valeurs aberrantes et au bruit des données que la régression linéaire classique.
• Hypothèses moins strictes : La méthode ne nécessite pas d'hypothèses strictes sur la distribution des données ou la forme de dépendance, ce qui la rend plus polyvalente.
• Convient aux données multi-colinéaires : La régression de Theil-Sen donne de bons résultats avec des données où les variables indépendantes sont fortement corrélées (problème de multicolinéarité).

Limites de la régression Theil-Sen :

• Complexité de calcul : Le calcul des pentes médianes pour toutes les paires de points de données peut prendre beaucoup de temps, en particulier pour les grands ensembles de données.
• Estimation du coefficient d'interception : Les écarts médians sont utilisés pour estimer le coefficient d'interception, ce qui peut entraîner un biais en présence de valeurs aberrantes.

La régression Theil-Sen est une méthode d'estimation pour la régression qui fournit une évaluation stable de la relation linéaire entre les variables indépendantes et la variable cible, en particulier en présence de valeurs aberrantes et de bruit de données. Cette méthode est utile lorsqu'une estimation stable est nécessaire dans des conditions de données réelles.

2.1.20.1. Code pour créer le TheilSenRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.TheilSenRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# TheilSenRegressor.py
# Le code démontre le processus d'entraînement du modèle TheilSenRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"

# crée un modèle Régresseur TheilSen
regression_model = TheilSenRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  TheilSenRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9962329196940459
Python  Mean Absolute Error: 6.338686004537594
Python  Mean Squared Error: 49.84886353898735
Python  
Python  TheilSenRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.996232919516505
Python  Mean Absolute Error: 6.338686370832071
Python  Mean Squared Error: 49.84886588834327
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  TheilSenRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962329196940459
Python  Mean Absolute Error: 6.338686004537594
Python  Mean Squared Error: 49.84886353898735
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

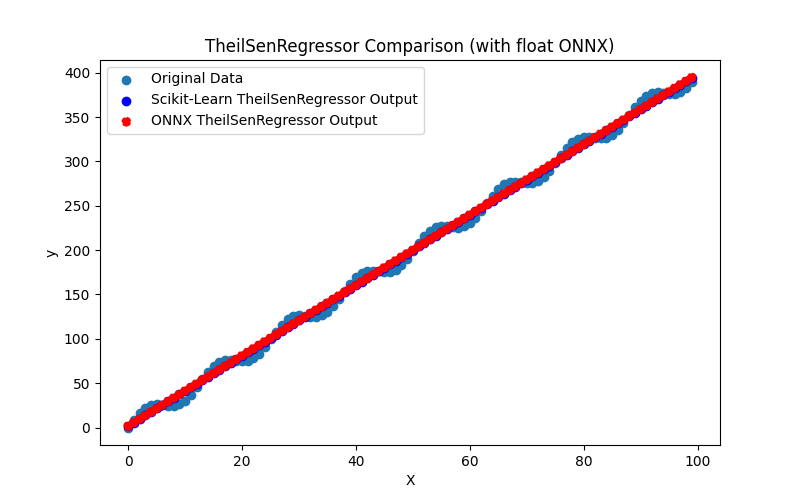
Fig. 67. Résultats de TheilSenRegressor.py (ONNX float)

2.1.20.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles enregistrés theil_sen_regressor_float.onnx et theil_sen_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                            TheilSenRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "TheilSenRegressor"
#define   ONNXFilenameFloat  "theil_sen_regressor_float.onnx"
#define   ONNXFilenameDouble "theil_sen_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

TheilSenRegressor (EURUSD,H1)   Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx)
TheilSenRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962329195165051
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3386863708320735
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 49.8488658883432691
TheilSenRegressor (EURUSD,H1)   
TheilSenRegressor (EURUSD,H1)   Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx)
TheilSenRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962329196940459
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3386860045375943
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 49.8488635389873735

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx)
Python  Mean Absolute Error: 6.338686004537594
MQL5:   Mean Absolute Error: 6.3386863708320735
        
Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx)
Python  Mean Absolute Error: 6.338686004537594
MQL5:   Mean Absolute Error: 6.3386860045375943

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 15 décimales.

2.1.20.3. Représentation ONNX de theil_sen_regressor_float.onnx et theil_sen_regressor_double.onnx

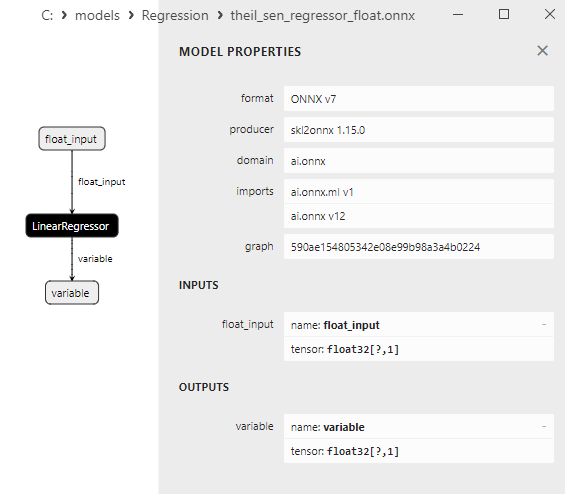
Fig. 68. Représentation ONNX de theil_sen_regressor_float.onnx dans Netron

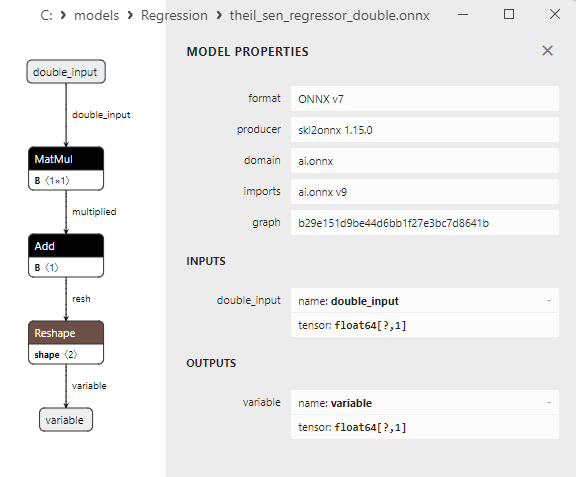
Fig. 69. Représentation ONNX de theil_sen_regressor_double.onnx dans Netron

2.1.21. sklearn.linear_model.LinearSVR

LinearSVR (Linear Support Vector Regression) est un modèle d'apprentissage automatique pour les tâches de régression basé sur la méthode des Support Vector Machines (SVM).

Cette méthode est utilisée pour trouver des relations linéaires entre les caractéristiques et la variable cible à l'aide d'un noyau linéaire.

Comment fonctionne LinearSVR :

1. Données d'Entrée : LinearSVR commence par un ensemble de données comprenant des caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Sélection d'un modèle linéaire : Le modèle suppose qu'il existe une relation linéaire entre les caractéristiques et la variable cible, décrite par une équation de régression linéaire.
3. Entraînement du modèle : LinearSVR trouve les valeurs optimales pour les coefficients du modèle en minimisant une fonction de perte qui prend en compte l'erreur de prédiction et une erreur acceptable (epsilon).
4. Générer des prédictions : Après l'entraînement, le modèle peut prédire les valeurs de la variable cible pour de nouvelles données sur la base des coefficients découverts.

Avantages de LinearSVR :

• Supporte la régression vectorielle : LinearSVR utilise le Support des Machines Vectorielles, qui permet de trouver la séparation optimale entre les données tout en tenant compte d'une erreur acceptable.
• Prise en charge de plusieurs fonctionnalités : Le modèle peut gérer des caractéristiques multiples et traiter des données en haute dimension.
• Régularisation : LinearSVR implique une régularisation, ce qui permet de lutter contre l'ajustement excessif et de garantir des prédictions plus stables.

Limites de LinearSVR :

• Linéarité : LinearSVR est contraint par l'utilisation de relations linéaires entre les caractéristiques et la variable cible. Dans le cas de relations complexes et non linéaires, le modèle peut ne pas être suffisamment flexible.
• Sensibilité aux valeurs aberrantes : Le modèle peut être sensible aux valeurs aberrantes des données et à l'erreur acceptable (epsilon).
• Incapacité à saisir des relations complexes : LinearSVR, comme d'autres modèles linéaires, n'est pas en mesure de saisir les relations non linéaires complexes entre les caractéristiques et la variable cible.

LinearSVR est un modèle d'apprentissage automatique de régression qui utilise la méthode de Support des Machines Vectorielles pour trouver des relations linéaires entre les caractéristiques et la variable cible. Il prend en charge la régularisation et peut être utilisé dans des tâches où le contrôle de l'erreur acceptable est essentiel. Toutefois, le modèle est limité par sa dépendance linéaire et peut être sensible aux valeurs aberrantes.

2.1.21.1. Code pour créer le modèle LinearSVR et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.LinearSVR, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# LinearSVR.py
# Le code démontre le processus d'entraînement du modèle LinearSVR, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LinearSVR"
onnx_model_filename = data_path + "linear_svr"

# crée un modèle SVR linéaire
linear_svr_model = LinearSVR()

# ajuste le modèle aux données
linear_svr_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = linear_svr_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(linear_svr_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(linear_svr_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  LinearSVR Original model (double)
Python  R-squared (Coefficient of determination): 0.9944935515149387
Python  Mean Absolute Error: 7.026852359381935
Python  Mean Squared Error: 72.86550241109444
Python  
Python  LinearSVR ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9944935580726729
Python  Mean Absolute Error: 7.026849848037511
Python  Mean Squared Error: 72.86541563418206
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  4
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  4
Python  
Python  LinearSVR ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9944935515149387
Python  Mean Absolute Error: 7.026852359381935
Python  Mean Squared Error: 72.86550241109444
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

Fig. 70. Résultats de LinearSVR.py (ONNX float)

2.1.21.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les fichiers linear_svr_float.onnx et linear_svr_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                    LinearSVR.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LinearSVR"
#define   ONNXFilenameFloat  "linear_svr_float.onnx"
#define   ONNXFilenameDouble "linear_svr_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

LinearSVR (EURUSD,H1)   Testing ONNX float: LinearSVR (linear_svr_float.onnx)
LinearSVR (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9944935580726729
LinearSVR (EURUSD,H1)   MQL5:   Mean Absolute Error: 7.0268498480375108
LinearSVR (EURUSD,H1)   MQL5:   Mean Squared Error: 72.8654156341820567
LinearSVR (EURUSD,H1)   
LinearSVR (EURUSD,H1)   Testing ONNX double: LinearSVR (linear_svr_double.onnx)
LinearSVR (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9944935515149387
LinearSVR (EURUSD,H1)   MQL5:   Mean Absolute Error: 7.0268523593819374
LinearSVR (EURUSD,H1)   MQL5:   Mean Squared Error: 72.8655024110944680

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: LinearSVR (linear_svr_float.onnx)
Python  Mean Absolute Error: 7.026852359381935
MQL5:   Mean Absolute Error: 7.0268498480375108
   
Testing ONNX double: LinearSVR (linear_svr_double.onnx)
Python  Mean Absolute Error: 7.026852359381935
MQL5:   Mean Absolute Error: 7.0268523593819374

Précision de la MAE ONNX float : 4 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.21.3. Représentation ONNX de linear_svr_float.onnx et linear_svr_double.onnx

Fig. 71. Représentation ONNX de linear_svr_float.onnx dans Netron

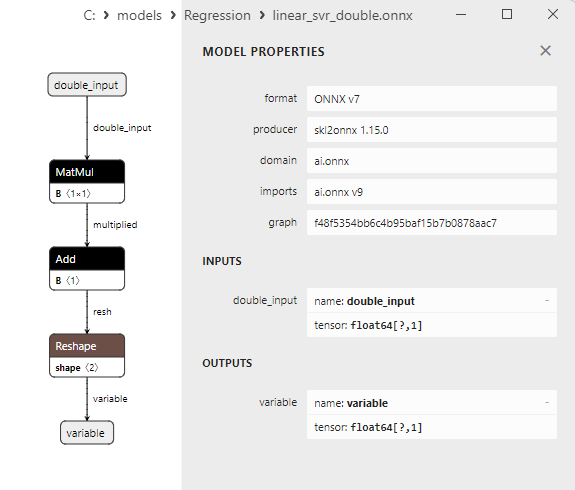
Fig. 72. Représentation ONNX de linear_svr_double.onnx dans Netron

2.1.22. sklearn.neural_network.MLPRegressor

MLPRegressor (Multi-Layer Perceptron Regressor) est un modèle d'apprentissage automatique qui utilise des réseaux neuronaux artificiels pour les tâches de régression.

Il s'agit d'un réseau neuronal multicouche comprenant plusieurs couches de neurones (y compris des couches d'entrée, cachées et de sortie) qui sont entraînées à prédire des valeurs continues de la variable cible.

Comment fonctionne MLPRegressor :

1. Données d'Entrée : Il commence par un ensemble de données contenant des caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Création d'un réseau neuronal multicouche : MLPRegressor utilise un réseau neuronal multicouche avec plusieurs couches cachées de neurones. Ces neurones sont reliés par des connexions pondérées et des fonctions d'activation.
3. Entraînement du modèle : MLPRegressor entraîne le réseau neuronal en ajustant les poids et les biais afin de minimiser une fonction de perte qui mesure la disparité entre les prédictions du réseau et les valeurs réelles de la variable cible. Ce résultat est obtenu grâce à des algorithmes de rétro-propagation.
4. Générer des prédictions : Après l'entraînement, le modèle peut prédire les valeurs des variables cibles pour de nouvelles données.

Avantages de MLPRegressor :

• Flexibilité : Les réseaux neuronaux multicouches peuvent modéliser des relations non linéaires complexes entre les caractéristiques et la variable cible.
• Polyvalence : MLPRegressor peut être utilisé pour diverses tâches de régression, y compris les problèmes de séries temporelles, l'approximation de fonctions, etc.
• Capacité de généralisation : Les réseaux neuronaux apprennent à partir des données et peuvent généraliser les dépendances trouvées dans les données d'apprentissage à de nouvelles données.

Limites de MLPRegressor :

• Complexité du modèle de base : Les grands réseaux neuronaux peuvent être coûteux en termes de calcul et nécessitent de nombreuses données pour l'apprentissage.
• Réglage des hyper-paramètres : Le choix des hyper-paramètres optimaux (nombre de couches, nombre de neurones dans chaque couche, taux d'apprentissage, etc.
• Susceptibilité à l'ajustement excessif : Les réseaux neuronaux de grande taille peuvent être sujets à un sur-ajustement si les données sont insuffisantes ou si la régularisation est insuffisante.

MLPRegressor représente un puissant modèle d'apprentissage automatique basé sur des réseaux neuronaux multicouches et peut être utilisé pour un large éventail de tâches de régression. Ce modèle est flexible mais nécessite un réglage et une formation méticuleux sur de grands volumes de données pour obtenir des résultats optimaux.

2.1.22.1. Code pour créer le modèle MLPRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.neural_network.MLPRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# MLPRegressor.py
# Le code démontre le processus d'entraînement du modèle MLPRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"

# crée un modèle MLP Régresseur
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)

# ajuste le modèle aux données
mlp_regressor_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = mlp_regressor_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  MLPRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9874070836467945
Python  Mean Absolute Error: 10.62249788982753
Python  Mean Squared Error: 166.63901957615224
Python  
Python  MLPRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9874070821340352
Python  Mean Absolute Error: 10.62249972216809
Python  Mean Squared Error: 166.63903959413219
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  MLPRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9874070836467945
Python  Mean Absolute Error: 10.622497889827532
Python  Mean Squared Error: 166.63901957615244
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  12
Python  double ONNX model precision:  14

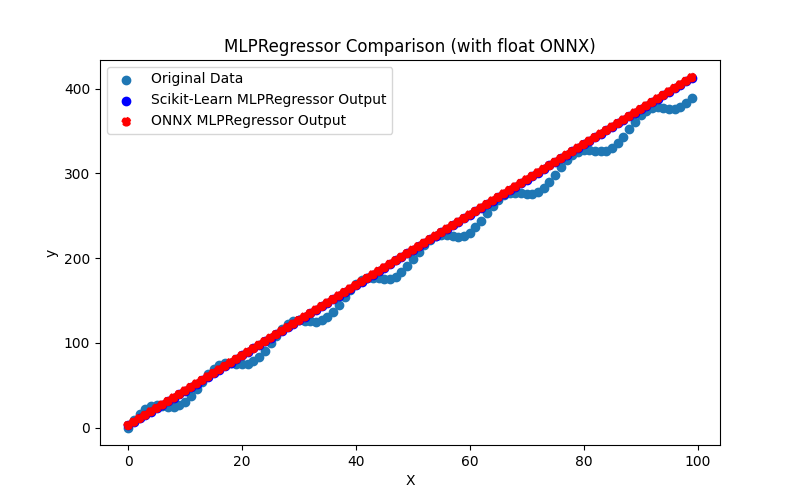
Fig. 73. Résultats du MLPRegressor.py (ONNX float)

2.1.22.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles mlp_regressor_float.onnx et mlp_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                 MLPRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "MLPRegressor"
#define   ONNXFilenameFloat  "mlp_regressor_float.onnx"
#define   ONNXFilenameDouble "mlp_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

MLPRegressor (EURUSD,H1)        Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx)
MLPRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9875198695654352
MLPRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 10.5596681685341309
MLPRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 165.1465507645494597
MLPRegressor (EURUSD,H1)        
MLPRegressor (EURUSD,H1)        Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx)
MLPRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9875198617341387
MLPRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 10.5596715833884609
MLPRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 165.1466543942046599

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx)
Python  Mean Absolute Error: 10.62249788982753
MQL5:   Mean Absolute Error: 10.6224997221680901

Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx)
Python  Mean Absolute Error: 10.62249788982753
MQL5:   Mean Absolute Error: 10.6224978898275282

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 13 décimales.

2.1.22.3. Représentation ONNX de mlp_regressor_float.onnx et mlp_regressor_double.onnx

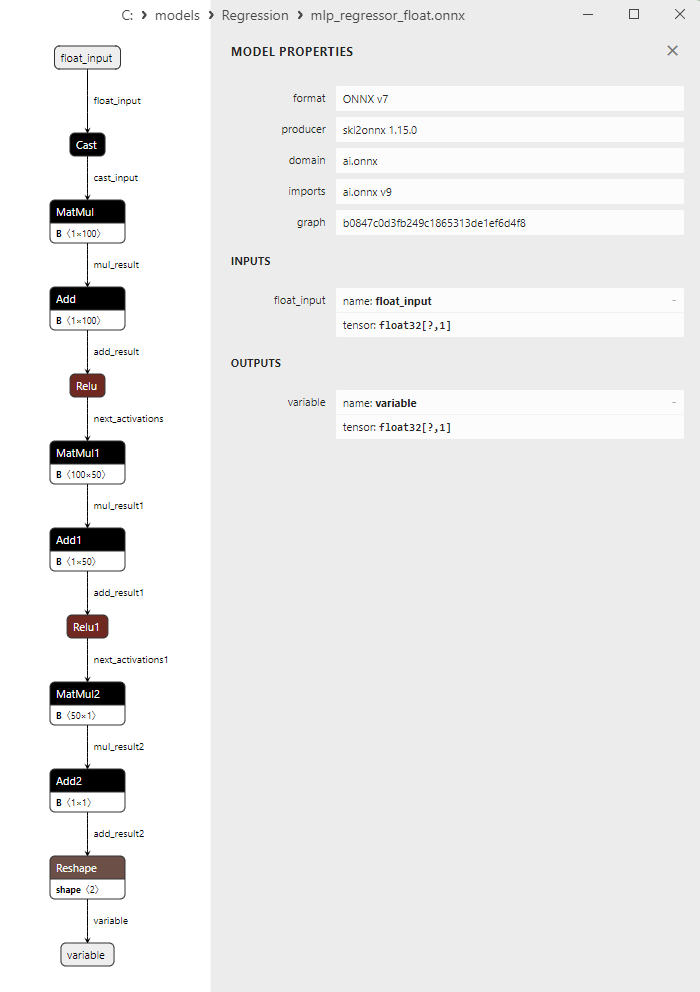
Fig. 74. Représentation ONNX du mlp_regressor_float.onnx dans Netron

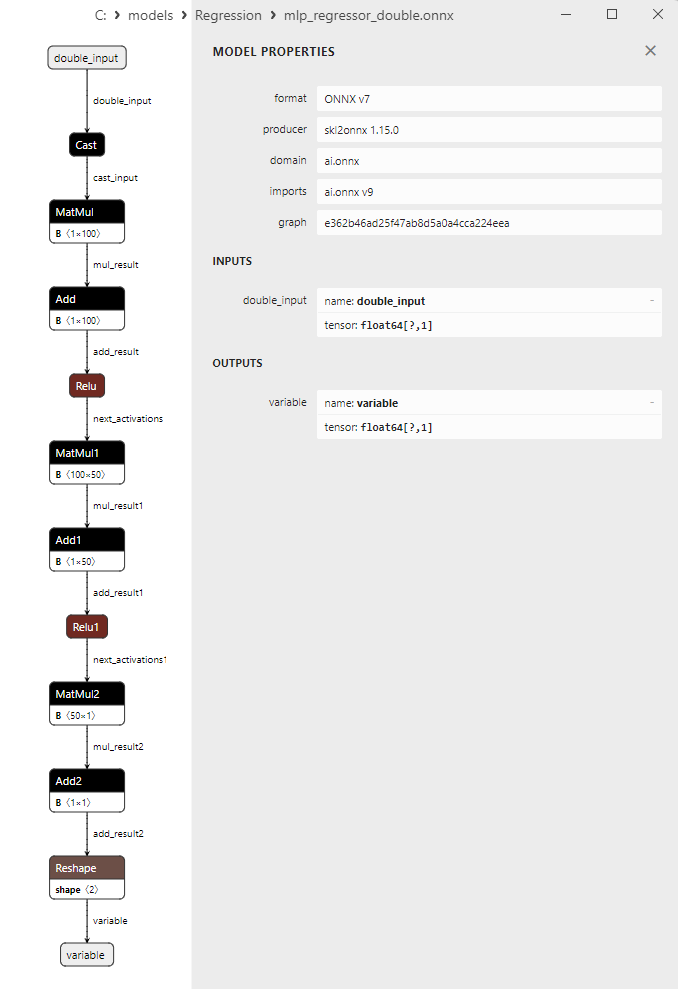
Fig. 75. Représentation ONNX de mlp_regressor_double.onnx dans Netron

2.1.23. sklearn.cross_decomposition.PLSRegression

PLSRegression (Partial Least Squares Regression) est une méthode d'apprentissage automatique utilisée pour résoudre les problèmes de régression.

Elle fait partie de la famille des méthodes PLS et est appliquée pour analyser et modéliser les relations entre deux ensembles de variables, dont l'un sert de prédicteurs et l'autre de variables cibles.

Comment fonctionne PLSRegression :

1. Données d'Entrée : Elle commence par deux ensembles de données, appelés X et Y. L'ensemble X contient des variables indépendantes (prédicteurs) et l'ensemble Y contient des variables cibles (dépendantes).
2. Sélection de combinaisons linéaires : PLSRegression identifie les combinaisons linéaires (composantes) dans les ensembles X et Y qui maximisent la covariance entre eux. Ces composantes sont appelées composantes PLS.
3. Maximiser la covariance : L'objectif principal de la régression PLS est de trouver les composantes PLS qui maximisent la covariance entre X et Y. Cela permet d'extraire les relations les plus informatives entre les prédicteurs et les variables cibles.
4. Entraînement du modèle : Une fois les composantes PLS trouvées, elles peuvent être utilisées pour créer un modèle qui prédit les valeurs Y en fonction de X.
5. Générer des prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs Y de nouvelles données à l'aide des valeurs X correspondantes.

Avantages de PLSRegression :

• Analyse de corrélation : PLSRegression permet d'analyser et de modéliser les corrélations entre deux ensembles de variables, ce qui peut être utile pour comprendre les relations entre les prédicteurs et les variables cibles.
• Réduction de la dimensionnalité : La méthode peut également être utilisée pour réduire la dimensionnalité des données en identifiant les composantes PLS les plus importantes.

Limites de la régression PLS :

• Sensibilité au choix du nombre de composants : La sélection du nombre optimal de composants PLS peut nécessiter une certaine expérimentation.
• Dépendance à l'égard de la structure des données : Les résultats de la régression PLS peuvent dépendre fortement de la structure des données et des corrélations entre elles.

La régression PLS est une méthode d'apprentissage automatique utilisée pour analyser et modéliser les corrélations entre deux ensembles de variables, dont l'un sert de prédicteurs et l'autre de variables cibles. Cette méthode permet d'étudier les relations entre les données et peut être utile pour réduire la dimensionnalité des données et prédire les valeurs des variables cibles sur la base de prédicteurs.

2.1.23.1. Code pour créer le modèle PLSRegression et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.cross_decomposition.PLSRegression, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# PLSRegression.py
# Le code démontre le processus d'apprentissage du modèle PLSRegression, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"

# crée un modèle de régression PLS
pls_model = PLSRegression(n_composants=1)

# ajuste le modèle aux données
pls_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = pls_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" Modèle ONNX (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  PLSRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281805
Python  
Python  PLSRegression ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382638567003
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.778145525764096
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  8
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  8
Python  
Python  PLSRegression ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281805
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  16

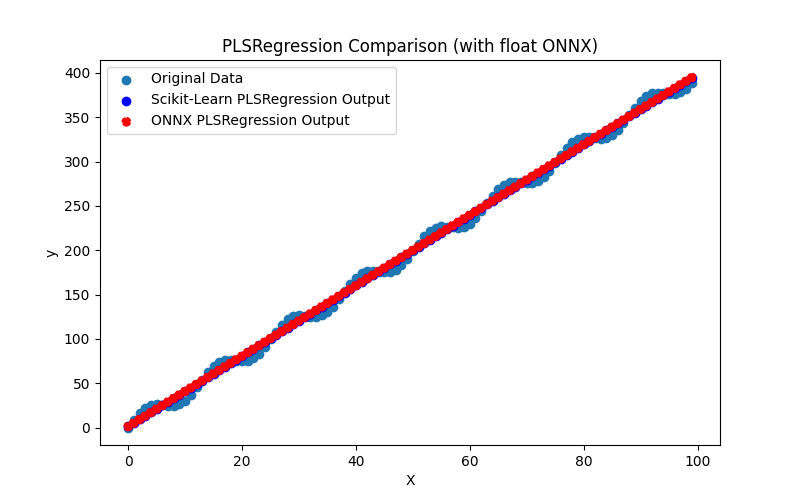
Fig. 76. Résultats de la régression PLS.py (ONNX float)

2.1.23.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles pls_regression_float.onnx et pls_regression_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                PLSRegression.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "PLSRegression"
#define   ONNXFilenameFloat  "pls_regression_float.onnx"
#define   ONNXFilenameDouble "pls_regression_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

PLSRegression (EURUSD,H1)       Testing ONNX float: PLSRegression (pls_regression_float.onnx)
PLSRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382638567003
PLSRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3477379221400145
PLSRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781455257640815
PLSRegression (EURUSD,H1)       
PLSRegression (EURUSD,H1)       Testing ONNX double: PLSRegression (pls_regression_double.onnx)
PLSRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
PLSRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3477379263364275
PLSRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781401712817839

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: PLSRegression (pls_regression_float.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477379221400145
       
Testing ONNX double: PLSRegression (pls_regression_double.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477379263364275

Précision de la MAE ONNX float : 8 décimales, Précision de la MAE ONNX double : 16 décimales.

2.1.23.3. Représentation ONNX de pls_regression_float.onnx et pls_regression_double.onnx

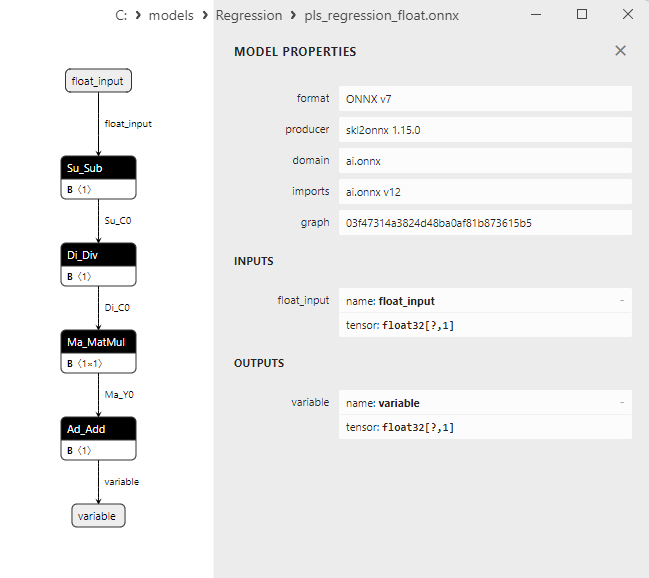
Fig. 77. Représentation ONNX de pls_regression_float.onnx dans Netron

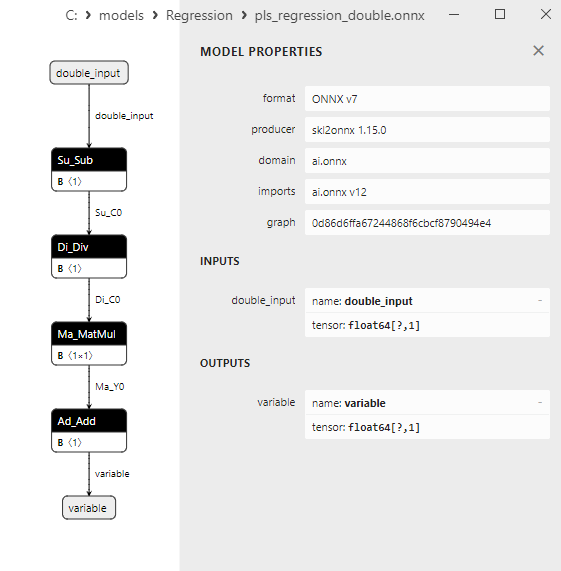
Fig. 78. Représentation ONNX de pls_regression_double.onnx dans Netron

2.1.24. sklearn.linear_model.TweedieRegressor

TweedieRegressor est une méthode de régression conçue pour résoudre les problèmes de régression à l'aide de la distribution de Tweedie. La distribution de Tweedie est une distribution de probabilité qui peut décrire un large éventail de données, y compris des données dont la structure de variance varie. TweedieRegressor est utilisé dans les tâches de régression où la variable cible possède des caractéristiques qui s'alignent sur la distribution de Tweedie.

Comment fonctionne TweedieRegressor :

1. Variable cible et distribution de Tweedie : TweedieRegressor suppose que la variable cible suit une distribution de Tweedie. La distribution de Tweedie dépend du paramètre "p", qui détermine la forme de la distribution et le degré de variance.
2. Entraînement du modèle : TweedieRegressor entraîne un modèle de régression pour prédire la variable cible sur la base de variables indépendantes (caractéristiques). Le modèle maximise la vraisemblance pour les données correspondant à la distribution de Tweedie.
3. Choix du paramètre "p" : La sélection du paramètre 'p' est un aspect crucial de l'utilisation de TweedieRegressor. Ce paramètre définit la forme et la variance de la distribution. Différentes valeurs de "p" correspondent à différents types de données ; par exemple, p=1 correspond à la distribution de Poisson, tandis que p=2 correspond à la distribution normale.
4. Transformer les réponses : Parfois, le modèle peut nécessiter des transformations des réponses (variables cibles) avant l'entraînement. Cette transformation concerne le paramètre "p" et peut impliquer des fonctions logarithmiques ou d'autres transformations pour se conformer à la distribution de Tweedie.

Avantages de TweedieRegressor :

• Capacité à modéliser des données à variance variable : La distribution de Tweedie peut s'adapter à des données ayant des structures de variance différentes, ce qui est précieux pour les données du monde réel où la variance peut varier.
• Variété de paramètres "p" : La possibilité de choisir différentes valeurs "p" permet de modéliser différents types de données.

Limites de TweedieRegressor :

• Complexité du choix du paramètre "p" : La sélection de la valeur "p" correcte peut nécessiter des connaissances sur les données et une expérimentation.
• Conformité à la distribution de Tweedie : Pour une application réussie de TweedieRegressor, la variable cible doit correspondre à la distribution de Tweedie. La non-conformité peut entraîner de mauvaises performances du modèle.

TweedieRegressor est une méthode de régression qui utilise la distribution de Tweedie pour modéliser des données avec des structures de variance variables. Cette méthode est utile dans les tâches de régression où la variable cible est conforme à la distribution de Tweedie et peut être réglée avec différentes valeurs du paramètre "p" pour une meilleure adaptation des données.

2.1.24.1. Code pour créer le modèle TweedieRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.TweedieRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# TweedieRegressor.py
# Le code démontre le processus d'entraînement du modèle TweedieRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"

# crée un modèle Tweedie Regressor
regression_model = TweedieRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_double))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

2023.10.31 11:39:36.223 Python  TweedieRegressor Original model (double)
2023.10.31 11:39:36.223 Python  R-squared (Coefficient of determination): 0.9962368328117072
2023.10.31 11:39:36.223 Python  Mean Absolute Error: 6.342397897667562
2023.10.31 11:39:36.223 Python  Mean Squared Error: 49.797082198408745
2023.10.31 11:39:36.223 Python  
2023.10.31 11:39:36.223 Python  TweedieRegressor ONNX model (float)
2023.10.31 11:39:36.223 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_float.onnx
2023.10.31 11:39:36.253 Python  Information about input tensors in ONNX:
2023.10.31 11:39:36.253 Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
2023.10.31 11:39:36.253 Python  Information about output tensors in ONNX:
2023.10.31 11:39:36.253 Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
2023.10.31 11:39:36.253 Python  R-squared (Coefficient of determination) 0.9962368338709323
2023.10.31 11:39:36.253 Python  Mean Absolute Error: 6.342397072978867
2023.10.31 11:39:36.253 Python  Mean Squared Error: 49.797068181938165
2023.10.31 11:39:36.253 Python  R^2 matching decimal places:  8
2023.10.31 11:39:36.253 Python  MAE matching decimal places:  6
2023.10.31 11:39:36.253 Python  MSE matching decimal places:  4
2023.10.31 11:39:36.253 Python  float ONNX model precision:  6
2023.10.31 11:39:36.613 Python  
2023.10.31 11:39:36.613 Python  TweedieRegressor ONNX model (double)
2023.10.31 11:39:36.613 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_double.onnx
2023.10.31 11:39:36.613 Python  Information about input tensors in ONNX:
2023.10.31 11:39:36.613 Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
2023.10.31 11:39:36.613 Python  Information about output tensors in ONNX:
2023.10.31 11:39:36.628 Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
2023.10.31 11:39:36.628 Python  R-squared (Coefficient of determination) 0.9962368328117072
2023.10.31 11:39:36.628 Python  Mean Absolute Error: 6.342397897667562
2023.10.31 11:39:36.628 Python  Mean Squared Error: 49.797082198408745
2023.10.31 11:39:36.628 Python  R^2 matching decimal places:  16
2023.10.31 11:39:36.628 Python  MAE matching decimal places:  15
2023.10.31 11:39:36.628 Python  MSE matching decimal places:  15
2023.10.31 11:39:36.628 Python  double ONNX model precision:  15

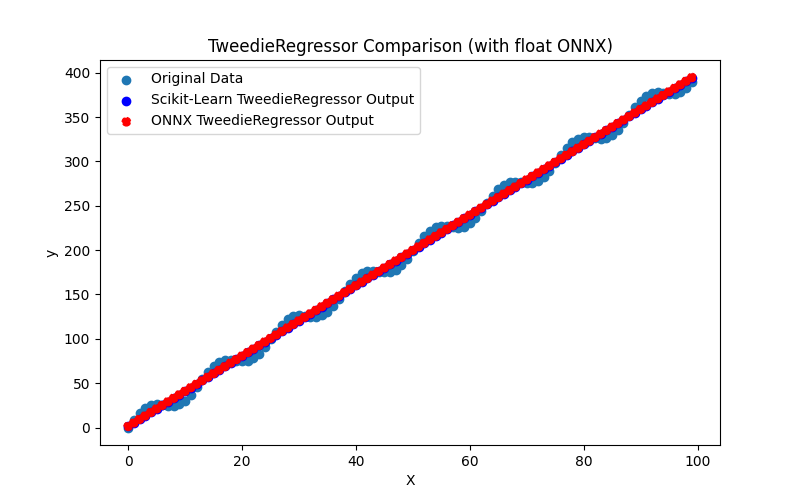
Fig. 79. Résultats de TweedieRegressor.py (ONNX float)

2.1.24.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles tweedie_regressor_float.onnx et tweedie_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                             TweedieRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "TweedieRegressor"
#define   ONNXFilenameFloat  "tweedie_regressor_float.onnx"
#define   ONNXFilenameDouble "tweedie_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

2023.10.31 11:42:20.113 TweedieRegressor (EURUSD,H1)    Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx)
2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962368338709323
2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3423970729788666
2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7970681819381653
2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1)    
2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1)    Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx)
2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962368328117072
2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3423978976675608
2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7970821984087593

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx)
Python  Mean Absolute Error: 6.342397897667562
MQL5:   Mean Absolute Error: 6.3423970729788666

Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx)
Python  Mean Absolute Error: 6.342397897667562
MQL5:   Mean Absolute Error: 6.3423978976675608

Précision de la MAE ONNX float : 6 décimales, Précision de la MAE ONNX double : 14 décimales.

2.1.24.3. Représentation ONNX de tweedie_regressor_float.onnx et tweedie_regressor_double.onnx

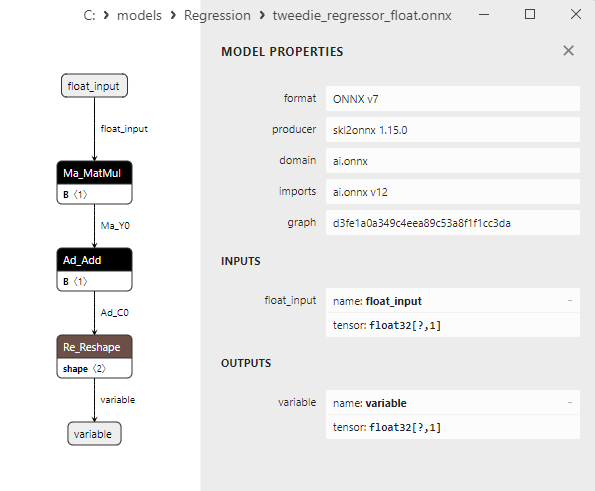
Fig. 80. Représentation ONNX de tweedie_regressor_float.onnx dans Netron

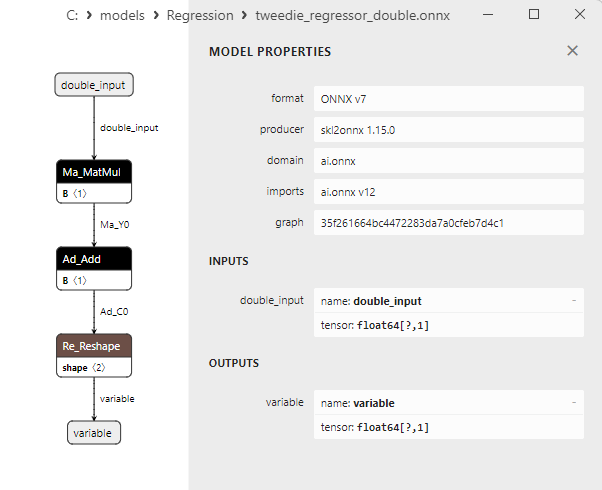
Fig. 81. Représentation ONNX de tweedie_regressor_double.onnx dans Netron

2.1.25. sklearn.linear_model.PoissonRegressor

PoissonRegressor est une méthode d'apprentissage automatique appliquée à la résolution de tâches de régression basées sur la distribution de Poisson.

Cette méthode convient lorsque la variable dépendante (variable cible) est une donnée de comptage, représentant le nombre d'événements qui se sont produits au cours d'une période de temps fixe ou dans un intervalle spatial fixe. PoissonRegressor modélise la relation entre les prédicteurs (variables indépendantes) et la variable cible en supposant que cette relation est conforme à la distribution de Poisson.

Comment fonctionne PoissonRegressor :

1. Données d'Entrée : On part d'un ensemble de données comprenant des caractéristiques (variables indépendantes) et la variable cible, qui représente le nombre d'événements.
2. Distribution de Poisson : La méthode PoissonRegressor modélise la variable cible en supposant qu'elle suit la distribution de Poisson. La distribution de Poisson convient à la modélisation d'événements qui se produisent à une intensité moyenne fixe dans un intervalle de temps ou une zone spatiale donnés.
3. Entraînement du modèle : PoissonRegressor forme un modèle qui estime les paramètres de la distribution de Poisson, en tenant compte des prédicteurs. Le modèle tente de trouver la meilleure adéquation aux données observées en utilisant la fonction de vraisemblance qui correspond à la distribution de Poisson.
4. Prédiction des valeurs de comptage : Après l'apprentissage, le modèle peut être utilisé pour prédire les valeurs de comptage (le nombre d'événements) sur de nouvelles données, et ces prédictions suivent également la distribution de Poisson.

Avantages de PoissonRegressor :

• Convient pour les données de comptage : PoissonRegressor convient aux tâches où la variable cible représente des données de comptage, telles que le nombre d'ordres, d'appels, etc.
• Spécificité de la distribution : Comme le modèle adhère à la distribution de Poisson, il peut être plus précis pour les données qui sont bien décrites par cette distribution.

Limites de PoissonRegressor :

• Ne convient que pour les données de comptage : PoissonRegressor n'est pas adapté à la régression lorsque la variable cible est continue et non comptée.
• Dépendance à l'égard de la sélection des caractéristiques : La qualité du modèle peut dépendre fortement de la sélection et de l'ingénierie des caractéristiques.

PoissonRegressor est une méthode d'apprentissage automatique utilisée pour résoudre les tâches de régression lorsque la variable cible représente des données de comptage et est modélisée à l'aide de la distribution de Poisson. Cette méthode est utile pour les tâches liées à des événements se produisant à une intensité fixe dans des intervalles de temps ou d'espace spécifiques.

2.1.25.1. Code pour créer le modèle PoissonRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.PoissonRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# PoissonRegressor.py
# Le code démontre le processus d'apprentissage du modèle PoissonRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# Fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"

# crée un modèle PoissonRegressor
regression_model = PoissonRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_double))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  PoissonRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9204304782362495
Python  Mean Absolute Error: 27.59790466048524
Python  Mean Squared Error: 1052.9242570153044
Python  
Python  PoissonRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9204305082536851
Python  Mean Absolute Error: 27.59790825165078
Python  Mean Squared Error: 1052.9238598018305
Python  R^2 matching decimal places:  6
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  2
Python  float ONNX model precision:  5
Python  
Python  PoissonRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9204304782362495
Python  Mean Absolute Error: 27.59790466048524
Python  Mean Squared Error: 1052.9242570153044
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  13
Python  double ONNX model precision:  14

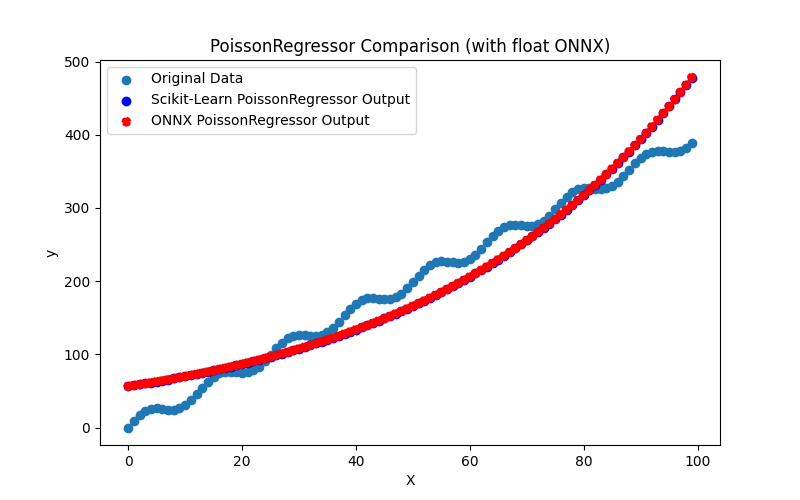
Fig. 82. Résultats du PoissonRegressor.py (ONNX float)

2.1.25.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles poisson_regressor_float.onnx et poisson_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                             PoissonRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "PoissonRegressor"
#define   ONNXFilenameFloat  "poisson_regressor_float.onnx"
#define   ONNXFilenameDouble "poisson_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

PoissonRegressor (EURUSD,H1)    Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx)
PoissonRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9204305082536851
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 27.5979082516507788
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 1052.9238598018305311
PoissonRegressor (EURUSD,H1)    
PoissonRegressor (EURUSD,H1)    Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx)
PoissonRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9204304782362493
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 27.5979046604852343
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 1052.9242570153051020

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx)
Python  Mean Absolute Error: 27.59790466048524
MQL5:   Mean Absolute Error: 27.5979082516507788
    
Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx)
Python  Mean Absolute Error: 27.59790466048524
MQL5:   Mean Absolute Error: 27.5979046604852343

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 13 décimales.

2.1.25.3. Représentation ONNX du poisson_regressor_float.onnx et du poisson_regressor_double.onnx

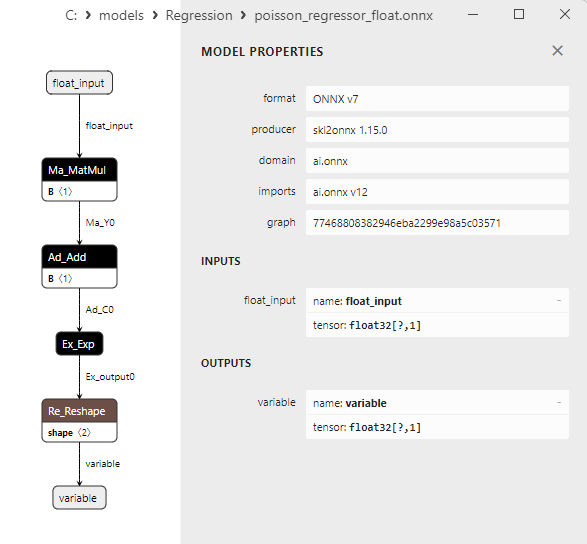
Fig. 83. Représentation ONNX de poisson_regressor_float.onnx dans Netron

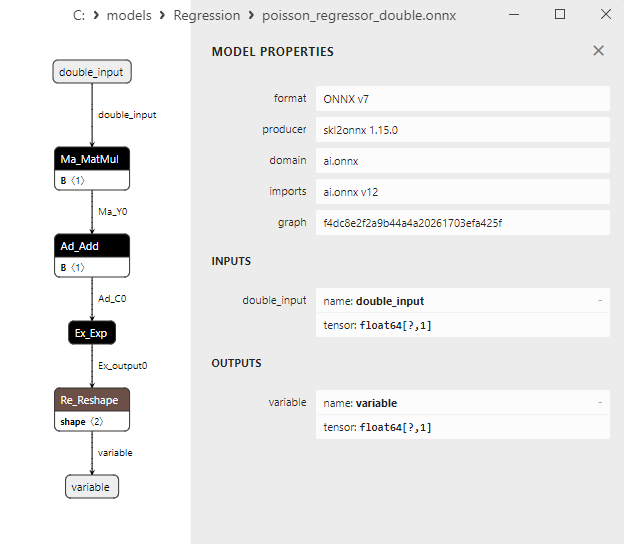
Fig. 84. Représentation ONNX de poisson_regressor_double.onnx dans Netron

2.1.26. sklearn.neighbors.RadiusNeighborsRegressor

RadiusNeighborsRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression. Il s'agit d'une variante de la méthode des k-Nearest Neighbors (k-NN, ou Voisins Les Plus Proches) conçue pour prédire les valeurs de la variable cible sur la base des voisins les plus proches dans l'espace des caractéristiques. Mais au lieu d'un nombre fixe de voisins (comme dans la méthode k-NN), RadiusNeighborsRegressor utilise un rayon fixe pour déterminer les voisins de chaque échantillon.

Fonctionnement de RadiusNeighborsRegressor :

1. Données d'Entrée : Commencer par un ensemble de données comprenant des caractéristiques (variables indépendantes) et la variable cible (continue).
2. Réglage du rayon : RadiusNeighborsRegressor nécessite la définition d'un rayon fixe pour déterminer les voisins les plus proches de chaque échantillon dans l'espace des caractéristiques.
3. Définition d’un voisin : Pour chaque échantillon, tous les points de données situés dans le rayon spécifié sont déterminés, devenant ainsi les voisins de cet échantillon.
4. Moyenne pondérée : Pour prédire la valeur de la variable cible pour chaque échantillon, les valeurs des variables cibles de ses voisins sont utilisées. Cette opération est souvent réalisée à l'aide d'une moyenne pondérée, où les poids dépendent de la distance entre les échantillons.
5. Prédiction : Après l'apprentissage, le modèle peut être utilisé pour prédire les valeurs de la variable cible sur de nouvelles données en se basant sur les voisins les plus proches dans l'espace des caractéristiques.

Avantages de RadiusNeighborsRegressor :

• Polyvalence : RadiusNeighborsRegressor peut être utilisé pour les tâches de régression, en particulier lorsque le nombre de voisins peut varier de manière significative en fonction du rayon.
• Résistance aux valeurs aberrantes : Une approche basée sur le voisinage peut être résistante aux valeurs aberrantes car le modèle ne prend en compte que les points de données proches.

Limites de RadiusNeighborsRegressor :

• Dépendance à la sélection du rayon : Le choix du bon rayon peut nécessiter des ajustements et des expérimentations.
• Complexité de calcul : Le traitement de grands ensembles de données peut nécessiter d'importantes ressources de calcul.

RadiusNeighborsRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression basées sur la méthode des k-Nearest Neighbors avec un rayon fixe. Cette méthode peut s'avérer précieuse dans les situations où le nombre de voisins peut varier en fonction du rayon et dans les cas où les données contiennent des valeurs aberrantes.

2.1.26.1. Code pour créer le RadiusNeighborsRegressor et l'exporter vers ONNX pour les float et double

Ce code crée le modèle sklearn.neighbors.RadiusNeighborsRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# RadiusNeighborsRegressor.py
# Le code démontre le processus d'entraînement du modèle RadiusNeighborsRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"

# crée un modèle RadiusNeighborsRegressor
regression_model = RadiusNeighborsRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  RadiusNeighborsRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9999521132921395
Python  Mean Absolute Error: 0.591458244376554
Python  Mean Squared Error: 0.6336732353950723
Python  
Python  RadiusNeighborsRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999999971
Python  Mean Absolute Error: 4.393654615473253e-06
Python  Mean Squared Error: 3.829042036424747e-11
Python  R^2 matching decimal places:  4
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  RadiusNeighborsRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 1.0
Python  Mean Absolute Error: 0.0
Python  Mean Squared Error: 0.0
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  double ONNX model precision:  0

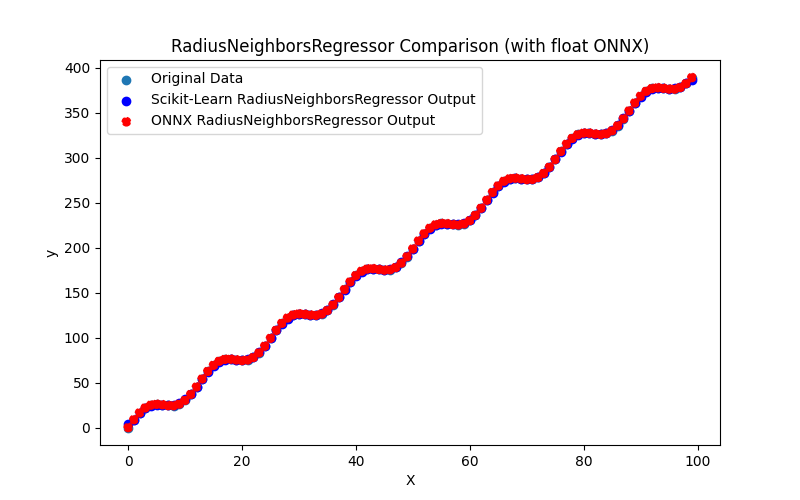
Fig. 85. Résultats de RadiusNeighborsRegressor.py (ONNX float)

2.1.26.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles radius_neighbors_regressor_float.onnx et radius_neighbors_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                     RadiusNeighborsRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RadiusNeighborsRegressor"
#define   ONNXFilenameFloat  "radius_neighbors_regressor_float.onnx"
#define   ONNXFilenameDouble "radius_neighbors_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

RadiusNeighborsRegressor (EURUSD,H1)    Testing ONNX float: RadiusNeighborsRegressor (radius_neighbors_regressor_float.onnx)
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9999999999999971
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000043936546155
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000382904
RadiusNeighborsRegressor (EURUSD,H1)    
RadiusNeighborsRegressor (EURUSD,H1)    Testing ONNX double: RadiusNeighborsRegressor (radius_neighbors_regressor_double.onnx)
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 1.0000000000000000
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000000000000000
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000000000

2.1.26.3. Représentation ONNX du radius_neighbors_regressor_float.onnx et du radius_neighbors_regressor_double.onnx

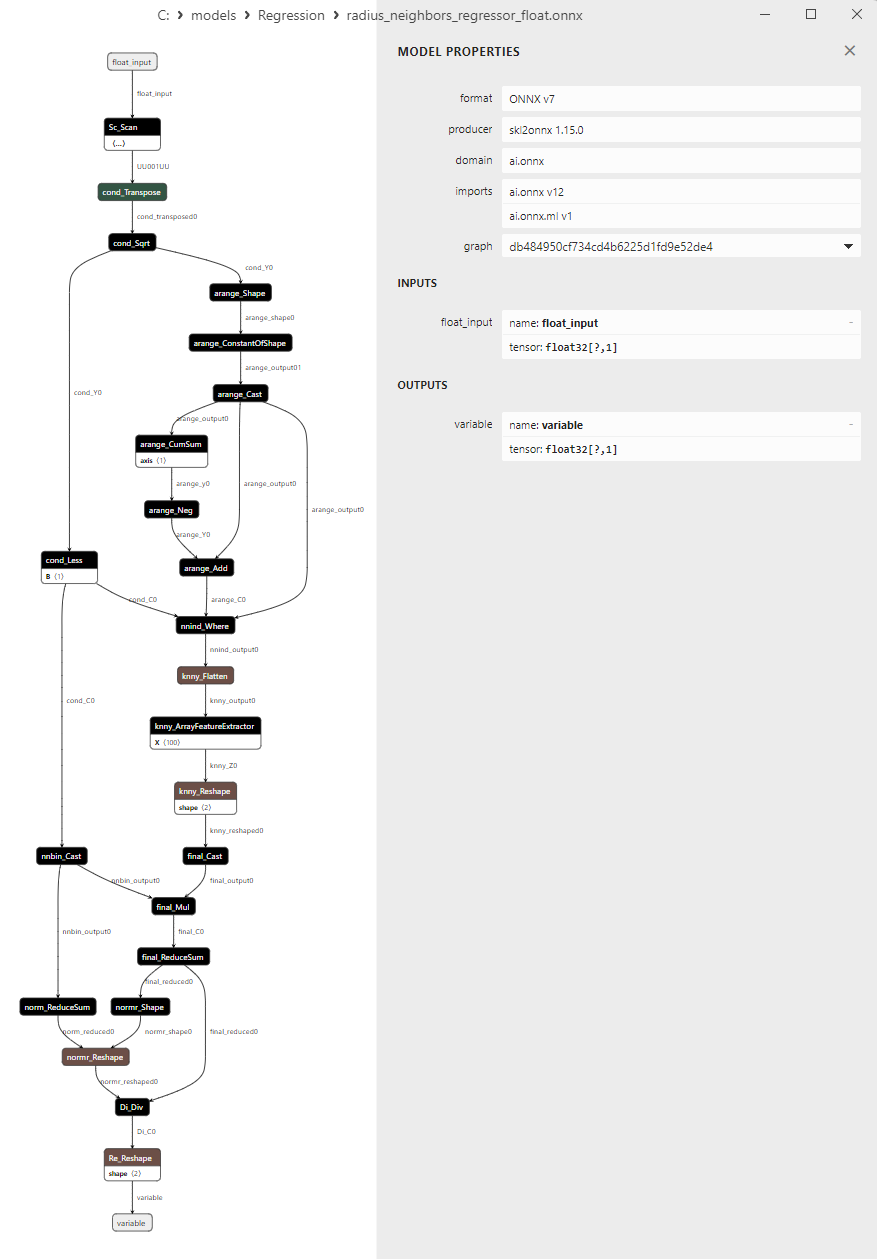
Fig. 86. Représentation ONNX de radius_neighbors_regressor_float.onnx dans Netron

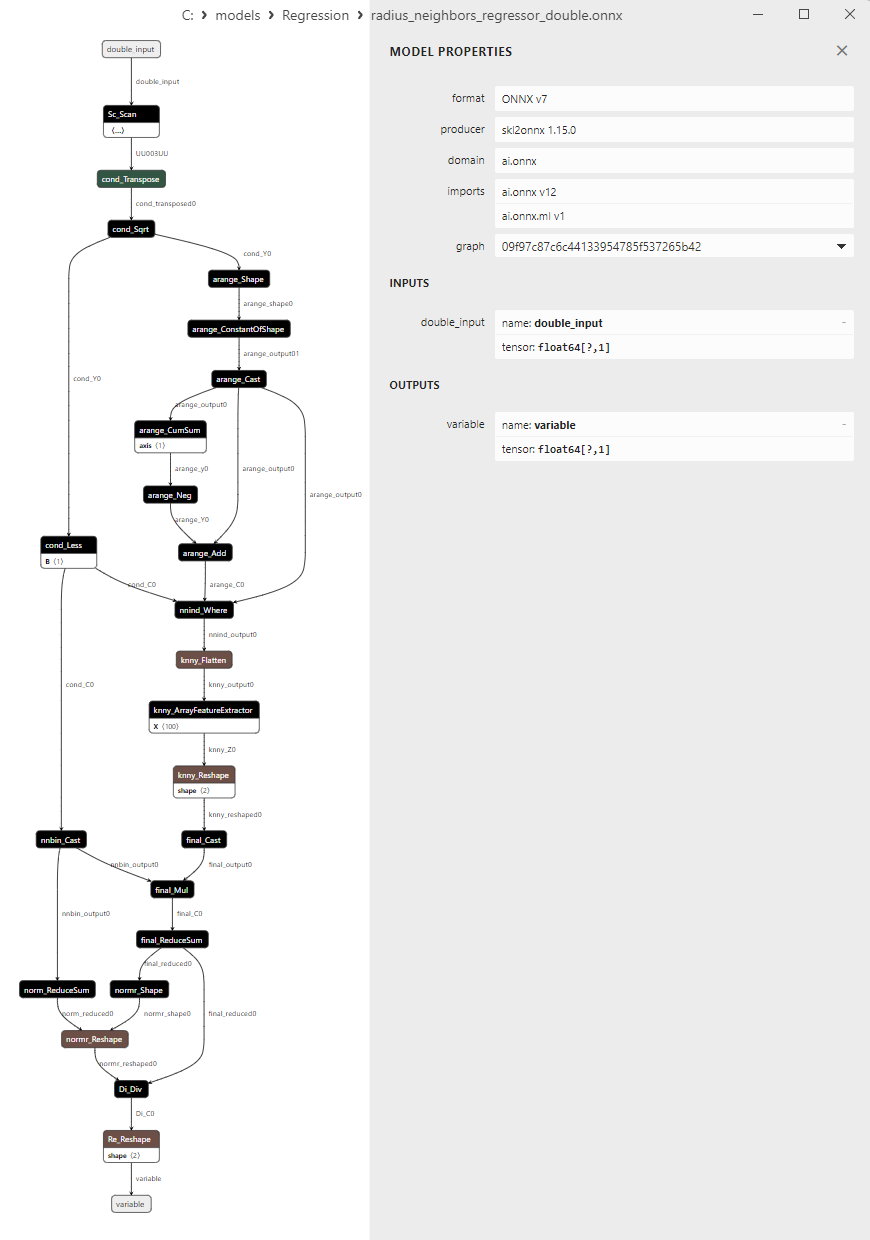
Fig. 87. ONNX-représentation de radius_neighbors_regressor_double.onnx dans Netron

2.1.27. sklearn.neighbors.KNeighborsRegressor

KNeighborsRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression.

Il appartient à la catégorie des algorithmes k-NN (k-Nearest Neighbors) et est utilisé pour prédire les valeurs numériques de la variable cible sur la base de la proximité (similarité) entre les objets dans l'ensemble de données d'apprentissage.

Fonctionnement de KNeighborsRegressor :

1. Données d'Entrée : Il commence par l'ensemble de données initial, comprenant les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Sélection du nombre de voisins (k) : Vous devez choisir le nombre de voisins les plus proches (k) à prendre en compte lors de la prédiction. Ce nombre est l'un des hyper-paramètres du modèle.
3. Calculer la proximité : Pour les nouvelles données (points pour lesquels des prédictions sont nécessaires), la distance ou la similarité entre ces données et tous les objets de l'ensemble de données d'apprentissage est calculée.
4. Choix des k voisins les plus proches : les k objets de l'ensemble de données d'apprentissage les plus proches des nouvelles données sont sélectionnés.
5. Prédiction : Pour les tâches de régression, la prédiction de la valeur de la variable cible pour de nouvelles données est calculée comme la valeur moyenne des variables cibles des k plus proches voisins.

Avantages de KNeighborsRegressor :

• Facilité d'utilisation : KNeighborsRegressor est un algorithme simple qui ne nécessite pas de prétraitement complexe des données.
• Nature non paramétrique : La méthode ne suppose pas une forme fonctionnelle spécifique de dépendance entre les caractéristiques et la variable cible, ce qui permet de modéliser diverses relations.
• Reproductibilité : Les résultats de KNeighborsRegressor peuvent être reproduits car les prédictions sont basées sur la proximité des données.

Limites de KNeighborsRegressor :

• Complexité de calcul : Le calcul des distances entre tous les points de l'ensemble de données d'apprentissage peut s'avérer coûteux en termes de calculs pour de grands volumes de données.
• Sensibilité au choix du nombre de voisins : La sélection de la valeur optimale de k nécessite un réglage et peut avoir un impact significatif sur les performances du modèle.
• Sensibilité au bruit : La méthode peut être sensible au bruit des données et aux valeurs aberrantes.

KNeighborsRegressor est utile dans les tâches de régression où il est essentiel de prendre en compte le voisinage des objets pour prédire la variable cible. Elle peut être particulièrement utile dans les situations où la relation entre les caractéristiques et la variable cible est non linéaire et complexe.

2.1.27.1. Code pour créer le modèle KNeighborsRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.neighbors.KNeighborsRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# KNeighborsRegressor.py
# Le code démontre le processus d'entraînement du modèle KNeighborsRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"

# crée un modèle de Régresseur de type KNeighbors
kneighbors_model = KNeighborsRegressor(n_neighbors=5)

# ajuste le modèle aux données
kneighbors_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = kneighbors_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  KNeighborsRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9995599863346534
Python  Mean Absolute Error: 1.7414210057117578
Python  Mean Squared Error: 5.822594523532273
Python  
Python  KNeighborsRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9995599867417418
Python  Mean Absolute Error: 1.7414195457976402
Python  Mean Squared Error: 5.8225891366283875
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  4
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  4
Python  
Python  KNeighborsRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9995599863346534
Python  Mean Absolute Error: 1.7414210057117583
Python  Mean Squared Error: 5.822594523532269
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  13
Python  double ONNX model precision:  14

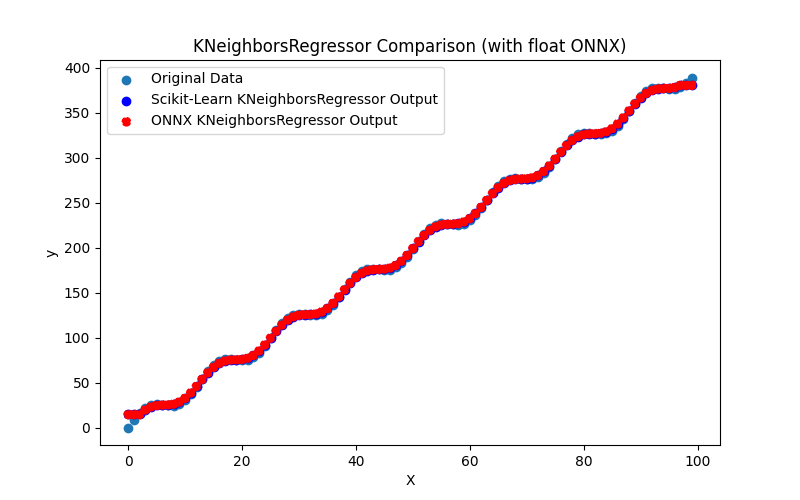
Fig. 88. Résultats de KNeighborsRegressor.py (ONNX float)

2.1.27.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles kneighbors_regressor_float.onnx et kneighbors_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                          KNeighborsRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "KNeighborsRegressor"
#define   ONNXFilenameFloat  "kneighbors_regressor_float.onnx"
#define   ONNXFilenameDouble "kneighbors_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

KNeighborsRegressor (EURUSD,H1) Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx)
KNeighborsRegressor (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9995599860116634
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Absolute Error: 1.7414200607817711
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Squared Error: 5.8225987975798184
KNeighborsRegressor (EURUSD,H1) 
KNeighborsRegressor (EURUSD,H1) Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx)
KNeighborsRegressor (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9995599863346534
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Absolute Error: 1.7414210057117601
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Squared Error: 5.8225945235322705

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx)
Python  Mean Absolute Error: 1.7414210057117578
MQL5:   Mean Absolute Error: 1.7414200607817711
 
Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx)
Python  Mean Absolute Error: 1.7414210057117578
MQL5:   Mean Absolute Error: 1.7414210057117601

Précision de la MAE ONNX float : 5 décimales, Précision de la MAX ONNX double : 13 décimales.

2.1.27.3. Représentation ONNX de kneighbors_regressor_float.onnx et kneighbors_regressor_double.onnx

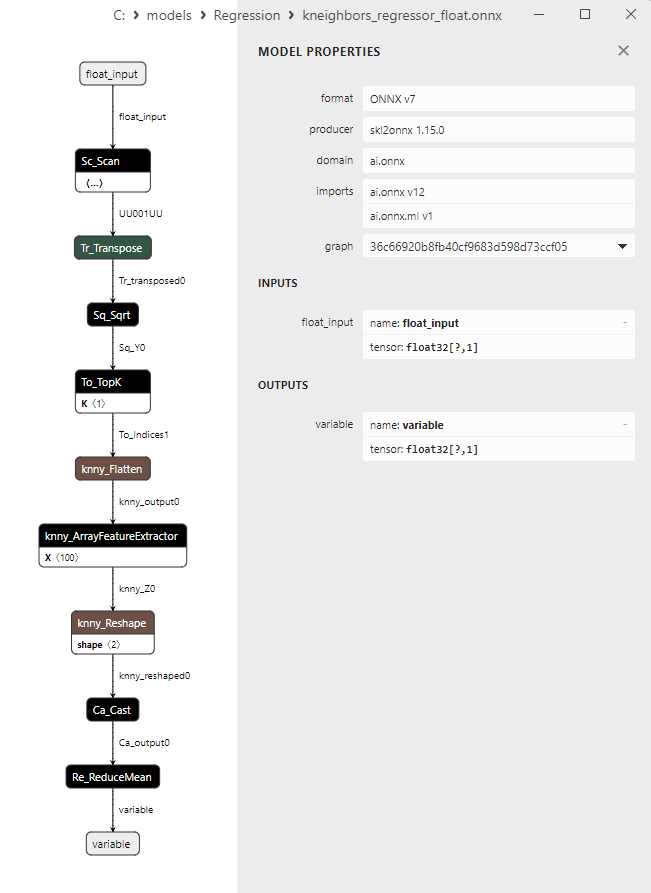
Fig. 89. Représentation ONNX de kneighbors_regressor_float.onnx dans Netron

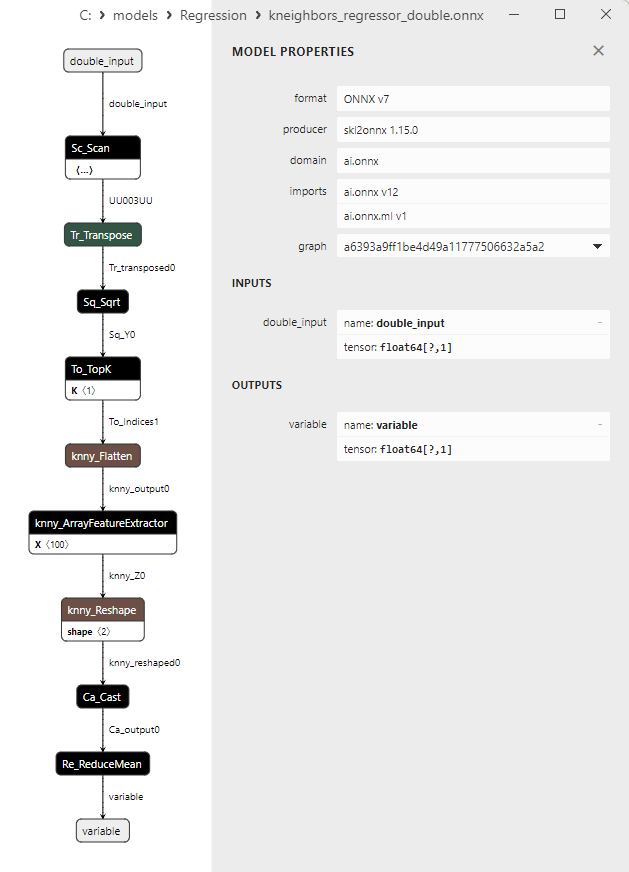
Fig. 90. Représentation ONNX de kneighbors_regressor_double.onnx dans Netron

2.1.28. sklearn.gaussian_process.GaussianProcessRegressor

GaussianProcessRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression qui permet de modéliser l'incertitude dans les prédictions.

Le Processus Gaussien (GP) est un outil puissant dans l'apprentissage automatique Bayésien et est utilisé pour modéliser des fonctions complexes et prédire les valeurs des variables cibles tout en tenant compte de l'incertitude.

Fonctionnement du GaussianProcessRegressor :

1. Données d'Entrée : Il commence par l'ensemble de données initial, comprenant les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Modélisation du processus Gaussien : Le processus Gaussien utilise un processus Gaussien, qui est un ensemble de variables aléatoires décrites par une distribution Gaussienne (normale). Le GP modélise non seulement les valeurs moyennes de chaque point de données, mais aussi la covariance (ou similarité) entre ces points.
3. Choix de la fonction de covariance : La sélection de la fonction de covariance (ou noyau) qui détermine l'interconnexion et la force entre les points de données est un aspect crucial du GP. Différentes fonctions de covariance peuvent être utilisées en fonction de la nature des données et de la tâche.
4. Entraînement du modèle : GaussianProcessRegressor entraîne le GP à l'aide des données d'apprentissage. Pendant l'apprentissage, le modèle ajuste les paramètres de la fonction de covariance et évalue l'incertitude des prédictions.
5. Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs des variables cibles pour de nouvelles données. Une caractéristique importante du GP est qu'il prédit non seulement la valeur moyenne, mais aussi un intervalle de confiance qui estime le niveau de confiance dans les prédictions.

Avantages de GaussianProcessRegressor :

• Modélisation de l'incertitude : Le GP permet de tenir compte de l'incertitude dans les prédictions, ce qui est utile dans les tâches où il est crucial de connaître la confiance dans les valeurs prédites.
• Flexibilité : Le GP peut modéliser différentes fonctions et ses fonctions de covariance peuvent être adaptées à différents types de données.
• Peu d'hyper-paramètres : La généralisation a un nombre relativement faible d'hyper-paramètres, ce qui simplifie la mise au point du modèle.

Limites de GaussianProcessRegressor :

• Complexité de calcul : Le GP peut s'avérer coûteux en termes de calcul, surtout lorsqu'il s'agit d'un grand volume de données.
• Inefficacité dans les espaces de haute dimension : Le GP peut perdre de son efficacité dans les tâches comportant de nombreuses caractéristiques en raison de la malédiction de la dimensionnalité.

GaussianProcessRegressor est utile dans les tâches de régression où la modélisation de l'incertitude et la fourniture de prédictions fiables sont cruciales. Cette méthode est fréquemment utilisée dans l'apprentissage automatique bayésien et dans la méta-analyse.

2.1.28.1. Code pour créer le modèle GaussianProcessRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.gaussian_process.GaussianProcessRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# GaussianProcessRegressor.py
# Le code démontre le processus d'apprentissage du modèle GaussianProcessRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des décimales dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"

# crée un modèle GaussianProcessRegressor
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)

# ajuste le modèle aux données
gp_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = gp_model.predict(X, return_std=False)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_double))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  GaussianProcessRegressor Original model (double)
Python  R-squared (Coefficient of determination): 1.0
Python  Mean Absolute Error: 3.504041501400934e-13
Python  Mean Squared Error: 1.6396606443650807e-25
Python  
Python  GaussianProcessRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: GPmean, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999999936
Python  Mean Absolute Error: 6.454076974495848e-06
Python  Mean Squared Error: 8.493606782250733e-11
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  GaussianProcessRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: GPmean, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 1.0
Python  Mean Absolute Error: 3.504041501400934e-13
Python  Mean Squared Error: 1.6396606443650807e-25
Python  R^2 matching decimal places:  1
Python  MAE matching decimal places:  19
Python  MSE matching decimal places:  20
Python  double ONNX model precision:  19

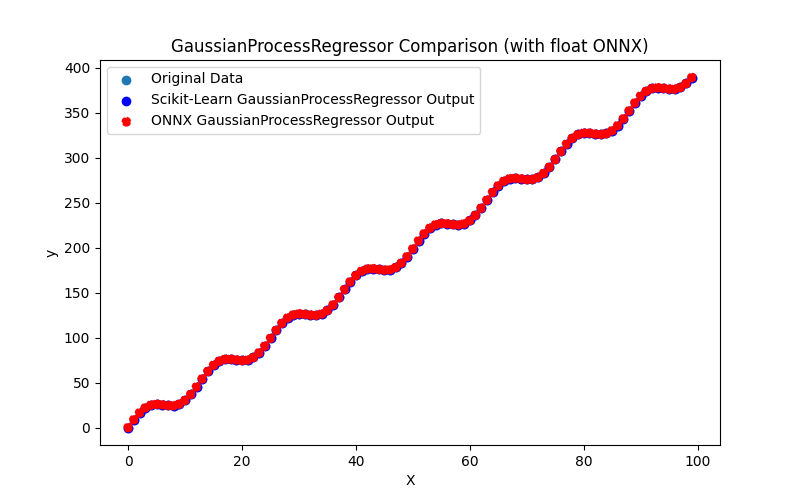
Fig. 91. Résultats de GaussianProcessRegressor.py (ONNX float)

2.1.28.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés gaussian_process_regressor_float.onnx et gaussian_process_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                     GaussianProcessRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "GaussianProcessRegressor"
#define   ONNXFilenameFloat  "gaussian_process_regressor_float.onnx"
#define   ONNXFilenameDouble "gaussian_process_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

GaussianProcessRegressor (EURUSD,H1)    Testing ONNX float: GaussianProcessRegressor (gaussian_process_regressor_float.onnx)
GaussianProcessRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9999999999999936
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000064540769745
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000849361
GaussianProcessRegressor (EURUSD,H1)    
GaussianProcessRegressor (EURUSD,H1)    Testing ONNX double: GaussianProcessRegressor (gaussian_process_regressor_double.onnx)
GaussianProcessRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 1.0000000000000000
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000000000003504
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000000000

2.1.28.3. Représentation ONNX du gaussian_process_regressor_float.onnx et du gaussian_process_regressor_double.onnx

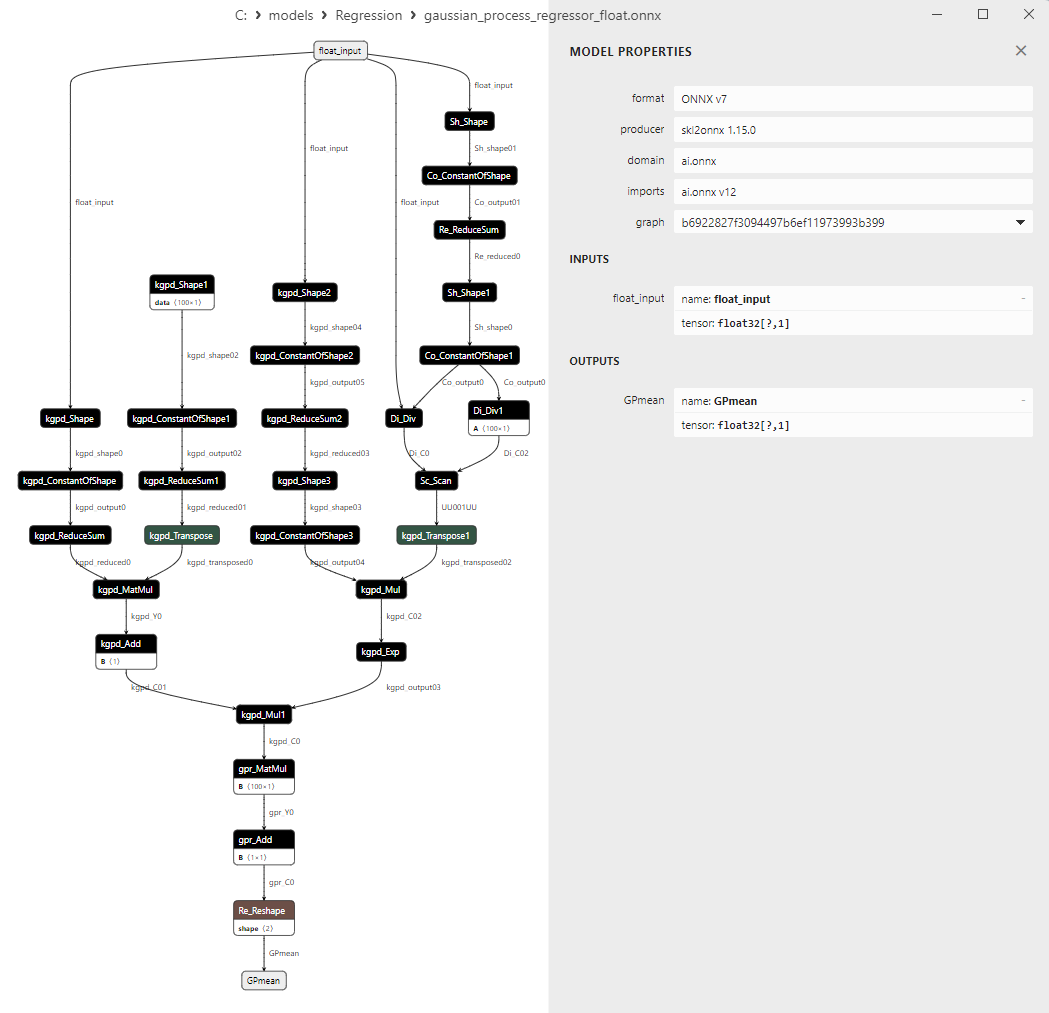
Fig. 92. Représentation ONNX du gaussian_process_regressor_float.onnx dans Netron

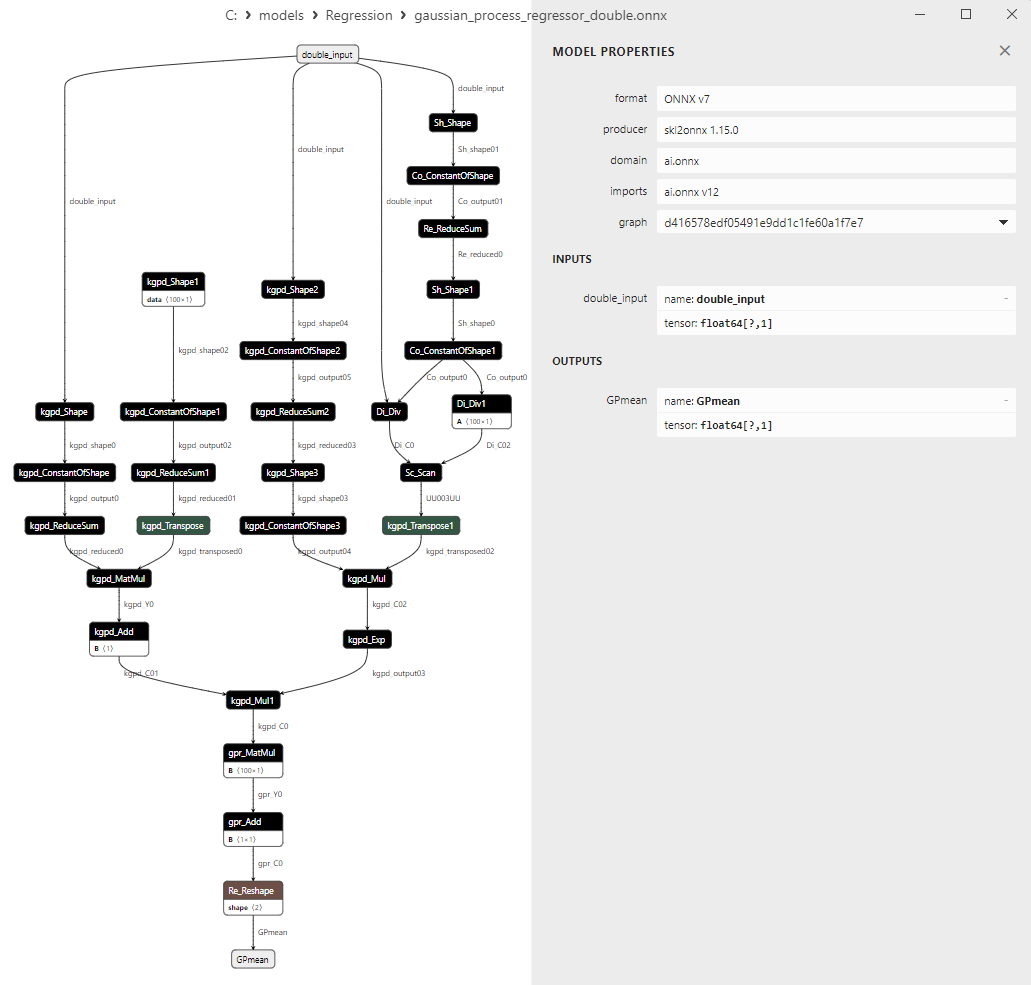
Fig. 93. Représentation ONNX du gaussian_process_regressor_double.onnx dans Netron

2.1.29. sklearn.linear_model.GammaRegressor

GammaRegressor est une méthode d'apprentissage automatique conçue pour les tâches de régression où la variable cible suit une distribution gamma.

La distribution gamma est une distribution de probabilité utilisée pour modéliser des variables aléatoires positives et continues. Cette méthode permet de modéliser et de prévoir des valeurs numériques positives, telles que le coût, le temps ou les proportions.

Comment fonctionne GammaRegressor :

1. Données d'Entrée : Il commence par l'ensemble de données initial, qui contient des caractéristiques (variables indépendantes) et des valeurs correspondantes de la variable cible suivant la distribution gamma.
2. Sélection de la fonction de perte : GammaRegressor utilise une fonction de perte qui correspond à la distribution gamma et prend en compte les particularités de cette distribution. Cela permet de modéliser les données tout en tenant compte de la non-négativité et de l'inclinaison à droite de la distribution gamma.
3. Entraînement du modèle : Le modèle est entraîné sur les données à l'aide de la fonction de perte choisie. Pendant l'apprentissage, il ajuste les paramètres du modèle afin de minimiser la fonction de perte.
4. Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs de la variable cible pour de nouvelles données.

Avantages de GammaRegressor :

• Modéliser les valeurs positives : Cette méthode est spécifiquement conçue pour modéliser des valeurs numériques positives, ce qui peut s'avérer utile dans les tâches où la variable cible est bornée.
• En considérant la forme de la distribution gamma : GammaRegressor prend en compte les caractéristiques de la distribution gamma, permettant une modélisation plus précise des données suivant cette distribution.
• Utilité en économétrie et en recherche médicale : La distribution gamma est fréquemment utilisée pour modéliser le coût, le temps d'attente et d'autres variables aléatoires positives en économétrie et en recherche médicale.

Limites de GammaRegressor :

• Limitation du type de données : Cette méthode ne convient qu'aux tâches de régression où la variable cible suit la distribution gamma ou des distributions similaires. Pour les données qui ne se conforment pas à une telle distribution, cette méthode peut ne pas être efficace.
• Nécessite le choix d'une fonction de perte : Le choix d'une fonction de perte appropriée peut nécessiter une connaissance de la distribution de la variable cible et de ses caractéristiques.

GammaRegressor est utile dans les tâches où il est nécessaire de modéliser et de prédire des valeurs numériques positives qui s'alignent sur la distribution gamma.

2.1.29.1. Code pour créer le modèle GammaRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.GammaRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# GammaRegressor.py
# Le code démontre le processus d'entraînement du modèle GammaRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)

model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"

# crée un modèle de Régresseur gamma
regression_model = GammaRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE correspondant aux décimales : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  GammaRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.7963797339354436
Python  Mean Absolute Error: 37.266200319422815
Python  Mean Squared Error: 2694.457784927322
Python  
Python  GammaRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.7963795030042045
Python  Mean Absolute Error: 37.266211754095956
Python  Mean Squared Error: 2694.4608407846144
Python  R^2 matching decimal places:  6
Python  MAE matching decimal places:  4
Python  MSE matching decimal places:  1
Python  float ONNX model precision:  4
Python  
Python  GammaRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.7963797339354436
Python  Mean Absolute Error: 37.266200319422815
Python  Mean Squared Error: 2694.457784927322
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  12
Python  double ONNX model precision:  15

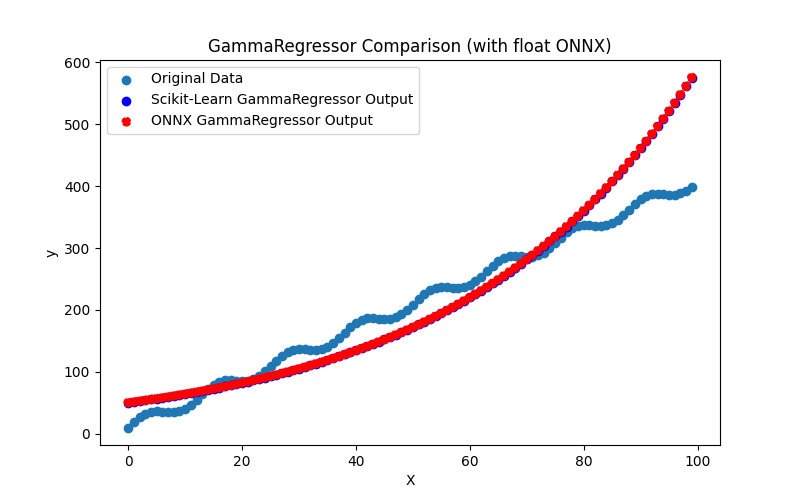
Fig. 94. Résultats de GammaRegressor.py (ONNX float)

2.1.29.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles enregistrés gamma_regressor_float.onnx et gamma_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                               GammaRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "GammaRegressor"
#define   ONNXFilenameFloat  "gamma_regressor_float.onnx"
#define   ONNXFilenameDouble "gamma_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(10+4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

GammaRegressor (EURUSD,H1)      Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx)
GammaRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.7963795030042045
GammaRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 37.2662117540959628
GammaRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 2694.4608407846144473
GammaRegressor (EURUSD,H1)      
GammaRegressor (EURUSD,H1)      Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx)
GammaRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.7963797339354435
GammaRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 37.2662003194228220
GammaRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 2694.4577849273218817

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx)
Python  Mean Absolute Error: 37.266200319422815
MQL5:   Mean Absolute Error: 37.2662117540959628
      
Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx)
Python  Mean Absolute Error: 37.266200319422815
MQL5:   Mean Absolute Error: 37.2662003194228220

Précision de la MAE ONNX float : 4 décimales, Précision de la MAE ONNX double : 13 décimales.

2.1.29.3. Représentation ONNX du gamma_regressor_float.onnx et du gamma_regressor_double.onnx

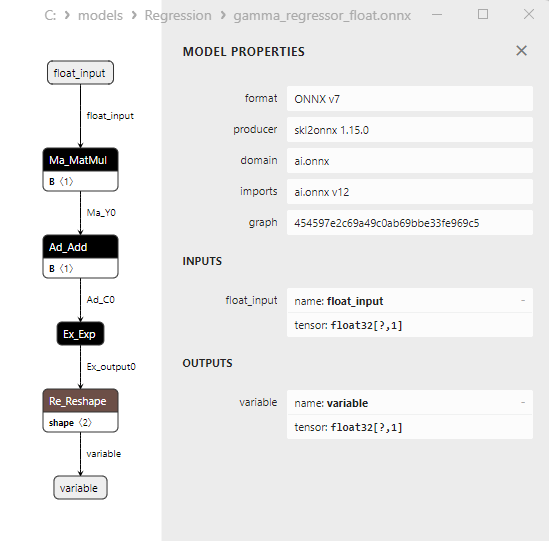
Fig. 95. Représentation ONNX de gamma_regressor_float.onnx dans Netron

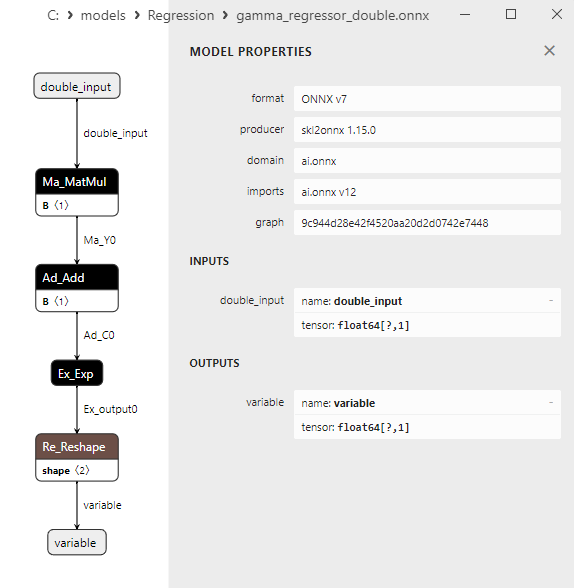
Fig. 96. Représentation ONNX de gamma_regressor_double.onnx dans Netron

2.1.30. sklearn.linear_model.SGDRegressor

SGDRegressor est une méthode de régression qui utilise la Descente Stochastique de Gradient (SGD) pour former un modèle de régression. Elle fait partie de la famille des modèles linéaires et peut être utilisée pour des tâches de régression. Les principales caractéristiques de SGDRegressor sont l'efficacité et la capacité à traiter de grands volumes de données.

Comment fonctionne SGDRegressor :

1. Régression Linéaire : Comme Ridge et Lasso, SGDRegressor vise à trouver une relation linéaire entre les variables indépendantes (caractéristiques) et la variable cible dans un problème de régression.
2. Descente Stochastique de Gradient : La base de SGDRegressor est la Descente Stochastique de Gradient. Au lieu de calculer les gradients sur l'ensemble des données d'apprentissage, elle met à jour le modèle sur la base de mini-lots de données sélectionnés de manière aléatoire. Cela permet de former efficacement des modèles et de travailler avec des ensembles de données importants.
3. Régularisation : SGDRegressor supporte les régularisations L1 et L2 (Lasso et Ridge). Cela permet de contrôler le sur-ajustement et d'améliorer la stabilité du modèle.
4. Hyper-paramètres : Comme Ridge et Lasso, SGDRegressor permet de régler des hyper-paramètres tels que le paramètre de régularisation (α, alpha) et le type de régularisation.

Avantages de SGDRegressor :

• Efficacité : SGDRegressor fonctionne bien avec les grands ensembles de données et entraîne efficacement les modèles sur des données étendues.
• Capacité de régularisation : La possibilité d'appliquer les régularisations L1 et L2 permet à cette méthode de gérer les problèmes de sur-ajustement.
• Descente de gradient adaptative : La descente de gradient stochastique permet de s'adapter à l'évolution des données et de former des modèles à la volée.

Limites de SGDRegressor :

• Sensibilité au choix des hyper-paramètres : L'ajustement des hyper-paramètres tels que le taux d'apprentissage et le coefficient de régularisation peut nécessiter une expérimentation.
• Ne converge pas toujours vers le minimum global : En raison de la nature stochastique de la descente de gradient, SGDRegressor ne converge pas toujours vers le minimum global de la fonction de perte.

SGDRegressor est une méthode de régression qui utilise la descente de gradient stochastique pour entraîner un modèle de régression. Elle est efficace, capable de traiter de grands ensembles de données et prend en charge la régularisation pour gérer l'ajustement excessif.

2.1.30.1. Code pour créer le modèle SGDRegressor et l'exporter vers ONNX pour les float et les double

Ce code crée le modèle sklearn.linear_model.SGDRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# SGDRegressor2.py
# Le code démontre le processus d'entraînement du modèle SGDRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)

model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"

# crée un modèle SGDRegressor
regression_model = SGDRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  SGDRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9961197872743282
Python  Mean Absolute Error: 0.6405924406136998
Python  Mean Squared Error: 0.5169867345998348
Python  
Python  SGDRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9961197876338647
Python  Mean Absolute Error: 0.6405924014799271
Python  Mean Squared Error: 0.5169866866963753
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  7
Python  MSE matching decimal places:  6
Python  float ONNX model precision:  7
Python  
Python  SGDRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9961197872743282
Python  Mean Absolute Error: 0.6405924406136998
Python  Mean Squared Error: 0.5169867345998348
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  16
Python  double ONNX model precision:  16

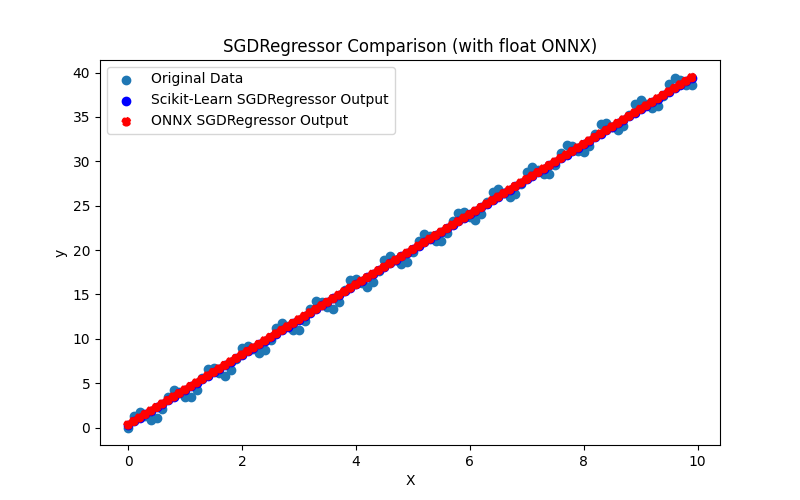
Fig. 97. Résultats de SGDRegressor.py (ONNX float)

2.1.30.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés sgd_regressor_float.onnx et sgd_rgressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                 SGDRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "SGDRegressor"
#define   ONNXFilenameFloat  "sgd_regressor_float.onnx"
#define   ONNXFilenameDouble "sgd_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i*0.1;
      y[i]=(double)(4*x[i] + sin(x[i]*10));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

SGDRegressor (EURUSD,H1)        Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx)
SGDRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9961197876338647
SGDRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 0.6405924014799272
SGDRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 0.5169866866963754
SGDRegressor (EURUSD,H1)        
SGDRegressor (EURUSD,H1)        Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx)
SGDRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9961197872743282
SGDRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 0.6405924406136998
SGDRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 0.5169867345998348

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx)
Python  Mean Absolute Error: 0.6405924406136998
MQL5:   Mean Absolute Error: 0.6405924014799272
        
Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx)
Python  Mean Absolute Error: 0.6405924406136998
MQL5:   Mean Absolute Error: 0.6405924406136998

Précision de la MAE ONNX float : 7 décimales, Précision de la MAE ONNX double : 16 décimales.

2.1.30.3. Représentation ONNX de sgd_regressor_float.onnx et sgd_regressor_double.onnx

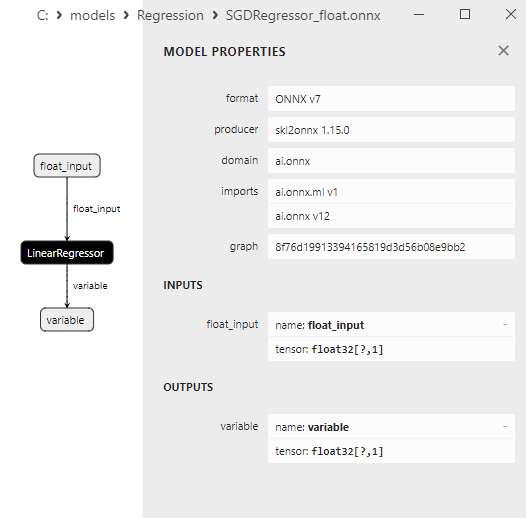
Fig. 98. Représentation ONNX de sgd_regressor_float.onnx dans Netron

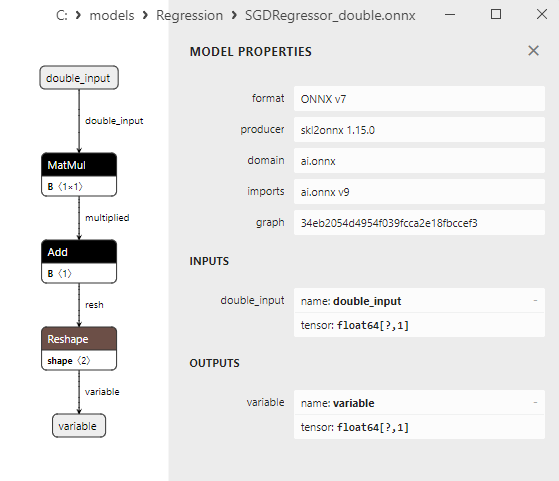
Fig. 99. Représentation ONNX de sgd_rgressor_double.onnx dans Netron

2.2. Modèles de régression de la bibliothèque Scikit-learn qui sont convertis uniquement en modèles ONNX de précision flottante

Cette section couvre les modèles qui ne peuvent fonctionner qu'avec la précision du float. Les convertir en ONNX avec une précision double conduit à des erreurs liées aux limitations du sous-ensembleai.onnx.ml des opérateurs ONNX.

2.2.1. sklearn.linear_model.AdaBoostRegressor

AdaBoostRegressor - est une méthode d'apprentissage automatique utilisée pour la régression, qui consiste à prédire des valeurs numériques (par exemple, les prix de l'immobilier, les volumes de vente, etc.)

Cette méthode est une variante de l'algorithme AdaBoost (Adaptive Boosting), initialement développé pour les tâches de classification.

Comment fonctionne AdaBoostRegressor :

1. Ensemble de données original : Il commence par l'ensemble de données original contenant des caractéristiques (variables indépendantes) et leurs variables cibles correspondantes (variables dépendantes que nous cherchons à prédire).
2. Initialisation du poids : Au départ, chaque point de données (observation) a le même poids, et le modèle est construit sur la base de cet ensemble de données pondérées.
3. Former les apprenants faibles : AdaBoostRegressor construit plusieurs modèles de régression faibles (par exemple, des arbres de décision) qui tentent de prédire la variable cible. Ces modèles sont appelés "apprenants faibles". Chaque apprenant faible est formé sur les données en tenant compte des poids de chaque observation.
4. Sélection des poids faibles de l'apprenant : AdaBoostRegressor calcule les poids de chaque apprenant faible en fonction de la performance de cet apprenant dans les prédictions. Les apprenants qui font des prédictions plus précises reçoivent un poids plus élevé, et vice versa.
5. Mise à jour des poids d'observation : Les poids des observations sont mis à jour de manière à ce que les observations précédemment mal prédites reçoivent un poids plus important, ce qui accroît leur importance pour le modèle suivant.
6. Prédiction finale : AdaBoostRegressor combine les prédictions de tous les apprenants faibles, en leur attribuant des poids en fonction de leurs performances. Il en résulte la prédiction finale du modèle.

Avantages de AdaBoostRegressor :

• Capacité d'Adaptation : AdaBoostRegressor s'adapte aux fonctions complexes et traite mieux les relations non linéaires.
• Réduction de l'ajustement excessif : AdaBoostRegressor utilise la régularisation par la mise à jour des poids d'observation, ce qui permet d'éviter l'ajustement excessif.
• Un ensemble puissant : En combinant plusieurs modèles faibles, AdaBoostRegressor peut créer des modèles forts capables de prédire la variable cible de manière assez précise.

Limites de AdaBoostRegressor :

• Sensibilité aux valeurs aberrantes : AdaBoostRegressor est sensible aux valeurs aberrantes dans les données, ce qui affecte la qualité de la prédiction.
• Coûts de calcul élevés : La construction de plusieurs apprenants faibles peut nécessiter davantage de ressources de calcul et de temps.
• Ce n'est pas toujours le meilleur choix : AdaBoostRegressor n'est pas toujours le choix optimal et, dans certains cas, d'autres méthodes de régression peuvent être plus performantes.

AdaBoostRegressor est une méthode d'apprentissage automatique utile, applicable à diverses tâches de régression, en particulier dans les situations où les données contiennent des dépendances complexes.

2.2.1.1. Code pour créer le modèle AdaBoostRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.AdaBoostRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# AdaBoostRegressor.py
# Le code démontre le processus d'entraînement du modèle AdaBoostRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"

# crée un modèle AdaBoostRegressor
regression_model = AdaBoostRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  AdaBoostRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9991257208809748
Python  Mean Absolute Error: 2.3678022748065457
Python  Mean Squared Error: 11.569124350863143
Python  
Python  AdaBoostRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9991257199849699
Python  Mean Absolute Error: 2.36780399225718
Python  Mean Squared Error: 11.569136207480646
Python  R^2 matching decimal places:  7
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  AdaBoostRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx

Ici, le modèle a été exporté en modèles ONNX pour les float et les double. Le modèle ONNX float a été exécuté avec succès, alors qu'il y a une erreur d'exécution avec le modèle double (erreurs dans l'onglet Erreurs) :

AdaBoostRegressor.py started    AdaBoostRegressor.py    1       1
Traceback (most recent call last):      AdaBoostRegressor.py    1       1
    onnx_session = ort.InferenceSession(onnx_filename)  AdaBoostRegressor.py    159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx failed:Type Error:       onnxruntime_inference_collection.py     424     1
AdaBoostRegressor.py finished in 3207 ms                5       1

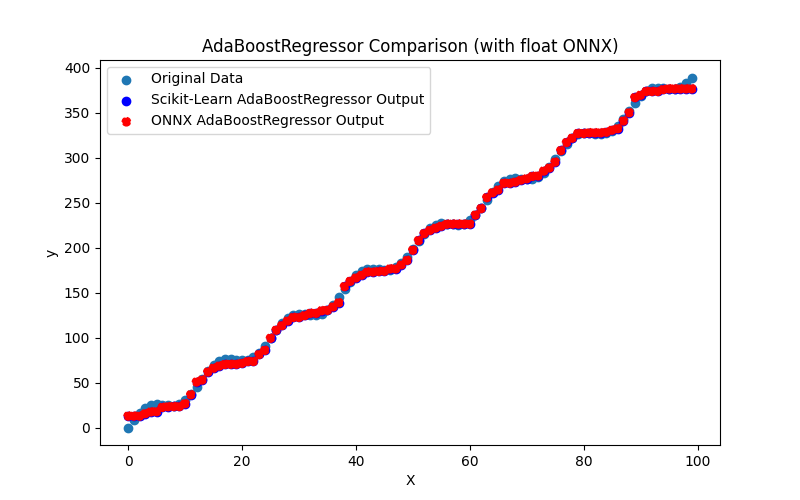
Fig. 100. Résultats de AdaBoostRegressor.py (ONNX float)

2.2.1.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés adaboost_regressor_float.onnx et adaboost_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                            AdaBoostRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "AdaBoostRegressor"
#define   ONNXFilenameFloat  "adaboost_regressor_float.onnx"
#define   ONNXFilenameDouble "adaboost_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

AdaBoostRegressor (EURUSD,H1)   
AdaBoostRegressor (EURUSD,H1)   Testing ONNX float: AdaBoostRegressor (adaboost_regressor_float.onnx)
AdaBoostRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9991257199849699
AdaBoostRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 2.3678039922571803
AdaBoostRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 11.5691362074806463
AdaBoostRegressor (EURUSD,H1)   
AdaBoostRegressor (EURUSD,H1)   Testing ONNX double: AdaBoostRegressor (adaboost_regressor_double.onnx)
AdaBoostRegressor (EURUSD,H1)   ONNX: cannot create session (OrtStatus: 1 'Type Error: Type parameter (T) of Optype (Mul) bound to different types (tensor(float) and tensor(double) in node (Mul).'), inspect code 'Scripts\Regression\AdaBoostRegressor.mq5' (133:16)
AdaBoostRegressor (EURUSD,H1)   model_name=AdaBoostRegressor OnnxCreate error 5800

Le modèle ONNX float a été exécuté avec succès, alors qu'il y a eu une erreur d'exécution avec le modèle double.

2.2.1.3. Représentation ONNX de adaboost_regressor_float.onnx et adaboost_regressor_double.onnx

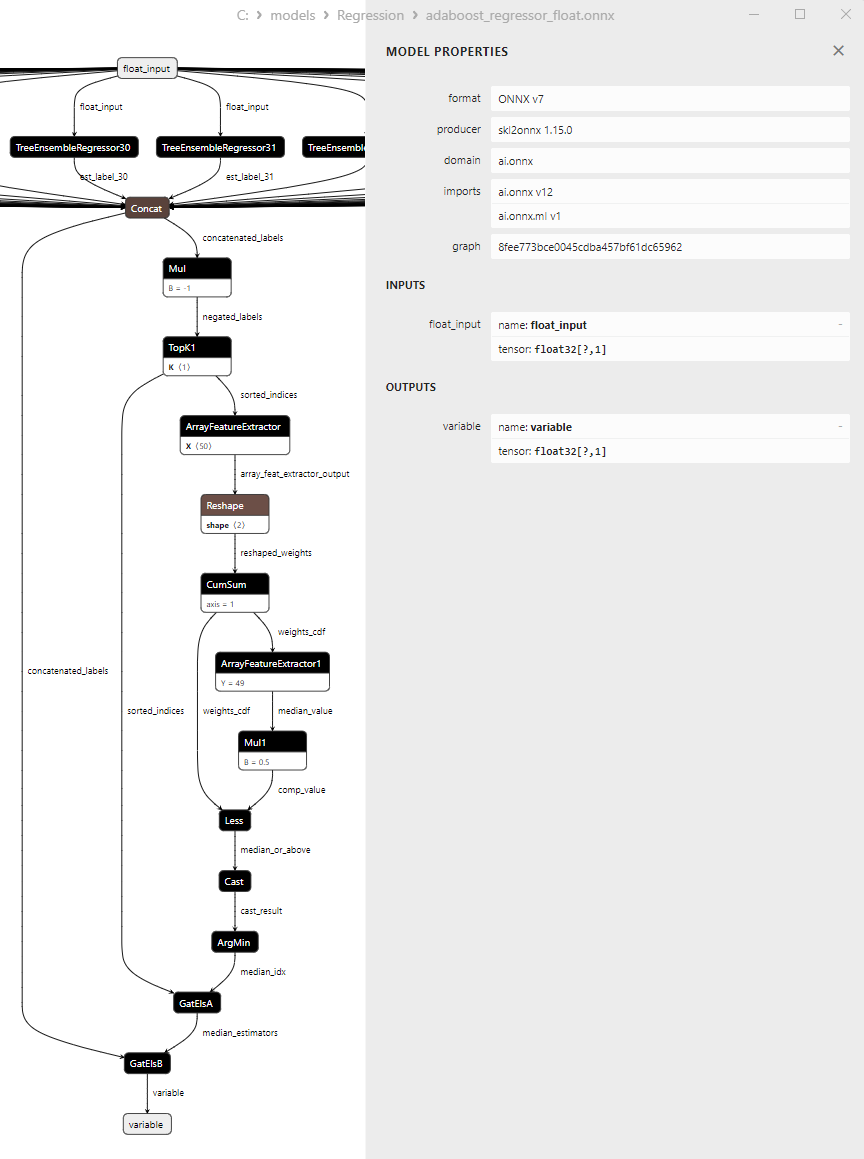
Fig. 101. Représentation ONNX de adaboost_regressor_float.onnx dans Netron

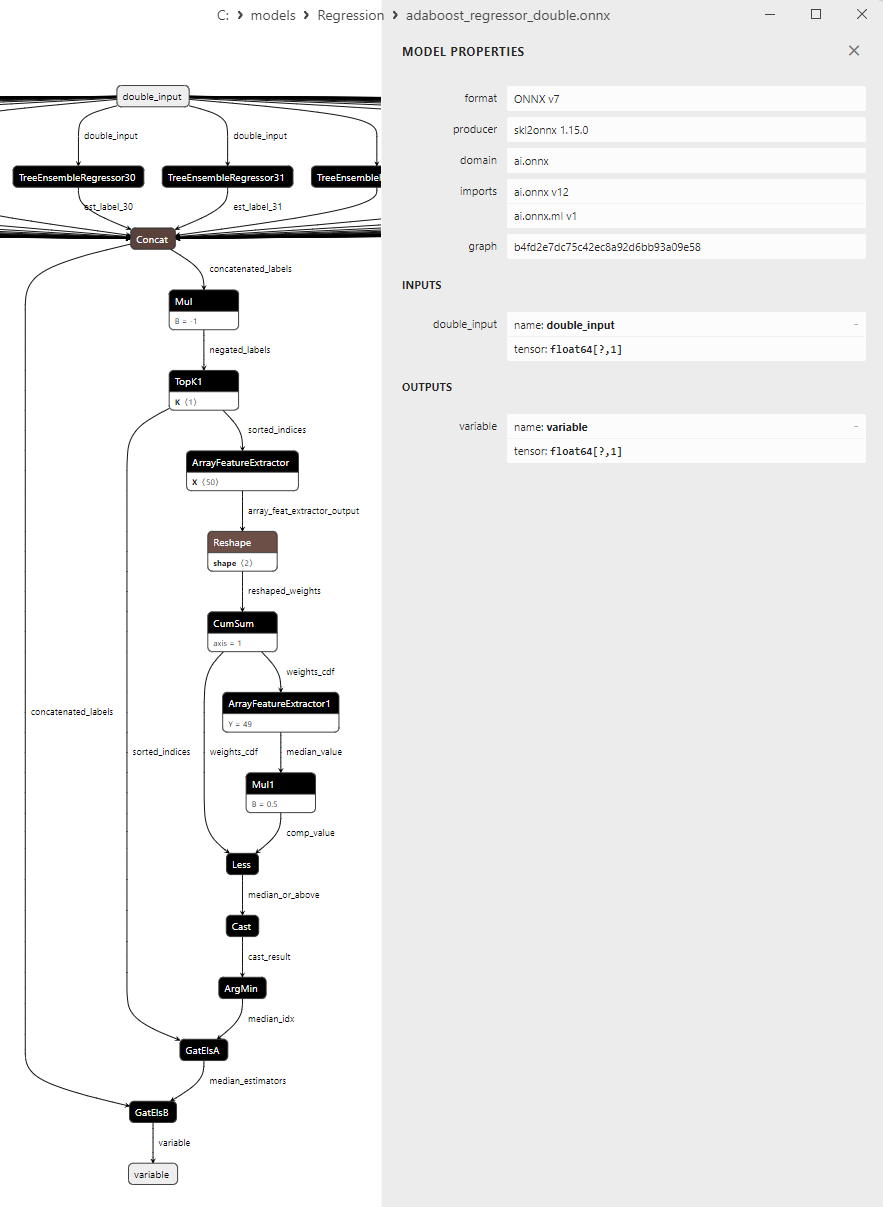
Fig. 102. Représentation ONNX de adaboost_regressor_double.onnx dans Netron

2.2.2. sklearn.linear_model.BaggingRegressor

BaggingRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression.

Il s'agit d'une méthode d'ensemble basée sur l'idée de "bagging" (Bootstrap Aggregating), qui implique la construction de plusieurs modèles de régression de base et la combinaison de leurs prédictions afin d'obtenir un résultat plus stable et plus précis.

Comment fonctionne le BaggingRegressor :

1. Ensemble de données original : Il commence par l'ensemble de données original contenant des caractéristiques (variables indépendantes) et leurs variables cibles correspondantes (variables dépendantes que nous cherchons à prédire).
2. Génération de sous-ensembles : BaggingRegressor crée aléatoirement plusieurs sous-ensembles (échantillons avec remplacement) à partir des données d'origine. Chaque sous-ensemble contient un ensemble aléatoire d'observations provenant des données originales.
3. Formation de modèles de régression de base : Pour chaque sous-ensemble, BaggingRegressor construit un modèle de régression de base distinct (par exemple, un arbre de décision, une forêt aléatoire, un modèle de régression linéaire, etc.)
4. Prédictions à partir de modèles de base : Chaque modèle de base est utilisé pour prédire la variable cible sur la base du sous-ensemble correspondant.
5. Moyenne ou combinaison : BaggingRegressor fait la moyenne ou combine les prédictions de tous les modèles de base pour obtenir la prédiction de régression finale.

Avantages du BaggingRegressor :

• Réduction des écarts : BaggingRegressor réduit la variance du modèle, ce qui le rend plus robuste aux fluctuations des données.
• Réduction de l'ajustement excessif : Comme le modèle est formé sur différents sous-ensembles de données, la méthode BaggingRegressor réduit généralement le risque de sur-ajustement.
• Amélioration de la généralisation : En combinant les prédictions de plusieurs modèles, BaggingRegressor fournit généralement des prévisions plus précises et plus stables.
• Large gamme de modèles de base : BaggingRegressor peut utiliser différents types de modèles de régression de base, ce qui en fait une méthode flexible.

Limites de BaggingRegressor :

• Il n'est pas toujours capable d'améliorer les performances lorsque le modèle de base est déjà performant sur les données.
• Le BaggingRegressor peut nécessiter plus de ressources de calcul et de temps que l'apprentissage d'un seul modèle.

BaggingRegressor est une méthode d'apprentissage automatique puissante qui peut être utile dans les tâches de régression, en particulier avec des données avec du bruit et la nécessité d'améliorer la stabilité des prédictions.

2.2.2.1. Code pour créer le modèle BaggingRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.BaggingRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# BaggingRegressor.py
# Le code démontre le processus d'entraînement du modèle BaggingRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"

# crée un modèle de Régresseur Bagging (Bagging Regressor)
regression_model = BaggingRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  
Python  BaggingRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9998128324923137
Python  Mean Absolute Error: 1.0257279210387649
Python  Mean Squared Error: 2.4767424083953005
Python  
Python  BaggingRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9998128317934672
Python  Mean Absolute Error: 1.0257282792130034
Python  Mean Squared Error: 2.4767516560614187
Python  R^2 matching decimal laces:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  BaggingRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx

Onglet Erreurs :

BaggingRegressor.py started     BaggingRegressor.py     1       1
Traceback (most recent call last):      BaggingRegressor.py     1       1
    onnx_session = ort.InferenceSession(onnx_filename)  BaggingRegressor.py     161     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx failed:Type Error: T      onnxruntime_inference_collection.py     424     1
BaggingRegressor.py finished in 3173 ms         5       1

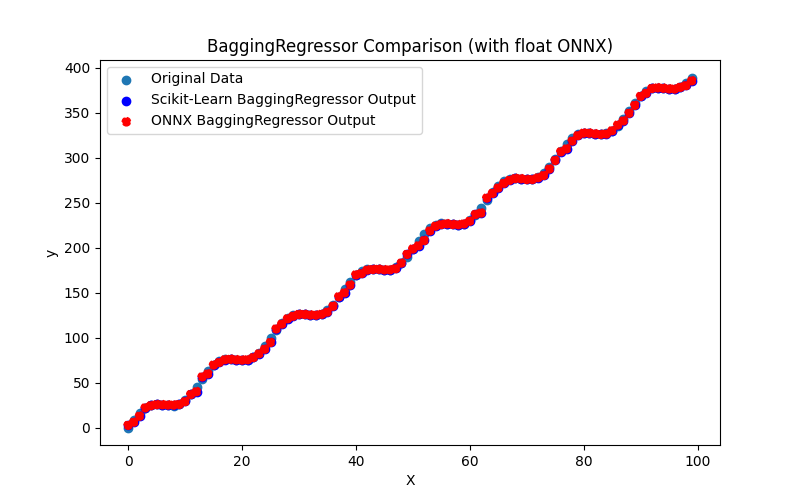
Fig. 103. Résultats du BaggingRegressor.py (ONNX float)

2.2.2.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les fichiers bagging_regressor_float.onnx et bagging_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                             BaggingRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "BaggingRegressor"
#define   ONNXFilenameFloat  "bagging_regressor_float.onnx"
#define   ONNXFilenameDouble "bagging_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

BaggingRegressor (EURUSD,H1)    Testing ONNX float: BaggingRegressor (bagging_regressor_float.onnx)
BaggingRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9998128317934672
BaggingRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 1.0257282792130034
BaggingRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 2.4767516560614196
BaggingRegressor (EURUSD,H1)    
BaggingRegressor (EURUSD,H1)    Testing ONNX double: BaggingRegressor (bagging_regressor_double.onnx)
BaggingRegressor (EURUSD,H1)    ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (ReduceMean) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\BaggingRegressor.mq5' (133:16)
BaggingRegressor (EURUSD,H1)    model_name=BaggingRegressor OnnxCreate error 5800

Le modèle ONNX calculé en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle en double.

2.2.2.3. Représentation ONNX du bagging_regressor_float.onnx et du bagging_regressor_double.onnx

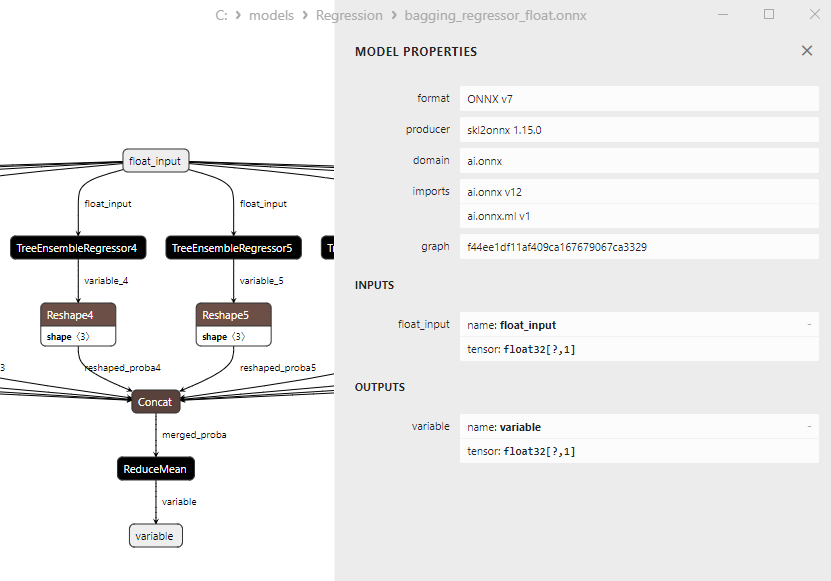
Fig. 104. Représentation ONNX du bagging_regressor_float.onnx dans Netron

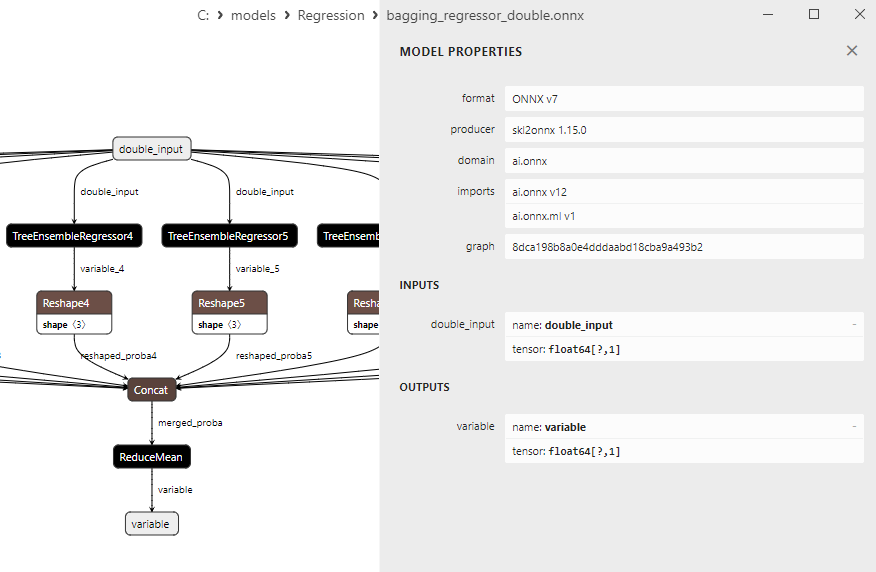
Fig. 105. Représentation ONNX du bagging_regressor_double.onnx dans Netron

2.2.3. sklearn.linear_model.DecisionTreeRegressor

DecisionTreeRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression, prédisant les valeurs numériques de la variable cible sur la base d'un ensemble de caractéristiques (variables indépendantes).

Cette méthode est basée sur la construction d'arbres de décision qui partitionnent l'espace des caractéristiques en intervalles et prédisent la valeur de la variable cible pour chaque intervalle.

Principe de fonctionnement de DecisionTreeRegressor :

1. Début de la construction : En commençant par l'ensemble de données initial contenant les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Sélection et répartition des caractéristiques : L'arbre de décision sélectionne une caractéristique et une valeur seuil qui divise les données en deux sous-groupes ou plus. Cette division est effectuée pour minimiser l'erreur quadratique moyenne (l'écart quadratique moyen entre les valeurs prédites et réelles de la variable cible) au sein de chaque sous-groupe.
3. Construction récursive : Le processus de sélection et de division des caractéristiques est répété pour chaque sous-groupe, créant ainsi des sous-arbres. Ce processus est effectué de manière récursive jusqu'à ce que certains critères d'arrêt soient remplis, tels que la profondeur maximale de l'arbre ou le nombre minimal d'échantillons dans un nœud.
4. Nœuds feuilles : Lorsque les critères d'arrêt sont remplis, des nœuds feuilles sont créés, prédisant les valeurs numériques de la variable cible pour les échantillons qui tombent dans un nœud feuille donné.
5. Prédiction : Pour les nouvelles données, l'arbre de décision est appliqué et les nouvelles observations traversent l'arbre jusqu'à ce qu'elles atteignent un nœud feuille qui prédit la valeur numérique de la variable cible.

Avantages de DecisionTreeRegressor :

• Interprétabilité : Les arbres de décision sont faciles à comprendre et à visualiser, ce qui les rend utiles pour expliquer la prise de décision des modèles.
• Robustesse des valeurs aberrantes : Les arbres de décision peuvent être robustes aux données aberrantes.
• Traitement des données numériques et catégorielles : Les arbres de décision peuvent traiter les caractéristiques numériques et catégorielles sans prétraitement supplémentaire.
• Sélection automatisée de caractéristiques : Les arbres peuvent sélectionner automatiquement les caractéristiques importantes, en ignorant celles qui sont moins pertinentes.

Limites de DecisionTreeRegressor :

• Vulnérabilité de l'ajustement excessif : Les arbres de décision peuvent être sujets à un sur-ajustement, en particulier s'ils sont trop profonds.
• Problèmes de généralisation : Les arbres de décision peuvent ne pas bien se généraliser aux données si elles ne sont pas incluses dans l'ensemble de formation.
• Ce n'est pas toujours un choix optimal : Dans certains cas, d'autres méthodes de régression, telles que la régression linéaire ou les voisins les plus proches, peuvent donner de meilleurs résultats.

DecisionTreeRegressor est une méthode précieuse pour les tâches de régression, en particulier lorsque la compréhension de la logique décisionnelle du modèle et la visualisation du processus sont cruciales.

2.2.3.1. Code pour créer le modèle DecisionTreeRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.linear_model.DecisionTreeRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# DecisionTreeRegressor.py
# Le code démontre le processus d'apprentissage du modèle DecisionTreeRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"

# crée un modèle de Régresseur d'arbre de décision
regression_model = DecisionTreeRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y)

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et effectue des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  DecisionTreeRegressor Original model (double)
Python  R-squared (Coefficient of determination): 1.0
Python  Mean Absolute Error: 0.0
Python  Mean Squared Error: 0.0
Python  
Python  DecisionTreeRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999999971
Python  Mean Absolute Error: 4.393654615473253e-06
Python  Mean Squared Error: 3.829042036424747e-11
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  DecisionTreeRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx

Onglet Erreurs :

DecisionTreeRegressor.py started        DecisionTreeRegressor.py        1       1
Traceback (most recent call last):      DecisionTreeRegressor.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  DecisionTreeRegressor.py        160     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx failed:Type Er      onnxruntime_inference_collection.py     424     1
DecisionTreeRegressor.py finished in 2957 ms            5       1

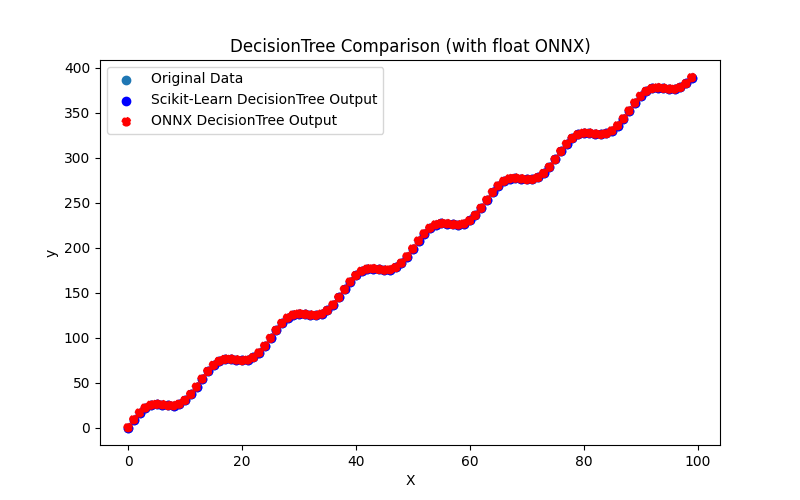
Fig. 106. Résultats de DecisionTreeRegressor.py (ONNX float)

2.2.3.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles decision_tree_regressor_float.onnx et decision_tree_regressor_double.onnx enregistrés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                        DecisionTreeRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "DecisionTreeRegressor"
#define   ONNXFilenameFloat  "decision_tree_regressor_float.onnx"
#define   ONNXFilenameDouble "decision_tree_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

DecisionTreeRegressor (EURUSD,H1)       Testing ONNX float: DecisionTreeRegressor (decision_tree_regressor_float.onnx)
DecisionTreeRegressor (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9999999999999971
DecisionTreeRegressor (EURUSD,H1)       MQL5:   Mean Absolute Error: 0.0000043936546155
DecisionTreeRegressor (EURUSD,H1)       MQL5:   Mean Squared Error: 0.0000000000382904
DecisionTreeRegressor (EURUSD,H1)       
DecisionTreeRegressor (EURUSD,H1)       Testing ONNX double: DecisionTreeRegressor (decision_tree_regressor_double.onnx)
DecisionTreeRegressor (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\DecisionTreeRegressor.mq5' (133:16)
DecisionTreeRegressor (EURUSD,H1)       model_name=DecisionTreeRegressor OnnxCreate error 5800

Le modèle ONNX calculé en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle en double.

2.2.3.3. Représentation ONNX de decision_tree_regressor_float.onnx et decision_tree_regressor_double.onnx

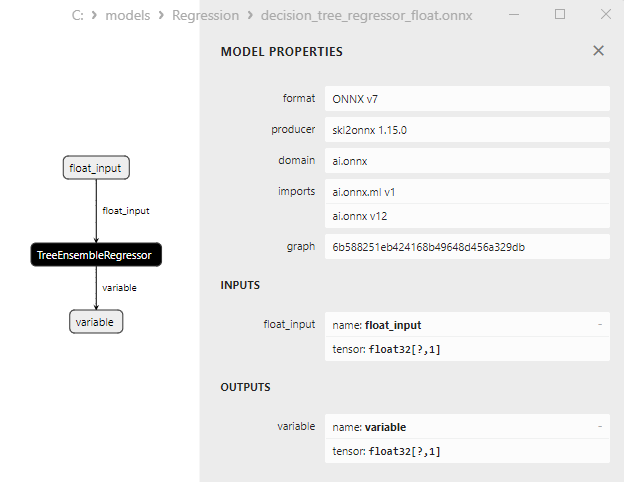
Fig. 107. Représentation ONNX de decision_tree_regressor_float.onnx dans Netron

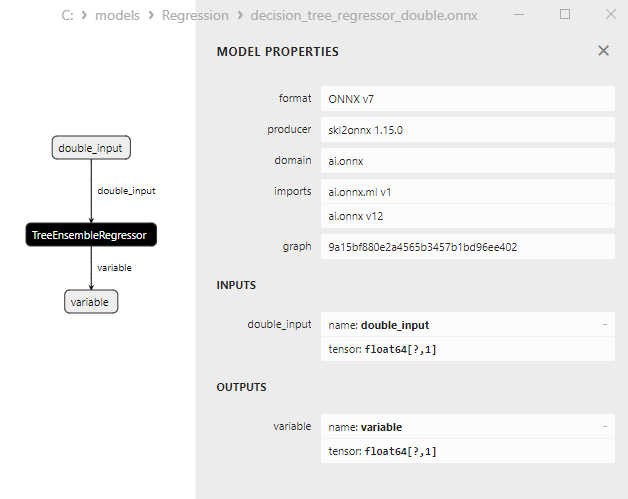
Fig. 108. Représentation ONNX de decision_tree_regressor_double.onnx dans Netron

2.2.4. sklearn.tree.ExtraTreeRegressor

ExtraTreeRegressor, ou Extremely Randomized Trees Regressor, est une méthode d'ensemble de régression basée sur des arbres de décision.

Cette méthode est une variante des forêts aléatoires et diffère en ce sens qu'au lieu de choisir la meilleure division pour chaque nœud de l'arbre, elle utilise des divisions aléatoires pour chaque nœud. Cela la rend plus aléatoire et plus rapide, ce qui peut être avantageux dans certaines situations.

Principe de fonctionnement de ExtraTreeRegressor :

1. Début de la construction : En commençant par l'ensemble de données initial contenant les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Le hasard dans les fractionnements : Contrairement aux arbres de décision classiques où la meilleure division est choisie, ExtraTreeRegressor utilise des valeurs seuils aléatoires pour diviser les nœuds de l'arbre. Le processus de fractionnement est ainsi plus aléatoire et moins susceptible d'être sur-ajouté.
3. Construction d'arbres : L'arbre est construit en divisant les nœuds sur la base de caractéristiques aléatoires et de valeurs seuils. Ce processus se poursuit jusqu'à ce que certains critères d'arrêt soient remplis, tels que la profondeur maximale de l'arbre ou le nombre minimal d'échantillons dans un nœud.
4. Ensemble d'arbres : ExtraTreeRegressor construit plusieurs arbres aléatoires de ce type, dont le nombre est contrôlé par l'hyper-paramètre "n_estimators".
5. Prédiction : Pour prédire la variable cible pour de nouvelles données, ExtraTreeRegressor fait simplement la moyenne des prédictions de tous les arbres de l'ensemble.

Avantages de ExtraTreeRegressor :

• Réduction de la sur-adaptation : L'utilisation d'un découpage aléatoire des nœuds rend la méthode moins sujette au sur-ajustement que les arbres de décision classiques.
• Parallélisme élevé : Comme les arbres sont construits indépendamment, ExtraTreeRegressor peut être facilement parallélisé pour l'apprentissage sur plusieurs processeurs.
• Formation rapide : Comparé à d'autres méthodes telles que le gradient boosting, ExtraTreeRegressor peut être formé plus rapidement.

Limites de ExtraTreeRegressor :

• Peut être moins précis : Dans certains cas, en particulier pour les petits ensembles de données, ExtraTreeRegressor peut être moins précis que des méthodes plus complexes.
• Moins interprétable : Comparé aux modèles linéaires, aux arbres de décision et à d'autres méthodes plus simples, ExtraTreeRegressor est généralement moins facile à interpréter.

ExtraTreeRegressor peut être une méthode de régression utile dans les situations où il est nécessaire de réduire le sur-ajustement et d'assurer une formation rapide.

2.2.4.1. Code pour créer le modèle ExtraTreeRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.tree.ExtraTreeRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# ExtraTreeRegressor.py
# Le code démontre le processus d'entraînement du modèle ExtraTreeRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"

# crée un modèle ExtraTreeRegressor
regression_model = ExtraTreeRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et les données de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

2023.10.30 14:40:57.665 Python  ExtraTreeRegressor Original model (double)
2023.10.30 14:40:57.665 Python  R-squared (Coefficient of determination): 1.0
2023.10.30 14:40:57.665 Python  Mean Absolute Error: 0.0
2023.10.30 14:40:57.665 Python  Mean Squared Error: 0.0
2023.10.30 14:40:57.681 Python  
2023.10.30 14:40:57.681 Python  ExtraTreeRegressor ONNX model (float)
2023.10.30 14:40:57.681 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_float.onnx
2023.10.30 14:40:57.681 Python  Information about input tensors in ONNX:
2023.10.30 14:40:57.681 Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
2023.10.30 14:40:57.681 Python  Information about output tensors in ONNX:
2023.10.30 14:40:57.681 Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
2023.10.30 14:40:57.681 Python  R-squared (Coefficient of determination) 0.9999999999999971
2023.10.30 14:40:57.681 Python  Mean Absolute Error: 4.393654615473253e-06
2023.10.30 14:40:57.681 Python  Mean Squared Error: 3.829042036424747e-11
2023.10.30 14:40:57.681 Python  R^2 matching decimal places:  0
2023.10.30 14:40:57.681 Python  MAE matching decimal places:  0
2023.10.30 14:40:57.681 Python  MSE matching decimal places:  0
2023.10.30 14:40:57.681 Python  float ONNX model precision:  0
2023.10.30 14:40:58.011 Python  
2023.10.30 14:40:58.011 Python  ExtraTreeRegressor ONNX model (double)
2023.10.30 14:40:58.011 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx

Onglet Erreurs :

ExtraTreeRegressor.py started   ExtraTreeRegressor.py   1       1
Traceback (most recent call last):      ExtraTreeRegressor.py   1       1
    onnx_session = ort.InferenceSession(onnx_filename)  ExtraTreeRegressor.py   159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx failed:Type Error      onnxruntime_inference_collection.py     424     1
ExtraTreeRegressor.py finished in 2980 ms               5       1

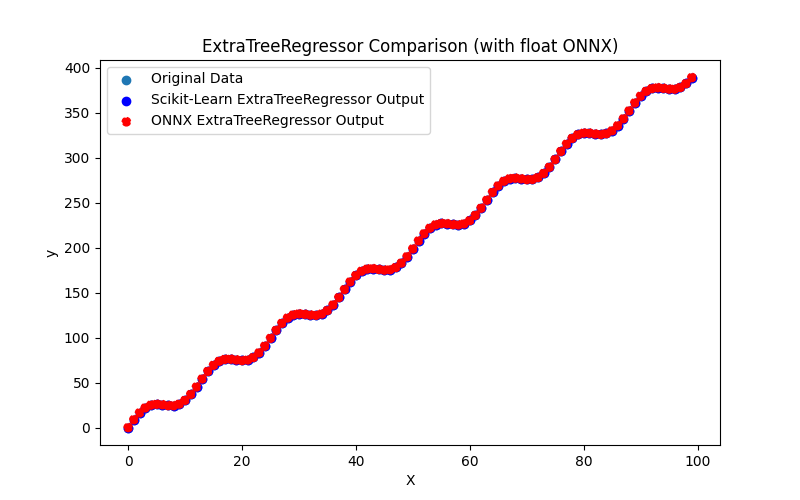
Fig. 109. Résultats de ExtraTreeRegressor.py (ONNX float)

2.2.4.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles extra_tree_regressor_float.onnx et extra_tree_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                           ExtraTreeRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ExtraTreeRegressor"
#define   ONNXFilenameFloat  "extra_tree_regressor_float.onnx"
#define   ONNXFilenameDouble "extra_tree_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

ExtraTreeRegressor (EURUSD,H1)  Testing ONNX float: ExtraTreeRegressor (extra_tree_regressor_float.onnx)
ExtraTreeRegressor (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9999999999999971
ExtraTreeRegressor (EURUSD,H1)  MQL5:   Mean Absolute Error: 0.0000043936546155
ExtraTreeRegressor (EURUSD,H1)  MQL5:   Mean Squared Error: 0.0000000000382904
ExtraTreeRegressor (EURUSD,H1)  
ExtraTreeRegressor (EURUSD,H1)  Testing ONNX double: ExtraTreeRegressor (extra_tree_regressor_double.onnx)
ExtraTreeRegressor (EURUSD,H1)  ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreeRegressor.mq5' (133:16)
ExtraTreeRegressor (EURUSD,H1)  model_name=ExtraTreeRegressor OnnxCreate error 5800

Le modèle ONNX en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double.

2.2.4.3. Représentation ONNX extra_tree_regressor_float.onnx et extra_tree_regressor_double.onnx

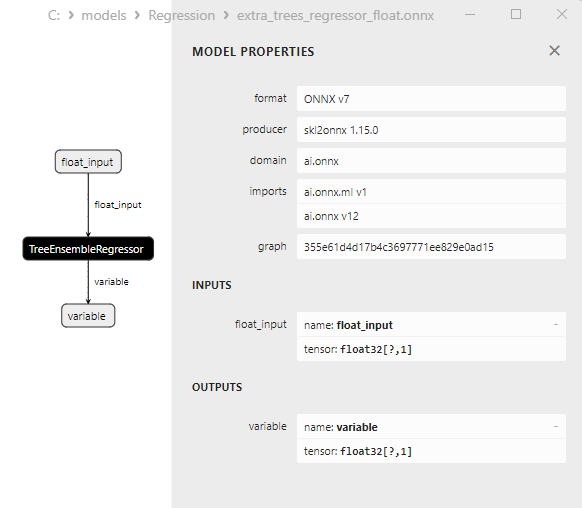
Fig. 110. Représentation ONNX de l'extra_tree_regressor_float.onnx dans Netron

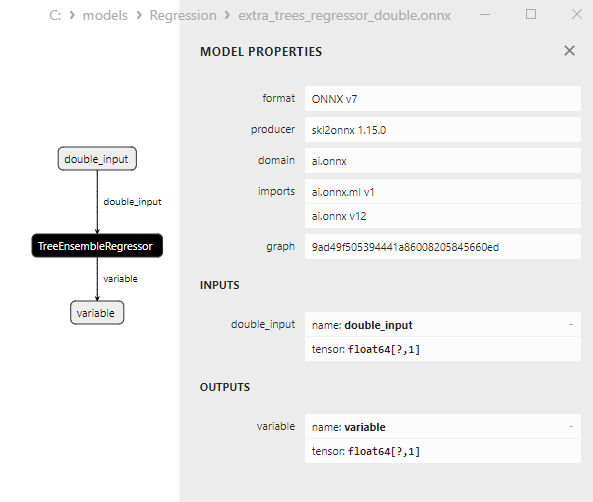
Fig. 111. Représentation ONNX de extra_tree_regressor_double.onnx dans Netron

2.2.5. sklearn.ensemble.ExtraTreesRegressor

ExtraTreesRegressor (Extremely Randomized Trees Regressor) est une méthode d'apprentissage automatique qui représente une variante des forêts aléatoires pour les tâches de régression.

Cette méthode utilise un ensemble d'arbres de décision pour prédire les valeurs numériques de la variable cible sur la base d'un ensemble de caractéristiques.

Comment fonctionne ExtraTreesRegressor :

1. Début de la Construction : Il commence par l'ensemble de données original, y compris les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Le hasard dans les fractionnements : Contrairement aux arbres de décision ordinaires où la meilleure division est sélectionnée pour diviser les nœuds, ExtraTreesRegressor utilise des valeurs de seuil aléatoires pour diviser les nœuds de l'arbre. Ce caractère aléatoire rend le processus de fractionnement plus arbitraire et moins sujet à des ajustements excessifs.
3. Construction d'Arbres : ExtraTreesRegressor construit plusieurs arbres de décision dans l'ensemble. Le nombre d'arbres est contrôlé par l'hyper-paramètre "n_estimators". Chaque arbre est formé sur un sous-échantillon aléatoire de données (avec remplacement) et sur des sous-ensembles aléatoires de caractéristiques.
4. Prédiction : Pour prédire la variable cible à partir de nouvelles données, ExtraTreesRegressor regroupe les prédictions de tous les arbres de l'ensemble (généralement en calculant une moyenne).

Avantages de ExtraTreesRegressor :

• Réduction du sur-ajustement : L'utilisation d'un découpage aléatoire des nœuds et d'un sous-échantillonnage des données rend la méthode moins sujette au sur-ajustement que les arbres de décision conventionnels.
• Parallélisme élevé : Comme les arbres sont construits indépendamment, ExtraTreesRegressor peut être facilement parallélisé pour l'apprentissage sur plusieurs processeurs.
• Robustesse face aux valeurs aberrantes : La méthode résiste généralement aux données aberrantes.
• Traitement des données numériques et catégorielles : ExtraTreesRegressor peut traiter les caractéristiques numériques et catégorielles sans prétraitement supplémentaire.

Limites de ExtraTreesRegressor :

• Peut nécessiter un réglage fin des hyper-paramètres : Bien que ExtraTreesRegressor fonctionne généralement bien avec les paramètres par défaut, un réglage fin des hyper-paramètres peut s'avérer nécessaire pour obtenir des performances maximales.
• Moins d'interprétabilité : Comme d'autres méthodes d'ensemble, ExtraTreesRegressor est moins facile à interpréter que des modèles plus simples tels que la régression linéaire.

ExtraTreesRegressor peut être une méthode bénéfique pour la régression dans diverses tâches, en particulier lorsqu'il est nécessaire de réduire le sur-ajustement et d'améliorer la généralisation du modèle.

2.2.5.1. Code pour créer le modèle ExtraTreesRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.ensemble.ExtraTreesRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# ExtraTreesRegressor.py
# Le code démontre le processus d'entraînement du modèle ExtraTreesRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"

# crée un modèle de Régresseur Extra Trees
regression_model = ExtraTreesRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  ExtraTreesRegressor Original model (double)
Python  R-squared (Coefficient of determination): 1.0
Python  Mean Absolute Error: 2.2302160118670144e-13
Python  Mean Squared Error: 8.41048471722451e-26
Python  
Python  ExtraTreesRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999998015
Python  Mean Absolute Error: 3.795239380975701e-05
Python  Mean Squared Error: 2.627067474763585e-09
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  ExtraTreesRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx

Onglet Erreurs :

ExtraTreesRegressor.py started  ExtraTreesRegressor.py  1       1
Traceback (most recent call last):      ExtraTreesRegressor.py  1       1
    onnx_session = ort.InferenceSession(onnx_filename)  ExtraTreesRegressor.py  160     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx failed:Type Erro      onnxruntime_inference_collection.py     424     1
ExtraTreesRegressor.py finished in 4654 ms              5       1

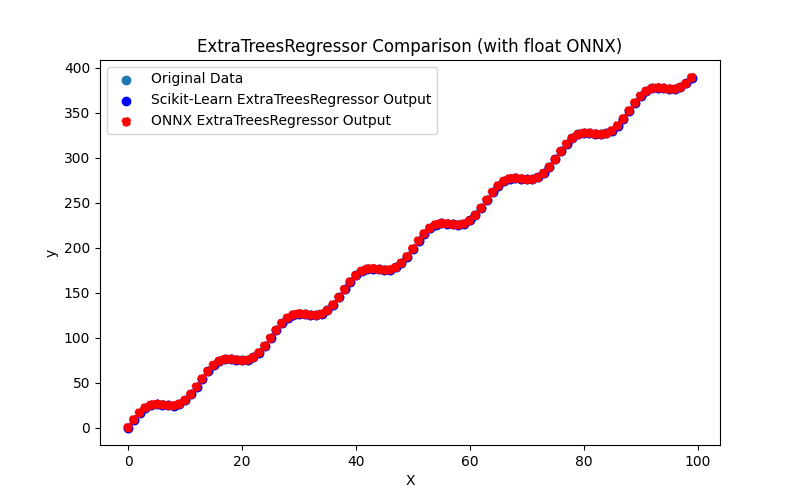
Fig. 112. Résultats de ExtraTreesRegressor.py (ONNX float)

2.2.5.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code crée les modèles extra_trees_regressor_float.onnx et extra_trees_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                          ExtraTreesRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ExtraTreesRegressor"
#define   ONNXFilenameFloat  "extra_trees_regressor_float.onnx"
#define   ONNXFilenameDouble "extra_trees_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

ExtraTreesRegressor (EURUSD,H1) Testing ONNX float: ExtraTreesRegressor (extra_trees_regressor_float.onnx)
ExtraTreesRegressor (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9999999999998015
ExtraTreesRegressor (EURUSD,H1) MQL5:   Mean Absolute Error: 0.0000379523938098
ExtraTreesRegressor (EURUSD,H1) MQL5:   Mean Squared Error: 0.0000000026270675
ExtraTreesRegressor (EURUSD,H1) 
ExtraTreesRegressor (EURUSD,H1) Testing ONNX double: ExtraTreesRegressor (extra_trees_regressor_double.onnx)
ExtraTreesRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreesRegressor.mq5' (133:16)
ExtraTreesRegressor (EURUSD,H1) model_name=ExtraTreesRegressor OnnxCreate error 5800

Le modèle ONNX en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double.

2.2.5.3. Représentation ONNX des extra_trees_regressor_float.onnx et extra_trees_regressor_double.onnx

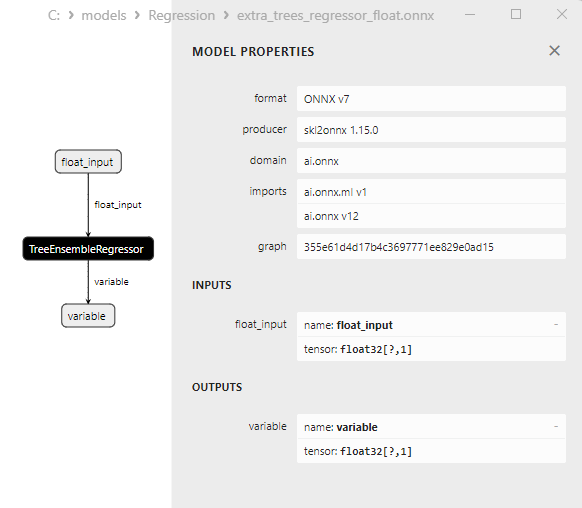
Fig. 113. Représentation ONNX de extra_trees_regressor_float.onnx dans Netron

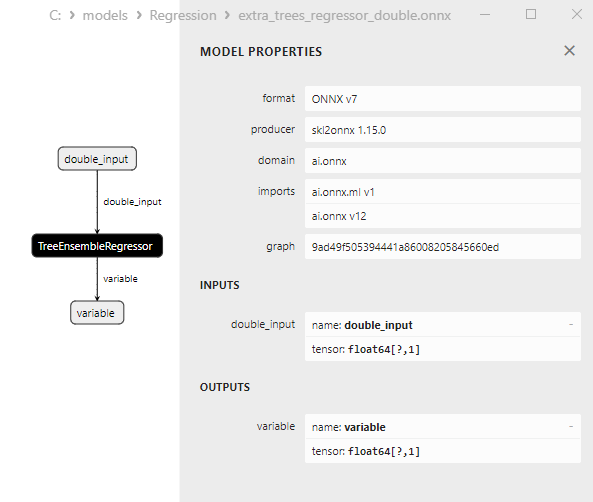
Fig. 114. Représentation ONNX de extra_trees_regressor_double.onnx dans Netron

2.2.6. sklearn.svm.NuSVR

NuSVR est une méthode d'apprentissage automatique utilisée pour les tâches de régression. Cette méthode est basée sur la Machine à Vecteur de Support (Support Vector Machine, SVM), mais elle est appliquée aux tâches de régression plutôt qu'aux tâches de classification.

NuSVR est une variante des SVM conçue pour résoudre les tâches de régression en prédisant les valeurs continues de la variable cible.

Comment fonctionne NuSVR :

1. Données d'Entrée : Elle commence par un ensemble de données comprenant des caractéristiques (variables indépendantes) et des valeurs de la variable cible (continue).
2. Sélection du noyau : NuSVR utilise des noyaux tels que des fonctions linéaires, polynomiales ou à base radiale (RBF) pour transformer les données dans un espace de plus grande dimension où un hyperplan de séparation linéaire peut être trouvé.
3. Définition du paramètre Nu : Le paramètre Nu contrôle la complexité du modèle et définit le nombre d'exemples d'apprentissage qui seront considérés comme aberrants. La valeur Nu doit être comprise entre 0 et 1, ce qui influe sur le nombre de vecteurs de soutien.
4. Construction de Vecteurs de Soutien : NuSVR vise à trouver un hyperplan de séparation optimal qui maximise l'écart entre cet hyperplan et les points d'échantillonnage les plus proches.
5. Entraînement du Modèle : Le modèle est entraîné de manière à minimiser l'erreur de régression et à respecter les contraintes associées au paramètre Nu.
6. Faire des Prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs de la variable cible sur de nouvelles données.

Avantages de NuSVR :

• Traitement des valeurs aberrantes : NuSVR permet de contrôler les valeurs aberrantes à l'aide du paramètre Nu, qui régule le nombre d'exemples d'apprentissage considérés comme aberrants.
• Noyaux Multiples : La méthode prend en charge différents types de noyaux, ce qui permet de modéliser des relations non linéaires complexes.

Limites de NuSVR :

• Sélection des Paramètres Nu : Le choix de la valeur correcte du paramètre Nu peut nécessiter quelques essais.
• Sensibilité de l'Echelle des Données : Les SVM, y compris NuSVR, peuvent être sensibles à l'échelle des données, de sorte qu'une standardisation ou une normalisation des caractéristiques peut être nécessaire.
• Complexité de Calcul : Pour les grands ensembles de données et les noyaux complexes, NuSVR peut s'avérer coûteux en termes de calcul.

NuSVR est une méthode d'apprentissage automatique pour les tâches de régression basée sur la méthode de la machine à vecteur de support (SVM). Il permet de prédire les valeurs continues de la variable cible et de gérer les valeurs aberrantes à l'aide du paramètre Nu.

2.2.6.1. Code pour créer le modèle NuSVR et l'exporter vers ONNX pour les float et les double

Ce code crée le modèle sklearn.svm.NuSVR, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# NuSVR.py
# Le code démontre le processus d'entraînement du modèle NuSVR, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"

# crée un modèle NuSVR
nusvr_model = NuSVR()

# ajuste le modèle aux données
nusvr_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = nusvr_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  NuSVR Original model (double)
Python  R-squared (Coefficient of determination): 0.2771437770527445
Python  Mean Absolute Error: 83.76666411704255
Python  Mean Squared Error: 9565.381751764757
Python  
Python  NuSVR ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_float.onnx
Python  Information about input tensors in ONNX:
1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.27714379657935495
Python  Mean Absolute Error: 83.766663385322
Python  Mean Squared Error: 9565.381493373838
Python  R^2 matching decimal places:  7
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  5
Python  
Python  NuSVR ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_double.onnx

Onglet Erreurs :

NuSVR.py started        NuSVR.py        1       1
Traceback (most recent call last):      NuSVR.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  NuSVR.py        159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess.initialize_session(providers, provider_options, disabled_optimizers)   onnxruntime_inference_collection.py     435     1
onnxruntime.capi.onnxruntime_pybind11_state.NotImplemented: [ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for SVMRegressor(1) node with name 'SVM'        onnxruntime_inference_collection.py     435     1
NuSVR.py finished in 2925 ms            5       1

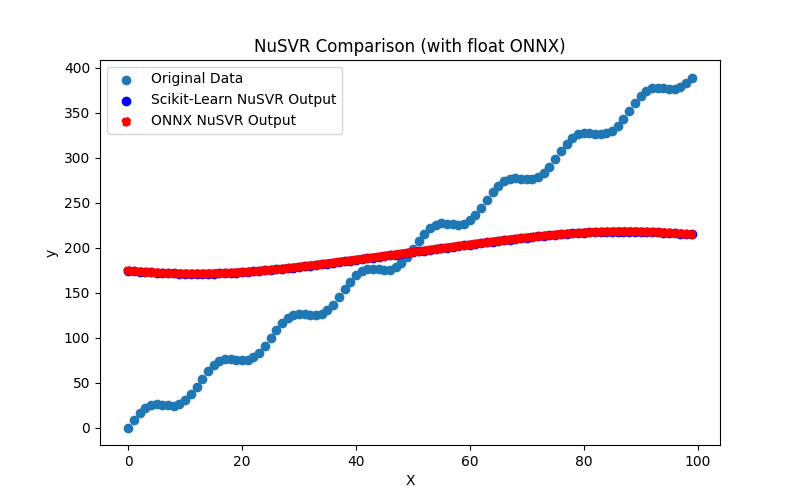
Fig. 115. Résultats du NuSVR.py (ONNX float)

2.2.6.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles sauvegardés nu_svr_float.onnx et nu_svr_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                        NuSVR.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "NuSVR"
#define   ONNXFilenameFloat  "nu_svr_float.onnx"
#define   ONNXFilenameDouble "nu_svr_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

NuSVR (EURUSD,H1)       Testing ONNX float: NuSVR (nu_svr_float.onnx)
NuSVR (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.2771437965793548
NuSVR (EURUSD,H1)       MQL5:   Mean Absolute Error: 83.7666633853219906
NuSVR (EURUSD,H1)       MQL5:   Mean Squared Error: 9565.3814933738358377
NuSVR (EURUSD,H1)       
NuSVR (EURUSD,H1)       Testing ONNX double: NuSVR (nu_svr_double.onnx)
NuSVR (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\Regression\NuSVR.mq5' (133:16)
NuSVR (EURUSD,H1)       model_name=NuSVR OnnxCreate error 5800

Le modèle ONNX en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double.

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: NuSVR (nu_svr_float.onnx)
Python  Mean Absolute Error: 83.76666411704255
MQL5:   Mean Absolute Error: 83.7666633853219906

2.2.6.3. Représentation ONNX de nu_svr_float.onnx et nu_svr_double.onnx

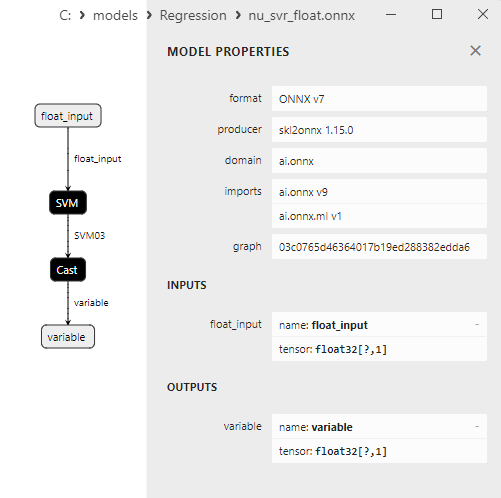
Fig. 116. Représentation ONNX du nu_svr_float.onnx dans Netron

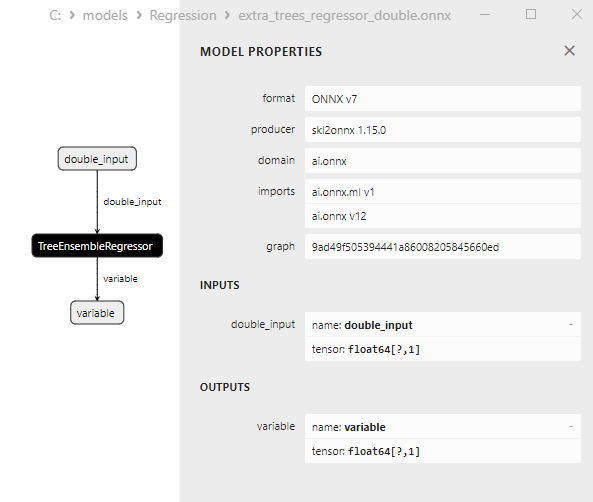
Fig. 117. Représentation ONNX du nu_svr_double.onnx dans Netron

2.2.7. sklearn.ensemble.RandomForestRegressor

RandomForestRegressor est une méthode d'apprentissage automatique utilisée pour résoudre les tâches de régression.

Il s'agit de l'une des méthodes les plus populaires basées sur l'apprentissage par ensembles et qui utilise l'algorithme Random Forest pour créer des modèles de régression puissants et robustes.

Voici comment fonctionne RandomForestRegressor :

1. Données d'Entrée : Elle commence par un ensemble de données comprenant des caractéristiques (variables indépendantes) et une variable cible (continue).
2. Random Forest : RandomForestRegressor utilise un ensemble d'arbres de décision pour résoudre la tâche de régression. Chaque arbre de la forêt s'efforce de prédire les valeurs de la variable cible.
3. Échantillonnage Bootstrap : Chaque arbre est formé à l'aide d'échantillons bootstrap, c'est-à-dire d'un échantillonnage aléatoire avec remplacement à partir de l'ensemble des données de formation. Cela permet de diversifier les données à partir desquelles chaque arbre apprend.
4. Sélection Aléatoire de Caractéristiques : Lors de la construction de chaque arbre, un sous-ensemble aléatoire de caractéristiques est également sélectionné, ce qui rend le modèle plus robuste et réduit les corrélations entre les arbres.
5. Calcul de la Moyenne des Prédictions : Une fois tous les arbres construits, RandomForestRegressor fait la moyenne de leurs prédictions ou les combine pour obtenir la prédiction de régression finale.

Avantages de RandomForestRegressor :

• Puissance et Robustesse : RandomForestRegressor est une méthode de régression puissante qui offre souvent de bonnes performances.
• Traitement des Données Volumineuses : Il gère bien les grands ensembles de données et peut prendre en charge une multitude de caractéristiques.
• Résilience au Sur-Ajustement : Grâce à l'échantillonnage bootstrap et à la sélection aléatoire des caractéristiques, la forêt aléatoire est généralement résistante à l'ajustement excessif.
• Estimation de l'importance des caractéristiques : Random Forest peut fournir des informations sur l'importance de chaque caractéristique dans la tâche de régression.

Limites de RandomForestRegressor :

• Manque d'Interprétabilité : Le modèle peut être moins facile à interpréter que les modèles linéaires.
• Le modèle n'est pas toujours le plus précis : Dans certaines tâches, des ensembles plus complexes peuvent s'avérer inutiles et des modèles linéaires peuvent être plus appropriés.

RandomForestRegressor est une méthode d'apprentissage automatique puissante pour les tâches de régression qui utilise un ensemble d'arbres de décision aléatoires pour créer un modèle de régression stable et performant. Cette méthode est particulièrement utile pour les tâches impliquant de grands ensembles de données et pour évaluer l'importance des caractéristiques.

2.2.7.1. Code pour créer le modèle RandomForestRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.ensemble.RandomForestRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# RandomForestRegressor.py
# Le code démontre le processus d'entraînement du modèle RandomForestRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"

# crée un modèle RandomForestRegressor
regression_model = RandomForestRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  RandomForestRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9998854509605539
Python  Mean Absolute Error: 0.9186485980852603
Python  Mean Squared Error: 1.5157997632401086
Python  
Python  RandomForestRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9998854516013125
Python  Mean Absolute Error: 0.9186420704511761
Python  Mean Squared Error: 1.515791284236419
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  5
Python  
Python  RandomForestRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx

Onglet Erreurs :

RandomForestRegressor.py started        RandomForestRegressor.py        1       1
Traceback (most recent call last):      RandomForestRegressor.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  RandomForestRegressor.py        159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx failed:Type Er      onnxruntime_inference_collection.py     424     1
RandomForestRegressor.py finished in 4392 ms            5       1

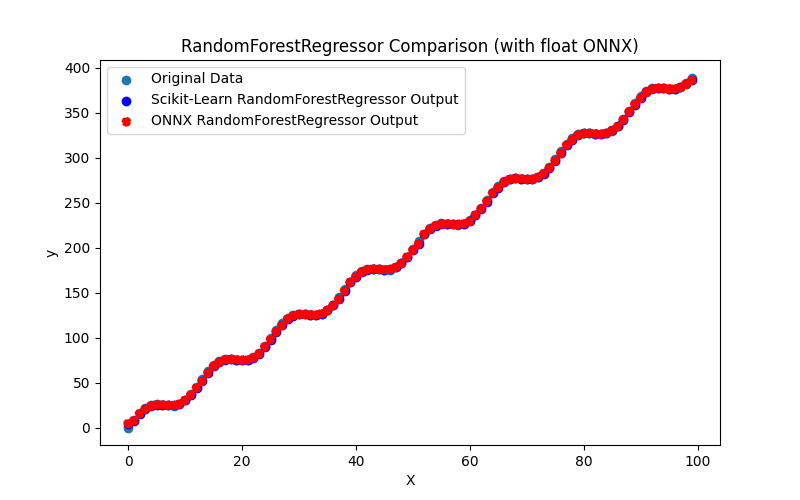
Fig. 118. Résultats de RandomForestRegressor.py (ONNX float)

2.2.7.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles random_forest_regressor_float.onnx et random_forest_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                        RandomForestRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RandomForestRegressor"
#define   ONNXFilenameFloat  "random_forest_regressor_float.onnx"
#define   ONNXFilenameDouble "random_forest_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

RandomForestRegressor (EURUSD,H1)       
RandomForestRegressor (EURUSD,H1)       Testing ONNX float: RandomForestRegressor (random_forest_regressor_float.onnx)
RandomForestRegressor (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9998854516013125
RandomForestRegressor (EURUSD,H1)       MQL5:   Mean Absolute Error: 0.9186420704511761
RandomForestRegressor (EURUSD,H1)       MQL5:   Mean Squared Error: 1.5157912842364190
RandomForestRegressor (EURUSD,H1)       
RandomForestRegressor (EURUSD,H1)       Testing ONNX double: RandomForestRegressor (random_forest_regressor_double.onnx)
RandomForestRegressor (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\RandomForestRegressor.mq5' (133:16)
RandomForestRegressor (EURUSD,H1)       model_name=RandomForestRegressor OnnxCreate error 5800

Le modèle ONNX float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double...

2.2.7.3. Représentation ONNX de random_forest_regressor_float.onnx et random_forest_regressor_double.onnx

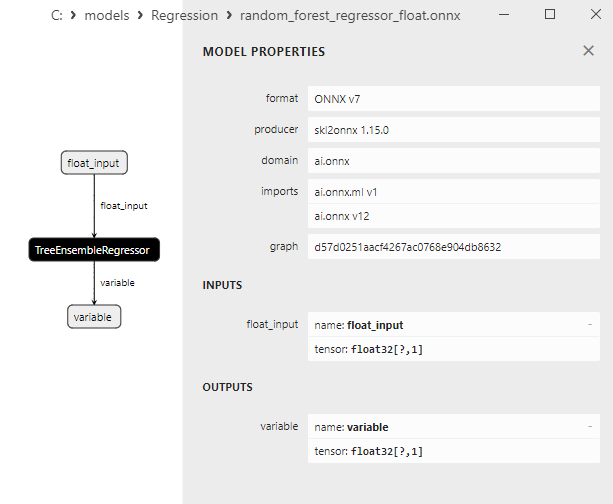
Fig. 119. Représentation ONNX de random_forest_regressor_float.onnx dans Netron

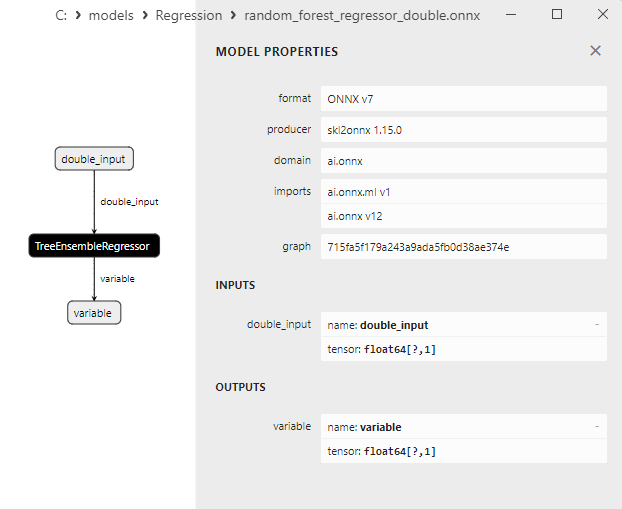
Fig. 120. Représentation ONNX de random_forest_regressor_double.onnx dans Netron

2.2.8. sklearn.ensemble.GradientBoostingRegressor

GradientBoostingRegressor est une méthode d'apprentissage automatique utilisée pour les tâches de régression. Elle fait partie de la famille des méthodes d'ensemble et repose sur l'idée de construire des modèles faibles et de les combiner en un modèle fort à l'aide de la méthode du gradient (gradient boosting).

Le renforcement du gradient est une technique qui permet d'améliorer les modèles en ajoutant de manière itérative des modèles faibles et en corrigeant les erreurs des modèles précédents.

Voici comment fonctionne GradientBoostingRegressor :

1. Initialisation : Il commence par l'ensemble de données original contenant des caractéristiques (variables indépendantes) et leurs valeurs cibles correspondantes.
2. Premier Modèle : Elle commence par l'apprentissage du premier modèle, souvent choisi comme un modèle de régression simple (par exemple, un arbre de décision) sur les données d'origine.
3. Résidus et Anti-Gradient : Les résidus, c'est-à-dire la différence entre les valeurs prédites par le premier modèle et les valeurs réelles de la variable cible, sont calculés. Ensuite, l'anti-gradient de cette fonction de perte est calculé, indiquant la direction à suivre pour améliorer le modèle.
4. Construire le Modèle Suivant : Le modèle suivant est construit, en se concentrant sur la prédiction de l'anti-gradient (erreurs du premier modèle). Ce modèle est entraîné sur les résidus et ajouté au premier modèle.
5. Itérations : Le processus de construction de nouveaux modèles et de correction des résidus est répété plusieurs fois. Chaque nouveau modèle prend en compte les résidus des modèles précédents et vise à améliorer les prévisions.
6. Combinaison de Modèles : Les prédictions de tous les modèles sont combinées dans la prédiction finale en établissant une moyenne ou en les pondérant en fonction de leur importance.

Avantages de GradientBoostingRegressor :

• Haute Performance : Le renforcement du gradient est une méthode puissante capable d'atteindre des performances élevées dans les tâches de régression.
• Robustesse face aux valeurs aberrantes : Il traite les données aberrantes et construit des modèles en tenant compte de cette incertitude.
• Sélection Automatique des Caractéristiques : Il sélectionne automatiquement les caractéristiques les plus importantes pour prédire la variable cible.
• Traitement de Diverses Fonctions de Perte : La méthode permet d'utiliser différentes fonctions de perte en fonction de la tâche à accomplir.

Limites de GradientBoostingRegressor :

• L'ajustement des hyper-paramètres est nécessaire : Pour obtenir des performances maximales, il est nécessaire d'ajuster les hyper-paramètres tels que le taux d'apprentissage, la profondeur de l'arbre et le nombre de modèles.
• Coûteux sur le plan des ressources de calcul : Le renforcement du gradient peut s'avérer coûteux en termes de calcul, en particulier lorsque les volumes de données sont importants et que le nombre d'arbres est élevé.

Le GradientBoostingRegressor est une méthode de régression puissante souvent utilisée dans des tâches pratiques pour obtenir des performances élevées avec un réglage correct des hyper-paramètres.

2.2.8.1. Code pour créer le modèle GradientBoostingRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.ensemble.GradientBoostingRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# GradientBoostingRegressor.py
# Le code démontre le processus d'entraînement du modèle GradientBoostingRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"

# crée un modèle de régresseur à renforcement de gradient (Gradient Boosting Regressor)
regression_model = GradientBoostingRegressor()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  GradientBoostingRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9999959514652565
Python  Mean Absolute Error: 0.15069342754017417
Python  Mean Squared Error: 0.053573282108575676
Python  
Python  GradientBoostingRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999959514739537
Python  Mean Absolute Error: 0.15069457426101718
Python  Mean Squared Error: 0.05357316702127665
Python  R^2 matching decimal places:  10
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  6
Python  float ONNX model precision:  5
Python  
Python  GradientBoostingRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx

Onglet Erreurs :

GradientBoostingRegressor.py started    GradientBoostingRegressor.py    1       1
Traceback (most recent call last):      GradientBoostingRegressor.py    1       1
    onnx_session = ort.InferenceSession(onnx_filename)  GradientBoostingRegressor.py    161     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     419     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     452     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx failed:Typ      onnxruntime_inference_collection.py     452     1
GradientBoostingRegressor.py finished in 3073 ms                5       1

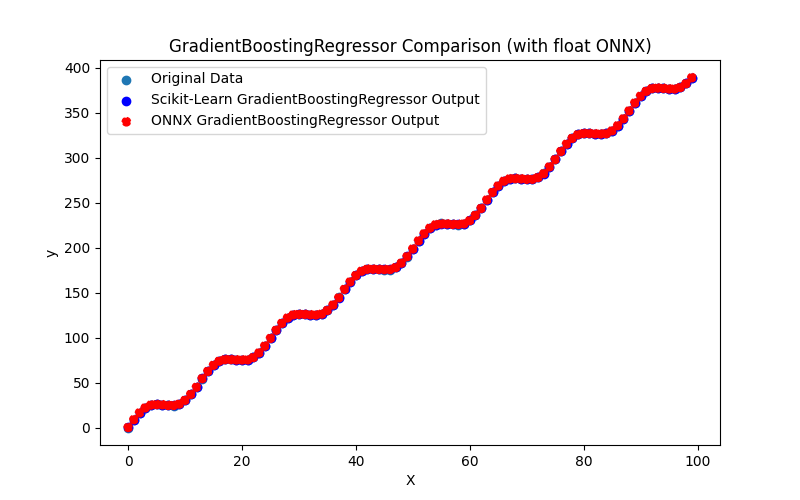
Fig. 121. Résultats de GradientBoostingRegressor.py (ONNX float)

2.2.8.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles gradient_boosting_regressor_float.onnx et gradient_boosting_regressor_double.onnx et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                    GradientBoostingRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "GradientBoostingRegressor"
#define   ONNXFilenameFloat  "gradient_boosting_regressor_float.onnx"
#define   ONNXFilenameDouble "gradient_boosting_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

GradientBoostingRegressor (EURUSD,H1)   Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx)
GradientBoostingRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9999959514739537
GradientBoostingRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 0.1506945742610172
GradientBoostingRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 0.0535731670212767
GradientBoostingRegressor (EURUSD,H1)   
GradientBoostingRegressor (EURUSD,H1)   Testing ONNX double: GradientBoostingRegressor (gradient_boosting_regressor_double.onnx)
GradientBoostingRegressor (EURUSD,H1)   ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\GradientBoostingRegressor.mq5' (133:16)
GradientBoostingRegressor (EURUSD,H1)   model_name=GradientBoostingRegressor OnnxCreate error 5800

Le modèle ONNX en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double.

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx)
Python  Mean Absolute Error: 0.15069342754017417
MQL5:   Mean Absolute Error: 0.1506945742610172

Précision de la MAE ONNX float : 5 décimales.

2.2.8.3. Représentation ONNX du gradient_boosting_regressor_float.onnx et du gradient_boosting_regressor_double.onnx

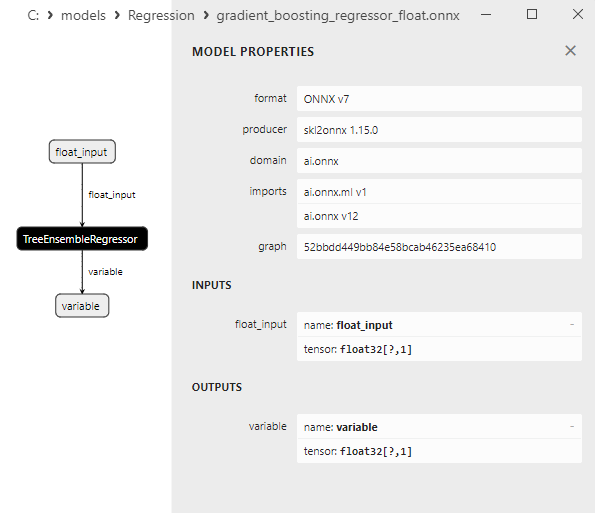
Fig. 122. Représentation ONNX du gradient_boosting_regressor_float.onnx dans Netron

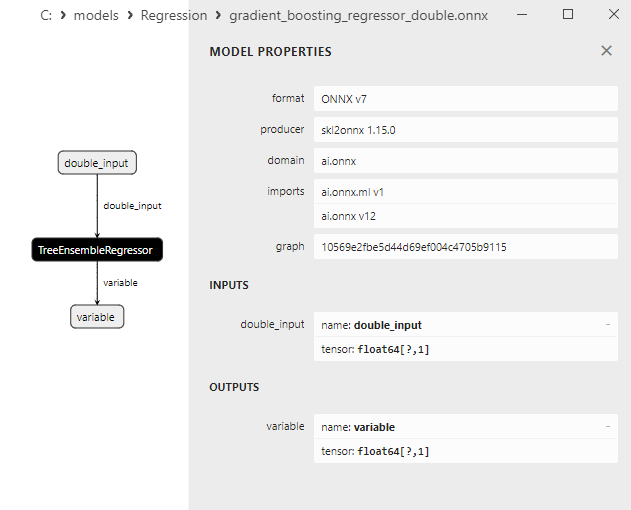
Fig. 123. Représentation ONNX du gradient_boosting_regressor_double.onnx dans Netron

2.2.9. sklearn.ensemble.HistGradientBoostingRegressor

HistGradientBoostingRegressor est une méthode d'apprentissage automatique qui représente une variante du renforcement du gradient optimisée pour travailler avec de grands ensembles de données.

Cette méthode est utilisée pour les tâches de régression, et son nom "Hist" signifie qu'elle utilise des méthodes basées sur les histogrammes pour accélérer le processus d'apprentissage.

Fonctionnement de HistGradientBoostingRegressor :

1. Initialisation : Il commence par l'ensemble de données original contenant des caractéristiques (variables indépendantes) et leurs valeurs cibles correspondantes.
2. Méthodes Basées sur les Histogrammes : Au lieu d'une division exacte des données au niveau des nœuds de l'arbre, HistGradientBoostingRegressor utilise des méthodes basées sur les histogrammes pour représenter efficacement les données sous forme d'histogrammes. Cela permet d'accélérer considérablement le processus de formation, en particulier pour les grands ensembles de données.
3. Construire des Arbres de Base : La méthode construit un ensemble d'arbres de décision de base appelés "arbres de décision à histogramme" en utilisant les représentations histogrammes des données. Ces arbres sont construits sur la base d'un renforcement du gradient et ajustés aux résidus du modèle précédent.
4. Formation Progressive : HistGradientBoostingRegressor ajoute progressivement de nouveaux arbres à l'ensemble, chaque arbre corrigeant les résidus des arbres précédents.
5. Combinaison de Modèles : Après avoir construit les arbres de base, les prédictions de tous les arbres sont combinées pour obtenir la prédiction finale.

Avantages de HistGradientBoostingRegressor :

• Haute Performance : Cette méthode est optimisée pour traiter de grands volumes de données et permet d'obtenir des performances élevées.
• Résistance au Bruit : HistGradientBoostingRegressor donne généralement de bons résultats, même en présence de bruit dans les données.
• Efficacité en Haute Dimension : La méthode peut traiter des tâches comportant un grand nombre de caractéristiques (données à haute dimension).
• Excellente Parallélisation : Elle peut paralléliser efficacement la formation sur plusieurs processeurs.

Limites de HistGradientBoostingRegressor :

• Nécessite l'ajustement des hyper-paramètres : Pour obtenir des performances maximales, il faut ajuster les hyper-paramètres tels que la profondeur de l'arbre et le nombre de modèles.
• Moins d'interprétabilité que les modèles linéaires : Comme d'autres méthodes d'ensemble, HistGradientBoostingRegressor est moins facile à interpréter que des modèles plus simples tels que la régression linéaire.

HistGradientBoostingRegressor peut être une méthode de régression utile pour les tâches impliquant de grands ensembles de données où la haute performance et l'efficacité des données à haute dimension sont essentielles.

2.2.9.1. Code pour créer le modèle HistGradientBoostingRegressor et l'exporter vers ONNX pour float et double

Ce code crée le modèle sklearn.ensemble.HistGradientBoostingRegressor, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# HistGradientBoostingRegressor.py
# Le code démontre le processus d'entraînement du modèle HistGradientBoostingRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"

# crée un modèle de Régresseur de Boosting de Gradient Basé sur l'Histogramme
hist_gradient_boosting_model = HistGradientBoostingRegressor()

# ajuste le modèle aux données
hist_gradient_boosting_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = hist_gradient_boosting_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  HistGradientBoostingRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9833421349506157
Python  Mean Absolute Error: 9.070567104488434
Python  Mean Squared Error: 220.4295035561544
Python  
Python  HistGradientBoostingRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9833421351962779
Python  Mean Absolute Error: 9.07056497799043
Python  Mean Squared Error: 220.42950030536645
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  5
Python  
Python  HistGradientBoostingRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx

Onglet Erreurs :

HistGradientBoostingRegressor.py started        HistGradientBoostingRegressor.py        1       1
Traceback (most recent call last):      HistGradientBoostingRegressor.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  HistGradientBoostingRegressor.py        161     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     419     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     452     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx faile      onnxruntime_inference_collection.py     452     1
HistGradientBoostingRegressor.py finished in 3100 ms            5       1

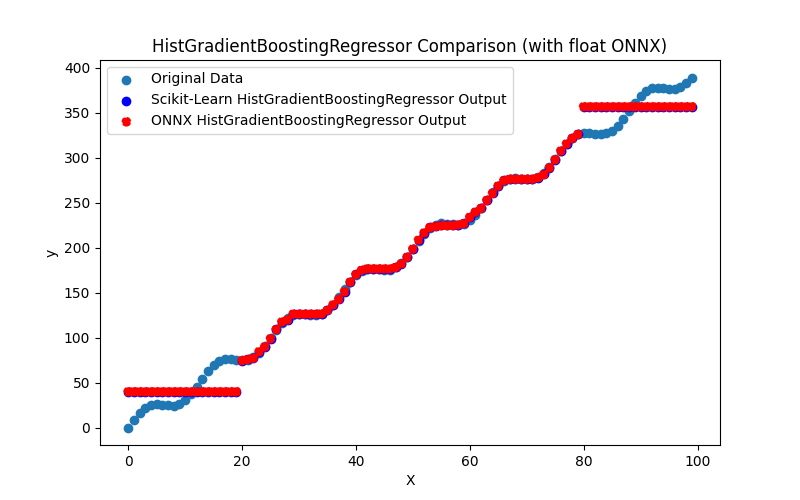
Fig. 124. Résultats de HistGradientBoostingRegressor.py (ONNX float)

2.2.9.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles hist_gradient_boosting_regressor_float.onnx et hist_gradient_boosting_regressor_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                HistGradientBoostingRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "HistGradientBoostingRegressor"
#define   ONNXFilenameFloat  "hist_gradient_boosting_regressor_float.onnx"
#define   ONNXFilenameDouble "hist_gradient_boosting_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

HistGradientBoostingRegressor (EURUSD,H1)       Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx)
HistGradientBoostingRegressor (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9833421351962779
HistGradientBoostingRegressor (EURUSD,H1)       MQL5:   Mean Absolute Error: 9.0705649779904292
HistGradientBoostingRegressor (EURUSD,H1)       MQL5:   Mean Squared Error: 220.4295003053665312
HistGradientBoostingRegressor (EURUSD,H1)       
HistGradientBoostingRegressor (EURUSD,H1)       Testing ONNX double: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_double.onnx)
HistGradientBoostingRegressor (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\HistGradientBoostingRegressor.mq5' (133:16)
HistGradientBoostingRegressor (EURUSD,H1)       model_name=HistGradientBoostingRegressor OnnxCreate error 5800

Le modèle ONNX en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double.

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx)
Python  Mean Absolute Error: 9.070567104488434
MQL5:   Mean Absolute Error: 9.0705649779904292

Précision de la MAE ONNX float : 5 décimales

2.2.9.3. Représentation ONNX de hist_gradient_boosting_regressor_float.onnx et hist_gradient_boosting_regressor_double.onnx  

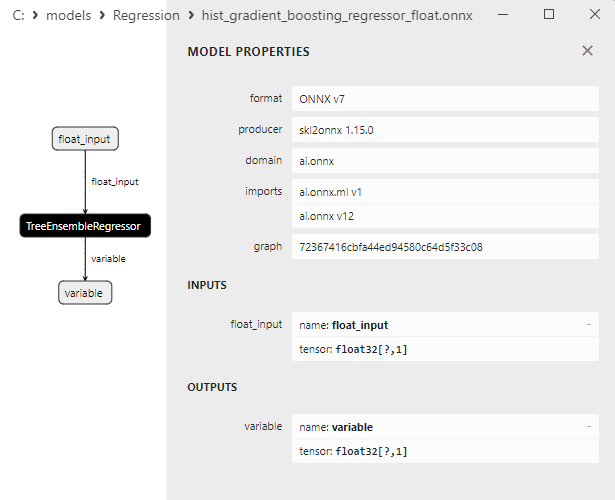
Fig. 125. Représentation ONNX de hist_gradient_boosting_regressor_float.onnx dans Netron

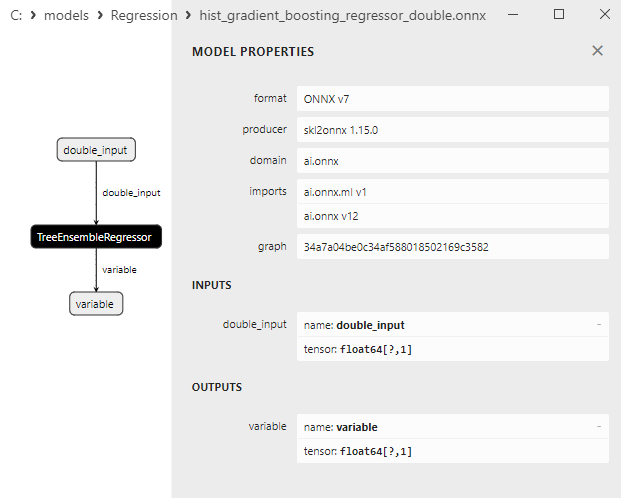
Fig. 126. Représentation ONNX de hist_gradient_boosting_regressor_double.onnx dans Netron

2.2.10. sklearn.svm.SVR

SVR (Support Vector Regression) est une méthode d'apprentissage automatique utilisée pour les tâches de régression. Il est basé sur le même concept que la Machine à Vecteurs de Support (SVM) pour la classification, mais il est adapté à la régression. L'objectif principal du SVR est de prédire les valeurs continues de la variable cible en se basant sur la distance moyenne maximale entre les points de données et la ligne de régression.

Comment fonctionne le SVR :

1. Définition de la Frontière : Comme le SVM, le SVR construit des frontières qui séparent les différentes classes de points de données. Au lieu de séparer les classes, le SVR vise à construire un "tube" autour des points de données, la largeur du tube étant contrôlée par un hyper-paramètre.
2. Variable cible et fonction de perte : Au lieu d'utiliser des classes comme dans la classification, le SVR traite des valeurs continues de la variable cible. Il minimise l'erreur de prédiction mesurée à l'aide d'une fonction de perte, telle que la différence quadratique entre les valeurs prédites et réelles.
3. Régularisation : Le SVR prend également en charge la régularisation, ce qui permet de contrôler la complexité du modèle et d'éviter l'ajustement excessif.
4. Fonctions du Noyau : Le SVR utilise généralement des fonctions de noyau qui lui permettent de gérer les dépendances non linéaires entre les caractéristiques et la variable cible. Les fonctions noyau les plus courantes sont les fonctions à base radiale (RBF), les fonctions polynomiales et les fonctions linéaires.

Avantages du SVR :

• Robustesse face aux valeurs aberrantes : Le SVR peut traiter les données aberrantes car il vise à minimiser l'erreur de prédiction.
• Prise en charge des dépendances non linéaires : L'utilisation de fonctions à noyau permet au SVR de modéliser des dépendances complexes et non linéaires entre les caractéristiques et la variable cible.
• Qualité de prédiction élevée : Dans les tâches de régression qui nécessitent des prédictions précises, le SVR peut fournir des résultats de haute qualité.

Limites du SVR :

• Sensibilité aux hyper-paramètres : Le choix de la fonction noyau et des paramètres du modèle, tels que la largeur du tube (hyper-paramètres), peut nécessiter un réglage et une optimisation minutieux.
• Complexité de Calcul : L'apprentissage du modèle SVR, en particulier lors de l'utilisation de fonctions de noyau complexes et de grands ensembles de données, peut s'avérer lourd en termes de calcul.

Le SVR est une méthode d'apprentissage automatique pour les tâches de régression basée sur l'idée de construire un "tube" autour des points de données afin de minimiser les erreurs de prédiction. Il est résistant aux valeurs aberrantes et capable de gérer des dépendances non linéaires, ce qui le rend utile pour diverses tâches de régression.

2.2.10.1. Code pour créer le modèle SVR et l'exporter vers ONNX pour les float et les double

Ce code crée le modèle sklearn.svm.SVR, l'entraîne sur des données synthétiques, enregistre le modèle au format ONNX et effectue des prédictions en utilisant des données d'entrée float et double. Il évalue également la précision du modèle original et des modèles exportés vers ONNX.

# SVR.py
# Le code démontre le processus d'entraînement d'un modèle SVR, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "SVR"
onnx_model_filename = data_path + "svr"

# crée un modèle SVR
regression_model = SVR()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  SVR Original model (double)
Python  R-squared (Coefficient of determination): 0.398243655775797
Python  Mean Absolute Error: 73.63683696034649
Python  Mean Squared Error: 7962.89631509593
Python  
Python  SVR ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.3982436352100983
Python  Mean Absolute Error: 73.63683840363255
Python  Mean Squared Error: 7962.896587236852
Python  R^2 matching decimal places:  7
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  5
Python  
Python  SVR ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_double.onnx

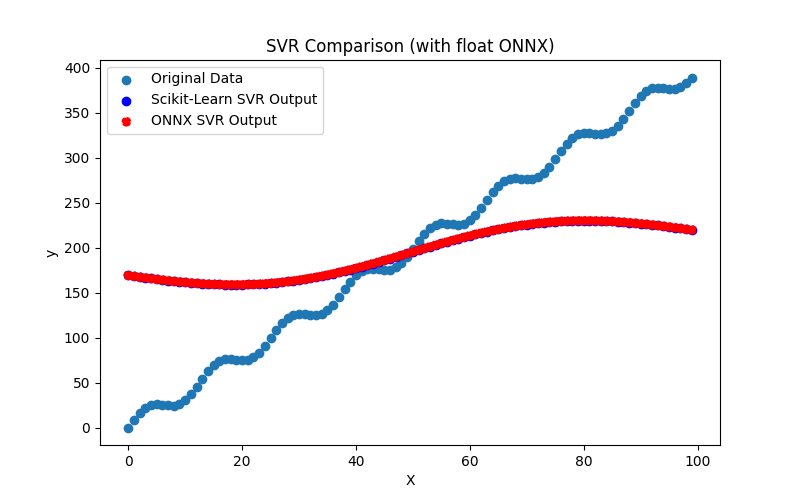
Fig. 127. Résultats du SVR.py (ONNX float)

2.2.10.2. Code MQL5 pour l'exécution des modèles ONNX

Ce code exécute les modèles svr_float.onnx et svr_double.onnx sauvegardés et démontre l'utilisation des métriques de régression dans MQL5.

//+------------------------------------------------------------------+
//|                                                          SVR.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "SVR"
#define   ONNXFilenameFloat  "svr_float.onnx"
#define   ONNXFilenameDouble "svr_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Sortie :

SVR (EURUSD,H1) Testing ONNX float: SVR (svr_float.onnx)
SVR (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.3982436352100981
SVR (EURUSD,H1) MQL5:   Mean Absolute Error: 73.6368384036325523
SVR (EURUSD,H1) MQL5:   Mean Squared Error: 7962.8965872368517012
SVR (EURUSD,H1) 
SVR (EURUSD,H1) Testing ONNX double: SVR (svr_double.onnx)
SVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\R\SVR.mq5' (133:16)
SVR (EURUSD,H1) model_name=SVR OnnxCreate error 5800

Le modèle ONNX en float s'est exécuté normalement, mais une erreur s'est produite lors de l'exécution du modèle ONNX en double.

Comparaison avec le modèle original de double précision en Python :

Testing ONNX float: SVR (svr_float.onnx)
Python  Mean Absolute Error: 73.63683696034649
MQL5:   Mean Absolute Error: 73.6368384036325523

Précision de la MAE ONNX float : 5 décimales

2.2.10.3. Représentation ONNX de svr_float.onnx et svr_double.onnx

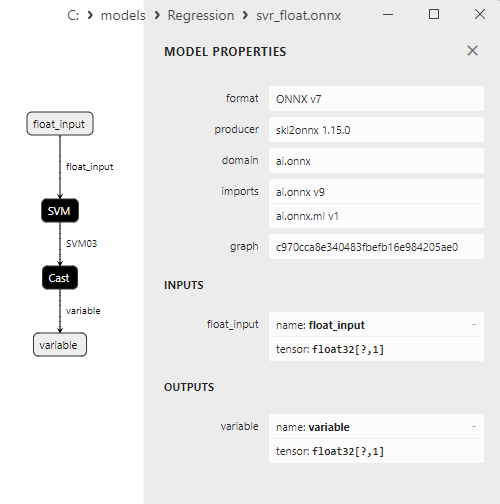
Fig. 128. Représentation ONNX de svr_float.onnx dans Netron

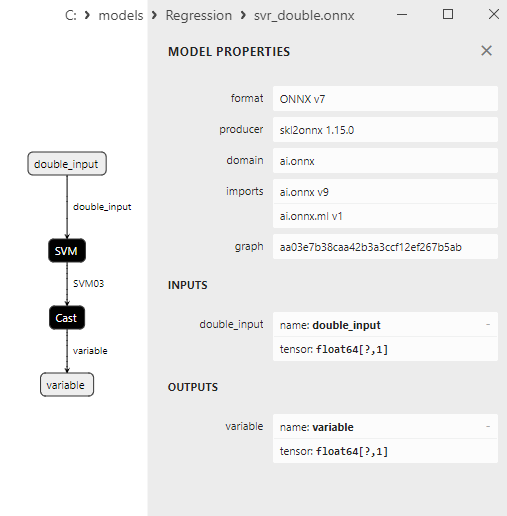
Fig. 129. Représentation ONNX de svr_double.onnx dans Netron

2.3. Modèles de régression ayant rencontré des problèmes lors de la conversion en ONNX

Certains modèles de régression n'ont pas pu être convertis au format ONNX par le convertisseur sklearn-onnx.

2.3.1. sklearn.dummy.DummyRegressor

DummyRegressor est une méthode d'apprentissage automatique utilisée dans les tâches de régression pour créer un modèle de base qui prédit la variable cible à l'aide de règles simples. Elle est précieuse pour la comparaison avec d'autres modèles plus complexes et l'évaluation de leurs performances. Cette méthode est souvent utilisée dans le cadre de l'évaluation de la qualité d'autres modèles de régression.

Le DummyRegressor offre plusieurs stratégies de prédiction :

1. "moyenne" (par défaut) : DummyRegressor prédit la valeur moyenne de la variable cible à partir de l'ensemble de données d'apprentissage. Cette stratégie est utile pour déterminer dans quelle mesure un autre modèle est meilleur que la simple prédiction de la moyenne.
2. "médiane" : DummyRegressor prédit la valeur médiane de la variable cible à partir de l'ensemble de données d'apprentissage.
3. "quantile" : DummyRegressor prédit la valeur du quantile de la variable cible (spécifiée par le paramètre quantile) à partir de l'ensemble de données d'apprentissage.
4. "constant" : DummyRegressor prédit une valeur constante fixée par l'utilisateur (à l'aide du paramètre strategy).

Avantages de DummyRegressor :

• Évaluation des Performances : DummyRegressor est utile pour évaluer la performance d'autres modèles plus complexes. Si votre modèle ne peut pas surpasser les prédictions faites par DummyRegressor, cela peut indiquer des problèmes dans le modèle.
• Comparaison avec les modèles de base : DummyRegressor permet de comparer les performances de modèles plus complexes par rapport à une base de référence (par exemple, une valeur moyenne ou médiane).
• Convivialité : DummyRegressor est facile à mettre en œuvre et à utiliser pour des analyses comparatives.

Limites de DummyRegressor :

• Pas pour une prédiction précise : DummyRegressor ne fournit que des prédictions de base et n'est pas destiné à des prévisions précises.
• Ignore les dépendances complexes : DummyRegressor ne tient pas compte des structures de données complexes et des dépendances des caractéristiques.
• Ne convient pas aux tâches nécessitant une prédiction précise : Dans les tâches de prédiction réelles, l'utilisation de DummyRegressor pour prévoir la variable cible est insuffisante.

DummyRegressor est un outil précieux pour une évaluation rapide et une comparaison des performances d'autres modèles de régression, mais il ne s'agit pas d'un modèle de régression sérieux et autonome.

2.3.1.1. Code pour la création du modèle DummyRegressor

# DummyRegressor.py
# Le code démontre le processus d'apprentissage du modèle DummyRegressor, son export au format ONNX (à la fois float et double), et la réalisation de prédictions en utilisant les modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"

# crée un modèle Dummy Regressor
regression_model = DummyRegressor(strategy="mean")

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-carré (Coefficient de Détermination):", r2)
print("Erreur Absolue Moyenne :", mae)
print("Erreur Quadratique Moyenne :", mse)

# convertit en modèle ONNX (float)
# définit letype de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  DummyRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.0
Python  Mean Absolute Error: 100.00329851715793
Python  Mean Squared Error: 13232.758393867645

Onglet Erreurs :

DummyRegressor.py started       DummyRegressor.py       1       1
Traceback (most recent call last):      DummyRegressor.py       1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     DummyRegressor.py       87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyRegressor'>'. _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
DummyRegressor.py finished in 2565 ms           19      1

2.3.2. sklearn.kernel_ridge.KernelRidge

KernelRidge est une méthode d'apprentissage automatique utilisée pour les tâches de régression. Il combine la méthode du noyau des Support Vector Machines (Kernel SVM) et la régression. KernelRidge permet de modéliser des relations complexes et non linéaires entre les caractéristiques et la variable cible à l'aide de fonctions à noyau.

Principe de fonctionnement de KernelRidge :

• Données d'Entrée : Il commence par l'ensemble de données original contenant les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
• Fonctions du noyau : KernelRidge utilise des fonctions à noyau (telles que polynomiale, RBF - fonction de base radiale, et autres) qui transforment les données dans un espace à haute dimension, permettant la modélisation de relations non linéaires plus complexes.
• Entraînement du modèle : Le modèle est entraîné sur les données en minimisant l'erreur quadratique moyenne entre les valeurs prédites et les valeurs réelles de la variable cible. Les fonctions du noyau sont utilisées pour prendre en compte les dépendances complexes.
• Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs de la variable cible pour de nouvelles données, en utilisant les mêmes fonctions de noyau.

Avantages de KernelRidge :

• Modélisation de relations non linéaires complexes : KernelRidge permet de modéliser des dépendances complexes et non linéaires entre les caractéristiques et la variable cible.
• Sélection de différents noyaux : Vous pouvez choisir différents noyaux en fonction de la nature des données et de la tâche.
• Régularisation : La méthode comprend une régularisation qui permet d'éviter l'ajustement excessif du modèle.

Limites de KernelRidge :

• Manque d'interprétabilité : Comme de nombreuses méthodes non linéaires, KernelRidge est moins facile à interpréter que les modèles linéaires.
• Complexité de calcul : L'utilisation de fonctions à noyau peut s'avérer coûteuse en termes de calculs lorsque les volumes de données sont importants et/ou que la dimension est élevée.
• Exigence de réglage des paramètres : Le choix du noyau et des paramètres du modèle appropriés nécessite des réglages et de l'expertise.

KernelRidge est utile dans les tâches de régression où les données présentent des dépendances complexes et non linéaires, et où un modèle capable de prendre en compte ces relations est nécessaire. Il est également utile dans les tâches où les fonctions de noyau peuvent être utilisées pour transformer les données en une représentation plus informative.

2.3.2.1. Code pour la création du modèle KernelRidge

# KernelRidge.py
# Le code démontre le processus d'entraînement du modèle KernelRidge, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"

# crée un modèle KernelRidge
regression_model = KernelRidge(alpha=1.0, kernel='linear')

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  KernelRidge Original model (double)
Python  R-squared (Coefficient of determination): 0.9962137909675411
Python  Mean Absolute Error: 6.36977985227399
Python  Mean Squared Error: 50.10198935520715

Onglet Erreurs :

KernelRidge.py started  KernelRidge.py  1       1
Traceback (most recent call last):      KernelRidge.py  1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     KernelRidge.py  87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.kernel_ridge.KernelRidge'>'.     _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
KernelRidge.py finished in 2516 ms              19      1

2.3.3. sklearn.isotonic.IsotonicRegression

IsotonicRegression - est une méthode d'apprentissage automatique utilisée pour les tâches de régression qui modélise une relation monotone entre les caractéristiques et la variable cible. Dans ce contexte, la "monotonicité" signifie qu'une augmentation de la valeur de l'une des caractéristiques entraîne une augmentation ou une diminution de la valeur de la variable cible, tout en préservant le sens du changement.

Principe de fonctionnement de la régression isotonique :

1. Données d'Entrée : Il commence par l'ensemble de données original contenant les caractéristiques (variables indépendantes) et les valeurs correspondantes de la variable cible.
2. Régression monotone : IsotonicRegression vise à trouver la meilleure fonction monotone qui décrit la relation entre les caractéristiques et la variable cible. Cette fonction peut être linéaire ou non linéaire mais doit rester monotone.
3. Entraînement du modèle : Le modèle est entraîné sur les données afin de déterminer les paramètres de la fonction monotone. Pendant l'apprentissage, le modèle tente de minimiser la somme des erreurs quadratiques entre les prédictions et les valeurs réelles de la variable cible.
4. Prédiction : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs de la variable cible pour de nouvelles données tout en maintenant la relation monotone.

Avantages de IsotonicRegression :

• Modélisation des relations monotones : Cette méthode est un choix idéal lorsque les données présentent des dépendances monotones et qu'il est important de conserver cette caractéristique dans le modèle.
• Interprétabilité : Les modèles monotones sont plus faciles à interpréter car ils permettent de définir clairement le sens de l'influence de chaque caractéristique sur la variable cible.

Limites de IsotonicRegression :

• Ne convient pas aux relations complexes et non linéaires : Cette méthode est limitée à la modélisation de relations monotones et n'est donc pas adaptée à la modélisation de dépendances non linéaires complexes.
• Réglage des paramètres : Certaines implémentations de la régression isotonique peuvent avoir des paramètres qui doivent être ajustés pour obtenir des performances optimales.

IsotonicRegression est utile dans les tâches où la monotonicité de la relation entre les caractéristiques et la variable cible est considérée comme un facteur important, et où il est nécessaire de construire un modèle qui préserve cette caractéristique.

2.3.3.1. Code pour la création des modèles IsotonicRegression

# IsotonicRegression.py
# Le code démontre le processus d'entraînement du modèle IsotonicRegression, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"

# crée un modèle IsotonicRegression
regression_model = IsotonicRegression()

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-carré (Coefficient de Détermination):", r2)
print("Erreur Absolue Moyenne :", mae)
print("Erreur Quadratique Moyenne :", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  IsotonicRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9999898125037958
Python  Mean Absolute Error: 0.20093409873424467
Python  Mean Squared Error: 0.13480867590911208

Onglet Erreurs :

IsotonicRegression.py started   IsotonicRegression.py   1       1
Traceback (most recent call last):      IsotonicRegression.py   1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     IsotonicRegression.py   87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.isotonic.IsotonicRegression'>'.  _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
IsotonicRegression.py finished in 2499 ms               19      1

2.3.4. sklearn.cross_decomposition.PLSCanonical

PLSCanonical (Partial Least Squares Canonical) est une méthode d'apprentissage automatique utilisée pour résoudre les problèmes de corrélation canonique. Il s'agit d'une extension de la méthode des Moindres Carrés Partiels (Partial Least Squares, PLS), appliquée à l'analyse et à la modélisation des relations entre deux ensembles de variables.

Principe de fonctionnement de PLSCanonical :

1. Données d'Entrée : Il commence par deux ensembles de données (X et Y), où chaque ensemble représente une collection de variables (caractéristiques). En général, X et Y contiennent des données corrélées, et la tâche consiste à trouver des combinaisons linéaires de caractéristiques qui maximisent la corrélation entre elles.
2. Sélection de combinaisons linéaires : PLSCanonical trouve des combinaisons linéaires (composantes) dans X et Y pour maximiser la corrélation entre les composantes des deux ensembles de données. Ces composantes sont appelées variables canoniques.
3. Recherche de corrélation maximale : L'objectif principal de PLSCanonical est de trouver des variables canoniques qui maximisent la corrélation entre X et Y, en mettant en évidence les relations les plus informatives entre les deux ensembles de données.
4. Entraînement du modèle : Une fois les variables canoniques trouvées, elles peuvent être utilisées pour créer un modèle qui prédit les valeurs Y en fonction de X.
5. Générer des prédictions : Après l'entraînement, le modèle peut être utilisé pour prédire les valeurs Y dans de nouvelles données à l'aide des valeurs X correspondantes.

Avantages de PLSCanonical :

• Analyse de corrélation : PLSCanonical permet d'analyser et de modéliser les corrélations entre deux ensembles de données, ce qui peut être utile pour comprendre les relations entre les variables.
• Réduction de la dimensionnalité : La méthode peut également être utilisée pour réduire la dimensionnalité des données, en mettant en évidence les composants les plus importants.

Limites de PLSCanonical :

• Sensibilité au choix du nombre de composants : La sélection du nombre optimal de variables canoniques peut nécessiter une certaine expérimentation.
• Dépendance à l'égard de la structure des données : Les résultats de PLSCanonical peuvent dépendre fortement de la structure des données et des corrélations entre elles.

PLSCanonical est une méthode d'apprentissage automatique utilisée pour analyser et modéliser les corrélations entre deux ensembles de variables. Cette méthode permet d'étudier les relations entre les données et peut être utile pour réduire la dimensionnalité des données et prédire des valeurs basées sur des composants corrélés.

2.3.4.1. Code pour la création du PLSCanonical

# PLSCanonical.py
# Le code démontre le processus d'entraînement du modèle PLSCanonical, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"

# crée un modèle PLSCanonical
regression_model = PLSCanonical(n_components=1)

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8, 5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  
Python  PLSCanonical Original model (double)
Python  R-squared (Coefficient of determination): 0.9962347199278333
Python  Mean Absolute Error: 6.3561407034365995
Python  Mean Squared Error: 49.82504148022689

Onglet Erreurs :

PLSCanonical.py started PLSCanonical.py 1       1
Traceback (most recent call last):      PLSCanonical.py 1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     PLSCanonical.py 87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.PLSCanonical'>'.        _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
PLSCanonical.py finished in 2513 ms             19      1

2.3.5. sklearn.cross_decomposition.CCA

Canonical Correlation Analysis (CCA) est une méthode d'analyse statistique multivariée utilisée pour étudier les relations entre deux ensembles de variables (ensemble X et ensemble Y). L'objectif principal de la CCA est de trouver des combinaisons linéaires de variables X et Y qui maximisent la corrélation entre elles. Ces combinaisons linéaires sont appelées variables canoniques.

Principe de fonctionnement de la CCA :

1. Données d'Entrée : Elle part de deux ensembles de variables X et Y. Ces ensembles peuvent contenir un nombre quelconque de variables, et la CCA tente de trouver des combinaisons linéaires qui maximisent la corrélation entre elles.
2. Construction de variables canoniques : La CCA identifie les variables canoniques dans X et Y qui maximisent leur corrélation. Ces variables canoniques sont des combinaisons linéaires des variables originales, une pour chaque indicateur canonique.
3. Évaluation de la corrélation : La CCA évalue la corrélation entre les paires de variables canoniques. Les variables canoniques sont généralement classées par corrélation décroissante, de sorte que la première paire présente la corrélation la plus élevée, la deuxième la plus élevée suivante, et ainsi de suite.
4. Interprétation : Les variables canoniques peuvent être interprétées en fonction de leur corrélation et de leur poids. Cela permet de comprendre quelles variables des ensembles X et Y sont les plus fortement liées.

Avantages de la CCA :

• Révèle les connexions cachées : La CCA peut aider à découvrir des corrélations cachées entre deux ensembles de variables qui peuvent ne pas être évidentes lors de l'analyse initiale.
• Robuste au bruit : La CCA peut tenir compte du bruit dans les données et se concentrer sur les corrélations les plus significatives.
• Applications multiples : La CCA peut être utilisée dans divers domaines, notamment les statistiques, la bio-informatique et la finance, afin d'étudier les relations entre des ensembles de variables.

Limites de la CCA :

• Nécessite plus de données : La CCA peut nécessiter une plus grande quantité de données que d'autres méthodes d'analyse pour estimer les corrélations de manière fiable.
• Relations linéaires : La CCA suppose des relations linéaires entre les variables, ce qui peut s'avérer insuffisant dans certains cas.
• Complexité d'interprétation : L'interprétation des variables canoniques peut être complexe, en particulier lorsqu'il y a de nombreuses variables dans les ensembles X et Y.

La CCA est utile lorsqu'il s'agit d'étudier la relation entre deux ensembles de variables et de découvrir des corrélations cachées.

2.3.5.1. Code pour la création du modèle CCA

# CCA.py
# Le code démontre le processus d'entraînement du modèle CCA, son export au format ONNX (à la fois float et double), et la réalisation de prédictions à l'aide des modèles ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# fonction de comparaison des décimales correspondantes
def compare_decimal_places(value1, value2):
    # convertit les deux valeurs en chaînes de caractères
    str_value1 = str(value1)
    str_value2 = str(value2)

    # trouve les positions des points décimaux dans les chaînes de caractères
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # si l'une des valeurs n'a pas de point décimal, retourne 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calcule le nombre de décimales
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # trouve le minimum du nombre de décimales
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialise un compteur pour les décimales correspondantes
    matching_count = 0

    # compare les caractères après la virgule
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# importe les bibliothèques nécessaires
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# génère des données synthétiques pour la régression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name="CCA"
onnx_model_filename = data_path + "cca"

# crée un modèle CCA
regression_model = CCA(n_components=1)

# ajuste le modèle aux données
regression_model.fit(X, y.ravel())

# prédit les valeurs pour l'ensemble du jeu de données
y_pred = regression_model.predict(X)

# évalue la performance du modèle
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convertit en modèle ONNX (float)
# définit le type de données d'entrée comme FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme FloatTensorType
initial_type_float = X.astype(np.float32)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-carré (Coefficient de Détermination)", r2_onnx_float)
print("Erreur Absolue Moyenne :", mae_onnx_float)
print("Erreur Quadratique Moyenne :", mse_onnx_float)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_float))
print("Précision du modèle ONNX float : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX float)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convertit en modèle ONNX (double)
# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# exporte le modèle au format ONNX
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# enregistre le modèle dans un fichier
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# affiche le chemin du modèle
print(f"ONNX model saved to {onnx_filename}")

# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# affiche les informations sur les tenseurs d'entrée dans ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# affiche les informations sur les tenseurs de sortie dans ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# définit le type de données d'entrée comme DoubleTensorType
initial_type_double = X.astype(np.float64)

# prédit les valeurs pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calcule et affiche les erreurs pour les modèles originaux et ONNX
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-carré (Coefficient de Détermination)", r2_onnx_double)
print("Erreur Absolue Moyenne :", mae_onnx_double)
print("Erreur Quadratique Moyenne :", mse_onnx_double)
print("R^2 matching decimal places : ", compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places : ", compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places : ", compare_decimal_places(mse, mse_onnx_double))
print("Précision du modèle ONNX double : ", compare_decimal_places(mae, mae_onnx_float))

# définit la taille de la figure
plt.figure(figsize=(8,5))
# trace les données originales et la ligne de régression
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparaison (avec ONNX double)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Sortie :

Python  CCA Original model (double)
Python  R-squared (Coefficient of determination): 0.9962347199278333
Python  Mean Absolute Error: 6.3561407034365995
Python  Mean Squared Error: 49.82504148022689

Onglet Erreurs :

CCA.py started  CCA.py  1       1
Traceback (most recent call last):      CCA.py  1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     CCA.py  87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.CCA'>'. _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
CCA.py finished in 2543 ms              19      1

Conclusion

L'article passe en revue 45 modèles de régression disponibles dans la bibliothèque Scikit-learn version 1.3.2.

1. Sur cet ensemble, 5 modèles ont rencontré des difficultés lors de la conversion au format ONNX :

1. DummyRegressor (Dummy Regressor) ;
2. KernelRidge (Kernel Ridge Regression) ;
3. IsotonicRegression (Isotonic Regression) ;
4. PLSCanonical (Partial Least Squares Canonical Analysis) ;
5. CCA (Canonical Correlation Analysis).

Ces modèles peuvent être trop complexes dans leur structure ou leur logique et peuvent utiliser des structures de données ou des algorithmes spécifiques qui ne sont pas entièrement compatibles avec le format ONNX.

2. Les 40 modèles restants ont été convertis avec succès en ONNX avec des calculs en précision flottante.

1. ARDRegression : Automatic Relevance Determination Regression (ARD) ;
2. BayesianRidge : Bayesian Ridge Regression avec régularisation ;
3. ElasticNet : Combinaison des régularisations L1 et L2 pour atténuer le sur-ajustement ;
4. ElasticNetCV : Elastic Net avec sélection automatique des paramètres de régularisation ;
5. HuberRegressor : Régression avec une sensibilité réduite aux valeurs aberrantes ;
6. Lars : Régression des Moindres Angles ;
   
7. LarsCV : Régression des Moindres Angles avec Validation Croisée ;
8. Lasso : Régression régularisée L1 pour la sélection des caractéristiques ;
   
9. LassoCV : Régression Lasso à Validation Croisée ;
10. LassoLars : Combinaison de Lasso et de LARS pour la régression ;
    
11. LassoLarsCV : Régression LassoLars à Validation Croisée ;
12. LassoLarsIC : Critères d'information pour la sélection des paramètres LassoLars ;
13. LinearRegression : Régression linéaire simple ;
14. Ridge : Régression linéaire avec régularisation L2 ;
    
15. RidgeCV : Régression Ridge à Validation Croisée ;
16. OrthogonalMatchingPursuit : Régression avec sélection orthogonale des caractéristiques ;
17. PassiveAggressiveRegressor : Régression avec une approche d'apprentissage passive-agressive ;
18. QuantileRegressor : Régression par quantile ;
19. RANSACRegressor : Régression avec la méthode RANdom SAmple Consensus ;
20. TheilSenRegressor : Régression non linéaire basée sur la méthode Theil-Sen.
21. LinearSVR : Régression vectorielle linéaire ;
22. MLPRegressor : Régression à l'aide d'un perceptron multicouche ;
23. PLSRegression : Régression des Moindres Carrés Partiels ;
24. TweedieRegressor : Régression basée sur la distribution de Tweedie ;
25. PoissonRegressor : Régression pour la modélisation des données distribuées selon Poisson ;
26. RadiusNeighborsRegressor: Régression basée sur les voisins de rayon ;
    
27. KNeighborsRegressor : Régression basée sur les voisins les plus proches ;
28. GaussianProcessRegressor : Régression basée sur les processus gaussiens ;
29. GammaRegressor : Régression pour la modélisation de données distribuées en gamma ;
30. SGDRegressor : Régression basée sur la descente stochastique du gradient ;
31. AdaBoostRegressor: Régression à l'aide de l'algorithme AdaBoost ;
32. BaggingRegressor: Régression à l'aide de la méthode Bagging ;
33. DecisionTreeRegressor: Régression basée sur un arbre de décision ;
34. ExtraTreeRegressor: Régression basée sur un arbre de décision supplémentaire ;
35. ExtraTreesRegressor: Régression avec arbres de décision supplémentaires ;
36. NuSVR: Régression linéaire continue à vecteur de support (SVR) ;
37. RandomForestRegressor: Régression avec un ensemble d'arbres de décision (Random Forest) ;
38. GradientBoostingRegressor: Régression avec renforcement du gradient ;
39. HistGradientBoostingRegressor: Régression avec renforcement du gradient de l'histogramme ;
40. SVR: Méthode de régression par vecteur de support.
    

3. La possibilité de convertir les modèles de régression en ONNX avec des calculs en double précision a également été explorée.

Un problème sérieux rencontré lors de la conversion des modèles en double précision dans ONNX est la limitation des opérateurs ML ai.onnx.ml.LinearRegressor, ai.onnx.ml.SVMRegressor, ai.onnx.ml.TreeEnsembleRegressor : leurs paramètres et valeurs de sortie sont de type float. Il s'agit essentiellement de composants de réduction de la précision et leur exécution dans des calculs en double précision est douteuse. Pour cette raison, la bibliothèque ONNX Runtime n'a pas implémenté certains opérateurs pour les modèles ONNX en double précision (des erreurs de nature NOT_IMPLEMENTED peuvent se produire) : 'Could not find an implementation for the node LinearRegressor:LinearRegressor(1)', 'Could not find an implementation for SVMRegressor(1) node with name 'SVM'', et ainsi de suite). Ainsi, dans le cadre de la spécification ONNX actuelle, il est impossible d'effectuer des opérations en double précision pour ces opérateurs ML.

Pour les modèles de régression linéaire, le convertisseur a permis de contourner la limitation de LinearRegressor : Les opérateurs ONNX MatMul() et Add() sont utilisés à la place. Grâce à cette approche, les 30 premiers modèles de la liste précédente ont été convertis avec succès en modèles ONNX avec des calculs en double précision, et ces modèles ont conservé la précision des modèles originaux en double précision.

Mais pour les opérateurs ML plus complexes tels que SVMRegressor et TreeEnsembleRegressor, ce résultat n'a pas été atteint. Donc, des modèles comme AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor et SVR ne sont actuellement disponibles que dans les modèles ONNX avec des calculs en float.

Résumé

L'article couvre 45 modèles de régression de la bibliothèqueScikit-learn version 1.3.2 et leurs résultats de conversion au format ONNX pour les calculs en float et en double précision.

Sur l'ensemble des modèles examinés, 5 se sont révélés complexes pour la conversion en ONNX. Ces modèles comprennent DummyRegressor, KernelRidge, IsotonicRegression, PLSCanonical et CCA. Leur structure ou leur logique complexe peut nécessiter une adaptation supplémentaire pour une conversion ONNX réussie.

Les 40 modèles de régression restants ont été transformés avec succès en format ONNX pour les float. Parmi ceux-là, 30 modèles ont également été convertis avec succès au format ONNX pour la double précision, en conservant leur précision

En raison de la limitation des opérateurs ML pour SVMRegressor et TreeEnsembleRegressor, les modèles AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor et SVR ne sont actuellement disponibles dans les modèles ONNX qu’avec les calculs en float.

Tous les scripts de l'article sont également disponibles dans le projet public MQL5\Shared Projects\Scikit.Regression.ONNX.