Mesure des Informations sur les Indicateurs

Introduction

L'apprentissage automatique s'appuie sur des données d'entraînement pour apprendre le comportement général du marché et, en fin de compte, faire des prédictions assez précises. L'algorithme d'apprentissage choisi doit se frayer un chemin à travers un échantillon soigneusement sélectionné pour en extraire des informations significatives. La raison pour laquelle de nombreuses personnes ne parviennent pas à appliquer avec succès ces outils sophistiqués est que la plupart des informations significatives sont cachées dans des données bruyantes. Il n'est peut-être pas évident pour de nombreux développeurs de stratégies que les ensembles de données que nous utilisons peuvent ne pas être appropriés pour l'apprentissage des modèles.

Les indicateurs peuvent être considérés comme des fournisseurs d'informations sur la série de prix sous-jacente à laquelle ils sont appliqués. En partant de ce principe, l'entropie peut être utilisée pour mesurer la quantité d'informations communiquées par un indicateur. À l'aide des étapes et des outils décrits dans le livre Testing and Tuning Market Trading Systems (TTMTS) de Timothy Masters, nous montrerons comment ces outils peuvent être utilisés pour évaluer la structure des données d'un indicateur.

Pourquoi mesurer les informations sur les indicateurs ?

Souvent, lorsqu'on utilise des outils d'apprentissage automatique pour élaborer une stratégie, on se contente de jeter toutes sortes de données sur les algorithmes dans l'espoir qu'il en ressortira quelque chose. En fin de compte, le succès dépendra de la qualité du (des) prédicteur(s) utilisé(s) dans le modèle. Et les prédicteurs efficaces présentent généralement certaines caractéristiques. L'une d'entre elles est chargée d'un important contenu informatif.

La quantité d'informations contenues dans les variables utilisées pour l'apprentissage des modèles est importante, mais elle n'est pas la seule condition d'un apprentissage efficace des modèles. Par conséquent, la mesure du contenu de l'information peut être utilisée pour sélectionner des indicateurs qui seraient autrement utilisés à l'aveuglette au cours du processus de formation.  C'est ici que s'applique le concept d'entropie.

Entropie

L’Entropie a déjà été discutée un certain nombre de fois sur MQL5.com. Je m'excuse auprès du lecteur car il devra subir une autre définition. Mais je promets qu'elle est essentielle pour comprendre l'application du concept. Les articles précédents ont présenté l'historique et la dérivation du calcul de l'entropie. Par souci de concision, nous commencerons donc par l'équation.

                                                        

H(X) désigne l'entropie de X, X étant une variable discrète représentant une variable arbitraire, par exemple un message. Le contenu du message ne peut prendre qu'un nombre fini de valeurs. Dans l'équation, cela se traduit par un petit x. Les petits x sont les valeurs observées des messages, telles que, si toutes les valeurs possibles de x étaient énumérées dans un ensemble, N.

Prenons l'exemple d'un dé non truqué. Les dés, lorsqu'ils sont lancés, peuvent être perçus comme fournissant des informations qui déterminent l'issue d'un jeu. Le dé a 6 faces uniques numérotées de 1 à 6. La probabilité d'observer l'un des nombres face vers le haut est de 1/6.

Dans cet exemple, le grand X serait le dé et le petit x pourrait être n'importe lequel des nombres peints sur les faces du dé. Tous sont placés dans l'ensemble N ={ 1, 2, 3, 4, 5, 6 }. En appliquant la formule, l'entropie de ce dé est de 0,7781.

                                                         

Considérons maintenant un autre dé, qui présente un défaut de fabrication. Il comporte 2 faces sur lesquelles est peint le même numéro. Pour ce dé défectueux, l'ensemble N des valeurs possibles est { 1, 1, 3, 4, 5, 6 }. En utilisant à nouveau la formule, nous obtenons une valeur d'entropie moyenne de 0,6778 .

                                                 

En comparant les valeurs, on constate que le contenu informatif a diminué. En analysant les deux dés, lorsque les probabilités d'observer chaque valeur possible sont toutes égales, l'équation de l'entropie produit sa plus grande valeur possible. L'entropie atteint donc sa moyenne maximale lorsque les probabilités de toutes les valeurs possibles sont égales.

Si l'on écarte les dés défectueux pour un indicateur qui produit des nombres réels traditionnels en sortie. X devient alors l'indicateur et le petit x sera la plage de valeurs que l'indicateur peut prendre. Avant d'aller plus loin, nous rencontrons un problème car l'équation de l'entropie traite strictement de variables discrètes. Il est possible de transformer l'équation pour travailler avec des variables continues, mais l'application d'une telle transformation serait difficile. Il est donc plus facile de s'en tenir au domaine des nombres discrets.

Calcul de l'entropie d'un indicateur

Pour appliquer l'équation de l'entropie à des variables continues, nous devons discrétiser les valeurs de l'indicateur, en divisant la plage de valeurs en intervalles de taille égale, puis en comptant le nombre de valeurs qui tombent dans chaque intervalle. Grâce à cette méthode, l'ensemble initial qui énumère la plage maximale de toutes les valeurs de l'indicateur est remplacé par des sous-ensembles dont chacun correspond aux intervalles sélectionnés.

Lorsqu'il s'agit de variables continues, la variation des probabilités des valeurs possibles que peut prendre la variable devient significative, car elle fournit une facette importante de l'application de l'entropie aux indicateurs.

Revenons au premier exemple des dés. Si nous divisons les valeurs finales d'entropie de chacun par le log(N) pour chacun des n respectifs. Le premier dé donne 1, alors que le dé défectueux donne 0,87. En divisant la valeur de l'entropie par le logarithme du nombre de valeurs que la variable peut prendre, on obtient une mesure relative à l'entropie maximale théorique de la variable. On parle alors d'entropie proportionnelle ou relative.

C'est cette valeur qui sera utile dans notre évaluation des indicateurs, car elle indiquera à quel point l'entropie de l'indicateur est proche de sa moyenne maximale théorique. Plus elle est proche de 1, le maximum, mieux c'est. Et tout ce qui se trouve à l'autre extrémité peut indiquer un indicateur qui serait un mauvais candidat pour une utilisation dans tout type d'effort d'apprentissage automatique. 

                                  

L'équation finale qui sera appliquée est présentée ci-dessus. Le code est implémenté ci-dessous sous la forme d'un script mql5 qui peut être téléchargé en pièce jointe à la fin de l'article. En utilisant le script, nous serons en mesure d'analyser la plupart des indicateurs.

Un script pour calculer l'entropie d'un indicateur

Le script est invoqué avec les paramètres suivants, réglables par l'utilisateur :

• TimeFrame - période sélectionnée pour analyser les valeurs de l'indicateur.
• IndicatorType - L'utilisateur peut ici sélectionner l'un des indicateurs intégrés pour l'analyse. Pour spécifier un indicateur personnalisé, sélectionnez l'option ’Indicateur personnalisé’ et saisissez le nom de l'indicateur dans la valeur du paramètre suivant.
  
• CustomIndicatorName - Si l'option ’Custom indicator’ a été sélectionnée pour le paramètre précédent, l'utilisateur doit saisir ici le nom correct de l'indicateur.
  
• UseDefaults - Si ce paramètre est fixé à true, les entrées utilisateur par défaut codées en dur dans l'indicateur seront utilisées.
  
• IndicatorParameterTypes - il s'agit d'une chaîne de caractères délimitée par des virgules qui énumère les types de données de l'indicateur dans le bon ordre. Un exemple d'entrée possible, en supposant que l'indicateur à analyser accepte 4 entrées de type double, entier, entier, chaîne respectivement, l'utilisateur doit simplement entrer "double, integer, integer, string ", la forme courte "d , i, i, s " est également supportée où d= double, i=integer (ou entier en français) et s=string (ou chaîne de caractères en français). Les valeurs des énumérations sont mappées sur le type entier.
  
• IndicatorParameterValues - Comme pour l'entrée précédente, il s'agit également d'une liste de valeurs délimitée par des virgules, par exemple, en reprenant l'exemple précédent, "0.5, 4, 5, string_value". En cas d'erreur dans la formulation des paramètres pour IndicatorParameterValues ou IndicatorParameterTypes, les valeurs par défaut de l'indicateur seront utilisées pour toutes les valeurs spécifiques qui ne peuvent pas être déchiffrées ou qui sont manquantes.
  Vérifiez les messages d'erreur dans l'onglet Experts. Notez qu'il n'est pas nécessaire d'inclure le nom de l'indicateur ici, si un indicateur personnalisé est considéré, il doit être spécifié par CustomIndicatorName.
• IndicatorBuffer - L'utilisateur peut stipuler lequel des buffers de l’indicateur doit être analysé.
  
• HistoryStart - Date de début de l'échantillon issu de l’historique.
  
• HistorySize - Nombre de barres à analyser par rapport à HistoryStart.
  
• Intervalles - Ce paramètre indique le nombre d'intervalles qui seront créés pour le processus de discrétisation. L'auteur de TTMTS spécifie 20 intervalles pour un échantillon de plusieurs milliers de personnes, 2 étant stipulé comme valeur minimale absolue.  J'ai ajouté ma propre touche à la valeur appropriée à utiliser ici en mettant en œuvre la possibilité de varier le nombre d'intervalles par rapport à la taille de l'échantillon, à savoir 51 pour 1000 échantillons. Cette option est disponible si l'utilisateur saisit une valeur inférieure à 2. Ainsi, pour être clair, il faut fixer l'intervalle à un nombre inférieur à 2 et le nombre d'intervalles utilisés changera en fonction du nombre de mesures analysées.
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Une remarque sur la valeur sélectionnée pour les intervalles : La modification du nombre d'intervalles utilisés dans le calcul fera varier la valeur finale de l'entropie. Lors de l'analyse, il serait judicieux d'assurer une certaine cohérence afin de minimiser les effets des données indépendantes utilisées. Dans le script, le calcul de l'entropie relative est encapsulé dans une fonction définie dans le fichier Entropy.mqh.

Le script affiche simplement la valeur d'entropie résultante dans l'onglet "experts". L'exécution du script pour divers indicateurs intégrés et personnalisés donne les résultats ci-dessous. Il est intéressant de noter que le William’s Percent Range a une entropie relative proche de la perfection. Si l'on compare avec l'indicateur Market Facilitation Index, les résultats sont décevants.

Grâce à ces résultats, nous pouvons prendre d'autres mesures pour traiter les données afin de les rendre accessibles aux algorithmes d'apprentissage automatique. Cela implique une analyse rigoureuse des propriétés statistiques de l'indicateur. L'étude de la distribution des valeurs de l'indicateur révélera tout problème d'asymétrie et de valeurs aberrantes. Tous ces éléments peuvent nuire à l'apprentissage du modèle.

À titre d'exemple, nous examinons certaines propriétés statistiques de deux indicateurs analysés ci-dessus.

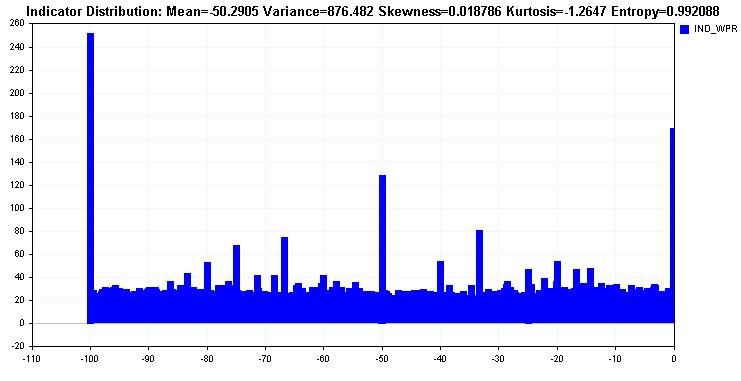
La distribution du William’s Percent Range montre que presque toutes les valeurs sont réparties sur l'ensemble de l’intervalle ; hormis le fait qu'elle soit multi-modale, la distribution est assez uniforme. Une telle distribution est idéale et se reflète dans la valeur de l'entropie.

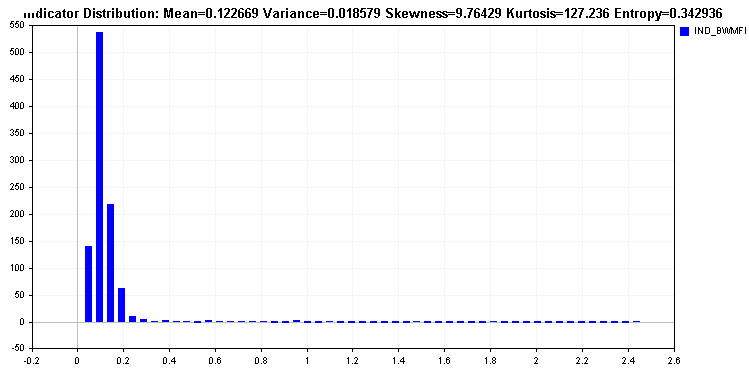
Cela contraste avec la distribution du Market Facilitation Index qui a une longue queue. Un tel indicateur serait problématique pour la plupart des algorithmes d'apprentissage et nécessite une transformation des valeurs. La transformation des valeurs devrait conduire à une amélioration de l'entropie relative de l'indicateur.

Améliorer le contenu des informations d'un indicateur

Il convient de préciser que les modifications qui augmentent l'entropie de l'indicateur ne doivent pas être considérées comme un moyen d'améliorer la précision des signaux fournis par l'indicateur. L'augmentation de l'entropie ne transformera pas un indicateur inutile en saint-graal. L'amélioration de l'entropie consiste à traiter les données de l'indicateur pour les utiliser efficacement dans des modèles prédictifs.

Cette option doit être envisagée lorsque la valeur de l'entropie est désespérément mauvaise, c'est-à-dire nettement inférieure à 0,5 et plus proche de zéro. Les seuils supérieurs sont purement arbitraires. Il appartient au développeur de choisir une valeur minimale acceptable. L'objectif est de produire une distribution des valeurs de l'indicateur qui soit aussi uniforme que possible. La décision d'appliquer une transformation doit être basée sur une analyse menée sur un échantillon important et représentatif des valeurs de l'indicateur.

La transformation appliquée ne doit pas modifier le comportement sous-jacent de l'indicateur. L'indicateur transformé doit avoir une forme similaire à celle de l'indicateur brut, par exemple l'emplacement des creux et des pics doit être similaire dans les deux séries. Si ce n'est pas le cas, nous risquons de perdre des informations potentiellement utiles.

Il existe de nombreuses méthodes de transformation qui ciblent différents aspects des imperfections des données de test. Nous n'examinerons que quelques transformations simples visant à corriger des défauts évidents révélés par une analyse statistique de base. Le pré-traitement est une vaste branche de l'apprentissage automatique. Il est conseillé à toute personne souhaitant maîtriser l'application des méthodes d'apprentissage automatique d'approfondir ses connaissances dans ce domaine.

Pour illustrer l'effet de certaines transformations, nous présentons un script qui a la possibilité d'appliquer différentes transformations et qui affiche également la distribution des données analysées. Le script met en œuvre 6 exemples de fonctions de transformation :

• la transformation de la fonction racine carrée est appropriée pour écraser les valeurs d'indicateurs occasionnels qui s'écartent considérablement de la majorité.

• la transformation de la racine cubique est une autre fonction d'écrasement qui s'applique le mieux aux indicateurs avec des valeurs négatives.

• la transformation logarithmique comprime les valeurs dans une plus large mesure que les transformations de compression mentionnées précédemment.

• les transformations de la tangente hyperbolique et de la logistique doivent être appliquées à des valeurs de données d'une échelle appropriée afin d'éviter les problèmes de production de nombres non valides (erreurs nan).

• la transformation extrême induit une uniformité extrême dans un ensemble de données. Elle ne doit être appliquée qu'aux indicateurs qui produisent principalement des valeurs uniques avec très peu de chiffres similaires.

Un script pour comparer les valeurs transformées des indicateurs

Par rapport au script précédent, il contient les mêmes entrées utilisateur pour spécifier l'indicateur à analyser. Les nouveaux intrants sont décrits ci-dessous :

• DisplayTime - le script affiche un graphique de la distribution de l'indicateur. DisplayTime est une valeur entière en secondes, qui correspond à la durée pendant laquelle le graphique sera visible avant d'être supprimé.

• ApplyTransfrom - est une valeur booléenne qui définit le mode du script. S'il est faux, le script dessine la distribution et affiche les statistiques de base de l'échantillon ainsi que l'entropie relative. Si true est activé, il applique une transformation aux valeurs brutes de l'indicateur et affiche les valeurs d'entropie relative avant et après la transformation. La distribution des échantillons modifiés peut également être dessinée sous forme de courbe en rouge.

• Select_transform - est une énumération fournissant les transformations décrites précédemment qui peuvent être appliquées pour éventuellement augmenter l'entropie de l'indicateur.

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

En poursuivant les exemples, nous comparons l'application des transformations de la racine carrée et de la racine cubique.

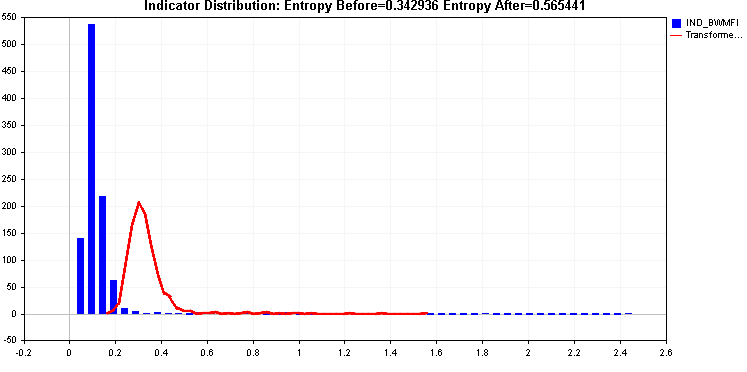
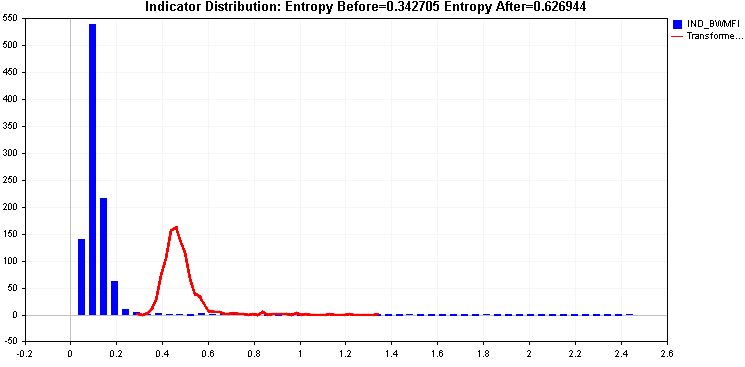
Toutes deux permettent d'améliorer l'entropie, mais cette queue droite pourrait être problématique, les deux transformées appliquées jusqu'à présent n'ayant pas été en mesure de la traiter efficacement.

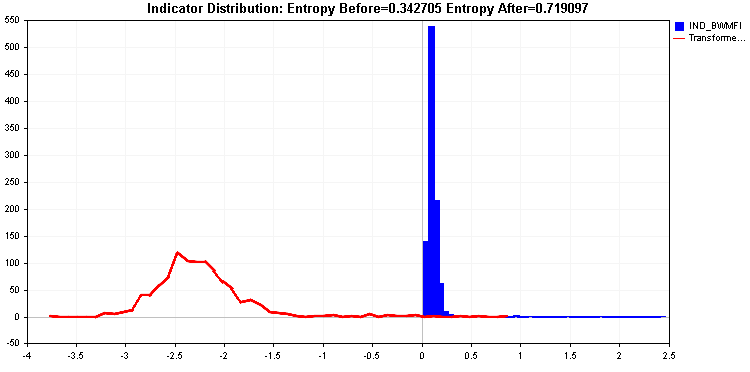
La transformée logarithmique produit une valeur d'entropie encore meilleure. Mais les queues sont assez significatives. En dernier recours, nous pouvons appliquer la transformation extrême.

Conclusion

Nous avons exploré le concept d'entropie pour évaluer la nécessité de transformer les valeurs des indicateurs avant de les utiliser dans l'apprentissage des modèles prédictifs.

Le concept a été mis en œuvre dans deux scripts. A savoir EntropyIndicatorAnalyis qui affiche l'entropie relative d'un échantillon dans l'onglet des experts. L'autre script IndicatorAnalysis va plus loin en dessinant la distribution des valeurs brutes et transformées des indicateurs et en affichant les valeurs d'entropie relative avant et après.

Si ces outils peuvent être utiles, il convient de noter qu'ils ne peuvent pas être appliqués à tous les types d'indicateurs. En général, les indicateurs basés sur des flèches qui contiennent des valeurs vides ne conviennent pas aux scripts décrits ici. Dans ce cas, d'autres techniques d'encodage sont nécessaires.

La transformation des données n'est qu'un sous-ensemble des étapes de pré-traitement possibles à prendre en compte lors de l'élaboration d'un modèle prédictif, quel qu'il soit. L'utilisation de ces techniques permettra d'extraire des relations vraiment uniques qui pourraient fournir l'avantage nécessaire pour battre les marchés.

Nom du fichier	Description
Mql5/Include/Entropy.mqh	fichier d’inclusion qui contient diverses définitions de fonctions utilisées pour calculer l'entropie ainsi que des fonctions utilitaires utilisées par les scripts joints.
Mql5/Scripts/IndicatorAnalysis.mq5	script qui affiche un graphique montrant la distribution des valeurs de l'indicateur, ainsi que son entropie.
Mql5/Scripts/EntropyIndicatorAnalysis	script qui peut être utilisé pour calculer l'entropie d'un indicateur