Approche brute de la recherche de motifs (partie VI) : Optimisation cyclique

Sommaire

• Introduction
• Routine
• Nouvel algorithme d'optimisation
• Critère d'optimisation le plus important
• Recherche automatique de configurations de trading
• Conclusion
• Liens

Introduction

Compte tenu du contenu de l'article précédent, je peux dire qu'il ne s'agit que d'une description superficielle de toutes les fonctions que j'ai introduites dans mon algorithme. Elles concernent non seulement l'automatisation complète de la création de l'EA, mais aussi des fonctions aussi importantes que l'automatisation complète de l'optimisation et de la sélection des résultats avec utilisation ultérieure pour le trading automatique, ou la création d'EAs plus progressifs que je vais montrer un peu plus loin.

Grâce à la symbiose entre les terminaux de trading, les EA universels et l'algorithme lui-même, vous pouvez vous débarrasser complètement du développement manuel ou, dans le pire des cas, réduire l'intensité du travail des améliorations possibles d'un ordre de grandeur, à condition que vous disposiez des capacités informatiques nécessaires. Dans cet article, je commencerai par décrire les aspects les plus importants de ces innovations.

Routine

Le facteur le plus important pour moi dans la création et les modifications ultérieures de ces solutions au fil du temps a été de comprendre la possibilité d'assurer une automatisation maximale des actions de routine. Les actions de routine, dans ce cas, comprennent tout travail humain non essentiel :

• Génération d'idées
• Création d'une théorie
• Rédaction du code en fonction de la théorie
• Correction du code
• Ré-optimisation constante de l'EA
• Sélection constante de l'EA
• Maintenance de l'EA
• Travail avec les terminaux
• Expériences et pratiques
• Autres

Comme vous pouvez le constater, le champ d'application de cette routine est assez large. Je considère cela précisément comme une routine, car j'ai pu prouver que toutes ces choses peuvent être automatisées. J'ai fourni une liste générale. Peu importe qui vous êtes – un trader algorithmique, un programmeur ou les deux. Peu importe que vous sachiez programmer ou non. Même si ce n'est pas le cas, vous rencontrerez de toute façon au moins la moitié de cette liste. Je ne parle pas des cas où vous avez acheté un EA sur le marché, l'avez lancé sur le graphique et vous vous êtes calmé en appuyant sur un bouton. Cela arrive bien sûr, mais extrêmement rarement.

En comprenant tout cela, j'ai d'abord dû automatiser les choses les plus évidentes. J'ai décrit conceptuellement toute cette optimisation dans un article précédent. Mais lorsque vous faites quelque chose comme cela, vous commencez à comprendre comment améliorer l'ensemble, sur la base de la fonctionnalité déjà mise en œuvre. Pour moi, les principales idées à ce sujet sont les suivantes :

• Améliorer le mécanisme d'optimisation
• Créer un mécanisme de fusion des EA (fusion des robots)
• Architecture correcte des chemins d'interaction de tous les composants.

Bien entendu, il s'agit d'une énumération assez brève. Je décrirai tout cela plus en détail. Par amélioration de l'optimisation, j'entends un ensemble de plusieurs facteurs à la fois. Tout cela est envisagé dans le cadre du paradigme choisi pour la construction de l'ensemble du système :

• Accélérer l'optimisation en éliminant les ticks.
• Accélérer l'optimisation en éliminant le contrôle de la courbe de profit entre les points de décision de trading.
• Améliorer la qualité de l'optimisation en introduisant des critères d'optimisation personnalisés.
• Maximiser l'efficacité de la période à venir.

Sur le forum de ce site web, vous trouverez encore des débats en cours sur la nécessité de l'optimisation et sur ses avantages. Auparavant, j'avais une attitude assez claire à l'égard de cette action, en grande partie grâce à l'influence de certains utilisateurs de forums et de sites web. Cet avis ne me dérange pas du tout. En ce qui concerne l'optimisation, tout dépend si vous savez l'utiliser correctement et quels sont vos objectifs. Si elle est utilisée correctement, cette action donne le résultat escompté. En général, il s'avère que cette action est extrêmement utile.

Beaucoup de gens n'aiment pas l'optimisation. Il y a deux raisons objectives à cela :

• Un manque de compréhension des principes de base (pourquoi, quoi et comment faire, comment sélectionner les résultats et tout ce qui s'y rapporte, y compris le manque d'expérience).
• Une imperfection des algorithmes d'optimisation.

En fait, ces deux facteurs se renforcent mutuellement. Pour être honnête, l'optimiseur de MetaTrader 5 est structurellement impeccable, mais il a encore besoin de nombreuses améliorations en termes de critères d'optimisation et de filtres possibles. Jusqu'à présent, toutes ces fonctionnalités s'apparentent à un bac à sable pour enfants. Peu de gens réfléchissent à la manière d'obtenir des périodes d'avance positives et, surtout, à la manière de contrôler ce processus. Cela fait longtemps que j'y pense. En fait, une bonne partie du présent article sera consacrée à ce sujet.

Nouvel algorithme d'optimisation

Outre les critères d'évaluation de base connus de tout backtest, nous pouvons proposer quelques caractéristiques combinées qui peuvent aider à multiplier la valeur de tout algorithme pour une sélection plus efficace des résultats et l'application ultérieure des paramètres. L'avantage de ces caractéristiques est qu'elles peuvent accélérer le processus de recherche de cadres de travail. Pour ce faire, j'ai créé une sorte de rapport de testeur de stratégie similaire à celui de MetaTrader :

figure 1

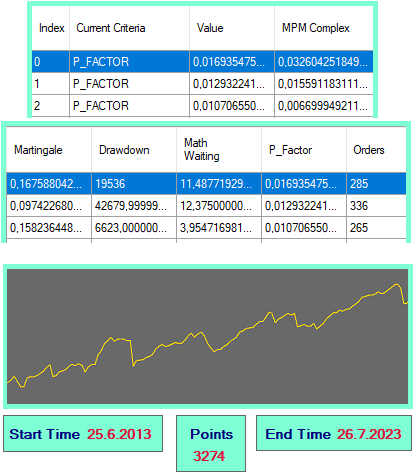
Grâce à cet outil, je peux choisir l'option qui me convient d'un simple clic. En cliquant, un paramètre est généré, que je peux immédiatement prendre et déplacer dans le dossier approprié du terminal, de sorte que les EA universels puissent le lire et commencer à négocier dessus. Si je le souhaite, je peux également cliquer sur le bouton pour générer un EA et il sera construit au cas où j'aurais besoin d'un EA séparé avec les paramètres câblés à l'intérieur. Il existe également une courbe de profit, qui est redessinée lorsque vous sélectionnez l'option suivante dans le tableau.

Déterminons ce qui est compté dans le tableau. Les éléments de base pour le calcul de ces caractéristiques sont les données suivantes :

1. Points : profit de l'ensemble du backtest en "_Point" de l'instrument correspondant.
2. Ordres : le nombre d'ordres complètement ouverts et fermés (ils se suivent dans un ordre strict, selon la règle "il ne peut y avoir qu'un seul ordre ouvert").
3. Drawdown: prélèvement sur le solde.

Sur la base de ces valeurs, les caractéristiques de trading suivantes sont calculées :

• Math Waiting : attentes mathématiques en points.
• Facteur P : analogue du facteur de profit normalisé dans l'intervalle [-1 ... 0 ... 1] (mon critère).
• Martingale : applicabilité de la martingale (mon critère).
• Complexe MPM : indicateur composite des trois précédents (mon critère).

Voyons maintenant comment ces critères sont calculés :

équations 1

Comme vous pouvez le constater, tous les critères que j'ai créés sont très simples et, surtout, faciles à comprendre. Étant donné que l'augmentation de chacun des critères indique que le résultat du backtest est meilleur en termes de théorie des probabilités, il devient possible de multiplier ces critères, comme je l'ai fait pour le critère MPM Complex. Une métrique commune permettra de trier plus efficacement les résultats en fonction de leur importance. En cas d'optimisations massives, il vous permettra de conserver davantage d'options de haute qualité et de supprimer davantage d'options de faible qualité, respectivement.

Notez également que dans ces calculs, tout se passe en points. Cela a un effet positif sur le processus d'optimisation. Pour les calculs, on utilise des quantités primaires strictement positives, qui sont toujours calculées au début. Tout le reste est calculé sur cette base. Je pense qu'il vaut la peine d'énumérer ces quantités primaires qui ne figurent pas dans le tableau :

• Points Plus : somme des bénéfices de chaque ordre rentable ou nul en points
• Points Moins : somme des modules de perte de chaque ordre non rentable en points.
• Drawdown : drawdown par solde (je le calcule à ma façon)

L'élément le plus intéressant est le mode de calcul du drawdown. Dans notre cas, il s'agit de la réduction maximale du solde relatif. Compte tenu du fait que mon algorithme de test refuse de suivre la courbe des fonds, d'autres types de drawdowns ne peuvent pas être calculés. Cependant, je pense qu'il serait utile de montrer comment je calcule ce drawdown :

figure 2

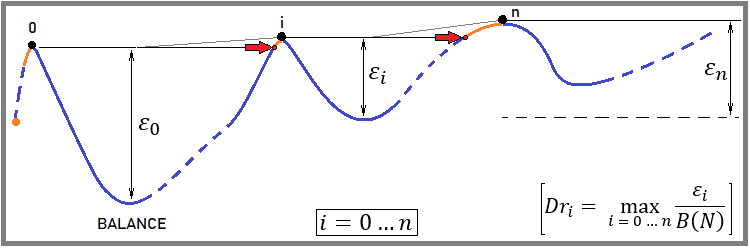
Sa définition est très simple :

1. Calcul du point de départ du backtest (le début du premier compte à rebours).
2. Si le trading commence par un bénéfice, nous déplaçons ce point vers le haut en suivant la croissance du solde, jusqu'à ce que la première valeur négative apparaisse (elle marque le début du calcul du drawdown).
3. Attendez que la balance atteigne le niveau du point de référence. Ensuite, définissez-le comme nouveau point de référence.
4. Nous revenons à la dernière section de la recherche de prélèvements et recherchons le point le plus bas (le montant des prélèvements dans cette section est calculé à partir de ce point).
5. Répétez l'ensemble du processus pour l'ensemble du backtest ou de la courbe de trading.

Le dernier cycle restera toujours inachevé. Mais sa réduction est également prise en compte, bien qu'il existe un potentiel d'augmentation si le test se poursuit. Mais ce n'est pas un élément particulièrement important.

Critère d'optimisation le plus important

Parlons maintenant du filtre le plus important. En fait, ce critère est le plus important lors de la sélection des résultats d'optimisation. Ce critère n'est pas inclus dans la fonctionnalité de l'optimiseur de MetaTrader 5, ce qui est dommage. Je vais donc fournir du matériel théorique pour que chacun puisse reproduire cet algorithme dans son propre code. Ce critère est multifonctionnel pour tout type de trading et fonctionne pour absolument toutes les courbes de profit, y compris les paris sportifs, les crypto-monnaies et tout ce à quoi vous pouvez penser. Ce critère est le suivant :

équations 2

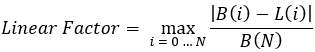
Voyons ce que contient cette équation :

• N — le nombre de positions de trading complètement ouvertes et fermées sur l'ensemble du backtest ou de la section de trading.
• B(i) — la valeur du solde après la position fermée "i" correspondante.
• L(i) — la ligne droite allant de zéro au dernier point du bilan (bilan final).

Nous devons effectuer deux backtests pour calculer ce paramètre. Le premier backtest calculera le solde final. Ensuite, il sera possible de calculer l'indicateur correspondant en sauvegardant la valeur de chaque point d'équilibre, afin qu'il ne soit pas nécessaire de faire des calculs inutiles. Ce calcul peut être qualifié de backtest répété. Cette équation peut être utilisée dans des testeurs personnalisés, qui peuvent être intégrés dans vos EA.

Il est important de noter que cet indicateur dans son ensemble peut être modifié pour une meilleure compréhension. Par exemple, comme ceci :

équations 3

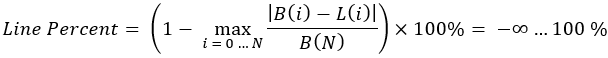
Cette équation est plus difficile à percevoir et à comprendre. Mais d'un point de vue pratique, un tel critère est commode car plus il est élevé, plus notre courbe d'équilibre ressemble à une ligne droite. J'ai abordé des questions similaires dans des articles précédents, mais je n'ai pas expliqué la signification de ces questions. Examinons d'abord la figure suivante :

figure 3

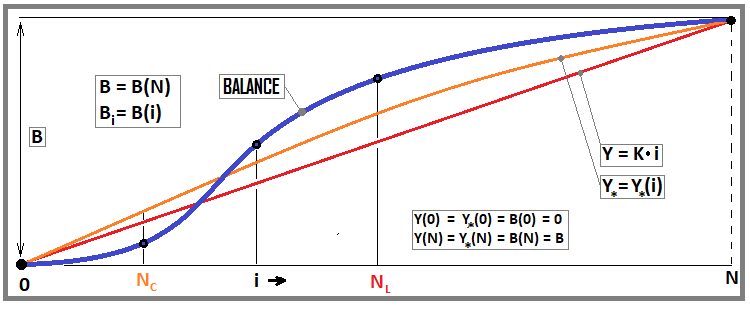
Cette figure montre une ligne d'équilibre et deux courbes : l'une relative à notre équation (rouge), et la seconde pour le critère modifié suivant (équations 11). Je le montrerai plus loin, mais concentrons-nous sur l'équation.

Si nous imaginons notre backtest comme un simple tableau de points avec des soldes, nous pouvons le représenter comme un échantillon statistique et lui appliquer les équations de la théorie des probabilités. Nous considérerons la ligne droite comme le modèle que nous cherchons à atteindre et la courbe de profit elle-même comme le flux de données réel qui cherche à atteindre notre modèle.

Il est important de comprendre que le facteur de linéarité indique la fiabilité de l'ensemble des critères de trading disponibles. Par ailleurs, une plus grande fiabilité des données peut indiquer une période à terme plus longue et plus favorable (transactions rentables à l'avenir). À proprement parler, j'aurais dû commencer à envisager ces choses en considérant les variables aléatoires. Mais il m'a semblé que cette présentation faciliterait la compréhension.

Créons une alternative analogue de notre facteur de linéarité, en tenant compte d'éventuels pics aléatoires. Pour cela, nous devrons introduire une variable aléatoire et sa moyenne pour le calcul ultérieur de la dispersion :

équations 4

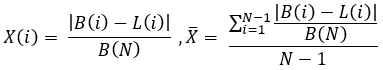
Pour une meilleure compréhension, il convient de préciser que nous avons "N" positions complètement ouvertes et fermées, qui se suivent strictement l'une après l'autre. Cela signifie que nous avons "N+1" points qui relient ces segments de la ligne d'équilibre. Le point zéro de toutes les lignes est commun, ses données fausseront donc les résultats dans le sens de l'amélioration, tout comme le dernier point. Par conséquent, nous les excluons des calculs. Il nous reste donc "N-1" points sur lesquels nous effectuerons des calculs.

Le choix de l'expression pour convertir les tableaux de valeurs de deux lignes en un seul s'est avéré très intéressant. Veuillez noter la fraction suivante :

équations 5

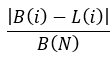
L'important est de diviser le tout par le solde final dans tous les cas. Nous ramenons ainsi tout à une valeur relative, ce qui garantit l'équivalence des caractéristiques calculées pour toutes les stratégies testées, sans exception. Ce n'est pas une coïncidence si la même fraction est présente dans le tout premier et simple critère du facteur de linéarité, puisqu'il est construit sur la même considération. Mais achevons la construction de notre critère alternatif. Pour ce faire, nous pouvons utiliser un concept bien connu, celui de la dispersion :

équations 6

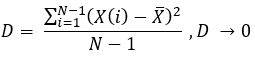
La dispersion n'est rien d'autre que la moyenne arithmétique de l'écart quadratique par rapport à la moyenne de l'ensemble de l'échantillon. J'y ai immédiatement substitué nos variables aléatoires, dont les expressions ont été définies plus haut. Une courbe idéale a un écart moyen de zéro et, par conséquent, la dispersion d'un échantillon donné sera également nulle. Sur cette base, il est facile de deviner que cette dispersion, en raison de sa structure - la variable aléatoire utilisée ou l'échantillon (au choix) - peut être utilisée comme un facteur de linéarité alternatif. Les deux critères peuvent également être utilisés en tandem pour contraindre plus efficacement les paramètres de l'échantillon, bien que, pour être honnête, je n'utilise que le premier critère.

Examinons un critère similaire, plus pratique, qui est également basé sur un nouveau facteur de linéarité que nous avons défini :

équations 7

Comme nous pouvons le constater, il est identique à un critère similaire, construit sur la base du premier (équations 2). Mais ces deux critères sont loin d'être la limite de ce qui peut être imaginé. Un fait évident qui plaide en faveur de cette considération est que ce critère est trop idéalisé et convient davantage à des modèles idéaux. Il sera extrêmement difficile d'ajuster un EA pour obtenir une correspondance plus ou moins importante. Je pense qu'il vaut la peine d'énumérer les facteurs négatifs qui seront évidents quelque temps après l'application des équations :

1. Réduction critique du nombre de transactions (réduit la fiabilité des résultats)
2. Rejet du nombre maximal de scénarios efficaces (selon la stratégie, la courbe ne tend pas toujours vers la ligne droite)

Ces lacunes sont très importantes, car l'objectif n'est pas d'écarter les bonnes stratégies, mais, au contraire, de trouver des critères nouveaux et améliorés qui soient exempts de ces lacunes. Ces inconvénients peuvent être totalement ou partiellement neutralisés par l'introduction simultanée de plusieurs lignes préférées, chacune d'entre elles pouvant être considérée comme un modèle acceptable ou préféré. Pour comprendre le nouveau critère amélioré, débarrassé de ces défauts, il suffit de comprendre le remplacement correspondant :

équations 8

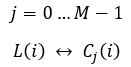
Nous pouvons ensuite calculer le facteur d'ajustement pour chaque courbe de la liste :

équations 9

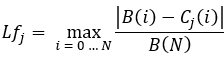
De même, nous pouvons également calculer un critère alternatif qui prend en compte des pics aléatoires pour chacune des courbes :

équations 10

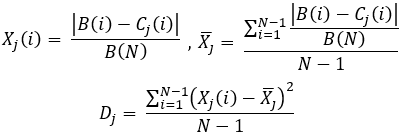
Nous devrons alors calculer les éléments suivants :

équations 11

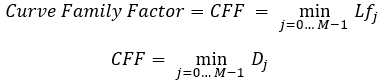
J'introduis ici un critère appelé facteur de famille de courbes (curve family factor). En effet, avec cette action, nous trouvons simultanément la courbe la plus similaire à notre courbe de trading, et nous trouvons immédiatement le facteur de correspondance avec elle. La courbe avec le facteur d'adaptation minimum est la plus proche de la situation réelle. Nous prenons sa valeur comme étant la valeur du critère modifié et, bien entendu, le calcul peut être effectué de deux manières, selon celle des deux variantes que nous préférons.

C'est très bien, mais ici, comme beaucoup l'ont remarqué, il y a des nuances liées à la sélection d'une telle famille de courbes. Pour décrire correctement une telle famille, on peut suivre diverses considérations, mais voici ce que j'en pense :

• Toutes les courbes ne doivent pas présenter de points d'inflexion (chaque point intermédiaire suivant doit être strictement supérieur au précédent).
• La courbe doit être concave (la pente de la courbe peut être constante ou augmenter).
• La concavité de la courbe doit être réglable (par exemple, l'ampleur de la déviation doit être réglée en fonction d'une valeur relative ou d'un pourcentage).
• Simplicité du modèle de courbe (il est préférable de baser le modèle sur des modèles graphiques initialement simples et compréhensibles).

Il ne s'agit que de la première variation de cette famille de courbes. Il est possible d'effectuer des variations plus importantes en tenant compte de toutes les configurations souhaitées, ce qui peut nous éviter complètement de perdre des paramètres de qualité. Je m'attellerai à cette tâche plus tard, mais pour l'instant je ne ferai qu'effleurer la stratégie originale de la famille des courbes concaves. J'ai pu créer une famille de ce type assez facilement grâce à mes connaissances en mathématiques. Permettez-moi de vous montrer immédiatement à quoi ressemble cette famille de courbes :

figure 4

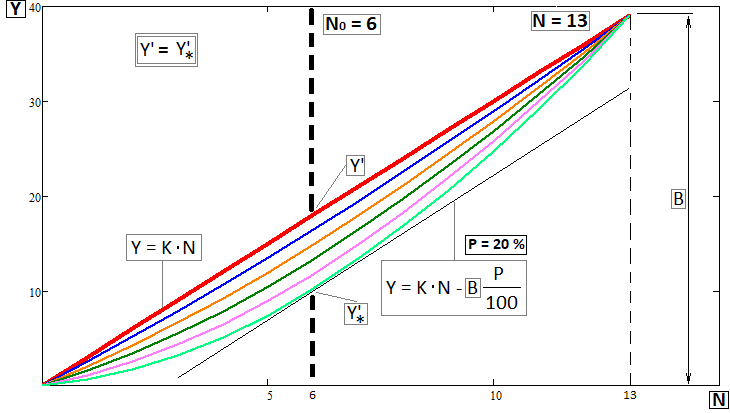
Pour construire cette famille, j'ai utilisé l'abstraction d'une tige élastique reposant sur des supports verticaux. Le degré de déviation d'une telle tige dépend du point d'application de la force et de son ampleur. Il est clair que cela ne ressemble que très peu à ce dont nous traitons ici, mais c'est suffisant pour développer une sorte de modèle visuellement similaire. Dans cette situation, il faut bien sûr commencer par déterminer la coordonnée de l'extremum, qui doit coïncider avec l'un des points du graphique de backtest, l'axe X étant représenté par les indices des trades à partir de zéro. Je la calcule comme suit :

équations 12

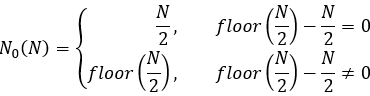
Il y a deux cas de figure : pour les "N" pairs et impairs. Si "N" est pair, il est impossible de le diviser simplement par deux, puisque l'indice doit être un nombre entier. D'ailleurs, j'ai représenté exactement ce cas dans la dernière image. Là, le point d'application de la force est un peu plus proche du début. Vous pouvez bien sûr faire l'inverse, un peu plus près de la fin, mais cela ne sera significatif que pour un petit nombre de transactions, comme je l'ai indiqué dans la figure. Au fur et à mesure que le nombre de transactions augmente, tout cela ne jouera plus aucun rôle significatif pour les algorithmes d'optimisation.

Après avoir fixé la valeur de déviation "P" en pourcentage et le solde final "B" du backtest, après avoir déterminé la coordonnée de l'extremum, nous pouvons commencer à calculer séquentiellement d'autres composants pour construire des expressions pour chacune des familles de courbes acceptées. Ensuite, nous avons besoin de la pente de la ligne droite reliant le début et la fin du backtest :

équations 13

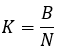
Une autre caractéristique de ces courbes est que l'angle tangent à chacune des courbes aux points d'abscisse "N0" est identique à "K". Lors de la construction d'équations, j'ai exigé cette condition de la tâche. Cela peut également être vu graphiquement dans la dernière figure (figure 4). Il y a quelques équations et identités là aussi. Passons à autre chose. Nous devons maintenant calculer la valeur suivante :

équations 14

 

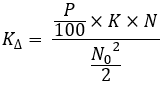
Gardez à l'esprit que "P" est réglé différemment pour chaque courbe de la famille. Au sens strict, il s'agit d'équations permettant de construire une courbe à partir d'une famille. Ces calculs doivent être répétés pour chaque courbe de la famille. Nous devons ensuite calculer un autre ratio important :

équations 15

Il n'est pas nécessaire d'approfondir la signification de ces structures. Elles ne sont créées que pour simplifier le processus de construction des courbes. Il reste à calculer le dernier ratio auxiliaire :

équations 16

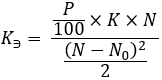
Maintenant, sur la base des données obtenues, nous pouvons obtenir une expression mathématique pour calculer les points de la courbe construite. Cependant, il faut d'abord préciser que la courbe n'est pas décrite par une seule équation. À gauche du point "N0", nous avons une équation, alors qu'une autre fonctionne à droite. Pour faciliter la compréhension, nous pouvons procéder de la manière suivante :

équations 17

Nous pouvons maintenant voir les équations finales :

équations 18

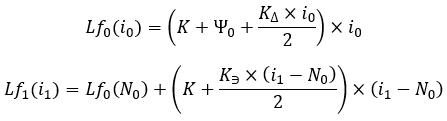
Nous pouvons également le démontrer de la manière suivante :

équations 19

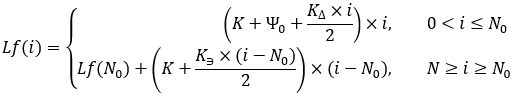
Strictement parlant, cette fonction doit être utilisée comme une fonction discrète et auxiliaire. Mais elle permet néanmoins de calculer des valeurs en "i" fractionnaires. Bien entendu, il est peu probable que cela nous soit utile dans le contexte de notre problème.

Puisque je donne ces mathématiques, je suis obligé de fournir des exemples de la mise en œuvre de l'algorithme. Je pense que tout le monde sera intéressé par l'obtention d'un code prêt à l'emploi qu'il sera plus facile d'adapter à ses systèmes. Commençons par définir les principales variables et méthodes qui simplifieront le calcul des quantités nécessaires :

//+------------------------------------------------------------------+
//| Number of lines in the balance model                             |
//+------------------------------------------------------------------+
#define Lines 11 

//+------------------------------------------------------------------+
//| Initializing variables                                           |
//+------------------------------------------------------------------+
double MaxPercent = 10.0;
double BalanceMidK[,Lines];
double Deviations[Lines];
int Segments;
double K;

//+------------------------------------------------------------------+
//| Method for initializing required variables and arrays            |
//| Parameters: number of segments and initial balance               |
//+------------------------------------------------------------------+
void InitLines(int SegmentsInput, double BalanceInput) 
{
  Segments = SegmentsInput;
  K = BalanceInput / Segments;
  ArrayResize(BalanceMidK,Segments+1);
  ZeroStartBalances();
  ZeroDeviations();
  BuildBalances();
}

//+------------------------------------------------------------------+
//| Resetting variables for incrementing balances                    |
//+------------------------------------------------------------------+
void ZeroStartBalances()
{
  for (int i = 0; i < Lines; i++ ) 
  {
      for (int j = 0; j <= Segments; j++)
      {
          BalanceMidK[j,i] = 0.0;
      }
  }
}

//+------------------------------------------------------------------+
//| Reset deviations                                                 |
//+------------------------------------------------------------------+
void ZeroDeviations()
{
  for (int i = 0; i < Lines; i++)
  {
      Deviations[i] = -1.0;
  }
}

Le code est conçu pour être réutilisable. Après le calcul suivant, vous pouvez calculer l'indicateur pour une courbe d'équilibre différente en appelant d'abord la méthode InitLines. Vous devez lui donner le solde final du backtest et le nombre de transactions, après quoi vous pouvez commencer à construire nos courbes sur la base de ces données :

//+------------------------------------------------------------------+
//| Constructing all balances                                        |
//+------------------------------------------------------------------+
void BuildBalances()
{
   int N0 = MathFloor(Segments / 2.0) - Segments / 2.0 == 0 ? Segments / 2 : (int)MathFloor(Segments / 2.0);//calculate first required N0
   for (int i = 0; i < Lines; i++)
   {
       if (i==0)//very first and straight line 
       {
           for (int j = 0; j <= Segments; j++)
           {
               BalanceMidK[j,i] = K*j;
           }
       }
       else//build curved lines
       {
           double ThisP = i * (MaxPercent / 10.0);//calculate current line curvature percentage
           double KDelta = ( (ThisP /100.0) * K * Segments) / (MathPow(N0,2)/2.0 );//calculation first auxiliary ratio
           double Psi0 = -KDelta * N0;//calculation second auxiliary ratio
           double KDelta1 = ((ThisP / 100.0) * K * Segments) / (MathPow(Segments-N0, 2) / 2.0);//calculate last auxiliary ratio
           //this completes the calculation of auxiliary ratios for a specific line, it is time to construct it

           for (int j = 0; j <= N0; j++)//construct the first half of the curve 
           {
               BalanceMidK[j,i] = (K + Psi0 + (KDelta * j) / 2.0) * j;
           }
           for (int j = N0; j <= Segments; j++)//construct the second half of the curve 
           {
               BalanceMidK[j,i] = BalanceMidK[i, N0] + (K + (KDelta1 * (j-N0)) / 2.0) * (j-N0);
           }
       }
   }
}

Veuillez noter que les "lignes" déterminent le nombre de courbes de notre famille. La concavité augmente progressivement à partir de zéro (à droite) et ainsi de suite jusqu'à MaxPercent, exactement comme je l'ai montré dans la figure correspondante. Vous pouvez ensuite calculer l'écart pour chacune des courbes et sélectionner la plus petite :

//+------------------------------------------------------------------+
//| Calculation of the minimum deviation from all lines              |
//| Parameters: initial balance passed via link                      |
//| Return: minimum deviation                                        |
//+------------------------------------------------------------------+
double CalculateMinDeviation(double &OriginalBalance[])
{
   //define maximum relative deviation for each curve 
   for (int i = 0; i < Lines; i++)
   {
       for (int j = 0; j <= Segments; j++)
       {
          double CurrentDeviation = OriginalBalance[Segments] ? MathAbs(OriginalBalance[j] - BalanceMidK[j, i]) / OriginalBalance[Segments] : -1.0;
          if (CurrentDeviation > Deviations[i])
          {
              Deviations[i] = CurrentDeviation;
          }           
       }
   }
    
   //determine curve with minimum deviation and deviation itself 
   double MinDeviation=0.0;
   for (int i = 0; i < Lines; i++)
   {
       if ( Deviations[i] != -1.0 && MinDeviation == 0.0)
       {
           MinDeviation = Deviations[i];
       }
       else if (Deviations[i] != -1.0 && Deviations[i] < MinDeviation)
       {
           MinDeviation = Deviations[i];
       }
   }
   return MinDeviation;
}

C'est ainsi que nous devons l'utiliser :

1. Définition du tableau de solde original OriginalBalance.
2. Déterminez sa longueur SegmentsInput et le solde final BalanceInput, et appelez la méthode InitLines.
3. Ensuite, nous construisons les courbes en appelant la méthode BuildBalances.
4. Puisque les courbes sont tracées, nous pouvons considérer notre critère CalculateMinDeviation amélioré pour la famille de courbes.

Le calcul du critère est ainsi terminé. Je pense que le calcul du facteur de famille de la courbe ne posera pas de difficultés. Il n'est pas nécessaire de le présenter ici.

Recherche automatique de configurations de trading 

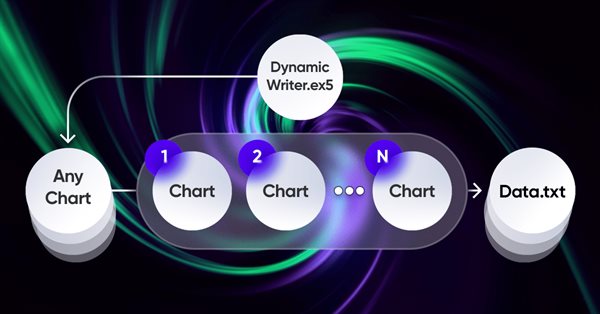
L'élément le plus important de toute cette idée est le système d'interaction entre le terminal et mon programme. Il s'agit en fait d'un optimiseur cyclique doté de critères d'optimisation avancés. Les plus importantes ont été abordées dans la section précédente. Pour que l'ensemble du système fonctionne, nous avons d'abord besoin d'une source de cotations, à savoir l'un des terminaux MetaTrader 5. Comme je l'ai déjà montré dans l'article précédent, les cotations sont écrites dans un fichier dans un format qui me convient. Cela se fait à l'aide d'un EA, qui fonctionne de manière assez étrange à première vue :

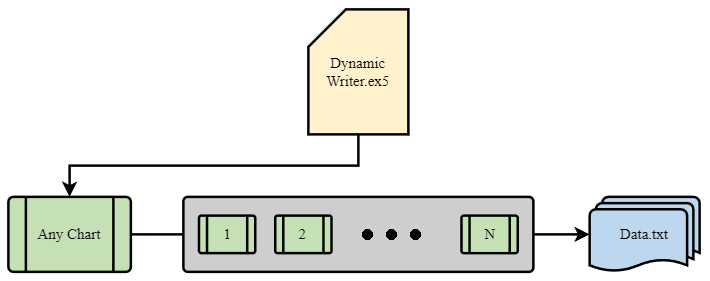
J'ai trouvé que c'était une expérience intéressante et bénéfique d'utiliser mon système unique pour le fonctionnement de l'EA. Il ne s'agit ici que d'une démonstration des problèmes que j'ai dû résoudre, mais tout ceci peut également être utilisé pour les EAs de trading :

 

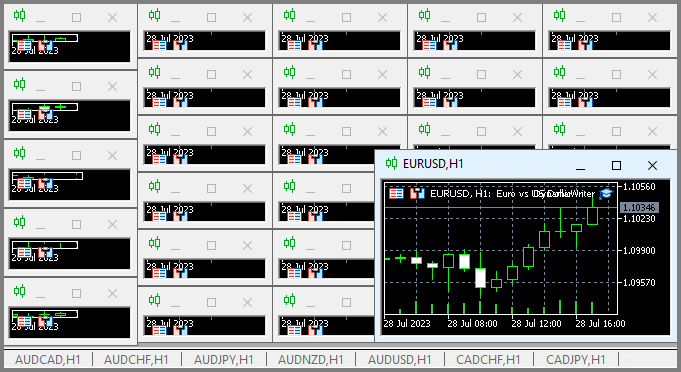
La particularité de ce système est que nous choisissons n'importe quel graphe. Il ne sera pas utilisé comme un outil de trading, afin d'éviter la duplication des données, mais il agira uniquement comme un gestionnaire de ticks ou un minuteur. Le reste des graphiques représente les instruments-périodes pour lesquels nous devons générer des cotations.

L’écriture des cotations se fait sous la forme d'une sélection aléatoire de cotations à l'aide d'un générateur de nombres aléatoires. Nous pouvons optimiser ce processus si nécessaire. L'écriture se produit après un certain temps d'utilisation de cette fonction de base :

//+------------------------------------------------------------------+
//| Function to write data if present                                |
//| Write quotes to file                                             |
//+------------------------------------------------------------------+
void WriteDataIfPresent()
{
    // Declare array to store quotes 
    MqlRates rates[];
    ArraySetAsSeries(rates, false);

    // Select a random chart from those we added to the workspace 
    ChartData Chart = SelectAnyChart();
    
    // If the file name string is not empty 
    if (Chart.FileNameString != "")
    {
        // Copy quotes and calculate the real number of bars
        int copied = CopyRates(Chart.SymbolX, Chart.PeriodX, 1,
                        int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX))),
                        rates);
        
        // Calculate ideal number of bars
        int ideal = int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX)));
        
        // Calculate percentage of received data 
        double Percent = 100.0 * copied / ideal;
        
        // If the received data is not very different from the desired data, 
        // then we accept them and write them to a file
        if (Percent >= 95.0)
        {
            // Open file (create it if it does not exist, 
            // otherwise, erase all the data it contained)
            OpenAndWriteStart(rates, Chart, CommonE); 
            WriteAllBars(rates); // Write all data to file
            WriteEnd(rates); // Add to end
            CloseFile(); // Close and save data file
        }
        else 
        {
            // If there are much fewer quotes than required for calculation 
            Print("Not enough data"); 
        }
    }
}

La fonction WriteDataIfPresent écrit les informations sur les cotations du graphique sélectionné dans un fichier si les données copiées représentent au moins 95% du nombre idéal de barres calculé sur la base des paramètres spécifiés. Si les données copiées sont inférieures à 95%, la fonction affiche le message "Pas assez de données". Si un fichier portant le nom donné n'existe pas, la fonction le crée.

Pour que ce code fonctionne, les éléments suivants doivent être décrits de manière complémentaire :

//+------------------------------------------------------------------+
//| ChartData structure                                              |
//| Objective: Storing the necessary chart data                      |
//+------------------------------------------------------------------+
struct ChartData {
    string FileNameString;
    string SymbolX;
    ENUM_TIMEFRAMES PeriodX;
};

//+------------------------------------------------------------------+
//| Randomindex function                                             |
//| Objective: Get a random number with uniform distribution         |
//+------------------------------------------------------------------+
int Randomindex(int start, int end) {
    return start + int((double(MathRand())/32767.0)*double(end-start+1));
}

//+------------------------------------------------------------------+
//| SelectAnyChart function                                          |
//| Objective: View all charts except current one and select one of  |
//|       them to write quotes                                       |
//+------------------------------------------------------------------+
ChartData SelectAnyChart() {
    ChartData chosenChart;
    chosenChart.FileNameString = "";
    int chartCount = 0;
    long currentChartId, previousChartId = ChartFirst();

    // Calculate number of charts
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;  
        }
        previousChartId = currentChartId;
        
        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }

    int randomChartIndex = Randomindex(0, chartCount - 1);
    chartCount = 0;
    currentChartId = ChartFirst(); 
    previousChartId = currentChartId;
    
    // Select random chart
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;
        }
        
        previousChartId = currentChartId;
        
        // Fill in selected chart data
        if (chartCount == randomChartIndex) {
            chosenChart.SymbolX = ChartSymbol(currentChartId);
            chosenChart.PeriodX = ChartPeriod(currentChartId);
            chosenChart.FileNameString = "DataHistory" + " " + chosenChart.SymbolX + " " + IntegerToString(CorrectPeriod(chosenChart.PeriodX));
        }
        
        if (chartCount > randomChartIndex) {
            break;
        }

        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }
       
    return chosenChart;
}

Ce code est utilisé pour enregistrer et analyser les données historiques des marchés financiers (cotations) pour différentes devises à partir de différents graphiques qui peuvent être ouverts dans le terminal à ce moment-là.

• La structure ChartData est utilisée pour stocker les données relatives à chaque graphique, notamment le nom du fichier, le symbole (paire de devises) et la période. 
• La fonction "Randomindex(start, end)" génère un nombre aléatoire entre "start" et "end". Cette option permet de sélectionner de manière aléatoire l'un des graphiques disponibles.
• SelectAnyChart() parcourt tous les graphiques ouverts et disponibles, à l'exception du graphique actuel, puis sélectionne au hasard l'un d'entre eux pour le traiter.

Les cotations générées sont automatiquement reprises par le programme, après quoi les configurations rentables sont automatiquement recherchées. L'automatisation de l'ensemble du processus est assez complexe, mais j'ai essayé de le condenser en une image :

figure 5

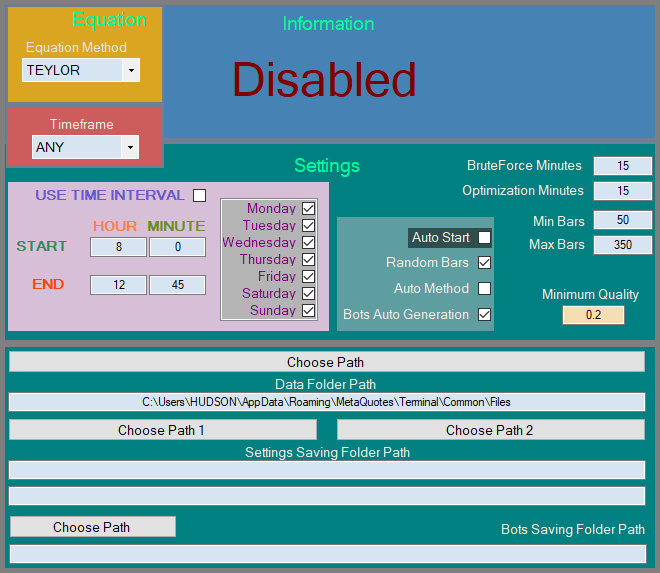
Cet algorithme se décline en 3 états :

1. Désactivé
2. En attente de cotations
3. Actif

Si l'EA pour l'enregistrement des cotations n'a pas encore généré de fichier unique ou si nous avons supprimé toutes les cotations du dossier spécifié, l'algorithme attend simplement qu'elles apparaissent et fait une pause. Quant à notre critère amélioré, que j'ai mis en œuvre pour vous dans le style MQL5, il est également mis en œuvre pour la force brute et l'optimisation :

figure 6

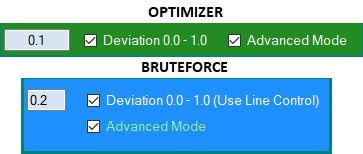
Le mode avancé utilise le facteur de famille de courbe, et l'algorithme standard n'utilise que le facteur de linéarité. Les autres améliorations sont trop nombreuses pour figurer dans cet article. Dans le prochain article, je présenterai mon nouvel algorithme de collage des expert advisors basé sur le modèle universel multidevises. Le modèle est lancé sur un seul graphique, mais traite tous les systèmes de trading fusionnés sans que chaque EA soit lancé sur son propre graphique. Certaines de ses fonctionnalités ont été utilisées dans cet article.

Conclusion

Dans cet article, nous avons examiné plus en détail les nouvelles opportunités et idées dans le domaine de l'automatisation du processus de développement et d'optimisation des systèmes de trading. Les principales réalisations sont le développement d'un nouvel algorithme d'optimisation, la création d'un mécanisme de synchronisation des terminaux et d'un optimiseur automatique, ainsi qu'un critère d'optimisation important - le facteur de courbe et la famille de courbes. Cela nous permet de réduire le temps de développement et d'améliorer la qualité des résultats obtenus.

La famille des courbes concaves, qui représente un modèle d'équilibre plus réaliste dans le contexte des périodes de backtest, constitue également un ajout important. Le calcul du facteur d'ajustement pour chaque courbe nous permet de sélectionner avec plus de précision les paramètres optimaux pour le trading automatisé.

Liens

• Approche brute de la recherche de motifs (Partie V) : Un nouvel angle
  
• Approche brute de la recherche de motifs (partie IV) : Fonctionnalité minimale
• Approche brute de la recherche de motifs (Partie III) : Nouveaux horizons
  
• Approche brute de la recherche de motifs (partie II) : Immersion
  
• Approche brute de la recherche de motifs