Biologisches Neuron zur Vorhersage von Finanzzeitreihen

Der moderne Handel befindet sich in einer Revolution. Neuronale Netze, genetische Algorithmen, Deep Learning – all diese Instrumente liefern beeindruckende Ergebnisse, haben aber oft einen entscheidenden Nachteil: Sie sind zu „mechanisch“ und nicht in der Lage, die subtile Natur der Marktschwankungen zu erfassen, die im Wesentlichen das Ergebnis des kollektiven Verhaltens der lebenden Marktteilnehmer sind.

In diesem Zusammenhang wird die Verwendung biologisch plausibler neuronaler Modelle besonders relevant. Anstatt abstrakte mathematische Konstrukte zu schaffen, haben wir uns an den fortschrittlichsten Computer im beobachtbaren Teil des Universums gewandt – das menschliche Gehirn. Unsere Forschungsgruppe hat ein einzigartiges System auf der Grundlage des Hodgkin-Huxley-Modells entwickelt, das nicht nur die Funktionalität, sondern auch die physikalische Natur neuronaler Prozesse simuliert.

Das mit dem Nobelpreis ausgezeichnete Hodgkin-Huxley-Modell beschreibt den Mechanismus der Erzeugung und Ausbreitung von Nervenimpulsen auf zellulärer Ebene. Warum aber könnte gerade dieses Modell der Schlüssel zum Verständnis der Finanzmärkte sein? Die Antwort liegt in der verblüffenden Analogie zwischen der Verbreitung von Nervenimpulsen im Gehirn und der Verbreitung von Informationen auf den Märkten. So wie Neuronen durch synaptische Verbindungen elektrische Signale austauschen, tauschen Marktteilnehmer durch Handelsgeschäfte Informationen aus.

Die Innovation unseres Ansatzes besteht darin, dass wir dem klassischen Modell eine plasmaähnliche Komponente hinzufügen. Wir betrachten ein neuronales Netz als ein dynamisches System, das in das „Plasma“ der Marktinformationen eingetaucht ist, wobei jedes Neuron das Verhalten anderer Neuronen nicht nur durch direkte Verbindungen, sondern auch durch die von ihm erzeugten elektromagnetischen Felder beeinflussen kann. Dadurch kann das System subtile Korrelationen und Beziehungen erfassen, die von herkömmlichen Algorithmen unbemerkt bleiben.

In diesem Artikel werden die Architektur des Systems, seine Funktionsweise und die Ergebnisse der praktischen Anwendung auf verschiedene Finanzinstrumente ausführlich dargestellt. Wir werden zeigen, wie ein biologisch inspirierter Ansatz eine neue Perspektive auf das Problem der finanziellen Zeitreihenprognose bieten und neue Horizonte im Bereich des algorithmischen Handels eröffnen kann.

Hodgkin-Huxley-Modell: Wenn Biologie auf Finanzen trifft

Stellen Sie sich ein Neuron vor – eine erstaunliche Zelle, die in der Lage ist, Informationen durch elektrische Impulse zu verarbeiten und zu übertragen. Diese grundlegende Einheit des Gehirns beschrieben Alan Hodgkin und Andrew Huxley in ihrer bahnbrechenden Arbeit, für die sie später den Nobelpreis erhielten. Ihr Modell war ein echter Durchbruch in den Neurowissenschaften, und stellen Sie sich nun vor, dass dasselbe Modell uns helfen kann, die Bewegungen der Finanzmärkte zu verstehen und vorherzusagen.

Das Herzstück des Modells ist eine mathematische Beschreibung, wie ein Neuron elektrische Impulse erzeugt. Genauso wie Händler auf eingehende Marktinformationen reagieren, reagiert ein Neuron auf eingehende Signale, indem es sein eigenes einzigartiges Aktivitätsmuster erzeugt. Werfen wir einen Blick auf den Code, der diesen erstaunlichen Prozess beschreibt:

class HodgkinHuxleyNeuron:
    def __init__(self):
        self.V = -65.0  # Initial resting potential
        self.m = 0.05   # Activation of sodium channels
        self.h = 0.6    # Inactivation of sodium channels
        self.n = 0.32   # Activation of potassium channels
        self.last_spike_time = float('-inf')

Tanz der Ionen: Wie Neuronen Entscheidungen treffen

Das Auffälligste am Hodgkin-Huxley-Modell ist die Beschreibung, wie Ionen durch die Neuronenmembran „tanzen“. Natrium und Kalium, die beiden Hauptakteure in diesem molekularen Ballett, bewegen sich durch spezielle Kanäle und erzeugen ein elektrisches Potenzial. Dies ist der Art und Weise sehr ähnlich, wie Auftragsflüsse Preisbewegungen auf dem Markt erzeugen. In unserem Handelssystem nutzen wir diese Analogie, indem wir die Marktdaten in Ionenströme umwandeln:

def ion_currents(self, V):
    I_Na = self.g_Na * (self.m ** 3) * self.h * (V - self.E_Na)  # Sodium current
    I_K = self.g_K * (self.n ** 4) * (V - self.E_K)             # Potassium current
    I_L = self.g_L * (V - self.E_L)                             # Leakage current
    return I_Na, I_K, I_L

Einfluss des Plasmas: Ein neuer Blick auf neuronale Netze

Wir sind über das klassische Modell hinausgegangen und haben das Konzept einer plasmaähnlichen Umgebung hinzugefügt. Stellen Sie sich vor, dass die Neuronen nicht nur durch Synapsen verbunden sind, sondern in das „Informationsplasma“ des Marktes eingetaucht sind. Jede Neuronenspitze erzeugt eine Welle des Einflusses, die mit der Zeit abklingt, so wie eine Nachricht auf dem Markt allmählich ihren Einfluss auf den Preis verliert:

def plasma_influence(self, current_time):
    time_since_spike = current_time - self.last_spike_time
    influence = self.plasma_strength * np.exp(-time_since_spike / self.plasma_decay)
    return influence * self.get_market_correlation()

Lernen durch die Zeit: Der STDP-Mechanismus

Der vielleicht spannendste Teil unseres Systems ist der Lernmechanismus, der auf der zeitlichen Abhängigkeit zwischen neuronalen Spikes (STDP) basiert. So wie ein Händler aus Erfahrung lernt, passen unsere Neuronen die Stärke ihrer Verbindungen an, je nachdem, wie erfolgreich sie Marktbewegungen vorhergesagt haben:

def update_synaptic_weights(self, pre_spike, post_spike, weight):
    delta_t = post_spike - pre_spike
    if delta_t > 0:
        return weight * (1 + self.A_plus * np.exp(-delta_t / self.tau_plus))
    else:
        return weight * (1 - self.A_minus * np.exp(delta_t / self.tau_minus))

Diese biologisch inspirierte Architektur ermöglicht es unserem System, nicht nur Marktdaten zu verarbeiten, sondern den Markt wie ein erfahrener Händler zu „fühlen“. Jedes Neuron wird zu einem Mini-Experten für seinen eigenen Aspekt der Marktdynamik, und ihre gemeinsame Arbeit führt zu bemerkenswert genauen Prognosen.

Systemarchitektur: von der Biologie zu Handelsentscheidungen

Stellen Sie sich das Gehirn eines Händlers vor, der den Markt analysiert. Tausende von Neuronen verarbeiten Informationen über Preise, Volumen, Indikatoren und Nachrichten. Diese natürliche Architektur haben wir in unserem System nachgebildet und mit den einzigartigen Eigenschaften von Plasma und elektromagnetischen Wechselwirkungen ergänzt.

Die Augen des Systems: Struktur der Eingabedaten

So wie das menschliche Gehirn Informationen über die Sinne aufnimmt, sammelt und verarbeitet unser System eine Vielzahl von Marktsignalen. Jeder Tick, jede Kursbewegung wird in neuronale Impulse umgesetzt. Werfen wir einen Blick auf den Code für die Datenvorverarbeitung:

class MarketFeatures:
    def __init__(self, window_size=20):
        self.window_size = window_size
        self.scaler = StandardScaler()
        
    def add_price(self, price: float, ohlc_data: pd.DataFrame) -> Dict[str, float]:
        features = {}
        
        # Technical indicators
        features['sma_10'] = self._calculate_sma(ohlc_data['close'], window=10)
        features['ema_20'] = self._calculate_ema(ohlc_data['close'], window=20)
        features['rsi'] = self._calculate_rsi(ohlc_data['close'], window=14)
        
        # Volumetric characteristics
        features['volume_sma'] = self._calculate_sma(ohlc_data['tick_volume'], window=10)
        
        # Temporal patterns
        features['hour'] = ohlc_data.index[-1].hour
        features['day_of_week'] = ohlc_data.index[-1].dayofweek
        
        return self.scaler.fit_transform(np.array(list(features.values())).reshape(1, -1))

Neuronales Netz: Eine Brücke zwischen Biologie und Mathematik

Das Herzstück unseres Systems ist eine hybride Architektur, die klassische neuronale Netze mit dem biologisch plausiblen Hodgkin-Huxley-Modell kombiniert. Jedes Neuron ist hier nicht nur eine mathematische Funktion, sondern ein kleines lebendes System:

class BioTradingModel(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(BioTradingModel, self).__init__()
        self.layers = nn.ModuleList([
            nn.Linear(input_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, output_size)
        ])
        
        # Biological neurons
        self.bio_neurons = [HodgkinHuxleyNeuron() for _ in range(hidden_size)]
        self.plasma_field = PlasmaField(hidden_size)

Plasmafeld: Eine neue Dimension der neuronalen Interaktionen

Die Einzigartigkeit unseres Systems liegt in der plasmaähnlichen Umgebung, in die die Neuronen eingetaucht sind. So wie elektromagnetische Felder den Raum durchdringen, schafft unser Plasma eine zusätzliche Ebene der Interaktion zwischen den Neuronen:

class PlasmaField:
    def __init__(self, size):
        self.field_strength = np.zeros(size)
        self.decay_rate = 0.95
        
    def update(self, neuron_activities):
        # Update the field based on neuron activity
        self.field_strength = self.field_strength * self.decay_rate
        self.field_strength += neuron_activities
        
    def get_influence(self, neuron_index):
        # Calculate the influence of a field on a specific neuron
        return np.sum(self.field_strength * np.exp(-self.distance_matrix[neuron_index]))

Lernmechanismus: Tanz der Neuronen und des Plasmas

In unserem System erfolgt die Ausbildung auf mehreren Ebenen gleichzeitig. Klassischer Gradientenabstieg wird mit biologischem STDP und Plasmadynamik kombiniert:

def train_step(self, inputs, target):
    # Straight pass
    predictions = self.forward(inputs)
    loss = self.criterion(predictions, target)
    
    # Backpropagation
    self.optimizer.zero_grad()
    loss.backward()
    
    # Biological education
    for i, neuron in enumerate(self.bio_neurons):
        # STDP update
        neuron.update_weights(self.last_spike_times)
        
        # Plasma modulation
        plasma_influence = self.plasma_field.get_influence(i)
        neuron.modulate_weights(plasma_influence)
    
    self.optimizer.step()
    return loss.item()

Diese mehrschichtige Architektur ermöglicht es dem System, nicht nur offensichtliche Muster in den Daten zu erfassen, sondern auch subtile, kaum wahrnehmbare Beziehungen zwischen verschiedenen Aspekten der Marktdynamik. Jede Komponente des Systems spielt ihre eigene, einzigartige Rolle, und ihre Synergie schafft etwas, das größer ist als die Summe seiner Teile – ein echtes künstliches Gehirn zur Analyse der Finanzmärkte.

Technische Indikatoren: Die digitalen Sinne unseres Systems

Wenn wir uns unser neuronales System als das künstliche Gehirn eines Traders vorstellen, dann sind die technischen Indikatoren seine Sinnesorgane. So wie der Mensch die Welt durch Sehen, Hören und Tasten wahrnimmt, verwendet unser System verschiedene Indikatoren, um den Markt in all seinen Erscheinungsformen zu „erspüren“.

Grundlegende Indikatoren: System-Vision

Beginnen wir mit den grundlegendsten Indikatoren – den gleitenden Durchschnitten. Sie sind wie die Vision unseres Systems, die es ihm ermöglicht, den zugrunde liegenden Trend durch das Marktrauschen hindurch zu erkennen:

def calculate_moving_averages(self, prices):
    def sma(window):
        return np.convolve(prices, np.ones(window)/window, mode='valid')
    
    def ema(window):
        alpha = 2 / (window + 1)
        kernel = alpha * (1 - alpha)**np.arange(window)
        return np.convolve(prices, kernel[::-1], mode='valid')
    
    return {
        'sma_fast': sma(10),  # Fast SMA for short-term trends 
        'sma_slow': sma(20),  # Slow SMA for long-term trends
        'ema_fast': ema(10),  # Exponential MA for fast response
        'ema_slow': ema(20)   # Slow EMA for sorting out noise
    }

Oszillatoren: Marktmomente wahrnehmen

RSI, Momentum und Stochastic sind die taktilen Rezeptoren unseres Systems. Sie ermöglichen es uns, die Stärke der Kursbewegung und potenzielle Umkehrpunkte zu „spüren“:

def calculate_oscillators(self, data):
    def rsi(prices, period=14):
        delta = np.diff(prices)
        gain = np.where(delta > 0, delta, 0)
        loss = np.where(delta < 0, -delta, 0)
        
        avg_gain = np.mean(gain[:period])
        avg_loss = np.mean(loss[:period])
        
        for i in range(period, len(gain)):
            avg_gain = (avg_gain * 13 + gain[i]) / 14
            avg_loss = (avg_loss * 13 + loss[i]) / 14
            
        rs = avg_gain / avg_loss
        return 100 - (100 / (1 + rs))
    
    return {
        'rsi': rsi(data['close']),
        'momentum': data['close'] - np.roll(data['close'], 10),
        'stoch_k': self._calculate_stochastic_k(data)
    }

Volatilität und Volumen: Die Systemanhörung

Volatilitäts- und Volumenmetriken sind wie die Ohren unseres Systems – sie nehmen das „Rauschen“ des Marktes und die Stärke der Bewegungen auf. Bollinger Bands und ATR helfen bei der Bewertung der Amplitude der Schwankungen, und Volumenindikatoren helfen bei der Beurteilung ihrer Bedeutung:

def measure_market_dynamics(self, data):
    def bollinger_bands(prices, window=20):
        sma = np.mean(prices[-window:])
        std = np.std(prices[-window:])
        return {
            'upper': sma + 2 * std,
            'lower': sma - 2 * std,
            'width': 4 * std / sma  # Normalized strip width
        }
    
    def volume_profile(volumes, prices):
        return {
            'volume_ma': np.mean(volumes[-10:]),
            'volume_trend': np.corrcoef(volumes[-20:], prices[-20:])[0,1],
            'volume_oscillator': (np.mean(volumes[-5:]) / np.mean(volumes[-20:]) - 1) * 100
        }
    
    volatility = bollinger_bands(data['close'])
    volume = volume_profile(data['volume'], data['close'])
    return {**volatility, **volume}

Normalisierung: Einstellen der Empfindlichkeit

So wie das menschliche Gehirn die Empfindlichkeit seiner Sinne an die Umgebungsbedingungen anpasst, passt unser System die Skala der Eingabedaten dynamisch an. Dies ist entscheidend für den stabilen Betrieb des neuronalen Netzes:

def normalize_features(self, features: dict) -> dict:
    class AdaptiveNormalizer:
        def __init__(self, window=100):
            self.window = window
            self.history = {}
            
        def update(self, feature_name, value):
            if feature_name not in self.history:
                self.history[feature_name] = []
            
            self.history[feature_name].append(value)
            if len(self.history[feature_name]) > self.window:
                self.history[feature_name].pop(0)
            
            mean = np.mean(self.history[feature_name])
            std = np.std(self.history[feature_name])
            return (value - mean) / (std + 1e-8)  # Avoid zero divide
    
    normalizer = AdaptiveNormalizer()
    return {name: normalizer.update(name, value) 
            for name, value in features.items()}

Alle diese Indikatoren und Merkmale wirken eng zusammen und ergeben ein mehrdimensionales Bild der Marktrealität. So wie das menschliche Gehirn Informationen aus allen Sinnesorganen integriert, fasst unser System Daten aus allen Indikatoren zu einer einzigen Darstellung der Marktsituation zusammen. Dies ermöglicht es, nicht nur einem Trend zu folgen oder auf einzelne Signale zu reagieren, sondern ein ganzheitliches Verständnis der Marktdynamik zu entwickeln.

Experimentelle Ergebnisse

Testmethode

Im Rahmen der Studie haben wir das System anhand historischer Daten für das Währungspaar EURUSD umfassend getestet. Der Zeithorizont betrug 5 Jahre unter Verwendung des täglichen Zeitrahmens D1. Nach den üblichen Prinzipien des maschinellen Lernens teilen wir die Daten in Trainings- und Testsätze im Verhältnis 80/20 auf. Daher wurden 1659 Datenpunkte für das Training und 415 für den Test verwendet. Das Modell durchlief 20 Trainingsiterationen mit verschiedenen Gewichtsinitialisierungen, um die optimale Konfiguration zu finden.

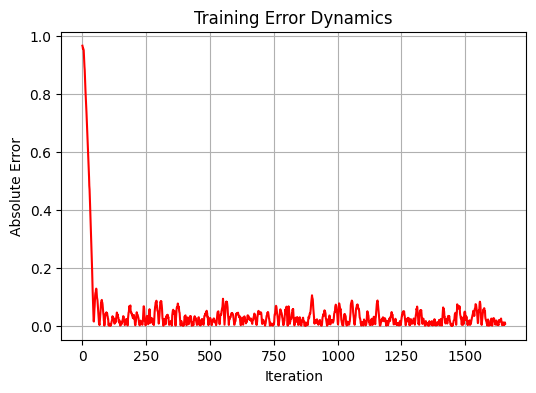
Leistungsanalyse

Bei der Analyse der Ergebnisse haben wir eine interessante Eigenschaft unseres Modells entdeckt. Anstatt zu versuchen, kurzfristige Kursbewegungen vorherzusagen, scheint das System darauf abzuzielen, eine Art „fairen“ Preis für das Währungspaar zu ermitteln. Diese Beobachtung wird durch die recht hohe Korrelation bei der Ausbildungsstichprobe bestätigt, die einen Wert von 0,583 mit einem relativ geringen Standardfehler von 0,012346 erreicht. Bei der Teststichprobe sinkt die Leistung des Modells jedoch erheblich: Die Korrelation fällt auf negative Werte (-0,108), und der MSE steigt um mehr als das 90fache und erreicht 1,156584.

Vergleich mit traditionellen Ansätzen

Unser biologisch inspiriertes Modell zeigt ein deutlich anderes Verhalten als klassische technische Indikatoren und neuronale Standardnetzwerke. Ihre Prognosen sind wesentlich unbeständiger. 

Es folgt ein Test mit einem Testmuster und einem Prognosehorizont von 15 Balken:

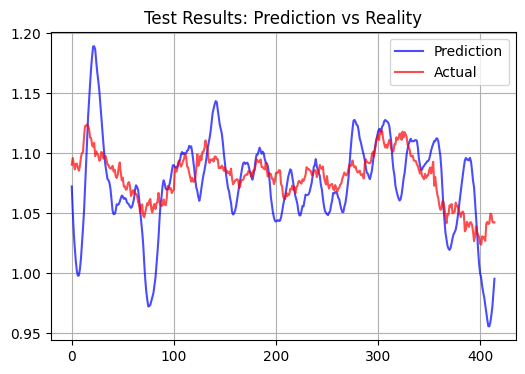
Statistische Leistungsindikatoren

Das signifikanteste Ergebnis der Modellleistung war das extrem niedrige Bestimmtheitsmaß (R²) für die Teststichprobe, das bei etwa 0,01 lag. Interessanterweise zeigt das Modell eine recht hohe Korrelation mit der Trainingsstichprobe, was auf seine Fähigkeit hinweist, langfristige Muster in den Daten zu erfassen. Außerdem enthalten die Modellprognosen oft deutlich sichtbare Ausschläge. Ob diese Spikes den kleinsten Kursbewegungen entsprechen und ob dies für Scalping geeignet ist, bleibt abzuwarten.

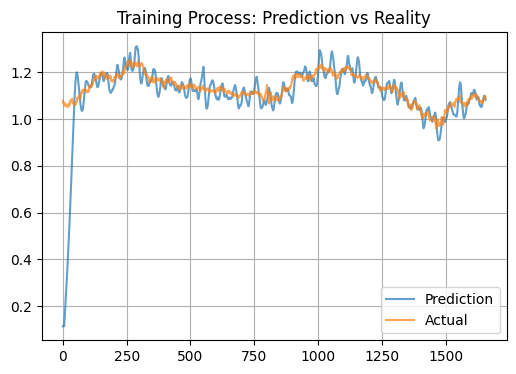
Merkmale und praktische Anwendung

Das beobachtete Verhalten des Modells kann durch seine biologische Natur erklärt werden. Das plasmaähnliche neuronale System scheint wie ein leistungsfähiger Filter zu wirken, der die Marktsignale erheblich verstärkt, und das Modell produziert übertriebene inkrementelle Prognosen. Der STDP-Mechanismus (Spike-Timing-Dependent Plasticity) sollte theoretisch zur Bildung stabiler Aktivierungsmuster führen, was zu einer Mittelwertbildung der Vorhersagen führt, und dementsprechend sollten wir ein unterschiedliches Bild des Test- und des Ist-Zustands erhalten. Ein zusätzlicher Faktor kann eine große Anzahl von Inputs in Form von technischen Indikatoren sein, die einen Überregulierungseffekt erzeugen.

Aus praktischer Sicht kann dieses Modell zur Bestimmung des kurzfristigen Niveaus des beizulegenden Zeitwerts eines Währungspaares verwendet werden. 

Schlussfolgerung

Unsere Forschung an einem biologisch inspirierten neuronalen System zur Vorhersage von Finanzmärkten hat unerwartete, aber faszinierende Ergebnisse erbracht. So wie das menschliche Gehirn in der Lage ist, intuitiv den „fairen“ Wert eines Vermögenswerts zu erkennen, hat unser Modell, das auf den Arbeitsprinzipien lebender Neuronen basiert, eine bemerkenswerte Fähigkeit bewiesen, fundamental gesunde Preisniveaus zu identifizieren.

Die Einführung einer plasmaähnlichen Umgebung in die Architektur des neuronalen Netzes schuf eine Art „kollektive Intelligenz“, bei der jedes Neuron den Betrieb des Systems nicht nur durch direkte Verbindungen, sondern auch durch weitreichende elektromagnetische Wechselwirkungen beeinflusst. Dieser Mechanismus hat sich als besonders effizient erwiesen, wenn es darum geht, das Marktrauschen auszublenden und langfristige Trends zu erkennen. 

Vielleicht hat dies eine tiefere Bedeutung. So wie sich biologische Systeme entwickelt haben, um langfristig zu überleben, strebt auch unser neuronales Netz, das nach ihrem Vorbild aufgebaut ist, danach, stabile, grundlegend solide Muster zu erkennen.

Bonus für diejenigen, die bis zum Ende lesen

Auf der Grundlage dieses Modells habe ich auch einen Indikator erstellt. Der Indikator lädt den Rest des Systems als Modul und öffnet sich in einem einfachen Fenster wie diesem:

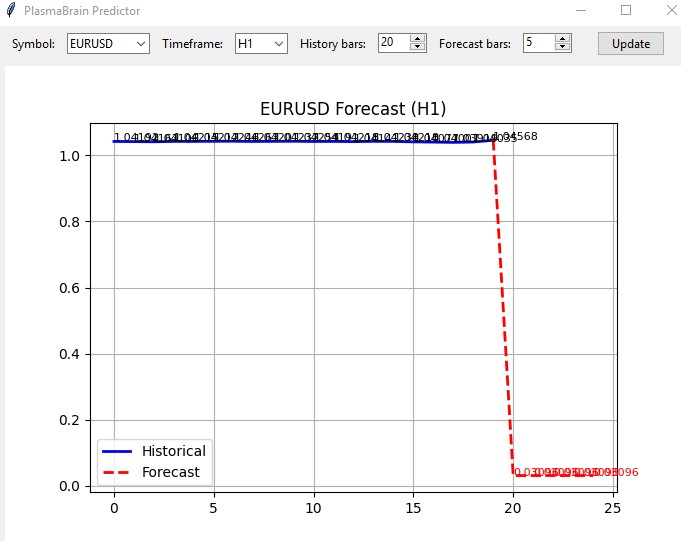
Ich habe ihn nicht live ausprobiert, aber wenn man bedenkt, dass alle anderen Systeme im Allgemeinen die gleiche Richtung vorhersagen, könnte der Indikator so funktionieren, wie er sollte.