
Neuronale Netze im Handel: Speichererweitertes kontextbezogenes Lernen (MacroHFT) für Kryptowährungsmärkte
Einführung
Die Finanzmärkte ziehen eine große Zahl von Anlegern an, weil sie leicht zugänglich sind und hohe Gewinne versprechen. Unter allen verfügbaren Anlageklassen zeichnen sich Kryptowährungen durch ihre außergewöhnliche Volatilität aus, die einzigartige Möglichkeiten zur Erzielung erheblicher Gewinne innerhalb kurzer Zeiträume bietet. Ein weiterer Vorteil ist der 24/7-Handelszyklus, der es den Händlern ermöglicht, Marktveränderungen zu verschiedenen Zeiten zu erfassen. Diese Volatilität birgt jedoch nicht nur Chancen, sondern auch erhebliche Risiken, die den Einsatz ausgefeilterer Managementstrategien erforderlich machen.
Um die Gewinne auf den Kryptowährungsmärkten zu maximieren, nutzen Händler häufig den Hochfrequenzhandel (HFT) – eine Form des algorithmischen Handels, der auf einer ultraschnellen Auftragsausführung basiert. HFT beherrscht seit langem die traditionellen Finanzmärkte und wird seit kurzem auch im Bereich der Kryptowährungen in großem Umfang eingesetzt. Es zeichnet sich nicht nur durch die Geschwindigkeit seiner Operationen aus, sondern auch durch seine Fähigkeit, enorme Datenmengen in Echtzeit zu verarbeiten, was es im schnelllebigen Umfeld der Kryptomärkte unverzichtbar macht.
Methoden des Verstärkungslernens (Reinforcement Learning, RL) werden im Finanzwesen immer beliebter, da sie komplexe sequentielle Entscheidungsprobleme lösen können. RL-Algorithmen können mehrdimensionale Daten verarbeiten, mehrere Parameter berücksichtigen und sich an wechselnde Umgebungen anpassen. Trotz erheblicher Fortschritte im Niederfrequenzhandel befinden sich wirksame Algorithmen für Hochfrequenzmärkte für Kryptowährungen jedoch noch in der Entwicklung. Diese Märkte sind gekennzeichnet durch hohe Volatilität, Instabilität und die Notwendigkeit, langfristige strategische Überlegungen mit schnellen taktischen Reaktionen in Einklang zu bringen.
Bestehende HFT-Algorithmen für Kryptowährungen stehen vor mehreren Herausforderungen, die ihre Wirksamkeit einschränken. Erstens werden die Märkte oft als einheitliche und stationäre Systeme behandelt, und viele Algorithmen stützen sich ausschließlich auf die Trendanalyse und vernachlässigen die Volatilität. Dieser Ansatz erschwert das Risikomanagement und verringert die Vorhersagegenauigkeit. Zweitens neigen viele Strategien zur Überanpassung und konzentrieren sich zu sehr auf eine begrenzte Anzahl von Marktmerkmalen. Dadurch verringert sich ihre Anpassungsfähigkeit an neue Bedingungen. Und schließlich fehlt es den einzelnen Handelsstrategien oft an ausreichender Flexibilität, um auf plötzliche Marktveränderungen zu reagieren – ein entscheidender Mangel in einem hochfrequenten Umfeld.
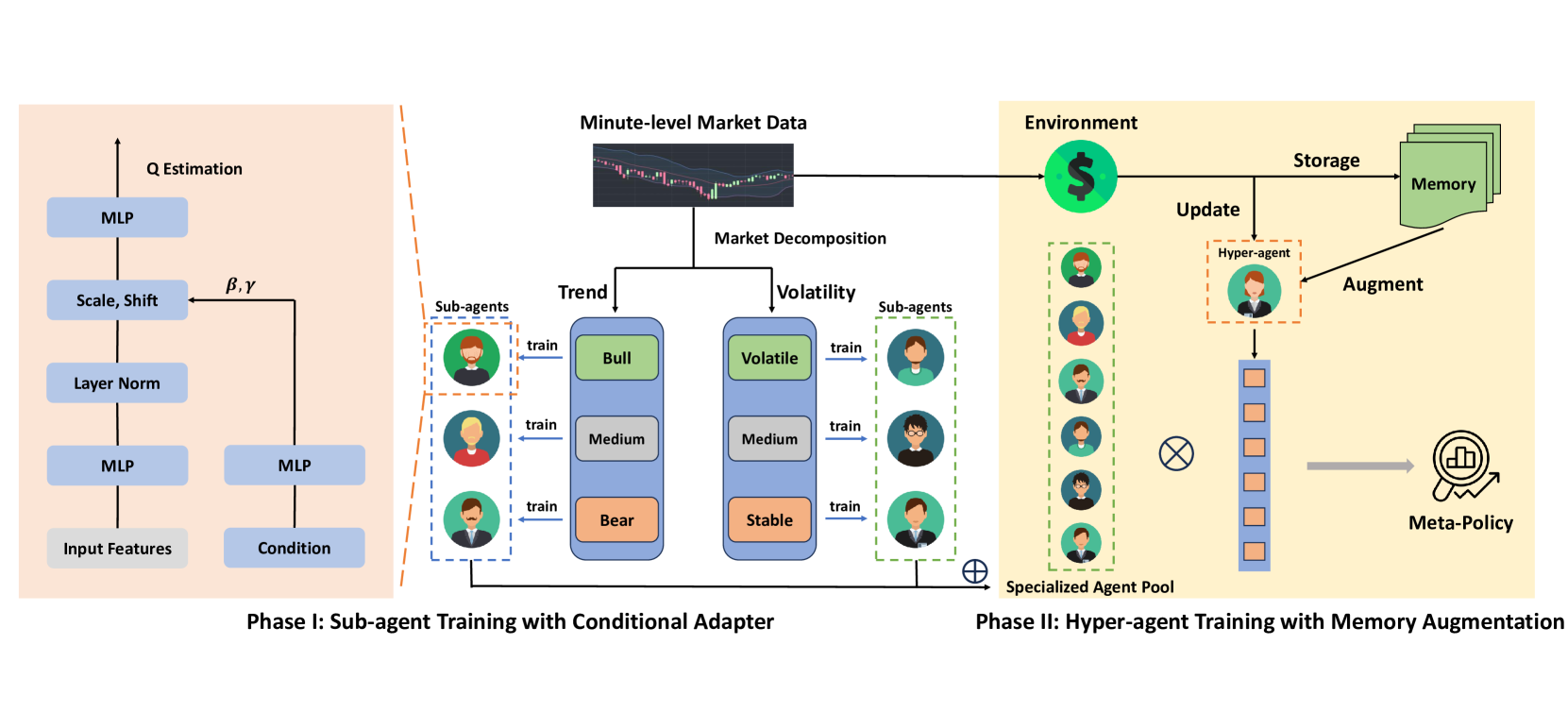
Eine mögliche Lösung für diese Herausforderungen wurde in dem Artikel „MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading“. Die Autoren schlagen MacroHFT vor, ein innovatives Framework, das auf kontextbezogenem Reinforcement Learning basiert und speziell für den Hochfrequenzhandel mit Kryptowährungen im Minutenbereich entwickelt wurde. MacroHFT bezieht makroökonomische und kontextbezogene Informationen ein, um die Entscheidungsqualität zu verbessern. Der Prozess umfasst zwei wichtige Phasen. Die erste ist die Marktklassifizierung, bei der der Markt anhand von Trend- und Volatilitätsindikatoren kategorisiert wird. Für jede Kategorie werden dann spezialisierte Unteragenten ausgebildet, die ihre Strategien dynamisch an die aktuellen Bedingungen anpassen können. Diese Untervermittler bieten Flexibilität und tragen den lokalen Marktgegebenheiten Rechnung.
In der zweiten Stufe integriert ein Hyperagent die Strategien der Unteragenten und optimiert ihren Einsatz auf der Grundlage der Marktdynamik. Ausgestattet mit einem Speichermodul, berücksichtigt es die jüngsten Erfahrungen, um stabile und adaptive Handelsstrategien zu entwickeln. Diese Struktur erhöht die Widerstandsfähigkeit des Systems gegenüber abrupten Marktveränderungen und verringert das Risiko.
Der Algorithmus von MacroHFT
Das MacroHFT-Framework ist eine innovative algorithmische Handelsplattform, die auf die Märkte für Kryptowährungen zugeschnitten ist, die sich durch hohe Volatilität und schnelle Schwankungen auszeichnen. Es basiert auf Methoden des Reinforcement Learning, die es ermöglichen, adaptive Algorithmen zu entwickeln, die das Marktverhalten analysieren und vorhersagen können. Die Grundidee besteht darin, spezialisierte Unteragenten, die jeweils für ein bestimmtes Marktszenario optimiert sind, und einen Hyperagenten zu integrieren, der sie koordiniert und so für Kohärenz und Gesamteffizienz sorgt.
Unter Bedingungen extremer Volatilität und schnellen Wandels ist es unzureichend, sich auf einen einzigen RL-Agenten zu verlassen. Die Marktbedingungen können sich zu schnell und unvorhersehbar ändern, als dass sich ein Algorithmus rechtzeitig anpassen könnte. Um dieses Problem zu lösen, werden im Rahmen von MacroHFT mehrere spezialisierte Unteragenten eingesetzt, die jeweils für unterschiedliche Marktumgebungen ausgebildet sind. Dies ermöglicht den Aufbau eines flexibleren und anpassungsfähigeren Systems.
Das Grundprinzip besteht in der Segmentierung und Klassifizierung von Marktdaten anhand zweier Schlüsselparameter: Trend und Volatilität. Die Marktdaten werden in Blöcke fester Länge unterteilt, die sowohl zum Training als auch zum Testen verwendet werden. Jedem Block werden Etiketten zugewiesen, die die Art der Marktbedingung kennzeichnen, was den Trainingsprozess für die Subagenten vereinfacht.
Der Kennzeichnungsprozess besteht aus zwei Schritten:
- Trend-Kennzeichnung. Jeder Datenblock wird mit einem Tiefpassfilter bearbeitet, um Rauschen zu entfernen und die Hauptkursrichtung hervorzuheben. Anschließend wird eine lineare Regression durchgeführt, wobei die Steigung als Trendindikator dient. Auf dieser Grundlage werden die Trends als positiv (aufwärts), neutral (seitwärts) oder negativ (abwärts) eingestuft.
- Volatilitätskennzeichnung. Zur Schätzung der Volatilität wird die durchschnittliche Preisänderung innerhalb jedes Blocks berechnet. Diese Werte werden in hohe, mittlere und niedrige Kategorien eingeteilt, wobei Quantile der Datenverteilung verwendet werden, um Schwellenwerte für die Kategorien festzulegen.
Somit erhält jeder Datenblock zwei Kennzeichnungen: eine für den Trend und eine für die Volatilität. Daraus ergeben sich sechs Marktzustandskategorien, die Trendtypen (aufwärts, seitwärts, abwärts) und Volatilitätsniveaus (hoch, mittel, niedrig) kombinieren. Aus dieser Segmentierung ergeben sich sechs Trainingsteilmengen, die jeweils zum Training eines für bestimmte Bedingungen optimierten Unteragenten verwendet werden. Die gleiche Kennzeichnungslogik wird auf die Testdaten angewandt, wobei Schwellenwerte verwendet werden, die aus dem Trainingssatz abgeleitet werden. Dieser Ansatz gewährleistet eine faire Leistungsbewertung.
Jeder Unteragent wird auf einer der sechs Datenuntermengen trainiert. Sie wird dann in der entsprechenden Kategorie getestet. Auf diese Weise entstehen spezialisierte Modelle, die auf bestimmte Umgebungen abgestimmt sind. So kann beispielsweise ein Unteragent in einem Aufwärtsmarkt mit hoher Volatilität am besten abschneiden, während ein anderer in einem Abwärtsmarkt mit niedriger Volatilität überragend ist. Diese modulare Architektur ermöglicht es dem System, sich dynamisch an sich verändernde Bedingungen anzupassen, was die Leistung erheblich verbessert.
Für das Training der Sub-Agenten wird die Methode Double Deep Q-Network (DDQN) mit einer dualen Architektur verwendet, die Marktindikatoren, kontextuelle Faktoren und die Position des Händlers berücksichtigt. Diese Datenströme werden durch separate neuronale Netzschichten verarbeitet und dann zu einer einheitlichen Darstellung zusammengeführt. Ein adaptiver Layer Norm Block verfeinert diese Darstellung und ermöglicht es dem Modell, spezifische Marktnuancen zu berücksichtigen, um eine flexible und präzise Entscheidungsfindung zu gewährleisten.
MacroHFT schafft somit sechs Sub-Agenten, die jeweils auf unterschiedliche Marktszenarien spezialisiert sind. Die daraus resultierenden Strategien werden von einem Hyper-Agenten integriert, der die Effizienz und Anpassungsfähigkeit des Systems unter den dynamischen Bedingungen der Kryptowährungsmärkte gewährleistet.
Der Hyper-Agent konsolidiert die Ergebnisse der Sub-Agenten zu einer flexiblen, effizienten Strategie, die sich an die Marktdynamik in Echtzeit anpassen kann. Es integriert die Entscheidungen der Subagenten mit Hilfe einer Softmax-basierten Meta-Politik. Dieser Ansatz verringert die übermäßige Abhängigkeit von einem einzelnen Unteragenten und bezieht gleichzeitig Erkenntnisse aus allen Systemkomponenten ein.
Einer der Hauptvorteile des Hyper-Agenten ist die Verwendung von Trend- und Volatilitätsindikatoren für eine schnelle Entscheidungsfindung, die eine schnelle Reaktion auf Marktveränderungen ermöglicht. Traditionelle, auf Markov-Entscheidungsprozessen (MDP) basierende Trainingsmethoden haben jedoch mit Problemen zu kämpfen, wie z. B. einer hohen Variabilität der Belohnungen und seltenen extremen Marktereignissen. Um diese Herausforderungen zu bewältigen, verfügt der Hyper-Agent über ein Speichermodul.
Das Speichermodul ist als eine Tabelle fester Größe implementiert, die Schlüsselvektoren von Zuständen und Aktionen speichert. Neue Erfahrungen werden hinzugefügt, indem ihre einstufigen Q-Wert-Schätzungen berechnet werden. Wenn die Kapazität der Tabelle erreicht ist, werden ältere Datensätze verworfen, um die wichtigsten Informationen zu erhalten. Während der Inferenz ruft der Hyper-Agent die relevantesten Einträge ab, indem er den L2-Abstand zwischen dem aktuellen Zustand und den gespeicherten Schlüsseln berechnet. Der endgültige Wert wird als gewichtete Summe der Speicherdaten berechnet.
Dieser Speichermechanismus verbessert auch die Handlungsbewertung des Hyper-Agenten. Durch Modifizierung der Verlustfunktion, um einen Term zur Speicheranpassung einzubeziehen, der die gespeicherten Speicherwerte mit den aktuellen Vorhersagen in Einklang bringt. Auf diese Weise erlernt das System stabilere Handelsstrategien, die in der Lage sind, plötzliche Marktschocks wirksam zu bewältigen.
MacroHFT verfügt über eine gut durchdachte Architektur, die es zu einem vielseitigen Handelsrahmen macht, der auf verschiedenen Finanzmärkten eingesetzt werden kann. Obwohl es ursprünglich für Kryptowährungen entwickelt wurde, lassen sich seine Methoden und Algorithmen auch auf andere Anlageklassen, einschließlich Aktien und Rohstoffe, übertragen.
Die Originalvisualisierung des MacroHFT-Rahmens ist unten zu sehen.
Implementation in MQL5
Nachdem wir die theoretischen Aspekte des MacroHFT-Rahmens analysiert haben, gehen wir nun zum praktischen Teil dieses Artikels über, in dem wir unsere eigene Implementierung der vorgeschlagenen Ansätze mit MQL5 vorstellen.
In dieser Implementierung behalten wir das Kernkonzept einer hierarchischen Modellarchitektur bei, führen jedoch erhebliche Änderungen an der Komponentenstruktur und dem Trainingsprozess ein. Zunächst entfällt die manuelle Segmentierung der Trainings- und Testdatensätze in beschriftete Blöcke, die nach Trend und Volatilitätsniveau kategorisiert sind. Zweitens trennen wir den Modellbildungsprozess nicht in zwei unterschiedliche Phasen. Stattdessen führen wir das gleichzeitige Training des Hyperagenten und der Subagenten in einem einheitlichen iterativen Prozess durch. Wir gehen davon aus, dass der Hyper-Agent während des Trainings in der Lage sein wird, Umweltzustände selbständig zu klassifizieren und den Agenten entsprechende Rollen zuzuweisen.
Wir werden keinen traditionellen tabellenbasierten Speicher für den Hyper-Agenten verwenden, sondern ihn durch einen dreischichtiges Speicherobjekt ersetzt, das im Rahmen von FinCon entwickelt wurde. Zusätzlich haben wir beschlossen, einen zuvor entwickelten Analysten-Agent in eine fortschrittlichere Architektur zu integrieren, um die Funktionalität der Unteragenten effizient zu implementieren. Unsere Arbeit an der Implementierung des MacroHFT-Rahmens beginnt also mit der Erstellung des Hyper-Agenten.
Aufbau des Hyper-Agenten
Nach der Beschreibung des MacroHFT-Rahmens durch die Autoren analysiert der Hyper-Agent den aktuellen Zustand der Umgebung, vergleicht ihn mit gespeicherten Speicherobjekten und gibt eine probabilistische Verteilung zurück, die die Klassifizierung des analysierten Zustands darstellt. Diese Klassifizierung kann sich auf den Trend oder die Volatilität der Marktbewegung beziehen. Die sich daraus ergebende Wahrscheinlichkeitsverteilung wird dann verwendet, um den Beitrag der einzelnen Unteragenten zur endgültigen Handelsentscheidung zu bestimmen. Die endgültige Entscheidung ergibt sich aus der Gewichtung der Ergebnisse der Unteragenten, je nachdem, wie gut sie mit den aktuellen Marktbedingungen übereinstimmen. Dieser Ansatz ermöglicht es, den gesamten Entscheidungsprozess dynamisch an die vorherrschenden Marktfaktoren anzupassen.
Mit anderen Worten: Wir müssen eine Komponente zur Klassifizierung von Zuständen schaffen, die in der Lage ist, das aktuelle Marktumfeld zu analysieren und dabei den Kontext der zuvor beobachteten und gespeicherten Zustände zu berücksichtigen. Dies geschieht durch die Analyse der Abfolge von Marktparametern und deren Korrelationen mit der aktuellen Situation. Historische Zustände helfen, langfristige Trends und verborgene Muster aufzudecken und ermöglichen so eine fundiertere Einordnung der aktuellen Marktlage.
Wir werden einen solchen Hyperagenten als ein Objekt namens CNeuronMacroHFTHyperAgent implementieren, dessen Struktur im Folgenden vorgestellt wird.
class CNeuronMacroHFTHyperAgent : public CNeuronSoftMaxOCL { protected: CNeuronMemoryDistil cMemory; CNeuronRMAT cStatePrepare; CNeuronTransposeOCL cTranspose; CNeuronConvOCL cScale; CNeuronBaseOCL cMLP[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMacroHFTHyperAgent(void) {}; ~CNeuronMacroHFTHyperAgent(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint agents, uint stack_size, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMacroHFTHyperAgent; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool Clear(void) override; };
Die Implementierung der Softmax-Schicht wird als übergeordnete Klasse verwendet. Diese Funktion wurde von den Autoren des MacroHFT-Rahmens zur Berechnung von Wahrscheinlichkeitsverteilungen vorgeschlagen. Sie spielt eine Schlüsselrolle bei der Bestimmung des Beitrags der einzelnen Unteragenten zur endgültigen Entscheidung und gewährleistet sowohl die Genauigkeit als auch die Anpassungsfähigkeit des Modells.
Die Struktur des Hyperagenten umfasst einen Standardsatz virtueller Methoden und mehrere interne Objekte, die als Grundlage für den Algorithmus zur Analyse des aktuellen Zustands der Umgebung dienen. Wir werden die Funktionalität dieser Komponenten bei der Implementierung der Klassenmethoden des Hyperagenten im Detail untersuchen.
Alle internen Objekte werden als statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt. Diese Methode benötigt eine Reihe von konstanten Parametern, die die Architektur des zu erstellenden Objekts eindeutig definieren.
bool CNeuronMacroHFTHyperAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint agents, uint stack_size, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, agents, optimization_type, batch)) return false; SetHeads(1); //--- int index = 0;
Im Methodenkörper rufen wir wie üblich zunächst die entsprechende Methode der übergeordneten Klasse auf. In diesem Fall handelt es sich um die Softmax-Funktionsschicht. Die erwartete Größe des Ergebnisvektors entspricht der Anzahl der verwendeten Subagenten, und dieser Wert wird vom aufrufenden Programm als Methodenparameter übergeben.
Als Nächstes gehen wir zur Initialisierung der internen Objekte über. Zunächst wird das Speichermodul initialisiert.
int index = 0; if(!cMemory.Init(0, 0, OpenCL, window, window_key, units_count, heads, stack_size, optimization, iBatch)) return false;
Zur Erkennung von Abhängigkeiten in den Daten, die den analysierten Umweltzustand darstellen, planen wir den Einsatz eines Transformators mit relativer Positionskodierung.
index++; if(!cStatePrepare.Init(0, index, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch)) return false;
Der nächste Schritt besteht darin, den analysierten Umweltzustand in einen Unterraum zu projizieren, dessen Dimensionalität der Anzahl der Unteragenten entspricht. Dies erfordert einen effizienten Projektionsmechanismus, der alle wichtigen Datenmerkmale beibehält. Auf den ersten Blick könnte eine normale voll verknüpfte oder eine Faltungsschicht verwendet werden. Angesichts des multimodalen Charakters der Zeitreihen ist es jedoch von entscheidender Bedeutung, die Struktur der univariaten Sequenzen zu erhalten, die wichtige Informationen enthalten, die andernfalls durch übermäßige Aggregation verloren gehen könnten.
Zuvor haben wir einen Transformator mit relativer Kodierung angewandt, um die Abhängigkeiten zwischen den Zeitschritten zu analysieren. Nun müssen wir diesen Prozess ergänzen, indem wir die Details der einzelnen univariaten Sequenzen festhalten. Zu diesem Zweck werden die Daten zunächst transponiert, um die Verarbeitung der univariaten Sequenzen in den nachfolgenden Operationen zu erleichtern.
index++; if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch)) return false;
Anschließend wenden wir eine Faltungsschicht an, die räumliche und zeitliche Merkmale aus diesen unitären Sequenzen extrahiert und ihre Interpretierbarkeit verbessert. Die Nichtlinearität wird durch die Aktivierungsfunktion des hyperbolischen Tangens (tanh) eingeführt.
index++; if(!cScale.Init(4 * agents, index, OpenCL, 3, 1, 1, units_count - 2, window, optimization, iBatch)) return false; cScale.SetActivationFunction(TANH);
Nach dieser Phase gehen wir zur Phase der Komprimierung der Schlüsseldaten über. Um die Dimensionalität zu reduzieren, wird eine zweischichtige MLP-Architektur verwendet. Die erste Schicht führt eine vorläufige Datenreduzierung durch und entfernt redundante Korrelationen und Rauschen. Die Verwendung der Aktivierungsfunktion Leaky ReLU (LReLU) hilft, Linearität bei Transformationen zu vermeiden. Die zweite Schicht schließt die Komprimierung ab und optimiert die Daten für die weitere Analyse.
index++; if(!cMLP[0].Init(agents, index, OpenCL, 4 * agents, optimization, iBatch)) return false; cMLP[0].SetActivationFunction(LReLU); index++; if(!cMLP[1].Init(0, index, OpenCL, agents, optimization, iBatch)) return false; cMLP[0].SetActivationFunction(None); //--- return true; }
Dieser Ansatz gewährleistet ein Gleichgewicht zwischen Informationserhalt und Modellvereinfachung, was für die Effektivität des Hyperagenten in Hochfrequenzhandelsumgebungen entscheidend ist.
Die verarbeiteten Daten werden dann über die Mechanismen, die von der zuvor initialisierten übergeordneten Klasse bereitgestellt werden, in den Wahrscheinlichkeitsraum übertragen. An diesem Punkt kann die Methode einen logischen Erfolgswert an das aufrufende Programm zurückgeben, womit der Initialisierungsprozess abgeschlossen ist.
Sobald die Initialisierung abgeschlossen ist, wird der Algorithmus des Vorwärtsdurchlaufs in der Methode feedForward implementiert. Hier ist alles ganz einfach und überschaubar.
bool CNeuronMacroHFTHyperAgent::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMemory.FeedForward(NeuronOCL)) return false;
Die Methode erhält als Parameter einen Zeiger auf das Quelldatenobjekt, das einen multimodalen Tensor enthält, der den analysierten Umweltzustand beschreibt. Dieser Zeiger wird sofort an die entsprechende Methode des Speichermoduls übergeben. In diesem Stadium wird die statische Beschreibung der Umwelt mit Informationen über die jüngste Dynamik angereichert, wodurch eine vollständigere und aktuellere Darstellung für die weitere Analyse entsteht. Die Integration dieses zeitlichen Kontextes ermöglicht eine präzisere Verfolgung der laufenden Veränderungen innerhalb des Systems und verbessert so die Effizienz der nachfolgenden Verarbeitungsalgorithmen.
Die verarbeiteten Daten aus der vorangegangenen Phase werden an den Aufmerksamkeitsblock weitergeleitet, der die Abhängigkeiten zwischen den verschiedenen Zeitpunkten innerhalb der analysierten Reihe ermittelt. Dieser Schritt deckt verborgene Zusammenhänge auf und verbessert die Genauigkeit der nachfolgenden Prognosen der Preisentwicklung.
if(!cStatePrepare.FeedForward(cMemory.AsObject())) return false;
Danach gehen wir zur Datenkompression über. Zunächst werden die Ergebnisse der vorangegangenen Analyse umgesetzt.
if(!cTranspose.FeedForward(cStatePrepare.AsObject())) return false;
Anschließend werden die einzelnen univariaten Sequenzen mit Hilfe einer Faltungsschicht komprimiert, wobei ihre Strukturinformationen erhalten bleiben.
if(!cScale.FeedForward(cTranspose.AsObject())) return false;
Dann projizieren wir den analysierten Umgebungszustand mit Hilfe des MLP in einen Unterraum mit vordefinierter Dimensionalität.
if(!cMLP[0].FeedForward(cScale.AsObject())) return false; if(!cMLP[1].FeedForward(cMLP[0].AsObject())) return false;
Nun müssen wir die erhaltenen Werte in den Wahrscheinlichkeitsraum übertragen. Dies geschieht durch den Aufruf der entsprechenden Softmax-Methode aus der übergeordneten Klasse, wobei die verarbeiteten Ergebnisse übergeben werden.
return CNeuronSoftMaxOCL::feedForward(cMLP[1].AsObject()); }
Dann geben wir das logische Ergebnis der Operation an den Aufrufer zurück und beenden die Ausführung der Methode.
Wie Sie vielleicht bemerkt haben, folgt der Algorithmus für den Vorwärtsdurchlauf des Hyperagenten einer linearen und transparenten Struktur. Die Algorithmen für die Rückwärtsdurchlauf-Methoden sind von ähnlich linearer Natur und relativ einfach für eine unabhängige Untersuchung.
An dieser Stelle schließen wir unseren Überblick über die Funktionsweise des Hyperagenten ab. Der vollständige Quellcode der vorgestellten Klasse, einschließlich aller Methoden, befindet sich im Anhang für diejenigen, die an weiteren Studien und praktischen Anwendungen interessiert sind. Weiter geht's. Wir gehen nun zur Integration der Agenten in einen einheitlichen Rahmen über.
Aufbau des MakroHFT-Rahmens
In diesem Stadium haben wir bereits die einzelnen Objekte der Unteragenten und des Hyperagenten. Es ist nun an der Zeit, sie in eine einheitliche, zusammenhängende Struktur zu integrieren, in der Algorithmen für den Datenaustausch zwischen den Modellkomponenten implementiert werden. Diese Aufgabe wird innerhalb des CNeuronMacroHFT-Objekts ausgeführt, das die Arbeitsabläufe der Datenverarbeitung verwaltet und optimiert. Die Struktur des neuen Objekts wird im Folgenden dargestellt.
class CNeuronMacroHFT : public CNeuronBaseOCL { protected: CNeuronTransposeOCL cTranspose; CNeuronFinConAgent caAgetnts[6]; CNeuronMacroHFTHyperAgent cHyperAgent; CNeuronBaseOCL cConcatenated; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMacroHFT(void) {}; ~CNeuronMacroHFT(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint stack_size, uint nactions, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMacroHFT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool Clear(void) override; };
Das neue Objekt enthält den bekannten Satz überschreibbarer virtueller Methoden, die Flexibilität bei der Implementierung seiner Funktionalität bieten. Unter den internen Objekten spielt der Hyper-Agent die zentrale koordinierende Rolle, während eine Reihe von sechs Unter-Agenten die Verarbeitung verschiedener Aspekte der Eingabedaten übernimmt. Eine detaillierte Beschreibung der Funktionalität interner Objekte und der Logik ihrer Interaktionen wird bei der Erstellung der Klassenmethoden erforscht.
Alle internen Objekte werden statisch deklariert. Dadurch können wir den Konstruktor und Destruktor der Klasse leer lassen. Die Initialisierung von deklarierten und geerbten Objekten wird in der Methode Init durchgeführt. Diese Methode akzeptiert mehrere konstante Parameter, die die Architektur des erstellten Objekts klar definieren.
bool CNeuronMacroHFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint stack_size, uint nactions, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, nactions, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir wie üblich die gleichnamige Methode der übergeordneten Klasse auf. Diese Methode implementiert bereits den Prozess der Initialisierung von abgeleiteten Objekten und Schnittstellen. In diesem Fall ist die übergeordnete Klasse eine vollständig verbundene Schicht, von der wir nur die grundlegenden Schnittstellen für die Interaktion mit externen Modellkomponenten benötigen. Die Ausgabe unseres neuen Objekts sollte den endgültigen Aktionstensor des Modells in Übereinstimmung mit den analysierten Marktbedingungen ergeben. Daher geben wir die Dimensionalität des Aktionsraums des Agenten als Parameter der Initialisierungsmethode der Elternklasse an.
Im ursprünglichen MacroHFT-Rahmen schlugen die Autoren vor, die Sub-Agenten nach Markttrend und Volatilität zu unterteilen. In unserer Version verwenden wir jedoch eine Aufteilung, die auf dem Sichtfeld des Marktes basiert. Unsere Untervermittler erhalten unterschiedliche Hochrechnungen der analysierten Marktdaten. Zur Bildung dieser Projektionen wird eine Datentranspositionsschicht verwendet.
int index = 0; if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch)) return false;
Als Nächstes initialisieren wir die Unteragenten. Die erste Hälfte von ihnen analysiert die Eingabedaten in ihrer ursprünglichen Form, während die zweite Hälfte ihre transponierte Darstellung verarbeitet. Um diese Initialisierung zu organisieren, richten wir zwei aufeinanderfolgende Schleifen ein, die jeweils die erforderliche Anzahl von Iterationen durchführen.
uint half = (caAgetnts.Size() + 1) / 2; for(uint i = 0; i < half; i++) { index++; if(!caAgetnts[i].Init(0, index, OpenCL, window, window_key, units_count, heads, stack_size, nactions, optimization, iBatch)) return false; } for(uint i = half; i < caAgetnts.Size(); i++) { index++; if(!caAgetnts[i].Init(0, index, OpenCL, units_count, window_key, window, heads, stack_size, nactions, optimization, iBatch)) return false; }
Anschließend initialisieren wir den Hyper-Agenten, der ebenfalls die ursprüngliche Marktdatendarstellung analysiert.
index++; if(!cHyperAgent.Init(0, index, OpenCL, window, window_key, units_count, heads, layers, caAgetnts.Size(), stack_size, optimization, iBatch)) return false;
Nach dem MacroHFT-Algorithmus müssen wir nun eine gewichtete Summierung der Ergebnisse der Subagenten vornehmen. Die Gewichte werden in diesem Fall durch den Hyper-Agenten erzeugt. Dieser Vorgang lässt sich leicht bewerkstelligen, indem die Matrix der Subagentenergebnisse mit dem vom Hyperagenten bereitgestellten Gewichtsvektor multipliziert wird. In unserer Implementierung werden die Ausgaben der Subagenten jedoch in separaten Objekten gespeichert. Daher erstellen wir ein zusätzliches Verkettungsobjekt, um die erforderlichen Vektoren zu einer einzigen Matrix zu kombinieren.
index++; if(!cConcatenated.Init(0, index, OpenCL, caAgetnts.Size()*nactions, optimization, iBatch)) return false; //--- return true; }
Die eigentliche Matrixmultiplikation wird im Rahmen des Vorwärtsdurchlauf-Prozesses durchgeführt. Im Moment geben wir einfach das logische Ergebnis der Initialisierung an das aufrufende Programm zurück und beenden die Init-Methode.
Unser nächster Schritt ist die Implementierung des Algorithmus für den Vorwärtsdurchlauf innerhalb der Methode feedForward. Wie zuvor erhält die Methode einen Zeiger auf das Eingabedatenobjekt, das wir sofort umwandeln.
bool CNeuronMacroHFT::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cTranspose.FeedForward(NeuronOCL)) return false;
Als Nächstes verarbeitet die eine Hälfte der Unteragenten die ursprüngliche Darstellung des analysierten Umweltzustands, während die andere Hälfte ihre transponierte Projektion verarbeitet.
uint total = caAgetnts.Size(); uint half = (total + 1) / 2; for(uint i = 0; i < half; i++) if(!caAgetnts[i].FeedForward(NeuronOCL)) return false;
for(uint i = half; i < total; i++) if(!caAgetnts[i].FeedForward(cTranspose.AsObject())) return false;
Der Hyper-Agent analysiert gleichzeitig auch die Originaldaten.
if(!cHyperAgent.FeedForward(NeuronOCL)) return false;
Anschließend fassen wir die Ergebnisse aller Subagenten in einer einzigen Matrix zusammen.
if(!Concat(caAgetnts[0].getOutput(), caAgetnts[1].getOutput(), caAgetnts[2].getOutput(), caAgetnts[3].getOutput(), cConcatenated.getPrevOutput(), Neurons(), Neurons(), Neurons(), Neurons(), 1) || !Concat(cConcatenated.getPrevOutput(), caAgetnts[4].getOutput(), caAgetnts[5].getOutput(), cConcatenated.getOutput(), 4 * Neurons(), Neurons(), Neurons(), 1)) return false;
In der sich ergebenden Matrix entspricht jede Zeile dem Output eines Unteragenten. Um die gewichtete Summe korrekt zu berechnen, multiplizieren wir den Gewichtsvektor (vom Hyper-Agenten) mit dieser Ergebnismatrix.
if(!MatMul(cHyperAgent.getOutput(), cConcatenated.getOutput(), Output, 1, total, Neurons(), 1)) return false; //--- return true; }
Die Ergebnisse dieser Matrixmultiplikation werden in den von der übergeordneten Klasse geerbten externen Schnittstellenpuffer geschrieben. Anschließend geben wir das logische Ergebnis der Operationen an das aufrufende Programm zurück und schließen die Methode ab.
Es ist erwähnenswert, dass der Algorithmus für den Vorwärtsdurchlauf trotz der eingeführten strukturellen Änderungen die ursprüngliche konzeptionelle Logik des MacroHFT-Rahmens vollständig beibehält. Dies gilt jedoch nicht für den Ausbildungsprozess, auf den wir im Folgenden eingehen werden.
Wie bereits erwähnt, haben die Autoren des MacroHFT-Rahmens den Trainingsdatensatz nach Markttrends und Volatilität in separate Teilmengen unterteilt. Jeder Teilagent wurde auf seiner jeweiligen Teilmenge trainiert. In unserer Implementierung schlagen wir jedoch vor, alle Agenten gleichzeitig zu trainieren. Dieser Prozess wird in den Methoden der Rückwärtsdurchläufe unserer Klasse implementiert.
Wir beginnen mit der Entwicklung eines Algorithmus zur Verteilung der Fehlergradienten auf die internen Objekte unserer Klasse und die Eingabedaten, und zwar im Verhältnis zu ihrem Einfluss auf die Gesamtleistung des Modells. Diese Funktion ist in der Methode calcInputGradients implementiert.
bool CNeuronMacroHFT::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Die Methode empfängt einen Zeiger auf das gleiche Eingangsdatenobjekt, das in der Vorwärtsdurchlauf verwendet wurde. Diesmal muss ihm jedoch der entsprechende Fehlergradient übergeben werden. Innerhalb der Methode überprüfen wir sofort die Gültigkeit des empfangenen Zeigers – denn wenn das Objekt nicht existiert, ist es unmöglich, Daten in dieses Objekt zu schreiben. In diesem Fall werden alle nachfolgenden Operationen sinnlos.
Wie Sie wissen, spiegelt der Fehlergradientenfluss die Vorgänge des Prozesses des Vorwärtsdurchlaufs wider, bewegt sich aber in die entgegengesetzte Richtung. Während der Vorwärtsdurchlauf mit der Matrixmultiplikation der Subagentenergebnisse und des Gewichtsvektors abgeschlossen wurde, beginnt der Rückwärtsdurchlauf mit der Verteilung des Fehlergradienten durch dieselbe Operation.
uint total = caAgetnts.Size(); if(!MatMulGrad(cHyperAgent.getOutput(), cHyperAgent.getGradient(), cConcatenated.getOutput(), cConcatenated.getGradient(), Gradient, 1, total, Neurons(), 1)) return false;
Es ist wichtig zu beachten, dass bei diesem Schritt der Gradient in zwei Informationsströme aufgeteilt wird. Die erste ist der Gradientenfluss des Hyperagenten. Über diesen Stream können wir den Fehler sofort auf die Ebene der Eingabedaten übertragen.
if(!NeuronOCL.calcHiddenGradients(cHyperAgent.AsObject())) return false;
Der zweite ist der Gradientenfluss der Subagenten. Bei der Gradientenverteilung durch Matrixmultiplikation erhalten wir Fehlerwerte auf der Ebene des verketteten Objekts. Natürlich erhält der Teilagent, der am meisten zum Output des Modells beigetragen hat, den größten Fehlergradienten. So können wir während des Trainings auf der Grundlage der vom Hyper-Agenten vorgenommenen Klassifizierungen des Umgebungszustands dynamisch Rollen an Sub-Agenten vergeben.
Anschließend verteilen wir die erhaltenen Gradientenwerte auf die entsprechenden Subagenten, indem wir eine Datenentkettung durchführen.
if(!DeConcat(cConcatenated.getPrevOutput(), caAgetnts[4].getGradient(), caAgetnts[5].getGradient(), cConcatenated.getGradient(), 4 * Neurons(), Neurons(), Neurons(), 1) || !DeConcat(caAgetnts[0].getGradient(), caAgetnts[1].getGradient(), caAgetnts[2].getGradient(), caAgetnts[3].getGradient(), cConcatenated.getPrevOutput(), Neurons(), Neurons(), Neurons(), Neurons(), 1)) return false;
Danach können wir die Fehlergradienten auf der Ebene der Eingabedaten entlang des Berechnungspfads jedes Unteragenten weitergeben. Hier sollten wir zwei Punkte beachten. Erstens enthält der Gradientenpuffer des Eingabedatenobjekts bereits Informationen, die vom Hyper-Agenten empfangen wurden, und diese müssen erhalten bleiben. Zu diesem Zweck wird der Zeiger des Gradientenpuffers vorübergehend durch einen anderen verfügbaren Puffer ersetzt, um das Überschreiben vorhandener Daten zu verhindern.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!temp || !NeuronOCL.SetGradient(cTranspose.getPrevOutput(), false)) return false;
Zweitens interagieren nicht alle Unteragenten direkt mit den Eingabedaten. Die Hälfte von ihnen verarbeitet transponierte Daten. Daher muss dies bei der Verteilung der Gradienten berücksichtigt werden. Wie beim Vorwärtsdurchlauf organisieren wir zwei sequentielle Schleifen. Die erste Schleife befasst sich mit den Unteragenten, die mit der direkten Eingabedarstellung arbeiten. Wir propagieren ihre Gradienten bis hinunter zur Eingabeebene und akkumulieren die Ergebnisse mit den zuvor gespeicherten Gradienten.
uint half = (total + 1) / 2; for(uint i = 0; i < half; i++) { if(!NeuronOCL.calcHiddenGradients(caAgetnts[i].AsObject())) return false; if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1)) return false; }
Die zweite Schleife spiegelt die erste wider, fügt aber einen zusätzlichen Schritt hinzu, indem sie die Gradienten durch die Datentranspositionsebene weiterleitet. Diese Schleife verarbeitet die andere Hälfte der Unteragenten.
for(uint i = half; i < total; i++) { if(!cTranspose.calcHiddenGradients(caAgetnts[i].AsObject()) || !NeuronOCL.calcHiddenGradients(cTranspose.AsObject())) return false; if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1)) return false; }
Sobald alle Schleifeniterationen erfolgreich abgeschlossen sind, werden die ursprünglichen Datenpufferzeiger wiederhergestellt. Anschließend beenden wir die Methode und geben das logische Erfolgsergebnis an das aufrufende Programm zurück.
Damit ist die Untersuchung der Algorithmen abgeschlossen, die zur Konstruktion der Methoden unseres neuen Koordinationsobjekts MacroHFT Framework verwendet werden. Den vollständigen Quellcode für alle vorgestellten Klassen und ihre Methoden finden Sie im Anhang.
Wir haben nun die Grenzen des Formats dieses Artikels erreicht, aber unsere Arbeit ist noch nicht abgeschlossen. Lassen Sie uns eine kurze Pause einlegen und im nächsten Artikel weitermachen. Wir werden die Implementierung abschließen und die Leistung der entwickelten Ansätze anhand realer historischer Marktdaten bewerten.
Schlussfolgerung
In diesem Artikel haben wir das MacroHFT-Framework untersucht, eine vielversprechende Lösung für den Hochfrequenzhandel mit Kryptowährungen. Dieser Rahmen berücksichtigt den makroökonomischen Kontext und die lokale Marktdynamik. Dies macht es zu einem leistungsstarken Instrument für professionelle Händler, die unter komplexen und volatilen Marktbedingungen ihre Rendite maximieren wollen.
Im praktischen Teil haben wir unsere eigene Interpretation der Kernkomponenten des Frameworks mit MQL5 umgesetzt. Im nächsten Schritt werden wir diese Arbeit vervollständigen und die Wirksamkeit der implementierten Ansätze anhand realer historischer Daten rigoros testen.
Referenzen
- MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading
- Andere Artikel dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modellausbildung Expert Advisor |
| 4 | Test.mq5 | Expert Advisor | Modellprüfung Expert Advisor |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16975
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Risikomanagement (Teil 1): Grundlagen für den Aufbau einer Risikomanagement-Klasse
Risikomanagement (Teil 1): Grundlagen für den Aufbau einer Risikomanagement-Klasse
 Dialektische Suche (DA)
Dialektische Suche (DA)
 Neuronale Netze im Handel: Multi-Task-Lernen auf der Grundlage des ResNeXt-Modells
Neuronale Netze im Handel: Multi-Task-Lernen auf der Grundlage des ResNeXt-Modells
 Neuronale Netze im Handel: Ein Multi-Agenten-System mit konzeptioneller Verstärkung (letzter Teil)
Neuronale Netze im Handel: Ein Multi-Agenten-System mit konzeptioneller Verstärkung (letzter Teil)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.