Risikomanagement (Teil 1): Grundlagen für den Aufbau einer Risikomanagement-Klasse

MetaTrader 5 — Beispiele | 28 Januar 2026, 08:57

Einführung

In diesem Artikel werden wir untersuchen, was Risikomanagement im Handel bedeutet und warum es für automatisierte Operationen unerlässlich ist. Wir werden mit den grundlegenden Konzepten beginnen, um zu verstehen, wie ein angemessenes Risikomanagement den Unterschied zwischen Erfolg und Misserfolg auf den Finanzmärkten ausmachen kann.

Später werden wir Schritt für Schritt eine MQL5-Klasse erstellen, die ein komplettes Risikomanagementsystem implementiert und die Kontrolle über wichtige Aspekte wie Losgröße, maximale Verluste und erwartete Gewinne ermöglicht.

Was ist Risikomanagement?

Das Risikomanagement ist ein Grundpfeiler jeder Handelsstrategie. Ihr Hauptzweck besteht darin, offene Positionen zu überwachen und zu kontrollieren, um sicherzustellen, dass die Verluste die vom Händler festgelegten Grenzen nicht überschreiten, z. B. tägliche, wöchentliche oder Gesamtverluste.

Darüber hinaus bestimmt das Risikomanagement die angemessene Losgröße für jeden Handel, basierend auf den Regeln und Präferenzen des Nutzers. Dadurch wird nicht nur das Kapital geschützt, sondern auch die Performance der Strategie optimiert, indem sichergestellt wird, dass die Handelsgeschäfte mit dem festgelegten Risikoprofil übereinstimmen.

Kurz gesagt, ein gutes Risikomanagement verringert nicht nur das Risiko katastrophaler Verluste, sondern bietet auch einen disziplinierten Rahmen für intelligente finanzielle Entscheidungen.

Bedeutung für den automatisierten Handel

Das Risikomanagement spielt beim automatisierten Handel eine entscheidende Rolle, da es als Kontrollsystem fungiert, das kostspielige Fehler wie übermäßiges Handeln oder das Eingehen unnötiger Risiken verhindert. Im Zusammenhang mit Handelsrobotern, bei denen Entscheidungen vollautomatisch getroffen werden, gewährleistet ein angemessenes Risikomanagement, dass Strategien diszipliniert und effizient ausgeführt werden.

Dies ist besonders wertvoll in Szenarien wie Finanzierungsherausforderungen, bei denen die Einhaltung strikter Tages-, Wochen- oder Totalverlustgrenzen den Unterschied zwischen Bestehen oder Nichtbestehen ausmachen kann. Das Risikomanagement ermöglicht die genaue Festlegung dieser Grenzen, um das Kapital des Nutzers zu schützen und die Leistung in einem wettbewerbsorientierten Umfeld zu optimieren.

Darüber hinaus hilft er dem Bot, strategischer vorzugehen, indem er klare Grenzen setzt, um übermäßiges Handeln oder das Eingehen unverhältnismäßiger Risiken zu vermeiden. Durch die automatische Berechnung von Losgrößen und die Begrenzung von Verlusten pro Handel schützt das Risikomanagement nicht nur das Kapital, sondern gibt dem Händler auch die Gewissheit, dass sein Bot innerhalb kontrollierter und sicherer Parameter arbeitet.

Schlüsselkonzepte im Risikomanagement

Bevor Sie mit der Programmierung beginnen, müssen Sie die wichtigsten Variablen und Konzepte des Risikomanagements verstehen. Diese Konzepte bilden die Grundlage für ein effektives System, das das Kapital des Nutzers schützt und einen kontrollierten Betrieb gewährleistet. Nachfolgend wird jede einzelne von ihnen aufgeschlüsselt:

1. Maximaler täglicher Verlust

Dies ist der maximale Verlust, den ein Bot innerhalb eines Tages (24 Stunden) anhäufen kann. Wird dieses Limit erreicht, schließt der Bot in der Regel alle offenen Handelsgeschäfte und setzt jegliche Handelsaktivität bis zum nächsten Tag aus. Dieses Konzept hilft zu verhindern, dass eine Serie von Verlustgeschäften das Kapital stark beeinträchtigt.

2. Maximaler wöchentlicher Verlust

Ähnlich wie das tägliche Verlustlimit, aber über einen einwöchigen Zeitraum angewendet. Überschreitet der Bot diesen Schwellenwert, stellt er den Handel bis zum Beginn der folgenden Woche ein. Dieser Parameter ist ideal, um erhebliche Verluste über längere Zeiträume zu vermeiden.

3. Maximaler Gesamtverlust

Dies ist die absolute Verlustgrenze, bei deren Erreichen eine spezielle Wiederherstellungsstrategie ausgelöst wird. Eine solche Strategie kann darin bestehen, die Losgrößen zu reduzieren und vorsichtiger zu handeln, um verlorenes Kapital allmählich zurückzugewinnen. Dieses Konzept trägt zur Kontrolle des Gesamtkontorisikos bei.

4. Maximaler Verlust pro Handel

Definiert den größten Verlust, den ein einzelner Handel verursachen kann. Dieser Wert ist von entscheidender Bedeutung, da er die automatische Berechnung der optimalen Losgröße für jeden Handel auf der Grundlage des Risikoniveaus ermöglicht, das der Nutzer zu akzeptieren bereit ist.

5. Tägliche, wöchentliche und Gesamtgewinne

Dies sind Variablen, die die kumulierten Gewinne über verschiedene Zeiträume hinweg erfassen. Diese Metriken sind nützlich, um die Leistung des automatisierten Roboters zu bewerten und die Strategien entsprechend den erzielten Ergebnissen anzupassen.

Erstellen der Include-Datei und Erläuterung des Plans

In diesem Abschnitt beginnen wir mit der Codierung unserer Include-Datei.

1. Klicken Sie im oberen Bereich Ihrer MetaTrader-Plattform auf die Schaltfläche „IDE“:

2. Klicken Sie in der oberen linken Ecke des MetaEditors auf die Registerkarte Datei und wählen Sie dann Neu. Das folgende Fenster wird angezeigt:

IDE-2

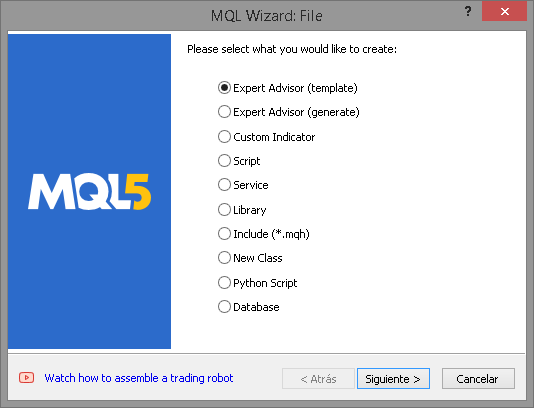
3. Wählen Sie „Include“ und klicken Sie auf Weiter:

IDE-3

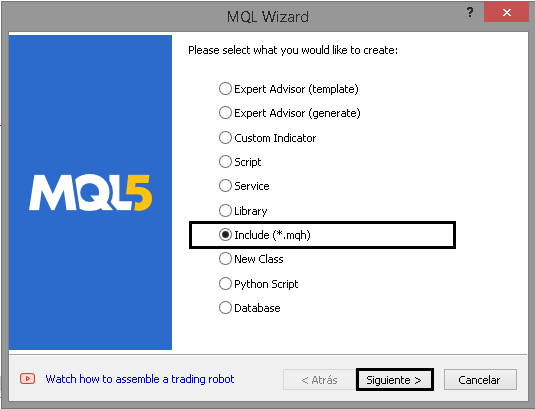
4. Richten Sie das Die Include-Datei ein, indem Sie einen Namen und einen Autor zuweisen:

IDE-4

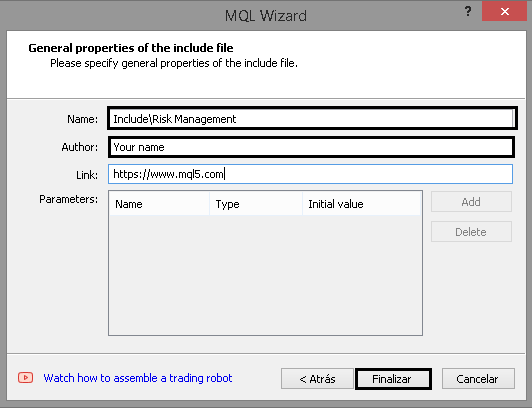
Die Erstellung der Datei ist abgeschlossen. Dies ist erst der Anfang. Lassen Sie uns nun den Plan durchgehen, wie unser Risikomanagementsystem funktionieren wird.

Das nachstehende Diagramm zeigt, wie das Risikomanagement funktioniert:

Plan-1

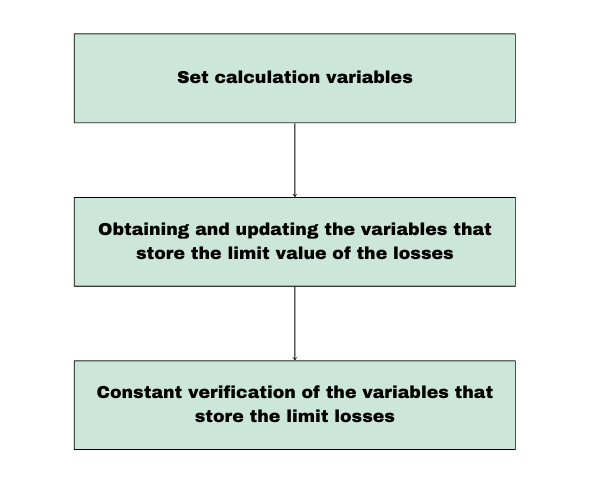
Abschnitt	Beschreibung	Durchführungshäufigkeit
1. Berechnungsvariablen festlegen	In dieser ersten Phase (die nur einmal durchgeführt wird) werden alle notwendigen Variablen für die Verlust- und Gewinnberechnung festgelegt. Zu den Hauptaufgaben gehören: Definition der magischen Zahl, um bestimmte Trades des Expert Advisors (EA) zu identifizieren. Festlegen des Anfangssaldos, besonders wichtig beim Handel auf finanzierten oder Prop-Firm-Konten. Angabe von Risikoprozentsätzen und Wahl, ob Verluste in Geld oder als Prozentsatz des Guthabens/Kapitals berechnet werden sollen. Wenn die prozentuale Methode gewählt wird, muss der Nutzer den Basiswert angeben, der für die Anwendung des Prozentsatzes verwendet wird (z. B. Gesamtsaldo, Kapital, Gesamtgewinn oder freie Marge).	Wird einmal ausgeführt, oder immer dann, wenn der EA konfiguriert ist.
2. Berechnung von Verlusten und Gewinnen	In dieser Phase wird der aktuelle Stand der Verluste und Gewinne des Kontos berechnet. Dazu gehören: Berechnung der kumulierten Gesamtverluste. Aufzeichnung täglicher, wöchentlicher oder handelsbezogener Gewinne. Vergleich der kumulierten Verluste mit den im vorherigen Abschnitt festgelegten Grenzen. Dieser Prozess wird je nach Bedarf der Nutzer regelmäßig durchgeführt.	Wird je nach Konfiguration täglich, bei Eröffnung eines Handelsgeschäfts oder wöchentlich ausgeführt.
3. Verifizierung in Echtzeit	Im laufenden Betrieb prüft der EA kontinuierlich (bei jedem Tick), ob die Stromverluste die festgelegten Grenzen nicht überschritten haben. Wenn eine Verlustvariable ihren Schwellenwert überschreitet, schließt der EA sofort alle offenen Positionen, um weitere Verluste zu verhindern.	Bei jedem Tick (Echtzeitverfahren).

Unter Berücksichtigung aller oben genannten Punkte können wir nun mit der Erstellung der ersten Funktionen beginnen.

Funktionen für die Losgrößenberechnung erstellen

Bevor wir die Klasse selbst entwickeln, müssen wir zunächst die Funktionen erstellen, mit denen wir die geeignete Losgröße berechnen können.

Berechnung der idealen Losgröße

Um die ideale Losgröße zu ermitteln, müssen wir zunächst das Brutto-Los berechnen, das das maximale Volumen darstellt, das unser Konto kaufen oder verkaufen kann. Diese Berechnung basiert auf der erforderlichen Marge (in der Währung des Kontos), um ein Los zu eröffnen. Sobald dieser Wert bekannt ist, teilen wir die freie Marge des Kontos durch die erforderliche Marge, runden das Ergebnis und erhalten so die maximale Losgröße, die für unser Konto zulässig ist.

Voraussetzungen

Bevor wir die Berechnung durchführen, müssen wir die erforderliche Marge pro Losgröße für ein bestimmtes Symbol ermitteln. In diesem Beispiel wird unser Symbol Gold (XAUUSD) sein, obwohl das gleiche Verfahren für jedes andere Finanzinstrument gilt.

Das Hauptziel besteht darin, eine solide Grundlage für die effiziente Berechnung von Losen zu schaffen, die sich dynamisch an den Kontostand und die verfügbare Marge anpassen.

MARGE-1

Wie dargestellt, beträgt die ungefähre Anfangsmarge, die für den Kauf einer Partie Gold erforderlich ist, 1.326 USD. Um die maximal zulässige Losgröße zu berechnen, dividieren wir daher einfach die verfügbare freie Marge des Kontos durch die erforderliche Marge pro Losgröße. Diese Beziehung kann wie folgt ausgedrückt werden:

MARGE-2

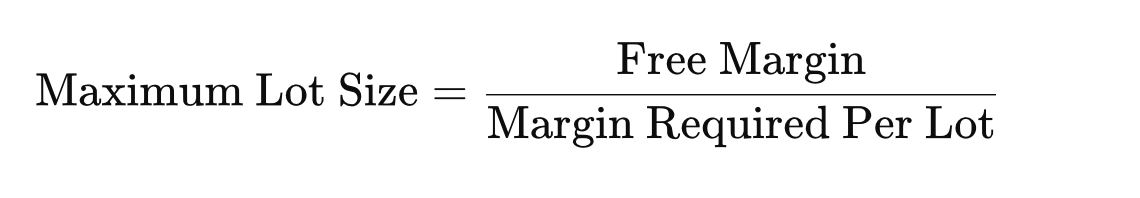
Freie Marge:

Die freie Marge ist das verfügbare Kapital auf Ihrem Konto, das zur Eröffnung neuer Handelsgeschäfte verwendet werden kann. Im MetaTrader wird er wie folgt berechnet:

Berechnen des Preises für jeden Auftragstyp
Da wir nun wissen, wie man die maximale Losgröße berechnet, besteht der nächste Schritt darin, diese Logik in Code umzusetzen. Zuvor müssen wir jedoch den Preis bestimmen, zu dem der Auftrag ausgeführt wird. Zu diesem Zweck erstellen wir eine Funktion namens PriceByOrderType, die den entsprechenden Preis auf der Grundlage des Auftragstyps berechnet und zurückgibt.

double PriceByOrderType(const string symbol, const ENUM_ORDER_TYPE order_type, double DEVIATION = 100, double STOP_LIMIT = 50)

Eingaben:

symbol: Das Handelssymbol (z.B. EURUSD), für das der Auftrag ausgeführt werden soll.
order_type: Die Art des Auftrags, basierend auf der Enumeration ENUM_ORDER_TYPE.
DEVIATION: Die zulässige Preisabweichung in Punkten.
STOP_LIMIT: Der Abstand in Punkten für Aufträge vom Typ STOP_LIMIT.

Schritt 1. Erstelle die erforderlichen Variablen

Zunächst werden die Variablen deklariert, in denen die Ziffern des Symbols, der Punktwert und die aktuellen Geld- und Briefkurse gespeichert werden, und zwar in einer MqlTick-Struktur.

int     digits=0; 
double  point=0; 
MqlTick tick={};

Schritt 2. Variablen Werte zuweisen

Wir verwenden integrierte Funktionen zum Abrufen der Symbolinformationen, wie z. B. Anzahl der Dezimalstellen, Punktwert und aktuelle Preise.

Ermittelt den Wert SYMBOL_POINT:

ResetLastError(); 
if(!SymbolInfoDouble(symbol, SYMBOL_POINT, point)) 
  { 
   Print("SymbolInfoDouble() failed. Error ", GetLastError()); 
   return 0; 
  }

Ermittelt den Wert SYMBOL_DIGITS:

long value=0; 
if(!SymbolInfoInteger(symbol, SYMBOL_DIGITS, value)) 
  { 
   Print("SymbolInfoInteger() failed. Error ", GetLastError()); 
   return 0; 
  } 
digits=(int)value;

Abrufen der aktuellen Symbolpreise:

if(!SymbolInfoTick(symbol, tick)) 
  { 
   Print("SymbolInfoTick() failed. Error ", GetLastError()); 
   return 0; 
  }

Schritt 3. Preisberechnung auf Basis der Auftragsart

Je nach Auftragsart geben wir den entsprechenden Preis mit Hilfe des Switch-Konstrukts zurück:

switch(order_type) 
  { 
   case ORDER_TYPE_BUY              :  return(tick.ask); 
   case ORDER_TYPE_SELL             :  return(tick.bid); 
   case ORDER_TYPE_BUY_LIMIT        :  return(NormalizeDouble(tick.ask - DEVIATION * point, digits)); 
   case ORDER_TYPE_SELL_LIMIT       :  return(NormalizeDouble(tick.bid + DEVIATION * point, digits)); 
   case ORDER_TYPE_BUY_STOP         :  return(NormalizeDouble(tick.ask + DEVIATION * point, digits)); 
   case ORDER_TYPE_SELL_STOP        :  return(NormalizeDouble(tick.bid - DEVIATION * point, digits)); 
   case ORDER_TYPE_BUY_STOP_LIMIT   :  return(NormalizeDouble(tick.ask + DEVIATION * point - STOP_LIMIT * point, digits)); 
   case ORDER_TYPE_SELL_STOP_LIMIT  :  return(NormalizeDouble(tick.bid - DEVIATION * point + STOP_LIMIT * point, digits)); 
   default                          :  return(0); 
  }

Hier ist die endgültige Implementierung der Funktion:

double PriceByOrderType(const string symbol, const ENUM_ORDER_TYPE order_type, double DEVIATION = 100, double STOP_LIMIT = 50) 
  {
   int     digits=0; 
   double  point=0; 
   MqlTick tick={}; 

//--- we get the Point value of the symbol
   ResetLastError(); 
   if(!SymbolInfoDouble(symbol, SYMBOL_POINT, point)) 
     { 
      Print("SymbolInfoDouble() failed. Error ", GetLastError()); 
      return 0; 
     } 

//--- we get the Digits value of the symbol
   long value=0; 
   if(!SymbolInfoInteger(symbol, SYMBOL_DIGITS, value)) 
     { 
      Print("SymbolInfoInteger() failed. Error ", GetLastError()); 
      return 0; 
     } 
   digits=(int)value; 

//--- we get the latest prices of the symbol
   if(!SymbolInfoTick(symbol, tick)) 
     { 
      Print("SymbolInfoTick() failed. Error ", GetLastError()); 
      return 0; 
     } 

//--- Depending on the type of order, we return the price
   switch(order_type) 
     { 
      case ORDER_TYPE_BUY              :  return(tick.ask); 
      case ORDER_TYPE_SELL             :  return(tick.bid); 
      case ORDER_TYPE_BUY_LIMIT        :  return(NormalizeDouble(tick.ask - DEVIATION * point, digits)); 
      case ORDER_TYPE_SELL_LIMIT       :  return(NormalizeDouble(tick.bid + DEVIATION * point, digits)); 
      case ORDER_TYPE_BUY_STOP         :  return(NormalizeDouble(tick.ask + DEVIATION * point, digits)); 
      case ORDER_TYPE_SELL_STOP        :  return(NormalizeDouble(tick.bid - DEVIATION * point, digits)); 
      case ORDER_TYPE_BUY_STOP_LIMIT   :  return(NormalizeDouble(tick.ask + DEVIATION * point - STOP_LIMIT * point, digits)); 
      case ORDER_TYPE_SELL_STOP_LIMIT  :  return(NormalizeDouble(tick.bid - DEVIATION * point + STOP_LIMIT * point, digits)); 
      default                          :  return(0); 
     } 
  }

Darüber hinaus benötigen wir eine Funktion, die die Marktauftragsart nach Auftragsart ermittelt:

ENUM_ORDER_TYPE MarketOrderByOrderType(ENUM_ORDER_TYPE type) 
  { 
   switch(type) 
     { 
      case ORDER_TYPE_BUY  : case ORDER_TYPE_BUY_LIMIT  : case ORDER_TYPE_BUY_STOP  : case ORDER_TYPE_BUY_STOP_LIMIT  : 
        return(ORDER_TYPE_BUY); 
      case ORDER_TYPE_SELL : case ORDER_TYPE_SELL_LIMIT : case ORDER_TYPE_SELL_STOP : case ORDER_TYPE_SELL_STOP_LIMIT : 
        return(ORDER_TYPE_SELL); 
     } 
   return(WRONG_VALUE); 
  }

Berechnung der maximalen Losgröße
GetMaxLot berechnet die maximale Losgröße, die auf der Grundlage der verfügbaren freien Marge und der angegebenen Auftragsart eröffnet werden kann. Es handelt sich um ein wichtiges Instrument des Risikomanagements, das sicherstellt, dass die Handelsgeschäfte den vom Broker festgelegten Margenanforderungen entsprechen.

1. Funktionsparameter erstellen

Die Funktion benötigt die folgenden Parameter:

double GetMaxLote(ENUM_ORDER_TYPE type, double DEVIATION = 100, double STOP_LIMIT = 50)

Type: Definiert die Auftragsart, z. B. ORDER_TYPE_BUY oder ORDER_TYPE_SELL. Dieser Parameter ist wichtig für die korrekte Berechnung von Preis und Gewinnspanne.
DEVIATION: Gibt die zulässige Abweichung in Punkten für schwebende Aufträge an. Der Standardwert ist 100.
STOP_LIMIT: Stellt die Entfernung in Punkten für STOP_LIMIT-Aufträge dar. Der Standardwert ist 50.

2. Initialisieren der erforderlichen Variablen

Vier Variablen vom Typ double und eine der Enumeration ORDER_TYPE werden zur Verwendung in den Berechnungen deklariert:

   //--- Set variables
   double VOLUME = 1.0; //Initial volume size
   ENUM_ORDER_TYPE new_type = MarketOrderByOrderType(type); 
   double price = PriceByOrderType(_Symbol, type, DEVIATION, STOP_LIMIT); // Price for the given order type
   double volume_step = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP); // Volume step for the symbol
   double margin = EMPTY_VALUE; // Required margin, initialized as empty

3. Berechnen der erforderliche Marge für eine Los

Die Funktion OrderCalcMargin wird verwendet, um die Marge zu ermitteln, die zur Eröffnung einer ganzen Losgröße unter den aktuellen Marktbedingungen erforderlich ist. Wenn die Funktion fehlschlägt, wird eine Fehlermeldung ausgegeben und die Funktion gibt 0 zurück:

ResetLastError(); 
if (!OrderCalcMargin(new_type, _Symbol, VOLUME, price, margin)) 
  { 
   Print("OrderCalcMargin() failed. Error ", GetLastError()); 
   return 0; // Exit the function if margin calculation fails
  }

4. Berechnen der maximale Losgröße

Zur Berechnung der maximalen Losgröße wird die oben genannte Formel angewendet. Dazu wird die freie Marge durch den erforderliche Marge geteilt, das Ergebnis entsprechend dem zulässigen Volumenschritt normalisiert und abgerundet, um Fehler zu vermeiden:

double result = MathFloor((AccountInfoDouble(ACCOUNT_MARGIN_FREE) / margin) / volume_step) * volume_step;

5. Rückgabe des Ergebnisses

Schließlich wird die berechnete maximale Losgröße zurückgegeben:

return result; // Return the maximum lot size

Vollständige Funktion:

double GetMaxLote(ENUM_ORDER_TYPE type, double DEVIATION = 100, double STOP_LIMIT = 50) 
  { 
   //--- Set variables
   double VOLUME = 1.0; // Initial volume size
   ENUM_ORDER_TYPE new_type = MarketOrderByOrderType(type); 
   double price = PriceByOrderType(_Symbol, type, DEVIATION, STOP_LIMIT); // Price for the given order type
   double volume_step = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP);    // Volume step for the symbol
   double margin = EMPTY_VALUE; // Required margin, initialized as empty
  
   //--- Get margin for one lot
   ResetLastError(); 
   if (!OrderCalcMargin(new_type, _Symbol, VOLUME, price, margin)) 
     { 
      Print("OrderCalcMargin() failed. Error ", GetLastError()); 
      return 0; // Exit the function if margin calculation fails
     }
   //--- Calculate the maximum lot size
   double result = MathFloor((AccountInfoDouble(ACCOUNT_MARGIN_FREE) / margin) / volume_step) * volume_step; 
   return result; // Return the maximum lot size
  }

Erstellen der Funktionen zur Gewinnberechnung

Nachdem die Funktionen zur Bestimmung der maximalen Losgröße fertiggestellt sind, werden in einem nächsten Schritt Funktionen entwickelt, die den Gewinn von einem bestimmten Datum bis zum aktuellen Zeitpunkt berechnen. Dies ist von entscheidender Bedeutung, da bei der Auswertung jedes Ticks festgestellt werden muss, ob eine maximale Verlustvariable überschritten wurde. Zu diesem Zweck verwenden wir Variablen, die Gewinndaten speichern. Um zum Beispiel zu überprüfen, ob der maximale Tagesverlust überschritten wurde, ist es wichtig, neben dem aktuellen Eigenkapital auch den kumulierten Tagesgewinn zu kennen.

Die Berechnung des aktuellen Gewinns erfolgt über Funktionen, die auf die Auftrags- und Transaktionshistorie zugreifen. So erhalten wir genaue und aktuelle Informationen über Gewinne und Verluste über einen bestimmten Zeitraum.

Detaillierte Funktionsbeschreibung

1. Variableninitialisierung und Fehlerrückstellung

double total_net_profit = 0.0; // Initialize the total net profit
ResetLastError(); // Reset any previous errors

total_net_profit: Initialisiert auf 0,0, was bedeutet, dass noch kein Nettogewinn berechnet wurde.
ResetLastError: Stellt sicher, dass alle vorherigen Fehler im Code gelöscht werden, bevor die Ausführung beginnt.

Überprüfung des Startdatums (start_date):

if((start_date > 0 || start_date != D'1971.01.01 00:00'))

In dieser Zeile wird geprüft, ob das angegebene start_date gültig ist (d. h. kein ungültiges Standarddatum wie 1971.01.01 oder ein Nulldatum). Ist das Datum gültig, fährt der Code mit der Auswahl des Handelsverlaufs fort.

3. Auswahl der Deal-Historie

if(!HistorySelect(start_date, TimeCurrent())) 
{
   Print("Error when selecting orders: ", _LastError); 
   return 0.0; // Exit if unable to select the history
}

HistorySelect: Wählt die Deal-Historie ab dem angegebenen Startdatum bis zum aktuellen Zeitpunkt (TimeCurrent) aus.
Schlägt die Auswahl der Historie fehl, wird eine Fehlermeldung ausgegeben, und die Funktion gibt 0 zurück.

4. Gesamtzahl der Deals abrufen

int total_deals = HistoryDealsTotal(); // Get the total number of deals in history

HistoryDealsTotal: Gibt die Gesamtzahl der Deals in der Handelshistorie zurück und ermöglicht die Iteration durch jeden Deal.

5. Iterieren durch alle Angebote

for(int i = 0; i < total_deals; i++)
{
   ulong deal_ticket = HistoryDealGetTicket(i); // Retrieve the deal ticket

An diesem Punkt beginnt eine for-Schleife, die alle Handelsgeschäfte in der Historie durchläuft.
HistoryDealGetTicket: Ruft das eindeutige Deal-Ticket an der Position i ab, das für den Zugriff auf die Details des Deals erforderlich ist.

6. Herausfiltern der Salden-Buchungen.

if(HistoryDealGetInteger(deal_ticket, DEAL_TYPE) == DEAL_TYPE_BALANCE) continue;

Handelt es sich bei dem Deal-Typ um eine Saldo-Operation (z. B. eine Einzahlung, eine Abhebung oder eine Anpassung und nicht um ein echtes Handelsgeschäft), wird er übersprungen und die Schleife wird mit dem nächsten Datensatz fortgesetzt.

7. Details zum Deal erhalten

ENUM_DEAL_ENTRY deal_entry = (ENUM_DEAL_ENTRY)HistoryDealGetInteger(deal_ticket, DEAL_ENTRY); // Get deal entry type
long deal_close_time_long = HistoryDealGetInteger(deal_ticket, DEAL_TIME);                    // Get deal close time (as long)
datetime deal_close_time = (datetime)deal_close_time_long;                                    // Explicit conversion to datetime
ulong position_id = HistoryDealGetInteger(deal_ticket, DEAL_POSITION_ID);                     // Get the position ID

deal_entry: Legt fest, ob es sich bei dem Handelsgeschäft um einen Zugang oder einen Abgang handelt (um zu bestimmen, ob es sich um ein Eröffnungs- oder ein Abschlussgeschäft handelt).
deal_close_time: Stellt den Zeitpunkt des Handelsgeschäftsabschlusses dar, der Einfachheit halber in ein Datum umgewandelt.
position_id: Die ID der Position, die mit dem Handelsgeschäft verbunden ist, nützlich zur Überprüfung der magischen Zahl.

8. Filtern der Deals nach Datum und Typ

if(deal_close_time >= start_date && (deal_entry == DEAL_ENTRY_OUT || deal_entry == DEAL_ENTRY_IN))

Die Bedingung stellt sicher, dass nur Handelsgeschäfte berücksichtigt werden, deren Abschlusszeitpunkt größer oder gleich dem Startdatum ist, und dass es sich um gültige Ein- oder Ausstiegsgeschäfte handelt.

9. Angebote nach magischer Zahl und Einschlussart filtern

if((HistoryDealGetInteger(deal_ticket, DEAL_MAGIC) == specific_magic || specific_magic == GetMagic(position_id)) 
   || include_all_magic == true)

HistoryDealGetInteger: Ermitteln der magischen Zahl des Deals.
Wenn die magische Zahl des Deals mit der angegebenen specific_magic übereinstimmt, oder wenn die Einbeziehung aller Deals erlaubt ist (include_all_magic == true), wird der Nettogewinn des Handelsgeschäfts berechnet.

10. Berechnen des Nettogewinns des Deals:

double deal_profit = HistoryDealGetDouble(deal_ticket, DEAL_PROFIT);         // Retrieve profit from the deal
double deal_commission = HistoryDealGetDouble(deal_ticket, DEAL_COMMISSION); // Retrieve commission
double deal_swap = HistoryDealGetDouble(deal_ticket, DEAL_SWAP);             // Retrieve swap fees
                  
double deal_net_profit = deal_profit + deal_commission + deal_swap;          // Calculate net profit for the deal
total_net_profit += deal_net_profit;                                         // Add to the total net profit

deal_profit: Ermittelt den Gewinn des Deals.
deal_commission: Ermittelt die für das Deals berechnete Provision.
deal_swap: Ermittelt den Swap (Zins oder Overnight-Gebühr).

Der Nettogewinn des Deals wird dann als Summe dieser drei Werte berechnet und zu total_net_profit addiert.

11. Rückgabe des Gesamtnettogewinns:

return NormalizeDouble(total_net_profit, 2); // Return the total net profit rounded to 2 decimals

Schließlich wird der gesamte Nettogewinn zurückgegeben, der mit NormalizeDouble auf zwei Dezimalstellen gerundet wird, um sicherzustellen, dass der Wert für die weitere Verwendung richtig formatiert ist.

Vollständige Funktion:

double GetNetProfitSince(bool include_all_magic, ulong specific_magic, datetime start_date)
{
   double total_net_profit = 0.0; // Initialize the total net profit
   ResetLastError();              // Reset any previous errors

   // Check if the start date is valid
   if((start_date > 0 || start_date != D'1971.01.01 00:00'))
   {   
      // Select the order history from the given start date to the current time
      if(!HistorySelect(start_date, TimeCurrent())) 
      {
         Print("Error when selecting orders: ", _LastError); 
         return 0.0; // Exit if unable to select the history
      }

      int total_deals = HistoryDealsTotal(); // Get the total number of deals in history
  
      // Iterate through all deals
      for(int i = 0; i < total_deals; i++)
      {
         ulong deal_ticket = HistoryDealGetTicket(i); // Retrieve the deal ticket

         // Skip balance-type deals
         if(HistoryDealGetInteger(deal_ticket, DEAL_TYPE) == DEAL_TYPE_BALANCE) continue;            

         ENUM_DEAL_ENTRY deal_entry = (ENUM_DEAL_ENTRY)HistoryDealGetInteger(deal_ticket, DEAL_ENTRY); // Get deal entry type
         long deal_close_time_long = HistoryDealGetInteger(deal_ticket, DEAL_TIME);                    // Get deal close time (as long)
         datetime deal_close_time = (datetime)deal_close_time_long;                                    // Explicit conversion to datetime
         ulong position_id = HistoryDealGetInteger(deal_ticket, DEAL_POSITION_ID);                     // Get the position ID

         // Check if the deal is within the specified date range and is a valid entry/exit deal
         if(deal_close_time >= start_date && (deal_entry == DEAL_ENTRY_OUT || deal_entry == DEAL_ENTRY_IN))
         {             
            // Check if the deal matches the specified magic number or if all deals are to be included
            if((HistoryDealGetInteger(deal_ticket, DEAL_MAGIC) == specific_magic || specific_magic == GetMagic(position_id)) 
               || include_all_magic == true)
            {
               double deal_profit = HistoryDealGetDouble(deal_ticket, DEAL_PROFIT);         // Retrieve profit from the deal
               double deal_commission = HistoryDealGetDouble(deal_ticket, DEAL_COMMISSION); // Retrieve commission
               double deal_swap = HistoryDealGetDouble(deal_ticket, DEAL_SWAP);             // Retrieve swap fees
               
               double deal_net_profit = deal_profit + deal_commission + deal_swap; // Calculate net profit for the deal
               total_net_profit += deal_net_profit; // Add to the total net profit
            }
         }
      }
   }
     
   return NormalizeDouble(total_net_profit, 2); // Return the total net profit rounded to 2 decimals
}

Zusätzliche Funktion zur Ermittlung der magischen Zahl der Bestellung:

ulong GetMagic(const ulong ticket)
{
HistoryOrderSelect(ticket);
return HistoryOrderGetInteger(ticket,ORDER_MAGIC); 
}

Praktischer Test mit einem einfachen Skript und einer Include-Datei

Wir werden nun eine Funktion erstellen, die eine absolute Entfernung in Punkteinheiten für das aktuelle Symbol umwandelt. Diese Umrechnung ist für den Handel von grundlegender Bedeutung, da Punkte das Standardmaß für die Berechnung von Kursniveaus, Stop-Loss und der Ziele sind.

Mathematische Formel
Die Formel zur Berechnung der Entfernung in Punkten ist einfach:

EXTRA-1

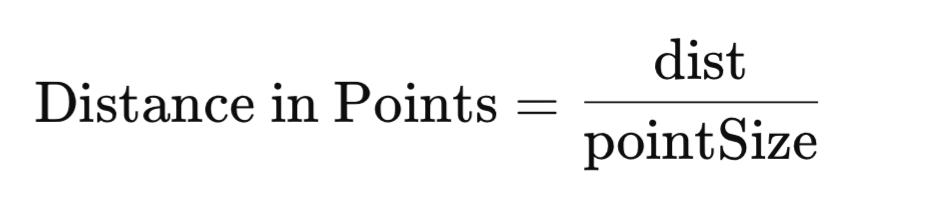
wobei:

dist ist die absolute Entfernung, die umgerechnet werden soll.
pointSize ist die Größe eines Punktes für das Finanzinstrument (z. B. 0,0001 für EUR/USD).

Darstellung der Formel im Code
Um diese Formel in MQL5 zu implementieren, gehen wir folgendermaßen vor:

Ermitteln der Punktgröße (pointSize).

Wir verwenden die Funktion SymbolInfoDouble, um die Punktgröße des aktuellen Symbols zu ermitteln. Der Parameter _Symbol steht für das aktuell ausgeführte Symbol, und SYMBOL_POINT liefert dessen Punktgröße.

double pointSize = SymbolInfoDouble(_Symbol, SYMBOL_POINT);

Wir teilen den Abstand durch die Punktgröße und wandeln ihn in eine ganze Zahl um

Wir teilen den Abstand (dist) durch die Punktgröße (pointSize), um die Anzahl der Punkte zu berechnen. Anschließend wird das Ergebnis mit int in eine ganze Zahl umgewandelt, da Punktwerte immer ganze Zahlen sind.

return (int)(dist / pointSize);

Vollständige Funktion
Nachfolgend ist die Funktion in ihrer endgültigen Form dargestellt:

int DistanceToPoint(double dist)
{
  double pointSize = SymbolInfoDouble(_Symbol, SYMBOL_POINT); // Get the point size for the current symbol
  return (int)(dist / pointSize); // Calculate and return the distance in points 
}

Um die in diesem Artikel behandelten Konzepte in die Praxis umzusetzen, werden wir zwei Skripte erstellen.

Als Nächstes werden wir zwei wichtige Funktionen entwickeln: eine zur Berechnung der idealen Losgröße auf der Grundlage des Risikos pro Handel und eine weitere zur Berechnung des idealen Stop Loss in Punkten für das Symbol auf der Grundlage der Losgröße und des Risikos pro Handel.

Funktion: Berechnung der idealen Losgröße, basierend auf dem Risiko pro Handelsgeschäft
Die Funktion GetIdealLot berechnet die ideale Losgröße (nlot) unter Berücksichtigung des maximal zulässigen Verlusts pro Handel und des StopLoss-Abstands (StopLoss). Auf diese Weise wird sichergestellt, dass alle Handelsgeschäfte das vom Nutzer festgelegte Risikolimit einhalten.

void GetIdealLot(
    double& nlot,                     // Calculated ideal lot
    double glot,                      // Gross Lot (max lot accorsing to the balance)
    double max_risk_per_operation,    // Maximum allowed risk per trade (in account currency)
    double& new_risk_per_operation,   // Calculated risk for the adjusted lot (in account currency)
    long StopLoss                     // Stop Loss distance (in points)
)

Parameter-Beschreibung

nlot: Die ideale Losgröße wird durch die Funktion angepasst.
glot: Die Bruttolosgröße (maximale Losgröße), die mit dem gesamten verfügbaren Kontoguthaben eröffnet werden kann.
max_risk_per_operation: Das maximal zulässige Risiko pro Handel, ausgedrückt in der Kontowährung.
new_risk_per_operation: Das tatsächliche Risiko des angepassten Handelsgeschäfts unter Berücksichtigung des berechneten Losgröße (nlot). Dieser Wert gibt an, wie viel wir verlieren würden, wenn der Kurs den Stop-Loss erreicht.
StopLoss: Der Stop-Loss-Abstand in Punkten.

1. Erste Verifizierung

Die Funktion prüft zunächst, ob der StopLoss-Wert größer als Null ist, da ein ungültiger StopLoss die Risikoberechnung unmöglich machen würde.

if(StopLoss <= 0)
{
    Print("[ERROR SL] Stop Loss distance is less than or equal to zero, now correct the stoploss distance: ", StopLoss);
    nlot = 0.0; 
    return;   
}

2. Variablen initialisieren

Die folgenden Variablen werden für spätere Berechnungen initialisiert:

spread: Der aktuelle Spread des Symbols.
tick_value: Der Wert pro Tick, der angibt, wie viel eine minimale Kursbewegung in Kontowährung ausmacht.
Schritt: Die minimal zulässige Erhöhung der Losgröße.

new_risk_per_operation = 0;  // Initialize the new risk
long spread = (long)SymbolInfoInteger(_Symbol, SYMBOL_SPREAD);
double tick_value = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE);
double step = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP);

3. Aktuelle Risikoberechnung (rpo)

Das aktuelle Risiko pro Operation (rpo) wird nach der folgenden Formel berechnet:

Der Code:

double rpo = (glot * (spread + 1 + (StopLoss * tick_value)));

4. Maximales Risiko prüfen

Die Funktion wertet aus, ob das aktuelle Risiko (rpo) das maximal akzeptable Risiko pro Deal (max_risk_per_operation) überschreitet:

Fall 1. Das Risiko übersteigt den Höchstwert

Die Losgröße wird proportional an das maximal akzeptable Risiko angepasst.
Die angepasste Partie wird auf die nächste zulässige Schrittweite abgerundet.
Es wird ein neues Risiko berechnet, das diesem angepassten Los entspricht.

if(rpo > max_risk_per_operation)
{
    double new_lot = (max_risk_per_operation / rpo) * glot;
    new_lot = MathFloor(new_lot / step) * step;
    new_risk_per_operation = new_lot * (spread + 1 + (StopLoss * tick_value));
    nlot = new_lot; 
}

Fall 2. Risiko innerhalb akzeptabler Grenzen

Überschreitet das aktuelle Risiko nicht den festgelegten Grenzwert, werden die ursprünglichen Werte beibehalten:

else
{
    new_risk_per_operation = rpo; // Current risk
    nlot = glot;                  // Gross lot
}

Schließlich erstellen wir die letzte Funktion, um den Stop-Loss auf der Grundlage des maximal zulässigen Verlusts pro Handel und der vom Nutzer angegebenen Losgröße zu berechnen:

long GetSL(const ENUM_ORDER_TYPE type , double risk_per_operation , double lot) 
{
 long spread = (long)SymbolInfoInteger(_Symbol, SYMBOL_SPREAD);
 double tick_value = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE);
 double result = ((risk_per_operation/lot)-spread-1)/tick_value;
 
return long(MathRound(result));
}

Parameter-Beschreibung

type: Auftragsart (Kauf oder Verkauf), obwohl sie in dieser Funktion nicht direkt verwendet wird.
risk_per_operation: maximal zulässiger Verlust pro Handel in Kontowährung.
lot: nutzerdefinierte Losgröße.

Schritt-für-Schritt-Logik

1. Grundlegende Formel

Die Grundformel für die Berechnung des Risikos pro Operation (rpo) lautet wie folgt:

In dieser Funktion werden wir den Stop-Loss isolieren, um seinen Wert auf der Grundlage von rpo, Losgröße und anderen relevanten Faktoren zu berechnen.

2. Isolierung des Stop Loss

Wir teilen beide Seiten der Gleichung durch die Losgröße:

RISIKO-2

Ziehe die Spanne und 1 von beiden Seiten ab:

RISIKO-3

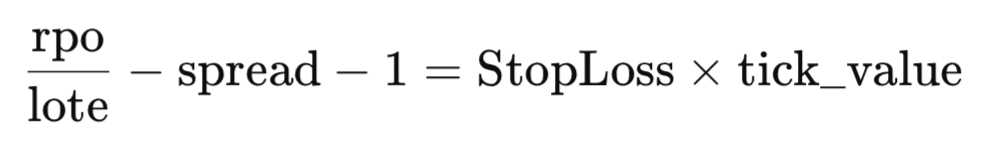
Dividiere durch tick_value, um den StopLoss zu isolieren:

RISIKO-4

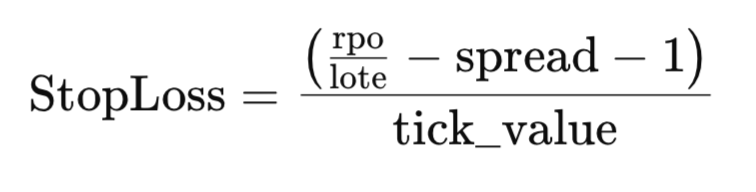
Umsetzung in Code
Die obige Formel wird direkt in die Berechnung im Funktionskörper übersetzt:

double result = ((risk_per_operation / lot) - spread - 1) / tick_value;

risk_per_operation / lot: Berechnet das Risiko pro Los.
- spread - 1: Subtrahiert den Spread und eine eventuelle zusätzliche Marge.
/ tick_value: Konvertiert das Ergebnis in Punkte, indem es durch den Tick-Wert geteilt wird.

Das Ergebnis wird dann gerundet und in long umgewandelt, damit es dem gewünschten Format entspricht.

return long(MathRound(result));

Schließlich werden wir zwei Skripte erstellen, um die ideale Losgröße und den idealen Stop-Loss (SL) entsprechend dem pro Handelsgeschäft definierten Risiko zu berechnen. Beide Skripte verwenden eine einfache, aber effiziente Logik zur Automatisierung dieser Berechnungen, die auf dem Kontostand und nutzerdefinierten Parametern basieren.

Erstes Drehbuch: Berechnung der idealen Losgröße
Dieses Skript berechnet die ideale Losgröße auf der Grundlage eines Risikoprozentsatzes pro Handel, eines in Punkten definierten Stop-Loss und des Auftragstyps.

Skript-Eigenschaften
- #property strict: Das stellt sicher, dass der Code die strengen Kompilierungsregeln einhält.
- #property script_show_inputs: Das ermöglicht dem Nutzer die Eingabe von Parametern über die grafische Oberfläche.
Input Parameters

input double percentage_risk_per_operation = 1.0; //Risk per operation in %
input long   sl = 600; //Stops Loss in points
input ENUM_ORDER_TYPE Order_Type = ORDER_TYPE_BUY; //Order Type

Berechnung des Risikos pro Handelsgeschäft

Die Formel berechnet den Betrag in der Kontowährung, den der Nutzer bereit ist, pro Handel zu riskieren, basierend auf dem festgelegten Prozentsatz:

double risk_per_operation = ((percentage_risk_per_operation/100.0) * AccountInfoDouble(ACCOUNT_BALANCE));

Aufrufen der Funktion zur Berechnung des idealen Losgröße

GetIdealLot(new_lot, GetMaxLote(Order_Type), risk_per_operation, new_risk_per_operation, sl);

Nutzer-Nachrichten: Details zu den berechneten Werten, wie z. B. die ideale Losgröße und das angepasste Risiko, werden sowohl auf der Konsole als auch auf dem Chart ausgedruckt, um eine einfache Referenz zu ermöglichen.

//+------------------------------------------------------------------+
//|                             Get Lot By Risk Per Trade and SL.mq5 |
//|                                                        Your name |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+ 
#property copyright "Your name"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property strict
#property script_show_inputs

input double percentage_risk_per_operation = 1.0; // Risk per operation in %
input long   sl = 600; // Stop Loss in points
input ENUM_ORDER_TYPE Order_Type = ORDER_TYPE_BUY; // Order Type

#include <Risk Management.mqh>

//+------------------------------------------------------------------+
//| Main script function                                             |
//+------------------------------------------------------------------+
void OnStart()
  {
   // Calculate the maximum allowable risk per operation in account currency
   double risk_per_operation = ((percentage_risk_per_operation / 100.0) * AccountInfoDouble(ACCOUNT_BALANCE));
   
   // Print input and calculated risk details
   Print("Risk Per operation: ", risk_per_operation);
   Print("SL in points: ", sl);
   Print("Order type: ", EnumToString(Order_Type));
   
   double new_lot;
   double new_risk_per_operation;
   
   // Calculate the ideal lot size
   GetIdealLot(new_lot, GetMaxLote(Order_Type), risk_per_operation, new_risk_per_operation, sl);
   
   // Check if the lot size is valid
   if (new_lot <= 0)
     {
      Print("The stop loss is too large or the risk per operation is low. Increase the risk or decrease the stop loss.");
     }
   else
     {
      // Display calculated values
      Print("Ideal Lot: ", new_lot);
      Print("Maximum loss with SL: ", sl, " | Lot: ", new_lot, " is: ", new_risk_per_operation);
      Comment("Ideal Lot: ", new_lot);
     }
   
   Sleep(1000);
   Comment(" ");
  }
//+------------------------------------------------------------------+

Zweites Skript: Berechnung des idealen SL
Dieses Skript berechnet den Stop-Loss in Punkten auf der Grundlage der vom Nutzer angegebenen Losgröße und des maximalen Risikos pro Handel.

input double percentage_risk_per_operation = 1.0; //Risk per operation in %
input double Lot = 0.01; //lot
input ENUM_ORDER_TYPE Order_Type = ORDER_TYPE_BUY; //Order Type

Berechnung der idealen sl: Die Funktion get sl wird verwendet, um den Stop Loss in Punkten zu bestimmen:

long new_sl = GetSL(Order_Type, risk_per_operation, Lot);

Ergebnisse prüfen: Wenn der berechnete Wert von sl ungültig ist (new_sl ist kleiner oder gleich 0), wird der Nutzer entsprechend benachrichtigt.

//+------------------------------------------------------------------+
//|                         Get Sl by risk per operation and lot.mq5 |
//|                                                        Your name |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Your name"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property strict
#property script_show_inputs

input double percentage_risk_per_operation = 1.0; // Risk per operation in %
input double Lot = 0.01; // Lot size
input ENUM_ORDER_TYPE Order_Type = ORDER_TYPE_BUY; // Order Type

#include <Risk Management.mqh>

//+------------------------------------------------------------------+
//| Main script function                                             |
//+------------------------------------------------------------------+
void OnStart()
  {
   // Calculate the maximum allowable risk per operation in account currency
   double risk_per_operation = ((percentage_risk_per_operation / 100.0) * AccountInfoDouble(ACCOUNT_BALANCE));
   
   // Print input and calculated risk details
   Print("Risk Per operation: ", risk_per_operation);
   Print("Lot size: ", Lot);
   Print("Order type: ", EnumToString(Order_Type));
   
   // Calculate the ideal stop loss
   long new_sl = GetSL(Order_Type, risk_per_operation, Lot);
   
   // Check if the SL is valid
   if (new_sl <= 0)
     {
      Print("The lot size is too high or the risk per operation is too low. Increase the risk or decrease the lot size.");
     }
   else
     {
      // Display calculated values
      Print("For lot: ", Lot, ", and risk: ", risk_per_operation, ", the ideal SL is: ", new_sl);
      Comment("Ideal SL: ", new_sl);
     }
   
   Sleep(1000);
   Comment(" ");
  }
//+------------------------------------------------------------------+

Um das Skript nun in die Praxis umzusetzen, verwenden wir es, um die ideale Losgröße auf der Grundlage des vorgegebenen Risikos pro Handel zu ermitteln. Wir werden es am Symbol XAUUSD testen, das für Gold steht.

SCRIPT-RISK-1

Mit Parametern wie einem Stop-Loss von 200 Pips und einem Risiko pro Handel von 1,0 % des Kontoguthabens und der Angabe der Auftragsart ORDER_TYPE_BUY sieht das Ergebnis wie folgt aus:

SCRIPT-RISK-2

Das auf der Registerkarte „Experten“ angezeigte Ergebnis entspricht einer Losgröße von 0,01 mit einem Stop-Loss von 200 Pips und einem Risiko pro Handel von 3,81, was 1 % des Kontostands entspricht.

Schlussfolgerung

Wir haben den ersten Teil dieser Serie abgeschlossen und uns auf die Entwicklung der Kernfunktionen konzentriert, die im Risikomanagementkurs verwendet werden. Diese Funktionen sind für die Gewinnermittlung und die Durchführung weiterer Berechnungen unerlässlich. Im nächsten Teil werden wir untersuchen, wie wir alles, was wir gelernt haben, mit Hilfe der MQL5-Steuerungsbibliotheken in eine grafische Oberfläche integrieren können.

Übersetzt aus dem Spanischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/es/articles/16820

Beigefügte Dateien |

ZIP herunterladen

Risk_Management.mqh (8.27 KB)

Get_Sl_by_risk_per_operation_and_lot.mq5 (3.84 KB)

Get_Lot_By_Risk_Per_Trade_and_SL.mq5 (2.07 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Neuronale Netze im Handel: Multi-Task-Lernen auf der Grundlage des ResNeXt-Modells

Ein auf ResNeXt basierendes Multi-Task-Learning-System optimiert die Analyse von Finanzdaten unter Berücksichtigung ihrer hohen Dimensionalität, Nichtlinearität und Zeitabhängigkeit. Die Verwendung von Gruppenfaltung und spezialisierten Köpfen ermöglicht es dem Modell, effektiv Schlüsselmerkmale aus den Eingabedaten zu extrahieren.

Neuronale Netze im Handel: Speichererweitertes kontextbezogenes Lernen (MacroHFT) für Kryptowährungsmärkte

Ich lade Sie ein, das MacroHFT-Framework zu erkunden, das kontextbewusstes Verstärkungslernen und eine Speicherverwendung anwendet, um Hochfrequenzhandelsentscheidungen für Kryptowährungen mithilfe von makroökonomischen Daten und adaptiven Agenten zu verbessern.

Risikomanagement (Teil 2): Implementierung der Losberechnung in einer grafischen Schnittstelle

In diesem Artikel werden wir uns ansehen, wie man die im vorherigen Artikel vorgestellten Konzepte mit Hilfe der leistungsstarken grafischen MQL5-Bibliotheken der Steuerelemente verbessern und effektiver anwenden kann. Wir werden Schritt für Schritt durch den Prozess der Erstellung einer voll funktionsfähigen GUI gehen. Ich werde die Ideen dahinter sowie den Zweck und die Funktionsweise der einzelnen Methoden erläutern. Darüber hinaus werden wir am Ende des Artikels das von uns erstellte Panel testen, um sicherzustellen, dass es korrekt funktioniert und die angegebenen Ziele erfüllt.

Dialektische Suche (DA)

Der Artikel stellt den dialektischen Algorithmus (DA) vor, eine neue globale Optimierungsmethode, die vom philosophischen Konzept der Dialektik inspiriert ist. Der Algorithmus macht sich eine einzigartige Aufteilung der Bevölkerung in spekulative und praktische Denker (thinker) zunutze. Tests zeigen eine beeindruckende Leistung von bis zu 98 % bei niedrigdimensionalen Problemen und eine Gesamteffizienz von 57,95 %. Der Artikel erläutert diese Metriken und präsentiert eine detaillierte Beschreibung des Algorithmus sowie die Ergebnisse von Experimenten mit verschiedenen Arten von Funktionen.