
Funktionen zur Aktivierung von Neuronen während des Trainings: Der Schlüssel zur schnellen Konvergenz?
Einführung
Im vorigen Artikel haben wir die Eigenschaften eines einfachen neuronalen MLP-Netzes als Approximator (Verstärkungslernen) im Handel untersucht. In diesem Fall wurde den Eigenschaften der Aktivierungsfunktionen keine besondere Aufmerksamkeit geschenkt, sondern das beliebte hyperbolische Tangens-Sigmoid verwendet. In einem der Artikel haben wir auch die Möglichkeiten des bekannten und weit verbreiteten ADAM-Algorithmus erörtert. Ich habe sie in eine unabhängige Populationsmethode der globalen ADAMm-Optimierung umgewandelt.
In diesem Artikel werden wir uns mit den Fähigkeiten eines neuronalen Netzes als Dateninterpolator (überwachtes Lernen) befassen, wobei wir uns auf die Eigenschaften der Aktivierungsfunktionen der Neuronen konzentrieren. Wir werden den in das neuronale Netz integrierten ADAM-Optimierungsalgorithmus verwenden (wie es bei der Anwendung neuronaler Netze üblich ist) und den Einfluss der Aktivierungsfunktion und ihrer Ableitung auf die Konvergenzrate des Optimierungsalgorithmus untersuchen.
Stellen Sie sich einen Fluss mit vielen Nebenflüssen vor. Im Normalzustand fließt das Wasser frei und bildet ein komplexes Muster aus Strömungen und Strudeln. Aber was passiert, wenn wir anfangen, ein System von Schleusen und Dämmen zu bauen? Wir werden in der Lage sein, den Wasserfluss zu kontrollieren, ihn in die richtige Richtung zu lenken und die Stärke der Strömung zu regulieren. Die Aktivierungsfunktion in neuronalen Netzen spielt eine ähnliche Rolle: Sie entscheidet, welche Signale durchgelassen werden und welche verzögert oder abgeschwächt werden sollen. Ohne sie wäre ein neuronales Netz nur eine Reihe von linearen Transformationen.
Die Aktivierungsfunktion verleiht dem neuronalen Netz eine Dynamik, die es ihm ermöglicht, subtile Nuancen in den Daten zu erfassen. Bei einer Gesichtserkennungsaufgabe zum Beispiel hilft eine Aktivierungsfunktion dem Netz, winzige Details wie den Bogen einer Augenbraue oder die Form eines Kinns zu erkennen. Die richtige Wahl der Aktivierungsfunktion wirkt sich darauf aus, wie ein neuronales Netz bei verschiedenen Aufgaben abschneidet. Einige Funktionen eignen sich besser für die Anfangsphase der Ausbildung und liefern klare und verständliche Signale. Andere Funktionen ermöglichen es dem Netz, in fortgeschrittenen Stadien subtilere Muster zu erkennen, während andere die unnötigen aussortieren und nur die wichtigsten übrig lassen.
Wenn wir die Eigenschaften von Aktivierungsfunktionen nicht kennen, können wir auf Probleme stoßen. Ein neuronales Netz kann beginnen, bei einfachen Aufgaben zu „stolpern“ oder wichtige Details zu „übersehen“. Der Hauptzweck von Aktivierungsfunktionen besteht darin, Nichtlinearität in das neuronale Netz einzuführen und die Ausgangswerte zu normalisieren.
Ziel dieses Artikels ist es, die mit der Verwendung verschiedener Aktivierungsfunktionen verbundenen Probleme und ihre Auswirkungen auf die Genauigkeit eines neuronalen Netzes beim Durchlaufen von Beispielpunkten (Interpolation) bei gleichzeitiger Minimierung des Fehlers zu ermitteln. Wir werden auch herausfinden, ob Aktivierungsfunktionen tatsächlich die Konvergenzrate beeinflussen oder ob dies eine Eigenschaft des verwendeten Optimierungsalgorithmus ist. Als Referenzalgorithmus verwenden wir eine modifizierte Population ADAMm, die Elemente der Stochastik nutzt, und führen Tests mit dem in MLP integrierten ADAM durch (klassische Verwendung). Letztere dürfte intuitiv im Vorteil sein, da sie dank der Ableitung der Aktivierungsfunktion direkten Zugriff auf den Gradienten der Fitnessfunktionsfläche hat. Gleichzeitig hat der stochastische ADAMm der Population keinen Zugang zur Ableitung und hat keine Ahnung von der Oberfläche des Optimierungsproblems. Mal sehen, was dabei herauskommt, und einige Schlussfolgerungen ziehen.
Der Artikel hat explorativen Charakter und die Schilderung folgt dem Ablauf eines Experiments.
Implementierung eines neuronalen MLP-Netzes mit eingebettetem ADAM
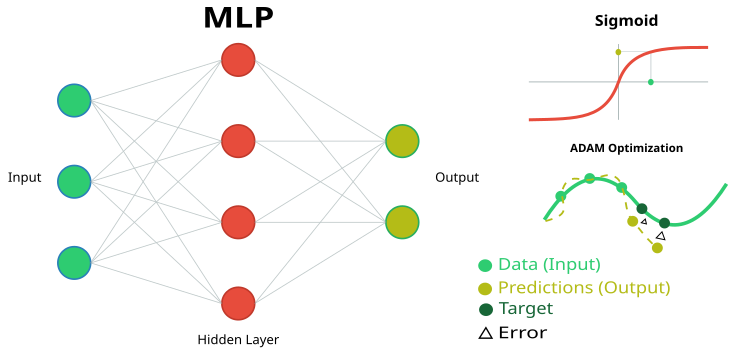
Abbildung 1. Schematische Darstellung des neuronalen MLP-Netzes und seines Trainings
Für die Durchführung der aktuellen Studie benötigen wir einen einfachen und transparenten MLP-Code für neuronale Netze, ohne spezielle Matrixberechnungen, die in der Sprache MQL5 enthalten sind. Auf diese Weise können wir klar verstehen, was genau in der Logik des neuronalen Netzes vor sich geht und wovon bestimmte Ergebnisse abhängen.
Wir werden ein mehrschichtiges Perzeptron (MLP) mit einem integrierten ADAM-Optimierungsalgorithmus (Adaptive Moment Estimation) implementieren. Eine Klasse und eine Struktur stellen einen Teil der Implementierung eines neuronalen Netzes dar, in dem die Hauptkomponenten definiert sind: Neuronen, Neuronenschichten und Gewichte.
1. Die Klasse C_Neuro stellt ein Neuron dar, das die Grundeinheit eines neuronalen Netzes ist.
- C_Neuron() ist ein Konstruktor, der die Werte der Eigenschaften „m“ und „v“ auf Null initialisiert. Diese Werte werden für den Optimierungsalgorithmus verwendet.
- out – der Ausgangswert des Neurons nach Anwendung der Aktivierungsfunktion.
- delta – das Fehlerdelta, das zur Berechnung des Gradienten beim Training verwendet wird.
- bias – ein zu den Neuroneneingängen hinzugefügter Bias-Wert.
- m und v werden verwendet, um die ersten und zweiten Momente für den Bias zu speichern, die von der ADAM-Optimierungsmethode verwendet werden.
2. Die Struktur S_NeuronLayer stellt eine Schicht von Neuronen dar. C_Neuron n[] ist ein Array von Neuronen in einer neuronalen Netzschicht.
Um die Gewichte zwischen den Neuronen zu speichern, verwenden wir einen objektorientierten Ansatz anstelle von einfachen zweidimensionalen Arrays. Sie basiert auf der Klasse C_Weight, die nicht nur das Verbindungsgewicht selbst speichert, sondern auch die Optimierungsparameter – das erste und zweite Moment, die im ADAM-Algorithmus verwendet werden. Die Datenstruktur ist hierarchisch aufgebaut: S_WeightsLayer enthält ein Array von S_WeightsLayerR-Strukturen, die ihrerseits Arrays von C_Weight-Objekten enthalten. Dies macht es einfach, jedes Gewicht im Netz durch eine klare Indexkette anzusprechen.
Um zum Beispiel das Gewicht der Verbindung zwischen dem ersten Neuron der Schicht 0 und dem zweiten Neuron der nächsten Schicht zu bezeichnen, verwenden wir die Notation: wL [0].nOnL [1].nOnR [2].w. Dabei bezeichnet der erste Index ein Paar benachbarter Schichten, der zweite ein Neuron in der linken Schicht und der dritte ein Neuron in der rechten Schicht.
//—————————————————————————————————————————————————————————————————————————————— // Neuron class class C_Neuron { public: C_Neuron () { m = 0.0; v = 0.0; } double out; // Neuron output after the activation function double delta; // Error delta double bias; // Bias double m; // First moment of displacement double v; // Second moment of displacement }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Structure of the neuron layer struct S_NeuronLayer { C_Neuron n []; // neurons in the layer }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Weight class class C_Weight { public: C_Weight () { w = 0.0; m = 0.0; v = 0.0; } double w; // Weight double m; // First moment double v; // Second moment }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— //Weight structure for neurons on the right struct S_WeightsLayerR { C_Weight nOnR []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— //Weight structure for neurons on the left struct S_WeightsLayer { S_WeightsLayerR nOnL []; }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_MLPa Multilayer Perceptron (MLP) implementiert die grundlegenden Funktionen eines neuronalen Netzes, einschließlich des Lernens durch Vorwärt- und Rückwärtsdurchlauf unter Verwendung des ADAM-Optimierungsalgorithmus. Schauen wir uns an, was es alles kann:
Struktur des Netzes:- Das Netz besteht aus aufeinanderfolgenden Schichten: Eingabe -> versteckte Schichten -> Ausgabeschicht.
- Jedes Neuron in einer Schicht ist mit allen Neuronen in der nächsten Schicht verbunden (vollständig verbundenes Netz).
- Init ist eine Methode zur Erstellung eines Netzes mit einer bestimmten Konfiguration.
- ImportWeights und ExportWeights – Laden und Speichern von Netzgewichten.
- ForwProp – Vorwärtsdurchlauf: Ermittlung der Reaktion des Netzes auf die Eingabedaten.
- BackProp – Netzwerk-Trainingsmethode, die auf den Rückwärtsdurchlauf von Fehlern basiert.
- alpha (0,001) – wie schnell das Netz lernt.
- beta1 (0,9) und beta2 (0,999) – Parameter, die dem Netz helfen, konsistent zu lernen.
- epsilon (1e-8) – eine kleine Zahl zum Schutz vor Division durch Null.
- BackProp speichert Informationen über die Größe der einzelnen Schichten (layersSize).
- Sie enthält alle Neuronen (nL) und die Gewichte zwischen ihnen (wL),
- sowie die Anzahl der Gewichte (wC) und der Schichten (nLC) im Auge behalten.
- actFunc verwendet die ausgewählte Aktivierungsfunktion.
Im Wesentlichen ist diese Klasse das „Gehirn“ eines neuronalen Netzes, das Eingabedaten annehmen, sie durch ein System von Neuronen und Gewichten verarbeiten, ein Ergebnis produzieren und aus seinen Fehlern lernen kann, wodurch die Genauigkeit seiner Vorhersagen schrittweise verbessert wird.
//+-----------------------------------------------------------------------------------------+ //| Multilayer Perceptron (MLP) class | //| Implements forward pass through a fully connected neural network and training using the | //| backpropagation of error by ADAM optimization algorithm | //| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout | //+-----------------------------------------------------------------------------------------+ class C_MLPa { public: //-------------------------------------------------------------------- ~C_MLPa () { delete actFunc; } C_MLPa () { alpha = 0.001; // Training speed beta1 = 0.9; // Decay ratio for the first moment beta2 = 0.999; // Decay ratio for the second moment epsilon = 1e-8; // Small constant for numerical stability } // Network initialization with the given configuration, Returns the total number of weights in the network, or 0 in case of an error int Init (int &layerConfig [], int actFuncType, int seed); bool ImportWeights (double &weights []); // Import weights bool ExportWeights (double &weights []); // Export weights // Forward pass through the network void ForwProp (double &inLayer [], // input values double &outLayer []); // output layer values // Error backpropagation with ADAM optimization algorithm void BackProp (double &errors []); // Get the total number of weights in the network int GetWcount () { return wC; } // ADAM optimization parameters double alpha; // Training speed double beta1; // Decay ratio for the first moment double beta2; // Decay ratio for the second moment double epsilon; // Small constant for numerical stability int layersSize []; // Size of each layer (number of neurons) S_NeuronLayer nL []; // Layers of neurons, example of access: nLayers [].n [].a S_WeightsLayer wL []; // Layers of weights between layers of neurons, example of access: wLayers [].nOnLeft [].nOnRight [].w private: //------------------------------------------------------------------- int wC; // Total number of weights in the network (including biases) int nLC; // Total number of neuron layers (including input and output ones) int wLC; // Total number of weight layers (between neuron layers) int t; // Iteration counter C_Base_ActFunc *actFunc; // Activation functions and their derivatives }; //——————————————————————————————————————————————————————————————————————————————
Die Init-Methode initialisiert die Struktur des mehrschichtigen Perzeptrons, indem sie die Anzahl der Neuronen in jeder Schicht festlegt, die Aktivierungsfunktion auswählt und Anfangsgewichte für die Neuronen erzeugt. Sie prüft die Gültigkeit der Netzkonfiguration und gibt die Gesamtzahl der erforderlichen Gewichte oder 0 im Falle eines Fehlers zurück.
Parameter:
- layerConfig[] – Array mit der Anzahl der Neuronen in jeder Netzschicht.
- actFuncType – Typ der Aktivierungsfunktion, die im neuronalen Netz verwendet werden soll (z. B. sigmoid, usw.).
- seed – ein Seed, der eine Zahl für den Zufallszahlengenerator initialisiert, was reproduzierbare Ergebnisse bei der Initialisierung von Gewichten ermöglicht.
Betriebslogik:
- Die Methode bestimmt die Anzahl der Schichten auf der Grundlage des übergebenen layerConfig-Arrays.
- Es wird sichergestellt, dass die Anzahl der Schichten mindestens 2 beträgt und dass jede Schicht eine positive Anzahl von Neuronen enthält. Wenn ein Fehler auftritt, wird eine Meldung angezeigt und die Ausführung beendet.
- Die Methode kopiert die Schichtgrößen in das Array layersSize und initialisiert die Arrays zur Speicherung der Neuronen und Gewichte.
- Sie berechnet die Gesamtzahl der Gewichte, die erforderlich sind, um die Neuronen zwischen den Schichten zu verbinden.
- Außerdem werden die Gewichte mit der Xavier-Methode initialisiert, was theoretisch dazu beiträgt, Probleme mit dem Abklingen oder Explodieren von Gradienten zu vermeiden.
- Je nach übergebenem Aktivierungsfunktionstyp erzeugt die Methode ein entsprechendes Aktivierungsfunktionsobjekt.
- Er initialisiert den Iterationszähler auf Null, der im ADAM-Algorithmus verwendet wird.
//+----------------------------------------------------------------------------+ //| Initialize the network | //| layerConfig - array with the number of neurons in each layer | //| Returns the total number of weights needed, or 0 in case of an error | //+----------------------------------------------------------------------------+ int C_MLPa::Init (int &layerConfig [], int actFuncType, int seed) { nLC = ArraySize (layerConfig); if (nLC < 2) { Print ("Network configuration error! Less than 2 layers!"); return 0; } // Check configuration for (int i = 0; i < nLC; i++) { if (layerConfig [i] <= 0) { Print ("Network configuration error! Layer #" + string (i + 1) + " contains 0 neurons!"); return 0; } } wLC = nLC - 1; ArrayCopy (layersSize, layerConfig, 0, 0, WHOLE_ARRAY); // Initialize neuron layers ArrayResize (nL, nLC); for (int i = 0; i < nLC; i++) { ArrayResize (nL [i].n, layersSize [i]); } // Initialize weight layers ArrayResize (wL, wLC); for (int w = 0; w < wLC; w++) { ArrayResize (wL [w].nOnL, layersSize [w]); for (int n = 0; n < layersSize [w]; n++) { ArrayResize (wL [w].nOnL [n].nOnR, layersSize [w + 1]); } } // Calculate the total number of weights wC = 0; for (int i = 0; i < nLC - 1; i++) wC += layersSize [i] * layersSize [i + 1] + layersSize [i + 1]; // Initialize weights double weights []; ArrayResize (weights, wC); srand (seed); //Xavier: U(-√(6/(n₁+n₂)), √(6/(n₁+n₂))) double n = sqrt (6.0 / (layersSize [0] + layersSize [nLC - 1])); for (int i = 0; i < wC; i++) { weights [i] = (2.0 * n) * (rand () / 32767.0) - n; } ImportWeights (weights); switch (actFuncType) { case eActACON: actFunc = new C_ActACON (); break; case eActAlgSigm: actFunc = new C_ActAlgSigm (); break; case eActBentIdent: actFunc = new C_ActBentIdent (); break; case eActRatSigm: actFunc = new C_ActRatSigm (); break; case eActSiLU: actFunc = new C_ActSiLU (); break; case eActSoftPlus: actFunc = new C_ActSoftPlus (); break; default: actFunc = new C_ActTanh (); break; } t = 0; return wC; } //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns zwei Methoden genauer an – ImportWeights und ExportWeights. Diese Methoden sind für den Import und Export von Gewichten und Verzerrungen eines mehrschichtigen Perzeptrons konzipiert. ImportWeights ist für den Import von Gewichten und Verzerrungen aus dem Array „weights“ in die Struktur des neuronalen Netzes zuständig.
Zunächst prüft die Methode, ob die Größe des übergebenen Arrays „weights“ mit der Anzahl der in der Variablen wC gespeicherten Gewichte übereinstimmt. Wenn die Größen nicht übereinstimmen, gibt die Methode „false“ zurück und zeigt damit einen Fehler an.
Die Variable wCNT wird verwendet, um den aktuellen Index im Array „Gewichte“ zu verfolgen.
Schleifen durch Schichten und Neuronen:
- Die äußere Schleife durchläuft jede Schicht, beginnend mit der zweiten Schicht (Index 1), da die erste Schicht die Eingabeschicht ist und keine Gewichte oder Verzerrungen hat.
- Die innere Schleife iteriert über jedes Neuron in der aktuellen Schicht.
- Für jedes Neuron wird der „bias“-Wert aus dem Array „weights“ gesetzt, und der Zähler wCNT wird inkrementiert.
- Eine verschachtelte Schleife durchläuft alle Neuronen der vorherigen Schicht und setzt die Gewichte, die die Neuronen der aktuellen Schicht mit den Neuronen der vorherigen Schicht verbinden.
ExportWeights – die Methode ist für den Export von Gewichten und Verzerrungen aus der Struktur des neuronalen Netzes in das Array „weights“ verantwortlich. Die Logik der Methode ist ähnlich wie die der Methode ImportWeights. Beide Methoden ermöglichen die Speicherung von Gewichten und Verzerrungen in einem externen Programm in Bezug auf die Netzklasse, die Verwendung des trainierten Netzes in der Zukunft und auch die Verwendung externer Optimierungsalgorithmen, wie z. B. Populationsalgorithmen.
//+----------------------------------------------------------------------------+ //| Import network weights and biases | //+----------------------------------------------------------------------------+ bool C_MLPa::ImportWeights (double &weights []) { if (ArraySize (weights) != wC) return false; int wCNT = 0; for (int ln = 1; ln < nLC; ln++) { for (int n = 0; n < layersSize [ln]; n++) { nL [ln].n [n].bias = weights [wCNT++]; for (int w = 0; w < layersSize [ln - 1]; w++) { wL [ln - 1].nOnL [w].nOnR [n].w = weights [wCNT++]; } } } return true; } //—————————————————————————————————————————————————————————————————————————————— //+----------------------------------------------------------------------------+ //| Export network weights and biases | //+----------------------------------------------------------------------------+ bool C_MLPa::ExportWeights (double &weights []) { ArrayResize (weights, wC); int wCNT = 0; for (int ln = 1; ln < nLC; ln++) { for (int n = 0; n < layersSize [ln]; n++) { weights [wCNT++] = nL [ln].n [n].bias; for (int w = 0; w < layersSize [ln - 1]; w++) { weights [wCNT++] = wL [ln - 1].nOnL [w].nOnR [n].w; } } } return true; } //——————————————————————————————————————————————————————————————————————————————
Bei der Methode ForwProp (Vorwärtsdurchlauf) werden die Werte aller Schichten eines mehrschichtigen Perzeptrons von der Eingabeschicht bis zur Ausgabeschicht sequentiell berechnet. Es nimmt Eingabewerte auf, verarbeitet sie durch versteckte Schichten und erzeugt Ausgabewerte. Parameter:
- inLayer[] – Array mit Eingabewerten für das neuronale Netz (in Abbildung 1 grün).
- outLayer[] – Array, in dem die Werte der Ausgabeschicht nach der Bearbeitung abgelegt werden (in Abbildung 1 gelb).
Die Methode initialisiert die Aktivierungswerte für die Neuronen der Eingabeschicht, indem sie die Eingabewerte aus dem Array inLayer in die entsprechenden Neuronen kopiert.
Handhabung von versteckten und Ausgabeschichten:
- Die äußere Schleife durchläuft alle Schichten, beginnend mit der zweiten Schicht (Index 1), da die erste Schicht die Eingabeschicht ist.
- Die innere Schleife durchläuft jedes Neuron der aktuellen Schicht.
- Für jedes Neuron wird die Summe der gewichteten Eingaben berechnet:
- Zunächst wird dem Neuron eine Vorspannung hinzugefügt.
- Die verschachtelte Schleife durchläuft alle Neuronen der vorherigen Schicht und addiert zu „val“ das Produkt aus dem Ausgabewert des Neurons der vorherigen Schicht und dem entsprechenden Gewicht.
- Nach der Berechnung der Summe wird die Aktivierungsfunktion auf „val“ angewendet, und das Ergebnis wird im Ausgangswert des Neurons der aktuellen Schicht gespeichert.
//+----------------------------------------------------------------------------+ //| Direct network pass | //| Calculate the values of all layers sequentially from input to output | //+----------------------------------------------------------------------------+ void C_MLPa::ForwProp (double &inLayer [], // input values double &outLayer []) // output layer values { double val; // Set the input layer activation values for (int n = 0; n < layersSize [0]; n++) { nL [0].n [n].out = inLayer [n]; } // Handle hidden and output layers for (int ln = 1; ln < nLC; ln++) { for (int n = 0; n < layersSize [ln]; n++) { val = nL [ln].n [n].bias; for (int w = 0; w < layersSize [ln - 1]; w++) { val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w; } nL [ln].n [n].out = actFunc.Activ (val); // Apply activation function } } // Set the output layer values for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out; } //——————————————————————————————————————————————————————————————————————————————
Die Methode BackProp implementiert den Rückwärtsdurchlauf der Fehler in einem mehrschichtigen Perzeptron. Es aktualisiert die Gewichte und Vorspannungen aller Schichten von der Ausgabe bis zur Eingabe mit Hilfe des ADAM-Optimierungsalgorithmus. Betriebslogik:
Die Variable „t“ wird inkrementiert, um die Anzahl der Iterationen zu verfolgen, und wird in der ADAM-Logikgleichung verwendet.
Berechnung der Deltas für alle Schichten:
- Die äußere Schleife durchläuft die Schichten in umgekehrter Reihenfolge, beginnend mit der Ausgabeschicht und endend mit der Eingabeschicht.
- Die innere Schleife geht durch die Neuronen der aktuellen Schicht.
- Handelt es sich bei der aktuellen Schicht um die Ausgangsschicht, wird das Delta als Produkt aus dem Fehler (errors[nCurr]) und der Ableitung der Aktivierungsfunktion für das Ausgangsneuron berechnet.
- Bei versteckten Schichten wird das Delta als Summe der Produkte aus den Deltas der nächsten Schicht und den entsprechenden Gewichten berechnet.
- Das Delta wird dann um die Ableitung der Aktivierungsfunktion angepasst, und das Ergebnis wird in nL[ln].n[nCurr].delta gespeichert.
- Die äußere Schleife durchläuft alle Ebenen, beginnend mit der zweiten Ebene.
- Für jedes Neuron der aktuellen Schicht werden die Bias-Momente „m“ und „v“ mit Hilfe der Parameter beta1 und beta2 aktualisiert.
- Dann werden die Verschiebungsmomente m_hat und v_hat angepasst.
- Schließlich wird die Verzerrung anhand der angepassten Momente aktualisiert.
- Die äußere Schlaufe geht durch alle Gewichtsschichten.
- Innere Schleifen durchlaufen die Neuronen der aktuellen Schicht und der nächsten Schicht.
- Für jedes Gewicht wird ein Gradient berechnet, der dann zur Aktualisierung der Momente „m“ und „v“ verwendet wird.
- Nach der Anpassung der Gewichtungsmomente m_hat und v_hat werden die Gewichte anhand der angepassten Momente aktualisiert.
//+----------------------------------------------------------------------------+ //| Backward network pass | //| Update the weights and biases of all layers from output to input | //+----------------------------------------------------------------------------+ void C_MLPa::BackProp (double &errors []) { t++; // Increase the iteration counter double delta; // current neuron delta double deltaNext; // delta of the neuron in the next layer connected to the current neuron double out; // neuron value after applying the activation function double deriv; // derivative double w; // weight for connecting the current neuron to the neuron of the next layer // 1. Calculating deltas for all layers ---------------------------------------- for (int ln = nLC - 1; ln > 0; ln--) // walk through layers in reverse order from output to input { for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++) // iterate through the neurons of the current layer { if (ln == nLC - 1) { delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out); } else { delta = 0.0; // Sum the products of the deltas of the next layer by the corresponding weights for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // pass the neurons of the next layer in the usual order { deltaNext = nL [ln + 1].n [nNext].delta; w = wL [ln].nOnL [nCurr].nOnR [nNext].w; delta += deltaNext * w; } } // Delta considering the derivative of the sigmoid out = nL [ln].n [nCurr].out; deriv = actFunc.Deriv (out); nL [ln].n [nCurr].delta = delta * deriv; } } // 2. Update biases using ADAM ------------------------------ for (int ln = 1; ln < nLC; ln++) { for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++) { delta = nL [ln].n [nCurr].delta; // Update displacement moments nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta; nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta; // Adjust displacement moments double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t)); double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t)); // Update bias nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon); } } // 3. Update weights using ADAM --------------------------------- for (int lw = 0; lw < wLC; lw++) { for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++) { for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++) { deltaNext = nL [lw + 1].n [nNext].delta; out = nL [lw].n [nCurr].out; double gradient = deltaNext * out; // Update moments for weights wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient; wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient; // Adjust weight moments double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t)); double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t)); // Update weight wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon); } } } } //——————————————————————————————————————————————————————————————————————————————
Code für den Prüfstand zum Rendern von Aktivierungsfunktionen
Der Prüfstand dient dazu, die korrekte Funktionsweise verschiedener Aktivierungsfunktionen, die in neuronalen Netzen verwendet werden, zu testen und sie in Form einer Grafik darzustellen. Die daraus resultierenden Bilder werden im weiteren Verlauf des Artikels zur visuellen Bewertung des Aussehens verwendet. Der Code ist recht einfach, und es ist nicht besonders sinnvoll, ihn zu beschreiben.
#include <Graphics\Graphic.mqh> #include <Math\AOs\NeuroNets\MLPa.mqh> #define SIZE_X 750 #define SIZE_Y 200 //--- input parameters input E_Act ACT = eActTanh; input int CNT = 10000; //—————————————————————————————————————————————————————————————————————————————— void OnStart () { ObjectDelete (ChartID (), "Test"); double activ []; double deriv []; //---------------------------------------------------------------------------- C_Base_ActFunc *act; switch (ACT) { default: act = new C_ActTanh (); break; case eActAlgSigm: act = new C_ActAlgSigm (); break; case eActRatSigm: act = new C_ActRatSigm (); break; case eActSoftPlus: act = new C_ActSoftPlus (); break; case eActBentIdent: act = new C_ActBentIdent (); break; case eActSiLU: act = new C_ActSiLU (); break; case eActACON: act = new C_ActACON (); break; case eActSnake: act = new C_ActSnake (); break; case eActSERF: act = new C_ActSERF (); break; } //---------------------------------------------------------------------------- ActFuncTest (act, activ, deriv, CNT, -10, 10); //---------------------------------------------------------------------------- CGraphic gr_test; gr_test.Create (0, "Test", 0, 0, 20, SIZE_X, SIZE_Y + 20); gr_test.YAxis ().Name (act.GetFuncName () + ": Value"); gr_test.YAxis ().NameSize (13); gr_test.HistorySymbolSize (10); gr_test.CurveAdd (activ, ColorToARGB (clrRed, 255), CURVE_LINES, "activ"); gr_test.CurveAdd (deriv, ColorToARGB (clrBlue, 255), CURVE_LINES, "deriv"); gr_test.CurvePlotAll (); gr_test.Redraw (true); gr_test.Update (); //---------------------------------------------------------------------------- delete act; } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void ActFuncTest (C_Base_ActFunc &act, double &arrayAct [], double &arrayDer [], int testCount, double min, double max) { Print (act.GetFuncName (), " [", min, "; ", max, "]"); Print (act.Activ (min), " ", act.Activ (0), " ", act.Activ (max)); Print (act.Deriv (min), " ", act.Deriv (0), " ", act.Deriv (max)); ArrayResize (arrayAct, testCount); ArrayResize (arrayDer, testCount); double x = 0.0; double step = (max - min) / testCount; for (int i = 0; i < testCount; i++) { x = min + step * i; arrayAct [i] = act.Activ (x); arrayDer [i] = act.Deriv (x); } } //——————————————————————————————————————————————————————————————————————————————
Code der Aktivierungsfunktionsklassen
Es gibt viele verschiedene Neuronen-Aktivierungsfunktionen, die für eine Vielzahl von Problemen mit neuronalen Netzen verwendet werden. Ich habe versucht, Funktionen auszuwählen, die sowohl den bekannten hyperbolischen Tangens als auch weniger bekannte Funktionen wie die Snake-Aktivierungsfunktion umfassen, während ich Funktionen ausschloss, die in Aussehen und Eigenschaften sehr ähnlich sind. Sie lassen sich bedingt in drei Gruppen einteilen:
- Funktionen des Sigmas,
- Nichtlineare Schalter,
- Periodische Funktionen.
Wir implementieren die Basisklasse C_Base_ActFunc für Neuronen-Aktivierungsfunktionen. Sie enthält zwei virtuelle Funktionen: Activ zur Berechnung der Aktivierung und Deriv zur Berechnung der Ableitung. Die Methode GetFuncName() gibt den Namen der Aktivierungsfunktion zurück, die in der geschützten Zelle funcName gespeichert ist. Die Klasse soll vererbt werden, um konkrete Implementierungen von Aktivierungsfunktionen zu erstellen. Durch die Erstellung des Aktivierungsfunktionsobjekts können wir die Berechnungen beschleunigen, da die mehrfache Verwendung von „if“ und „switch“ entfällt.
//—————————————————————————————————————————————————————————————————————————————— // Base class of the neuron activation function class C_Base_ActFunc { public: virtual double Activ (double inp) = 0; // Virtual activation function virtual double Deriv (double inp) = 0; // Virtual derivative function string GetFuncName () {return funcName;} protected: string funcName; }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_ActTanh implementiert die hyperbolische Tangens-Aktivierungsfunktion und ihre Ableitung und erbt von der Basisklasse C_Base_ActFunc. Im Klassenkonstruktor wird der Name der Aktivierungsfunktion in der Variablen funcName auf ActTanh gesetzt. Aktivierungsmethode:
- Activ (double x) berechnet den Wert der Aktivierungsfunktion des hyperbolischen Tangens anhand der Gleichung: f(x) = 2 / (1 + exp ( – 2 ⋅ (x)) – 1. Diese Gleichung wandelt die Eingabe „x“ in den Bereich von -1 bis 1 um.
- Deriv(double x) berechnet die Ableitung der Aktivierungsfunktion. Die Ableitung des hyperbolischen Tangens wird wie folgt ausgedrückt: f′(x) = 1 – (f (x)) ^ 2, wobei f(x) der Wert der Aktivierungsfunktion ist, der für das aktuelle „x“ berechnet wurde. Die Ableitung zeigt, wie schnell sich eine Funktion in Bezug auf den Eingangswert ändert.
//—————————————————————————————————————————————————————————————————————————————— // Hyperbolic tangent class C_ActTanh : public C_Base_ActFunc { public: C_ActTanh () {funcName = "ActTanh";} double Activ (double x) { return 2.0 / (1.0 + exp (-2 * (x))) - 1.0; } double Deriv (double x) { //1 - (f(x))^2 double fx = Activ (x); return 1.0 - fx * fx; } }; //——————————————————————————————————————————————————————————————————————————————
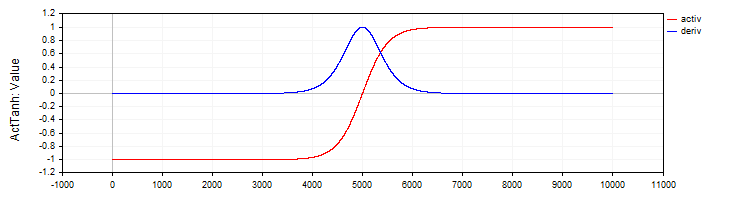
Abbildung 2. Hyperbolischer Tangens und seine Ableitung
Die Klasse C_ActAlgSigm implementiert, ähnlich wie die Klasse C_ActTanh, das algebraische Sigmoid als Aktivierungsfunktion mit Methoden zur Berechnung der Aktivierung und ihrer Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // Algebraic sigmoid class C_ActAlgSigm : public C_Base_ActFunc { public: C_ActAlgSigm () {funcName = "ActAlgSigm";} double Activ (double x) { return x / sqrt (1.0 + x * x); } double Deriv (double x) { // (1 / sqrt (1 + x * x))^3 double d = 1.0 / sqrt (1.0 + x * x); return d * d * d; } }; //——————————————————————————————————————————————————————————————————————————————
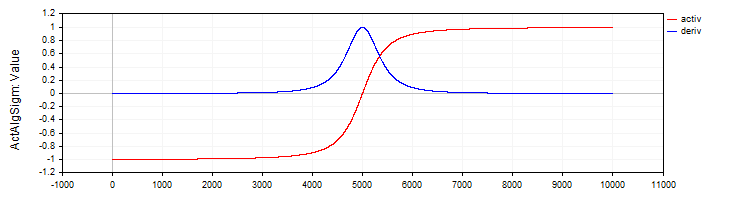
Abbildung 3. Algebraisches Sigmoid und seine Ableitung
Die Klasse C_ActRatSigm implementiert ein rationales Sigmoid mit Aktivierungs- und Ableitungsmethoden.
//—————————————————————————————————————————————————————————————————————————————— // Rational sigmoid class C_ActRatSigm : public C_Base_ActFunc { public: C_ActRatSigm () {funcName = "ActRatSigm";} double Activ (double x) { return x / (1.0 + fabs (x)); } double Deriv (double x) { //1 / (1 + abs (x))^2 double d = 1.0 + fabs (x); return 1.0 / (d * d); } }; //——————————————————————————————————————————————————————————————————————————————
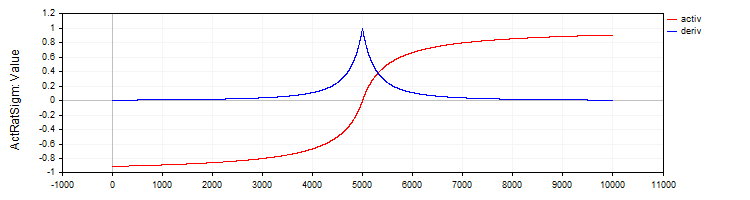
Abbildung 4. Rationales Sigmoid und seine Ableitung
Die Klasse C_ActSoftPlus implementiert die Softplus-Aktivierungsfunktion und ihre Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // Softplus class C_ActSoftPlus : public C_Base_ActFunc { public: C_ActSoftPlus () {funcName = "ActSoftPlus";} double Activ (double x) { return log (1.0 + exp (x)); } double Deriv (double x) { return 1.0 / (1.0 + exp (-x)); } }; //——————————————————————————————————————————————————————————————————————————————
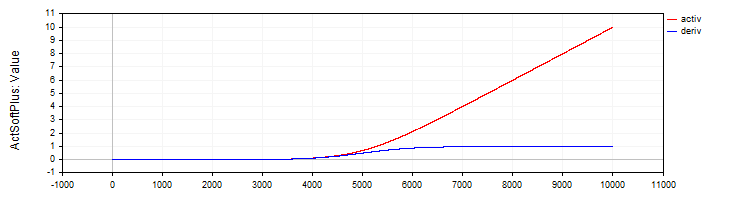
Abbildung 5. SoftPlus-Funktion und ihre Ableitung
Die Klasse C_ActBentIdent implementiert die Aktivierungsfunktion Bent Identity und ihre Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // Bent Identity class C_ActBentIdent : public C_Base_ActFunc { public: C_ActBentIdent () {funcName = "ActBentIdent";} double Activ (double x) { return (sqrt (x * x + 1.0) - 1.0) / 2.0 + x; } double Deriv (double x) { return x / (2.0 * sqrt (x * x + 1.0)) + 1.0; } }; //——————————————————————————————————————————————————————————————————————————————
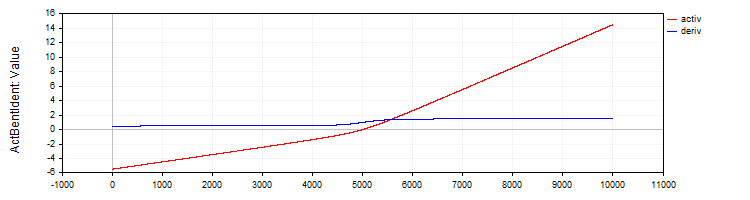
Abbildung 6. Bent Identity-Funktion und ihre Ableitung
Die Klasse C_ActSiLU bietet eine Implementierung der SiLU-Aktivierungsfunktion und ihrer Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // SiLU (Swish) class C_ActSiLU : public C_Base_ActFunc { public: C_ActSiLU () {funcName = "ActSiLU";} double Activ (double x) { return x / (1.0 + exp (-x)); } double Deriv (double x) { if (x == 0.0) return 0.5; // f(x) + (f(x)*(1 - f(x)))/ x double fx = Activ (x); return fx + (fx * (1.0 - fx)) / x; } }; //——————————————————————————————————————————————————————————————————————————————
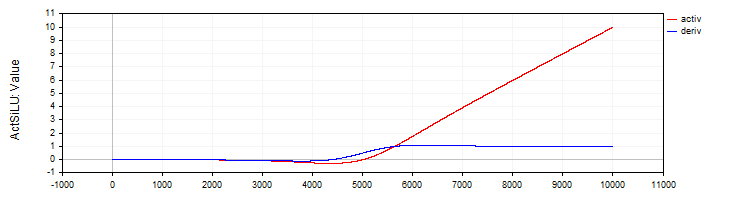
Abbildung 7. SiLU-Funktion und ihre Ableitung
Die C_ActACON implementiert die ACON-Aktivierungsfunktion und ihre Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // ACON class C_ActACON : public C_Base_ActFunc { public: C_ActACON () {funcName = "ActACON";} double Activ (double x) { return (x * cos (x) + sin (x)) / (1.0 + fabs (x)); } double Deriv (double x) { if (x == 0.0) return 2.0; //[2 * cos(x) - x * sin(x)] / [|x| + 1] - x * (sin(x) + x * cos(x)) / [|x| * ((|x| + 1)²)] double sinX = sin (x); double cosX = cos (x); double fabsX = fabs (x); double fabsXp = fabsX + 1.0; // Divide the equation into two parts double part1 = (2.0 * cosX - x * sinX) / fabsXp; double part2 = -x * (sinX + x * cosX) / (fabsX * fabsXp * fabsXp); return part1 + part2; } }; //——————————————————————————————————————————————————————————————————————————————
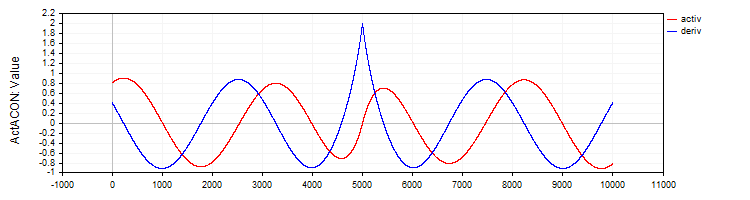
Abbildung 8. ACON-Funktion und ihre Ableitung
Die Klasse C_ActSERF implementiert die SERF-Aktivierungsfunktion und ihre Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // SERF (sigmoid-weighted exponential straightening function) class C_ActSERF : public C_Base_ActFunc { public: C_ActSERF () { alpha = 0.5; funcName = "ActSERF"; } double Activ (double x) { double sigmoid = 1.0 / (1.0 + exp (-alpha * x)); if (x >= 0) return sigmoid * x; else return sigmoid * (exp (x) - 1.0); } double Deriv (double x) { double sigmoid = 1.0 / (1.0 + exp (-alpha * x)); double sigmoidDeriv = alpha * sigmoid * (1.0 - sigmoid); double e = exp (x); if (x >= 0) return sigmoid + x * sigmoidDeriv; else return sigmoid * e + (e - 1.0) * sigmoidDeriv; } private: double alpha; }; //——————————————————————————————————————————————————————————————————————————————
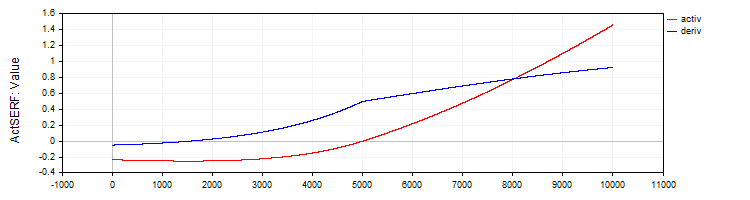
Abbildung 9. SERF-Funktion und ihre Ableitung
Die Klasse C_ActSNAKE implementiert die Aktivierungsfunktion SNAKE und ihre Ableitung.
//—————————————————————————————————————————————————————————————————————————————— // Snake (periodic activation function) class C_ActSnake : public C_Base_ActFunc { public: C_ActSnake () { frequency = 1; funcName = "ActSnake"; } double Activ (double x) { double sinx = sin (frequency * x); return x + sinx * sinx; } double Deriv (double x) { double fx = frequency * x; return 1.0 + 2.0 * sin (fx) * cos (fx) * frequency; } private: double frequency; }; //——————————————————————————————————————————————————————————————————————————————
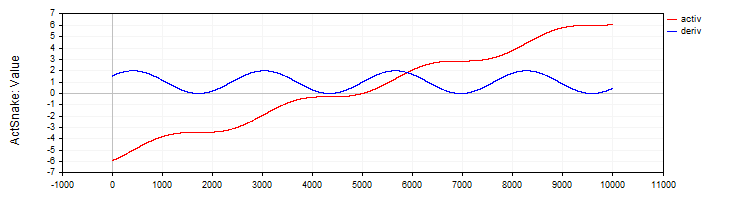
Abbildung 10. Funktion SNAKE und ihre Ableitung
Testen von Aktivierungsfunktionen
Nun ist es an der Zeit, sich anzusehen, wie ein MLP-Netz mit verschiedenen Aktivierungsfunktionen trainiert wird. Die Komplexität der Aktivierungsfunktion für den Optimierungsalgorithmus lässt sich an der 1-1-1-MLP-Konfiguration mit nur einem Beispiel im Training (ein Eingabewert und ein Zielwert) deutlich demonstrieren.
Auf den ersten Blick mag dies nicht offensichtlich erscheinen. Warum weckt eine so einfache Aufgabe das Interesse? Dies ist ein wichtiger methodischer Punkt: Die Verwendung eines einzigen Datenpunkts ermöglicht es uns, die Komplexität der Aktivierungsfunktion selbst und ihre Auswirkungen auf die Optimierung zu isolieren und zu untersuchen. Wenn wir mit einem großen Datensatz arbeiten, beeinflussen viele Faktoren das Training: die Verteilung der Daten, die Abhängigkeiten zwischen den Beispielen und wie sich ihr Einfluss beim Durchlaufen der Aktivierungsfunktion manifestiert. Durch die Verwendung von nur einem Punkt werden all diese externen Faktoren eliminiert und wir können uns darauf konzentrieren, wie schwierig es für den Optimierungsalgorithmus ist, mit einer bestimmten Aktivierungsfunktion zu arbeiten.
Der Punkt ist, dass ein neuronales Netz, das durch einen einzigen Punkt der interpolierten Funktion geht, eine unendliche Anzahl von Gewichtungsoptionen haben kann. Dies mag unglaublich erscheinen, ergibt sich aber aus der Gleichung in * w + b = out, wobei in ein Netzeingang, w ein Gewicht, b ein Bias und out ein Netzausgang für die Konfiguration 1-1 ist.
Bei dieser Konfiguration gibt es keine Probleme, sie treten jedoch auf, wenn eine weitere Schicht hinzugefügt wird – die 1-1-1-Konfiguration. In diesem Fall wird selbst das einfachste Problem für den Optimierungsalgorithmus nicht mehr trivial, da der Suchraum für eine Lösung deutlich komplexer wird: Jetzt muss die richtige Kombination von Gewichten durch die Zwischenschicht mit ihrer Aktivierungsfunktion gefunden werden. Diese Komplexität ermöglicht es uns zu bewerten, wie effektiv verschiedene Optimierungsalgorithmen mit der Gewichtsabstimmung umgehen, wenn sie mit verschiedenen Aktivierungsfunktionen arbeiten.
Nachfolgend finden Sie Tabellen mit den Ergebnissen der ADAM-Algorithmen in der klassischen Implementierung und der Population ADAMm. Für beide Algorithmen wurden 10.000 Iterationen durchgeführt. Bei dem populationsbasierten Algorithmus wurde das Vorhandensein der Population berücksichtigt, und die Gesamtzahl der Berechnungen des neuronalen Netzes blieb gleich. Die Ausdrucke geben den Pseudozufallszahlengenerator an (um problematische Trainingsläufe zu reproduzieren), die Iteration, die das beste Ergebnis lieferte, und das Ergebnis für die aktuelle Epoche, ein Vielfaches von 1000.
Die Gewichte wurden mit Zufallszahlen nach der Xavier-Methode für ADAM und mit Zufallszahlen im Bereich [-10; 10] für ADAMm initialisiert. Es wurden mehrere Tests mit verschiedenen Körnern durchgeführt, und die schlechtesten Ergebnisse wurden ausgewählt. Die Auswahl der Gewichte wurde entweder abgeschlossen, wenn die maximale Anzahl der Iterationen erreicht war oder wenn der Fehler unter 0,000001 sank.
Tabelle der Ergebnisse für sigmoidale Aktivierungsfunktionen:
| Tanh | AlgSigm | RatSigm |
|---|---|---|
| MLP config: 1|1|1, Weights: 4, Activation func: eActTanh, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActAlgSigm, Seed: 4 -----Integrated ADAM----- 0: 0.1878131682539310, 0: 0.18781316825393096 0: 0.1878131682539310, 1000: 0.22880505258129305 0: 0.1878131682539310, 2000: 0.2395439537933131 0: 0.1878131682539310, 3000: 0.24376284285887292 0: 0.1878131682539310, 4000: 0.24584964230029535 0: 0.1878131682539310, 5000: 0.2470364071634453 0: 0.1878131682539310, 6000: 0.24777681648987268 0: 0.1878131682539310, 7000: 0.2482702131676117 0: 0.1878131682539310, 8000: 0.24861563983949608 0: 0.1878131682539310, 9000: 0.2488669473265396 Best result iteration: 0, Err: 0.187813 -----Population-based ADAMm----- 0: 0.2481251241755712 1000: 0.0000009070157679 Best result iteration: 1000, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActRatSigm, Seed: 4 -----Integrated ADAM----- 0: 0.0354471509280691, 0: 0.03544715092806905 0: 0.0354471509280691, 1000: 0.10064226929576263 0: 0.0354471509280691, 2000: 0.13866170841306655 0: 0.0354471509280691, 3000: 0.16067944018111643 0: 0.0354471509280691, 4000: 0.17502946224977484 0: 0.0354471509280691, 5000: 0.18520767592761297 0: 0.0354471509280691, 6000: 0.19285431843628092 0: 0.0354471509280691, 7000: 0.1988366186290051 0: 0.0354471509280691, 8000: 0.20365853142896836 0: 0.0354471509280691, 9000: 0.20763502064394074 Best result iteration: 0, Err: 0.035447 -----Population-based ADAMm----- 0: 0.1928944265733889 Best result iteration: 688, Err: 0.000000 |
Tabelle der Ergebnisse für Aktivierungsfunktionen vom Typ SiLU:
| SoftPlus | BentIdent | SiLU |
|---|---|---|
| MLP config: 1|1|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 131.77685264891647 0: 0.5380138004155748, 2000: 1996.1250363225556 0: 0.5380138004155748, 3000: 8050.259717531171 0: 0.5380138004155748, 4000: 20321.169969814575 0: 0.5380138004155748, 5000: 40601.21872791767 0: 0.5380138004155748, 6000: 70655.44591598355 0: 0.5380138004155748, 7000: 112311.81150857621 0: 0.5380138004155748, 8000: 167489.98562842538 0: 0.5380138004155748, 9000: 238207.27978678182 Best result iteration: 0, Err: 0.538014 -----Population-based ADAMm----- 0: 18.4801637203493884 778: 0.0000022070092175 Best result iteration: 1176, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 185.646717568436 0: 15.1221330593320857, 2000: 1003.1026112225994 0: 15.1221330593320857, 3000: 2955.8393027057205 0: 15.1221330593320857, 4000: 6429.902382962495 0: 15.1221330593320857, 5000: 11774.781156010686 0: 15.1221330593320857, 6000: 19342.379583340015 0: 15.1221330593320857, 7000: 29501.355075464813 0: 15.1221330593320857, 8000: 42640.534930000824 0: 15.1221330593320857, 9000: 59168.850722337185 Best result iteration: 0, Err: 15.122133 -----Population-based ADAMm----- 0: 7818.0964949082390376 Best result iteration: 15, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActSiLU, Seed: 2 -----Integrated ADAM----- 0: 0.0021199944516222, 0: 0.0021199944516222444 0: 0.0021199944516222, 1000: 4.924850697388685 0: 0.0021199944516222, 2000: 14.827133542234415 0: 0.0021199944516222, 3000: 28.814259008218087 0: 0.0021199944516222, 4000: 45.93517121925276 0: 0.0021199944516222, 5000: 65.82077308420028 0: 0.0021199944516222, 6000: 88.26782602934948 0: 0.0021199944516222, 7000: 113.15535264604428 0: 0.0021199944516222, 8000: 140.41067538093935 0: 0.0021199944516222, 9000: 169.9878269747845 Best result iteration: 0, Err: 0.002120 -----Population-based ADAMm----- 0: 17.2288020548757288 1000: 0.0000030959186317 Best result iteration: 1150, Err: 0.000001 |
Tabelle der Ergebnisse für periodische Aktivierungsfunktionen:
| ACON | SERF | Snake |
|---|---|---|
| MLP config: 1|1|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0.0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0.0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 481, Err: 0.000000 | MLP config: 1|1|1, Weights: 4, Activation func: eActSERF, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActSnake, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001 |
Wir können nun vorläufige Schlussfolgerungen über die Komplexität der Aktivierungsfunktionen für das klassische Gradienten-ADAM und das Populations-ADAMm ziehen. Obwohl das reguläre ADAM direkte Informationen über den Gradienten der Aktivierungsfunktion hat, d.h. es kennt buchstäblich die Richtung des steilsten Abstiegs, ist es an dieser scheinbar einfachen Aufgabe gescheitert. ACON erwies sich als die einfachste Funktion für ADAM. Es ist auf diesem Typ, dass es in der Lage war, den Fehler konsequent zu minimieren. Funktionen wie SiLU erwiesen sich jedoch als problematisch: Der Fehler nahm nicht nur nicht ab, sondern auch schnell zu. Es ist offensichtlich, dass ADAM, da es nicht über die Randbedingungen für Gewicht und Vorspannung verfügte, die falsche Richtung wählte und die Gewichtswerte erhöhte. Die Gewichte flogen frei zur Seite, ungebremst und buchstäblich weggeblasen vom gerichteten Wind der Ableitung der Aktivierungsfunktion.
Das Problem wird nur schlimmer, wenn man mehr Neuronen in Schichten verwendet, da jedes Neuron als Eingabe die Summe der Produkte aus den Ausgaben der Neuronen der vorherigen Schicht und dem entsprechenden Gewicht erhält. So kann die Summe so groß werden, dass es unmöglich wird, die Exponentialfunktion korrekt zu berechnen.
Wie wir sehen können, stellt keine der Aktivierungsfunktionen ein Problem für die Population ADAMm dar. Die Konvergenz ist bei allen gleich, und nur bei einigen übersteigt die Anzahl der Iterationen leicht 1000.
Verfeinerung der Aktivierungsfunktionsklassen, MLP und ADAM
Um die Situation mit vereinzelte Gewichten im neuronalen Netz zu korrigieren, werden wir Änderungen an den Aktivierungsfunktionsklassen vornehmen. Auf diese Weise können wir die Grenzen der entsprechenden Funktionen verfolgen und die Anhäufung einer großen Summe verhindern, wenn sie einem Neuron zugeführt wird, und auch die Werte der Gewichte und Verzerrungen selbst werden begrenzt.
Ich werde der Basisklasse die Methoden GetBoundUp und GetBoundLo hinzufügen, die den Zugriff auf die Grenzen der entsprechenden Aktivierungsfunktionen ermöglichen, sodass andere Klassen oder Funktionen Informationen über die zulässigen Werte erhalten können.
Nachstehend finden Sie den Code für die Basisklasse und die hyperbolische Tangens-Klasse mit einigen Änderungen (der Rest des Codes bleibt unverändert). Die übrigen Klassen anderer Aktivierungsfunktionen werden auf ähnliche Weise implementiert, mit ihren eigenen entsprechenden Grenzen.
//—————————————————————————————————————————————————————————————————————————————— // Base class of the neuron activation function class C_Base_ActFunc { public: double GetBoundUp () { return boundUp;} double GetBoundLo () { return boundLo;} protected: double boundUp; // upper bound of the input range double boundLo; // lower bound of the input range }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Hyperbolic tangent class C_ActTanh : public C_Base_ActFunc { public: C_ActTanh () { boundUp = 6.0; boundLo = -6.0; } }; //——————————————————————————————————————————————————————————————————————————————
Jetzt ergänzen wir eine Validierung der Summenwerte zum MLP-Vorwärtspass-Methodencode hinzu, bevor wir sie in die Neuronenaktivierungsfunktion einspeisen, um sicherzustellen, dass sie nicht über die festgelegten Grenzen hinausgehen. Es macht keinen Sinn, den Betrag über die festgelegten Grenzen hinaus zu erhöhen. Außerdem ermöglicht dies einen frühen Stopp bei der Berechnung der Summe für eine Netzkonfiguration mit einer großen Anzahl von Neuronen in Schichten, was die Berechnungen erheblich beschleunigen kann.
Prüfung der oberen Grenze: Dieser Codeschnipsel prüft, ob der aktuelle Wert der Summe größer ist als die eingestellte Obergrenze. Ist der Wert größer als diese Grenze, wird er gleich dieser Grenze gesetzt und die Schleifenausführung beendet. Die untere Grenze wird auf ähnliche Weise überprüft.
//+----------------------------------------------------------------------------+ //| Direct network pass | //| Calculate the values of all layers sequentially from input to output | //+----------------------------------------------------------------------------+ void C_MLPa::ForwProp (double &inLayer [], // input values double &outLayer []) // output layer values { double val; // Set the input layer activation values for (int n = 0; n < layersSize [0]; n++) { nL [0].n [n].out = inLayer [n]; } // Handle hidden and output layers for (int ln = 1; ln < nLC; ln++) { for (int n = 0; n < layersSize [ln]; n++) { val = nL [ln].n [n].bias; for (int w = 0; w < layersSize [ln - 1]; w++) { val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w; if (val > actFunc.GetBoundUp ()) { val = actFunc.GetBoundUp (); break; } if (val < actFunc.GetBoundLo ()) { val = actFunc.GetBoundLo (); break; } } nL [ln].n [n].out = actFunc.Activ (val); // Apply activation function } } // Set the output layer values for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out; } //——————————————————————————————————————————————————————————————————————————————
Ergänzen wir nun den Code zur Überprüfung der Grenzen zur Backpropagation-Methode. In diesen Ergänzungen wird die Logik implementiert, die die Werte der Offsets und Gewichte von den festgelegten Grenzen auf die Rückwärtsgrenze spiegelt. Es muss sichergestellt werden, dass die Werte nicht außerhalb der zulässigen Bereiche liegen, um eine unkontrollierte Erhöhung oder Verringerung der Gewichte und Verzerrungen zu verhindern.
Ein einfaches Abschneiden der Werte an der Grenze würde zu einer Stagnation im Training führen, da das Gewicht einfach an die Grenze stoßen würde und eine Änderung der Gewichte unmöglich wäre. Gerade um solche Situationen zu vermeiden, werden Überlegungen angestellt, anstatt Werte zu reduzieren. Dies sorgt für eine „Wiederbelebung“ oder eine Art „Aufrüttlung“ bei der Anpassung der Gewichte und Verzerrungen.
//+----------------------------------------------------------------------------+ //| Backward network pass | //| Update the weights and biases of all layers from output to input | //+----------------------------------------------------------------------------+ void C_MLPa::BackProp (double &errors []) { t++; // Increase the iteration counter double delta; // current neuron delta double deltaNext; // delta of the neuron in the next layer connected to the current neuron double out; // neuron value after applying the activation function double deriv; // derivative double w; // weight for connecting the current neuron to the neuron of the next layer double bias; // bias // 1. Calculating deltas for all layers ---------------------------------------- for (int ln = nLC - 1; ln > 0; ln--) // walk through layers in reverse order from output to input { for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++) // iterate through the neurons of the current layer { if (ln == nLC - 1) { delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out); } else { delta = 0.0; // Sum the products of the deltas of the next layer by the corresponding weights for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // pass the neurons of the next layer in the usual order { deltaNext = nL [ln + 1].n [nNext].delta; w = wL [ln].nOnL [nCurr].nOnR [nNext].w; delta += deltaNext * w; } } // Delta considering the derivative of the sigmoid out = nL [ln].n [nCurr].out; deriv = actFunc.Deriv (out); nL [ln].n [nCurr].delta = delta * deriv; } } // 2. Update biases using ADAM ------------------------------ for (int ln = 1; ln < nLC; ln++) { for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++) { delta = nL [ln].n [nCurr].delta; // Update displacement moments nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta; nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta; // Adjust displacement moments double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t)); double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t)); // Update bias nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon); bias = nL [ln].n [nCurr].bias; if (bias < actFunc.GetBoundLo ()) { nL [ln].n [nCurr].bias = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - bias); // reflect from the bottom border } else if (bias > actFunc.GetBoundUp ()) { nL [ln].n [nCurr].bias = actFunc.GetBoundLo () + (bias - actFunc.GetBoundUp ()); // reflect from the upper border } } } // 3. Update weights using ADAM --------------------------------- for (int lw = 0; lw < wLC; lw++) { for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++) { for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++) { deltaNext = nL [lw + 1].n [nNext].delta; out = nL [lw].n [nCurr].out; double gradient = deltaNext * out; // Update moments for weights wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient; wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient; // Adjust weight moments double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t)); double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t)); // Update weight wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon); w = wL [lw].nOnL [nCurr].nOnR [nNext].w; if (w < actFunc.GetBoundLo ()) { wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - w); // reflect from the lower border } else if (w > actFunc.GetBoundUp ()) { wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundLo () + (w - actFunc.GetBoundUp ()); // reflect from the upper border } } } } } //——————————————————————————————————————————————————————————————————————————————
Wiederholen wir nun die gleichen Tests wie oben und betrachten wir die Ergebnisse. Jetzt gibt es keine Explosion der Gewichte und kein lawinenartiges Anwachsen der Fehler beim Training.
Tabelle der Ergebnisse für sigmoidale Aktivierungsfunktionen:
| Tanh | AlgSigm | RatSigm |
|---|---|---|
| MLP config: 1|1|1, Weights: 4, Activation func: eActTanh, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActAlgSigm, Seed: 2 -----Integrated ADAM----- 0: 0.0095411465043040, 0: 0.009541146504303972 0: 0.0095411465043040, 1000: 0.20977102640908893 0: 0.0095411465043040, 2000: 0.23464558094398064 0: 0.0095411465043040, 3000: 0.23657904914082925 0: 0.0095411465043040, 4000: 0.17812555648593617 0: 0.0095411465043040, 5000: 2.1749975763135927 0: 0.0095411465043040, 6000: 2.2093668968051166 0: 0.0095411465043040, 7000: 2.1657244506071813 0: 0.0095411465043040, 8000: 1.9330415523200173 0: 0.0095411465043040, 9000: 0.10441382194622865 Best result iteration: 0, Err: 0.009541 -----Population-based ADAMm----- 0: 0.2201830630768654 Best result iteration: 750, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActRatSigm, Seed: 1 -----Integrated ADAM----- 0: 1.2866075458561122, 0: 1.2866075458561121 1000: 0.2796061866784148, 1000: 0.2796061866784148 2000: 0.0450819127087337, 2000: 0.04508191270873367 3000: 0.0200306843648248, 3000: 0.020030684364824806 4000: 0.0098744349153286, 4000: 0.009874434915328582 5000: 0.0049448920462547, 5000: 0.00494489204625467 6000: 0.0024344513388710, 6000: 0.00243445133887102 7000: 0.0011602603038120, 7000: 0.0011602603038120354 8000: 0.0005316894732581, 8000: 0.0005316894732581081 9000: 0.0002339388712666, 9000: 0.00023393887126662818 Best result iteration: 9999, Err: 0.000099 -----Population-based ADAMm----- 0: 1.8418367346938778 Best result iteration: 645, Err: 0.000000 |
Tabelle der Ergebnisse für Aktivierungsfunktionen vom Typ SiLU:
| SoftPlus | BentIdent | SiLU |
|---|---|---|
| MLP config: 1|1|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 12.377378915308087 0: 0.5380138004155748, 2000: 12.377378915308087 3000: 0.1996421769021168, 3000: 0.19964217690211675 4000: 0.1985425345613517, 4000: 0.19854253456135168 5000: 0.1966512639256550, 5000: 0.19665126392565502 6000: 0.1933509943676914, 6000: 0.1933509943676914 7000: 0.1874142582090466, 7000: 0.18741425820904659 8000: 0.1762132792048514, 8000: 0.17621327920485136 9000: 0.1538331138702293, 9000: 0.15383311387022927 Best result iteration: 9999, Err: 0.109364 -----Population-based ADAMm----- 0: 12.3773789153080873 Best result iteration: 677, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 25.619316876852988 1922: 8.6344718719116980, 2000: 8.634471871911698 1922: 8.6344718719116980, 3000: 8.634471871911698 1922: 8.6344718719116980, 4000: 8.634471871911698 1922: 8.6344718719116980, 5000: 8.634471871911698 1922: 8.6344718719116980, 6000: 8.634471871911698 6652: 4.3033564303197833, 7000: 8.634471871911698 6652: 4.3033564303197833, 8000: 8.634471871911698 6652: 4.3033564303197833, 9000: 7.11489380279475 Best result iteration: 9999, Err: 3.589207 -----Population-based ADAMm----- 0: 25.6193168768529880 Best result iteration: 15, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActSiLU, Seed: 4 -----Integrated ADAM----- 0: 0.6585816582701970, 0: 0.658581658270197 0: 0.6585816582701970, 1000: 5.142928362480306 1393: 0.3271208998291733, 2000: 0.32712089982917325 1393: 0.3271208998291733, 3000: 0.32712089982917325 1393: 0.3271208998291733, 4000: 0.4029355474095988 5000: 0.0114993205601383, 5000: 0.011499320560138332 6000: 0.0003946998191595, 6000: 0.00039469981915948605 7000: 0.0000686308316624, 7000: 0.00006863083166239227 8000: 0.0000176901182322, 8000: 0.000017690118232197302 9000: 0.0000053723044223, 9000: 0.000005372304422295116 Best result iteration: 9999, Err: 0.000002 -----Population-based ADAMm----- 0: 19.9499415647445524 1000: 0.0000057228950379 Best result iteration: 1051, Err: 0.000000 |
Tabelle der Ergebnisse für periodische Aktivierungsfunktionen:
| ACON | SERF | Snake |
|---|---|---|
| MLP config: 1|1|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0.0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0.0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 300, Err: 0.000000 | MLP config: 1|1|1, Weights: 4, Activation func: eActSERF, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001 | MLP config: 1|1|1, Weights: 4, Activation func: eActSnake, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001 |
Zusammenfassung
Fassen wir also unsere Forschungsergebnisse zusammen. Ich möchte Sie an das Wesentliche des Experiments erinnern: Wir haben zwei Optimierungsalgorithmen genommen, die auf derselben Logik aufbauen, aber grundlegend unterschiedlich arbeiten. Die erste (klassische ADAM) ist ein eingebauter Optimierer, der innerhalb des neuronalen Netzes arbeitet, mit direktem Zugriff auf die Aktivierungsfunktionen und die gesamte interne Struktur – wie ein Navigator mit einer detaillierten Karte des Gebiets. Der zweite (Population ADAMm) ist ein externer Optimierer, der mit dem neuronalen Netz als „Black Box“ arbeitet, ohne jegliche Informationen über seine interne Struktur oder die Besonderheiten der Aufgabe – wie ein Reisender, der seinen Weg anhand der Sterne und der allgemeinen Richtung findet.
Wir haben für beide Algorithmen dasselbe neuronale Netz als Untersuchungsgegenstand verwendet. Dies ist von entscheidender Bedeutung, da es uns ermöglicht, die Quelle potenzieller Probleme zu lokalisieren: Wenn wir auf Schwierigkeiten mit bestimmten Aktivierungsfunktionen stoßen, können wir sicher sein, dass es sich nicht um ein Problem mit dem neuronalen Netz selbst handelt, sondern mit der Art und Weise, wie der Optimierungsalgorithmus mit diesen Funktionen interagiert.
Diese Versuchsanordnung ermöglicht es uns, deutlich zu sehen, wie verschiedene Aktivierungsfunktionen im Zusammenhang mit verschiedenen Optimierungsansätzen funktionieren. Es ist wichtig anzumerken, dass wir die Generalisierungsfähigkeit des Netzes oder seine Leistung bei neuen Daten bewusst nicht berücksichtigen. Unser Ziel ist es, den gegenseitigen Einfluss von Aktivierungsfunktionen und Optimierungsalgorithmen, ihre Kompatibilität und die Effizienz ihrer Interaktion zu untersuchen.
Mit diesem Ansatz können wir uns ein klares Bild davon machen, wie verschiedene Optimierungsstrategien bei verschiedenen Aktivierungsfunktionen abschneiden, ohne den Einfluss externer Faktoren. Die Ergebnisse des Experiments zeigen deutlich, dass ein „blinder“ externer Optimierer manchmal effizienter sein kann als ein Algorithmus, der über vollständige Informationen über die Netzstruktur verfügt.
Für alle Aktivierungsfunktionen zeigte das externe ADAMm eine schnelle und stabile Konvergenz, was darauf hindeutet, dass die Eigenschaften der Aktivierungsfunktion keine wesentliche Rolle für sie spielen. Das normale, integrierte ADAM stieß dagegen auf ernste Probleme.
Betrachten wir nun das Verhalten des eingebauten ADAM auf jede der Aktivierungsfunktionen und fassen wir sie in den folgenden Schlussfolgerungen zusammen:
1. Problematische Funktionen (Hängenbleiben oder langsame Konvergenz):
- TanH (hyperbolischer Tangens)
- AlgSigm (algebraisches Sigmoid)
- SERF (sigmoid-gewichtete exponentielle Begradigung)
- Snake (periodische Funktion)
2. Erfolgreiche Fälle (Konvergenz):
- RatSigm (rationales Sigmoid), die beste der Sigmoid-Funktionen
- SoftPlus
- BentIdent
- SiLU (Swish), der Beste der zweiten Gruppe
- ACON (adaptive Funktion), die beste der periodischen Funktionen
3. Muster:
Klassische Sigmoidfunktionen (TanH, AlgSigm) haben das Problem, dass sie stecken bleiben. Modernere adaptive Funktionen (ACON, SiLU) zeigen eine bessere Konvergenz. Von den periodischen Funktionen zeigt ACON Konvergenz, während Snake stecken bleibt.
In der vorliegenden Studie wird daher ein umfassender Ansatz zur Optimierung neuronaler Netze entwickelt, der die Gewichtskontrolle, die Grenzen der Aktivierungsfunktion und den Lernprozess in einem einzigen, miteinander verbundenen System vereint. Die wichtigste Neuerung war die Einführung der Methoden GetBoundUp und GetBoundLo, die es jeder Aktivierungsfunktion ermöglichen, ihre eigenen Grenzen zu definieren, die dann zur Verwaltung der Netzgewichte verwendet werden. Dieser Mechanismus wird durch ein System zur frühzeitigen Beendigung der Summierung bei Erreichen von Grenzen ergänzt, das nicht nur redundante Berechnungen, insbesondere in großen Netzen, verhindert, sondern auch die Kontrolle der Werte vor Anwendung der Aktivierungsfunktion gewährleistet.
Ein besonders wichtiges Element war der Mechanismus der Gewichtsreflexion, der im Gegensatz zum traditionellen Pruning oder zur Normalisierung eine Stagnation beim Lernen verhindert, indem er die Gewichte „schüttelt“, wenn sie ihre Grenzen erreichen. Diese Lösung ermöglicht es, die Gewichte auch in kritischen Situationen zu ändern, um die Kontinuität des Trainingsprozesses zu gewährleisten. Die Systemintegration all dieser Komponenten schafft einen effektiven Mechanismus zur Verhinderung von Gewichtsstreuung, ohne dass die Flexibilität des Trainings verloren geht, was besonders wichtig ist, wenn mit verschiedenen Aktivierungsfunktionen gearbeitet wird. Dieser integrierte Ansatz löst nicht nur das Problem der Gewichtskontrolle, sondern eröffnet auch neue Perspektiven für das Verständnis der Wechselwirkungen zwischen den verschiedenen Komponenten des neuronalen Netzes während des Trainings.
Die Studie deutet nicht darauf hin, dass ADAM beim Training neuronaler Netze nutzlos ist, sondern lenkt die Aufmerksamkeit auf seine Reaktion auf bestimmte Aktivierungsfunktionen. Für große neuronale Netze gibt es vielleicht überhaupt keine Alternative (außer den modernen Analoga der Gradientenabstiegsmethoden). Dies könnte das nächste Thema sein, um die Effizienz von ADAM (als Vertreter moderner Optimierungsalgorithmen, die die Methode eines Rückwärtsdurchlaufs verwenden) im Zusammenhang mit großen neuronalen Netzen zu untersuchen, sowie den Einfluss der Wahl der Aktivierungsfunktionen auf die Generalisierungsfähigkeit des Netzes und die Stabilität seines Betriebs bei neuen Daten.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | MLPa.mqh | Skript | Neuronales MLP-Netz mit ADAM |
| 4 | Tests and Drawing act func.mq5 | Skript | Skript zur visuellen Konstruktion von Aktivierungsfunktionen |
| 5 | Test act func in training.mq5 | Skript | MLP-Trainingsskript mit ADAM und ADAMm |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16845
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze im Handel: Ein Agent mit geschichtetem Speicher
Neuronale Netze im Handel: Ein Agent mit geschichtetem Speicher
 Diskretisierungsmethoden für Preisbewegungen in Python
Diskretisierungsmethoden für Preisbewegungen in Python
 Evolutionärer Handelsalgorithmus mit Verstärkungslernen und Auslöschung von schwachen Individuen (ETARE)
Evolutionärer Handelsalgorithmus mit Verstärkungslernen und Auslöschung von schwachen Individuen (ETARE)
 Big Bang – Big Crunch (BBBC) Algorithmus
Big Bang – Big Crunch (BBBC) Algorithmus
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Ich glaube, es gab ein Missverständnis zwischen dem, was ich sagen wollte, und dem, was ich tatsächlich in Textform formuliert habe.
Ich werde versuchen, dieses Mal etwas deutlicher zu sein 🙂 Wenn wir KLASSIFIZIEREN Dinge, wie Bilder, Gegenstände, Zahlen, Töne, kurz gesagt, wo Wahrscheinlichkeiten herrschen werden. Wir müssen die Werte innerhalb des neuronalen Netzes so begrenzen, dass sie in einen bestimmten Bereich fallen. Dieser Bereich liegt in der Regel zwischen -1 und 1, kann aber auch zwischen 0 und 1 liegen, je nachdem, wie schnell die Trefferquote ist und wie die Eingangsinformationen behandelt werden, mit denen das Netz in Berührung kommen soll, und wie es sein eigenes Lernen am besten steuert, um die Klassifizierung der Dinge zu erstellen. IN DIESEM FALL BENÖTIGEN WIR Aktivierungsfunktionen. Genau, um die Werte in diesem Bereich zu halten. Am Ende haben wir die Möglichkeit, Werte in Bezug auf die Wahrscheinlichkeit zu generieren, dass die Eingabe das eine oder das andere ist. Das ist eine Tatsache, und ich bestreite sie nicht. Das geht so weit, dass wir die Eingabedaten oft normalisieren oder standardisieren müssen.
Neuronale Netze werden jedoch nicht nur zur Klassifizierung von Dingen verwendet, sondern können und werden auch zur Speicherung von Wissen eingesetzt. In diesem Fall sollten Aktivierungsfunktionen in vielen Fällen verworfen werden. Detail: Es gibt Fälle, in denen wir Dinge einschränken müssen. Aber das sind sehr spezielle Fälle. Das liegt daran, dass diese Funktionen das Netz daran hindern, seinen Zweck zu erfüllen. Und der besteht eben darin, Wissen zu bewahren. Und in der Tat stimme ich teilweise mit Stanislav Korotkys Bemerkung überein, dass das Netz in diesen Fällen auf etwas reduziert werden kann, das einer einzelnen Schicht entspricht, wenn wir keine Aktivierungsfunktionen verwenden. Aber wenn dies geschieht, wäre es einer von mehreren Fällen, da es Fälle gibt, in denen ein einzelnes Polynom mit mehreren Variablen nicht ausreicht, um Wissen zu repräsentieren, oder besser gesagt zu behalten. In diesem Fall müssten wir zusätzliche Schichten verwenden, damit das Ergebnis wirklich repliziert werden kann. Oder es können neue Schichten erzeugt werden. Es ist ein bisschen verwirrend, das so zu erklären, ohne eine richtige Demonstration. Aber es funktioniert.
Das große Problem ist, dass in den letzten 10 Jahren, wenn ich mich recht erinnere, alles mit künstlicher Intelligenz und neuronalen Netzen in Verbindung gebracht wurde, weil es gerade in Mode ist. Obwohl das Geschäft erst in den letzten fünf Jahren so richtig in Schwung gekommen ist. Viele Menschen wissen gar nicht, was sie wirklich sind. Oder wie sie eigentlich funktionieren. Das liegt daran, dass alle, die ich sehe, immer fertige Frameworks verwenden. Und das hilft überhaupt nicht, um zu verstehen, wie neuronale Netze funktionieren. Sie sind einfach eine Gleichung mit mehreren Variablen. Sie werden schon seit Jahrzehnten in akademischen Kreisen untersucht. Und selbst als sie aus der akademischen Welt kamen, wurden sie nie mit so viel Tamtam angekündigt. In der Anfangsphase und für eine lange Zeit WURDEN AKTIVIERUNGSFUNKTIONEN NICHT VERWENDET. Aber der Zweck der Netze, die damals noch nicht einmal neuronale Netze genannt wurden, war ein anderer. Weil aber drei Leute von ihnen profitieren wollten, wurden sie in einer Art und Weise propagiert, die meiner Meinung nach nicht ganz richtig war. Richtig wäre es, zumindest aus meiner Sicht, wenn sie richtig erklärt würden. Eben um nicht so viel Verwirrung bei vielen Menschen zu stiften. Aber gut, die drei verdienen eine Menge Geld, während die Menschen mehr verloren sind als ein Hund, der von einem Umzugswagen gefallen ist. Auf jeden Fall möchte ich Sie nicht davon abhalten, neue Artikel zu schreiben, Andrey Dik, aber ich möchte, dass Sie weiter studieren und versuchen, sich noch tiefer in dieses Thema zu vertiefen. Ich habe gesehen, dass Sie versucht haben, das System mit reinem MQL5 zu erstellen. Was im Übrigen sehr gut ist. Das hat meine Aufmerksamkeit erregt und mich erkennen lassen, dass Ihr Artikel sehr gut geschrieben und geplant ist. Ich wollte Sie nur auf diesen speziellen Punkt aufmerksam machen und Sie dazu bringen, ein wenig mehr darüber nachzudenken. In der Tat ist dieses Thema sehr interessant und es gibt vieles, was nur wenige wissen. Aber Sie haben sich damit befasst und es studiert.
Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍
...
Ihr Beitrag ist so, als würden Sie sagen: "Ein Turbojet-Triebwerk ist eigentlich eine Dampfmaschine, wie sie ursprünglich konzipiert wurde."
Als Aktivierungsfunktion kann alles verwendet werden, sogar Cosinus, das Ergebnis liegt auf dem Niveau der gängigen Funktionen. Es wird empfohlen, relu (mit Bias 0,1(es wird nichtempfohlen, eszusammen mit der Random-Walk-Initialisierungzu verwenden )) zu verwenden , weil es einfach (schnelles Zählen) und besser lernend ist: Diese Blöcke sind leicht zu optimieren, weil sie linearen Blöcken sehr ähnlich sind.Der einzige Unterschiedbesteht darin, dass ein linearer Gleichrichtungsblock in der Hälfte seinesDefinitionsbereichs 0 ausgibt. Daher bleibt die Ableitung eines linearen Gleichrichtungsblocks überall dort groß, wo der Block aktiv ist. Die Gradienten sind nicht nur groß, sie sind auch konsistent. Die zweite Ableitung der Gleichrichtungsoperation ist überall Null, und die ersteAbleitung ist überall dort 1, wo der Block aktiv ist. Das bedeutet, dass die Richtung des Gradienten für das Lernen viel nützlicher ist, als wenn die Aktivierungsfunktion Effekten zweiter Ordnungunterliegt ... Bei der Initialisierung der affinen Transformationsparameter empfiehlt es sich,allen Elementen von beinen kleinen positiven Wert zuzuweisen, z. B. 0,1. Dann ist es sehr wahrscheinlich, dass der lineare Entzerrungsblock im Anfangszeitpunkt für die meisten Trainingsbeispiele aktiv ist und die Ableitung von Null verschieden ist.
Im Gegensatz zu stückweise linearenBlöcken liegen sigmoidaleBlöcke im größten Teil ihres Definitionsbereichs nahe der Asymptote - sie nähern sich einem hohen Wert, wenn zgegen unendlich tendiert , und einem niedrigen Wert , wenn zgegen minus unendlich tendiert .Eine hohe Empfindlichkeit haben sienur in der Nähe von Null. Aufgrund der Sättigung von sigmoidalen Blöcken wird das Gradientenlernen stark behindert. Daher wird ihre Verwendung als versteckte Blöcke in Vorwärtspropagationsnetzen heutzutage nicht empfohlen ... Wenn es notwendig ist, eine sigmoidale Aktivierungsfunktion zu verwenden, ist es besser, den hyperbolischen Tangens anstelle des logistischen Sigmoid zu nehmen . Sie ist näher an der Identitätsfunktion in dem Sinne, dass tanh(0) = 0, während σ(0) = 1/2 ist. Da tanh in der Nähe von Nulleiner Identitätsfunktion ähnelt ,ähnelt das Training eines tiefen neuronalenNetzes dem Training eines linearen Modells , vorausgesetzt, die Aktivierungssignale des Netzes können niedrig gehalten werden.In diesem Fall wird das Training eines Netzes mit der Aktivierungsfunktion tanh vereinfacht.
Für lstm müssen wir sigmoid oder arctangent verwenden(es wird empfohlen, den Offsetfür die Vergessensöffnung auf 1 zu setzen): Sigmoidale Aktivierungsfunktionen werden immer noch verwendet, aber nicht in Feedforward-Netzen . Rekurrente Netze, viele probabilistische Modelle und einige Autokoder haben zusätzliche Anforderungen, die die Verwendung von stückweise linearen Aktivierungsfunktionen ausschließen und sigmoidale Blöcke trotz Sättigungsproblemen geeignetermachen .
Lineare Aktivierung und Parameterreduktion: Wenn jede Schicht des Netzes nur aus linearen Transformationen besteht , ist das Netz als Ganzes linear. Einige Schichten können jedoch auch rein linear sein - das ist in Ordnung. Betrachten wir eine Schicht eines neuronalen Netzes, die n Eingänge und p Ausgängehat . Sie kann durch zwei Schichten ersetzt werden, eine mit einer Gewichtsmatrix U und die andere mit einer Gewichtsmatrix V. Wenn die erste Schicht keine Aktivierungsfunktion hat, haben wir die Gewichtsmatrix der ursprünglichen Schicht auf der Grundlage von Wim Wesentlichen in Multiplikatoren zerlegt . Wenn Uq Ausgänge erzeugt , dann enthaltenU und V zusammen nur (n + p)q Parameter, während Wnp Parameter enthält . Bei kleinen q können die Parametereinsparungenerheblich sein. Der Vorteil ist eine Einschränkung - die lineare Transformation muss einen niedrigen Rang haben, aber solche Verbindungen mit niedrigem Rang sind oft ausreichend. Lineare versteckte Blöcke bietenalso eine effiziente Möglichkeit, die Anzahl derNetzparameterzu reduzieren.
Relu ist besser für tiefe Netze: Trotz der Beliebtheit der Rektifikation in frühen Modellen wurde sie in den 1980er Jahren fast durchgängig durch Sigmoid ersetzt, weil sie für sehr kleine neuronale Netzebesser funktioniert .
Aber sie ist generell besser: Bei kleinen Datensätzen ist die Verwendung von gleichrichtenden Nichtlinearitäten sogar wichtiger als das Lernen von Gewichten der verborgenen Schicht.Zufällige Gewichte reichen aus, um nützlicheInformationen durch das Netz mit linearer Entzerrungweiterzugeben, so dass die klassifizierendeAusgabeschicht darauf trainiert werden kann, verschiedene MerkmalsvektorenaufKlassenidentifikatorenabzubilden. Wenn mehr Daten zur Verfügung stehen, beginnt der Lernprozess, so viel nützliches Wissen zu extrahieren , dass er die zufällig ausgewähltenParameter übertrifft... Das Lernen ist in gleichgerichteten linearen Netzen viel einfacher als in tiefen Netzen, derenAktivierungsfunktionen durch Krümmung oder zweiseitige Sättigung gekennzeichnet sind...
Ich glaube, es gab ein Missverständnis zwischen dem, was ich sagen wollte, und dem, was ich tatsächlich in Textform dargelegt habe.
Ich werde versuchen, dieses Mal etwas deutlicher zu sein 🙂 Wenn wir KATEGORISIEREN Dinge wie Bilder, Objekte, Formen, Geräusche, kurz gesagt, wo Wahrscheinlichkeiten herrschen werden. Wir müssen die Werte im neuronalen Netz so einschränken, dass sie in einen bestimmten Bereich fallen. Normalerweise liegt dieser Bereich zwischen -1 und 1. Er kann aber auch zwischen 0 und 1 liegen, je nachdem, wie schnell, mit welcher Geschwindigkeit und auf welche Weise die Eingangsinformationen, die das Netz lernen soll, verarbeitet werden und wie es sein Lernen am besten ausrichtet, um eine Klassifizierung der Dinge zu erstellen. IN DIESEM FALL BENÖTIGEN WIR Aktivierungsfunktionen. Sie sollen die Werte innerhalb dieses Bereichs halten. Am Ende werden wir ein Mittel haben, um Werte in Bezug auf die Wahrscheinlichkeit zu erzeugen, dass die Eingaben das eine oder das andere sind. Das ist eine Tatsache, und ich bestreite sie nicht. Das geht so weit, dass wir die Eingabedaten oft normalisieren oder standardisieren müssen.
Neuronale Netze werden jedoch nicht nur zur Klassifizierung verwendet, sondern können und werden auch zur Wissensspeicherung eingesetzt. In diesem Fall sollten Aktivierungsfunktionen in vielen Fällen verworfen werden. Detail: Es gibt Fälle, in denen wir etwas einschränken müssen. Aber das sind sehr spezielle Fälle. Der Punkt ist, dass diese Funktionen das Netz daran hindern, seinen Zweck zu erfüllen. Und der besteht darin, Wissen zu bewahren. Und in der Tat stimme ich teilweise mit Stanislav Korotskys Bemerkung überein, dass das Netz in solchen Fällen auf etwas reduziert werden kann, das einer einzelnen Schicht entspricht, wenn man keine Aktivierungsfunktionen verwendet. Aber wenn dies geschieht, ist es einer von mehreren Fällen, denn es gibt Fälle, in denen ein einzelnes Polynom mit mehreren Variablen nicht ausreicht, um Wissen zu repräsentieren oder, besser gesagt, zu speichern. In diesem Fall müssen wir zusätzliche Schichten verwenden, damit das Ergebnis tatsächlich reproduziert werden kann. Alternativ können auch neue Schichten erzeugt werden. Es ist ein bisschen verwirrend, das so zu erklären, ohne eine richtige Demonstration. Aber es funktioniert.
Das große Problem ist, dass sich in den letzten 10 Jahren, wenn ich mich recht erinnere, alles um künstliche Intelligenz und neuronale Netze gedreht hat, weil jetzt alles in Mode ist. Obwohl das Geschäft erst in den letzten fünf Jahren richtig aufgeblüht ist. Viele Menschen wissen gar nicht, was diese Dinge wirklich sind. Und wie sie eigentlich funktionieren. Das liegt daran, dass alle, denen ich begegne, immer mit Standard-Frameworks arbeiten. Und das hilft überhaupt nicht, um zu verstehen, wie neuronale Netze funktionieren. Es ist nur eine Gleichung mit ein paar Variablen. Sie werden seit Jahrzehnten in der Wissenschaft erforscht. Und selbst wenn sie die akademische Welt verlassen haben, wurden sie nie mit so viel Pomp angekündigt. Ursprünglich, und für eine lange Zeit WURDEN AKTIVIERUNGSFUNKTIONEN NICHT VERWENDET. Aber der Zweck der Netze, die damals noch nicht einmal neuronale Netze genannt wurden, war ein anderer. Aber weil drei Leute daraus Kapital schlagen wollten, wurden sie gehypt, was ich für etwas falsch halte. Richtig wäre es, zumindest aus meiner Sicht, gewesen, ihr Wesen richtig zu erklären. Genau, um nicht in den Köpfen vieler Menschen Verwirrung zu stiften. Aber das ist in Ordnung, die drei verdienen eine Menge Geld und die Leute sind verirrter als ein Hund, der von einem Müllwagen fällt. Wie auch immer, ich möchte Sie nicht davon abhalten, weitere Artikel zu schreiben, Andrew Dick, aber ich möchte, dass Sie weiter lernen und versuchen, noch tiefer in dieses Thema einzutauchen. Ich habe gesehen, dass Sie versucht haben, mit reinem MQL5 ein System zu erstellen. Das ist im Übrigen sehr gut. Es hat meine Aufmerksamkeit erregt und ich habe festgestellt, dass Ihr Artikel sehr gut geschrieben und geplant ist. Ich wollte Sie nur auf diesen Punkt aufmerksam machen und Sie dazu bringen, ein wenig mehr darüber nachzudenken. Dieses Thema ist wirklich sehr interessant und nicht viele Menschen wissen darüber Bescheid. Aber Sie haben es aufgegriffen und recherchiert.
Ja, die Nichtlinearität ist ein indirekter Effekt, den die Aktivierungsphasen haben. Sie waren ursprünglich dazu gedacht, von einem Bereich der Zieldefinition auf einen anderen zu übertragen, zum Beispiel für Klassifikationsaufgaben. "Nichtlinearität" kann auf verschiedene Weise erreicht werden, z. B. durch Erhöhung der Anzahl der Merkmale oder durch deren Transformation oder durch Kernel, die Merkmale transformieren.
Das einfachste Beispiel ist die logistische Regression, die trotz der Aktivierungsfunktion am Ende linear bleibt.
In mehrschichtigen Netzen wird die Nichtlinearität jedoch durch die Anzahl der Schichten mit Aktivierungsfunktionen erreicht, einfach als Folge von Kernel-Transformationen.Historischer Hintergrund:
Sie haben Recht, dass die Konzepte, die der logistischen Regression und den frühen neuronalen Netzen zugrunde liegen, vor den modernen tiefen neuronalen Netzen entwickelt wurden.
Werfen wir einen Blick auf die Chronologie:
Dielogistische Funktion wurde im 19. Jahrhundert entwickelt. Ihre Verwendung als statistisches Modell für die Klassifizierung (logistische Regression) wurde Mitte des 20. Jahrhunderts (etwa in den 1940er bis 50er Jahren) populär.
Das erste mathematische Modell eines Neurons (das Modell von McCulloch und Pitts) mit einer Aktivierungsfunktion erschien 1943. Es verwendete eine einfache Schwellenwertfunktion.
Das Perceptron, ein einschichtiges neuronales Netz, wurde 1958 von Frank Rosenblatt entwickelt. Es verwendete eine Schwellenwert-Aktivierungsfunktion und konnte nur linear trennbare Probleme lösen.
DerDurchbruch im Bereich des tiefen Lernens und der mehrschichtigen Netze kam erst mit der Einführung des Backpropagation-Algorithmus, der 1986 von Rumelhart, Hinton und Williams populär gemacht wurde.
Dieser Algorithmus machte das Training mehrschichtiger neuronaler Netze praktisch und zeigte, dass dafür nicht nur Schwellenwerte, sondern auch differenzierbare nichtlineare Aktivierungsfunktionen (wie Sigmoid und später ReLU) erforderlich sind.
Schlussfolgerung:
Historisch gesehen stellt sich Folgendes heraus:
Zunächst gab es Modelle (logistische Regression, Perceptron), die im Wesentlichen einschichtige Modelle waren.
Bei diesen Modellen wirkte die Aktivierungsfunktion tatsächlich wie eine Transformation in den gewünschten Bereich (von einer linearen Summe zu einer binären Klasse oder Wahrscheinlichkeit), da das gesamte Modell linear blieb.
Später, mit dem Aufkommen der mehrschichtigen Netze, kam der Aktivierungsfunktion eine neue, wesentlich wichtigere Rolle zu - die Einführung von Nichtlinearität in die versteckten Schichten, damit das Netz lernen kann.