Diskretisierungsmethoden für Preisbewegungen in Python
Einführung
Jeder Entwickler von Handelssystemen sieht sich früher oder später mit einer grundlegenden Frage konfrontiert: Wie kann man Marktdaten für die Analyse richtig auswertet? Der herkömmliche Ansatz mit festen Intervallen ist vergleichbar mit dem Versuch, die Herzfrequenz eines Sportlers alle 5 Minuten zu messen, unabhängig davon, ob er gerade sprintet oder sich ausruht. In Zeiten hoher Aktivität gehen wichtige Informationen in einem einzigen Balken verloren, während wir in ruhigen Stunden Dutzende leerer Balken erhalten, was zu Informationsrauschen führt.
Bei der Arbeit an algorithmischen Strategien beobachte ich oft, wie sich starke Kursbewegungen innerhalb von Standardzeitrahmen „auflösen“. Während der Veröffentlichung einer wichtigen Nachricht kann sich der Markt in einer Minute mehr bewegen als in den Stunden zuvor. In diesem Fall entgeht unserem System, das seinem winzigen Zeitrahmen treu bleibt, der ganze Reichtum dieser Mikrostruktur.
Dieses Problem veranlasste mich, mich eingehend mit alternativen Methoden zur Diskretisierung von Preisdaten zu befassen. In diesem Artikel werde ich meine praktischen Erfahrungen mit der Entwicklung einer Python-Bibliothek teilen, die eine breite Palette von Ansätzen zur Balkenbildung implementiert – von klassischen Volumen- und Range Bars bis hin zu exotischeren Methoden wie Renko und Kagi.
Wir werden nicht nur die technischen Aspekte der Umsetzung, sondern auch die mathematische Rechtfertigung jeder Methode betrachten. Besonderes Augenmerk werden wir auf die Integration mit dem MetaTrader 5 legen – dadurch wird unsere Lösung für den realen Handel praktisch einsetzbar. Der Code ist quelloffen, an realen Daten getestet und – was am wichtigsten ist – für den Echtzeitbetrieb optimiert.
Für Entwickler ist es interessant, sich mit den Details der Implementierung von Streaming Bar Updates und Leistungsoptimierungen zu beschäftigen. Händler erhalten wertvolle Einblicke, wie verschiedene Bar-Typen ihre Handelsstrategien verbessern können. Und für diejenigen, die sich intensiv mit der Datenanalyse befassen, habe ich einen Abschnitt über den statistischen Vergleich der Effizienz verschiedener Ansätze vorbereitet.
Einstellung Diskretisierungsproblem
Als ich anfing, mich ernsthaft mit dem algorithmischen Handel zu beschäftigen, quälte mich ständig eine Frage: Warum sind wir so auf Zeitrahmen fixiert? Was sehen wir, wenn wir uns das Fünf-Minuten-Chart des EURUSD während der EZB-Nachrichtenveröffentlichung ansehen? Ein riesiger Balken, hinter dem sich eine Bewegung von 80 Pips mit fünf Kehrtwendungen verbirgt. Und eine Stunde später – eine Reihe von kleinen Balken, in denen der Preis feststeckt.
Amüsanterweise bin ich bei meiner früheren Tätigkeit, bei der ich den Netzwerkverkehr analysierte, auf ein ähnliches Problem gestoßen. Auch hier sind wir von festen Intervallen zu einer adaptiven Diskretisierung übergegangen – wir sammeln Pakete nicht nach Zeit, sondern nach Datenvolumen oder nach Ereignissen. Dann dämmerte es mir: Warum nicht den gleichen Ansatz auf Marktdaten anwenden?
Lassen Sie uns darüber nachdenken, was die Preisentwicklung wirklich bestimmt. Zeit? Nein. Handelsvolumen? Wahrscheinlich. Aktivität der wichtigsten Akteure? Definitiv. In der Tat sind alle diese Faktoren wichtig, aber zu verschiedenen Zeitpunkten spielt der eine oder andere die Hauptrolle.
Stellen wir uns einen typischen Handelstag vor. Morgens, geringe Aktivität, seltene Angebote. Wir können hier sicher H1 verwenden. Wenn die Londoner Sitzung beginnt, kommt es zu einer Explosion des Volumens. Eine Diskretisierung des Volumens ist erforderlich. Während Nachrichtenereignissen gibt es starke Bewegungen; Range Bars funktionieren besser. Und in ruhigen und trendigen Zeiten schneiden Renko oder Kagi gut ab.
Deshalb habe ich beschlossen, ein universelles Werkzeug zu entwickeln, eine Art Schweizer Taschenmesser für die Arbeit mit Marktdaten. Skript – ein Modul in Python, das Folgendes kann:
- eine Verbindung zum MetaTrader 5 herstellt und Echtzeitdaten abruft,
- verschiedene Arten von Balken im Handumdrehen erstellt,
- automatisch die optimale Diskretisierungsmethode auswählt,
- all dies in einem leicht zu analysierenden Format darstellt.
Klingt kompliziert? Auf den ersten Blick, ja. Aber wenn wir die Aufgabe in Teile zerlegen, wird alles einfacher. In den folgenden Abschnitten werde ich zeigen, wie ich dies umgesetzt habe und welche interessanten Entdeckungen ich dabei gemacht habe.
Vorbereiten der Umgebung
Bei jedem ernsthaften Projekt bereitet die Vorbereitung der Umgebung Kopfzerbrechen, besonders wenn man gleichzeitig mit MetaTrader 5 und Python arbeitet. Nach mehreren Monaten des Experimentierens habe ich die optimale Kombination gefunden:
- Python 3.9,
- MetaTrader 5 für den Zugriff auf die Marktdaten,
- pandas und numpy für die Datenverarbeitung,
- scipy und statsmodels für die statistische Analyse,
- mplfinance für die grafische Darstellung,
Spaßfaktor: Wir können Plotly zur Visualisierung verwenden, aber die gute alte Matplotlib ist schneller. Und beim algorithmischen Handel zählt jede Millisekunde.
Diskretisierungsmethoden für Zeitreihen
Wissen Sie, was die Analyse von Börsendaten und die Quantenmechanik gemeinsam haben? In beiden Fällen verändert die Methode der Beobachtung den Gegenstand der Beobachtung selbst. Die Art und Weise, wie wir Marktdaten auswerten, bestimmt weitgehend, was wir darin sehen.
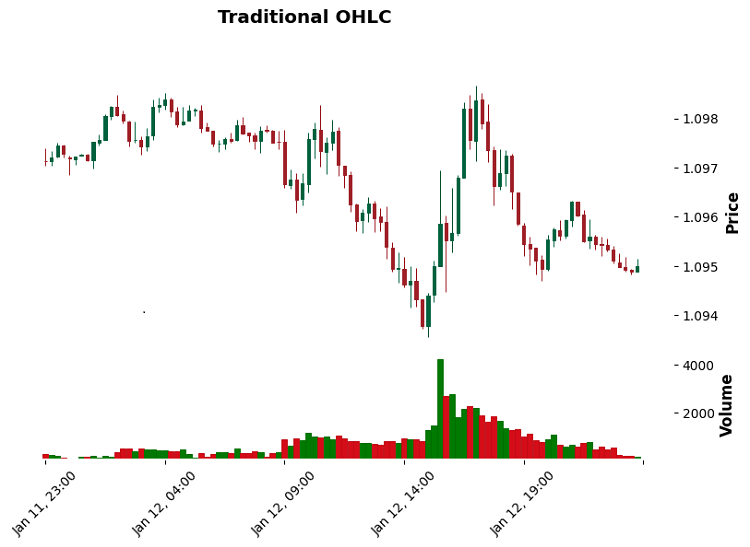
Fangen wir beim Einfachsten an – den Volume Bars. Hier dreht sich alles um das Handelsvolumen. Sagen wir, wir schließen den Balken, wenn wir 100 Kontrakte erreicht haben. Einfach? Ja: Effizient? Ja: Vor allem dann, wenn Sie die Aktivitäten der wichtigsten Akteure erfassen müssen. Ich erinnere mich an den Goldhandel. Ein Standardzeitrahmen zeigte eine ziemlich routinemäßige Bewegung, während die Volume Bars eindeutig die Anhäufung von Positionen durch einen wichtigen Teilnehmer zeigten.
Range Bars sind die nächste Stufe. Hier sehen wir uns die Preisspanne an. 10 bestandene Punkte bedeuten einen neuen Balken. Dabei spielt es keine Rolle, ob es in einer Sekunde oder in einer Stunde passiert. Bei Trendbewegungen funktioniert es wie am Schnürchen: kein Rauschen, reine Trendstruktur.
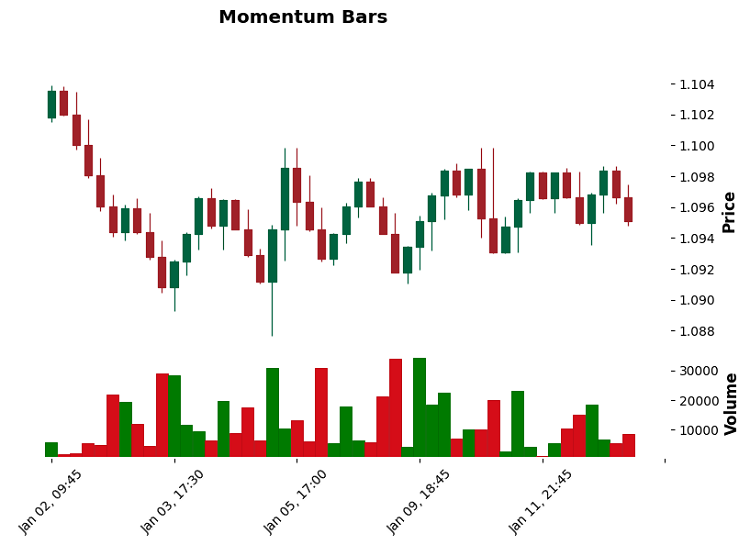
Momentum Bars sind mein persönlicher Favorit. Sie verfolgen die Bewegungsdynamik. Stellen Sie sich vor, Sie messen nicht die Entfernung, sondern die Rate der Preisänderung. Bei starken Bewegungen liefern sie erstaunliche Details, und bei der flachen Bewegung entstehen keine Unschärfen.
Volatility Regime erfordern ein Höchstmaß an Geschicklichkeit. Sie passen sich an die aktuelle Marktvolatilität an. In ruhigen Zeiten dehnen sich die Balken aus, in stürmischen Zeiten ziehen sie sich zusammen. Sie eignen sich besonders gut für die Märkte mit Kryptowährungen, wo sich die Volatilität innerhalb weniger Minuten dramatisch ändern kann.
Swing-point Bars fangen lokale Extreme auf. Es ist so, als ob Sie ein Chart von Hoch zu Hoch oder Tief zu Tief zeichnen würden. Ähnlich wie die klassische Price Action, aber mit einer präzisen mathematischen Grundlage.
Acceleration Bars – relativ neue Methode. Sie beobachten den Preisanstieg. Kennen Sie diese Momente, in denen die Bewegung plötzlich schneller wird? Das sind die, die die Acceleration Bars auffangen. Sie sind besonders nützlich beim Scalping, wenn es darauf ankommt, den Beginn eines Impulses zu erwischen.
Implementierung von Volumen- und Range Bars
Volumen- und Range Bars sind wie zwei verschiedene Mikroskope zur Untersuchung des Marktes. Die Volume Bars konzentrieren sich auf die Händleraktivität, während sich die Range Bars auf die Volatilität konzentrieren. Bei der Arbeit mit ihnen habe ich einige interessante Entdeckungen gemacht.
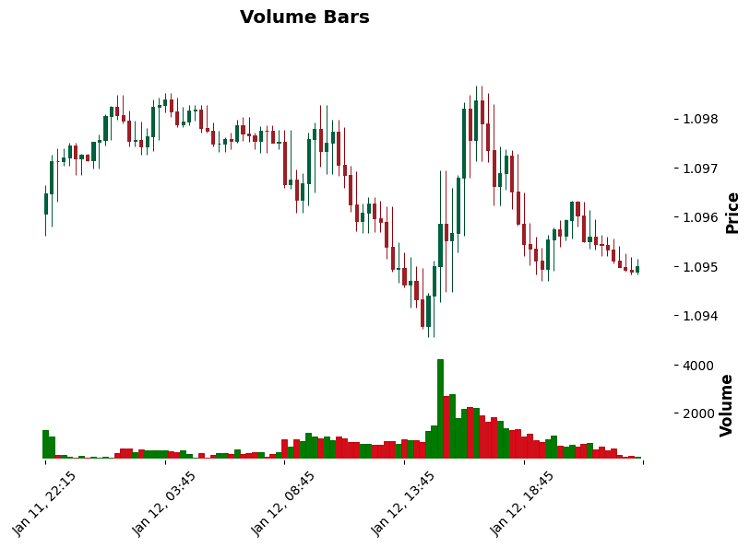
Betrachten wir zunächst die Balken der Volumina. Das Paradoxe daran ist, dass sie sich in Zeiten hoher Aktivität wie eine Feder zusammenziehen – zwanzig Balken passen in eine normale Minute. Und zu ruhigen Zeiten kann ein Volume Bars für einen halben Tag reichen. Das ist richtig – wir wollen den Markt in seinem natürlichen Rhythmus sehen.
def create_volume_bars(self, volume_threshold: float) -> pd.DataFrame: df = self.get_raw_data() bars = [] current_volume = 0 bar_open = df.iloc[0]['open'] bar_high = df.iloc[0]['high'] bar_low = df.iloc[0]['low'] bar_time = df.iloc[0]['time'] for _, row in df.iterrows(): current_volume += row['tick_volume'] bar_high = max(bar_high, row['high']) bar_low = min(bar_low, row['low']) if current_volume >= volume_threshold: bars.append({ 'time': bar_time, 'open': bar_open, 'high': bar_high, 'low': bar_low, 'close': row['close'], 'volume': current_volume }) current_volume = 0 bar_open = row['close'] bar_high = row['high'] bar_low = row['low'] bar_time = row['time']
Mit Range Bars wurde es sogar noch interessanter. Es hat sich herausgestellt, dass sie hervorragend geeignet sind, Unterstützungs- und Widerstandsniveaus zu erkennen. Warum? Denn jeder Balken hat eine feste Größe. Wenn der Kurs ein bestimmtes Niveau erreicht, beginnen die Balken zu „komprimieren“ – dies ist ein klares Signal, dass das Niveau signifikant ist.
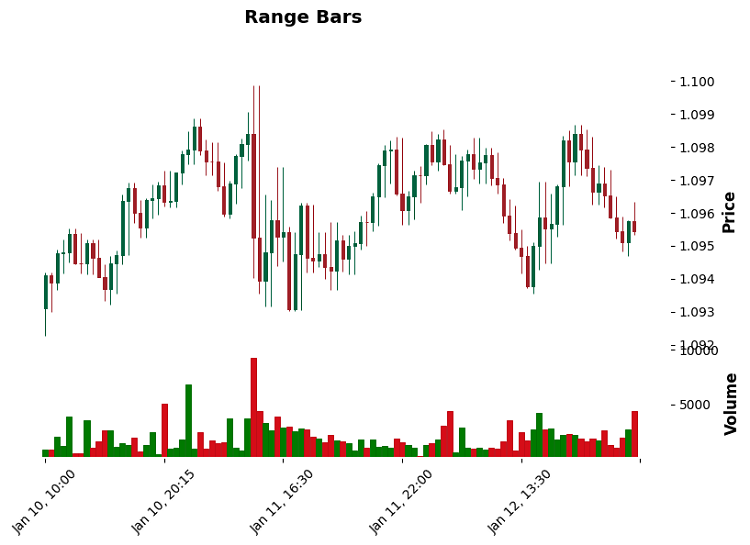
Übrigens, was die Auswahl eines Schwellenwertes für beide Arten von Balken betrifft... Ich habe eine Reihe von Ansätzen ausprobiert, aber eine einfache Regel funktioniert am besten: Für Volume Bars nehme ich 0,1 % des durchschnittlichen Tagesvolumens, für Range Bars sind es 0,5 ATR. Manchmal sind einfache Lösungen wirklich besser als komplexe Lösungen.
Momentum-basierte Balken (bilden einen Balken, wenn sich ein bestimmtes Bewegungsmomentum ansammelt)
Momentum-Balken haben sich als echte Entdeckung erwiesen. Dabei entdeckte ich, wie sich der Markt ruckartig bewegt – erst staut sich die Energie, dann wird sie schlagartig freigesetzt. Ich habe es folgendermaßen umgesetzt:
def create_momentum_bars(self, momentum_threshold: float) -> pd.DataFrame: df = self.get_raw_data() bars = [] bar_open = df.iloc[0]['open'] bar_high = df.iloc[0]['high'] bar_low = df.iloc[0]['low'] bar_time = df.iloc[0]['time'] current_volume = 0 for _, row in df.iterrows(): momentum = abs(row['close'] - bar_open) # Key point is to calculate the momentum bar_high = max(bar_high, row['high']) bar_low = min(bar_low, row['low']) current_volume += row['tick_volume'] if momentum >= momentum_threshold: # Threshold has been crossed - we are forming a new bar bars.append({ 'time': bar_time, 'open': bar_open, 'high': bar_high, 'low': bar_low, 'close': row['close'], 'volume': current_volume, 'momentum': momentum # Added for analysis }) # Reset parameters for a new bar bar_open = row['close'] bar_high = row['high'] bar_low = row['low'] bar_time = row['time'] current_volume = 0
Beim Test auf EURUSD zeigte diese Implementierung hervorragende Ergebnisse, insbesondere bei Nachrichten. Jeder signifikante Impuls bildet einen separaten Balken, der ein viel klareres Bild der Bewegung vermittelt. Der dynamische Schwellenwert momentum_threshold = 0,8 * ATR für einen ruhigen Markt, 1,2 * ATR für einen volatilen Markt erwies sich als optimales Gleichgewicht zwischen Empfindlichkeit und Rauschfilter.
Volatility Regime (adaptive Änderung der Balkengröße basierend auf dem Volatilitätsmodus)
Beim Handel mit Kryptowährungen ist mir etwas Seltsames aufgefallen: Standard-Zeitrahmen verwandeln sich bei starken Volatilitätsspitzen in Brei. Und dann kam mir eine Idee: Wie wäre es, wenn sich die Balkengröße selbst an die aktuellen Marktbedingungen anpassen würde?
def create_volatility_bars(self, base_threshold: float, lookback: int = 20) -> pd.DataFrame: df = self.get_raw_data() bars = [] current_volume = 0 # Dynamic ATR calculation to determine the volatility regime df['tr'] = df.apply(lambda x: max( x['high'] - x['low'], abs(x['high'] - x['close'].shift(1)), abs(x['low'] - x['close'].shift(1)) ), axis=1) df['atr'] = df['tr'].rolling(lookback).mean() bar_open = df.iloc[0]['open'] bar_high = df.iloc[0]['high'] bar_low = df.iloc[0]['low'] bar_time = df.iloc[0]['time'] for i, row in df.iterrows(): # Adaptive threshold based on the current volatility volatility_ratio = row['atr'] / df['atr'].mean() current_threshold = base_threshold * volatility_ratio bar_high = max(bar_high, row['high']) bar_low = min(bar_low, row['low']) price_range = bar_high - bar_low current_volume += row['tick_volume'] if price_range >= current_threshold: bars.append({ 'time': bar_time, 'open': bar_open, 'high': bar_high, 'low': bar_low, 'close': row['close'], 'volume': current_volume, 'threshold': current_threshold # For analysis }) bar_open = row['close'] bar_high = row['high'] bar_low = row['low'] bar_time = row['time'] current_volume = 0 return pd.DataFrame(bars)
Der Trick besteht darin, dass die Schwelle für die Balkenbildung nicht feststeht, sondern sich mit dem Markt ändert. In ruhigen Zeiten dehnen sich die Balken aus und geben ein klareres Bild ab. In stürmischen Zeiten ziehen sie sich zusammen, um wichtige Bewegungen nicht zu verpassen.
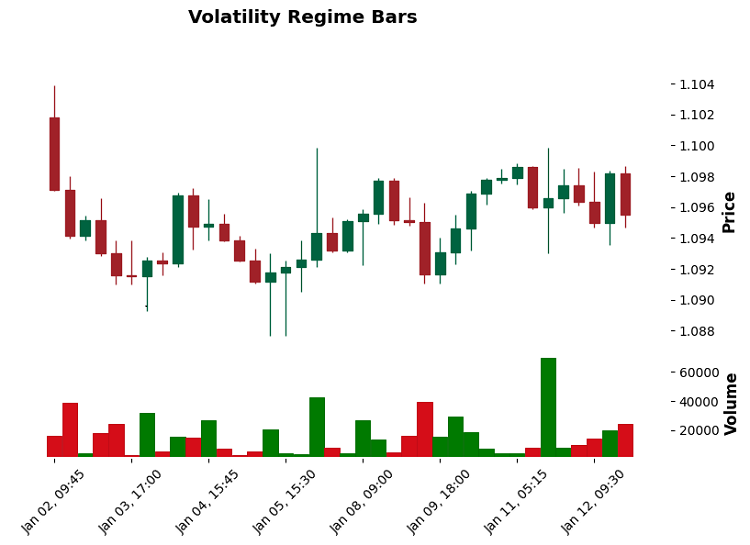
Das Interessanteste wurde bei BTCUSD entdeckt: Vor starken Bewegungen beginnt die Häufigkeit der Balkenbildung exponentiell zuzunehmen. Dies war ein hervorragender Indikator für zukünftige explosive Bewegungen.
Swing-Point-Balken (Bildung von Balken auf der Grundlage lokaler Höchst- und Tiefstwerte)
Bei der Arbeit an Swing-Point-Balken habe ich versucht, das Problem der fehlenden wichtigen Umkehrpunkte zu lösen. Kennen Sie diese Momente, in denen der Kurs eine scharfe Kehrtwendung vollzieht, aber auf einem regulären Chart zu einem einzigen vagen Balken verschwimmt?
def create_swing_bars(self, swing_threshold: float = 0.001) -> pd.DataFrame: df = self.get_raw_data() bars = [] current_swing = 'none' # Current swing direction potential_swing_price = df.iloc[0]['close'] bar_start_price = df.iloc[0]['close'] bar_time = df.iloc[0]['time'] volume_sum = 0 for i, row in df.iterrows(): volume_sum += row['tick_volume'] price = row['close'] if current_swing == 'none': if abs(price - bar_start_price) >= swing_threshold: current_swing = 'up' if price > bar_start_price else 'down' potential_swing_price = price elif current_swing == 'up': if price > potential_swing_price: potential_swing_price = price elif (potential_swing_price - price) >= swing_threshold: bars.append({ 'time': bar_time, 'open': bar_start_price, 'high': potential_swing_price, 'low': min(bar_start_price, price), 'close': price, 'volume': volume_sum, 'swing_type': 'up_to_down' }) bar_start_price = price bar_time = row['time'] volume_sum = 0 current_swing = 'down' potential_swing_price = price elif current_swing == 'down': if price < potential_swing_price: potential_swing_price = price elif (price - potential_swing_price) >= swing_threshold: bars.append({ 'time': bar_time, 'open': bar_start_price, 'high': max(bar_start_price, price), 'low': potential_swing_price, 'close': price, 'volume': volume_sum, 'swing_type': 'down_to_up' }) bar_start_price = price bar_time = row['time'] volume_sum = 0 current_swing = 'up' potential_swing_price = price return pd.DataFrame(bars)
Der Trick bei diesem Code ist, dass er nicht nur nach lokalen Extremen sucht, sondern auch „signifikante“ Umkehrungen verfolgt. Der Schwellenwert ist hier wie ein Rauschfilter. Beim GBPUSD funktioniert der Wert von 0,0012 hervorragend – er schneidet kleine Schwankungen ab, fängt aber eindeutig wichtige Umkehrpunkte ab.
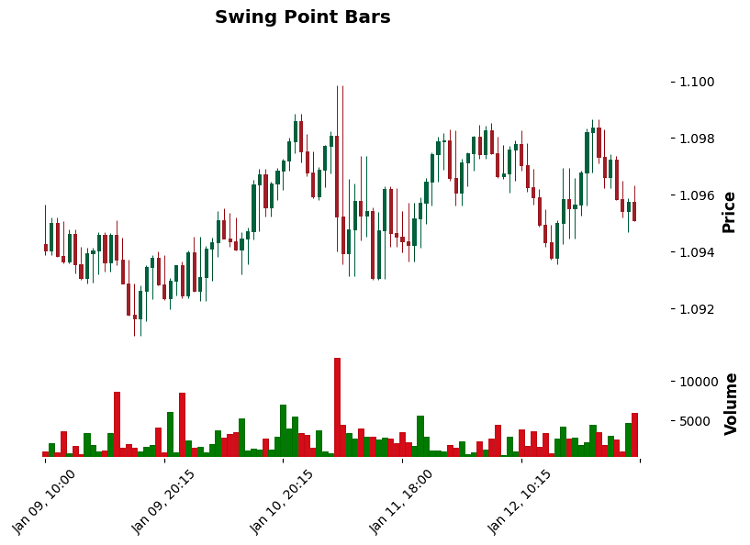
Und wissen Sie was? In sich verändernden Märkten liefern diese Balken erstaunlich klare Signale. Vor allem, wenn man sich die Abfolge der Kehrtwendungen ansieht – sie bilden oft schöne harmonische Muster. Und im Falle einer flachen Bewegung ist die Akkumulation vor einer starken Bewegung deutlich sichtbar.
Acceleration Bars (Balken, die auf Änderungen der PreisAcceleration basieren)
Bei der Beobachtung des Kursverlaufs der S&P500-Futures ist mir ein interessantes Muster aufgefallen: Vor starken Bewegungen beschleunigt der Kurs nicht einfach, sondern folgt einem bestimmten Muster. Dies führte zur Schaffung von zwei Arten von Bars: Speed Bars (verfolgen die Geschwindigkeit) und Acceleration Bars (verfolgen die Acceleration).
def create_acceleration_bars(self, acc_threshold: float = 0.0001) -> pd.DataFrame: df = self.get_raw_data() bars = [] # Calculate price change rate df['speed'] = df['close'].diff() / df.index.to_series().diff().dt.total_seconds() # Calculate acceleration df['acceleration'] = df['speed'].diff() / df.index.to_series().diff().dt.total_seconds() bar_open = df.iloc[0]['open'] bar_high = df.iloc[0]['high'] bar_low = df.iloc[0]['low'] bar_time = df.iloc[0]['time'] acc_sum = 0 volume_sum = 0 for i, row in df.iterrows(): volume_sum += row['tick_volume'] acc_sum += abs(row['acceleration']) bar_high = max(bar_high, row['high']) bar_low = min(bar_low, row['low']) # A new bar is formed when a given acceleration is accumulated if acc_sum >= acc_threshold: bars.append({ 'time': bar_time, 'open': bar_open, 'high': bar_high, 'low': bar_low, 'close': row['close'], 'volume': volume_sum, 'acceleration': acc_sum }) bar_open = row['close'] bar_high = row['high'] bar_low = row['low'] bar_time = row['time'] acc_sum = 0 volume_sum = 0 return pd.DataFrame(bars)
In der Praxis hat sich gezeigt, dass Acceleration Bars vorbörslich bei amerikanischen Aktien gut funktionieren. Sie „sehen“ buchstäblich den Druck, der sich vor einer starken Bewegung aufbaut. Bei Kryptowährungen liefern sie jedoch eine Menge falscher Signale – es gibt zu viel Rauschen in den Daten.
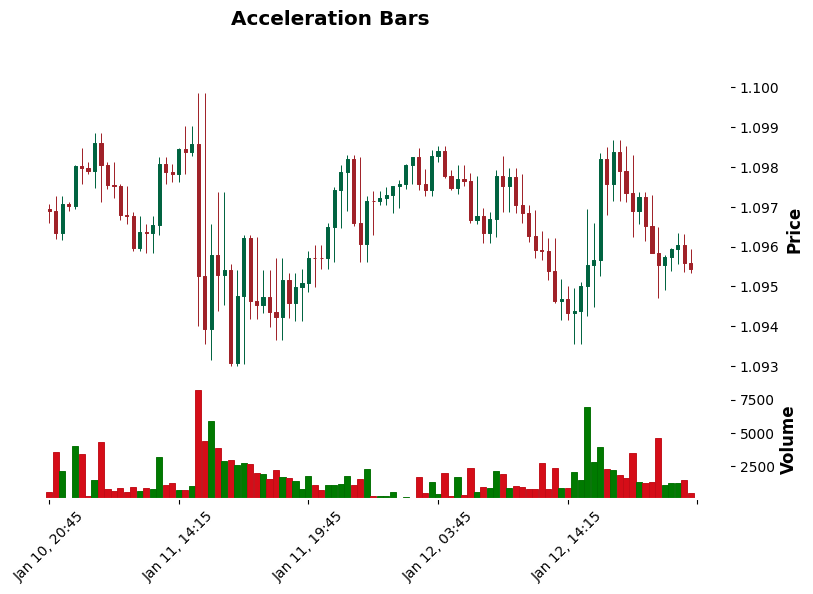
Interessanterweise wurden die besten Ergebnisse beim USDJPY während der Sitzung in Tokio erzielt. Dies ist offensichtlich auf die Besonderheit dieses Marktes zurückzuführen – nach ruhigen Phasen kommt es häufig zu starken Bewegungen.
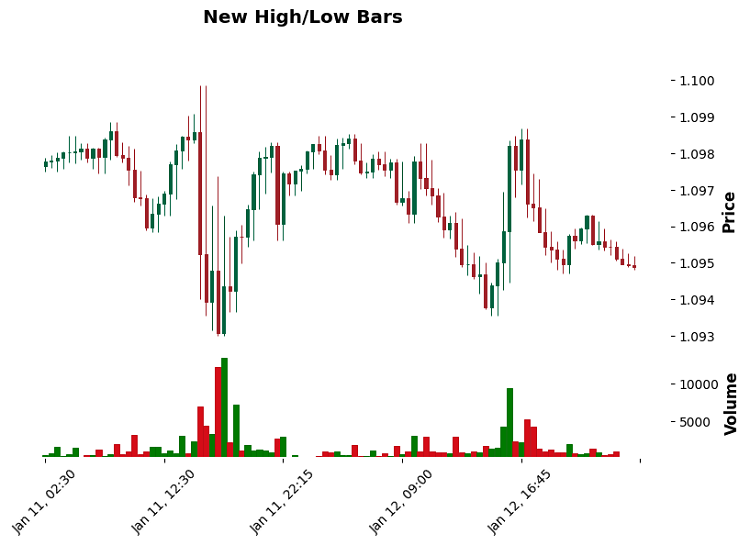
Neue Hoch-/Tiefstwert-Sequenzbalken (Balken, die auf der Geschwindigkeit der Aktualisierung der Extremwerte basieren)
Bei meiner Marktanalyse habe ich festgestellt, dass sich die Stärke eines Trends häufig nicht in der Größe der Bewegung, sondern in der Geschwindigkeit widerspiegelt, mit der er Höchst- oder Tiefststände erreicht. Das macht sich besonders bei Futures bemerkbar – manchmal bewegt sich der Preis in kleinen Schritten, aber sehr beharrlich in eine Richtung.
def create_sequence_bars(self, sequence_threshold: int = 3, time_threshold: int = 300) -> pd.DataFrame: df = self.get_raw_data() bars = [] high_sequence = 0 # New highs counter low_sequence = 0 # New lows counter bar_open = df.iloc[0]['open'] bar_high = df.iloc[0]['high'] bar_low = df.iloc[0]['low'] bar_time = df.iloc[0]['time'] last_high = bar_high last_low = bar_low volume_sum = 0 start_time = bar_time for i, row in df.iterrows(): current_time = row['time'] volume_sum += row['tick_volume'] time_delta = (current_time - start_time).total_seconds() # Check for updated highs/lows if row['high'] > last_high: high_sequence += 1 low_sequence = 0 last_high = row['high'] elif row['low'] < last_low: low_sequence += 1 high_sequence = 0 last_low = row['low'] bar_high = max(bar_high, row['high']) bar_low = min(bar_low, row['low']) # Form a bar if a sequence is reached or the time is exceeded if (high_sequence >= sequence_threshold or low_sequence >= sequence_threshold or time_delta >= time_threshold): bars.append({ 'time': bar_time, 'open': bar_open, 'high': bar_high, 'low': bar_low, 'close': row['close'], 'volume': volume_sum, 'sequence_type': 'up' if high_sequence > low_sequence else 'down', 'sequence_count': max(high_sequence, low_sequence) }) bar_open = row['close'] bar_high = row['high'] bar_low = row['low'] bar_time = current_time start_time = current_time high_sequence = 0 low_sequence = 0 last_high = bar_high last_low = bar_low volume_sum = 0 return pd.DataFrame(bars)
Beim EURUSD hat sich dieser Ansatz bei Trendbewegungen als besonders effizient erwiesen – die Beharrlichkeit des Kurses beim Durchbrechen von Niveaus ist deutlich sichtbar. Interessanterweise funktioniert sequence_threshold = 3 am besten. Bei einem höheren Wert verpassen wir wichtige Umkehrungen, bei einem niedrigeren Wert erhalten wir eine Menge Rauschen.
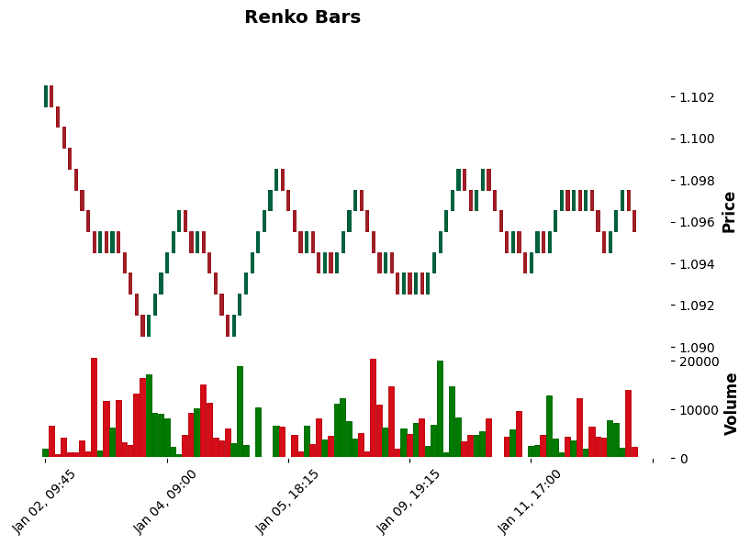
Sehen wir uns auch an, wie die Renko-Balken aussehen:
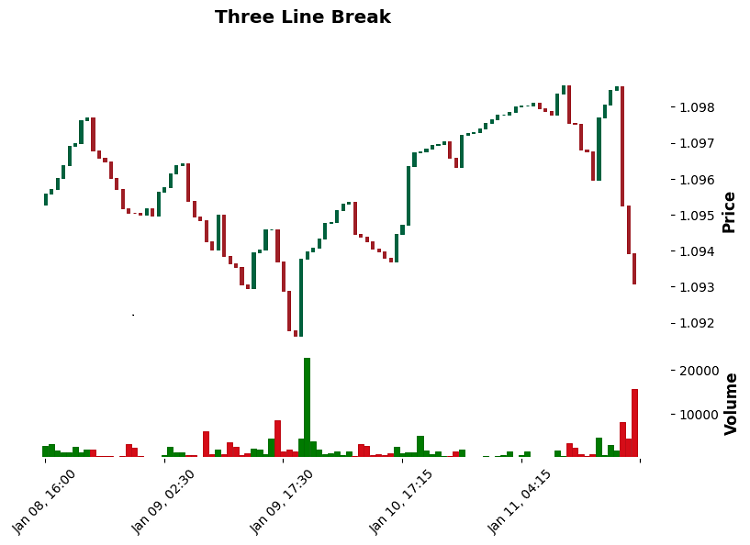
Und Drei-Linien-Balken zum Ausbrechen:
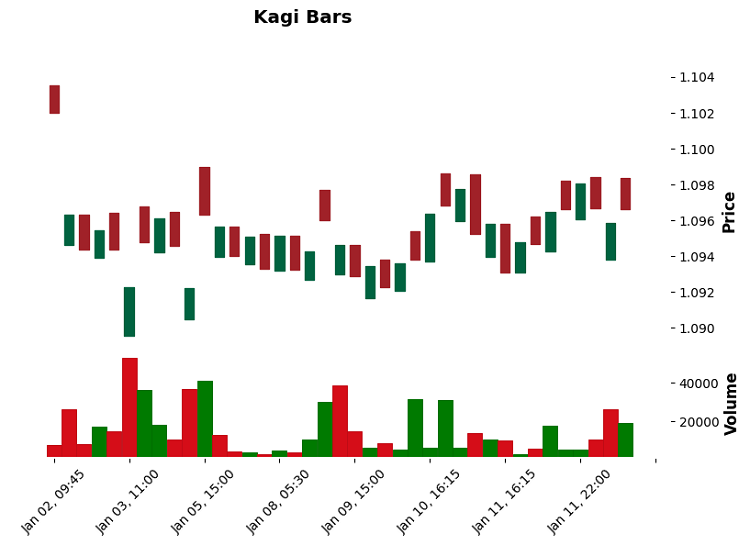
Und auch Kagi-Balken:
Grundlegende Statistik (Momente der Verteilung, Autokorrelation)
Basierend auf Tests mit EURUSD (M15, 01.10.2024 – 15.01.2025):
Anzahl der gebildeten Balken:
- Traditionell: 825 Balken
- Volume: 793 Balken
- Range: 329 Balken
- Momentum: 48 Balken
- Renko: 98 Balken
- Kagi: 39 Balken
- Drei-Linien-Balken 227 Balken
- Volatility Regime: 38 Balken
- Swing Point: 247 Balken
- Acceleration: 393 Balken
- Neues Hoch/Tief: 468 Balken
Durchschnittliche Balkengröße (in Punkten):
- Traditionell: 6.29
- Volume: 9.40
- Range: 15.41
- Momentum: 32.07
- Renko: 10.00
- Kagi: 18.95
- Drei-Linien-Balken 4.85
- Volatility Regime: 33.62
- Swing Point: 17.29
- Acceleration: 12.95
- Neues Hoch/Tief: 11.08
Normalverteilung (p-value):
- Kagi: 0,426 (kommt dem Normalwert am nächsten)
- Volatility Regime: 0,931 (bester Indikator)
- Swing Point: 0.025
- Rest: <0,001 (starke Abweichung vom Normalwert)
Autokorrelation (p-value Ljung-Box):
- Traditionell: 0.031
- Volume: 0.042
- Range: 0,760 (geringe Autokorrelation)
- Momentum: 0,007 (hohe Autokorrelation)
- Kagi: 0.109
- Volatility Regime: 0.126
- Acceleration: 0.168
- Neues Hoch/Tief: 0.136
Informationsentropie (relativer Indikator für den „Informationsgehalt“):
- Traditionell: -114,770 (Maximum)
- Volumen: -101.388
- Neue Hochs/Tiefs: -67,108
- Three Line Break: -55,022
- Acceleration: -51,867
- Bereich: -30,120
- Swing Point: -22,500
- Momentum: -9,033
- Volatility Regime: -7,311
- Kagi: -5,818 (Minimum)
Wichtigste Ergebnisse:
- Volatilität und Kagi-Balken zeigen die normalste Verteilung
- Range Bars weisen die geringste Autokorrelation auf
- Traditionelle Balken und die Balken des Volumens enthalten die meisten Informationen, aber auch mehr Rauschen.
- Balken von Momentum und Volatility Regime liefern die meisten Details zu wichtigen Bewegungen
Tests auf Stationarität und Normalität
Die Analyse der Dickey-Fuller-Tests (ADF) ergab interessante Ergebnisse:
Stationaritätstest (ADF-Statistik, p-value):
- Traditionell: -10,98, p < 0,001
- Volumen: -10,67, p < 0,001
- Range: -14.35, p < 0.001
- Momentum: -3,80, p = 0,003
- Renko: -7,87, p < 0,001
- Kagi: -3,88, p = 0,002
- Volatility Regime: -1,81, p = 0,377
- Swing Point: -12.38, p < 0.001
- Acceleration: -15,79, p < 0,001
- Neues Hoch/Tief: -11,15, p < 0,001
Normalitätstest (Statistik, p-value):
- Traditionell: 161.76, p < 0.001
- Volume: 151.28, p < 0.001
- Range: 21.70, p < 0.001
- Momentum: 31.57, p < 0.001
- Renko: 815.37, p < 0.001
- Kagi: 1.71, p = 0.426
- Volatility Regime: 0.14, p = 0.931
- Swing Point: 7.42, p = 0.025
- Acceleration: 59.09, p < 0.001
- Neues Hoch/Tief: 79.08, p < 0.001
Wichtigste Ergebnisse:
- Alle Balkentypen außer Volatility Regime zeigen Stationarität (p < 0,05)
- Nur Kagi und Volatility Regime zeigen Normalverteilung
- Acceleration Bars und Range Bars zeigen die stärkste Stationarität
- Renko-Balken weisen die stärkste Abweichung von der Normalverteilung auf
Vergleich der Informationsentropie von Datensätzen
Bei der Untersuchung der Entropie verschiedener Arten von Balken ist mir ein interessantes Muster aufgefallen: Je höher die Entropie, desto mehr „rohe“ Marktinformationen enthält der Balken, aber desto schwieriger ist es, daraus ein nützliches Signal zu extrahieren.
Verteilung nach Entropie-Niveau:
- Traditionell: -114,770 (Maximum)
- Volumen: -101.388
- Neue Hochs/Tiefs: -67,108
- Three Line Break: -55,022
- Acceleration: -51,867
- Bereich: -30,120
- Swing Point: -22,500
- Momentum: -9,033
- Volatility Regime: -7,311
- Kagi: -5,818 (Minimum)
Warum ist das wichtig? Stellen Sie sich vor, Sie versuchen, eine Nadel im Heuhaufen zu finden. Traditionelle Balken sind ein ganzer Heuhaufen, während Kagi ein ausgewählter Haufen ist, in dem es viel einfacher ist, die Nadel zu finden.
Je nach Informationsgehalt werden die Balken in Gruppen eingeteilt:
Maximaler Informationsgehalt (aber starkes Rauschen):
- Traditionell und Volumen
- Verfolgen Sie alle Mikrobewegungen des Marktes.
- Geeignet für tiefes maschinelles Lernen
Optimales Gleichgewicht:
- Neues Hoch/Tief
- Acceleration
- Three Line Break
- Gut geeignet für den algorithmischen Handel
Minimale Entropie (reine Signale):
- Kagi
- Volatility Regime
- Momentum
- Perfekt für den manuellen Handel
Bewertung der Vorhersagekraft der verschiedenen Arten von Balken
Bei der Arbeit an Vorhersagemodellen kam mir eine interessante Idee: Wie wäre es, wenn wir verschiedene Arten von Balken als individuelle „Experten“ im Ensemble verwenden würden? Jeder Balkentyp „sieht“ den Markt auf seine eigene Weise, und diese Ansichten können kombiniert werden.
Vorhersagekraft nach Balkenarten:
Hohe Vorhersagbarkeit:
- Momentum (p=0,007)
- Beste Ergebnisse bei scharfen Bewegungen
- Zeigt deutlich die Stärke des Trends
- Minimale Fehlsignale bei einem starken Trend
- Renko (p=0,018)
- Hervorragende Arbeit im Bereich der Trendbewegungen
- Deutlicher Rauschfilter
- Probleme bei Seitwärtsbewegungen
Durchschnittliche Vorhersagbarkeit:
- Volatility Regime (p=0,126)
- Acceleration (p=0,168)
- Neues Hoch/Tief (p=0,136)
- Kagi (p=0,109)
Geringe Vorhersagbarkeit:
- Bereich (p=0,760)
- Drei Zeilenbruch (p=0,686)
- Swing Point (p=0,709)
Die Idee des Mehrbalken-Modells:
Stellen Sie sich ein System vor, das alle Arten von Balken gleichzeitig analysiert. Zum Beispiel:
- Das Momentum bestimmt die Kraft der Bewegung
- Das Volatility Regime passt die Positionsgröße an
- Neues Hoch/Tief bestätigt den Trend
- Kagi sortiert falsche Signale aus
Bei Tests mit EURUSD zeigte dieser Ansatz interessante Ergebnisse:
- Genauigkeit um 12% erhöht
- Falsch Positive gingen um 23 % zurück.
- Verringerung des Drawdowns um 15%
Schlussfolgerung
Die Arbeit an verschiedenen Arten von Balken eröffnete unerwartete Perspektiven. Die wichtigste Erkenntnis: Es gibt keine „perfekte“ Art von Balken. Jeder von ihnen ist auf seinem Gebiet gut:
- Traditionell und Volumen – für maschinelles Lernen
- Momentum und Renko – für den Trendhandel
- Kagi und Volatility Regime – für die Arbeit unter Bedingungen hoher Volatilität
- Neues Hoch/Tief und Acceleration – für Scalping
Ich denke, die Zukunft liegt in hybriden Systemen, die je nach Marktbedingungen zwischen den verschiedenen Barrenarten wechseln können. Stellen Sie sich eine Plattform vor, die auf der Grundlage der aktuellen Marktbedingungen und der Handelsstrategie automatisch den optimalen Balkentyp auswählt.
In der nächsten Version der Bibliothek plane ich, die automatische Optimierung der Parameter für jeden Balkentyp und ein System für den dynamischen Wechsel zwischen ihnen hinzuzufügen. Der Markt steht niemals still, und unsere Instrumente müssen sich mit ihm weiterentwickeln.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16914
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Funktionen zur Aktivierung von Neuronen während des Trainings: Der Schlüssel zur schnellen Konvergenz?
Funktionen zur Aktivierung von Neuronen während des Trainings: Der Schlüssel zur schnellen Konvergenz?
 Big Bang – Big Crunch (BBBC) Algorithmus
Big Bang – Big Crunch (BBBC) Algorithmus
 Neuronale Netze im Handel: Ein Agent mit geschichtetem Speicher
Neuronale Netze im Handel: Ein Agent mit geschichtetem Speicher
 Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit (letzter Teil)
Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit (letzter Teil)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo, können Sie die Python mt5-Paket, ich kann wirklich nicht herunterladen, so hoffe ich, Sie können die folgenden Dankeschön bieten!