Zyklen im Handel

Einführung

Die Hauptaufgabe eines Händlers besteht darin, Kursbewegungen vorherzusagen. Händler erstellen ihre Prognosen auf der Grundlage des einen oder anderen Modells. Eines der einfachsten und anschaulichsten Modelle ist das Modell der zyklischen Preisbewegung.

Die Grundidee hinter jedem zyklischen Muster ist, dass verschiedene Faktoren zusammenwirken, um Zyklen in der Preisbewegung zu schaffen. Diese Zyklen können sich in ihrer Dauer und Stärke voneinander unterscheiden. Wenn Sie die Parameter dieser Zyklen kennen, werden die Handelsoperationen sehr einfach: Öffnen Sie eine Kaufposition, wenn der Zyklus sein Minimum erreicht hat, und verkaufen Sie, wenn der Zyklus sein Maximum erreicht hat.

Schauen wir uns an, wie dieses Modell in der Praxis angewendet werden kann.

Einfacher Zyklus

Bei der Beschreibung von Zyklen werden in der Regel die trigonometrischen Funktionen Sinus und Kosinus verwendet. Der Zyklus kann aber auch auf andere Weise definiert werden - mit Hilfe von Finite Differenzen.

Betrachten wir zum Beispiel eine Gleichung, bei der die zweite Differenz proportional zum Wert der Zeitreihe ist:

Dies ist die Gleichung eines Harmonischen Oszillators. Auf den ersten Blick ist daran nichts Besonderes. Diese Gleichung hat jedoch eine interessante Eigenschaft. Liegt der Wert des R-Verhältnisses im Bereich von 0 bis 4, so kann diese Gleichung nur zu einer Sinuskurve gehören. Dieses Verhältnis hängt von der Dauer des Zyklus N ab. Mit anderen Worten, sein Wert kann so gewählt werden, dass die Gleichung nur auf Zyklen mit einer bestimmten Häufigkeit reagiert:

Nun wollen wir sehen, wie diese Gleichung in der Praxis angewendet werden kann. Wenn wir es auf die Preise p[] anwenden, benötigen wir den Wert des m-Niveaus, um das der Preis schwankt.

Um die Berechnung dieses Durchschnittswertes zu vermeiden, werde ich zu einem kleinen Trick greifen. Erinnern wir uns daran, was mathematisch gesehen passiert, wenn ein Zyklus einen Maximal- oder Minimalpunkt erreicht. In diesen Momenten wechselt die 1. Ableitung das Vorzeichen.

Anstelle der Ableitung verwenden wir die 1. Differenz der ursprünglichen Gleichung. Dies ist das schwierige Schicksal eines Händlers - nach Unterschieden aus Unterschieden zu suchen. Aber dieser Ansatz vereinfacht die Berechnungen erheblich. Wir müssen nur den Wert des R-Verhältnisses festlegen. Die endgültige Form der Gleichung lautet wie folgt:

Ich werde solche Gleichungen auch als Handelsalgorithmus-Gleichungen bezeichnen. Auf der Grundlage dieser Gleichung können wir eine Handelsstrategie entwickeln. Zunächst möchte ich eine kleine Ergänzung vornehmen - wir können anstelle des aktuellen Kurses eine beliebige Version des herkömmlichen gleitenden Durchschnitts verwenden. Das Wesen der Strategie selbst ist sehr einfach. Öffnungs- und Schließungspositionen entstehen, wenn sich das Vorzeichen der Gleichung ändert:

• von negativ zu positiv - Kaufen, Verkauf schließen;
• von positiv zu negativ - Verkaufen, Kauf schließen.

Die Änderung der EA-Bilanz kann folgendermaßen aussehen.

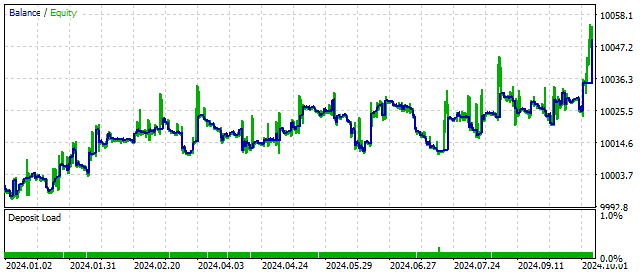
Diese Handelsstrategie hat Perspektiven. Aber es muss noch verbessert werden.

Zyklus mit Dämpfung

Die oben beschriebene Strategie hat einen gravierenden Nachteil. Sie beruht auf der Annahme, dass der Zyklus noch recht lange andauern wird. Im wirklichen Leben hängt der Zyklus von vielen externen Faktoren ab und kann fast unmittelbar nach seinem Beginn zusammenbrechen.

Um diesen Nachteil zu beseitigen, können wir das Modell eines harmonischen Oszillators mit Dämpfung der Schwingungen verwenden. Die Gleichung eines solchen Zyklus wird ebenfalls durch endliche Differenzen aufgestellt:

Der Parameter S bestimmt, wie schnell die Schwingungen abklingen. Je höher dieser Wert ist, desto schneller erfolgt die Dämpfung. Der kritische Wert dieses Parameters kann anhand der folgenden Gleichung ermittelt werden:

Ab diesem Wert wird die Bewegung des Oszillators nicht mehr oszillierend.

Wir wissen bereits, was mit einer solchen Gleichung zu tun ist. Wir müssen seine 1. Differenz finden, die Handelssignale erzeugt.

Durch Hinzufügen eines neuen Parameters kann die Handelsstrategie flexibler und rentabler werden. So sieht zum Beispiel die Veränderung des Saldos bei einem kritischen Wert von S aus.

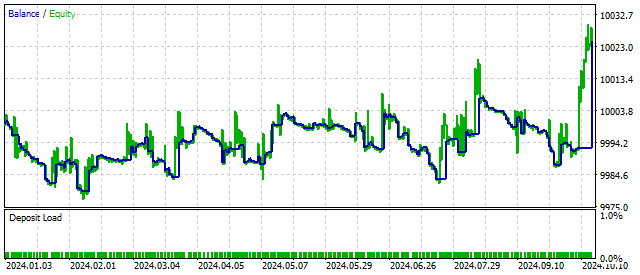
Per Definition sollte der Parameter S positiv sein. Diese Anforderung ist jedoch nicht zwingend. Setzt man für diesen Parameter einen negativen Wert, so beschreibt die ursprüngliche Gleichung Schwingungen mit einer immer größer werdenden Amplitude. Auf diese Weise kann EA auf den Beginn des Zyklus reagieren und möglicherweise die Rentabilität erhöhen. Die Handelsergebnisse könnten in diesem Fall wie folgt aussehen:

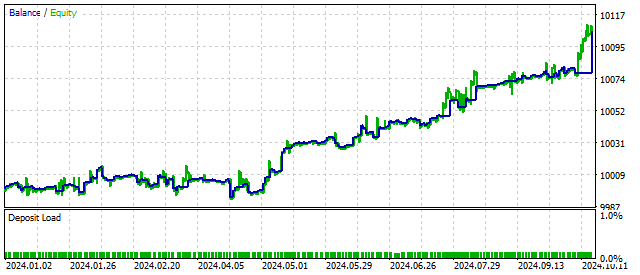
Wie Sie sehen können, kann eine höhere Komplexität des Zyklusmodells die Handelsergebnisse verbessern. Versuchen wir, das Modell noch weiter zu verkomplizieren.

Elliott-Wellen

Das Prinzp der Elliott-Wellen ist schon seit langem bekannt und wird im Handel häufig verwendet. Versuchen wir nun, das zyklische Modell auf Elliott-Wellen anzuwenden.

Die ersten fünf Elliott-Wellen können als Summe von zwei Sinuswellen mit unterschiedlichen Amplituden und Perioden simuliert werden:

In diesem Fall sollten die folgenden Bedingungen erfüllt sein:

Daraus ergibt sich etwa folgendes Bild:

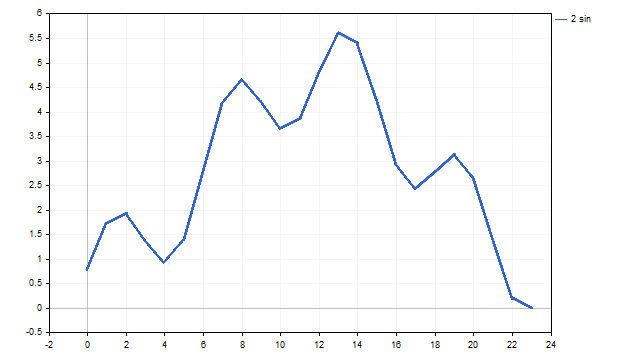
Es sieht nicht genau so aus wie in den Büchern - ein bisschen eckig, aber ziemlich ähnlich.

Wir können die Summe von zwei Sinuskurven mit Hilfe von finiten Differenzen simulieren:

wobei - der Wert der endlichen Differenz der Ordnung n auf dem Preisstand mit dem Index i. Wir wissen bereits, was wir mit dieser Gleichung tun können - die Differenz aus der Summe der Differenzen ermitteln und Handelssignale erhalten:

Die Verwendung der Summe von zwei Sinuskurven ermöglicht es, den EA an komplexere Marktsituationen anzupassen. Die Verwendung dieses Handelsalgorithmus kann sowohl zu einer Zunahme der Markteintritte als auch zu einer Verbesserung ihrer Rentabilität führen.

Dies ist das Ergebnis, das ein auf dem Elliott-Wellen-Prinzip basierender EA anzeigen kann:

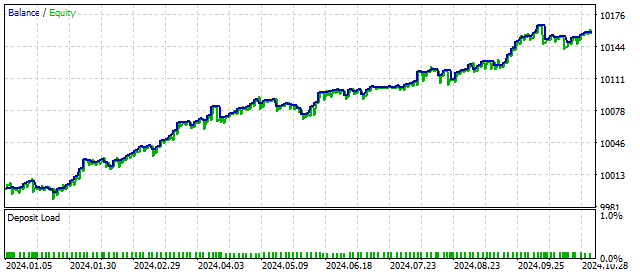
Wie Sie sehen können, kann selbst eine kleine Komplikation des zyklischen Modells positive Ergebnisse bringen.

Verallgemeinerter harmonischer Oszillator

Wir haben uns bereits drei Modelle angeschaut, die auf dem harmonischen Oszillator basieren. Jedes dieser Modelle basierte auf seinen eigenen ursprünglichen Annahmen. Aber als Ergebnis haben wir immer noch eine Summe endlicher Differenzen.

Wir können ein allgemeineres Modell erstellen. Das Wesen dieses Modells ist sehr einfach - zuerst nehmen wir die Differenz einer vorbestimmten Ordnung und addieren sie zu den Differenzen der niedrigeren Ordnungen, bis hinunter zur 1. In diesem Fall wird jede Differenz niedriger Ordnung mit einem eigenen Gewichtungsfaktor berücksichtigt.

Ich habe zum Beispiel die Differenz der 7. Ordnung genommen. Die Gleichung für den Handelsalgorithmus lautet dann wie folgt:

Ein solches Modell kann eine Vielzahl von Kombinationen von Zyklen und deren Verhalten umfassen. Wir haben bereits gesehen, dass eine höhere Komplexität des Modells die Handelsergebnisse verbessert. In diesem Fall kann sich der Saldo wie folgt ändern:

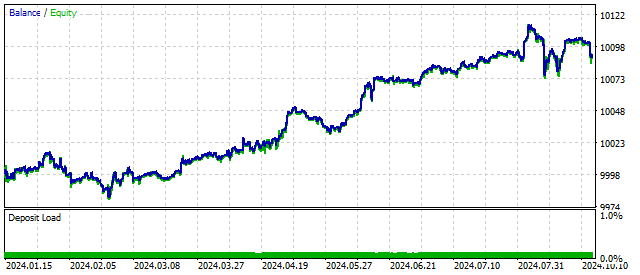
Die Erhöhung der Ordnung der führenden Differenz macht das Modell flexibler. Der generalisierte Oszillator reagiert nur auf bestimmte Preiskombinationen. Mit anderen Worten: Es wird nach bestimmten Mustern gesucht. Gleichzeitig müssen Sie bedenken, dass die Muster umso seltener auftreten, je höher die Ordnung des Oszillators ist.

Ein weiteres Merkmal dieses Algorithmus ist, dass die Verhältnisse in sehr weiten Grenzen variieren können. Selbst die Beurteilung dieser Grenzen kann schwierig sein. Andererseits können Sie durch die Auswahl von Kennzahlen den Algorithmus so konfigurieren, dass er auf nichtzyklische Muster im Preisverhalten reagiert.

Nichtlineare Oszillatoren

Lineare Modelle sind einfach und intuitiv. Das Preisverhalten auf dem Markt kann aber auch nicht-linear sein. So lässt sich beispielsweise eine starke Preisveränderung leichter mit nichtlinearen Modellen beschreiben. Der Hauptvorteil nichtlinearer Modelle besteht darin, dass sie ein sehr komplexes Zeitreihenverhalten beschreiben können. Wenn Sie die WorteChaos“ und "Stochastizität hören, dann haben Sie es höchstwahrscheinlich mit nichtlinearen Modellen zu tun.

Eines der einfachsten Modelle ist der Signaturoszillator. Seine Gleichung ist in vielerlei Hinsicht dem harmonischen Oszillator ähnlich. Die Vorzeichenfunktion wird als nichtlineare Funktion verwendet. Die Gleichung des Handelsalgorithmus sieht wie folgt aus:

wobei „sign“ die Vorzeichenfunktion ist.

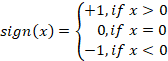
Dank dieser Funktion kann der Oszillator in 5 verschiedenen Modi arbeiten. Der Wechsel der Modi hängt von der Preisentwicklung ab. Die Nichtlinearität des Oszillators lässt uns hoffen, dass der Handel mit seiner Hilfe flexibler und stabiler wird. Die Veränderung des Saldos nach diesem Algorithmus könnte folgendermaßen aussehen:

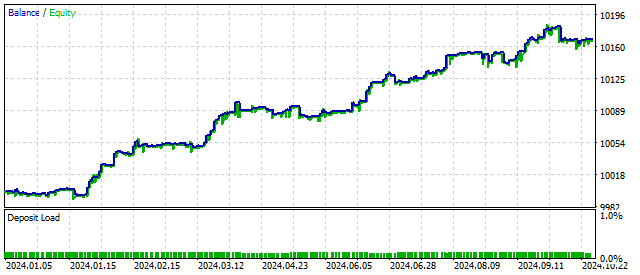
Betrachten wir nun einen Oszillator mit quadratischer Nichtlinearität. Die Gleichung ist sehr einfach:

Um diese Gleichung in der Praxis anwenden zu können, müssen wir sie noch etwas verfeinern.

Zunächst einmal brauchen wir ein Durchschnittsniveau, um das der Preis schwankt. Ich möchte Sie daran erinnern, dass wir anstelle der realen Preise auch deren geglätteten Wert (SMA) verwenden können. Dann entspricht das durchschnittliche Niveau dem Durchschnittswert der gleitenden Durchschnitte.

Die Berechnung des Durchschnitts der Durchschnittswerte mag zunächst etwas unheimlich erscheinen. Im Jahr 1910 veröffentlichte Andrey Markov sein Werk „Calculating Finite Differences“. In dieser Arbeit zeigte er, dass die Bildung eines Durchschnitts aus einer großen Anzahl von SMAs der Anwendung eines LWMA auf alle Werte der Zeitreihe gleichkommt. Auch hier haben die endlichen Differenzen die Berechnungen vereinfacht.

Die Gleichung für den Handelsalgorithmus des quadratischen Oszillators lautet wie folgt:

Die quadratische Nichtlinearität ermöglicht ein sanfteres Umschalten der Oszillatorbetriebsarten, allerdings mit einer größeren Amplitude. Dies kann die Handelsergebnisse verbessern.

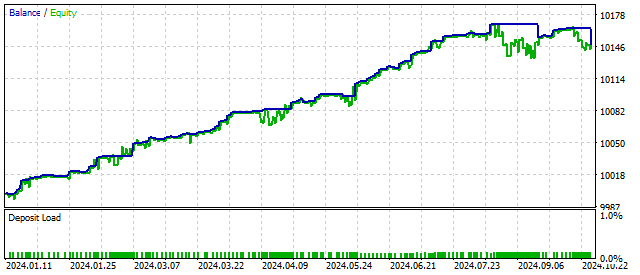
Ein weiteres Beispiel für quadratische Nichtlinearität ist der van der Pol Oszillator. Dieser Oszillator war eines der ersten Beispiele für die Simulation von deterministischem Chaos. Aufgrund ihrer Eigenschaften findet die Van-der-Pol-Gleichung nicht nur in der Oszillator-Theorie Anwendung, sondern auch in anderen Bereichen - Physik, Biologie usw.

Der Van-der-Pol-Oszillator selbst ist eine Modifikation des Oszillators mit quadratischer Nichtlinearität, und die Gleichung für seinen Handelsalgorithmus sieht wie folgt aus:

Auf den ersten Blick sollte dieser Oszillator instabil sein. Die Parameter können in einem weiten Bereich verändert werden, ohne dass sich dies auf die Handelsergebnisse auswirkt.

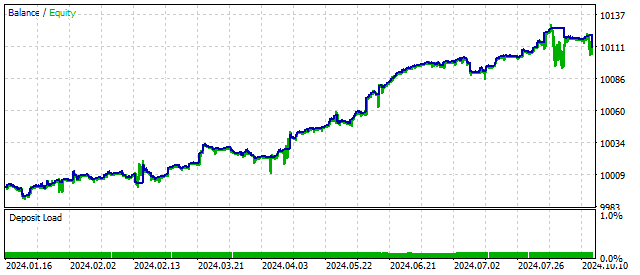
Im Jahr 1918 untersuchte Georg Duffing die Gleichung eines Oszillators mit kubischer Nichtlinearität. Dieser Oszillator kann auch ein chaotisches Kursverhalten simulieren. Aber er hat noch eine weitere Eigenschaft: Je nach äußeren Bedingungen und seinen Parametern kann dieser Oszillator zwei stabile Zustände annehmen.

Die Gleichung des Duffing-Oszillator-Handelsalgorithmus ist die Summe aus einem harmonischen Oszillator 3. Grades und kubischen Binom:

Die Leistung dieses Oszillators ist mit der anderer nichtlinearer Modelle vergleichbar.

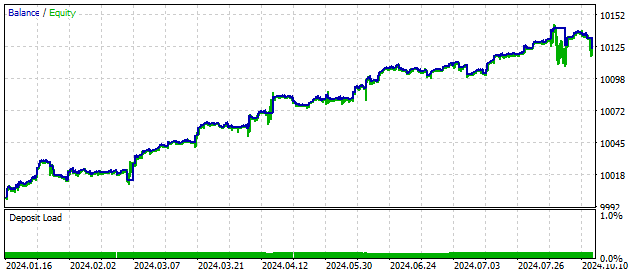
Im Allgemeinen können viele nicht-lineare Modelle erstellt werden. Jede nichtlineare Funktion kann zu einem Chaosgenerator werden. Die Nichtlinearität der drei früheren Oszillatoren beruhte auf einigen physikalischen Prinzipien und Ideen. Die Ökonophysik ist eine nützliche Richtung, aber es ist keineswegs notwendig, ihr immer zu folgen.

Zum Beispiel werde ich dem Handelsalgorithmus auf der Grundlage der logarithmischen Funktion Nichtlinearität hinzufügen:

Sie werden sich fragen: Woher kommen diese Logarithmen, und aus welchen Gründen habe ich sie hinzugefügt? Meine Antwort ist ganz einfach: Ich wollte es so.

Aber wenn ich Zeit habe, über die Antwort nachzudenken, wird sie ein wenig anders ausfallen. Was ist der Unterschied zwischen aufeinanderfolgenden Preisen? Sagen wir 100 Punkte. Und was ist mit der Differenz zwischen den Logarithmen dieser Preise? Wird es dort etwas anderes als Nullen geben? Hier ist meine neue Antwort: Auf der linken Seite haben wir einen regulären Oszillator, und auf der rechten Seite haben wir einen Filter, der die Eröffnung von Positionen beeinflussen kann. Der Filter zeigt sich nur, wenn sich der Preis stark bewegt. Wir überprüfen seine Arbeit.

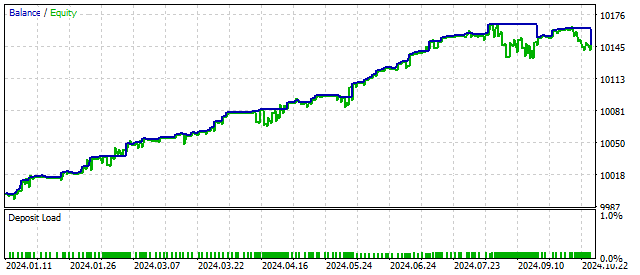
Das Ergebnis ähnelt dem Betrieb eines Oszillators mit quadratischer Nichtlinearität. Der Filter funktioniert. Es ist jedoch wichtig, daran zu denken, dass alle Ideen zunächst im Tester getestet werden sollten, bevor sie in der Praxis angewendet werden.

Externe Kräfte

Bislang haben wir uns mit autonomen Oszillatoren befasst. Stellen Sie sich ein Pendel vor. Sie schwingt gleichmäßig von einer Seite zur anderen. Seine Zyklen wiederholen sich immer wieder. Warum dieses Pendel schwingt, warum es auf diese bestimmte Weise schwingt - das sind Fragen, die wir nicht beantworten können. Dies ist ein Beispiel für einen freilaufenden Oszillator.

Jetzt geben Sie dem Pendel einen Schubs. Erst in die eine, dann in die andere Richtung. Die Pendelzyklen begannen sich zu verändern - ihre momentane Frequenz und Amplitude änderte sich. Unter dem Einfluss äußerer Kräfte hat das Pendel aufgehört, autonom zu sein.

Versuchen wir nun, den gleichen Ansatz auf den harmonischen Oszillator anzuwenden. Die Gleichung wird sich ändern und wie folgt aussehen:

wobei F[n] eine äußere Kraft ist. Was für eine Art von Kraft ist das, wie wirkt sie, wohin ist sie gerichtet - ich weiß nichts darüber. Ich gehe einfach davon aus, dass sie existiert. Und nun stellt sich die Frage: Ist eine solche Komplizierung des Modells gerechtfertigt? Beantworten wir die Frage.

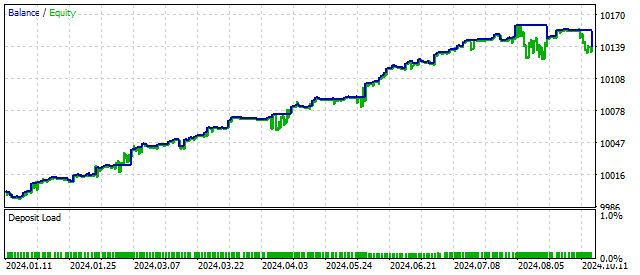
Ich kam zu diesem Ergebnis, indem ich annahm, dass diese externe Kraft wie folgt mit den Preiswerten zusammenhängt:

Ich habe diese Annahme nur aus einem Grund gemacht - ich habe im gesamten Artikel über endliche Differenzen gesprochen, und in diesem Fall habe ich auch die Verhältnisse der 2ten Differenz verwendet. Es steht Ihnen frei, Ihre eigenen Annahmen zu treffen. Die äußere Kraft kann sich beispielsweise auf die Differenz zwischen Schluss- und Eröffnungskursen, Tick-Volumen usw. beziehen. Sie können auch ein Element der Nichtlinearität hinzufügen:

Schließlich kann diese unbekannte Kraft von mehreren Komponenten abhängen. Fassen Sie so viel wie möglich und so lange wie möglich zusammen. Jede Annahme, die Sie treffen, kann sich positiv auf Ihre Handelsergebnisse auswirken.

Schlussfolgerung

Wie Sie sehen, ist die Verwendung zyklischer Muster im Handel durchaus gerechtfertigt. Der Hauptvorteil solcher Modelle besteht darin, dass sie Hunderte von Parameterkombinationen enthalten, die über einen langen Zeitraum hinweg ein stabiles Ergebnis liefern. Der Händler muss mehrere Dutzend Optionen auswählen, die nicht miteinander korrelieren.

In diesem Artikel habe ich nur einige der beliebtesten Oszillatoren erwähnt. Es gibt noch eine ganze Reihe von Lösungen, die (unter anderem) zur Erstellung zyklischer Modelle verwendet werden können.

Ich habe den EA unter den folgenden Bedingungen getestet: EURUSD, H1, 2024.01.01 - 2024.10.30

Die folgenden Programme wurden bei der Erstellung dieses Artikels verwendet:

Name	Typ	Beschreibung
Harmonischer Oszillator	EA	iPeriode - Periodenlänge für den gleitende Durchschnitt Typ - gleitender Durchschnittstyp R - Oszillatorverhältnis, zulässiger Wert: 1 ... 399
Gedämpfter harmonischer Oszillator	EA	S - Kippverhältnis, zulässiger Wert: -1000 ... +1000
scr Elliott-Welle	Skript	A1, A2 - Amplituden der Sinuskurven N1, N2 - Periodenlängen der Sinuskurven Width - Linienbreite Pause - Verzögerung bei der Anzeige des Ergebnisses Screenshot - wenn „true“, dann wird das Bild erstellt und im Ordner „Files“ gespeichert
Elliott-Welle	EA	R, S - Oszillator-Verhältnisse, akzeptabler Wert: 0 ... 1000
Verallgemeinerter harmonischer Oszillator	EA	zulässiger Wert der Verhältnisse: -1000 ... +1000
Vorzeichen-Oszillator	EA
Quadratischer Oszillator	EA
Van-der-Pol-Oszillator	EA
Duffing-Oszillator	EA
Logarithmischer Oszillator	EA
Nicht-autonomer Oszillator	EA