Algorithmen zur Optimierung mit Populationen: der Algorithmus Simulated Annealing (SA). Teil I

Inhalt

1. Einführung
2. Der Algorithmus
3. Testergebnisse

1. Einführung

Der Algorithmus des Simulated Annealing, der simulierten Abkühlung, wurde 1983 von Scott Kirkpatrick, George Gelatt und Mario Vecchi entwickelt. Bei der Untersuchung der Eigenschaften von Flüssigkeiten und Feststoffen bei hohen Temperaturen wurde festgestellt, dass das Metall in einen flüssigen Zustand übergeht und die Teilchen zufällig verteilt sind, während der Zustand mit minimaler Energie unter der Bedingung einer ausreichend hohen Anfangstemperatur und einer ausreichend langen Abkühlzeit erreicht wird. Wenn diese Bedingung nicht erfüllt ist, befindet sich das Material in einem metastabilen Zustand mit nicht minimaler Energie - dies wird als Aushärtung bezeichnet, die in einer starken Abkühlung des Materials besteht. In diesem Fall hat die atomare Struktur keine Symmetrie (anisotroper Zustand oder ungleichmäßige Eigenschaften des Materials innerhalb des Kristallgitters).

Während des langsamen Abkühlens geht das Material ebenfalls in einen festen Zustand über, allerdings mit geordneten Atomen und mit Symmetrie, sodass vorgeschlagen wurde, diesen Prozess zu nutzen, um einen Optimierungsalgorithmus zu entwickeln, der bei komplexen Problemen ein globales Optimum finden kann. Der Algorithmus wurde auch als Methode zur Lösung von kombinatorischen Optimierungsproblemen vorgeschlagen.

Die Grundidee des Algorithmus basiert also auf einem mathematischen Prozessanalogon von glühendem Metall. Während des Abkühlens wird das Metall auf eine hohe Temperatur erhitzt und dann langsam abgekühlt, damit sich die Metallmoleküle bewegen und in stabilere Zustände überführen können, während innere Spannungen im Metall abgebaut und interkristalline Defekte beseitigt werden. Der Begriff „annealing“ (Abkühlen) wird auch mit der thermodynamischen freien Energie in Verbindung gebracht, die eine Eigenschaft des Materials ist und von seinem Zustand abhängt.

Der Optimierungsalgorithmus des simulierten Abkühlens verwendet ein ähnliches Verfahren. Der Algorithmus wendet Vorgänge an, die dem Aufheizen und Abkühlen des Materials ähneln. Der Algorithmus beginnt seine Arbeit mit einer Anfangssituation, die zufällig sein kann oder aus früheren Iterationen stammt. Dann wendet er Operationen an, um den Zustand der Situation zu ändern, die zufällig oder kontrolliert sein können, um einen neuen Zustand zu erhalten, auch wenn dieser schlechter ist als der aktuelle. Die Wahrscheinlichkeit, eine schlechtere Entscheidung zu treffen, wird durch eine „Abkühlungsfunktion“ bestimmt, die die Wahrscheinlichkeit, eine schlechtere Entscheidung zu treffen, im Laufe der Zeit verringert und es dem Algorithmus ermöglicht, vorübergehend aus lokalen Optima „herauszuspringen“ und anderswo im Suchraum nach besseren Lösungen zu suchen.

Der Algorithmus der simulierte Abkühlung (Simulated Annealing, SA) basiert auf drei Hauptkonzepten:

• Anwendung des Zufalls: Der Algorithmus verwendet Zufallsoperationen, um den Zustand der Situation zu ändern und den nächsten Zustand zu wählen. Auf diese Weise können verschiedene Regionen des Suchraums erkundet werden, und es kann vermieden werden, in lokalen Optima stecken zu bleiben.

• Akzeptieren schlechterer Entscheidungen: SA ist einer der wenigen Algorithmen, der mit einer gewissen Wahrscheinlichkeit schlechtere Entscheidungen gegenüber besseren Entscheidungen bevorzugt.

• Schrittweise Verringerung der Wahrscheinlichkeit, schlechtere Entscheidungen zu treffen: Der Algorithmus nutzt einen „Abkühlungsprozess“, der die Wahrscheinlichkeit schlechterer Entscheidungen mit der Zeit verringert. Auf diese Weise können wir den Suchraum zunächst breiter erkunden und uns dann auf die Verbesserung der Lösung konzentrieren, wobei wir ein Gleichgewicht zwischen der Erkundung und der Nutzung des Suchraums herstellen.

Der Optimierungsalgorithmus des simulierten Abkühlens ist eine der Methoden der Metaheuristik, die eine Klasse von Algorithmen zur Lösung komplexer Optimierungsprobleme beschreibt. Sie basieren auf heuristischen Methoden, die die Suche nach Näherungslösungen im Suchraum ermöglichen, ohne dass eine vollständige Suche nach allen möglichen Optionen erforderlich ist. Der Zufall ist eines der Schlüsselelemente von Metaheuristiken, das es ihnen ermöglicht, neue und vielversprechende Lösungsbereiche zu entdecken. Der Algorithmus gehört zu einer Gruppe von Algorithmen, die „stochastische Optimierungsmethoden“ genannt werden.

Der SA-Algorithmus hat seine Nachteile, die wir im Folgenden erörtern werden. Es wurden weitere Algorithmen auf der Grundlage von SA entwickelt, wie Adaptive Simulated Annealing (ASA) und Quantum Normalization (QN), auch bekannt als Quantum Annealing (QA).

2. Der Algorithmus

Die von den Autoren vorgeschlagene Grundversion des Algorithmus des simulierten Abkühlens ist äußerst einfach, aber es ist nicht leicht, sich die Funktionsweise des Algorithmus vorzustellen, ohne die grafische Darstellung des Temperaturänderungsprozesses und der Wahrscheinlichkeit der schlechtesten Entscheidungen zu veranschaulichen.

Lassen Sie es uns Schritt für Schritt herausfinden. Der Algorithmus beginnt seine Arbeit mit einer bestimmten hohen Anfangstemperatur (externer Parameter), die dem erhitzten Material in der Metallurgie entspricht. Eine hohe Temperatur bedeutet eine hohe Energie der Moleküle, die sich aus verschiedenen Energiezuständen (entweder niedriger oder höher) bewegen. Ähnlich wie bei diesem Prozess der hochenergetischen Bewegung in Metall kann das System mit einer gewissen Wahrscheinlichkeit schlechtere Entscheidungen treffen.

Wenn wir uns die Bewegung eines Skifahrers vom Gipfel eines Berges aus vorstellen, dann kann er, wenn er sich in einer örtlichen Ebene befindet, zu dem Schluss kommen, dass er den Fuß des Berges erreicht hat. Um sicherzugehen, dass die Entscheidung richtig ist, müssen wir unsere Position leicht verschlechtern und uns auf eine gewisse Höhe erheben, um mit noch größerer Geschwindigkeit hinunterzueilen. Das ist der Punkt, an dem es darum geht, schlechtere Entscheidungen mit einer gewissen Wahrscheinlichkeit zu treffen. Um aus der lokalen „Falle“ herauszukommen, wurde der Algorithmus der „Quantenabkühlung“ entwickelt, der die Quanteneffekte simuliert, die entstehen, wenn man sich an zwei Orten gleichzeitig aufhält, und bei dem man durch Tunneln über „Mauern“ springen kann.

Zur Beschreibung des simulierten Abkühlens werden mehrere einfache Gleichungen verwendet. Gleichung zur Energieberechnung:

E = f (x)

Mit anderen Worten: E stellt den Wert der Fitnessfunktion für den aktuellen Zustand des Agenten dar.

Gleichung zur Berechnung der Energieänderung:

ΔE = E_new - E_old

wobei:

• ΔE - Energieänderung beim Übergang vom aktuellen Zustand zu einem neuen Zustand (die Differenz der Werte der Fitnessfunktion bei zwei aufeinanderfolgenden Iterationen)
  
• E_new - Energiewert für den neuen Zustand
• E_old - Energiewert für den vorherigen Zustand

Gleichung zur Berechnung der Wahrscheinlichkeit, eine schlechtere Entscheidung zu treffen:

P = exp (-ΔE / T)

wobei:

• P - Wahrscheinlichkeit, eine schlechtere Entscheidung zu treffen
• T - aktuelle Temperatur

Aus dem nachstehenden Diagramm, das die Abhängigkeit der P-Wahrscheinlichkeit zeigt, wird deutlich, dass ein höheres ΔE einer geringeren Wahrscheinlichkeit entspricht. Das bedeutet, dass mit abnehmender Temperatur die Wahrscheinlichkeit hochenergetischer Übergänge nach unten schneller abnimmt als Übergänge mit geringeren Energieunterschieden. Mit anderen Worten: Der Algorithmus geht immer weniger Risiko ein, um aus der „Falle“ herauszukommen, durch die Versuche, die Situation zu verbessern. Das Wahrscheinlichkeitsdiagramm ist in Abbildung 1 dargestellt, wobei der Übersichtlichkeit halber ein linearer Temperaturabfall verwendet wird, obwohl der Algorithmus eine nichtlineare Temperaturänderung verwendet.

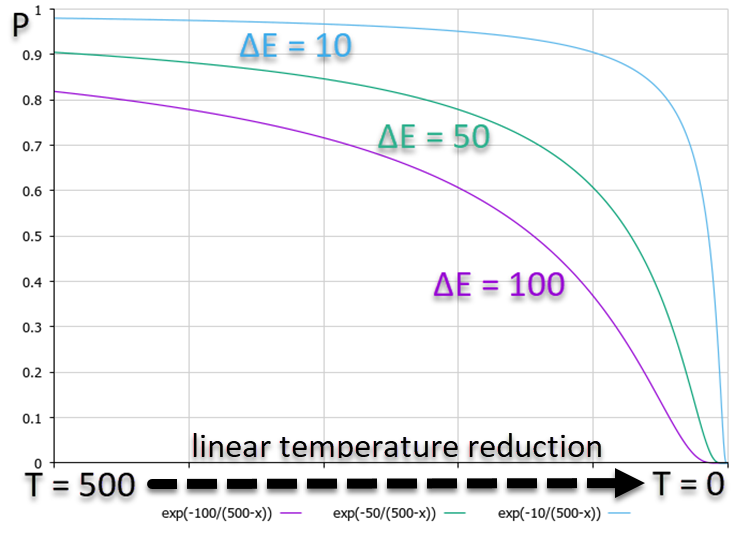
Abbildung 1. Grafik der Entscheidungswahrscheinlichkeiten in Abhängigkeit von der Energie, die sich bei einer linearen Abnahme der Temperatur zum Schlechteren verändert

Gleichung zur Aktualisierung der Temperatur:

Tnew = α * Tprev

wobei:

• α - das Abkühlungsverhältnis. α liegt normalerweise im Bereich von 0,8 bis 0,99
• Tnew - neue Temperatur
• Tprev - vorherige Temperatur
  

Der Graph der Temperaturänderung bei jeder Iteration mit α = 0,99, 0,8, 0,5 und 0,1 bei der Ausgangstemperatur T = 500 ist in Abbildung 2 dargestellt. Die Temperatur sinkt allmählich, was der Abkühlung des Materials entspricht. Die Verringerung der Temperatur bei jeder Iteration führt zu einer Verringerung der Wahrscheinlichkeit, schlechtere Entscheidungen zu treffen, was einer Abnahme der Fähigkeit der Moleküle entspricht, ihren Energiezustand zu ändern, wenn die Temperatur sinkt.

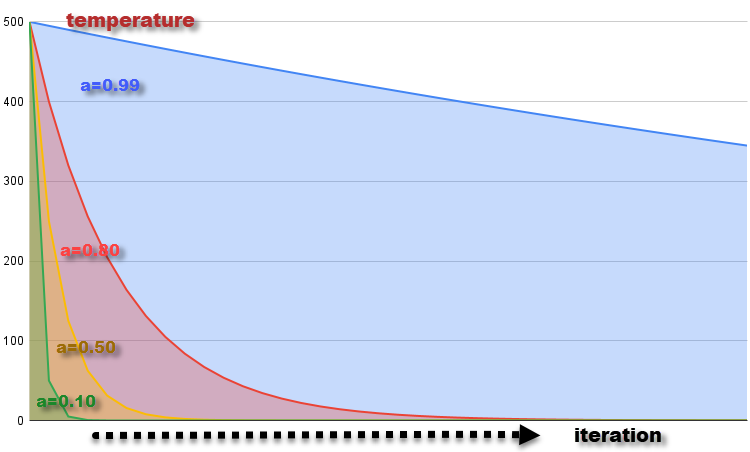
Abbildung 2. Temperaturänderungsdiagramm mit α = 0,99, 0,8, 0,5 und 0,1

Gleichung zur Erzeugung eines neuen Systemzustands:

x_new = GenerateNeighbor (x)

wobei:

• x_new - ein neuer Zustand, der auf der Grundlage des aktuellen x-Zustands erzeugt wird
  
• GenerateNeighbor (x) - die Funktion, die einen neuen Zustand erzeugt, indem sie zufällige Änderungen mit einer gleichmäßigen Verteilung am aktuellen Zustand vornimmt
  

Da wir nun alle theoretischen Grundlagen des Algorithmus der simulierten Abkühlens, wird es uns nicht schwer fallen, SA-Code zu schreiben. Wir können die Bewegung von Molekülen, die ihren Energiezustand ändern, in Form einer Struktur (S_Agent) darstellen, die Informationen über den Agenten im Optimierungsproblem enthält. Felder und Strukturmethoden:

• Init (int coords) - Methode initialisiert den Agenten und weist Speicher für die Arrays „c“ und „cPrev“ der Größe „coords“ zu. Er setzt auch die Anfangswerte von „f“ und „fPrev“ auf „-DBL_MAX“ (negative Unendlichkeit).
• c [] - das Feld „c“ stellt die Koordinaten des Agenten im Optimierungsraum dar.
  
• cPrev [] - das Array „cPrev“ stellt die vorherigen Koordinaten des Agenten dar.
  
• f - der Wert der Fitnessfunktion für die aktuellen Koordinaten des Agenten,
  
• fPrev - der vorherige Wert der Fitnessfunktion des Agenten.
  

//————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f     = -DBL_MAX;
    fPrev = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//————————————————————————————————————————

Beschreiben wir die SA-Algorithmusklasse und nennen sie C_AO_SA. Sie wird sich als sehr einfach erweisen, da sie nichts Ungewöhnliches enthält, das wir nicht schon vorher verwendet haben, mit Ausnahme von spezifischen thermischen Variablen und Konstanten.

Felder und Methoden der Klasse:

• cB [] - Array mit den besten Koordinaten, die der Optimierungsalgorithmus zum Zeitpunkt der aktuellen Iteration gefunden hat.
  
• fB - Wert der Fitnessfunktion für die besten Koordinaten,
  
• a [] - das Array steht für die Agenten. Es wird verwendet, um Informationen über jeden Agenten in einem Optimierungsproblem zu speichern. Jedes Element des Arrays ist eine Instanz der Struktur S_Agent Struktur.
• rangeMax [] - Array der maximalen Suchbereichswerte für jede Koordinate, die zur Bestimmung der oberen Suchgrenze für jede Agentenkoordinate verwendet werden.
• rangeMin [] - Array der minimalen Suchbereichswerte für jede Koordinate, die zur Bestimmung der unteren Suchgrenze für jede Agentenkoordinate verwendet werden.
• rangeStep [] - das Array stellt Suchschritte für jede Koordinate dar,
• Init (const int coordsP, const int popSizeP, const double tP, const double aP, const double dP) - die Methode initialisiert den Optimierungsalgorithmus und akzeptiert folgende Parameter: Anzahl der Koordinaten „coordsP“, Populationsgröße „popSizeP“, Anfangstemperatur „tP“, Temperaturreduktionsverhältnis „aP“ und Diffusionskoeffizient „dP“. Die Methode initialisiert die Felder der Klasse und des Agenten.
• Moving () - die Methode verschiebt die Agenten während der Optimierung und verwendet den Algorithmus zur Bestimmung der neuen Koordinaten der Agenten.
• Revision () - die Methode führt eine Revision und Aktualisierung der besten Koordinaten und der Fitnessfunktion auf der Grundlage der aktuellen Werte der Agenten durch.
• SeInDiSp (double In, double InMin, double InMax, double Step) - die private Methode zur Normalisierung des Wertes von „In“ im Bereich von „InMin“ bis „InMax“ mit einem Schritt von „Step“.
• RNDfromCI (double min, double max) - private Methode zur Erzeugung einer Zufallszahl in einem bestimmten Bereich von „min“ bis „max“.

Es ist zu beachten, dass das dP-Diffusionsverhältnis in der ursprünglichen SA-Version nicht vorhanden ist. Die Idee der Autoren war es, einen neuen Zustand des Systems und dementsprechend eine neue Koordinate der Agenten über den gesamten Bereich von „min“ bis „max“ für jede Koordinate zu erzeugen. Dies entspräche einer chaotischen Bewegung der Moleküle im gesamten „Volumen“ des geglühten Metalls. Meine Experimente haben gezeigt, dass sich die Ergebnisse verbessern, wenn der Bereich der Molekülschwingungen auf ein bestimmtes Intervall, ausgedrückt in Teilen des gesamten zulässigen Intervalls, begrenzt wird. Genau das ist das Ziel des Parameters Diffusionsverhältnis - den Bereich der möglichen Vermischung von Molekülen zu begrenzen.

Um Ergebnisse zu erhalten, die der ursprünglichen SA entsprechen, setzen wir den Parameter einfach auf 1 (Standardwert 0,2).

//————————————————————————————————————————
class C_AO_SA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double tP,           //temperature
                     const double aP,           //temperature reduction coefficient
                     const double dP);          //diffusion coefficient


  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double T;
  private: double α;
  private: double d;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//————————————————————————————————————————

Die Funktion Init dient als Initialisierungsmethode, die alle Felder der Klasse initialisiert und die Größen der notwendigen Arrays verteilt, damit der Optimierungsalgorithmus funktioniert.

//————————————————————————————————————————
void C_AO_SA::Init (const int    coordsP,      //coordinates number
                    const int    popSizeP,     //population size
                    const double tP,           //temperature
                    const double aP,           //temperature reduction coefficient
                    const double dP)           //diffusion coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords     = coordsP;
  popSize    = popSizeP;
  T          = tP;
  α          = aP;
  d          = dP;

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//————————————————————————————————————————

Schreiben wir die Methode Moving, um Agenten im Suchraum zu bewegen.
Bei der ersten Iteration, wenn der Algorithmus gerade gestartet wurde, ist das Flag „revision“ gleich „false“. Es ist notwendig, die Agenten der Population mit Anfangswerten zu initialisieren, die im Bereich der [min;max]-Koordinaten mit einer Gleichverteilung liegen. Wir normalisieren die erhaltenen Werte der Koordinaten der Agenten mit der Funktion SeInDiS, um den erforderlichen Bewegungsschritt beizubehalten. Als nächstes wird das Flag „revision“ auf „true“ gesetzt, um anzuzeigen, dass die Operatoren des Algorithmus des simulierten Abkühlens in der nächsten Iteration angewendet werden müssen.

Wäre dies die ursprüngliche SA, dann würden wir so vorgehen wie in der ersten Iteration, d. h. wir würden auch in der zweiten und den folgenden Iterationen Zufallszahlen in einem bestimmten Bereich mit einer gleichmäßigen Verteilung erzeugen. In unserer leicht korrigierten Version werden wir dasselbe tun, aber mit einer Anpassung des Wertebereichs, wodurch der Bereich der Diffusionswechselwirkung der Moleküle im Metall begrenzt wird, während die Bewegung von dem Ort aus erfolgt, an dem sich das Molekül bei der vorherigen Iteration befand. Wir normalisieren die erhaltenen Werte der Koordinaten der Agenten mit der Funktion SeInDiS, um den erforderlichen Bewegungsschritt beizubehalten.

//————————————————————————————————————————
void C_AO_SA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (-0.1, 0.1);
      a [i].c [c] = a [i].cPrev [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
      a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//————————————————————————————————————————

Während wir bei der Methode „Moving“ neue Zustände des Systems erzeugt haben, d.h. die Moleküle in der Schmelze bewegt haben, werden wir bei der Methode „Revision“ die „Wärmebilanz“ und die Wahrscheinlichkeit des Übergangs der Moleküle in einen neuen Zustand berechnen.

Zu Beginn der Methode überprüfen wir die Werte aller Fitnessfunktionen der Agenten. Wenn wir Werte finden, die besser sind als der globale Wert, werden wir ihn aktualisieren.

Dann führen wir in der „for“-Schleife die folgenden Aktionen für jeden Agenten in der Population durch:

• der Wert „ΔE“ wird als absoluter Wert der Differenz zwischen „a[i].f“ und „a[i].fPrev“ berechnet, d. h. der Differenz zwischen den Werten der Fitnessfunktion bei der aktuellen und der vorherigen Iteration.

Wenn der Wert von „a[i].f“ größer ist als der Wert von „a[i].fPrev“ (d. h. die aktuelle Fitness ist besser als die vorherige), wird der folgende Codeblock ausgeführt:

• der Wert „a[i].fPrev“ wird durch „a[i].f“ ersetzt,
• die Werte des Arrays „a[i].cPrev“ werden aus dem Array „a[i].c“ kopiert.

Andernfalls wird der folgende Codeblock ausgeführt (der aktuelle Wert der Fitnessfunktion ist schlechter als der vorherige):

• der Wahrscheinlichkeitswert „P“ wird als Exponent des negativen Verhältnisses von „ΔE“ zu „T“ berechnet,
• eine Zufallszahl wird aus dem Bereich [0,0;1,0] für „rnd“ erzeugt, um die Wahrscheinlichkeit des Übergangs in einen neuen Zustand zu modellieren, der schlechter ist als der vorherige.

Wenn der Wert von „rnd“ kleiner ist als der Wert von „P“ (d. h. die Wahrscheinlichkeit ist erfüllt), dann:

• der Wert „a[i].fPrev“ wird durch „a[i].f“ ersetzt,
• die Werte des Arrays „a[i].cPrev“ werden aus dem Array „a[i].c“ kopiert.

Der Temperaturwert „T“ wird mit dem thermischen Verhältnis „α“ multipliziert, sodass die Temperatur bei jeder neuen Iteration abnimmt.

//————————————————————————————————————————
void C_AO_SA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double ΔE;
  double P;

  for (int i = 0; i < popSize; i++)
  {
    ΔE = fabs (a [i].f - a [i].fPrev);

    if (a [i].f > a [i].fPrev)
    {
      a [i].fPrev = a [i].f;
      ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
    else
    {
      P = exp (-ΔE / T);
      rnd = RNDfromCI (0, 1.0);

      if (rnd < P)
      {
        a [i].fPrev = a [i].f;
        ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
      }

    }
  }

  T = α * T;
}
//————————————————————————————————————————

3. Testergebnisse

Die Testergebnisse des ursprünglichen Algorithmus mit der Erzeugung von Zufallszahlen im gesamten zulässigen Wertebereich:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 61.3646399742684
Score: 0.76034
25 Rastrigin's; Func runs 10000 result: 47.454223750487884
Score: 0.58798
500 Rastrigin's; Func runs 10000 result: 39.06494648961887
Score: 0.48404
=============================
5 Forest's; Func runs 10000 result: 0.4708272303190655
Score: 0.26632
25 Forest's; Func runs 10000 result: 0.17553657864203864
Score: 0.09929
500 Forest's; Func runs 10000 result: 0.0538869772164491
Score: 0.03048
=============================
5 Megacity's; Func runs 10000 result: 2.6
Score: 0.21667
25 Megacity's; Func runs 10000 result: 1.0
Score: 0.08333
500 Megacity's; Func runs 10000 result: 0.3044
Score: 0.02537
=============================
All score: 2.55383

Die Testergebnisse des Algorithmus ergänzt mit dem Diffusionsverhältnis:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 65.78409729002105
Score: 0.81510
25 Rastrigin's; Func runs 10000 result: 52.25447043222567
Score: 0.64746
500 Rastrigin's; Func runs 10000 result: 40.40159931988021
Score: 0.50060
=============================
5 Forest's; Func runs 10000 result: 0.5814827554067439
Score: 0.32892
25 Forest's; Func runs 10000 result: 0.23156336186841173
Score: 0.13098
500 Forest's; Func runs 10000 result: 0.06760002887601002
Score: 0.03824
=============================
5 Megacity's; Func runs 10000 result: 2.92
Score: 0.24333
25 Megacity's; Func runs 10000 result: 1.256
Score: 0.10467
500 Megacity's; Func runs 10000 result: 0.33840000000000003
Score: 0.02820
=============================
All score: 2.83750

Es ist zu erkennen, dass sich die Leistung des Algorithmus durch die Anwendung des Diffusionsverhältnisses merklich verbessert hat. Der ursprüngliche Algorithmus musste verbessert werden, um in unsere Tabelle aufgenommen zu werden. Es ist überraschend, dass ein so bekanntes und beliebtes Optimierungsverfahren so schwache Ergebnisse liefert, zumal es beim Training neuronaler Netze eingesetzt wird.

Die SA-Visualisierung zeigte keine Auffälligkeiten im Verhalten der Agenten im Suchraum. Die Punkte verhalten sich chaotisch, ohne Strukturen zu bilden, die der thermischen Brownschen Bewegung ähneln. Außerdem bleibt der Algorithmus in lokalen Extremen stecken, und die Konvergenz lässt zu wünschen übrig, obwohl es nicht an Populationsvielfalt mangelt, d. h. die Population ist am Ende der Iterationen nicht erschöpft.

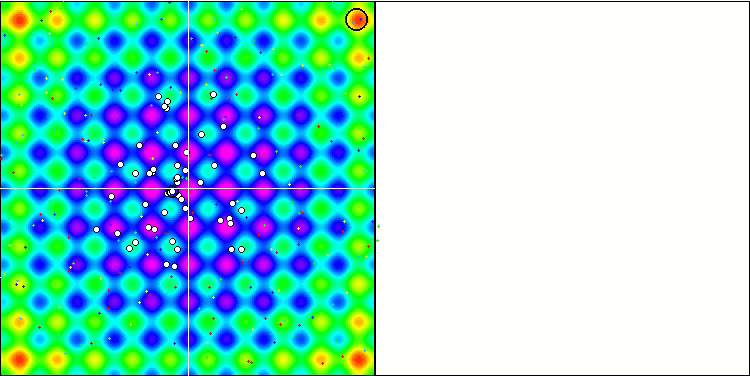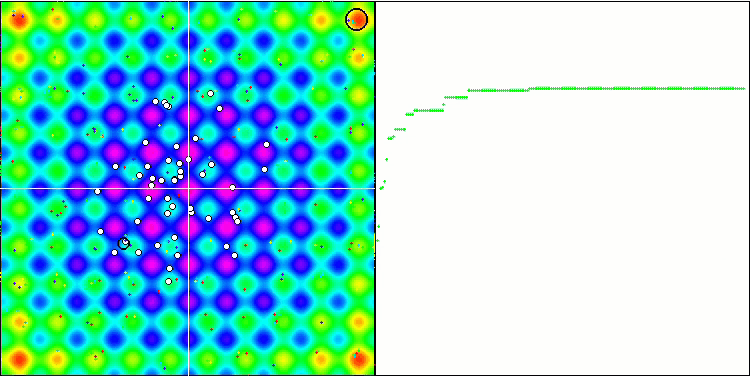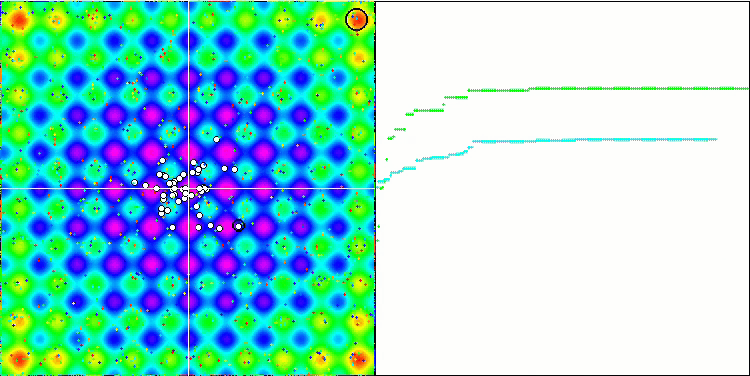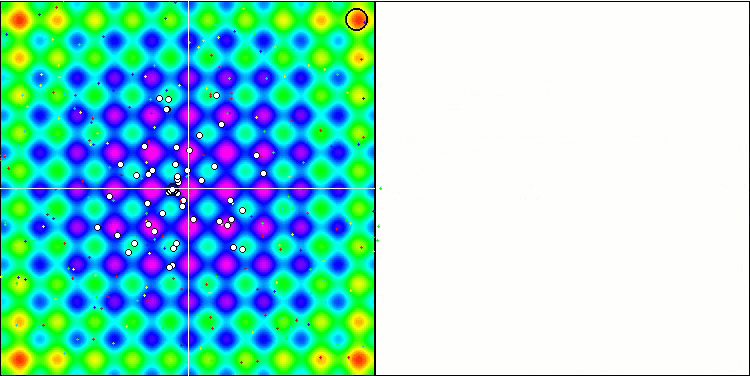
  SA mit der Testfunktion Rastrigin

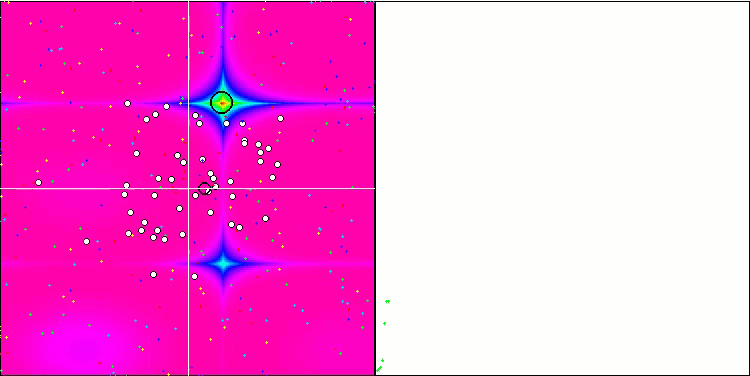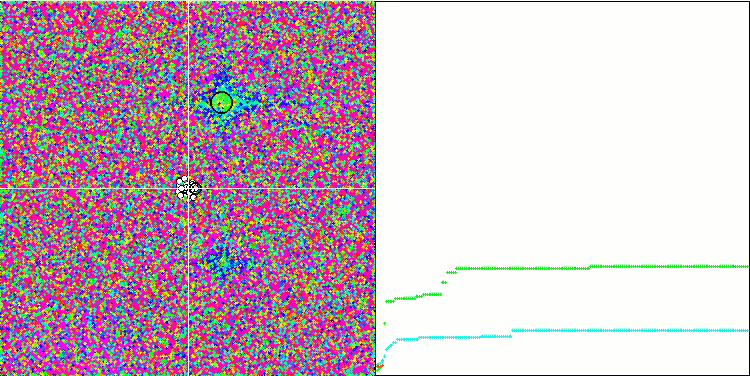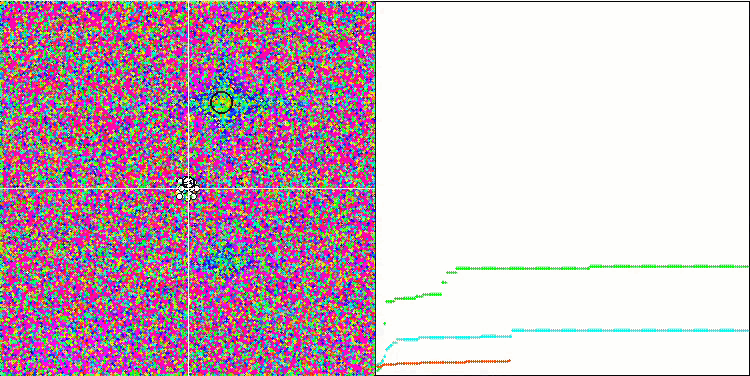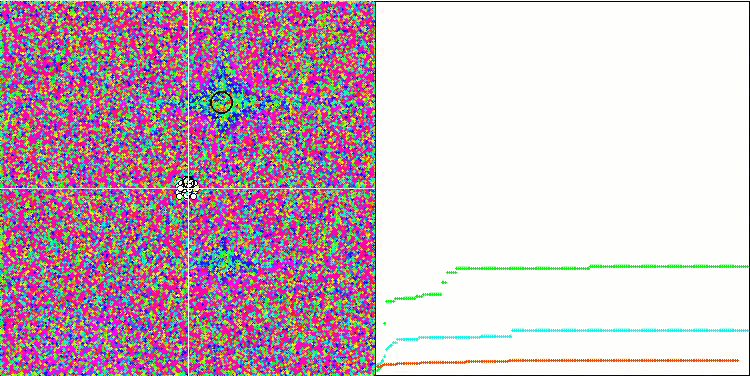
  SA mit der Testfunktion Forest

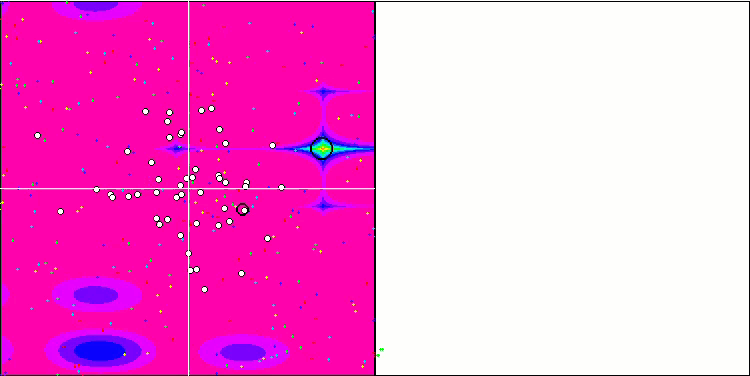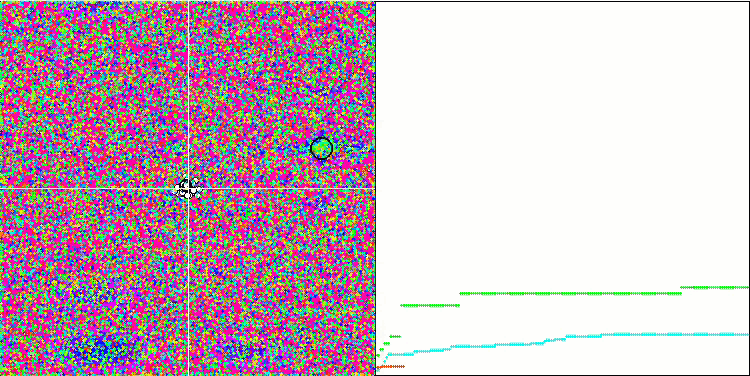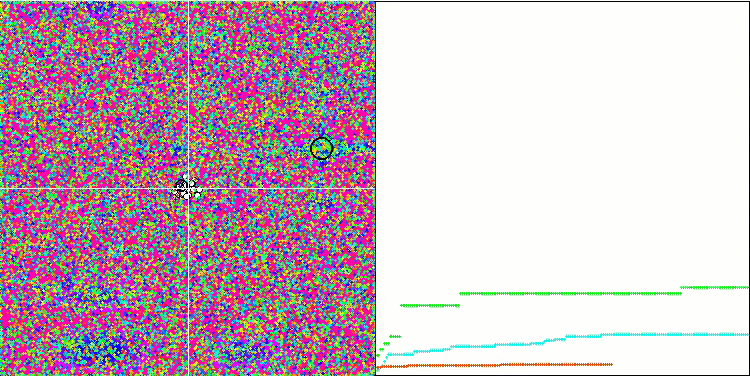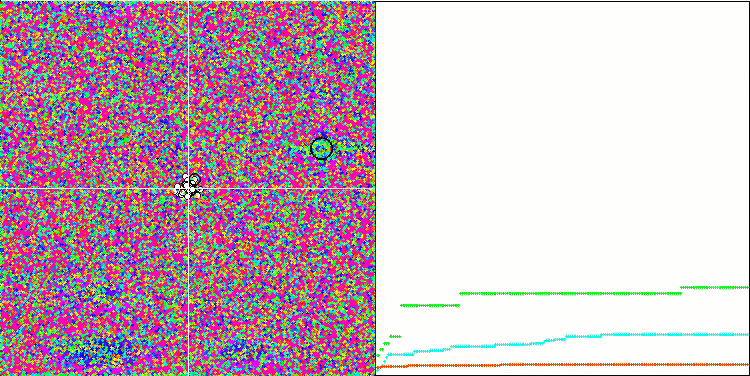
   SA mit der Testfunktion Megacity

Der Algorithmus des simulierten Abkühlens rangiert am Ende der Tabelle. Aus der Vergleichstabelle geht hervor, dass der Algorithmus in den einzelnen Tests keine besonderen Merkmale aufweist. Alle Ergebnisse sind unterdurchschnittlich. Es gibt Algorithmen in der Tabelle, wie z. B. CSS, die in einigen Tests hervorragende Ergebnisse zeigen, obwohl sie am Ende der Tabelle stehen. Leider gehört der SA-Algorithmus nicht dazu.

#	AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastische Diffusionssuche M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	1.00000	2.99265	1.00000	1.00000	1.00000	3.00000	100.000
2	SSG	Setzen, Säen und Wachsen	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.83760	2.21081	0.54782	0.61841	0.99522	2.16146	77.683
3	DE	differentielle Evolution	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.65510	2.50112	0.90000	0.52237	0.12031	1.54268	73.099
4	HS	Harmoniesuche	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.37529	2.04919	0.71739	0.71842	0.41338	1.84919	70.623
5	IWO	Optimierung mit invasiven Unkräutern	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.26613	1.28755	0.57391	0.30527	0.33130	1.21048	48.250
6	ACOm	Ameisen-Kolonie-Optimierung M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.64798	2.19925	0.71739	0.63947	0.05579	1.41265	47.387
7	MEC	Evolutionäre Berechnung des Geistes	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.21324	1.09615	0.66957	0.30000	0.26045	1.23002	44.049
8	SDOm	Optimierung der Spiraldynamik M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.37600	1.36183	0.35653	0.15262	0.25842	0.76758	40.289
9	NMm	Nelder-Mead-Verfahren M	0.88433	0.48306	0.45945	1.82685	0.46155	0.24379	0.21903	0.92437	0.46088	0.25658	0.16810	0.88555	39.660
10	COAm	Kuckuck-Optimierungsalgorithmus M	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.13842	0.95200	0.52174	0.24079	0.17001	0.93254	37.830
11	FAm	Firefly-Algorithmus M	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.41704	1.21519	0.24783	0.20526	0.35090	0.80398	33.139
12	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.11177	0.79355	0.40435	0.19474	0.13859	0.73768	29.766
13	BA	Fledermaus-Algorithmus	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.21769	0.54488	0.21305	0.07632	0.17288	0.46225	29.499
14	CSS	Suche geladener Systeme	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.13638	0.29452	0.07392	0.00000	0.03465	0.10856	27.930
15	GSA	Algorithmus für die Schwerkraftsuche	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.27812	0.84322	0.42609	0.25525	0.00000	0.68134	27.807
16	BFO	Optimierung der bakteriellen Futtersuche	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.17298	0.75026	0.37392	0.24211	0.18841	0.80444	27.542
17	EM	elektromagnetismusähnlicher Algorithmus	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	19.002
18	SFL	schlurfender Froschsprung	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.02221	0.25063	0.19565	0.04474	0.06607	0.30646	13.200
19	SA	simuliertes Abkühlen	0.36938	0.21640	0.10018	0.68595	0.20341	0.07832	0.09372	0.37545	0.16956	0.08422	0.10394	0.35772	13.138
20	MA	Affen-Algorithmus	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.07482	0.22852	0.15652	0.03553	0.10669	0.29874	11.777
21	FSS	Fischschulsuche	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.05458	0.21647	0.12175	0.03947	0.08244	0.24366	11.332
22	IWDm	intelligente Wassertropfen M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.05112	0.38916	0.22609	0.05659	0.05054	0.33322	10.423
23	PSO	Partikelschwarmoptimierung	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.18207	0.44175	0.16956	0.04737	0.01947	0.23641	8.426
24	RND	zufällig	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03949	0.20648	0.12175	0.03290	0.04898	0.20363	5.054
25	GWO	Grauer-Wolf-Optimierung	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02545	0.31812	1.000

Zusammenfassung

Der Algorithmus des simulierten Abkühlens hat mehrere Schwächen, die seine Wirksamkeit bei der Lösung einiger Optimierungsprobleme einschränken können. Einige dieser Schwächen sind:

• Abhängigkeit vom Anfangszustand: Wie viele andere Optimierungsmethoden kann auch das simulierte Abkühlen von einer zufällig gewählten Anfangslösung abhängen. Wenn die Ausgangslösung schlecht ist, kann der Algorithmus in einem lokalen Optimum stecken bleiben und kein globales Optimum finden.
  
  Es ist zu beachten, dass der Algorithmus eine Abstimmung von Parametern wie der „Anfangstemperatur“ und der Temperaturänderungsstufe erfordert, die die Wahrscheinlichkeit einer schlechten Entscheidung beeinflussen. Diese Parameter wirken sich auf die Leistung und die Qualität der Lösungen aus, sodass die Auswahl und Abstimmung der Parameter wichtige Aspekte bei der Anwendung eines simulierten Abkühlens auf ein bestimmtes Optimierungsproblem sind. Die Festlegung dieser Parameter kann eine Herausforderung sein. Falsche Einstellungen können zu schlechten Ergebnissen führen. Die Standardeinstellungen wurden gewählt, um die besten Ergebnisse bei den Testmerkmalen zu erzielen.
  
  
• Ein weiterer Schwachpunkt des simulierten Abkühlens ist die Möglichkeit, in lokalen Extremas hängen zu bleiben. Dies ist der Fall, wenn der Algorithmus eine optimale Lösung findet, die ein lokales Extremum, aber kein globales Extremum ist. In diesem Fall kann der Algorithmus nicht weiterkommen und bleibt am lokalen Optimum stehen. Dies ist in der obigen Visualisierung sehr deutlich zu erkennen.
  
  
• Langsame Konvergenzrate: SA kann bei der Konvergenz zu einer optimalen Lösung langsam sein, insbesondere bei komplexen Optimierungsproblemen. Der Grund dafür ist, dass der Algorithmus mit Zufällen arbeitet und möglicherweise schlechtere Entscheidungen trifft, was den Optimierungsprozess verlangsamen kann.
  
  
• Notwendigkeit einer großen Anzahl von Iterationen: Um eine optimale Lösung zu erreichen, kann der Simulated Annealing-Algorithmus eine große Anzahl von Iterationen erfordern. Dies kann ein Problem für Aufgaben sein, bei denen die Ausführungszeit ein kritischer Faktor ist.
  
  
• Geringe Effizienz bei der Lösung von Problemen mit einer großen Anzahl von Variablen: SA kann bei der Lösung von Problemen mit einer großen Anzahl von Variablen unwirksam sein, da der Suchraum zu groß sein kann. In diesem Fall können andere Optimierungsmethoden, wie genetische Algorithmen oder gradientenbasierte Optimierungsmethoden, effektiver sein. Der Algorithmus kommt mit einer kleinen Anzahl von Variablen (1-2) gut zurecht, wie jeder Algorithmus, selbst ein einfacher Zufalls-RND.

Es gibt mehrere Verbesserungsmöglichkeiten für das simulierte Abkühlen, um seine Leistung und Effizienz zu steigern:

1. Modifizierung der Kühlfunktion: Die Kühlfunktion ist ein wichtiger Parameter des Algorithmus, der die Kühlgeschwindigkeit und die Temperatur des Systems regelt.

2. Anwendung effizienterer Methoden zur Auswahl des nächsten Zustands: Bei SA wird der nächste Zustand zufällig ausgewählt. Es gibt jedoch effizientere Methoden für die Auswahl des nächsten Zustands, z. B. Mutations- und Crossover-Methoden.

3. Verwendung adaptiver Parameter: Die Parameter des Algorithmus, wie z. B. die Anfangstemperatur und das Abkühlungsverhältnis, können je nach den Merkmalen des Optimierungsproblems adaptiv angepasst werden.

4. Verwendung einer Kombination von Algorithmen: SA kann mit anderen Optimierungsalgorithmen, wie genetischen Algorithmen oder Gradientenabstiegsmethoden, kombiniert werden, um die Optimierungsleistung und -effizienz zu verbessern.

Die Verwendung unterschiedlicher Verteilungen einer Zufallsvariablen bei der Erzeugung eines neuen Systemzustands anstelle einer gleichmäßigen Verteilung trug nicht zur Verbesserung der Ergebnisse bei. Es gibt jedoch eine Möglichkeit, diesen sehr bekannten und beliebten Algorithmus so radikal zu verändern, dass er mit den Spitzenreitern mithalten kann. Wie ist das möglich? Ich werde diese Methode im zweiten Teil des Artikels teilen und über alle Phasen der Änderung sprechen. Aber wie wir wissen, gibt es keinen universellen Weg, einen Optimierungsalgorithmus zu verbessern, und es hängt allein von der Suchstrategie im Algorithmus selbst ab. Die Verbesserung betrifft daher nur den guten alten (aber praktisch nutzlosen) Algorithmus des simulierten Abkühlens.

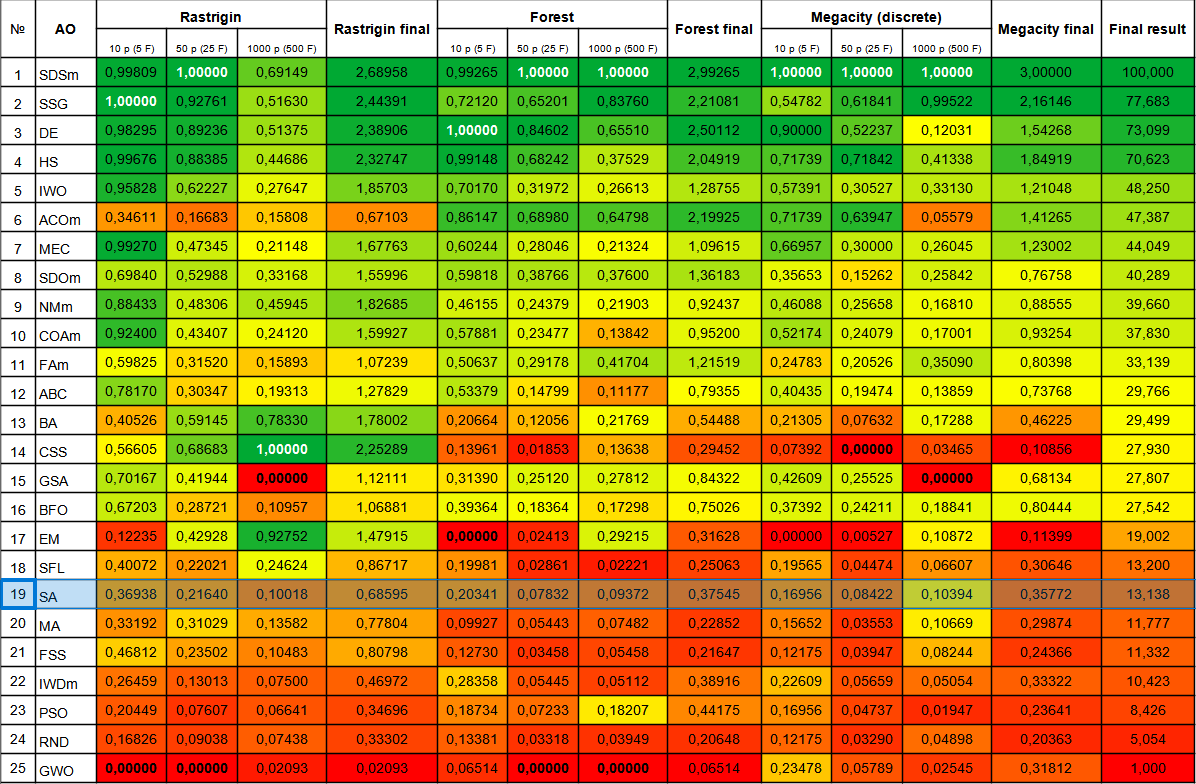
Abb. 3. Farbabstufung der Algorithmen gemäß den einschlägigen Tests

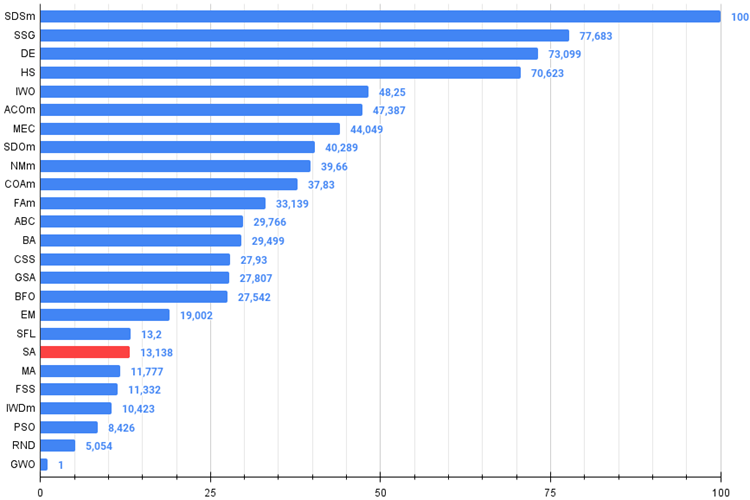
Abb. 4. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,

das Archiv enthält das Skript zur Berechnung der Bewertungstabelle nach der im Artikel angewandten Methode)

SA Vor- und Nachteile:

Vorteile:

1. Eine kleine Anzahl externer Parameter.
2. Hohe Arbeitsgeschwindigkeit.
3. Sehr einfache Umsetzung.
   

Nachteile

1. Unklare Einstellungen (es ist nicht klar, wie und was die Temperatur beeinflusst).
   
2. Sehr schlechte Skalierbarkeit.
3. Hohe Streuung der Ergebnisse.
4. Tendenz, in lokalen Extrema stecken zu bleiben.
5. Schlechte Konvergenz.

Dem Artikel ist ein Archiv mit aktualisierten Versionen der in früheren Artikeln beschriebenen Algorithmuscodes beigefügt. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.