Expert Advisor auf der Grundlage des universellen MLP-Approximators

Inhalt

1. Einführung
2. Eintauchen in die Probleme der Ausbildung
   
3. Universal-Approximator
4. Implementierung von MLP als Teil eines Trading EA

Einführung

Wenn es um neuronale Netze geht, stellen sich viele Menschen komplexe Algorithmen und umständliche technische Details vor. Im Kern ist ein neuronales Netz eine Komposition von Funktionen, wobei jede Schicht aus einer Kombination einer linearen Transformation und einer nichtlinearen Aktivierungsfunktion besteht. Wenn wir dies in eine Gleichung einsetzen, sieht sie wie folgt aus:

F(x) = f2(f1(x))

wobei f1 die Funktion der ersten Schicht und f2 die Funktion der zweiten Schicht ist.

Viele Menschen denken, dass neuronale Netze etwas unglaublich Komplexes und schwer zu Verstehendes sind, aber ich möchte sie mit einfachen Worten erklären, damit jeder sie aus einer anderen Perspektive sehen kann. Es gibt viele verschiedene Architekturen neuronaler Netze, die jeweils für bestimmte Aufgaben konzipiert sind. In diesem Artikel konzentrieren wir uns auf das einfachste mehrschichtige Perzeptron (MLP), das durch nichtlineare Funktionen Transformationen an den Eingangsinformationen vornimmt. Wenn wir die Netzwerkarchitektur kennen, können wir sie in eine analytische Form bringen, bei der jede Aktivierungsfunktion in den Neuronen als nichtlinearer Transformator dient.

Jede Schicht des Netzes enthält eine Gruppe von Neuronen, die Informationen verarbeiten, die viele nichtlineare Transformationen durchlaufen. Das mehrschichtige Perzeptron ist in der Lage, Aufgaben wie Annäherung, Klassifizierung und Extrapolation durchzuführen. Die allgemeine Gleichung, die die Funktionsweise des Perzeptrons beschreibt, wird mit Hilfe von Gewichten angepasst, sodass es an verschiedene Aufgabenstellungen angepasst werden kann.

Interessanterweise können wir diesen Approximator in jedes Handelssystem integrieren. Betrachtet man ein neuronales Netz, ohne Optimierer wie SGD oder ADAM zu erwähnen, kann MLP als Informationstransformator verwendet werden. Zum Beispiel kann es die Marktbedingungen analysieren - sei es eine Flaute, ein Trend oder eine Übergangsphase - und darauf basierend verschiedene Handelsstrategien anwenden. Wir können auch ein neuronales Netz verwenden, um Indikatordaten in Handelssignale umzuwandeln.

In diesem Artikel wollen wir mit dem Mythos der Komplexität neuronaler Netze aufräumen und zeigen, wie man, abgesehen von den komplexen Details der Gewichtung und Optimierung, einen auf einem neuronalen Netz basierenden Handels-EA erstellen kann, ohne tiefgreifende Kenntnisse des maschinellen Lernens zu haben. Wir werden den Prozess der Erstellung eines EA Schritt für Schritt durchgehen, von der Datenerfassung und -aufbereitung bis zum Training des Modells und seiner Integration in eine Handelsstrategie.

Eintauchen in die Probleme der Ausbildung

Es gibt drei Haupttypen von Schulungen. Wir interessieren uns für die Nuancen dieser Arten, wie sie für die Analyse von Marktdaten gelten. Der in diesem Artikel vorgestellte Ansatz zielt darauf ab, die Unzulänglichkeiten dieser Ausbildungsformen zu berücksichtigen.

Überwachtes Lernen. Das Modell wird auf markierten Daten trainiert und macht Vorhersagen auf der Grundlage von Beispielen. Zielfunktion: Minimierung des Fehlers der Vorhersage gegenüber dem Zielwert (z. B. MSE-Fehler). Dieser Ansatz hat jedoch eine Reihe von Nachteilen. Sie erfordert eine beträchtliche Menge an qualitativ hochwertigen markierten Daten, was im Kontext von Zeitreihen eine große Herausforderung darstellt. Wenn wir klare und zuverlässige Beispiele haben, anhand derer wir trainieren können, wie z. B. bei der Handschrifterkennung oder der Erkennung von Bildinhalten, dann verläuft das Training reibungslos. Das neuronale Netz lernt, genau das zu erkennen, wofür es trainiert wurde.

Bei Zeitreihen ist die Situation anders: Es ist äußerst schwierig, die Daten so zu kennzeichnen, dass man sich auf ihre Zuverlässigkeit und Relevanz verlassen kann. In der Praxis stellt sich heraus, dass das Netz das lernt, was wir annehmen, und nicht das, was tatsächlich für den untersuchten Prozess relevant ist. Viele Autoren betonen, dass ein erfolgreiches überwachtes Training die Verwendung von „guten“ Kennzeichnungen voraussetzt, aber der Grad ihrer Qualität im Kontext von Zeitreihen ist oft schwer im Voraus zu bestimmen.

Daraus ergeben sich andere subjektive Einschätzungen der Qualität des Trainings, wie z.B. „überanpassung“. Es wird auch das künstliche Konzept des „Rauschens“ eingeführt, was bedeutet, dass ein übermäßig „überangepasstes“ Netz sich Rauschdaten und nicht die Hauptmuster merken könnte. Sie werden nirgendwo klare Definitionen und Quantifizierungen von „Rauschen“ und „Überanpassung“ finden, eben weil sie bei der Zeitreihenanalyse subjektiv sind. Daher sollte man sich darüber im Klaren sein, dass bei der Anwendung des überwachten Lernens auf Zeitreihen viele Nuancen berücksichtigt werden müssen, die schwer zu algorithmisieren sind und die Stabilität des Modells bei neuen Daten erheblich beeinflussen.

Unüberwachtes Lernen. Das Modell selbst sucht nach verborgenen Strukturen in nicht gekennzeichneten Daten. Die Zielfunktionen können je nach Methode unterschiedlich sein. Es ist schwierig, die Qualität der erzielten Ergebnisse zu beurteilen, da es keine eindeutigen Anhaltspunkte für eine Überprüfung gibt. Das Modell findet möglicherweise keine nützlichen Muster, wenn die Daten keine klare Struktur aufweisen, und es ist nicht bekannt, ob in den Daten tatsächlich Strukturen gefunden wurden, die in direktem Zusammenhang mit dem „Trägerprozess“ stehen.

Zu den Methoden, die traditionell als unüberwachtes Lernen eingestuft werden, gehören: K-means, Self-Organizing Maps (SOM) und andere. Alle diese Methoden werden anhand ihrer spezifischen Zielfunktionen trainiert.

Betrachten wir einige Beispiele:

• K-means. Minimierung der internen Cluster-Varianz, die als Summe der Quadrate der Abstände zwischen jedem Punkt und seinem Clusterzentrum definiert ist.
• Hauptkomponentenanalyse (Principal component analysis, PCA). Maximierung der Varianz der Projektionen von Daten auf neue Achsen (Hauptkomponenten).
• Entscheidungsbäume (Decision trees, DT). Minimierung von Entropie, Gini-Index, Streuung und anderen.
  

Verstärkungslernen (Reinforcement learning). Zielfunktion: Gesamtbelohnung. Es handelt sich um eine Technik des maschinellen Lernens, bei der ein Agent (z. B. ein Programm oder ein Roboter) durch Interaktion mit seiner Umgebung lernt, Entscheidungen zu treffen. Der Agent erhält je nach seinen Aktionen eine Belohnung oder eine Strafe. Das Ziel des Agenten ist es, die Gesamtbelohnung durch Lernen aus Erfahrung zu maximieren.

Die Ergebnisse können aufgrund des zufälligen Charakters des Trainings instabil sein, was es schwierig macht, das Verhalten des Modells vorherzusagen, und es ist nicht immer für Probleme geeignet, bei denen es kein klares System von Belohnungen und Bestrafungen gibt, was das Lernen weniger effektiv machen kann. Verstärkungslernen ist in der Regel mit vielen praktischen Problemen verbunden: die Schwierigkeit der Darstellung der objektiven Verstärkungsfunktion bei der Verwendung von Lernalgorithmen für neuronale Netze wie ADAM und dergleichen, da es notwendig ist, die Werte der Zielfunktion auf einen Bereich nahe [-1;1] zu normalisieren. Dabei werden die Ableitungen der Aktivierungsfunktion in den Neuronen berechnet und der Fehler durch das Netz zurückgeführt, um die Gewichte anzupassen und eine „Gewichtsexplosion“ und ähnliche Effekte zu vermeiden, die das neuronale Netz zum Stillstand bringen.

Wir haben uns oben die herkömmliche Klassifizierung der Ausbildungsarten angesehen. Wie Sie sehen können, basieren sie alle auf der Minimierung/Maximierung einer Zielfunktion. Dann wird deutlich, dass der Hauptunterschied zwischen ihnen nur in einem Punkt besteht - dem Fehlen oder Vorhandensein eines „Vorgesetzten“. Wenn dies nicht der Fall ist, hängt die Einteilung der Ausbildungsarten von den Besonderheiten der zu optimierenden Zielfunktion ab.

Meiner Meinung nach kann die Klassifizierung von Trainingsarten als überwachtes Lernen dargestellt werden, wenn es Zielwerte gibt (Minimierung des Vorhersagefehlers in Bezug auf das Ziel) und als unüberwachtes Lernen, wenn es keine Zielwerte gibt. Die Unterarten des unüberwachten Lernens hängen von der Art der Zielfunktion ab, die auf Dateneigenschaften (Abstand, Dichte usw.), der Systemleistung (integrierte Metriken wie Gewinn, Produktivität usw.), Verteilungen (für generative Modelle) und anderen Bewertungskriterien basiert.

Universal-Approximator

Der von mir vorgeschlagene Ansatz gehört zur zweiten Art - dem unüberwachten Lernen. Bei dieser Methode versuchen wir nicht, dem neuronalen Netz beizubringen, wie man richtig handelt, und wir sagen ihm nicht, wo es Positionen eröffnen oder schließen soll, da wir selbst die Antwort auf diese Fragen nicht kennen. Stattdessen überlassen wir es dem Netzwerk, seine eigenen Handelsentscheidungen zu treffen, und unsere Aufgabe ist es, seine gesamten Handelsergebnisse zu bewerten.

In diesem Fall brauchen wir die Bewertungsfunktion nicht zu normalisieren oder uns um Probleme wie „Gewichtsexplosionen“ und „Netzwerkstillstand“ zu kümmern, da sie bei diesem Ansatz nicht auftreten. Wir trennen das neuronale Netz logischerweise vom Optimierungsalgorithmus und geben ihm nur die Aufgabe, die Eingabedaten in eine neue Art von Informationen umzuwandeln, die die Fähigkeiten des Händlers widerspiegeln. Im Grunde genommen wandeln wir einfach eine Art von Informationen in eine andere um, ohne die Muster in den Zeitreihen zu verstehen oder zu wissen, wie man handelt, um einen Gewinn zu erzielen.

Ein neuronales Netz wie das MLP (Multilayer Perceptron) ist für diese Aufgabe ideal geeignet, was durch das universelle Approximationstheorem bestätigt wird. Dieses Theorem besagt, dass neuronale Netze jede kontinuierliche Funktion approximieren können. In unserem Fall verstehen wir unter „kontinuierlicher Funktion“ einen Prozess, der in der analysierten Zeitreihe auftritt. Mit diesem Ansatz entfällt die Notwendigkeit, auf künstliche und subjektive Begriffe wie „Rauschen“ und „Überanpassung“ zurückzugreifen, die keinen quantitativen Wert haben.

Um eine Vorstellung davon zu bekommen, wie das funktioniert, genügt ein Blick auf Abbildung 1. Wir füttern MLP mit einigen Informationen, die sich auf die aktuellen Marktdaten beziehen (das können OHLC-Bar-Preise, Indikatorwerte usw. sein), und am Ausgang erhalten wir einsatzbereite Handelssignale. Nachdem wir die Historie eines Handelssymbols durchlaufen haben, können wir die Zielfunktion berechnen, bei der es sich um eine integrale Bewertung (oder einen Komplex von Bewertungen) der Handelsergebnisse handelt, und die Netzwerkgewichte mit einem externen Optimierungsalgorithmus anpassen, um die Zielfunktion zu maximieren, die die Qualität der Handelsergebnisse des neuronalen Netzwerks beschreibt.

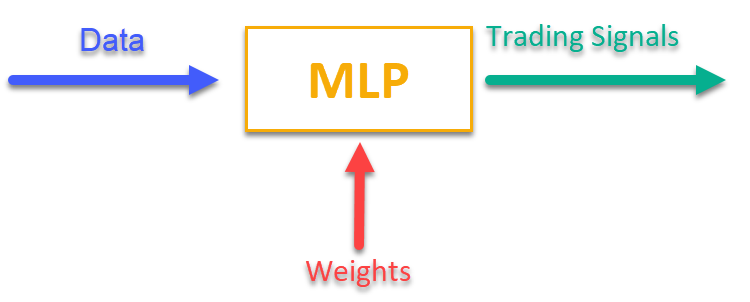
Abbildung 1. Umwandlung einer Art von Information in eine andere

Implementierung von MLP als Teil eines Trading EA

Zuerst schreiben wir die MLP-Klasse, dann betten wir die Klasse in den EA ein. Die Artikel enthalten viele verschiedene Implementierungen von Netzen unterschiedlicher Architekturen, aber ich werde meine Version von MLP zeigen, die genau ein neuronales Netz ist, ohne einen Optimierer.

Deklarieren wir eine Klasse C_MLP, die ein mehrschichtiges Perzeptron (MLP) implementiert. Wesentliche Merkmale:

1. Init() - die Initialisierung konfiguriert das Netz in Abhängigkeit von der gewünschten Anzahl der Schichten und der Anzahl der Neuronen in jeder Schicht und gibt die Gesamtzahl der Gewichte zurück.

2. ANN() - ein Vorwärtsdurchlauf von der ersten Eingabeschicht bis zur letzten Ausgabeschicht, die Methode nimmt Eingabedaten und Gewichte, berechnet die Ausgabewerte des Netzes (siehe Abb. 1).

3. GetWcount() - Gesamtzahl der Gewichte im Netz.

4. LayerCalc() - Berechnung der Netzwerkschicht.

Interne Elemente:

• Schichten speichern die Werte der Neuronen
• weightsCNT - Gesamtzahl der Gewichte
• layersCNT - Gesamtzahl der Schichten

Mit dieser Klasse können wir ein neuronales MLP-Netz mit einer beliebigen Anzahl versteckter Schichten und einer beliebigen Anzahl von Neuronen in diesen Schichten erstellen.

//+----------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                          |
//| Implement a forward pass through a fully connected neural network          |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                            |
//+----------------------------------------------------------------------------+
class C_MLP
{
  public: //--------------------------------------------------------------------

  // Initialize the network with the given configuration
  // Return the total number of weights in the network, or 0 in case of an error
  int Init (int &layerConfig []);

  // Calculate the values of all layers sequentially from input to output
  void ANN (double &inLayer  [],  // input values
            double &weights  [],  // network weights (including biases)
            double &outLayer []); // output layer values

  // Get the total number of weights in the network
  int GetWcount () { return weightsCNT; }

  int layerConf []; // Network configuration - number of neurons in each layer

  private: //-------------------------------------------------------------------
  // Structure for storing the neural network layer
  struct S_Layer
  {
      double l [];     // Neuron values
  };

  S_Layer layers [];    // Array of all network layers
  int     weightsCNT;   // Total number of weights in the network (including biases)
  int     layersCNT;    // Total number of layers (including input and output ones)
  int     cnt_W;        // Current index in the weights array when traversing the network
  double  temp;         // Temporary variable to store the sum of the weighted inputs

  // Calculate values of one layer of the network
  void LayerCalc (double   &inLayer  [], // values of neurons of the previous layer
                  double   &weights  [], // array of weights and biases of the entire network
                  double   &outLayer [], // array for writing values of the current layer
                  const int inSize,      // number of neurons in the input layer
                  const int outSize);    // outSize  - number of neurons in the output layer
};

Ein mehrschichtiges Perzeptron (MLP) wird mit einer bestimmten Schichtkonfiguration initialisiert. Die wichtigsten Schritte:

1. Überprüfe die Konfiguration:

• Prüfe, ob das Netz mindestens 2 Schichten hat (Eingabe und Ausgabe).
• Überprüfe, ob es in jeder Schicht mindestens 1 Neuron gibt. Wenn die Bedingungen nicht erfüllt sind, wird eine Fehlermeldung angezeigt und die Funktion gibt 0 zurück.

2. Speichere die Konfiguration der einzelnen Ebenen für den schnellen Zugriff auf das Array layerconf.

3. Erstelle die Arrays der Schichten: Für die Neuronen in jeder Schicht wird Speicher zugewiesen.

4. Gewichtsanzahl: Die Gesamtzahl der Gewichte im Netz wird berechnet, einschließlich der Verzerrungen für jedes Neuron.

Die Funktion liefert die Gesamtzahl der Gewichte oder 0 im Falle eines Fehlers.

//+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLP::Init (int &layerConfig [])
{
  // Check that the network has at least 2 layers (input and output)
  layersCNT = ArraySize (layerConfig);
  if (layersCNT < 2)
  {
    Print ("Error Net config! Layers less than 2!");
    return 0;
  }

  // Check that each layer has at least 1 neuron
  for (int i = 0; i < layersCNT; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Error Net config! Layer No." + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  // Save network configuration
  ArrayCopy (layerConf, layerConfig, 0, 0, WHOLE_ARRAY);

  // Create an array of layers
  ArrayResize (layers, layersCNT);

  // Allocate memory for neurons of each layer
  for (int i = 0; i < layersCNT; i++)
  {
    ArrayResize (layers [i].l, layerConfig [i]);
  }

  // Calculate the total number of weights in the network
  weightsCNT = 0;
  for (int i = 0; i < layersCNT - 1; i++)
  {
    // For each neuron of the next layer we need:
    // - one bias value
    // - weights for connections with all neurons of the current layer
    weightsCNT += layerConf [i] * layerConf [i + 1] + layerConf [i + 1];
  }

  return weightsCNT;
}

Die Methode LayerCalc führt Berechnungen für eine einzelne Schicht eines neuronalen Netzes durch und verwendet dabei den hyperbolischen Tangens als Aktivierungsfunktion. Die wichtigsten Schritte:

1. Eingabe- und Ausgabeparameter:

• inLayer[] - Array der Eingabewerte der vorherigen Schicht
• weights[] - weights-Array enthält Offsets und Gewichte für die Links
• outLayer[] - Array zur Speicherung der Ausgangswerte der aktuellen Schicht
• inSize - Anzahl der Neuronen in der Eingabeschicht
• outSize - Anzahl der Neuronen in der Ausgabeschicht

2. Durchlaufen Sie die Neuronen der Ausgabeschicht. Für jedes Neuron in der Ausgabeschicht:

• beginne mit einem Bias-Werten
• addiere gewichtete Eingabewerte (jeder Eingabewert wird mit dem entsprechenden Gewicht multipliziert)
• der Wert der Aktivierungsfunktion für ein Neuron wird berechnet

3. Anwendung der Aktivierungsfunktion:

• verwende den hyperbolischen Tangens, um einen Wert nichtlinear in einen Bereich zwischen -1 und 1 zu transformieren
• das Ergebnis wird in das Ausgabe-Array outLayer[] geschrieben

//+----------------------------------------------------------------------------+
//| Calculate values of one layer of the network                               |
//| Implement the equation: y = tanh(bias + w1*x1 + w2*x2 + ... + wn*xn)       |
//+----------------------------------------------------------------------------+
void C_MLP::LayerCalc (double    &inLayer  [],
                       double    &weights  [],
                       double    &outLayer [],
                       const int  inSize,
                       const int  outSize)
{
  // Calculate the value for each neuron in the output layer
  for (int i = 0; i < outSize; i++)
  {
    // Start with the bias value for the current neuron
    temp = weights [cnt_W];
    cnt_W++;

    // Add weighted inputs from each neuron in the previous layer
    for (int u = 0; u < inSize; u++)
    {
      temp += inLayer [u] * weights [cnt_W];
      cnt_W++;
    }

    // Apply the "hyperbolic tangent" activation function
    // f(x) = 2/(1 + e^(-x)) - 1
    // Range of values f(x): [-1, 1]
    outLayer [i] = 2.0 / (1.0 + exp (-temp)) - 1.0;
  }
}

Wir setzen die Arbeit eines künstlichen neuronalen Netzes um, indem wir nacheinander die Werte aller Schichten berechnen - von der Eingabe bis zur Ausgabe. 

1. Eingabe- und Ausgabeparameter:

• inLayer[] - Array von Eingabewerten, die in das neuronale Netz eingespeist werden
• weights[] - Array von Gewichten, das sowohl die Gewichte für die Verbindungen zwischen den Neuronen als auch die Verzerrungen enthält
• outLayer[] - Array, das die Ausgangswerte der letzten Schicht des neuronalen Netzes enthält

2. Gewichtszähler zurücksetzen: Die Variable cnt_W, die die aktuelle Position im Gewichtsfeld festhält, wird vor Beginn der Berechnung auf 0 zurückgesetzt.

3. Kopieren von Eingabedaten: Eingabedaten aus inLayer werden mit der Funktion ArrayCopy in die erste Schicht des Netzes kopiert.

4. Schleife durch die Schichten:

• die Schleife geht durch alle Schichten des neuronalen Netzes.
• Für jede Schicht wird die Funktion LayerCalc aufgerufen, um die Werte für die aktuelle Schicht auf der Grundlage der Ausgangswerte der vorherigen Schicht, der Gewichte und der Größen der Schichten zu berechnen.

5. Nachdem alle Schichten ihre Berechnungen abgeschlossen haben, werden die Ausgangswerte der letzten Schicht mit Hilfe der Funktion ArrayCopy in die Schicht outLayer kopiert.

//+----------------------------------------------------------------------------+
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLP::ANN (double &inLayer  [],  // input values
                 double &weights  [],  // network weights (including biases)
                 double &outLayer [])  // output layer values
{
  // Reset the weight counter before starting the pass
  cnt_W = 0;

  // Copy the input data to the first layer of the network
  ArrayCopy (layers [0].l, inLayer, 0, 0, WHOLE_ARRAY);

  // Calculate the values of each layer sequentially
  for (int i = 0; i < layersCNT - 1; i++)
  {
    LayerCalc (layers    [i].l,     // output of the previous layer
               weights,             // network weights (including bias)
               layers    [i + 1].l, // next layer
               layerConf [i],       // size of current layer
               layerConf [i + 1]);  // size of the next layer
  }

  // Copy the values of the last layer to the output array
  ArrayCopy (outLayer, layers [layersCNT - 1].l, 0, 0, WHOLE_ARRAY);
}

Es ist an der Zeit, einen Advisor für eine automatische Handelsstrategie zu schreiben, die maschinelles Lernen auf der Grundlage des neuronalen MLP-Netzes verwendet.

1. Wir werden Bibliotheken für Handelsoperationen, die Handhabung von Handelssymbolinformationen, mathematische Funktionen, mehrschichtige Perzeptrons (MLP) und Optimierungsalgorithmen miteinander verbinden.

2. Handelsparameter - Positionsvolumen, Beginn und Ende der Handelszeit. Trainingsparameter - Auswahl des Optimierers, Struktur des neuronalen Netzes, Anzahl der zu analysierenden Balken, Tiefe der Trainingshistorie, Gültigkeitsdauer des Modells und Signalschwelle.

3. Deklaration von Klassen und Variablen - Klassenobjekte für Dienstprogramme, neuronales Netz und Variablen zum Speichern von Eingabedaten, Gewichten und der letzten Trainingszeit.

#include "#Symbol.mqh"
#include <Math\AOs\Utilities.mqh>
#include <Math\AOs\NeuroNets\MLP.mqh>
#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>

//------------------------------------------------------------------------------
input group    "---Trade parameters-------------------";
input double   Lot_P              = 0.01;   // Position volume
input int      StartTradeH_P      = 3;      // Trading start time
input int      EndTradeH_P        = 12;     // Trading end time

input group    "---Training parameters----------------";
input E_AO     OptimizerSelect_P  = AO_CLA; // Select optimizer
input int      NumbTestFuncRuns_P = 5000;   // Total number of function runs
input string   MLPstructure_P     = "1|1";  // Hidden layers, <4|6|2> - three hidden layers
input int      BarsAnalysis_P     = 3;      // Number of bars to analyze
input int      DepthHistoryBars_P = 10000;  // History depth for training in bars 
input int      RetrainingPeriod_P = 12;     // Duration in hours of the model's relevance
input double   SigThr_P           = 0.5;    // Signal threshold

//------------------------------------------------------------------------------
C_AO_Utilities U;
C_MLP          NN;
int            InpSigNumber;
int            WeightsNumber;
double         Inputs  [];
double         Weights [];
double         Outs    [1];
datetime       LastTrainingTime = 0;

C_Symbol       S;
C_NewBar       B;
int            HandleS;
int            HandleR;

Ich wählte das Erste, was mir in den Sinn kam, als Daten, die dem neuronalen Netz zur Verarbeitung übergeben wurden: OHLC - Balkenpreise (standardmäßig in den Einstellungen, 3 vorherige Balken vor dem aktuellen) und die Werte der RSI- und Stochastik-Indikatoren für diese Balken. Die Funktion OnInit () initialisiert eine Handelsstrategie, die ein neuronales Netz verwendet. 

1. Initialisiere die Indikatoren - Objekte für RSI und Stochastic werden erstellt.

2. Berechne die Anzahl der Eingangssignale für das Netz auf der Grundlage des Eingangs BarsAnalysis_P.

3. Richte die Struktur des neuronalen Netzes ein - die Eingabeparameterzeile mit der Netzkonfiguration wird geteilt, die Gültigkeit der Anzahl der Schichten und Neuronen wird überprüft. Der Input-String-Parameter gibt die Anzahl der versteckten Schichten des Netzes und der Neuronen in ihnen an. Standardmäßig ist der Parameter „1|1“, was 2 versteckte Schichten im Netz mit je einem Neuron bedeutet.

4. Initialisierung des neuronalen Netzes - die Methode wird aufgerufen, um das Netz zu initialisieren, Arrays für Gewichte und Eingabedaten werden erstellt.

5. Informationsausgabe - Daten über die Anzahl der Schichten und Netzparameter werden gedruckt.

6. Gibt einen erfolgreichen Initialisierungsstatus zurück.

Die Funktion stellt sicher, dass alle notwendigen Komponenten für das Funktionieren der Handelsstrategie vorbereitet sind.

//——————————————————————————————————————————————————————————————————————————————
int OnInit ()
{
  //----------------------------------------------------------------------------
  // Initializing indicators: Stochastic and RSI
  HandleS = iStochastic (_Symbol, PERIOD_CURRENT, 5, 3, 3, MODE_EMA, STO_LOWHIGH);
  HandleR = iRSI        (_Symbol, PERIOD_CURRENT, 14, PRICE_TYPICAL);

  // Calculate the number of inputs to the neural network based on the number of bars to analyze
  InpSigNumber = BarsAnalysis_P * 2 + BarsAnalysis_P * 4;

  // Display information about the number of inputs
  Print ("Number of network logins  : ", InpSigNumber);

  //----------------------------------------------------------------------------
  // Initialize the structure of the multilayer MLP
  string sepResult [];
  int layersNumb = StringSplit (MLPstructure_P, StringGetCharacter ("|", 0), sepResult);

  // Check if the number of hidden layers is greater than 0
  if (layersNumb < 1)
  {
    Print ("Network configuration error, hidden layers < 1...");
    return INIT_FAILED; // Return initialization error
  }

  // Increase the number of layers by 2 (input and output)
  layersNumb += 2;

  // Initialize array for neural network configuration
  int nnConf [];
  ArrayResize (nnConf, layersNumb);

  // Set the number of inputs and outputs in the network configuration
  nnConf [0] = InpSigNumber;   // Input layer
  nnConf [layersNumb - 1] = 1; // Output layer

  // Filling the hidden layers configuration
  for (int i = 1; i < layersNumb - 1; i++)
  {
    nnConf [i] = (int)StringToInteger (sepResult [i - 1]); // Convert a string value to an integer

    // Check that the number of neurons in a layer is greater than 0
    if (nnConf [i] < 1)
    {
      Print ("Network configuration error, in layer ", i, " <= 0 neurons...");
      return INIT_FAILED; // Return initialization error
    }
  }

  // Initialize the neural network and get the number of weights
  WeightsNumber = NN.Init (nnConf);
  if (WeightsNumber <= 0)
  {
    Print ("Error initializing MLP network...");
    return INIT_FAILED; // Return initialization error
  }

  // Resize the input array and weights
  ArrayResize (Inputs,  InpSigNumber);
  ArrayResize (Weights, WeightsNumber);

  // Initialize weights with random values in the range [-1, 1] (for debugging)
  for (int i = 0; i < WeightsNumber; i++)
      Weights [i] = 2 * (rand () / 32767.0) - 1;

  // Output network configuration information
  Print ("Number of all layers     : ", layersNumb);
  Print ("Number of network parameters: ", WeightsNumber);

  //----------------------------------------------------------------------------
  // Initialize the trade and bar classes
  S.Init (_Symbol);
  B.Init (_Symbol, PERIOD_CURRENT);

  return (INIT_SUCCEEDED); // Return successful initialization result
}
//——————————————————————————————————————————————————————————————————————————————

Die Hauptlogik der Handelsstrategie ist in der Funktion OnTick () implementiert. Die Strategie ist einfach: Wenn das Signal des Neurons der Ausgabeschicht den in den Parametern festgelegten Schwellenwert überschreitet, wird das Signal als entsprechend der Kauf-/Verkaufsrichtung interpretiert, und wenn es keine offenen Positionen gibt und die aktuelle Zeit für den Handel erlaubt ist, eröffnen wir eine Position. Die Position wird geschlossen, wenn das neuronale Netz ein gegenteiliges Signal erhält, oder sie wird zwangsweise geschlossen, wenn die für den Handel vorgesehene Zeit endet. Lassen Sie uns die wichtigsten Schritte der Strategie aufzählen:

1. Prüfe, ob ein neues Training erforderlich ist. Wenn seit dem letzten Training genügend Zeit vergangen ist, wird das Training des neuronalen Netzes gestartet. Im Falle eines Fehlers wird eine Meldung angezeigt.

2. Testen des neuen Balkens. Wenn der aktuelle Tick nicht der Beginn eines neuen Balkens ist, wird die Ausführung der Funktion abgebrochen.

3. Empfangen von Daten. Der Code fragt Kursdaten (Eröffnungs-, Schlusskurs, Höchst- und Tiefstkurs) und Indikatorwerte (RSI und Stochastic) ab.

4. Normalisierung der Daten. Die Maximal- und Minimalwerte werden unter den empfangenen Symbolpreisdaten gefunden, woraufhin alle Daten im Bereich von -1 bis 1 normalisiert werden.

5. Vorhersage. Die normalisierten Daten werden in ein neuronales Netz eingespeist, um Ausgangssignale zu erzeugen.

6. Generierung eines Handelssignals. Auf der Grundlage der Ausgangsdaten wird ein Kauf- (1) oder Verkaufssignal (-1) generiert.

7. Positionsmanagement. Wenn die aktuelle Position dem Signal widerspricht, wird es geschlossen. Fällt das Signal zur Eröffnung einer neuen Position mit der zulässigen Zeit zusammen, wird die Position eröffnet. Andernfalls wird eine offene Position geschlossen.

Somit implementiert die Logik in OnTick() den gesamten Zyklus des automatisierten Handels, einschließlich Training, Datenerfassung, Normalisierung, Prognosen und Positionsmanagement.

//——————————————————————————————————————————————————————————————————————————————
void OnTick ()
{
  // Check if the neural network needs to be retrained
  if (TimeCurrent () - LastTrainingTime >= RetrainingPeriod_P * 3600)
  {
    // Start the neural network training
    if (Training ()) LastTrainingTime = TimeCurrent (); // Update last training time
    else             Print ("Training error...");      // Display an error message

    return; // Complete function execution
  }

  //----------------------------------------------------------------------------
  // Check if the current tick is the start of a new bar
  if (!B.IsNewBar ()) return;

  //----------------------------------------------------------------------------
  // Declare arrays to store price and indicator data
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  // Get price data
  if (CopyRates (_Symbol, PERIOD_CURRENT, 1, BarsAnalysis_P, rates) != BarsAnalysis_P) return;

  // Get Stochastic values
  if (CopyBuffer (HandleS, 0, 1, BarsAnalysis_P, sto) != BarsAnalysis_P) return;
  // Get RSI values
  if (CopyBuffer (HandleR, 0, 1, BarsAnalysis_P, rsi) != BarsAnalysis_P) return;

  // Initialize variables to normalize data
  int wCNT   = 0;
  double max = -DBL_MAX; // Initial value for maximum
  double min =  DBL_MAX; // Initial value for minimum

  // Find the maximum and minimum among high and low
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    if (rates [b].high > max) max = rates [b].high; // Update the maximum
    if (rates [b].low  < min) min = rates [b].low;  // Update the minimum
  }

  // Normalization of input data for neural network
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    Inputs [wCNT] = U.Scale (rates [b].high,  min, max, -1, 1); wCNT++; // Normalizing high
    Inputs [wCNT] = U.Scale (rates [b].low,   min, max, -1, 1); wCNT++; // Normalizing low
    Inputs [wCNT] = U.Scale (rates [b].open,  min, max, -1, 1); wCNT++; // Normalizing open
    Inputs [wCNT] = U.Scale (rates [b].close, min, max, -1, 1); wCNT++; // Normalizing close

    Inputs [wCNT] = U.Scale (sto   [b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
    Inputs [wCNT] = U.Scale (rsi   [b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
  }

  // Convert data from Inputs to Outs
  NN.ANN (Inputs, Weights, Outs);

  //----------------------------------------------------------------------------
  // Generate a trading signal based on the output of a neural network
  int signal = 0;
  if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
  if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

  // Get the type of open position
  int posType = S.GetPosType ();
  S.GetTick ();

  if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
  {
    if (!S.PosClose ("", ORDER_FILLING_FOK) != 0) posType = 0;
    else return;
  }

  MqlDateTime time;
  TimeToStruct (TimeCurrent (), time);

  // Check the allowed time for trading
  if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P)
  {
    // Open a new position depending on the signal
    if (posType == 0 && signal != 0) S.PosOpen (signal, Lot_P, "", ORDER_FILLING_FOK, 0, 0.0, 0.0, 1);
  }
  else
  {
    if (posType != 0) S.PosClose ("", ORDER_FILLING_FOK);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Als Nächstes wollen wir uns das Training eines neuronalen Netzes mit historischen Daten ansehen:

1. Empfangen von Daten. Historische Kursdaten werden zusammen mit RSI- und Stochastik-Indikatorwerten geladen.

2. Festlegung der Handelszeit. Es wird ein Array erstellt, das angibt, welche Balken in die zulässige Handelszeit fallen.

3. Einstellung der Optimierungsparameter. Die Grenzen und Parameterschritte für die Optimierung werden initialisiert.

4. Auswahl eines Optimierungsalgorithmus. Definietion eines Optimierungsalgorithmus und Angabe der Populationsgröße.

5. Die Hauptschleife der Gewichtsoptimierung im neuronalen Netz: 

• Für jede Lösung in der Population wird der Wert der Zielfunktion berechnet, um ihre Qualität zu bewerten.
• die Lösungspopulation wird auf der Grundlage der Ergebnisse aktualisiert.

6. Ausgabe der Ergebnisse. Der Name des Algorithmus und das beste Ergebnis werden gedruckt, und die besten Parameter werden in das Array der Gewichte kopiert.

7. Der vom Objekt Optimierungsalgorithmus belegte Speicher wird freigegeben.

Die Funktion führt ein Training des neuronalen Netzes durch, um auf der Grundlage historischer Daten die besten Parameter zu finden.

//——————————————————————————————————————————————————————————————————————————————
bool Training ()
{
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  int bars = CopyRates (_Symbol, PERIOD_CURRENT, 1, DepthHistoryBars_P, rates);
  Print ("Training on history of ", bars, " bars");
  if (CopyBuffer (HandleS, 0, 1, DepthHistoryBars_P, sto) != bars) return false;
  if (CopyBuffer (HandleR, 0, 1, DepthHistoryBars_P, rsi) != bars) return false;

  MqlDateTime time;
  bool truTradeTime []; ArrayResize (truTradeTime, bars); ArrayInitialize (truTradeTime, false);
  for (int i = 0; i < bars; i++)
  {
    TimeToStruct (rates [i].time, time);
    if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P) truTradeTime [i] = true;
  }

  //----------------------------------------------------------------------------
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = NumbTestFuncRuns_P / popSize; // Total number of epochs (iterations) for optimization

  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps

  ArrayResize (rangeMin,  WeightsNumber);              // Resize 'min' borders array
  ArrayResize (rangeMax,  WeightsNumber);              // Resize 'max' borders array
  ArrayResize (rangeStep, WeightsNumber);              // Resize the steps array

  for (int i = 0; i < WeightsNumber; i++)
  {
    rangeMax  [i] =  5.0;
    rangeMin  [i] = -5.0;
    rangeStep [i] = 0.01;
  }

  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (OptimizerSelect_P);             // Select an optimization algorithm

  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)

  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs

  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = TargetFunction (ao.a [set].c, rates, rsi, sto, truTradeTime); //FF.CalcFunc (ao.a [set].c); //ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }

  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB);
  ArrayCopy (Weights, ao.cB);
  delete ao;                                           // Release the memory occupied by the algorithm object

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Wir implementieren die Zielfunktion zur Bewertung der Effizienz einer Handelsstrategie mit Hilfe eines neuronalen Netzes.

1. Initialisierung von Variablen. Festlegen der Variablen, um Gewinne, Verluste, die Anzahl der Trades und andere Parameter zu verfolgen.

2. Umgang mit historischen Daten. Die Schleife durchläuft die historischen Daten und prüft, ob die Eröffnung von Positionen für den aktuellen Balken zulässig ist.

3. Normalisierung der Daten. Für jeden Balken werden die Kurswerte (Höchst-, Tiefst-, Eröffnungs- und Schlusskurs) und die Indikatoren (RSI und Stochastik) für die anschließende Übertragung an das neuronale Netz normalisiert.

4. Signalvorhersage. Die normalisierten Daten werden in ein neuronales Netz eingespeist, das Handelssignale (Kauf oder Verkauf) erzeugt.

5. Virtuelle Positionen werden gemäß der Handelsstrategie in OnTick () verwaltet.

6. Berechnen Sie das Ergebnis. Am Ende der Funktion wird die Gesamtgewinn-/Verlustquote berechnet, die mit der Anzahl der Geschäfte multipliziert wird, wobei ein Reduktionsfaktor für das Ungleichgewicht zwischen Käufen und Verkäufen berücksichtigt wird.

Die Funktion bewertet die Effizienz einer Handelsstrategie durch die Analyse von Gewinnen und Verlusten auf der Grundlage von Signalen, die von einem neuronalen Netz generiert werden, und gibt einen numerischen Wert zurück, der die Qualität der Strategie widerspiegelt (im Wesentlichen führt die Funktion einen Durchlauf durch die Geschichte zurück von der aktuellen Position des Handels EA in der Zeit).

//——————————————————————————————————————————————————————————————————————————————
double TargetFunction (double &weights [], MqlRates &rates [], double &rsi [], double &sto [], bool &truTradeTime [])
{
  int bars = ArraySize (rates);

  // Initialize variables to normalize data
  int    wCNT       = 0;
  double max        = 0.0;
  double min        = 0.0;
  int    signal     = 0;
  double profit     = 0.0;
  double allProfit  = 0.0;
  double allLoss    = 0.0;
  int    dealsNumb  = 0;
  int    sells      = 0;
  int    buys       = 0;
  int    posType    = 0;
  double posOpPrice = 0.0;
  double posClPrice = 0.0;

  // Run through history
  for (int h = BarsAnalysis_P; h < bars - 1; h++)
  {
    if (!truTradeTime [h])
    {
      if (posType != 0)
      {
        posClPrice = rates [h].open;
        profit = (posClPrice - posOpPrice) * signal - 0.00003;

        if (profit > 0.0) allProfit += profit;
        else              allLoss   += -profit;

        if (posType == 1) buys++;
        else              sells++;

        allProfit += profit;
        posType = 0;
      }

      continue;
    }

    max  = -DBL_MAX; // Initial value for maximum
    min  =  DBL_MAX; // Initial value for minimum

    // Find the maximum and minimum among high and low
    for (int b = 1; b <= BarsAnalysis_P; b++)
    {
      if (rates [h - b].high > max) max = rates [h - b].high; // Update maximum
      if (rates [h - b].low  < min) min = rates [h - b].low;  // Update minimum
    }

    // Normalization of input data for neural network
    wCNT = 0;
    for (int b = BarsAnalysis_P; b >= 1; b--)
    {
      Inputs [wCNT] = U.Scale (rates [h - b].high,  min, max, -1, 1); wCNT++; // Normalizing high
      Inputs [wCNT] = U.Scale (rates [h - b].low,   min, max, -1, 1); wCNT++; // Normalizing low
      Inputs [wCNT] = U.Scale (rates [h - b].open,  min, max, -1, 1); wCNT++; // Normalizing open
      Inputs [wCNT] = U.Scale (rates [h - b].close, min, max, -1, 1); wCNT++; // Normalizing close

      Inputs [wCNT] = U.Scale (sto   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
      Inputs [wCNT] = U.Scale (rsi   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
    }

    // Convert data from Inputs to Outs
    NN.ANN (Inputs, weights, Outs);

    //----------------------------------------------------------------------------
    // Generate a trading signal based on the output of a neural network
    signal = 0;
    if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
    if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

    if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
    {
      posClPrice = rates [h].open;
      profit = (posClPrice - posOpPrice) * signal - 0.00003;

      if (profit > 0.0) allProfit += profit;
      else              allLoss   += -profit;

      if (posType == 1) buys++;
      else              sells++;

      allProfit += profit;
      posType = 0;
    }

    if (posType == 0 && signal != 0)
    {
      posType = signal;
      posOpPrice = rates [h].open;
    }
  }

  dealsNumb = buys + sells;

  double ko = 1.0;
  if (sells == 0 || buys == 0) return -DBL_MAX;
  if (sells / buys > 1.5 || buys / sells > 1.5) ko = 0.001;

  return (allProfit / (allLoss + DBL_EPSILON)) * dealsNumb;
}
//——————————————————————————————————————————————————————————————————————————————

Abbildung 2 zeigt eine grafische Darstellung des Gleichgewichts der Handelsergebnisse, die mit einem MLP-basierten EA auf neuen, dem neuronalen Netz unbekannten Daten erzielt wurden. Die Eingabe sind normalisierte OHLC-Kurswerte sowie RSI- und Stochastik-Indikatoren, die auf der Grundlage der angegebenen Anzahl von Balken berechnet werden. Der EA handelt so lange, wie das neuronale Netzwerk auf dem neuesten Stand ist; andernfalls trainiert er das Netzwerk und setzt dann den Handel fort. Die in Abbildung 2 dargestellten Ergebnisse spiegeln also die Leistung bei OOS (out of sample) wider.

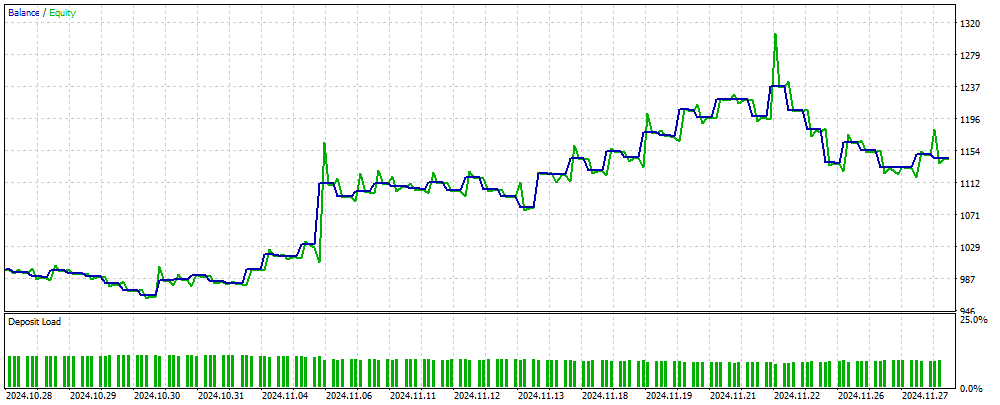
Abbildung 2. Das Ergebnis der EA-Operation auf Daten, die der MLP nicht bekannt sind

Zusammenfassung

In diesem Artikel wird eine einfache und zugängliche Methode zur Verwendung eines neuronalen Netzwerks in einem Handels-EA vorgestellt, die für ein breites Spektrum von Händlern geeignet ist und keine tiefgreifenden Kenntnisse auf dem Gebiet des maschinellen Lernens erfordert. Mit dieser Methode entfällt die Notwendigkeit, die Zielfunktionswerte zu normalisieren, um sie als Fehler in das neuronale Netz einzuspeisen, und es sind auch keine Methoden zur Vermeidung einer „Gewichtsexplosion“ erforderlich. Darüber hinaus löst es das Problem des „Staus im Netz“ und bietet intuitives Training mit visueller Kontrolle der Ergebnisse.

Es ist zu beachten, dass der EA nicht über die notwendigen Kontrollen bei der Durchführung von Handelsgeschäften verfügt und nur zu Informationszwecken dient.

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	#C_AO.mqh	Include	Übergeordnete Klasse von Populationsoptimierungsalgorithmen
2	#C_AO_enum.mqh	Include	Aufzählung von Algorithmen zur Populationsoptimierung
3	Utilities.mqh	Include	Bibliothek der Hilfsfunktionen
4	#Symbol.mqh	Include	Bibliothek der Handels- und Hilfsfunktionen
5	ANN EA.mq5	Expert Advisor	EA auf Basis eines neuronalen MLP-Netzwerks