Algorithmen zur Optimierung mit Populationen Künstliches Bienenvolk (Artificial Bee Colony, ABC)

MetaTrader 5 — Beispiele | 24 Januar 2023, 09:38

243

Andrey Dik

Inhalt

1. Einführung

Soziale Insekten sind hochentwickelte Lebewesen, die viele komplexe Aufgaben erfüllen, die von vielen einzelnen Insekten nicht ausgeführt werden. Kommunikation, komplexer Nestbau, Umweltkontrolle, Schutz und Arbeitsteilung sind nur einige der Verhaltensweisen, die Honigbienen entwickelt haben, um in sozialen Kolonien zu gedeihen.
Bienen gehören zu den Schwarmwesen und zeigen außergewöhnliche Fähigkeiten, optimale Lösungen zu finden. In der Natur finden sie in der Nähe des Bienenstocks Blütentrauben, um Nektar und Pollen zu sammeln. Manchmal kann der Suchradius bis zu mehreren Kilometern betragen. Die umstimmenden Bienen teilen ihre Ergebnisse in einem improvisierten Tanz mit.

Auf den ersten Blick scheint dies unmöglich zu sein, aber sie sind in der Lage, sich gegenseitig durch rhythmische Bewegungen Informationen über die geografische Position zu übermitteln. Je nach Intensität des Tanzes ihrer Geschwister ziehen die Bienen Rückschlüsse auf die Anzahl der Blüten und die geschätzte Menge an Nektar an einem bestimmten Ort. Je mehr potenzielle Nahrung, desto aktiver findet der Tanz statt. Dieses ungewöhnliche Phänomen wurde Mitte des 20. Jahrhunderts von dem Insektenforscher Karl von Frisch entdeckt.

Viele Jahre lang wurden die Methoden der Bienensuche ausschließlich von Biologen erforscht. Das Interesse an der Anwendung des Schwarmverhaltens bei der Entwicklung neuer Optimierungsalgorithmen wuchs jedoch. Im Jahr 2005 wurde Professor Dervis Karaboga auf die Forschungsergebnisse aufmerksam. Er veröffentlichte einen wissenschaftlichen Artikel und beschrieb als erster das Modell der Schwarmintelligenz, das sich vor allem am Bienentanz orientiert. Das Modell wurde als künstliches Bienenvolk bezeichnet.

2. Beschreibung des Algorithmus

Es gibt viele Implementierungen eines künstlichen Bienenvolks(artificial bee colony, ABC) die sich in den Grundsätzen der Verwaltung der Bienen in einem Bienenstock und in den Regeln für die Erkundung des Gebiets unterscheiden. In diesem Artikel werde ich über meine Interpretation der klassischen Version des Algorithmus sprechen.

Die Idee des Algorithmus basiert auf dem Verhalten der Bienen bei der Suche nach Orten, an denen sie so viel Nektar wie möglich bekommen können. Zunächst fliegen alle Bienen aus dem Bienenstock in eine zufällige Richtung, um als Kundschafterbienen Gebiete zu finden, in denen es Nektar gibt. Danach kehren die Bienen zum Bienenstock zurück und teilen den anderen auf besondere Weise mit, wo und wie viel Nektar sie gefunden haben.

Die Arbeitsbienen werden zu den Fundorten geschickt. Je mehr Nektar in diesem Gebiet zu finden sein soll, desto mehr Bienen fliegen in diese Richtung. Die Kundschafterbienen fliegen wieder weg, um nach anderen Gebieten zu suchen, aber schon in der Nähe der gefundenen Gebiete. So werden alle Bienen in zwei Arten unterteilt: Arbeitsbienen, die Nektar sammeln, und Kundschafterbienen, die neue Gebiete erkunden. Die Nektarsammelgebiete haben einen Wert, der der Menge an Nektar entspricht, die sie enthalten. Regionen eines niedrigeren Ranges werden relativ zu einer Region eines höheren Ranges entlang einer Linie verschoben, die durch die Zentren der Regionen verläuft.

Die Verteilung der Arbeitsbienen nach Regionen ist in Abbildung 1 schematisch dargestellt.

ABCarea

Abb. 1. Die Anzahl der Bienen in den Gebieten hängt von der Rangfolge der Gebiete ab

Gebiet 1 hat einen höheren Rang, da es den meisten Nektar enthält und daher mehr Bienen dorthin fliegen. Anhand der Anzahl der Bienen können wir visuell feststellen, dass das Gebiet 4 den niedrigsten Rang (Wert) hat. Informationen über den Wert der einzelnen Gebiete werden von den Bienen in Form eines speziellen Tanzes gemeldet. Jeder Bienenstock hat seinen eigenen Tanz, bei dem die Richtung und die Menge des Nektars in der Umgebung programmiert wird.

Angenommen, der Ort des globalen Extremums ist das Gebiet, in dem es den meisten Nektar gibt, und es gibt nur ein solches Gebiet. An anderen Stellen gibt es Nektar, wenn auch in geringerer Menge. Bienen leben in einem mehrdimensionalen Raum, in dem jede Koordinate einen Parameter der zu optimierenden Funktion darstellt. Die gefundene Nektarmenge ist der Wert der Zielfunktion an diesem Punkt, wenn wir nach einem globalen Maximum suchen. Wenn wir nach einem globalen Minimum suchen, genügt es, die Zielfunktion mit -1 zu multiplizieren.

Da die Nektarsammelgebiete einen bestimmten Wert haben, hat nur das Gebiet mit dem höchsten Rang das Recht, sich zu dem Punkt mit der höchsten Nektarkonzentration zu bewegen (Zentrumsverschiebung). Gebiete mit einem niedrigeren Rang werden in das Zentrum der höchsten Konzentration verschoben und auf die Überschneidung mit einem Gebiet eines höheren Ranges überprüft. Auf diese Weise wird die Konzentration der Bienen in einem engen, kleinen Gebiet verhindert und der Suchraum wird von den Arbeitsbienen so effizient wie möglich bedient, wodurch die Erschöpfung der Nahrungsquelle verhindert wird. In Bezug auf die Optimierung bedeutet dies, dass das Steckenbleiben in lokalen Extrema vermieden oder minimiert wird. Nachdem die Gebiete verstreut und relativ zueinander entlang der Rangkette in Richtung ihres Optimums verschoben wurden, werden ihre Nachbarschaften zusätzlich von Kundschafterbienen untersucht.

Viele Imker empfehlen, Kundschafterbienen in zufällige Bereiche des Suchraums zu schicken, aber meine Erfahrung zeigt, dass der praktische Wert eines solchen „Kundschaftens“ gegen Null geht und nur für eine und zwei Dimensionen nützlich ist. Mit anderen Worten: Wenn es sich um mehrdimensionale Räume handelt, dann nehmen die Freiheitsgrade geometrisch zu, und es ist unglaublich schwierig, zufällig über eine wertvollere Nektarquelle zu stolpern. Die Ressourcen des Bienenstocks werden nur verschwendet. Viel sinnvoller ist es, Kundschafterinnen in die Nachbarschaft der bereits bekannten Suchgebiete zu schicken, damit die Koordinaten nicht verstreut, sondern gezielt auf die Zonen möglicher Nektarquellen konzentriert werden.

Wenn sich die Flächen überschneiden, muss der Mittelpunkt so verschoben werden, dass die Flächen nur die Ränder berühren. Dies ist in Abbildung 2 dargestellt.

ABCcrossArea

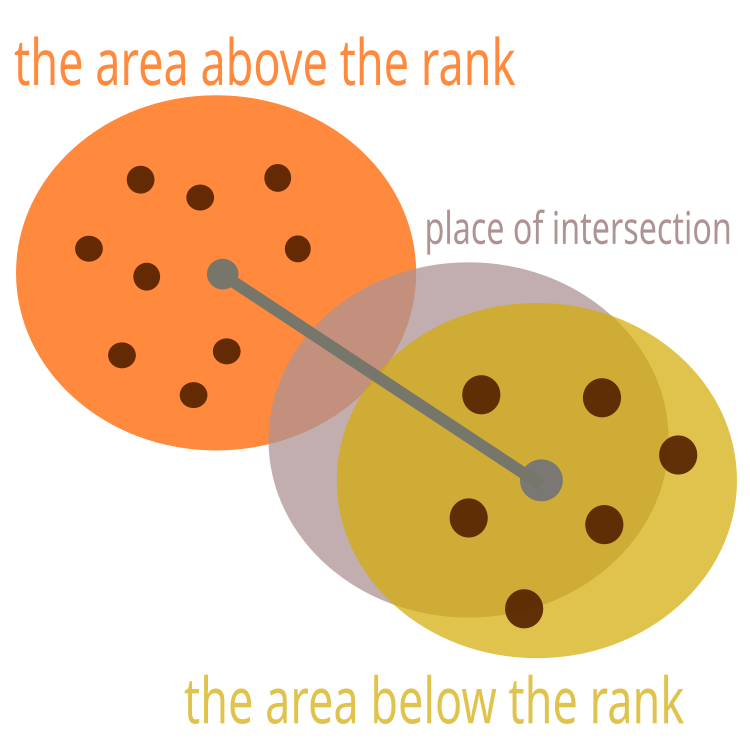
Abb. 2. Das Gebiet mit einem niedrigeren Rang sollte verschoben werden

Der Rang der Gebiete ist nicht starr festgelegt, sondern wird dynamisch gebildet. Die Funde von Kundschafterbienen werden dem Gebiet zugeordnet, in dessen Nähe sie geflogen sind. Falls eine wertvollere Nahrungsquelle entdeckt wird, wird das Zentrum des Gebiets dorthin verlagert. Es könnte sogar die neue beste Nektarsammelstelle werden. Die übrigen Bereiche werden nun relativ dazu verschoben. Mit anderen Worten: Sie werden entlang der Rangkette relativ zu ihm verschoben.

Die Methode der Informationsübermittlung, die als Bienentanz bezeichnet wird, ist ein wesentliches Element der Strategie des Bienenstocks als Ganzes. Es ist notwendig, die verfügbaren Ressourcen des Bienenstocks möglichst rationell auf die zu bearbeitenden Flächen zu verteilen, daher sollte die Anzahl der entsandten Bienen proportional zum Wert der Fläche sein. Das bedeutet, dass eine gleiche Anzahl von Bienen in gleichwertige Gebiete geschickt wird.

Kommen wir nun zum Algorithmus selbst. Die Ausführungsschritte sind im Folgenden aufgeführt:

Alle Bienen fliegen nach dem Zufallsprinzip als Kundschafter durch den Suchraum.
Wir messen die von jeder Biene aufgenommene Nektarmenge.
Sortieren der Bienen.
Zuweisen der Flächen entsprechend der von den Bienen ermittelten Nektarmenge.
Entsendung von Arbeitsbienen in das Gebiet. Je mehr Nektar in dem Gebiet vorhanden ist, desto mehr Bienen werden geschickt.
Aussenden von Kundschafterbienen in der Nähe eines zufällig ausgewählten Gebiets.
Messung der von jeder Biene aufgenommenen Nektarmenge.
Reihung der Gebiete nach der Menge des Nektars.
Wiederholen ab Schritt 4, bis das Stoppkriterium erfüllt ist.

Um die visuelle Wahrnehmung zu erleichtern, wird der Algorithmus in Abbildung 3 als Blockdiagramm dargestellt.

ABCsceme

Abb. 3. Blockschaltbild des Algorithmus

Beschreiben wir den Code des Bienenvolk-Algorithmus genauer.

Eine Biene ist eine elementare und grundlegende logische Einheit des Algorithmus. Sie kann durch eine Struktur beschrieben werden. Wie Sie sich vielleicht erinnern, wird ein Bienenstandort anhand von Koordinaten, der Zugehörigkeit zu dem Gebiet, in dem Nektar gesammelt wurde, und der Nektarmenge bestimmt. Die Bienen des Bienenstocks werden dann durch ein Array dargestellt. Auf jeden kann über seinen Index zugegriffen werden.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bee
{
  double c []; //coordinates
  int    aInd; //area index
  double n;    //nectar
};
//——————————————————————————————————————————————————————————————————————————————

Die zweite, größere logische Einheit ist das Gebiet der Nektarsammlung. Es wird durch den Mittelpunkt und den Punkt der größten Nektarkonzentration und die Nektarmenge definiert, die den Wert des Gebietes bestimmt. In dem Gebiet mit dem höchsten Rang (dem ersten in der Liste) stimmen die Koordinaten des Zentrums und der höchsten Nektarkonzentration überein. Bei den Gebieten an zweiter und unterer Stelle der Liste stimmen sie möglicherweise nicht überein, da sie verschoben wurden. Die Initialisierung des Gebietes schließt mit dem Zurücksetzen des Nektarmengenindikators und der Verteilung der Koordinaten auf die entsprechende Anzahl von Parametern der optimierten Funktion ab.

//——————————————————————————————————————————————————————————————————————————————
struct S_Area
{
  void Init (int coordinatesNumber)
  {
    n = -DBL_MAX;

    ArrayResize (cC, coordinatesNumber);
    ArrayResize (cB, coordinatesNumber);
  }

  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Beschreiben wir den Tanz der Bienen als eine Struktur, deren Anordnung der Anzahl der Bereiche entspricht.

//——————————————————————————————————————————————————————————————————————————————
struct S_BeeDance
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Ich werde den Bienenstock als eine Klasse beschreiben, die Suchgebiete, Bienen, beste Koordinaten und die größte Menge an Nektar in allen Iterationen findet. Außerdem werden hier alle notwendigen Methoden zum Sortieren von Bienen und Flächen sowie zum Bewegen von Bienen und Flächen relativ zueinander definiert. Hier sehen wir die bereits bekannten Funktionsdeklarationen für die vorherigen Algorithmen: Erzeugung zufälliger, gleichmäßig verteilter Zahlen, Skalierung auf einen Bereich und Auswahl einer Zahl aus einem Bereich mit einem Schritt.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABC //Bees Hive
{
  //============================================================================
  public: S_Area areas     []; //nectar collection areas
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Bee  bees      []; //all the bees of the hive
  public: double cB        []; //best coordinates
  public: double nB;           //nectar of the best coordinates

  public: void InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP); //scout area radius

  public: void TasksForBees ();
  public: void CollectingNectar ();

  //============================================================================
  private: void   BeeFlight      (double &cC [] , S_Bee &bee);
  private: void   ScoutBeeFlight (double &cC [] , S_Bee &bee);
  private: void   MarkUpAreas    ();
  private: void   SortingBees    ();
  private: void   SortingAreas   ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: int    coordinates;      //coordinates number
  private: int    beesNumber;       //the number of all bees
  private: int    workerBeesNumber; //worker bees number
  private: int    areasNumber;      //areas number
  private: S_Bee  beesT       [];   //temporary, for sorting
  private: S_Area areasT      [];   //temporary, for sorting
  private: int    indA        [];   //array for indexes when sorting
  private: double valA        [];   //array for nectar values when sorting
  private: int    indB        [];   //array for indexes when sorting
  private: double valB        [];   //array for nectar values when sorting
  private: double areasRadius [];   //radius for each coordinate
  private: double scoutRadius [];   //scout radius for each coordinate

  private: double collectionRadius;   //collection radius
  private: double scoutAreaRadius;    //scout area radius
  private: double hypersphereRadius;  //hypersphere radius
  private: double distHyperspCenters; //distance hyperspheres centers
  private: double scoutHyperspRadius; //scout hypersphere radius
  private: bool   scouting;           //scouting flag

  private: S_BeeDance beeDance [];    //bee dance
};
//——————————————————————————————————————————————————————————————————————————————

Jede neue Optimierung sollte unbedingt mit der Initialisierung der Klasse beginnen. Der Wert der Nektarmenge wird für den gesamten Bienenstock und für einzelne Bienen sowie für Bereiche zurückgesetzt.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP)  //scout area radius
{
  MathSrand (GetTickCount ());
  scouting = false;
  nB       = -DBL_MAX;

  coordinates      = coordinatesP;
  beesNumber       = beesNumberP;
  workerBeesNumber = workerBeesNumberP;
  areasNumber      = areasNumberP < 3 ? 3 : areasNumberP;

  collectionRadius = collectionRadiusP; //collection radius
  scoutAreaRadius  = scoutAreaRadiusP;  //scout area radius

  ArrayResize (areas,  areasNumber);
  ArrayResize (areasT, areasNumber);
  for (int i = 0; i < areasNumber; i++)
  {
    areas  [i].Init (coordinates);
    areasT [i].Init (coordinates);
  }

  ArrayResize (beeDance, areasNumber);

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (indA, areasNumber);
  ArrayResize (valA, areasNumber);

  ArrayResize (areasRadius, coordinates);
  ArrayResize (scoutRadius, coordinates);
  for (int i = 0; i < coordinates; i++)
  {
    areasRadius [i] = (rangeMax [i] - rangeMin [i]) * collectionRadius;
    scoutRadius [i] = (rangeMax [i] - rangeMin [i]) * scoutAreaRadius;
  }

  double sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += areasRadius [i] * areasRadius [i];
  hypersphereRadius  = MathSqrt (sqr) * collectionRadius;

  distHyperspCenters = hypersphereRadius * 2.0;

  sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += scoutRadius [i] * scoutRadius [i];
  scoutHyperspRadius = MathSqrt (sqr) * scoutAreaRadius;

  ArrayResize (indB, beesNumber);
  ArrayResize (valB, beesNumber);

  ArrayResize (bees,  beesNumber);
  ArrayResize (beesT, beesNumber);
  for (int i = 0; i < beesNumber; i++)
  {
    ArrayResize (bees  [i].c, coordinates);
    ArrayResize (beesT [i].c, coordinates);
    bees  [i].n = -DBL_MAX;
    beesT [i].n = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die einfachste und auch klassenübergreifende Methode ist die Verteilung von Aufgaben an Bienen. Alles ist einfach hier. Wenn die Gebiete noch nicht erkundet wurden, setzen wir den Nektarwert für den gesamten Bienenstock zurück und starten die Gebietsmarkierung. Wir rufen die Methode in jeder Epoche auf, bis der Wert der Fitnessfunktion erreicht ist.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::TasksForBees ()
{
  if (!scouting)
  {
    nB = -DBL_MAX;
  }
  MarkUpAreas ();
}
//——————————————————————————————————————————————————————————————————————————————

Die zweite öffentliche Methode wird in jeder Epoche aufgerufen. Der Start sollte erfolgen, nachdem der Wert der Fitnessfunktion ermittelt wurde. In diesem Fall sortieren wir die Bienen nach dem Wert des Nektars und kopieren die Koordinaten und die Nektarmenge der ersten Bienen in der Liste in die entsprechenden Bereiche, wenn noch keine Erkundung stattgefunden hat. Wenn die Erkundung bereits stattgefunden hat, kopieren wir die Koordinaten und die Nektarmenge in dem Gebiet, in dem der Nektar gesammelt wurde, sofern sich die Ergebnisse verbessert haben. Außerdem aktualisieren wir die besten Ergebnisse für den gesamten Bienenstock.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::CollectingNectar ()
{
  if (!scouting)
  {
    SortingBees ();

    for (int a = 0; a <areasNumber; a++)
    {
      ArrayCopy (areas [a].cB, bees [a].c, 0, 0, WHOLE_ARRAY);
      areas [a].n = bees [a].n;
    }

    scouting = true;
  }
  else
  {
    //transfer the nectar to the hive---------------------------------------------
    for (int b = 0; b < beesNumber; b++)
    {
      if (bees [b].n > areas [bees [b].aInd].n)
      {
        ArrayCopy (areas [bees [b].aInd].cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        areas [bees [b].aInd].n = bees [b].n;
      }

      if (bees [b].n > nB)
      {
        ArrayCopy (cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        nB = bees [b].n;
      }
    }

    SortingAreas ();
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode MarkUpAreas () ist es wert, im Detail besprochen zu werden. Zerlegen wir den Code in seine Teile.

Bevor die Gebiete erkundet werden und keine Informationen über das Auffinden von Blüten zum Nektarsammeln vorliegen, schicken wir alle Bienen zu einer ersten Erkundung. In dieser Phase spielen alle Bienen die Rolle von Kundschafterinnen. Da es keine Informationen über den Nektar gibt, schicken wir Kundschafter in eine zufällige Richtung und erzeugen Zufallszahlen, die gleichmäßig über den Koordinatenbereich verteilt sind.

//if the areas is not scouting - send all the bees to scouting----------------
if (!scouting)
{
  for (int b = 0; b < beesNumber; b++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      bees [b].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      bees [b].c [c] = SeInDiSp  (bees [b].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Nachdem die Gebiete erkundet wurden, müssen die Koordinaten der maximalen Nektarkonzentration in die Mitte des Gebiets kopiert werden. Mit anderen Worten, es ist notwendig, das Gebiet an einen besseren Ort zu verlegen. Nachdem wir diese Aktion durchgeführt haben, müssen wir sicherstellen, dass die Fläche nicht die Fläche eines höheren Ranges überschneidet. Wir können den Schnittpunkt von Flächen überprüfen, indem wir den Abstand zwischen ihren Mittelpunkten messen. Die Flächen überschneiden sich, wenn der Abstand zwischen den Zentren kleiner als zwei Radien ist (einer der Parameter des Algorithmus). Wird eine Überschneidung festgestellt, so wird die Fläche auf einen Punkt in einem Abstand von zwei Radien übertragen, während die Koordinaten des besten Ergebnisses (die Koordinaten der maximalen Nektarkonzentration) an der gleichen Stelle verbleiben. Die Gebiete sind also ständig in Bewegung. Die besten Gebiete zwingen den Rest verschoben zu werden. Die übrigen Gebiete können, während sie sich verschieben, zu einer reichhaltigeren Nahrungsquelle gelangen und nach der Sortierung, die in der nächsten Methode erfolgt, die besten werden.

for (int s = 0; s < areasNumber; s++)
{
  //move the center of the area to the best point in with more nectar-------
  ArrayCopy (areas [s].cC, areas [s].cB, 0, 0, WHOLE_ARRAY);

  //ordinary area-----------------------------------------------------------
  if (s != 0)
  {
    //check if there is no intersection of a region with a region of higher rank
    //measure the distance from the centers of the regions
    double centersDistance = 0.0;

    for (int c = 0; c < coordinates; c++) centersDistance += pow (areas [s].cC [c] - areas [s - 1].cC [c], 2.0);
    centersDistance = MathSqrt (centersDistance);

    //the areas intersect, then need to move the current area
    if (centersDistance < distHyperspCenters)
    {
      double incrementFactor = (distHyperspCenters - centersDistance) / centersDistance;
      double coordDistance   = 0.0;

      for (int c = 0; c < coordinates; c++)
      {
        coordDistance = areas [s].cC [c] - areas [s - 1].cC [c];
        areas [s].cC [c] = areas [s].cC [c] + (coordDistance * incrementFactor);

        areas [s].cC [c] = SeInDiSp (areas [s].cC [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}

Hier findet der Tanz der Bienen statt. Anhand von Informationen über die Richtung und die Menge des Nektars in den Regionen und unter Anwendung einer Zufallskomponente markieren wir das Verteilungsgebiet einer Zufallszahl so, dass die Wahrscheinlichkeit, dass eine Biene bei der nächsten Iteration ein Gebiet wählt, proportional zur Nektarmenge in diesem Gebiet ist. Vereinfacht ausgedrückt, werden auf der Zahlenlinie Segmente eingezeichnet, deren Länge der Differenz zwischen dem Nektarwert jedes Gebiets und dem schlechtesten Gebiet entspricht.

//send bees to the marked areas-----------------------------------------------
double r = 0.0;

beeDance [0].start = bees [0].n;
beeDance [0].end   = beeDance [0].start + (bees [0].n - bees [areasNumber - 1].n);

for (int a = 1; a < areasNumber; a++)
{
  if (a != areasNumber - 1)
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a].n - bees [areasNumber - 1].n);
  }
  else
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a - 1].n - bees [a].n) * 0.1;
  }
}

In diesem Teil des Methodencodes erfolgt eine zufällige Auswahl des Gebiets mit der durch den Tanz der Arbeitsbienen übermittelten Wahrscheinlichkeit. Dazu erzeugen wir eine Zufallszahl in dem Bereich, der durch Markierung auf der Zahlenreihe mit einem Tanz entsteht. Für die Kundschafter spielt der Tanz keine Rolle, da sie mit gleicher Wahrscheinlichkeit in die Nähe jedes der Gebiete fliegen und so die Suchmöglichkeiten der Bienenstrategie erweitern. Wie in der Natur hat jeder Teilnehmer des Bienenstocks einen bestimmten Wert und spielt eine Rolle.

for (int b = 0; b < beesNumber; b++)
{
  if (b < workerBeesNumber)
  {
    r = RNDfromCI(beeDance [0].start, beeDance [areasNumber - 1].end);
        
    for (int a = 0; a < areasNumber; a++)
    {
      if (beeDance [a].start <= r && r < beeDance [a].end)
      {
        bees [b].aInd = a;
        break;
      }
    }

    BeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
  else
  {
    //choose the area to send the bees there
    r = RNDfromCI (0.0, areasNumber - 1);

    bees [b].aInd = (int)r; //area index

    ScoutBeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
}

Diese private Methode implementiert den Flug einer Biene. Hier ist alles einfach, auch wenn es auf den ersten Blick unverständlich und kompliziert aussieht. Die Biene fliegt zu einem Bereich mit einer kubischen Wahrscheinlichkeitsverschiebung näher zum Zentrum. Die Wahrscheinlichkeit nimmt also vom Zentrum des Gebiets zu seinen Rändern hin ab. Vergessen wir nicht, dass dies die Mitte des Gebiets ist und nicht die beste Position, die wir zuvor gefunden haben. Selbst bei dieser einfachen Handlung lässt sich die Strategie der Biene nachvollziehen, die eine kontinuierliche Suche nach neuen Nahrungsquellen gewährleistet.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::BeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (0.0, 1.0);
    r  = r * r * r;
    r = Scale (r, 0.0, 1.0, 0.0, areasRadius [c], false);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Anders als bei der vorherigen Methode wird hier der Flug der Kundschafterbienen beschrieben. Die Biene fliegt außerhalb des Gebiets innerhalb des in den Algorithmuseinstellungen festgelegten Radius. Obwohl die Einstellung dieselbe ist, werden die Radien bei der Initialisierung der Klasse vorher berechnet, da die Koordinatenbereiche unterschiedlich sein können und die Radien daher angemessen sein sollten. Um eine Kundschafterbienen auszuschicken, müssen wir eine Zufallszahl im Bereich zwischen dem Radius des Gebiets und der Summe aus dem Radius des Gebiets und dem Radius der Erkundung erzeugen und dann einfach den resultierenden Wert zum Mittelpunkt des Gebiets addieren. Auf diese einfache Art und Weise befindet sich die Kundschafterbienen zufällig in der Nähe des Gebiets, während die Koordinaten nicht über den gesamten Suchraum verstreut sind.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::ScoutBeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (areasRadius [c], areasRadius [c] + scoutRadius [c]);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Der Algorithmus verfügt über zwei spezifische Methoden - das Sortieren der Bienen und der Flächen. Ihn zu beschreiben, macht keinen Sinn, es ist nur der bekannte und einfache Bubble-Sort. Ich verwende ihm in fast allen Optimierungsalgorithmen (wo überhaupt eine Sortierung erforderlich ist), weil diese Methode einfach und leicht für bestimmte Aufgaben zu modifizieren ist und gleichzeitig eine der besten Geschwindigkeiten unter allen Sortiermethoden bietet.

//——————————————————————————————————————————————————————————————————————————————
//Sorting of bees
void C_AO_ABC::SortingBees ()
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Sorting of areas
void C_AO_ABC::SortingAreas ()
//——————————————————————————————————————————————————————————————————————————————

Es ist an der Zeit, den gesamten berücksichtigten Code zu sammeln und zu kompilieren. Nach dem Ausführen des Teststandes können wir die folgenden Animationen sehen, die das Verhalten des Bienenalgorithmus zeigen. Die Bienen werden eindeutig in getrennten Bereichen beobachtet. Wir können sehen, wie sich die Bereiche gegenseitig verdrängen. Die Genauigkeit und die Anzahl der auffälligen „Schwärme“ hängen von den Einstellungen des Algorithmus ab.

Skin

ACO mit der Testfunktion Skin

Forest

ACO mit der Testfunktion Forest

Megacity

ACO mit der Testfunktion Megacity

Hier sind die Ergebnisse des Algorithmus für die Testfunktionen:

2022.11.21 13:14:06.669    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    1 Skin; Funktionsdurchläufe 1000 Ergebnis: 14.018634225602678; Funktionsdurchläufe 10000 Ergebnis: 14.06060189007221
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.99772; Score2: 1.00000
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    20 Skins; Funktionsdurchläufe 1000 Ergebnis: 7.459929501115262; Funktionsdurchläufe 10000 Ergebnis: 8.320771456653533
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.64085; Score2: 0.68769
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    500 Skins; Funktionsdurchläufe 1000 Ergebnis: 4.69267387794685; Funktionsdurchläufe 10000 Ergebnis: 4.838631770950824
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.49029; Score2: 0.49823
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    1 Forest; Funktionsdurchläufe 1000 Ergebnis: 15.063567301715784; Funktionsdurchläufe 10000 Ergebnis: 15.912087696850861
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.94435; Score2: 0.99755
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    20 Forests; Funktionsdurchläufe 1000 Ergebnis: 3.0207584941876133; Funktionsdurchläufe 10000 Ergebnis: 4.1918977577943295
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.18937; Score2: 0.26279
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    500 Forests; Funktionsdurchläufe 1000 Ergebnis: 1.2004991531402736; Funktionsdurchläufe 10000 Ergebnis: 1.288357831462411
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.07526; Score2: 0.08077
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    1 Megacity; Funktionsdurchläufe 1000 Ergebnis: 10.4; Funktionsdurchläufe 10000 Ergebnis: 15.0
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.69333; Score2: 1.00000
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 1000 Ergebnis: 1.5499999999999998; Funktionsdurchläufe 10000 Ergebnis: 2.31
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.10333; Score2: 0.15400
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 1000 Ergebnis: 0.6180000000000001; Funktionsdurchläufe 10000 Ergebnis: 0.6568
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.04120; Score2: 0.04379
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    All score for C_AO_ABC: 0.49447371765340953

Der Algorithmus hat für die beiden Testfunktionen mit zwei Variablen vollständig konvergiert, was ein hervorragender Indikator für Konvergenz ist. Es wäre verfrüht, die übrigen Ergebnisse zu bewerten. Es ist besser, die Ergebnisse in einer Tabelle zusammenzustellen und Schlussfolgerungen im Vergleich mit anderen Optimierungsalgorithmen zu ziehen.

3. Geänderte Version

Bei der Entwicklung und dem Entwurf von Optimierungsalgorithmen stellt sich immer die Frage: „Funktioniert der Algorithmus wie vorgesehen oder gibt es irgendwo im Code einen Fehler?“ Der stochastische Suchprozess ist von Natur aus zufällig, daher ist nicht klar, ob die Optimierungsergebnisse durch den Algorithmus erzielt wurden oder ob irgendwo ein Fehler aufgetreten ist und das Ergebnis wirklich nicht zufällig ist. Bei der Entwicklung des Bienenvolk-Algorithmus bin ich auf ein ähnliches Phänomen gestoßen. Beim ersten von fünf Tests in der Testmenge blieb der Algorithmus offensichtlich an den Punkten hängen, an denen er die Suche begonnen hatte, und versuchte nicht, überhaupt zu konvergieren. Dieser Fehler wurde auf eine vom Standpunkt der Logik her völlig unglaubliche Weise gelöst. Ich musste lediglich die Klasse der Bienen bei der ersten Epoche ein weiteres Mal initialisieren, obwohl die Klasse bereits vor dem Start der Epochen vorinitialisiert war (String 142 in Test_AO_ABC.mq5). Wenn es jemandem gelingt, dieses Geheimnis zu lüften, würde ich mich freuen, die Lösung in den Kommentaren zu erfahren.

Zum Teil aufgrund der obigen Ausführungen und zum Teil aufgrund der nicht ganz zufriedenstellenden Ergebnisse der ersten Tests (obwohl später klar wurde, dass ich mit den Einstellungen des Algorithmus experimentieren musste), kam ich auf die Idee, die Bienensuchstrategie zu ändern. In der ursprünglichen Version fliegen die Bienen im Verhältnis zum Flächenwert. Bei dem neuen Algorithmus sollte es in jedem Gebiet eine feste Anzahl von Bienen geben. Mit anderen Worten: Unabhängig vom Rang des Gebietes hat jedes von ihnen immer die gleiche Anzahl von Bienen. Daher wurde das Gebiet logischerweise in das Konzept des „Bienenschwarms“ umgewandelt.

Anstelle der Bereichsstruktur wird nun die folgende Struktur verwendet:

//——————————————————————————————————————————————————————————————————————————————
struct S_BeesSwarm
{
  void Init (int coordinatesNumber, int beesNumber)
  {
    ArrayResize (bees, beesNumber);

    for (int i = 0; i < beesNumber; i++)
    {
      ArrayResize (bees [i].c, coordinatesNumber);
      bees [i].n = -DBL_MAX;
    }

    n = -DBL_MAX;

    ArrayResize     (cC, coordinatesNumber);
    ArrayInitialize (cC, -DBL_MAX);
  }

  S_Bee  bees []; //bees
  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Diese Struktur hat auch eine Initialisierungsfunktion, aber zusätzlich gibt es das Array bees[].

Im Allgemeinen ist der Rest des Codes der klassischen Version sehr ähnlich und wir sollten sich nicht zu sehr darauf konzentrieren. Der Code ist im Archiv unten beigefügt. Es lohnt sich, die Unterschiede in der Logik der Algorithmen besonders zu beachten. Schritt für Schritt sieht das folgendermaßen aus:

Anlegen eines Zentrums für den ersten Schwarm an und platzieren der Bienen um dieses Zentrum herum.
Anlegen eines Zentrums für die nachfolgenden Schwärme an und prüfen, ob der Abstand zwischen dem Zentrum und den vorherigen Schwärmen größer oder gleich R*2 (zwei Radien) ist, platzieren der Bienen in der Nähe des Zentrums.
Aussenden der Kundschafterbienen, sodass jede der Bienen einen Abstand größer oder gleich R (Radius) zu den anderen Schwärmen hat.
Ermitteln des Wertes der Fitnessfunktion für alle Bienen.
Sortieren der Schwärme.
Platzieren der Bienen um die Mitte eines jeden Schwarms.
Wiederholen ab Schritt 4, bis das Stoppkriterium erfüllt ist.

Wie Sie vielleicht schon bemerkt haben, gibt es einen grundlegenden Unterschied in der Suchstrategie. Während in der klassischen Version jedes Gebiet eine andere Anzahl von Bienen haben kann, sind die Schwärme hier immer gleich groß. Auf diese Weise wird sichergestellt, dass Gebiete auch dann weiter erforscht werden, wenn die Nahrungsquelle versiegt, sodass eine gründlichere Erkundung der Oberfläche im Hyperraum möglich ist. Die Tests bestätigen die Legitimität dieses Ansatzes. Die Ergebnisse werden besser. Kundschafterbienen fliegen nicht in der Nähe von Bereichen, sondern in die freie Bereiche des Raums, und zwar nach den Regeln der Bereiche, wie in der klassischen Version. In der klassischen Version der Bienen verhalten sich die Kundschafterinnen nicht so wie beschrieben, da sie sich in eine völlig zufällige Richtung verstreuen, ohne sich darum zu kümmern, dass sie in bereits erforschte Gebiete gelangen können, wodurch ihre grundlegendste Erkundung verloren geht. Der letzte Schwarm in der Reihe ist der Kundschafterschwarms. Auch für diesen Schwarm gilt die Regel „Nicht in den Raum eines anderen eindringen“, aber nicht für den Schwarm als Ganzes, sondern für die Kundschafterbienen selbst.

Nachstehend sind die Ergebnisse der geänderten Version aufgeführt:

2022.11.21 21:53:19.695    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    1 Skin; Funktionsdurchläufe 1000 Ergebnis: 14.009060385607679; Funktionsdurchläufe 10000 Ergebnis: 14.060603974847265
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    Score1: 0.99720; Score2: 1.00000
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 1000 Ergebnis: 7.826824877236677; Funktionsdurchläufe 10000 Ergebnis: 8.735832346695558
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    Score1: 0.66082; Score2: 0.71028
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 1000 Ergebnis: 4.645933304640949; Funktionsdurchläufe 10000 Ergebnis: 4.844246724239038
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    Score1: 0.48774; Score2: 0.49853
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    1 Forest; Funktionsdurchläufe 1000 Ergebnis: 15.44507700105064; Funktionsdurchläufe 10000 Ergebnis: 15.662273922787355
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    Score1: 0.96827; Score2: 0.98188
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 1000 Ergebnis: 3.6397442648278924; Funktionsdurchläufe 10000 Ergebnis: 4.759146560755886
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    Score1: 0.22818; Score2: 0.29836
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 1000 Ergebnis: 1.2349621811342104; Funktionsdurchläufe 10000 Ergebnis: 1.4191098624570897
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    Score1: 0.07742; Score2: 0.08897
2022.11.21 21:54:01.112    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    1 Megacity; Funktionsdurchläufe 1000 Ergebnis: 12.0; Funktionsdurchläufe 10000 Ergebnis: 15.0
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    Score1: 0.80000; Score2: 1.00000
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 1000 Ergebnis: 1.7; Funktionsdurchläufe 10000 Ergebnis: 2.35
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    Score1: 0.11333; Score2: 0.15667
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 1000 Ergebnis: 0.572; Funktionsdurchläufe 10000 Ergebnis: 0.67
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    Score1: 0.03813; Score2: 0.04467
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    All score for C_AO_ABCm: 0.508357869056105

Wir können sehen, dass der modifizierte Algorithmus den Erfolg bei zwei Funktionen mit zwei Variablen wiederholt und eine 100%ige Konvergenz aufweist. Im Allgemeinen haben sich die Ergebnisse verbessert, die Endnote ist höher geworden: 0.50836. Leider ist dies keine wesentliche Verbesserung der Ergebnisse. Konvergenzprobleme bei Funktionen mit einer großen Anzahl von Variablen sind mit der klassischen Version der Algorithmusimplementierung vergleichbar.

Übrigens gibt es in der geänderten Version keinen Fehler, der eine Neuinitialisierung des Bienen erfordert.

4. Testergebnisse

AO	Durchläufe	Skin			Forest			Megacity (diskret)			Endergebnis
AO	Durchläufe	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	Endergebnis
ACOm	1000	0.99502	0.69826	0.50498	0.99087	0.22374	0.08408	0.78667	0.11667	0.04224	0.54688
ACOm	10,000	0.99599	0.86403	0.58800	0.99302	0.65571	0.17442	0.78667	0.26133	0.08208	0.54688
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
RND	10,000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283	0.51254
ABCm	1000	0.99720	0.66082	0.48774	0.96827	0.22818	0.07742	0.80000	0.11333	0.03813	0.50836
ABCm	10,000	1.00000	0.71028	0.49853	0.98188	0.29836	0.08897	1.00000	0.15667	0.04467	0.50836
ABC	1000	0.99772	0.64085	0.49029	0.94435	0.18937	0.07526	0.69333	0.10333	0.04120	0.49447
ABC	10,000	1.00000	0.68769	0.49823	0.99755	0.26279	0.08077	1.00000	0.15400	0.04379	0.49447
PSO	1000	0.98436	0.72243	0.65483	0.71122	0.15603	0.08727	0.53333	0.08000	0.04085	0.47695
PSO	10,000	0.99836	0.72329	0.65483	0.97615	0.19640	0.09219	0.82667	0.10600	0.04085	0.47695

Fassen wir zusammen. Überraschenderweise zeigte der Bienenvolk-Algorithmus in allen fünf Tests 100 % Konvergenz bei zwei Testfunktionen, „smooth Skin“ und „discrete Megacity“, und demonstrierte damit eine phänomenale Geschwindigkeit und Qualität der Konvergenz. Dies gilt jedoch nur für Funktionen mit zwei Variablen. In Bezug auf die Skalierbarkeit ist der Algorithmus den anderen Mitgliedern der Bewertungstabelle unterlegen. Funktionen mit mehreren Variablen gehören definitiv nicht zu den Stärken eines Bienenvolkes. Dies zeigt sich sowohl in der Animation des Prüfstands als auch in den Ergebnissen der Tabelle.

Beim ABC-Algorithmus muss der Nutzer mehrere Parameter wie Schwarmgröße, Anzahl der Späher und Gebietsradien einstellen. Wenn diese Einstellungen für eine bestimmte Anwendung nicht angemessen gewählt werden, kann der Algorithmus vorzeitig oder überhaupt nicht konvergieren. Darüber hinaus hat ABC Nachteile wie langsame Konvergenz bei komplexen Funktionen, lokale Lösungserfassung und mittelmäßige Sucheigenschaften.

Vorteile:
1. Relativ schnell.
2. Phänomenale Konvergenz für glatte und diskrete Funktionen mit wenigen Variablen.

Nachteile
1. Starker Einfluss der Algorithmusparameter auf das Ergebnis.
2. Nicht-Universellität.
3. Feststecken in lokalen Extremen.
4. Durchschnittliche Skalierbarkeit.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11736

Beigefügte Dateien |

ZIP herunterladen

94_The_world_of_AO_qABCn.zip (44.93 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

DoEasy. Steuerung (Teil 27): Arbeiten am WinForms Objekt der ProgressBar

In diesem Artikel werde ich die Entwicklung des ProgressBar-Steuerelements fortsetzen. Insbesondere werde ich die Funktionen zur Verwaltung des Fortschrittsbalkens und der visuellen Effekte erstellen.

Nicht-lineare Indikatoren

In diesem Artikel werde ich versuchen, einige Möglichkeiten zur Erstellung nichtlinearer Indikatoren und deren Verwendung im Handel zu besprechen. In der MetaTrader-Handelsplattform gibt es eine ganze Reihe von Indikatoren, die nicht-lineare Ansätze verwenden.

Algorithmen zur Optimierung mit Populationen Grauer-Wolf-Optimierung (GWO)

Betrachten wir einen der neuesten modernen Optimierungsalgorithmen - die Grey-Wolf-Optimierung. Das originelle Verhalten bei Testfunktionen macht diesen Algorithmus zu einem der interessantesten unter den zuvor besprochenen Algorithmen. Dies ist einer der besten Algorithmen für das Training neuronaler Netze, glatte Funktionen mit vielen Variablen.

DoEasy. Steuerung (Teil 26): Fertigstellung des WinForms-Objekts ToolTip und Weiterführung der Entwicklung der ProgressBar

In diesem Artikel werde ich die Entwicklung des ToolTip-Steuerelements abschließen und mit der Entwicklung des WinForms-Objekts der ProgressBar beginnen. Bei der Arbeit an Objekten werde ich universelle Funktionen für die Animation von Steuerelementen und deren Komponenten entwickeln.