
Optimierungsmethoden der ALGLIB-Bibliothek (Teil II)
Inhalt
- Einführung
- Optimierungsmethoden der ALGLIB-Bibliothek:
- BC (Box Constrained Optimization)
- NLC (Nichtlineare eingeschränkte Optimierung mit Lagrangeschem Algorithmus)
- LM (Levenberg-Marquardt-Verfahren)
- Tabelle der in den ALGLIB-Methoden verwendeten Funktionen
- Prüfmethoden
Einführung
Im ersten Teil unserer Untersuchung über die Optimierungsalgorithmen der ALGLIB-Bibliothek in der Standardauslieferung von MetaTrader 5 haben wir die folgenden Algorithmen gründlich untersucht: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden-Fletcher-Goldfarb-Shanno) und NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). Wir haben uns nicht nur mit ihren theoretischen Grundlagen beschäftigt, sondern auch eine einfache Möglichkeit diskutiert, sie auf Optimierungsprobleme anzuwenden.
In diesem Artikel werden wir die verbleibenden Methoden des ALGLIB-Arsenals näher betrachten. Besonderes Augenmerk wird dabei auf die Prüfung komplexer mehrdimensionaler Funktionen gelegt, die es uns ermöglichen, einen ganzheitlichen Blick auf die Effizienz der einzelnen Methoden zu werfen. Abschließend werden wir eine umfassende Analyse der erzielten Ergebnisse durchführen und praktische Empfehlungen für die Wahl des optimalen Algorithmus für bestimmte Aufgabentypen geben.
BC (Box Constrained Optimization)
Optimierung mit Randbedingungen (constraints) der Box: Das Unterprogramm minimiert die Funktion F(x) mit N Argumenten unter Berücksichtigung von Box-Bedingungen (einige der Randbedingungen der Box sind eigentlich Gleichheiten). Dieser Optimierer verwendet einen Algorithmus, der dem BLEIC-Algorithmus (linearer Optimierer der Randbedingung) ähnelt, aber das alleinige Vorhandensein von Randbedingungen der Box ermöglicht schnellere Strategien zur Aktivierung der Randbedingungen. Bei großen Problemen mit mehreren aktiven Randbedingungen in der Lösung kann dieser Optimierer schneller sein als BLEIC.
Lassen Sie mich einfacher erklären, was eine Box-gebundene Optimierung ist. Es handelt sich um einen Optimierungsalgorithmus, der nach der besten Lösung sucht, der mit Randbedingungen der Box arbeitet (bei denen jede Variable innerhalb bestimmter Grenzen liegen muss) und im Wesentlichen nach dem Minimum einer Funktion sucht, bei der alle Variablen innerhalb bestimmter Bereiche liegen müssen. Das Hauptmerkmal des Algorithmus ist, dass er BLEIC ähnlich ist, aber schneller arbeitet und speziell für die Arbeit mit Bereichsrestriktionen optimiert ist.
Bedingungen: Der Ausgangspunkt muss machbar sein oder in der Nähe der machbaren Region liegen, und die Funktion muss über die gesamte machbare Region definiert sein.
Um die BC-Methode und andere in der ALGLIB-Bibliothek zu verwenden, müssen wir die Datei verbinden (die Bibliothek wird mit dem MetaTrader 5-Terminal geliefert, der Nutzer muss nichts zusätzlich installieren).
#include <Math\Alglib\alglib.mqh> Lassen Sie uns ein Skript entwickeln - ein Beispiel für effektives Arbeiten mit ALGLIB-Methoden. Ich werde die wichtigsten Schritte hervorheben, die für die Arbeit mit ALGLIB-Methoden typisch sind. Identische Codeblöcke werden ebenfalls in der entsprechenden Farbe hervorgehoben.
1. Wir definieren die Randbedingungen des Problems, wie die Anzahl der Starts der Fitnessfunktion (Zielfunktion), die Bereiche der zu optimierenden Parameter und deren Schritt. Für die ALGLIB-Methoden müssen die Startwerte der „x“-optimierten Parameter (die Methoden sind deterministisch und die Ergebnisse hängen vollständig von den Anfangswerten ab, daher werden wir die Zufallszahlengenerierung im Bereich der Problemparameter anwenden) sowie die „s“-Skala (die Methoden reagieren empfindlich auf die Skala der Parameter im Verhältnis zueinander, in diesem Fall setzen wir die Skala auf „1“) zugewiesen werden.
2. Wir deklarieren die Objekte, die für das Funktionieren des Algorithmus erforderlich sind.
3. Wir legen die externen Parameter des Algorithmus fest (Einstellungen).
4. Wir initialisieren den Algorithmus durch Übergabe der Bereiche und Schritte der zu optimierenden Parameter sowie der externen Parameter des Algorithmus an die Methode.
5. Wir optimieren.
6. Wir erhalten die Optimierungsergebnisse zur weiteren Verwendung.
Denken Sie daran, dass der Nutzer keine Möglichkeit hat, den Optimierungsprozess zu beeinflussen oder ihn zu stoppen. Die Methode führt alle Operationen unabhängig voneinander aus und ruft die Fitnessfunktion innerhalb ihres Prozesses auf. Der Algorithmus kann die Fitnessfunktion beliebig oft aufrufen (wobei er sich an einem vom Nutzer festgelegten Parameter orientiert). Der Nutzer kann die maximale Anzahl der zulässigen Aufrufe kontrollieren, indem er der Methode einen Stoppbefehl übergibt.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinBCReport rep; // Set the parameters of the BC optimization algorithm------------------------------ double diffStep = 0.00001; double epsg = 1e-16; double epsf = 1e-16; CAlglib::MinBCCreateF (x, diffStep, fFunc.state); CAlglib::MinBCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinBCSetScale (fFunc.state, s); CAlglib::MinBCSetCond (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns); CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinBCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Da die Methode die Fitnessfunktion selbst aufruft (und nicht vom Nutzerprogramm aus), muss der Aufruf der Fitnessfunktion in einer Klasse verpackt werden, die von einer übergeordneten Klasse in der ALGLIB erbt (diese übergeordneten Klassen sind für verschiedene Methoden unterschiedlich). Deklarieren wir die Wrapper-Klasse als C_OptimizedFunction und legen die folgenden Methoden in der Klasse fest:
1. Func () ist eine virtuelle Methode, die in abgeleiteten Klassen außer Kraft gesetzt wird.2. Init () - Initialisierung der Klassenparameter. Innerhalb der Methode:
- Die Variablen für die Anzahl der Durchläufe und den besten Wert der Funktion werden initialisiert.
- Die Arrays c und cB sind für die Speicherung von Koordinaten reserviert.
Variablen:
- state - Objekt vom Typ CMinBCState, das für die BC-Methode spezifisch ist, wird beim Aufruf statischer Methoden des Algorithmus und beim Aufruf der Stopp-Methode verwendet.
- numberLaunches - aktuelle Anzahl der Starts (notwendig, um eine unkontrollierte oder zu lange Ausführung der Fitnessfunktion zu verhindern).
- maxNumbLaunchesAllowed - maximal zulässige Anzahl von Starts.
- fB - bester gefundener Wert der Fitnessfunktion.
- c [] - Array der aktuellen Koordinaten.
- cB [] - Array zum Speichern der besten Suchkoordinaten.
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_Func class C_OptimizedFunction : public CNDimensional_Func { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void Func (CRowDouble &x, double &func, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinBCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Func von C_OptimizedFunction ist für den Zugriff auf die Fitnessfunktion des Nutzers vorgesehen. Sie nimmt als Argumente den Vektor x (eine der Varianten der optimierten Parameter des Problems, die von der Optimierungsmethode vorgeschlagen werden), das Argument func, um den berechneten Wert der zurückgegebenen Fitnessfunktion zu akzeptieren, und das Objekt obj (dessen Zweck mir unklar ist, vielleicht ist es für die Fähigkeit reserviert, zusätzliche Informationen an/von der Methode zu übergeben). Die wichtigsten Etappen der Methode:
- Der Zähler numberLaunches wird erhöht. Ihr Ziel ist es, die Anzahl der Methodenaufrufe von Func zu verfolgen.
- Wenn die Anzahl der Starts den zulässigen Wert von maxNumbLaunchesAllowed überschreitet, setzt die Funktion den Wert vonfunc in DBL_MAX (den Maximalwert vom Typ „double“, ALGLIB-Methoden sind darauf ausgelegt, Funktionen zu minimieren, dieser Wert bedeutet die schlechtestmögliche Lösung). Dann rufen wir die Funktion MinBCRequestTermination auf, die der BC-Methode signalisieren soll, die Optimierung zu beenden.
- Anschließend werden die Werte aus dem Vektor x in das Array c der Schleife kopiert. Dies ist notwendig, um diese Werte an die Fitnessfunktion des Nutzers weiterzugeben.
- Die Funktion ObjectiveFunction wird aufgerufen. Sie berechnet den Wert der Zielfunktion für die aktuellen Werte im Array c. Das Ergebnis wird in ffVal gespeichert, während der Wert von func auf den negativen Wert von ffVal gesetzt wird (wir optimieren ein invertiertes Paraboloid, das maximiert werden muss, und BC minimiert die Funktion, also drehen wir den Wert um).
- Wenn der aktuelle Wert von ffVal den vorhergehenden besten Wert von fB übersteigt, wird fB aktualisiert und das Array cB kopiert den aktuellen Zustand von c. Dies ermöglicht es uns, den besten gefundenen Wert der Zielfunktion mit den entsprechenden Parametern zu verfolgen und bei Bedarf später darauf zurückzugreifen.
Die Funktion Func implementiert einen Aufruf einer nutzerdefinierten Fitnessfunktion und verfolgt, wie oft diese Funktion aufgerufen wurde, wobei die besten Ergebnisse aktualisiert werden. Sie steuert auch die Stoppbedingungen, wenn die Anzahl der Starts einen festgelegten Grenzwert überschreitet.
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { func = DBL_MAX; CAlglib::MinBCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); func = -ffVal; // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Nachdem wir das Testskript mit dem BC-Algorithmus zur Optimierung der Parabelfunktion ausgeführt haben, erhalten wir das folgende Ergebnis im Ausdruck:
Leider setzte der Algorithmus trotz der Aufforderung, die Optimierung mit der Methode MinBCRequestTermination zu beenden, den Prozess fort und versuchte, über die Grenze von 10.000 Durchläufen hinaus auf die Fitnessfunktion zuzugreifen.
Versuchen wir nun, die BC nicht einzuschränken und ihr die Möglichkeit zu geben, nach eigenem Ermessen zu handeln. Das Ergebnis sieht wie folgt aus:
Wie wir sehen, ist BC in der Lage, vollständig auf der Parabelfunktion zu konvergieren, aber in diesem Fall ist es unmöglich, die erforderliche Anzahl von Durchläufen der Zielfunktion im Voraus zu schätzen.
Der Schritt der Differenzierung ist ein wichtiger Bestandteil des Algorithmus. Wenn wir z. B. einen sehr kleinen Schritt verwenden, z. B. 1e-16 anstelle von 0,00001, dann bleibt der Algorithmus vorzeitig stehen, mit folgendem Ergebnis:
NLC (Nichtlineare eingeschränkte Optimierung mit vorkonditioniertem erweiterten Lagrangeschen Algorithmus)
Dieser nichtlineare Optimierungsalgorithmus mit Randbedingungen ermöglicht die Minimierung einer komplexen Zielfunktion F(x) mit N Variablen unter Berücksichtigung verschiedener Randbedingungen: Randbedingungen an den Grenzen der Variablen (min <= x <= max), lineare Ungleichheiten und Gleichheiten, nichtlineare Gleichheiten G(x) = 0, nichtlineare Ungleichheiten H(x) <= 0.
Stellen Sie sich vor, Sie haben ein schwieriges Ziel, das Sie erreichen wollen, aber es gibt einige Einschränkungen, gegen die Sie nicht verstoßen können. Sie wollen zum Beispiel die Verkaufsgewinne maximieren, dürfen aber eine bestimmte Höhe der Gemeinkosten nicht überschreiten. Der ALGLIB-Algorithmus hilft bei der Lösung dieser Art von eingeschränkten Optimierungsproblemen. Das funktioniert folgendermaßen:
1. Sie geben dem Algorithmus einen Ausgangspunkt - eine erste Vermutung, wie das Ziel zu erreichen ist. Dieser Punkt muss alle Randbedingungen erfüllen.
2. Der Algorithmus beginnt dann, sich von diesem Ausgangspunkt aus langsam zu bewegen und sich Schritt für Schritt der optimalen Lösung zu nähern. Bei jedem Schritt wird ein Hilfsproblem gelöst, um zu verstehen, in welche Richtung es weitergehen soll.
3. Um diesen Prozess zu beschleunigen, verwendet der Algorithmus eine spezielle Technik namens „preconditioning“ (Vorkonditionierung). Das bedeutet, dass es seine „Schritte“ an die Struktur der Aufgabe anpasst, um schneller voranzukommen.
4. Nach mehreren Iterationen findet der Algorithmus schließlich eine Lösung, die Ihre Zielfunktion minimiert (z. B. den Overhead minimiert) und gleichzeitig alle Randbedingungen erfüllt.
Die Nutzer können zwischen drei verschiedenen Lösungsmodellen wählen, die für Probleme unterschiedlicher Größe und Komplexität geeignet sind und in ALGLIB implementiert wurden:
SQP (sequentielle quadratische Programmierung) wird für mittelgroße Probleme mit schwierigen Zielfunktionen empfohlen.
AUL (vorkonditionierte augmentierte Lagrangesche Methode) wird für große Probleme oder solche mit einfachen (schnellen) Zielfunktionen empfohlen.
SLP (sequentielle lineare Programmierung) ist langsamer, aber robuster in komplexen Fällen.
Experimente mit Testfunktionen haben die Effizienz des AUL-Lösers gezeigt, andere Löser sind im Code auskommentiert.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinNLCReport rep; // Setting parameters of the NLC optimization algorithm----------------------------- double diffStep = 0.00001; double rho = 1000.0; int outerits = 5; CAlglib::MinNLCCreateF (x, diffStep, fFunc.state); CAlglib::MinNLCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinNLCSetScale (fFunc.state, s); CAlglib::MinNLCSetCond (fFunc.state, rangeStep, numbTestFuncRuns); //CAlglib::MinNLCSetAlgoSQP (fFunc.state); CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits); //CAlglib::MinNLCSetAlgoSLP (fFunc.state); CAlglib::MinNLCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinNLCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
In NLC wird der Variablentyp „state“ auf CMinNLCState gesetzt.
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinNLCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
Fordern Sie den Abbruch des Optimierungsprozesses mit dem Befehl MinNLCRequestTermination an.
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); CAlglib::MinNLCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Nachdem wir das Testskript mit dem NLC-Algorithmus zur Optimierung der Parabelfunktion ausgeführt haben, erhalten wir das folgende Ergebnis im Ausdruck:
NLC, bestes Ergebnis: 0.8858935739350294, Anzahl der Funktionsstarts: 28007
Da die Anzahl der Starts der Zielfunktion nicht begrenzt ist, konvergiert NLC vollständig, führt aber auf dem Weg dorthin über eine Million Iterationen durch:
NLC, bestes Ergebnis: 1.0, Anzahl der Funktionsstarts: 1092273
Bei einem sehr kleinen Schritt von 1e-16 bricht der Algorithmus nicht vorzeitig ab, wie z. B. die BC-Methode, sondern zeigt ein etwas schlechteres Ergebnis als bei einem Schritt von 0,00001.
NLC, bestes Ergebnis: 0.8543715192632731, Anzahl der Funktionsstarts: 20005
LM (Levenberg-Marquardt-Verfahren)
Die Levenberg-Marquardt-Methode (LM) ist ein weit verbreiteter Optimierungsalgorithmus zur Lösung nichtlinearer Probleme der kleinsten Quadrate. Diese Methode ist bei Kurven- und Oberflächenanpassungsproblemen wirksam.
Die Grundidee von LM kombiniert zwei Optimierungstechniken: die Gradientenabstiegsmethode und die Gauß-Newton-Methode. Dadurch kann sich der Algorithmus an die Form der Zielfunktion anpassen. So funktioniert es:
- Bei jeder Iteration berechnet der Algorithmus die Schrittrichtung mit einer Kombination aus Gradientenabstieg und Approximation zweiter Ordnung.
- Das Dämpfungsverhältnis (λ) wird automatisch angepasst, um die Schrittgröße und das Gleichgewicht zwischen den beiden Methoden zu steuern.
Stellen Sie sich vor, Sie versuchen, den tiefsten Punkt eines Gebirges zu finden, aber Sie haben nur eine Karte mit unscharfen Kanten. Die Levenberg-Marquardt-Methode ist wie ein intelligentes Navigationsgerät, das zwei Wege kombiniert, um einen Weg zu finden:
1. Die erste Methode (Gauß-Newton-Methode) ist schnell, aber riskant. Es ist, als würde man gerade einen Abhang hinunterlaufen. Das funktioniert gut, wenn man sich in der Nähe des Ziels befindet, aber man könnte stolpern, wenn das Gelände schwierig ist.
2. Die zweite Methode (Gradientenabstieg) ist langsam, aber zuverlässig. Es ist, als würde man vorsichtig in kleinen Schritten hinabsteigen. Es ist langsamer, aber sicherer. Er funktioniert auch in schwierigem Gelände gut.
Der Algorithmus wechselt auf intelligente Weise zwischen diesen beiden Methoden. Wenn der Weg frei ist, verwendet es die schnelle Methode, aber wenn die Situation schwierig ist, schaltet es in einen hohen Alarmmodus. Es stellt automatisch eine Schrittweite ein.
Außerdem kann er in einem lokalen Minimum stecken bleiben. Der Algorithmus erfordert eine gute anfängliche Annäherung (man muss ungefähr wissen, wo man suchen muss) und ist nicht sehr effektiv für Probleme mit einer großen Anzahl von Parametern (mehr als 100).
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; double rangeMin [], rangeMax [], rangeStep; ArrayResize (rangeMin, params); ArrayResize (rangeMax, params); for (int i = 0; i < params; i++) { rangeMin [i] = -10; rangeMax [i] = 10; } rangeStep = DBL_EPSILON; double x []; double s []; ArrayResize (x, params); ArrayResize (s, params); ArrayInitialize (s, 1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinLMReportShell rep; // Set the parameters of the LM optimization algorithm------------------------------ double diffStep = 1e-16;//0.00001; CAlglib::MinLMCreateV (1, x, diffStep, fFunc.state); CAlglib::MinLMSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinLMSetScale (fFunc.state, s); CAlglib::MinLMSetCond (fFunc.state, rangeStep, numbTestFuncRuns); CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj); CAlglib::MinLMResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Für LM wird der Variablentyp „state“ auf CMinLMStateShell gesetzt.
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinLMStateShell state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
Wie bei den vorherigen Optimierungsmethoden begrenzen wir die Anzahl der Aufrufe der Zielfunktion, aber die LM-Methode ist die einzige, für die kein Stopp-Befehl vorgesehen ist. Es wäre logisch, das Vorhandensein der Funktion MinLMRequestTermination zu erwarten.
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); //CAlglib::MinLMRequestTermination (state); // such method does not exist return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Nachdem wir das Testskript mit dem LM-Algorithmus zur Optimierung der Parabelfunktion ausgeführt haben, erhalten wir das folgende Ergebnis im Ausdruck:
LM, bestes Ergebnis: 0.6776047308612422, Anzahl der Funktionsstarts: 4003
Die LM-Methode stoppte beim 4003. Durchlauf der Zielfunktion, sodass die Aufhebung der Beschränkungen für die Anzahl der Iterationen zum gleichen Ergebnis führt, da der Algorithmus vor Erreichen der „Obergrenze“ von 10.000 Iterationen stecken blieb:
Wenn wir eine sehr kleine Schrittweite von 1e-16 verwenden, stoppt der Algorithmus sogar noch früher, nämlich beim 2001sten Lauf der Zielfunktion:
LM, bestes Ergebnis: 0.6670839162547625, Anzahl der Funktionsstarts: 2001
Tabelle der in den ALGLIB-Methoden verwendeten Funktionen
ALGLIB-Optimierungsmethoden verwenden verschiedene Arten von Variablen als Anfangswerte und Randbedingungen der Box, verschiedene Arten von übergeordneten Klassen der Zielfunktion und Sätze von Objekten, die für die Optimierung benötigt werden, sowie verschiedene Listen von aufzurufenden Funktionen. Dies kann es schwierig machen, Programme, die diese Methoden verwenden, intuitiv zu schreiben.
Um das Wissen über ALGLIB-Optimierungsmethoden leichter zu verstehen und zu strukturieren, habe ich eine Übersichtstabelle erstellt. Es wird Programmierern helfen, sich schnell zurechtzufinden und ihre Projekte richtig zu optimieren.
| Optimierungsalgorithmus | Funktion Typ FF | Typ der Variablen | Objekt-Liste | Liste der aufgerufenen Methoden |
| BLEIC | Func | double | 1) Kobjekt 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell | 1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination |
| LBFGS | Func | double | 1) Kobjekt 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell | 1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination |
| NS | FVec | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState | 1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination |
| BC | Func | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState | 1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination |
| NLC | Fvec | CRowDouble | 1) Kobjekt 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState | 1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination |
| LM | FVec | double | 1) Kobjekt 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell | 1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (existiert nicht) |
Prüfmethoden
Nach dem Studium der Optimierungsmethoden der ALGLIB-Bibliothek stellt sich natürlich die Frage, welche dieser Methoden für bestimmte Aufgaben zu wählen ist. Verschiedene Arten von Optimierungsproblemen können je nach der gewählten Methode mit unterschiedlicher Effizienz gelöst werden. Um diese wichtige Frage zu beantworten, werden wir komplexe Testfunktionen verwenden, die sich als besonders realitätsnah erwiesen haben. Diese Funktionen stellen typische Fälle dar: glatte Funktionen werden durch die Testfunktion Hilly dargestellt, glatte mit scharfen Scheitelpunkten (differenzierbar nicht auf ihrer gesamten Definition) - durch Forest, während eine rein diskrete Funktion Megacity ist.
Die Tests werden mit 50 Wiederholungen pro Test und einer Höchstzahl von 10.000 Zielfunktionsaufrufen durchgeführt. Wir werden ein Bench-Skript zum Testen vorbereiten und dabei die BC-Methode als Beispiel verwenden. Auf diese Weise erhalten wir genauere und repräsentativere Ergebnisse, die uns helfen, die am besten geeignete Optimierungsmethode für jede spezifische Aufgabe zu wählen.
Implementieren wir die Funktion FuncTests, die Testläufe zur Optimierung unter Verwendung der entsprechenden ALGLIB-Methode durchführt. Die Funktion wird es uns ermöglichen, Daten über die Leistung von Methoden zu sammeln und ihre Arbeit zu visualisieren sowie Konvergenzdiagramme zu erstellen.
Listen wir kurz auf, was die Funktion FuncTests tut:
- Sie akzeptiert eine Testzielfunktion, die Anzahl der Tests, die Farbe der Visualisierung und Variablen für das Gesamtergebnis.
- Wenn Video aktiviert ist, wird die Funktion dargestellt.
- Sie legt die Grenzen für die Prüfung fest und initialisiert Variablen für die Ergebnisse.
- Sie erzeugt zufällige Eingabedaten und führt die Optimierung mit Hilfe der CAlglib-Bibliothek durch.
- Sie verfolgt die Anzahl der Aufrufe der Zielfunktion und die besten Ergebnisse.
- Sie berechnet und zeigt durchschnittliche Ergebnisse an.
- Sie aktualisiert die Gesamtpunktzahl auf der Grundlage der aktuellen Tests.
//—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, // Reference to the target function object const int funcCount, // Number of functions to test const color clrConv, // Visualization color double &allScore, // Total score of all tests double &allTests) // Total number of tests { if (funcCount <= 0) return; // If the number of functions = 0, exit the function allTests++; // Increase the total number of tests if (Video_P) // If visualization is enabled { ST.DrawFunctionGraph (f); // Draw the function graph ST.SendGraphToCanvas (); // Send the graph to the canvas ST.MaxMinDr (f); // Determine the maximum and minimum of the function ST.Update (); // Update the visualization } //---------------------------------------------------------------------------- C_AO_Utilities Ut; // Utilities for handling numbers int xConv = 0.0; // Variable for converting along the X axis int yConv = 0.0; // Variable for converting along the Y axis double aveResult = 0.0; // Average test result int aveRunsFF = 0; // Average number of function runs int params = funcCount * 2; // Number of parameters (2 for each function) int epochCount = NumbTestFuncRuns_P / PopSize_P; // Number of epochs //---------------------------------------------------------------------------- CRowDouble bndl; bndl.Resize (params); // Array for lower bounds CRowDouble bndu; bndu.Resize (params); // Array for upper bounds for (int i = 0; i < funcCount; i++) // Fill the boundaries for each function { bndu.Set (i * 2, f.GetMaxRangeX ()); // Set the upper boundary by X bndl.Set (i * 2, f.GetMinRangeX ()); // Set the lower boundary by X bndu.Set (i * 2 + 1, f.GetMaxRangeY ()); // Set the upper bound by Y bndl.Set (i * 2 + 1, f.GetMinRangeY ()); // Set the lower boundary by Y } CRowDouble x; x.Resize (params); // Array for parameter values CRowDouble s; s.Resize (params); // Array for scaling s.Fill (1); // Fill the array with ones for (int test = 0; test < NumberRepetTest_P; test++) // Run the tests { for (int i = 0; i < funcCount; i++) // For each function { x.Set (i * 2, Ut.RNDfromCI (bndl [i * 2], bndu [i * 2])); // Generate random values by X x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Generate random values by Y } //-------------------------------------------------------------------------- CObject obj; // Object for storing results C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Initialize the optimization function CNDimensional_Rep frep; // Representation of multidimensional space CMinBCState state; // State of the minimization method CMinBCReport rep; // Minimization report double epsg = 1e-16; // Parameter for gradient stop condition double epsf = 1e-16; // Parameter for the stop condition by function value CAlglib::MinBCCreateF (x, DiffStep_P, state); // Create minimization state CAlglib::MinBCSetBC (state, bndl, bndu); // Set the boundaries CAlglib::MinBCSetScale (state, s); // Set scaling CAlglib::MinBCSetCond (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P); // Set conditions CAlglib::MinBCOptimize (state, fFunc, frep, obj); // Optimization CAlglib::MinBCResults (state, x, rep); // Get results //-------------------------------------------------------------------------- aveRunsFF += fFunc.numberLaunches; // Sum up the number of function runs aveResult += -fFunc.bestMIN; // Sum up the best minimum found } aveRunsFF /= NumberRepetTest_P; // Calculate the average number of runs aveResult /= NumberRepetTest_P; // Calculate the average result double score = aveResult; // Estimate based on average result Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Output test results allScore += score; // Update the overall score } //——————————————————————————————————————————————————————————————————————————————
Führen wir die Tests nacheinander für alle in Frage kommenden Optimierungsmethoden der ALGLIB-Bibliothek durch. Nachstehend finden Sie Ausdrucke der Testergebnisse für die jeweiligen Methoden, die wie folgt zu lesen sind:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8| - Methodenabkürzung, vollständiger Name, Differenzierungsschritt (optional zusätzliche Methodenparameter).
5 Hilly's - Anzahl der entsprechenden Testzielfunktionen in einem multivariaten Problem.
Func runs: 2178(10000) - Anzahl der Durchläufe der Zielfunktion - die Anzahl der Versuche, Methoden der Zielfunktion aufzurufen und die angegebene gewünschte „Obergrenze“ für die Anzahl der Durchläufe.
result: 0.38483704535107116 - durchschnittliches Ergebnis für 50 Testläufe.
Ausdruck der Leistung der BLEIC-Methode bei den Testzielfunktionen:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|
=============================
5 Hilly's; Func runs: 2178(10000); result: 0.38483704535107116
25 Hilly's; Func runs: 10130(10000); result: 0.3572376879336238
500 Hilly's; Func runs: 11989(10000); result: 0.2676346390264618
=============================
5 Forest's; Func runs: 1757(10000); result: 0.28835869530001046
25 Forest's; Func runs: 9383(10000); result: 0.22629722977214342
500 Forest's; Func runs: 14978(10000); result: 0.16606494305819486
=============================
5 Megacity's; Func runs: 1211(10000); result: 0.13815384615384615
25 Megacity's; Func runs: 9363(10000); result: 0.12640000000000004
500 Megacity's; Func runs: 15147(10000); result: 0.09791692307692391
=============================
All score: 2.05290 (22.81%)
Ausdruck der Leistung der L-BFGS-Methode bei den Testzielfunktionen:
L-BFGS|limited memory BFGS method for large scale optimization|0.9|
=============================
5 Hilly's; Func runs: 5625(10000); Ergebnis: 0.38480050402327626
25 Hilly's; Func runs: 10391(10000); Ergebnis: 0.2944296786579764
500 Hilly's; Func runs: 41530(10000); Ergebnis: 0.25091140645623417
=============================
5 Forest's; Func runs: 3514(10000); Ergebnis: 0.2508946897150378
25 Forest's; Func runs: 9105(10000); Ergebnis: 0.19753907736098766
500 Forest's; Func runs: 40010(10000); Ergebnis: 0.1483916309143011
=============================
5 Megacity's; Func runs: 916(10000); Ergebnis: 0.12430769230769222
25 Megacity's; Func runs: 4639(10000); Ergebnis: 0.10633846153846153
500 Megacity's; Func runs: 39369(10000); Ergebnis: 0.09022461538461606
=============================
All score: 1.84784 (20.53%)
Ausdruck der Leistung der NS-Methode bei den Testzielfunktionen:
NS|nonsmooth nonconvex optimization|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs: 10171(10000); result: 0.3716823351189392
25 Hilly's; Func runs: 11152(10000); result: 0.30271115043870767
500 Hilly's; Func runs: 1006503(10000); result: 0.2481831526729561
=============================
5 Forest's; Func runs: 10167(10000); result: 0.4432983184931045
25 Forest's; Func runs: 11221(10000); result: 0.20891527876847327
500 Forest's; Func runs: 1006503(10000); result: 0.15071828612481414
=============================
5 Megacity's; Func runs: 7530(10000); result: 0.15076923076923068
25 Megacity's; Func runs: 11069(10000); result: 0.12480000000000002
500 Megacity's; Func runs: 1006503(10000); result: 0.09143076923076995
=============================
All score: 2.09251 (23.25%)
Ausdruck der Leistung der BC-Methode bei den Testzielfunktionen:
BC|box constrained optimization with fast activation of multiple box constraints|0.9|
=============================
5 Hilly's; Func runs: 1732(10000); result: 0.37512809463286956
25 Hilly's; Func runs: 9763(10000); result: 0.3542591015005374
500 Hilly's; Func runs: 22312(10000); result: 0.26434986025328294
=============================
5 Forest's; Func runs: 1564(10000); result: 0.28431712294752914
25 Forest's; Func runs: 8844(10000); result: 0.23891148588644037
500 Forest's; Func runs: 15202(10000); result: 0.16925473100070892
=============================
5 Megacity's; Func runs: 1052(10000); result: 0.12307692307692313
25 Megacity's; Func runs: 9095(10000); result: 0.12787692307692308
500 Megacity's; Func runs: 20002(10000); result: 0.09740000000000082
=============================
All score: 2.03457 (22.61%)
Ausdruck der Leistung der NLC-Methode bei den Testzielfunktionen:
NLC|nonlinearly constrained optimization with preconditioned augmented lagrangian algorithm|0.8|1000.0|5|
=============================
5 Hilly's; Func runs: 8956(10000); result: 0.4270442612182801
25 Hilly's; Func runs: 10628(10000); result: 0.3222093696838907
500 Hilly's; Func runs: 48172(10000); result: 0.24687323917487405
=============================
5 Forest's; Func runs: 8357(10000); result: 0.3230697968403923
25 Forest's; Func runs: 10584(10000); result: 0.2340843463074393
500 Forest's; Func runs: 48572(10000); result: 0.14792910131023018
=============================
5 Megacity's; Func runs: 5673(10000); result: 0.13599999999999995
25 Megacity's; Func runs: 10560(10000); result: 0.1168615384615385
500 Megacity's; Func runs: 47611(10000); result: 0.09196923076923148
=============================
All score: 2.04604 (22.73%)
Ausdruck der Leistung der LM-Methode bei den Testzielfunktionen:
LM|improved levenberg-marquardt algorithm|0.0001|
=============================
5 Hilly's; Func runs: 496(10000); Ergebnis: 0.2779179366819541
25 Hilly's; Func runs: 4383(10000); result: 0.26680986645907423
500 Hilly's; Func runs: 10045(10000); result: 0.27253276065962373
=============================
5 Forest's; Func runs: 516(10000); result: 0.1549127879839302
25 Forest's; Func runs: 3727(10000); result: 0.14964009375922901
500 Forest's; Func runs: 10051(10000); result: 0.1481206726095718
=============================
5 Megacity's; Func runs: 21(10000); result: 0.0926153846153846
25 Megacity's; Func runs: 101(10000); result: 0.09040000000000001
500 Megacity's; Func runs: 2081(10000); result: 0.08909230769230835
=============================
All score: 1.54204 (17.13%)
Jetzt können wir das Verhalten der Algorithmen bei Testfunktionen klar analysieren. Die meisten Methoden zeichnen sich dadurch aus, dass die Arbeit vorzeitig beendet wird, bevor das Limit für die Anzahl der Durchläufe der Zielfunktion ausgeschöpft ist (in den Parametern haben wir ein Limit von 10.000 Iterationen festgelegt). Das Levenberg-Marquardt (LM)-Verfahren für das diskrete Megacity-Problem mit einer Dimension von 1.000 Parametern stoppte zum Beispiel im Durchschnitt nach 2.081 Iterationen und mit einer Dimension von 10 nur nach 21 Iterationen. Gleichzeitig wurde bei glatten, Hilly-Funktionen mit dieser Methode versucht, das Minimum in einer wesentlich größeren Anzahl von Iterationen zu finden. Bei anderen Methoden wurden dagegen mehr als eine Million Aufrufe der Zielfunktion durchgeführt.
Nachfolgend werden die Leistungen der NS-Methode (die am besten abschnitt) und der LM-Methode (die am schlechtesten abschnitt) dargestellt.
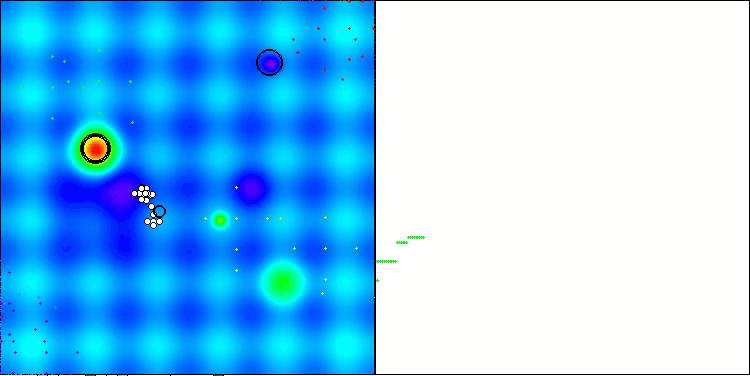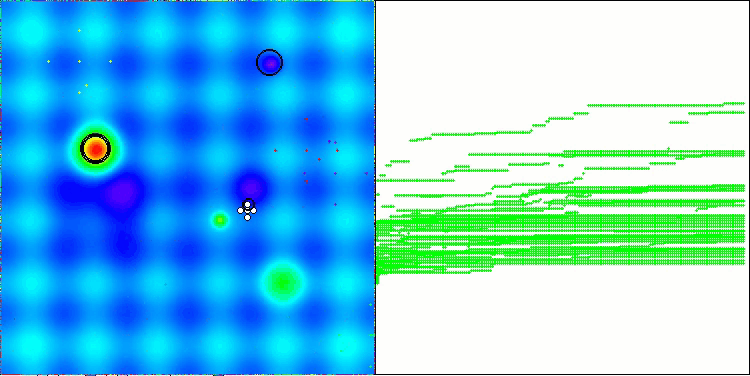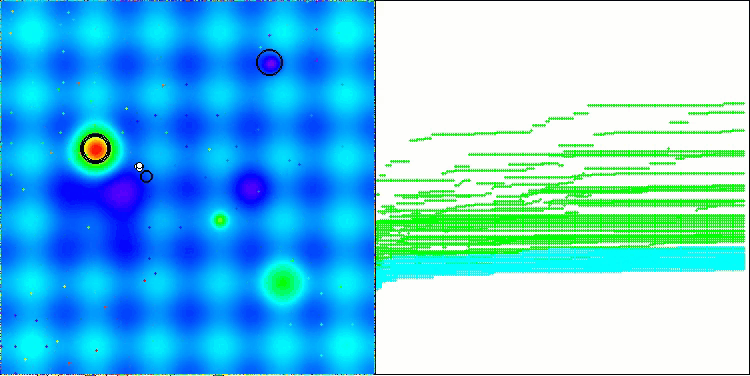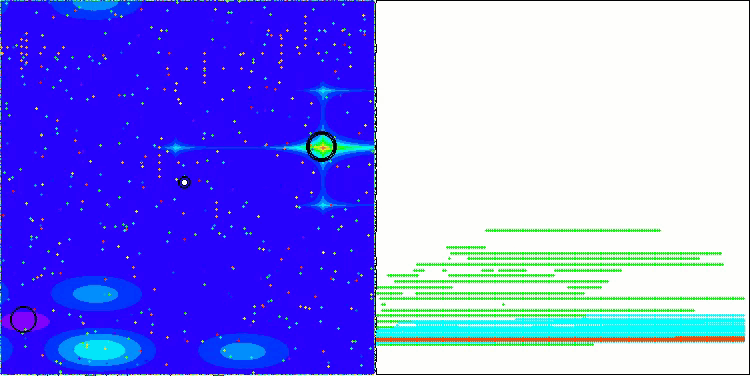
NS mit der Testfunktion Hilly
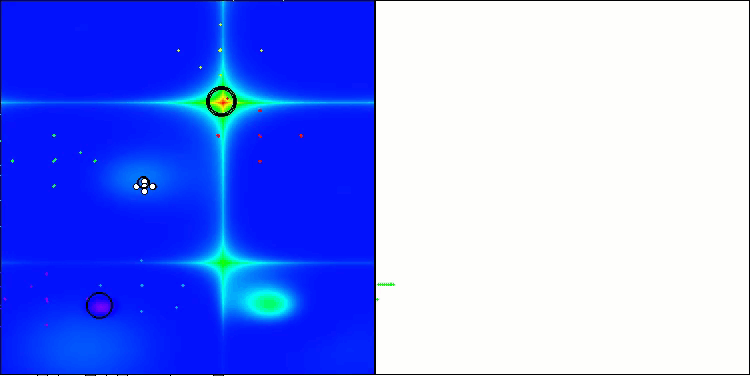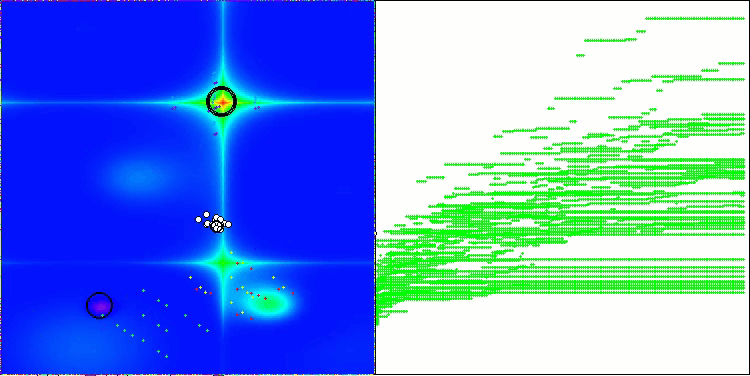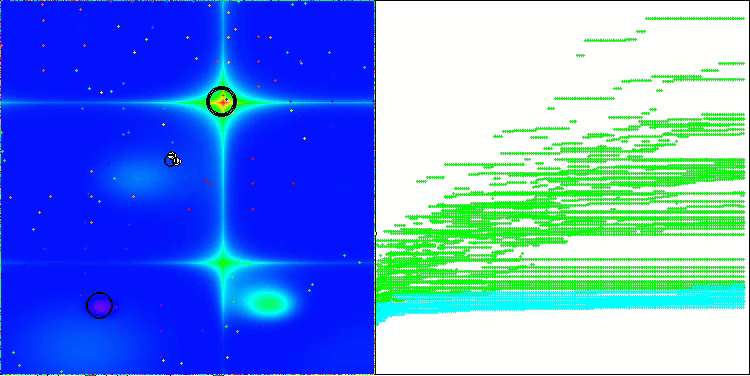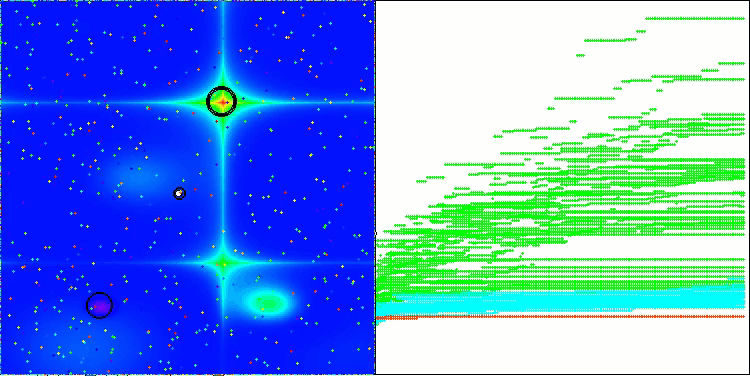
NS mit der Testfunktion Forest
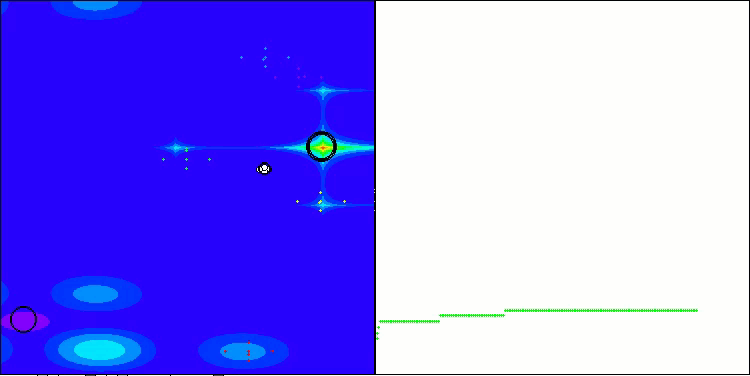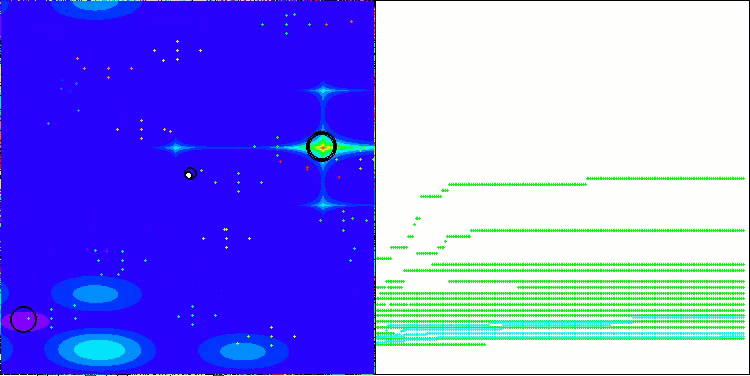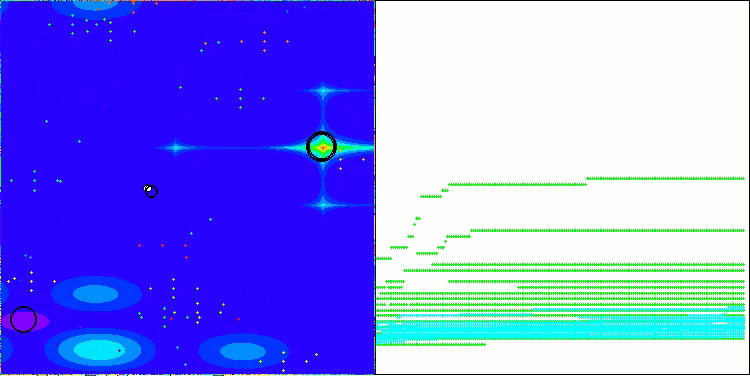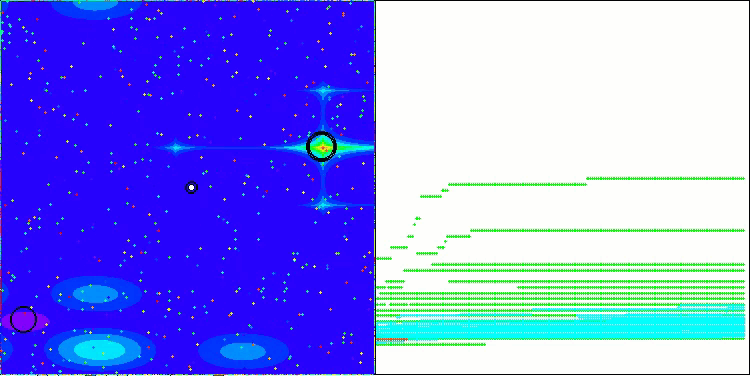
NS mit der Testfunktion Megacity
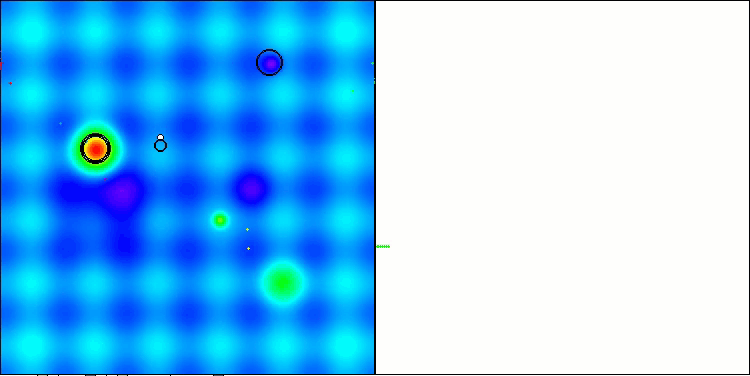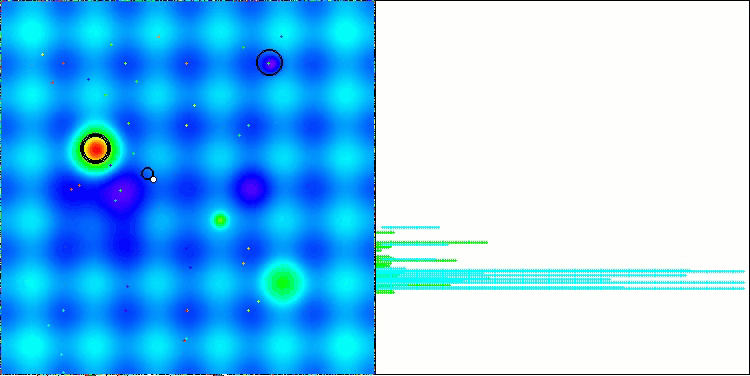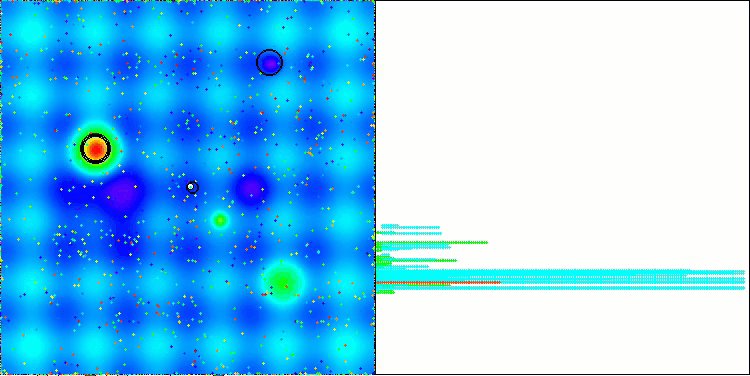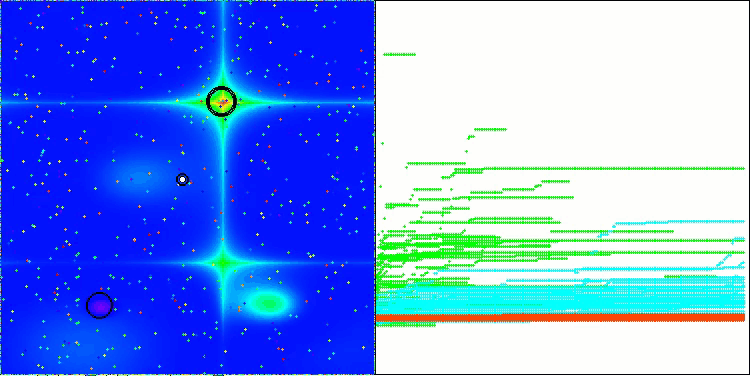
LM mit der Testfunktion Hilly
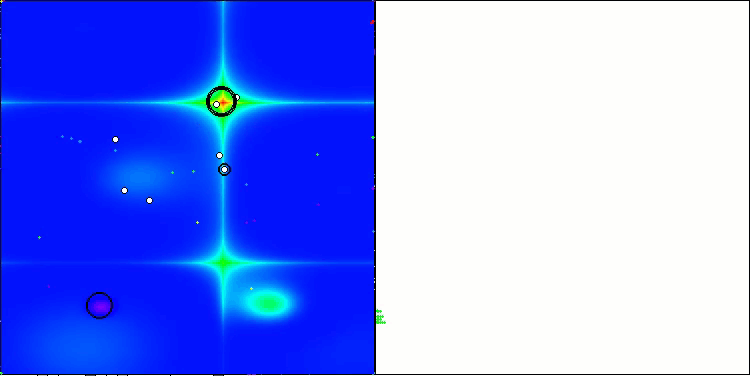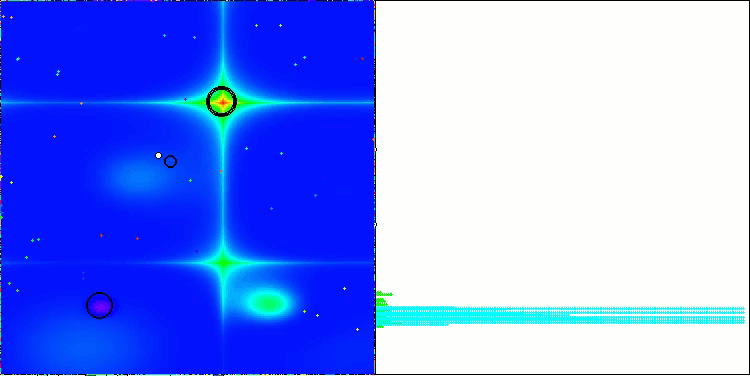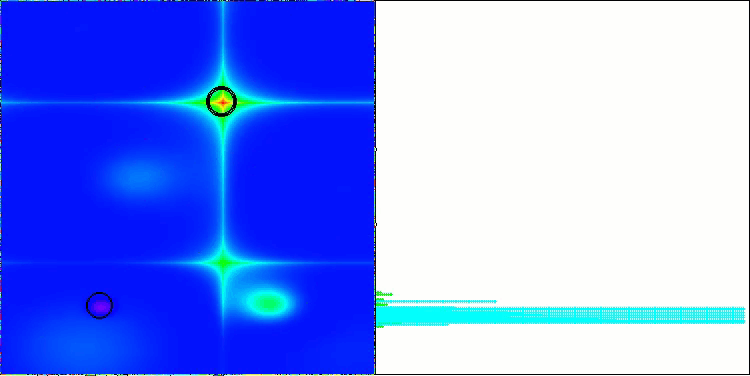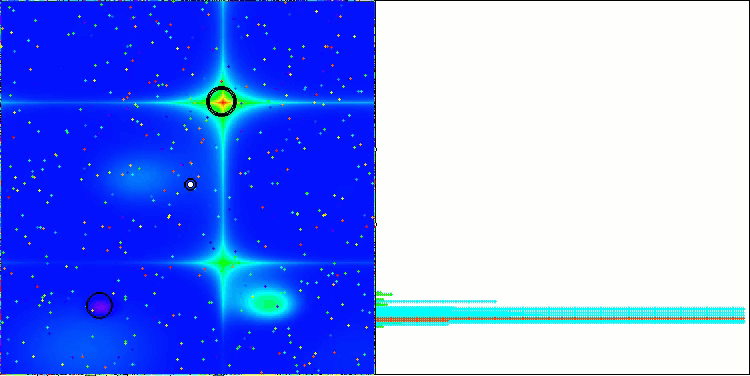
LM mit der Testfunktion Forest
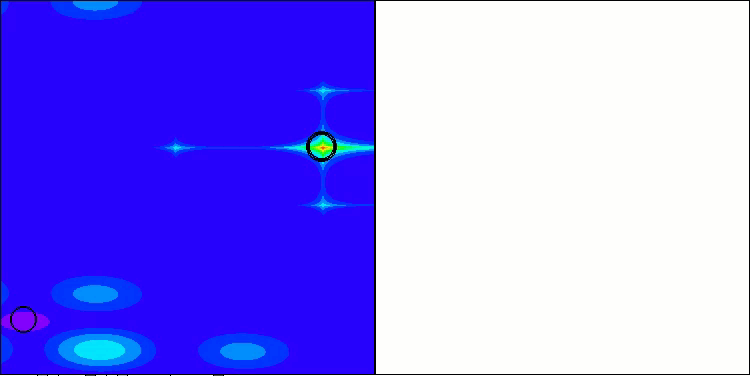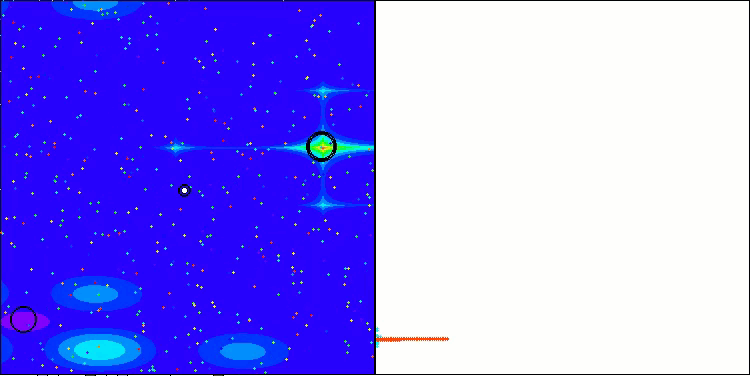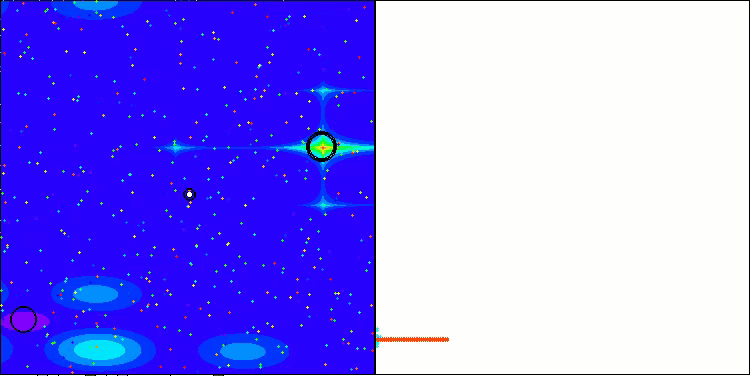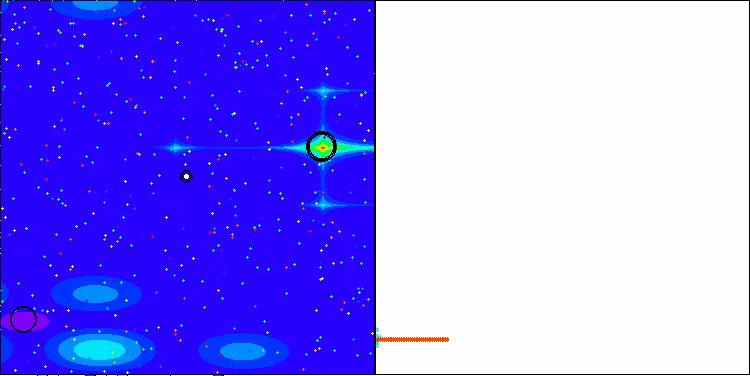
LM mit der Testfunktion Megacity
Fassen wir die erzielten Ergebnisse in einer Tabelle zusammen.

Farbabstufung der Algorithmen nach den entsprechenden Tests
Zusammenfassung
In zwei Artikeln haben wir uns mit Optimierungsmethoden aus der ALGLIB-Bibliothek beschäftigt und untersucht, wie sie in Anwenderprogramme integriert werden können, sowie die Möglichkeiten der Interaktion mit den Methodenfunktionen. Darüber hinaus haben wir Tests durchgeführt, um die Stärken und Schwächen der Algorithmen zu ermitteln. Lassen Sie uns kurz zusammenfassen:
- Bei glatten Funktionen (Hilly) mit niedriger Dimension zeigte die NLC-Methode die besten Ergebnisse, während bei hohen Dimensionen die LM-Methode die Nase vorn hatte.
- Bei glatten Funktionen mit scharfen Extrema (Forest) in niedrigen Dimensionen zeigte die NS-Methode die besten Ergebnisse, und in hohen Dimensionen war die BC-Methode die beste.
- Beim diskreten Megacity-Problem in kleinen Dimensionen hat die NS-Methode die Führung übernommen, während in großen Dimensionen die BLEIC-Methode die erste war.
Die Unterschiede in den Ergebnissen der Methoden sind unbedeutend, die Abweichungen liegen im Rahmen der eigenen Ergebnisse, jedoch kann die NS-Methode als universeller bezeichnet werden, während es nicht möglich ist, sie zwangsweise zu beenden.
Die Codes, die dem Artikel beigefügt sind, enthalten alles, was Sie brauchen, um Optimierungsmethoden in Ihren Projekten zu verwenden und ihre Fähigkeiten visuell zu sehen und zu bewerten.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Simple test ALGLIB BLEIC.mq5 | Skript | Testskript für die Arbeit mit BLEIC |
| 2 | Simple test ALGLIB LBFGS.mq5 | Skript | Testskript für die Arbeit mit L-BFGS |
| 3 | Simple test ALGLIB NS.mq5 | Skript | Testskript für die Arbeit mit NS |
| 4 | Simple test ALGLIB BC.mq5 | Skript | Testskript für die Arbeit mit BC |
| 5 | Simple test ALGLIB NLC.mq5 | Skript | Testskript für die Arbeit mit NLC |
| 6 | Simple test ALGLIB LM.mq5 | Skript | Testskript für die Arbeit mit LM |
| 7 | Test_minBLEIC.mq5 | Skript | Testskript für BLEIC |
| 8 | Test_minLBFGS.mq5 | Skript | Testskript für L-BFGS |
| 9 | Test_minNS.mq5 | Skript | Testskript für NS |
| 10 | Test_minBC.mq5 | Skript | Testskript für BC |
| 11 | Test_minNLC.mq5 | Skript | Testskript für NLC |
| 12 | Test_minLM.mq5 | Skript | Testskript für LM |
| 13 | CalculationTestResults.mq5 | Skript | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 14 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 15 | TestStandFunctions.mqh | Include | Bibliothek der Testfunktionen |
| 16 | Utilities.mqh | Include | Bibliothek der Hilfsfunktionen |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16164
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung fortschrittlicher ICT-Handelssysteme: Implementierung von Orderblöcken in einem Indikator
Entwicklung fortschrittlicher ICT-Handelssysteme: Implementierung von Orderblöcken in einem Indikator
 SQLite-Fähigkeiten in MQL5: Beispiel für ein Dashboard mit Handelsstatistiken nach Symbolen und magischen Zahlen
SQLite-Fähigkeiten in MQL5: Beispiel für ein Dashboard mit Handelsstatistiken nach Symbolen und magischen Zahlen
 Neuronale Netze im Handel: Direktionale Diffusionsmodelle (DDM)
Neuronale Netze im Handel: Direktionale Diffusionsmodelle (DDM)
 Neuronale Netze im Handel: Knotenadaptive Graphendarstellung mit NAFS
Neuronale Netze im Handel: Knotenadaptive Graphendarstellung mit NAFS
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
1. Es ist noch nicht sichergestellt, dass die Optimierer von alglib korrekt verwendet werden.
1. Sie können alles in Frage stellen, aber es ist immer viel konstruktiver, von der Position vollständiger Quellcodes und korrekter, reproduzierbarer Tests aus zu sprechen.
2) Man kann ein optimales Ergebnis auf einer zweidimensionalen Megacity erhalten, wenn man 9 Milliarden Menschen bittet, mit ihren Fingern wahllos in ein leeres Blatt Papier zu stechen, hinter dem die Oberfläche der Funktion verborgen ist (einer von ihnen wird mit Sicherheit sehr nahe am Globalen sein und sagen, dass er es ist, der das Problem erfolgreich gelöst hat). Aber wir müssen die optimale Lösung nicht in 9 Milliarden Versuchen durch zufälliges Stochern finden, sondern in 10 000 mit Hilfe einer Strategie.
Je höher das durchschnittliche Ergebnis einer Reihe unabhängiger Tests ist (Stabilität, Wiederholbarkeit der Ergebnisse), desto besser ist die getestete Methode im Vergleich zum Zufallsstochern für eine bestimmte Art von Problem (bei einigen Problemen unterscheiden sich einige Methoden nicht wesentlich vom Zufallsstochern, bei anderen sind sie sehr effektiv).
Das ist der Sinn des Testens und Vergleichens verschiedener Algorithmen, für die nicht nur eine Testfunktion, sondern drei verschiedene mit unterschiedlichen Eigenschaften als Benchmarks herangezogen werden, so dass man die Anwendbarkeit verschiedener Algorithmen auf verschiedene Aufgaben, ihre Grenzen und Fähigkeiten bei verschiedenen Aufgaben klar erkennen kann. So kann man sich der Lösung von Optimierungsproblemen auf sinnvolle Weise nähern.
In Zukunft werde ich lieber spezifische Fragen zum Inhalt des Artikels und zu den Codes beantworten.
Wir nehmen die Methoden der lokalen Optimierung, wenden sie auf das globale Problem an und vergleichen sie mit den Methoden der globalen Optimierung. Das ist es, worüber ich spreche.
Ich spreche darüber, wie wir diese Methoden für die globale Optimierung anpassen können. Die einfachste Möglichkeit besteht darin, die Anzahl der Initialisierungen zu erhöhen.
Wenn ich es richtig verstanden habe, werden Adam usw. auf Geschwindigkeit und nicht auf Qualität getrimmt.
Es wäre interessant zu sehen, wie die Bewertung ausfällt, wenn sie durch die Zeit und nicht durch die Anzahl der Wiederholungen begrenzt wird.
Wenn ich das richtig verstanden habe, geht es bei Adam usw. um Geschwindigkeit, nicht um Qualität.
Es wäre interessant zu sehen, wie die Bewertung ausfällt, wenn sie durch die Zeit und nicht durch die Anzahl der Wiederholungen begrenzt wird.
Die Algorithmen der ADAM-Familie (AdamW, RAdam, AdaBelief und andere) sowie SGD, SGRAD und andere (es gibt viele davon) wurden als moderner Ersatz für die klassischen Gradientenmethoden entwickelt und sind darauf ausgelegt, Probleme mit großen Dimensionen ohne Kenntnis der analytischen Formel zu lösen, oft zum Training neuronaler Netze (alle haben ihre Vor- und Nachteile). Es gibt auch interessante Lion-Methoden von Google (2023) und einige andere sehr aktuelle Methoden. Es ist sehr interessant, sich mit diesem Thema zu befassen, vor allem im Zusammenhang mit dem Training neuronaler Netze, bei dem es nützlich und informativ ist, eine Zieloberfläche für ein einfaches (oder vielleicht auch komplexes) Beispiel zu erstellen und Experimente durchzuführen (mit dem Parsing ihrer Innereien, mit einer eingehenden Untersuchung der Eigenschaften der Methoden, einer sorgfältigen Bewertung ihrer Fähigkeiten - alles, was wir wollen).
Es gibt keine zeitlichen Beschränkungen, an die man gebunden wäre. Ein Nutzer wird in einer Minute 1 Million Zugriffe auf das Ziel durchführen, ein anderer 1 Milliarde. Wie können wir Algos unter solchen Bedingungen vergleichen? Deshalb verwenden wir ein Limit für die Anzahl der Treffer und vergleichen die Effizienz innerhalb dieses Limits.
Bei zeitlichen Beschränkungen gibt es nichts, woran man sich binden könnte. Ein Nutzer wird in einer Minute 1 Million Zugriffe auf das Ziel durchführen, ein anderer 1 Milliarde. Wie können wir unter solchen Bedingungen Algos miteinander vergleichen? Deshalb verwenden wir eine Obergrenze für die Anzahl der Treffer und vergleichen die Effizienz innerhalb dieser Grenze.
Bindung an den PC des Autors. Nehmen Sie die Zeit von 10000 Iterationen von ANS als Basis.
Meine Ergebnisse mit dem Code von fxsaber:
PS-Codegröße als zusätzliche Metrik (wie komplex ist die Implementierung des Algorithmus)