种群优化算法：模拟各向同性退火（SIA）算法。第 II 部分

MetaTrader 5 — 示例 | 24 七月 2024, 09:58

654

Andrey Dik

内容

1. 概述
2. 算法
3. 测试结果

1. 概述

在第一部分中，我们研究了模拟退火（SA）算法的传统版本。该算法基于三个主要概念：应用随机性、做出更糟糕的决策、及逐渐降低做出更糟糕决策的概率。应用随机性可以探索搜索空间的不同区域，并避免陷入局部优化状态。接受具有一定概率的更差决策，允许算法暂时“跳出”局部优化，并在搜索空间的其它地方寻找更好的解，从而允许它首先探索更广泛地搜索空间，然后再专注于改善解。

SA 算法的思想是基于金属退火的模拟。预热的金属逐渐冷却，导致其结构发生变化。类似地，模拟退火算法从高温（做出更差决策的概率较高）开始，逐渐降低温度（降低做出更差决策的概率），这应该有助于算法收敛到最优解。

该算法从初始解开始运作，该初始解可以是随机的，也可从以前的迭代中获得。然后，它应用运算来更改解的状态（可以是随机的、或受控的），从而获得新状态，即便它比当前状态更差。做出更差决策的概率由“冷却”函数决定，该函数会随着时间的推移降低做出更差决策的概率。

使用若干简单的方程来描述模拟退火。计算能量变化的方程允许我们判定适应度函数值在两次连续迭代中的差值。计算做出更差决定的概率的方程式判定接受新状态的概率，同时考虑到能量和当前温度的差值。

使用模拟退火算法时需要调整的重要参数是初始温度和冷却比。设置这些参数会对解的性能和品质产生重大影响，并且是一个算法的弱点 — 由于参数对性能的影响不明显，因此难以选择参数。此外，这两个参数相互影响：温度的升高几乎可以被冷却比的降低所取代。

在本文的第一部分，我们辩证了该算法的主要问题：

参数调优：SA 算法的参数，如初始温度和冷却系数，可以显著影响其性能和效率。设置这些参数可能具有挑战性，需要进行实验才能获得最优值。

陷于局部极值的问题：为了克服它，我们可以应用各种策略，例如在结合现有算法策略工具生成新解时选择最合适的随机变量分布，以及考虑可能的解，从而提高组合能力。

提高收敛速度：为了加快收敛速度，可以修改冷却函数，以便令系统温度更快地降低（或使用不同形式的冷却函数）。我们还可以修改算法中选择下一个状态的方法，其中考虑了有关先前所传递状态的信息。

提升含有大量变量的 SA 算法的效率：这是绝大多数算法最困难的问题之一。随着变量数量的增加，搜索空间的复杂性增长速度远远快于在搜索策略中使用特殊方法所能考虑到的速度。

多维空间中的主要问题之一是变量可能组合的急剧暴涨。随着变量数量的增加，需要探索的可能系统状态的数量呈指数级增长。这导致优化算法面临空间复杂度的问题。

空间复杂度意味着搜索空间的大小随着变量数量的增加而呈指数增长。例如，如果我们有 10 个变量，每个变量可以取 10 个值，那么可能的组合总数等于 10^10，即 100 亿次，尽管事实上我们只会尝试 10000 次（适应度函数运行次数）。在如此多的组合中找到最佳解成为一项极其困难的任务。另外，值得注意的是，在我们的测试中，我们的优化函数步长参数取 0。这意味着算法的条件异常困难。它们当中能很好地解决如此复杂测试问题的那些胜者，几乎可以保证在不太复杂的实际问题上表现得更好（所有其它条件相同）。

2. 算法

模拟退火算法非常简单，真的很难想象如何进一步改进。这就像把一杯水变成一杯迷人的葡萄酒 — 魔术行为。事实上，如果生成的新数值是均匀分布的，并且做出最差决策的思路完全违反了构建优化算法的通常逻辑，那么可以改进什么呢？

我们看看上一篇文章结果的打印输出，以便直观地将后续实验结果与原始模拟退火（SA）算法的初始参考结果进行比较：

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 65.78409729002105
Score: 0.81510
25 Rastrigin's; Func runs 10000 result: 52.25447043222567
Score: 0.64746
500 Rastrigin's; Func runs 10000 result: 40.40159931988021
Score: 0.50060
=============================
5 Forest's; Func runs 10000 result: 0.5814827554067439
Score: 0.32892
25 Forest's; Func runs 10000 result: 0.23156336186841173
Score: 0.13098
500 Forest's; Func runs 10000 result: 0.06760002887601002
Score: 0.03824
=============================
5 Megacity's; Func runs 10000 result: 2.92
Score: 0.24333
25 Megacity's; Func runs 10000 result: 1.256
Score: 0.10467
500 Megacity's; Func runs 10000 result: 0.33840000000000003
Score: 0.02820
=============================
All score: 2.83750

我们尝试在生成系统的新状态时，通过将随机变量的均匀分布替换为正态变量来改善结果。

我们将使用模拟退火算法类作为新 SIA 算法的基础，因此我们不会提供该类的方法和功能的叙述，因为所有这些在本文的第一部分已经完成。

然后，我们可以使用逆函数方法生成一个具有正态分布的随机数。假设我们想生成一个具有正态分布的 “x” 数字，mu（平均值）和 sigma（标准差）。然后我们可以使用以下等式：

x = z0 * sigma + mu

其中：

z0 - 使用公式计算：

z0 = sqrt (-2 * log (u1)) * cos(2 * Pi * u2)

其中：

u1* - 范围 (0.0;1.0] 内的随机数（此处的 “最小值” 不包括在范围内）
u2** - 范围 [0.0;1.0] 内随机数字
* 和 ** - 两个分布均匀的独立随机数

在上一篇文章中，我们在 SA 算法中添加了一个扩散比参数，该参数限制了随机数生成的范围。正是在这个数域内，我们应该生成随机数。

我们编写模拟扩散的 C_AO_SIA 类方法 — “Diffusion”。该方法生成一个随机数，其正态分布最多为两个标准差。我们将超出这些边界的数值包装在“内部”，而不会丢失分布的形状（我们将在以下文章中更详细地检阅它）。

知道标准差（sigma）的数值后，我们可以将该数值范围转换为模拟扩散所需的范围。为此，我们使用 Scale 缩放函数。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SIA::Diffusion (const double value, const double rMin, const double rMax, const double step)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN))* cos (2 * M_PI * u2);

  double sigma = 2.0;//Sigma > 8.583864105157389 ? 8.583864105157389 : Sigma;

  if (z0 >=  sigma) z0 = RNDfromCI (0.0,    sigma);
  if (z0 <= -sigma) z0 = RNDfromCI (-sigma, 0.0);

  double dist = d * (rMax - rMin);

  if (z0 >= 0.0) return Scale (z0, 0.0,    sigma, value,        value + dist, false);
  else           return Scale (z0, -sigma, 0.0,   value - dist, value,        false);
}
//——————————————————————————————————————————————————————————————————————————————

在 Moving 方法中，我们将调用如下的 Diffusion 方法：

for (int i = 0; i < popSize; i++)
{
   for (int c = 0; c < coords; c++)
   {
     a [i].c [c] = Diffusion (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
     a [i].c [c] = SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
   } 
}

按所做的更改（用正态分布替换均匀分布）运行测试后，我们得到了以下结果：

C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 60.999013617749895
Score: 0.75581
25 Rastrigin's; Func runs 10000 result: 47.993562806349246
Score: 0.59467
500 Rastrigin's; Func runs 10000 result: 40.00575378955945
Score: 0.49569
=============================
5 Forest's; Func runs 10000 result: 0.41673083215719087
Score: 0.23572
25 Forest's; Func runs 10000 result: 0.16700842421505407
Score: 0.09447
500 Forest's; Func runs 10000 result: 0.049538421252065555
Score: 0.02802
=============================
5 Megacity's; Func runs 10000 result: 2.7600000000000002
Score: 0.23000
25 Megacity's; Func runs 10000 result: 0.9039999999999999
Score: 0.07533
500 Megacity's; Func runs 10000 result: 0.28
Score: 0.02333
=============================
All score: 2.53305

当我们在模拟退火算法中改变随机变量的分布时，就像在任何其它算法中一样，这肯定会影响其操作和结果。该算法的原始方程使用均匀分布生成随机步骤来探索解空间。这种分布确保了所有可能步骤的概率相等。

当我们用正态分布替换均匀分布时，算法的概率特性发生了变化。正态分布在均值附近达到峰值，并在远离均值时减小。这意味着使用正态分布生成的随机步骤将集中在均值附近。偏离均值的步骤不太可能发生。在我们的例子中，“平均值”是我们想要改进的原始坐标值。

这种分布的变化显然导致探索解空间的步骤变化较少。该算法似乎变得更加局部化，并且无法探索解空间中更远或不太可能的区域。

上述测试表明，在这种情况下，与均匀分布的随机变量相比，使用正态分布导致最终结果略有下降，但在统计学上显见恶化（如本文第一部分所示）。这些结果是用两个标准差获得的，增加 sigma（标准差）值会导致结果进一步出现统计学上的显见恶化。

由此我们得出结论，在这种特殊情况下，将分布的形状更改为更尖锐的形状会令结果恶化。

既然我们已经意识到在原始算法中“锐化”分布的形状是没有好处的，那么我们来看看另一种方式。我们假设在原始算法中，金属中的分子，或者说是晶体的整个扩散区内，没有足够的机会交换能量，以便将其均匀地分布在整个金属体积中。在这种情况下，我们可以提出以下想法：让晶体在交换能量的同时交换分子。

具有不同能量的晶体之间的分子交换，将允许个体之间的坐标转移。因此，分子将成为某种能量载体，能够平滑整个金属体的能量分布。由于晶格和分子之间的这种相互作用，能量将会更均匀地分布，这将实现更稳定和最优的系统配置。换言之，我们将尝试增加金属结构中的各向同性。

各向同性是物体或系统在所有方向上保持相同特征、或属性的性质。简单来说，如果一个对象或系统在各个方向上的外观和行为都相同，那么它就是各向同性的。因此，各向同性意味着没有首选的方向或方向，并且对象或系统在所有方向上都被认为是相同或均匀的。

为了模拟金属在所有方向上的性质均衡（增加各向同性），我们需要针对 Moving 方法进行修改。

代码的逻辑如下：针对 “popSize” 种群的每个元素、和每个 “coords” 坐标执行迭代：

调用 RNDfromCI 函数在 0 到 “popSize” 的范围内生成一个随机整数 “r”，从而在种群中随机选择一个个体
检查条件：如果所选个体的适应度函数值大于被更改个体的适应度值，则我们复制最优个体的坐标，否则个体的坐标不变
调用 RNDfromCI 函数生成一个 [-0.1;0.1] 范围内随机数 “rnd”
通过将 “rnd”, (rangeMax[c] - rangeMin[c]) 和 “d” 的乘积相加来更新坐标值，即在扩散范围内添加一个随机增量
调用 SeInDiSp 函数检查结果坐标，令其在允许的范围内，并执行所需的步骤

int    r   = 0;
double rnd = 0.0;

for (int i = 0; i < popSize; i++)
{
  for (int c = 0; c < coords; c++)
  {
      
    r = (int)RNDfromCI (0, popSize);
    if (r >= popSize) r = popSize - 1;

    if (a [r].fPrev > a [i].fPrev)
    {
      a [i].c [c] = a [r].cPrev [c];
    }
    else
    {
      a [i].c [c] = a [i].cPrev [c];
    }
      
    rnd = RNDfromCI (-0.1, 0.1);
    a [i].c [c] = a [i].c [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
    a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

采用具有均匀分布、和各向同性的相同参数进行退火的结果：

C_AO_SIA:50:1000.0:0.1:0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.52391137534615
Score: 0.99774
25 Rastrigin's; Func runs 10000 result: 77.70887543197314
Score: 0.96286
500 Rastrigin's; Func runs 10000 result: 57.43358792423487
Score: 0.71163
=============================
5 Forest's; Func runs 10000 result: 1.5720970326889474
Score: 0.88926
25 Forest's; Func runs 10000 result: 1.0118351454323513
Score: 0.57234
500 Forest's; Func runs 10000 result: 0.3391169587652742
Score: 0.19182
=============================
5 Megacity's; Func runs 10000 result: 6.76
Score: 0.56333
25 Megacity's; Func runs 10000 result: 5.263999999999999
Score: 0.43867
500 Megacity's; Func runs 10000 result: 1.4908
Score: 0.12423
=============================
All score: 5.45188

使用递增各向同性，其中分子在具有不同能量的晶体之间交换，导致算法结果的显著改善。这是对领导地位的宣示。

基于所叙述的过程可以得出的结论：

个体之间的坐标转移：具有不同能量的晶体之间的分子交换，允许在算法中的个体之间传输坐标信息。这有助于更有效、更快速地搜索最优解，因为有关优秀解的信息会传输给其它个体
能量分布平滑：具有不同能量的晶体之间交换分子的过程，可以平滑整个金属体的能量分布。这意味着能量将更均匀地分布，这有助于避免局部最小值，并实现更稳定、和最优系统配置

现在，在通过添加各向同性显著改善结果之后，我们再次尝试添加正态分布（首先我们执行增加各向同性的操作，并将具有正态分布的增量添加到结果值当中）。

附加各向同性增强 + 正态分布的退火结果：

C_AO_SIA:50:1000.0:0.1:0.05
=============================
5 Rastrigin's; Func runs 10000 result: 78.39172420614801
Score: 0.97132
25 Rastrigin's; Func runs 10000 result: 66.41980717898778
Score: 0.82298
500 Rastrigin's; Func runs 10000 result: 47.62039509425823
Score: 0.59004
=============================
5 Forest's; Func runs 10000 result: 1.243327107341557
Score: 0.70329
25 Forest's; Func runs 10000 result: 0.7588262864735575
Score: 0.42923
500 Forest's; Func runs 10000 result: 0.13750740782669305
Score: 0.07778
=============================
5 Megacity's; Func runs 10000 result: 6.8
Score: 0.56667
25 Megacity's; Func runs 10000 result: 2.776
Score: 0.23133
500 Megacity's; Func runs 10000 result: 0.46959999999999996
Score: 0.03913
=============================
All score: 4.43177

结果已显著恶化。

在模拟退火算法中生成正态分布增量，并没有带来任何改善。应用各向同性增强后，正态分布增量能否提供预期效果？预期尚未得到证实。这可以通过以下事实来解释：在应用各向同性增强后，仍然均匀的分布允许对解空间进行更均匀的探索，从而允许算法在偏好不强烈偏置的情况下探索不同的区域。尝试使用正态分布细化现有坐标未成功。这限制了对算法领域的更广泛探索。

我们进行最后一个实验，以便最终得出结论，在应用各向同性增加后，随机变量的增量均匀分布。我们将通过使用二次分布来更准确地探索已知坐标的邻域。如果将均匀分布的随机变量提高到二次方，则得到的分布称为随机变量的平方分布、或二次方分布。

具有相同参数的模拟退火算法的结果，包括各向同性增强+锐化二次方分布：

C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 70.23675927985173
Score: 0.87027
25 Rastrigin's; Func runs 10000 result: 56.86176837508631
Score: 0.70455
500 Rastrigin's; Func runs 10000 result: 43.100825665204596
Score: 0.53404
=============================
5 Forest's; Func runs 10000 result: 0.9361317757226002
Score: 0.52952
25 Forest's; Func runs 10000 result: 0.25320813586138297
Score: 0.14323
500 Forest's; Func runs 10000 result: 0.0570263375476293
Score: 0.03226
=============================
5 Megacity's; Func runs 10000 result: 4.2
Score: 0.35000
25 Megacity's; Func runs 10000 result: 1.296
Score: 0.10800
500 Megacity's; Func runs 10000 result: 0.2976
Score: 0.02480
=============================
All score: 3.29667

针对均匀分布的随机变量进行平方也没有产生积极的影响。性能的下降甚至比使用正态分布更严重。
现在，我们摆脱模拟退火算法的另一个缺点 — 选择设置的困难，以及温度和温度降低比的组合，因为这两个参数相互影响。为了将这两个参数连接到一起，将温度降低函数和概率更差决策函数结合起来。我们应用双曲弧余弦函数：

(1 - delta) * (acosh (-(x^3 - 3))) / 1,765

其中：

delta - 最后两次迭代时适应度函数值之间的差值，归一化到范围 [0.0;1.0]
x - 常规化算法世代步长

temp ch

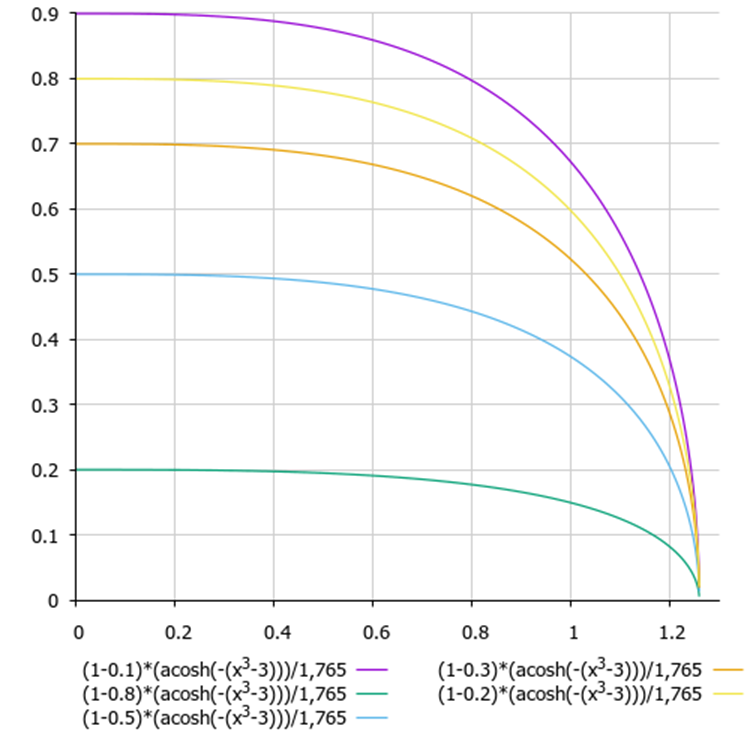
图例 1. 对能量差和当前世代（y - 能量差，x - 世代）的依赖图

3. 测试结果

SIA 试验台结果：

C_AO_SIA:100:0.01:0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.49732910930824
Score: 0.99741
25 Rastrigin's; Func runs 10000 result: 78.48411039606445
Score: 0.97246
500 Rastrigin's; Func runs 10000 result: 56.26829697982381
Score: 0.69720
=============================
5 Forest's; Func runs 10000 result: 1.6491133508905373
Score: 0.93282
25 Forest's; Func runs 10000 result: 1.3608802086313785
Score: 0.76978
500 Forest's; Func runs 10000 result: 0.31584037846210056
Score: 0.17866
=============================
5 Megacity's; Func runs 10000 result: 8.6
Score: 0.71667
25 Megacity's; Func runs 10000 result: 6.152
Score: 0.51267
500 Megacity's; Func runs 10000 result: 1.0544
Score: 0.08787
=============================
All score: 5.86552

结果令人印象深刻。此外，参数数量减少了一个。

算法操作的可视化显示了对个体的单独聚类的清晰划分，并涵盖了所有重要的局部极值。该图像类似于凝固金属的实际结晶。我们可以清楚地看到所有测试（包括具有许多变量的测试）的出色收敛性。

rastrigin

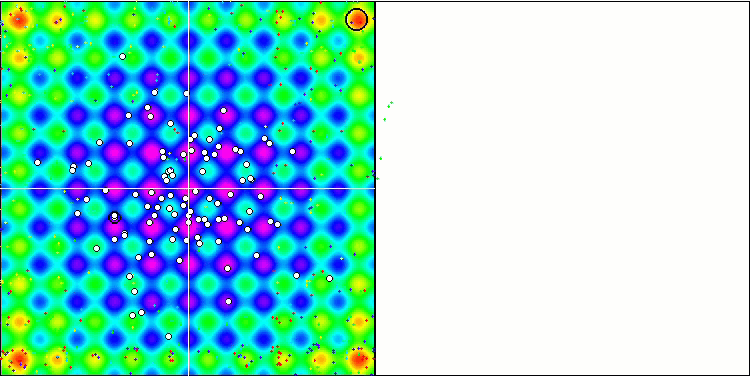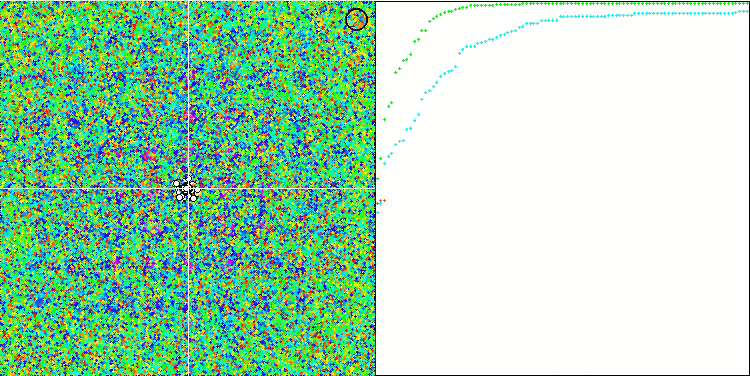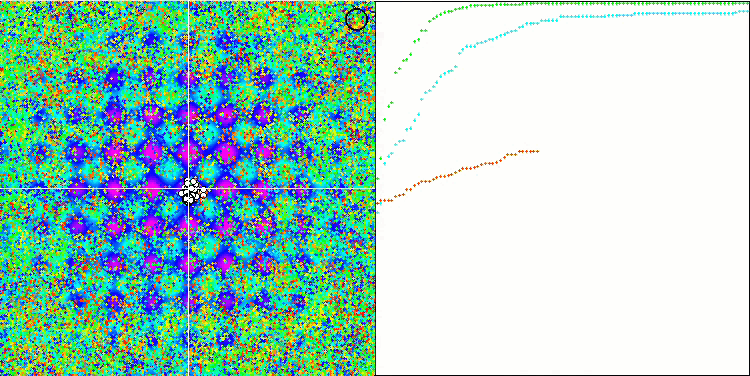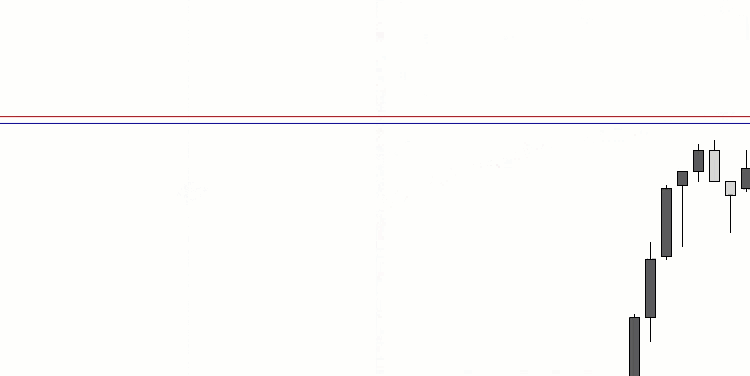
SIA 基于 Rastrigin 测试函数

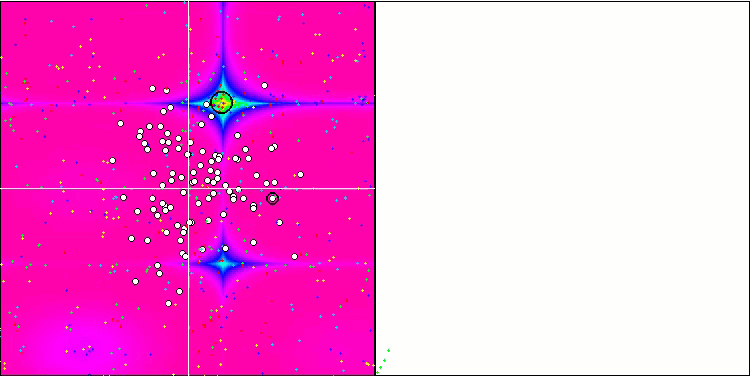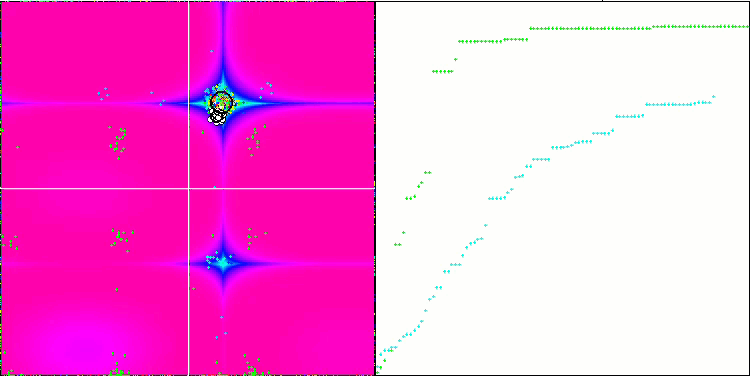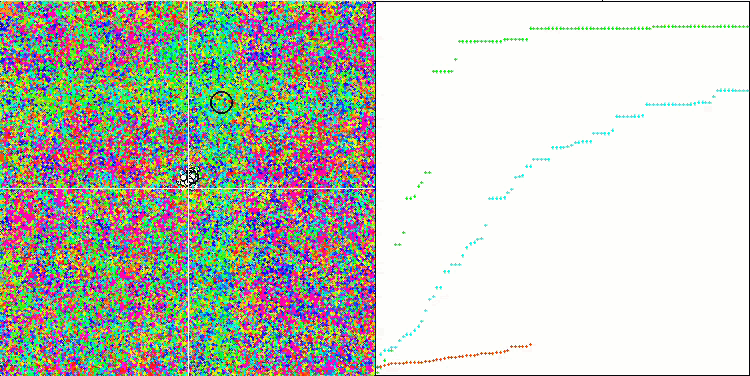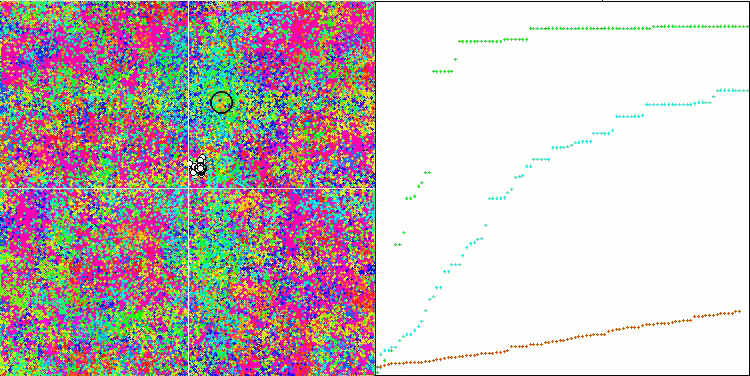
SIA 基于 Forest 测试函数

megacity

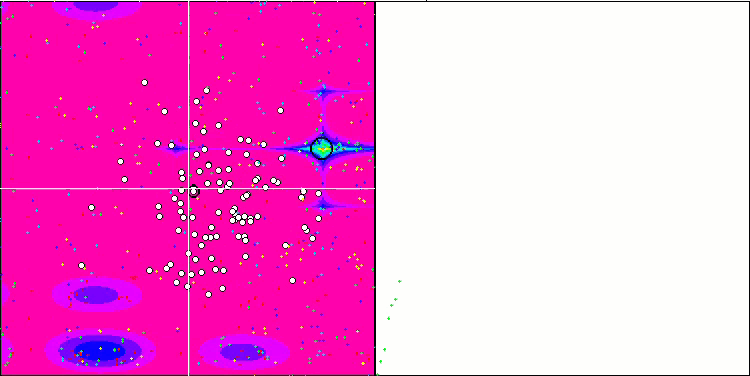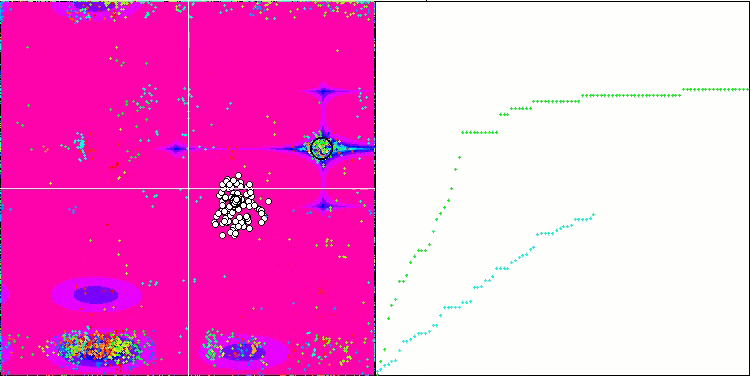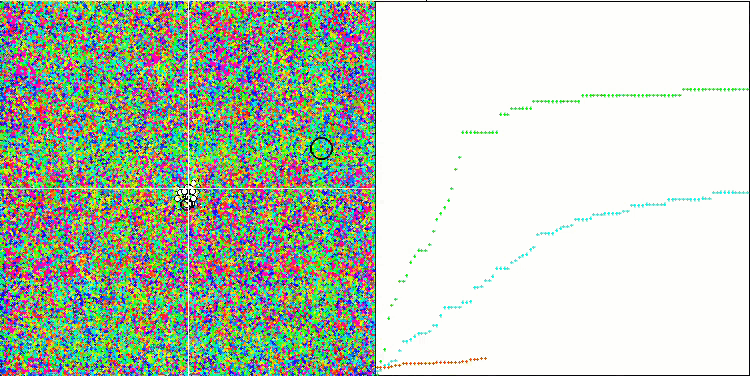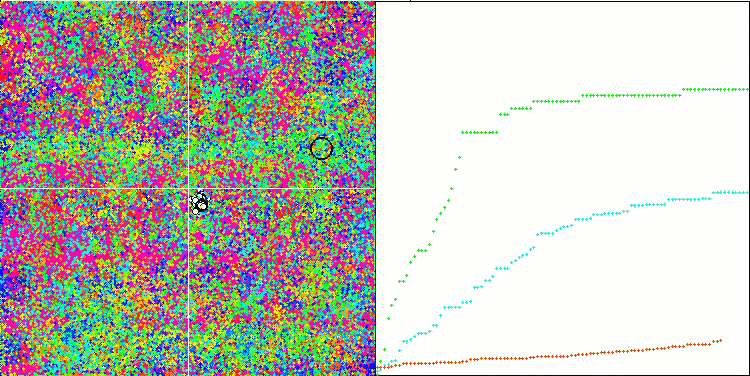
SIA 基于 Megacity 测试函数

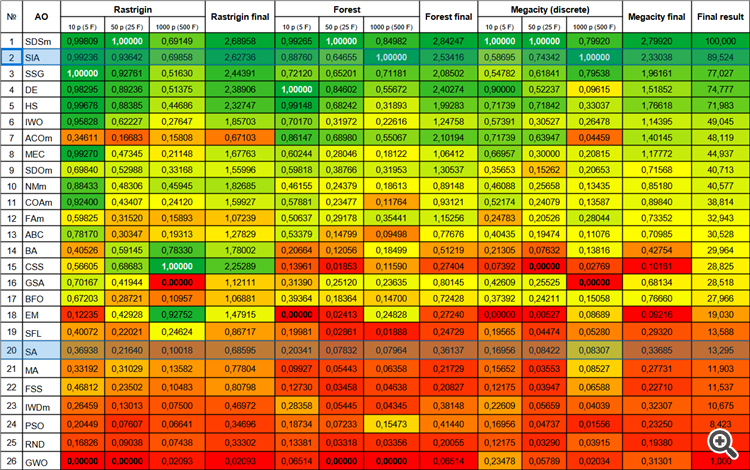
模拟各向同性退火的新算法（SIA，2023 年）在两个最困难的测试（尖锐 Forest，及具有 1000 个变量的离散 Megacity）中取代了 SDSm，在评级表格中排名第二。

#	AO	说明	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果
#	AO	说明	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Rastrigin 最终	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest 最终	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity 最终	最终结果
1	SDSm	随机扩散搜索 M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	0,84982	2,84247	1.00000	1.00000	0,79920	2,79920	100.000
2	SIA	模拟各向同性退火	0.99236	0.93642	0.69858	2.62736	0.88760	0.64655	1.00000	2.53416	0.58695	0.74342	1.00000	2.33038	89.524
3	SSG	树苗播种和生长	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.71181	2.08502	0.54782	0.61841	0.79538	1.96161	77.027
4	DE	差分进化	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.55672	2.40274	0.90000	0.52237	0.09615	1.51852	74.777
5	HS	谐声搜索	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.31893	1.99283	0.71739	0.71842	0.33037	1.76618	71.983
6	IWO	入侵性杂草优化	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.22616	1.24758	0.57391	0.30527	0.26478	1.14395	49.045
7	ACOm	蚁群优化 M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.55067	2.10194	0.71739	0.63947	0.04459	1.40145	48.119
8	MEC	心智进化计算	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.18122	1.06412	0.66957	0.30000	0.20815	1.17772	44.937
9	SDOm	螺旋动力学优化 M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.31953	1.30537	0.35653	0.15262	0.20653	0.71568	40.713
10	NMm	Nelder-Mead 方法 M	0.88433	0.48306	0.45945	1.82685	0.46155	0.24379	0.18613	0.89148	0.46088	0.25658	0.13435	0.85180	40.577
11	COAm	布谷鸟优化算法 M	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.11764	0.93121	0.52174	0.24079	0.13587	0.89840	38.814
12	FAm	萤火虫算法 M	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.35441	1.15256	0.24783	0.20526	0.28044	0.73352	32.943
13	ABC	人工蜂群	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.09498	0.77676	0.40435	0.19474	0.11076	0.70985	30.528
14	BA	蝙蝠算法	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.18499	0.51219	0.21305	0.07632	0.13816	0.42754	29.964
15	CSS	收费系统搜索	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.11590	0.27404	0.07392	0.00000	0.02769	0.10161	28.825
16	GSA	重力搜索算法	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.23635	0.80145	0.42609	0.25525	0.00000	0.68134	28.518
17	BFO	细菌觅食优化	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.14700	0.72428	0.37392	0.24211	0.15058	0.76660	27.966
18	EM	类电磁算法	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.24828	0.27240	0.00000	0.00527	0.08689	0.09216	19.030
19	SFL	蛙跳	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.01888	0.24729	0.19565	0.04474	0.05280	0.29320	13.588
20	SA	模拟退火	0.36938	0.21640	0.10018	0.68595	0.20341	0.07832	0.07964	0.36137	0.16956	0.08422	0.08307	0.33685	13.295
21	MA	猴子算法	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.06358	0.21729	0.15652	0.03553	0.08527	0.27731	11.903
22	FSS	鱼群搜索	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.04638	0.20827	0.12175	0.03947	0.06588	0.22710	11.537
23	IWDm	智能水滴 M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.04345	0.38148	0.22609	0.05659	0.04039	0.32307	10.675
24	PSO	粒子群优化	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.15473	0.41440	0.16956	0.04737	0.01556	0.23250	8.423
25	RND	随机	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03356	0.20055	0.12175	0.03290	0.03915	0.19380	5.097
26	GWO	灰狼优化器	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02034	0.31301	1.000

总结

基于所进行的实验，及对结果的分析，我们可以得出以下结论：

新的模拟各向同性退火（SIA）算法在优化具有多个变量的函数方面取得了令人印象深刻的结果。这表明该算法在高维空间中寻找最优解的效率。
该算法在具有锐化和离散特征的函数上显示出特别好的结果。这可能是由于 SIA 允许我们均匀地探索解空间，即使在复杂和不规则的区域也能找到最优点。
总体而言，新的 SIA 算法是一个强大的优化工具。由于搜索策略的成功组合，该算法具有质的新属性，并在寻找最优解方面表现出很高的效率。

在新的 SIA 算法中，除了种群大小外，只有两个参数（温度和扩散比），而不是 SA 中的三个参数。此外，现在温度参数非常容易理解，用一些抽象温度的部分表示，默认等于 0.01。

基于对结果的研究和分析，我们可以自信地推荐 SIA 算法用于训练神经网络，以及处理拥有许多参数的问题、以及复杂组合问题。

图例 2. 算法的颜色渐变是根据相关测试

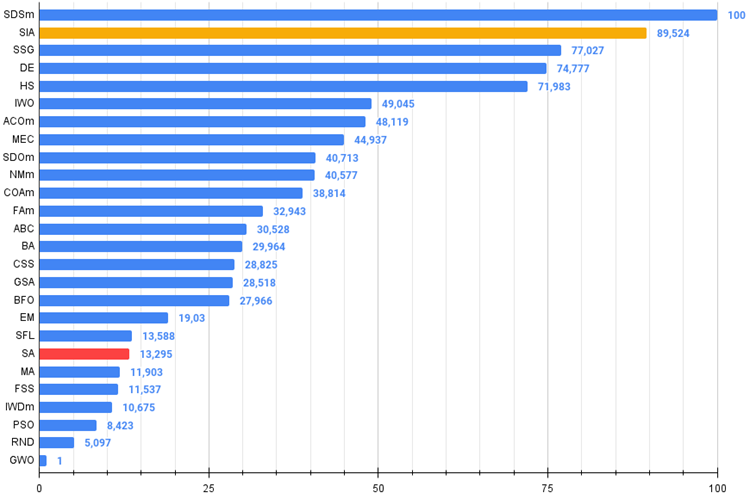
图例 3. 算法测试结果的直方图（标尺从 0 到 100，越多越好，

存档包含文章中应用的计算评级表格的方法脚本）。

SIA 的优点和缺点：

优势：

外部参数的数量最小。
高效解决各种问题。
计算资源负载低。
易于实现。
抗粘连性。
在平滑和复杂的离散函数上都有可喜的结果。
高收敛性。

缺点：

未找到。

本文附有一个存档，其中包含前几篇文章中讲述的算法代码的当前更新版本。文章作者不对规范算法讲述的绝对准确性负责。对其中进行了多处修改，从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/13870

附加的文件 |

下载ZIP

26_The_world_of_AO_SIA.zip (437.92 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论

掌握 MQL5：从入门到精通（第二部分）基本数据类型和变量的使用

这是初学者系列的延续。本文将介绍如何创建常量和变量、写入日期、颜色和其他有用的数据。我们将学习如何创建枚举，如一周中的天数或线条样式（实线、虚线等）。变量和表达式是编程的基础。它们肯定存在于99%以上的程序中，因此理解它们至关重要。因此，如果你是编程新手，这篇文章会对你非常有用。所需的编程知识水平：非常基础，在我上一篇文章（见开头的链接）的范围内。

图表上的历史仓位及其盈利/亏损图指标

在本文中，我将探讨根据交易历史获取已平仓头寸信息的选项。此外，我将创建一个简单的指标，以图表的形式显示每个柱形上仓位的大致盈利/亏损。

MQL5 中的定量分析：实现有前途的算法

我们将分析什么是定量分析，以及主要参与者如何运用定量分析的问题。我们将用 MQL5 语言创建一种定量分析算法。

多交易品种多周期指标中的颜色缓冲区

在本文中，我们将回顾多交易品种、多周期指标中指标缓冲区的结构，并在图表上组织这些指标的彩色缓冲区的显示。