MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
种群优化算法：鸟群算法（BSA）

种群优化算法：鸟群算法（BSA）

MetaTrader 5 — 示例 | 29 十月 2024, 11:01
376 0
Andrey Dik
Andrey Dik

内容

概述
算法描述
测试结果


1. 概述

鸟类是令人惊叹的生物，在自然界和生态系统中都占据重要地位。鸟类被认为是从其最近的亲属——恐龙进化而来的。最著名的例子之一是已知最古老的鸟类始祖鸟，它生活在大约1.5亿年前。鸟类通常作为判断环境健康的指标，因为数量和行为的变化可以表明生态系统中出现的问题，如污染、栖息地丧失和气候变化。地球上已知有超过1万种鸟类，每一种都有其独特的生活方式适应性。

有些鸟类能够飞行很长的距离，有些能够潜入深海，还有些拥有惊人的发声能力。鸟类在生态系统中扮演着重要的角色，它们传播植物种子，控制昆虫和其他动物的数量，并且是捕食者们的食物来源。许多鸟类会进行长途迁徙，在迁徙过程中，它们与同种的其他成员一起生活、互动，成群结队地旅行数千公里以寻找食物或繁殖地。这一现象突显了鸟类出色的导航技能、耐力、群体互动和合作能力。. 鸟类的极具多样性使其成为我们星球的重要组成部分。

鸟群算法（Bird Swarm Algorithm，简称BSA）是一种令人兴奋的受生物启发的进化算法，是基于鸟群社会互动和行为的群体智能。BSA由Meng及其同伴于2015年开发，是一种独特的优化方法，它结合了鸟类行为的三个关键方面：飞行、觅食和警戒。在电子鸟群中，每只“鸟”都有各自的战术和策略，由此诞生了一个充满算法智能和创造力的独特的集体交互系统。在这里，重要的不仅是个人的努力，还有在追求优化这一共同目标过程中的相互合作、交流和支持。  

在BSA中，不同的个体可能采用不同的搜索策略。鸟类可以在飞行、警戒和觅食行为之间随机切换。该仿生设计算法包括基于全局适应度和个体适应度的觅食策略。鸟类也会尝试向种群中心移动（这可能会与其他鸟类产生竞争）或远离鸟群。鸟类的行为包括常规的飞行和迁徙，以及在生产者（给予者）和乞讨者（接受者）角色之间进行切换。在BSA中，每一次迭代，每个个体都有自己的搜索策略，这使得该算法具有多面性，并能够充分发挥其作用。

然而，与许多种群智能算法一样，BSA可能会出现早熟收敛并导致局部最优。为了实现基于种群优化算法的快速且高精度的收敛，已经采取各种方法实现均衡开发和研究。

BSA算法以鸟类行为作为基础，受到自然界中鸟类群体互动行为的启发：

  • 集群行为。许多鸟类，如椋鸟、燕子和鹅，在飞行时会表现出集群行为。这种行为有助于它们在迁徙或觅食过程中减少空气阻力并节省能量。
  • 沟通。鸟类使用不同类型的沟通方式，如声音、手势或姿态来相互传递信息。这使得它们能够协调行动、向同类发出危险警告以及协调食物搜寻。
  • 适应性。鸟类对变化的环境因素具有很高的适应性。它们能够迅速对危险、天气变化和食物供应的变化做出反应，并根据情况调整其行为和迁徙路线。
  • 领导与追随。在鸟群中，通常有一只领头鸟决定飞行方向，其他鸟类跟随它飞行。这体现了领导与追随的原则，该原则也被用于BSA算法中，以便高效地找出最优解。

BSA算法利用这些鸟类行为的原则来开发一种高效的优化技术，该技术模拟鸟群的集体行为来解决各种优化问题。BSA不仅仅是一种算法，也是一场精彩的优化世界之旅，鸟类的社会互动成为了高效解决复杂问题的灵感来源。


2. 算法

让我们更详细地探讨BSA算法的逻辑。虽然初次接触该算法可能会令人觉得复杂和困惑，但通过逐步分析，我们会更容易理解它。在开始编写代码之前，我们先来开发一个该算法的伪代码，作为我们实现算法的基础。通过这个伪代码，我们更容易地理解BSA算法。

鸟群算法（BSA）伪代码是对模拟鸟群行为算法的高级描述：

1. 初始化N个解和相关参数
2. 生成新的解决方案：
3. 当鸟类在飞行时：
    4. 当鸟类作为生产者（给予者）时：
        5. 寻找新的食物来源时：
    6. 除此之外：        7. 乞讨鸟跟随生产鸟
8. 除此之外：    9. 鸟类正在觅食：
        10. 鸟类正在进食
    11. 除此之外：        12. 鸟类保持警惕
13. 评估新解决方案
14. 更新解决方案
15. 如果已达到停止标准：
    16. 算法完成
17. 除此之外：    18. 返回第2步


对于寻找新食物地点的鸟类，第5点的方程式为：

 xn = RNDg (min, max, producerPower)

其中：

  • xn - 新坐标值
  • RNDg - 以当前坐标为中心的正态分布随机数
  • min and max - 分布边界
  • producerPower - 生产鸟的标准偏差

根据该方程，繁殖鸟类可以在整个搜索空间中向任何方向迁移，其当前位置附近的概率增加。这使得鸟类能够探索新的区域寻找食物。

对于跟随生产鸟的乞讨鸟，第7点的方程式为：

xn = x + (xK - x) * FL * RNDg (-1.0, 1.0, scroungerPower)

其中：

  • xn - 新坐标值
  • x -史上乞讨鸟的最佳坐标
  • xK - 史上生产鸟的最佳坐标，其中选择种群中位置为K的随机鸟类作为生产鸟。
  • RNDg - 正态分布的随机数，分布中心为0，边界为“-1.0”和“1.0”
  • scroungerPower - 乞讨鸟的标准偏差

该方程表明，乞讨鸟的位置依据它的最佳坐标和群中最优个体的最佳坐标而确定（生产鸟不是根据其最佳坐标确定，而是由当前坐标确定）。这模拟了跟随团队领导者的行为。

第10点的方程式代表不在飞行而处于喂食期的鸟类：

xn = x + (p - x) * C * r1 + (g - x) * S * r2

其中：

  • xn - 新坐标值
  • x - 当前坐标
  • p - 史上鸟类觅食的最佳坐标
  • g - 史上最佳种群坐标（最优全局解）
  • r1 - 活动范围内的均匀分散随机数[0.0 ... 1.0]
  • r2 - 活动范围内的均匀分散随机数[0.0 ... 1.0]
  • C - 认知比例，外部参数
  • S - 社会比例，外部参数

该方程描述了觅食的时刻，此时鸟类的行为是基于其自身经验（当前位置和过去最佳位置）以及鸟群的经验。

第12点方程式代表处于警惕状态时的鸟类：

xn = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2

其中：

  • xn - 新坐标值
  • x - 史上最警惕的鸟类协调
  • r1 - 活动范围内的均匀分散随机数[0.0 ... 1.0]
  • r2- 活动范围内的均匀分散随机数[0.0 ... 1.0]
  • mean [c] - 基于鸟群中所有鸟类最佳坐标的c-th坐标平均值

A1 - 影响鸟群中心平均坐标的修正率：

A1 = a1 * exp (-pFit * N / (sumFit + e)) 

其中：

  • a1 - 比例，外部参数
  • e = DBL_MIN, 不能除以0
  • pFit - 鸟儿保持警惕状态时的最佳健康情况
  • sumFit - 鸟群中最合适的鸟的总数
  • N - 鸟群中的鸟数

A2 - 校正比例，考虑所选的观察鸟的位置（已落入警戒鸟的视野内）对后者行为的影响。A2方程：

A2 = a2 * exp (((pFit - pFitK) / (|pFitK - pFit| + e)) * (N * pFitK / (sumFit + e)))

其中：

  • a2 - 比例，外部参数
  • e = DBL_MIN, 不能除以0
  • pFit - 鸟儿保持警惕状态时的最佳健康情况
  • pFitK - 从种群中随机选择的第K只鸟（已落入警戒鸟的视野内的鸟儿）的最佳适应性
  • sumFit - 鸟群中最合适的鸟的总数
  • N - 鸟群中的鸟数

因此，警惕的鸟儿会监视其周围环境，这使得它能够及时警告其同伴存在的危险。这是算法中描述的所有行为中最复杂的一种，它考虑了种群中所有鸟儿的适应性，以及警惕的鸟儿自身的适应性和被选为观察对象的鸟儿的适应性。从本质上讲，在给定其视野范围内另一只鸟儿的位置的情况下，警惕的鸟儿会朝着种群整体适应度提高的方向移动。

伪代码中高亮显示的文本对应于图1中所示BSA的逻辑元素。

BSA

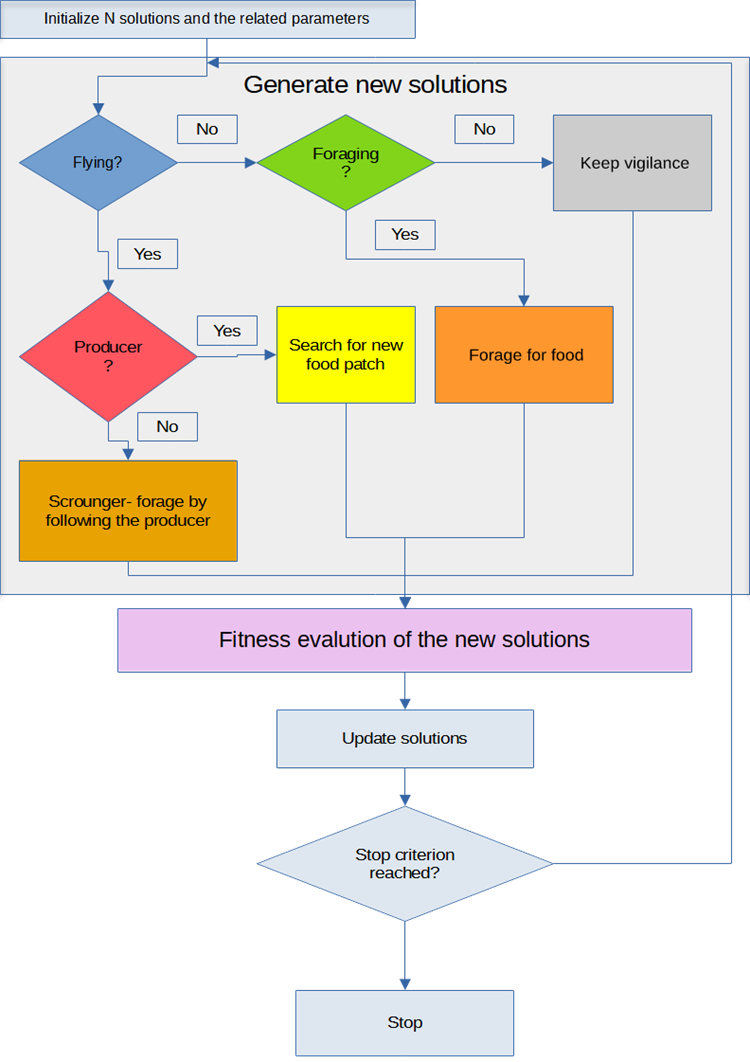
Figure 1. BSA 算法逻辑图

图1中的图表是BSA算法的可视化表示，它模拟了鸟群的行为。算法的关键特征：

  1. 初始化解决方案。该算法先初始化一组解决方案及其相关参数。这涉及在搜索空间中鸟群（或解决方案）的初始分布。
  2. 飞行行为。在算法运行过程中，每只鸟都可以被设置为“飞行”或“不飞行”。这一条件会影响鸟儿发现新解决方案的能力。 
  3. 觅食行为。如果一只鸟处于“飞行”状态，它既可以成为“生产鸟”，寻找有食物的新地区，也可以成为跟随生产鸟的“乞讨鸟”。
  4. 觅食行为。如果一只鸟“没在飞行”，它要么在觅食，要么在保持警觉。这可能代表了一种对环境的预测或观察状态。
  5. 评估与更新解决方案。在生成新的解决方案后，会对其适应性或质量进行评估。
  6. 停止准则。算法会持续进行生成和更新解决方案的循环，直到达到某个停止准则位置。这个停止准则可能是达到一定的迭代次数、解决方案质量达到某一水平，或其他标准。

我想强调的是，BSA是一个在搜索最优解过程中能够自适应和演化的动态算法。

现在我们来运行BSA算法代码。对于每个智能体，我们定义了S_BSA_Agent结构，这将是优化问题的一个独立解决方案，也是鸟群中鸟儿的描述。

该结构包含以下字段：

  • cBest[] - 用于存储最佳代理坐标的数组。
  • fBest - 用于存储最佳智能体适应性得分的变量。
  • Init - 初始化结构字段S_BSA_Agent的代码结构。它使用“coords”整数型参数，通过ArrayResize函数来调整“cBest”数组的大小。

我们将“fBest”变量的初始值设置为可能的最小双精度浮点数，这代表着可能存在的最差适应性。

//——————————————————————————————————————————————————————————————————————————————
struct S_BSA_Agent
{
    double cBest []; //best coordinates
    double fBest;    //best fitness

    void Init (int coords)
    {
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

让我们为BSA定义一个C_AO_BSA类，该类继承自表示种群算法基类的C_AO，其包含以下字段和方法：

1. 公共字段:

  • <b0>ao_name </b0>- 优化算法名称。
  • <b0>ao_desc </b0>- 优化算法描述。
  • <b0>popSize </b0>- 种群规模。
  • <b0>params </b0>- 算法参数数组。
  • flyingProb - 飞行概率。
  • producerProb - 生产概率。
  • foragingProb - 觅食概率。
  • a1 - a1常量[0...2].
  • a2 - a2常量[0...2].
  • C - 认知比例。
  • S - 社会比例。
  • FL - FL常量[0...2].
  • producerPower - 生产行为的标准偏差。
  • scroungerPower - 乞讨行为的标准偏差。

2. 可用的选项有：

  • C_AO_BSA - 初始化类字段的类构造函数。
  • <b0>SetParams </b0>- 算法参数设置方法。
  • <b0>Init </b0>- 算法初始化方法。该方法需要最小和最大搜索范围、搜索步长和迭代次数。
  • <b0>Moving </b0>- 智能体移动方法。
  • <b0>Revision </b0>- 智能体修改方法。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BSA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BSA () { }
  C_AO_BSA ()
  {
    ao_name = "BSA";
    ao_desc = "Bird Swarm Algorithm";

    popSize        = 20;  //population size

    flyingProb     = 0.8;  //Flight probability
    producerProb   = 0.25; //Producer probability
    foragingProb   = 0.55; //Foraging probability
    a1             = 0.6;  //a1 constant [0...2]
    a2             = 0.05; //a2 constant [0...2]
    C              = 0.05; //Cognitive coefficient
    S              = 1.1;  //Social coefficient
    FL             = 1.75; //FL constant [0...2]
    producerPower  = 7.05; //Producer power
    scroungerPower = 2.60; //Scrounger power

    ArrayResize (params, 11);

    params [0].name = "popSize";         params [0].val  = popSize;

    params [1].name  = "flyingProb";     params [1].val  = flyingProb;
    params [2].name  = "producerProb";   params [2].val  = producerProb;
    params [3].name  = "foragingProb";   params [3].val  = foragingProb;
    params [4].name  = "a1";             params [4].val  = a1;
    params [5].name  = "a2";             params [5].val  = a2;
    params [6].name  = "C";              params [6].val  = C;
    params [7].name  = "S";              params [7].val  = S;
    params [8].name  = "FL";             params [8].val  = FL;
    params [9].name  = "producerPower";  params [9].val  = producerPower;
    params [10].name = "scroungerPower"; params [10].val = scroungerPower;
  }

  void SetParams ()
  {
    popSize        = (int)params [0].val;

    flyingProb     = params [1].val;
    producerProb   = params [2].val;
    foragingProb   = params [3].val;
    a1             = params [4].val;
    a2             = params [5].val;
    C              = params [6].val;
    S              = params [7].val;
    FL             = params [8].val;
    producerPower  = params [9].val;
    scroungerPower = params [10].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double flyingProb;      //Flight probability
  double producerProb;    //Producer probability
  double foragingProb;    //Foraging probability
  double a1;              //a1 constant [0...2]
  double a2;              //a2 constant [0...2]
  double C;               //Cognitive coefficient
  double S;               //Social coefficient
  double FL;              //FL constant [0...2]
  double producerPower;   //Producer power
  double scroungerPower;  //Scrounger power

  S_BSA_Agent agent [];


  private: //-------------------------------------------------------------------
  double mean [];  //represents the element of the average position of the whole bird’s swarm
  double N;
  double e;        //epsilon

  void BirdProducer  (int pos);
  void BirdScrounger (int pos);
  void BirdForaging  (int pos);
  void BirdVigilance (int pos);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSA类的Init方法用于根据传递的参数初始化类变量。该方法使用 StandardInit 方法执行标准初始化，需要输入最小搜索范围、最大搜索范围以及搜索步长作为参数。

如果标准初始化成功，该方法将继续初始化“N”和“e”变量。将“N”的值设置为“popSize”（种群规模），而“e”是初始化epsilon的最小双精度值。

该方法将“agent”（智能体）数组的大小调整为“popSize”的大小。对于“智能体”（agent）数组或集合中的每个元素，都会调用 Init 方法，并传入一个名为 coords 的参数。“mean”数组也被改为与“coords”相同的大小。该数组用于存储鸟类的平均种群坐标。

如果初始化成功，该方法返回“true”，否则返回“false”。

该方法使用给定的参数初始化BSA优化算法，并为其执行优化做好准备。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BSA::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)  //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (mean, coords);

  N = popSize;
  e = DBL_MIN;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSA类的Moving方法用于在优化过程中移动智能体。该方法执行以下操作：

  • 如果“revision”值为“false”，则使用指定范围内的随机值初始化智能体的坐标“a[i].c[c]”。当 "revision" 标识的值设置为 "true" 时，退出该方法。
  • 如果“revision”值不是'false'，则使用方程和概率为每个智能体计算新的坐标。

在第二个及之后的迭代周期中，该方法会调用函数来确定鸟群中每只鸟的行为，这取决于符合条件的概率： 

  • 如果满足飞行概率—“flyingProb”，则智能体处于“飞行”模式。在这种情况下，有两种可能的行为选项：

  1. 如果概率小于“producerProb”（生产鸟概率），则智能体是“生产鸟”，正在寻找新的觅食地点。
  2. 否则，智能体是“乞讨鸟”，会跟随生产鸟。
  • 如果智能体“不在飞行”，则有以下两种可能的行为选项：
  1. 如果概率小于“foragingProb”（觅食概率），则智能体会“觅食”食物。 
  2. 否则，智能体处于“警觉”状态。

该方法负责根据当前迭代周期、随机值和概率，更新BSA优化算法中智能体的坐标。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //bird is flying------------------------------------------------------------
    if (u.RNDprobab () < flyingProb)
    {
      //bird producer
      if (u.RNDprobab () < producerProb) BirdProducer  (i); //bird is looking for a new place to eat
      //bird is not a producer
      else                               BirdScrounger (i); //scrounger follows the  producer
    }
    //bird is not flying--------------------------------------------------------
    else
    {
      //bird foraging
      if (u.RNDprobab () < foragingProb) BirdForaging  (i); //bird feeds
      //bird is not foraging
      else                               BirdVigilance (i); //bird vigilance
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

在C_AO_BSA类中，BirdProducer方法用于模拟BSA算法中“生产鸟”的行为。该方法执行以下操作：

  • 初始化变量“x”，用于存储鸟类的当前位置。
  • 对于每个智能体的坐标，执行以下操作：
    • 将“x”值设置为当前代理坐标。
    • 使用高斯分布更新“x”值，其中均值为当前坐标，范围和标准差由“rangeMin”（范围最小值）、“rangeMax”（范围最大值）和“producerPower”（生产鸟能力）值确定。
    • 使用SeInDiSp方法设置智能体坐标的新值，该方法根据搜索范围和步长调整“x”值。

此方法模拟了BSA算法中“生产鸟”的行为，该行为使用高斯分布探索搜索空间，以寻找新的食物来源位置（即新的潜在解决方案）。

//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdProducer  (int pos)
{
  double x = 0.0; //bird position

  for (int c = 0; c < coords; c++)
  {
    x = a [pos].c [c];
    x = u.GaussDistribution (x, rangeMin [c], rangeMax [c], producerPower);

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

在C_AO_BSA类中，模拟“乞讨鸟”行为的方法是BirdScrounger函数。它执行以下操作：

  • 1. 初始化变量“K”、“x”和“xK”。“K”是鸟群中随机选择的一只鸟的位置，“x”是当前鸟儿的最佳位置，而“xK”是鸟群中随机选择的鸟儿当前的最佳位置。
  • 2. 遍历所有坐标。
    • 随机选择一只不是当前鸟的鸟儿。
    • 根据当前鸟儿和随机选择的鸟儿的最佳位置来更新“x”和“xK”。
    • 使用高斯分布来更新“x”。
    • 最后，使用SeInDiSp方法更新鸟类的当前位置，根据搜索范围和步长调整“x”值。

该方法使用高斯分布模拟BSA算法中的“乞讨鸟”行为，该行为跟随“生产鸟”（即相对于生产鸟的位置调整自身的位置）。

//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdScrounger (int pos)
{
  int    K  = 0;   //position of a randomly selected bird in a swarm
  double x  = 0.0; //best bird position
  double xK = 0.0; //current best position of a randomly selected bird in a swarm

  for (int c = 0; c < coords; c++)
  {
    do K = u.RNDminusOne (popSize);
    while (K == pos);

    x  = agent [pos].cBest [c];
    xK = agent   [K].cBest [c];

    x = x + (xK - x) * FL * u.GaussDistribution (0, -1.0, 1.0, scroungerPower);

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

在C_AO_BSA类中，BirdForaging方法是为那些当前不飞行且正在进食的鸟类设计的。该方法对所有坐标执行以下循环操作：

  • 根据鸟类的当前位置、最佳位置以及全局最佳位置来更新“x”、“p”和“g”值。
  • 生成两个随机数“r1”和“r2”。
  • 使用这些随机数以及“C”和“S”常量来更新“x”。
  • 调整SeInDiSp函数得到的鸟类位置。
//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdForaging  (int pos)
{
  double x  = 0.0; //current bird position
  double p  = 0.0; //best bird position
  double g  = 0.0; //best global position
  double r1 = 0.0; //uniform random number [0.0 ... 1.0]
  double r2 = 0.0; //uniform random number [0.0 ... 1.0]

  for (int c = 0; c < coords; c++)
  {
    x = a     [pos].c     [c];
    p = agent [pos].cBest [c];
    g = cB                [c];

    r1 = u.RNDprobab ();
    r2 = u.RNDprobab ();

    x = x + (p - x) * C * r1 + (g - x) * S * r2;

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

模拟处于警惕状态的鸟类行为最新、最复杂的方法是鸟类警戒。它执行以下操作：

  • 计算鸟群中所有鸟儿的最佳适应性值的总和。
  • 计算鸟群中所有鸟在每个坐标上的平均值。
  • 随机选择一只不是当前鸟的鸟儿。
  • 基于当前鸟儿和随机选择的鸟儿的最佳适应性值来更新“pFit”和“pFitK”。
  • 通过“pFit”、“pFitK”、“N”、“sumFit”和“e”的指数函数来计算“A1”和“A2”。
  • 遍历所有坐标。 
    • 生成两个随机数“r1”和“r2”。
    • 根据当前鸟儿和随机选择的鸟儿的最佳位置来更新“x”和“xK”。
    • 通过 "A1", "A2", "r1" and "r2"更新"x" 。
    • 使用SeInDiSp函数调整当前鸟的位置。
//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdVigilance (int pos)
{
  int    K      = 0;   //position of a randomly selected bird in a swarm
  double sumFit = 0.0; //best birds fitness sum
  double pFitK  = 0.0; //best fitness of a randomly selected bird
  double pFit   = 0.0; //best bird fitness
  double A1     = 0.0;
  double A2     = 0.0;
  double r1     = 0.0; //uniform random number [ 0.0 ... 1.0]
  double r2     = 0.0; //uniform random number [-1.0 ... 1.0]
  double x      = 0.0; //best bird position
  double xK     = 0.0; //best position of a randomly selected bird in a swarm

  ArrayInitialize (mean, 0.0);

  for (int i = 0; i < popSize; i++) sumFit += agent [i].fBest;

  for (int c = 0; c < coords; c++)
  {
    for (int i = 0; i < popSize; i++) mean [c] += a [i].c [c];

    mean [c] /= popSize;
  }

  do K = u.RNDminusOne (popSize);
  while (K == pos);

  pFit  = agent [pos].fBest;
  pFitK = agent   [K].fBest;

  A1 = a1 * exp (-pFit * N / (sumFit + e));
  A2 = a2 * exp (((pFit - pFitK) / (fabs (pFitK - pFit) + e)) * (N * pFitK / (sumFit + e)));

  for (int c = 0; c < coords; c++)
  {
    r1 = u.RNDprobab ();
    r2 = u.RNDfromCI (-1, 1);

    x  = agent [pos].cBest [c];
    xK = agent   [K].cBest [c];

    x = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2;

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

使用C_AO_BSA类的Revision方法更新最佳全局解和更新智能体的最佳位置。该方法执行以下操作：

  • 更新全局解。
  • 更新之前的最佳适应性函数值和智能体坐标。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fBest)
    {
      agent [i].fBest = a [i].f;
      ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 测试结果

我希望更详细地探讨鸟群算法（BSA）应用于各种函数集上的结果。在所有测试函数中，鸟群算法（BSA）的总体得分为4.80947，这相当于占最大可能得分的53.44%。这一结果表明了该算法的整体效率。使用鸟群算法很有可能解决不同函数上的各种优化问题。

BSA|鸟群算法|20.0|0.8|0.25|0.55|0.6|0.05|0.05|1.1|1.75|7.05|2.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.8930600046782612
25 Hilly's; Func runs: 10000; result: 0.6489975525320968
500 Hilly's; Func runs: 10000; result: 0.262496551797822
=============================
5 Forest's; Func runs: 10000; result: 0.9241962617798402
25 Forest's; Func runs: 10000; result: 0.7112057472851052
500 Forest's; Func runs: 10000; result: 0.24938963509983267
=============================
5 Megacity's; Func runs: 10000; result: 0.6938461538461538
25 Megacity's; Func runs: 10000; result: 0.3261538461538461
500 Megacity's; Func runs: 10000; result: 0.1001230769230778
=============================
总分: 4.80947 (53.44%)

算法操作的可视化结果显示，在不同测试函数上，结果存在显著的差异。尽管该算法能够成功地覆盖局部表面区域，但也可能会陷入局部陷阱。这限制了其达到全局最优的能力，并可能导致其在寻找最优解的过程中缺乏稳定性。

在Skin测试函数上的可视化结果仅仅是算法操作的一个示例，并不影响其在评分表中的结果。.

Hilly值

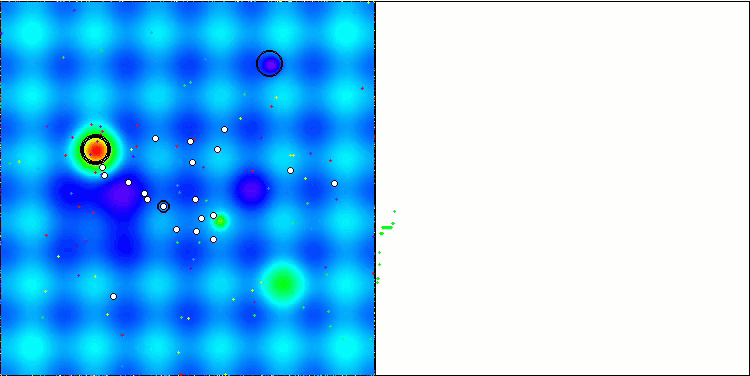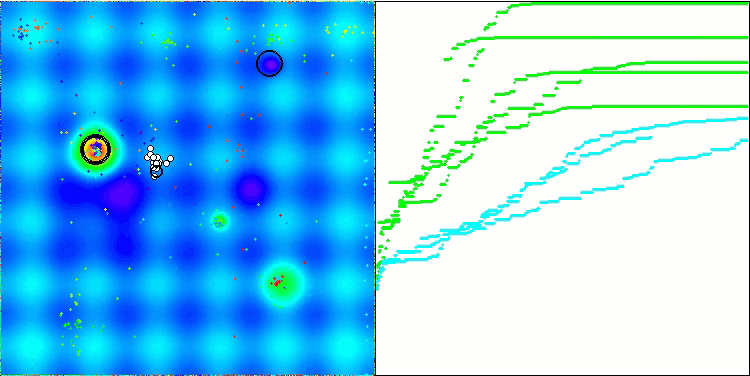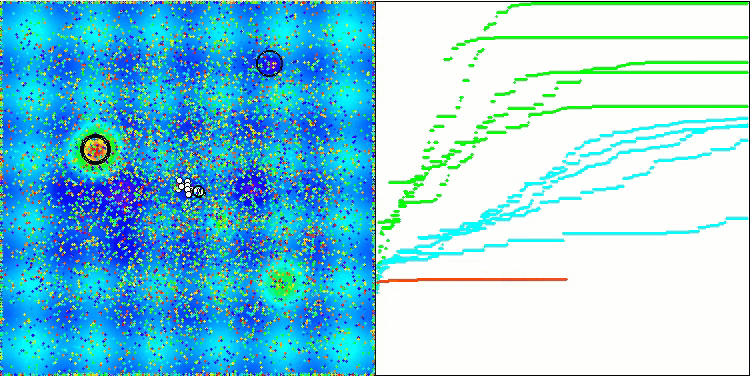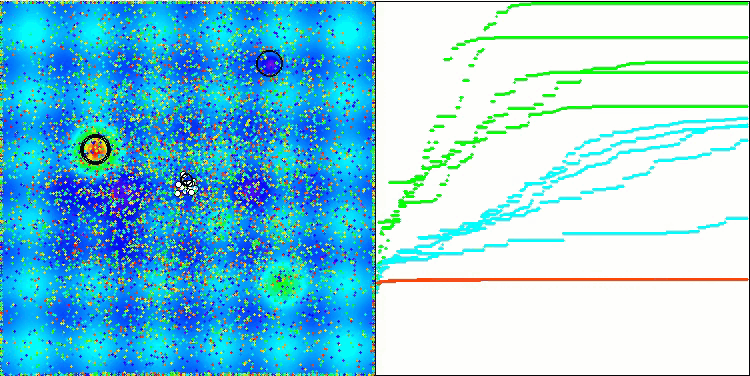
  BSA 对 Hilly 的测试影响

Forest值

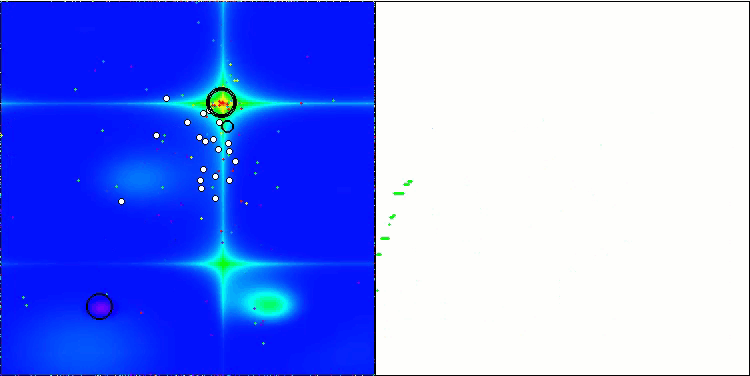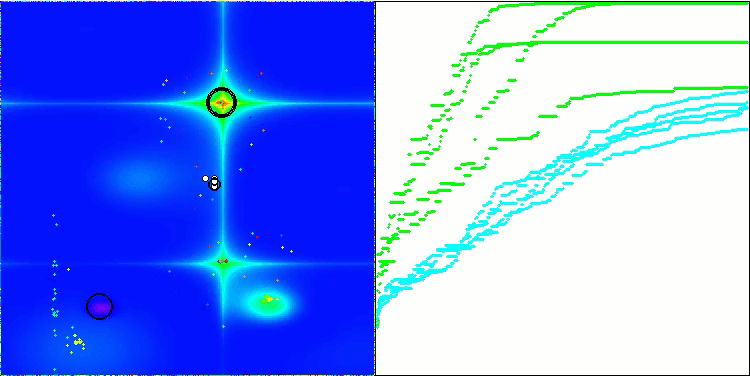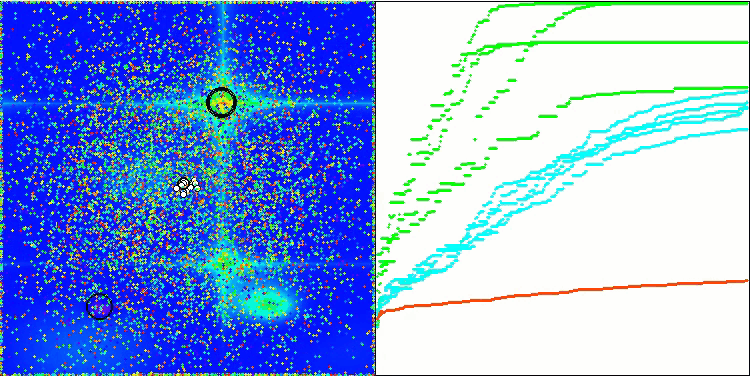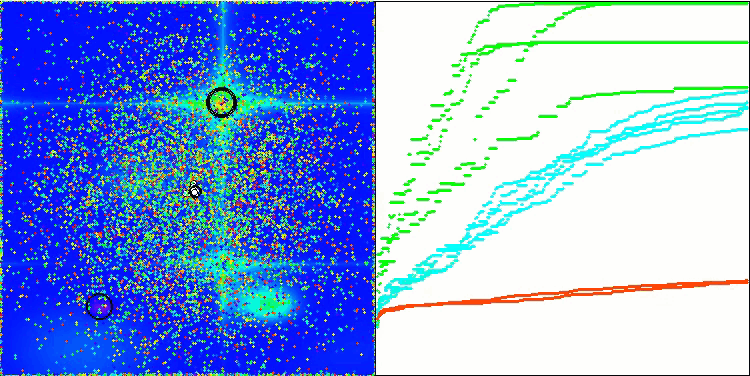
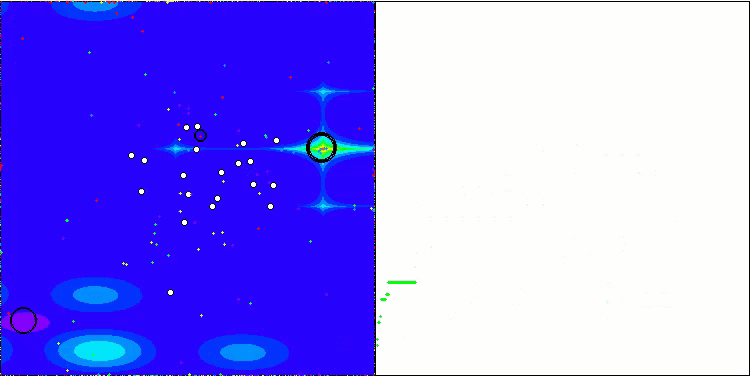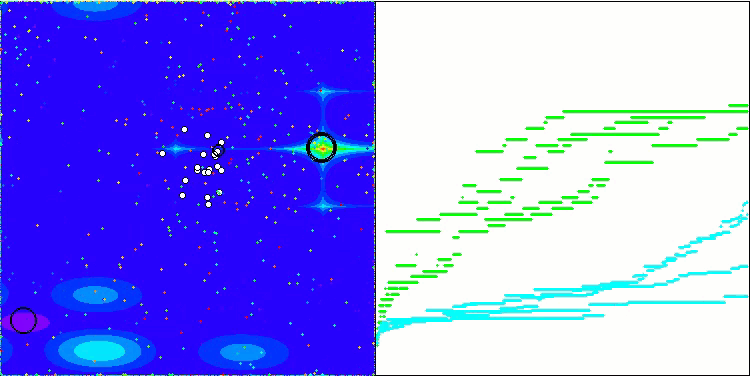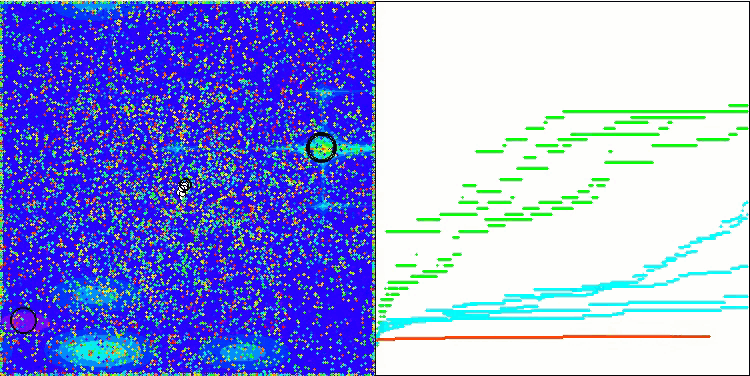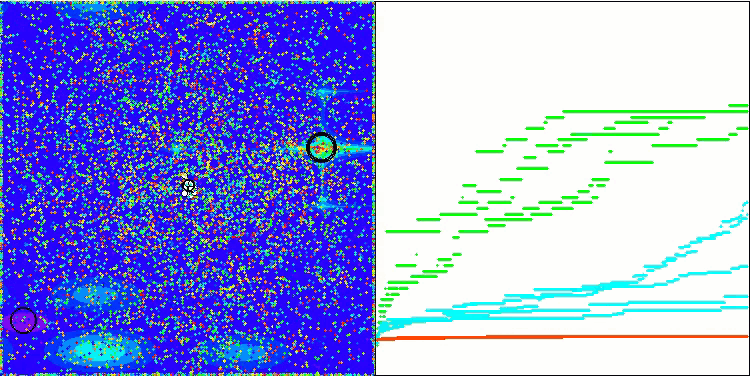
  BSA 对 Forest 的测试影响

Megacity

BSA 对Megacity 的测试影响

Skin

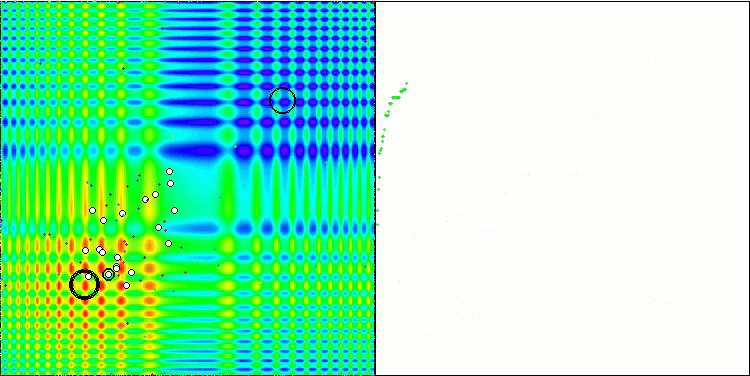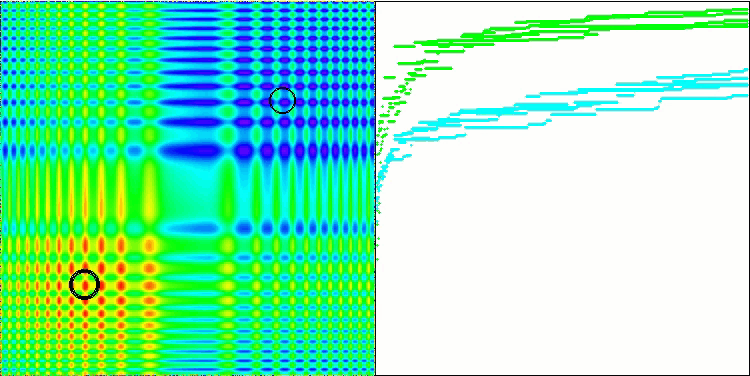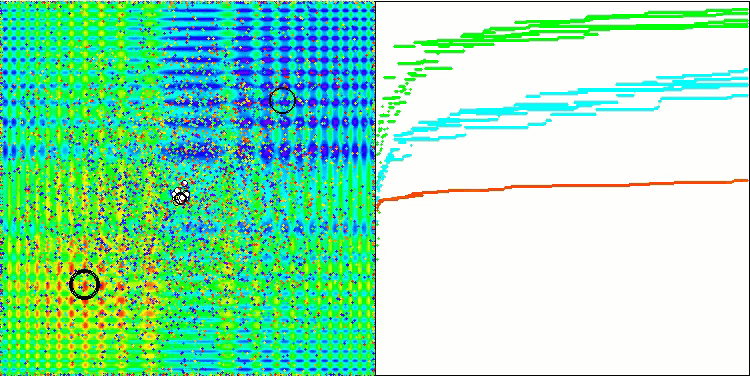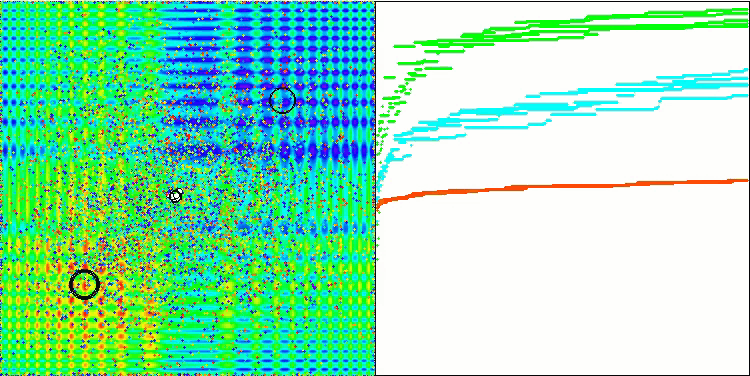
BSA对 Skin 的测试影响

值得注意的是，在变量数量众多的平滑Hilly 测试函数上，该算法表现得极为低效，在所有列入考虑的算法中，其评分结果位列最后。尽管在高维森林和离散函数上，与其他算法（包括评分表中排名更高的算法）相比，鸟群算法（BSA）仍然展现出不错的结果。

# AO 说明 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA 二进制遗传算法 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O) 进化策略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA 模拟退火算法 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA 鸟群算法 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
12 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
13 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
14 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
15 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
16 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
17 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
18 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
19 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
20 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
21 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
22 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
23 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
24 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
25 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
26 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
27 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
28 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
29 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
30 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
31 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
32 GWO 灰狼优化算法 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
33 CSS 人工电场算法 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
34 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


总结

鸟群算法（BSA）是一种优秀的研究工具，其丰富的逻辑体现了鸟群多样化的状态和策略，激发了人们的想象力。研究这个算法对我来说很有趣，因为它内部包含复杂的动态机制，其中鸟类的个体和群体行为受到不同条件和组合的影响。

BSA的复杂性还体现在它基于大量需要仔细调整的参数上，以实现最佳结果。为了优化算法参数，我编写了一个进化算法（Evolutionary Algorithm, EA），使其能够在标准MetaTrader 5测试器的数学计算模式下工作，从而能够找到优秀的外部参数，这些参数确保了该算法在评级中获得了第7名的成绩。该算法仍有进一步改进的潜力，我鼓励对此感兴趣的人对其进行继续实验。我认为，由于鸟类行为执行顺序和序列组合的多样性存在许多变化（本文探讨了4种行为类型），该算法未来仍有可能取得更好的实验结果。 

tab

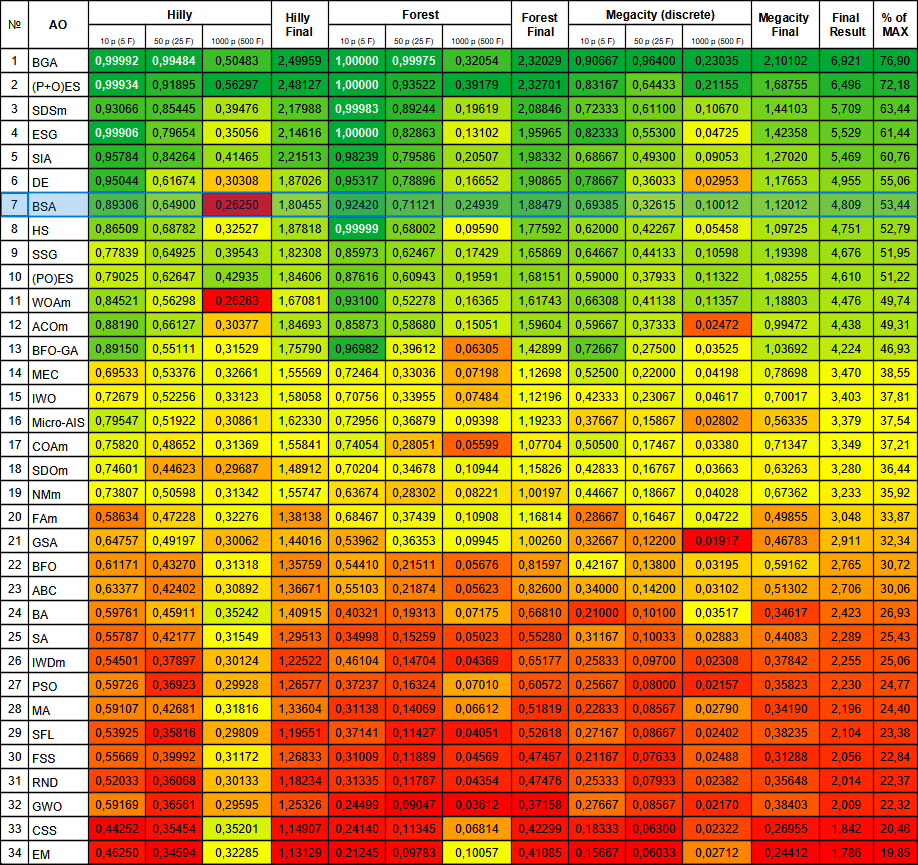
Figure 2. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示

图表

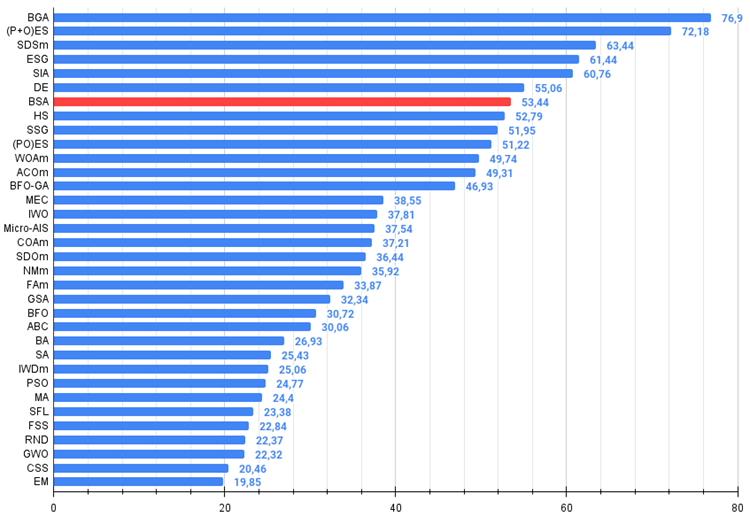
Figure 3. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）。

BSA的优缺点：

优势：

  1. 在尖锐森林函数和高维离散模型问题上取得了良好的结果。

缺点：

  1. 复杂的实现难度。
  2. 低收敛性。
  3. 在诸如Hilly等平滑函数上，可扩展性低（高维任务存在问题）。

本文附有一个包含当前代码版本的电子档案。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14491

附加的文件 |
下载ZIP
BSA.zip (28.34 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
您应当知道的 MQL5 向导技术（第 11 部分）：数字墙 您应当知道的 MQL5 向导技术（第 11 部分）：数字墙
数字墙（Number Walls）是线性回移寄存器的一种变体，其通过检查收敛性来预筛选序列来达到可预测性。我们看看这些思路如何运用在 MQL5。
神经网络实践：割线 神经网络实践：割线
正如理论部分已经解释的那样，在使用神经网络时，我们需要使用线性回归和导数。为什么呢？原因是线性回归是现存最简单的公式之一。从本质上讲，线性回归只是一种仿射函数。然而，当我们谈论神经网络时，我们对直接线性回归的影响并不感兴趣。我们感兴趣的是生成这条直线的方程。我们对创建出的线并不感兴趣。你知道我们需要理解的主要方程吗？如果没有，我建议您阅读这篇文章来了解它。
非平稳过程和伪回归 非平稳过程和伪回归
本文基于蒙特卡洛模拟，展示了回归分析非平稳过程时产生的伪回归现象。
神经网络变得简单（第 74 部分）：自适应轨迹预测 神经网络变得简单（第 74 部分）：自适应轨迹预测
本文介绍了一种相当有效的多个体轨迹预测方法，其可适配各种环境条件。